Optimized General Uniform Quantum State Preparation

1  Introduction

All quantum unstructured search algorithms begin with a uniform superposition representing the search space that is then gradually modified through interference to arrive at a superposition of only correct answers. Typically, uniform state preparation is performed using Hadamard gates, which put a wire into equal superposition of 0 and 1. However, using Hadamard gates to create a uniform superposition means that the size of the search space can only be 2k where k is the number of wires. This means additional nonsensical answers are introduced that decrease search efficiency.

As mentioned in [1], there is need in some cases for a restricted search space. Mukherjee describes a process to find a potential unitary of an initializer for such a restricted search space, namely the Gram-Schmidt procedure. While this works to run this process on a simulator, it cannot be run on an actual quantum computer without first implementing a sequence of gates for this unitary. He gives [2–4] as examples to implement the unitary but these do not leverage what is known about the search space and thus do not maximize depth efficiency. In searching for an implementation, we discovered that another potential unitary for the initializer is a Quantum Fourier Transform with an Nth root of unity. However, we could not find any implementation of this for any N that is not 2k. This process also introduces similar inefficiencies because it imposes unnecessary constraints on the unitary matrix. The only condition necessary for such a state initializer is

U|0⟩⌈log2⁡N⌉=1N∑n=0N−1|n(2)⟩(1)

We developed an algorithm that accomplishes this while minimizing 2-wire gate complexity.

The current optimal solver for general non-uniform state-preparation is [5]. For a state represented by d wires, the depth of circuits created by this solver is O(Nd) with constant ancillary wires and O(log⁡(Nd)) with O(Ndlog⁡N) ancillary qubits. However, in scenarios where only a uniform superposition is required, as is often the case in unstructured search problems, our proposed solver offers a notable efficiency advantage. With a reduced circuit depth of O(log2⁡N), fewer 2-wire gates, and the absence of ancillary wires, our solver not only streamlines the preparation process but also minimizes resource requirements, and the opportunity for error [6], making it a more efficient choice for such applications.

As an example of an unstructured search application of our solver, we will focus hereafter specifically on Graph Coloring Problems. A graph G consists of a set of vertices/nodes V and a set of edges E. Each vertex v has a set of Nv possible colors of which it can exhibit exactly one. An edge between two vertices constitutes a constraint that those two vertices cannot be the same color. A solution to G is a coloring such that each vertex has been assigned a color from among its color-set and all constraints are satisfied.

We have implemented a Grover’s Algorithm [7] based approach to such problems as described in [1] to demonstrate an application of our algorithm. For this implementation, each vertex v∈V is represented by ⌈log2⁡Nv⌉ wires. As such, the number of wires needed to solve a given graph is

E+1+∑vV⌈log2⁡Nv⌉(2)

Using Hadamard gates for state preparation means a search space that is

∏vV2⌈log2⁡Nv⌉(3)

which is significantly greater than or equal to the restricted search space

∏vV2log2⁡Nv=∏vVNv(4)

Consequently, using Hadamard gates for state preparation can mean a significant reduction in efficiency, as the number of repetitions needed is proportional to the square root of the size of the search space. If instead we create a restricted superposition of any given number of states, we can significantly decrease the number of repetitions of Grover’s Algorithm that are needed.

This optimization is applicable not only for Graph Coloring Problems, but (at minimum) all applications of Grover’s Algorithm. Previously, Grover’s Algorithm has been successfully employed to obtain quantum speedup for various combinatorial optimization problems ([8–12]) all of which can potentially be further optimized via this modification. One thing to note for Grover’s Algorithm in particular, is that the sub-circuit for generating the restricted superposition is needed not only for the initializer but for the mirror of the diffuser in each repetition, making it very important to minimize the number of inefficient 2 wire gates. We believe we have developed an optimal general case solver for the uniform state preparation circuit of any possible N.

2  Process

2.1 Algorithm

The circuit for the uniform superposition of N states needs j = ⌈log2⁡N⌉ wires. If N is a multiple of 2i for some integer i greater than 0, the first i wires do not need to be entangled because they have an equal desired probability of 1 and 0 independent of the other wires (line 4). Once those wires are in superposition, the other wires need to be entangled beginning with the highest order wire. The angle function is used to determine the angle of RY gate to apply to this wire to achieve the desired probability of 1 and 0. For the subsequent wires, in order of decreasing magnitude, if their corresponding digit in (N−1)(2) is 1, the angle function is used to determine the angle of CRY gate to apply to that wire with the most recently rotated wire as the control. This “upward arc” of the algorithm generates the largest element of the superposition.

A subsequent “downward arc” back-fills the remaining elements. First the lowest order wire outside of the first i wires is put into equal superposition anti-controlled by the next lowest order wire that was rotated in the upward arc (recorded in line 9). This is because among the states in the superposition where that control wire holds 0 at this point in the process, half should hold 1 in the target wire. This is repeated on each wire in order of increasing magnitude, excluding the highest order wire, each controlled by the next lowest order wire that was entangled in the upward arc.

The desired probability of observing 1 on the highest order wire is the proportion of states in the desired superposition that have 1 on that bit, thus p = nmod2xn for the highest order wire. For the other wires, the desired probability of observing 1 on the target wire coincident with observing 1 on the control wire is the proportion of states in the superposition that have 1 in the target bit given 1 in the control bit, thus p = nmod2xnmod2clast where clast is the last element of c. The desired magnitude of the 1 state for a given wire is m = p and to achieve that magnitude we perform an RY or CRY rotation by 2sin−1⁡(m) depending on whether the wire is of the highest magnitude.

2.2 Efficiency

The number of 2-wire gates required to create a uniform superposition for any given N is equal to count1(N − 1) – 2 maxp(N) + ⌈log2⁡N⌉ – 2, where count1(x)$ is the number of bits holding 1 in the binary representation of x and maxp(x) is the maximum integer i such that x/2i is an integer greater than 1. This can be written mathematically as

∑i=1⌈log2⁡N⌉−1(⌊nmod2i2i−1⌋−2⌊1−(N2imod1)⌋)+⌈log2⁡N⌉−1(5)

which is O(log2⁡N).

2.3 Example 1

Suppose we wanted a superposition of 7 states, see Fig. 1. This superposition consists of elements 0 through 6, which are represented in binary as 000, 001, 010, 011, 100, 101, and 110. The wires that represent the value of each bit are labeled in order of decreasing magnitude, q2, q1, q0. Of these 7 states, 3 begin with 1. Thus we want a 3/7 probability of observing 1 on the highest order qubit, q2. The magnitude of the 1 state for this qubit should then be 3/7. In order to obtain this magnitude, we perform a RY rotation on q2 by 2sin−1⁡3/7. Of the 3 states with 1 in q2, 1 has 1 in q1. Thus we perform a 2sin−1⁡1/3 CRY rotation on q1 controlled by q2. Of the 6 states that do not have 1 in both q1 and q2, half have 1 in q0. We perform a π2 CRY rotation on q0 anti-controlled by q1. Finally, of the 4 states with 0 in q2, half have 1 in q1. The last operation is a π2 CRY rotation on q1 anti-controlled by q2.

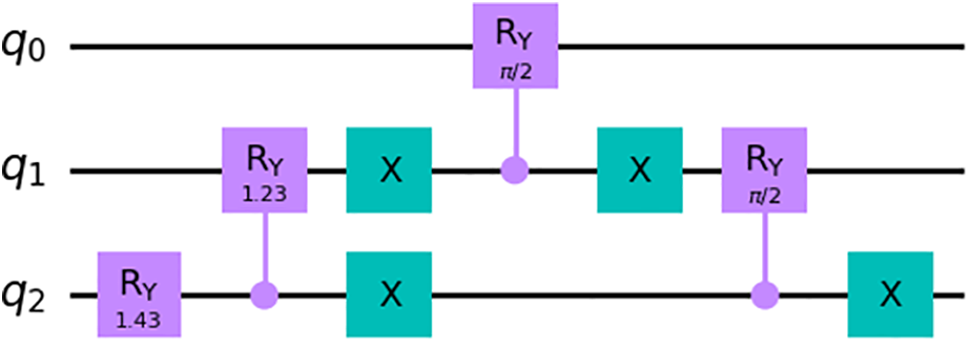
Figure 1: Circuit to initialize a uniform superposition of 7 states

2.4 Example 2

Suppose instead that we wanted a superposition of 22 states, see Fig. 2. We follow the same general process with a few modifications. First, because 22 is even, the superposition has an even distribution of 1 and 0 in q0, so it can be put into uniform superposition on its own via a π2 RY rotation and not entangled. Second, the largest element in the superposition, 21, is represented in binary as 10101. Because q3 in 21(2) holds 0, after performing an RY on q4, we skip q3 and perform a CRY on q2. For the same reason, when we perform the π2 anti-controlled CRY rotations on the downward arc of the circuit, q3 is not the control when q2 is rotated. Instead it is controlled by q4.

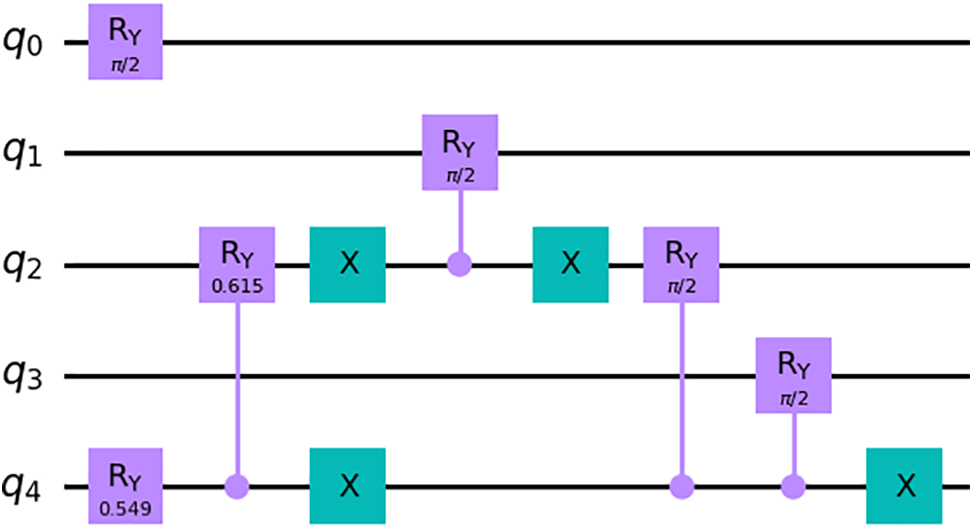
Figure 2: Circuit to initialize a uniform superposition of 22 states

3  Results

3.1 Simulator vs. Quantum Computer

All results in this section come from the circuit for N = 27, see Fig. 3.

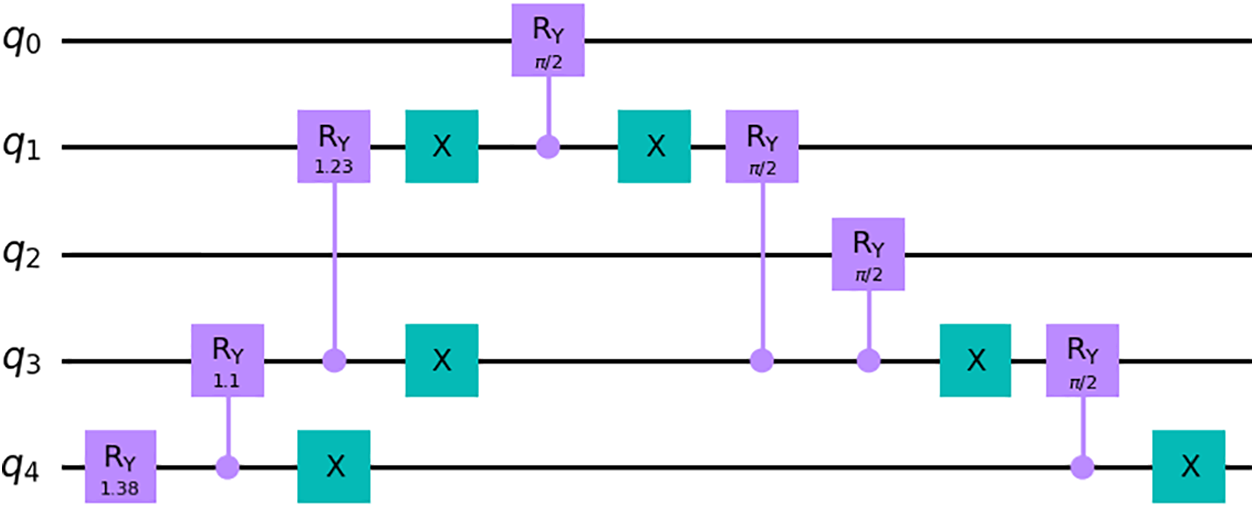
Figure 3: Circuit to initialize a uniform superposition of 27 states

When run on a noiseless simulator, the algorithm creates a perfect superposition of N states, however, each noisy simulator has a different consistent bias when running, see Fig. 4a, likely stemming from inexact rotation angles. Each quantum computer also has a different bias that is consistent across runs in the same calibration, see Fig. 4b. However, when a histogram for the frequency of each output is constructed with all of the results from the simulators and the machines, see Fig. 4c, the mean bias is very small, though the variance varies greatly between them. This indicates that the bias results from flaws in the hardware, and that the algorithm is sound in principle.

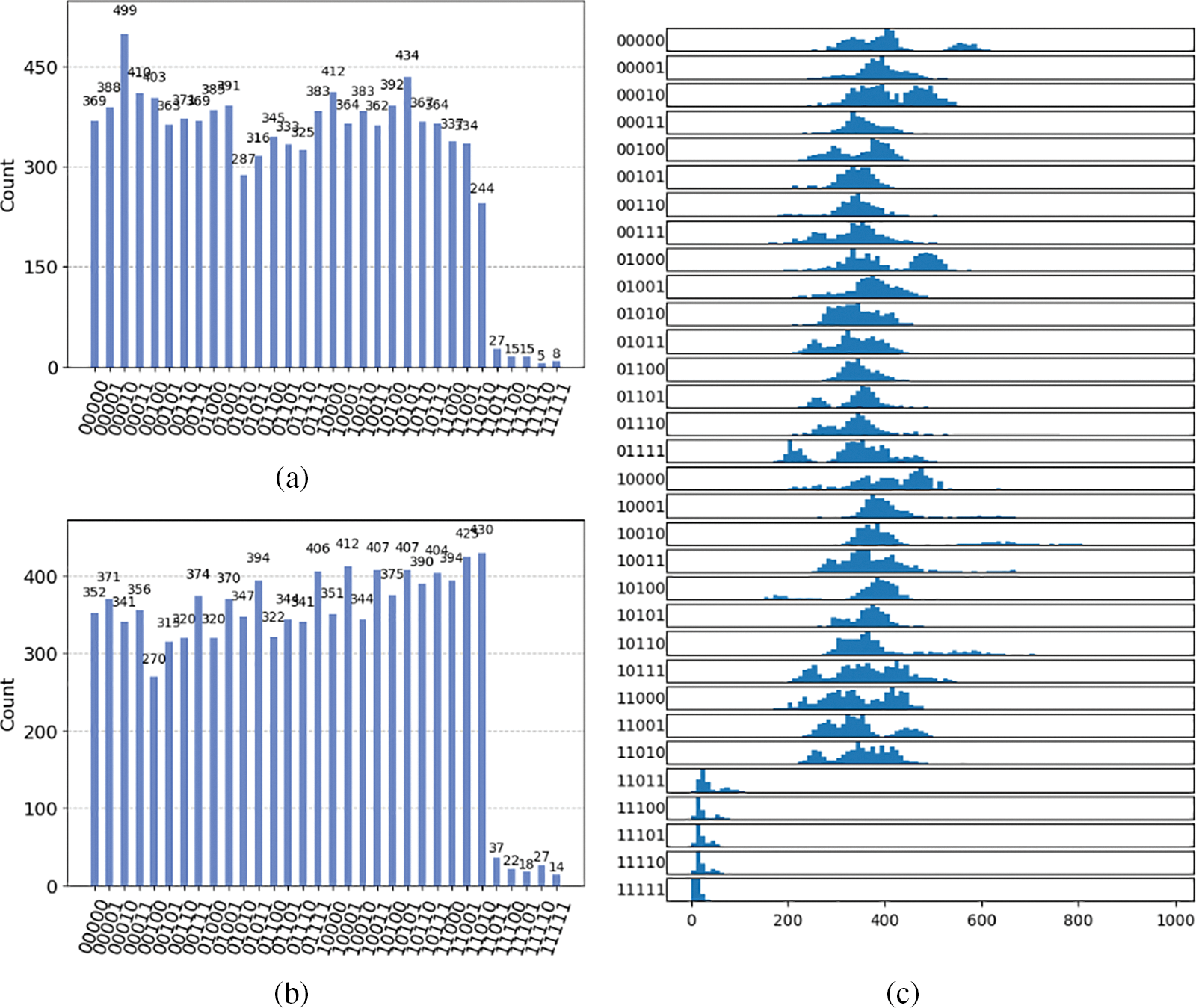
Figure 4: Frequency of each state in the superposition for N = 27 with 10,000 shots when run on (a) IonQ’s aria noise simulator and (b) their aria machine. (c) Histogram for each state in the superposition for N = 27 with 10,000 shots and results combined from IonQ’s harmony and aria noise simulators, their harmony machine, and two different calibrations of their aria machine across 100 runs of each

It may be of note that the bias when run on a quantum computer is not consistent across calibrations. This was discovered when a group of identical runs on IonQ’s harmony machine were spread out over the course of 2 weeks and thus were run under different calibrations, see Fig. 5. In this way, the circuits generated by this solver can incidentally be used as a test of the fidelity of a calibration including 2-wire gates.

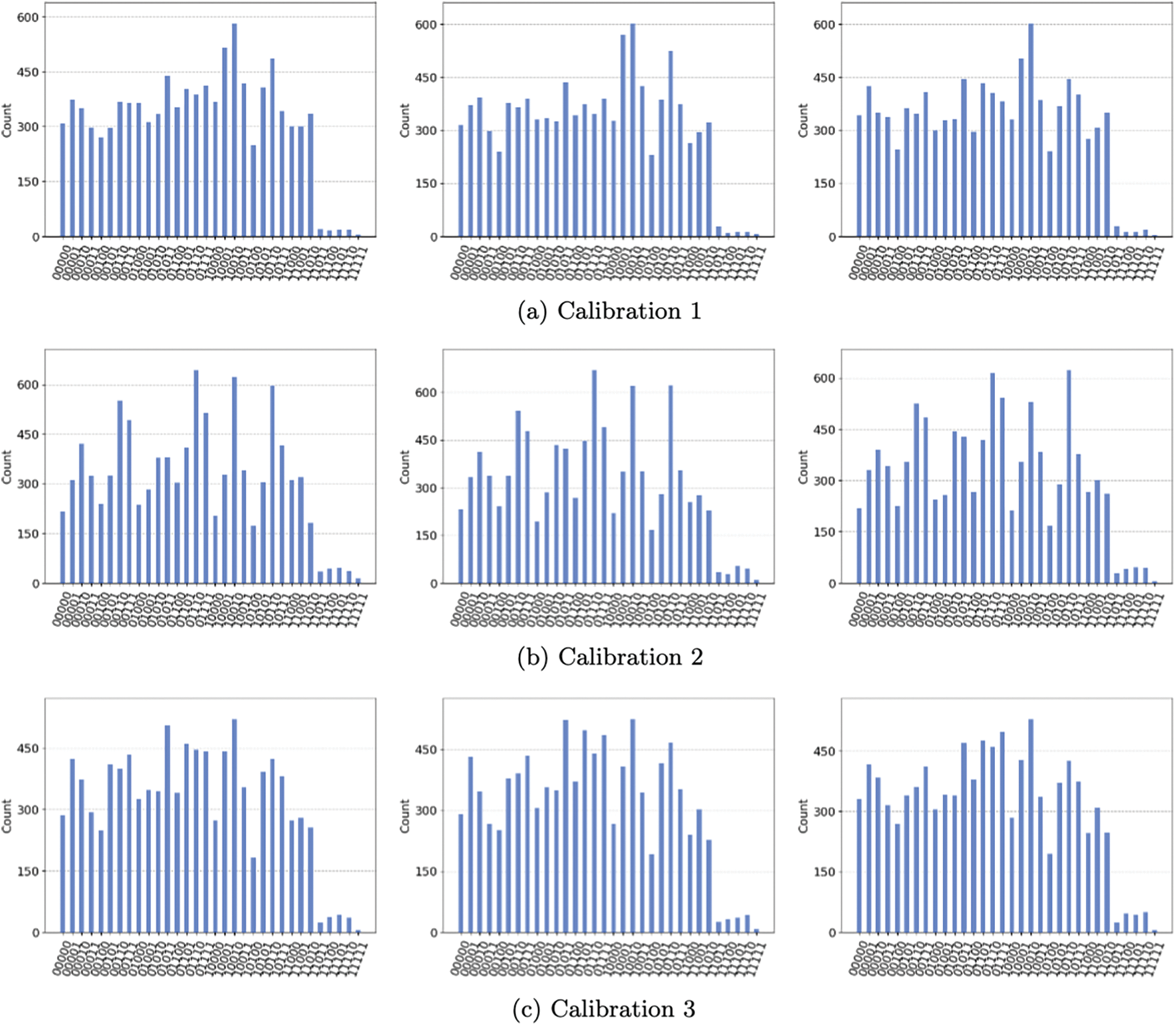
Figure 5: Consistent bias across consecutive runs of N = 27 on IonQ harmony but not across calibrations

3.2 Simulated Modified Grover’s Algorithm

When applying this process to Grover’s Algorithm for Graph Coloring problems, we saw a remarkable improvement in efficiency that was polynomially proportional to 2⌈log2⁡N⌉−N and exponentially proportional to the number of vertices/nodes in the graph. This seems to arise naturally from the difference in search space observed in Eqs. (3) and (4). On graphs where 2⌈log2⁡N⌉−N>1, see Figs. 6b, 6c, the modified algorithm is more efficient regardless of the number of nodes. However, for certain trivial graph problems where 2⌈log2⁡N⌉−N=1, a small decrease in efficiency was seen, but this is irrelevant because all such graph problems were trivial and solving is only necessary for non-trivial graph problems. Examples where this is the case include 3-color graphs with 3 or less nodes, see Fig. 6a, and 7-color graphs with 7 or less nodes, see Fig. 6d. For these graphs, the modified algorithm seems to over-shoot the solution on low-iteration runs and thus requires more runs than the original algorithm to regain a correct solution. However, as the number of nodes increases, the two efficiencies converge until they cross, and the modified algorithm becomes more efficient for the non-trivial graphs. This is clear in Fig. 6a, and though Fig. 6d ends at 7 nodes, the same trend can be extrapolated. Similar results were observed with both noisy and noise-less simulators.

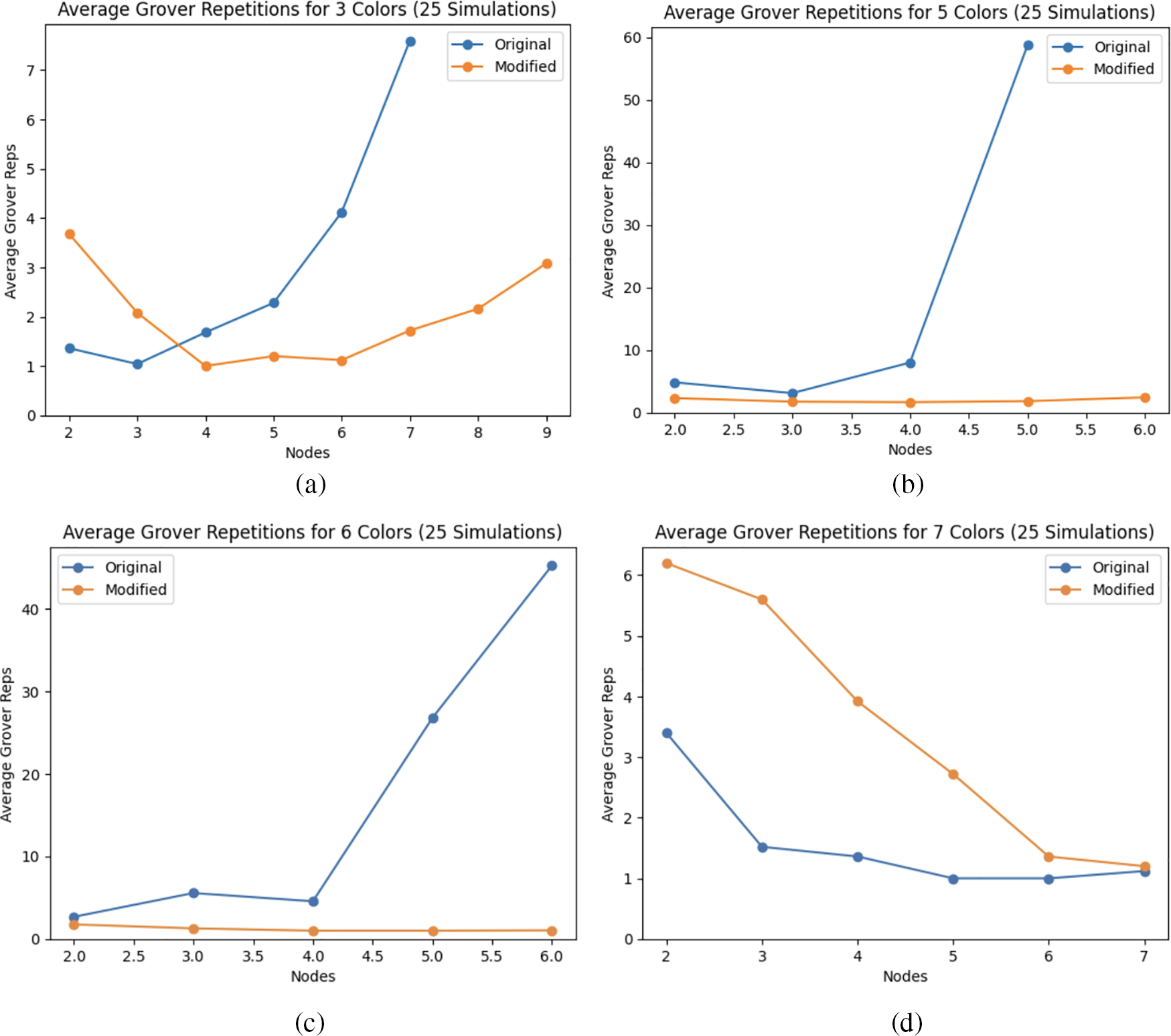
Figure 6: Average number of Grover repetitions needed to observe correct answers via a stochastic iterative stepping process as suggested in [13] for a line graph with (a) 3, (b) 5, (c) 6, and (d) 7 colors. These results were simulated on the qiskit Aer simulator with the qiskit FakeVigo noise model. Other approaches to estimate repetitions include [14–16]

Unfortunately, trivial graphs predominate in these experiments because of the limitations of the simulator on which they were conducted. When more nodes were attempted than shown in the datapoints, the simulator failed either due to time out, or simply being unable to handle the number of wires required, see Eq. (2). It is notable that timeout always occurred with fewer or equal nodes for the original version than for the modified version. Graphs where N=2k are not included because no modification is made in those cases.

With this modified version of Grover’s Algorithm, the initializer and the mirror of the diffuser both have increased depth in each iteration. We have already discussed how we limit the depth of our circuits so that this increased depth is minimized, but the increase in depth is also negligible in comparison to the depth of the oracle and the decomposition of the multi-controlled CNOT in the diffuser, both of which are unchanged by our modification. The data in Fig. 6 demonstrate that as a trade-off for this slight increase in the depth of each iteration, we can significantly reduce the number of iterations required to reach a correct solution. Overall, this balances out to significantly decrease the overall depth of Grover’s Algorithm.

4  Conclusion

We were able to accomplish a significant improvement in the efficiency of quantum unstructured search by eliminating the auxiliary search space created by traditional methods of state preparation while minimizing the number of 2-wire gates required to do so. Although we have only provided the example of a Grover’s Algorithm approach to graph coloring problems as a viable application, colleagues of ours have already begun making use of these state preparations to improve the efficiency of quantum walk, machine learning, and other applications. This solver can be used to varying degrees of effect to modify any algorithm that requires a uniform state preparation that is unattainable via simple Hadamard superposition.

Acknowledgement: Thank you to Dr. Franz Klein from University of Maryland for his advisory role, helping me to consider potential applications of my work and for his advice and revisions during the writing of this paper.

Funding Statement: The author received no specific funding for this work.

Author Contributions: Mark Levin was the sole researcher and author of this work.

Availability of Data and Materials: All data in this work can be generated using https://github.com/TheMLevin/GroverGraphSolver.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Mukherjee, “A grover search-based algorithm for the list coloring problem,” arXiv:2108.09061, 2022. [Google Scholar]

2. R. Roberts, C. K. Li, and X. Yin, “Decomposition of unitary matrices and quantum gates,” Int. J. Quantum. Inf., vol. 11, no. 1, pp. 1350015, 2013. doi: 10.48550/arXiv.1210.7366. [Google Scholar] [CrossRef]

3. Mikko Mött önen et al., “Quantum circuits for general multiqubit gates,” Phys. Rev. Lett., vol. 93, no. 13, pp. 130502, 2004. doi: 10.1142/S0219749913500159. [Google Scholar] [CrossRef]

4. Mikko Mött önen Juha, J. J. Vartiainen, and M. M. Salomaa, “Efficient decomposition of quantum gates,” Phys. Rev. Lett., vol. 93, no. 13, pp. 130502, 2004. doi: 10.1103/PhysRevLett.92.177902. [Google Scholar] [PubMed] [CrossRef]

5. X. M. Zhang, T. Li, and X. Yuan, “Quantum state preparation with optimal circuit depth: Implementations and applications,” Phys. Rev. Lett., vol. 129, pp. 230504, 2022. doi: 10.1103/PhysRevLett.129.230504. [Google Scholar] [PubMed] [CrossRef]

6. F. Yan et al., “Tunable coupling scheme for implementing high-fidelity two-qubit gates,” Phys. Rev. Appl., vol. 10, no. 5, pp. 054062, 2018. doi: 10.1103/PhysRevApplied.10.054062. [Google Scholar] [CrossRef]

7. L. K. Grover, “A fast quantum mechanical algorithm for database search,” in Proc. Twenty-Eighth Annu. ACM Symp. Theory Comput., 1996, pp. 212–219. [Google Scholar]

8. S. Jeffery, R. Kothari, F. L. Gall, and F. Magniez, “Improving quantum query complexity of boolean matrix multiplication using graph collision,” Algorithmica, vol. 76, no. 1, pp. 1–16, 2016. doi: 10.48550/arXiv.1112.5855. [Google Scholar] [CrossRef]

9. K. Khadiev and A. Ilikaev, “Quantum algorithms for the most frequently string search, intersection of two string sequences and sorting of strings problems,” in Theory and Practice of Natural Computing, Cham: Springer, 2019, pp. 234–245. [Google Scholar]

10. D. Kravchenko, K. Khadiev, and D. Serov, “On the quantum and classical complexity of solving subtraction games,” in Computer Science—Theory and Applications, Cham: Springer, 2019, pp. 228–236. [Google Scholar]

11. T. Lee, F. Magniez, and M. Santha, “Improved quantum query algorithms for triangle detection and associativity testing,” Algorithmica, vol. 77, no. 2, pp. 459–486, 2017. doi: 10.48550/arXiv.1210.1014. [Google Scholar] [CrossRef]

12. A. Shukla and P. Vedula, “Trajectory optimization using quantum computing,” J. Global. Optim., vol. 75, no. 1, pp. 199–225, 2019. doi: 10.1007/s10898-019-00754-5. [Google Scholar] [CrossRef]

13. M. Boyer et al., “Tight bounds on quantum searching,” arXiv:quant-ph/9605034, 1996. [Google Scholar]

14. C. Durr and P. Hoyer, “A quantum algorithm for finding the minimum,” arXiv: quant-ph/9607014, 1996. [Google Scholar]

15. S. Aaronson and P. Rall, “Quantum approximate counting, simplified,” in Symp. Simpl. Algorithms, SIAM, 2020, pp. 24–32. [Google Scholar]

16. M. Mosca, “Counting by quantum eigenvalue estimation,” Theor. Comput. Sci., vol. 264, no. 1, pp. 139–153, 2001. doi: 10.1016/S0304-3975(00)00217-6. [Google Scholar] [CrossRef]