 Open Access
Open Access
ARTICLE
Tensile Properties and Prediction Model of Recombinant Bamboo at Different Temperatures
College of Civil Engineering, Nanjing Forestry University, Nanjing, 210037, China
* Corresponding Author: Yang Wei. Email:
Journal of Renewable Materials 2023, 11(6), 2695-2712. https://doi.org/10.32604/jrm.2023.025711
Received 25 July 2022; Accepted 24 August 2022; Issue published 27 April 2023
Abstract
The destruction of recombinant bamboo depends on many factors, and the complex ambient temperature is an important factor affecting its basic mechanical properties. To investigate the failure mechanism and stress–strain relationship of recombinant bamboo at different temperatures, eighteen tensile specimens of recombinant bamboo were tested. The results showed that with increasing ambient temperature, the typical failure modes of recombinant bamboo were flush fracture, toothed failure, and serrated failure. The ultimate tensile strength, ultimate strain and elastic modulus of recombinant bamboo decreased with increasing temperature, and the ultimate tensile stress decreased from 154.07 to 96.55 MPa, a decrease of 37.33%, and the ultimate strain decreased from 0.011 to 0.008, a decrease of 26.57%. Based on the Ramberg-Osgood model and the pseudo‒elastic design method, a predictive model was established for the tensile stress–strain relationship of recombinant bamboo considering the temperature level. The model can accurately evaluate the tensile stress–strain relationship of recombinant bamboo under different temperature conditions.Graphic Abstract
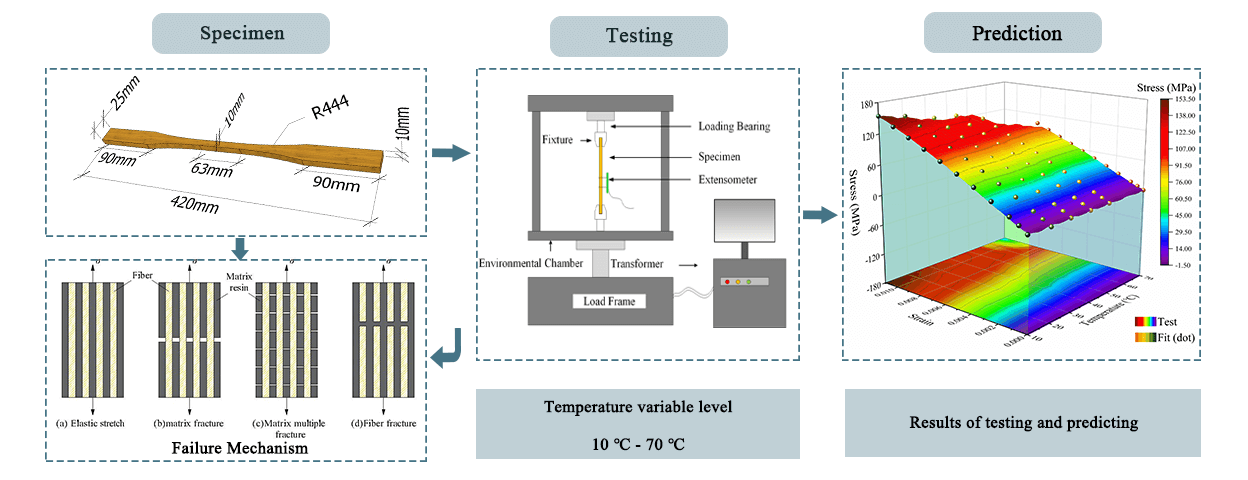
Keywords
Recombinant bamboo is a kind of environmentally friendly bamboo-based fibre composite material that has been widely used in building structures due to its excellent mechanical properties [1–5]. Its mechanical properties are similar to those of wood [6,7], which can be considered an anisotropic viscoelastic polymer matrix composite with strong temperature sensitivity [8,9]. Therefore, it is essential to study the effects of temperature on basic mechanical properties.
The basic mechanical properties of bamboo are influenced by a variety of factors [10,11]. In addition to the bamboo species [12], the composition and distribution of bamboo fibre structure [13], and the volume content of bamboo fibre [14,15], environmental factors also have a certain impact on the application of bamboo. In the past, there have been some studies on the effect of humidity on the basic mechanical properties of bamboo [16,17], and sufficient studies have proved that humidity can degrade the basic mechanical properties of bamboo [18–20]. In contrast, temperature has a greater effect on the properties of bamboo composites. In terms of heat treatment, Hou et al. [21] discussed the effect of temperature level on the physical and mechanical properties of recombinant bamboo and found that the internal bond strength and static bending strength of recombinant bamboo decreased after heat treatment at high temperatures. Brito et al. [22] verified that heat treatment improves the physical characteristics but causes a reduction in the mechanical properties of glued laminated (glulam) bamboo. In the process of application, Wang et al. [23] studied the mechanical properties of unidirectional and multidirectional composite engineering bamboo boards used in laminated bamboo structures at high temperatures. Xu et al. [24,25] reported the stress–strain relationship of laminated bamboo at elevated temperatures. Cui et al. [26,27] analysed the effect of temperature on the failure mode of the specimen and summarized the variation rule of yield strength with temperature.
The above content mainly studied the influence of humidity and high-temperature treatment on the basic mechanical properties of recombinant bamboo. However, there are few studies on the influence of temperature factors considering the use environment on the basic mechanical properties of bamboo. In this work, the effect of ambient temperature on the basic mechanical properties of recombinant bamboo tensile specimens was studied. By discussing the failure mechanism of tensile specimens at different temperatures, the typical failure modes of recombinant bamboo were summarized. Based on the analysis of the relationship between tensile stress, strain, and temperature, the variation law of relevant parameters of the elastic–plastic constitutive model was obtained, and the prediction model considering the influence of temperature was proposed to provide a useful reference for the analysis and design of the bamboo structure.
Bamboo with a growth cycle of 3∼4 years from Huangshan, Anhui Province, China was selected as a raw material [28,29]. Recombinant bamboo has high strength and good uniformity [30]. The processing technique is shown in Fig. 1. The detailed production of recombinant bamboo involves five main steps. The bamboo culms were cut into desired lengths, the bamboo pieces were split vertically with a bamboo cutter, the bamboo wax was removed, and the bamboo pieces were flattened and processed into interconnected and longitudinal bamboo fibres. Then, the bamboo fibres were placed in a tunnel chamber to dry until the moisture content was less than 7%. Then, the bamboo fibres were dipped in the glue (phenol glue) for 10 min, the amount of dipping glue was approximately 5%∼10% of the dry mass of the bamboo fibres, and the recombinant bamboo was dried to the required moisture content (10% ± 2%). The impregnated bamboo fibres were directly placed on the hot-pressed backing board, and the board was pressed at a certain temperature and pressure of 4∼6 MPa to achieve the desired size (e.g., 2400 mm × 120 mm × 50 mm). The test showed that the average density of the recombinant bamboo was 1.23 g/cm3, the moisture content was 8.4%, and the internal adhesive strength was 3.57 MPa.

Figure 1: Production of recombinant bamboo
2.2 Specimens and Test Schemes
According to the standards of “General requirements for the physical and mechanical test of wood” [31] and “Standard Test Methods for Small Clear Specimens of Timber” [32], dumbbell-shaped recombinant bamboo tensile specimens were composed of a gripping section, a transition arc, and a working section. The size of the holding section was 90 mm (length), 25 mm (width), and 10 mm (height); the radius of the transition arc was 444 mm; the size of the working section was 63 mm (length), 10 mm (width), and 10 mm (height); and the total length of the specimen was 420 mm. The recombinant bamboo specimen was shown in Fig. 2, which was cut along the grain direction of the recombinant bamboo beam. Its surface was smooth without burrs, and its bottom was perpendicular to its side.
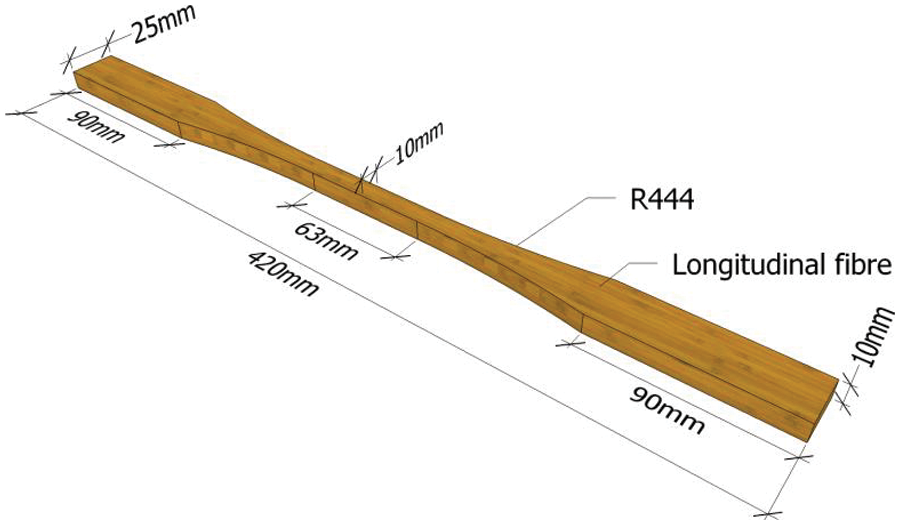
Figure 2: Dumbbell-type tensile specimen of recombinant bamboo (dimensions in mm)
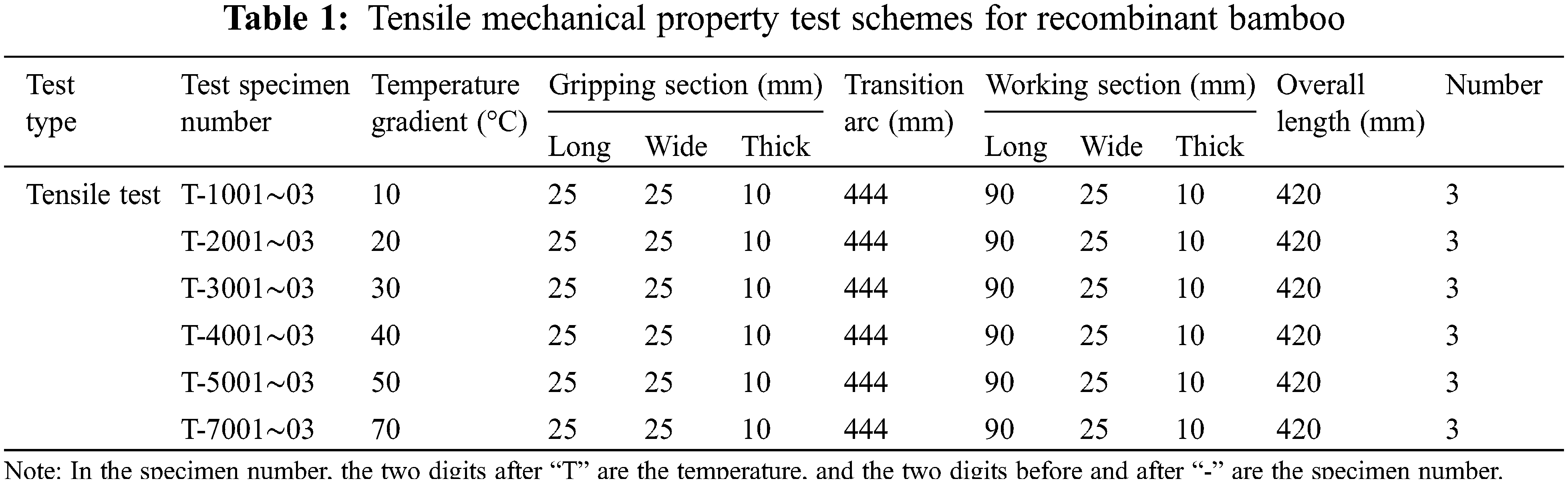
To ensure the reliability of the test data on the mechanical properties of the recombinant bamboo, three tensile specimens of equal size were selected for parallel testing. Considering the influence of temperature on the tensile properties of recombinant bamboo, the humidity was set at 50% (constant), the test parameters were temperature (10°C, 20°C, 30°C, 40°C, 50°C, 70°C), and the tensile specimen was divided into six groups for a total of eighteen specimens. A test plan is shown in Table 1.
2.3 Experimental Instruments and Methods
A microcomputer-controlled universal testing machine (UTM5504-GD) and a high- and low-temperature testing chamber (WGDY-7350 L) were used to test the tensile strength of the specimen, as shown in Fig. 3. The maximum test load of the universal testing machine was 50 kN, the temperature range of the high- and low-temperature testing chambers is −70°C∼350°C, and the humidity was 20%∼100%. Additionally, a reliable high- and low-temperature extensometer (EAG-050 M-0200-S) was used to monitor the deformation of the specimen. The extensometer’s distance length was 50 mm, the measurement range was +20%/−10%, and the temperature range was −40°C∼100°C. The combined system can be used to test the mechanical properties of composite materials.

Figure 3: Loading diagram of recombinant bamboo in a tensile test
Tensile specimens were placed in an environment box with preset temperature and humidity in advance and maintained for no less than 24 h. Then, tensile specimens were loaded, maintained, and loaded. Under the condition of variable temperature, the sensor of the creep tester collects load and displacement data in real time. According to the “Method of testing in tensile strength parallel to the grain of the wood” [33], the tensile specimen was loaded. To eliminate the error caused by the contact gap between the clamping piece of the tensile fixture and the specimen surface, the tensile specimen must be preloaded to 2 kN at a speed of 50 N/s, and the load was reduced to 0 kN. Then, the specimen was loaded at a speed of 0.5 mm/min until failure. During the experiment, the failure of the recombinant bamboo specimen was observed and recorded. According to the test results, the strength, displacement, elastic modulus, and other results can be obtained, and the corresponding stress–strain test curve can be obtained.
3.1.1 Tensile Failure Mechanism
With the increase in the external load, the longitudinal tensile deformation of the unidirectional fibre composite material can be divided into four stages, as shown in Fig. 4. Fibre elastic deformation occurred, but the matrix underwent transverse fracture; the fibre continued elastic deformation, and the matrix exhibited many fractures. Fibre fracture followed by fracture of the unidirectional fibre composite. The existence of the above four stages depends on many factors. In addition to the basic mechanical properties of the fibre and the matrix, it was also affected by the working environment. Due to the joint action of complex factors, the fracture time and fracture section of the matrix and the fibre were not the same. Based on qualitative analysis of the fracture mechanism, Kelly et al. [34] established a prediction model of tensile strength, and Zhu et al. [35] proposed a unified theory of longitudinal tensile of unidirectional composite materials. In the case of known fibre strength, matrix content, and matrix strength, the above model can quantitatively describe the stress–strain relationship, but it needs to be based on the statistics and analysis of many tests. Therefore, the tensile failure mode of the recombinant bamboo was considered only from the failure mechanism.
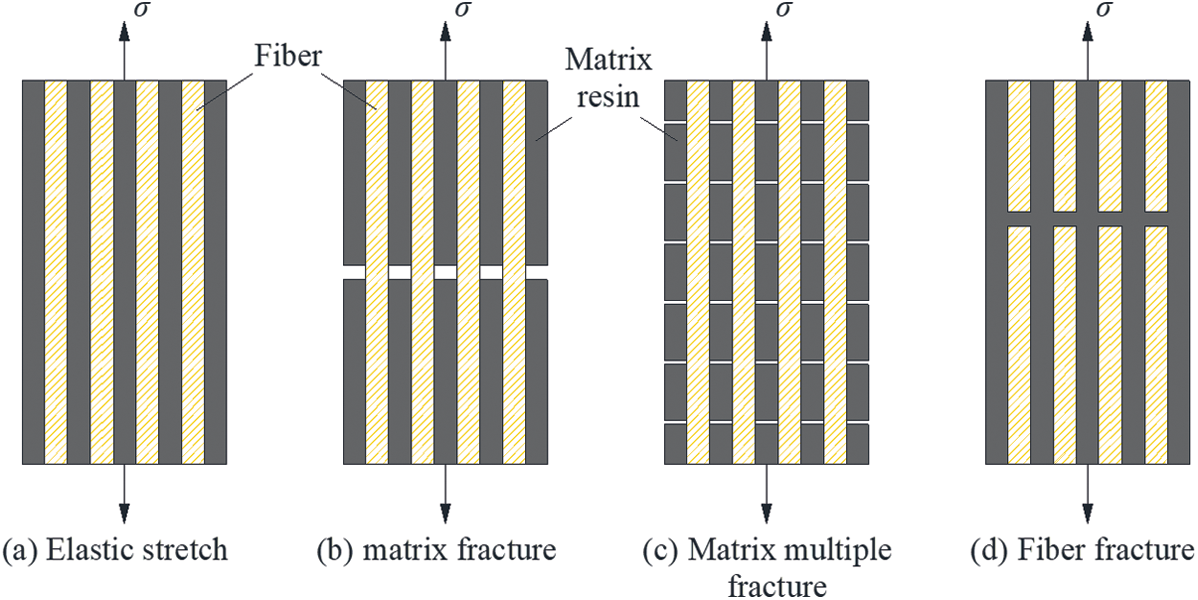
Figure 4: Main tensile failure stages of unidirectional fibre composites [26]
3.1.2 Discrimination of the Tensile Failure Mode
The elastoplasticity of the fibre and matrix is significantly affected by temperature. The failure mode of a tensile specimen of recombinant bamboo was analysed to determine the influence of temperature on the tensile properties of recombinant bamboo. Fig. 5 shows the failure modes of the recombinant bamboo tensile sample with increasing temperature. It can be seen from the damaged specimens that there were mainly three failure modes. When the temperature was lower, tensile failure modes of the specimens for the “flush fracture” mode, early tensile test, the reorganization of the bamboo found no abnormal noise. When the load was close to the ultimate load, the cross-section fast fracture occurs in the effective area of the tensile specimen, the fracture surface was flush, and the tensile capacity of the specimen loses instantly, as shown in Fig. 5a. The main reason is that both the matrix and bamboo fibre are hard and brittle when the temperature was low (10°C). The tensile strength of the recombinant bamboo is greatly affected by the strength of the bamboo fibre bundle. When the tensile strength reached the tensile strength of the bamboo fibre bundle, the recombinant bamboo suddenly broke. When the temperature rose to 30°C, the tensile specimen exhibits a “toothed failure” model. In the process of the tensile test, the reorganization of the bamboo tensile specimen with slight noise, and the bamboo fibre begins to break. Because of the additional load on the fibre fracture attached to the substrate to matrix cracking, the fracture of the fibre cross-section in the corresponding place, and the effective cross-sectional area of the matrix was reduced. In the effective area, the recombinant bamboo presents a tooth-like fracture form, and the tensile strength of the specimen was lost, as shown in Fig. 5f. When the temperature was 70°C, with increasing temperature, the matrix softened, the fibre underwent transverse debonding, and the fibre began to fracture. When the fibre broke, the load transferred to the matrix was very large, which the matrix could not bear, leading to the fracture of the matrix immediately, and the pattern of “serrated failure” appeared in the recombinant bamboo tensile specimen.

Figure 5: Failure mode of a tensile specimen of recombinant bamboo
3.2.1 Tensile Stress and Strain
To facilitate the analysis of the mechanical properties of the recombinant bamboo, the stress–strain curve of the tensile test of the recombinant bamboo was drawn, as shown in Fig. 6. As seen from Fig. 6, the form of the stress–strain curve of the tensile strength of recombinant bamboo changes with increasing temperature, and the strain rate increased with increasing temperature. When the temperature was low (10°C), as shown in Fig. 6a, the strain rate was low, and the stress–strain curve of the tensile test of recombinant bamboo did not show the properties of nonlinear viscoelastic materials. When the temperature was high (70°C), as shown in Fig. 6f, the strain rate is high, and the stress–strain curve of the tensile test of the recombinant bamboo presents obvious properties of nonlinear viscoelastic materials. By Figs. 6a–6f, due to the increase in temperature, the diffusion capacity of atoms increases, the tiny voids inside the recombinant bamboo increase, the deformation ability of the recombinant bamboo increases under high-temperature conditions, the matrix slips, and the fibres soften and lose effective bonding with the matrix. The tensile strength decreased with increasing temperature, the strain decreased with increasing temperature, and the strain rate increased with increasing temperature.

Figure 6: Stress and strain test results of recombinant bamboo under tensile loading
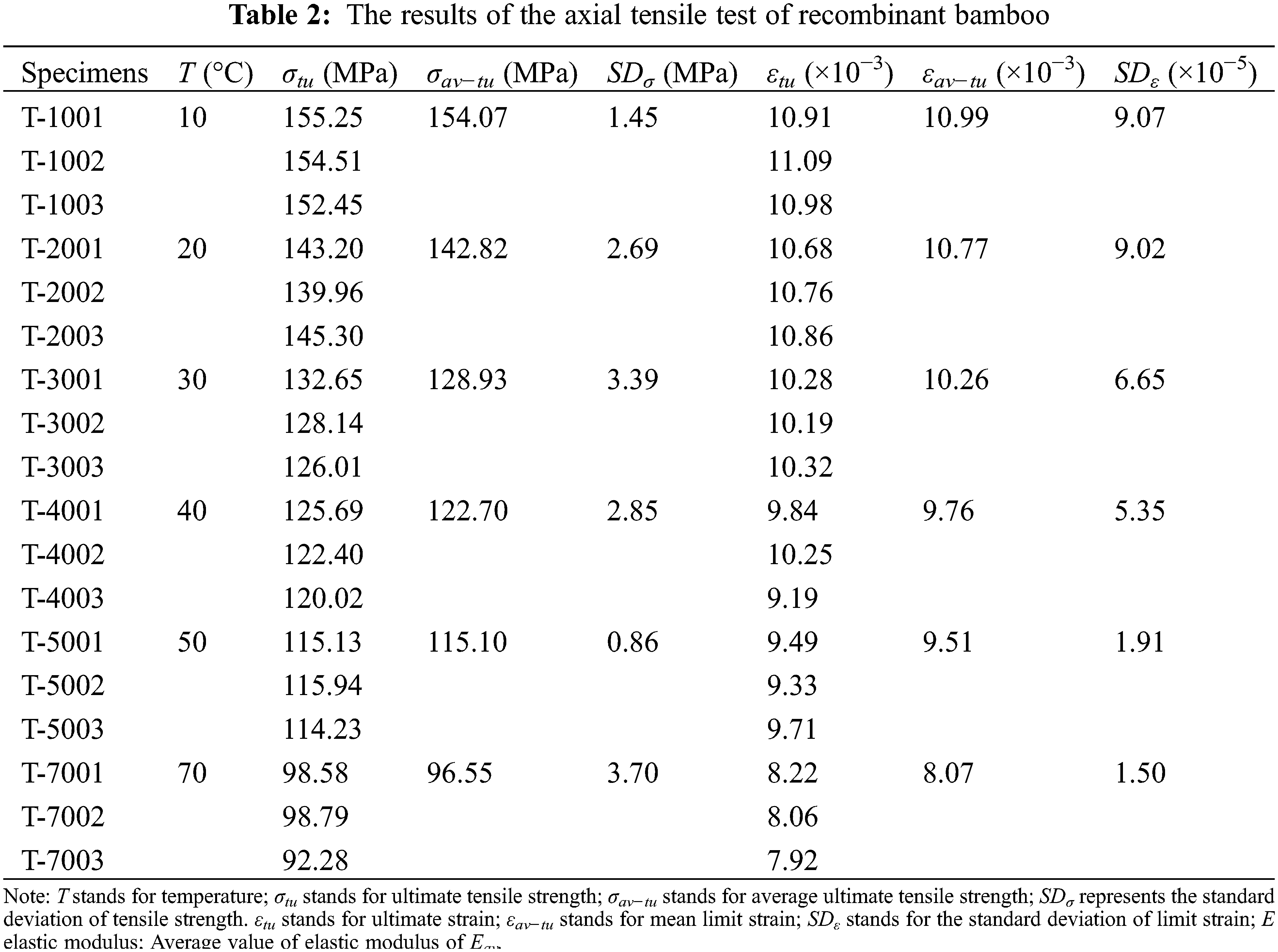
Fig. 6 shows the ultimate tensile strength and ultimate strain values of each group of specimens. The mean value of the test data of each group was obtained by using analysis software, and the ultimate tensile strength and ultimate strain of the mean curve were statistically analysed. The statistical results are shown in Table 2. It can be seen from the statistical results that the standard deviation of ultimate tensile strength and ultimate strain was small, indicating that the dispersion of test data was small, and the test results were satisfactory.
3.2.2 Effect of Temperature on Ultimate Tensile Stress and Strain
To study the effect of temperature on the ultimate tensile strength and ultimate tensile strain of recombinant bamboo, the relationship between temperature, σav-tu, and εav−tu was established according to the statistical results in Table 2, as shown in Fig. 7. It can be seen in Fig. 7 and Table 2 that the ultimate stress decreased with increasing temperature. Under normal temperature conditions (10°C∼50°C), the ultimate tensile strength decreased from 154.07 to 115.10 MPa, the amount of decrease was 38.97 MPa, and the decay rate of the ultimate tensile strength with temperature was 0.97 MPa/°C. In the high-temperature range (50°C∼70°C), the ultimate tensile strength decreased from 115.10 to 96.55 MPa, the amount of decrease was 18.55 MPa, and the decay rate of the ultimate tensile strength with temperature was 0.92 MPa/°C. The ultimate strain in the normal temperature range (10°C∼50°C) decreased from 0.0109 to 0.0095, the decrease was 0.0015, and the ultimate strain decreases with temperature. The decay rate was 0.000037/°C. In the high-temperature range (50°C∼70°C), the ultimate strain decreased from 0.00951 to 0.00807, and the amount of decrease was 0.00144. The decay rate of the ultimate strain with temperature was 0.000072/°C, the decay rate was faster, and its decay rate was twice that of the normal temperature decay rate. Therefore, recombinant bamboo was more suitable for use in the normal temperature range (10°C∼50°C).
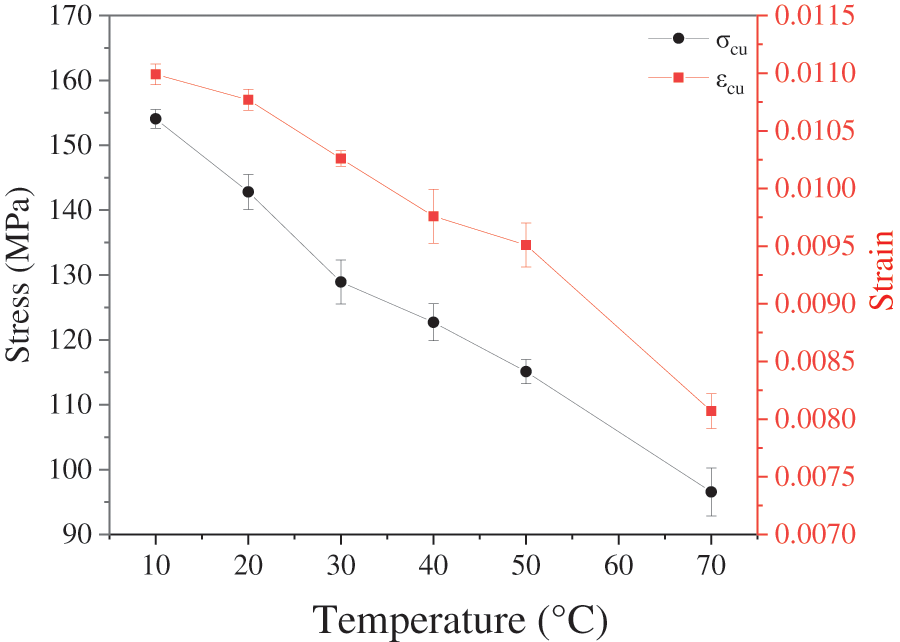
Figure 7: The relationship between temperature and ultimate stress and strain
3.2.3 Reduction Factors for Stress and Strain
Considering the influence of temperature on the ultimate strength and strain of the recombinant bamboo tensile specimen, the reduction factor method was used to treat the ultimate tensile stress and strain of the recombinant bamboo to quickly estimate the ultimate stress and strain of the tensile specimen at a specific temperature. The reduction factors are shown in Eqs. (1) and (4).
The reduction factor of tensile stress (ησ,T) is:
Since at 20°C the ησ,T = 1, thus
where ησ,T is the reduction factor of stress; T is the temperature,°C; σT is the stress at temperature T,
The reduction factor of tensile strain (ηε,T) is:
Since at 20°C the ηε,T = 1, thus
where ηε,T is the reduction factor of strain; T is the temperature,°C; εT is the strain at temperature T;
The reference temperature was selected as 20°C, and the reduction coefficient was calculated by using Eqs. (3) and (6). The fitting curve between temperature and reduction factor was drawn according to the calculated results, expressed by Eqs. (7) and (8), as shown in Fig. 8.
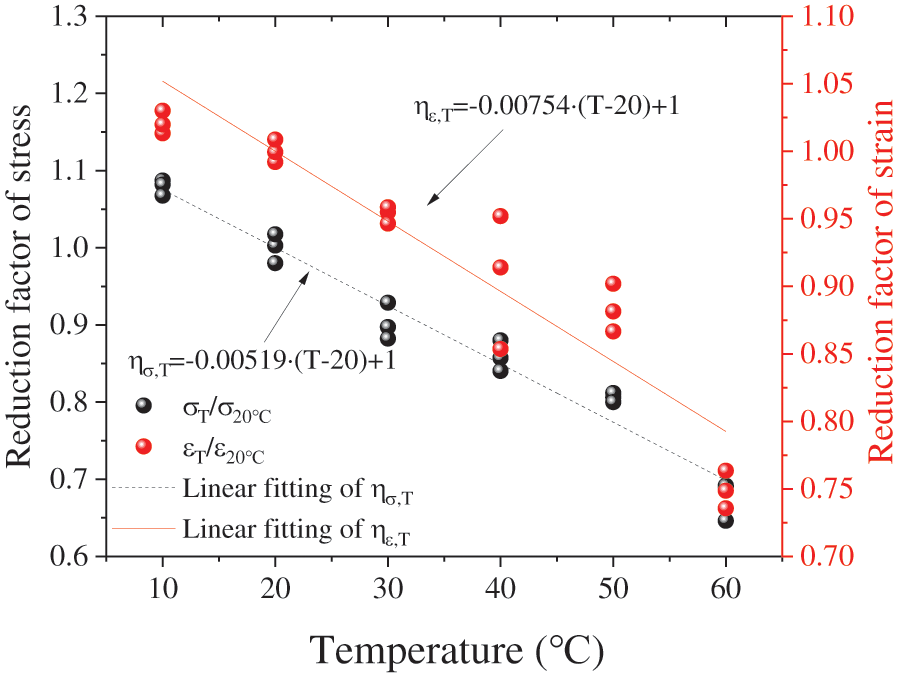
Figure 8: The relationship between the reduction factors and temperature
The reduction factor of tensile stress (ησ,T) is:
where ησ,T is the reduction factor of stress and T is the temperature,°C.
The reduction factor of tensile strain (ηε,T) is:
where ηε,T is the reduction factor of strain and T is the temperature,°C.
Fig. 8 shows that the reduction factor (ησ,T, ηε,T) decreases with increasing temperature, and the reduction factor of strain was greater than that of stress. The results showed that temperature had a significant effect on the ultimate stress and that the ultimate strain had a strong temperature sensitivity.
4 Mathematical Model and Analysis
In fact, the tensile properties of recombinant bamboo showed some properties of nonlinear viscoelastic materials. The stress of nonlinear viscoelastic materials was a function of strain and time, as shown in Fig. 9. In addition, the stress of viscoelastic materials was related not only to strain and time but also to temperature sensitivity. The experimental results showed that under the condition of elevated temperature, recombinant bamboo showed some viscoelastic plastic deformation. The nonlinear viscoelastic constitutive equation of behaviour was related to time. Due to the reorganization of the bamboo, the bearing capacity of the tensile test of the time was shorter, so the elastic–plastic model was considered to analyse the stress–strain relationship of the tensile test. The elastoplastic model is shown in Fig. 10.
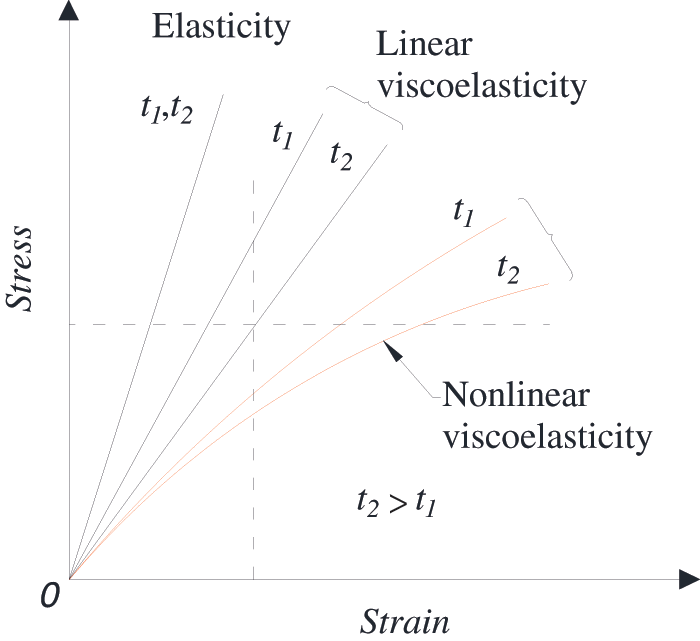
Figure 9: Stress–strain relationship of elastic and viscoelastic materials
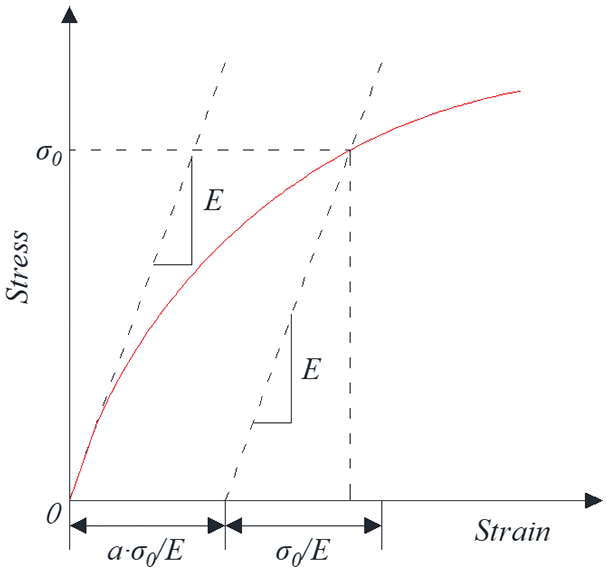
Figure 10: Ramberg-Osgood model
The Ramberg-Osgood model is a nonlinear deformation formula that does not consider the time factor [36]. Since the strain was only related to stress, it is a static equation consisting of mutually independent elastic deformation and plastic deformation. The two do not affect each other in the tensile process. The nonlinear stress–strain relationship can be described [37], as shown in Eq. (11).
where ε represents the total deformation; σ stands for tensile stress, MPa; εe stands for elastic deformation; εp stands for plastic deformation; E stands for elastic modulus, MPa; k and n are constants.
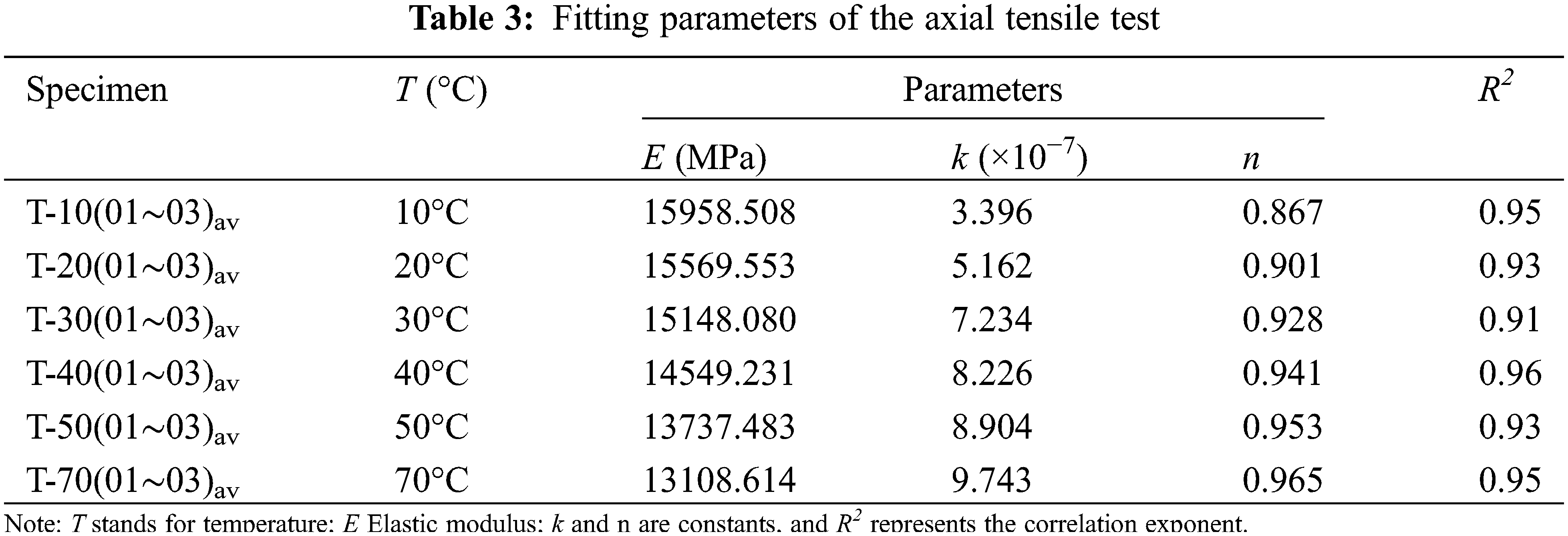
The mean value of the test data at a single temperature was fitted. The fitting results and test data are shown in Fig. 11, and the fitted parameters are statistically shown in Table 3. The statistical results showed that the correlation coefficients (R2) of each fitting curve were close to 1.0 within the ultimate tensile strain range, indicating that the Ramberg-Osgood model can fit the linear and nonlinear parts of the test data well. As seen from Fig. 11, with the increase in temperature, the stress–strain curve of the recombinant bamboo can be divided into two stages: the first stage was the elastic stage, and the stress–strain curve showed a linear growth trend; the second stage was the elastic–plastic stage, the stress exceeds the elastic limit, the axial stress growth rate decreases, and the stress–strain curve presents a nonlinear reduction state. When the temperature was 10°C, the tensile strength of the recombinant bamboo was large, and the plastic stage of its stress–strain curve was not obvious, showing a strong elastic state. When the temperature was 70°C, after the online elastic stage, the stress develops slowly and lags behind the growth of strain. The plastic stage after yield was more obvious, showing the properties of viscoelastic materials. When the temperature was between 10°C and 70°C, the ultimate tensile strength and ultimate strain of recombinant bamboo decrease with increasing temperature, and the nonlinear characteristics of the stress–strain curve become increasingly significant.
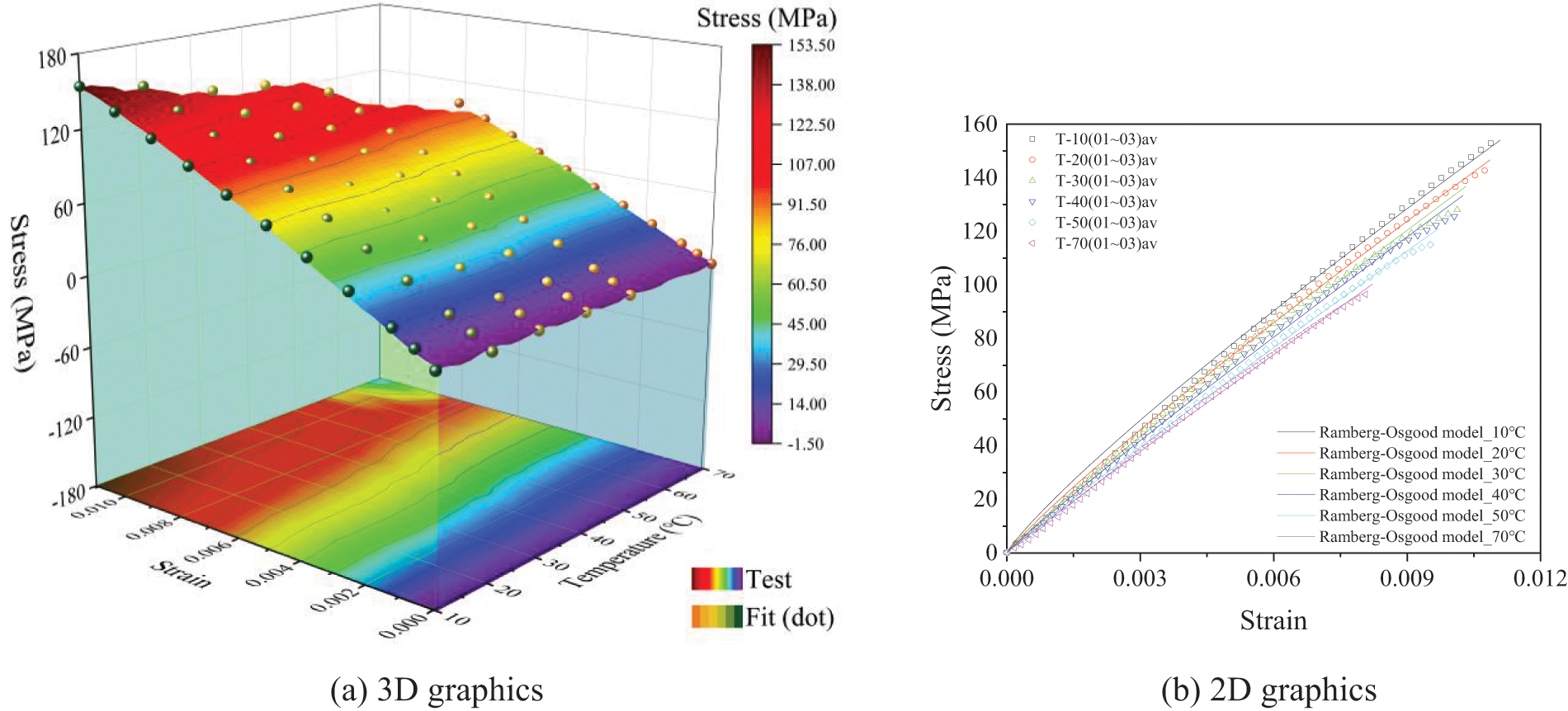
Figure 11: Fitting results of the stress–strain relationship of the recombinant bamboo tensile test
4.3 Analysis of Modulus Parameters
Under the experimental conditions of different temperatures, the parameters (E, k, n) of the Ramberg-Osgood model were estimated by the nonlinear least square method. Fig. 11 and Table 3 show that the model fitting results are in good agreement with the experimental curve. Table 3 shows that the elastic modulus (E) of the recombinant bamboo material in the direction of the grain was higher, which was mainly due to the comprehensive effect of the fibre and matrix. In the Ramberg-Osgood model, plastic deformation was affected by E, k, and n. The larger the parameters k and n were, the smaller E was, and the more likely the material was to undergo plastic deformation. According to the fitting results, the k value was large, while the n value was small, so the plastic deformation of the recombinant bamboo along the grain tensile test is smaller than that of the compression and bending test. According to Fig. 12, the E value decreases with increasing temperature, while the lnk and n values increase with increasing temperature. Therefore, the plasticity of the tensile specimen of recombinant bamboo increased with increasing temperature.
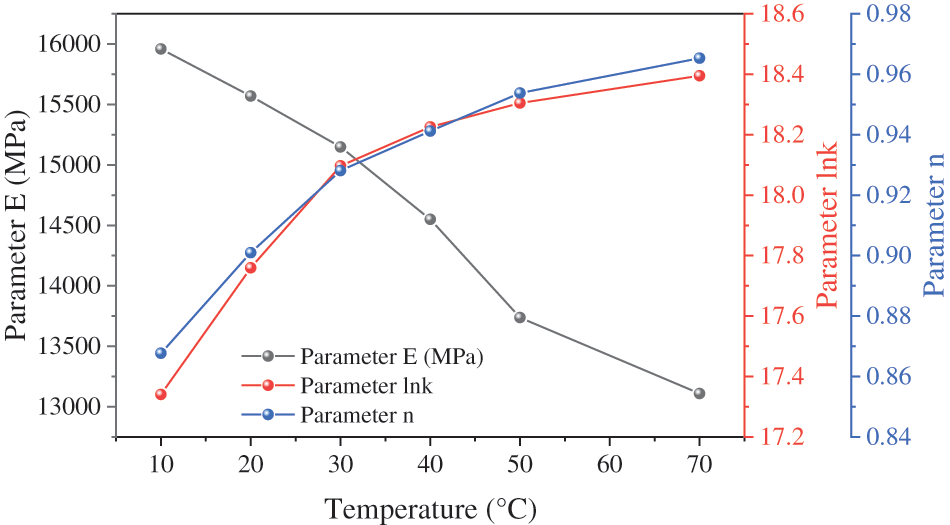
Figure 12: Relationship between model parameters and temperature
The stress–strain relationship of the specimen at different temperature levels is shown in Fig. 12. Based on these mean stress–strain curves, the fitting curves of the Ramberg-Osgood model at different temperatures can be obtained. Referring to the pseudo-elastic method [38], according to the relevant parameters (E, k, n) of the fitting results, the functional relationship (E(T), k(T), n(T)) between the model parameters and the temperature was established, and a further stress–strain prediction model considering temperature effects was developed.
5.1 Establishment Method of the Prediction Model
Based on the above discussion, the dependence between the elastic modulus and temperature can be described by a functional relationship. Due to the large value of k, to better display the relationship between k and temperature, lnk is taken to replace k. Linear and nonlinear function equation were used to relate the variation of three parameters with temperature, as shown in Eq. (12).
where ai, bi and ci (i = 1,…, 3) are the fitting coefficients and T stands for temperature,°C.
Eq. (12) was used to fit the parameters in Table 3, and the temperature-dependent fitting coefficients a, b and c are as follows:
Fig. 13 shows the fitting results related to temperature, where the line is the fitting curve. The linear and nonlinear function equation in Eq. (12) can describe the dependence of model parameters lnk, n, and E on temperature.
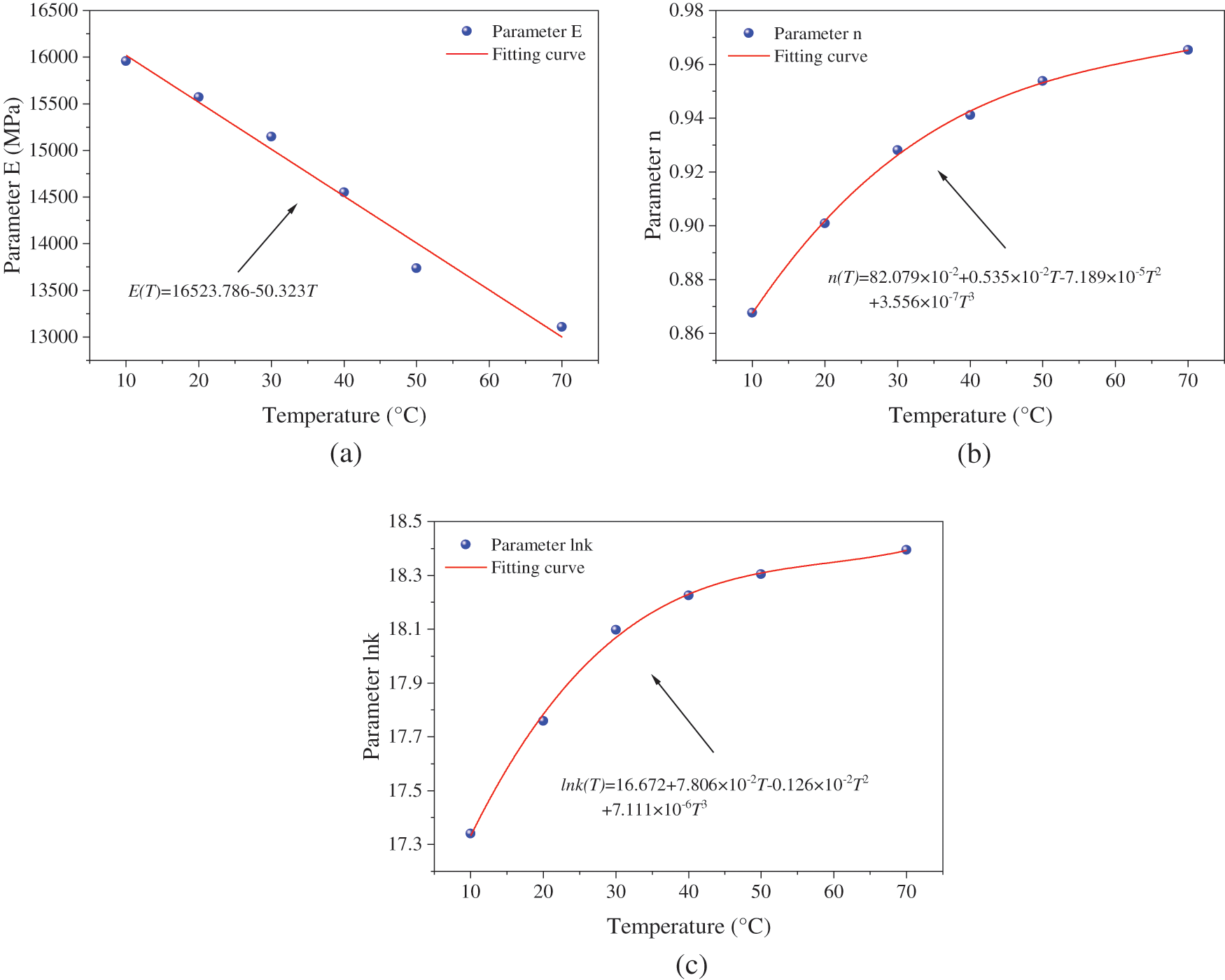
Figure 13: The function relationship between model parameters and temperature
By substituting Eq. (13) into Eq. (12) and the parameters in Eq. (12) into Eq. (11), the tensile stress–strain constitutive model considering the influence of temperature can be obtained:
Based on the above results, the stress–strain prediction model of recombinant bamboo tensile specimens under different temperature conditions was obtained as follows:
10°C temperature level:
20°C temperature level:
30°C temperature level:
40°C temperature level:
50°C temperature level:
70°C temperature level:
5.3 Validation of the Predictive Model
To verify the applicability of the prediction model, the calculation results of the prediction model at different temperatures were compared with the experimental data, as shown in Fig. 14. The results showed that the established model can describe the stress–strain relationship of the recombinant bamboo tensile specimens well, including the elastic stage in the early stage and the plastic stage in the middle and late stages of the stress–strain curve. The model can more accurately evaluate the stress–strain behaviour of recombinant bamboo under different loading levels.
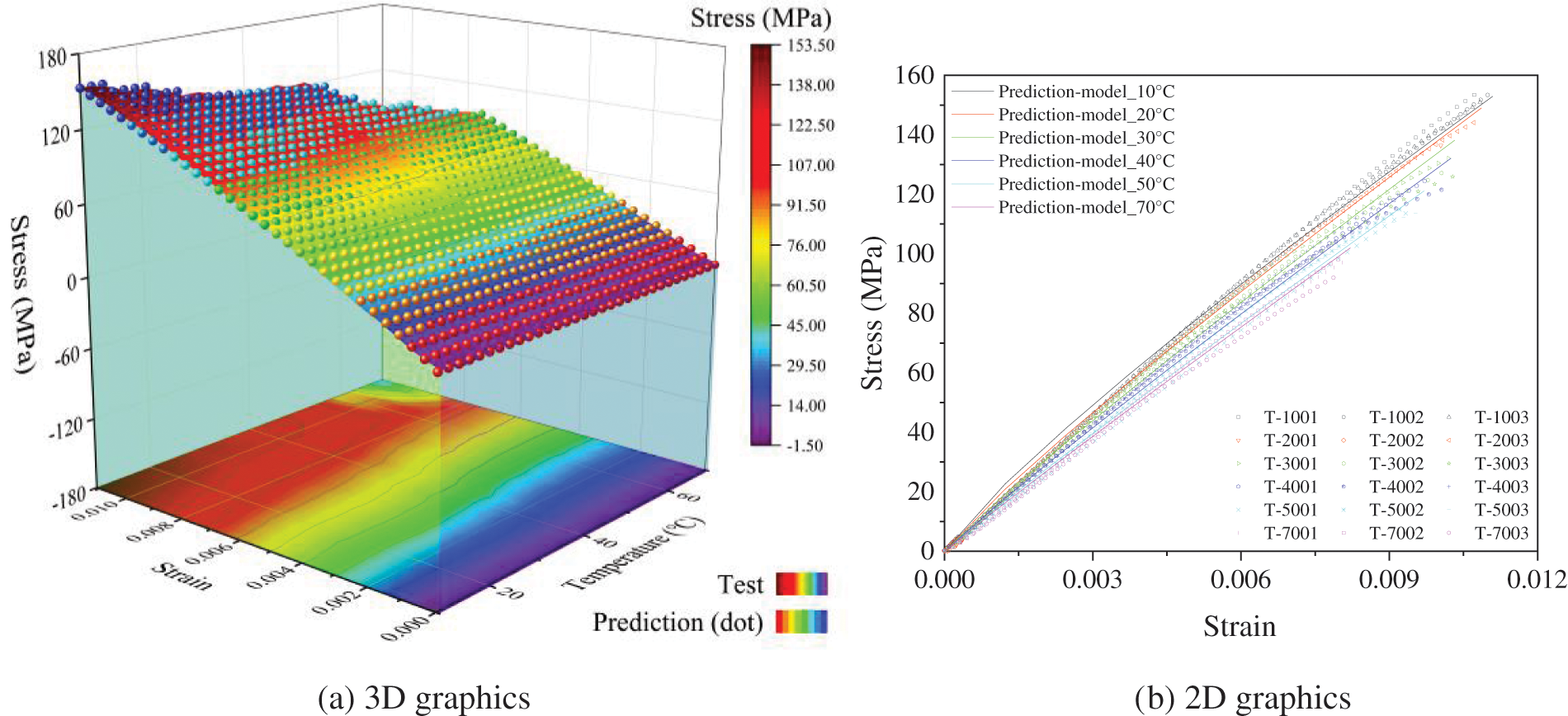
Figure 14: The predicted tensile strength
The tensile properties of recombinant bamboo were tested at different temperatures to investigate the failure mechanism and determine the failure mode of the recombinant bamboo tensile specimen. The effect of temperature on stress and strain was summarized, and the reduction factors of stress and strain were calculated. A prediction model for tensile strength considering temperature was established. The results are as follows:
(1) Under the action of continuous loading, with increasing ambient temperature, the typical failure modes of the recombinant bamboo specimen were fracture failure, tooth failure, and sawtooth failure. That is, with increasing temperature, its damage form intensifies.
(2) The ultimate tensile strength and ultimate strain of recombinant bamboo decreased as the temperature increased; the ultimate tensile stress decreased from 154.07 to 96.55 MPa, a decrease of 37.33%, and the ultimate strain decreased from 0.0109 to 0.0081, a decrease of 26.57%. Both the strength reduction factor (ησ,T) and the modulus reduction factor (ηE,T) decrease exponentially with increasing temperature.
(3) The fitting results of the Ramberg-Osgood model to the experimental data showed that the elastic modulus (E) decreases with increasing temperature, and the model correlation coefficient (K, n) increases with increasing temperature; therefore, the plasticity of the recombinant bamboo increases with increasing temperature.
(4) Based on the Ramberg-Osgood model, a tensile stress–strain prediction model considering the temperature level was established. The model can accurately evaluate the stress–strain relationship of recombinant bamboo under the condition of considering the effect of temperature.
This study mainly considered the effect of temperature on the tensile properties of recombinant bamboo and established a stress–strain prediction model considering the effect of temperature. However, many factors affect the basic mechanical properties of recombinant bamboos, such as humidity and long-term ageing. In addition, the coupling of multiple factors has not been discussed. Their effects on the mechanical properties of recombinant bamboo will be the focus of the next phase of research.
Funding Statement: The authors wish to express their gratitude to the National Natural Science Foundation of China (Nos. 51208262, 51778300), Key Research and Development Project of Jiangsu Province (No. BE2020703), Natural Science Foundation of Jiangsu Province (No. BK20191390), Six Talent Peaks Project of Jiangsu Province (JZ-017), and Qinglan Project of Jiangsu Province for financially supporting this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Wei, Y., Zhao, K., Hang, C., Chen, S., Ding, M. (2020). Experimental study on the creep behavior of recombinant bamboo. Journal of Renewable Materials, 8(3), 251–257. https://doi.org/10.32604/jrm.2020.08779 [Google Scholar] [CrossRef]
2. Chen, G., Wu, J., Jiang, H., Zhou, T., Li, X. et al. (2020). Evaluation of OSB webbed laminated bamboo lumber box-shaped joists with a circular web hole. Journal of Building Engineering, 29(5), 101129. https://doi.org/10.1016/j.jobe.2019.101129 [Google Scholar] [CrossRef]
3. Li, H., Wang, L., Wei, Y., Wang, B. J. (2022). Off-axis compressive behavior of cross-laminated bamboo and timber wall elements. Structures, 35(1), 452–468. https://doi.org/10.1016/j.istruc.2021.11.009 [Google Scholar] [CrossRef]
4. Zhang, J., Tong, K., Shan, Q., Li, Y. (2022). Examining mechanical behavior of steel-bamboo composite I-section column under long-term loading. Journal of Building Engineering, 45, 103583. https://doi.org/10.1016/j.jobe.2021.103583 [Google Scholar] [CrossRef]
5. Nkeuwa, W. N., Zhang, J., Semple, K. E., Chen, M., Xia, Y. et al. (2022). Bamboo-based composites: A review on fundamentals and processes of bamboo bonding. Composites Part B: Engineering, 235, 109776. https://doi.org/10.1016/j.compositesb.2022.109776 [Google Scholar] [CrossRef]
6. Nie, Y., Wei, Y., Zhao, K., Ding, M., Huang, L. (2022). Compressive performance of bamboo sheet twining tube-confined recycled aggregate concrete columns. Construction and Building Materials, 323, 126544. https://doi.org/10.1016/j.conbuildmat.2022.126544 [Google Scholar] [CrossRef]
7. Chen, S., Wei, Y., Zhao, K., Dong, F., Huang, L. (2022). Experimental investigation on the flexural behavior of laminated bamboo-timber I-beams. Journal of Building Engineering, 46, 103651. https://doi.org/10.1016/j.jobe.2021.103651 [Google Scholar] [CrossRef]
8. Luo, X., Wang, X., Ren, H., Zhang, S., Zhong, Y. (2022). Long-term mechanical properties of bamboo scrimber. Construction and Building Materials, 338, 127659. https://doi.org/10.1016/j.conbuildmat.2022.127659 [Google Scholar] [CrossRef]
9. Akinbade, Y., Harries, K. A. (2021). Is the rule of mixture appropriate for assessing bamboo material properties? Construction and Building Materials, 267, 120955. https://doi.org/10.1016/j.conbuildmat.2020.120955 [Google Scholar] [CrossRef]
10. Wei, Y., Chen, S., Tang, S., Zheng, K., Wang, J. (2022). Mechanical behavior of bamboo composite tubes under axial compression. Construction and Building Materials, 339, 127681. https://doi.org/10.1016/j.conbuildmat.2022.127681 [Google Scholar] [CrossRef]
11. Tian, L. M., Kou, Y. F., Hao, J. P. (2019). Axial compressive behaviour of sprayed composite mortar–original bamboo composite columns. Construction and Building Materials, 215, 726–736. https://doi.org/10.1016/j.conbuildmat.2019.04.234 [Google Scholar] [CrossRef]
12. Chung, K. F., Yu, W. (2002). Mechanical properties of structural bamboo for bamboo scaffoldings. Engineering Structures, 24(4), 429–442. https://doi.org/10.1016/S0141-0296(01)00110-9 [Google Scholar] [CrossRef]
13. Obataya, E., Kitin, P., Yamauchi, H. (2007). Bending characteristics of bamboo (Phyllostachys pubescens) with respect to its fiber–foam composite structure. Wood Science and Technology, 41(5), 385–400. https://doi.org/10.1007/s00226-007-0127-8 [Google Scholar] [CrossRef]
14. Lo, T. Y., Cui, H., Tang, P., Leung, H. (2008). Strength analysis of bamboo by microscopic investigation of bamboo fibre. Construction and Building Materials, 22(7), 1532–1535. https://doi.org/10.1016/j.conbuildmat.2007.03.031 [Google Scholar] [CrossRef]
15. Kou, Y. F., Tian, L. M., Jin, B. B. (2022). Axial compressive behavior of bamboo slices twining tube-confined concrete. European Journal of Wood and Wood Products, 80(1), 115–129. https://doi.org/10.1007/s00107-021-01737-8 [Google Scholar] [CrossRef]
16. Zhang, X., Li, J., Yu, Y., Wang, H. (2018). Investigating the water vapor sorption behavior of bamboo with two sorption models. Journal of Materials Science, 53(11), 8241–8249. https://doi.org/10.1007/s10853-018-2166-y [Google Scholar] [CrossRef]
17. Yuan, J., Fang, C., Chen, Q., Fei, B. (2021). Observing bamboo dimensional change caused by humidity. Construction and Building Materials, 309, 124988. https://doi.org/10.1016/j.conbuildmat.2021.124988 [Google Scholar] [CrossRef]
18. Zou, Z., Wu, J., Zhang, X. (2019). Influence of moisture content on mechanical properties of bamboo scrimber. Journal of Materials in Civil Engineering, 31(7), 06019004. https://doi.org/10.1061/(ASCE)MT.1943-5533.0002746 [Google Scholar] [CrossRef]
19. Askarinejad, S., Kotowski, P., Shalchy, F., Rahbar, N. (2015). Effects of humidity on shear behavior of bamboo. Theoretical and Applied Mechanics Letters, 5(6), 236–243. https://doi.org/10.1016/j.taml.2015.11.007 [Google Scholar] [CrossRef]
20. Wei, Y., Tang, S., Ji, X., Zhao, K., Li, G. (2020). Stress-strain behavior and model of bamboo scrimber under cyclic axial compression. Engineering Structures, 209, 110279. https://doi.org/10.1016/j.engstruct.2020.110279 [Google Scholar] [CrossRef]
21. Hou, R., Liu, Y., Li, X. (2013). Effects of heat treatment on physical-mechanical properties of reconstituted bamboo lumber (RBL). Journal of Central South University of Technology, 33(2), 101–104. https://doi.org/10.14067/j.cnki.1673-923x.2013.02.023 [Google Scholar] [CrossRef]
22. Brito, F. M. S., Paes, J. B., da Silva Oliveira, J. T., Arantes, M. D. C., Vidaurre, G. B. et al. (2018). Physico-mechanical characterization of heat-treated glued laminated bamboo. Construction and Building Materials, 190, 719–727. https://doi.org/10.1016/j.conbuildmat.2018.09.057 [Google Scholar] [CrossRef]
23. Wang, R., Li, Z., Zhang, Z., Yue, K. (2022). Influence of temperature on the mechanical properties of engineered bamboo laminate. Construction and Building Materials, 341, 127825. https://doi.org/10.1016/j.conbuildmat.2022.127825 [Google Scholar] [CrossRef]
24. Xu, M., Cui, Z., Tu, L., Xia, Q., Chen, Z. (2019). The effect of elevated temperatures on the mechanical properties of laminated bamboo. Construction and Building Materials, 226, 32–43. https://doi.org/10.1016/j.conbuildmat.2019.07.274 [Google Scholar] [CrossRef]
25. Xu, M., Cui, Z., Chen, Z., Xiang, J. (2017). Experimental study on compressive and tensile properties of a bamboo scrimber at elevated temperatures. Construction and Building Materials, 151, 732–741. https://doi.org/10.1016/j.conbuildmat.2017.06.128 [Google Scholar] [CrossRef]
26. Cui, Z., Wang, F., Xu, M., Chen, Z. (2017). Experimental study on embedding strength of bamboo scrimber parallel to grain at high temperatures. Journal of Southeast University (Natural Science Edition), 47(6), 1174–1179. https://doi.org/10.3969/j.issn.1001-0505.2017.06.015 [Google Scholar] [CrossRef]
27. Cui, Z., Xu, M., Tu, L., Chen, Z., Hui, B. (2020). Determination of dowel-bearing strength of laminated bamboo at elevated temperatures. Journal of Building Engineering, 30, 101258. https://doi.org/10.1016/j.jobe.2020.101258 [Google Scholar] [CrossRef]
28. Wang, P., Wang, Y., Yang, S., Zhang, F., Li, D. et al. (2018). Effect of age on the fiber morphological characteristics of dendrocalamus farinosus. Journal of Anhui Agricultural University, 45(5), 853–860. https://doi.org/10.13610/j.cnki.1672-352x.20181025.001 [Google Scholar] [CrossRef]
29. Wei, Y., Chen, S., Tang, S., Peng, D., Zhao, K. (2022). Mechanical response of timber beams strengthened with variable amounts of CFRP and bamboo scrimber layers. Journal of Composites for Construction, 26(4), 04022038. https://doi.org/10.1016/j.conbuildmat.2022.127681 [Google Scholar] [CrossRef]
30. Lv, Q. F., Ding, Y., Liu, Y. (2019). Study of the bond behaviour between basalt fibre-reinforced polymer bar/sheet and bamboo engineering materials. Advances in Structural Engineering, 22, 3121–3133. https://doi.org/10.1177/1369433219858725 [Google Scholar] [CrossRef]
31. GB/T (2009). General requirements for physical and mechanical tests of wood. GB/T 1928-2009. Beijing, China: Standard Press of China. [Google Scholar]
32. ASTM (2009). Standard test methods for small clear specimens of timber. ASTM D143-09. West Conshohocken, USA: American Society for Testing Materials. [Google Scholar]
33. GB/T (2009). Method of testing in tensile strength parallel to grain of wood. GB/T 1938-2009. Beijing, China: Standard Press of China. [Google Scholar]
34. Kelly, A., Davies, G. (2013). The principles of the fibre reinforcement of metals. Metallurgical Reviews, 10(1), 1–77. https://doi.org/10.1179/mtlr.1965.10.1.1 [Google Scholar] [CrossRef]
35. Zhu, Y., Zhou, B., He, G., Zheng, Z. (1989). A statistical theory of composite materials strength. Journal of Composite Materials, 23(3), 280–287. https://doi.org/10.1177/002199838902300305 [Google Scholar] [CrossRef]
36. Shao, B., Chen, B., Cao, Y., Fang, Y., Song, Y. et al. (2021). Nonlinear tensile behavior of cotton fabric reinforced polypropylene composites. Journal of Applied Polymer Science, 138(5), 49780. https://doi.org/10.1002/a49780 [Google Scholar] [CrossRef]
37. Duan, X., Yuan, H., Tang, W., He, J., Guan, X. (2021). A general temperature-dependent stress–strain constitutive model for polymer-bonded composite materials. Polymers, 13(9), 1393. https://doi.org/10.3390/polym13091393 [Google Scholar] [PubMed] [CrossRef]
38. Christensen, R. M. (2012). Mechanics of composite materials. Mineola, New York: Courier Corporation. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools