 Open Access
Open Access
ARTICLE
A Combined Denoising Method of Adaptive VMD and Wavelet Threshold for Gear Health Monitoring
School of Mechanical Engineering, Hebei University of Science and Technology, Shijiazhuang, 050018, China
* Corresponding Author: Guangfei Jia. Email:
(This article belongs to the Special Issue: Sensing Data Based Structural Health Monitoring in Engineering)
Structural Durability & Health Monitoring 2025, 19(4), 1057-1072. https://doi.org/10.32604/sdhm.2025.061805
Received 03 December 2024; Accepted 13 February 2025; Issue published 30 June 2025
Abstract
Considering the noise problem of the acquisition signals from mechanical transmission systems, a novel denoising method is proposed that combines Variational Mode Decomposition (VMD) with wavelet thresholding. The key innovation of this method lies in the optimization of VMD parameters K and using the improved Horned Lizard Optimization Algorithm (IHLOA). An inertia weight parameter is introduced into the random walk strategy of HLOA, and the related formula is improved. The acquisition signal can be adaptively decomposed into some Intrinsic Mode Functions (IMFs), and the high-noise IMFs are identified based on a correlation coefficient-variance method. Further noise reduction is achieved using wavelet thresholding. The proposed method is validated using simulated signals and experimental signals, and simulation results indicate that the proposed method surpasses original VMD, Empirical Mode Decomposition (EMD), and wavelet thresholding in terms of Signal-to-Noise Ratio (SNR) and Root Mean Square Error (RMSE), and experimental results indicate that the proposed method can effectively remove noise in terms of three evaluation metrics. Furthermore, compared with Feature Mode Decomposition (FMD) and Multichannel Singular Spectrum Analysis (MSSA), this method has a better envelope spectrum. This method not only provides a solution for noise reduction in signal processing but also holds significant potential for applications in structural health monitoring and fault diagnosis.Graphic Abstract
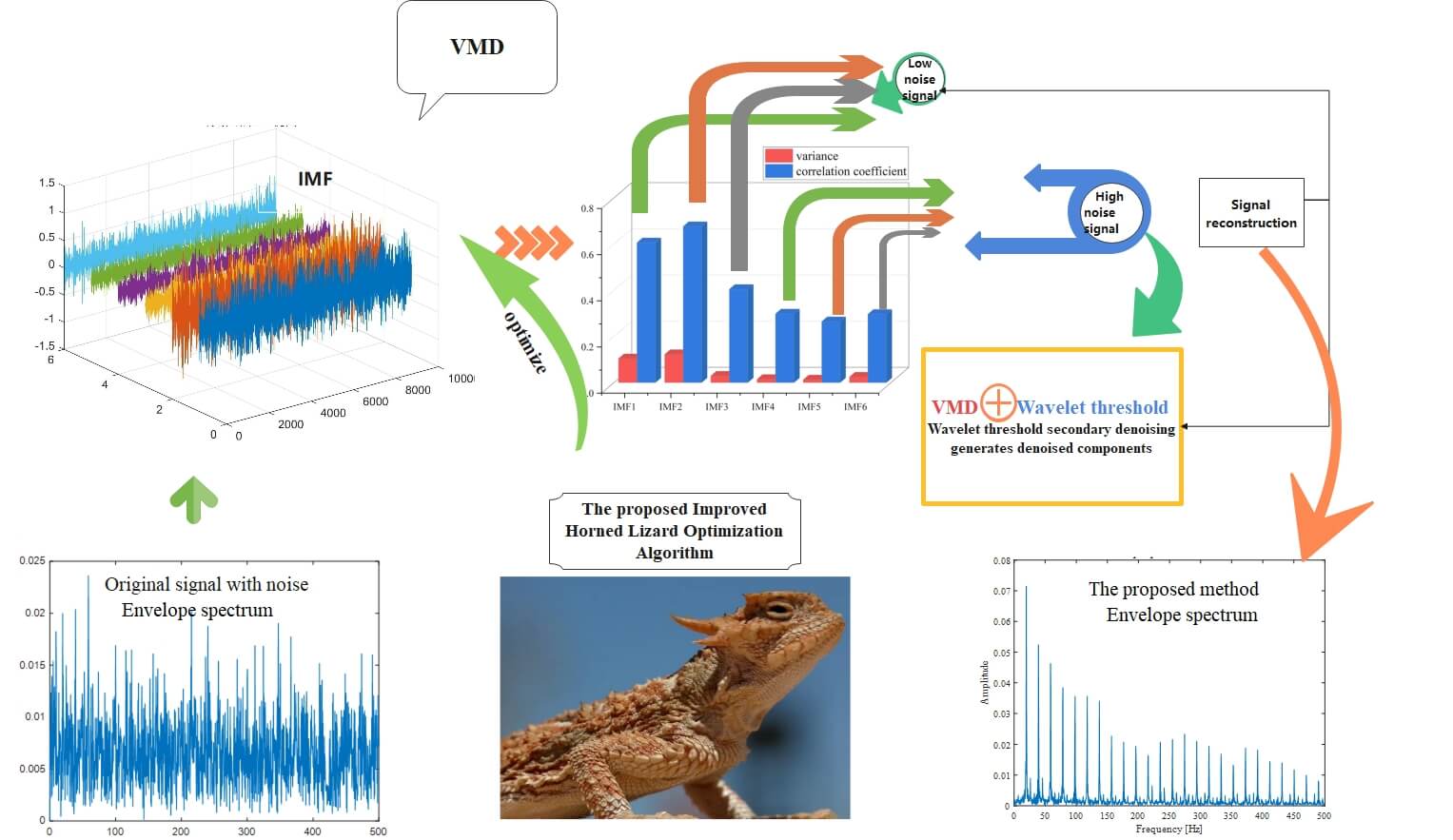
Keywords
In the diagnosis of mechanical system faults, vibration monitoring is a commonly used technique [1,2]. However, the complicated vibration signals generated by equipment during prolonged operation are often contaminated by noise interference, which may come from sources such as the external environment, sensor errors, and other factors. These noises can obscure critical information in the signals, thereby compromising the accuracy of fault diagnosis. To enhance diagnostic accuracy, researchers have proposed various denoising methods [3,4], among which signal decomposition techniques, such as EMD [5,6] and VMD [7,8], are widely applied. Currently, research on health monitoring and fault diagnosis of mechanical systems focuses on improving signal processing and feature extraction methods. Toffghi Niaki et al. [9] proposed a novel approach for early gearbox fault monitoring by combining VMD (Variational Mode Decomposition) and TSA (Time Synchronous Averaging) techniques. Matania et al. [10] introduced a cross-machine health monitoring method to address data scarcity issues and target domain adaptation. Wang et al. [11] analyzed vibration signals using the AR (Auto-Regressive) model to capture gear fault feature patterns. These studies have advanced the development of mechanical fault diagnosis technology, achieving significant progress particularly in signal processing and cross-domain applications. Wang et al. [12] developed gear signal decomposition techniques, providing new methods for analyzing complex vibration signals. The aforementioned methods have made substantial progress in the application of signal processing. Nevertheless, traditional noise reduction methods often struggle to handle complicated vibration signals, necessitating the development of more advanced techniques.
The EMD method has inherent advantages in analyzing non-stationary and nonlinear signals [13], and it can also be used for signal denoising. However, EMD is prone to problems such as mode aliasing and the endpoint effects. With the progress of research, the EEMD method [14,15] was introduced, which adds white noise to mitigate these issues. Nonetheless, the white noise in EEMD cannot entirely eliminate the problems. The CEEMD method [16] was proposed to further reduce the impact of white noise. Even with these improvements, CEEMD still encounters residual noise in the signal reconstruction process. To solve this problem, the CEEMDAN method [17] was proposed, incorporating adaptive noise to optimize the decomposition process. Nevertheless, EMD and its derivatives continue to face challenges such as mode aliasing and residual noise in the analysis of complex signals.
Based on wavelet analysis, Gilles proposed the Empirical Wavelet Transform (EWT) [18], which is achieved by segmenting the Fourier frequency. However, this segmentation can result in the splitting of characteristic signals into different modes [19]. To solve these problems, VMD [20,21] was introduced, which utilized classical Wiener filtering, Hilbert transform, and frequency mixing for adaptive signal decomposition. Then, the decomposition results can be denoised through filtering or reconstruction. Usually, the parameters K and
Due to the ability of VMD to preserve functional signal components for reconstruction, it effectively removes the noise in the original signal. However, some details may be lost during this process. To further improve the decomposition quality of vibration signals, this paper proposes the use of wavelet thresholding for secondary denoising of IMFs that contain high noise level after adaptive VMD decomposition. Specifically, wavelet thresholding is applied to process these high-noise IMFs, effectively suppressing the noise while preserving the main features of the signal. This secondary denoising allows for more accurate extraction of meaningful information from the signal, enhancing the overall effectiveness of vibration signal processing.
2 IHLOA-VMD-Wavelet Thresholding Combined Denoising Method
The combined denoising method consists of two steps. The first step involves decomposing the original vibration signal using VMD. The second step applies wavelet thresholding to denoise the high-noise components. Finally, the original signal with reduced noise content is reconstructed by combining the secondary denoised components, resulting in a new signal.
VMD improves signal denoising by imposing constraints on the center frequency and bandwidth of each mode. Additionally, VMD demonstrates high computational efficiency when processing large-scale datasets. However, the modal number K and penalty parameter
The main steps of the combined denoising method are shown in Fig. 1:
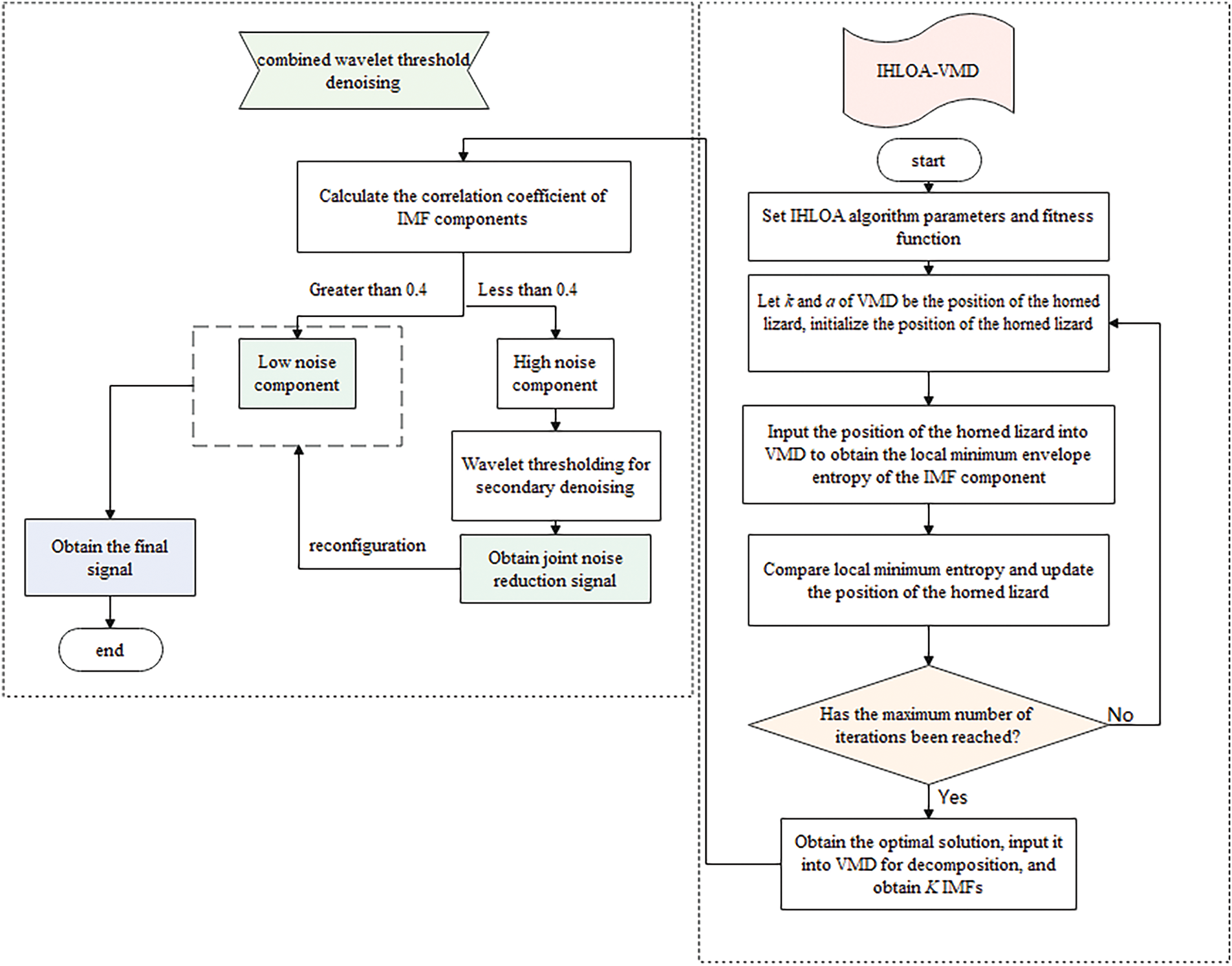
Figure 1: IHLOA-VMD wavelet threshold joint denoising method
(1) Input the vibration signal, set the HLOA population size to 30, and the number of iterations to 10. Use envelope entropy as the fitness function.
(2) Set the range of the number of decomposition modes K to
(3) Input the positions of the horned lizards into VMD to obtain the local minimum of the envelope entropy for the decomposed IMF components.
(4) Compare the envelope entropy values and update the horned lizard positions accordingly.
(5) Check if the stopping condition is met. If not, continue the optimization process and output the optimal parameter combination.
(6) The IHLOA algorithm optimizes the VMD, which then decomposes the signal into K IMFs.
(7) Screen high- and low-noise components based on the correlation coefficient-variance.
(8) After reconstructing the high-noise components, apply wavelet thresholding for secondary denoising, and combine the processed high-noise components with the low-noise components to obtain a combined denoised signal.
3 The Improved Horned Lizard Optimization Algorithm
3.1 Theoretical Basis for Improved Horned Lizard Optimization Algorithm
However, in the HLOA, as the number of iterations increases, the algorithm’s convergence speed accelerates, but it struggles to escape from local optimal solutions. To address this issue, the HLOA is improved by introducing an inertia weight parameter
The inertia weight parameter
In the equation: t—The current iteration number.
Original Position Update Formula:
Improved Position Update Formula:
3.2 Performance Evaluation of Improved Algorithm
The performance of the IHLOA is validated using essential standard test functions, as shown in Fig. 2. It can be observed that the convergence speed of the IHLOA is faster than that of other algorithms. Its fitness value decreases exponentially, indicating a strong global search capability. The IHLOA can quickly escape local optima and demonstrates good local search ability. The improved HLOA enhances both global and local search capabilities, resulting in better convergence speed and search accuracy.
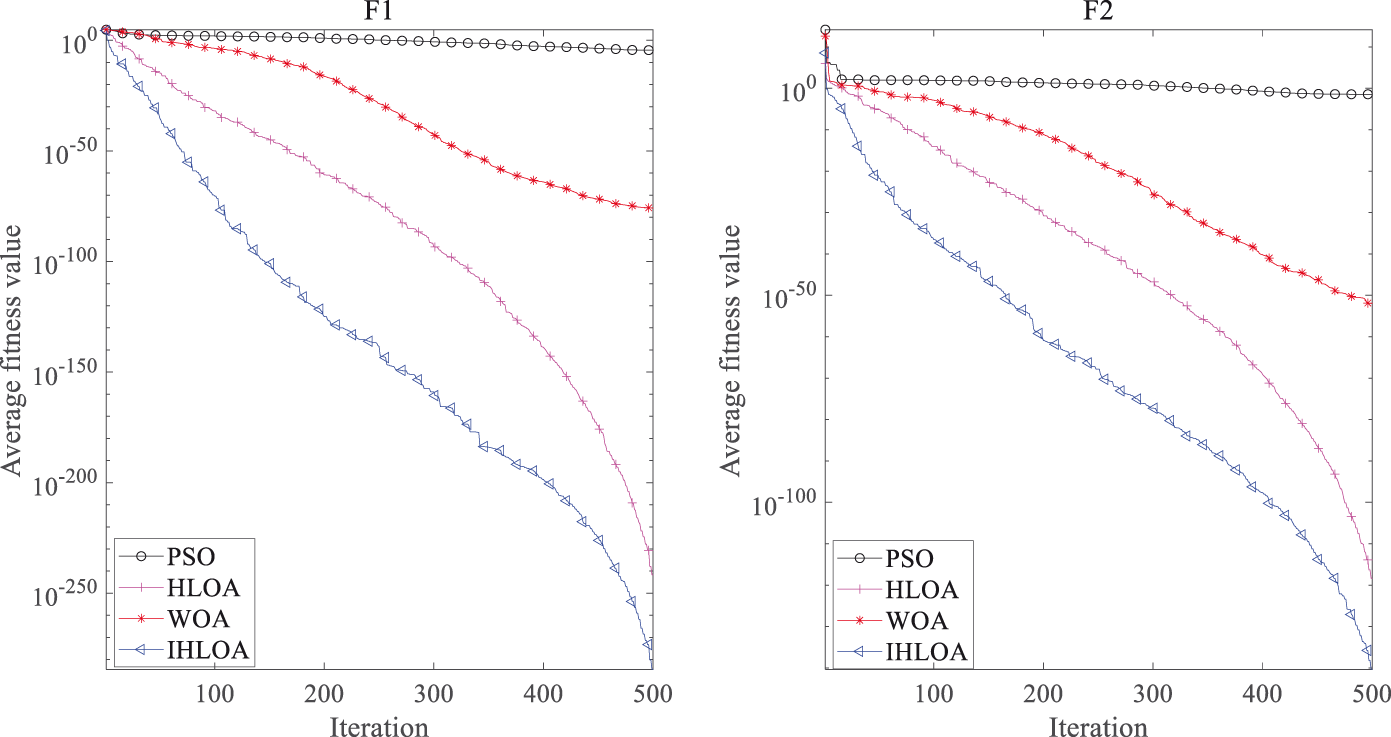
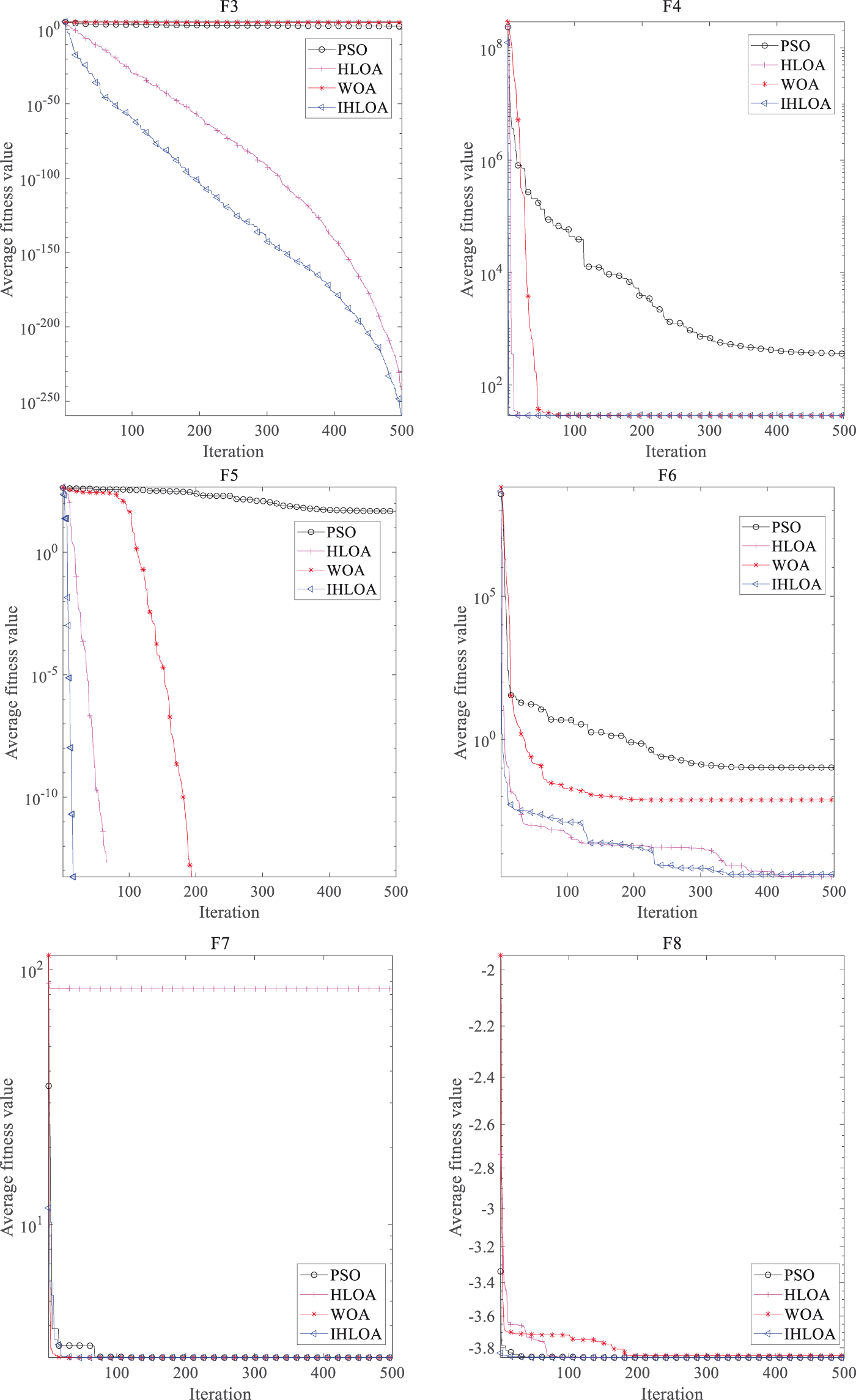
Figure 2: Convergence curves of different algorithms from F1 to F8
4.1 Case 1: Simulated Signal with Noise
In order to verify the denoising effect of IHLOA-VMD-wavelet thresholding secondary denoising method, the simulated signal is used, as follows:
Among them, nt is random Gaussian white noise with a standard deviation of 0.2 added; The sampling frequency is
From Fig. 3, it is evident that the denoising method combining VMD and wavelet thresholding closely matches the original signal plot, indicating that a significant amount of noise has been eliminated. However, when using only wavelet denoising, the time-domain plot still contains residual noise.
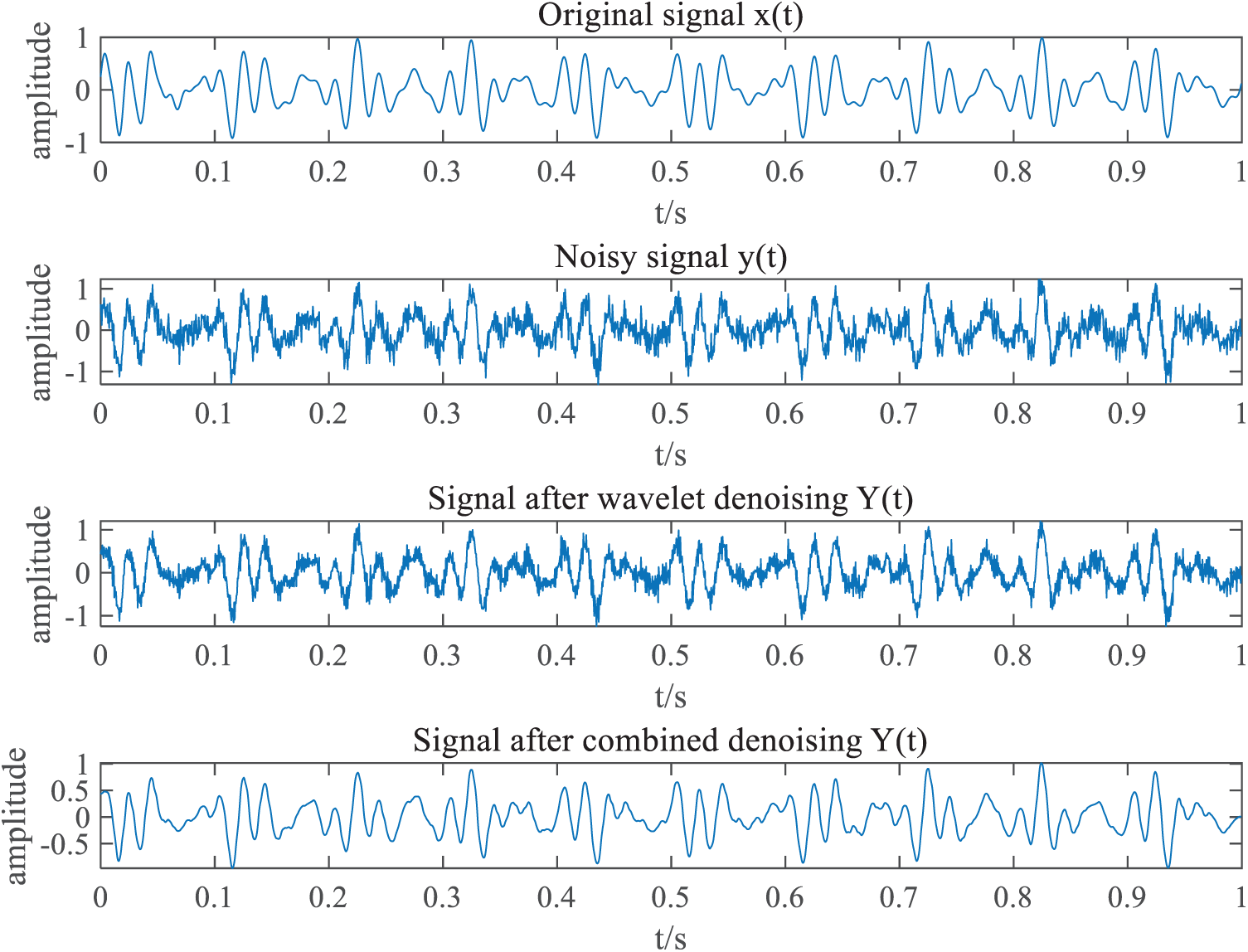
Figure 3: Time-domain diagram of simulated signal before and after denoising
To further verify the denoising effects, the following methods were applied to process the signal: VMD denoising, wavelet thresholding denoising, EMD denoising, CEEMDAN-wavelet thresholding denoising, and IHLOA-VMD-wavelet thresholding Combined denoising. The root mean squared error (RMSE) and signal-to-noise ratio (SNR) for each of the five denoising methods were calculated using the respective formulas.
Table 1 shows that the method proposed in this paper achieves the highest SNR and the smallest RMSE. A higher SNR indicates that more noise has been removed, resulting in a better denoising effect. The mean squared error measures the difference between the original signal and the denoised signal; a smaller mean squared error indicates that the denoised signal is closer to the original signal. Therefore, it can be concluded that the proposed method demonstrates superior denoising performance, making it both more effective and efficient.

4.2 Case 2: Experimental Verification of Helical Gears
The gear data is sourced from the open-source dataset provided by Zamanian et al. [27–29]. Fig. 4 shows the gearbox test bench, which is designed to simulate and collect vibration signals from gears with different fault types, providing a solid foundation for subsequent model validation and performance evaluation. In the experiment, vibration signals were collected under a

Figure 4: Gearbox test stand
The WOA, HLOA, and IHLOA algorithms were employed to search for the optimal parameters of VMD, with the minimum envelope entropy serving as the fitness function. Fig. 5 illustrates the variation of the function values. From the figure, it can be observed that IHLOA-VMD converges to the optimal solution within the third iteration. Compared to the WOA and HLOA algorithms, IHLOA shows superior search capability, faster convergence, and can efficiently identify the optimal VMD parameters. It has been proven that the improved HLOA effectively avoids getting trapped in local optima, thereby enhancing the algorithm’s overall performance.
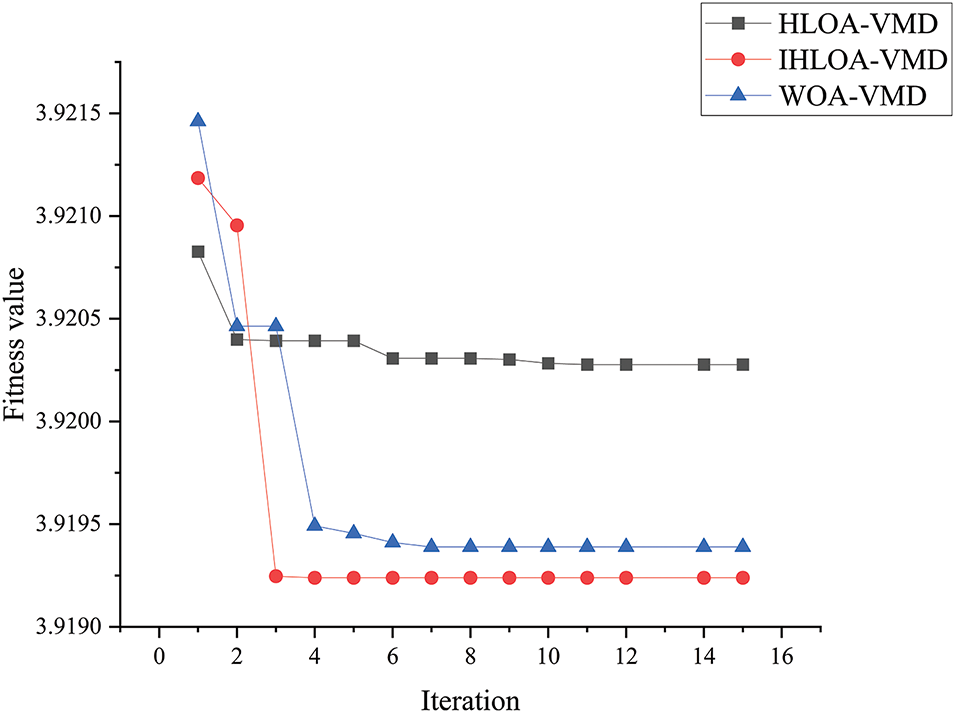
Figure 5: Variation of fitness function values for the fault signal of a helical gear with missing teeth
To verify the effectiveness of the proposed method, the correlation coefficient-variance of the six IMFs components decomposed by IHLOA-VMD were calculated, and the results are shown in Fig. 6. When the correlation coefficient-variance is very low, the explanatory power of the overall data is limited, and it may predominantly represent noise, failing to reflect the essential characteristics of the signal. Therefore, the components are classified into low-noise and high-noise components based on the correlation coefficient-variance. The low-noise component refers to the relatively pure part of the signal with minimal noise or interference, which closely resembles the original signal. In contrast, the high-noise component contains significant noise and interference, leading to poor performance after VMD processing. Due to the substantial impact of noise, the quality of this part of the signal is compromised. Since the high-noise component still contains useful information, wavelet thresholding is applied for secondary denoising to mitigate its influence.
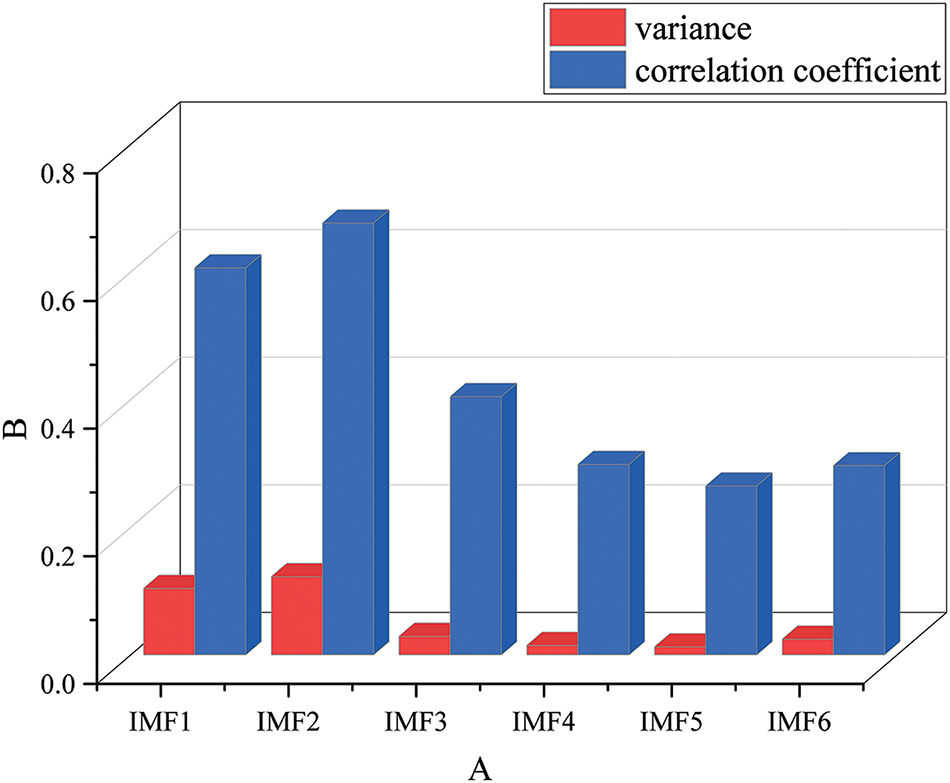
Figure 6: Correlation coefficients of various IMF vectors
By selecting IMF components with relatively low correlation coefficient-variance as high-noise components, high-variance modes typically represent the effective parts of the signal. In contrast, low-variance modes often contain noise or irrelevant information. Variance analysis helps in understanding the distribution of signal components and facilitates the separation of noisy signals from effective ones for reconstruction. Wavelet thresholding is then applied for secondary denoising, after which the denoised IMF components are reconstructed from the low-noise signal to produce the final denoised signal.
Since noise-free signals are unattainable, using SNR and root mean square error RMSE as evaluation indicators poses challenges. Therefore, Root of Variance Ratio (RVR) is introduced as a smoothness indicator, primarily used to assess the smoothness of the denoised signal. The closer its value is to 0, the better the smoothness, indicating more effective denoising. The Signal Energy Ratio (SER) is employed to measure the change in signal energy before and after denoising. A higher SER value generally reflects better preservation of the signal’s main energy and effective suppression of noise components. Additionally, the Noise Mode (NM) index is used to evaluate changes in signal energy; a larger NM value indicates better preservation of the signal’s effective components during the denoising process.
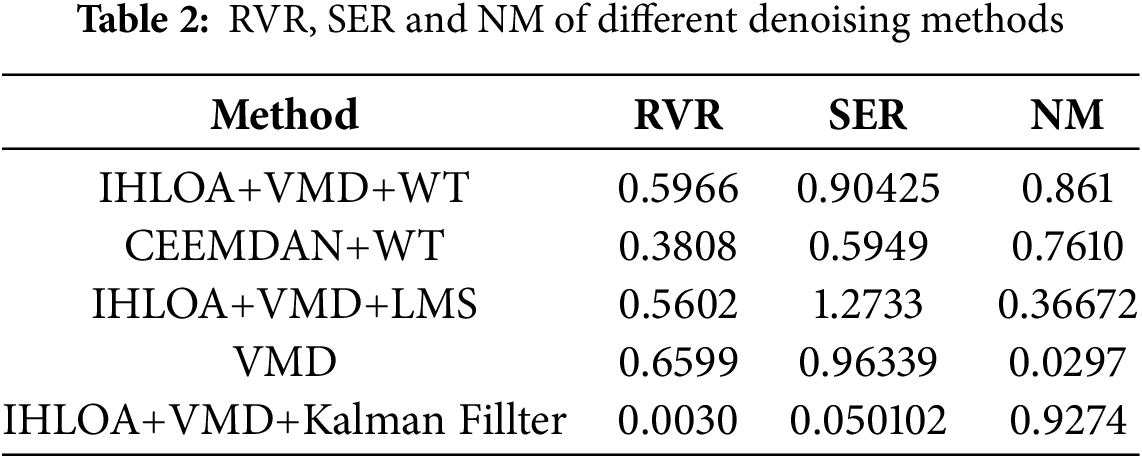
Table 2 shows a performance comparison of different methods based on three indicators: RVR, SER, and NM. The method proposed in this paper demonstrates significant advantages in overall performance: the RVR is 0.5966, which, although not the lowest, strikes a good balance; the SER is 0.90425, second only to VMD, and the NM is as high as 0.861, indicating a favorable balance between accuracy and denoising effect. In contrast, while VMD performs well on SER, its NM value is the lowest at only 0.0297, suggesting insufficient stability and overall performance. Therefore, the method proposed in this paper offers better noise reduction and broader applicability.
4.3 Case 3: Experimental Verification of Bevel Gear
To further validate the noise reduction method proposed in this paper for practical applications, using the gear dataset provided by HUST [30]. This dataset provides useful resources for research in gear fault diagnosis. Specifically, Fig. 7 illustrates the gearbox test bench at HUST. The design of this test bench allows for the simulation of various types of gear faults and the collection of their vibration signals, providing a solid foundation for subsequent experimental validation.

Figure 7: Gearbox test bench at HUST
The sampling frequency of the experiment is
When analyzing the IMF components processed by IHLOA-VMD, the correlation coefficient-variance of each component was first calculated, and the results were summarized in Fig. 8. IMF components with lower correlation coefficient-variance values were selected and reconstructed to form a new signal. Wavelet thresholding was then applied to this new signal, and the processed components were combined with those having higher correlation coefficient-variance values for final signal reconstruction, resulting in the denoised signal.
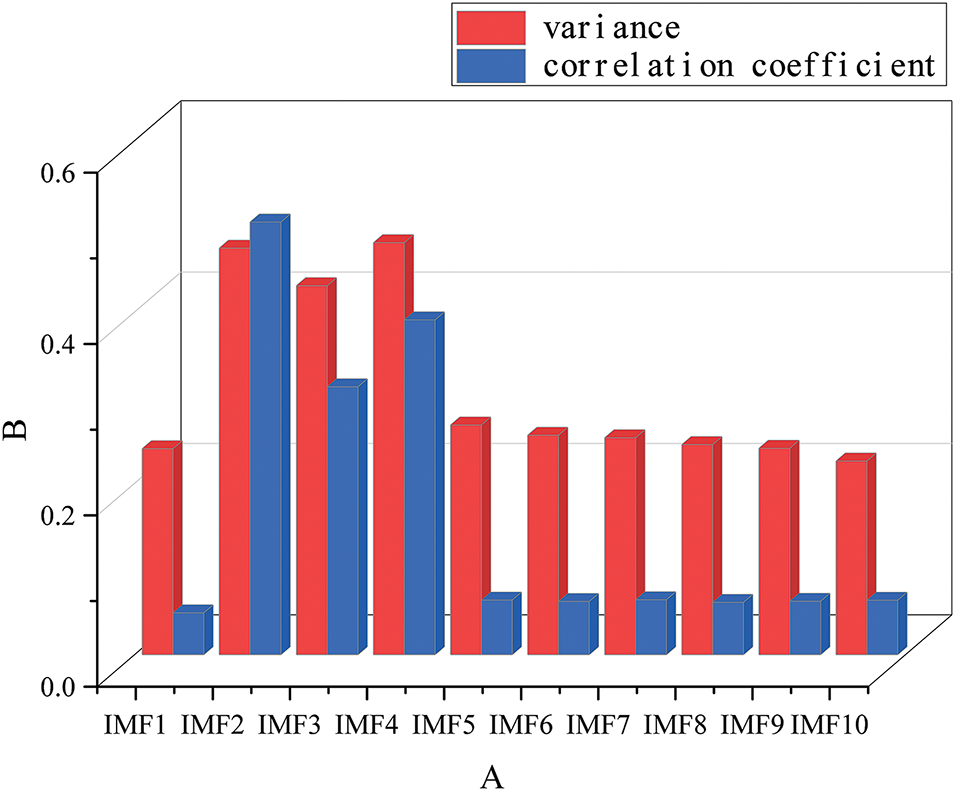
Figure 8: Correlation coefficients of various IMF vectors
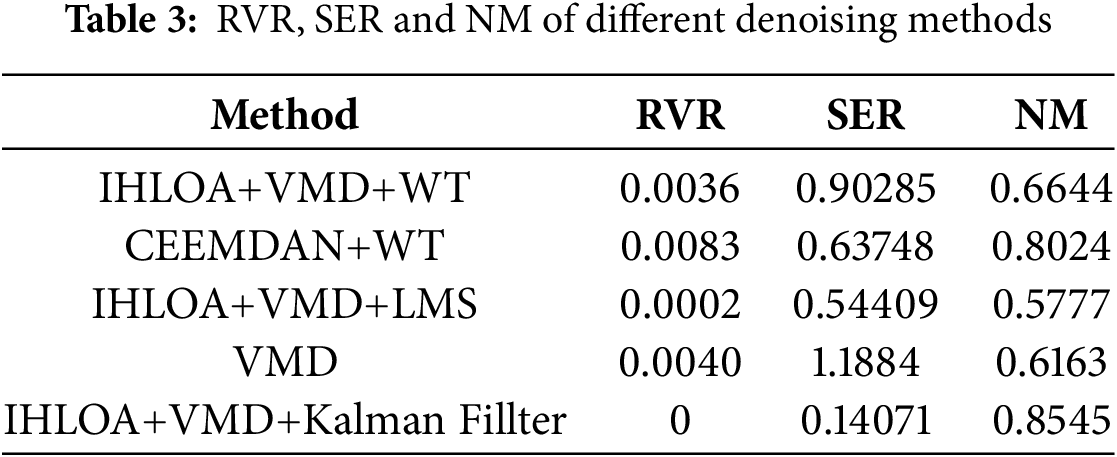
Subsequently, the method proposed in this paper demonstrates strong performance by comparing the performance of different methods based on these evaluation indicators, particularly the data presented in the Table 3. Its RVR is only 0.0036, which is close to the minimum value, indicating extremely low deviation in signal recovery. The SER is 0.90285, the second-highest value, reflecting a good signal-to-noise ratio. Additionally, the NM value is 0.6644, balancing both stability and denoising effectiveness. In contrast, although VMD achieved the highest SER value of 1.1884, its RVR and NM performance were poor, indicating a lack of overall balance. Therefore, the method proposed in this paper offers comprehensive advantages across multiple indicators, with significant improvements in noise suppression and signal preservation.
To verify the universality of this method under different fault conditions, the signal of a broken tooth gear was used, and experimental verification was conducted following the same methodology. The PSO, WOA, HLOA, and IHLOA algorithms were employed to search for the optimal parameters of VMD, using the minimum envelope entropy as the fitness function. The function values are shown in the Fig. 9. It can be observed from the figure that IHLOA-VMD finds the optimal solution the fastest. Compared to WOA, HLOA, and PSO algorithms, it exhibits stronger search capability and faster convergence speed and can efficiently identify the optimal parameters of VMD.
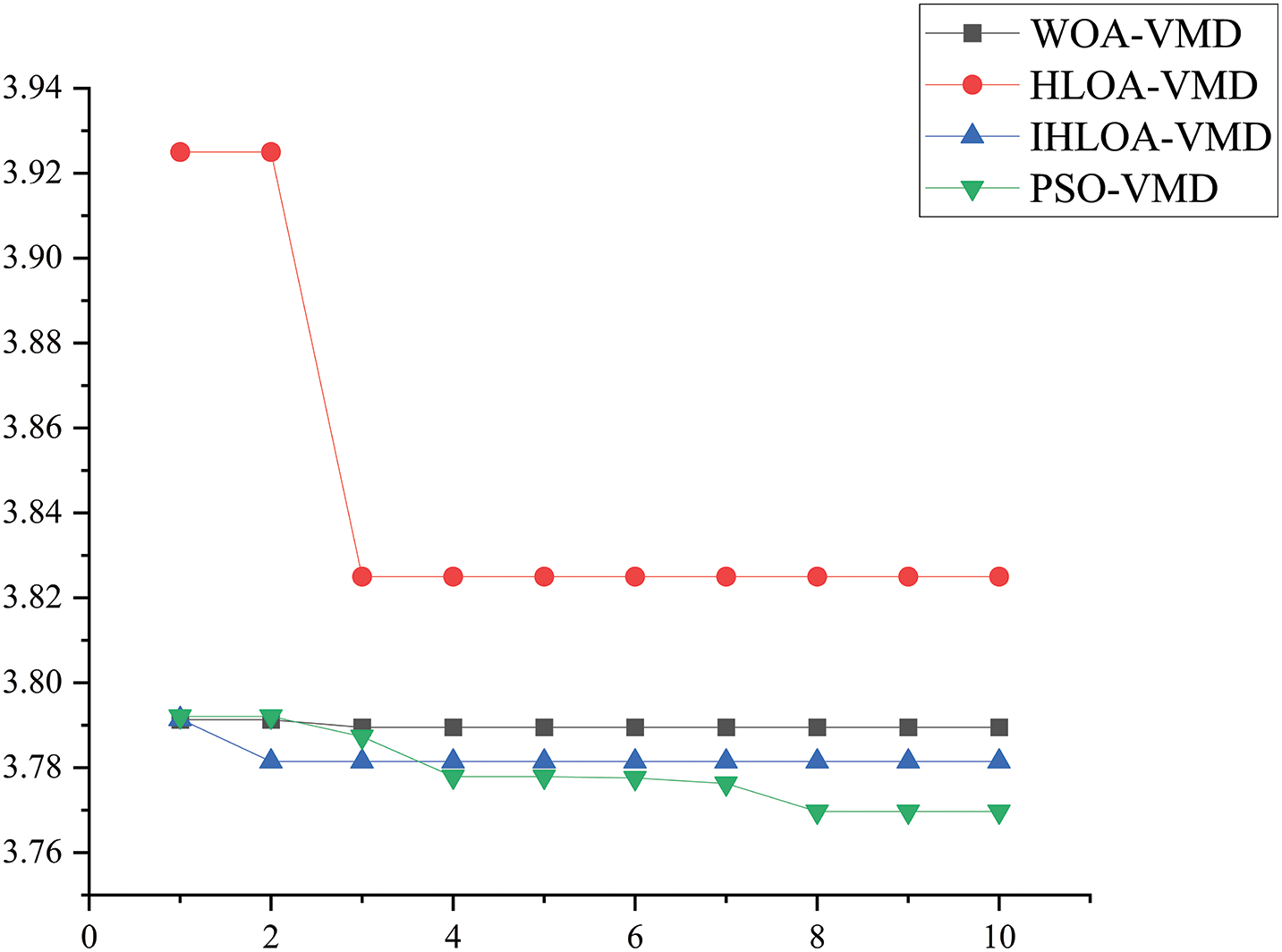
Figure 9: Changes in the fitness function value of the fault signal of a broken gear
The de-noised broken tooth signal obtained using the method proposed in this paper was compared with the de-noising effects of other methods. Verification was conducted using the three aforementioned indicators, and the results are shown in the Fig. 10: the symbol A represents IHLOA+VMD+Wavelet Threshold, the symbol B represents IHLOA+VMD+LMS, the symbol C represents IHLOA+VMD+Kalman Filter, and the symbol D represents CEEMDAN+Wavelet Threshold. Fig. 10 shows that the proposed method in this paper demonstrates superior performance in signal processing and noise reduction. In particular, it exhibits significant advantages regarding SER and NM, making it highly suitable for complex signal decomposition and noise suppression tasks.
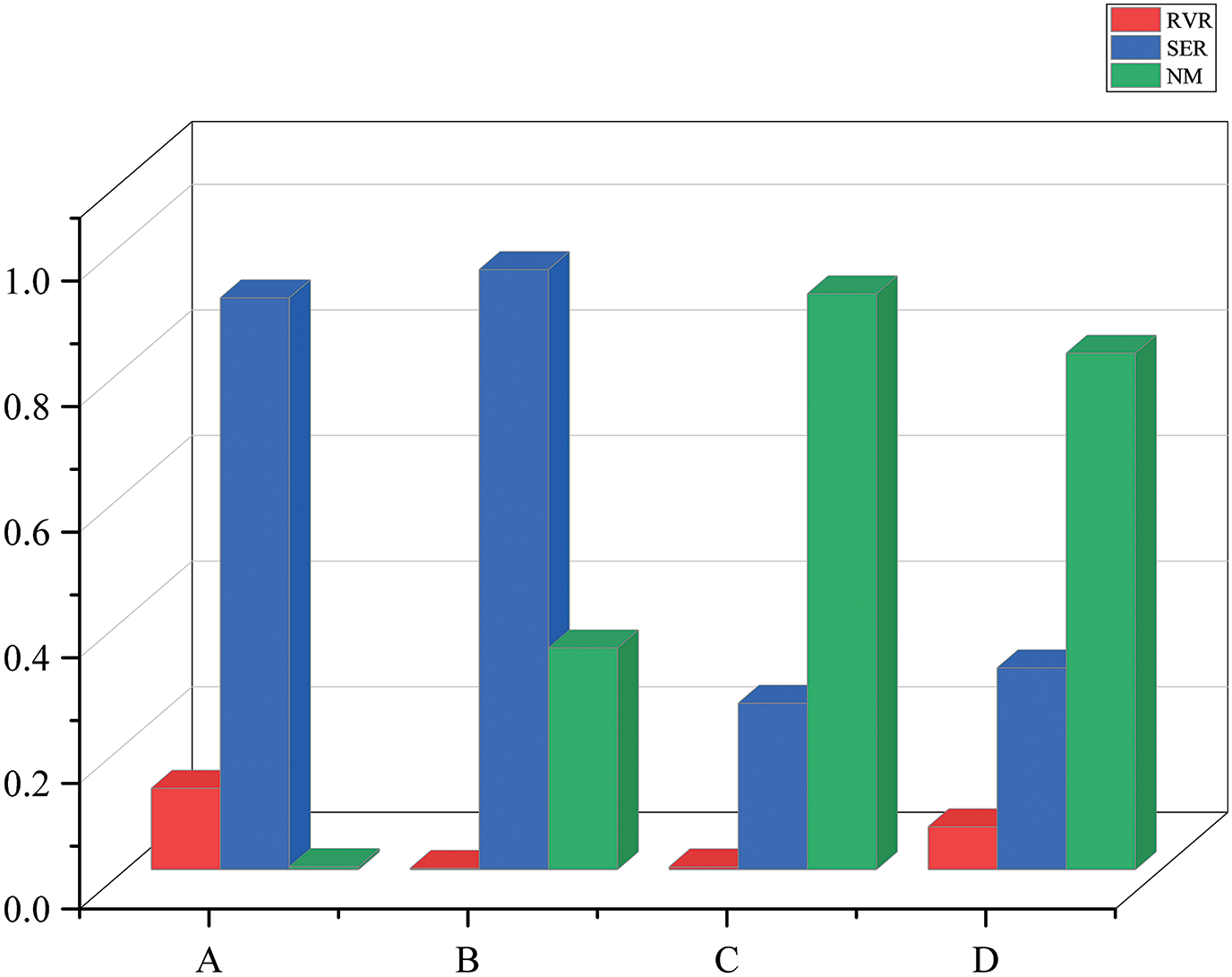
Figure 10: RVR, SER and NM of different denoising methods
Through the experimental comparisons presented above, although the method proposed in this paper may take slightly longer than the individual VMD and wavelet thresholding methods, the processing time is mainly influenced by the operating conditions, the number of iterations, and the population size of the optimization algorithm. However, the proposed method significantly enhances noise reduction and signal reconstruction performance through a multi-step process, demonstrating superior processing effects. In real-time condition monitoring of equipment, processing time is certainly important, but diagnostic accuracy and reliability are equally crucial. Considering both time efficiency and performance superiority, the method proposed in this paper, under multiple evaluation criteria, is more suitable for application in real-time monitoring systems for equipment, providing effective fault detection and early early fault prediction while ensuring high-quality processing.
The envelope spectrum of the original signal for the tooth breakage fault with 1 dB noise and the envelope spectrum after de-noising using IHLOA+VMD+Wavelet Threshold are shown in the Fig. 11 for comparison. Observing the de-noised envelope spectrum, it is evident that the meshing fault frequency is clearly visible after de-noising, and the sideband frequency features can be extracted. The spectral lines distributed uniformly on both sides of the harmonic frequencies are relatively lower. Therefore, the method proposed in this paper can effectively extract fault frequencies under noisy conditions, suppress the impact of noise on the signal, and demonstrate a certain degree of robustness against noise.
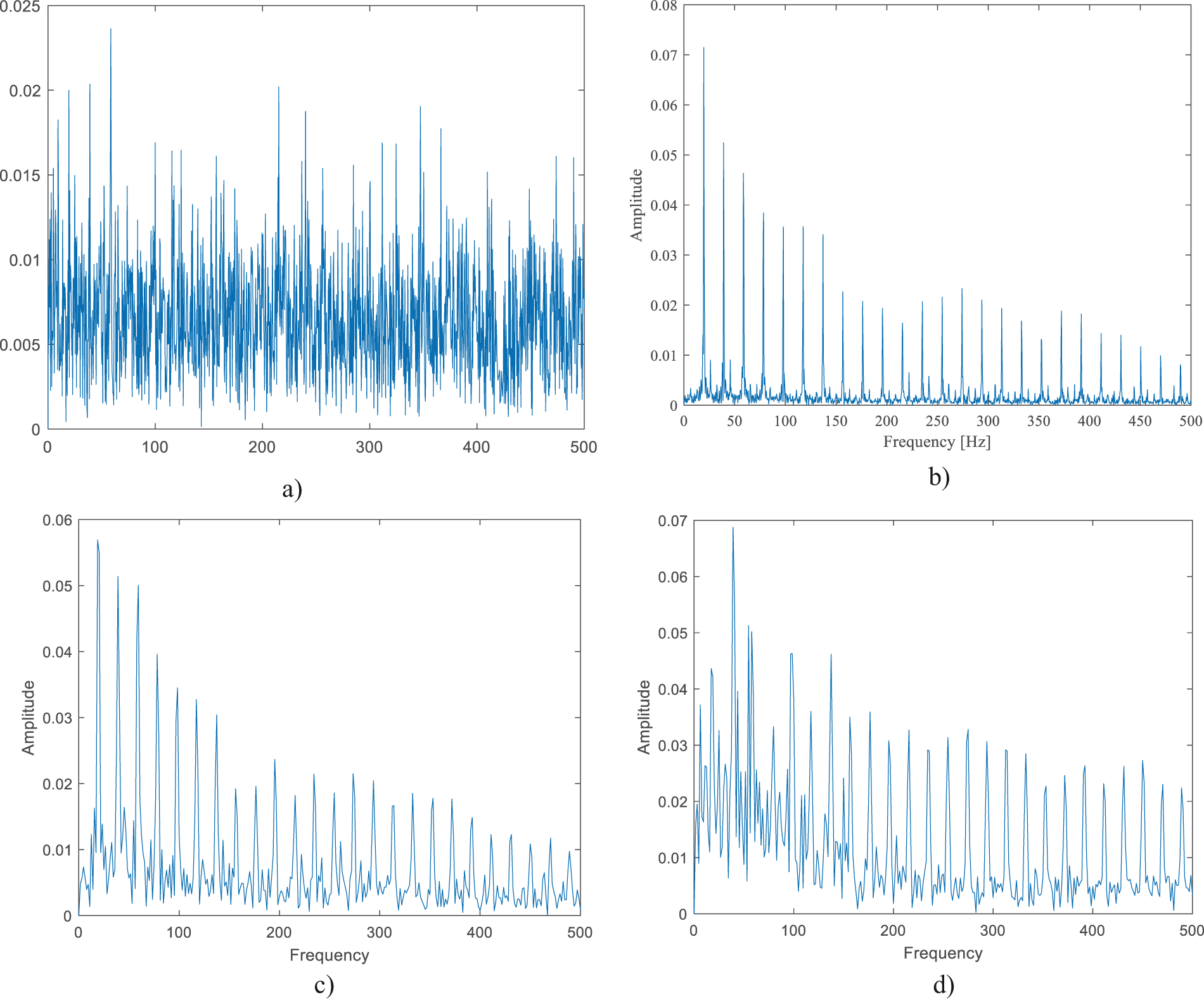
Figure 11: Envelope spectrum (a) Original signal with 1 dB noise (b) Envelope spectrum of the proposed method (c) Envelope spectrum of MSSA method (d) Envelope spectrum of IHLOA-FMD method
To validate the effectiveness of the proposed method, this paper compares the envelope spectra generated by the IHLOA-FMD method and the Multivariate Singular Spectrum Analysis (MSSA) method. From the results, it can be observed that the MSSA method’s envelope spectrum still exhibits relatively high spectral lines on both sides, indicating the presence of noticeable residual noise. Additionally, the overall amplitude of the envelope is lower than that achieved by the proposed method, reflecting its limited ability to extract signal features effectively. In contrast, the IHLOA-FMD method’s envelope spectrum shows more disorganized spectral line distributions on both sides, suggesting weaker noise suppression and insufficient de-noising performance. A comprehensive analysis demonstrates that the proposed method outperforms both in terms of de-noising effectiveness and signal feature extraction. It particularly shows strong robustness against noise interference, further validating the effectiveness and practical value of the proposed approach.
The IHLOA is proposed to optimize the VMD parameters and wavelet thresholding for combined denoising to reduce the noise of the acquisition signals from mechanical transmission systems. The main conclusions are as follows:
(1) To enhance the optimization efficiency of the HLOA algorithm and avoid local optima, an inertia weight parameter is incorporated into the random walk strategy. A comparison among HLOA, PSO, WOA, and IHLOA is conducted using eight standard benchmark functions. The results indicate that IHLOA significantly improves global and local search capabilities, overall convergence speed, and search accuracy.
(2) The IHLOA algorithm is employed to optimize the parameters of VMD, effectively mitigating mode aliasing and endpoint effects and achieving notable noise reduction. To retain useful information within high-noise components, wavelet thresholding is applied as a secondary denoising step. Simulation results validate the method’s effectiveness, achieving a Signal-to-Noise Ratio (SNR) of 17.7776 and a Root Mean Square Error (RMSE) of 0.0447. Compared to other methods, this method achieves a higher SNR and a lower RMSE.
(3) Through the validation of signals related to gear tooth breakage and tooth loss, the results demonstrate that the proposed method can be effectively applied to other gear faults. By comparing the three indicators—RVR, SER, and NM—it has been verified that the method excels in noise reduction, successfully minimizing noise interference in the signals. The experimental results fully prove the effectiveness and advantages of the method in signal denoising. Furthermore, by comparing the denoised signal waveforms of this method with those of IHLOA-FMD and Multivariate Singular Spectrum Analysis (MSSA), it is shown that the proposed method exhibits strong robustness in the presence of noise interference, thereby validating its effectiveness.
In short, the proposed IHLOA-VMD-wavelet thresholding method provides a robust solution for noise suppression in vibration signals and ensures accurate feature extraction. These capabilities are essential for ensuring the safety and reliability of mechanical systems in prognostic and health management.
Acknowledgement: None.
Funding Statement: The research was supported by Central Guidance on Local Science and Technology Development Fund of Hebei Province (Grant No. 226Z1906G), funded by Science Research Project of Hebei Education Department (CXY2024038), funded by Basic Research Project of Shijiazhuang University in Hebei Province (241791157A), National Natural Science Foundation of China (52206224).
Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Guangfei Jia; data collection: Jinqiu Yang; analysis and interpretation of results: Guangfei Jia, Hanwen Liang; draft manuscript preparation: Jinqiu Yang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| SNR | Signal-to-Noise Ratio |
| RMSE | Root Mean Square Error |
| EMD | Empirical Mode Decomposition |
| EEMD | Ensemble Empirical Mode Decomposition |
| CEEMD | Complementary Ensemble Empirical Mode Decomposition |
| CEEMDAN | Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise |
| VMD | Variational Mode Decomposition |
| FMD | Feature Mode Decomposition |
| MSSA | Multichannel Singular Spectrum Analysis |
| PSO | Particle Swarm Optimization |
| WOA | Whale Optimization Algorithm |
| HLOA | Horned Lizard Optimization Algorithm |
| IHLOA | Improve Horned Lizard Optimization Algorithm |
| IMF | Intrinsic Mode Function |
| SER | Signal Energy Ratio |
| NM | Noise Modulus |
| WT | Wavelet Thresholding |
| RVR | Root of Variance Ratio |
| GMF | Gear Mesh Frequency |
| EWT | Empirical Wavelet Transform |
References
1. Hu Y, Guo R, Wang H, Zhao R, Ning R, Huang Z, et al. Gear-fault monitoring and digital twin demonstration of aircraft engine based on piezoelectric vibration sensor for engine health management. Nano Energy. 2025;133:110448. doi:10.1016/j.nanoen.2024.110448. [Google Scholar] [CrossRef]
2. Zhang L, He X, Chen J, Liu J. Fault diagnoses of a nonlinear cracked rotor-bearing system based on vibration energy space and incremental learning approach. J Sound Vib. 2025;600:118785. doi:10.1016/j.jsv.2024.118785. [Google Scholar] [CrossRef]
3. Jia GF, Guo FW, Wu Z, Cui CX, Yang JJ. A noise reduction method for multiple signals combining computed order tracking based on chirplet path pursuit and distributed compressed sensing. Struct Durab Health Monit. 2023;17(5):383–405. doi:10.32604/sdhm.2023.026885. [Google Scholar] [CrossRef]
4. Cheng J, Yang Y, Hu NQ, Cheng Z, Cheng JS. A noise reduction method based on adaptive weighted symplectic geometry decomposition and its application in early gear fault diagnosis. Mech Syst Signal Process. 2021;149(15):107351. doi:10.1016/j.ymssp.2020.107351. [Google Scholar] [CrossRef]
5. Zhang Z, Liu X, Shu R, Xie F, Wang F, Liu Z, et al. A novel noise reduction method for space-borne full waveforms based on empirical mode decomposition. Optik. 2020;202:163581. doi:10.1016/j.ijleo.2019.163581. [Google Scholar] [CrossRef]
6. Wang J, Du G, Zhu Z, Shen C, He Q. Fault diagnosis of rotating machines based on the EMD manifold. Mech Syst Signal Process. 2020;135(1):106443. doi:10.1016/j.ymssp.2019.106443. [Google Scholar] [CrossRef]
7. Mao B, Bu Z, Xu B, Gong H, Li Y, Wang H, et al. Denoising method based on VMD-PCC in φ-OTDR system. Opt Fiber Technol. 2022;74(3):103081. doi:10.1016/j.yofte.2022.103081. [Google Scholar] [CrossRef]
8. Li Z, Xiao J, Ding X, Wang L, Yang Y, Zhang W, et al. A new raw signal fusion method using reweighted VMD for early crack fault diagnosis at spline tooth of clutch friction disc. Measurement. 2023;220:113414. [Google Scholar]
9. Toffghi Niaki S, Alavi H, Ohadi A. Incipient fault detection of helical gearbox based on variational mode decomposition and time synchronous averaging. Struct Health Monit. 2023;22(2):1494–512. doi:10.1177/14759217221108489. [Google Scholar] [CrossRef]
10. Matania O, Klein R, Bortman J. Transfer across different machines by transfer function estimation. Front Arttf Intell. 2022;5:811073. doi:10.3389/frai.2022.811073. [Google Scholar] [PubMed] [CrossRef]
11. Wang W, Wong AK. Autoregressive model-based gear fault diagnosis. J Vib Acoust. 2002;124(2):172–9. doi:10.1115/1.1456905. [Google Scholar] [CrossRef]
12. Wang WJ, McFadden PD. Decomposition of gear motion signals and its application to gearbox diagnostics. J Vib Acoust. 1995;117:363–9. doi:10.1115/1.2874462. [Google Scholar] [CrossRef]
13. Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc Royal Soc London Ser A: Math Phys Eng Sci. 1998;454(1971):903–95. doi:10.1098/rspa.1998.0193. [Google Scholar] [PubMed] [CrossRef]
14. Wu Z, Huang NE. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adaptive Data Anal. 2009;1(1):1–41. doi:10.1142/S1793536909000047. [Google Scholar] [CrossRef]
15. Chen C, Luo Y, Liu J, Yi Y, Zeng W, Wang S, et al. Joint sound denoising with EEMD and improved wavelet threshold for real-time drilling lithology identification. Measurement. 2024;238(1):115363. doi:10.1016/j.measurement.2024.115363. [Google Scholar] [CrossRef]
16. Yeh JR, Shieh JS, Huang NE. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method. Adv Adapt Data Anal. 2010;2(2):135–56. doi:10.1142/S1793536910000422. [Google Scholar] [CrossRef]
17. María ET, Marcelo AC, Gastón S, Flandrin P. A complete ensemble empirical mode decomposition with adaptive noise. In: 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). 2011 May 22–27; Prague, Czech Republic. doi:10.1109/ICASSP.2011.5947265. [Google Scholar] [CrossRef]
18. Gilles J. Empirical wavelet transform. Signal Process. 2013;61(16):3999–4010. [Google Scholar]
19. Li Z, Chen J, Zi Y, Pan J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of highspeed locomotive. Mech Syst Signal Process. 2017;85(11):512–29. doi:10.1016/j.ymssp.2016.08.042. [Google Scholar] [CrossRef]
20. Chen HH. A vibration signal processing method based on SE-PSO-VMD for ultrasonic machining. Syst Soft Comput. 2024;6(14):20081. doi:10.1016/j.sasc.2024.200081. [Google Scholar] [CrossRef]
21. Dragomiretskiy K, Zosso D. Variational mode decomposition. IEEE Trans Signal Process. 2013;62(3):531–44. doi:10.1109/TSP.2013.2288675. [Google Scholar] [CrossRef]
22. Jiang H, Lu H, Zhou J, Liu M. Fault diagnosis of rolling bearings in VMD and GWOELM. J Phys: Conf Ser. 2023;2496(1):012013. doi:10.1088/1742-6596/2496/1/012013. [Google Scholar] [CrossRef]
23. Lin Y, Xiao M, Liu H, Li Z, Zhou S, Xu X, et al. Gear fault diagnosis based on CS-improved variational mode decomposition and probabilistic neural network. Measurement. 2022;192(19):110913. doi:10.1016/j.measurement.2022.110913. [Google Scholar] [CrossRef]
24. Zhang X, Miao Q, Zhang H, Wang L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech Syst Signal Process. 2018;108(12):58–72. doi:10.1016/j.ymssp.2017.11.029. [Google Scholar] [CrossRef]
25. Ding J, Huang L, Xiao D, Li X. GMPSO-VMD algorithm and its application to rolling bearing fault feature extraction. Sensors. 2020;20(7):1946. doi:10.3390/s20071946. [Google Scholar] [PubMed] [CrossRef]
26. Peraza-Vázquez H, Peña-Delgado A, Merino-Treviño M, Morales-Cepeda AB, Sinha N. A novel metaheuristic inspired by horned lizard defense tactics. Artif Intell Rev. 2024;57(3):59. doi:10.1007/s10462-023-10653-7. [Google Scholar] [CrossRef]
27. Zamanian AH. Experimental dataset for gear fault diagnosis. 2014. doi:10.13140/RG.2.2.28152.44802/2. [Google Scholar] [CrossRef]
28. Zamanian AH, Ohadi A. Gear fault diagnosis based on Gaussian correlation of vibrations signals and wavelet coefficients. Applied Soft Comput. 2011;11(8):4807–19. doi:10.1016/j.asoc.2011.06.020. [Google Scholar] [CrossRef]
29. Zamanian AH, Ohadi A. Gearbox fault detection through PSO exact wavelet analysis and SVM classifier. In: 18th Annual International Conference on Mechanical Engineering—ISME; May 2010; Tehran, Iran: Sharif University of Technology. doi:10.13140/RG.2.1.4983.3442. [Google Scholar] [CrossRef]
30. Zhao C, Zio E, Shen WM. Domain generalization for cross-domain fault diagnosis: an application-oriented perspective and a benchmark study. Reliab Eng Syst Saf. 2024;245:109964. doi:10.1016/j.ress.2024.109964. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools