Magnetic Field Effect and Heat Transfer of Nanofluids within Waveform Microchannel

1  Introduction

The use of advanced and efficient cooling systems to sustain the reliable and effective operation of devices with microelectronic parts and the like is inevitable. The dramatic increase in heat transfer in microchannels has led to their use as heat dissipation devices in microelectronic equipment. High heat transfer, small size, the need of a small amount of cooling fluid is the characteristics of microchannels. Expanding the surface of cooling devices by changing the geometry of heat channels, such as corrugating the surface of the channel, causes changes in the efficiency of heat exchangers. Changing the flow rate or suspending solid particles in a fluid is also one of the methods used to increase heat transfer. Creating a magnetic field according to the current regime can also increase or even decrease the amount of heat transfer. In the following, the studies that have been done in this field were reviewed. Most researches have shown that with the addition of nanoparticles with relatively high thermal conductivity to the base fluid, the thermal performance of the nanofluid will be enhanced [1]. Heris et al. [2] used water-aluminum oxide nanofluids in a triangular cross-sectional channel under constant heat flux boundary conditions in the wall to investigate the forced displacement heat transfer in a laminar-flow process in the laboratory. The outcomes proved the pure water lab heat transfer coefficient is lower than the nanofluid laboratory heat transfer coefficient. Furthermore, it is more distinguished than the one calculated in theory. Nanofluids have particular properties that distinguish them entirely from a mixture of two-phase fluids in which the particles are micro or millimeter in size [3]. Zarringhalam et al. [4] investigated the effect of Reynolds number and volume fraction on pressure drop and heat transfer coefficient of copper oxide and water of nanofluid experimentally. Results revealed that the heat transfer coefficient of the base fluid is commonly lower than the nanofluids. Observations additionally showed growing the volume fraction coefficient and Reynolds number, improving the heat transfer coefficient and the Nusselt number. However, the magnitude of this improvement is more evident in lower Reynolds. Öğüt et al. [5] studied the heat transfer of turbulent nanofluid on corrugated trapezoidal plate heat exchangers with boundary conditions on a wall with constant heat flux numerically. Examining the impacts of nanofluids on the heat transfer flow and rate, they observed growing nanoparticle concentration rises heat transfer. In addition, they observed using nanofluids in the trapezoidal channel improves the performance of heating systems and leads to the design of more dense and small heat exchangers. Shehzad et al. [6] used the Bangirno model in a wavy channel to examine nanofluid free displacement heat transfer effects in which thermos diffusion and the brown motion simultaneous impacts are analyzed. Peng et al. [7] investigated nanofluids heat transfer using three homogeneous single and two-phase Euler-Euler and two-phase Euler-Lagrange methods and compared them with similar experimental results. They found that among the used models, the Euler-Lagrange model presented the most precise analysis, while the single-phase had the lowest precision. Zabilhi et al. [8] conducted a simultaneous experimental and numerical study for water-aluminum oxide nanofluids in the form of slow flow in an equilateral triangle cross-section channel and constant heat flux, which resulted in increased heat transfer rate with increasing nanoparticle volume concentration. Ducts with non-flat plates have many applications because they increase the level of heat transfer. Among these channels are sinusoidal channels that enhance heat transfer and have less effect on the unfavorable pressure gradient along the channel. Wavy channels are found in many engineering applications [9]. Chai et al. [10] increased the rate of microchannel heat transfer by considering various ribs in the lateral canal walls. Moreover, with rising Reynolds number, the use of different ribs due to the improvement in pressure drop in the microchannel misses its advantage as an efficient method of improving heat transfer. Ahmed et al. [11] investigated the flow of a nanofluid in a corrugated channel using numerical methods and changing the Reynolds number (between 100 and 400) and changing the volume percentage of nanoparticles (from zero to 5%). They examined the influence of these parameters on heat transfer. Zhou et al. [12] presented the best length-to-amplitude ratio utilizing the finite volume method and corrugated wall geometric simulation as the main factor to improve the efficiency of heat transfer. In one study, Moon et al. [13] applied three-dimensional numerical simulations for investigating the development of heat transfer in micro-and multi-harmonic corrugated channels at the square cross-section. With more attention to channel surface geometry effect and using the Nusselt number ratio in wavy channels directly, they analyzed the cold water parametrically in different Reynolds. The more beneficial form of a corrugated microchannel heat sink was proposed by Lin et al. [14]. They changed the amplitude and wavelength by the flow direction. The formation of vortices increased heat transfer and was connected to the curved walls, which caused the cooling to mix and improved the heat transfer among the channel wall and the coolant.

Kirsch et al. [15] investigated the performance of corrugated ducts pressure drop and heat transfer. Due to the current created by the wave structure, they showed that short-wavelength channels have a higher pressure drop than high-wavelength channels, and increasing the wavelength improves the heat transfer performance. Skullong et al. [16] studied the solar-air heating channel heat transfer using corrugated grooves with a pair of trapezoidal fins located on the absorber plate. It showed that corrugated grooves with a pair of trapezoidal fins caused a notable increase in heat transfer compared to a smooth channel, and both trapezoidal fins alone displayed extremely higher heat transfer but the corrugated grooves caused a significant pressure drop. Yadav et al. [17] examined increasing a microchannel heat transfer using a large surface area. Comparing rectangular microchannels with cylindrical microphones, they concluded that the performance of the microchannel heat transfer was better than microphones. Furthermore, in the presence of wide surface microchannels, the average surface temperature decreases. The magnetic field affects both forced and free movement. The use of a magnetic field in free movement reduces the velocity near the wall and lessens heat transfer [18]. Malekpour et al. [19] studied the impact of magnetic fields on free movement in a triangular chamber. They utilized Hartmann numbers up to 80 to the chamber and noted that developing the Hartmann number decreased the fluid velocity in the triangular chamber and reduced free movement heat transfer. Unlike free displacement, in forced displacement, the magnetic field flattens the velocity profile, which increases velocity near the channel walls and enhances the heat transfer coefficient. The nanofluid particles are orients regularly by the magnetic field that result in more communication between the nanoparticles. Consequently, in a nanofluid stream, the utilization of a favorable magnetic field can dramatically increase heat transfer [20]. Aminfar et al. [21] examined the non-uniform magnetic field impact of electric current in a magnetic fluid. They determined that the magnetic field improves the heat transfer coefficient up to 22% and prevents nanoparticles from settling. Nourazar et al. [22] numerically analyzed the nanoparticles’ flow under a magnetic field on a flat plate. Motozawa et al. [23] experimentally investigated the impact of a magnetic field on the slow current heat transfer in a rectangular channel. Their results confirmed that the magnetic field application increases the heat transfer coefficient and enhances the heat transfer up to 20%. Çelik [24] examined the impact of a magnetic field on current in a channel with a rectangular cross-section and examined up to Hartmann 1000. Rashidi et al. [25] examined nanofluids’ conduction and heat transfer in a vertical channel with a sinusoidal wall under the impact of a magnetic field and discovered the increase in gradient number for nanofluids with different volume fractions, develops the average Nusselt number. In addition, with raising the Hartmann’s number, the average Nusselt increases. Heidary et al. [9] numerically studied the heat transfer and flow field in a nanofluid wavy channel and showed that the heat transfer in the channels could be enhanced by 50% with adding nanoparticles and usage wavy horizontal walls. Al-Zurfi et al. [26] numerically investigated the flow field and heat transfer performance in fixed and rotating wave channels with different shapes. They found that as the rotation velocity increased, the lower wall heat transfer coefficient increased significantly,while the upper wall heat transfer coefficient increased slightly. Alsabery et al. [27] numerically investigated the mechanisms of increasing convective heat transfer with two-phase water nanofluids in a three-dimensional horizontal wavy channel with high and low wavy surfaces with uniform temperature and adiabatic conditions, respectively. The results indicated that nanofluid flow in the undulating channel is higher, especially at higher volume fractions of nanoparticles and Reynolds numbers. Also, higher convective heat transfer is achieved by increasing the flow mixing due to the increase in oscillation frequency. Mehta et al. [28] evaluated the thermo-fluidic and entropy generation characteristics for laminar forced convective flow through a wavy channel at different Prandtl (Pr) numbers. Their results indicated that the channel performance coefficient (PF) with different Prandell numbers showed non-uniform behavior at lower Reynolds number and uniform behavior at higher Reynolds number. Elsafy et al. [29] investigated the performance of three fluids with forced convection in a wave channel. Their results revealed that the wavy channel provides better heat gain than the straight channel with the same dimensions. Porous materials enhanced heat extraction at the expense of pressure drop. 1% TiO2 nanofluid in water provided the highest performance evaluation criteria.

In this paper, the forced convection of nano fluids flow in the presence of a magnetic field in the corrugated microchannel was examined. The novelty of this study is use of simple coordinate transformation to transform wavy surface to flat surface. The transform stream vorticity and energy equations are solved by Spline Alternating Direction Implicit (SADI) method. Since the SADI method can evaluate the spatial derivative terms directly without any finite difference discretization, the gradient boundary conditions may be represented more accurately, and irregular boundaries are easier to deal with. By considering the boundary conditions, the effect of parameters such as nanofluid volume fraction, wave amplitude, Hartmann number, Reynolds number, and magnetic field in the wavy microchannel have been investigated. The innovation of this paper is the use of mapping in corrugated microchannels to solve vortex flow equations in forced heat transfer. By drawing medium and local Nusselt diagrams in different modes of these parameters and comparing them with each other, we have tried to provide the most optimal model for increasing heat transfer in a corrugated microchannel.

2  Problem Mathematical Formulation

Fig. 1 shows the coordinate system and physical model of the problem. Viscous dissipation is insignificant and is not considered. The above assumptions are designed to maintain the theoretical model as simple as possible. In this coordinate system, x is along the wavy surface in the flow direction, and y is the flow perpendicular. The equation of wavy surface equation is as follows:

S(X)=L+αsin⁡(π(x¯−xs¯)L).(1)

where L is average vertical distance from the center of the channel and α is the magnitude of the wave length domain.

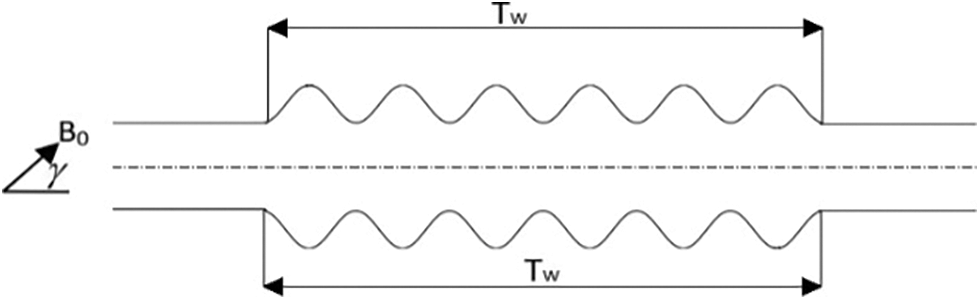
Figure 1: The temperature is at the wavy surface (Tw) and the magnetic field the microchannel at an angle γ

The upper and lower wavy surfaces correspond to constant temperature Tw, which is above the ambient temperature T∞. The beginning and end of the microchannel are flat, the wall of which is adiabatic in this part. The nanofluid temperature is assumed to be T0. The fluid flow is under uniform magnetic field B0 so that γ is the direction of the magnetic field with the horizontal axis and in this study, γ = π/ 6.

The governing equations in this method for an uncompressible flow, stable and two-dimensional are presented as follows:

∂u¯∂x¯+∂v¯∂y¯=0,(2)

u¯∂u¯∂x¯+v¯∂u¯∂y¯=−1ρnf∂p∂x¯+v¯nf(∂2u¯∂x¯2+∂2u¯∂y¯2) - σnfu¯ρnfB02sin2γ+σnfv¯ρnfB02sin⁡γcosγ,(3)

u¯∂v¯∂x¯+v¯∂v¯∂y¯=−1ρnf∂p∂y¯+νnf(∂2v¯∂x¯2+∂2v¯∂y¯2)−σnfv¯ρnfB02cos2γ+σnfu¯ρnfB02sin⁡γcos⁡γ,(4)

u¯∂T∂x¯+v¯∂T∂y¯=αnf(∂2T∂x¯2+∂2T∂y¯2).(5)

In the above equations, u and v are the velocities of the fluid in the x and y directions, ρnf, p, T and B0 are density, pressure, the temperature of the fluid and the magnetic field, respectively.

The effective density, dynamic viscosity, and nanofluids heat capacity are represented as follows [30–33]:

ρnf=ρf(1−ϕ)+ρsϕ,(6)

μnf=(1+2.5ϕ)μf,(7)

(ρCp)nf=(ρCp)f(1−ϕ)+(ρCp)sϕ.(8)

In this paper, assuming the spherical shape for nanoparticles, the Maxwell-Garnet relationship is used to determine the thermal conductivity, which is determined as follows [34]:

knf=(ks+2kf−2ϕ(kf−ks)ks+2kf+ϕ(kf−ks))kf.(9)

Also, the effective nanofluid electrical conductivity from the Maxwell relation is written as follows [35]:

σnfσf=1+3(σsσf−1)ϕ(σsσf+2)−(σsσf−1)ϕ.(10)

The flow and rotation functions are described as follows:

v¯=−∂ψ∂x¯.(11)

ωz=(∂v¯∂x¯−∂u¯∂y¯).(12)

The flow function in the continuity equation and the rotation equation is obtained from removing the pressure gradient among the momentum equations and extracting Eq. (5) in the y-direction and decreasing it from the derivative of Eq. (6) in the x-direction as follows:

u¯∂Ω∂x¯+v¯∂Ω∂y¯=µnfρnf(∂2Ω∂x¯2+∂2Ω∂y¯2)+σnfρnfB02[−cos2⁡γ∂v¯∂x¯+ sinγcos⁡γ∂u¯∂x¯+ sin2γ∂u¯∂y¯− sinγcos⁡γ∂v¯∂y¯].(13)

Dimensional variables for dimensionless equations are defined as follows:

ω=ΩLU∞,ψ=ψU∞L,u=u¯U∞,v=v¯U∞,x =x¯L,y=y¯L,θ=T−T∞T−TW, Ha=LB0σfµf, Re=u L ν.(14)

where Ha and Re are the Hartmann and Reynolds number of the base fluid, respectively. Also, the thermophysical properties of the copper oxide and base fluid are given in Table 1.

By placing dimensionless variables in the equations of continuity, momentum and energy are as follows:

∂2ψ∂x2+∂2ψ∂y2=−ω,(15)

u∂ω∂x+ v∂ω∂y=1Re(µnf/µfρnf/ρf)(∂2ω∂x2+∂2ω∂y2)+(σnf/σfρnf/ρf)Ha2Re[cos2⁡γ∂2ψ∂x2+sin2⁡γ∂2ψ∂y2+2 sinγcos⁡γ∂2ψ∂x ∂y],(16)

u∂θ∂x+v ∂θ∂y=1Re Pr(knf/kf(ρCp)nf/(ρCp)f)(∂2θ∂x2+∂2θ∂y2).(17)

The wavy surface becomes a flat surface, to solve the surface we use the following transform:

ξ=x ,η=ys(x).(18)

Therefore, using it in an equation, the wavy surface turns to a flat surface. These equations are

∂2ψ∂ξ2+(ηx2+ηy2)∂2ψ∂η2+2ηx∂2ψ∂ξ∂η+(ηxx+ηyy)∂ψ∂η=−ω(19)

u(∂ω∂ξ+ηx∂ω∂η)+vηy∂ω∂η=(1+2.5ϕ+6.2ϕ2)((1−ϕ)+ρsρfϕ)(1Re)[∂2ω∂ξ2+(ηx2+ηy2)∂2ω∂η2+2ηx∂2ω∂ξ∂η+(ηxx+ηyy)∂ω∂η]+Ha2Re[+3(σsσf−1)ϕ(σsσf+2)−(σsσf−1)ϕ](1(1−ϕ)+ρsρfϕ)×[cos2γ(ηx2∂2ψ∂ξ2+2ηx∂2ψ∂ξ∂η+ηx2∂2ψ∂η2+ηxx∂ψ∂η)+sin2γ(ηy2∂2ψ∂ξ2+ηy2∂2ψ∂η2)+2sinγcos⁡γ(ηy∂2ψ∂ξ∂η+ηxηy∂2ψ∂η2+ηxy∂ψ∂η)](20)

u(∂T∂ξ+ηx∂T∂η)+vηy∂T∂η=1RePr(ks−2ϕ(kf−ks)+2kfks−2ϕ(kf−ks)+2kf(1−ϕ)+(ρCp)s(ρCp)fϕ)(∂2T∂ξ2+(ηx2+ηy2)∂2T∂η2+2ηx∂2T∂ξ∂η+(ηxx+ηyy)∂T∂η).(21)

where the boundary conditions are as follows:

u=ηy∂ψ∂η,v=−(∂ψ∂ξ+ηx∂ψ∂η),ηy=1s(x),ηx=−ys′(x)s(x)2,ηxx=y(2s′2+ss″)s(x)3,ηyy = 0(22)

η=1,u=v=0→ψ= cte=1,θ=1On the wall(23)

η=0,ψ=ω=0∂θ∂η=0Microchannel center(24)

ψ=32(η−η33)ω=−3y,,θ=0Microchannel input(25)

∂ω∂ξ=0∂ψ∂ξ=0∂u∂ξ=0∂v∂ξ=0∂θ∂ξ=0Microchannel output(26)

The local Nusselt number is described as follows:

Nux=(∂T/∂n)x¯Tw−T0.(27)

∂T/∂n is a derivative of the vector perpendicular to the corrugated surface of the object, which is defined as follows. Eventually, after dimensioning and changing the corrugated surface variable to smooth, the Nusselt number is written as follows.

The mean Nusselt number is determined by combining the local Nusselt numbers on the upper wall of the microchannel as follows [37]:

∂T∂n=(∂T∂x)2+(∂T∂y)2.(28)

Nux=(ηx2+ηy2)1/2∂θ∂η(knfkf),(29)

Num=1S¯∫x0xLNuxdS=1S¯(knfkf)∫x0xL(ηx2+ηy2)1/2∂θ∂ηdξ(30)

which in the above relation S¯ is equal to

S¯(ξ)=∫x0xL⁡(1+S¯′2)dξ.(31)

The coefficient of skin friction Cf is also defined as follows [37]:

Re Cf=(ηy2−ηx2)∂2ψ∂η2.(32)

ReCf=(ηy2−ηx2)∂2ψ∂η2.(33)

3  Numerical Solution Method

Having the boundary condition, the spline alternating direction implicit method [38,39] has been used to solve the governing dimensionless differential Eqs. (19)–(21). Using the false transient technique, Eqs. (19)–(21) can be written in the following form:

φi,j=Fi,jn+Gi,jmi,jn+1+Si,jmi,jn+1.(34)

where ∅ represents u or θ or the first and second derivatives of ∅ with respect to y, i, j refer to the computational nodes where n is time step. Fi,j, Gi,j and Si,j are the known coefficients evaluated at the previous time step. Eq. (34) may be written in tri-diagonal form using cubic spline collocation [39].

Ai,jΩi.j−1+Bi,jΩi.j+Ci,jΩi.j+1=Di,j(35)

where Ω represents u or θ or first and second derivative. Eq. (34) can be solved, using Tomas algorithm.

In this research, the iteration process is continued until the convergence criterion, is achieved

Ωi,jn+1−Ωi,jnΩmaxn<5×10−5.(36)

4  Results and Discussions

A very important issue in numerical simulation is to ensure that the number of mesh points is adequate. To achieve enough points, we start the calculation with a suitable mesh and gradually increase the mesh points number, by that from several points onwards, the effect of the mesh on the results is negligible for the above problem, 50 × 360, 60 × 740, 75 × 1000 and 80 × 1480 mesh has been used. To diminish the computational cost of the software, 75 × 1000 mesh has been used (Fig. 2).

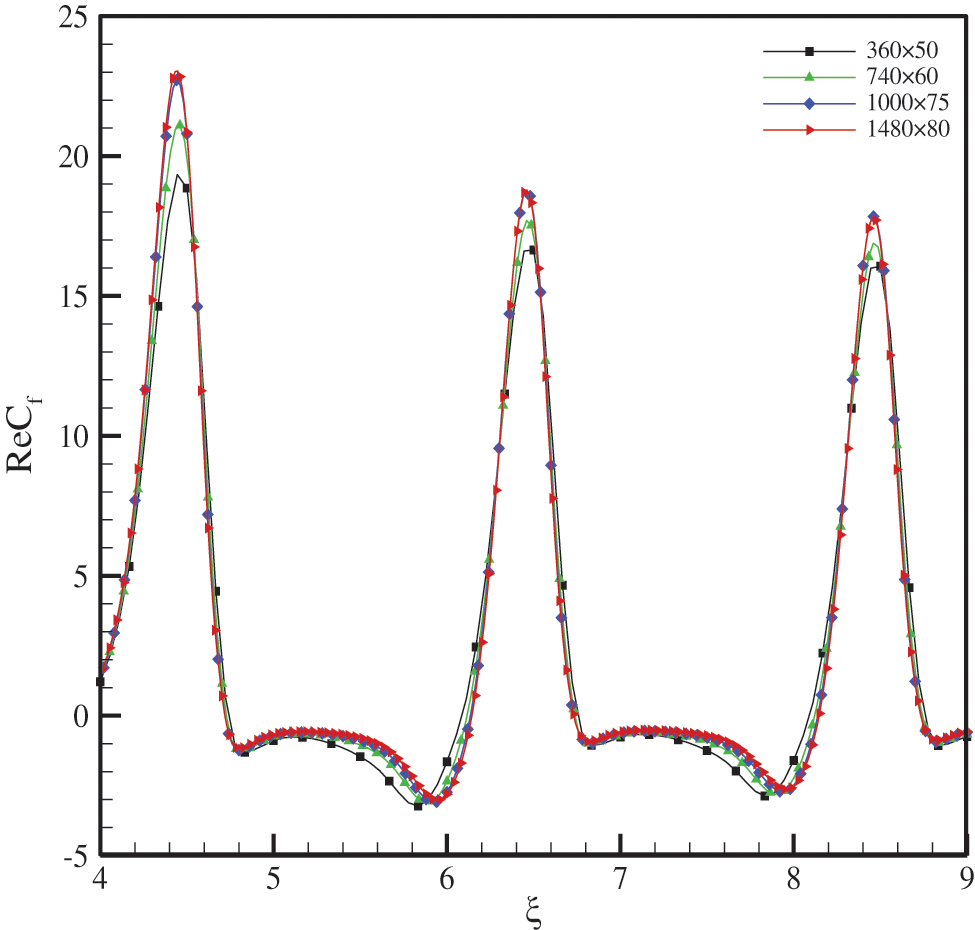
Figure 2: Investigation of the effect of network number on surface friction coefficient at α = 0.2, Re = 300, Pr = 6.83

Verifying the code results are examined with the values of the research of Wang et al. [37]. It can be seen that in Figs. 3 and 4, the coefficient of surface friction and local Nusselt obtained from the present study are very close to the outcomes of Wang et al. [37].

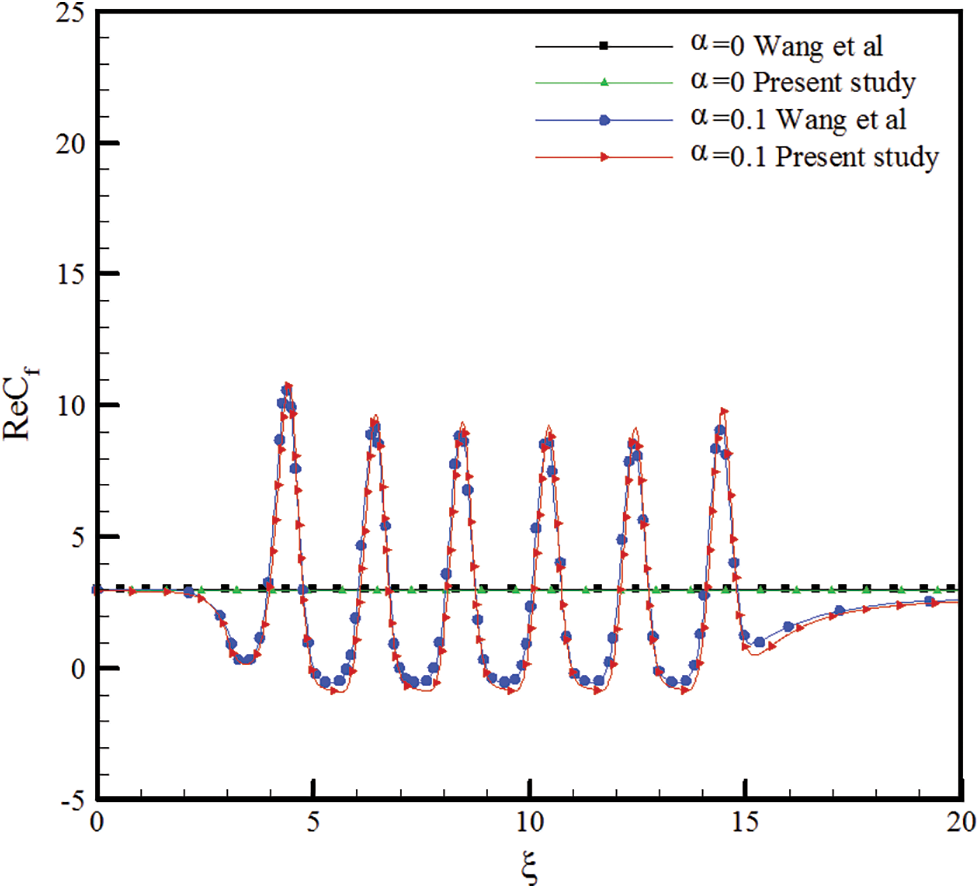
Figure 3: Results of this study compare with Wang et al. [37] for friction coefficient at Re = 500, Pr = 6.83

Figure 4: Results of this study compare with Wang et al. [37] for local Nusselt in Re = 500, Pr = 6.83

Figs. 5 and 6 show the microchannel wave amplitude parameter impact on local and mean Nusselt number at Ha = 5, Re = 500, and volume fraction of 0.1. Medium Nusselt in wavy microchannels with shorter wavelengths, such as α = 0.1, are only slightly larger than planar microchannels, whereas when the wave amplitude increases to 0.2 and 0.3, the average Nusselt suddenly increases dramatically. This occurs due to the creation of a secondary current that causes the fluid to rotate and create a vortex, and as the amplitude of the wave rises, the flow line becomes more vortexes. In Fig. 5, in the convergent part of the microchannel, where the channel height is minimal, the local Nusselt number also increases due to the increase in velocity. While in the part of the channel where the height is maximum, the local Nusselt number also decreases due to the reduction of the velocity slope and temperature.

Figure 5: Local Nusselt diagram in the wave amplitude of α = 0, 0.1, 0.2, 0.3

Figure 6: The average Nusselt diagram in the amplitude waves of α = 0, 0.1, 0.2, 0.3

Fig. 7 shows how the vortex forms at the peak of the wave and the stream line in the microchannel at the wavelength of 0.2. As it is known, the proximity of the stream lines in the wave fall part is more than the wave rise part.

Figure 7: How to form a vortex in the wavy part of the microchannel in the wave amplitude of 0.2

Figs. 8 and 9 show the changes in the impact of volume fraction on mean and local Nusselt at Reynolds number 200, wavelength 0.2, and Prandtl number 6.93. Raising the volume fraction of the base fluid nanoparticles improves the effective thermal conductivity of the nanofluid. As a result, Nusselt number and heat transfer are improved.

Figure 8: Local Nusselt diagram for different volume fractions, Re = 200 and Ha = 10

Figure 9: Diagram of medium Nusselt of different volume fractions, Re = 200 and Ha = 10

Figs. 10 and 11 show the flow line diagram in Reynolds number 200, wavelength 0.2 and volume fraction 0.1 and various Hartmann numbers. As the Hartmann number rises, the probability of a vortex in the wall decreases, and this is because of the gross velocity near the wall. Fig. 12 indicates the stream and temperature contour. Therefore, by increasing the Hartmann number near the wall, the gradient of the temperature rises. Consequently, the local and mean Nusselt number (shapes) increases and the heat transfer rate raises.

Figure 10: Local Nusselt diagram in different Hartmann numbers

Figure 11: Mean Nusselt diagram in different Hartmann numbers

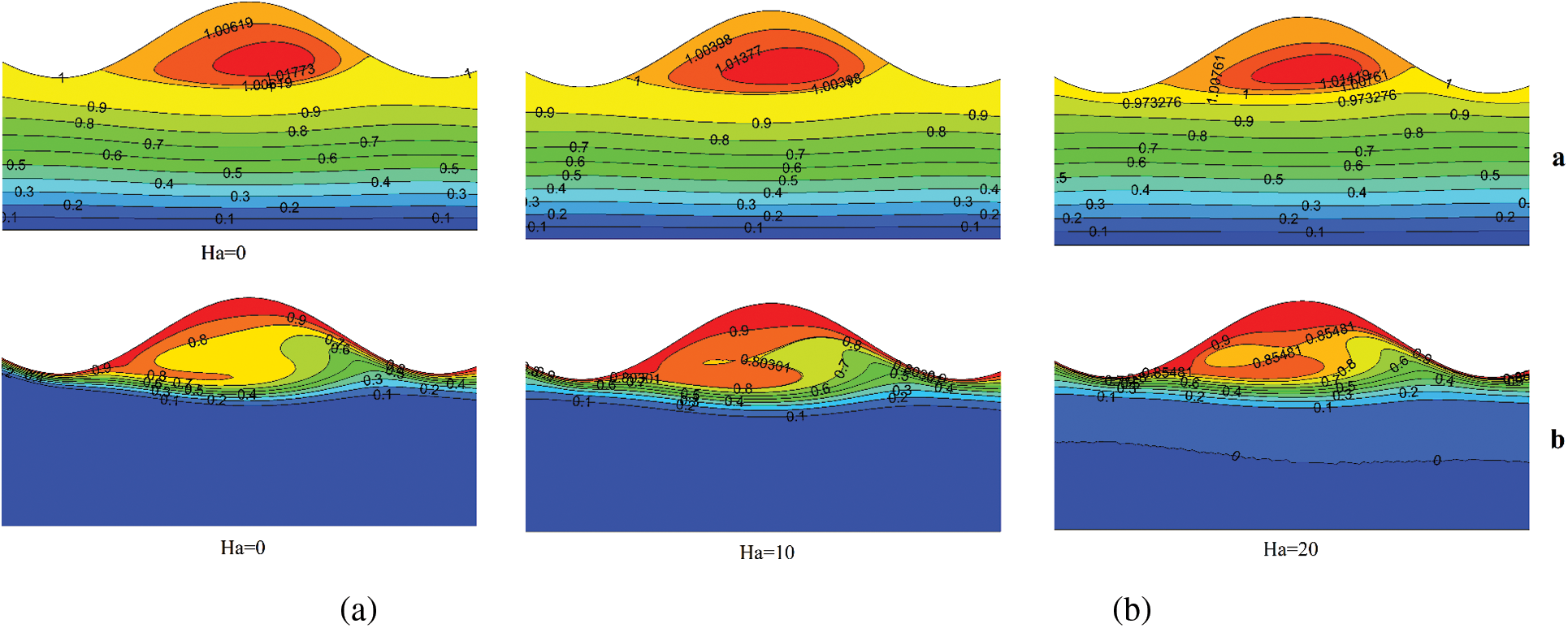
Figure 12: Stream contour (a) and temperature contour (b) for different Hartmann numbers

5  Conclusion

In this research, the forced convection heat transfer with nanofluid flow in a wavy microchannel in the presence of a magnetic field was examined numerically. A simple transformation and the spline alternating direction implicit method (SADI) were employed to analyze. Nanoparticle volume fraction, wave length amplitude, and Hartmann number impact on heat transfer properties and fluid stream were investigated. Outcomes indicate that adding high conductivity nanoparticles to the base fluid improves the heat transfer property of the fluid, which raises the average Nusselt number of a microchannel. This upward trend intensifies with the increment in Reynolds number because of the formation of larger vortices. With microchannel deformation from parallel to wavvy due to the creation of secondary current in the corrugated parts of the microchannel, an increasing trend of heat transfer is observed. The corrugation of the microchannel also increased the nanofluid efficiency in heat transfer. In addition, outcomes show that by increasing Hartmann number, the velocity of the flow near the corrugated wall of the microchannel rises and the velocity profile near the wall becomes smoother, which improves the nature of the heat transfer. As the Reynolds number rises, the more inertial force is applied to the current and the effect of the Hartmann number increases. These results, which have been obtained by making changes in various parameters, are beneficial in designing a compact and optimal heat exchanger.

Acknowledgement: The researchers would like to thank the Deanship of Scientific Research, Qassim University, for funding the publication of this project.

Funding Statement: This work was partially supported by College of Science and Arts, Qassim University, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Aminossadati, S. M., Raisi, A., Ghasemi, B. (2011). Effects of magnetic field on nanofluid forced convection in a partially heated microchannel. International Journal of Non-Linear Mechanics, 46(10), 1373–1382. DOI 10.1016/j.ijnonlinmec.2011.07.013. [Google Scholar] [CrossRef]

 2.  Heris, S. Z., Edalati, Z., Noie, S. H., Mahian, O. (2014). Experimental investigation of Al2O3/water nanofluid through equilateral triangular duct with constant wall heat flux in laminar flow. Heat Transfer Engineering, 35(13), 1173–1182. DOI 10.1080/01457632.2013.870002. [Google Scholar] [CrossRef]

 3.  Singh, A. K. (2008). Thermal conductivity of nanofluids. Defence Science Journal, 58(5), 600–607. DOI 10.14429/dsj.58.1682. [Google Scholar] [CrossRef]

 4.  Zarringhalam, M., Karimipour, A., Toghraie, D. (2016). Experimental study of the effect of solid volume fraction and Reynolds number on heat transfer coefficient and pressure drop of CuO–water nanofluid. Experimental Thermal and Fluid Science, 76, 342–351. DOI 10.1016/j.expthermflusci.2016.03.026. [Google Scholar] [CrossRef]

 5.  Öğüt, E. B., Dilki, S. (2019). Effect of prandlt number on turbulent heat transfer of corrugated trapezoidal plate heat exchangers using nanofluids. The Online Journal of Science and Technology, 9(2), 144–155. [Google Scholar]

 6.  Shehzad, N., Zeeshan, A., Ellahi, R., Vafai, K. (2016). Convective heat transfer of nanofluid in a wavy channel: Buongiorno’s mathematical model. Journal of Molecular Liquids, 222, 446–455. DOI 10.1016/j.molliq.2016.07.052. [Google Scholar] [CrossRef]

 7.  Peng, W., Bai, M. L., Lv, J. Z., Zhang, L., Cui, W. Z. et al. (2013). Comparison of multidimensional simulation models for nanofluids flow characteristics. Numerical Heat Transfer, Part B: Fundamentals, 63(1), 62–83. [Google Scholar]

 8.  Zabihi, K., Gholamian, F., Vasefi, S. I. (2013). Experimental and numerical investigation of Al2O3-water nanofluid inside a triangular tube. World Applied Sciences Journal, 22(5), 601–607. [Google Scholar]

 9.  Heidary, H., Kermani, M. J. (2010). Effect of nano-particles on forced convection in sinusoidal-wall channel. International Communications in Heat and Mass Transfer, 37(10), 1520–1527. DOI 10.1016/j.icheatmasstransfer.2010.08.018. [Google Scholar] [CrossRef]

10. Chai, L., Xia, G. D., Wang, H. S. (2016). Numerical study of laminar flow and heat transfer in microchannel heat sink with offset ribs on sidewalls. Applied Thermal Engineering, 92, 32–41. DOI 10.1016/j.applthermaleng.2015.09.071. [Google Scholar] [CrossRef]

11. Ahmed, M. A., Shuaib, N. H., Yusoff, M. Z. (2012). Numerical investigations on the heat transfer enhancement in a wavy channel using nanofluid. International Journal of Heat and Mass Transfer, 55(21–22), 5891–5898. DOI 10.1016/j.ijheatmasstransfer.2012.05.086. [Google Scholar] [CrossRef]

12. Zhou, J., Hatami, M., Song, D., Jing, D. (2016). Design of microchannel heat sink with wavy channel and its time-efficient optimization with combined RSM and FVM methods. International Journal of Heat and Mass Transfer, 103, 715–724. DOI 10.1016/j.ijheatmasstransfer.2016.07.100. [Google Scholar] [CrossRef]

13. Moon, J., Pacheco, J. R., Pacheco-Vega, A. (2018). Heat transfer enhancement in wavy micro-channels through multiharmonic surfaces. ASME International Mechanical Engineering Congress and Exposition, vol. 52125, V08BT10A004. Pittsburgh, Pennsylvania, USA, American Society of Mechanical Engineers. [Google Scholar]

14. Lin, L., Zhao, J., Lu, G., Wang, X. D., Yan, W. M. (2017). Heat transfer enhancement in microchannel heat sink by wavy channel with changing wavelength/amplitude. International Journal of Thermal Sciences, 118, 423–434. DOI 10.1016/j.ijthermalsci.2017.05.013. [Google Scholar] [CrossRef]

15. Kirsch, K. L., Thole, K. A. (2017). Heat transfer and pressure loss measurements in additively manufactured wavy microchannels. Journal of Turbomachinery, 139(1), 11007. DOI 10.1115/1.4034342. [Google Scholar] [CrossRef]

16. Skullong, S., Promvonge, P., Thianpong, C., Jayranaiwachira, N., Pimsarn, M. (2017). Heat transfer augmentation in a solar air heater channel with combined winglets and wavy grooves on absorber plate. Applied Thermal Engineering, 122, 268–284. DOI 10.1016/j.applthermaleng.2017.04.158. [Google Scholar] [CrossRef]

17. Yadav, V., Baghel, K., Kumar, R., Kadam, S. T. (2016). Numerical investigation of heat transfer in extended surface microchannels. International Journal of Heat and Mass Transfer, 93, 612–622. DOI 10.1016/j.ijheatmasstransfer.2015.10.023. [Google Scholar] [CrossRef]

18. Kefayati, G. R. (2013). Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with sinusoidal temperature distribution. Powder Technology, 243, 171–183. DOI 10.1016/j.powtec.2013.03.047. [Google Scholar] [CrossRef]

19. Malekpour, A., Ghasemi, B. (2013). Magnetic field effect on natural convection in a nanofluidfilled triangular enclosure. Modares Mechanical Engineering, 3(13), 10–21. [Google Scholar]

20. Mehdipour, M., Pooladsanj, S., Saidi, M. H. (2013). Numerical study of evaporation effects on heat transfer in falling film. 15th Fluid Dynamics Conference, Bandar Abbas. [Google Scholar]

21. Aminfar, H., Mohammadpourfard, M., Zonouzi, S. A. (2013). Numerical study of the ferrofluid flow and heat transfer through a rectangular duct in the presence of a non-uniform transverse magnetic field. Journal of Magnetism and Magnetic Materials, 327, 31–42. DOI 10.1016/j.jmmm.2012.09.011. [Google Scholar] [CrossRef]

22. Nourazar, S. S., Habibi Matin, M., Simiari, M. (2011). The HPM applied to MHD nanofluid flow over a horizontal stretching plate. Journal of Applied Mathematics, 2011. DOI 10.1155/2011/876437. [Google Scholar] [CrossRef]

23. Motozawa, M., Chang, J., Sawada, T., Kawaguchi, Y. (2010). Effect of magnetic field on heat transfer in rectangular duct flow of a magnetic fluid. Physics Procedia, 9, 190–193. DOI 10.1016/j.phpro.2010.11.043. [Google Scholar] [CrossRef]

24. Çelik, İ (2012). Solution of magnetohydrodynamic flow in a rectangular duct by chebyshev polynomial method. Applied Mathematics, 2(3), 58–65. [Google Scholar]

25. Rashidi, M. M., Nasiri, M., Khezerloo, M., Laraqi, N. (2016). Numerical investigation of magnetic field effect on mixed convection heat transfer of nanofluid in a channel with sinusoidal walls. Journal of Magnetism and Magnetic Materials, 401, 159–168. DOI 10.1016/j.jmmm.2015.10.034. [Google Scholar] [CrossRef]

26. Al-Zurfi, N., Alhusseny, A., Nasser, A. (2020). Effect of rotation on forced convection in wavy wall channels. International Journal of Heat and Mass Transfer, 149, 119177. DOI 10.1016/j.ijheatmasstransfer.2019.119177. [Google Scholar] [CrossRef]

27. Alsabery, A. I., Sidik, N. A. C., Hashim, I., Muhammad, N. M. (2022). Impacts of two-phase nanofluid approach toward forced convection heat transfer within a 3D wavy horizontal channel. Chinese Journal of Physics, 77, 350–365. DOI 10.1016/j.cjph.2021.10.049. [Google Scholar] [CrossRef]

28. Mehta, S. K., Pati, S. (2020). Numerical study of thermo-hydraulic characteristics for forced convective flow through wavy channel at different Prandtl numbers. Journal of Thermal Analysis and Calorimetry, 141(6), 2429–2451. DOI 10.1007/s10973-020-09412-5. [Google Scholar] [CrossRef]

29. Elsafy, K. M., Saghir, M. Z. (2021). Forced convection in wavy microchannels porous media using TiO2 and Al2O3–Cu nanoparticles in water base fluids: Numerical results. Micromachines, 12(6), 654. DOI 10.3390/mi12060654. [Google Scholar] [CrossRef]

30. Mahmoudi, A., Mejri, I., Abbassi, M. A., Omri, A. (2014). Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with linear temperature distribution. Powder Technology, 256, 257–271. DOI 10.1016/j.powtec.2014.02.032. [Google Scholar] [CrossRef]

31. Maxwell, J. C. (1873). A treatise on electricity and magnetism, vol. 1. UK: Clarendon Press. [Google Scholar]

32. Murshed, S. M. S., Leong, K. C., Yang, C. (2005). Enhanced thermal conductivity of TiO2–water based nanofluids. International Journal of Thermal Sciences, 44(4), 367–373. DOI 10.1016/j.ijthermalsci.2004.12.005. [Google Scholar] [CrossRef]

33. Timofeeva, E. V., Routbort, J. L., Singh, D. (2009). Particle shape effects on thermophysical properties of alumina nanofluids. Journal of Applied Physics, 106(1), 014304. DOI 10.1063/1.3155999. [Google Scholar] [CrossRef]

34. Sheikholeslami, M., Rashidi, M. M., Ganji, D. D. (2015). Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4–water nanofluid. Computer Methods in Applied Mechanics and Engineering, 294, 299–312. DOI 10.1016/j.cma.2015.06.010. [Google Scholar] [CrossRef]

35. Sheikholeslami, M., Ganji, D. D. (2014). Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer. Energy, 75, 400–410. DOI 10.1016/j.energy.2014.07.089. [Google Scholar] [CrossRef]

36. Javaherdeh, K., Moslemi, M., Shahbazi, M. (2017). Natural convection of nanofluid in a wavy cavity in the presence of magnetic field on variable heat surface temperature. Journal of Mechanical Science and Technology, 31(4), 1937–1945. DOI 10.1007/s12206-017-0342-7. [Google Scholar] [CrossRef]

37. Wang, C. C., Chen, C. K. (2002). Forced convection in a wavy-wall channel. International Journal of Heat and Mass Transfer, 45(12), 2587–2595. DOI 10.1016/S0017-9310(01)00335-0. [Google Scholar] [CrossRef]

38. Rubin, S. G., Graves Jr, R. A. (1975). Viscous flow solutions with a cubic spline approximation. Computers & Fluids, 3(1), 1–36. DOI 10.1016/0045-7930(75)90006-7. [Google Scholar] [CrossRef]

39. Wang, P., Kahawita, R. (1983). Numerical integration of partial differential equations using cubic splines. International Journal of Computer Mathematics, 13(3–4), 271–286. DOI 10.1080/00207168308803369. [Google Scholar] [CrossRef]