Mathematical Modeling and Evaluation of Reliability Parameters Based on Survival Possibilities under Uncertain Environment

1  Introduction

In the past three decades, one of the challenging endeavors has been the design and manufacturing of large-scale reliable systems. These large-scale reliable systems are used in various application areas. Some of them are military applications, space exploration, commercial operations, and others deal in power distribution. Unlike the manufacturing of components, the manufacturing of such reliable systems includes the broader aspects of organizing composite manufacturing tools, operating organization and costs, as well as maintenance schedules, plus the skills required to make the system performance as an integrated entity too.

The study field of reliability engineering contains various activities, of which reliability modeling happens to be one area of the utmost significant. The traditional solution techniques are applied extensively based on probabilistic techniques, while the system survival probability is formulated by considering the statistical information (reliabilities or survival probabilities) of its sub-systems or components. In 1982, Martz et al. [1] studied the Bayesian reliability with a detailed analysis. The statistical information is obtained most of the time subjectively. They used a methodology to deal with the reliability in machine systems, with an application to error possibility. Gupta et al. [2] used the hybrid data to study the reliability parameters of a conveyor model.

A fuzzy set is adopted to cope with the uncertainty in mathematical models. In 1965, Zadeh [3] introduced fuzzy sets. Later in 1968, Zadeh [4] presented the concept of probability measures of fuzzy events. Over a short span, several researchers presented their works with reliability applications using fuzzy sets (Dubois et al. [5], Keller et al. [6], Onisawa [7], etc.). In the meantime, Onisawa [8] studied system reliability modeling with the application of fuzzy sets. Cai et al. [9] proposed the possibility concept to deal with uncertainty. They presented fuzzy variables to study the fuzzy reliability. Human reliability was studied with the help of fuzziness (Liang et al. [10], and Huang [11]). Some applications of fuzzy sets to reliability analysis were investigated by Bowles et al. [12], Murata [13], and Bing et al. [14]. In 2002, a risk assessment approach was investigated for implementing the uncertainty using fuzzy set theory by Cho et al. [15].

In 2007, Hryniewicz [16] used the fuzzy triangular numbers to determine the reliability parameters. After that, Karimi et al. [17] presented a novel technique related to fuzzy probability. They studied the risk assessment model for natural hazards. Later, some authors extended the risk concept to a fuzzy risk matrix in various ways. The reliability assessment and situation assessment were studied by using the multi-criteria decision-making approaches by Lu et al. [18], and then extended by Ding et al. [19]. Jain [20] studied the piecewise quadratic fuzzy number and presented the close interval approximation to fuzzy fractional programming problems. There are many papers related to the investigation of a mathematical model to handle the uncertainty to risk analysis. Later, Gargama et al. [21] extended fault and event tree analysis for failure mode effects using fuzzy logic. They presented an application to a fault and event tree analysis. In 2021, Varghese et al. [22] formulated a reliability model and evaluated using various fuzzy numbers, for instance, pendant, hexant, and fuzzy octant numbers.

Several researchers used the fuzzy interval to deal with uncertainty in reliability models (Washio et al. [23], Utkin et al. [24], etc.). The uncertainty in fault trees was studied for bridge construction by many researchers. Wu [25] presented a novel approach based on closed fuzzy numbers for reliability analysis. The fuzzy probability has an extended role in reliability analysis, which was presented by numerous authors (Yu et al. [26], Ung et al. [27], etc.). Purba et al. [28] studied the nuclear event reliability data to evaluate the reliability parameters. They considered the data related to failure possibility by using a new defuzzification method based on area. Arunraj et al. [29] proposed a novel approach based on the fuzzy set theory as well as Monte Carlo simulation. They presented the modeling under uncertainty and risk. In 2014, Purba et al. [30] presented a qualitative data processing approach. They used their approach for the assessment of fuzzy reliability. Maity et al. [31] developed a multi-objective transportation model considering the cost reliability in an uncertain environment. Recently, Yi et al. [32] introduced the triangular intuitionistic fuzzy number for reliability systems and decision making. They used the possible characteristics of fuzzy triangular numbers. Reliability evaluation and analysis have been studied by many authors in an uncertain environment. Examples are, but not limited to: Liu et al. [33], Li et al. [34], Xu et al. [35], Yang et al. [36], Jin et al. [37], and Zuo [38].

The above-reported literature review reveals the scope still remaining to innovate and study regarding both survival possibilities and the closed interval approximation of fuzzy numbers. Thus, a research gap is realized. In this paper, the reliability methods for modeling and evaluation based on survival possibilities and closed interval approximation of fuzzy numbers are introduced.

The outlay of the paper is constructed as follows: Section 2 introduces some of the notation and index needed in the problem formulation. In Section 3, reliability in possibility environment is discussed. Section 4 introduces the approximation of closed interval of piecewise quadratic fuzzy number for evaluation of the reliability with numerical example illustrates the efficiency of the method. Finally, some concluding remarks are reported in Section 5.

2  Preliminaries

In this section, some basics and concepts based on fuzzy numbers, piecewise quadratic fuzzy numbers, and their closed approximation intervals are recalled.

Definition 1. (Jain [20]). A piecewise quadratic fuzzy number (PQFN) is denoted by a~PQ=(a1,a2,a3,a4,a5), where a1≤a2≤a3≤a4≤a5 are real numbers and is characterized with the membership function μa~PQ is defined by (see Fig. 1)

μa~PQ={0, x<a1; 121(a2−a1)2(x−a1)2, a1≤x≤a2;121(a3−a2)2(x−a3)2+1, a2≤x≤a3;121(a4−a3)2(x−a3)2+1, a3≤x≤a4;121(a5−a4)2(x−a5)2, a4≤x≤a5;0, x>a5.

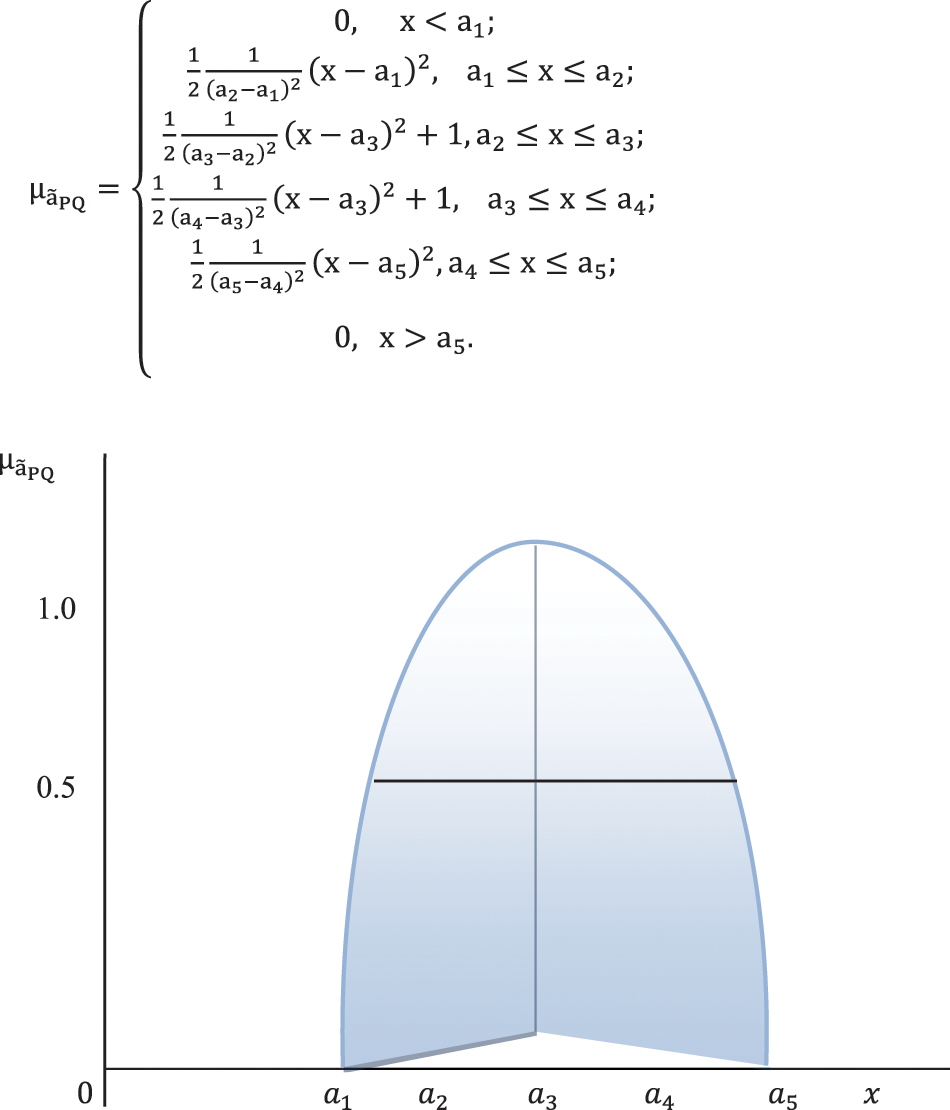
Figure 1: Graph of a PQFN

The interval of confidence at a level α for the PQFN is defined as

(a~PQ)α=[a1+2(a2−a1)α,a5−2(a5−a4)α];∀α∈[0,1].

Definition 2. (Jain [20]). An interval approximation [A]=[(aα)L,(aα)U] of a PQFN A~ is referred as the approximation of a closed interval, when

(aα)L=inf{x∈R:μA~≥0.5},and (aα)U=sup{x∈R:μA~≥0.5}.

Definition 3. (Jain [20]). The associated ordinary numbers of PQFN corresponding to the closed interval approximation [A]=[(aα)L, (aα)U] is A^=(aα)L+ (aα)U2.

3  Possibility Theory of Reliability

Consider a fuzzy number A~ with membership function μA~(t)∈[0,1], t∈[0, ∞). This fuzzy number represents a fuzzy data on the breakdown of a component at time t. Therefore, we have Eq. (1):

μA~(t)=0, for t=0.(1)

Also, consider the fuzzy number represents the possibility of failure at time t,t∈[0,∞). Thus, a law of possibilities of failure can be written as Eq. (2):

Ψ(t)=μA~(t).(2)

Remark 1: The possibility law of failure in (2) gives the possibility of failure occurring at time t.

Remark 2: A~ is not necessarily a unimodal fuzzy number (i.e., μA~(t) may have a flat at the top for μA~(t)=0).

Now, consider φ as the time to failure, where we have Ψ(t=φ)=μA~(t=φ)=1. Since μA~(t) is not necessarily a unimodal, φ may be over [φ1, φ2].

The cumulative failure possibility distribution of Ψ(t) over the interval [0,t]∈ℜ+ is expressed by Eq. (3):

Λ(t)=Vv=0t⁡Ψ(t), t≤φ.(3)

For t≥φ, we have Eq. (4) below:

Λ(t)=1.(4)

Therefore, Λ(t)=Ψ(t) until t≤φ, and after that Λ(t)=1. In addition, we can define another representation law of possibility that the equipment will be surviving (i.e., operating at the time t), namely the law of survival possibility which is denoted by Ω(t) and defined as the complement of the cumulative failure possibility distribution (Fig. 2), by Eq. (5) below:

Ω(t)=1−Λ(t).(5)

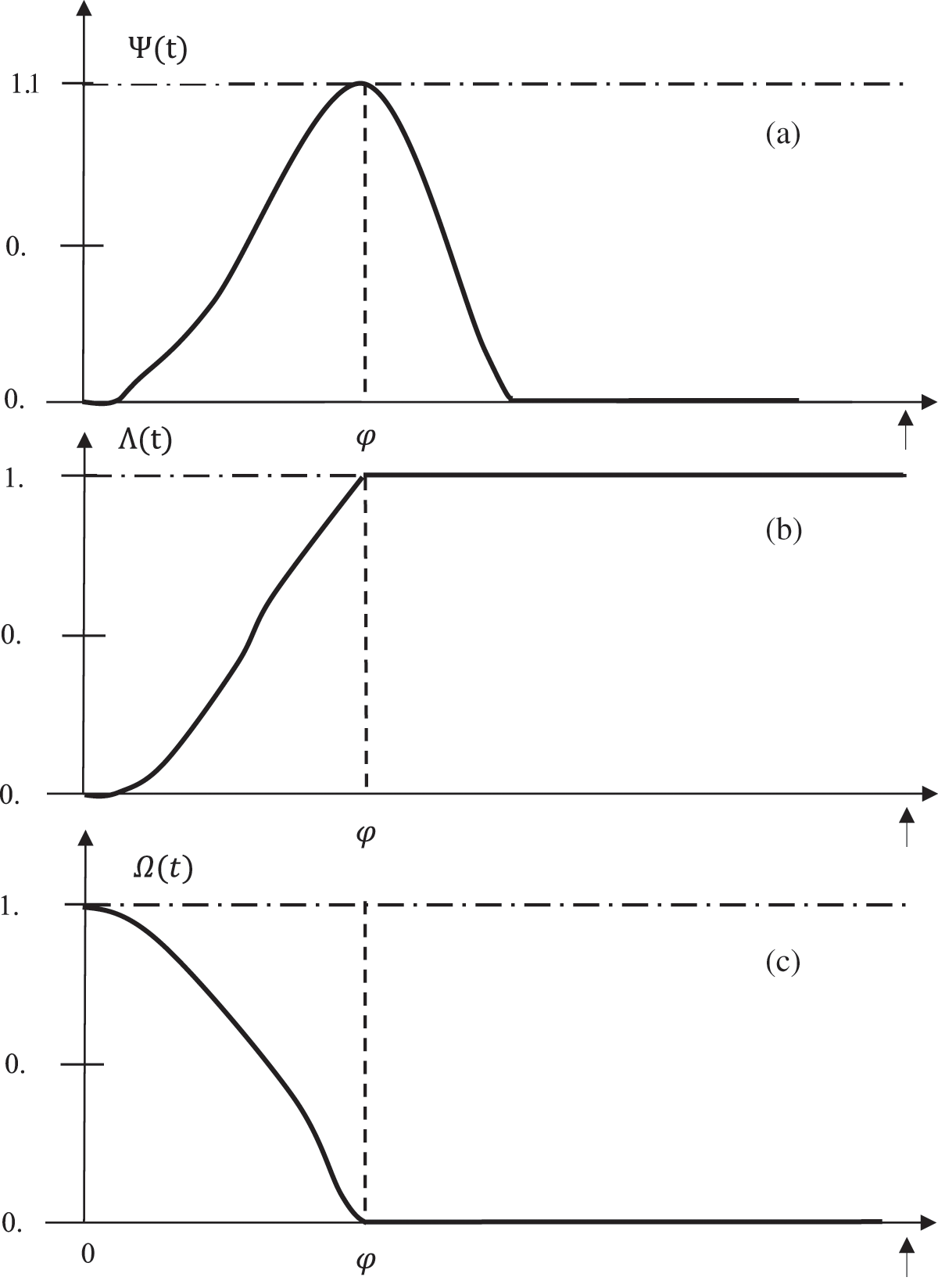
Figure 2: Possibility of failure, Ψ(t), the law of failure possibility (cumulative failure possibility distribution), Λ(t), and the law of survival possibility Ω(t)

Assume that Ψ(0)=0, but Ψ(0) may not be zero if the failure occurs immediately after the beginning of the service. In this case Ψ(t) and Λ(t)  occur at the origin with Ψ(0)=α<1 and Ω(t) will be Ω(0)=1−α which is lower than 1. Therefore, Ω(0) changes stepwise from 1 to (1−α) at the beginning of the service.

In the probability theory of reliability, the logarithmic derivative of the reliability function ω(t) is the failure rate ψ(t) as expressed by Eq. (6) below:

ψ(t)=ω′(t)ω(t).(6)

Similarly, in the possible theory of reliability, we characterize the failure rate by Eq. (7) as follows:

ψ(t)=Ω′(t)Ω(t).(7)

The below demonstrated Table 1 gives the failure rate which is based on the possibility theory, Ψ(t),Λ(t) and Ω(t)

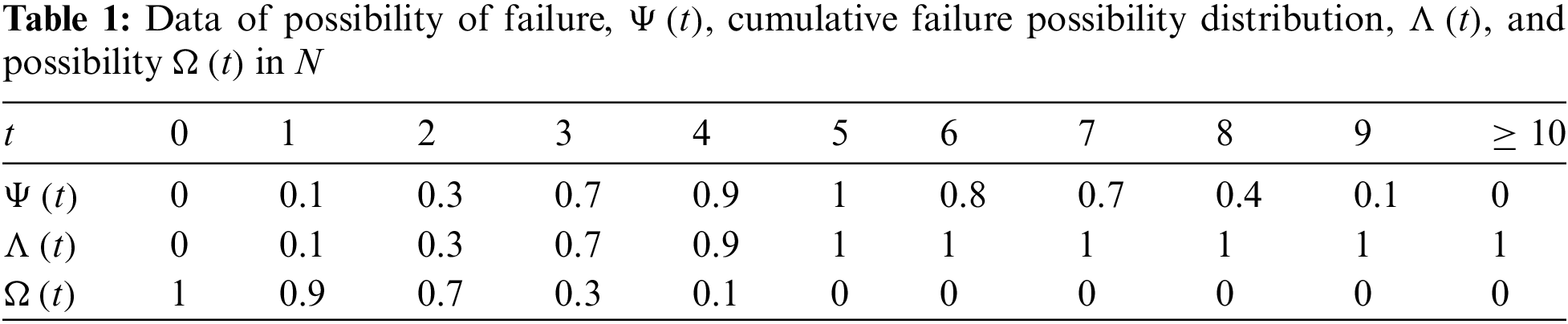
In the case of t∈N, the failure rate defined in Eq. (7) can be modified to rewrite by Eq. (8) below:

ψ(t)=Ω(t−1)−Ω(t)Ω(t−1),t=1,2,…(8)

If the failure rate ψ(t) is considered as basic data, the law of survival possibility (or reliability function) with the help of Eq. (7) is given as (Figs. 3 & 4):

dΩ(t)dt+ψ(t)Ω(t)=0,Ω(0)=1,t∈R+,(9)

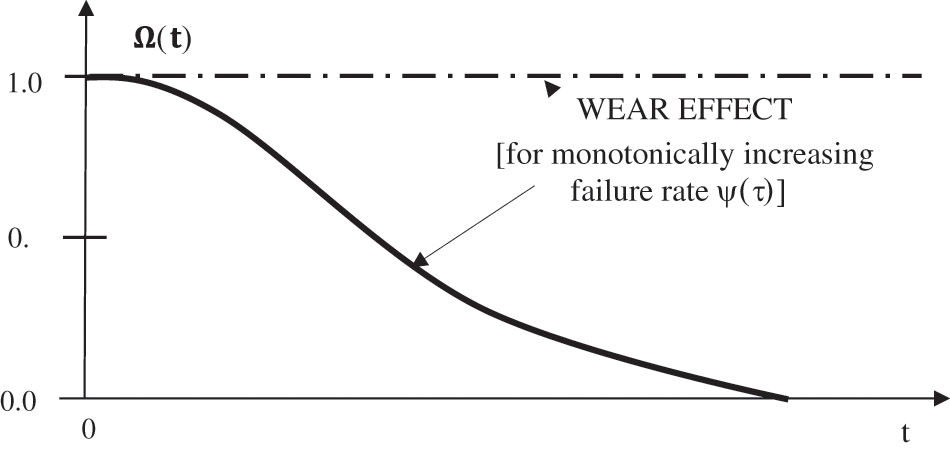
Figure 3: Survival possibility with monotonically increasing failure rate ψ(t)

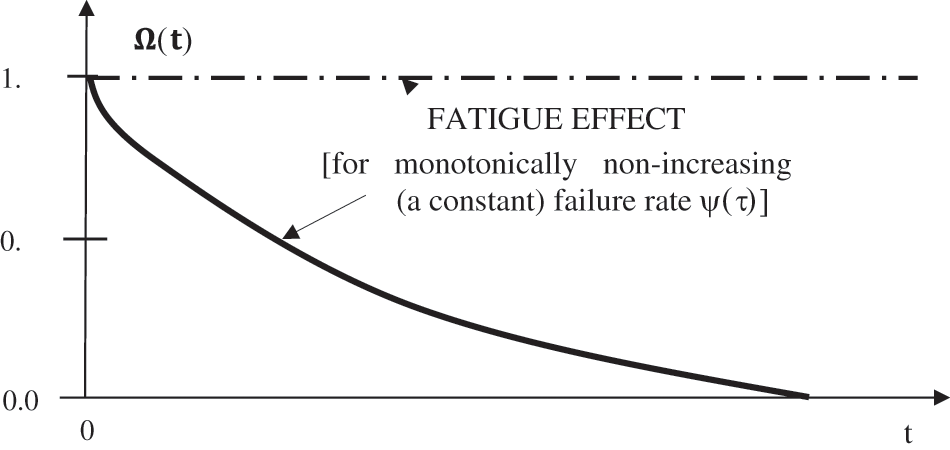
Figure 4: Survival possibility with monotonically non-increasing failure rate ψ(t)

For t∈N and by using Eq. (8) the reliability function is provided by Eq. (10) as follows:

Ω(t−1)−Ω(t)(1−ψ(t))=0,Ω(0)=1,t∈N.(10)

Remark 3:

(i)   The failure rate ψ(t) is always non-negative.

(ii)   ψ(t) is not necessarily monotone.

(iii)   Once can get the initial failure rate ψ(t)>0.

The solution of the differential Eq. (9) gives the Survival possibility in terms of the possibilistic failure rate by Eq. (11) as follows:

Ω(t)=e−∫vt⁡ψ(t)du,t∈ℜ+.(11)

For t∈N, the solution of differential Eq. (10) can be obtained recursively by Eq. (12) as follows:

Ω(1)=1−ψ(0),

Ω(2)=(1−ψ(1))(1−ψ(0)),

Ω(3)=(1−ψ(2))(1−ψ(1))(1−ψ(0)),

···

Ω(t)=(1−ψ(t−1))(1−ψ(t−2))…(1−ψ(1))(1−ψ(0))

=∏v=0t−1⁡(1−ψ(t−v)).(12)

Here ψ(t−1)=1, \Omega (t)=0 giving the time to failure t=φ.

Now, we examine some examples of reliability function as follows:

1.    ψ(t)=ψ0= a fixed value for the failure rate.

The corresponding survival function is written by Eq. (13) as follows:

Ω(t)=e−∫v=0t⁡ψ0du=e−ψ0t(Exponential survival law).(13)

2.     ψ(t)=ψ0t= a ramp type failure rate, and

Ω(t)=e−∫v=0t⁡ψ0tdu=e−ψ02t,t≥0(Truncated bell survival).(14)

There is another indicator of reliability called cumulative failure rate K(t), which is defined Eqs. (15) and (16) as

K(t)=∫v=0t⁡ψ(v)dvin ℜ+,and(15)

K(t)=∑v=0t⁡ψ(v), in {\mathbb N}.(16)

It is noted in the Eq. (17) below:

ψ(t)=poss (A~>t).(17)

Proceeding in the same way, we obtain Eq. (18) as follows:

ω(t)=Pr(A~>t).(18)

Now, let us consider the case where a system is introduced into a new service at t=a. The survival function is conditioned on t=a. Thus, we obtain Eq. (19):

Ω(a+t)=Ω(a) . Ωa(t).(19)

Here, it is observed that Ωa(t) is the survival function of the equipment of the age a from the time it begins its service. Thus, Ωa(t) is conditional possibility conditioned on survival age from t=0tot=a, which is given by Eq. (20):

Ωa(t)=Ω(a+t)Ω(a).(20)

The corresponding failure rate is computed by Eq. (21) as follows:

ψa(t)=ψ(a+t),(21)

In addition, the cumulative failure rate is given by Eq. (22) as below:

Ka(t)=∫v=0t⁡ \psi (a+v)dv

=K(a+t)− K(a).(22)

4  Approximation of a Closed Interval for Piece-Wise Quadratic Fuzzy Numbers for Reliability Evaluating

This section is divided into two sub-sections as follows.

4.1 Approximation of Closed Interval

Consider the situation where an expert is uncertain about the estimation of model parameters. Instead of describing the reliability function using one survival law, he/she gives two subjective functions forming an interval of confidence. For example, he/she gives

Ω∘(t): The lower law of survival,

Ω∘(t): The upper law of survival.

Through the closed interval approximation, the subjective survival law can be represented by Eq. (23) below:

Ωα(t)=[Ω∘α(t),Ω∘α(t)];∀t∈ℜ+.(23)

Theorem 1. At a given time t

ψ1(t)≥ψ2(t)⇒Ω1(t)≤Ω2(t); ∀ t∈ℜ+.(24)

Proof

From the Definition of the failure rate and the survival function, we have

ψ1(t)≥ψ2(t)⇒∫v=0t⁡ψ1(v) dv≥∫v=0t⁡ψ2(v) dv

⇒−∫v=0t⁡ψ1(v) dv≤−∫v=0t⁡ψ2(v) dv

⇒ e−∫v=0t⁡ψ1(v) dv≤e−∫v=0t⁡ψ2(v) dv

⇒ Ω1(t)≤Ω2(t).

This completes the proof.

Theorem 2. Let ψα(t)=[ψ∘α(t), ψ∘α(t)];∀t∈ℜ+ be the closed interval approximation of piecewise quadratic fuzzy numbers of failure rate with Ω∘α(t)≤Ω∘α(t) and Ωα(t)=[Ω∘α(t),Ω∘α(t)] be the corresponding closed interval approximation of possibility of survival. Then, we have the Eq. (25) as follows:

ψα(t)∈[,ψ∘α(t), ψ∘α(t)]⇒Ωα(t)∈[Ω∘α(t),Ω∘α(t)].(25)

4.2 Reliability Evaluating

In this sub-section, we present some examples as follows:

Example 1. Let the closed interval approximation of the failure rate be given by

ψα(t)=[ψ∘α(t)=γ1, ψ∘α(t)=γ2], γ2≥γ1.

The corresponding closed interval approximation for the survival law is presented by Eq. (26) as follows:

Ωα(t)=[Ω∘α(t)=e−γ2t,Ω∘α(t)=e−γ1t](26)

The data of failure rate and survival law for the Example 1 is illustrated in Table 2 below:

Now, let the failure rate be

ψα(t)=[ψ∘α(t)=t γ1, ψ∘α(t)=t γ2].

Then, the corresponding survival law is presented by Eq. (27) as follows:

Ωα(t)=[Ω∘α(t)=e−γ22t2,Ω∘α(t)=e−γ12t2].(27)

The failure rate is not necessary monotonic, but the cumulative failure rate is always monotonic as in the definition, therefore we obtain Eq. (28) below:

K(t)=∫0t⁡ψ(u)du.(28)

The closed interval approximation of the cumulative failure rate is expressed by Eq. (29) as under:

Kα(t)=[K2α(t),K1α(t)].(29)

In addition, it is possible to define in another way the closed interval approximation for the survival law Ω(t) using the inverse time function t(Ω) instead of the survival function. In this case, the closed interval approximation for time to survival with reliability Ω is as in Eq. (30) below:

A~(Ω)=[t∘ (Ω), t∘ (Ω)].(30)

Lemma 3. For all t,t1,t2∈R, we have Eqs. (31)–(32) as under:

1.Ω1(t)≤Ω2(t)⇔t1(Ω)≤t2(Ω),(31)

2.t(Ω)∈[t∘(Ω),t∘(Ω)]⇔Ω(t)∈[Ω∘(t),Ω∘(t)].(32)

Example 2. We have Eqs. (33)–(34) as follows:

(a)t=−1ψlnlnΩ,correspond toΩ(t)=e−ψt,(33)

(b)t=−2ψlnlnΩ,correspond toΩ(t)=e−ψ2t2(34)

The corresponding closed intervals approximation for time to survival forallΩ∈[0,1], are in Eqs. (35)–(36) below:

1.A~=A~(Ω)=[t∘(Ω),t∘(Ω)]=[−1ψ∘lnlnΩ,−1ψ∘lnlnΩ],(35)

2.A~=A~(Ω)=[−2ψ∘lnlnΩ,−2ψ∘lnlnΩ]=[t∘(Ω),t∘(Ω)].(36)

The divergence of these two cases is evaluated and are expressed in Eq. (37) as under:

ξ(Ω)=t∘(Ω)−t∘(Ω).(37)

It is quite evident that for ξ(Ω) increases monotonically when Ω decreases with ξ(Ω→0). In the reliability theory, it is usual to consider the mean failure time t¯. In the possibility theory of reliability, t¯ is defined by Eqs. (38)–(39) as below:

(i)t¯=∫t=0∞⁡Ω(t)dt, t∈ℜ+,(38)

(ii)t¯=∑t=0∞⁡Ω(t),t∈N.(39)

In terms of failure rate, (t), t¯ is defined by Eqs. (40)–(41) as follows:

1.t¯=∫t=0∞⁡e∫v=0t⁡ψ(v)dvdt, v, t∈ℜ+,(40)

2.t¯=∑t=0∞⁡∏v=0t⁡(1−ψ(t−v)), t, v∈N.(41)

By applying the survival law, one can write t¯ as presented in Eq. (42) below:

t¯=∑t=1∞⁡t(Ω(t−1)−Ω(t)),t∈N.(42)

Example 3. Consider an example using the failure rate and the survival law given in this Table 3:

Using Eq. (41), the mean failure rate is given by Eq. (43) as follows:

t¯=1+1+0.85+0.646+0.381+0.182+0.045+0.004=4.108(43)

Also, the mean failure rate using Eq. (42) is given by Eq. (44) below:

t¯=2(0.15)+3(0.204)+4(0.265)+5(0.199)+6(0.137)=7(0.041)+8(0.004)

=4.018(44)

Thus, the closed interval approximation for the mean failure time t¯ (referring to Table 2) is given by t¯=[t¯∘,t¯∘]=[3.732,4.448].

Remark 4. It is trivial to observe that t¯1 is less than or equal to t¯2 as presented by Eq. (45) below:

Ω1(t)≤Ω2(t)⇔t¯1≤t¯2.(45)

5  Conclusions and Future Research Directions

In industrial problems, the performance of the system reliability is of utmost concern. Thus, the outcomes for the failure of one or more machines are required to compute with extreme care. In this paper, we have demonstrated that when uncertainty is associated with the system, the reliability function, as well as some other similar criteria, are formulated as a mathematical model using the closed interval approximations of a piecewise quadratic fuzzy number. Apart from this, the intervals of confidence of fuzzy numbers, instead of the probabilistic, are also used in suggested modeling to handle the associated uncertainty. Extensions of the possibilistic criteria to several scenarios of reliability evaluation may lead to some interesting studies. There are several future possibilities to extend the proposed work in many application areas. One can consider the fuzzy type-2 sets (Tang et al. [39]), neutrosophic sets [40], and LR possibilistic variables [41] and deal with the uncertainty for further extensions of current research.

Acknowledgement: Researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Martz, H. F., Waller, R. A. (1982). Bayesian reliability analysis. John Wiley & Sons, New York. [Google Scholar]

 2.  Gupta, S., Bhattacharya, J. (2007). Reliability analysis of a conveyor system using hybrid data. Quality and Reliability Engineering International, 23(7), 867–882. DOI 10.1002/(ISSN)1099-1638. [Google Scholar] [CrossRef]

 3.  Zadeh, L. A. (1965). Fuzzy sets. Information Control, 8(1), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]

 4.  Zadeh, L. A. (1968). Probability measures of fuzzy events. Journal of Mathematical Analysis and Applications, 23, 421–428. DOI 10.1016/0022-247X(68)90078-4. [Google Scholar] [CrossRef]

 5.  Dubois, D., Prade, H. (1980). Fuzzy sets and systems; Theory and Applications. New York: Academic Press. [Google Scholar]

 6.  Keller, A. Z., Zaitri, C. K. (1989). Further applications of fuzzy logic to reliability assessment. Microelectronics Reliability, 29, 399–404. DOI 10.1016/0026-2714(89)90627-6. [Google Scholar] [CrossRef]

 7.  Onisawa, T. (1989). Fuzzy theory in reliability analysis. Fuzzy Sets and Systems, 30(3), 361–363. DOI 10.1016/0165-0114(89)90031-6. [Google Scholar] [CrossRef]

 8.  Onisawa, T. (1990). An application of fuzzy concept to modeling of reliability analysis. Fuzzy Sets and Systems, 37, 267–286. DOI 10.1016/0165-0114(90)90026-3. [Google Scholar] [CrossRef]

 9.  Cai, K. Y., Wen, C. Y., Zhang, M. L. (1991). Fuzzy variables as a basis for a theory of fuzzy reliability in the possibility context. Fuzzy Sets and Systems, 42, 145–172. DOI 10.1016/0165-0114(91)90143-E. [Google Scholar] [CrossRef]

10. Liang, G. H., Wang, M. J. (1993). Evaluating human reliability using fuzzy relation. Microelectronics Reliability, 33, 63–80. DOI 10.1016/0026-2714(93)90046-2. [Google Scholar] [CrossRef]

11. Huang, H. Z. (1995). Reliability analysis method in the presence of fuzziness attached to operating time. Microelectronics Reliability, 35, 1483–1487. DOI 10.1016/0026-2714(94)00173-L. [Google Scholar] [CrossRef]

12. Bowles, J. B., Pelaez, C. E. (1995). Fuzzy logic prioritization of failures in a system failure mode, effects and criticality analysis. Reliability Engineering and System Safety, 50(2), 203–213. DOI 10.1016/0951-8320(95)00068-D. [Google Scholar] [CrossRef]

13. Murata, T. (1995). An application of fuzzy set theory to reliability analysis. In: Onisawa T., Kacprzyk J. (Eds.Reliability and safety analyses under fuzziness. Studies in fuzziness, vol. 4. Physica, Heidelberg. DOI 10.1007/978-3-7908-1898-7_13. [Google Scholar] [CrossRef]

14. Bing, L., Meilin, Z., Kai, X. (2000). A practical engineering method for fuzzy reliability analysis of mechanical structures. Reliability Engineering and System Safety, 67(3), 311–315. DOI 10.1016/S0951-8320(99)00073-3. [Google Scholar] [CrossRef]

15. Cho, H. N., Choi, H. H., Kim, Y. B. (2002). A risk assessment methodology for incorporating uncertainties using fuzzy concepts. Reliability Engineering and System Safety, 78(2), 173–183. DOI 10.1016/S0951-8320(02)00158-8. [Google Scholar] [CrossRef]

16. Hryniewicz, O. (2007). Fuzzy sets in the evaluation of reliability. In: Evitin, G. (Ed.Computational intelligence in reliability engineering new metaheuristics, neural and fuzzy techniques in Reliability, pp. 363–386. Berlin, Heidelberg: Springer-Verlag. [Google Scholar]

17. Karimi, I., Hüllermeier, E. (2007). Risk assessment system of natural hazards: A new approach based on fuzzy probability. Fuzzy Sets and Systems, 158(9), 987–999. DOI 10.1016/j.fss.2006.12.013. [Google Scholar] [CrossRef]

18. Lu, J., Zhang, G., Ruan, D. (2008). Intelligent multi-criteria fuzzy group decision-making for situation assessments. Soft Computing, 12(3), 289–299. DOI 10.1007/s00500-007-0197-4. [Google Scholar] [CrossRef]

19. Ding Y., Lisnianski, L. (2008). Fuzzy universal generating functions for multi-state system reliability assessment. Fuzzy Sets and Systems, 159(3), 307–324. DOI 10.1016/j.fss.2007.06.004. [Google Scholar] [CrossRef]

20. Jain, S. (2010). Close interval approximation of piecewise quadratic fuzzy numbers for fuzzy fractional program. Iranian Journal of Operations Research, 2(1), 77–88. [Google Scholar]

21. Gargama, H., Chaturvedi, S. K. (2011). Criticality assessment models for failure mode effects and criticality analysis using fuzzy logic. IEEE Transactions on Reliability, 60(1), 102–110. DOI 10.1109/TR.2010.2103672. [Google Scholar] [CrossRef]

22. Varghese, P. J., Rosario, G. M. (2021). A study on reliability using pendant, hexant, octant fuzzy numbers. Journal of Reliability and Statistical Studies, 14(2), 491–526. DOI 10.13052/jrss0974-8024.1426. [Google Scholar] [CrossRef]

23. Washio, T., Kitamura, M. (1995). Human reliability analysis with fuzzy interval. In: Nisawa, T. Kacprzyk, J. (Eds.Reliability and safety analyses under fuzziness, pp. 233–244.Physica-Verlag, Heidelberg [Google Scholar]

24. Utkin, L. V., Gurov, S. V., Shubinsky, M. I. (1996). Reliability growth in the probability and possibility contexts. Microelectronics Reliability, 36(9), 1155–1166. DOI 10.1016/0026-2714(95)00179-4. [Google Scholar] [CrossRef]

25. Wu, H. C. (1997). Fuzzy reliability analysis based on closed fuzzy numbers. Information Science, 103, 135–159. DOI 10.1016/S0020-0255(97)00059-5. [Google Scholar] [CrossRef]

26. Yu, D., Park, W. S. (2000). Combination and evaluation of expert opinions characterized in terms of fuzzy probabilities. Annals of Nuclear Energy, 27(8), 713–726. DOI 10.1016/S0306-4549(00)82012-5. [Google Scholar] [CrossRef]

27. Ung, S. T., Shen, W. M. (2011). A novel human error probability assessment using fuzzy modeling. Risk Analysis, 31(5), 745–757. DOI 10.1111/j.1539-6924.2010.01536.x. [Google Scholar] [CrossRef]

28. Purba, J. H., Lu, J., Ruan, D., Zhang, G. (2012). An area defuzzification technique to assess nuclear event reliability data from failure possibilities. International Journal of Computational Intelligence and Applications, 11(4), 1250022, DOI 10.1142/S1469026812500228. [Google Scholar] [CrossRef]

29. Arunraj, N. S., Mandal, S., Maiti, J. (2013). Modeling uncertainty in risk assessment: An integrated approach with fuzzy set theory and monte carlo simulation. Accident Analysis and Prevention, 55, 242–255. DOI 10.1016/j.aap.2013.03.007. [Google Scholar] [CrossRef]

30. Purba, J. H., Lu, J., Zhang, G., Pedrycz, W. (2014). A fuzzy reliability assessment of basic events of fault trees through qualitative data processing. Fuzzy Sets and Systems, 243, 50–69. DOI 10.1016/j.fss.2013.06.009. [Google Scholar] [CrossRef]

31. Maity, G., Roy, S. K., Verdegay, J. L. (2016). Multi-objective transportation problem with cost reliability under uncertain environment. International Journal of Computational Intelligence Systems, 9, 839–849. DOI 10.1080/18756891.2016.1237184. [Google Scholar] [CrossRef]

32. Yi, Z. H., Li, H. Q. (2018). Triangular norm-based cuts and possibility characteristics of triangular intuitionistic fuzzy numbers for decision making. International Journal of Intelligent Systems, 33(6), 1165–1179. DOI 10.1002/int.21974. [Google Scholar] [CrossRef]

33. Liu, B., Zhang, Z., Wen, Y., Kang, S., Guo, Y. et al. (2020). Reliability analysis for complex systems subject to competing failure processes in an uncertain environment. Journal of Intelligent & Fuzzy Systems, 39, 4331–4339. DOI 10.3233/JIFS-200343. [Google Scholar] [CrossRef]

34. Li, Y., Peng, R., Kucukkoc, I., Tang, X., Wei, F. (2020). System reliability optimization for an assembly line under uncertain random environment. Computers & Industrial Engineering, 146, 106540. DOI 10.1016/j.cie.2020.106540. [Google Scholar] [CrossRef]

35. Xu, Q., Zhu, Y. (2020). Uncertain random optimization models based on system reliability. International Journal of Computational Intelligence Systems, 13, 1498–1506. DOI 10.2991/ijcis.d.200915.002. [Google Scholar] [CrossRef]

36. Yang, Y., Huang, S., Wen, M., Chen, X., Zhang, Q. et al.(2021). Analyzing travel time belief reliability in road network under uncertain random environment. Soft Computing, 25, 10053–10065. DOI 10.1007/s00500-021-05940-w. [Google Scholar] [CrossRef]

37. Jin, T., Xia, H., Gao, S. (2021). Reliability analysis of the uncertain fractional-order dynamic system with state constraint. Mathematical Methods in the Applied Sciences, 45, 2615–2637. DOI 10.1002/mma.7943. [Google Scholar] [CrossRef]

38. Zuo, M. J. (2021). System reliability and system resilience. Frontiers of Engineering Management, 8, 615–619. DOI 10.1007/s42524-021-0176-y. [Google Scholar] [CrossRef]

39. Tang, Z., Lu, Z. (2014). Reliability-based design optimization for the structures with fuzzy variables and uncertain-but-bounded variables. Journal of Aerospace Information Systems, 11, 412–422. DOI 10.2514/1.I010140. [Google Scholar] [CrossRef]

40. Khalifa, H. A., Kumar, P., Mirjalili, S. (2021). A KKM approach for inverse capacitated transportation problem in neutrosophic environment. Sādhanā, 46, 166. DOI 10.1007/s12046-021-01682-5. [Google Scholar] [CrossRef]

41. Khalifa, H. A., Kumar, P. (2022). A goal programming approach for multi-objective linear fractional programming problem with LR possibilistic variables. International Journal of System Assurance Engineering and Management, 13, 2053–2061. DOI 10.1007/s13198-022-01618-0. [Google Scholar] [CrossRef]