Topology Optimization of Stiffener Layout Design for Box Type Load-Bearing Component under Thermo-Mechanical Coupling

1  Introduction

Stiffened structures are applied widely in aeronautics, machine tool, automobile, and so on. These structures are composed of an unstiffened structure (plate or shell element) and stiffeners (Beam elements). The proper distribution of stiffeners on the structure can improve the structural mechanical performance effectively [1]. Recently, with the requirements of the products’ precision increasing, the accuracy of the machining center has become extremely severe. The deformation of the machining center body (Box type load-bearing component) is the key factor that influences the accuracy of the machining center because it will be amplified by dimensional chain transmission from the body to the cutter. The deformation of the body mainly comes from load and temperature during work. In mechanics, the deformation can be controlled by improving the structure stiffness with increasing stiffener. In thermotic, the heat generated by the manufacturing process will lead to local deformation of the body, which is controlled by heat conduction optimization. Meanwhile, design objection of advanced machining center not only strive for excellent mechanical performances but also seek economic advantages for customers [2–4]. Thus, controlling the deformation under thermo-mechanical coupling without substantially increasing materials has been done to develop methodologies and approaches.

The internal structure optimization of box type support load-bearing component is the stiffener layout optimization design, essentially. In traditional, the stiffener layout design is usually referring to the regular shape, such as shape ‘#’, shape ‘*’, shape ‘X’, and so on. It is no doubt that the regular shape stiffener layout is simple to design and easy to manufacture, but actually, the stiffener layout design is still blind because it is difficult to improve both mechanics and thermotics of load-bearing components for requiring stiffness and material savings effectively. Therefore, a new optimization method for stiffener layout design should be developed, especially for the structure under thermo-mechanical coupling.

Actually, stiffener layout optimization is the problem for searching optimal material distribution [5], and topology optimization has become the most popular tool for stiffener layout design [6]. The advantage of structure topology optimization is using the same material to obtain better mechanics and thermotics performance [7]. According to the evolutionary and degeneration in natural phenomena, topology has developed two kinds of principles: one is the degeneration principle, which is filling adequate materials into the microstructure before optimization, then the microstructure will be filtered and deleted to obtain optimal microstructure layout; the other is the evolutionary principle, which is developed a series potential link element (stiffener) in the structure firstly, then calculate the contributions of different link element (stiffener) for structure and choice the link elements (stiffener) which contribution is larger than others, on this basis, continue to grow link element (stiffener) and choice again, finally, completing link element (stiffener) grow by iteration to obtain optimal structure. The processing shows the survival of the fittest.

The homogenization method and the density method as the traditional structure topology optimization methods are adopted frequently [8]. Bendsoe et al. [5] developed the homogenization method, which converted the topology optimization problem to the dimensional optimization problem to seek the optimal distribution in the material space, then the structure satisfies load and other conditions. The defects of the homogenization method are too many design variables and the checkerboard phenomenon. Based on their homogenization theory, a lot of excellent research results for the optimal topology of stiffened plate structures have been obtained. Krog et al. [9] proposed an approach to deal with topology optimization of statically loaded or freely vibrating disk and plate structures. Ansola et al. [10] presented a combined shape and reinforcement layout optimization method of shell structures, the geometry of shell mid-plane and the layout of surface stiffeners on the shell are optimized simultaneously. Afonso et al. [11] presented an integrated design tool that includes developments, integration, and applications for the structural optimization of variable thickness plates and free-form shells to obtain optimum designs. This approach overcomes the drawbacks of both topology optimization and structural shape optimization procedures. Variable density method assumed that the material is composed of several elements whose densities are from 0 to 1. Then, seeking materials distribution for optimal performance of structure under a certain material. Mao et al. [12] applied the Solid Isotropic Material with Penalization (SIMP) method to design the battery rack in an AUV, and obtained the optimization results under different ratios of force and thermal loads. The results demonstrated that topology optimization could reduce the temperature gradient of the battery rack structure while bearing the force load. Although this method cannot be validated which is global optimality, it improved the larger variables problem of the homogenization method and simplicity of operator. The chess board problem is still in existence. The traditional optimization methods are simple and easy to operate, but have a disadvantage that the design procedure may fail if the layout is not formed a stiffener-like pattern.

To overcome the disadvantage of traditional optimization methods, some new methods were developed. Bojczuk et al. [13] presented a method to optimize the layout and shape of stiffeners in plates. The heuristic algorithm is used to find optimal reinforcement, both loaded in a plane and in bending Kirchhoff’s plates are considered. In addition, the minimization or maximization of arbitrary objective functions of displacements, strains, stresses, or reactions with the constraint imposed on the structure cost is also considered. Kimmel [14] developed Level Set Method (LSM), the low dimensional curved line or surface is described implicitly. The advantages of LSM are: both shape and topology are optimized simultaneously, no checkerboard phenomenon, without intermediate density units and so on. The defections of LSM method are converging slowly and computational efficiency is low. Steven et al. [15] proposed the Evolutionary Structure Optimization (ESO) method, which is based on the concept of gradually removing redundant material to achieve an optimal design. Ding et al. [16,17] proposed a new topology optimization method for the generation of stiffener layout based on the growth mechanism of branching systems in nature, and named the bionic growth method. Then, Li et al. [18] presented a multidiscipline topology optimization method to produce the stiffener layout for plate/shell structures, which simulated the emergence of complex branching patterns copying the self-optimization of leaf veins, and on this basis, developed a novel approach for designing the stiffener layout inside machine tools [19].

In the structure optimization for heat conduction, it is still focus on cross-sectional area optimization [20] and interval of heat dissipation channel [21], including density penalty function method [22], Evolutionary Structure Optimization (ESO) method [23] and Level Set Method (LSM) method [24,25]. The thermal compliance is an objective function [26], and the optimal heat conduction coefficient distribution of structure is obtained the thermal compliance is minimum. Some researchers use the temperature variance to evaluate the uniformity of the whole structure temperature distribution [27]. Zhang et al. [28] proposed evaluating indicators of structure heat dissipate performance by geometric average temperature. Zuo et al. [29] deduced the governing equations and optimization model for topology optimization under thermo-mechanical coupling, and an adjoint method is used to calculate the sensitivity of structure’s response. Takezawa et al. [30] developed a structure optimization method based on SIMP. Zhang et al. [31] linked reliability design with topology optimization design, Yan et al. [32,33] and Chen et al. [34] carried out topology optimization design for multi-material mechanisms. Recently, to satisfy the green manufacturing, increasing material developed fast, and topology optimization based on the increasing material principled is derived. This method uses a material increasing method on the key position of structure to achieve structure optimally. This work developed an adaptive growth algorithm based on increasing material principle for topology optimization of stiffener layout design under thermo-mechanical coupling.

To optimal stiffeners layout pattern of box type load-bearing component, this paper is organized as follows: Firstly, constructs the equivalent model of box type support of the machining center under thermo-mechanical coupling, then the stiffness diffusion theory is extended to the load and heat conduction model to develop structure adaptive growth algorithm. Secondly, extends the optimization objective to minimum strain energy and thermal compliance, then an adaptive growth algorithm is developed to optimize stiffener layout under thermo-mechanical coupling. Thirdly, to evaluate the method, the stiffener layout of square shell under thermo-mechanical coupling is optimized by the adaptive growth algorithm. Finally, the adaptive growth algorithm is used to optimize the stiffener of box type support.

2  Adaptive Growth Algorithm under Thermo-Mechanical Coupling

The principle of adaptive growth algorithm under thermo-mechanical coupling is the calculation of two parallel levels of the objective function, load, and heat conduction. The two parallel levels of objective function and optimization are connected by stiffener.

In the adaptive growth algorithm of structure load optimization, the objective of the optimization is to find the stiffener which can be minimized the whole strain energy. In adaptive growth considering thermal loads, the objective of the optimization is to find a layout of the heat conduction rod to a minimum heat dissipation of structure.

The adaptive growth algorithm of this paper can construct the connection between the adaptive growth algorithm of structure and heat conduction structure, and the unit of connection is the growth stiffener. The growth stiffeners under thermal coupling are improved in terms of structural stiffness and heat dissipation. In terms of load, it is equivalent to adding a stiffener. At the heat level, it is equivalent to adding a high thermal conductivity rod.

After the stiffener growth, both the stiffness matrix and heat conduction stiffness matrix are updated based on the stiffness diffusion theory. The stiffness matrix updated under thermo-mechanical coupling is shown in Fig. 1.

Figure 1: Stiffness matrix updated under thermo-mechanical coupling

The interrelationship between the high heat conduction rod and stiffener is considered during the stiffener growth. The flow chart of growth stiffener layout under thermo-mechanical coupling is shown in Fig. 2.

Figure 2: The flow chart of growth stiffener layout under thermo-mechanical coupling

Considering the influence of thermo-mechanical coupling, the weighting factor is used to represent the influence of compliance and heat dissipation. The optimization goal is to optimize the comprehensive performance of the stiffener, and the density of the stiffener is the design variable. Under the condition of a given volume constraint, find the stiffener distribution of the best structure. In the multi-objective topology optimization problem, the topology optimization model is as follows:

find:x=[x1,x2,…,xn]Min:f=wE+(1−w)Qs.t.KU=FKTT=pV=∑i=1nxivi0<xmin≤xi≤1(1)

where w represents weighted coefficients, representing the proportion of heat dissipation weakness and compliance; xi is the design variable (the relative density); E and Q are the objective functions of structural flexibility and heat dissipation weakness; f is the topology optimization objective function; KT and K are stiffness matrix and heat conduction stiffness matrix; v is the volume of the design domain.

The flow of the adaptive growth algorithm under thermo-mechanical coupling is as follows:

(1)   Set the specific size of the box type load-bearing component, and the correlation coefficient of material properties, including elastic modulus, Poisson’s ratio, and thermal conductivity.

(2)   At the structural level and the heat level, the upper surface of the box type load-bearing component is divided into grids. The grid division at the structural level and heat level is completely consistent, this is, keeping the same grid size.

(3)   The overall stiffness matrix Struct_K of the base structure divided by free quadrilateral element grid and the overall stiffness matrix Heat_K of the base structure divided by free quadrilateral element grid are calculated.

(4)   Selected seed growth points at the selected structural level and at the heat level.

(5)   The structural seed growth point and the heat conduction seed growth point grow at the same time, and the mutual influence relationship is considered during the growth process.

(6)   Stiffness diffusion is carried out on the stiffener at the structural level. At the same time, the growth stiffener generated at the heat level is replaced by the stiffener at the same position. Then introduce the stiffener to the structural level, and stiffness diffusion for the stiffener. Finally, the overall stiffness matrix updated at the structural level is obtained.

(7)   Stiffness diffusion is carried out on the high heat conduction rod of the heat level. At the same time, the growth ribs generated at the structural level are replaced by high thermal conductivity rods in the same position and introduced to the heat level. Then stiffness diffusion for the high thermal conductivity rods. Finally, the overall stiffness matrix of the updated at the heat level is obtained.

(8)   When the growing rib grows out of the boundary or the total volume of the growing rib reaches the predetermined upper limit, the growth is stopped. Otherwise, the growth is continued.

(9)   Finally, the structural layout of the growth rib under the action of thermo-mechanical coupling is obtained.

3  The Stiffener Layout Optimization Design of Square Shell

The square shell is shown in Fig. 3. The size is 480mm×480mm×5 mm, heat conductivity is k0=40W/(m⋅K). There is a uniform heat source on the plate and the heat flux is 100W/m2, the edges of square shell are heat insulation. The heat radiation is from the middle point of one edge, O, which is kept at a constant temperature, 0°C. The material thermal conductivity of growth stiffener is k=100W/(m⋅K). In addition, a vertical load is applied on the center of plate and the edges of plate are fixed. The stiffener will be grown adaptive under thermo-mechanical coupling.

Figure 3: Square shell case model

3.1 Temperature Distribution and Deformation under Thermo-Mechanical Coupling of Square Shell with Initial Condition

The temperature distribution and thermo-mechanical coupling with initial condition are shown in Fig. 4. The temperature distribution of the structure without stiffeners in Fig. 4 shows that the maximum temperature is 118.592°C, and the maximum deformation of structure without stiffener is 0.84057 mm.

Figure 4: Temperature distribution and structural deformation with initial condition

3.2 Temperature Distribution and Structural Deformation under Thermo-Mechanical Coupling of Shape “#” Stiffener Layout

The temperature distribution and structural deformation under thermo-mechanical coupling of shape “#” stiffener layout are shown in Fig. 5. The temperature distribution of the structure without stiffeners in Fig. 4 shows that the maximum temperature is 118.592°C, and the maximum deformation of structure without stiffener is 0.84057 mm.

Figure 5: Temperature distribution and structural deformation of shape “#” layout under thermo-mechanical coupling

3.3 The Temperature Distribution and Structural Deformation of Stiffener Layout by Adaptive Growth Algorithm under Thermal-Mechanical Coupling

Applying the proposed adaptive growth algorithm of this paper to stiffener layout design, the growth situations from Step 1 to Step 30 are shown in Fig. 6. The conditions of stiffener growth stop under thermo-mechanical coupling as follows:

i.   The volume of growth stiffener exceed limit;

ii.   The stiffener grows to a point beyond the pre-defined boundary;

iii.   The growth steps exceed preset.

Figure 6: Stiffener growth of square shell under thermo-mechanical coupling

After growth stiffener layout optimization, the temperature distribution and structure of growth stiffener under thermo-mechanical coupling are analyzed by ANSYS, the results are shown in Fig. 7.

Figure 7: The temperature distribution of growth stiffener under thermo-mechanical coupling

Comparing the temperature distribution and the deformation of the structure without stiffener, the structure with shape ‘#’ stiffener layout and the structure with stiffener layout, which is grown by an adaptive growth algorithm. In the temperature distribution, the maximum temperature of the structure without stiffener is 118.592°C, the structure with shape ‘#’ stiffener layout is 102.488°C, and the structure with growth stiffener layout is 76.265°C. In the structural deformation, the maximum deformation of structure without stiffener is 0.84057 mm, the structure with shape ‘#’ stiffener layout is 0.83017 mm, and the structure with growth stiffener layout is 0.79382 mm.

From the results, we can conclude that using the adaptive growth algorithm to optimize stiffener layout of square shell, both the maximum temperature and structural deformation are decreased significantly. Compared with the analysis results of the structure with shape ‘#’ stiffener layout and structure with growth stiffener layout, the maximum temperature and structural deformation with growth stiffener layout are decreased 25.59% and 4.38%, respectively.

The results of square shell show the superiority of the adaptive growth algorithm for stiffener layout optimization under thermo-mechanical coupling:

(1)   Improving the structure stiffness and decreasing temperature simultaneously;

(2)   Saving the material compared with the shape ‘#’ stiffener layout to obtain the same performance;

(3)   The adaptive growth algorithm is more efficient.

4  The Body of Machining Center Stiffener Layout Optimization under Thermo-Mechanical Coupling

Using adaptive growth algorithm of this paper proposed, the stiffener layout of the body (load-bearing box type component) of M800 machining center is optimized. Before stiffener optimization, the body is equivalent to a simple model. The simplified model of the body is shown in Fig. 8.

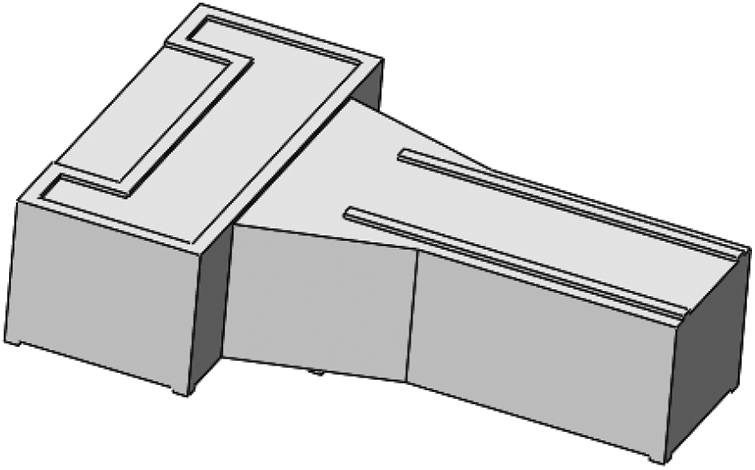
Figure 8: The simplified model of the body of M800 machining center

4.1 Constraint Condition

The load conditions of the body are shown in Fig. 9. Vertical loading applied on the surface which connects with a column, is F = 1250 N, and on the surface which connects with a slider, is F = 987.5 N. It is shown in Fig. 9a. The edges of the top surface are fixed during stiffener optimization. It is shown in Fig. 9b that the heat generation by guide way movement is considered, so the heat flow constraint of guideway is added, hear flow = 120 W, which is applied on the top surface of the guide way. Fig. 9c shows that the edges of the top surface are applied fixed temperature constraint, 22°C.

Figure 9: The constraint condition

4.2 The Stiffener Layout Optimization of the Body under Thermo-Mechanical Coupling

The optimization is from the top surface of body; the ground structure and thermal are built, and the seed point and stiffness spread radius are set up. Then the stiffener is grown by an adaptive growth algorithm. The processing of stiffener growth is shown in Fig. 10. It can be seen from Fig. 10 that as the iteration progresses, a certain volume of growth stiffener is gradually filled into the structure, and the maximum temperature and maximum deformation of the structure decrease.

Figure 10: The processing of stiffener layout design under thermo-mechanical coupling

After the stiffener growth, the stiffener layout should be round to obtain the growth rhythm, and simplified some repeat growth stiffener, the processing of simplified is shown in Fig. 11. After simplification, the structure of the growth stiffener is shown in Fig. 12. The simplified growth stiffener is remodeled, and the structure and heat dissipation are compared with the “#” stiffener.

Figure 11: The processing of stiffener simplified

Figure 12: The structure of body with growth stiffener

4.3 The Temperature Distribution and Structural Deformation of Machining Center Body with Growth Stiffener

The models of the body with shape ‘#’ stiffener layout and with growth stiffener layout are shown in Fig. 13.

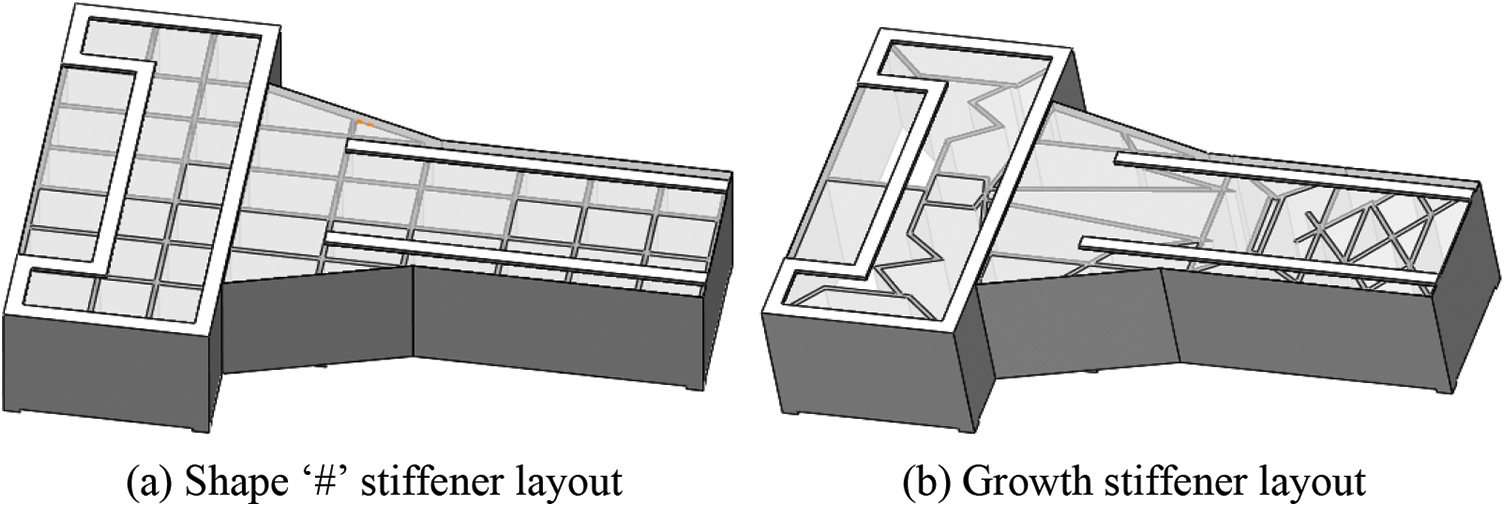
Figure 13: The models of the body with different stiffener layout

The temperature distribution and structural deformation of body with shape ‘#’ stiffener layout and growth stiffener layout under thermo-mechanical coupling are shown in Figs. 14 and 15.

Figure 14: The temperature distribution and structural deformation of body with shape ‘#’ stiffener layout

Figure 15: The temperature distribution and structural deformation of body with growth stiffener layout

Comparing the analysis results of temperature distribution and structural deformation with two different stiffener layouts, shape “#” stiffener layout and growth stiffener layout, we can conclude that the maximum temperature of the body with a growth stiffener layout by using an adaptive growth algorithm decreased from 26.387°C to 25.965°C, dropping 1.6%. The structural deformation under thermo-mechanical coupling is also decreased obviously. The maximum structural deformation of the body with shape ‘#’ stiffener layout is 7.4159 μm, and the maximum structural deformation of the body with growth stiffener layout is 5.8492 μm, dropping 1.5667 μm, 21.1%.

5  Conclusion

This paper developed an adaptive growth algorithm for stiffener layout design under thermo-mechanical coupling based on the topology optimization theory of heat conduction and stiffening structurally. Compared with the regular shape stiffener layout, both the temperature and structural deformation of the structure with the growth stiffener layout is reduced obviously. The square shell case shows the adaptive growth algorithm for stiffener layout design is more effective, practicable, and applicable. Using this approach, the stiffener layout of box type load-bearing components is optimized, and the temperature and deformation are reduced obviously compared with the traditional stiffener layout.

From the numerical results, we can conclude as follows:

(1)   The adaptive growth algorithm based on thermo-mechanical coupling can improve the stiffness and heat dissipation performance of the structure through stiffeners. The maximum temperature and structural deformation of structure with growth stiffener layout are reduced obviously.

(2)   The stiffener layout optimization of square shell shows that the maximum temperature and the deformation under thermo-mechanical coupling of the structure with growth stiffener are 76.265°C and 0.79382 mm. Comparing the structure with shape ‘#’ stiffener, the maximum temperature and deformation decreased by 25.59% and 4.38%, respectively.

The stiffener layout optimization of the machining center body shows the maximum temperature and the deformation under thermo-mechanical coupling of the structure of the body with growth stiffener are 25.965°C and 5.8492 μm. Comparing the structure of body with shape ‘#’ stiffener, the maximum temperature and deformation decreased by 1.6% and 21.1%, respectively.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work is supported by National Natural Science Foundation of China (No. 52075445) and Science, Technology and Innovation Commission of Shenzhen Municipality (No. JCYJ20190806151013025).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Souza, B. F., Anflor, C. T. M., Jorge, A. B. (2021). Application of modified adaptive morphogenesis and robust optimization algorithms for thin stiffened plates. Engineering with Computers, 1–17. DOI 10.1007/s00366-021-01465-w. [Google Scholar] [CrossRef]

 2.  Zulaika, J. J., Campa, F. J., LopezdeLacalle, L. N. (2011). An integrated process-machine approach for designing productive and lightweight milling machines. International Journal of Machine Tools and Manufacture, 51(7–8), 591–604. DOI 10.1016/j.ijmachtools.2011.04.003. [Google Scholar] [CrossRef]

 3.  Kroll, L., Blau, P., Wabner, M., Frie, U., Eulitz, J. et al. (2011). Lightweight components for energy-efficient machine tools. CIRP Journal of Manufacturing Science and Technology, 4(2), 148–160. DOI 10.1016/j.cirpj.2011.04.002. [Google Scholar] [CrossRef]

 4.  Gontarz, A. M., Hanni, F., Weiss, L. B., Wegener, K. (2012). Machine tool optimization strategies for ecologic and economic efficiency. Proceedings of Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 227(1), 54–61. DOI 10.1177/0954405412464932. [Google Scholar] [CrossRef]

 5.  Bendsoe, M. P., Kikuchi, N. (1988). Generating optimal topologies in structural design using homogenization method. Computer Methods in Applied Mechanics and Engineering, 71(2), 197–224. DOI 10.1016/0045-7825(88)90086-2. [Google Scholar] [CrossRef]

 6.  Cui, M., Luo, C., Li, G., Pan, M. (2019). The parameterized level set method for structural topology optimization with shape sensitivity constraint factor. Engineering with Computers, 37(2), 855–872. DOI 10.1007/s00366-019-00860-8. [Google Scholar] [CrossRef]

 7.  Shen, W., Ohsaki, M. (2021). Geometry and topology optimization of plane frames for compliance minimization using force density method for geometry model. Engineering with Computers, 37(3), 2029–2046. DOI 10.1007/s00366-019-00923-w. [Google Scholar] [CrossRef]

 8.  Pham, Q. H., Phan, D. H. (2020). Polygonal topology optimization for Reissner–Mindlin plates. Engineering with Computers, 38(1), 141–154. DOI 10.1007/s00366-020-01047-2. [Google Scholar] [CrossRef]

 9.  Krog, L. A., Olhoff, N. (1999). Optimum topology and reinforcement design of disk and plate structures with multiple stiffness and eigenfrequency objectives. Computers & Structures, 72(4/5), 535–563. DOI 10.1016/S0045-7949(98)00326-5. [Google Scholar] [CrossRef]

10. Ansola, R., Canales, J., Tarrago, J. A., Rasmussen, J. (2004). Combined shape and reinforcement layout optimization of shell structures. Structural Multidisciplinary Optimization, 27(4), 219–227. DOI 10.1007/s00158-004-0399-7. [Google Scholar] [CrossRef]

11. Afonso, S., Sienz, J., Belbidia, F. (2005). Structural optimization strategies for simple and integrally stiffened plates and shells. Engineering Computations, 22(4), 429–452. DOI 10.1108/02644400510598769. [Google Scholar] [CrossRef]

12. Mao, Z. Y., Yan, S. K. (2018). Design and analysis of the thermal-stress coupled topology optimization of the battery rack in an AUV. Ocean Engineering, 148, 401–411. DOI 10.1016/j.oceaneng.2017.11.025. [Google Scholar] [CrossRef]

13. Bojczuk, D., Szteleblak, W. (2008). Optimization of layout and shape of stiffeners in 2D structures. Computers and Structures, 86(13–14), 1436–1446. DOI 10.1016/j.compstruc.2007.05.005. [Google Scholar] [CrossRef]

14. Kimmel, R. (2004). The Osher-Sethian level set method. In: Numerical geometry of images: Theory, algorithms, and applications. New York: Springer. DOI 10.1007/978-0-387-21637-9_4. [Google Scholar] [CrossRef]

15. Steven, G. P., Querin, O. M., Xie, Y. M. (1998). Evolutionary structural optimization (ESO) using a bidirectional algorithm. Engineering Computations, 15(8), 1031–1048. DOI 10.1108/02644409810244129. [Google Scholar] [CrossRef]

16. Ding, X., Yamazaki, K. (2004). Stiffener layout design for plate structures by growing and branching tree model (application to vibration-proof design). Structural Multidisciplinary Optimization, 26(1/2), 99–110. DOI 10.1007/s00158-003-0309-4. [Google Scholar] [CrossRef]

17. Ding, X., Yamazaki, K. (2005). Adaptive growth technique of stiffener layout pattern for plate and shell structures to achieve minimum compliance. Engineering Optimization, 37(3), 259–76. DOI 10.1080/0305215512331328231. [Google Scholar] [CrossRef]

18. Li, B. T., Hong, J., Yan, S. N., Liu, Z. F. (2013). Multidiscipline topology optimization of stiffened plate/shell structures inspired by growth mechanisms of leaf veins in nature. Mathematical Problems in Engineering, 2013, 444–449. DOI 10.1155/2013/653895. [Google Scholar] [CrossRef]

19. Li, B. T., Hong, J., Liu, Z. F. (2014). Stiffness design of machine toll structures by a biologically inspired topology optimization method. International Journal of Machine Tools & Manufacture, 84(6), 33–44. [Google Scholar]

20. Tejani, G. G., Kumar, S., Gandomi, A. H. (2021). Multi-objective heat transfer search algorithm for truss optimization. Engineering with Computers, 37(1), 641–662. DOI 10.1007/s00366-019-00846-6. [Google Scholar] [CrossRef]

21. Ding, X., Yamazaki, K. (2007). Constructal design of cooling channel in heat transfer system by utilizing optimality of branch systems in nature. Journal of Heat Transfer, 129(3), 245–255. DOI 10.1115/1.2426357. [Google Scholar] [CrossRef]

22. Mao, H. P., Su, T. X., Li, J. J., Wang, Y. H. (2013). A new variable density method for topology optimization of continuum structures. Journal of Machine Design, 30(5), 38–41. [Google Scholar]

23. Huang, X., Xie, Y. M. (2010). A further review of eso type methods for topology optimization. Structural and Multidisciplinary Optimization, 41(5), 671–683. DOI 10.1007/s00158-010-0487-9. [Google Scholar] [CrossRef]

24. Zhuang, C., Xiong, Z., Ding, H. (2010). Topology optimization of multi-material for the heat conduction problem based on the level set method. Engineering Optimization, 42(9), 811–831. DOI 10.1080/03052150903443780. [Google Scholar] [CrossRef]

25. Zhuang, C., Xiong, Z., Ding, H. (2007). A level set method for topology optimization of heat conduction problem under multiple load cases. Computer Methods in Applied Mechanics and Engineering, 196(4/6), 1074–1084. DOI 10.1016/j.cma.2006.08.005. [Google Scholar] [CrossRef]

26. Guo, Z. Y., Cheng, X. G., Xia, Z. Z. (2003). The principle of minimum heat transfer potential capacity dissipation and its application in heat conduction optimization. Chinese Science Bulletin, 48(1), 1–25. [Google Scholar]

27. Cheng, X. T., Xu, X. H., Liang, X. G. (2009). The uniformity of temperature field and temperature gradient field. Science in China Press, 39(10), 1730–1735. [Google Scholar]

28. Zhang, Y. C., Liu, S. T. (2008). Mathematical model for optimal design of heat conduction structure design. Progress in Natural Science, 18(6), 680–685. DOI 10.1016/j.pnsc.2008.01.010. [Google Scholar] [CrossRef]

29. Zuo, K. T., Qiang, Q., Zhao, Y. D., Chen, L. P. (2005). Research on the topology optimization about thermo-structural coupling field. Chinese Journal of Solid Mechanics, 26(4), 447–452. [Google Scholar]

30. Takezawa, A., Yoon, G. H., Jeong, S. H., Kobashi, M., Kitamura, M. (2014). Structural topology optimization with strength and heat conduction constraints. Computer Methods in Applied Mechanics & Engineering, 276, 341–361. DOI 10.1016/j.cma.2014.04.003. [Google Scholar] [CrossRef]

31. Zhang, L., Zhao, Q., Chen, J. (2022). Reliability-based topology optimization of thermo-elastic structures with stress constraint. Mathematics, 10(7), 1091. DOI 10.3390/math10071091. [Google Scholar] [CrossRef]

32. Yan, J., Sui, Q., Fan, Z., Duan, Z. (2022). Multi-material and multiscale topology design optimization of thermoelastic lattice structures. Computer Modeling in Engineering & Sciences, 130(2), 967–986. DOI 10.32604/cmes.2022.017708. [Google Scholar] [CrossRef]

33. Yan, J., Xu, Q., Fan, Z., Duan, Z., Du, H. et al. (2021). Thermoelastic structural topology optimization based on moving morphable components framework. Computer Modeling in Engineering & Sciences, 128(3), 1179–1196. DOI 10.32604/cmes.2021.016950. [Google Scholar] [CrossRef]

34. Chen, J., Zhao, Q., Zhang, L. (2022). Multi-material topology optimization of thermo-elastic structures with stress constraint. Mathematics, 10(8), 1216. DOI 10.3390/math10081216. [Google Scholar] [CrossRef]