 Open Access
Open Access
ARTICLE
Two-Sided Stable Matching Decision-Making Method Considering Matching Intention under a Hesitant Fuzzy Environment
1 School of Management, Shanghai University of Engineering Science, Shanghai, 201620, China
2 School of Information Management, Jiangxi University of Finance and Economics, Nanchang, 330013, China
* Corresponding Author: Qi Yue. Email:
(This article belongs to the Special Issue: Decision making Modeling, Methods and Applications of Advanced Fuzzy Theory in Engineering and Science)
Computer Modeling in Engineering & Sciences 2023, 135(2), 1603-1623. https://doi.org/10.32604/cmes.2022.022956
Received 02 April 2022; Accepted 01 July 2022; Issue published 27 October 2022
Abstract
In this paper, a stable two-sided matching (TSM) method considering the matching intention of agents under a hesitant fuzzy environment is proposed. The method uses a hesitant fuzzy element (HFE) as its basis. First, the HFE preference matrix is transformed into the normalized HFE preference matrix. On this basis, the distance and the projection of the normalized HFEs on positive and negative ideal solutions are calculated. Then, the normalized HFEs are transformed into agent satisfactions. Considering the stable matching constraints, a multiobjective programming model with the objective of maximizing the satisfactions of two-sided agents is constructed. Based on the agent satisfaction matrix, the matching intention matrix of two-sided agents is built. According to the agent satisfaction matrix and matching intention matrix, the comprehensive satisfaction matrix is set up. Furthermore, the multiobjective programming model based on satisfactions is transformed into a multiobjective programming model based on comprehensive satisfactions. Using the G-S algorithm, the multiobjective programming model based on comprehensive satisfactions is solved, and then the best TSM scheme is obtained. Finally, a terminal distribution example is used to verify the feasibility and effectiveness of the proposed method.Keywords
In the process of two-sided matching decision-making (TSMDM), two-sided agents yield the preference information according to their own needs and produce a reasonable matching scheme. The TSMDM problem widely exists in various fields, such as the freight source matching problem [1], blockchain-based task matching problem [2], cap-trade matching problem in carbon emissions [3], mentor-mentee matching problem [4], emergency rescue personnel and task matching problem [5] and so on. Gale et al. [6] first studied TSMDM problems with ordinal preferences. After the initial study, different types of preference information were used in the TSMDM problems, such as the linguistic term, ordinal number and interval number. For instance, Tong et al. [7] proposed a two-sided matching (TSM) model based on the preference information of linguistic terms. Pittel [8] proposed a TSM model under strict preference order. Hu et al. [9] presented a stable TSM model with one-side preference. Antler [10] studied TSMDM problems based on the endogenous preference ordinal number and proposed a new TSMDM method. Many scholars at home and abroad are devoting increasing attention to TSMDM because of the important roles of TSMDM theory and methodology in economic activities.
Currently, the preference information provided by people is often vague or uncertain due to the subjectivity and fuzziness of human thinking [11]. Thus, preference information based on different forms of fuzzy sets has been noticed and studied by many scholars, including intuitionistic fuzzy sets, interval intuitionistic fuzzy sets, and triangular fuzzy numbers [12–14]. These types of fuzzy sets mostly contain a membership and nonmembership element. However, in some decision-making scenarios, the decision-maker may not provide a single evaluation value, but rather multiple evaluation values. In addition, multiple decision-makers may give different evaluation information at the same time, and they may not convince each other due to conflicting opinions. For instance, in a venture investment matching problem, five experts in the field of venture capital may assign different evaluation values with respect to venture capital enterprises, such as 0.5, 0.4, 0.6, 0.8 and 0.7. The traditional fuzzy sets mentioned above cannot effectively maintain the integrity of decision information. Compared with the traditional fuzzy sets mentioned above, the hesitant fuzzy set (HFS) proposed by Torra can maximize the retention of initial decision information due to the multiple membership degrees [15]. In the case mentioned above, the preference information given by five experts can be described by the hesitant fuzzy element (HFE) {0.5, 0.4, 0.6, 0.8, 0.7}. Therefore, the TSMDM considering HFS preferences also has important research value.
Relevant studies on HFS have emerged in different fields. First, the basic theory regarding HFS has been generalized. For instance, Xu et al. [16] proposed various hesitant ordered weighted distance measures and corresponding hesitant ordered weighted similarity measures. Following Xu and Xia's [17] research, a brand-new distance measure and similarity measure for higher order HFS were given in Farhadinia’s study. Liang et al. [18] developed a novel utility function for HFS. Liao et al. [19] proposed brand-new hesitant fuzzy weighted operators, including the hesitant power average operator, weighted hesitant power average operator, ordered weighted hesitant power average operator and hybrid weighted hesitant power average operator. Moreover, the application scope of HFS has expanded. For instance, a novel multiattribute group decision-making model based on the hesitant fuzzy superiority and inferiority ranking method and the interval-valued hesitant fuzzy superiority and inferiority ranking method was proposed by Ma et al. [20]. Ullah [21] developed a new multiattribute group decision-making model based on the fuzzy picture Maclaurin symmetric mean operator.
In addition, according to the aforementioned literature, there have been many studies on the application of HFS in the TSMDM problem. For instance, Zhang et al. [22] established a stable TSM model considering multi-granular hesitant fuzzy linguistic term information and proposed an example for the matching of green building technology supply and demand to verify the effectiveness of this model. Li et al. [23] studied the complex product manufacturing problem and proposed a TSMDM method considering dual-hesitant fuzzy information. Yue et al. [24] developed a new HFS score function and constructed the corresponding TSMDM model. Zhang et al. [25] proposed a two-sided matching method considering regret aversion psychological behavior and matching aspiration to solve TSM problems with intuitionistic fuzzy preference information. Xiang et al. [26] constructed a novel TSM model considering hesitancy and ambiguity and proposed a novel Pareto refining method, which can be applied in high-end equipment cloud manufacturing platform matching problems.
Although a considerable number of scholars have explored the TSMDM problem under HFS preferences from a variety of perspectives and have achieved some promising results, there are some deficiencies in the existing research.
First, in the TSMDM with HFS preference information, it is vital for decision-makers to find a reasonable tool to transform HFS preferences into exact values. In most of the existing studies, the TOPSIS method based on the distance measure or biprojection technology has been widely used in the TSMDM problem with HFS preference information. However, the above methods may still result in the loss of decision-making information in some cases. Hence, it would be meaningful to create an effective method to compute agent satisfaction.
Second, the matching intention coefficient, which reflects the matching intention of two-sided agents, plays an important role in the TSMDM problem. For some TSMDM problems, the matching intention coefficient may affect the final TSM result. However, it seems that the matching intention coefficient has been neglected in the aforementioned TSMDM model. Therefore, it would be practicable to develop a method to obtain the matching intention coefficient of two-sided agents in the TSMDM problem with HFS preference information.
Third, stability is of great significance for two-sided agents to achieve a reasonable and satisfactory matching result. However, this topic has not been fully discussed by many existing studies on the TSMDM problem in HFS preference environments. Thus, it is necessary to consider the stability of the TSMDM problem based on HFS preference information.
To overcome these deficiencies, this paper aims to develop a reasonable and effective method to cope with the TSMDM problem considering HFS preferences. Moreover, a TSMDM model with HFS preferences considering the matching intention coefficient is constructed. The key contributions of this work are as follows. First, we create an effective method to compute the agent satisfaction, which uses the distance measure and bi-projection technology. Second, we develop an effective method for calculating the matching intention coefficient of two-sided agents. Finally, a TSMDM model with HFS preference information considering stable matching constraints and matching intention is constructed.
The remaining structure of this paper is as follows: In Section 2, some relevant concepts of the TSM, HFS and HFE, and stable matching are presented. The stable TSM problem with HFS preference information considering matching intention is described in Section 3. Section 4 describes the TSMDM method with HFSs using TOPSIS technology. In Section 5, a TSM case is applied to verify the effectiveness and feasibility of the proposed method. Section 6 summarizes this paper.
In this section, we first introduce the basic concepts of the TSM, HFS and HFE. Then, the stable matching based on satisfaction is briefly described.
There are two agent sets in the TSM problem, namely,
Definition 1. [22] Let
2.2 Hesitant Fuzzy Set and Hesitant Fuzzy Element
Definition 2. [24] Assume
Definition 3. [16] Let
where
2.3 Stable Matching Based on Satisfaction
In the real TSMDM scenario, we assume that
Definition 4. [22] If neither of the following conditions occurs in a TSM
(i)
(ii)
then
3 Stable Two-Sided Matching Problem Considering Matching Intention
In this section, we introduce the TSMDM problem based on HFE preference information considering the matching intention.
In the TSMDM problem, two-sided agents usually hesitate to assign their own preferences among multiple membership degrees. Therefore, to show the hesitancy and fuzziness of the evaluation information in TSMDM activities, we assume that two-sided agents provide hesitant fuzzy preference information. Furthermore, assume
The problem studied in this paper is as follows: how to construct a TSM model considering the matching intention and stable matching conditions according to the HFE preference matrices
4 Two-Sided Matching Decision-Making Based on Hesitant Fuzzy Elements
In this section, the TSMDM method based on HFE considering matching intention is presented. First, the HFE matrices are transformed into standardized HFE matrices. Then, the agent satisfaction matrices are calculated by using the TOPSIS and biprojection technology-based methods. Third, the TSM model considering the matching intention and stability is constructed by using the multiobject planning method. Finally, the optimal TSM scheme is obtained through the G-S algorithm.
4.1 Standardized Hesitant Fuzzy Element Matrix
According to Definition 2, we know that l signifies the number of elements in the HFE. However, the number of elements in the two HFEs is not the same in many decision scenarios. Therefore, the HFE is normalized based on the method proposed in the reference [23]. Assuming two HFEs
The normalized HFE matrices
Therefore, the length
4.2 Construction of the Agent Satisfaction Matrix
The normalized HFE matrix is processed according to TOPSIS technology, and the following definitions are given with reference to the reference [24] and Definition 3.
Definition 5. [23] Given a normalized HFE matrix
Definition 6. Let the normalized HFE, the positive ideal solution HFE and negative ideal solution HFE be
where
Definition 7. [23] Let the normalized HFE, the positive ideal solution HFE and negative ideal solution HFE be
According to Definition 6 and Definition 7 and the calculation theory of closeness in reference [24], the definitions of combined closeness are given below.
Definition 8. Let
where
In Eq. (8), the larger the combined closeness
Definition 9. [23] Given a normalized HFE matrix
Definition 10. Let the normalized HFE, the positive ideal solution HFE and negative ideal solution HFE be
where
Definition 11. [23] Let the normalized HFE, the positive ideal solution HFE and negative ideal solution HFE be
According to Definition 9, Definition 10, and the calculation theory of closeness in reference [24], the definitions of combined closeness are given below.
Definition 12. Let
where
In Eq. (15), the larger the combined closeness
4.3 Construction of a Two-Sided Matching Model Considering the Matching Intention and Stability
Based on the satisfaction matrices
where
Referring to the references [24,25], we know that the matching intention coefficient is associated with agent satisfaction and matching diversity. Thus, the optimal model for determining the matching intention coefficient considering matching satisfaction and matching diversity is constructed as follows:
To solve Model (M-2), the Lagrange function is introduced as follows:
Then, let
Hence, the optimal solution can be obtained on the basis of Eqs. (17) and (18), in which
Furthermore, the standardized matching intention coefficient can be computed by normalizing Eq. (19), in which
To concretely illustrate the calculation method of the matching intention coefficient given above, we take an example with three agents of each side.
Example 1. Let
then, the matching intention coefficient can be computed through Eq. (20) as follows:
According to Eq. (20), the matching intention coefficient matrix
Therefore, Model (M-1) is transformed into Model (M-3) based on the comprehensive satisfactions
4.4 Solution Process of the Two-Sided Matching Model Based on the G-S Algorithm
The framework of the solution process for TSM Model (M-3) based on the G-S algorithm is shown in Algorithm 1; then, the detailed procedures are presented as follows:
Step 1. For each agent
Step 2. For each agent
Step 3. For agent
Step 4. For other two-sided agents of side V and side U, rank all remaining agents of side V and side U according to the comprehensive satisfactions. Then, return to Step 2 until all agents of side U are matched.

4.5 Steps of Two-Sided Matching Decision-Making with Hesitation Fuzzy Set Preference
In summary, the steps of stable HFE TSMDM considering matching intention are given below:
Step 1. Transform HFE preference matrices
Step 2. Transform normalized HFE matrices
Step 3. Construct the TSM Model (M-1) based on the satisfaction matrices
Step 4. Calculate the matching intention coefficient matrix
Step 5. Transform satisfactions
Step 6. Transform Model (M-1) into Model (M-3) based on the comprehensive satisfactions
Step 7. Determine the stable alternative of TSM by solving Model (M-3) through Algorithm 1.
In the business activities of enterprises, the terminal distribution problem is the last link in the enterprise supply chain. Currently, the quality of terminal distribution will affect the overall benefit of enterprises, so the terminal distribution plays an important role in the supply chain. At the same time, there are two decision-makers in a terminal distribution problem, namely, freight cars and terminal distribution centers. The decision-making process may be affected by many factors; therefore, we will consider a distribution problem between freight cars and terminal delivery points as an example to verify the validity and feasibility of the TSM model proposed in this paper. The framework of the proposed case is given in Fig. 1. In addition, a comparison analysis is presented to clarify the advantage of the proposed model.
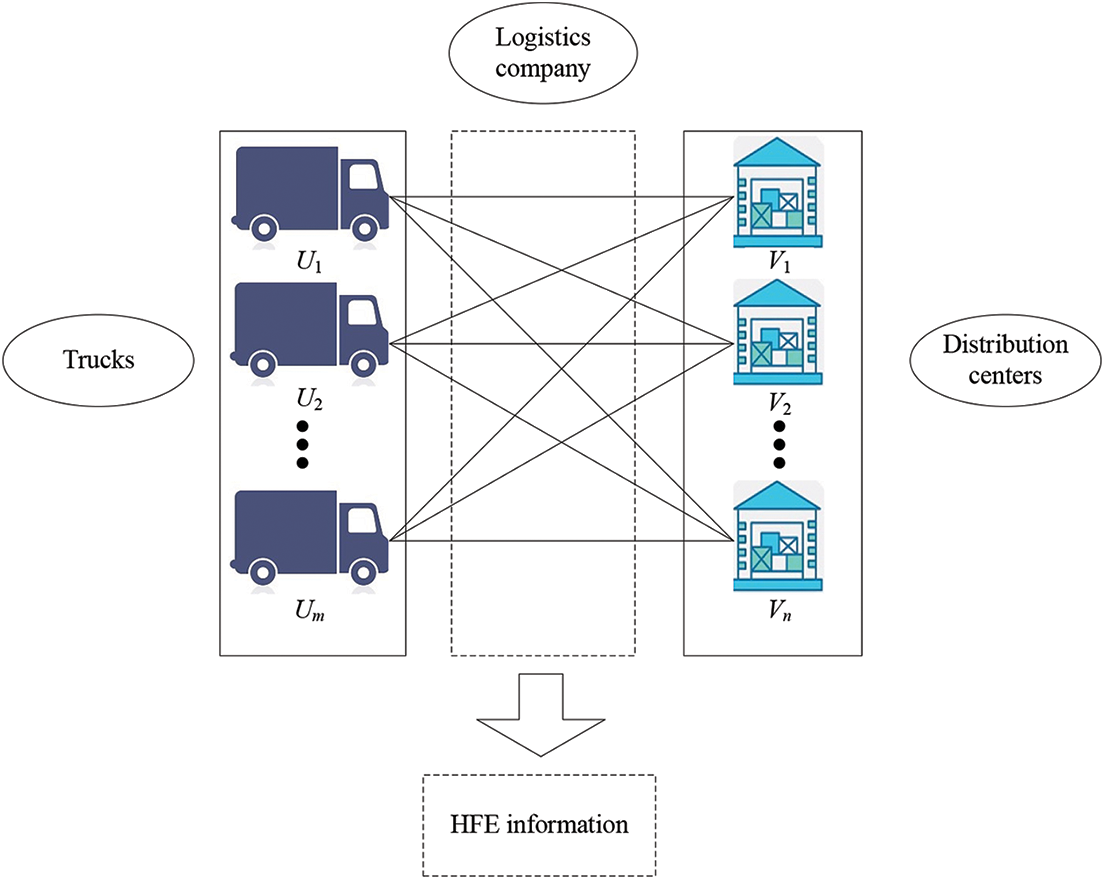
Figure 1: Framework of the terminal distribution problem
5.1 Steps of Two-Sided Matching Decision-Making with Hesitation Fuzzy Set Preference
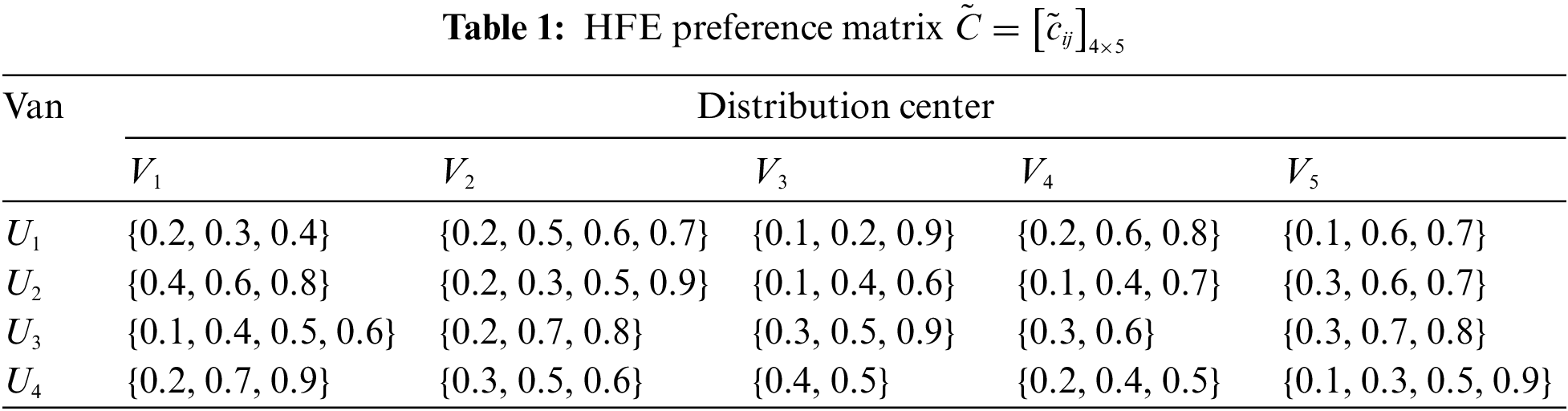
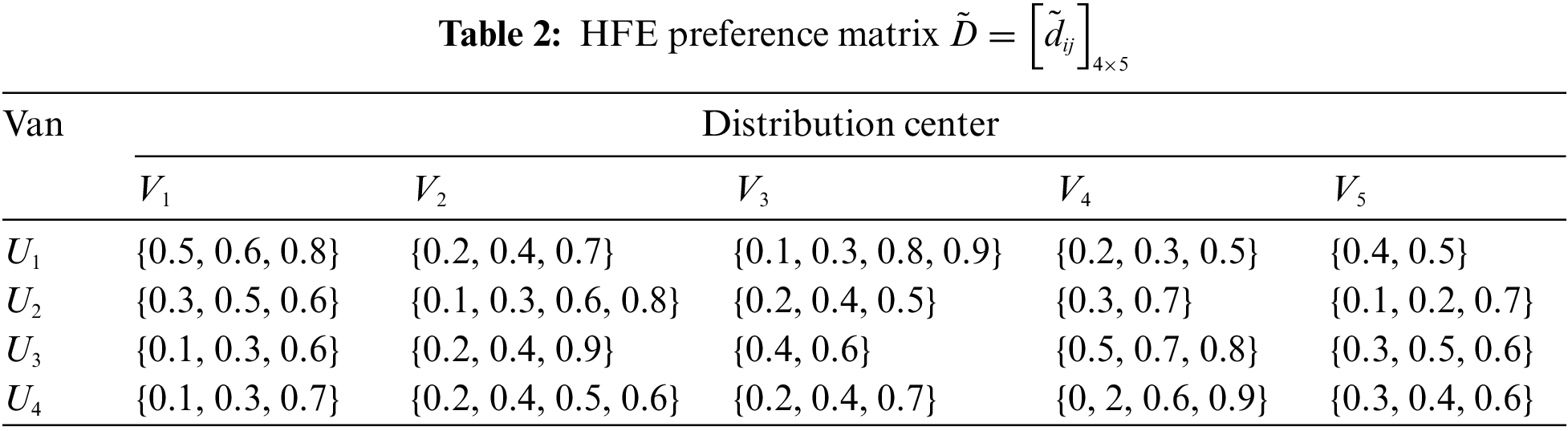
GH is a third-party logistics enterprise specializing in LCL transportation. In a certain terminal distribution task, GH Company needs to arrange four trucks
The proposed method is adopted to solve the problem, and the solution steps are displayed as follows.
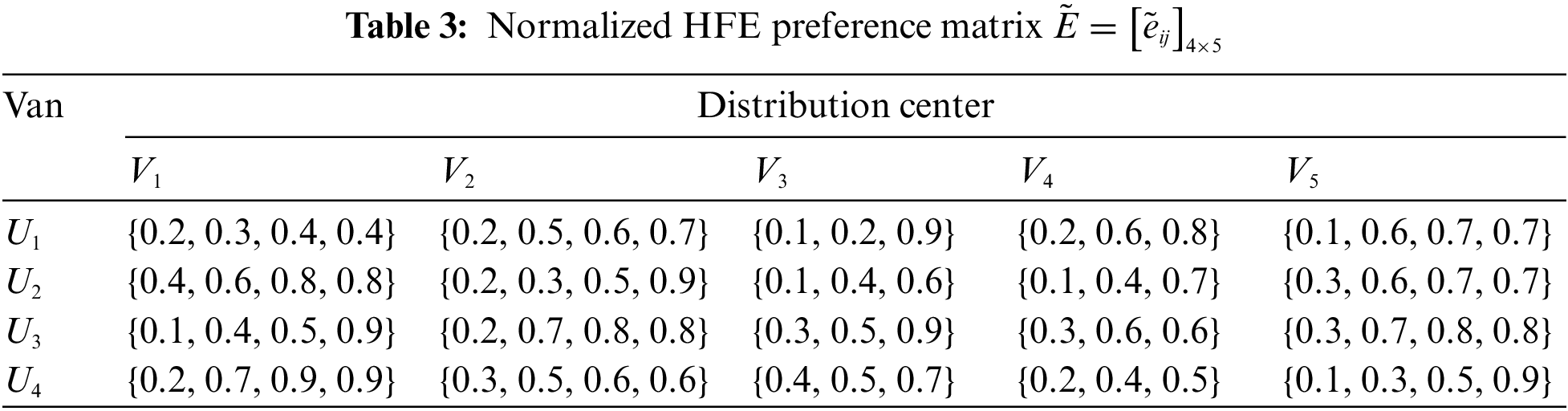
Step 1. Transform the HFE preference matrices
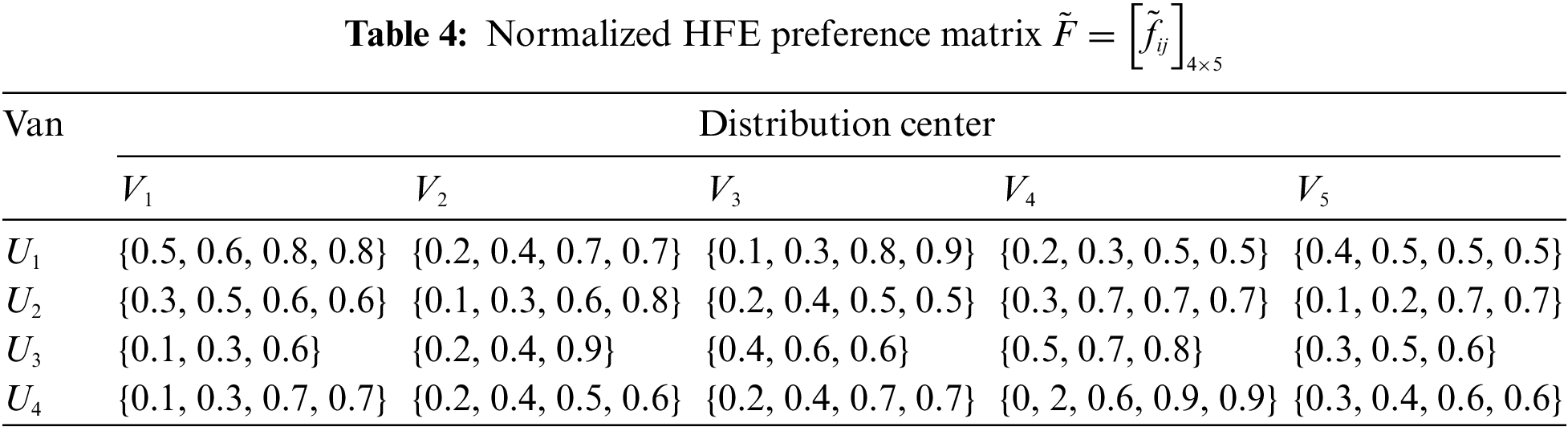
Step 2. Calculate the positive solutions for two-sided normalized HFE matrices through Eqs. (2) and (9): {0.4, 0.7, 0.9, 0.9}, {0.3, 0.7, 0.8, 0.9}, {0.4, 0.5, 0.9}, {0.4, 0.6, 0.8}, {0.3, 0.7, 0.8, 0.9}, {0.5, 0.6, 0.8, 0.9}, {0.3, 0.7, 0.7, 0.8}, {0.5, 0.7, 0.9}, {0.3, 0.6, 0.9, 0.9}. Calculate the negative solutions for two-sided normalized HFE matrices through Eqs. (3) and (10): {0.1, 0.3, 0.4, 0.4}, {0.2, 0.3, 0.5, 0.6}, {0.1, 0.2, 0.6}, {0.1, 0.4, 0.5}, {0.1, 0.3, 0.5, 0.7}, {0.1, 0.3, 0.5, 0.5}, {0.1, 0.2, 0.5, 0.5}, {0.1, 0.3, 0.6}, {0.1, 0.3, 0.5, 0.6}.
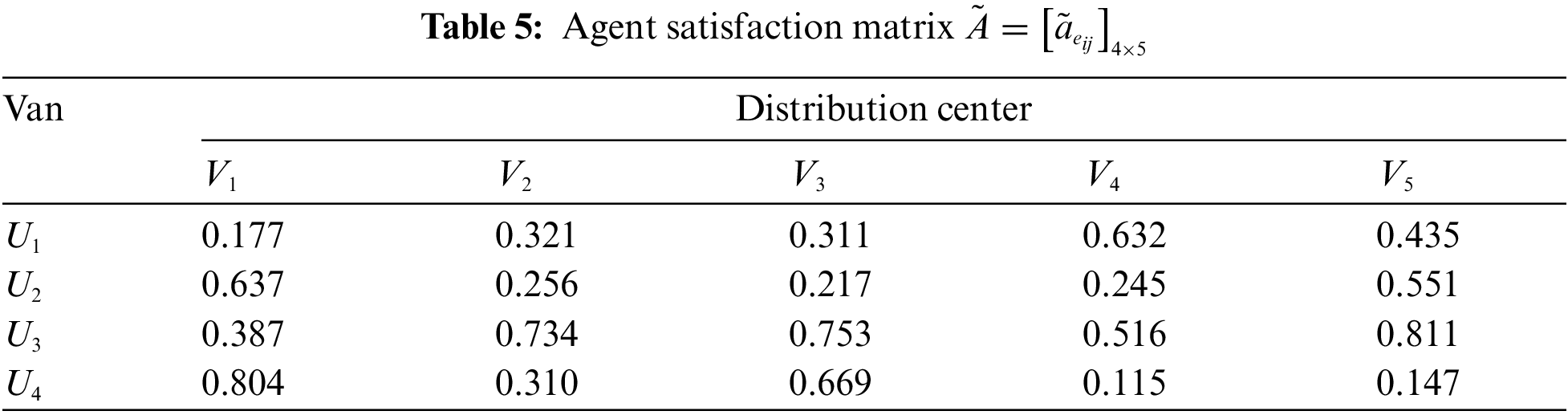
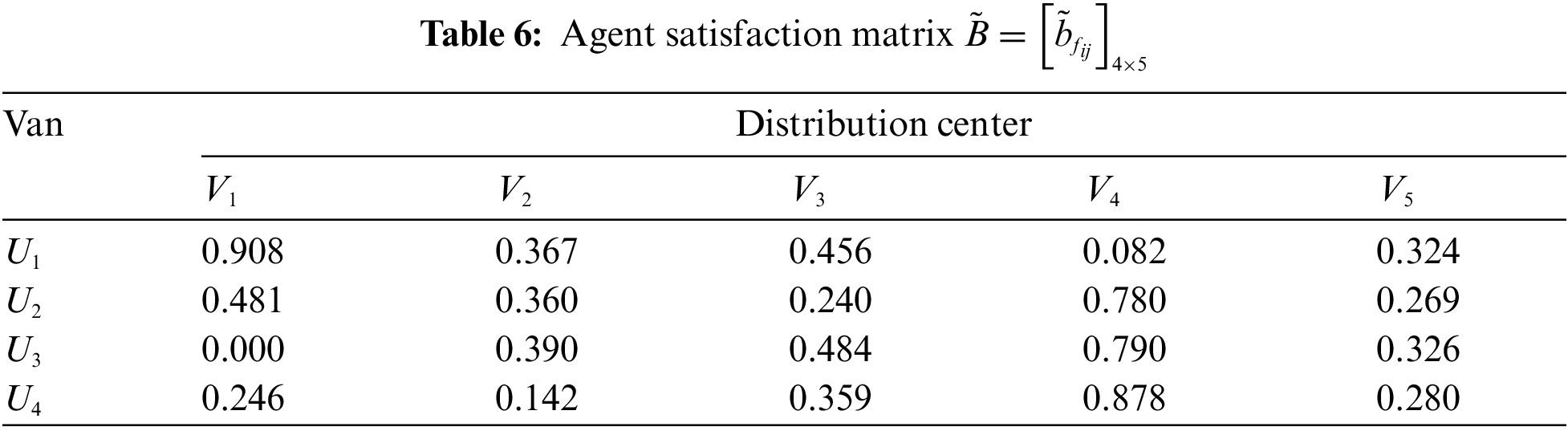
Construct the agent satisfaction matrices
Step 3. Then, Model (M-1) considering the stable matching constraints is constructed as:
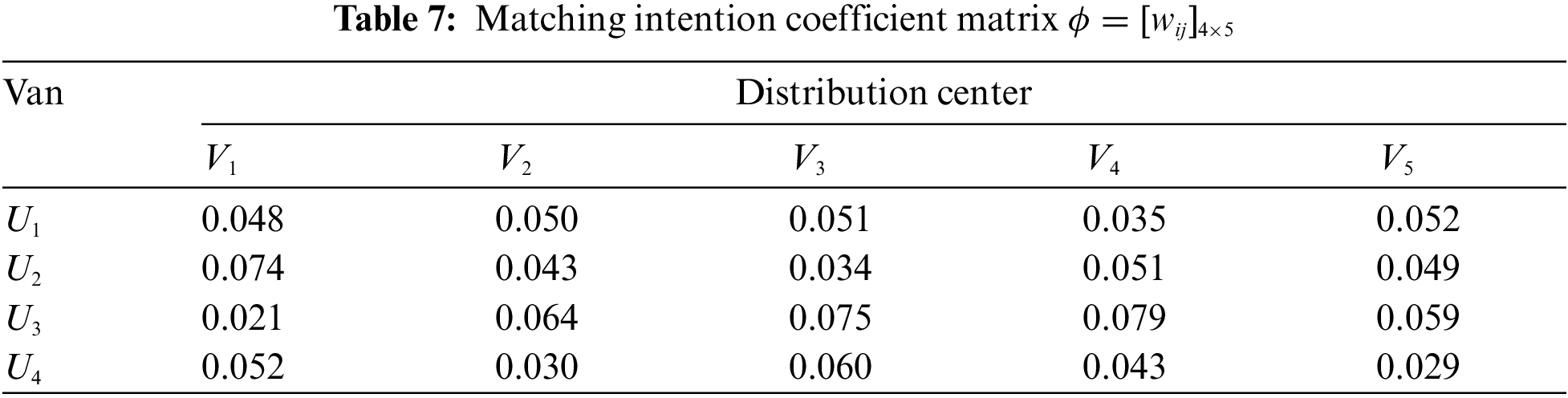
Step 4. Based on the satisfaction matrices
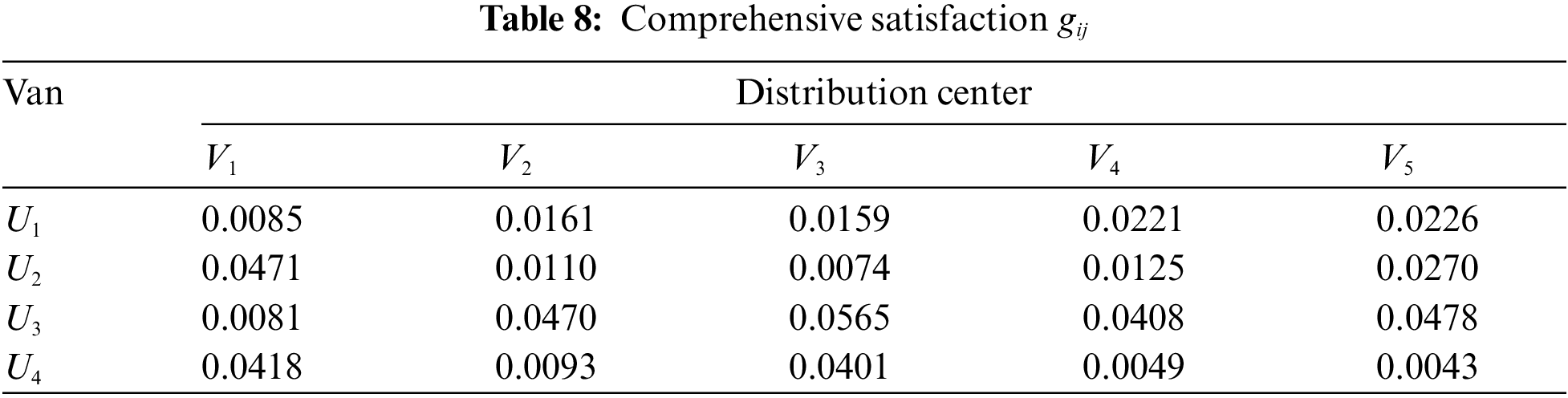
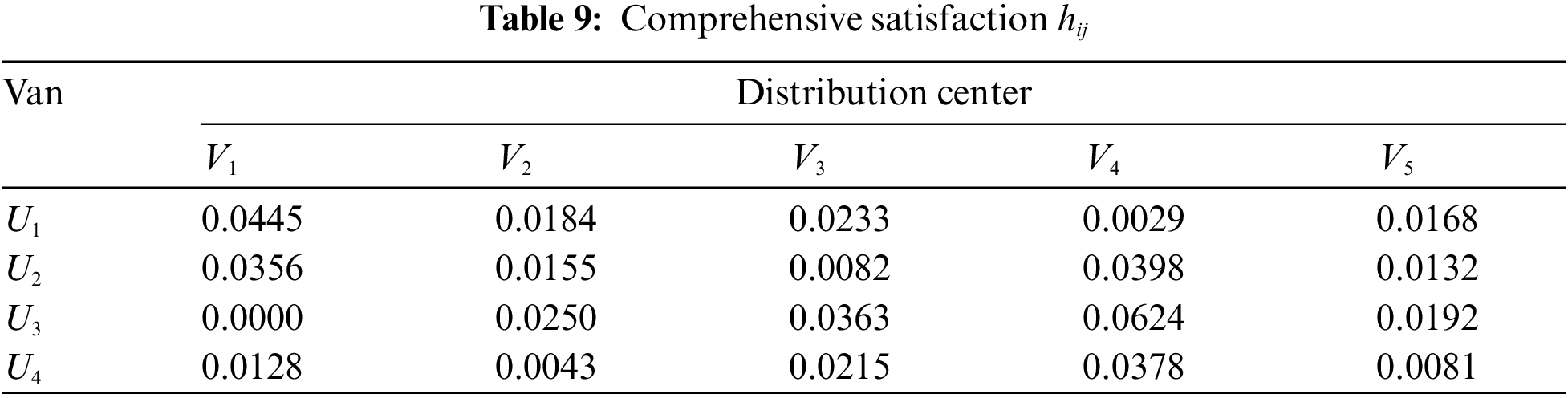
Step 5. Transform Model (M-1) into Model (M-3) based on the comprehensive satisfactions
Step 6. Determine a stable alternative of TSM by solving Model (M-3), as shown in Table 10.
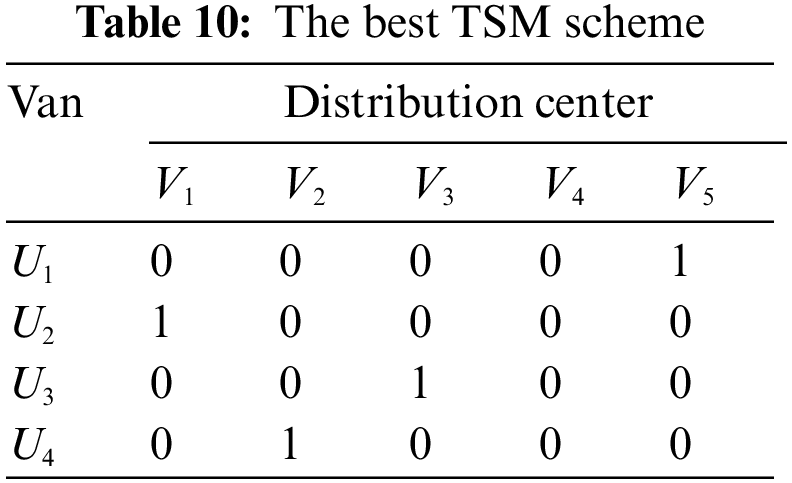
Therefore, the best TSM is
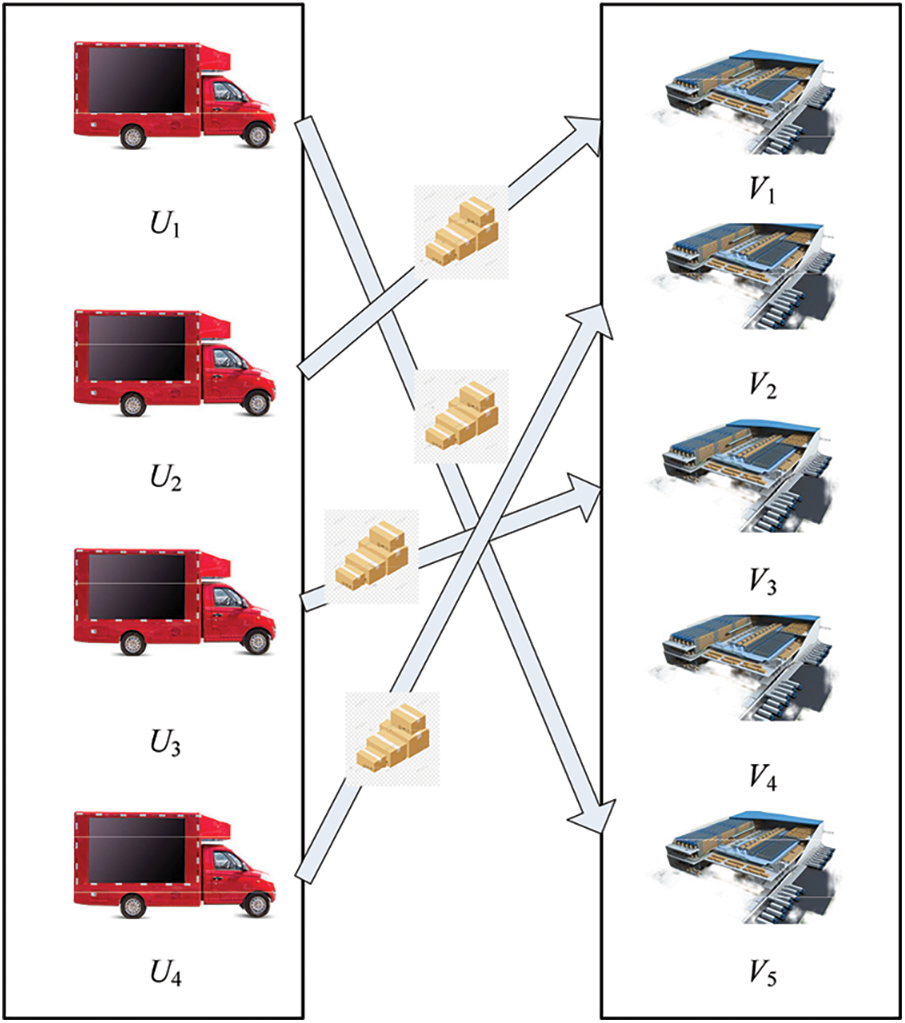
Figure 2: The best TSM scheme between cars and terminal distribution centers
Furthermore, we reconstruct Model (M-4) without the stable constraint:
Then, the matching scheme can be obtained by solving TSM Model (M-4), as shown in Table 11.
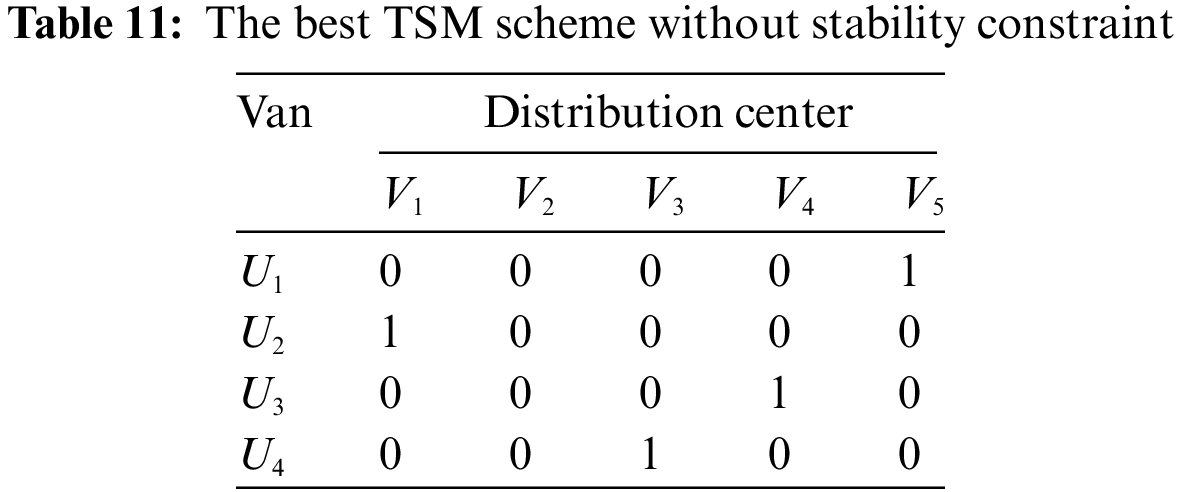
Hence, the best TSM scheme is determined from Table 11, i.e.,

As seen from Table 12, in the best TSM schemes obtained through method I and method II, only
First, there are several kinds of methods for dealing with fuzzy preference information, such as the TOPSIS method based on distance measures or biprojection technology. This paper adopted a brand-new method to deal with fuzzy preference information, which contains distance measures and biprojection technology. To further state the effectiveness of the method proposed in this paper, we compare the proposed method for handling hesitant fuzzy information with two methods given in references [16] and [23]. Reference [23] only adopted the biprojection technology for transforming fuzzy preference information into exact values. Meanwhile, reference [16] adopted only the distance measure for transforming fuzzy preference information into exact values. The TSM results obtained by different methods are displayed in Table 13. From Table 13, it can be concluded that the TSM results obtained by the mentioned methods are different. Meanwhile, the methods proposed in references [23] and [16] may cause deviations in hesitant preference information in the process of conversion. Furthermore, the method proposed in this paper can effectively synthesize the advantages of the two methods proposed in the references [23] and [16]. Therefore, the proposed method can guarantee the integrity of decision-making evaluation information.

Second, many of the existing TSMDM studies ignored the matching intention of two-sided agents. In this paper, the proposed TSMDM method considered the matching intention of matching agents, which can be applied to minimize the diversity of the TSM scheme.
Third, stability plays a significant role in the TSMDM process because the unstable matching pair may hinder the formation of matching results even if the satisfaction of two-sided agents is high. From the aforementioned research, we find that stability has not been fully considered in TSMDM problems in hesitant fuzzy preference environments. Hence, the one-to-one stable matching constraints are integrated into the TSMDM model developed in this paper, which can not only maximize the satisfaction of two-sided agents but also ensure a stable TSM scheme.
In this paper, a TSM decision-making model considering the matching intention and stability of two-sided agents under hesitant fuzzy preference is proposed. In this method, the normalized HFE is transformed into the agent satisfaction after normalizing the HFE preference information. A multiobjective programming model considering the agent satisfactions and the stable matching constraint is constructed. Based on the agent satisfaction matrices, the matching intention coefficient matrix is calculated, and then the comprehensive satisfaction matrices are calculated. Furthermore, the multiobjective programming model based on the satisfactions is transformed into the multiobjective programming model based on the comprehensive satisfactions. The best TSM scheme can be obtained by solving the developed model.
The main innovation of this paper can be denoted as follows: First, the TSM scheme obtained by the method proposed in this paper can reflect the matching intention of two-sided agents; second, the proposed method ensures the stability of the matching scheme. The TSM method proposed in this paper provides a new perspective for studying the TSM problem under the condition of HFS.
Further research work can be conducted as follows:
(1) In the proposed TSMDM method, we present a novel method including distance measures and biprojection technology for dealing with hesitant fuzzy preference information. However, due to the complex decision-making environment, the proposed distance measures may not fully reveal the comments of the decision-makers who have various preferences. Therefore, it could be practicable to develop a brand-new distance measure for HFS and the corresponding TOPSIS method.
(2) For some TSMDM problems, two-sided agents may provide multiple hesitant fuzzy preference information, such as probability hesitant fuzzy sets, interval hesitant fuzzy sets, and probability interval hesitant fuzzy sets. These would be interesting topics for developing a TSMDM model with multiple hesitant fuzzy preference information.
(3) It is meaningful to conduct research on the TSMDM problem considering bipolar hesitant fuzzy sets and T-spherical fuzzy sets [27] which can be used to solve decision-making problems in dynamic scenarios.
Funding Statement: This work was partly supported by the National Natural Science Foundation of China (Grant No. 71861015), the Humanities and Social Science Foundation of the Ministry of Education of China (Grant No. 18YJA630047), and the Distinguished Young Scholar Talent of Jiangxi Province (Grant No. 20192BCBL23008).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Wang, Z. H., Li, Y. Y., Gu, F., Guo, J. F., Wu, X. J. (2020). Two-sided matching and strategic selection on freight resource sharing platforms. Physical A: Statistical Mechanics and its Applications, 559, 125014. DOI 10.1016/j.physa.2020.125014. [Google Scholar] [CrossRef]
2. Maha, K., Hadi, O., Shakti, S., Rabeb, M., Anis, O. (2021). Two-sided preferences task matching mechanisms for blockchain-based crowdsourcing. Journal of Network and Computer Applications, 191, 103155. DOI 10.1016/j.jnca.2021.103155. [Google Scholar] [CrossRef]
3. Ren, Z. T., Lei, R. B., Gao, S. X. (2017). Two-sided matching and game on investing in carbon emission reduction technology under a cap-and-trade system. Journal of Cleaner Production, 282, 124436. DOI 10.1016/j.jclepro.2020.124436. [Google Scholar] [CrossRef]
4. Christian, H., Margeret, H., Vlasnik, S. L. (2018). Finding optimal mentor-mentee matches: A case study in applied two-sided matching. Heliyon, 4(6), e00634. DOI 10.1016/j.heliyon.2018.e00634. [Google Scholar] [CrossRef]
5. Chen, S. Q., Wang, Y. M., Shi, H. L., Zhang, X. X. (2019). A decision-making method for uncertain matching between volunteer teams and rescue tasks. International Journal of Disaster Risk Reduction, 58, 102138. DOI 10.1016/j.ijdrr.2021.102138. [Google Scholar] [CrossRef]
6. Gale, D., Shapley, L. S. (1962). College admissions and the stability of the marriage. American Mathematical Monthly, 69(1), 9–15. DOI 10.1080/00029890.1962.11989827. [Google Scholar] [CrossRef]
7. Tong, H. G., Zhu, J. J. (2020). New peer effect-based approach for service matching in cloud manufacturing under uncertain preferences. Applied Soft Computing, 94, 106444. DOI 10.1016/j.asoc.2020.106444. [Google Scholar] [CrossRef]
8. Pittel, B. (2020). On random stable matchings: Cyclic ones with strict preferences and two-sided ones with partially ordered preference. Advances in Applied Mathematics, 120, 102061. DOI 10.1016/j.aam.2020.102061. [Google Scholar] [CrossRef]
9. Hu, G. J., Li, J. T., Tang, R. (2020). The revealed preference theory of stable matchings with one-sided preferences. Games and Economic Behavior, 124, 305–318. DOI 10.1016/j.geb.2020.08.015. [Google Scholar] [CrossRef]
10. Antler, Y. (2015). Two-sided matching with endogenous preferences. American Economic Journal: Microeconomics, 7(3), 241–258. DOI 10.1257/mic.20130272. [Google Scholar] [CrossRef]
11. Chen, J., Song, K. (2013). Two-sided matching in the loan market. International Journal of Industrial Organization, 31(2), 145–152. DOI 10.1016/j.ijindorg.2012.12.002. [Google Scholar] [CrossRef]
12. Liang, Z. C., Yang, Y., Liao, S. G. (2021). Interval-valued intuitionistic fuzzy two-sided matching model considering level of automation. Applied Soft Computing, 116, 108252. DOI 10.1016/j.asoc.2021.108252. [Google Scholar] [CrossRef]
13. Yin, S., Li, B. Z. (2018). Matching management of supply and demand of green building technologies based on a novel matching method with intuitionistic fuzzy sets. Journal of Cleaner Production, 201, 748–763. DOI 10.1016/j.jclepro.2018.08.055. [Google Scholar] [CrossRef]
14. Yu, D. J., Xu, Z. S. (2020). Intuitionistic fuzzy two-sided matching model and its application to personnel-position matching problems. Journal of the Operational Research Society, 71(2), 312–321. DOI 10.1080/01605682.2018.1546662. [Google Scholar] [CrossRef]
15. Torra, V. (2010). Hesitant fuzzy sets. International Journal of Intelligent Systems, 25(6), 529–539. DOI 10.1002/int.20418. [Google Scholar] [CrossRef]
16. Xu, Z. S., Xia, M. M. (2011). Distance and similarity measures for hesitant fuzzy sets. Information Sciences, 181(11), 2128–2138. DOI 10.1016/j.ins.2011.01.028. [Google Scholar] [CrossRef]
17. Farhadinia, B. (2014). Distance and similarity measures for higher order hesitant fuzzy sets. Knowledge-Based Systems, 55, 43–48. DOI 10.1016/j.knosys.2013.10.008. [Google Scholar] [CrossRef]
18. Liang, W., Wang, J. Y., Deng, Z. (2022). HFGLDS: Hesitant fuzzy gained and lost dominance score method based on hesitant fuzzy utility function for multi-criteria decision making. IEEE Access, 10, 20407–20419. DOI 10.1109/ACCESS.2022.3152209. [Google Scholar] [CrossRef]
19. Liao, H. C., Wu, X. L., Keikha, A., Hafezalkotob, A. (2018). Power average-based score function and extension rule of hesitant fuzzy set and the hesitant power average operators. Journal of Intelligent & Fuzzy Systems, 35(3), 3873–3882. DOI 10.3233/JIFS-18794. [Google Scholar] [CrossRef]
20. Ma, Z. J., Zhang, N., Dai, Y. (2014). A novel SIR method for multiple attributes group decision making problem under hesitant fuzzy environment. Journal of Intelligent & Fuzzy Systems, 26(5), 2119–2130. DOI 10.3233/IFS-130887. [Google Scholar] [CrossRef]
21. Ahmadian, B., Ullah, G. (2021). Picture fuzzy maclaurin symmetric mean operators and their applications in solving multi-attribute decision-making problems. Mathematical Problems in Engineering, 2021, 1098631. DOI 10.1155/2021/1098631. [Google Scholar] [CrossRef]
22. Zhang, Z., Gao, J. L., Gao, Y., Yu, W. W. (2020). Two-sided matching decision making with multi-granular hesitant fuzzy linguistic term sets and incomplete criteria weight information. Expert Systems with Applications, 168, 114311. DOI 10.1016/j.eswa.2020.114311. [Google Scholar] [CrossRef]
23. Li, B. D., Yang, Y., Su, J. F., Wang, S. (2021). Two-sided matching model for complex product manufacturing tasks based on dual hesitant fuzzy preference information. Knowledge-Based Systems, 186, 104989. DOI 10.1016/j.knosys.2019.104989. [Google Scholar] [CrossRef]
24. Yue, Q., Zhang, L. L. (2020). Two-sided matching for hesitant fuzzy numbers in smart intelligent technique transfer. Mechanical Systems and Signal Processing, 139, 106643. DOI 10.1016/j.ymssp.2020.106643. [Google Scholar] [CrossRef]
25. Zhang, D., Dai, H. J., Liu, X. R. (2020). Intuitionistic fuzzy two-sided matching method considering regret aversion and matching aspiration. Operations Research and Management Science, 29(10), 132–139 (in Chinese). DOI 10.12005/orms.2020.0264. [Google Scholar] [CrossRef]
26. Xiang, N., Dou, Y. J., Xia, B. Y., Yang, K. W., Tan, Y. J. (2022). High-end equipment: An improved two-sided based S&M matching and a novel pareto refining method considering consistency. Expert Systems with Applications, 202, 117175. DOI 10.1016/j.eswa.2022.117175. [Google Scholar] [CrossRef]
27. Mahmood, T., Ullah, K., Khan, Q., Jan, N. (2019). An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Computing and Applications, 31(11), 7041–7053. DOI 10.1007/s00521-018-3521-2. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools