Qualia Role-Based Quantity Relation Extraction for Solving Algebra Story Problems

1  Introduction

Automatically solving math word problem (MWP) is a long-standing artificial intelligence (AI) challenge problem that dates back to the 1960s [1]. An automatic problem solver can be a key enabling technology for intelligent learning systems [2], such as for auto grading, peer math tutoring, etc. In recent years, automatic problem solving has attracted significant interest from the AI community and several neural network-based solvers were built for solving MWPs. Despite the great success of deep neural networks achieved in many other fields over the last few years, there are still many challenges in designing such kinds of solvers that can meet the needs of applications like intelligent tutoring. For example, it is hard for a neural solver to handle and describe the math object relations which are fundamental facts for mathematical expression generation. In this paper, we focus on designing algorithms for solving algebra story problems stated in Chinese with the ability of math entity relationship representation and quantity relation extraction.

Algebra story problem [3] is a sub-category of MWPs, which uses a short story to present mathematical properties of math objects. Quantity relations hidden in the mathematical properties of the interconnected math objects are essential information for solving the problem. In practice, some of the quantity relations are presented implicitly by the properties of the interconnected objects, but others may be hidden in the story text. As shown in Fig. 1, the key information for solving this problem lies in the L3 level relations of “length” between “square” and “circle”. Therefore, it is important for a problem solver to have the ability of quantity relation acquisition from the implicit properties of objects hidden in story text.

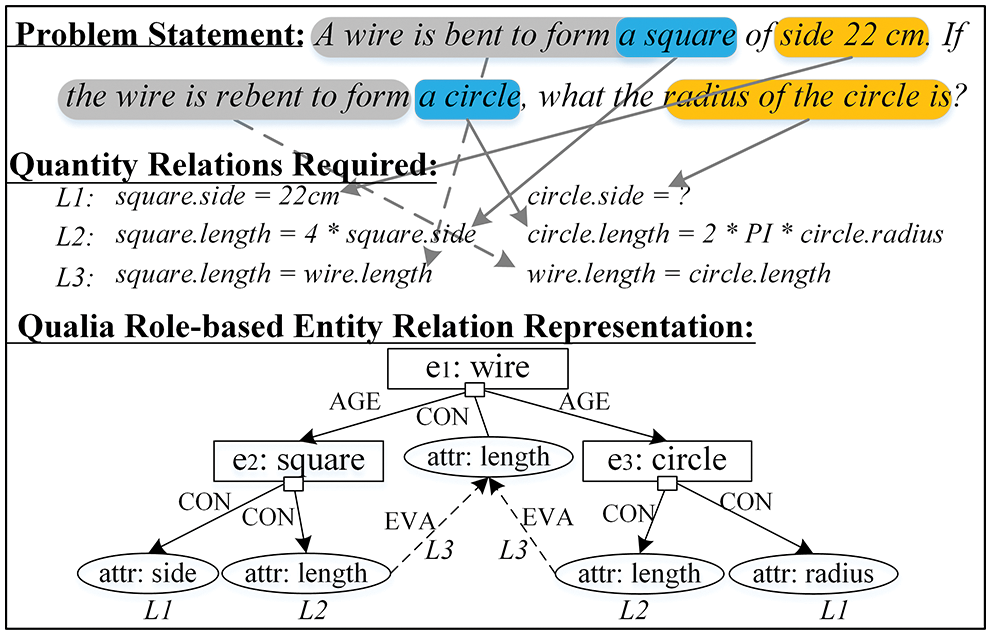
Figure 1: An example of quantity relation representation by using qualia role-related EDG

Traditional MWP solvers, such as rule-based methods [4,5] and semantic parsing-based methods [6–9], utilize heuristic rules or templates to locate and extract quantity relations from the problem statements. Mandal et al. [10], for example, demonstrated the use of a mixed approach of using the rule-based information and semantic role labeling to represent a MWP and generate the answer. Despite a good explanation of these methods, they have only been proven effective on fine-scale datasets. Recent works have focused on solving this problem on large-scale datasets by training an end-to-end neural network to directly map the problem text into a mathematical expression [11–16]. Although they seem to obtain satisfying performance, such end-to-end neural models suffer from several drawbacks being applied in practical tutoring systems. First, the ability of expression generation drops dramatically in sophisticated scenarios. Most neural solvers utilize an end-to-end model to derive the math expression directly to avoid entity recognition and quantity relation extraction. For example, retrieval models are used in early deep neural solvers [15] to obtain the equation. These models can only handle the predefined equations lack of generation ability for new equations that are not existent in the training data set. Recent state-of-the-art neural solvers, such as GTS [17], Graph2Tree [13,14], SMART [18], were designed to translate the problem text into an expression tree (e.g., equation tree) which greatly improved the generation ability of new equations. However, such end-to-end neural models were trained to generate an entire math expression which lacks of the supporting information to explain the composition of the generated math expression.

To represent the relations between quantities mentioned in the problem text, Roy et al. [11] proposed the concept of unit dependency graph (UDG) to connect the given numbers and the question being asked, which leverages two types of classifiers to predict the operations between quantities. The classifiers were trained on dataset with domain knowledge-based annotations to constrain the UDG generation as well as to explain the output expression. Yu et al. [19] proposed a framework for solving arithmetic word problems which use a set of syntactic-semantic (S2) models to bridge the problem text and the mathematical expressions. The improved S2 models were designed to solve various types of mathematical problems, e.g., direct current circuit problems [20], plane geometry problems [21], etc., which proved the efficiency of this method. However, the S2 model still suffers from insufficient ability of deriving quantity relations in more sophisticated scenarios which lack explicit syntactic-semantic patterns, such as the “length” between the “wire” and the “square”. Generally, such hidden information is usually indicated by incomplete S2 structures or hidden events, which are deeply related with qualia roles of entities in linguistics research [22,23].

Inspired by their work, we propose an EDG method to represent the quantity relations for solving algebra story problems stated in Chinese. The proposed method leverages qualia roles [22,23] to present the interconnections of the objects as well as the properties associated with the objects. In each EDG, objects are divided into math entities and math attributes which are connected to each other according to the qualia roles defined on the basis of the relation between the math entities and attributes. Quantity relations extracted from the interconnected math entities and attributes are taken as the supplementary inputs of the problem solver to improve the performance of problem solving. Recalling the example shown in Fig. 1, by using the qualia role-based entity dependency graph, the L3 level relations could be represented through the “EVA” role between the entity “square” and “circle”, which can be translated into the relations of “square.length=wire.length” and “wire.length=circle.length” finally.

The main contributions of this paper lie in:

1)   A qualia role-related entity dependency graph (EDG) is proposed to efficiently represent the quantity relations presented by the properties of the interconnected math objects, especially for those literally uncorrelated math objects in algebra story problems stated in Chinese.

2)   An algorithm is designed to extract quantity relations from the built EDG to improve the algebra story problem solving.

The rest of the paper is organized as follows. Section 2 describes the related research of quantity relation extraction. Sections 3 and 4 introduce the entity-dependency graph, the algorithm and application of extracting the quantity relations and the experimental results are presented in Section 5. We conclude this paper in Section 6.

2  Related Work

2.1 Algebra Story Problem Solving

This paper aims to build a graph-based representation method to improve the efficiency of quantity relation extraction for solving algebra story problems stated in Chinese. As discussed above, the algebra story problem is a sub-category of the math word problem which is much more complex than other math word problems such as arithmetic word problems [3]. Hence, in this section, we discuss the related work of solving math word problems, not just algebra story problems. The math word problem solvers can be divided into three categories: rule-based, semantic parsing-based and end-to-end method.

Rule-Based Method. Early solvers used rule-based methods to solve math word problems, which leverage predefined rules or templates to extract quantity relation from the problem text. A computer program, WORDPRO [4] was proposed in the 1980s. By manually defining rules, the program converts text in a particular format into propositions, and then makes simple inferences about these propositions to solve one-step problems. Bakman [24] proposed another system ROBUST which is an improvement on WORDPRO by defining a wider range of rules that enable it to solve free-format multi-step problems. Yuhui et al. [5] expanded this method to solve multi-step addition and subtraction algebra story problems by using a fixed frame. All these methods leverage fine defined rules to represent the input problems and can only work on small and closed data set of problems. Besides, the rules could be inefficient in a complicated context of problems.

Semantic Parsing-Based Method. With the development of natural language processing (NLP) technologies, researchers use semantic parsing to extract quantity relations from the problem text to avoid the huge work of manual rule construction. Roy et al. [6] made a first attempt to map text segments into quantity-value representation (QVR) by using text features and part of speech tags. The method of tracking the changes of quantity relation state with verbs was described in [7] which can be used to solve some numerical state change problems, but only in addition and subtraction. Another approach to semantic analysis described in [8] which is to extract relations by defining expressions named schema that match text. A tag-based algebra story problems solver was proposed in [9] which analyzes and transforms the text into predefined tag-based logic forms to achieve relation extraction. Mandal et al. [10] proposed an approach to extract the key entities and their attributes and quantities for solving addition-subtraction type arithmetic MWP. The problem of these semantic parsing methods is that they are too sensitive to interference information, and the performance of quantity relations extraction is significantly reduced when complex text is encountered.

End-to-End Method. Recent years, a number of researchers try to solve algebra story problems by generating a mathematical expression directly from the problem text. In [11], tree model is proposed to construct an expression tree. Then, the concept of unit dependency graph [11] is proposed to optimize the construction process of the tree. Inspired by this work, Wang et al. [12] attempted to use deep reinforcement learning to generate expression trees. Slightly different from expression trees, the concept of equation trees is proposed in [25]. Expression trees differ from equation trees in whether they contain unknowns in tree nodes, but are essentially equivalent.

Other researchers adopt the deep learning approach and obtain an expression from the problem text through training on the big data set without manual intervention, so as to calculate and solve the target. A method to align the quantities in the text with the template by pre-defining the equation template and using the deep learning is proposed in [26]. Wang et al. [15] made the first attempt to use a deep neural network to generate expressions for solving algebra story problems. In [27], a neural math solver based on an encoder-decoder framework was proposed to generate expressions. Although the number of researchers studying the end-to-end method is increasing, solving algebra story problems is not only about obtaining a result, because it is the retention of intermediate process that makes sense for the intelligent tutoring system, and this is the biggest problem of these methods that do not extract numeric relations.

2.2 Entity Relation Representation

The quantity relations and solution goals in algebra story problems are presented associated with math objects and recognizing the math object and identifying the relationship between the math objects is the fundamental work before quantity relation extraction. In the field of natural language processing (NLP), objects are usually named entities and a fair amount of work has been done on entity relation representation. This section introduces the general approaches of entity relation representation in NLP: semantic relation-based method, semantic framework-based method, and commonsense network-based method.

The semantic relation-based method classifies words according to the lexical meaning to obtain the relations between words, such as WordNet [28]. The WordNet is a database of English words developed by Princeton University in 1985. First, the words are divided according to the four parts of speech: noun, verb, adjective, and adverb, and then words are grouped according to the connections between different lexical meanings. WordNet defined four semantic relations: synonyms, hyponymy, antonymy, and meronymy. WordNet is an inductive lexicon not associated in meaning [29] but simultaneously present in the context.

The method based on semantic framework takes the semantic context of natural language into constructing lexical associations, such as FrameNet database [30]. which are organized by lexical meanings, the core of the FrameNet is to link words through semantic frameworks. The FrameNet consists of lexicon, annotated example sentences and the FrameNet database. The lexicon contains the definitions of word meaning, the annotated example sentences store the application examples of words, and the FrameNet database represents numerous patterns of the semantic framework [31]. The semantic framework is the core of FrameNet, which defines the framework’s name, meaning, and relation [29], and the lexical units. By defining a semantic framework, FrameNet can represent relationships when they exist simultaneously in a natural language context but where the entities are not lexically related. However, if the entities to be described do not have an associated semantic context frame defined in FrameNet, it is impossible to relate them.

The commonsense network-based method represents general commonsense information, such as ConceptNet [32]. ConceptNet is a dataset to track commonsense associations between entities. ConceptNet can construct associations between entities not directly related lexically or semantically. The combination and association of ConceptNet entities neglect the linguistic relevance of entities, making the relationships between entities dependent on commonsense. ConceptNet does not have the linguistic discipline for the existence of regularisations and formalization in algebra story problems. Therefore, ConceptNet is not adapted to modeling entity relations in algebra story problems.

As described in [23], a qualia role is proposed and designed to indicate a word’s meaning by a set of relations, called qualia, between the concept of the word and another concept that the word evokes. In [22], a more elaborated set of semantic roles (e.g., formal role, constitutive role, agentive role and telic role) is proposed to represent the meaning of nominals as well as the hidden information that is not overtly expressed in the syntax. The qualia role framework is described as follows: [α,QUALIA=[F,C,T,A]], where F=Formal denotes what kind of thing is it, what is its nature; C=Constitutive denotes what it make of, what are its constituents; T=Telic denotes what is it for, how does it function; A=Agentive denotes how did it come into being, what brought it about.

Later, Yuan [23] extended the semantic roles to 10 categories to form a more complete qualia structure of nouns, verbs and adjectives in Chinese.

The qualia role explores subjective evaluation and objective attribute of the math objects within an individual framework, which coincides with the expectation of the S2 method but is more powerful in understanding concept relations of linguistic expressions. In this paper, benefiting from this framework, the qualia role is chosen to modeling the quantity relations of math objects in sophisticated scenarios for solving algebra story problems stated in Chinese.

3  The Proposed Method

In this section, a qualia role-based entity dependency graph (EDG) is introduced to represent quantity relations for solving algebra story problems. An EDG is composed by a node set N and an edge set A. Each node ni in N denotes a math object in the problem text and each edge aij denotes the interconnection between the nodes ni and nj which could be used to generate quantity relations. Hence, the key issue of the EDG method is to identify the math objects and relationship between the math objects. In the following, we give a further discussion on the EDG generation and quantity relation extraction.

3.1 Math Entities in Algebra Story Problems

In an algebra story problem, quantities are mostly associated with the attributes that belong to math objects and the attributes are related to each other according to the interconnections of the math objects. Quantity relations are formed from the source formula of the attribute(s) of an individual math object or the attribute relation(s) between the interconnected math objects.

For example, in the case of “A 2000 lbs car with a speed of 50 km/h”, the quantities of “2000 lbs” and “50 km/h” are both associated with the entity “car”, but each refers a specific attribute (e.g., “2000 lbs” refers to the weight of the car, “50 km/h” refers to the speed of the car). To distinguish the quantities of various attributes is essential to prevent solvers from invalid operations that against the elemental principles of mathematics. For example, it is meaningless to plus “2000 lbs” and “50 km/h”. However, in most current MWP solvers, attributes of “weight”, “speed” and “car” are modeled as equal objects and it is hard to distinguish the entities and the associated attributes.

In this paper, the detected objects are divided into two categories: math entity and math attribute, from the perspective of semantic roles.

•   Math Entity (ME): Math entity is a noun object with math attribute(s).

•   Math Attribute (MA): Math attribute is a noun object that refers to the attribute of a math entity, which usually associates with a numerical value and a unit.

Both MA and ME are terms generated from math objects, which are annotated as nouns but different for mathematical property presentation. Generally, MAs represent numeric values associated with the math attributes of math entities. While MEs are used to distinguish different math entities. As a result, the quantity relations can be a hierarchical structure of “ME−MA−Value”.

To note that not all the math attributes are presented explicitly in the problem text. For example, in statement of “a 2 m long wire”, the quantity “2 m long” describes the attribute length of the wire which is not given. In such cases, an unit parsing is applied to complete the missing MEs.

Another issue is that the boundary between math attributes and math entities is not static, i.e., there is a variable semantic role. For example, in the case of “the leg of the table is 5 inches height”, here “the leg” is an attribute of the entity “the table”, but in some time, it is also an entity with an attribute “height”. In such case, the algorithm needs to determine the specific role of the object according to the context. Besides, entities may be missed as the idiomatic usage in a language. For example, “A storybook consists of 50 pages. Ming reads ten pages on the first day and five pages more on the second day”. The problem does not explicitly state the mathematical entity underlying the ten and five more pages. However, it requires an algorithm to construct the implicit entity of “sub-page”, which forms the Constitute and Unit semantic roles with the storybook and the numerical value.

3.2 Math Entity Relationship Modeling

In the qualia role description system, entity relationships are modeled by the qualia roles of entities. Specifically, the materiality roles of entities are determined by the type and syntactic structure, and we use ten qualia roles [23] to describe the math entity relationships in Chinese math word problems. As a result, the math entity relationship can be described as a qualia structure denoted as QS and each element qs in QS is structured as a tuple of <esrc,edst,r,f,p>, where esrc and edst are two math entities, r denotes the semantic role of edst associated with esrc, f denotes the source formulas related to r, p denotes the syntax pattern related to r.

•   Formal (FOR): the taxonomic information about the math entity (the is-a relation).

•   Constitutive (CON): the parts and constitution of a math entity (part-of or made-of relation).

•   Telic (TEL): the purpose and function of a math entity (the used-for or functions-as relation).

•   Agentive (AGE): the origin of a math entity (the created-by relation).

•   Unit (UNI): the corresponding quantifier of a math entity.

•   Evaluation (EVA): the subjective evaluation and emotion about the math entity.

•   Material (MAT): materials used to reflect the creation of the math entity.

•   Action (ACT): the habitual action, behavior, or activity of a math entity.

•   Handle (HAN): the habitual action, behavior, and influence of people or other things on a math entity.

•   Orientation (ORI): the relation between the position and direction of a person or other thing and the place, time, etc., indicated by.

Recalling the example of wire-square-circle problem above, the dependency between “wire” and “square” can be represented by a constitutive role (CON). The dependency between of “square” and “side” can be represented by an agentive role (AGE).

Entity dependency presents the relationship that exists between different entities. The relationship can be described as a graph called entity-dependency graph (EDG). We define the EDG as a tuple (N,A) consisting of nodes N and edges A. The nodes represent entities and the links represent the dependencies. Entity dependency in problem text exists in the following two situations. One is when entities are used to present the attributes of others. Take “weight of a tiger” for example, the entity “weight” is used to specify the attribute of another entity “tiger”, which means that it can not be treated as the principal subject in presenting numeric values. Similar examples such as the “length”, “width” and “area” of a rectangle, the “radius” or “diameter” of a circle. In this situation, entity dependency is implied by domain knowledge, and it can be specified either explicit or implicit. Another situation is when entities are used as syntactic modifiers. Examples such as “tigers in the zoo”, where the entities “zoo” and “tiger” constitute an adjunct relation. In this situation, numeric values are used to present the attributes of either a single entity (e.g., “tiger”) or the compound entity of “zoo−tiger”, which depends on the problem context. This section presents a detailed discussion of the types of entity dependency in algebra story problems.

As shown in Fig. 2, entity relationships can be classified into three fundamental types, each type refers to a sub-graph.

Figure 2: The category of entity relationships. (a) G1: Attribute relationship; (b) G2: Coordinate relationship; (c) G3: Convergence relationship

Attribute Relationship Sub-graph: describes the attributes of a math entity, such as the quantity, length, weight, speed, etc., which usually associates with qualia roles of FOR and UNI.

Coordinate Relationship Sub-graph: describes a concurrent relationship between two or more entities, e.g., a comparative relationship, a multiplicative/proportional relationship, etc., which usually associates with qualia roles of EVA, MAT and ORI.

Convergence Relationship Sub-graph: describes the convergent relationship between two or more math entities, e.g., the summation relation, which usually associates with qualia roles of CON, TEL, ACT, HAN, MAT, and ORI.

As a result, entity relationships could be organized as a network named entity dependency graph (EDG in short) which is composed by the above three relationship networks. In the field of math word problem solving, we can build a static EDG that contains domain knowledge and commonsense knowledge to store and represent the attribute relations of entities. Besides, EDG can be also used to represent the dynamic relations of entities given by the problem text. In the end, all the static relations and dynamic relations are integrated into a single EDG. Next, we give an introduction to how the quantity relations are represented and stored in an EDG.

3.3 Quantity Relation Representation

According to the definition of the categories of entity relationships, quantity relations in algebra story problems could be divided into the following three categories:

Attribute Relation. Attribute relation usually presents a numeric value for an attribute (as shown in formula (1)) of a math entity. The numeric value is given or known by the input problem. Another frequently existed attribute relation is the quantity transformation between multiple attributes (as shown in formula (2)). For example, the relation between the radius and the circumference of a circle. These attribute relations are not directly presented by the input problem, but could be inferred out following certain knowledge. Therefore, in this case, a domain knowledge base is needed and a tiny inference engine should be designed to obtain attribute relations.

r1,i=c(1)

r1,i=domain_formula(r1,j,r1,k,…)(2)

where r1,i,r1,j,r1,k,… denote the attributes of the math entity e1o as shown in Fig. 2a, c is a constant extracted from the input problem, domain_formula() is a source formula on attributes r1,i,r1,j,r1,k,…

Comparable Relation. The comparable relation describes a comparative or multiplicative relationship between two math entities with the same type of attribute, such as a relation of “more or less than”, “times”, etc.

r1,i=c⊕r2,i(3)

c=r1,i⊙r2,i(4)

where ⊕ denotes operator + or ×, ⊙ is an operator from − or ÷. Comparable relations could be translated from the coordinate relationship sub-graph as shown in Fig. 2b.

Convergence Relation. The aggregate relation in a convergence relationship describes a total relation of the same type attribute between multiple math entities as expressed in formula (5), which usually refers to “total”, “sum”, etc. Convergence relations could be translated from the convergence relationship sub-graph as shown in Fig. 2c.

r0,i=r1,i+r2,i+⋯(5)

where i=1,…,n, n represents the entity number involved in the convergence operation. By using the above formulas, the entity relationship sub-graphs defined in Fig. 2 could be translated into quantity expressions for solving the input problem.

The above types of quantity relations exist everywhere in algebra story problems. The difference between each category is that the attribute relation is used to represent the quantities of the attributes within an attribute sub-graph Ga, which could be written as a constant expression or an expression with two or more attributes of the math entity in Ga. The comparable relation and the convergence relation are used to represent quantity relations of the same attribute between different math entities but are fit for different typologies of sub-graphs. For a coordinate sub-graph, expressions can be obtained from the source formulas of the comparable relations, and for a convergence sub-graph, expressions can be obtained from the source formulas of the convergence relations. Therefore, the task of quantity relation extraction can be divided into two sub-tasks of EDG construction and sub-graph identification.

4  Quantity Relation Extraction

This section introduces the algorithms of quantity relation extraction from a given problem, including the processes of EDG construction and sub-graph identification. Firstly, a generation algorithm is introduced to build an instance graph of entity relation network, called entity-dependency graph (EDG), from an input problem text. Then, an extraction algorithm is introduced to obtain quantity relations from the generated EDG.

4.1 Entity-Dependency Graph Generation

To build the EDG for each input problem, we first create a node set N based on the result of part-of-speech annotation. Then, edges aij are added according to the syntactic dependency and the qualia role of the nodes. The complete process of EDG generation is described in Algorithm 1 which contains two main processes: node generation and edge generation.

Node Generation A graph EDG has two types of nodes: ME nodes and MA nodes, which correspond to math entities and math attributes separately. To generate the nodes, part-of-speech (POS) analyzing [33] is adopted to obtain all the math objects from the original text. Then, attribute checking is implemented to identify entity objects and attribute objects and ME nodes and MA nodes are created correspondingly. Implicit MA nodes as discussed in Section 3.1 are added before the edge generation.

Edge Generation An edge could to added to connect either two ME nodes, or between a ME node and a MA node if there exists a qualia relationship between the two nodes. Ten types of qualia relationships as described in Section 3.2 determine to add which edges.

Take the problem shown in Fig. 1 as an example, to generate the EDG nodes, nouns of “wire”, “square”, “side”, “circle” and “radius” annotated by a POS analyzer could perceive as the original math objects. Then, an attribute analyzing is implemented according to the qualia roles described by the knowledge base QRKB, to distinguish ME nodes “wire”, “square” and “circle” from MA nodes “side” and “radius”. In the end, a qualia relationship analysis determines when to add which edges. For example, when a constitutive relation is detected between the MA node “side” and the ME node “square”, an edge between nodes “side” and “square” is added. Similar operations can be done to add a new edge between the ME node “wire” and “square” because of an agentive relation.

4.2 Quantity Relation Extraction from EDG

As discussed in Section 3, entity relationships are categorized into three categories and quantity relations can be obtained by using formulas (1)–(5). Therefore, the task of quantity relation extraction is to identify the categories of the sub-graph in the generated EDG. The process of quantity relation extraction is described in Algorithm 2.

The core task of Algorithm 2 is to search out all the sub-graphs Gi in directly graph G, and let each Gi refers to one category of entity relationship as discussed in Section 3. To identify the category of a sub-graph composed by (pi,pj), we only need to test the node type of pj. If pj is an attribute node, then (pi,pj) belongs to an attribute sub-graph associated with entity node pi. Otherwise, (pi,pj) belongs to a concurrent sub-graph. Therefore, the algorithm first travels all the nodes to find out attribute relation sub-graphs. Then, the concurrency relation sub-graphs are searched out, denoted as G3. To identify the convergence sub-graph and the compound sub-graph, we implement a further analysis on G3. Specifically, if the sub-graph G3 only has two nodes, then it can be identified as a convergence sub-graph G2. Finally, the left sub-graphs in G3 are considered as convergence sub-graphs. The output relations are translated from the identified sub-graphs according to formulas (1)–(5).

For example in Fig. 1, when the sub-graph G1=(e2:square,attr:side,attr:length) is identified, an expression of “e2.length=4×e2.side” could be extracted from G1. Similarly, an area calculation expression “e2.area=e2.side×e2.side” could also be generated if keyword “area” is involved in the input problem.

Though some AWP solvers can directly use the generated expressions, most of the neural solvers cannot accept these expressions directly. To address the incompatible issue, the expressions need to be transformed into natural language statements to input to the solvers.

5  Experimental Evaluation

In this section, we introduce the experimental results of the proposed method compared to the state-of-the-art on the public dataset stated in Chinese, Math23K.

Dataset. Math23K [15] is a large-scale data set widely used in math problem solver evaluation, which contains story problems and non-story problems (e.g., equation, formula, number, etc.) in stage of primary school in China. In this paper, we apply EDG to represent the quantity relations for solving algebra story problems. According to Mayer’s [3] work, algebra story problems can be divided into several categories with different propositional structures and story lines which affect the complexity of the EDG and the quantity relations. To evaluate the performance of the proposed algorithms on different problem categories, we curate the new data set from Math23k with 6028 problems which are classified into five categories:

•   Proportion: problems involve or require proportions.

•   Unitary: problems involve total quantities and require the quantity per day, minute, etc.

•   Interest rate: problems involve or require the interest and interest rate.

•   Summation: problems involve the partial values and require the total value.

•   Motion: problems involve or require the distance, time and speed.

Compared with Mayer’s work, we merged several simple categories into a more comprehensive category. For example, in Mayer’s work, the DRT (distance-rate-time) problems and Motion problems are divided into two separate categories. While in our experiment, these two categories are merged into a single group named Motion as they have similar graph structures and source formulas.

To build the new data set, we first create a set of keywords for each category, and then a classifier accomplishes the classification work. In the end, we group the selected 6028 problems into five categories, including 1377 proportion problems, 1115 unitary problems, 239 interest rate problems, 1464 summation problems, and 1833 motion problems. Table 1 gives the detailed information of the new dataset.

Baselines. The methods to be compared are listed as below:

•   S2 method [19]: A framework for solving explicit algebra story problems which uses a set of syntactic-semantic (S2) models to transform a natural language math problem to a formal representation of quantity relations to produce the solution.

•   GTS [17]: A goal-driven tree-structured math word problem solver which uses a top-down goal decomposition process to generate solution expressions. GTS is considered to be a foundation work for most of the recent tree-based deep neural MWP solvers.

•   Graph2Tree [14]: A tree-based MWP solvers that combines the merits of the quantity comparison graph and quantity cell graph for problem encoding, and a decoder similar to GTS is applied to generate the solution expression.

•   Qualia role-based entity dependency graph (EDG in short): the method proposed in this paper.

All the above baseline methods are built on the dataset of Math23K which is stated in Chinese. Another similar work employed UDG [11] to represent the relationships among the quantities and the questions for solving English arithmetic word problems. It was heavily dependent on manual features and conditions for both classification and unit dependency reference and was not selected as the baseline for problem solving performance evaluation in this paper.

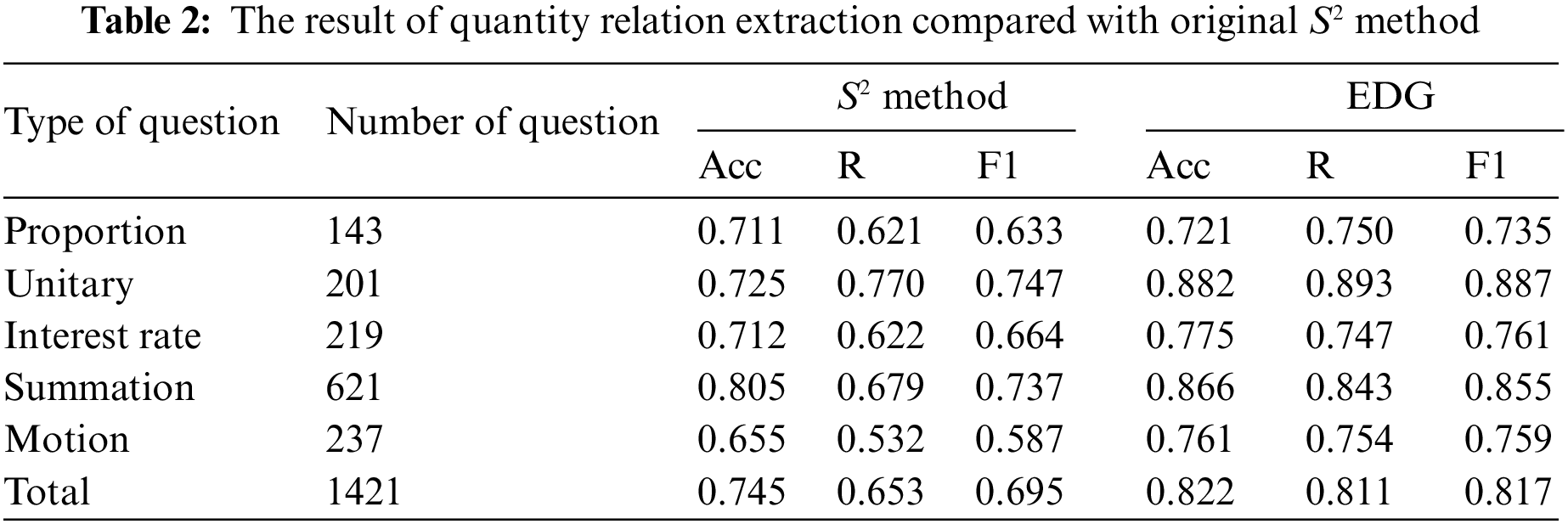
5.1 Performance on Quantity Relation Extraction

As the performance of quantity relation extraction is not evaluated by all the neural solvers, we only compare the result to the S2 method. The test uses accuracy (Acc), recall (R) and F1-score as metrics to evaluate the performance of quantity relation extraction. A big challenge is that there is a lack of large scale ground-truth for quantity relation evaluation. Therefore, we randomly choose 1421 problems from the new dataset and add the quantity relation labels for each problem. Comparison with S2 method, Table 2 summarizes the comparison of the answer accuracy on the test set with regard to problem types. The proposed EDG model significantly outperforms the S2 method nearly 7.7% in terms of the overall accuracy. More specifically, EDG outperforms the neural models by 15.7% and 10.6% on the Unitary and Motion problems.

5.2 Performance on Problem Solving

Inspired by [34], a prompt learning mechanism is implemented to evaluate the performance of problem solving. In our experiment, the original problem text, as well as the output of Algorithm 2, were encoded together and were taken as input of the MWP solvers, e.g., GTS, Graph2Tree. The accuracy of problem solving is then evaluated as shown in Table 3.

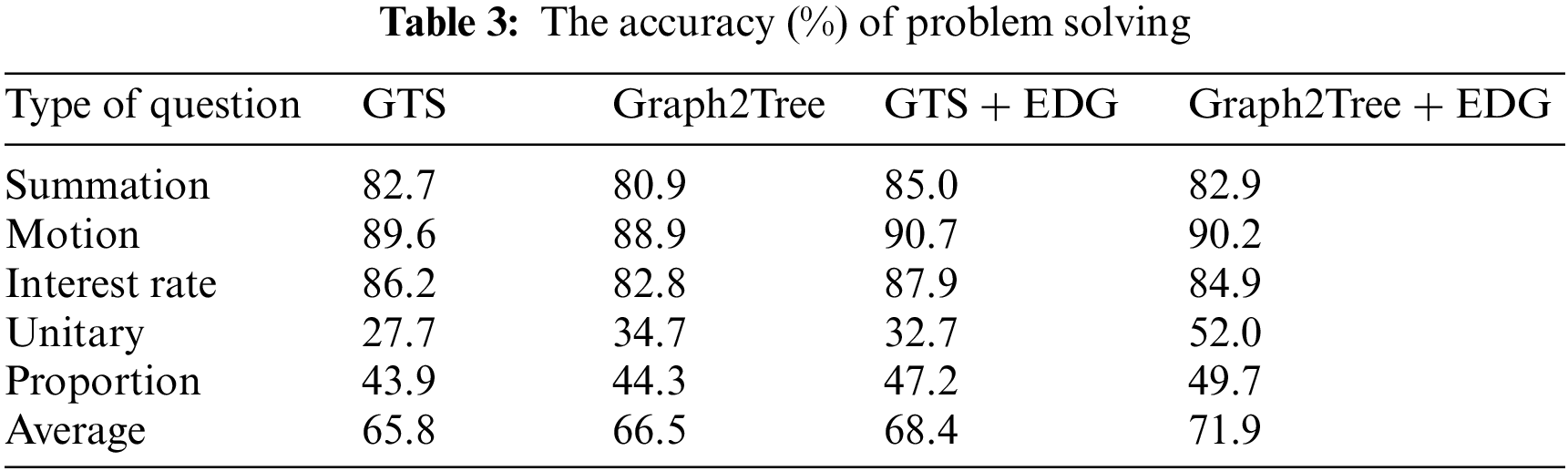
From Table 3, we can observe that benefiting from the EDG tasks, the average accuracy is up to 71.9% and 68.4% by injecting the extracted quantity relations into Graph2Tree and GTS models separately. Significant improvements (5%, 3.3%) were achieved on questions of Unitary and Proportion after integrating EDG method into Grahp2Tree model, which shows our method is more feasible for solving WMPs in case of more implicit relations are needed.

5.3 Comparative Analysis on Graph-Based Representation

For most MWP solvers, problem texts are treated as an unstructured word sequence. However, the relationships among the math objects involved in the text, such as math entities and attributes, are structured information with corresponding hidden domain knowledge. This structured information can be organized as a tree or graph [11,14,35] to improve the final performance. As shown in Fig. 3a, Roy et al. [11] used unit dependency graph (UDG) to represent the relationship between the numbers and the question being asked. Here, “66” and “10” are connected via a “SAME UNIT” edge, hence they can be added or subtracted, “8” is connected to the goal question node with an “DEN UNIT” edge, indicating that some expression will be divided by “8” to get the answer’s unit. To enrich the representation of a quantity, Zhang et al. [14] (as shown in Fig. 3b) leverage two graphs, including a quantity comparison graph and a quantity cell graph, to model the relationships between the descriptive words associated with a quantity. To associate the phrase structure information, the dependency parsing [35] (as shown in Fig. 3c) is implemented to link with two word nodes using syntactic constituency information to construct quantity graphs.

Figure 3: Comparison of graph-based quantity relation representation ((a) Unit dependency graph [11]; (b) Constituency tree augmented text graph [35]; (c) Quantity comparison graph and quantity cell graph [14]; (d) Entity dependence graph)

Compared with the above three types of graphs, the proposed entity-dependency graph (EDG) can be used to represent the relationship among the quantities and math entities in sophisticated scenarios. In each constructed EDG (as shown in Fig. 3d), math entities (e.g., “Isabel”, “flower”, “bouquets”) and quantities, as well as the associated nouns, verbs, adjectives, units, and rates that describe a quantity, are listed as nodes. Entity relationships are modeled according to the qualia roles of entities. For example, the edge <Isabel, flower, ACT> denotes an Action relationship between entities “Isabel” and “flower”, and <flower, bouquets, AGE> denotes an Agentive relationship between entities “flower” and “bouquets”. Quantity nodes associated to math entities denote the attribute values assigned to the connected math entities. Possible advantages of EDG are summarized below:

1)   It is a first attempt to integrate nodes of math entities, attributes and quantities into a single graph which provides more indicative information for solution tree construction.

2)   The qualia structure is used to model the relationships among math entities, which allows us to avoid the heavily manual work of semantic role labeling for text parsing.

3)   The edges in the constructed EDG can be easily formed into path(s) by integrating a lite inference engine to generate an interpretable solution.

6  Conclusion

Quantity relation extraction is essential for building MWP solvers, especially for those solvers built for intelligent tutoring systems. This paper proposed a qualia role-based entity-dependency graph (EDG) to represent quantity relations for solving algebra story problems stated in Chinese. Algorithms were designed to generate the EDG and to extract mathematical expressions from the generated EDG. Finally, the extracted mathematical expressions are used as the input of the solver to calculate the final answer. Experimental results showed that the proposed method achieved up to 7% promotion on the average accuracy on quantity relation extraction and 5% promotion on problem solving compared to baseline methods.

Despite the encouraging results that have been achieved, there is room for improvement. First, the proposed method can only be applied to solve algebra story problems stated in Chinese currently. In future work, we will continue working on developing an extended qualia role knowledge base to support solving problems stated in other languages, such as English. Second, further research is needed to improve the capability of mathematical property representation. Mathematical properties are much more complex than numerical values and some new encoding mechanisms should be discussed when constructing the EDG. Recent research results on natural language processing and deep neural symbol networks will be considered for extracting the math entities in varieties of MWPs and modeling the relationship between the extracted math entities. In the end, we will also explore the possibility of using entity-dependency graph to improve the interpretability of the generated solutions.

Funding Statement: This work is supported by the National Natural Science Foundation of China (Nos. 62177024, 62007014), the Humanities and Social Sciences Youth Fund of the Ministry of Education (No. 20YJC880024), China Post Doctoral Science Foundation (No. 2019M652678) and the Fundamental Research Funds for the Central Universities (No. CCNU20ZT019).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Zhang, D., Wang, L., Zhang, L., Dai, B. T., Shen, H. T. (2019). The gap of semantic parsing: A survey on automatic math word problem solvers. IEEE Transactions on Pattern Analysis and Machine Intelligence, 42(9), 2287–2305. DOI 10.1109/TPAMI.34. [Google Scholar] [CrossRef]

 2.  Mandal, S., Naskar, S. K. (2021). Classifying and solving arithmetic math word problems--An intelligent math solver. IEEE Transactions on Learning Technologies, 14(1), 28–41. DOI 10.1109/TLT.2021.3057805. [Google Scholar] [CrossRef]

 3.  Mayer, R. E. (1981). Frequency norms and structural analysis of algebra story problems into families, categories, and templates. Instructional Science, 10(2), 135–175. DOI 10.1007/BF00132515. [Google Scholar] [CrossRef]

 4.  Fletcher, C. R. (1985). Understanding and solving arithmetic word problems: A computer simulation. Behavior Research Methods, Instruments, & Computers, 17(5), 565–571. DOI 10.3758/BF03207654. [Google Scholar] [CrossRef]

 5.  Ma, Y., Ying, Z., Cui, G., Ren, Y., Huang, R. (2010). Frame-based calculus of solving arithmetic multi-step addition and subtraction word problems. Procedings of the 2010 Second International Workshop on Education Technology and Computer Science, vol. 2, pp. 476–479. Wuhan, China. [Google Scholar]

 6.  Roy, S., Vieira, T., Roth, D. (2015). Reasoning about quantities in natural language. Transactions of the Association for Computational Linguistics, 3, 1–13. DOI 10.1162/tacl_a_00118. [Google Scholar] [CrossRef]

 7.  Hosseini, M. J., Hajishirzi, H., Etzioni, O., Kushman, N. (2014). Learning to solve arithmetic word problems with verb categorization. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, pp. 523–533. Doha, Qatar. [Google Scholar]

 8.  Sundaram, S. S., Khemani, D. (2015). Natural language processing for solving simple word problems. Proceedings of the 12th International Conference on Natural Language Processing, pp. 394–402. Trivandrum, India. [Google Scholar]

 9.  Liang, C. C., Hsu, K. Y., Huang, C. T., Li, C. M., Miao, S. Y. et al. (2016). A Tag-based statistical English math word problem solver with understanding, reasoning and explanation. Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, pp. 4254–4255. San Diego, USA. [Google Scholar]

10. Mandal, S., Naskar, S. K. (2019). Solving arithmetic word problems by object oriented modeling and query-based information processing. International Journal on Artificial Intelligence Tools, 28(4), 1940002. DOI 10.1142/S0218213019400025. [Google Scholar] [CrossRef]

11. Roy, S., Roth, D. (2017). Unit dependency graph and its application to arithmetic word problem solving. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 31, no. 1. San Francisco, USA. [Google Scholar]

12. Wang, L., Zhang, D., Gao, L., Song, J., Guo, L. et al. (2018). MathDQN: Solving arithmetic word problems via deep reinforcement learning. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, no. 1. New Orleans, USA. [Google Scholar]

13. Wu, Q., Zhang, Q., Wei, Z. (2021). An edge-enhanced hierarchical graph-to-tree network for math word problem solving. Proceedings of the Association for Computational Linguistics: EMNLP 2021, pp. 1473–1482. Seattle, USA. [Google Scholar]

14. Zhang, J., Wang, L., Lee, R. K. W., Bin, Y., Wang, Y. et al. (2020). Graph-to-tree learning for solving math word problems. Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. [Google Scholar]

15. Wang, Y., Liu, X., Shi, S. (2017). Deep neural solver for math word problems. Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pp. 845–854. Copenhagen, Denmark. [Google Scholar]

16. Qin, J., Liang, X., Hong, Y., Tang, J., Lin, L. (2021). Neural-symbolic solver for math word problems with auxiliary tasks. Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing. arXiv preprint arXiv:2107.01431. [Google Scholar]

17. Xie, Z., Sun, S. (2019). A Goal-driven tree-structured neural model for math word problems. Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 5299–5305. Macao, China. [Google Scholar]

18. Hong, Y., Li, Q., Gong, R., Ciao, D., Huang, S. et al. (2021). SMART: A situation model for algebra story problems via attributed grammar. Proceedings of the 2021 AAAI Conference on Artificial Intelligence. https://www.aaai.org/AAAI21Papers/AAAI-8166.HongY.pdf. [Google Scholar]

19. Yu, X., Wang, M., Gan, W., He, B., Ye, N. (2019). A framework for solving explicit arithmetic word problems and proving plane geometry theorems. International Journal of Pattern Recognition and Artificial Intelligence, 33(7), 1940005. DOI 10.1142/S0218001419400056. [Google Scholar] [CrossRef]

20. He, B., Yu, X., Jian, P., Zhang, T. (2020). A relation based algorithm for solving direct current circuit problems. Applied Intelligence, 50(7), 2293–2309. DOI 10.1007/s10489-020-01667-7. [Google Scholar] [CrossRef]

21. Yu, X., Gan, W., Wang, M. (2017). Understanding explicit arithmetic word problems and explicit plane geometry problems using syntax-semantics models. Proceedings of the 2017 International Conference on Asian Language Processing, Singapore. [Google Scholar]

22. Pustejovsky, J. (1991). The generative lexicon. Computational Linguistics, 17, 409–441. [Google Scholar]

23. Yuan, Y. L. (2013). A study of Chinese semantic knowledge system based on the theory of generative lexicon and argument structure. Jorunal of Chinese Information Processing, 27(6), 23–30. [Google Scholar]

24. Bakman, Y. (2007). Robust understanding of word problems with extraneous information. arXiv preprint Math/0701393. [Google Scholar]

25. Koncel-Kedziorski, R., Hajishirzi, H., Sabharwal, A., Etzioni, O., Ang, S. D. (2015). Parsing algebraic word problems into equations. Transactions of the Association for Computational Linguistics, 3, 585–597. DOI 10.1162/tacl_a_00160. [Google Scholar] [CrossRef]

26. Kushman, N., Artzi, Y., Zettlemoyer, L., Barzilay, R. (2014). Learning to automatically solve algebra word problems. Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, Baltimore, Maryland. [Google Scholar]

27. Chiang, T. R., Chen, Y. N. (2018). Semantically-aligned equation generation for solving and reasoning math word problems. arXiv preprint arXiv:1811.00720. [Google Scholar]

28. Miller, G. A. (1998). WordNet: An electronic lexical database. Cambridge, MA, USA: MIT Press. [Google Scholar]

29. Baker, C. F., Fillmore, C. J., Lowe, J. B. (1998). The Berkeley framenet project. Proceedings of the 17th International Conference on Computational Linguistics, Patna, India. [Google Scholar]

30. Fillmore, C. J., Johnson, C. R., Petruck, M. R. (2003). Background to framenet. International Journal of Lexicography, 16(3), 235–250. DOI 10.1093/ijl/16.3.235. [Google Scholar] [CrossRef]

31. Semantics, F. C. J. F., Fillmore, C. J. (1982). Linguistics in the morning calm, pp. 111–137. Seoul: Hanshin Publishing Co. [Google Scholar]

32. Liu, H., Singh, P. (2004). ConceptNet-A practical commonsense reasoning tool-kit. BT Technology Journal, 22(4), 211–226. DOI 10.1023/B:BTTJ.0000047600.45421.6d. [Google Scholar] [CrossRef]

33. He, H. (2020). HanLP: Han language processing. https://github.com/hankcs/HanLP. [Google Scholar]

34. Liang, Z., Zhang, J., Shao, J., Zhang, X. (2021). MWP-BERT: A strong baseline for math word problems. arXiv preprint arXiv:2107.13435. [Google Scholar]

35. Li, S., Wu, L., Feng, S., Xu, F., Xu, F. et al. (2020). Graph-to-tree neural networks for learning structured input-output translation with applications to semantic parsing and math word problem. Findings of the Association for Computational Linguistics: EMNLP 2020. DOI 10.18653/v1/2020.findings-emnlp. [Google Scholar] [CrossRef]