Aggregate Point Cloud Geometric Features for Processing

1  Introduction

With the rapid development of 3D vision sensors such as RGB-D cameras, 3D point cloud data has proliferated, which can provide rich 3D geometric information. The analysis of 3D point clouds is receiving more and more attention as they can be used in many aspects such as autonomous driving, robotics, and remote sensing [1]. Intelligent (automatic, efficient, and reliable) feature learning and representation of these massive point cloud data is a key problem for 3D understanding (including 3D object recognition, semantic segmentation and 3D object generation, etc.).

Thanks to deep learning’s powerful ability to learn features, deep learning has attracted extensive attention. It has also achieved fruitful results in the field of image understanding over the past few years [2–10]. As traditional 3D point cloud features rely on artificial design, they cannot describe semantic information at a high level, making adaptations to complex real-life situations difficult. However, deep learning methods with autonomous feature learning capacity have great advantages in these aspects. Since point clouds are disordered and unstructured, traditional deep learning methods that work well on 2D images cannot be directly used to process point clouds. Inferring shape information from these irregular points is complicated.

In order to process point clouds using raw data, Qi et al. proposed PointNet [8], which uses multilayer perceptrons (MLPs) with shared parameters to map each point to a high-dimensional feature space, and then passes in a Max Pooling layer to extract global features. Since PointNet mainly focuses on the overall features and ignores the neighborhood structure information, it is difficult for PointNet to capture local geometric structure information. Qi et al. proposed PointNet++ [9], which introduces a multilayer network structure in PointNet to better capture geometric structure information from the neighborhood of each point. The network structure for PointNet++ is similar to image convolutional neural network. PointNet++ extracts local neighborhood features using PointNet as basic components and abstracts the extracted features layer by layer using a hierarchical network structure. Due to their simplicity and powerful presentation, many networks have been developed based on PointNet and PointNet++ [6,11–18].

Local feature aggregation is an important basic operation that has been extensively studied in recent years [6,14,19], which is mainly used to discover the correlations between points in local regions. For each key point, its neighbors are first grouped according to predefined rules (e.g., KNN). Next, the features between query points and neighboring points are passed into various point-based transformations and aggregation modules for local geometric feature extraction.

Local feature aggregation can incorporate some prior knowledge into local features by predefined rules. For example, KNN-based approaches explicitly assume that local features are related to neighboring points and independent of non-adjacent features in same layers. They incorporate this information into local features by KNN. However, the above operation lacks long-range relations, Li et al. proposed a non-local module to capture them [6]. It not only considers neighboring points, but also the whole point cloud sampling points. It incorporates this priori information into the local features by L-NL Module.

We argue that these approaches are insufficient to extract long-range relations. For this reason, we propose an end-to-end point cloud processing network named TGNet, which can efficiently, robustly, and adequately depict the geometry of point clouds. Fig. 1 intuitively compares our aggregation method with local and non-local aggregation methods. Compared with local aggregation approaches, our method can better capture long-range dependencies. Compared with non-local aggregation approaches, our method avoids the global point-to-point mapping and can extract geometric features more efficiently.

Our main contributions can be summarized as follows:

1.    We propose a novel robust end-to-end point cloud processing network, named TGNet, which can effectively enhance point clouds processing.

2.    We design a local feature grouping block TGSG (Tree Graph Sampling and Grouping) that enables our network to better trade off the balance of local and long-range dependencies.

3.    We further design a transformer-based point cloud aggregation block TGA, which can efficiently aggregate Tree Graph features.

Figure 1: Common aggregations and tree graph (our) aggregation. Red points denote key points, yellow points denote query points and green circles denote query range. Left: local aggregation method. Middle: non-local aggregation method. Right: our aggregation method (Note that our query points are in the feature space)

Our approach achieves state-of-the-art performance in extensive experiments on point cloud classification, segmentation, and normal estimation, which validates the effectiveness of our work.

We note that an earlier version of this paper appeared in [20]. This manuscript has been expanded, revised, and refined based on conference papers. Our description of the method provides a more complete explanation. In the experiments section, supplementary experiments and visualizations have been added to further understand our model.

2  Related Work

2.1 Deep Learning on Point Cloud

The biggest challenge of point cloud processing is its unstructured representations. According to the form of the data input to neural network, existing learning methods can be classified as volume-based [2,4,5,7,10], projection-based [3,21–24], and point-based methods [8,9,11,14,16–18,25–31]. Projection-based methods project an unstructured point cloud into a set of 2D images, while volume-based methods transform the point cloud into regular 3D grids. Then, the task is completed using 2D or 3D convolutional neural networks. These methods do not use raw point cloud directly and suffer from explicit information loss and extensive computation. For volume-based methods, low-resolution voxelization will result in the loss of detailed structural information of objects, while high-resolution voxelization will result in huge memory and computational requirements. For projection-based methods, they are more sensitive to viewpoints selection and object occlusion. Furthermore, such methods cannot adequately extract geometric and structural information from 3D point clouds due to information loss during 3D-to-2D projection.

PointNet is a pioneer of point-based methods, which directly uses raw point clouds as input to neural networks to extract point cloud features through shared MLP and global Max Pooling. To capture delicate geometric structures from local regions, Qi et al. proposed a hierarchical network PointNet++ [9]. Local features are learned from local geometric structures and abstracted layer by layer. The point-based approach does not require any voxelization or projection and thus does not introduce explicit information loss and is gaining popularity. Following them, recent work has focused on designing advanced convolution operations, considering a wider range of neighborhoods and adaptive aggregation of query points. In this paper, point-based approach is also used to construct our network.

2.2 Advanced Convolution Operations

Although unstructured point clouds make it difficult to design convolution kernels, advanced convolution kernels in recent literature have overcome these drawbacks and achieved promising results on basic point cloud analysis tasks. Current 3D convolution methods can be divided into continuous [11,13,16,17], discrete [28,32] and graph-based convolution methods [12]. Continuous convolution methods define the convolution operation depending on the spatial distribution of local regions. The convolution output is a weighted combination of adjacent point features, and the convolution weights of adjacent points are determined based on their spatial distribution to the centroids. For example, RS-CNN [17] maps predefined low-level neighborhood relationships (e.g., relative position and distance) to high-level feature relationships via MLPs and uses them to determine the weights of neighborhood points. In PointConv [16], the convolution kernel is considered as a nonlinear function of local neighborhood point coordinates, consisting of weight and density functions. The weight functions are learned by MLPs, and the kernelized density estimates are used to learn the density functions.

Discrete convolution method defines a convolution operation on regular grids, where the offset about the centroid determines the weights of the neighboring points. In GeoConv [32], Edge features are decomposed into six bases, which encourages the network to learn edge features independently along each base. Then, the features are aggregated according to the geometric relationships between the edge features and the bases. Learning in this way can preserve the geometric structure information of point clouds.

Graph-based convolution methods use a graph to organize raw unordered 3D point cloud, where the vertices of the graph are defined by points in the point cloud, and the directed edges of the graph are generated by combining the centroids and neighboring points. Features learning and aggregation are performed in spatial or spectral domains. In DGCNN [12], its graph is built in feature space and changes as features are extracted. EdgeConv is used to generate edge features and search for neighbors in their feature space.

2.3 Wider Range of Neighborhoods

Due to the geometric structure of the point cloud itself, it is difficult to determine precisely which global points are associated with local point cloud features. During the information extraction and abstraction process, local features are roughly assumed to be associated only with neighboring points. Recent state-of-the-art methods in literatures attempt to address the above difficulties and achieve promising results on basic point cloud analysis tasks. SOCNN [33] and PointASNL [6] sample global and local points and then fuse them with features. With these computed features, point cloud processing can be executed with greater accuracy and robustness.

Unlike all existing sampling methods, we follow explicit rules for sampling and grouping points on the surface of the point cloud. In this way, our local features will contain rich information describing the shape and geometry of the object.

2.4 Adaptive Aggregation

There are currently two main types of feature aggregation operators: local and non-local. Local feature aggregation operators fuse existing features of neighboring points to obtain new features. After that, the new features are abstracted layer by layer through a hierarchical network structure to get global features. Different from the local feature aggregation operator, non-local aggregation operators introduce global information when computing local features. Non-local aggregation operators start with nonlocal neural networks [34], which essentially use self-attention to compute a new feature by fusing the features of neighboring points with global information. Due to the success of the transformer in vision tasks [35–37] and the fact that the transformer [38] itself has inherently permutation invariant and is well suited for point cloud processing, the transformer has received extensive attention in extracting non-local features for point cloud processing [14,19]. As a representative, Qi et al. propose PCT [14], where global features are used to learn multi-to-one feature mappings after transformation and aggregation.

Unlike the two feature aggregation operators mentioned above, we argue that point cloud processing can be better achieved by taking special consideration of local geometry. By aggregating additional geometric information, local features will carry more information and thus achieve better results.

3  Method

In this paper, we design a novel framework TGNet (Tree Graph Network), which improves the ability to extract local features and brings the global information into point representation. TGNet consists of several TGSG (Tree Graph Sampling and Grouping) blocks for sampling and grouping and TGA (Tree Graph Aggregation) blocks for aggregating features. For each block, the TGSG block first receives the output from the previous block. It then follows explicit rules for sampling, grouping, and simple processing, which can assemble additional information about the geometric structure of local regions. TGA block uses a self-attention mechanism to aggregate Tree Graph to obtain new features for the next module.

We first introduce the TGSG block in Section 3.1 and the TGA block in Section 3.2, respectively. Then, the TGSG and TGA blocks are combined in a hierarchical manner to form our TGNet proposed in Section 3.3.

3.1 Tree Graph Sampling and Grouping (TGSG) Block

A point cloud is a set of three-dimensional coordinate points in spatial space, denoted as P={p1,p2,…,pn}∈RN×3. Relatively, its features can be expressed as F={f1,f2,…,fn}∈RN×3 which can represent a variety of information, including color, surface normal, geometric structure, and high-level semantic information. In a hierarchical network framework, the output of the previous layer is the input of the subsequent layer, and the subsequent layer abstracts the features of the previous layer. In different feature layers, the feature F of the point cloud carries different information.

We first construct a graph G=(V,E) containing nodes V and edges E based on the spatial relationships of the 3D point cloud. Each vertex corresponds to a point in the point cloud, and each point is connected to its spatially adjacent K nearest points by edges. In this way, we transform the point cloud into a graph feature space.

Using the definition of the curve in CurveNet [39], a curve of length l can be generated from a series of points in the features space F such that ci={ci,1,ci,2,…,ci,l}∈RD×l. Unlike them, we adopt a deterministic strategy where our curves follow a specific explicit rule π extending in the feature space. Deterministic strategies can reduce learnable parameters and achieves similar results as non-deterministic strategies. In Fig. 2a, m curves of length l extending in different directions form a Tree Graph, such that TG={c1,c2,…,cm}∈RD×l×m. Local point clouds with different geometries can form different Tree Graph, while these Tree Graph can carry their geometric information. Fig. 2a shows a Tree Graph with 5 curves.

Figure 2: Illustration of TGSG block. (a) Tree graph with 5 curves in point cloud feature space. (b) illustration for tree graph. ci−1, ci and ci+1 denote curves of tree graph. Red balls denote the nodes of curves. Green balls in the center are the key point for feature aggregation. Green circle denotes the query range of node ci+1,3. (c) Convolution kernel operation on image I. (d) Using the GAP operation on the feature map to create the vector z

Next, we will describe the construction process of Tree Graph in detail as shown in Fig. 2b. We first randomly sample the starting points in feature space to get Ps={ps1,ps2,…,psv|ps∗∈P} and the corresponding feature Fs={fs1,fs2,…,fsv|fs∗∈F}. Due to the high computational efficiency of KNN, we obtain the neighborhood N(f) of each point feature f by this method. Then, we iteratively obtain the nodes ci,j of the curve ci in the point cloud using predefined strategy π:

ci,j+1=π(ci,j)(1)

where ci,0 is numerically equal to fs, that is ci,0=fs.

In our neural network model TGNet, we use a simpler approach as strategy π, which can ensure that the curves extend as far as possible in all directions. The node ci,j+1 on ci can be obtained by executing the predefined policy π.

ci,j+1=π(ci,j)={argmaxfk(DViTfk)j=0,k=1,2,…,Kargmaxci,j,k((DViT+ti,j)Tci,j,k)j≠0,k=1,2,…,K(2)

where DVi is the learnable direction vector of the ith curve ci, fk∈N(fs) is the neighboring feature of p and ci,j,k∈N(ci,j) is neighboring feature of ci,j. ti,j represents the direction vector between point ci,j−1 and ci,j:

ti,j=ci,j−ci,j−1(3)

In this way, we can obtain a Tree Graph that contains both local and non-global long-range information.

When the number of m increases, the query points and query ranges will be more clustered around the center point because the curve will become more. When the number of l increases, the query points and query ranges will be farther from the center point because the curve will be longer. So, we can adjust m and l to enable the network to balance local information and long-range dependencies. When the product of m and l is constant, increasing the length of l enables the network to obtain more information over long distances. Conversely, decreasing l allows the network to focus more on local information.

In Fig. 2c, we convert the graph TG into an image I∈Rm×l×D of size m×l with dimension D using the following manner:

I=[c1c2c3⋮cm]=[c1,1c1,2c1,3⋯c1,lc2,1c2,2c2,3⋯c2,lc3,1c3,2c3,3⋯c3,l⋮⋮⋮⋱⋮cm,1cm,2cm,3⋯cm,l]m×l×D(4)

Note that ci,j an element F.

In the above way, we obtain a tensor similar to an image feature map. In Fig. 2d, we use a simple method to process the image I to get local features. We obtain the local features I′∈RNs×D′×l×m of the starting points of each Tree Graph image Is={I1,I2,…,INs}∈RNs×D×l×m by a convolution kernel of size 3 × 3. Then use GAP (global average pooling) on the image to get z∈RNs×D′. Finally, we convert image Is to a vector z to represent the entire Tree Graph, which is used to represent the local geometric structure information.

3.2 Tree Graph Aggregation (TGA) Block

With the TGSG block, we obtain a Tree Graph containing local information and non-global long-range dependency information. In this subsection, we will use TGA block to fuse Tree Graph and global information into local features. To simplify the notation, we define the local features of the point cloud as x∈RN×D. We take advantage of the cross-attention to fuse feature z into local feature x. The multi-head cross attention from local to global is defined as follows:

x′=x+LN([Attn(zhWhQ,xhWhK,xhWhV)])h=1:hmWo(5)

With multi-head cross attention (MCA) and feed forward layer (FFN), H can be computed as:

H=x′+LN(FFN(x′))(6)

x and z are split as x=[xh] and z=[zh](1≤h≤hm) for multi-head attention with hm heads. WhQ, WhK and WhV are the projection matrix in the hth head. Who is used to merge multiple heads together. LN is layer normalization function. Attn is standard attention function as:

Attn(Q,K,V)=softmax(QKTdk)V(7)

Absolute and relative positions of the point cloud are very important. As shown in Fig. 3, we incorporate them into. H. We concatenate P (the absolute spatial positions), PK (neighboring points spatial positions) and P−PK. The concatenated features are mapped to higher dimensions through a single layer MLP. Hk−H added with PK are passed into another MLP layer and Max Pooling layer get result xout.

Figure 3: Tree graph aggregation block

3.3 Tree Graph Network (TGNet)

Fig. 4 shows the architecture of a TGNet (Tree Graph network), which stacks several TGSG blocks and TGA blocks. It starts with a local feature extraction block (LFE), which takes key points’ absolute position, neighboring points’ relative position, and neighboring points’ absolute position as input. LFE contains an MLP layer and a Max Pooling layer to initially extract point cloud features. In all TGSGs, the length and the number of curves are set to 5. In all TGAs, the number of attention heads is 3, and the ratio in FFN is 2 instead of 4 to reduce computations. In this paper, TGNet is used for point cloud classification, segmentation, and surface normal estimation, which can all be trained in an end-to-end manner.

For classification, the point cloud is passed into a local feature extraction block (LFE) to initially extract local features. The extracted local features are abstracted layer by layer through 8 TGSA and TGA modules, and the global features are obtained by Max-Pooling. Finally, we get class scores by using two layers of MLPs. The category with the highest score is what TGNet’s prediction.

The point cloud segmentation task is similar to the normal estimation task, and we use almost the same architecture. We all use attention U-Net style networks to learn multi-level representations. For segmentation, its outputs per point prediction score for semantic labels. For normal estimation, it outputs per point normal prediction.

Figure 4: Top:TGNet applied to point cloud classification task. Bottom:TGNet applied to point cloud segmentation and normal estimation task

4  Experiments

We evaluate our network on multiple point cloud processing tasks, including point cloud classification, segmentation, and normal estimation. To further understand TGNet, we also performed ablation experiments and visualizations to help further understand our network.

4.1 Classification

We evaluate TGNet on ModelNet40 [2] for classification, which contains 12311 CAD models of 3D objects belonging to 40 categories. The dataset consists of two parts: the training dataset contains 9843 objects, and the test dataset contains 2468 objects. We uniformly sample 1024 points from the surface of each CAD model. For processing purposes, all 3D point clouds are normalized to a unit sphere. During training, we augment the data by scaling in the range [0.67, 1.5] and panning in the range [−0.2, 0.2]. We trained our network for 200 epochs, using SGD with a learning rate of 0.001, and reduced the learning rate to 0.0001 using cosine annealing. The batch sizes for training and testing are set to 48 and 24, respectively.

Table 1 reports the results of our TGNet and current most advanced methods. In contrast to other methods, ours uses only 1024 sampling points and does not require additional surface normals. In addition, when we do not use the voting strategy [17], our method achieves a state-of-the-art score of 93.8, which is already better than many methods. Surprisingly, our method achieves 94.0 accuracies using the voting strategy. These improvements demonstrate the robustness of TGNet to various geometric shapes.

4.2 Segmentation

We evaluate the ability of our network for fine-grained shape analysis on the ShapeNetPart [44] benchmark. ShapeNetPart dataset contains 16881 shape models in 16 categories, labeled as 50 segmentation parts. We use 12137 models for training and the rest for validation and testing. We uniformly select 2048 points from each model as input to our network. We train our network for 200 epochs with a learning rate of 0.05 and a batch size of 32. Table 2 summarizes the comparison of current advanced methods, where TGNet achieves the best performance of 86.5% overall mIoU. Segmentation is a more difficult task than shape classification. Even without fine-tuning parameters, our method still achieves high scores. The effectiveness of our Tree Graph features strategy is confirmed. Fig. 5 shows our segmentation results. The segmentation predictions made by TGNet are very close to the ground truth.

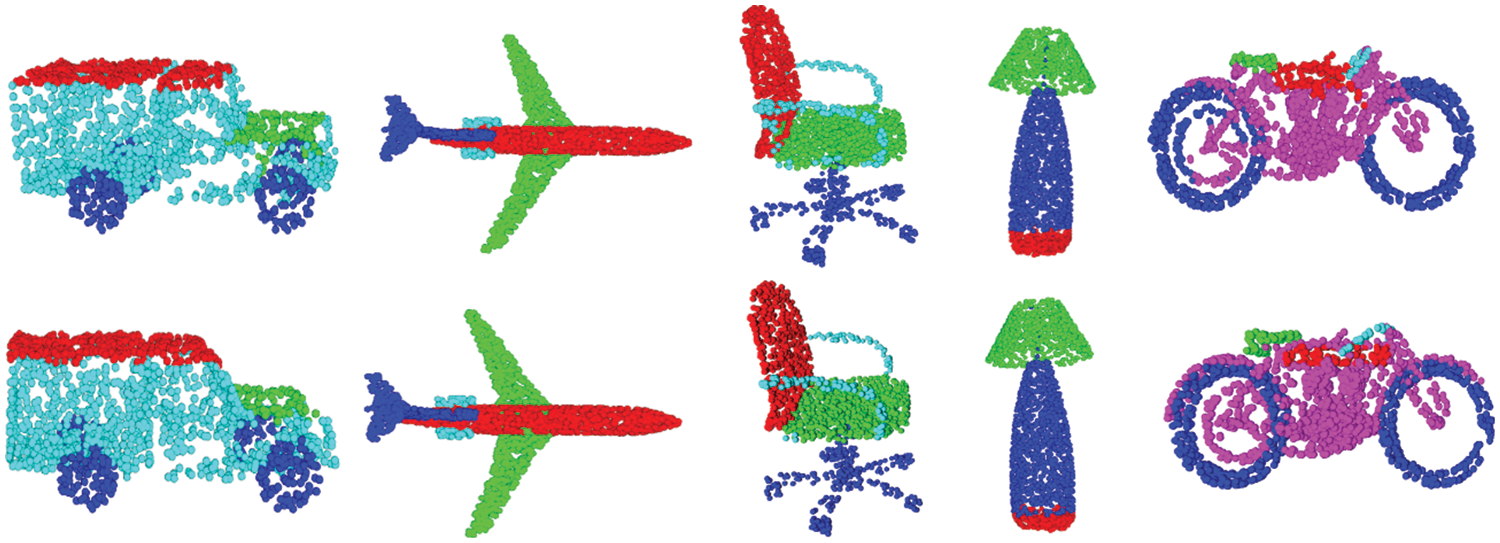
Figure 5: Segmentation results on ShapeNetPart benchmark. Top: ground truth; Bottom: ours

4.3 Normal Estimation

Normal estimation is essential to many 3D point cloud processing tasks, such as 3D surface reconstruction and rendering. It is a very challenging task that requires a comprehensive understanding of object geometry. We evaluate normal estimation on the ModelNet40 dataset as a supervised regression task. We train for 200 epochs using a structure similar to point cloud segmentation, where the input is 1024 uniformly sampled points. Table 3 shows the average cosine error results for TGNet and current state-of-the-art methods. Our network shows excellent performance with an average error of only 0.12. Our method gives excellent results demonstrating that TGNet can understand 3D model shapes very well. Fig. 6 summarizes the normal estimation results of our method. The surface normals predicted by TGNet are very close to ground truth. Even complex 3D models, such as airplanes, can be estimated accurately.

Figure 6: Normal estimation results on ModelNet40

4.4 Ablation Studies

We performed numerous experiments on the dataset ModelNet40 to evaluate the network entirely. Table 4 shows the ablation result. First, we introduce our baseline method for making comparisons. To replace TGSG, we use KNN for sampling and grouping and use shared MLPs to ensure that the features of their outputs have the same dimensions. TGA module is replaced by PNL (point nonlocal cell) of PointASNL. The accuracy of the baseline is only 92.8%. The impact is investigated by simply replacing TGNet’s components to the baseline architecture.

For model B, our method shows a 0.4% improvement over the baseline when using TGSG for model B. In contrast with the baseline, TG is used to sample and group geometric information. This illustrates the effectiveness of our Tree Graph in capturing geometric information. For model C, our method shows a 0.6% improvement over the baseline when using TGA. This illustrates the effectiveness of our TGA in aggregating local and non-local information. Our model TGNet achieved an accuracy of 93.8 after using TGSG blocks and TGA blocks. The ablation experiment shows that introducing more geometric information into the local features by explicit methods can effectively improve the point cloud processing.

4.5 More Experiments on TGNet

As mentioned before, adjusting the values of m and l enables TGNet to tradeoff local information with long-range dependent information. In this subsection, we use different number of curves and nodes for experiments on the ModelNet40 dataset. As shown in Fig. 7, we perform five experiments, and the product of l and m for each experiment is 24 except the third time, which is 25. When m equals 5 and l equals 5. We obtain the best accuracy of 93.8% experimental results.

Figure 7: Test result of using different number of m and l for experiments. The number of curves m=3 and the number of nodes l=8 are denoted m3l8. The other cases (m4l6, m5l5, m6l4, m8l3) are similar to m3l8

The experiments show that simply increasing the number of curves or the number of nodes does not lead to better results when the number of learnable parameters is close. The best results can only be achieved with a reasonable trade-off between locally and remotely relevant information.

4.6 Visualization for Tree Graph

In this subsection, we visualize shallow Tree Graphs to further understand it. Since the deep Tree Graph has more high-level semantic information, a local point feature may even represent the entire point cloud geometric information. We cannot map the deep Tree Graph to the geometric space, so we do not discuss the deep Tree Graph in this subsection.

Our Tree Graph consists of several lines extending in different directions in feature space. However, in contrast to curves in feature space, curves do not extend in one direction. In Fig. 8, we can clearly see that the nodes of the curve (also known as query points) are mainly concentrated in the corners and edges of the point cloud. These points can provide robust geometric information for the feature calculation of the center points (also known as key points). Our Tree Graphs aggregate these robust regions with distinct geometric structures as input to the next layer of the network. This is where our method differs from others and why our method is more effective.

Figure 8: Visualization for tree graph. Black balls are the center of tree graph. Blue-green balls are the points of point clouds. Others are the node of curves

5  Conclusion

In this paper, we propose a novel method TGNet, which obtains Tree Graphs with local and non-global long-range dependencies by explicit sampling and grouping rules. The aggregation of features is then performed in a cross-attention mechanism. In this way, the geometric spatial distribution of the point cloud can be explicitly reasoned about, and the geometric shape information can be incorporated into the local features. Due to these advantages mentioned above, our approach can achieve state-of-the-art results on several point cloud object analysis tasks.

Acknowledgement: Portions of this work were presented at the 8th International Conference on Virtual Reality in 2022, TGNet: Aggregating Geometric Features for 3D Point Cloud Processing.

Funding Statement: This research was supported by the National Natural Science Foundation of China (Grant Nos. 91948203, 52075532).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Chen, X., Ma, H., Wan, J., Li, B., Xia, T. (2017). Multi-view 3D object detection network for autonomous driving. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1907–1915. Honolulu, HI. [Google Scholar]

 2.  Wu, Z., Song, S., Khosla, A., Yu, F., Zhang, L. et al. (2015). 3D shapenets: A deep representation for volumetric shapes. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1912–1920. Boston, MA. [Google Scholar]

 3.  Su, H., Maji, S., Kalogerakis, E., Learned-Miller, E. (2015). Multi-view convolutional neural networks for 3D shape recognition. Proceedings of the IEEE International Conference on Computer Vision, pp. 945–953. Santiago, CHILE. [Google Scholar]

 4.  Wang, P. S., Liu, Y., Guo, Y. X., Sun, C. Y., Tong, X. (2017). O-CNN: Octree-based convolutional neural networks for 3D shape analysis. ACM Transactions on Graphics, 36(4), 1–11. [Google Scholar]

 5.  Riegler, G., Osman Ulusoy, A., Geiger, A. (2017). OctNet: Learning deep 3D representations at high resolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3577–3586. Honolulu, HI, USA. [Google Scholar]

 6.  Yan, X., Zheng, C., Li, Z., Wang, S., Cui, S. (2020). PointASNL: Robust point clouds processing using nonlocal neural networks with adaptive sampling. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5589–5598. Seattle, WA, USA. [Google Scholar]

 7.  Le, T., Duan, Y. (2018). PointGrid: A deep network for 3D shape understanding. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 9204–9214. Salt Lake City, UT, USA. [Google Scholar]

 8.  Qi, C. R., Su, H., Mo, K., Guibas, L. J. (2017). PointNet: Deep learning on point sets for 3D classification and segmentation. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 652–660. Honolulu, HI. [Google Scholar]

 9.  Qi, C. R., Yi, L., Su, H., Guibas, L. J. (2017). PointNet++: Deep hierarchical feature learning on point sets in a metric space. Advances in Neural Information Processing Systems, 30, 5105–5114. [Google Scholar]

10. Maturana, D., Scherer, S. (2015). VoxNet: A 3D convolutional neural network for real-time object recognition. 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 922–928. Hamburg, Germany, IEEE. [Google Scholar]

11. Liu, Y., Fan, B., Meng, G., Lu, J., Xiang, S. et al. (2019). DensePoint: Learning densely contextual representation for efficient point cloud processing. Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 5239–5248. Seoul, Korea (South). [Google Scholar]

12. Wang, Y., Sun, Y., Liu, Z., Sarma, S. E., Bronstein, M. M. et al. (2019). Dynamic graph CNN for learning on point clouds. ACM Transactions on Graphics, 38(5), 1–12. [Google Scholar]

13. Thomas, H., Qi, C. R., Deschaud, J. E., Marcotegui, B., Goulette, F. et al. (2019). KPConv: Flexible and deformable convolution for point clouds. Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 6411–6420. Seoul, Korea (South). [Google Scholar]

14. Guo, M. H., Cai, J. X., Liu, Z. N., Mu, T. J., Martin, R. R. et al. (2021). PCT: Point cloud transformer. Computational Visual Media, 7(2), 187–199. [Google Scholar]

15. Atzmon, M., Maron, H., Lipman, Y. (2018). Point convolutional neural networks by extension operators. arXiv preprint arXiv:1803.10091. [Google Scholar]

16. Wu, W., Qi, Z., Fuxin, L. (2019). PointConv: Deep convolutional networks on 3D point clouds. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 9621–9630. Long Beach, CA. [Google Scholar]

17. Liu, Y., Fan, B., Xiang, S., Pan, C. (2019). Relation-shape convolutional neural network for point cloud analysis. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 8895–8904. Long Beach, CA, USA. [Google Scholar]

18. Li, J., Chen, B. M., Lee, G. H. (2018). So-Net: Self-organizing network for point cloud analysis. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 9397–9406. Salt Lake City, UT, USA. [Google Scholar]

19. Zhao, H., Jiang, L., Jia, J., Torr, P. H., Koltun, V. (2021). Point transformer. Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 16259–16268. [Google Scholar]

20. Li, Y., Xia, R., Zhao, J., Chen, Y., Zou, H. (2022). TGNet: Aggregating geometric features for 3D point cloud processing. 2022 8th International Conference on Virtual Reality (ICVR), pp. 55–61. Nanjing, China, IEEE. [Google Scholar]

21. Ma, C., Guo, Y., Yang, J., An, W. (2018). Learning multi-view representation with LSTM for 3-D shape recognition and retrieval. IEEE Transactions on Multimedia, 21(5), 1169–1182. [Google Scholar]

22. Feng, Y., Zhang, Z., Zhao, X., Ji, R., Gao, Y. (2018). GvCNN: Group-view convolutional neural networks for 3D shape recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 264–272. Salt Lake City, UT, USA. [Google Scholar]

23. Qi, C. R., Su, H., Nießner, M., Dai, A., Yan, M. et al. (2016). Volumetric and multi-view CNNs for object classification on 3D data. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5648–5656. Las Vegas, NV, USA. [Google Scholar]

24. Yu, T., Meng, J., Yuan, J. (2018). Multi-view harmonized bilinear network for 3D object recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 186–194. Salt Lake City, UT. [Google Scholar]

25. Biasotti, S., Lavoué, G., Falcidieno, B., Pratikakis, I. (2019). Generalizing discrete convolutions for unstructured point clouds. DOI 10.2312/3dor.20191064. [Google Scholar] [CrossRef]

26. Esteves, C., Allen-Blanchette, C., Makadia, A., Daniilidis, K. (2018). Learning so(3) equivariant representations with spherical CNNs. Proceedings of the European Conference on Computer Vision (ECCV), pp. 52–68. Munich, GERMANY. [Google Scholar]

27. Lei, H., Akhtar, N., Mian, A. (2019). Octree guided cnn with spherical kernels for 3D point clouds. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 9631–9640. Long Beach, CA. [Google Scholar]

28. Li, Y., Bu, R., Sun, M., Wu, W., Di, X. et al. (2018). PointCNN: Convolution on X-transformed points. 32nd Conference on Neural Information Processing Systems (NIPS), pp. 820–830. Montreal, CANADA. [Google Scholar]

29. Hua, B. S., Tran, M. K., Yeung, S. K. (2018). Pointwise convolutional neural networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 984–993. Salt Lake City, UT, USA. [Google Scholar]

30. Zhang, Z., Hua, B. S., Rosen, D. W., Yeung, S. K. (2019). Rotation invariant convolutions for 3D point clouds deep learning. 2019 International Conference on 3D Vision (3DV), pp. 204–213. Quebec City, QC, Canada, IEEE. [Google Scholar]

31. Duan, Y., Zheng, Y., Lu, J., Zhou, J., Tian, Q. (2019). Structural relational reasoning of point clouds. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 949–958. Long Beach, CA, USA. [Google Scholar]

32. Li, Y., Bu, R., Sun, M., Wu, W., Di, X. et al. (2018). PointCNN: Convolution on X-transformed points. 32nd Conference on Neural Information Processing Systems (NIPS), Montreal, CANADA. [Google Scholar]

33. Lan, S., Yu, R., Yu, G., Davis, L. S. (2019). Modeling local geometric structure of 3D point clouds using geo-CNN. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 998–1008. Long Beach, CA, USA. [Google Scholar]

34. Zhang, C., Song, Y., Yao, L., Cai, W. (2020). Shape-oriented convolution neural network for point cloud analysis. Proceedings of the AAAI Conference on Artificial Intelligence, pp. 12773–12780. New York, NY. [Google Scholar]

35. Wang, X., Girshick, R., Gupta, A., He, K. (2018). Non-local neural networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 7794–7803. Salt Lake City, UT. [Google Scholar]

36. Chen, Y., Dai, X., Chen, D., Liu, M., Dong, X. et al. (2021). Mobile-former: Bridging mobilenet and transformer. arXiv preprint arXiv:2108.05895. [Google Scholar]

37. Devlin, J., Chang, M. W., Lee, K., Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805. [Google Scholar]

38. Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y. et al. (2021). Swin transformer: Hierarchical vision transformer using shifted windows. Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 10012–10022. [Google Scholar]

39. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L. et al. (2017). Attention is all you need. Advances in Neural Information Processing Systems, 30, 5998–6008. [Google Scholar]

40. Xiang, T., Zhang, C., Song, Y., Yu, J., Cai, W. (2021). Walk in the cloud: Learning curves for point clouds shape analysis. Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 915–924. [Google Scholar]

41. Joseph-Rivlin, M., Zvirin, A., Kimmel, R. (2019). Momen(e)t: Flavor the moments in learning to classify shapes. Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, South Korea. [Google Scholar]

42. Yang, J., Zhang, Q., Ni, B., Li, L., Liu, J. et al. (2019). Modeling point clouds with self-attention and gumbel subset sampling. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 3323–3332. Long Beach, CA. [Google Scholar]

43. Zhao, H., Jiang, L., Fu, C. W., Jia, J. (2019). Pointweb: Enhancing local neighborhood features for point cloud processing. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5565–5573. Long Beach, CA, USA. [Google Scholar]

44. Xu, Y., Fan, T., Xu, M., Zeng, L., Qiao, Y. (2018). SpiderCNN: Deep learning on point sets with parameterized convolutional filters. Proceedings of the European Conference on Computer Vision (ECCV), pp. 87–102. Munich, Germany. [Google Scholar]

45. Chang, A. X., Funkhouser, T., Guibas, L., Hanrahan, P., Huang, Q. et al. (2015). ShapeNet: An information-rich 3D model repository. arXiv preprint arXiv:1512.03012. [Google Scholar]