 Open Access
Open Access
ARTICLE
A New Hybrid Hierarchical Parallel Algorithm to Enhance the Performance of Large-Scale Structural Analysis Based on Heterogeneous Multicore Clusters
1 School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China
2 Aerospace System Engineering Shanghai, Shanghai, 201108, China
3 School of Aerospace, Mechanical and Mechatronic Engineering, University of Sydney, Sydney, NSW, 2006, Australia
* Corresponding Author: Xianlong Jin. Email:
Computer Modeling in Engineering & Sciences 2023, 136(1), 135-155. https://doi.org/10.32604/cmes.2023.025166
Received 24 June 2022; Accepted 07 September 2022; Issue published 05 January 2023
Abstract
Heterogeneous multicore clusters are becoming more popular for high-performance computing due to their great computing power and cost-to-performance effectiveness nowadays. Nevertheless, parallel efficiency degradation is still a problem in large-scale structural analysis based on heterogeneous multicore clusters. To solve it, a hybrid hierarchical parallel algorithm (HHPA) is proposed on the basis of the conventional domain decomposition algorithm (CDDA) and the parallel sparse solver. In this new algorithm, a three-layer parallelization of the computational procedure is introduced to enable the separation of the communication of inter-nodes, heterogeneous-core-groups (HCGs) and inside-heterogeneous-core-groups through mapping computing tasks to various hardware layers. This approach can not only achieve load balancing at different layers efficiently but can also improve the communication rate significantly through hierarchical communication. Additionally, the proposed hybrid parallel approach in this article can reduce the interface equation size and further reduce the solution time, which can make up for the shortcoming of growing communication overheads with the increase of interface equation size when employing CDDA. Moreover, the distributed sparse storage of a large amount of data is introduced to improve memory access. By solving benchmark instances on the Shenwei-Taihuzhiguang supercomputer, the results show that the proposed method can obtain higher speedup and parallel efficiency compared with CDDA and more superior extensibility of parallel partition compared with the two-level parallel computing algorithm (TPCA).Keywords
Nomenclature
| HHPA | Hybrid hierarchical parallel algorithm proposed in this paper |
| CDDA | Conventional domain decomposition algorithm |
| TPCA | Two-level parallel computing algorithm |
| HCG | Heterogeneous-core-group |
| DOF | Degree of freedom |
| UI(t + Δt) | Displacement at the moment of t + Δt to the internal node |
| UB(t + Δt) | Displacement at the moment of t + Δt to the boundary node |
| FI(t + Δt) | External load at the moment of t + Δt to the internal node |
| FB(t + Δt) | External load at the moment of t + Δt to the boundary node |
| Effective stiffness matrix | |
| Effective external load vector | |
| I | Internal DOF |
| B | Boundary DOF |
| K | Stiffness matrix |
| M | Mass matrix |
| F | External load vector |
| Node displacement at nth time step | |
| Node velocity at nth time step | |
| Node acceleration at nth time step | |
| Condensed stiffness matrix | |
| Condensed external load vector | |
| XB(t + Δt) | Boundary node displacement |
| Differential operator | |
| N | Interpolation matrix |
| D | Elastic matrix for the finite element analysis |
| n | Number of DOFs |
| Niter | Number of substeps in structural transient finite element analysis |
| K | Iterations of parallel PCG |
With the development of transportation, energy exploration and exploitation, aerospace industry, etc., there have been increasing demands for developing complex large or ultra-large systems, such as highspeed-multiple-unit trains, 3000-meter-ultradeep drilling rigs, large aircraft, heavy-duty fracturing trucks, and optimizing major engineering projects, including cross-river tunnels and skyscrapers [1,2]. Research and development related to these particular equipment systems usually involve systemic complex dynamical evaluations for their performance and utilize the finite element method to execute high-performance computing [3]. However, applying finite element analysis in complex systems faces a high degree of freedom (DOF) and contains various factors such as nonlinear and complicated boundary conditions, making it high computational complexity and requiring enormous amounts of computational power. Therefore, it challenges the traditional finite element method and tools [4]. In the conventional finite element approach, some vital local details are often sacrificed for a simplified model to guarantee the calculation efficiency in large or ultra-large systems. As a result, the prediction ability for these details will be lost, accompanied by a lower computational precision. Compared to the conventional finite element method, fine modeling of complex dynamical systems has higher accuracy and can predict essential details, but it requires heavy computing based on large-scale or ultra-large-scale finite element models. Consequently, efficient solutions of fine modeling cannot be obtained on traditional serial computers [5]. Nowadays, parallel supercomputers have been developed rapidly. The research and explorations of parallel algorithms provide a feasible way to solve large and ultra-large complex systems and thus attract researchers’ attention worldwide.
Currently, two main research algorithms are commonly used as finite element parallel solution algorithms. One is starting from the most time-consuming linear equations in the finite element structural analysis to find the effective parallel computing method for solving linear equations [6–8]. The other one starts from the parallelism of the finite element method itself to develop a parallel domain decomposition method [9–11]. Specifically, the research of parallel algorithms for linear equations is mainly focusing on two methods, the direct scheme [6,12] and the iterative scheme [13,14]. In the direct method, the exact solution of the system can be obtained within the expected calculation steps through sorting algorithm, triangular decomposition, and back substituting. However, the required memory space and computing power will grow rapidly with the increase of the calculation scale, so its scalability is not as good as the iterative method [6,12]. The iterative approach improves the solution results through multiple iterations to achieve a convergence interval within the allowable error range of the exact solution. The memory required in the iterative process is relatively small, and it is easy to achieve parallelization. However, the iterative method cannot guarantee a convergence within a reasonable time, and the convergence of ill-conditioned problems with considerable condition number [7,13]. In the field of parallel computing on CDDA, the hybrid method with direct and iterative approaches has been employed by researchers. They start from the parallelism of the finite element problem itself, dividing the complex problem into smaller sub-tasks for parallel processing, and applying the direct method on sub-tasks and iterative method on sub-domains. The hybrid method takes both advantage of direct and iterative schemes, which can improve parallel efficiency. And thus, it has been widely used in the finite elements structural field [2,15–19]. Based on the CDDA, Miao et al. [15] designed a hierarchical parallel calculation method in finite element analysis for static structures. This method was later applied to a high-rise building to find its parallel solution to static structural characteristics. El Gharbi et al. [16] utilized the CDDA to design a two-level parallel mesh algorithm. And they applied the algorithm to complete the mesh for a turbine blade. Koric et al. [17] brought the CDDA to solve the static structural characteristics of a charge air cooler under the unstructured grids. Fialko et al. [18] used the CDDA to obtain the parallel solution of the static characteristics of a multi-storey building. Klawonn et al. [19] also combined CDDA with the
Regarding the hardware in high-performance computing, parallel computing systems usually employ distributed storage parallel mode, which mainly includes the homogeneous supercomputers [20] and the heterogeneous supercomputers [21]. Specifically, heterogeneous supercomputers have become the mainstream in high-performance computers due to their excellent computing power and high cost-to-performance effectiveness. Heterogeneous supercomputers are often equipped with multicore CPUs, also with GPUs and many integrated cores (MIC) processors or heterogeneous groups to complete the computing tasks. The APU project from the AMD Company is such an example [22]. Other examples include the Echolen project, led by the NVIDIA [23], The Runnemede project, led by Intel Corporation [24], the ‘Shenwei-Taihuzhiguang’ project from Wuxi-Hending Company [2], etc. On this basis, researchers have ported and improved CDDA to solve the structural performance of large-scale and ultra-large-scale finite element systems and achieved remarkable results [25,26]. Xue et al. [25] gained the numerical simulation of the three-dimensional compressible Euler atmospheric model system using the CDDA based on the CPU-MIC architecture. With the base of CPU-MIC architecture on CDDA, Miao et al. [26] designed a new hybrid solver with TPCA for large-scale structural analysis. And it was applied to the parallel computation of a tunnel to find its dynamic characteristics. Moreover, the different storage mechanisms and non-uniform communication latencies on the heterogeneous multicore distributed groups also introduce new challenges for the design of efficient parallel algorithms in large-scale structural analysis [27]. Thus, the keys to improving the efficiency of the finite element parallel algorithm of the heterogeneous supercomputer are: (1) to balance loads of computational tasks and hardware topology architecture of the heterogeneous multicore clusters; (2) to store the large-scale data generated in the computing process and (3) to guarantee the communication between inter-node and intra-node, within and between heterogeneous groups.
The main contribution of this paper is to provide a novel hybrid solver that is aware of the characteristics of heterogeneous multicore clusters and fully exploits their computing power to achieve optimal performance. In the proposed algorithm, the hybrid parallel partitioning is adopted based on the mesh partition and data partition, which reduces the assembling scale of global interface equations. And it improves the memory access efficiency of data by introducing distributed sparse storage of data in the computing process. By utilizing the computing tasks and the mapping of hardware topology structure on the heterogeneous multicore clusters, this method can also realize a three-layer parallelization in the computation procedure: the inter-nodes parallelization, the HCGS parallelization, and the inside-HCGs parallelization. This method not only achieves load balancing at different levels in an effective way but also improves communication efficiency by separating the communication. As a consequence, the work in this paper can be provided as a reference for porting the finite element structural analysis on the ‘Shenwei’ heterogeneous multicore processor and other heterogeneous processors to optimize the performance of large-scale parallel implementations.
The rest of this paper is organized as follows: In Section 2, the related works CDDA and TPCA are introduced to solve the structural large-scale finite element analysis. Then, in Section 3, the HHPA proposed with mesh partition, data partition and the implementation of HHPA with the best respect for the architecture of the Shenwei heterogeneous multicore processor is described. In Section 4, two numerical experiments are presented. Finally, conclusions are drawn in Section 5.
To present the proposed algorithm, some parallel computing algorithms for large-scale finite element analysis are introduced for better understanding.
Applying CDDA to solve the large-scale finite element structural analysis, the finite element mesh will first be partitioned into series sub-domains [28], as shown in Fig. 1.
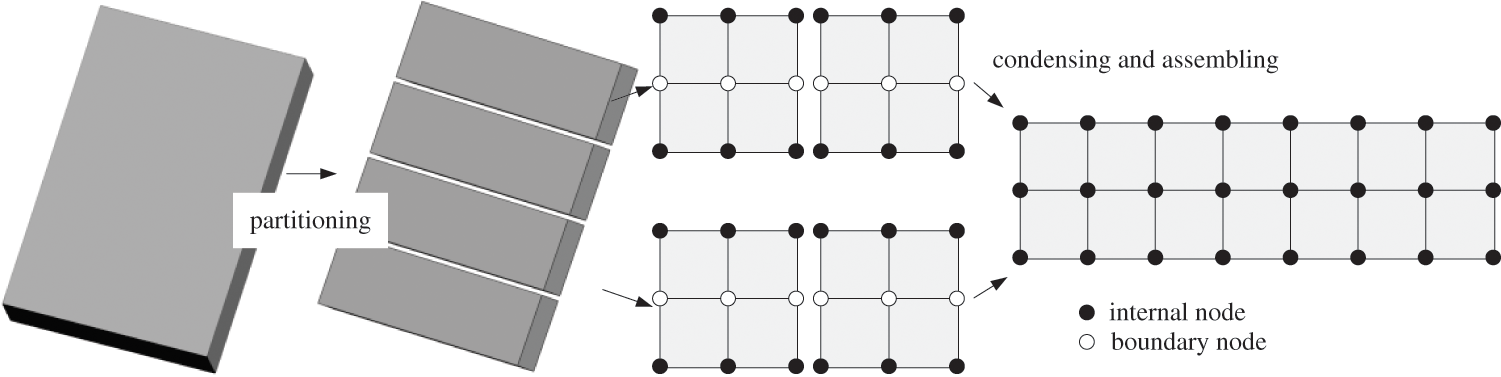
Figure 1: Partitioning and condensation of CDDA
The system equations of partitioned sub-domains at the moment of t + Δt can be expressed as the following equation equivalently with Schur formulation [15–19]:
In the Eqs. (2)~(3), the values of a0∼a7 are decided by α, δ, αm, αf together, which are calculated by Eq. (4):
Eliminate the internal DOFs to obtain the interface equation that only with the unknowns of the boundary DOFs:
Combining the interface equations from Eq. (5) in every sub-domain and solving them using parallel PCG algorithm can determine
Finally, calculate the stress σ/strain ɛ of each sub-domain through Eqs. (9) and (10) by substituting the internal and boundary displacement synchronously as follows:
To reduce memory and calculation amount, the procedure of finding inverse matrixes should be avoided [31]. Considered that
TPCA [16] was proposed to improve the parallel efficiency of large-scale structural dynamic analysis through two-level partitioning and two-level condensation based on CDDA, as shown in Fig. 2.
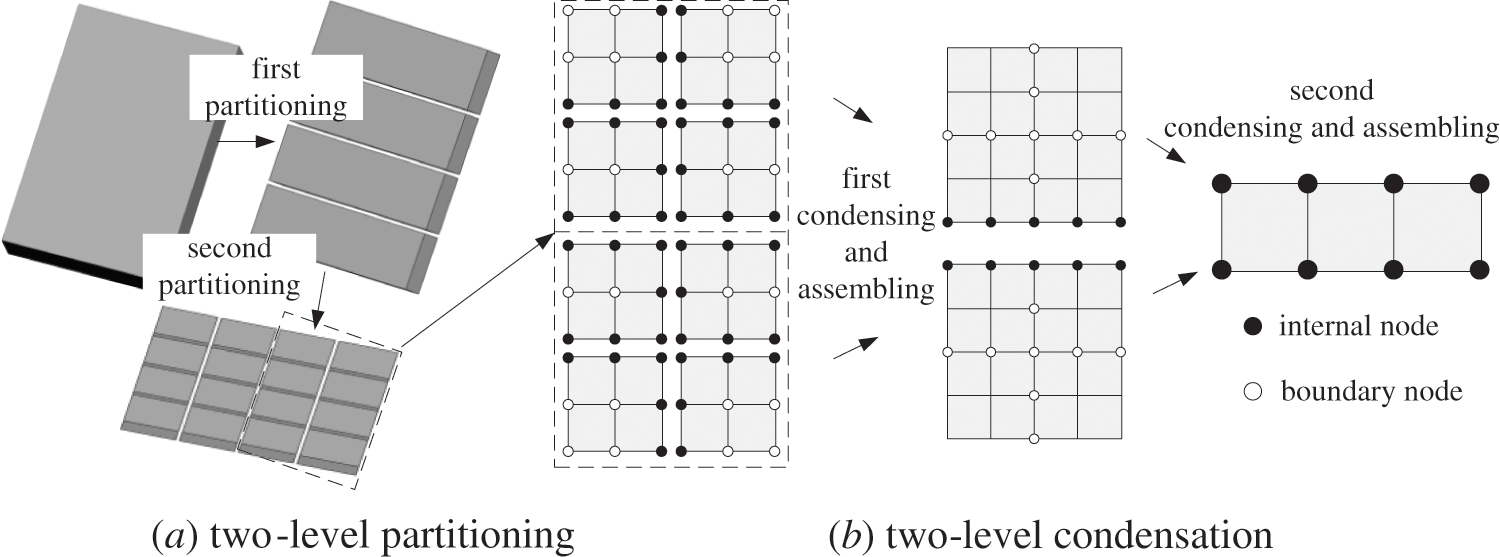
Figure 2: Partitioning and condensation of TPCA
Compared with CDDA, TPCA can reduce the solution scale of the overall interface equations of the system through multilayer partition and multi-condensation and thus can effectively improve the parallel efficiency of finding the solution. However, TPCA will require additional time in condensing sub-domains, assembling and solving the interface equations in sub-domains level 2 with the increasing number of sub-tasks, and therefore will limit the efficiency of the parallel system to a certain degree.
3 Proposed HHPA Based on Shenwei Heterogeneous Multicore Processor
To reduce time in condensing sub-domains, assembling and solving the interface equations in sub-domains level 2 with the increasing number of sub-tasks, HHPA was proposed o the basis of CDDA and parallel sparse solver, as shown in Fig. 3.
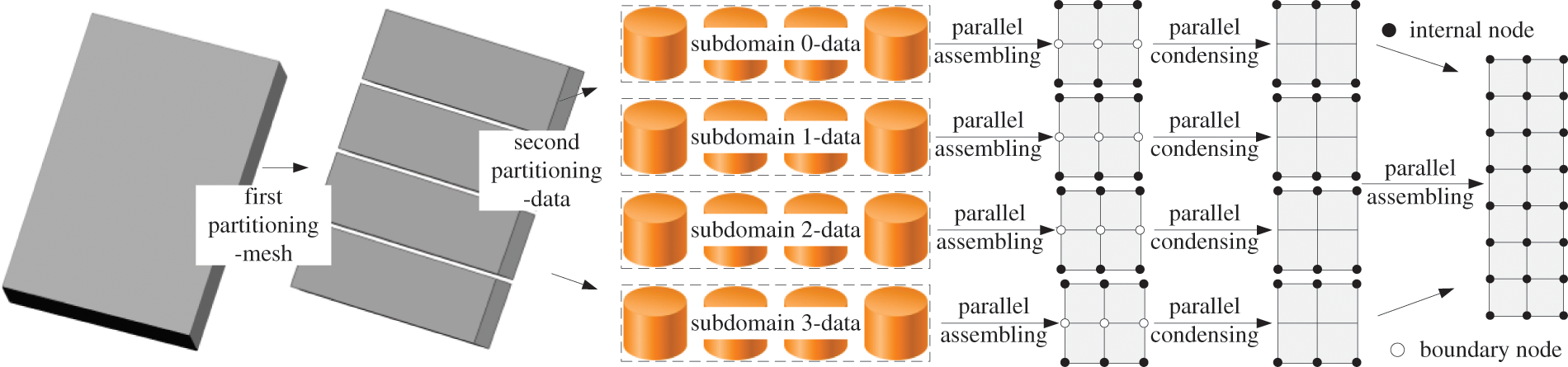
Figure 3: Partitioning and condensation of HHPA
There are two partition methods, namely mesh partition and data partition. For each subdomain, the nodes can be divided into internal node and boundary node according to mesh partition. The system equations of partitioned sub-domains at the moment of t + Δt can be expressed as Eq. (1).
The differences between the different approaches CDDA, TPCA and HHPA are shown in Table 1. Also, Fig. 4 demonstrates the block diagram of the proposed algorithm. During the parallel computing, each subdomain in level 1 is assigned to a node. All the subdomains in level 2 derived from the same subdomain in level 1 are assigned to different cores within the same node. Besides, MPI process 0 in each node is applied to take charge of operations of the corresponding subdomain in level 1 and the solution of global interface equations. The process of HHPA can be divided into steps as follows.
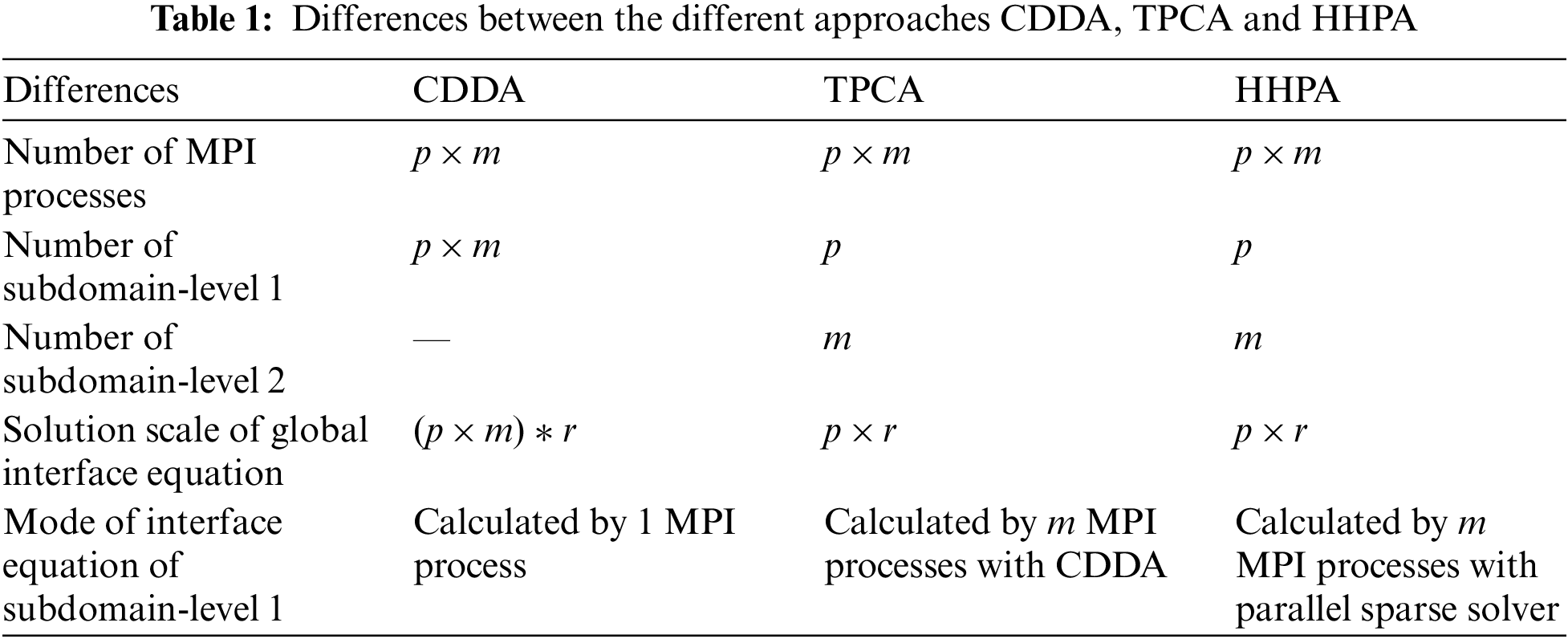
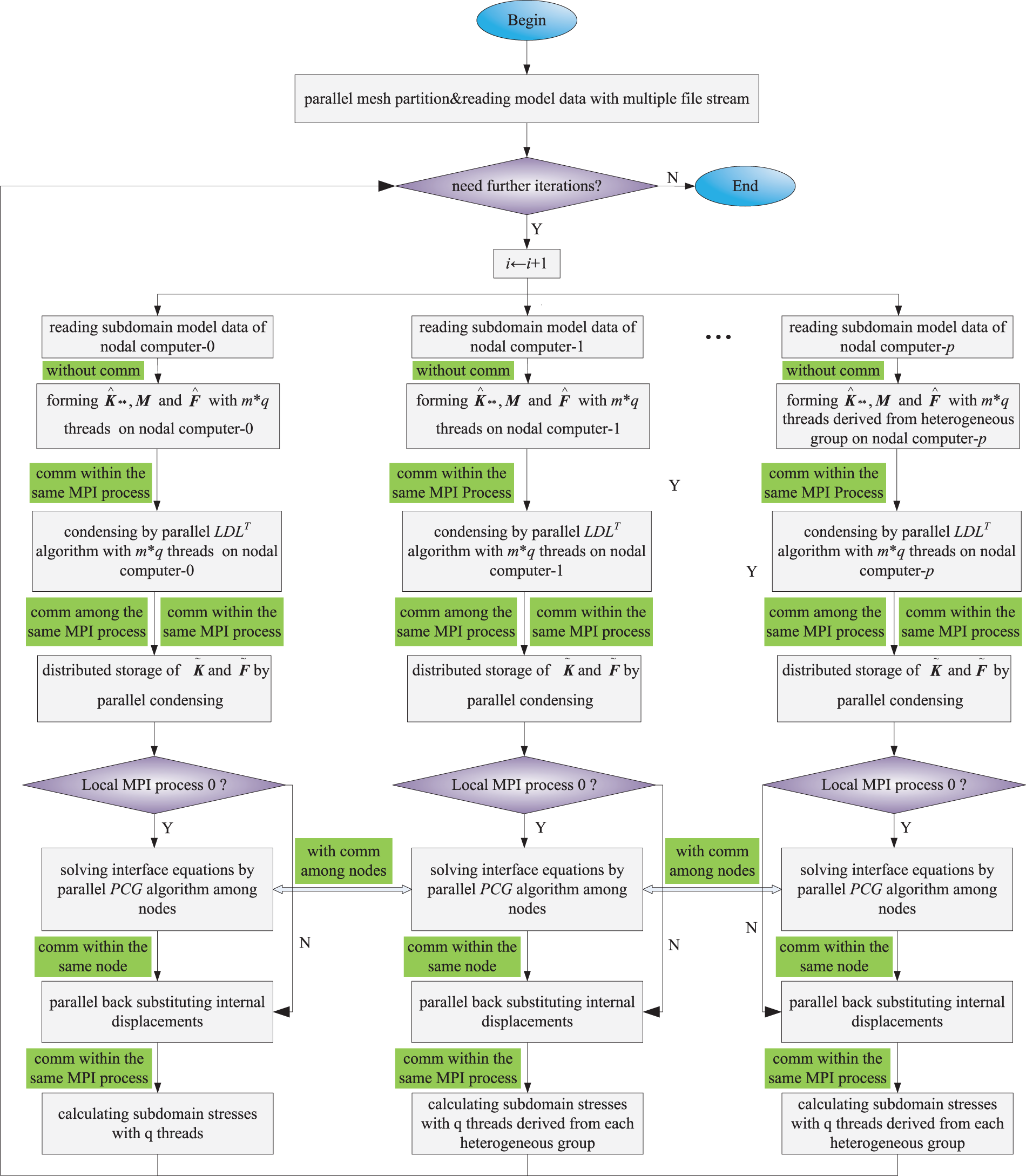
Figure 4: Block diagram of proposed HHPA
Step 1: Prepare data for domain decomposition parallel computing of mesh partition. Data contains information on finite element models (element stiffness matrix, mass matrix and external load vector) and partition information files. There is no communication for this step.
Step 2: Create p × m processes on the node side synchronously. Every m of the MPI process is responsible for one sub-domain data file data reading, where p represents the number of nodes participating in parallel computing and m represents the number of heterogeneous cluster terminals on each node. There is no communication for this step.
Step 3: Each MPI process will derive q threads from the heterogeneous group to assemble
Step 4: Every MPI process of each node uses its derived q threads to join the condensing based on Eqs. (5)~(7) for each sub-domain synchronously. And then distribute and save
Step 5: Use the derived q threads to solve interface equations by parallel PCG algorithm with communication among nodes.
Step 6: Use the heterogeneous clusters in each node to solve the internal displacement with parallel back substituting according to Eqs. (9)~(10). There exists communication within and among the MPI process. There exists communication within and among the MPI process.
Step 7: Use the derived q threads to back substitute to get the value of the stress σ/strain ɛ for each sub-domain. And then distribute and store the calculation results in corresponding shared memory space in the MPI process. There exists communication within and among the MPI process.
Step 8: If there is no need for further iterations, stop calculation; else back to Step 2.
3.2 Architecture and Execution Mode of Shenwei Processor
Shenwei-Taihuzhiguang supercomputer is based on Shenwei heterogeneous multicore processor [2]. The architecture of the Shenwei heterogeneous multicore is shown in Fig. 5. Every Shenwei heterogeneous multicore processor includes four HCGs, and each HCG shares 32 G of memory. Every single HCG consists of one computational control core and 64 computing cores. The communication between the HCGs adopts the bidirectional 14 Gbits/s bandwidth. And the communication between the computational control and the computing core adopts the DMA method to get bulk access to the main memory. The local storage space of the computing core is 64 KB, and the command storage space is 16 KB.
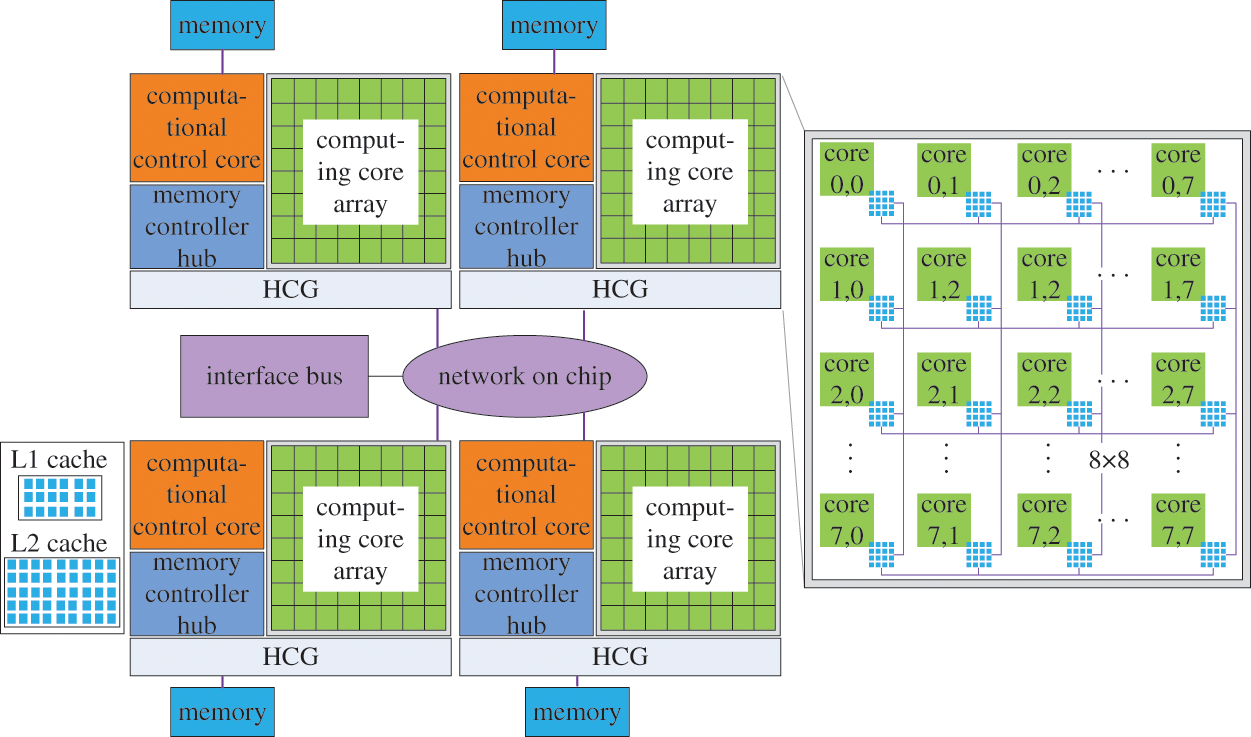
Figure 5: Architecture of Shenwei heterogeneous multicore processor
The application modes of Shenwei heterogeneous multicore processors mainly include the private mode and the full-chip shared mode of the HCGs. For the private mode of heterogeneous-core groups, every HCGs at each node shares 8 G memory space; On the other hand, for the full-chip mode of the HCGs, the full-chip has 32 G memory, or 16 G memory can be used by one MPI process. Since the computing power in the full-chip mode of the HCG is weaker, it is often used in the case of large memory requirements. Therefore, our project mainly adopts the private mode of the HCG to design the hybrid hierarchical parallel computing method for large-scale finite element structures.
3.3 Task Mapping of Parallel Algorithms
Mapping the computing tasks to different hardware layers of heterogeneous multicore supercomputers can achieve a balance-load among different nodes, as well as implement efficacious partitioning in communication, thereby significantly reducing communication overheads [32].
Based on CDDA, considering the hardware architecture of heterogeneous multicore supercomputers, the design of task mapping of HHPA for large-scale finite element structural analysis is shown in Fig. 6. When performing task mapping, the initial mesh in the sub-domains and the interface equation systems will be mapped according to the node order. The condensing of each sub-domain and the internal back substituting within each sub-domain will be mapped corresponding to the HCGs within the internal node. And the mapping of data calculations within HCGs is based on the computing core.
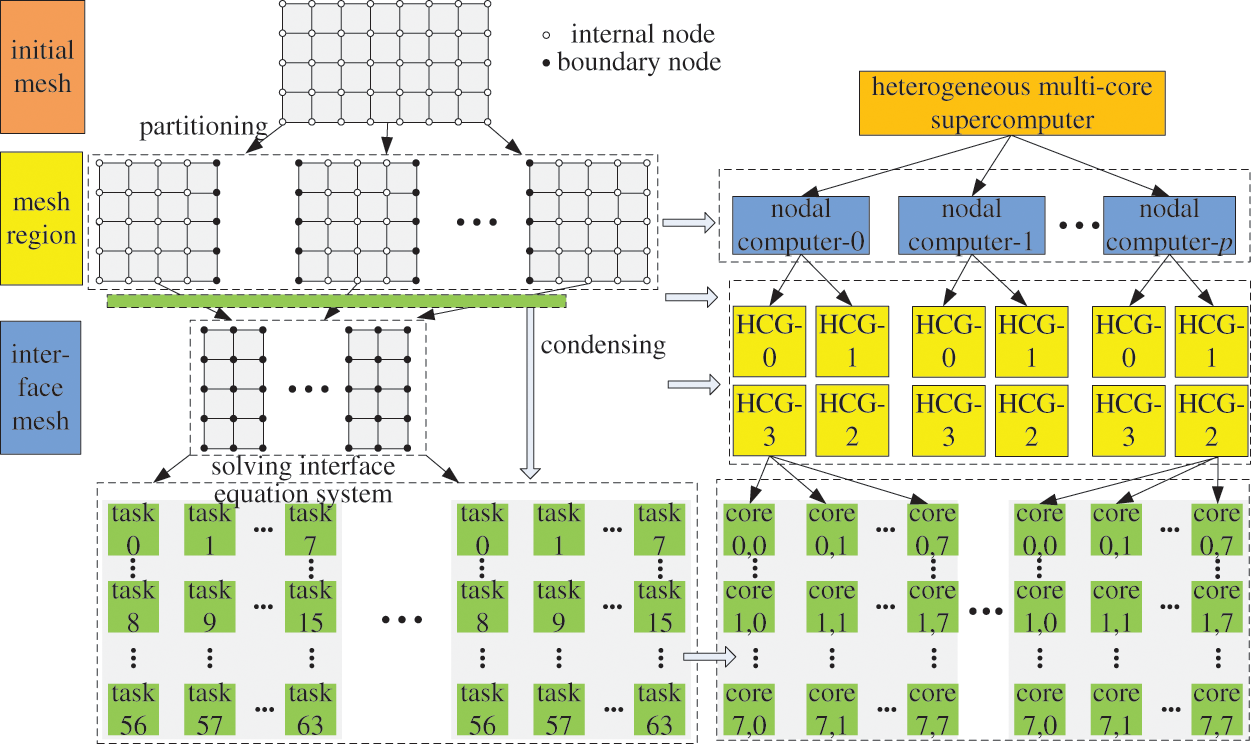
Figure 6: Task mapping of HHPA for structural large-scale finite element analysis
3.4 Large-Scale Parallel Computing Mechanism
Consider the fact that the communication efficiency of intra-node is much higher than inter-node. And the efficiency within the same HCG is much higher than that among the HCGs in heterogeneous multicore distributed storage computers. Thus, the key to reducing the overheads raised from communication and cooperation in the calculation is to separate and minimize the communication between intra-node and inter-node and the communication among the HCG and within the HCG. Based on the multilayer and multigrain parallel computing approach to large-scale finite element structural analysis, a computing strategy with a three-parallel layer has been designed, as shown in Fig. 7.
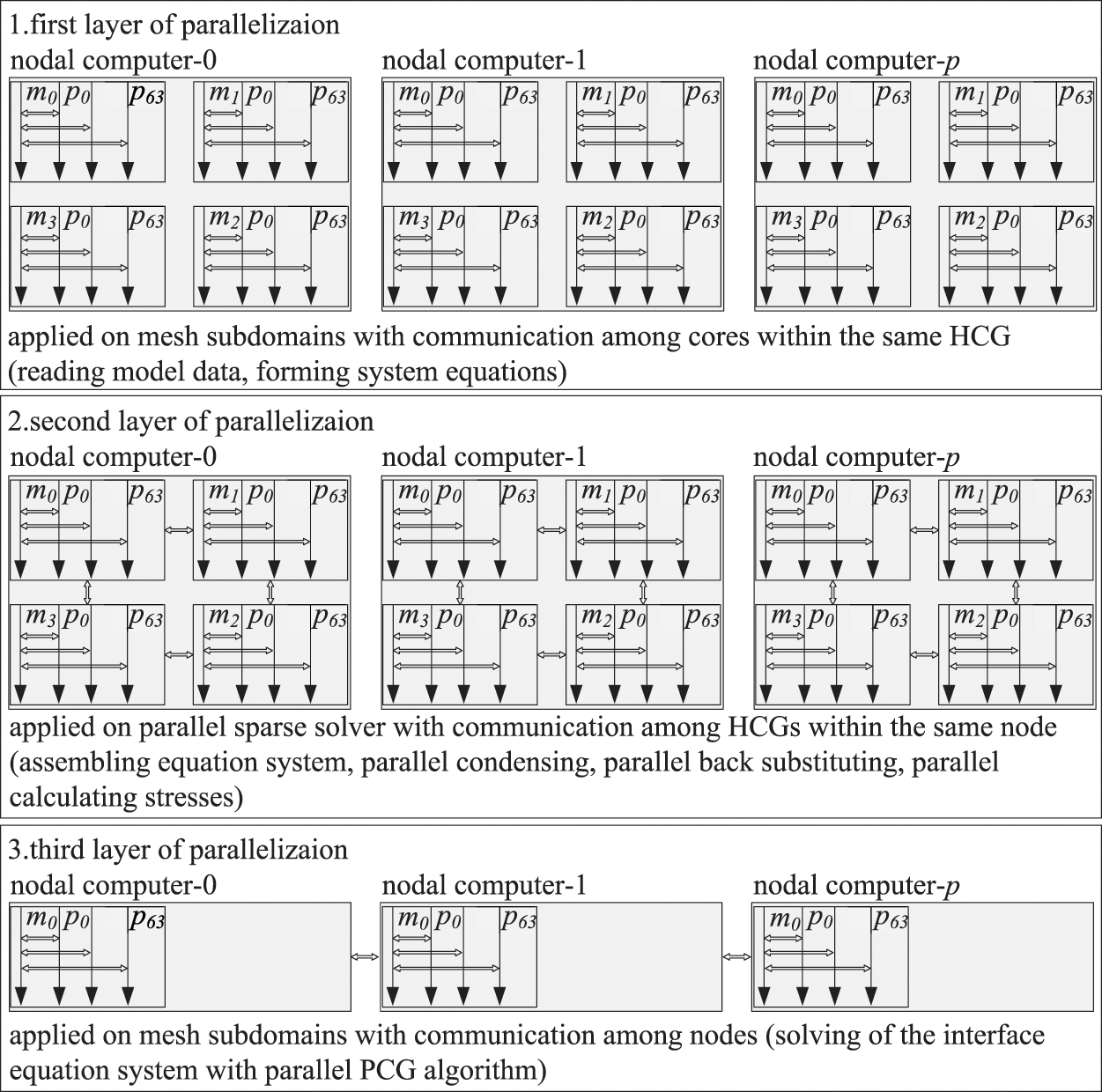
Figure 7: Scheme of three-layer parallelization
The first layer parallelization: In every node, m processes are responsible for processing one mesh subdomain, and all processes are operated synchronously. There is no data interaction between processes, but data interactions exist between the computational control cores and the computing cores within the process. Data progress procedure including computational control cores read the model data in sub-domain, and computing cores assemble the system equations for parallel computing of sub-domains. To save the memory space and to reduce the amount of computation, compressed sparse column techniques are applied to store the local stiffness matrix of each sub-domain.
The second layer parallelization: In this layer, based on the LDLT algorithm, each node starts m processes simultaneously to carry out condensation and back substitution for the corresponding mesh sub-domain. Communications exist between different HCGs within the same node, and communications also exist in the computational control cores and the computing cores in one HCG. Compressed sparse column techniques are used here for distributed storage of computational data in the procedure. After calculations, the result data will be sent to the main HCG corresponding to each node named No. 0, which is in charge of assembling the effective stiffness matrix and the effective load vector corresponding to its mesh sub-domain.
SuperLU [33] is a library that implements algorithms for parallel and serially solving of sparse linear equations. SuperLU_S can provide serial LDLT algorithm. And SuperLU_D can provide parallel LDLT algorithm, which is used in the second layer parallelization of proposed HHPA. However, the SuperLU_D cannot use the computing cores of the HCG directly. Through MPI or OpenMPI library, SuperLU_D can only call the computational control core of the HCG. Considering that the implementation process of the parallel LDLT algorithm mainly includes parallel LDLT decomposition and parallel solution of triangular systems of linear equations, the heterogeneous multicore acceleration is utilized to improve process improvement. The primary operations for computing are matrix-vector calculus and data communications. The communication procedure between different HCGs is realized by adopting the MPI library, and Athread library is utilized to achieve communication within each HCG. Matrix-vector calculus mainly includes addition, subtraction, multiplication and division. Taking vector multiplication a = b × c as an example (a, b, c are storage arrays in the process of arbitrary matrix-vector operations), the implementation process is shown in Fig. 8. The 64 computing cores on each HCG read the corresponding data from the memory space synchronously, where the memory of this data segment must be less than 64 KB. And the data will return to specific locations after calculation. The communication only exists in the computational control cores and computing cores.
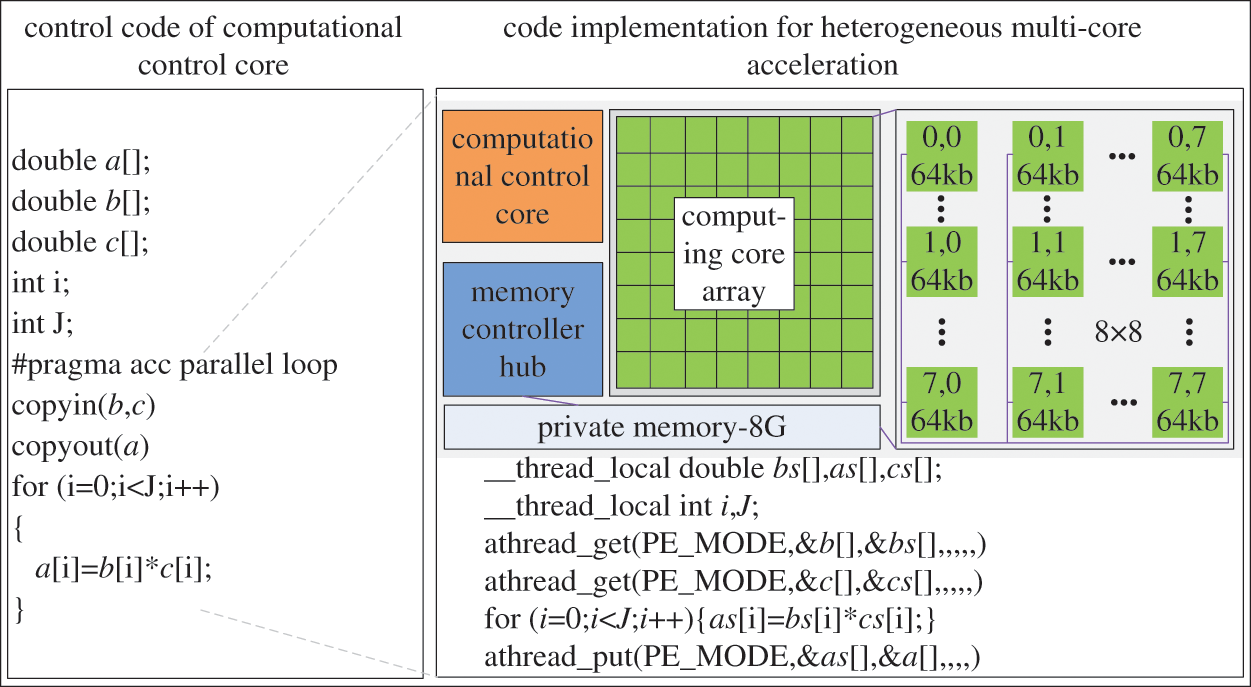
Figure 8: Vector matrix multiplication on heterogeneous multicore acceleration
The third layer parallelization: In the third layer, interface equations of the sub-domains are solved based on the parallel PCG algorithm. Only one HCG participates in computing and communication in each node, as illustrated in Fig. 9. The diagonal preconditioners are constructed locally using the condensed stiffness matrices of subdomains in level 1 [26,34]. The diagonal preconditioning requires solving the system
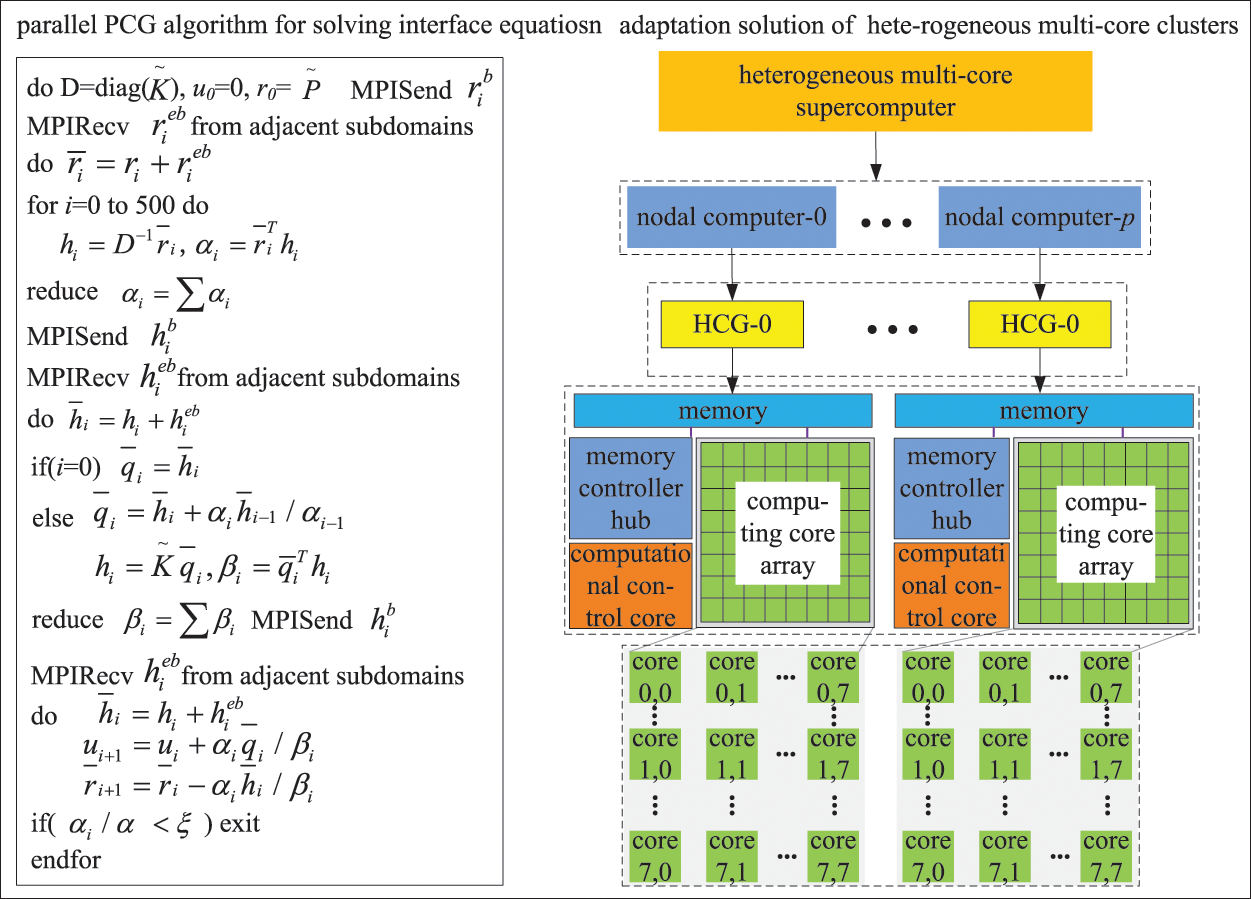
Figure 9: Parallel PCG algorithms
During the solving procedure, the effective stiffness matrix and effective load vector of each sub-domain are distributed and stored in the memory space of the corresponding HCG. Similarly, the intermediate results are stored in matrix-vector product form based on compressed sparse column distributed storage. Global communications only exist between neighboring sub-domains. And just a few dot product operations and computations for overall iterative error require global communications. Local communications are restricted within the computational control core and the computing cores of each HCG. Hence, this method can remarkably reduce the amount of communication and speed up the computing efficiency.
To sum up, HHPA can limit the majority of local communications within the node and ensure there is one HCG to participate in global communication for each node. At the same time, each HCG confines a large amount of communication between the computational control cores and the computing cores through multicore acceleration. And also guarantee that only the computing control cores participate in the communication between the core groups for each HCG. Through this operation, communications between intra-node and inter-node and the communication within and among HCGs can be separated effectively. As a result, it reduces the communication and cooperation overheads in the computing process and improves communication efficiency.
4 Numerical Experiments and Discussion
To verify the performance of the proposed algorithm, the Shenwei-Taihuzhiguang supercomputer is employed for testing, and each node operates four HCGs during the test.
A cube model was used to evaluate the performance of the parallel algorithm. The model and its load-time curve are shown in Fig. 10. The cube is fixed at its left end face, and the right end face is under a uniform sinusoidal load with a peak force of 106 N. The cube is 20 m in length, 10 m in width and 10 m in height. After discretizing with tetrahedral element, the model contains 6,886,981 elements, 7,037,638 nodes, and 11,007,819 DOFs. The material assigned to this model with an Elastic Modulus of 210 Gpa, Poisson’s ratio of 0.3 and density of 7850 Kg/m3.
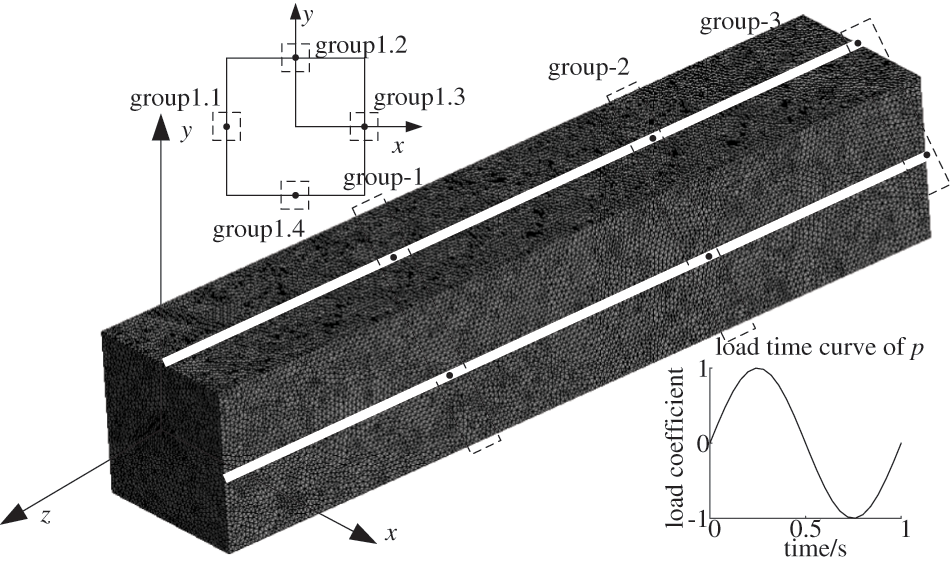
Figure 10: Finite element model of cube and load time curve for p
In parallel computing, the operating number of nodes should be 32, 64, 96, and 128, respectively. The criterions of the parallel PCG in CDDA, TPCA and HHPA are 1e-8. The sub-domains should be prepared in advance to correspond to the total number of nodes when applying HHPA proposed in this article. When applying TPCA, the sub-domains in level 2 should be prepared to correspond to four times the total node number [15]. And for CDDA, the pre-prepared sub-domains should also match the 4 times total number of nodes. SuperLU_S is adopted by CDDA and TPCA in the condensation of the subdomains.
In order to verify the accuracy of the parallel algorithm computation, 12 sampling points are picked, as shown in Fig. 10. The goodness-of-fit with the theoretical solution is adopted to evaluate the precision of the solution based on the three algorithms, as shown in Fig. 11. The definition of goodness-of-fit is shown in Eq. (12):
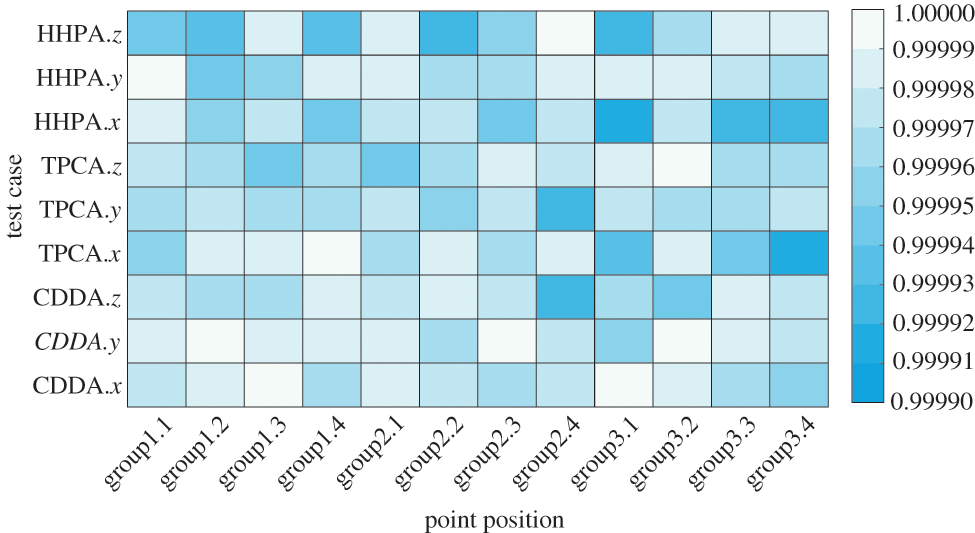
Figure 11: R2 value of different methods
In Eq. (12), n represents the number of the sampling points with the changing of the time curve, which is 25. Yi is the theoretical solution (the displacement changes with time in x, y, and z directions). Xi is the finite element solution (the displacement changes with time in x, y, and z directions).
It can be observed from Fig. 11 that whether using the CDDA, TPCA, or HHPA proposed in this paper, the displacement-time curve in all directions for all sampling points is in good agreement with the theoretical solution based on the elasticity and solid mechanics, with the goodness-of-fit close to 1. Hence, the computational accuracy of the CDDA, TPCA and HHPA is reasonable. However, there are some minor differences between CDDA, TPCA and HHPA. This is because the ordering of operations and rounding errors in calculation with CDDA, TPCA and HHPA are slightly different.
The detailed results for the cube model of the CDDA, TPCA, and HHPA are shown in Tables 2–3. The performance of parallel algorithm for cube model of the CDDA, TPCA, and HHPA is shown in Fig. 12.
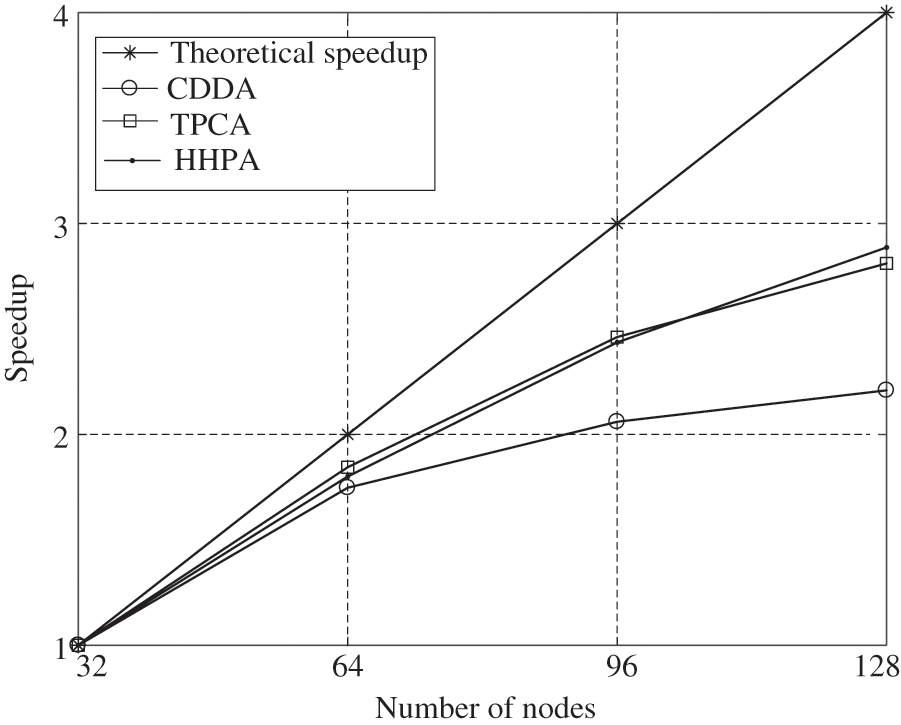
Figure 12: Performance of parallel algorithms for cube
In Table 3, the total time for parallel computing starts from calculating system equations and ends when obtaining the deformation/strain/stress solutions for every sub-domain. Solution time for level 1 with TPCA includes: assembling system equations of level 1 and the level 2 sub-domains, condensing level 2 sub-domains, solving interface equations with the parallel algorithm of level 1 and level 2 sub-domains, and back substituting the internal DOFs for level 1 and level 2 sub-domains. Solution time for level 1 with HHPA includes: assembling level 1 sub-domains, condensing level 1 sub-domains with the parallel solution of level 2 sub-domains, solving interface equations with the parallel algorithm of level 1 sub-domains, and parallel back substituting the internal DOFs for level 2 sub-domains. Compared to the CDDA, both TPCA and HHPA proposed in this article can achieve higher speedup and parallel efficiency, which is shown in Fig. 12. This is because the scale and condition number grow dramatically with the increase of sub-domains in the CDDA, which results in longer solving time for the interface equations, and a weaker overall parallel efficiency. Compared with the TPCA, when the number of level-1 sub-domain is small, the computing efficiency and speedup of HHPA proposed in this article are relatively low. But with the increase in the level-1 sub-domains, this algorithm comes with relatively high parallel computing efficiency and speedup. From the mathematics point of view, TPCA and CDDA have the same interface equations of level 1. When the number of level 1 sub-domain is small, the scale and condition number of the system equations are larger. Although utilizing the parallel solvers can save time for assembling the level 2 sub-domain system equations, condensing, and solving time for the level 2 interface equations, the time to solve the sub-domain system is still relatively high. Thus, it has lower parallel efficiency and speedup. Nevertheless, with more sub-domains in level 1, the scale and condition number of the system equations become smaller, and there is no need for assembling, condensing and solving for the level 2 subdomains. Therefore, the parallel solvers take advantage of reducing the total solving time. At the same time, HHPA realized the communication separation of inter-nodes and the communication within and among heterogeneous groups through the three-layer parallelization. As a consequence, it can noticeably reduce the time in solving the level 1 sub-domain and achieve better speedup and parallel efficiency under large-scale partitions.
The time complexity of CDDA, TPCA, and HHPA is analyzed as follows. It starts with the calculation of Eqs. (2) and (3). All of them took O(n). The calculation of Eq. (5) took O(n2). And the calculation of Eqs. (6)~(10) took O(n3/2). Time complexity of CDDA is
4.2 Case of a Cable-Stayed Bridge in Shock Wave
A double-layer cable-stayed bridge system is used to perform dynamic structural analysis based on the calculating system of HHPA. The development of the double-layer cable-stayed bridge system is significant for solving the dual use of highways and light rails problem and improving traffic efficiency. The strict and high requirements for the safety and stability of the system make it a tough challenge for large-scale numerical modeling. The overall modeling of the finite element system needs to consider detailed modeling and be able to reflect the local response. The overall finite element model is shown in Fig. 13, including the H main tower base, H main tower crown, transitional pier, assistant pier, girder, etc. After meshing with tetrahedral elements, this model is composed of 17,637,501 elements, 10,367,815 nodes and 21,835,902 DOFs. When under dangerous working conditions, the main loads usually come from the seismic wave and their own weight. Therefore, the structural dynamics analysis mainly considers the deformation and stress of the bridge under seismic loads and its gravity. Specifically, the seismic waves are the MEX natural waves, which are input in three directions of the bridge bottom simultaneously, and their overall amplitude is modulated proportionally.
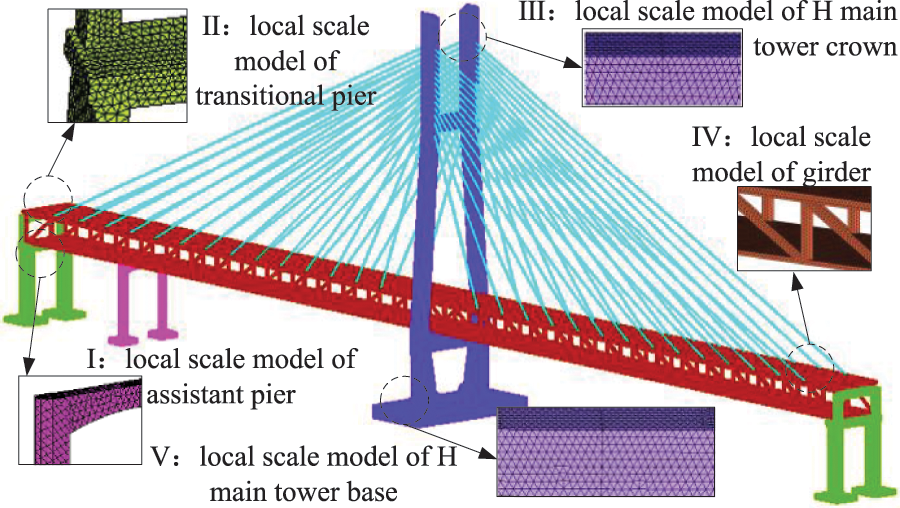
Figure 13: Whole finite element model of cable-stayed bridge
In parallel computing, the operating number of nodes is 96, 192, 288, and 384, respectively. The calculation results of TPCA and HHPA proposed in this article are presented in Tables 4–5. The performance of parallel algorithm for cable-stayed bridge of the CDDA, TPCA, and HHPA are shown in Fig. 14.
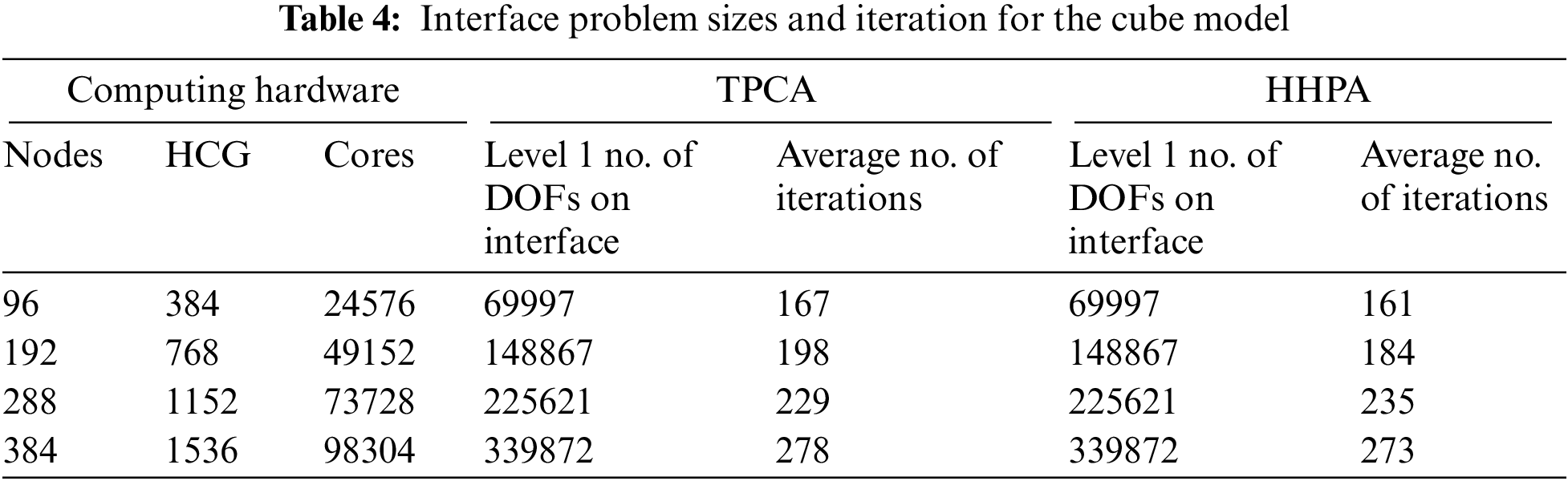
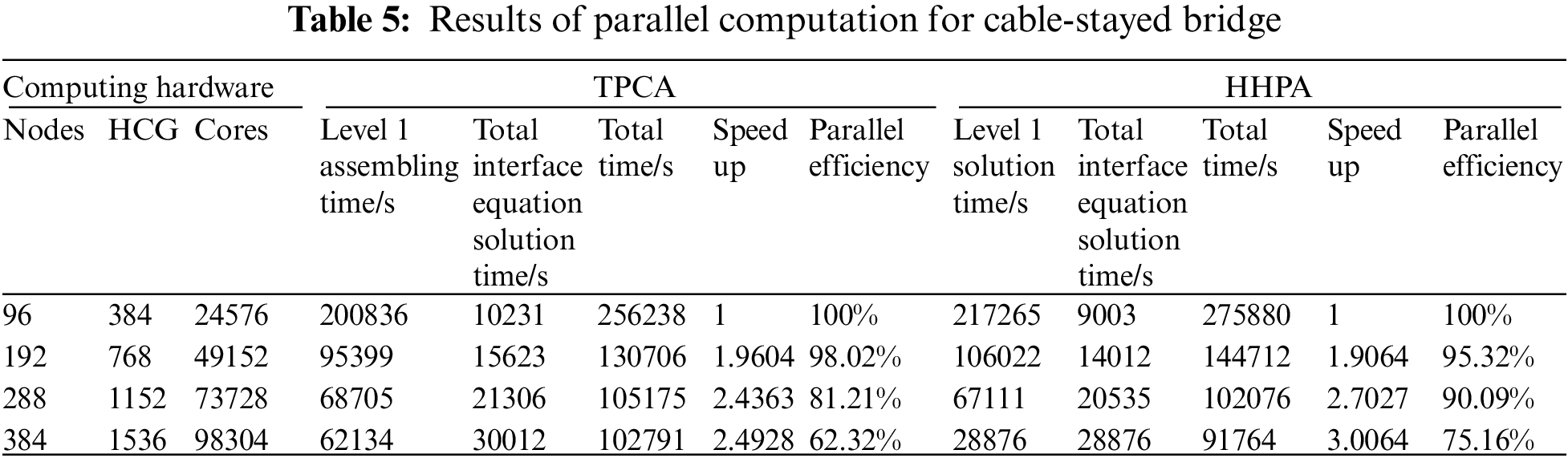
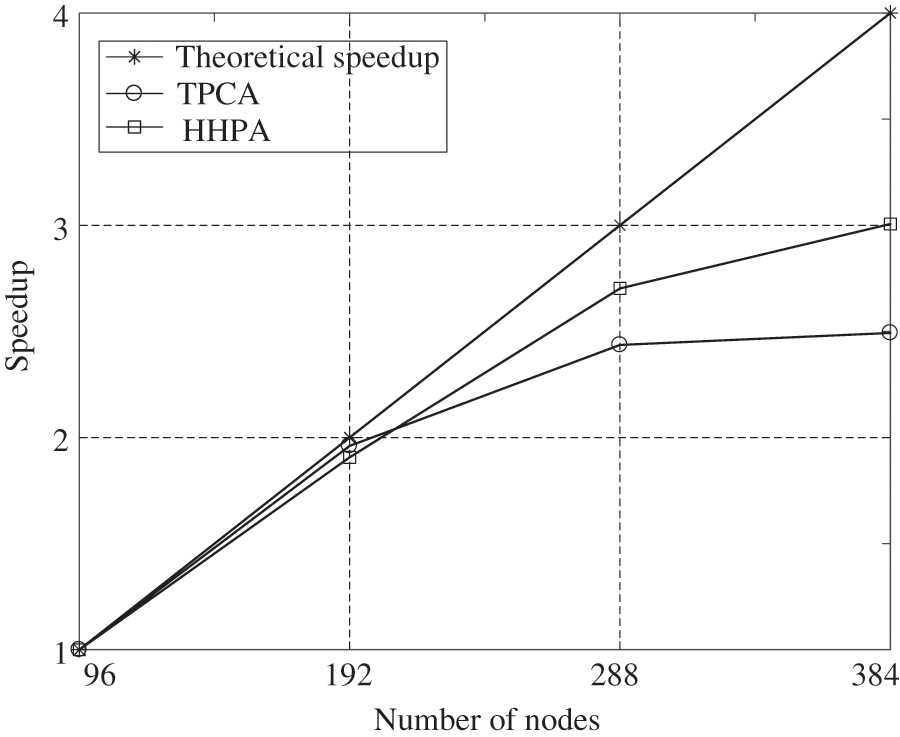
Figure 14: Performance of parallel algorithms for cable-stayed bridge
It can be seen from Table 5 that HHPA and TPCA almost obtain the same computing time for the interface equations. This is because the scales of the interface equations of the two methods are approximately the same. When under 96 nodes or 192 nodes, the total computing time of HHPA in this paper is higher than that of TPCA. This result is consistent with Miao’s [15] findings based on the parallel computation under a multicore environment. The main reason behind the phenomenon is when the partition scale is relatively small, the computing scale for the sub-domain is rather large, causing the bandwidth of every sub-domain system to be too large in turn. This raises the computing memory space requirements for each sub-system and accompanies a serious increment in the computing amount. As a consequence, it affects the parallel computing efficiency. On the contrary, when under 288 nodes or 384 nodes, our HHPA consumes less time than TPCA. This is because when the partition scale gets larger, the sub-domain scale will effectively shrink in computing, which will further cause a decrease in the bandwidth of every sub-domain system. Also, compared to the homogeneous groups under a multicore environment, the heterogeneous groups under the heterogeneous condition have superior computation ability, which can speed up the parallel solution for equations. In general, these factors make the total computation time shorter in level 1 equations based on HHPA than that time for the TPCA, considering the assembling, condensing, solving and back substituting for the level 2 equations. And therefore, when under a larger scale partition, HHPA proposed in this article owns a higher efficiency and speedup, which is shown in Fig. 14.
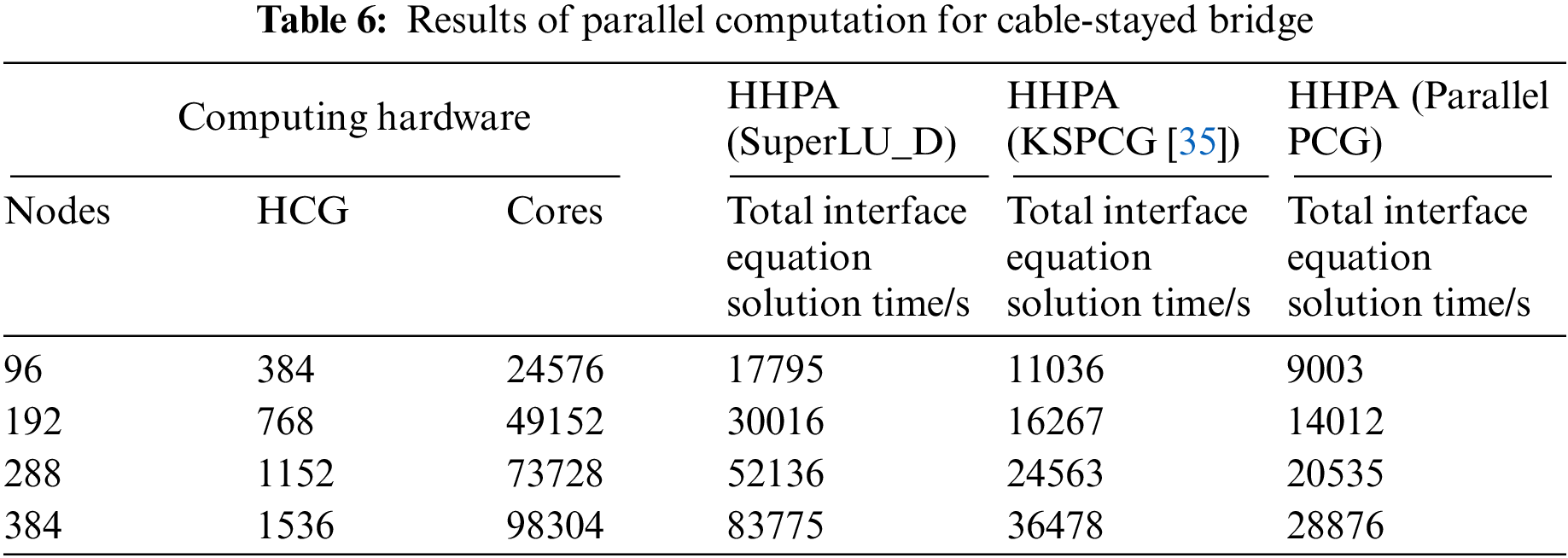
The calculation results of HHPA with different parallel solvers on the solving of global interface equations are shown in Table 6.
In Table 6, the global interface equations are solved by different parallel solvers SuperLU_D, KSPCG in PetSc and parallel PCG. It can be seen from the Table 6 that when using HHPA with SuperLU_D to solve the global interface equations, the solution time increases sharply with the increase of subdomains. Although the global interface equations adopt compressed sparse column technique for storage and the SuperLU_D is only applied in the lower triangle decomposition when conducting triangular decomposition, the global interface equations are still highly dense. Also, the triangular decomposition will further increase the density of the original equations. As a consequence, the sets and triangular decomposition require a large amount of memory. Besides, it also needs a lot of communication and calculation. With the increase of subdomain, the scale of the global interface equations also gets larger. Companies with more expense in storage, communication and computing, and take a longer time to solve the global interface equations. On the contrary, when utilizing the KSPCG and the parallel PCG, because of the use of the iterate method, the local communication involved in the equation parallel solution only exists between neighbor subdomains. Only a few dot product operations and computations for overall iterative errors need global communications. Thus, the KSPCG and the parallel PCG can achieve the calculation in a shorter computing time. Additionally, the solving time of parallel PCG is less than KSPCG. It is because all processes need to participate in global communication when solving global interface equations with KSPCG. And the parallel PCG only uses 1 MPI process within the same node. Hence, the overhead increment in inter-process communication and synchronization will greatly increase the solution time of global interface equations.
(1) To lower the computational efficiency loss when solving systemically large-scale or ultra-large-scale structure finite element problems with heterogeneous multicore distributed storage computers, the HHPA for finite element analysis is proposed based on research and understanding of CDDA, TPCA, parallel solver, and multilayer communication strategy architecture. This method not only reduces the scale of interface equations but also considerably saves computing time. Moreover, a three-layer parallelization has been applied successfully during the computational procedure to separate the communication of inter-nodes, heterogeneous-core-groups and inside-heterogeneous-core-groups. Thereby, this method largely increases communication efficiency.
(2) The typical numerical example shows that when the scale of the partition is comparatively small, the parallel efficiency of this approach is better than CDDA but worse than TPCA. When the scale of the sub-domain is relatively large, this method can achieve a higher speedup and parallel efficiency than TPCA. The results of this paper can be provided as a reference for finite element structural analysis software operating on ‘Shenwei’ heterogeneous multicore processors and can be ported to other heterogeneous processors for large-scale parallel computing. It can also be provided as a practical reference for large equipment systems and the dynamics of complex engineering systems under fine modeling in parallel computing.
Funding Statement: This work is supported by the National Natural Science Foundation of China (Grant No. 11772192).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Kennedy, G. J., Martins, J. R. (2014). A parallel finite-element framework for large-scale gradient-based design optimization of high-performance structures. Finite Elements in Analysis and Design, 87, 56–73. DOI 10.1016/j.finel.2014.04.011. [Google Scholar] [CrossRef]
2. Xu, S., Wang, W., Zhang, J., Jiang, J. R., Jin, Z. et al. (2021). High performance computing algorithm and software for heterogeneous computing. Journal of Software, 32(8), 2365–2376. [Google Scholar]
3. Gao, R., Li, X. (2021). Design and mechanical properties analysis of radially graded porous scaffolds. Journal of Mechanical Engineering, 57(3), 220–226. DOI 10.3901/JME.2021.03.220. [Google Scholar] [CrossRef]
4. Ni, P. H., Law, S. S. (2016). Hybrid computational strategy for structural damage detection with short-term monitoring data. Mechanical Systems and Signal Processing, 70, 650–663. DOI 10.1016/j.ymssp.2015.09.031. [Google Scholar] [CrossRef]
5. Kurc, Ö. (2010). Workload distribution framework for the parallel solution of large structural models on heterogeneous PC clusters. Journal of Computing in Civil Engineering, 24(2), 151–160. DOI 10.1061/(ASCE)CP.1943-5487.0000019. [Google Scholar] [CrossRef]
6. Zuo, S., Lin, Z., García-Doñoro, D., Zhang, Y., Zhao, X. (2021). A parallel direct domain decomposition solver based on schur complement for electromagnetic finite element analysis. IEEE Antennas and Wireless Propagation Letters, 20(4), 458–462. DOI 10.1109/LAWP.2021.3053566. [Google Scholar] [CrossRef]
7. Wang, Y., Gu, Y., Liu, J. (2020). A domain-decomposition generalized finite difference method for stress analysis in three-dimensional composite materials. Applied Mathematics Letters, 104, 106226. DOI 10.1016/j.aml.2020.106226. [Google Scholar] [CrossRef]
8. Phillips, J. C., Hardy, D. J., Maia, J. D., Stone, J. E., Ribeiro et al. (2020). Scalable molecular dynamics on CPU and GPU architectures with NAMD. The Journal of Chemical Physics, 153(4), 044130. DOI 10.1063/5.0014475. [Google Scholar] [CrossRef]
9. Zhang, W., Zhong, Z. H., Peng, C., Yuan, W. H., Wu, W. (2021). GPU-accelerated smoothed particle finite element method for large deformation analysis in geomechanics. Computers and Geotechnics, 129, 103856. DOI 10.1016/j.compgeo.2020.103856. [Google Scholar] [CrossRef]
10. Li, Z., Shan, Q., Ning, J., Li, Y., Guo, K. et al. (2022). AMG-CG method for numerical analysis of high-rise structures on heterogeneous platforms with GPUs. Computers and Concrete, 29(2), 93–105. [Google Scholar]
11. He, X., Wang, K., Feng, Y., Lv, L., Liu, T. (2022). An implementation of MPI and hybrid OpenMP/MPI parallelization strategies for an implicit 3D DDG solver. Computers & Fluids, 241, 105455. DOI 10.1016/j.compfluid.2022.105455. [Google Scholar] [CrossRef]
12. Paszyńska, A. (2017). Graph-grammar greedy algorithm for reutilization of partial LU factorization over 3D tetrahedral grids. Journal of Computational Science, 18, 143–152. DOI 10.1016/j.jocs.2016.10.003. [Google Scholar] [CrossRef]
13. Łoś, M., Schaefer, R., Paszyński, M. (2018). Parallel space–time hp adaptive discretization scheme for parabolic problems. Journal of Computational and Applied Mathematics, 344, 819–835. DOI 10.1016/j.cam.2017.12.005. [Google Scholar] [CrossRef]
14. Peng, X., Chen, G., Yu, P., Zhang, Y., Guo, L. et al. (2019). Parallel computing of three-dimensional discontinuous deformation analysis based on OpenMP. Computers and Geotechnics, 106, 304–313. DOI 10.1016/j.compgeo.2018.11.016. [Google Scholar] [CrossRef]
15. Miao, X., Jin, X., Ding, J. (2014). A hierarchical parallel computing approach for structural static finite element analysis. Acta Mechanica Sinica, 46(4), 611–618. [Google Scholar]
16. El Gharbi, Y., Parret-Fréaud, A., Bovet, C., Gosselet, P. (2021). Two-level substructuring and parallel mesh generation for domain decomposition methods. Finite Elements in Analysis and Design, 192, 103484. DOI 10.1016/j.finel.2020.103484. [Google Scholar] [CrossRef]
17. Koric, S., Lu, Q., Guleryuz, E. (2014). Evaluation of massively parallel linear sparse solvers on unstructured finite element meshes. Computers & Structures, 141, 19–25. DOI 10.1016/j.compstruc.2014.05.009. [Google Scholar] [CrossRef]
18. Fialko, S. (2021). Parallel finite element solver for multi-core computers with shared memory. Computers & Mathematics with Applications, 94, 1–14. DOI 10.1016/j.camwa.2021.04.013. [Google Scholar] [CrossRef]
19. Klawonn, A., Köhler, S., Lanser, M., Rheinbach, O. (2020). Computational homogenization with million-way parallelism using domain decomposition methods. Computational Mechanics, 65(1), 1–22. DOI 10.1007/s00466-019-01749-5. [Google Scholar] [CrossRef]
20. Gasparini, L., Rodrigues, J. R., Augusto, D. A., Carvalho, L. M., Conopoima, C. et al. (2021). Hybrid parallel iterative sparse linear solver framework for reservoir geomechanical and flow simulation. Journal of Computational Science, 51, 101330. DOI 10.1016/j.jocs.2021.101330. [Google Scholar] [CrossRef]
21. Ghysels, P., Synk, R. (2022). High performance sparse multifrontal solvers on modern GPUs. Parallel Computing, 110, 102897. DOI 10.1016/j.parco.2022.102897. [Google Scholar] [CrossRef]
22. Daga, M., Aji, A. M., Feng, W. C. (2011). On the efficacy of a fused CPU+GPU processor (or APU) for parallel computing. 2011 Symposium on Application Accelerators in High-Performance Computing, pp. 141–149. Knoxville, TN, USA. [Google Scholar]
23. Keckler, S. W., Dally, W. J., Khailany, B., Garland, M., Glasco, D. (2011). GPUs and the future of parallel computing. IEEE Micro, 31(5), 7–17. DOI 10.1109/MM.2011.89. [Google Scholar] [CrossRef]
24. Carter, N. P., Agrawal, A., Borkar, S., Cledat, R., David, H. et al. (2013). Runnemede, an architecture for ubiquitous high-performance computing. 2013 IEEE 19th International Symposium on High Performance Computer Architecture (HPCA), pp. 198–209. Shenzhen, China. [Google Scholar]
25. Xue, W., Yang, C., Fu, H., Wang, X., Xu, Y. et al. (2014). Ultra-scalable CPU-MIC acceleration of mesoscale atmospheric modeling on Tianhe-2. IEEE Transactions on Computers, 64(8), 2382–2393. DOI 10.1109/TC.2014.2366754. [Google Scholar] [CrossRef]
26. Miao, X., Jin, X., Ding, J. (2016). Improving the parallel efficiency of large-scale structural dynamic analysis using a hierarchical approach. The International Journal of High Performance Computing Applications, 30(2), 156–168. DOI 10.1177/1094342015581402. [Google Scholar] [CrossRef]
27. Shirvani, M. H. (2020). A hybrid meta-heuristic algorithm for scientific workflow scheduling in heterogeneous distributed computing systems. Engineering Applications of Artificial Intelligence, 90, 103501. DOI 10.1016/j.engappai.2020.103501. [Google Scholar] [CrossRef]
28. Dostál, Z., Horák, D. (2003). Scalability and FETI based algorithm for large discretized variational inequalities. Mathematics and Computers in Simulation, 61(3–6), 347–357. DOI 10.1016/S0378-4754(02)00088-5. [Google Scholar] [CrossRef]
29. Bathe, K. J., Noh, G. (2012). Insight into an implicit time integration scheme for structural dynamics. Computers & Structures, 98, 1–6. DOI 10.1016/j.compstruc.2012.01.009. [Google Scholar] [CrossRef]
30. Chen, D., Yang, J., Kitipornchai, S. (2016). Free and forced vibrations of shear deformable functionally graded porous beams. International Journal of Mechanical Sciences, 108, 14–22. DOI 10.1016/j.ijmecsci.2016.01.025. [Google Scholar] [CrossRef]
31. Hughes, T. J. R. (1987). The finite element method linear static and dynamic finite element analysis. Computer Methods in Applied Mechanics and Engineering, 65(2), 191. DOI 10.1016/0045-7825(87)90013-2. [Google Scholar] [CrossRef]
32. Hosseini Shirvani, M., Noorian Talouki, R. (2022). Bi-objective scheduling algorithm for scientific workflows on cloud computing platform with makespan and monetary cost minimization approach. Complex & Intelligent Systems, 8(2), 1085–1114. DOI 10.1007/s40747-021-00528-1. [Google Scholar] [CrossRef]
33. Li, X. S., Demmel, J. W. (2003). SuperLU_DIST, A scalable distributed-memory sparse direct solver for unsymmetric linear systems. ACM Transactions on Mathematical Software, 29(2), 110–140. DOI 10.1145/779359.779361. [Google Scholar] [CrossRef]
34. Rao, A. R. M. (2005). MPI-based parallel finite element approaches for implicit nonlinear dynamic analysis employing sparse PCG solvers. Advances in Engineering Software, 36(3), 181–198. DOI 10.1016/j.advengsoft.2004.10.004. [Google Scholar] [CrossRef]
35. Balay, S., Buschelman, K., Eijkhout, V., Gropp, W. D., Kaushik, D. et al. (2022). PETSc users manual. Technical Report ANL-95/11–Revision 3.17. Argonne National Laboratory. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools