 Open Access
Open Access
ARTICLE
Fractional Order Modeling of Predicting COVID-19 with Isolation and Vaccination Strategies in Morocco
1 Laboratory of Engineering Sciences for Energy, National School of Applied Sciences, Chouaib Doukkali University, El Jadida, 10002, Morocco
2 Department of Mathematics, Faculty of Sciences, Chouaib Doukkali University, El Jadida, 10002, Morocco
3 Department of Mathematics, Hodeidah University, Al-Hudaydah, 91911, Yemen
4 Department of Mathematics and Sciences, Prince Sultan University, Riyadh, 11586, Saudi Arabia
5 Department of Mathematics, University of Malakand, Chakdara Dir (L), Khyber Pakhtankhawa, 18000, Pakistan
6 Department of Medical Research, China Medical University, Taichung, 40402, Taiwan
* Corresponding Author: Thabet Abdeljawad. Email:
(This article belongs to the Special Issue: Applications of Fractional Operators in Modeling Real-world Problems: Theory, Computation, and Applications)
Computer Modeling in Engineering & Sciences 2023, 136(2), 1931-1950. https://doi.org/10.32604/cmes.2023.025033
Received 28 April 2022; Accepted 16 August 2022; Issue published 06 February 2023
Abstract
In this work, we present a model that uses the fractional order Caputo derivative for the novel Coronavirus disease 2019 (COVID-19) with different hospitalization strategies for severe and mild cases and incorporate an awareness program. We generalize the SEIR model of the spread of COVID-19 with a private focus on the transmissibility of people who are aware of the disease and follow preventative health measures and people who are ignorant of the disease and do not follow preventive health measures. Moreover, individuals with severe, mild symptoms and asymptomatically infected are also considered. The basic reproduction number () and local stability of the disease-free equilibrium (DFE) in terms of are investigated. Also, the uniqueness and existence of the solution are studied. Numerical simulations are performed by using some real values of parameters. Furthermore, the immunization of a sample of aware susceptible individuals in the proposed model to forecast the effect of the vaccination is also considered. Also, an investigation of the effect of public awareness on transmission dynamics is one of our aim in this work. Finally, a prediction about the evolution of COVID-19 in 1000 days is given. For the qualitative theory of the existence of a solution, we use some tools of nonlinear analysis, including Lipschitz criteria. Also, for the numerical interpretation, we use the Adams-Moulton-Bashforth procedure. All the numerical results are presented graphically.Keywords
COVID-19 is an infectious viral disease brought about by a virus known as severe acute syndrome Coronavirus [1]. This virus was first reported at the end of 2019 in Wuhan, China. Then, it was reported in other places in China surprisingly [2]. In three months, the disease was transmitted in many countries of the world. Therefore, in April 2020, the World Health Organization (WHO) announced it as an outbreak. Its symptoms involve breathing trouble, exhaustion, fever, dry hack, sleepiness, conjunctivitis, chest torment, loss of discourse, loose bowels, and painful throat. Furthermore, in serious cases, pneumonia, multiorgan letdown, intense respiratory pain condition, septic shock, abnormal heart rhythm, myocarditis, blood clumps, cardiovascular breakdown, encephalitis, stroke, and Guillain Barré disorder, reciprocal lung entrance have been reported [3,4]. Additionally, a few patients might experience the ill effects of looseness of the bowels, loss of craving, taste, or smell, with no indications of breathing problem [5–7].
Investigating infectious diseases through various procedures is an attractive area of research in recent times. One of the important areas in this regard is devoted to the mathematical modeling of infectious diseases. Mathematical modeling is a powerful tool to study infectious diseases for analysis of the dynamic of diseases and backing control systems [8]. Plenty of research work has been published by researchers. The mentioned work is devoted to investigating disease transmission dynamics and their control. In the same fashion to understand the dynamics of COVID-19 and the tracking down—of the reasonable result of the outbreak is helpful for public health initiatives and consciousness programs, for which significant work has been published, and we refer to a few such as [9–14].
Fractional calculus can more precisely describe natural phenomena as compared to ordinary calculus, where derivatives and integrations have integer-orders. Numerous scientists have given more attention to investigating the dynamics of fractional-order models regarding the COVID-19 pandemic [15–38]. There are many papers showing the effectiveness of fractional calculus (see [39–45]). Further, the dynamics of a stochastic epidemic model has been studied, for which we refer [46,47] and mathematical modeling of COVID-19 pandemic using the Caputo-Fabrizio fractional derivative (see [48]). Also, a model of COVID-19 disease has been investigated under the stochastic concept in [49].
In this research work, an SEIR-type model that concentrates on the transmission dynamics of the COVID-19 outbreak are considered. Here, with a special spotlight on the transmissibility of people with mild, severe, and without side effects like the existence of people who tested positive for sharp, mild, or asymptomatic manifestations, and separating infectious compartment into two fundamental compartments of hospitalized people with mild symptoms and those in dense care units are involved in our proposed model.
This work is organized as: Part 2 is devoted to the formulation of the proposed model for COVID-19. In Parts 3 and 4, we analyze the proposed model with fractional order. Some qualitative analysis, computation of
Here in this section, the proposed model is formulated. The flowchart of the model is given in Fig. 1 to understand the evolution of the mentioned disease. Let the total human population at time
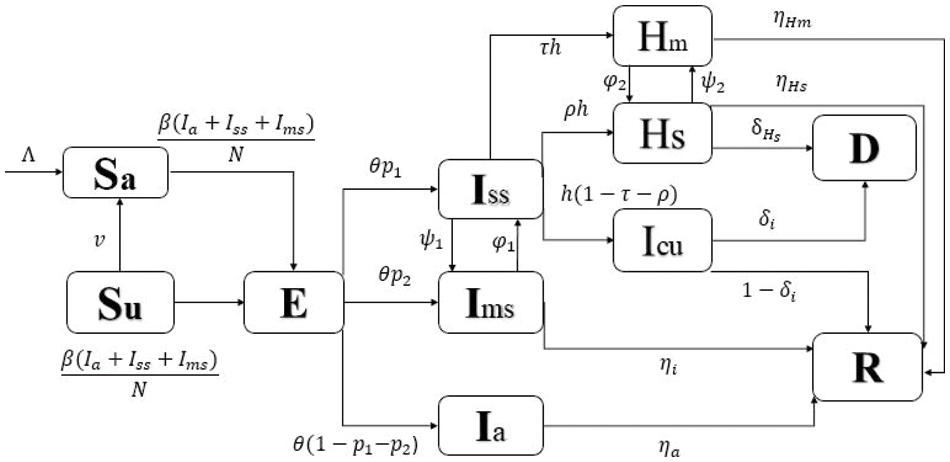
Figure 1: Flowchart of model (1)
Thus, we have
From Fig. 1, we formulate our proposed model as
with initial conditions as
In this part, we recall some definitions from fractional calculus which are needed throughout the paper.
Definition 3.1. [50] The Caputo fractional derivative of f of order
where
The fractional integral [51] having of order
where
Now, let us present the fractional order model of the COVID-19 by means of the Caputo derivative as follows:
In this part, we study the existence of a solution for the fractional order model Eq. (4). The existence theory is an important consequence of applied analysis and has many applications. It provides us with whether the model we study exists or not and if it exists whether it has a solution or not. If a problem has a solution, whether it will be unique or multiple. It also helps us in investigating the qualitative behavior of the solution to the problem.
Consider the following subsystem:
Since
Therefore, to study the existence and uniqueness of solutions of the system Eq. (4), we focus to study Eq. (5).
Assume that
Applying the fractional integral to Eq. (5), it follows from initial conditions that
Assume that
Theorem 4.1. The kernels
hold.
Proof. Let
Similarly
Thus,
Theorem 4.2. The model Eq. (4) has a unique solution provided
when
Proof. The proof for the above result is the same as the proof of Theorem 1 in [52].
5 Reproductive Number and Stability Analysis
We follow the references [53,54] to calculate
The DFE point is given by
and
It follows that the Jacobian matrices of
Thus, the
The reported result below is given in Theorem 2 of [54].
Theorem 5.1. The DFE
6 Fractional Order Model with Vaccination
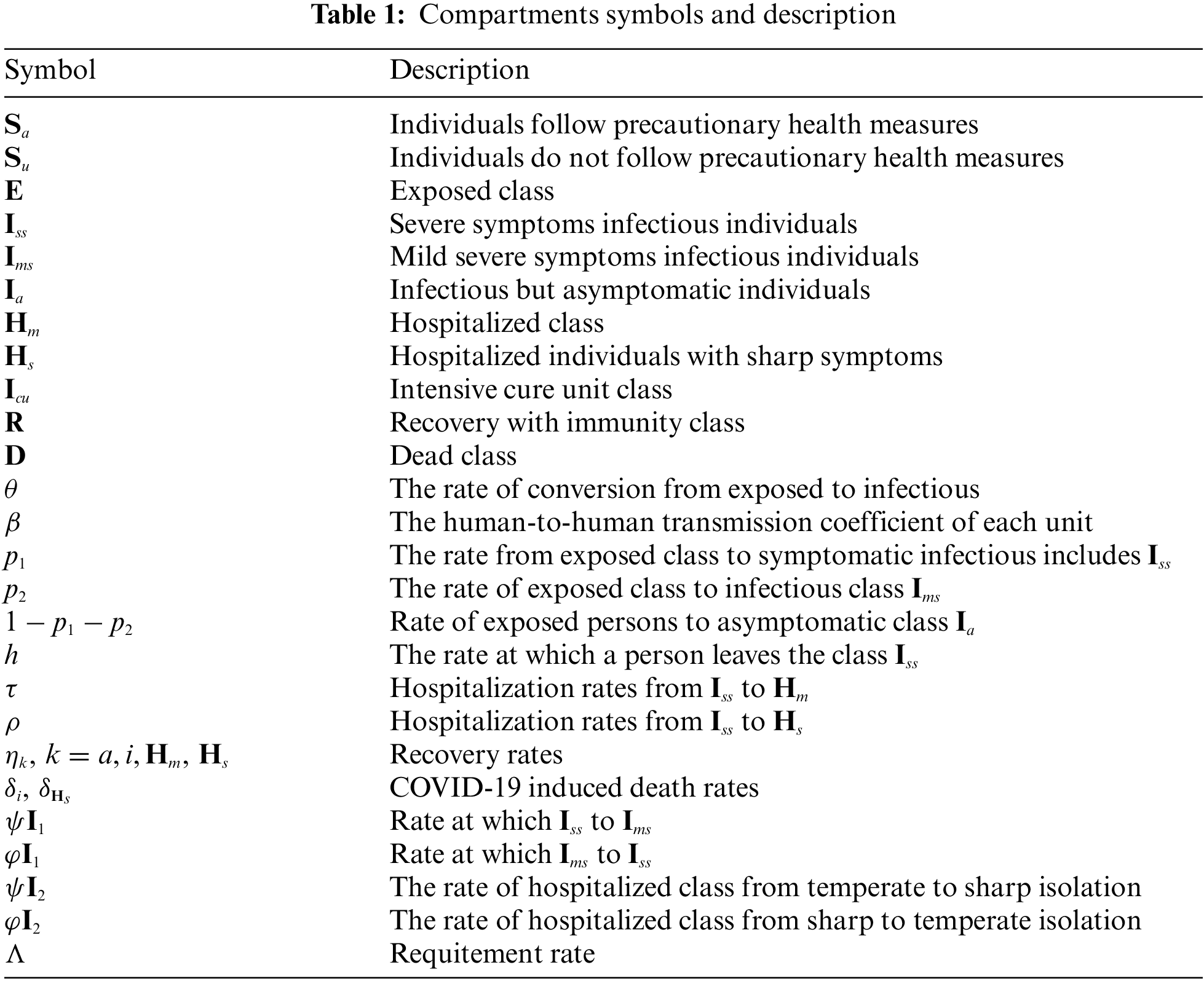
In this part, we discuss the fractional order model with vaccination which is overseeing and controlling contagious diseases by giving security to powerless and susceptible individuals. We suppose that a specified proportion p of people in the mindful susceptible class are vaccinated. For this situation, inoculated people are moved to another compartment
Figure 2: Flowchart of the fractional model (10)
We can interpret this diagram into fractional differential equations as follows:
with
The components of infection in this model are,
Theorem 6.1. The reproduction number
Proof. Let
and
By the differential of
and
Thus, the
Theorem 6.2. The DFE
Proof. The proof is given in the Theorem 2 of [54].
The critical percentage of the population
In the numerical analysis of traditional differential equations, various numerical methods have been established. Among various numerical procedures, Adams’s methods represent one of the most used and studied classes of implicit (Adams-Moulton) and explicit (Adams-Bashforth) linear multistep methods. The aforementioned methods have gotten much popularity among researchers due to their good stability properties, reasonable computational cost, and simplicity of implementation. Therefore, several authors have extended the aforementioned methods. In particular, the mentioned procedures have also been extended to deal with fractional order differential equations numerically. A predictor-corrector algorithm has been extended to fractional differential equations with the corresponding Adams-Moulton-Bashforth procedure for traditional differential equations. The numerical method used to solve the model is the predictor-corrector method for fractional differential equations in [55]. Consider, the problem with fractional order
where
where
We extend the afore given scheme in Eq. (12) for our considered model Eq. (4) to simulate the results. The numerical simulations for fractional dynamic of the considered model Eqs. (4) and (10) are performed as the case study of Morocco. The parameters values are given in the Table 2 for the numerical interpretation. Also we compute the value of the reproduction number as
In Fig. 3, the confirmed infected and death cases are described daily from July 01, 2020, to January 01, 2021, which is a total of 185 days. We implement numerical simulations to compare the results of our model with the real data in Fig. 3. The forecasted evolution of the outbreak of COVID-19 without and with vaccination in Morocco can be seen in Figs. 4 and 5, respectively.
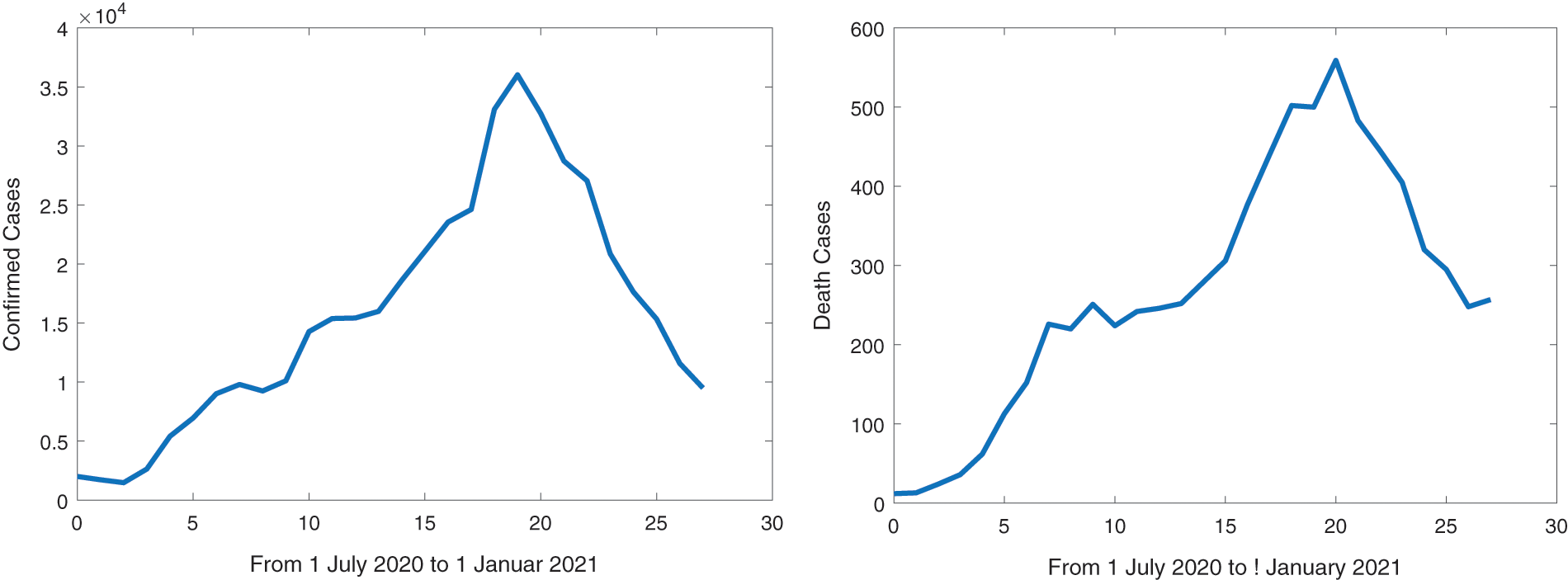
Figure 3: Evolution of COVID-19 in Morocco per day
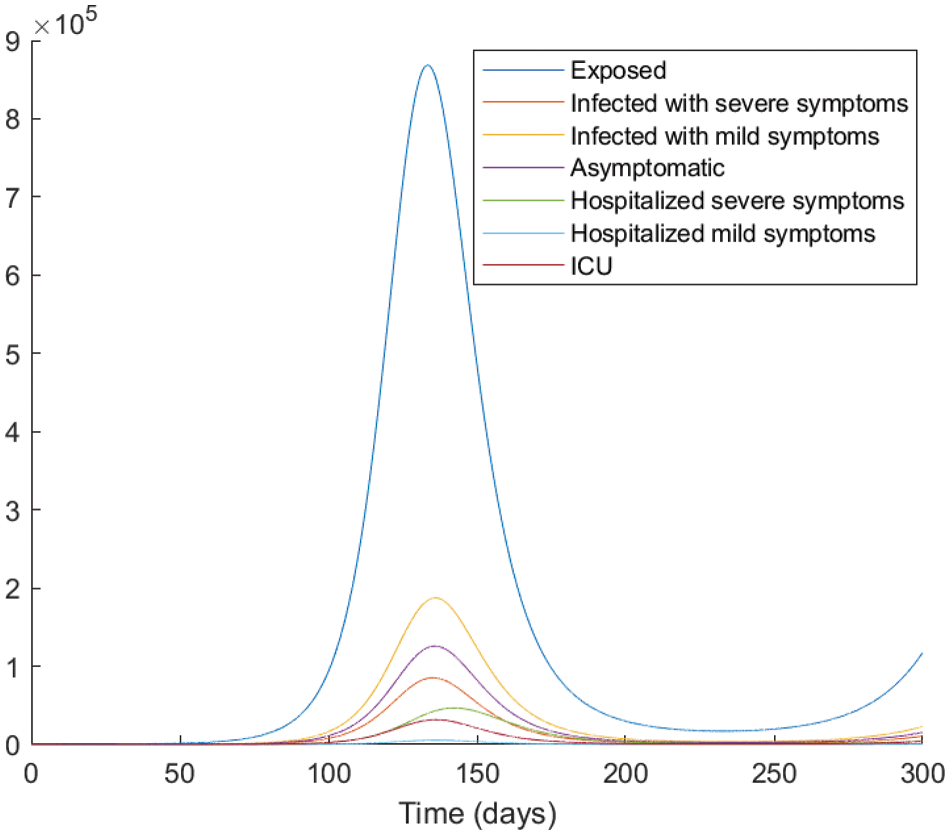
Figure 4: The evolution of the epidemic predicted by the fractional model (4) with
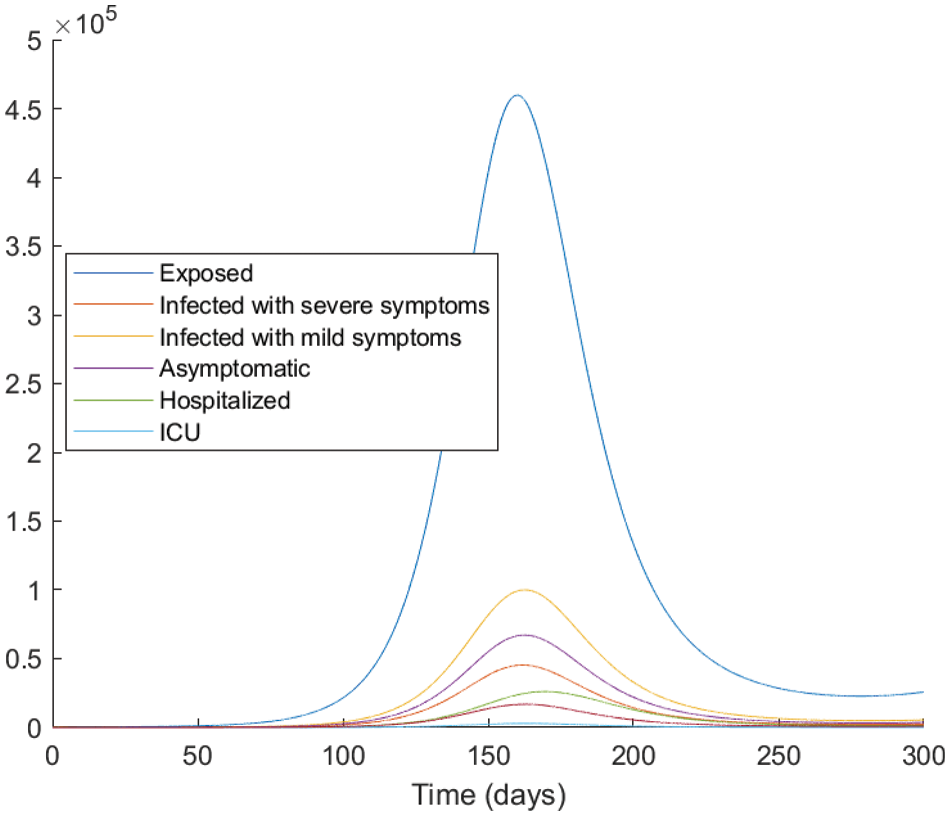
Figure 5: The evolution of the epidemic predicted by the fractional model vaccinated with
From the analysis of the acquired graphs, we observe that the population of the infected class decreases significantly by decreasing the fractional order of the derivative and the endemic state of the disease goes to the disease-free state in all the cases deliberated. Besides, we demonstrate that our fractional order model well describes the actual data of daily confirmed, recovered, and death cases. In Fig. 5, we note that the plot is much flatter than that in Fig. 4. As well, the curve for asymptomatic individuals is almost identical to the x-axis, and this indicates the importance of the vaccination approach to overcome the pandemic.
In Fig. 6, we give the graphical results of the suggested model (4) to analyze the effect of the fractional order.
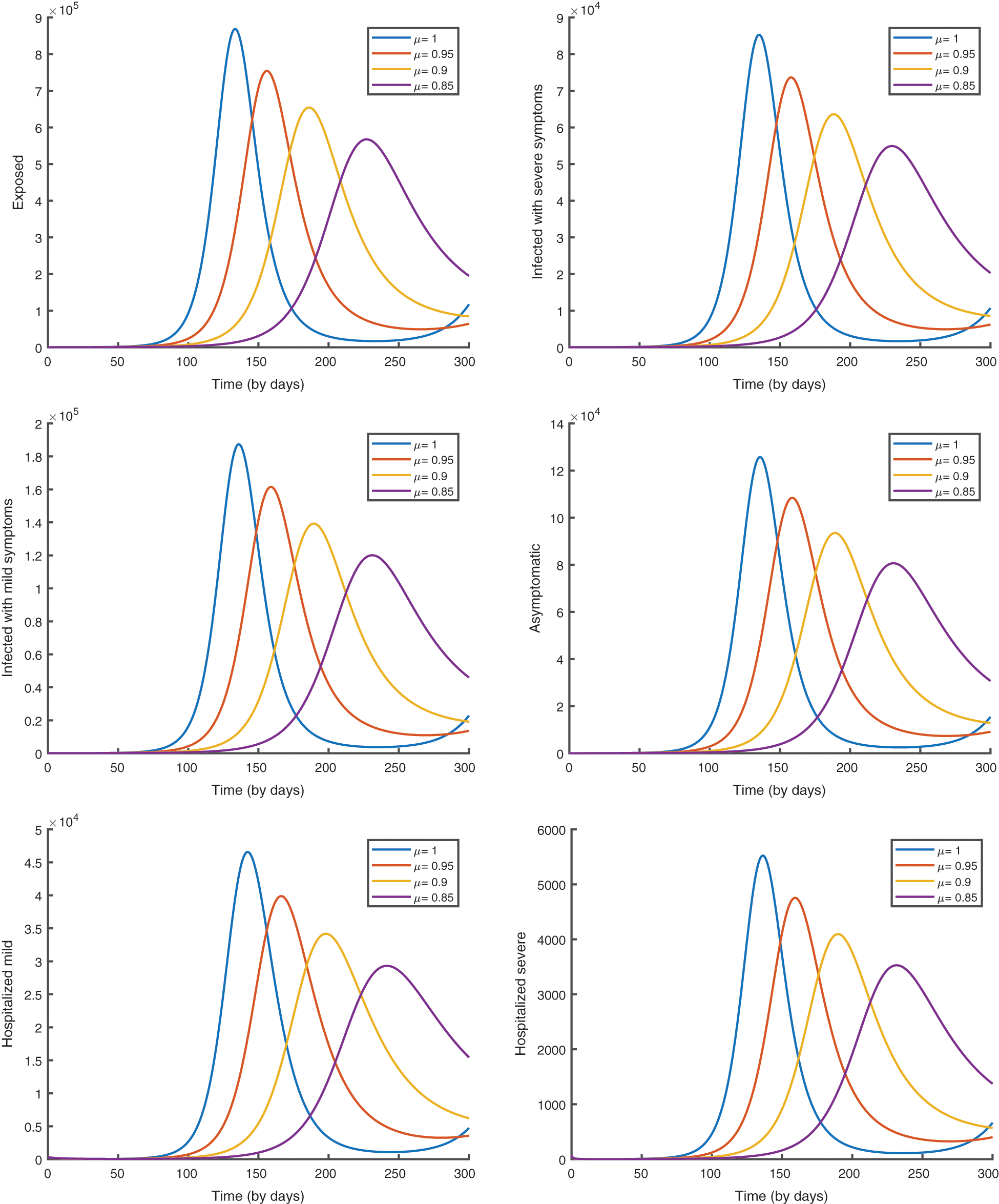
Figure 6: The evolution of the epidemic predicted by the model (4)
In Fig. 7, we give the graphical results of the suggested vaccination model (10) to analyze the influence of the fractional order.
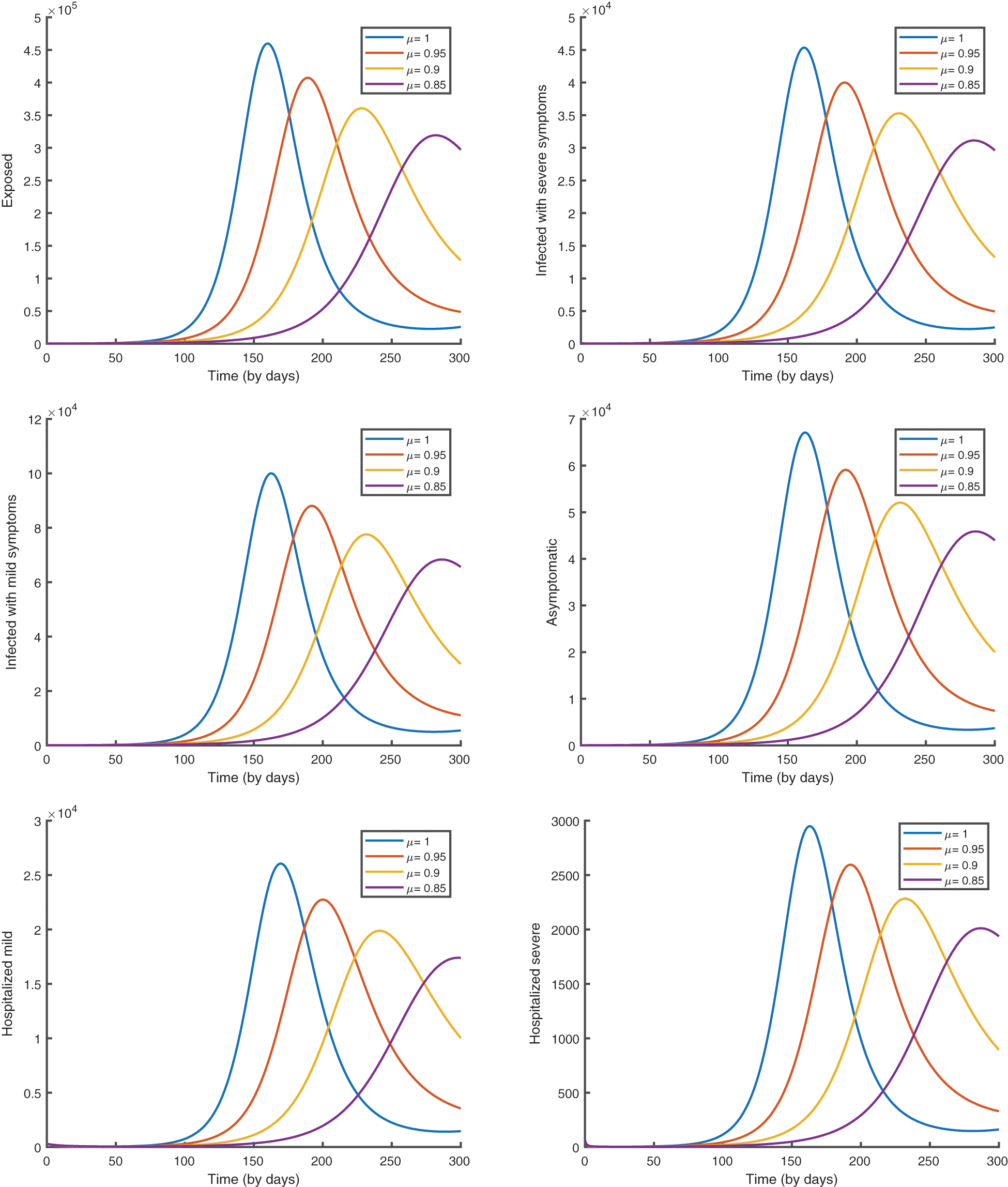
Figure 7: Epidemic evolution predicted by the fractional vaccination model (10)
We represent the spread of infection without vaccination in Fig. 8 and with vaccination in Fig. 9, for a period of 1000 days.
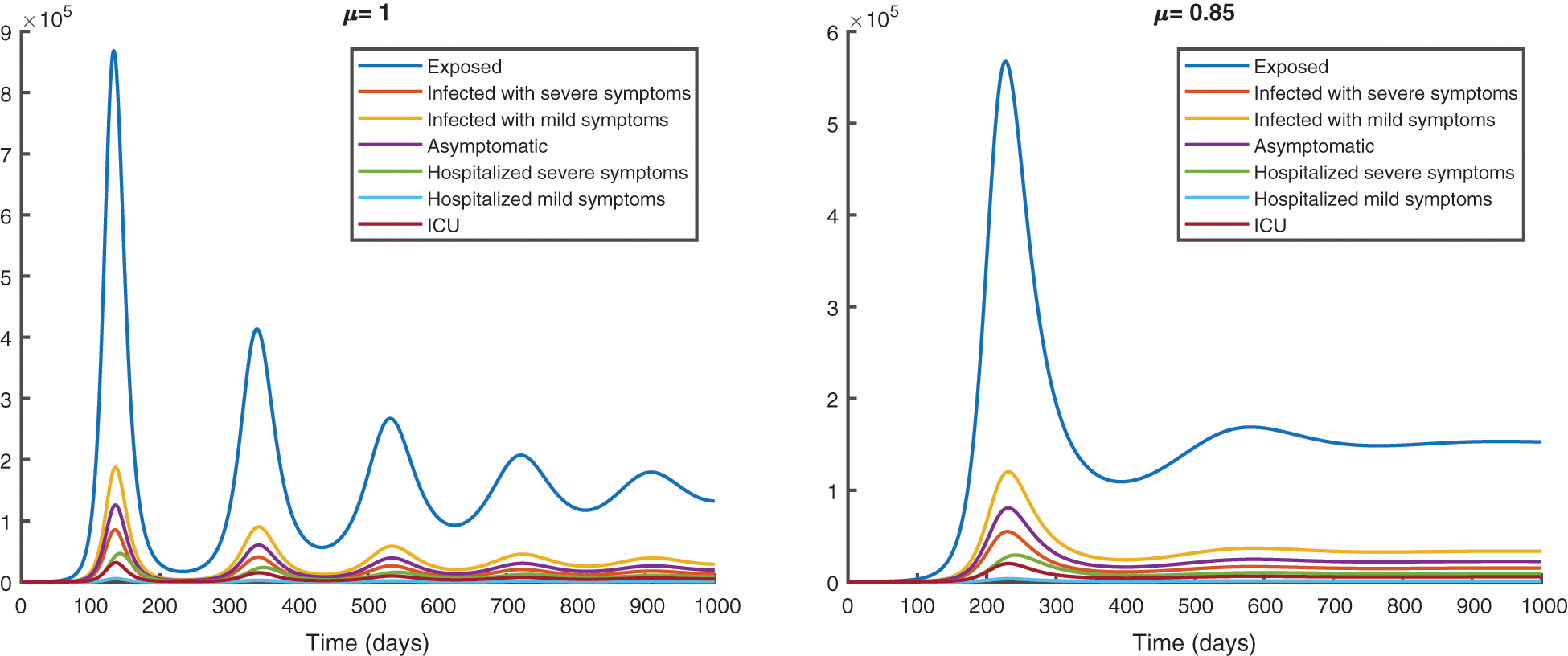
Figure 8: Epidemic evolution predicted by the fractional model
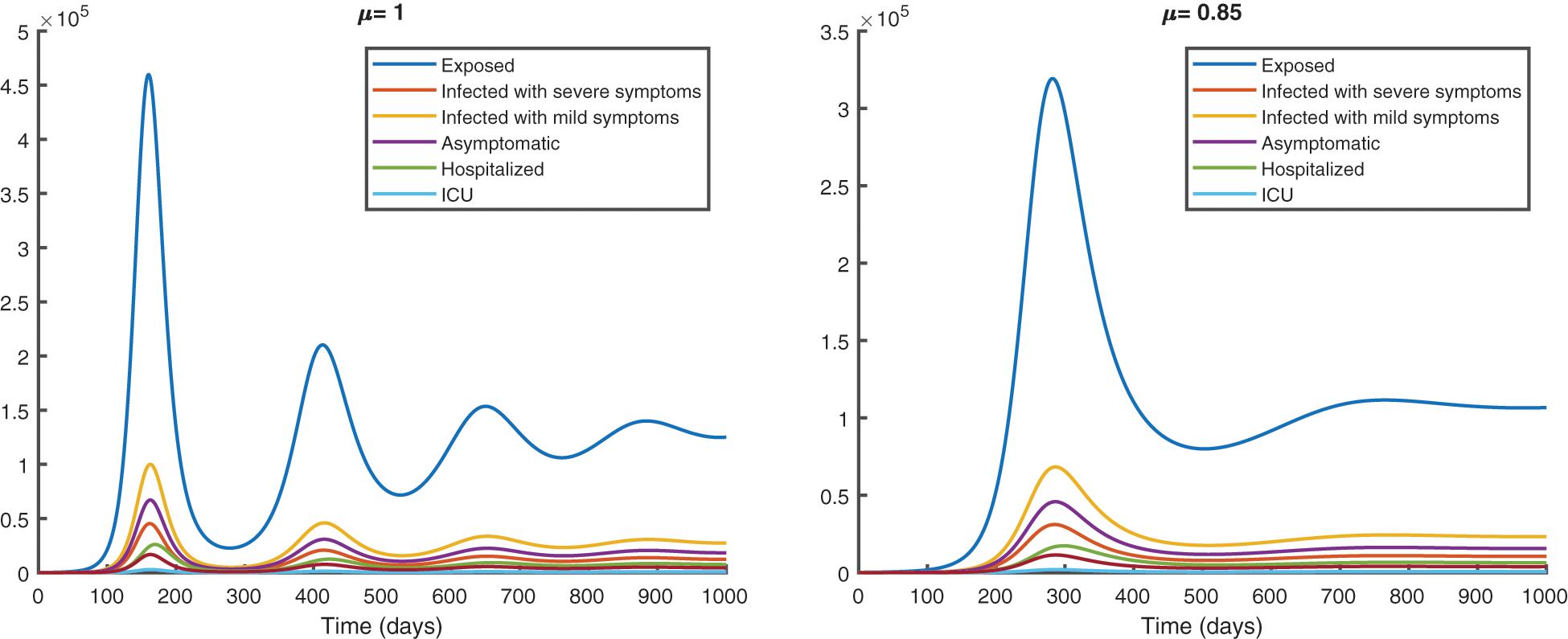
Figure 9: Epidemic evolution predicted by the fractional vaccination model
In this manuscript, we have given an analysis of the fractional order model of COVID-19, with theoretical calculations. We have established sufficient conditions for the existence theory using some tools of nonlinear analysis. The existence theory is an important area of research in recent times. Also, we have computed the basic reproductive number
Acknowledgement: The authors Kamal Shah, and Thabet Abdeljawad would like to thank Prince Sultan University for the support through the TAS Research Lab.
Funding Statement: The authors Kamal Shah, and Thabet Abdeljawad would like to thank Prince Sultan University for paying the APC.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Lai, C. C., Shih, T. P., Ko, W. C., Tang, H. J., Hsueh, P. R. (2020). Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and coronavirus disease-2019 (COVID-19The epidemic and the challenges. International Journal of Antimicrobial Agents, 55(3), 105924. DOI 10.1016/j.ijantimicag.2020.105924. [Google Scholar] [CrossRef]
2. Baba, I. A., Ahmed, I., Al-Mdallal, Q. M., Jarad, F., Yunusa, S. (2022). Numerical and theoretical analysis of an awareness COVID-19 epidemic model via generalized Atangana-Baleanu fractional derivative. Journal of Applied Mathematics and Computational Mechanics, 21(1), 7–18. DOI 10.17512/jamcm.2022.1.01. [Google Scholar] [CrossRef]
3. Bedford, J., Enria, D., Giesecke, J., Heymann, D. L., Ihekweazu, C. et al. (2020). COVID-19: Towards controlling of a pandemic. The Lancet, 395(10229), 1015–1018. DOI 10.1016/S0140-6736(20)30673-5. [Google Scholar] [CrossRef]
4. Memon, Z., Qureshi, S., Memon, B. R. (2021). Assessing the role of quarantine and isolation as control strategies for COVID-19 outbreak: A case study. Chaos, Solitons & Fractals, 144, 110655. DOI 10.1016/j.chaos.2021.110655. [Google Scholar] [CrossRef]
5. Guo, Y. R., Cao, Q. D., Hong, Z. S., Tan, Y. Y., Chen, S. D. et al. (2020). The origin, transmission and clinical therapies on coronavirus disease 2019 (COVID-19) outbreak–an update on the status. Military Medical Research, 7(1), 1–10. DOI 10.1186/s40779-020-00240-0. [Google Scholar] [CrossRef]
6. Lauer, S. A., Grantz, K. H., Bi, Q., Jones, F. K., Zheng, Q. et al. (2020). The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Annals of Internal Medicine, 172(9), 577–582. DOI 10.7326/M20-0504. [Google Scholar] [CrossRef]
7. Liu, J., Liao, X., Qian, S., Yuan, J., Wang, F. et al. (2020). Community transmission of severe acute respiratory syndrome coronavirus 2, Shenzhen, China, 2020. Emerging Infectious Diseases, 26(6), 1320–1323. DOI 10.3201/eid2606.200239. [Google Scholar] [CrossRef]
8. Momoh, A. A., Ibrahim, M. O., Uwanta, I. J., Manga, S. B. (2013). Mathematical model for control of measles epidemiology. International Journal of Pure and Applied Mathematics, 87(5), 707–718. DOI 10.12732/ijpam.v87i5.4. [Google Scholar] [CrossRef]
9. Wu, P., Hao, X., Lau, E. H., Wong, J. Y., Leung, K. S. et al. (2020). Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan, China, as at 22 January 2020. Eurosurveillance, 25(3), 2000044. DOI 10.2807/1560-7917.ES.2020.25.3.2000044. [Google Scholar] [CrossRef]
10. Tang, B., Wang, X., Li, Q., Bragazzi, N. L., Tang, S. et al. (2020). Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. Journal of Clinical Medicine, 9(2), 462. DOI 10.3390/jcm9020462. [Google Scholar] [CrossRef]
11. Peter, O. J., Qureshi, S., Yusuf, A., Al-Shomrani, M., Idowu, A. A. (2021). A new mathematical model of COVID-19 using real data from Pakistan. Results in Physics, 24, 104098. DOI 10.1016/j.rinp.2021.104098. [Google Scholar] [CrossRef]
12. Abdullahi, I., Baba, B. A., Nasidi, B. (2021). Optimal control model for the transmission of novel COVID-19. Computers, Materials, & Continua, 66(3), 3089–3106. DOI 10.32604/cmc.2021.012301. [Google Scholar] [CrossRef]
13. Mahmoudi, M. R., Baleanu, D., Band, S. S., Mosavi, A. (2021). Factor analysis approach to classify COVID-19 datasets in several regions. Results in Physics, 25, 104071. DOI 10.1016/j.rinp.2021.104071. [Google Scholar] [CrossRef]
14. Qureshi, S., Yusuf, A. (2019). Mathematical modeling for the impacts of deforestation on wildlife species using caputo differential operator. Chaos, Solitons & Fractals, 126, 32–40. DOI 10.1016/j.chaos.2019.05.037. [Google Scholar] [CrossRef]
15. Sindhu, T. N., Shafiq, A., Al-Mdallal, Q. M. (2021). On the analysis of number of deaths due to COVID-19 outbreak data using a new class of distributions. Results in Physics, 21, 103747. DOI 10.1016/j.rinp.2020.103747. [Google Scholar] [CrossRef]
16. Khan, M. A., Atangana, A. (2020). Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alexandria Engineering Journal, 59(4), 2379–2389. DOI 10.1016/j.aej.2020.02.033. [Google Scholar] [CrossRef]
17. Shafiq, A., Lone, S. A., Sindhu, T. N., El Khatib, Y., Al-Mdallal, Q. M. et al. (2021). A new modified Kies Fréchet distribution: Applications of mortality rate of COVID-19. Results in Physics, 28, 104638. DOI 10.1016/j.rinp.2021.104638. [Google Scholar] [CrossRef]
18. Thabet, S., Abdo, M. S., Shah, K. (2021). Theoretical and numerical analysis for transmission dynamics of COVID-19 mathematical model involving Caputo-Fabrizio derivative. Advances in Difference Equations, 2021(1), 1–17. DOI 10.1186/s13662-021-03316-w. [Google Scholar] [CrossRef]
19. Abdulwasaa, M. A., Abdo, M. S., Shah, K., Nofal, T. A., Panchal, S. K. et al. (2021). Fractal-fractional mathematical modeling and forecasting of new cases and deaths of COVID-19 epidemic outbreaks in India. Results in Physics, 20, 103702. DOI 10.1016/j.rinp.2020.103702. [Google Scholar] [CrossRef]
20. Redhwan, S. S., Abdo, M. S., Shah, K., Abdeljawad, T., Dawood, S. et al. (2020). Mathematical modeling for the outbreak of the coronavirus (COVID-19) under fractional nonlocal operator. Results in Physics, 19, 103610. DOI 10.1016/j.rinp.2020.103610. [Google Scholar] [CrossRef]
21. Thabet, S. T., Abdo, M. S., Shah, K., Abdeljawad, T. (2020). Study of transmission dynamics of COVID-19 mathematical model under ABC fractional order derivative. Results in Physics, 19, 103507. DOI 10.1016/j.rinp.2020.103507. [Google Scholar] [CrossRef]
22. Sindhu, T. N., Shafiq, A., Al-Mdallal, Q. M. (2021). Exponentiated transformation of gumbel type-II distribution for modeling COVID-19 data. Alexandria Engineering Journal, 60(1), 671–689. DOI 10.1016/j.aej.2020.09.060. [Google Scholar] [CrossRef]
23. Akgül, A., Ahmed, N., Raza, A., Iqbal, Z., Rafiq, M. et al. (2021). New applications related to COVID-19. Results in Physics, 20, 103663. DOI 10.1016/j.rinp.2020.103663. [Google Scholar] [CrossRef]
24. Gao, W., Veeresha, P., Baskonus, H. M., Prakasha, D. G., Kumar, P. (2020). A new study of unreported cases of 2019-nCOV epidemic outbreaks. Chaos, Solitons & Fractals, 138, 109929. DOI 10.1016/j.chaos.2020.109929. [Google Scholar] [CrossRef]
25. Singh, H., Srivastava, H. M., Hammouch, Z., Nisar, K. S. (2021). Numerical simulation and stability analysis for the fractional-order dynamics of COVID-19. Results in Physics, 20, 103722. DOI 10.1016/j.rinp.2020.103722. [Google Scholar] [CrossRef]
26. Alshomrani, A. S., Ullah, M. Z., Baleanu, D. (2021). Caputo SIR model for COVID-19 under optimized fractional order. Advances in Difference Equations, 2021(1), 1–17. DOI 10.1186/s13662-021-03345-5. [Google Scholar] [CrossRef]
27. Habenom, H., Aychluh, M., Suthar, D. L., Al-Mdallal, Q., Purohit, S. D. (2022). Modeling and analysis on the transmission of COVID-19 pandemic in Ethiopia. Alexandria Engineering Journal, 61(7), 5323–5342. DOI 10.1016/j.aej.2021.10.054. [Google Scholar] [CrossRef]
28. Gao, W., Baskonus, H. M., Shi, L. (2020). New investigation of bats-hosts-reservoir-people coronavirus model and application to 2019-nCoV system. Advances in Difference Equations, 2020(1), 1–11. DOI 10.1186/s13662-020-02831-6. [Google Scholar] [CrossRef]
29. Naik, P. A., Yavuz, M., Qureshi, S., Zu, J., Townley, S. (2020). Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. The European Physical Journal Plus, 135(10), 1–42. DOI 10.1140/epjp/s13360-020-00819-5. [Google Scholar] [CrossRef]
30. Srivastava, H. M., Jan, R., Jan, A., Deebani, W., Shutaywi, M. (2021). Fractional-calculus analysis of the transmission dynamics of the dengue infection. Chaos: An Interdisciplinary Journal of Nonlinear Science, 31(5), 053130. DOI 10.1063/5.0050452. [Google Scholar] [CrossRef]
31. Boulaaras, S., Jan, R., Khan, A., Ahsan, M. (2022). Dynamical analysis of the transmission of dengue fever via Caputo-Fabrizio fractional derivative. Chaos, Solitons & Fractals: X, 8, 100072. DOI 10.1016/j.csfx.2022.100072. [Google Scholar] [CrossRef]
32. Baleanu, D., Fernandez, A. (2019). On fractional operators and their classifications. Mathematics, 7(9), 830. DOI 10.3390/math7090830. [Google Scholar] [CrossRef]
33. Gao, W., Veeresha, P., Prakasha, D. G., Baskonus, H. M. (2020). Novel dynamic structures of 2019-nCoV with nonlocal operator via powerful computational technique. Biology, 9(5), 107. DOI 10.3390/biology9050107. [Google Scholar] [CrossRef]
34. Jajarmi, A., Ghanbari, B., Baleanu, D. (2019). A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence. Chaos: An Interdisciplinary Journal of Nonlinear Science, 29(9), 093111. DOI 10.1063/1.5112177. [Google Scholar] [CrossRef]
35. Acay, B., Bas, E., Abdeljawad, T. (2020). Fractional economic models based on market equilibrium in the frame of different type kernels. Chaos, Solitons & Fractals, 130, 109438. DOI 10.1016/j.chaos.2019.109438. [Google Scholar] [CrossRef]
36. Uçar, S., Uçar, E., Özdemir, N., Hammouch, Z. (2019). Mathematical analysis and numerical simulation for a smoking model with Atangana-Baleanu derivative. Chaos, Solitons & Fractals, 118, 300–306. DOI 10.1016/j.chaos.2018.12.003. [Google Scholar] [CrossRef]
37. Khan, M. A., Atangana, A., Alzahrani, E. (2020). The dynamics of COVID-19 with quarantined and isolation. Advances in Difference Equations, 2020(1), 1–22. DOI 10.1186/s13662-020-02882-9. [Google Scholar] [CrossRef]
38. Wrapp, D., Wang, N., Corbett, K. S., Goldsmith, J. A., Hsieh, C. L. et al. (2020). Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science, 367(6483), 1260–1263. DOI 10.1126/science.abb2507. [Google Scholar] [CrossRef]
39. Kumar, P., Erturk, V. S., Nisar, K. S., Jamshed, W., Mohamed, M. S. (2022). Fractional dynamics of 2019-nCOV in Spain at different transmission rate with an idea of optimal control problem formulation. Alexandria Engineering Journal, 61(3), 2204–2219. DOI 10.1016/j.aej.2021.07.005. [Google Scholar] [CrossRef]
40. Arfan, M., Alrabaiah, H., Rahman, M. U., Sun, Y. L., Hashim, A. S. et al. (2021). Investigation of fractal-fractional order model of COVID-19 in Pakistan under Atangana-Baleanu Caputo (ABC) derivative. Results in Physics, 24, 104046. DOI 10.1016/j.rinp.2021.104046. [Google Scholar] [CrossRef]
41. Boudaoui, A., El hadj Moussa, Y., Hammouch, Z., Ullah, S. (2021). A fractional-order model describing the dynamics of the novel coronavirus (COVID-19) with nonsingular kernel. Chaos, Solitons & Fractals, 146, 110859. DOI 10.1016/j.chaos.2021.110859. [Google Scholar] [CrossRef]
42. Zeb, A., Kumar, P., Erturk, V. S., Sitthiwirattham, T. (2022). A new study on two different vaccinated fractional-order COVID-19 models via numerical algorithms. Journal of King Saud University-Science, 34(4), 101914. DOI 10.1016/j.jksus.2022.101914. [Google Scholar] [CrossRef]
43. Alalyani, A., Saber, S. (2022). Stability analysis and numerical simulations of the fractional COVID-19 pandemic model. International Journal of Nonlinear Sciences and Numerical Simulation, 2022, 1–14. DOI 10.1515/ijnsns-2021-0042. [Google Scholar] [CrossRef]
44. Allegretti, S., Bulai, I. M., Marino, R., Menandro, M. A., Parisi, K. (2021). Vaccination effect conjoint to fraction of avoided contacts for a Sars-Cov-2 mathematical model. Mathematical Modelling and Numerical Simulation with Applications, 1(2), 56–66. DOI 10.53391/mmnsa.2021.01.006. [Google Scholar] [CrossRef]
45. Özköse, F., Yavuz, M., Senel, M. T., Habbireeh, R. (2022). Fractional order modelling of omicron SARS-CoV-2 variant containing heart attack effect using real data from the United Kingdom. Chaos, Solitons & Fractals, 157, 111954. DOI 10.1016/j.chaos.2022.111954. [Google Scholar] [CrossRef]
46. Alsakaji, H. J., Rihan, F. A., Hashish, A. (2022). Dynamics of a stochastic epidemic model with vaccination and multiple time-delays for COVID-19 in the UAE. Complexity, 2022. DOI 10.1155/2022/4247800. [Google Scholar] [CrossRef]
47. Rihan, F. A., Alsakaji, H. J. (2021). Dynamics of a stochastic delay differential model for COVID-19 infection with asymptomatic infected and interacting people: Case study in the UAE. Results in Physics, 28, 104658. DOI 10.1016/j.rinp.2021.104658. [Google Scholar] [CrossRef]
48. Pandey, P., Gómez-Aguilar, J. F., Kaabar, M. K., Siri, Z., Abd Allah, A. M. (2022). Mathematical modeling of COVID-19 pandemic in India using Caputo-Fabrizio fractional derivative. Computers in Biology and Medicine, 145, 105518. DOI 10.1016/j.compbiomed.2022.105518. [Google Scholar] [CrossRef]
49. Mahrouf, M., Boukhouima, A., Zine, H., Lotfi, E. M., Torres, D. F. et al. (2021). Modeling and forecasting of COVID-19 spreading by delayed stochastic differential equations. Axioms, 10(1), 18. DOI 10.3390/axioms10010018. [Google Scholar] [CrossRef]
50. Kilbas, A. A., Marichev, O. I., Samko, S. G. (1993). Fractional integrals and derivatives (Theory and applications). Gordon and Breach, Switzerland: Elesvier. [Google Scholar]
51. Podlubny, I., Magin, R. L., Trymorush, I. (2017). Niels Henrik Abel and the birth of fractional calculus. Fractional Calculus and Applied Analysis, 20(5), 1068–1075. DOI 10.1515/fca-2017-0057. [Google Scholar] [CrossRef]
52. Yusuf, A., Acay, B., Mustapha, U. T., Inc, M., Baleanu, D. (2021). Mathematical modeling of pine wilt disease with Caputo fractional operator. Chaos, Solitons & Fractals, 143, 110569. DOI 10.1016/j.chaos.2020.110569. [Google Scholar] [CrossRef]
53. Diekmann, O., Heesterbeek, J. A. P., Metz, J. A. (1990). On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. Journal of Mathematical Biology, 28(4), 365–382. DOI 10.1007/BF00178324. [Google Scholar] [CrossRef]
54. Van den Driessche, P., Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 180(1–2), 29–48. DOI 10.1016/S0025-5564(02)00108-6. [Google Scholar] [CrossRef]
55. Garrappa, R. (2010). On linear stability of predictor-corrector algorithms for fractional differential equations. International Journal of Computer Mathematics, 87(10), 2281–2290. DOI 10.1080/00207160802624331. [Google Scholar] [CrossRef]
56. Amouch, M., Karim, N. (2021). Modeling the dynamic of COVID-19 with different types of transmissions. Chaos, Solitons & Fractals, 150, 111188. DOI 10.1016/j.chaos.2021.111188. [Google Scholar] [CrossRef]
57. Zine, H., Boukhouima, A., Lotfi, E. M., Mahrouf, M., Torres, D. F. et al. (2020). A stochastic time-delayed model for the effectiveness of Moroccan COVID-19 deconfinement strategy. Mathematical Modelling of Natural Phenomena, 15, 50. DOI 10.1051/mmnp/2020040. [Google Scholar] [CrossRef]
58. Kada, D., Labzai, A., Balatif, O., Rachik, M., Labriji, E. H. (2020). Spread of COVID-19 in Morocco discrete mathematical modeling: Optimal control strategies and cost-effectiveness analysis. Journal of Mathematical and Computational Science, 10(5), 2070–2093. [Google Scholar]
59. Musa, S. S., Qureshi, S., Zhao, S., Yusuf, A., Mustapha, U. T. et al. (2021). Mathematical modeling of COVID-19 epidemic with effect of awareness programs. Infectious Disease Modelling, 6, 448–460. DOI 10.1016/j.idm.2021.01.012. [Google Scholar] [CrossRef]
60. Abu-Shady, M., Kaabar, M. K. (2021). A generalized definition of the fractional derivative with applications. Mathematical Problems in Engineering, 2021. DOI 10.1155/2021/9444803. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF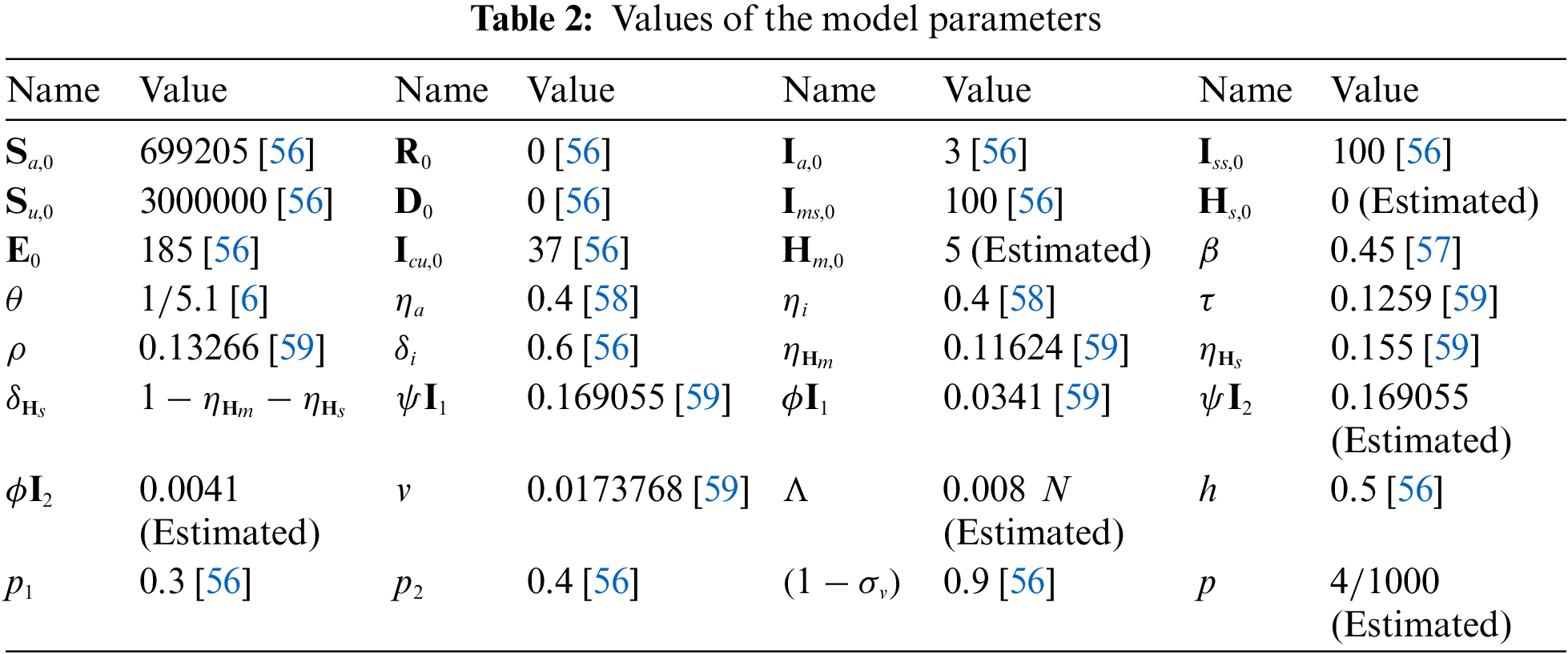
 Downloads
Downloads
 Citation Tools
Citation Tools