 Open Access
Open Access
ARTICLE
Effect of Particle Orientation on Heat Transfer in Arrays of Prolate Particles
1
School of Chemical Engineering and Technology, Xi’an Jiaotong University, Xi’an, China
2
State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an, China
* Corresponding Author: Qiang Zhou. Email:
(This article belongs to the Special Issue: Advanced Computational Models for Decision-Making of Complex Systems in Engineering)
Computer Modeling in Engineering & Sciences 2023, 136(2), 1509-1526. https://doi.org/10.32604/cmes.2023.025308
Received 07 July 2022; Accepted 26 September 2022; Issue published 06 February 2023
Abstract
Direct Numerical Simulations have been carried out to study the forced convection heat transfer of flow through fixed prolate particles for a variety of aspect ratios ar = {5/4, 5/3, 5/1} with Reynolds number (Re) up to 100. Three variations of the solid volume fraction c = {0.1, 0.2, 0.3} with four Hermans orientation factors S = {−0.5, 0, 0.5, 1} are studied. It has been found that changes in S cause prominent variations in the Nusselt number. In general, Nusselt number increases with the decrease of S. For all three aspect ratios, the Nusselt number remains a linear function of S at different c and Re. Therefore, it is concluded that, for heat transfer from prolate muti-particle system, the effects of orientations cannot be ignored. A new correlation for Nusselt number has been developed for arrays of prolate particles using the simulation data as a function of Re, c, S and ar.Graphic Abstract
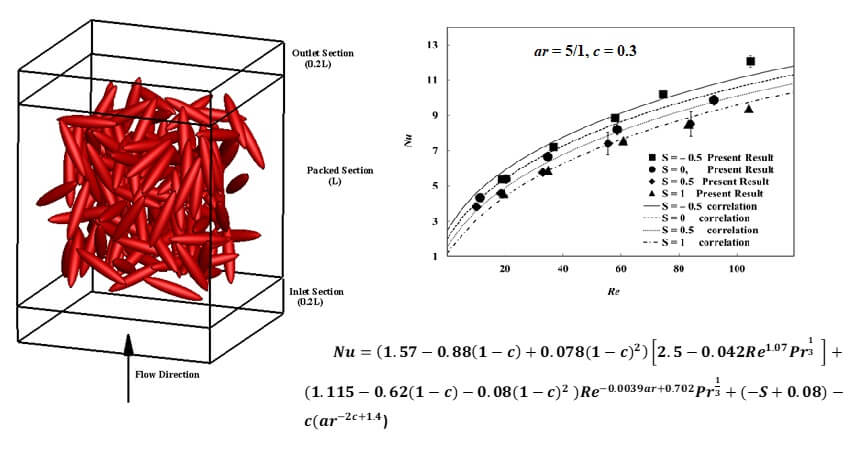
Keywords
Nomenclature
| c | solid volume fraction |
| particle equivalent diameter | |
| U | superficial gas velocities |
| Re | Reynolds number |
| S | Hermans orientation factors |
| distribution functions | |
| relaxation factors | |
| source term in momentum equation | |
| source term in heat equation | |
| fluid thermal conductivity | |
| h | convective heat transfer coefficient |
| Nu | Nusselt number |
| average temperature of slice | |
| volume of slice | |
| number of slices | |
| specific surface area | |
| heat flux from particles to the fluid phase | |
| signed level set function | |
| gas velocity in flow direction | |
| angle | |
| a, b | particle semi major and minor axis |
| ar | aspect ratio |
| n | number of solid particles |
| L | length of cubic computational domain |
| kinematic viscosity | |
| thermal viscosity | |
| Pr | Prandtl number |
Gas-solid flows are defined by the flow of gases through suspended particles of solids. These flows are present in many industrial processes and arise in several natural phenomena as well. These flows are encountered in processes such as drying of food items, particulate pollution control, pneumatic transport, combustion of coal, solid waste ignition, sand blasting, plasma-arc coating, rocket propellant combustion and fluidized bed mixing [1–7]. Gas-solid flows are also found in solar energy transport by graphite suspension flows and in nuclear reactor cooling. The optimal design of the engineering processes and precise interpretation of the natural phenomena that involve such flows require a systematic understanding of the principles of these flows.
Computational fluid dynamics (CFD) plays an essential role in the analysis of the performance of the reactor hardware. To enhance the role of CFD for the estimation of the performance and safe operation of these reactors, various models are used to explore such physical processes. Direct numerical simulations (DNSs) are an important CFD technique that can be used for the prediction of heat transfer between gas and solid phases. Generally, researchers use Nusselt number correlations developed by Gunn [8] and Wakao et al. [9] for spherical particles. In a previous study, DNS combined with the immersed boundary method (IBM) was used to study heat transfer of particulate flows [10]. Temperature field and fluid velocity were computed by solving the improved energy and momentum equations. Huang et al. investigated heat transfer in assemblies of spherical particles using the immersed boundary thermal lattice Boltzmann method [11]. Influences of particle velocity fluctuations were studied in detail. A new technique has been used to solve the dense fluid particle system heat transfer by Deen et al. [12]. Cup mixing average temperature was used during this investigation and a fixed Eulerian grid was utilized in the computational domain. At higher values of superficial velocities, a considerable amount of bed expansion was obtained. In another investigation, DNSs were used to solve the heat transfer problem of bidisperse arrays of spherical particles [13]. Chen et al. [14] used thermal lattice Boltzmann with immersed boundary method to simulate the heat transfer of stationary spherical particles for different values of solid volume fractions and Reynolds number.
Heat transfer of non-spherical particles not only depends on the solid volume fraction and Reynolds number but their orientation may play a significant role in forced convection. In practical applications ellipsoidal particles of different sizes are available. However, most of the particles encountered in practical applications are not spherical in shape, and the particle orientation and shape considerably affect the heat transfer in gas-solid flows. There is a great need to investigate the effect of particle orientation and shape on the heat transfer performance. Ke et al. [15] studied the flow and heat transfer characteristics of scalene single prolate ellipsoidal particles having different aspect ratios (ar). Nusselt number and drag coefficients were calculated and their correlations were presented with Reynolds number range of 25 to 200. Furthermore, they analyzed the effects of orientations of particles on Nusselt number with respect to flow direction. Chen et al. investigated the heat transfer from quadric cubes to the surrounding fluid for Reynolds number range of 1 to 100 using the immersed boundary thermal lattice Boltzmann method [16]. They confirmed the validation of method by performing numerical simulations of heat transfer from single ellipsoidal particles with ar = 2 for two different orientations. It was reported that the Nusselt number of assemblies of spherical particles is smaller as compared to the assemblies of superquadric cubes. Alawadhi [17] computed the forced convection flow of elliptical array with different inclinations by using the finite element method. Five cylinders were placed in a row and their inclination angle was increased from first to the last one. Reynolds number was varied from 125 to 1000 for the simulations and ratio of minor to major axis of the particles was kept as 0.5. He found that the change in inclinations of ellipsoidal particles placed in a row resulted in heat transfer enhancement. In another research work, effect of variation of angles of cubic and ellipsoidal particles with the flow direction was investigated using ANSYS Fluent [18]. Drag and Nusselt number correlations were presented that included an additional term to consider the effect of orientations. For Reynolds number of 200, change in angles of attack from 0 to 90 degrees resulted in a variation of up to 12% for ellipsoidal particle and up to 7% for cubic particle in their Nusselt numbers.
The solid volume fraction and Reynolds numbers are also very important in the non-spherical particles system. He et al. [19] performed the numerical simulations of ellipsoidal particles for a variety of solid volume fractions (0.1 to 0.35) and Reynolds numbers (10 to 200). They utilized the Generalized Incompressible Direct and Large Eddy Simulation of Turbulence (GenIDLEST) based in-house code. They developed a Nusselt number correlation for ellipsoidal particles with ar = 5/2 using the simulation data. Li et al. [20] used DNS to study the effects of orientations of prolate particles on the drag force in creeping flow regime. They found that drag force decreased with the increase of Hermans orientation factor S when flow was parallel with the reference direction. Basit et al. [21] performed the heat transfer studies of prolate particles with ar = 5/2 using the immersed boundary thermal lattice Boltzmann method proposed in [11]. Four different S in the range of [−0.5, 1] were used with three different solid volume fractions, i.e., 0.1, 0.2 and 0.3. The results showed that Nusselt number increased with the decrease of S. It was demonstrated that the impact of orientations on the heat transfer of prolate particulate system was evident. For solid volume fraction of 0.2 with aspect ratio of 5 and Reynolds number of 20, Nusselt number for S = −0.5 was found to be 28% higher than the arrays of particles with S = 1. The literature related to the heat transfer of prolate particles for various shape is very limited. Moreover, the available literature only consider the effect of solid volume fraction on the forced convection heat transfer. There is a great need to explore the effects of variation of orientations on forced convection heat transfer from prolate particle assemblies of various aspect ratios because particles of various sizes are usually used in practical engineering operations [22,23]. Moreover, to the best of the knowledge of the authors, no investigation of the heat transfer problem of flows through arrays of prolate particles for various aspect ratios, solid volume fractions and Hermans orientation factors has been reported in the literature.
Hence, in the present work, DNSs are performed to investigate the heat transfer in gas-solid flows with prolate particles. Flows with particles of three aspect ratios, i.e., ar = {5/4, 5/3, 5/1} at Reynolds numbers of up-to 100 are simulated. For each aspect ratio three different solid volume fractions c = {0.1, 0.2, 0.3} with four Hermans orientation factors S = {–0.5, 0, 0.5, 1} are considered. Three realizations are used for each case and the results are averaged out to reduce the statistical errors. The effect of S, c and ar on the heat transfer phenomenon for the arrays of prolate particles has been formulated in the form of Nusselt number correlation.
The adopted three dimensional immersed boundary thermal lattice Boltzmann method is implemented with
Eqs. (1) and (2) are the basic equations in the Lattice Boltzmann method representing the momentum and energy equation respectively.
2.1 Nusselt Number Calculations
Nusselt number represents the dimensionless temperature gradient at the surface and it provides a measure of the convective heat transfer occurring at the surface. It is defined as:
In Eq. (3), h is the convective heat transfer coefficient, k is the fluid thermal conductivity and D is the particle equivalent diameter. The equivalent diameter is defined by 2(ab2)1/3, where a and b are the lengths of semi major axis and semi minor axis of the prolate particle respectively Reynolds number is obtained by using equivalent diameter and superficial gas velocities (U) from Re = ρUD/μ. In the present research, the Nusselt number is obtained by the creation of slices of unit thickness along the stream-wise direction. Average temperature of a slice is calculated by:
More details of this method can be found in [11].
where Vslice is the volume of slice (L2) and Nslice is the number of slices. The specific surface area is represented by ap which is identified by 6c/D. The Prandtl number is defined by using the expression of
2.2 Generation of Random Arrays with Different Orientations
Random assemblies of prolate particles with different S are generated using the Monte Carlo method [20]. Hermans orientation factor S is normally used in polymer processing to describe the orientations of polymer chains [27]. In a three-dimensional case, where the particles make many different orientations, S proves to be a good parameter to quantify these orientations [28]. Functional form of S is given as:
where φ is the angle amongst semi major axis of the prolate particle and the reference direction. In this work, the reference direction is aligned with the positive z direction. For generation of arrays of prolate, values of S, average angle φ and its deviations need to be specified for a given solid volume fraction. More details about the generation of arrays can be found in the [20]. Range of S has been varied from −0.5 to 1, where S = 0 displays random orientations of particles, S = 1 represents the absolute alignment of particles along the reference direction, whereas S = −0.5 signifies placement of particles normal to the reference direction as shown in Fig. 1. During the generation of assemblies, contact of the particles is not allowed and if such an event occurs, the placement of particle is dismissed at that point and another position is searched for that particle. In a fluidized bed, position of solid particles is arbitrary in nature, therefore, present strategy offers a reasonable representation of the process of placement of particles in the arrays. Aspect ratio and solid volume fractions are defined below:

Figure 1: Prolate arrays ar = 5, c = 0.1 (a) S = −0.5 (b) S = 0 (c) S = 0.5 (d) S = 1
3 Geometry Definition and Code Validation
3.1 Geometry and Boundary Conditions
Domain size of 1.4 L is used in the following simulations where L is the side length of packed cubic unit. Inlet and outlet section of size 0.2 L has been used. An illustrative depiction of the computational domain is presented in Fig. 2. The boundary conditions are the same as used in [21]. Prolate particles are kept at higher temperature of 1 and fluid temperature at the inlet is specified to be 0. Prandtl number is chosen as unity. Gas flows parallel to the positive z direction. The fluid phase stands still at the initial state. It is driven by a constant pressure gradient implemented in the computational domain. Temperature gradient has been set equal to zero at the outlet. The simulations have been performed for low Reynolds number range, i.e., up to 100. Prolate particles with ar = {5/4, 5/3, 5/1} and c = {0.1, 0.2, 0.3} are studied. For each c, arrays with four Hermans orientation factor, i.e., S = {−0.5, 0, 0.5, 1} have been simulated. Three different grid sizes, i.e., d/Δx = 8, 12, 16 are used for each case, where d is the length of the minor axis diameter of the particles. The result for each configuration is obtained by applying Richardson Extrapolation method using the data from the three grids for each case. Final results are averaged from three different configurations for each combination of c, Re and S. Each configuration signifies a realization for the prescribed simulation parameters.

Figure 2: Schematic depiction of computational domain (ar = 5, S = 0, c = 0.2)
In [21], extensive validation of the present IB-LBM code was performed by the authors for multi-particle system with aspect ratio of 5/2 (ar = 2.5, S = 0) and the results were compared with those of He et al. [19]. Detailed heat transfer studies of prolate particles (ar = 2.5) for a variety of c, Re and S were performed using the present code. In the present work, validation of code is further performed for a single prolate particle with ar = 2. The results are compared with the correlation presented by Richter et al. [18] who used ANSYS FLUENT™ V14.0 package for the simulation of a single ellipsoidal particle. The single particle is placed at a 45-degree angle with the flow direction in the computational domain. Nusselt number of the single particle at the dilute limit (c = 0) is obtained by extrapolating the results from five different solid volume fractions ranging from 0.002 to 0.03. This is because it is not possible to perform such simulation in a finite computational domain with zero solid volume fraction. The maximum deviation of the obtained results at c = 0 from the correlation presented by Richter et al. [18] is less than 3% as shown in Fig. 3. The comparison shows a good agreement with the literature results.

Figure 3: The Nusselt number of a single ellipsoidal particle (ar = 2) placed at 45-degree angle with the flow direction
After performing the validation of the computer code, the effects of various parameters on Nusselt number are studied. Based on the simulation data, a correlation for Nusselt number is formulated. Further details on the simulation results and the proposed correlation are presented in the following sub-sections.
4.1 Arrays of Prolate Particles with ar = 5/4
A series of DNSs are performed for prolate particles with aspect ratio of 5/4. Three solid volume fractions are considered for four different values of S. Nusselt number at the start of energy exchange process has a higher value due to large temperature gradient, however, it approaches a steady state value after some time as shown in Fig. 4.

Figure 4: Average Nusselt number with non-dimensional time (
Particles, placed with their major axes normal to the flow direction (S = −0.5), are simulated for three solid volume fractions and the results are plotted in Fig. 5a. The data points in the figure have been obtained from the DNS whereas the curved lines have been plotted from the correlation developed from the simulation data, which is presented in Eq. (8). This graph shows that Nusselt number increases with the solid volume fraction and Reynolds number. The heat transfer from an array of randomly oriented prolate particles (i.e., S = 0) is studied and the results are shown in Fig. 5b.
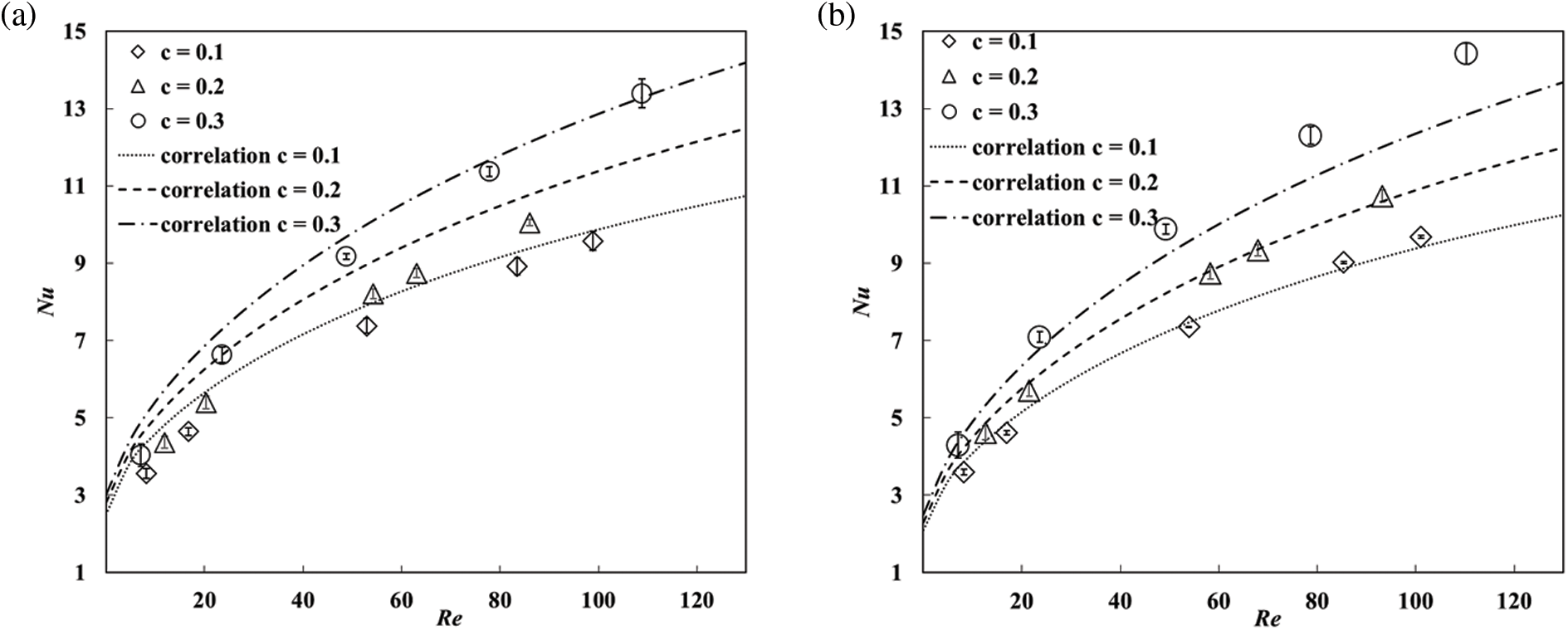

Figure 5: Nusselt number of prolate particles with ar = 5/4 for different Reynolds numbers, solid volume fractions and Hermans orientation factors. Flow direction is parallel to reference direction. Error bars denote standard deviation in Nusselt number found from three different samples of configurations. Curves are obtained from the correlation given in Eq. (8). (a) S = −0.5, (b) S = 0 (c) S = 0.5, (d) S = 1
To further explore the effects of the orientations on Nusselt number, assemblies with S = 0.5, and S = 1 are also simulated and the results are shown in Figs. 5c and 5d, respectively. By closely observing these graphs, it can be concluded that forced convection strength is the lowest for S = 1 when compared with other orientations. This is because the particles of this orientation have smaller projected cross-section area along the flow direction. The fluid phase could flow smoothly along the particle surface with less velocity fluctuations, which results in smaller Nusselt number. Generally, the arrays containing the particles which are placed with their major axes perpendicular to the flow direction display higher values of Nusselt number. It should be mentioned that Li et al. [20] found that the drag force experienced in arrays decreased as S increased. This could also be used to explain the decreasing trend of Nusselt number with the increase of S considering that drag reduction generally causes reduced heat transfer between the fluid and particle phases. At 0.1 value of solid volume fractions S = −0.5 shows 16% increase in Nusselt number when compared with S = 1 for Reynolds number of 80. Moreover, it is also observed that at the lower values of Reynolds numbers the effect of solid volume fraction is small. For random orientation with S = 0 at Reynolds number of 80 the increase in Nusselt number is 15% for solid volume fractions variation from 0.1 to 0.2.
Similarly, DNSs of flow past arrays of prolate particles with ar = 5/3 and 5/1 are performed in this work. The decreasing trend of Nusselt number with the increase of S becomes more evident. Nusselt number of prolate particles with ar = 5/3 and 5/1 for different Reynolds numbers, solid volume fractions and Hermans orientation factors are shown in Figs. 6 and 7, respectively. Symbols are obtained from the DNSs and the curved lines are obtained from the correlation given in Eq. (8). By using the simulation data of all the aspect ratios with different orientation, Nusselt number correlation has been developed which is given below:
where c is the solid volume fraction, ar is the aspect ratio of particle, S is the Hermans orientation factor, Re is the Reynolds number. The Nusselt number increases with the Reynolds number for all the four values of Hermans orientation factor as it is the main driving force in the forced convection process. Moreover, at a fixed Reynolds number Nusselt number rises with the increase in solid volume fraction. In the case of random orientation for aspect ratio of 5/1 this increment at Reynolds number of 80 is 14% for the increase of solid volume fraction from 0.1 to 0.2 (Fig. 7b). Furthermore, at Reynolds number of 20 for aspect ratio of 5/1 and solid volume fraction of 0.1 arrays with S = −0.5 shows 30% more Nu when compared with S = 1 arrays (Fig. 7).

Figure 6: Nusselt number of prolate particles with ar = 5/3 for different Reynolds numbers, solid volume fractions and Hermans orientation factors. Flow is parallel to the reference direction. Error bars denote standard deviation in Nusselt number found from three different samples of configurations. Curves are obtained from the correlation given in Eq. (8). (a) S = −0.5, (b) S = 0 (c) S = 0.5, (d) S = 1


Figure 7: Nusselt number of prolate particles with ar = 5/1 for different Reynolds numbers, solid volume fractions and Hermans orientation factors. Flow is parallel to the reference direction. Error bars denote the standard deviation in Nusselt number found from three different samples of configurations. Curves are obtained from the correlation given in Eq. (8). (a) S = −0.5, (b) S = 0 (c) S = 0.5, (d) S = 1
The Nusselt number for the single particle depends only on the two parameters which are the Reynolds number and Prandtl numbers. However, in the case of many particles the effects of c are also very important. In the present research the effects of ar and S in addition with the variation of Re and c have been studied on the Nusselt number. Therefore, the variations of new terms have been accommodated by adding extra terms which incorporate their effects on Nu as mentioned in Eq. (8). Power of the Prandtl number in the correlation is set to be equal to 1/3 which comes theoretically from the boundary layer theory. All the other coefficients are set in such a way that it fits well with the simulations data. Selection of the term –S + 0.08 in Eq. (8) has been made on the basis that the maximum values of Nusselt number exist at S = −0.5 and minimum values of Nusselt number occur at S = 1. Also, the trend of the variation of the Nusselt number with the Hermans orientation factor outcome with a linear variation, therefore, the power of S has been selected to be unity. The trend of linearity of Nu with S remains obvious for all the aspect ratios of particles. Hence in the case of non-spherical particles, the Nusselt number depends on the Hermans orientation factor which has been discussed in more detail in the next section.
5 Impact of Hermans Orientation Factors
The Herman orientation factor is an important factor in forced convection heat transfer of prolate particle. Therefore, for a clearer illustration of the varying trend of Nusselt number with S, the results from different S at the same solid volume fraction of 0.3 are shown in Figs. 8 and 9 for ar = 5/3 and 5/1, respectively. It can be seen that, at ar = 5/3, when Re is around 100, the Nusselt number decreases approximately 12% as S increases from −0.5 to 1. While at ar = 5/1, the decreasing trend is more significant and the decrease becomes 14%. Figs. 8 and 9 show that dependence of the Nusselt number on the Hermans orientation factor is prominent for both aspect ratios.

Figure 8: Effect of Hermans orientation factor on Nusselt number for ar = 5/3, c = 0.3. The line is depicted by Eq. (8)
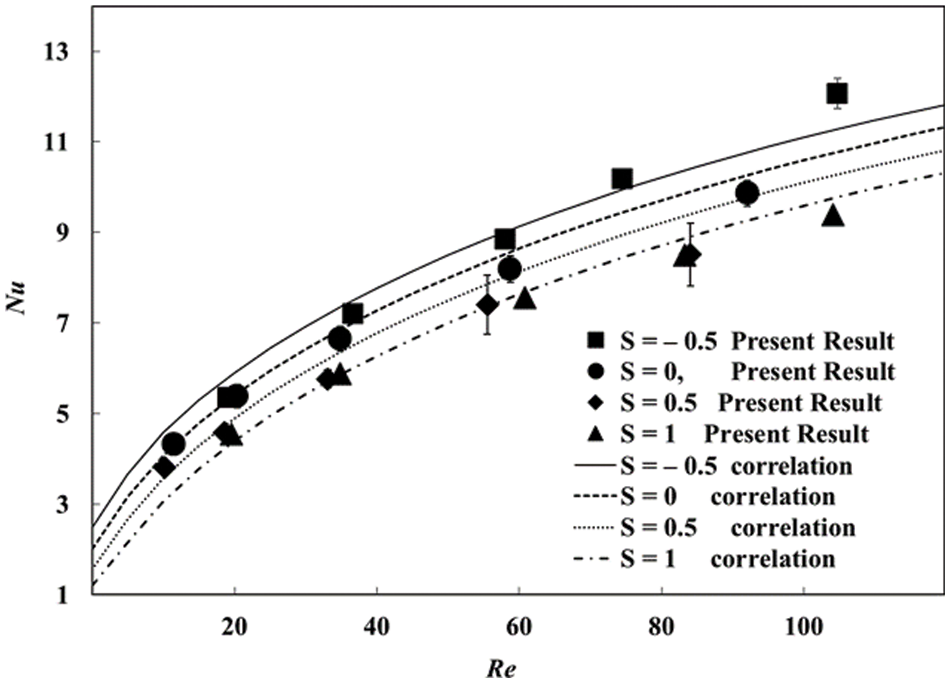
Figure 9: Effect of Hermans orientation factors for ar = 5/1, c = 0.3, correlation given in Eq. (8)
The impact of Herman’s orientation factor is pronounced for a range of aspect ratios for different values of solid volume fraction and Reynolds number. All these effects have been incorporated in Eq. (8) in previous section. The correlation developed in Eq. (8) has been plotted in Fig. 10 with the all simulations data. It can be observed that the deviation of the correlation with simulation values is less than 13% for majority of the data points with some of the data points having deviation of 20%. The values of different variables are ar = {5/4, 5/3, 5/1}, S = {–0.5, 0, 0.5, 1}, c = {0.1, 0.2, 0.3}. The selection of different coefficients in Eq. (8) ensures that the maximum deviation of correlation results the simulation data remains less than 13% for majority of the data points [29].

Figure 10: Comparison between Nusselt numbers of the simulations and correlation in Eq. (8)
The correlation presented in Eq. (8) is a modified form of the correlation put forth by the authors in a previous work [21]. The presented correlation has been improved by including the effect of aspect ratios. The correlation presented in [21] was valid only for an aspect ratio of 5/2, but Eq. (8) has been formulated based on the aspect ratios of {5/4, 5/3, 5/1}. Therefore, this correlation can predict the Nusselt numbers from arrays of prolate particles with aspect ratios in this range. A comparison of the data of [21] for an aspect ratio of 5/2 with the new correlation (Eq. (8)) is plotted in Fig. 11. Maximum deviation of the results of present correlation with the data of [21] remains within 10%. Therefore, it can be concluded that the new correlation is applicable for a range of aspect ratios of multi-particle systems. Moreover, it is equally valid for a range of Hermans orientation factors, solid volume fraction and Reynolds number. Non-spherical particulate systems are important to explore due to their applicability in the industry. Therefore, the present research will provide a new road map in the heat transfer process.

Figure 11: Comparison between the simulated Nusselt number of [21] and obtained from the correlation in Eq. (8) with aspect ratio of 5/2
From the correlation presented in Eq. (8), the variation of Nusselt number with Hermans orientation factors for two different values of Reynolds number = 20, 80 is presented for different aspect ratios in Fig. 12. The arrays oriented perpendicular to the flow direction (S = −0.5) show higher values of Nusselt number as compared with other arrays. From these graphs, it can be concluded that prolate particles with aspect ratio of 5/4 and 5/3 show linear variation with S for both Reynolds number of 20 and 80. Prolate arrays having an aspect ratio of 5/4 with c = 0.2, Reynolds number of 80 for S = −0.5 result in Nusselt number enhancement of 5%, 9% and 14% over S = 0, S = 0.5 and S = 1, respectively. For the arrays with S = −0.5 for an aspect ratio of 5/3, c = 0.2 and Reynolds number of 80 show 5%, 10% and 14% increase in forced convection over S = 0, S = 0.5 and S = 1, respectively. Prolate particles with larger aspect ratios are like needle shape ellipsoids which behaves as the bluff and slender bodies for S = −0.5 and S = 1, respectively [30,31]. Needle shaped arrays with ar = 5/1, c = 0.2 and Reynolds number of 80 for S = −0.5 result in 6%, 11% and 17% enhancement in heat transfer over S = 0, S = 0.5 and S = 1, respectively. With the increase of aspect ratio, the particles transform into more needle like shapes that are more susceptible to the effects of variations in S. Furthermore, it can be concluded that the Nusselt number depends on the Hermans Orientation factors and effects of particle orientations on heat transfer from arrays of prolate particles cannot be ignored even for smaller aspect ratios. The maximum percent increase in Nusselt number caused by S can be calculated using Eq. (9) which is given below:
where


Figure 12: Nusselt number vs. Hermans orientation factor first row ar = 5/4, second row ar = 5/3, third row ar = 5/1 (a) Re = 20 (b) Re = 80
Fig. 13 presents the percentage increase in Nusselt number calculated from Eq. (9). This graph shows that for an aspect ratio of 5, Nusselt number enhancement of 13 to 46 percent is obtained for three different solid volume fractions due to the variation of S. With the increase of Reynolds number, the percent increase in Nusselt number decreases for all values of the solid volume fraction.

Figure 13: Nusselt number enhancement caused by S for various c with ar = 5
Heat transfer from prolate particles for three different aspect ratios, i.e., 5/4, 5/3 and 5/1 has been simulated using the immersed boundary thermal lattice Boltzmann method. Arrays of particles have been created using the Monte Carlo method for three different solid volume fractions i.e., {0.1, 0.2, 0.3} and four different values of Hermans orientation factors, i.e., {−0.5, 0, 0.5, 1}. It is found that the Nusselt number increases with the rise of the solid volume fraction and Reynolds number. A more important finding is that, even for smaller aspect ratios, changes in S cause a significant variation in the Nusselt number. For prolate particles with various aspect ratios, the Nusselt number increases linearly with the decrease of S. Particularly, the Nusselt number enhancement vary between 46% to 13% for the solid volume fractions from 0.1 to 0.3 for ar = 5. Therefore, the effect of particle orientation should be considered in simulations of practical fluid-particle flows with prolate particles. The developed model of the present research can be used in the Computational Fluid Dynamic–Discrete Element Method (CFD-DEM) for the heat transfer analysis of the prolate particles. This work only performs simulations for prolate particles. The investigation of heat transfer properties of flows past arrays of other non-spherical particles is left as future work.
Funding Statement: This computation was supported by the HPC Platform of Xi’an Jiaotong University. We are grateful for the financial support by the Natural Science Foundation of China (21978228, 22078255). We are also grateful for the financial support by Shaanxi Creative Talents Promotion Plan-Technological Innovation Team (2019TD-039), the Fundamental Research Funds for the Central Universities (Creative Team Plan No. cxtd2017004 in Xi’an Jiaotong University) and the China Scholarship Council (CSC, 2017GXZ021009).
Conflicts of Interest: The authors declare that they have no known conflicts of interest or personal relationships that could have appeared to influence the work reported in this paper.
References
1. Panahi, A., Levendis, Y. A., Vorobiev, N., Schiemann, M. (2017). Direct observations on the combustion characteristics of miscanthus and beechwood biomass including fusion and spherodization. Fuel Processing Technology, 166, 41–49. DOI 10.1016/j.fuproc.2017.05.029. [Google Scholar] [CrossRef]
2. Klinzing, G. E. (2016). Novel, unusual and new videos and pictures in pneumatic conveying. Powder Technology, 296, 53–58. DOI 10.1016/j.powtec.2015.07.021. [Google Scholar] [CrossRef]
3. Kuang, S., Zhou, M., Yu, A. (2020). CFD-DEM modelling and simulation of pneumatic conveying: A review. Powder Technology, 365, 186–207. DOI 10.1016/j.powtec.2019.02.011. [Google Scholar] [CrossRef]
4. He, J., Zhang, L., Yao, Z., Che, H., Gong, S. et al. (2020). Source apportionment of particulate matter based on numerical simulation during a severe pollution period in Tangshan, North China. Environmental Pollution, 266, 115133–115145. DOI 10.1016/j.envpol.2020.115133. [Google Scholar] [CrossRef]
5. Debiagi, P., Nicolai, H., Han, W., Janicka, J., Hasse, C. (2020). Machine learning for predictive coal combustion CFD simulations—from detailed kinetics to HDMR reduced-order models. Fuel, 274, 117720–117731. DOI 10.1016/j.fuel.2020.117720. [Google Scholar] [CrossRef]
6. Azmir, J., Hou, Q., Yu, A. (2019). CFD-DEM simulation of drying of food grains with particle shrinkage. Powder Technology, 792–802. DOI 10.1016/j.powtec.2018.11.097. [Google Scholar] [CrossRef]
7. Salehi, M. S., Askarishahi, M., Radl, S. (2020). Quantification of solid mixing in bubbling fluidized beds via Two-fluid model simulations. Industrial and Engineering Chemistry Research, 59, 10606–10621. DOI 10.1021/acs.iecr.9b06343. [Google Scholar] [CrossRef]
8. Gunn, D. J. (1978). Transfer of heat or mass to particles in fixed and fluidised beds. International Journal of Heat and Mass Transfer, 21, 467–476. DOI 10.1016/0017-9310(78)90080-7. [Google Scholar] [CrossRef]
9. Wakao, N., Kaguei, S., Funazkri, T. (1979). Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds. correlation of Nusselt numbers. Chemical Engineering Science, 34, 325–336. DOI 10.1016/0009-2509(79)85064-2. [Google Scholar] [CrossRef]
10. Feng, Z. G., Musong, S. G. (2014). Direct numerical simulation of heat and mass transfer of spheres in a fluidized bed. Powder Technology, 262, 62–70. DOI 10.1016/j.powtec.2014.04.019. [Google Scholar] [CrossRef]
11. Huang, Z., Zhang, C., Jiang, M., Wang, H., Zhou, Q. (2019). Effects of particle velocity fluctuations on inter-phase heat transfer in gas-solid flows. Chemical Engineering Science, 206, 375–386. DOI 10.1016/j.ces.2019.05.047. [Google Scholar] [CrossRef]
12. Deen, N. G., Kriebitzsch, S. H. L., van der Hoef, M. A., Kuipers, J. A. M. (2012). Direct numerical simulation of flow and heat transfer in dense fluid-particle systems. Chemical Engineering Science, 81, 329–344. DOI 10.1016/j.ces.2012.06.055. [Google Scholar] [CrossRef]
13. Tavassoli, H., Peters, E. A. J. F., Kuipers, J. A. M. (2017). Direct numerical simulation of non-isothermal flow through dense bidisperse random arrays of spheres. Powder Technology, 314, 291–298. DOI 10.1016/j.powtec.2016.09.088. [Google Scholar] [CrossRef]
14. Chen, Y., Müller, C. R. (2019). Lattice Boltzmann simulation of gas-solid heat transfer in random assemblies of spheres: The effect of solids volume fraction on the average Nusselt number for Re ≤ 100. Chemical Engineering Journal, 361, 1392–1399. DOI 10.1016/j.cej.2018.10.182. [Google Scholar] [CrossRef]
15. Ke, C., Shu, S., Zhang, H., Yuan, H. (2018). Drag coefficient and averaged Nusselt number of a scalene prolate ellipsoid. Applied Mathematical Modelling, 64, 556–571. DOI 10.1016/j.apm.2018.07.055. [Google Scholar] [CrossRef]
16. Chen, Y., Müller, C. R. (2020). Gas-solid heat transfer in assemblies of cubes for ReV ≤ 100. Chemical Engineering Science, 216, 115478–115486. DOI 10.1016/j.ces.2020.115478. [Google Scholar] [CrossRef]
17. Alawadhi, E. M. (2010). Laminar forced convection flow past an in-line elliptical cylinder array with inclination. Journal of Heat Transfer, 132, 1–10. DOI 10.1115/1.4000061. [Google Scholar] [CrossRef]
18. Richter, A., Nikrityuk, P. A. (2013). New correlations for heat and fluid flow past ellipsoidal and cubic particles at different angles of attack. Powder Technology, 249, 463–474. DOI 10.1016/j.powtec.2013.08.044. [Google Scholar] [CrossRef]
19. He, L., Tafti, D. K. (2017). Heat transfer in an assembly of ellipsoidal particles at low to moderate reynolds numbers. International Journal of Heat and Mass Transfer, 114, 324–336. DOI 10.1016/j.ijheatmasstransfer.2017.06.068. [Google Scholar] [CrossRef]
20. Li, X., Jiang, M., Huang, Z., Zhou, Q. (2019). Effect of particle orientation on the drag force in random arrays of prolate ellipsoids in low-reynolds-number flows. American Institute of Chemical Engineers Journals, 65, 1–11. DOI 10.1002/aic.16621. [Google Scholar] [CrossRef]
21. Basit, R., Li, X., Huang, Z., Zhou, Q. (2020). Heat transfer studies of arrays of prolate particles in Gas-solid flows. Mathematical Problems in Engineering, 2020, 1–12. DOI 10.1155/2020/6639172. [Google Scholar] [CrossRef]
22. Gubba, S. R., Ma, L., Pourkashanian, M., Williams, A. (2011). Influence of particle shape and internal thermal gradients of biomass particles on pulverised coal/biomass co-fired flames. Fuel Processing Technology, 92, 2185–2195. DOI 10.1016/j.fuproc.2011.07.003. [Google Scholar] [CrossRef]
23. Sami, M., Annamalai, K., Wooldridge, M. (2001). Co-firing of coal and biomass fuel blends. Progress in Energy and Combustion Science, 27, 171–214. DOI 10.1016/S0360-1285(00)00020-4. [Google Scholar] [CrossRef]
24. Qiang, Z., Fan, L. S. (2015). Direct numerical simulation of moderate-reynolds-number flow past arrays of rotating spheres. Physics of Fluids, 27, 396–423. [Google Scholar]
25. Qiang, Z., Fan, L. S. (2014). A second-order accurate immersed boundary-lattice Boltzmann method for particle-laden flows. Journal of Computational Physics, 268, 269–301. DOI 10.1016/j.jcp.2014.02.038. [Google Scholar] [CrossRef]
26. Seta, T. (2013). Implicit temperature-correction-based immersed-boundary thermal lattice Boltzmann method for the simulation of natural convection. Physical Review E, 87(6), 063304. DOI 10.1103/PhysRevE.87.063304. [Google Scholar] [CrossRef]
27. White, J. L., Spruiell, J. E. (1983). The specification of orientation and its development in polymer processing. Polymer Engineering and Science, 23, 247–256. DOI 10.1002/(ISSN)1548-2634. [Google Scholar] [CrossRef]
28. Li, X., Jiang, M., Huang, Z., Zhou, Q. (2020). Effect of particle orientation on the drag force in random arrays of oblate ellipsoids in low-reynolds-number flows. AIChE Journal, 67, 1, e17040. 1–12. DOI 10.1002/aic.17040. [Google Scholar] [CrossRef]
29. Sparrow, E. M., Abraham, J. P., Tong, J. C. K. (2004). Archival correlations for average heat transfer coefficients for non-circular and circular cylinders and for spheres in cross-flow. International Journal of Heat and Mass Transfer, 47, 5285–5296. DOI 10.1016/j.ijheatmasstransfer.2004.06.024. [Google Scholar] [CrossRef]
30. Epstein, N., Masliyah, J. H. (1972). Creeping flow through clusters of spheroids and elliptical cylinders. Chemical Engineering Journal, 3, 169–175. DOI 10.1016/0300-9467(72)85019-6. [Google Scholar] [CrossRef]
31. Fröhlich, K., Meinke, M., Schröder, W. (2020). Correlations for inclined prolates based on highly resolved simulations. Journal of Fluid Mechanics, 901, 1–34. DOI 10.1017/jfm.2020.482. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools