 Open Access
Open Access
ARTICLE
Aggregation Operators for Decision Making Based on q-Rung Orthopair Fuzzy Hypersoft Sets: An Application in Real Estate Project
1
Department of Mathematics and Statistics, Hazara University Mansehra, 21120, Pakistan
2
Department of Mathematics, Faculty of Arts and Sciences, Yildiz Technical University, Esenler, Istanbul, 34210, Turkey
3
Faculty of Organizational Sciences, University of Belgrade, Belgrade, 11000, Serbia
4
Department of Computer Science and Information Engineering, National University of Kaohsiung, Kaohsiung, 804, Taiwan
5
Department of Computer Science and Engineering, National Sun Yat-sen University, Kaohsiung, 804, Taiwan
* Corresponding Author: Hafiz Abdul Wahab. Email:
(This article belongs to the Special Issue: Advanced Computational Models for Decision-Making of Complex Systems in Engineering)
Computer Modeling in Engineering & Sciences 2023, 136(3), 3141-3156. https://doi.org/10.32604/cmes.2023.026169
Received 20 August 2022; Accepted 01 November 2022; Issue published 09 March 2023
Abstract
In this paper, a decision-making problem with a q-rung orthopair fuzzy hypersoft environment is developed, and two operators of ordered weighted average and induced ordered weighted average are developed. Several fundamental features are also derived. The induced ordered weighted average operator is essential in a q-ROFH environment as the induced ordered aggregation operators are special cases of the existing aggregation operators that already exist in q-ROFH environments. The main function of these operators is to help decision-makers gain a complete understanding of uncertain facts. The proposed aggregation operator is applied to a decision-making problem, with the aim of selecting the most promising real estate project for investment.Graphic Abstract
Keywords
Decision making [1] is a crucial aspect of our daily lives. Due to the complexity and subjectivity of complex alternatives, decision-makers are frequently confronted with a considerable measure of ambiguity in decision-making problems. To address these problems, Zadeh [2] developed fuzzy set theory. Each element of such set is assigned a membership value, between 0 and 1. The fuzzy set theory has a significant impact on the decision-making process. The fuzzy set theory has numerous applications in numerous domains of engineering, humanities, health, and physical sciences. In recent years, fuzzy set theory has also been utilized in the fields of energy, medicine, materials, economics, and nearly every other scientific discipline. There must be uncertainty if the decision-makers do not have sufficient knowledge to deal with the data necessary to express their preference for the object. Experts mostly consider membership and non-membership values in the decision-making process that the fuzzy set cannot handle. Using the framework of fuzzy multisets, Du et al. [3] developed a multicriteria group decision-making method in 2021, which accounts for varying degrees of risk associated with each criterion.
To deal with this type of circumstance, Atanassov [4,5] proposed intuitionistic fuzzy sets, whose primary components are intuitionistic fuzzy numbers (IFN). Intuitionistic fuzzy numbers are defined by a membership function and a non-membership function, with the condition that the sum of the membership and non-membership grades is less than or equal to one. When the sum is greater than 1, the intuitionistic fuzzy sets do not work under specific conditions. Several operations on intuitionistic fuzzy sets were developed by De et al. [6,7] and incorporated into Sanchez’s method for medical diagnosis. The distance between intuitionistic fuzzy sets was discussed by Szmidt et al. [8]. Using intuitionistic fuzzy sets as a theme, Gulzar et al. [9] introduced the t-intuitionistic fuzzy subgroup with basic algebraic properties and complex intuitionistic fuzzy sets in group theory and its applications. In some instances, when the sum of the degrees of MM and NMM is greater than 1, their sum of squares may be less than or equal to 1. Intuitionistic fuzzy sets fail in this situation.
To address these problems, Yager [10] proposed a novel concept known as the Pythagorean fuzzy set, a generalization of the intuitionistic fuzzy sets. The quadratic sum of membership and non-membership is less than or equal to 1, distinguishing it from other entities. Intuitionistic fuzzy sets and Pythagorean fuzzy sets are incredibly valuable for characterising fuzzy data. It is obvious that the Pythagorean fuzzy set can represent more decision-making information and is more inclusive than the intuitionistic fuzzy set. However, the Pythagorean fuzzy set frequently fails when the decision-maker is able to specify the degree of the membership and non-membership in a particular case where their sum is greater than 1. Some findings for Pythagorean fuzzy sets were developed in 2015 [11]. Pythagorean fuzzy sets, as well as a more refined approach to linguistic, Garg [12] utilized Pythagorean fuzzy sets for MCDM problems.
Yager [13] came up with q-rung orthopair fuzzy sets (q-ROFS), the key feature of which is that the sum of the
In order to address the issue of making group decisions based on several criteria, Zulqarnain et al. [15] developed certain aggregation operators inside the framework of the Interval-Valued Pythagorean fuzzy soft set. After transforming the function F into a multi-valued function, Smarandache [16] introduced the hypersoft set. Hypersoft sets are a fundamental mathematical tool for dealing with ambiguity and uncertainty in problem-based decision-making. Zulqarnain et al. [17,18] developed the Pythagorean fuzzy hypersoft sets, along with fundamental operations and techniques. By combining these concepts, Khan et al. [19] constructed a new structure called q-rung orthopair fuzzy hypersoft sets (q-ROFHSs). In q-ROFHSs, the multi-parameter membership and non-membership grades are limited to the
It is crucial to understand the aggregation operators in the q-rung orthopair fuzzy environment and other types of fuzzy sets for tackling problems involving decision-making. In order to solve the decision-making techniques, the induced intuitionistic fuzzy ordered weighted geometric (I-IFOWG) and induced interval-valued intuitionistic fuzzy ordered weighted geometric (I-IIFOWG) operators were developed by Wei [20]. The induced generalised intuitionistic fuzzy ordered weighted averaging (I-GIFOWA) and induced generalised interval-valued intuitionistic fuzzy ordered weighted averaging (I-GIIFOWA) operators were introduced by Xu et al. [21]. For the sake of better decision-making, Zulqarnain et al. [22] also explored a variety of aggregation operators in a Pythagorean fuzzy hypersoft environment. Basic aggregation operators, such as the weighted average and weighted geometric operators were designed by Liu et al. [23], and they were applied in a scenario based on q-rung orthopair fuzzy information. Several fundamental operations and exponential aggregation operators were developed by Peng et al. [24] for the q-rung orthopair fuzzy set. Two aggregation operators the complex q-rung orthopair fuzzy weighted average (Cq-ROFWA) and the complex q-rung orthopair fuzzy weighted geometric (Cq-ROFWG) were introduced by Liu et al. [25]. For a complex q-rung orthopair fuzzy (Cq-ROF) environment, Garg et al. [26] developed power aggregation operations. The q-rung orthopair fuzzy hypersoft weighted average (q-ROFHWA) and q-rung orthopair fuzzy hypersoft weighted geometric (q-ROFHWG) aggregation operators were developed by Khan et al. [27] for use in decision-making problems.
Due to the inadequacies of such mathematical modelling problems, we proposed q-ROFHS baesd mathematical model of such daily life problems in decision-making. For these mathematical models in the q-ROFH context, some aggregation operators and decision-making approaches are required. Therefore, we developed ordered weighted average and induced ordered weighted average aggregation operators in the q-ROFH environment.
Here are some of the key aspects of this research:
• The q-ROFHS process expert data with multi-sub-attributes of uncertainty in order to make decisions.
• Important aggregation operators in the decision-making process include ordered weighted average and induced ordered weighted average.
• Using basic operational laws, properties of the ordered weighted average and induced ordered weighted average aggregation operator.
• A novel decision-making technique was presented by using the proposed aggregation operators.
• Research is conducted within a real company to determine the efficacy and viability of the proposed method. The interpretations demonstrate that the predefined model is more practical and reliable for understanding the facts.
The remaining study of this article is organized as follows. In Section 2, briefly some basic materials related to the proposed structure are introduced. Section 3 consists of ordered weighted average and induced ordered weighted average operators with properties. In Section 4, the algorithm of the proposed structure is presented based on aggregation operators. A real-life application is also presented in this section. Section 5 describes the comparative analysis of the proposed structure with existing structures. Section 6 presents the conclusion and future work.
In this section, we compile some basic data that will be utilised to construct the structure of the article.
Definition 2.1 (16). The pair
Definition 2.2 (19). Let
where
(a)
(b)
(c) A is a q-rung orthopair fuzzy over Y with
(d)
Here
Definition 2.3 (19). The score function of the q-ROFHNs is defined as
3 Ordered and Induced Ordered Weighted Average Aggregation Operators
In this section, we use the concept of ordered weighted averaging operator and develop the q-rung orthopair fuzzy hypersoft ordered weighted averaging operator (q-ROFHOWA) and the induced-q-rung orthopair fuzzy hypersoft ordered weighted averaging operator (I-q-ROFHOWA).
Definition 3.1. An ordered weighted averaging q-rung orthopair fuzzy hypersoft (q-ROFHOWA) operator is defined as:
where
Theorem 3.1. Let
Proof. The q-ROFHOWA operator can be proved using the principle of mathematical induction as follows. For
For
So, Eq. (2) is true for all
Now we prove the equation for
So, it is valid for
Remark 3.2. If the value of q is fixed, which is
Remark 3.3. If the value of q is fixed, which is
Remark 3.4. If there are single parameters, which is
Remark 3.5. From the above remarks, it is clear that IFHOWA, PFHOWA and q-ROFSOWA operators are the special cases of the proposed q-ROFHOWA operator.
The I-q-ROFHSOWA operator is idempotent, bounded and monotonic. These can be proved by the following theorem:
(Idempotency) Let
Proof. As we know,
(Boundedness) Let
Proof. Let
so
As
Let
If
If
If
So by Eqs. (14) and (15), we get
Definition 3.2. An induced q-rung orthopair fuzzy hypersoft ordered weighted averaging (I-q-ROFHSOWA) operator is defined as:
where
Theorem 3.6. Let
where
Proof. The I-q-ROFHOWA operator can be proved using the principle of mathematical induction as follows. For
For
So, Eq. (2) is true for
Now we prove the equation for
So, it is valid for
Example 3.7. Let Y be the set of decision makers to decide the best laptop given as
The I-q-ROFHSOWA operator is idempotent, bounded and monotonic. These properties can be proved by the following theorems:
(Idempotency) Let
where
i. Let
(Boundedness) Let
(Monotonicity) Let
4 Decision Making with q-ROFHOWA I-q-ROFHOWA Operator
Here we will analyze the applicability of the q-ROFHOWA and I-q-ROFHOWA operators and show their fundamental aspects. As mentioned earlier, the q-ROFHOWA operator provides a parameterized family of aggregation functions, but the I-q-ROFHOWA operator has the fundamental aspect of reordering the arguments to be aggregated, based on the order inducing variable. Also, the inducing order determines the generation of q-ROF measures. The following part provides an illustration of the above-mentioned innovative approaches. We analyze a group decision-making problem where an ordinary person studies the real-estate and decides which real estate developer’s project is the best and worth investing. Also, they want to know about the soundness and reliability of real-estate developers. So, in this case, we want to reveal some of the attributes of the real estate before investing in a project. We choose four agents (alternatives) of different companies of real estate, which are represented as follows:
1. Agent 1
2. Agent 2
3. Agent 3
4. Agent 4
After careful review of the information, the group of experts establishes the following information about investment in a real estate project. The following are some attributes of real estate from different companies agents:
U = {Ability to deliver, Property location,Valuation of the property}
We also consider their respective attributes, i.e.,
A committee of decision makers has a weight vector (.32, .12, .36, 20), and thus
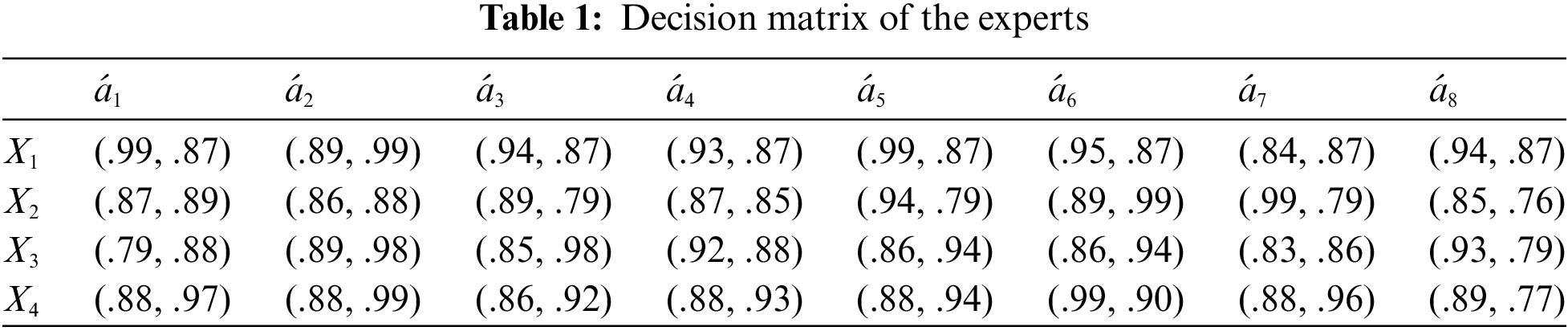






Calculate the score value by using Definition 2.3, which is
In this section, some current techniques under the existing structures, namely q-ROFS, q-ROFSS, and our proposed structure of q-ROFHSS have been compared in order to show the effectiveness of the proposed model. We have developed the MADM technique under the q-ROFHSOWA and I-q-ROFHSOWA operators. Our proposed technique can explain the most suitable results of DM problems. Since the proposed model is competent and adaptable, it can continue working hard despite any disruptions that may occur. The results obtained from the proposed techniques are different as compared to hybrid techniques. The results show that the operator of the proposed structure is more capable, reliable and effective. Fig. 1 shows a graphical ranking order of the alternatives to our proposed technique compared to the existing techniques.

Figure 1: Graphical representation of existing studies with proposed study
In this study, we developed a new decision-making technique under the q-rung orthopair fuzzy hypersoft environment with the induced ordered weighted averaging operator. We have initiated two types of operators i.e., ordered weighted averaging operator and induced ordered weighted averaging operator. The induced ordered weighted averaging operator is very helpful in decision-making problems with q-rung orthopair fuzzy hypersoft numbers under uncertain conditions. We have also studied some of its basic results and properties. All attribute values are considered by the method described in this article for selecting a real estate project based on the computation of aggregation operators from considered data in the form of membership and non-membership. Finally, we developed an application in an MADM problem. In this problem, we discussed the selection of the best real-estate project for investment. The induced ordered weighted averaging operator is very useful for this problem because this operator represents the uncertain data in the best form under q-rung orthopair fuzzy hypersoft numbers. This decision-making technique proves the information in the best way because in this process the decision-maker uses the order-inducing strategy. The main feature of the suggested strategy is that it offers a useful and adaptable way to effectively help the DM in uncertain situations. In addition, the proposed method can be used both for q-rung orthopair fuzzy hypersoft numbers and q-rung orthopair fuzzy soft numbers, which accurately represent the uncertainty. We plan to use the aggregation operator to solve DM problems in the future when dealing with more ambiguous data, including interval-valued q-rung orthopair fuzzy hypersoft sets, and interval-valued q-rung orthopair fuzzy hypersoft linguistic term sets.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Mishra, A. R., Rani, P., Krishankumar, R., Ravichandran, K., Kar, S. (2021). An extended fuzzy decision-making framework using hesitant fuzzy sets for the drug selection to treat the mild symptoms of coronavirus disease 2019 (COVID-19). Applied Soft Computing, 103, 107155. https://doi.org/10.1016/j.asoc.2021.107155 [Google Scholar] [PubMed] [CrossRef]
2. Zadeh, L. A. (1965). Information and control. Fuzzy Sets, 8(3), 338–353. [Google Scholar]
3. Du, C., Ye, J. (2021). Weighted parameterized correlation coefficients of indeterminacy fuzzy multisets and their multicriteria group decision making method with different decision risks. Computer Modeling in Engineering & Sciences, 129(1), 341–354. https://doi.org/10.32604/cmes.2021.016758 [Google Scholar] [CrossRef]
4. Atanassov, K. T. (1989). More on intuitionistic fuzzy sets. Fuzzy Sets and Systems, 33(1), 37–45. https://doi.org/10.1016/0165-0114(89)90215-7 [Google Scholar] [CrossRef]
5. Atanassov, K. T. (1999). Intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets. Studies in fuzziness and soft computing, physica, vol. 35, pp. 1–137. Heidelberg: Springer. [Google Scholar]
6. De, S. K., Biswas, R., Roy, A. R. (2000). Some operations on intuitionistic fuzzy sets. Fuzzy Sets and Systems, 114(3), 477–484. https://doi.org/10.1016/S0165-0114(98)00191-2 [Google Scholar] [CrossRef]
7. De, S. K., Biswas, R., Roy, A. R. (2001). An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets and Systems, 117(2), 209–213. https://doi.org/10.1016/S0165-0114(98)00235-8 [Google Scholar] [CrossRef]
8. Szmidt, E., Kacprzyk, J. (2000). Distances between intuitionistic fuzzy sets. Fuzzy Sets and Systems, 114(3), 505–518. https://doi.org/10.1016/S0165-0114(98)00244-9 [Google Scholar] [CrossRef]
9. Gulzar, M., Mateen, M. H., Alghazzawi, D., Kausar, N. (2020). A novel applications of complex intuitionistic fuzzy sets in group theory. IEEE Access, 8, 196075–196085. https://doi.org/10.1109/ACCESS.2020.3034626 [Google Scholar] [CrossRef]
10. Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. https://doi.org/10.1109/TFUZZ.2013.2278989 [Google Scholar] [CrossRef]
11. Peng, X., Yang, Y. (2015). Some results for pythagorean fuzzy sets. International Journal of Intelligent Systems, 30(11), 1133–1160. https://doi.org/10.1002/int.21738 [Google Scholar] [CrossRef]
12. Garg, H. (2018). Linguistic pythagorean fuzzy sets and its applications in multiattribute decision-making process. International Journal of Intelligent Systems, 33(6), 1234–1263. https://doi.org/10.1002/int.21979 [Google Scholar] [CrossRef]
13. Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems, 25(5), 1222–1230. https://doi.org/10.1109/TFUZZ.2016.2604005 [Google Scholar] [CrossRef]
14. Madasi, J. D., Khan, S., Kausar, N., Pamucar, D., Gulistan, M. et al. (2022). N-Cubic q-rung orthopair fuzzy sets: Analysis of the use of mobile app in the education sector. Computational Intelligence and Neuroscience, 2022, 1–24. https://doi.org/10.1155/2022/9984314 [Google Scholar] [PubMed] [CrossRef]
15. Zulqarnain, R. M., Siddique, I., Iampan, A., Baleanu, D. (2022). Aggregation operators for interval-valued pythagorean fuzzy soft set with their application to solve multi-attribute group decision making problem. Computer Modeling in Engineering & Sciences, 131(3), 1717–1750. https://doi.org/10.32604/cmes.2022.019408 [Google Scholar] [CrossRef]
16. Smarandache, F. (2018). Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets and Systems, 22(1), 168–170. [Google Scholar]
17. Zulqarnain, R. M., Xin, X. L., Saeed, M. (2021). A development of pythagorean fuzzy hypersoft set with basic operations and decision-making approach based on the correlation coefficient. Theory and Application of Hypersoft Set, 40(6), 149–168. [Google Scholar]
18. Siddique, I., Zulqarnain, R. M., Ali, R., Jarad, F., Iampan, A. (2021). Multicriteria decision-making approach for aggregation operators of pythagorean fuzzy hypersoft sets. Computational Intelligence and Neuroscience, 2021, 2036506. https://doi.org/10.1155/2021/2036506 [Google Scholar] [PubMed] [CrossRef]
19. Khan, S., Gulistan, M., Wahab, H. A. (2022). Development of the structure of q-rung orthopair fuzzy hypersoft set with basic operations. Punjab University Journal of Mathematics, 53(12), 881–892. [Google Scholar]
20. Wei, G. (2010). Some induced geometric aggregation operators with intuitionistic fuzzy information and their application to group decision making. Applied Soft Computing, 10(2), 423–431. https://doi.org/10.1016/j.asoc.2009.08.009 [Google Scholar] [CrossRef]
21. Xu, Y., Wang, H. (2012). The induced generalized aggregation operators for intuitionistic fuzzy sets and their application in group decision making. Applied Soft Computing, 12(3), 1168–1179. https://doi.org/10.1016/j.asoc.2011.11.003 [Google Scholar] [CrossRef]
22. Zulqarnain, R. M., Siddique, I., Ali, R., Jarad, F., Iampan, A. (2021). Multicriteria decision-making approach for pythagorean fuzzy hypersoft sets interaction aggregation operators. Mathematical Problems in Engineering, 2021, 9964492. https://doi.org/10.1155/2021/9964492 [Google Scholar] [CrossRef]
23. Liu, P., Wang, P. (2018). Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. International Journal of Intelligent Systems, 33(2), 259–280. https://doi.org/10.1002/int.21927 [Google Scholar] [CrossRef]
24. Peng, X., Dai, J., Garg, H. (2018). Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. International Journal of Intelligent Systems, 33(11), 2255–2282. https://doi.org/10.1002/int.22028 [Google Scholar] [CrossRef]
25. Liu, P., Mahmood, T., Ali, Z. (2019). Complex q-rung orthopair fuzzy aggregation operators and their applications in multi-attribute group decision making. Information, 11(1), 5. https://doi.org/10.3390/info11010005 [Google Scholar] [CrossRef]
26. Garg, H., Gwak, J., Mahmood, T., Ali, Z. (2020). Power aggregation operators and vikor methods for complex q-rung orthopair fuzzy sets and their applications. Mathematics, 8(4), 538. https://doi.org/10.3390/info1101000510.3390/math8040538 [Google Scholar] [CrossRef]
27. Khan, S., Gulistan, M., Kausar, N., Kousar, S., Pamucar, D. et al. (2022). Analysis of cryptocurrency market by using q-rung orthopair fuzzy hypersoft set algorithm based on aggregation operators. Complexity, 2022, 7257449. https://doi.org/10.1155/2022/7257449 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools