 Open Access
Open Access
REVIEW
Review of Recent Trends in the Hybridisation of Preprocessing-Based and Parameter Optimisation-Based Hybrid Models to Forecast Univariate Streamflow
1 Department of Civil Engineering, University of Maysan, Maysan, 57000, Iraq
2 Department of Civil Engineering, Wasit University, Wasit, 52001, Iraq
3 College of Engineering, University of Warith Al-Anbiyaa, Karbala, 56001, Iraq
4 Department of Civil Environmental and Natural Resources Engineering, Lulea University of Technology, Lulea, 971 87, Sweden
5 Department of Computer Science, Faculty of Computer Science and Information Technology, Universiti Putra Malaysia, Serdang, 43400, Malaysia
* Corresponding Author: Nadhir Al-Ansari. Email:
Computer Modeling in Engineering & Sciences 2024, 138(1), 1-41. https://doi.org/10.32604/cmes.2023.027954
Received 23 November 2022; Accepted 23 March 2023; Issue published 22 September 2023
Abstract
Forecasting river flow is crucial for optimal planning, management, and sustainability using freshwater resources. Many machine learning (ML) approaches have been enhanced to improve streamflow prediction. Hybrid techniques have been viewed as a viable method for enhancing the accuracy of univariate streamflow estimation when compared to standalone approaches. Current researchers have also emphasised using hybrid models to improve forecast accuracy. Accordingly, this paper conducts an updated literature review of applications of hybrid models in estimating streamflow over the last five years, summarising data preprocessing, univariate machine learning modelling strategy, advantages and disadvantages of standalone ML techniques, hybrid models, and performance metrics. This study focuses on two types of hybrid models: parameter optimisation-based hybrid models (OBH) and hybridisation of parameter optimisation-based and preprocessing-based hybrid models (HOPH). Overall, this research supports the idea that meta-heuristic approaches precisely improve ML techniques. It's also one of the first efforts to comprehensively examine the efficiency of various meta-heuristic approaches (classified into four primary classes) hybridised with ML techniques. This study revealed that previous research applied swarm, evolutionary, physics, and hybrid metaheuristics with 77%, 61%, 12%, and 12%, respectively. Finally, there is still room for improving OBH and HOPH models by examining different data pre-processing techniques and metaheuristic algorithms.Graphic Abstract
Keywords
Nomenclature
| MLP | Multi-layer perceptron |
| RNN | Recurrent neural network |
| ANFIS | Adaptive neuro-fuzzy inference system |
| GEP | Gene expression programming |
| GP | Genetic programming |
| MLR | Multi-linear regression |
| LSTM | Long-short-term memory |
| SVR | Support vector regression |
| ANN | Artificial neural network |
| ELM | Extreme learning machines |
| AR | Auto-regression method |
| GRU | Gated recurrent unit |
| LSSVM | Least-squares support vector machine |
| ARMA | Auto regressive moving average |
| RF | Random forest |
| M5RT | M5 regression tree |
| CANFIS | Coactive neuro-fuzzy inference system |
| PNN | Polynomial neural network |
| FNN | Feed-forward neural network |
| BL | Bi-linear |
| ERNN | Elman recurrent neural network |
| GA | Genetic algorithm |
| DE | Differential evolution |
| FPA | Flower pollination algorithm |
| CSA | Cooperation search algorithm |
| CS | Cuckoo search |
| SCE-UA | Shuffled complex evolution |
| SCA | Sine cosine algorithm |
| SFA | Sunflower optimisation |
| WOA | Whale optimisation algorithm |
| GWO | Gray wolf optimisation |
| SSA | Sparrow search algorithm |
| PSO | Particle swarm optimisation |
| IPSO | Improved particle swarm optimisation |
| QPSO | Quantum-behaved particle swarm optimisation |
| WT | Wavelet transform |
| ICEE | Improved complete ensemble empirical |
| IGWO | Improved grey wolf optimiser |
| IWD | Intelligent water drop |
| FA | Firefly algorithm |
| PSOGSA | Particle swarm optimisation gravitational search algorithms |
| PSOMVO | Particle swarm optimisation-multi-verse optimiser |
| EO | Equilibrium optimisation |
| HGSO | Henry gases solubility optimisation |
| NPO | Nuclear reaction optimisation |
| WDO | Wind driven optimisation |
| MVO | Multi-verse optimisation |
| GSA | Gravitational search algorithm |
| MI | Mutual information |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MAD | Mean absolute deviation |
| MSE | Mean square error |
| AE | Absolute error |
| ME | Mean error |
| RE | Relative error |
| MARE | Mean absolute relative error |
| RAE | Relative absolute error |
| R | Pearson’s correlation coefficient |
| R2 | Coefficient of determination |
| Ce | Coefficient of efficiency |
| Wl | Willmott index |
| CI | Confidence index |
| PI | Persistence index |
| STD | Standard deviation |
| QR | Qualification rate |
| D | Agreement index |
| SD | Standard deviation |
| PFC | Peak flow criteria |
| LFC | Low flow criteria |
| SNR | Signal-to-noise ratio |
| CC | Correlation coefficient |
| ACOR | Ant colony optimisation for continuous domain |
| VAF | Variance account |
| RSR | RMSE-observations standard deviation ratio |
| ABC | Artificial bee colony |
| TLBO | Teaching‑learning based optimisation |
| ACO | Ant colony optimisation |
| ALO | Ant‑lion optimisation |
| ICA | Imperialist competitive algorithm |
| MPA | Marine predator algorithm |
| SMA | Slim mold algorithm |
| SI | Scatter index |
| MBE | Mean bias error |
| BART | Bayesian additive regression tree |
| EMPA | Extended marine predators algorithm |
| GBO | Gradient-based optimiser |
| TL | Time lag |
| NRMSE | Normalised root mean square error |
| TSVR | Twin support vector machine |
| EWT | Efficient wavelet transform |
| EEMD | Ensemble empirical mode decomposition |
| AHELM | Asymmetric huber loss function-based ELM |
Water scarcity, high requests for electricity consumption, irrigation requirements, industrial and residential uses are the primary issues compelling academics to precisely estimate streamflow for the effective use of freshwater resources [1,2]. Moreover, streamflow estimation is essential for flood forecasting and warning, environmental flow analysis, food risk management, hydropower generation, irrigation systems, and water quality management [3–5]. In the past, multiple regression and autoregressive moving average methods were utilized as conventional models for streamflow forecasting. However, these models rely on static data and work well only when the data has linear distribution and is regularly distributed [6–8]. In contrast, streamflow time series data usually has nonlinear and unstable characteristics. Thus, based on linear distribution, these approaches are then unsuitable for capturing the features of hydrological time series [9–13]. Alternatively, machine learning (ML) approaches are highly helpful in modelling natural systems since they do not require equations and assumptions depending on physical procedures, which are frequently needed in other models. These strategies have also resulted in effective outcomes and frequently outperformed conventional approaches [14–16]. As a toolbox, high-level programming languages, including Python, NeuroSolutions, MATLAB, etc., are successful and effective [17]. Hence, various techniques have been evolved to improve streamflow forecast: support vector regression (SVR) [18,19], adaptive neuro-fuzzy inference systems (ANFIS) [20,21], random forest (RF) [22], and artificial neural networks (ANN) [9,14,23–27]. However, ML models fall short of capturing hydrological processes, particularly in records with frequent high and variable streamflow. In addition, these models encounter issues through the training procedure, including over-fitting or trapping in search of global optimums [28,29]. Therefore, several nature-inspired and evolutionary algorithms locating the global optimum have been combined with ML techniques to overcome these limitations [30].
The hybrid techniques combine various models for supporting (manipulating the data) and optimising the primary method [31]. Some research has shown that combined approaches are superior to single techniques in terms of streamflow estimation, such as Kilinc et al. [32], Tikhamarine et al. [33], Shyama et al. [34], Zaini et al. [35], Adnan et al. [36], and Tikhamarine et al. [37]. Hybrid prediction models have been recently prioritised over standalone approaches in hydrology issues. Fig. 1 shows the percentage number of research on combined methods performed to simulate univariate streamflow over the last five years (from 2018 to 2022).

Figure 1: A percentage of research on combined ML techniques was applied to simulate univariate streamflow during the last five years
Multiple combined techniques have been advanced and effectively used to enhance the precision of univariate streamflow prediction. According to Hajirahimi et al. [38], combined approaches are classified into several types. However, this study focuses only on two groups:
1) The parameter optimisation-based hybrid models (OBH): The rationale behind OBH models is to make use of optimisation methods [29,39] and integrate the models with nature-inspired algorithms to estimate the optimum hyperparameters of ML methods such as Kilinc et al. [32], Adnan et al. [40], and Kilinc et al. [41].
2) Hybridisation of parameter optimisation-based and preprocessing-based hybrid models (HOPH): It is developed by combining the metaheuristic algorithms with the preprocessing-based hybrid models (PBH) models to seek appropriate parameters [38]. This hybrid method has been successfully studied for hydrological research such as Tikhamarine et al. [37] and Zakhrouf et al. [42].
The reason behind studying these hybrid models in detail is because they enhanced predictive performance and are better than standalone methods, as demonstrated in Table 4 through the comparison between the column, which contains all models (Models Used), and the column (Best Model). It can notice that the combined technique superior to the single methods.
The univariate prediction technique is a data-driven modelling strategy that uses the same time series data as input, such as streamflow time series data [43]. Consequently, when only streamflow data are available, the forecasting model will rely on the best streamflow lag data scenario [44]. A univariate approach is especially prevalent in watersheds with limited data. The univariate time series forecasting approach is more flexible and applicable than traditional hydrological modelling in basin-scale hydrological forecasting, which typically requires large amounts of data, especially for river basins with low availability [43]. Therefore, univariate data-driven prediction has become more prevalent recently in hydrological predicting, as shown by Pham et al. [45], Marques et al. [46], Kabbilawsh et al. [47], Danandeh et al. [48], Hu et al. [49] and Sammen et al. [50].
Different metaheuristic optimisation methods could solve various issues for diverse application fields. The significant benefits of optimisation approaches are their capability to choose the optimum values for system hyperparameters across a wide range of operating situations [51,52]. Ahmed et al. [28] classified the metaheuristic into the evolutionary group, swarm group, physics group, and hybrid group. The studies that used this method, such as Jiang et al. [53], Feng et al. [54], Adnan et al. [36], Ren et al. [55], Fatemeh et al. [56] and Zhao et al. [57]. In addition, data preprocessing techniques have a significant potential benefit for enhancing the effectiveness of prediction models [58]. It can be categorised into three steps, which are, firstly, data normalisation. Secondly, data cleansing has received more importance recently. Multiple signal pre-treatment methods have been used for cleanning and/or locate the stochastic, seasonal, and trend signals of streamflow time series, including wavelet transform (WT) [8,59–61] and singular spectrum analysis (SSA) [62–67]. Finally, selecting the best model input, such as mutual information (MI) [53,68–72].
In addition, many other review articles have introduced the uses of machine learning to predict streamflow [43,73–76], whose keywords and essential features are summarised in Table 1.
Literature on streamflow estimation can be seen from numerous angles. Ibrahim et al. [74] analysed papers on hybrid artificial intelligence (AI) and optimisation of flow prediction. This review focused on ANN, the support vector machine (SVM), SVR, ANFIS, and AI techniques optimised using genetic algorithm (GA), particle swarm optimisation (PSO), and artificial bee colony (ABC). The study suggested that ML models can be used for advanced methodologies and future hybrid models. Troin et al. [75] investigated methods and strategies for forecasting streamflow for forty years and stated that ANN is the most well-known method for predicting streamflow. Furthermore, combined forecast techniques are a well-established field of research that covers a wide variety of practical applications.
Many studies on the development application of naturalisation procedures and the primary obstacles associated with the methods have been examined and evaluated. Naturalisation procedures are used when natural flows cannot be measured directly and must instead be calculated. Terrier et al. [76] provided literature with an overview of streamflow naturalisation approaches. The study revealed that the creation of hybrid approaches resulted from difficulty estimating the natural flow without human intervention and accumulating a long enough series to calculate robust hydrological indicators. Belvederesi et al. [73] focused on streamflow forecasting in cold and ungauged areas in previous studies. They showed the importance of developing hybrid models in such watersheds to aid flood prediction and warning and resource management challenges.
Zhenghao et al. [43] categorised the publications on data-driven models for univariate streamflow predictions: traditional and AI-based techniques. Traditional data-driven methods can be simply applied, such as auto-regressive integrated moving averages (ARIMA), multiple linear regressive (MLR), and auto-regressive moving averages with the exogenous term (ARMAX). The most widely employed AI-based data-driven techniques are SVM, ANN, ANFIS, genetic programming (GP), and least squares support vector machine (LSSVM). Finally, hybrid models incorporate both a data-driven technique and a data preprocessing method. The PSO, and GA, are widely used to determine ML hyperparameters, and wavelet decomposition (WD) is widely used as a data preprocessing approach. Additionally, researchers prefer hybrid models that integrate preprocessing techniques with novel data-driven techniques for streamflow predicting.
All the above reviewers in their studies considering the climate changes with streamflow, except Zhenghao et al. [43], discussed the univariate streamflow using data-driven models until 2018. One limitation of zhang’s study was that it did not consider the three preprocessing steps.
To this end, in all the above review papers, there is rarely a focus on univariate streamflow prediction.
In this context, the contributions made in this work could be introduced in detail below:
1-Collect previous studies and present them in coherent groups to shed light on the hybrid methods currently employed in univariate streamflow forecasting. Particularly meta-heuristic algorithms that incorporate machine learning. 2-Explain and show the outcomes of using various algorithms in prior studies, highlighting the most common and successful varieties, and providing some recommendations for future investigations. 3-Focus on how these algorithms help improve the reliability of predictions. 4-Identify potential research pathways to help academics by illuminating the available options and gaps in this field.
The current research is up to date and explores using OBH and HOPH for univariate streamflow anticipating only ML models. Fig. 2 presents all ML models and metaheuristic algorithms according to the finding of the summarised papers published from 2018 to 2022 that are considered in the present study. Thus, this study concentrated on combined ML approaches and their classification capability, including approaches for data pre-processing. Additionally, Fig. 3 displays the general framework of streamflow prediction in this research.

Figure 2: All models and metaheuristics discussed in this paper are based on studies over the last five years

Figure 3: The framework of streamflow simulation
ML models have been utilised over decades and have gained considerable attention recently. This is because it can manage large volumes of data and permit nonlinear structures by applying complex mathematical processes [77]. Typically, these algorithms can be classified into two groups: unsupervised and supervised training. In order to generate new data with the benefit of prior knowledge, supervised learning uses labelled training data [78]. Various machine learning algorithms have been developed for predicting issues, such as ANNs [79–84], ANFIS [85–89], SVR [90–93], k-nearest neighbour (k-NN) [94–98], and multi-layer perceptron (MLP) [56,99–102]. The pros and cons of the most prevalent ML approaches are briefed in Table 2.
It plays a critical role in estimating variables by endorsing high precision and minimal processing costs throughout the training stage, where noisy and undependable data may badly influence the training stage and lead to a flawed model [77]. These techniques are also fundamental to the data mining procedure by endorsing high precision and minimal processing costs throughout the training stage [107]. Additionally, these techniques are essential for ensuring that all independent factors receive equal consideration throughout the training stage and for accelerating the procedure [108]. Data preprocessing techniques have been used effectively in a variety of fields of research, e.g., forecasting irrigation water [109], monthly rainfall [65], and drought prediction [110]. The preprocessing data method comprises three steps: normalisation, cleaning, and selecting the optimal predictors, as indicated in Zubaidi et al. [111].
The goal of data normalisation is to provide each ANN model with input data that is normally or nearly normally distributed and has the same range of values [112]. As a result, the convergence of the weights and biases will be more stable, and the outliers’ impact will be reduced [58,113].
The step of cleaning data seeks to identify outliers and noise [114]. Then, treat the outliers if found and remove noise from normalised time series to mitigate the scale of error and enhance the regression value [115]. Outliers and noise negatively influence data analysis and the models’ performance, so it is essential to determine and treat or remove undesirable values from the data [116].
3.3 Choosing the Best Predictors
Selecting the optimum predictors is one of the key processes in data preprocessing and evolving a viable prediction model [117]. When applying the univariate strategy, various techniques, such as the mutual information method [16,118,119], are employed to choose the optimal antecedent lags scenario [39]. According to the current research, only 42% of the academics made use of data normalisation, 19% employed data cleaning, and 45% used best model input choice techniques. Table 3 summarises data preprocessing based on earlier research evaluated in this study.
4 State of Art of Hybrid Models
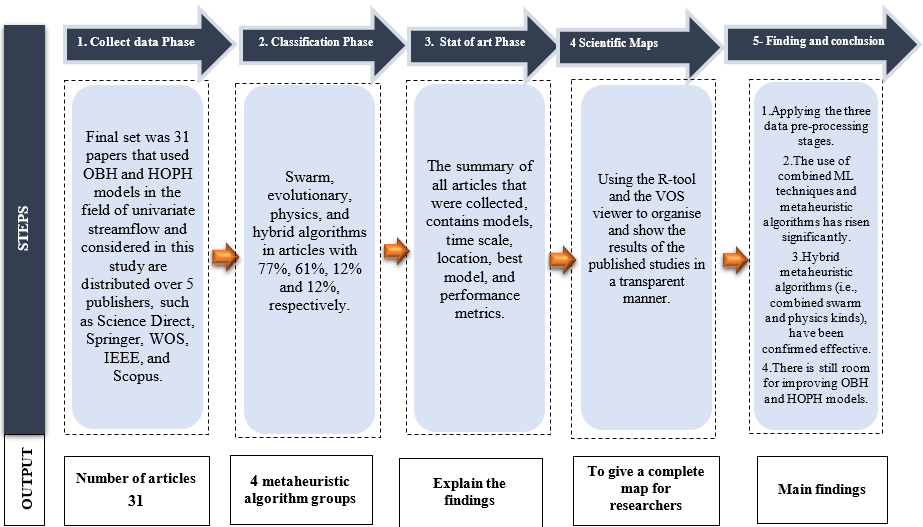
This section will discuss the papers that the combined technique incorporates a couple or more methods: one works as the main technique and the rest as a pre-or post-processing technique. Recently, coupled techniques have been proposed to build flexible and effective techniques and increase the precision of single algorithms’ forecasts [77]. This study focuses on two types of combined methods: parameter optimisation-based hybrid models (OBH) and model hybridisation based on parameter optimisation and preprocessing (HOPH) [38]. Fig. 4 shows the best hybrid for OBH and HOPH models, and Table 4 demonstrates various research that applied hybrid models to forecast univariate streamflow over the period that this study focused on. The number of research reviewed in this paper is 31 research including six studies of the OBH model and 25 studies of HOPH model. The next sections review the summary of all research that were collected, contains models, time scale, location, best model, and performance metrics.

Figure 4: Classification of the hybrid models utilised for streamflow forecasting

4.1 The Parameter Optimisation Based Hybrid Models (OBH)
The key idea behind these methods is to characterise the learning process and locate ML model hyperparameters through the use of optimisation methods [38]. According to the nature-based method, a metaheuristic optimisation algorithm can be developed to address hydrological issues. Bio-inspired optimisation algorithms have proven useful in streamflow investigations for parameter estimation [135]. Moreover, various forms of metaheuristic algorithms are employed for this issue. The metaheuristic algorithms imitate mathematical procedures via imitating natural processes, such as animal behaviour, physical annealing, and biological evolution [39].
The firefly algorithm (FFA), genetic algorithm (GA), grey wolf optimisation (GWO), particle swarm optimisation (PSO), and differential evolution (DE) are all hybrids of ANFIS and nature-inspired optimisation algorithms that are used for streamflow simulation across three prediction perspectives: the short-term (daily time scale), the intermediate-term (weekly to monthly scale), and the long-term (annually). From June 2005 to December 2016 in the southwest of Iran, fifteen various input-output vectors were utilised for training the hybrid streamflow forecasting model. The results showed that on all time scales, the hybrid algorithms proposed exceeded the traditional ANFIS models. Values of R2, RMSE, NSE, and RAE were improved by 12%, 10%, 18.5%, and 14.3% for the short-term, 15%, 13%, 20%, and 21.1% for the medium-term, and 10.3%, 7.5%, 10.5%, and 14% for the long-term, respectively [30]. The ideal models were ANFIS_GWO1, ANFIS_GWO7, and ANFIS_GWO11.
Additionally, Kilinc et al. [32] combined a long_short_term memory (LSTM) with GA for streamflow forecasting. The GA-LSTM approach was implemented using daily streamflow data of the Beyderesi_Kılayak station (Sep 2000–Jun 2019) and of Yazıköy station (Dec 2000–Jun 2018) in the Euphrates River, Turkey. The findings demonstrated that the suggested GA-LSTM reduced the prediction error more effectively than the benchmark models (i.e., LSTM and Linear Regression) with MAE = 0.2865 m3/s, RMSE = 0.7795 m3/s, MAPE = 5.2819, SD = 0.0973, and R2 = 0.9689.
Moreover, compared the M5 Regression Tree (M5RT) models to 2 hybrid approaches, ANN GA and ANFIS GA, for forecasting streamflow in four distinct time-lag input combinations. For this research, we utilised monthly streamflow data from the 2 Rivers in Pakistan. When comparing the ANFIS GA and ANN GA to the M5RT models, it was discovered that the hybrid models performed better in terms of prediction. The results demonstrated that the ANN-GA model with three historical streamflow and periodicity input outperformed the ANFIS_GA model in Kunhar River (RMSE: 31.16 m3/s, MAE: 18.67 m3/s, and R2: 0.891).
Also, a hybridisation of a gated recurrent unit (GRU) with a grey wolf algorithm (GWO) was used for estimating the streamflow of Üçtepe and Tuzla stations in Turkey from 2000 to 2009. The comparative model and linear regression were used to compare the hybrid model’s precision. Based on their findings, the GWO-GRU combined technique was superior to the standard methods in all statistical parameters except standard deviation (SD) at the Üctepe station and the entire Tuzla station. At Üçtepe, the flow measurement station (FMS), RMSE and MAE of the single GRU method were 124.57, 184.06 m3/s, respectively, whereas that of the hybrid model were 82.93 and 85.93 m3/s, respectively, resulting in improvements of around 34% in RMSE and 53% in MAE. In addition, the Tuzla station’s GWO-GRU and linear regression R2 values were 0.9827 and 0.9558, respectively. It also supported the potential of the hybrid GWO-GRU model for forecasting issues [41].
Samui et al. [130] employed three metaheuristic algorithms to enhance the ANN model to predict the daily streamflow of the Euphrates River relying on several historical data. The metaheuristic algorithms are ABC, TLBO, ACO, ALO, and ICA. Data were collected in a 2102-gauge station in Turkey from 1981 to 2010. The outcomes display that the ANN_ALO technique remained superior considering the performance criteria such as R2 = 0.962, NSE = 0.962, RMSE = 0.061 m3/s, MAE = 0.029 m3/s, and MARE = 0.003.
Nguyen et al. [132] used the genetic algorithm (GA) to determine the bayesian additive regression tree (BART) model’s variables in the most efficient manner possible. As a result, a novel hybrid GA-BART model was suggested for estimating hourly streamflow in the Jungrang urban basin, which is located on the Han River in South Korea with data (2003–2020). The GA-BART approach produced better results compared to the MLR and GA-SVR models. In comparison to models using different input predictors, the statistical results showed that the hybrid GA-BART model performed better than the other models for the hourly streamflow estimate with an RMSE = 25.12 m3/s, MAE = 8.00 m3/s, NSE = 0.96, CC = 0.98, and MAPE = 9.0%.
4.2 Hybridisation of Parameter Optimisation‑Based and Pre Processing‑Based Hybrid Models (HOPH)
By combining optimisation methods with pre-processing-based hybrid (PBH) models, HOPH models can determine the best settings for their pre-processing stage or assess the correct weights to use when adding up the results of its decompositional elements’ predictions [38].
Tikhamarine et al. [37] analysed the model of SVR using four algorithms (i.e., grey_wolf optimiser (GWO), shuffled_complex_evolution_algorithm (SCE_UA), Multi_verse optimiser (MVO), and PSO). The aforementioned approach was then used to develop hybrid models that combine wavelet transform with SVR in order to make predictions about the monthly streamflows at the Ain Bedra and Fermatou stations in Algeria between 1970 and 1995. Finally, both the basic and hybrid models were compared. In comparison to other hybrid models, the created hybrid (GWO_WSVR) presented somewhat higher NSE (95.72%) and coefficient of determination (0.9786) and lower RMSE (0.6433 m3/s) and MAE (0.3047 m3/s) values.
Zhao et al. [61] also used the ICEEWT-IGWO-GRU model to estimate monthly streamflow prediction from 1956 to 2016 for the Shangjingyou station and from 1958 to 2016 for the Fenhe reservoir station in Taiyuan. They revealed that ICEEWT_IGWO_GRU was advanced to the single GRU model, so the values of MAE and RMSE were reduced by 50% and 52% for the two stations.
When it comes to daily streamflow forecasting, Niu et al. [123] developed a hybrid model based on variational mode decomposition (VMD), extreme learning machine (ELM), and sine cosine algorithm (SCA). For this reason, we decided to breakdown the original streamflow series using the VMD method of data processing. This analysis makes use of daily streamflow measurements taken at Danjiangkou Reservoir on the Han River in China between 1 January 2005 and 31 December 2019. The outcomes showed that compared with the control models, such as ANN, SVM, and ARMA, the hybrid method gave rise to high accuracy in predicting streamflow. The GVMD-ELM technique had the best performance (RMSE = 50.48% m3/s, MAPE = 63.06 m3/s, CE = 12.75 and R = 0.986).
Zakhrouf et al. [42] have established the discrete wavelet transform-based feed-forward neural networks (WFFNNs-GA) model for the multi-day-ahead streamflow prediction using three different evolutionary techniques (i.e., MIMO, MIMO, and MIMO). In this analysis, we utilised data collected over a period of 14 years along the Chellif River in Algeria. Five statistical indices (root-mean-squared error, signal-to-noise ratio, correlation coefficient, nash-Sutcliffe efficiency, and peak flow criterion) were used to evaluate the suggested models. Outcomes demonstrated that the WFFNNs-GA model based on the MISMO evolutionary approach provided the best accuracy (i.e., RMSE (m3/s) = 1.550, SNR = 0.066, CC = 0.998, NSE (%) = 99.565, and PFC = 0.081). Results further supported the claim that hybrid models based on comparable evolutionary methodologies estimate results more accurately than solo models.
Moreover, Zakhrouf et al. [129] used a hybrid approach, combining wavelet (W) with data-driven models (ANN, ANFIS, and GA) to predict daily river flow in Northern Algeria. They analysed data from 12 years. Comparisons were also made between the WANN-GA and WANFIS-GA models and their individual counterparts, including ANN and ANFIS. Coefficients of determination (R2) achieved by using the WANFIS-GA and WANN-GA models were 87.2% and 78.9%, respectively, whereas those obtained using the individual models (i.e., ANFIS and ANN) were 56% and 57%, respectively. For the peak values during the testing period (RMSE = 12.1545 m3/s, MARE = 106.785%, R = 0.934, R2 = 0.872, and EC (%) = 87.32), the WANFIS-GA model provided an excellent match for the observed data.
Furthermore, the MLP is integrated with three physics-inspired algorithms (i.e., equilibrium optimisation (EO-MLP), nuclear reaction optimisation (NRO-MLP), and henry gas solubility optimisation (HGSO-MLP)) to forecast the monthly streamflow. Ahmed et al. [28] compared these hybrid models with two_neural network standalone models MLP and Recurrent Neural Network (RNN) and nine metaheuristic algorithms: evolutionary-inspired (genetic_algorithm (GA-MLP), differential evolution (DE_MLP), and flower pollination algorithm (FPA-MLP), swarm-inspired (particle swarm optimisation (PSO-MLP)), whale optimisation algorithm (WOA_MLP), grey wolf optimisation (GWO-MLP) and sparrow search algorithm (SSA-MLP), and two physics-inspired algorithms ((wind-driven optimisation (WDO-MLP) and multi-verse optimisation (MVO_MLP)). The case study was the Nile River, with 130 years of monthly natural streamflow between 1887 and 2000. Their findings indicated that physics-inspired models were more reliable in capturing the streamflow patterns. The NRO had the best accuracy with the lowest RMSE of 2.35, MAE of 1.356, MAPE of 16.747, the highest WI of 0.957, and R of 0.924. The study also concluded that enhancing the NRO algorithm with MLP may result in a reliable method for monthly streamflow predictions.
Azad et al. [120] also trained the ANFIS by GA, the ant colony optimisation for the continuous domain (ACOR), and PSO to predict river flow 1, 3, 5, and 7 days ahead. The data was collected from five stations, the upstream stations, including Eskandare (U1) and Ghaleh-Shahrukh (U2), and the downstream ones, including Saad-Tanzimi (D1), Pole-Zamankkhan (D2), and Cham-Aseeman (D3) in Iran for three years. Results demonstrated the PSO enhanced performance of ANFIS so that averages of R2, RMSE (
Moreover, a gene expression program (GEP) was added to the (GA) to create a unique hybrid model for forecasting streamflow in an intermittent stream one month ahead of time. Results from the GEP-GA were compared to those from the classic GP, the GEP, multiple linear regression, and the GEP-linear regression models. They used a monthly streamflow data set for the region of northwest Iran from 1978 to 2008 for their study. As shown by the results, the GEP-GA performed better than all of the reference models (RMSE = 249.6, NSE = 0.523) [121].
Three machine-learning approaches were employed to predict monthly streamflow in Egypt from 1871 to 2000. These methods were SVM, multilayer perceptron neural network (MLPNN), and ANN. The above methods were hybridised with the GWO algorithm. Auto-regression (AR) was used for comparative analysis purposes. So, single models, such as SVM, MLPNN, and ANN, performed less well than combined ones. Among all the combined techniques, the SVR-GWO technique was the best in terms of estimating streamflow, based on statistical criteria (i.e., RMSE = 2.0570 m3/s, MAE = 1.2005 m3/s, R = 0.9363, NSE =0.8728, and WI = 0.9671) [33].
An ELM was also combined with GA, the PSO algorithm, and upgraded particle swarm optimisation (IPSO) to raise the accuracy of monthly streamflow predictions using one delay time. The models were trained with data from the Chaohe River, in China, from January 1956 to December 2010. This research demonstrated that the developed procedure (ELM-IPSO) had a greater prediction accuracy when compared to AR, ANN, ELM-GA, and ELM-PSO approaches. The ELM-IPSO also had the lowest MAE, RMSE, and RE values throughout the training and prediction stages and the highest NSE and R values, indicating that ELM-IPSO is a practical approach for predicting monthly streamflow with MAE = 1.16 m3/s, RMSE = 1.46 m3/s, RE = −11.04%, NSE = 0.78, and R = 0.89 [53].
Feng et al. [54] used the ANN model with five meta-heuristic algorithms, namely the cooperation search algorithm (CSA), PSO, DE, gravitational search algorithm (GSA), and quantum-behaved particle swarm optimisation (QPSO) to predict the monthly flow. The study was done in the Yangtze River, China; the flow data of three Gorge stations lasted from 1890 to 2019, while the data of the Gaochang station lasted from 1940 to 2019. They modelled the ANN using 12 input scenarios (M1 to M12). The experimental results indicated that the hybrid method ANN-CSA consistently outperformed the control models and produced superior predicting outcomes during the training and testing stages in various scenarios; the evaluation result was (RMSE = 3653.3034 m3/s, MAPE = 18.5002, R = 0.9198, and CE = 0.8457).
In another study, the ANFIS was combined with the particle swarm optimisation (ANFIS_PSO), genetic algorithm (ANFIS_GA), and differential evolution algorithm (ANFIS-DE) to predict monthly streamflow. The data was collected from one station (ID 3527410) in Malaysia from 2000 to 2014. The results suggested that integrating long antecedent data increases forecasting accuracy, as the model can capture seasonal patterns and the current trend in time series. The model with five input variables (t _1, t _2, t_3, t_6, t_12) was superior to the best, with a 68% improvement in prediction accuracy over the model with a single input variable (t_1). The results revealed that the PSO improved the capability of the ANFIS model (RMSE = 7.96; MAE = 2.34; R2 = 0.998 and WI = 0.994) more than GA and DE in forecasting streamflow. Comparing evolutionary optimisation methods revealed that PSO is superior to GA and DE for optimising ANFIS functions. The precision of the ANFIS-PSO technique was somewhat greater than that of the ANFI-SGA and ANFIS-DE techniques (24% and 20%, respectively), and it was 25% more accurate than the non-hybrid ANFIS model. Therefore, the ANFIS-PSO model could accurately predict highly stochastic stream flow in a tropicalsetting [122].
A hybridisation of ANN and SVR with GA and (SVR, RF) was done using the grid search algorithm to simulate river flow from Jan 1991–Nov 2010. The historical data under 5 input scenarios were created (1st Model, 2nd Model,…, 5th Model) to predict streamflow in the Tigris River in Iraq. The results indicated that the SVR-GA model was the most accurate at predicting monthly river flow (i.e., ME = −14.73, RMSE = 100.78 m3/s, MAE = 81.585 m3/s, MPE = −214.02, MAPE = 670.30, and R2 = 0.96). Consequently, it was applicable to improve the flow of river forecasting capability by utilising the suggested hybrid model [19].
The multilayer perceptron (MLP) was hybridised with multiple metaheuristic algorithms: sunflower optimisation (SFA), the genetic algorithm (GA), and particle swarm optimisation (PSO) predict six lags of daily streamflow in two stations, Jam Seyed Omar (JSO) and Muda Di Jeniang (MDJ) in Malaysia. The MLP-SFA was compared to the conventional MLP and two other hybrid MLP models (MLP-PSO, MLP-GA). The assessment yielded the following outcomes: at the MDJ station (PBIAS = 0.18, MAE = 0.29 m3/s, NSE = 0.93, RMSE = 0.45 m3/s, d = 0.95), and at the JSO station (PBIAS = 0.16, MAE = 0.27 m3/s, NSE = 0.93, RMSE = 0.37 m3/s, d = 0.94). Compared to previous models, the MLP-SFA might reduce RMSE by 12%~21% at the JSO station and 8%~24% at the MDJ station. The results demonstrated that using MLP with optimisation methods led to the enhancement of the accuracy of the standalone MLP model [50].
Meshram et al. [126] suggested a novel hybrid technique (FNN-PSOGSA) for simulating monthly streamflow. The data was collected from Garber station of the Turkey River in Iowa from 1990 to 2016. This study utilised the PSOGSA for the perfect preparation of the FNN model. The model with two input variables (Qt-1, Qt-2) was superior. They were comparing revealed that FNN-PSOGSA is superior to the standard FNN and FNN_PSO models with RMSE = 24.42 m3/s and MAE = 16.47 m3/s, and the maximum rate of NSE = 0.652, WI = 0.864. The findings also show that the FNN-PSOGSA model is a workable strategy for estimating streamflow and increasing forecasting accuracy.
Abdul Kareem et al. [131] developed three combined models to forecast univariate streamflow of the Tigris River in Maysan Province, Iraq, over 11 years. The procedure comprises data preprocessing and an ANN method combined with CPSOCGSA, MPA, and SMA algorithms. The outcomes reveal that the ANN-CPSOCGSA algorithm offers the better solution based on multiple statistical tests, such as R2 = 0.91, RMSE = 1.07 m3/s, MAE = 1.07 m3/s, and MARE = 1.01.
Zhao et al. [57] used monthly streamflow data collected at the Shangjingyou and Fenhe reservoir sites between the years 1956 and 2016. Comparisons are made between the LSSVM and ELM models and the monthly and sequential IGWO-GRU. The results showed that the hybrid IGWO-GRU method outperformed the other models in estimating monthly streamflow. The IGWO-GRU model reduced the MAPE values by an average of 55.8% compared with the ELM model. Likewise, it yielded a qr value of 97.22% in the Fenhe reservoir station and 86.11% in the Shangjingyou station; this falls under the “very good” and “good” grade categories, respectively. The monthly IGWO-GRU technique was determined to be a more accurate estimating tool, with an average qualification rate of 91.66 percent at two stations (RMSE = 19.615 m3/s, NSE = 0.675, R = 0.896, MAPE = 0.060, and qr = 97.22%), (RMSE = 147.666 m3/s, NSE = 0.922, R = 0.971, MAPE = 0.049, and qr = 86.11%) was the evaluation result for Shangjingyou and Fenhe reservoir stations, respectively.
Pham et al. [45] assessed a new procedure, which coupled the multi-layer perceptron neural network (MLP-NN) with the IWD algorithm to predict monthly streamflow. Nong Son and Thanh My Stations at the Vu Gia Thu Bon River basin were used to collecting historical river streamflow data (1978–2016). The MLP-IWD model was evaluated by four different scenarios for the model input–output architecture. Additionally, the classical MLP-NN model was compared with a proposed hybrid model. The MLP-IWD model offered the best performance (with R2 = 0.80, RMSE = 73.70 m3/s, RE =195.08, NSE = 0.70 and MAE = 55.01 m3/s) for Thanh My station and (with R2 = 0.83, RMSE = 173.65 m3/s, RE = 47.75, NSE = 0.784 and MAE = 123.20 m3/s) for Nong Son station.
Tripura et al. [124] examined the applicability and ability of a hybrid coactive neuro-fuzzy inference system (CANFIS), with a genetic algorithm (CANFIS-GA) and a firefly algorithm (CANFIS-FA), in simulating hourly streamflow. The data were obtained from a Barak River system in Assam, India, from 2000 to 2005. Furthermore, the hybrid models were compared to traditional CANFIS, ANN, and probabilistic neural networks (PNN). The outcomes expression that the suggested CANFIS-FA model outperformed the conventional CANFIS, CANFIS-GA, ANN, and PNN estimates (MAPE = 0.06%, the coefficient of correlation r = 0.99965, and RMSE = 3.92 m3/s).
Kilinc [125] created and implemented an innovative hybrid model using LSTM coupled with the PSO. The proposed hybrid model was compared with statistical methods, including linear regression and the autoregressive integrated moving average (ARIMA). This study employed daily streamflow data from three stations, including Karasu (2010–2019), Demirköprü (2010–2019) and Samandağ (2009–2018), located along the Orontes River basin, Turkey. The hybrid PSO-LSTM strategy gave more promising accuracy results and produced greater performance than the benchmark and linear regression techniques while simulating daily streamflow. For example, the results of the Samandağ station values exhibited the highest R2 (0.9749) RMSE (1.2557 m3/s), MAE (0.1025 m3/s), MAPE (10.2574) and lowest standard deviation (−0.1541).
Mohammadi et al. [127] employed three hybrid techniques include, MLP_PSO, MLP_PSOMVO, and MLP-BL, to predict the daily streamflow. Statistical criteria were used to evaluate the above-boosted methods against MLP and BL. Four hydrometric stations are utilised, two in Canada (Brantford and Galt) on the Grand River and two in the United States (Macon and Elkton, on the Ocmulgee and Umpqua rivers, respectively) to measure daily streamflows from 1998 to 2018. Results reveal that the boosted approaches, especially the boosted MLP-BL, are superior to the baseline models in terms of their ability to accurately estimate daily streamflows. It yields, for example, R2 = 0.994, MAE = 3.53 m3/s, and RMSE = 6.426 m3/s for Brantford station in the testing stage.
Zakhrouf et al. [128] integrated three deep learning techniques (i.e., ERNN, LSTM, and GRU) and one machine learning method (i.e., FFNN) by combining each model with the PSO algorithm to simulate the daily streamflow data in Sidi Aich and Ponteba Defluent stations, Algeria over six years. The results of the testing stage indicate that the GRUII two-stage combined technique delivers the best results compared with the rest of the models. It offers NSE = 0.7337, SNR = 0.5159, and RMSE = 35.241 m3/s for Sidi Aich station and NSE = 0.8703, SNR = 0.3600, and RMSE = 11.074 m3/s for Ponteba Defluent station.
Adnan et al. [5] established and applied an innovative hybrid model utilising two optimisation methods: the PSO and GWO, coupled with the ELM. The data used are monthly streamflow from 1980 to 2011 on the Mangla catchment in the north of Pakistan. In addition, the proposed hybrid model was contrasted with four models, including the standalone ELM, a hybrid of ELM-PSO, ELM-GWO, and binary hybrid ELM-PSOGSA (a hybrid of PSO with gravitational search algorithm) methods. According to the evaluation results, the developed coupled model ELM-PSOGWO outperformedthe standalone ELM, hybrid ELM-PSO, ELM-GWO, and binary hybrid PSOGSA methods, with the lowest RMSE = 55.14 m3/s, MAE = 46.59 m3/s, and both a high R2 and NSE of 0.925, 0.919 in the test phase respectively. Furthermore, the outcomes reveal the potential of the ELM-PSOGWO model to be recommended for monthly streamflow prediction.
Ikram et al. [133] assessed a new procedure, which joined the ANN with the extended marine predators’ algorithm (EMPA) (i.e., ANN-EMPA) to predict monthly streamflow. The Upper Indus Basin (UIB) of northern Pakistan was used to collect river streamflow data (1974–2008). Additionally, the new method ANN-EMPA was compared with the hybrids ANN-MPA, ANN-GWO, ANN-GA, and ANN-PSO methods. The ANN-EMPA model offered the best performance with the lowest RMSE = 131.80 m3/s, MAE = 84.44 m3/s, and the highest NSE = 0.9532. Additionally, the ANN-EMPA enhanced the RMSE, MAE, and Nash–Sutcliffe efficiency of ANN-PSO by 4.8%, 4.1%, and 0.5%, ANN-GA by 6.2%, 5.6% and 0.6%, ANNGWO by 3.7%, 4.4% and 0.5%, and ANN-MPA by 3.2%, 7.5% and 0.3%, respectively.
Adnan et al. [134] used the gradient-based optimisation (GBO) algorithm to develop the ANFIS model for estimating monthly streamflow. The models were built using antecedent streamflow data collected from 1974 to 2009 and were based on two significant sub-basins of the Upper Indus Basin (UIB), namely the Astore and Gilgit basins in northern Pakistan. The accuracy of ANFIS-GBO was evaluated in comparison to ANFIS, ANFIS-GWO, ANFIS-PSO, ANFIS-ACO, ANFIS-GA, and ANFIS-DE. The GBO successfully improved the estimated precision of the ANFIS model by optimising its parameters. The outcomes indicated that the ANFIS-GBO model improved the forecast precision of other hybrid models with root mean square error (RMSE) = 28%–29.5%, normalised RMSE = 28%–26.9%, mean absolute error = 28.7%–40.4%, determination coefficient = 11.2%–20.1%, and Nash Sutcliffe Efficiency = 10.4%–20.9%, respectively. The results of the Astore Station values in the test period were R2 (0.853), RMSE (53.97 m3/s), MAE (33.69 m3/s), and NSE (0.843). Likewise, Gilgit Station yielded in the test period R2 (0.923), RMSE (93.5 m3/s), MAE (48.63 m3/s), and NSE (0.915).
A continual stream of both applied and theoretical material makes keeping up with it difficult. Several authors have suggested using the R-tool and the VOS viewer to organise and show the results of the published studies in a transparent manner [136]. The bibliometrics technique is distinguished by its high reliability and transparency in interpreting research results. Furthermore, these instruments are simple to utilise and are commonly accessible because they have been established and shared by the crowd. The bibliometric method was utilised in this study, as will be demonstrated below.
5.1 Country Scientific Production
It displays the total number of articles published by the country, researchers, and institution. Fig. 5 depicts a graphic map of univariate streamflow data prediction using OBH and HOPH models. It has five colours. Maximum scientific output is represented by the deepest blue, while the lightest blue shows the minimum output. Gray indicates no significant scientific contribution. The highest levels of scientific output are found in Turkey, China, Algeria, Iran, and Malaysia, all of which can help advance the scientific understanding of researchers and policymakers.

Figure 5: The country’s scientific production map of studies on OBH and HOPH models were utilised to forecast univariate streamflow during the last five years
This word cloud investigates the most often occurring and significant words in the prior investigations. Fig. 6 provides the most important concepts from the study literature in an effort to provide a summary and reorganise the data. Word sizes range from tiny to enormous. A higher frequency of occurrence was found for larger words. Thinner words are those that appear less frequently in the literature. Essential aspects of the current corpus of knowledge include river flow, hybrid model, particle swarm, swarm optimisation, and genetic algorithm. The results of the existing research suggest that optimisation algorithms are crucial factors to think about when trying to enhance ML approaches in univariate streamflow prediction models.

Figure 6: A provides essential concepts from the academic literature
It is constructed utilising the current literature’s most frequently occurring phrases. Researchers, academics, and practitioners in a given subject may find the network structure revealed by co-occurrence analysis to be particularly useful, as it can help us understand the theoretical underpinnings of that field. Fig. 7 shows the co-occurrence networks of several frequently used phrases. When it comes to previous literature, the greatest knots signify recurring topics. Optimisation techniques are among the most commonly utilised words by earlier researchers in the univariate streamflow forecast models since they may help researchers employ data networks in their attempts to reorganise the existing information and conclusions.

Figure 7: A co-occurrence network structure
There are potentially useful connections between journals, universities, and countries. We suggest a new three-field structure in Fig. 8 that shows the relationships among the most important journals on the left, affiliations in the middle, and countries on the right. For this topic, we observed that most publications were written by writers from Malaysia, Iran, and China and published in environmental research and water resources management. The most common academic affiliations in this field are with the University of Duy Tan, the University of Malaya, and the Ilia State University. In general, Fig. 8 provides a positive image for new authors to depend on.

Figure 8: Three-field plot
5.5 Co-Occurrence Networks Authors
It is vital to identify the authors who have had the most impact on the field, which gives an impression to new researchers and provides them with consultants in their work. Similarly, gaining knowledge of author collaboration patterns in the literature might provide light on where the discipline is headed. The most influential writers in the field are summarised in Fig. 9. The two most influential writers are Yaseen and Wang.

Figure 9: A co-occurrence network authors
5.6 Journal Index Distribution
Additionally, the 31 papers that used OBH and HOPH models in the field of univariate streamflow and considered in this study are distributed over seven publishers, such as Science Direct, Springer, MDPI, IEEE, Taylor & Francis, and Hindawi, are given in the pie chart shown in Fig. 10.

Figure 10: Journal index distribution
The prediction precision is determined by comparing the measured and estimated flows. Different performance evaluations are used to assess the model’s predictive capabilities. An individual assessment may not be sufficient to determine the model(s)’ efficacy and dependability [124,137]. Additionally, the criteria employed to evaluate the accuracy of the predicting technique are crucial because they influence the selection of the optimal strategy or scenario [78,138]. Also, graphical plots, such as a Taylor diagram [139], Violin diagrams [1], and scatter plots [140,141], were used to assess the predicting efficiency of the suggested methodologies. According to the finding of the current study, 77% of the researchers made use of scatter plots, 9% used the Violin diagrams, and 32% employed a Taylor diagram (see Fig. 8). The following are the most commonly used criteria based on earlier research that are divided into three main categories:
6.1.1 Root Mean Square Error (RMSE)
RMSE is the average squared deviation between the estimated and measured outputs. It is utilised for assessing the nonlinear error; this is an excellent measure of forecast accuracy [78,138]. The Equation for determining RMSE is exposed in Eq. (1):
where Yi is: the forecast value, Xi is the actual value, X ̅: mean of the actual value, Y ̅: the mean of the predicted value, N: the total number, i: counter.
6.1.2 Mean Absolute Error (MAE)
MAE estimates the mean of error magnitudes without regard to their direction. In other words, this is the mean absolute deviation between the predicted and actual values [142].
6.1.3 Mean Absolute Percentage Error (MAPE)
MAPE is an objective statistic utilised to assess relative error by comparing predicted and observed data. MAPE is frequently insensitive to large magnitudes but sensitive to smaller magnitudes [54,143].
It represents the percentage error values between actual and anticipated values [144].
6.2.2 Mean Absolute Relative Error (MARE)
This measure represents the average absolute error compared to the observed record. It is also known as the relative mean error [145,146].
6.3.1 Determination Coefficient (R2)
The R2 indicates the degree of correlation between the expected and measured values. The R2 values range from 0 to 1: 1 means the whole relationship between the data set and the line drawn across data, and 0 indicates that there is no meaningful relationship between the type of data and the line drawn through them [39,120].
6.3.2 Nash-Sutcliffe-Efficiency (NSE)
NSE was evolved by Nash et al. [147] in 1970. It measures the fit of hydrological models; When NSE equals 1, the model perfectly matches the measured data; NSE = 0, model forecasts are as accurate as the mean of the empirical data [148].
The SI is a dimensionless measure of a model’s relative accuracy. The model's accuracy is considered poor if SI ⩾ 30%, acceptable if 20% < SI < 30%, good if 10% < SI < 20%, and excellent if SI < 10% [149,150].
Fig. 11 shows the details of the prediction evaluation metrics and the papers’ number utilising them.

Figure 11: Prediction evaluation metrics vs. number of papers
Ahmed et al. [28] advised that the proposed models could be evaluated using data from various research regions with varying climatic circumstances. Also, potential avenues for enhancing the performance of the suggested methods might be achieved by hybridising or evolving new variations of NRO before combining it with MLP. Additionally, Azad et al. [120] recommended (I) examining the performance of other acceptable evolutionary algorithms (EA) approaches and comparing them to the methods described in this study (ANFIS-GA, ANFIS-PSO, AFIS-ACOR). (II) using the offered methods of research (ANFIS-GA, ANFIS-PSO, ANFIS-ACOR) to anticipate other hydrological phenomena, (III) comparing the performance of the planned combined approach (ANFIS-PSO) to other well-known methods, such as ANNs, SVR, and GEP. Danandeh et al. [121] also applied GEP-GA and GEP-LR for monthly streamflow forecasting. The recommendation was that future research might benefit from both preprocessing and post-processing methods to enhance the precision of GEP projections.
Tikhamarine et al. [33] proposed that the enhanced revised algorithm of GWO can be implemented in future research to advance the hyper-parameters optimisation and prevent local optima trapping. In addition, it is necessary to enhance the searching algorithm for the GWO to produce a rapid convergence method. Also, various advanced meta-heuristic techniques should be examined to enhance streamflow prediction. Tao et al. [19] suggested employing the mutual information (MI) statistical approach as a preliminary step in creating forecasting models to extract highly correlated data. Tikhamarine et al. [37] proposed using various meta-heuristic techniques, such as the slap swarm algorithm and grasshopper optimisation methods.
Additionally, based on an analysis of previous research, hybrid models could be enhanced in the following ways:
1. Applying the three data preprocessing stages significantly impacts the performance and precision of a model's target. Therefore, it is suggested that more significant effort should be spent using data pre-treatment methods, such as singular spectrum analysis (SSA) and empirical mode decomposition (EMD), for denoising data. Additionally, establishing the ideal predictor combination scenario. Hence, it prefers expanding the use of the mutual information method better than the try-and-error method.
2. The use of combined ML techniques and metaheuristic algorithms for univariate streamflow forecasts has risen significantly recently. However, there is still an area for streamflow prediction improvement.
3. Recently, hybrid metaheuristic algorithms, such as CPSOCGSA (i.e., combined swarm and physics kinds), have been confirmed effective. It would be useful to extend the current findings by examining different combinations of metaheuristic algorithms types.
4. There is still room for improving OBH and HOPH models by examining different data pre-processing techniques and metaheuristic algorithms.
There are a couple of limitations to this research. Firstly, some studies may have been missed because they did not utilise the identified search terms in their title or abstract; however, the study covered previous studies very well. The second aspect is that the field is expanding so quickly that a timely survey is complex. The last limitation means that a snapshot of search activity in this active research direction does not reflect the fact that the algorithms are used but rather reflects the response to our research question, which is the aim of this research.
This study has reviewed the previous studies on typically used univariate approaches regarding prediction performance and accuracy. Since machine learning models are currently receiving more attention for streamflow prediction due to their simplicity and lower data needs compared to general hydrological techniques. This paper reviewed the recent univariate streamflow forecasting works for the last five years.
A variety of factors influence the effectiveness and accuracy of the prediction technique. Therefore, approaches were selected and compared based on data preprocessing, a univariate data-driven modelling strategy, a suitable timescale, and metaheuristic algorithms integrated into the model. Recent studies have demonstrated that different traditional ML techniques no longer produce the best accurate results. The features and limitations of ML techniques have several disadvantages, including a slow convergence rate and difficulty readily sliding into local minima. Hybrid models can address the limitations problems, involving a couple or more processes; the first works as the main method and the rest as pre- or post-processing. A combination of ML techniques and meta-heuristic optimisation techniques has been made. Consequently, hybrid models represent the most effective instruments for enhancing the precision of streamflow forecasts, such as a comprehensive hybrid approach that integrates preprocessing techniques and metaheuristic algorithms such as (OBH and HOPH).
This paper has concluded that the researchers employed swarm, evolutionary, physics, and hybrid algorithms in their articles with 77%, 61%, 12% and 12%, respectively. Also, the best model was 58% for the swarm, followed by 26% for evolutionary, 10% for hybrid, 3% for physics, and 3% for other models.
In general, this research supports the idea that meta-heuristic approaches precisely improve ML techniques. It is also one of the first efforts to comprehensively examine the efficiency of various meta-heuristic approaches (classified into four primary classes) hybridised with ML techniques. There are a number of ways in which these results advance our knowledge of HOPH and OBH techniques. As there is still potential for improvement in HOPH and OBH techniques for univariate streamflow forecast techniques, it would be beneficial for academics to conduct further research into the role of meta-heuristic approaches and data pre-processing techniques. Lastly, the availability of reliable univariate streamflow data drove a balance between water demand and supply that achieves sustainability. Moreover, Decision-makers should take into account the results of this study to have a scientific view of the current and expected research directions.
Acknowledgement: This paper’s logical organisation and content quality have been enhanced, so the authors thank anonymous reviewers and journal editors for assistance.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: B.A.K., S.L.Z.; data collection: B.A.K., S.L.Z., N.A.-A.; analysis and interpretation of results: B.A.K., S.L.Z., N.A.-A., Y.R.M.; draft manuscript preparation: B.A.K., S.L.Z., N.A.-A. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Ikram, R. M. A., Hazarika, B. B., Gupta, D., Heddam, S., Kisi, O. (2022). Streamflow prediction in mountainous region using new machine learning and data preprocessing methods: A case study. Neural Computing and Applications, 105(3), 107282. https://doi.org/10.1007/s00521-022-08163-8 [Google Scholar] [CrossRef]
2. Siddiqi, T. A., Ashraf, S., Khan, S. A., Iqbal, M. J. (2021). Estimation of data-driven streamflow predicting models using machine learning methods. Arabian Journal of Geosciences, 14(11), 1058. https://doi.org/10.1007/s12517-021-07446-z [Google Scholar] [CrossRef]
3. Jozaghi, A., Shen, H., Ghazvinian, M., Seo, D. J., Zhang, Y. et al. (2021). Multi-model streamflow prediction using conditional bias-penalised multiple linear regression. Stochastic Environmental Research and Risk Assessment, 35(11), 2355–2373. https://doi.org/10.1007/s00477-021-02048-3 [Google Scholar] [CrossRef]
4. Rahimzad, M., Moghaddam, N. A., Zolfonoon, H., Soltani, J., Danandeh, M. A. et al. (2021). Performance comparison of an LSTM-based deep learning model versus conventional machine learning algorithms for streamflow forecasting. Water Resources Management, 35(12), 4167–4187. https://doi.org/10.1007/s11269-021-02937-w [Google Scholar] [CrossRef]
5. Adnan, R. M., Reham, R. M., Ozgur, K., Zaher, Mundher, Y. et al. (2021). Improving streamflow prediction using a new hybrid ELM model combined with hybrid particle swarm optimization and grey wolf optimization. Knowledge-Based Systems, 230(6), 107379. https://doi.org/10.1016/j.knosys.2021.107379 [Google Scholar] [CrossRef]
6. Alsumaiei, A. A., Alrashidi, M. S. (2020). Hydrometeorological drought forecasting in hyper-arid climates using nonlinear autoregressive neural networks. Water, 12(9), 2611. https://doi.org/10.3390/w12092611 [Google Scholar] [CrossRef]
7. Khan M. H., Muhammad N. S., El-Shafie A. (2020). Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. Journal of Hydrology, 590(1995), 125380. https://doi.org/10.1016/j.jhydrol.2020.125380 [Google Scholar] [CrossRef]
8. Evkaya, O., Sevinç, K. F. (2020). Forecasting drought using neural network approaches with transformed time series data. Journal of Applied Statistics, 48(13–15), 2591–2606. https://doi.org/10.1080/02664763.2020.1867829 [Google Scholar] [PubMed] [CrossRef]
9. Hassan, M., Hassan, I. (2021). Improving artificial neural network based streamflow forecasting models through data preprocessing. KSCE Journal of Civil Engineering, 25(9), 3583–3595. https://doi.org/10.1007/s12205-021-1859-y [Google Scholar] [CrossRef]
10. Peng, T., Zhou, J., Zhang, C., Fu, W. (2017). Streamflow forecasting using empirical wavelet transform and artificial neural networks. Water, 9(6), 406. https://doi.org/10.3390/w9060406 [Google Scholar] [CrossRef]
11. Wang, K., Band, S. S., Ameri, R., Biyari, M., Hai, T. et al. (2022). Performance improvement of machine learning models via wavelet theory in estimating monthly river streamflow. Engineering Applications of Computational Fluid Mechanics, 16(1), 1833–1848. https://doi.org/10.1080/19942060.2022.2119281 [Google Scholar] [CrossRef]
12. Wang, L., Li, X., Ma, C., Bai, Y. (2019). Improving the prediction accuracy of monthly streamflow using a data-driven model based on a double-processing strategy. Journal of Hydrology, 573(15), 733–745. https://doi.org/10.1016/j.jhydrol.2019.03.101 [Google Scholar] [CrossRef]
13. Zhang, X., Peng, Y., Zhang, C., Wang, B. (2015). Are hybrid models integrated with data preprocessing techniques suitable for monthly streamflow forecasting? Some experiment evidences. Journal of Hydrology, 530(1–2), 137–152. https://doi.org/10.1016/j.jhydrol.2015.09.047 [Google Scholar] [CrossRef]
14. Poul A. K., Shourian M., Ebrahimi H. (2019). A comparative study of MLR, KNN, ANN and ANFIS models with wavelet transform in monthly stream flow prediction. Water Resources Management, 33(8), 2907–2923. https://doi.org/10.1007/s11269-019-02273-0 [Google Scholar] [CrossRef]
15. Reis, G. B., da Silva, D. D., Fernandes, F. E. I., Moreira, M. C., Veloso, G. V. et al. (2021). Effect of environmental covariable selection in the hydrological modeling using machine learning models to predict daily streamflow. Journal of Environmental Management, 290, 112625. https://doi.org/10.1016/j.jenvman.2021.112625 [Google Scholar] [PubMed] [CrossRef]
16. Shu, X., Ding, W., Peng, Y., Wang, Z., Wu, J. et al. (2021). Monthly streamflow forecasting using convolutional neural network. Water Resources Management, 35(15), 5089–5104. https://doi.org/10.1007/s11269-021-02961-w [Google Scholar] [CrossRef]
17. Bach, H. C., Torkil, J., Dang, T. T., Emerton, L., Facon, T. et al. (2011). From local water she management to integrated river basin management at national and transboundary levels. Watershed Management Scientific Report, 1, 4–5. [Google Scholar]
18. Meng, E., Huang, S., Huang, Q., Fang, W., Wang, H. et al. (2021). A hybrid VMD-SVM model for practical streamflow prediction using an innovative input selection framework. Water Resources Management, 35(4), 1321–1337. https://doi.org/10.1007/s11269-021-02786-7 [Google Scholar] [CrossRef]
19. Tao, H., Al-Sulttani, A. O., Salih, A., Ali, Z. H., Al-Ansari, N. et al. (2020). Training and testing data division influence on hybrid machine learning model process: Application of river flow forecasting. Complexity, 2020(5), 1–22. https://doi.org/10.1155/2020/8844367 [Google Scholar] [CrossRef]
20. Ehteram, M., Afan, H. A., Dianatikhah, M., Ahmed, A. N., Ming, F. C. et al. (2019). Assessing the predictability of an improved ANFIS model for monthly streamflow using lagged climate indices as predictors. Water, 11(6), 1130. https://doi.org/10.3390/w11061130 [Google Scholar] [CrossRef]
21. Meshram, S. G., Meshram, C., Santos, C. A. G., Benzougagh, B., Khedher, K. M. (2021). Streamflow prediction based on artificial intelligence techniques. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 46(3), 2393–2403. https://doi.org/10.1007/s40996-021-00696-7 [Google Scholar] [CrossRef]
22. Hu, Y., Wang, J., Liu, T., Li, B., Tang, T. et al. (2018). Long-term streamflow forecasting using SWAT through the integration of the random forests precipitation generator: Case study of Danjiangkou Reservoir. Hydrology Research, 49(5), 1513–1527. https://doi.org/10.2166/nh.2017.085 [Google Scholar] [CrossRef]
23. Gunathilake, M. B., Karunanayake, C., Gunathilake, A. S., Marasingha, N., Samarasinghe, J. T. et al. (2021). Hydrological models and artificial neural networks (ANNs) to simulate streamflow in a tropical catchment of Sri Lanka. Applied Computational Intelligence and Soft Computing, 2021(4), 1–9. https://doi.org/10.1155/2021/6683389 [Google Scholar] [CrossRef]
24. Hadi, S. J., Tombul, M. (2018). Streamflow forecasting using four wavelet transformation combinations approaches with data-driven models: A comparative study. Water Resources Management, 32(14), 4661–4679. https://doi.org/10.1007/s11269-018-2077-3 [Google Scholar] [CrossRef]
25. Halit, A., Mohammad, T. S., Kambiz, F., Ramendra, P. (2021). Artificial intelligence modelling integrated with singular spectral analysis and seasonal-trend decomposition using loess approaches for streamflow predictions. Journal of Hydrology, 600(1), 126506. https://doi.org/10.1016/j.jhydrol.2021.126506 [Google Scholar] [CrossRef]
26. Li, F. F., Wang, Z. Y., Zhao, X., Xie, E., Qiu, J. (2019). Decomposition-ANN methods for long-term discharge prediction based on fisher’s ordered clustering with MESA. Water Resources Management, 33(9), 3095–3110. https://doi.org/10.1007/s11269-019-02295-8 [Google Scholar] [CrossRef]
27. Mohammed, M., Alquraish, M. K. (2021). Remote-sensing-based streamflow forecasting using artificial neural network and support vector machine models. Remote Sensing, 13(20), 4147. https://doi.org/10.3390/rs13204147 [Google Scholar] [CrossRef]
28. Ahmed, A. N., Van, L. T., Hung, N. D., Van, T., Kisi, O. et al. (2021). A comprehensive comparison of recent developed meta-heuristic algorithms for streamflow time series forecasting problem. Applied Soft Computing, 105, 107282. https://doi.org/10.1016/j.asoc.2021.107282 [Google Scholar] [CrossRef]
29. Khairan, H. E., Zubaidi, S. L., Muhsen, Y. R., Al-Ansari, N. (2022). Parameter optimisation-based hybrid reference evapotranspiration prediction models: A systematic review of current implementations and future research directions. Atmosphere, 14(1), 77. https://doi.org/10.3390/atmos14010077 [Google Scholar] [CrossRef]
30. Riahi, M. H., Dehghani, M., Memarzadeh, R., Gharabaghi, B. (2021). Short to long-term forecasting of river flows by heuristic optimisation algorithms hybridised with ANFIS. Water Resources Management, 35(4), 1149–1166. https://doi.org/10.1007/s11269-020-02756-5 [Google Scholar] [CrossRef]
31. Zubaidi, S. L., Hashim, K., Ethaib, S., Al-Bdairi, N. S. S., Al-Bugharbee, H. et al. (2022). A novel methodology to predict monthly municipal water demand based on weather variables scenario. Journal of King Saud University—Engineering Sciences, 34(3), 163–169. https://doi.org/10.1016/j.jksues.2020.09.011 [Google Scholar] [CrossRef]
32. Kilinc, H. C., Haznedar, B. (2022a). A hybrid model for streamflow forecasting in the basin of euphrates. Water, 14(1), 80. https://doi.org/10.3390/w14010080 [Google Scholar] [CrossRef]
33. Tikhamarine, Y., Souag, G. D., Najah, A. A., Kisi, O., El-Shafie, A. (2019a). Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (GWO) algorithm. Journal of Hydrology, 582, 124435. https://doi.org/10.1016/j.jhydrol.2019.124435 [Google Scholar] [CrossRef]
34. Shyama, D., Choudhury, P. (2020). River flow prediction with memory-based artificial neural networks: A case study of the Dholai river basin. International Journal of Advanced Intelligence Paradigms, 15(1), 51–62. https://doi.org/10.1504/IJAIP.2020.104106 [Google Scholar] [CrossRef]
35. Zaini, N., Malek, M. A., Yusoff, M., Osmi, S. F. C., Mardi, N. H. et al. (2018). Bat algorithm and neural network for monthly streamflow prediction. AIP Conference Proceedings, 2030, 020260-020261–020260-020266. https://doi.org/10.1063/1.5066901 [Google Scholar] [CrossRef]
36. Adnan, R. M., Kisi, O., Mostafa, R. R., Ahmed, A. N., El-Shafie, A. (2022). The potential of a novel support vector machine trained with modified mayfly optimization algorithm for streamflow prediction. Hydrological Sciences Journal, 67(2), 161–174. https://doi.org/10.1080/02626667.2021.2012182 [Google Scholar] [CrossRef]
37. Tikhamarine, Y., Souag-Gamane, D., Kisi, O. (2019b). A new intelligent method for monthly streamflow prediction: Hybrid wavelet support vector regression based on grey wolf optimizer (WSVR-GWO). Arabian Journal of Geosciences, 12(17), 540. https://doi.org/10.1007/s12517-019-4697-1 [Google Scholar] [CrossRef]
38. Hajirahimi, Z., Khashei, M. (2022). Hybridization of hybrid structures for time series forecasting: A review. Artificial Intelligence Review, 56(2), 1201–1261. https://doi.org/10.1007/s10462-022-10199-0 [Google Scholar] [CrossRef]
39. Alawsi, M. A., Zubaidi, S. L., Al-Bdairi, N. S. S., Al-Ansari, N., Hashim, K. (2022). Drought forecasting: A review and assessment of the hybrid techniques and data pre-processing. Hydrology, 9(7), 115. https://doi.org/10.3390/hydrology9070115 [Google Scholar] [CrossRef]
40. Adnan, R. M., Liang, Z., Kuriqi, A., Kisi, O., Malik, A. et al. (2020). Streamflow forecasting using heuristic machine learning methods. Proceedings of 2020 2nd International Conference on Computer and Information Sciences (ICCIS), pp. 1–6. Aljouf, Saudi Arabia. [Google Scholar]
41. Kilinc, H. C., Yurtsever, A. (2022b). Short-term streamflow forecasting using hybrid deep learning model based on grey wolf algorithm for hydrological time series. Sustainability, 14(6), 3352. https://doi.org/10.3390/su14063352 [Google Scholar] [CrossRef]
42. Zakhrouf, M., Bouchelkia, H., Stamboul, M., Kim, S. (2019). Novel hybrid approaches based on evolutionary strategy for streamflow forecasting in the Chellif River, Algeria. Acta Geophysica, 68(1), 167–180. https://doi.org/10.1007/s11600-019-00380-5 [Google Scholar] [CrossRef]
43. Zhenghao, Z., Zhang, Q., Singh, V. P. (2018). Univariate streamflow forecasting using commonly used data-driven models: Literature review and case study. Hydrological Sciences Journal, 63(7), 1091–1111. https://doi.org/10.1080/02626667.2018.1469756 [Google Scholar] [CrossRef]
44. Shiri, J., Kisi, O. (2010). Short-term and long-term streamflow forecasting using a wavelet and neuro-fuzzy conjunction model. Journal of Hydrology, 394(3–4), 486–493. https://doi.org/10.1016/j.jhydrol.2010.10.008 [Google Scholar] [CrossRef]
45. Pham, Q. B., Afan, H. A., Mohammadi, B., Ahmed, A. N., Linh, N. T. T. et al. (2020). Hybrid model to improve the river streamflow forecasting utilising multi-layer perceptron-based intelligent water drop optimisation algorithm. Soft Computing, 24(23), 18039–18056. https://doi.org/10.1007/s00500-020-05058-5 [Google Scholar] [CrossRef]
46. Marques, C. A. F., Ferreira, J. A., Rocha, A., Castanheira, J. M., Melo-Gonçalves, P. et al. (2006). Singular spectrum analysis and forecasting of hydrological time series. Physics and Chemistry of the Earth, Parts A/B/C, 31(18), 1172–1179. https://doi.org/10.1016/j.pce.2006.02.061 [Google Scholar] [CrossRef]
47. Kabbilawsh, P., Kumar, D. S., Chithra, N. R. (2022). Performance evaluation of univariate time-series techniques for forecasting monthly rainfall data. Journal of Water and Climate Change, 13(12), 4151–4176. https://doi.org/10.2166/wcc.2022.107 [Google Scholar] [CrossRef]
48. Danandeh Mehr, A., Safari, M. J. S. (2021). Genetic programming for streamflow forecasting. In: Advances in streamflow forecasting, pp. 193–214. Elsevier, Amsterdam, Netherlands. https://doi.org/10.1016/B978-0-12-820673-7.00007-X [Google Scholar] [CrossRef]
49. Hu, M., Li, W., Yan, K., Ji, Z., Hu, H. (2019). Modern machine learning techniques for univariate tunnel settlement forecasting: A comparative study. Mathematical Problems in Engineering, 2019(10), 1–12. https://doi.org/10.1155/2019/7057612 [Google Scholar] [CrossRef]
50. Sammen, S. S., Ehteram, M., Abba, S. I., Abdulkadir, R. A., Ahmed, A. N. et al. (2021). A new soft computing model for daily streamflow forecasting. Stochastic Environmental Research and Risk Assessment, 35(12), 2479–2491. https://doi.org/10.1007/s00477-021-02012-1 [Google Scholar] [CrossRef]
51. Ahmed, M. S., Mohamed, A., Khatib, T., Shareef, H., Homod, R. Z. et al. (2017). Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy and Buildings, 138(3), 215–227. https://doi.org/10.1016/j.enbuild.2016.12.052 [Google Scholar] [CrossRef]
52. Zubaidi, S. L., Abdulkareem, I. H., Hashim, K. S., Al-Bugharbee, H., Ridha, H. M. et al. (2020). Hybridised artificial neural network model with slime mould algorithm: A novel methodology for prediction of urban stochastic water demand. Water, 12(10), 2692. https://doi.org/10.3390/w12102692 [Google Scholar] [CrossRef]
53. Jiang, Y., Bao, X., Hao, S., Zhao, H., Li, X. et al. (2020). Monthly streamflow forecasting using ELM-IPSO based on phase space reconstruction. Water Resources Management, 34(11), 3515–3531. https://doi.org/10.1007/s11269-020-02631-3 [Google Scholar] [CrossRef]
54. Feng, Z. K, Niu, W. J. (2021). Hybrid artificial neural network and cooperation search algorithm for nonlinear river flow time series forecasting in humid and semi-humid regions. Knowledge-Based Systems, 211, 106580. https://doi.org/10.1016/j.knosys.2020.106580 [Google Scholar] [CrossRef]
55. Ren, K., Wang, X., Shi, X., Qu, J., Fang, W. (2021). Examination and comparison of binary metaheuristic wrapper-based input variable selection for local and global climate information-driven one-step monthly streamflow forecasting. Journal of Hydrology, 597, 126152. https://doi.org/10.1016/j.jhydrol.2021.126152 [Google Scholar] [CrossRef]
56. Fatemeh, M. E. B., Ali, N. A., Huang, Y. H., Mosavi, A. E. S. (2021). Streamflow prediction with large climate indices using several hybrid multilayer perceptrons and copula Bayesian model averaging. Ecological Indicators, 133(1), 108285. https://doi.org/10.1016/j.ecolind.2021.108285 [Google Scholar] [CrossRef]
57. Zhao, X., Lv, H., Wei, Y., Lv, S., Zhu, X. (2021a). Streamflow forecasting via two types of predictive structure-based gated recurrent unit models. Water, 13(1), 91. https://doi.org/10.3390/w13010091 [Google Scholar] [CrossRef]
58. Zubaidi, S. L., Martorell, O. S., Al-Bugharbee, H., Olier, I., Hashim, K. S. et al. (2020). Urban water demand prediction for a city that suffers from climate change and population growth: Gauteng province case study. Water, 12(7), 1885. https://doi.org/10.3390/w12071885 [Google Scholar] [CrossRef]
59. Altunkaynak, A., Kartal, E. (2019). Performance comparison of continuous Wavelet-Fuzzy and discrete Wavelet-Fuzzy models for water level predictions at northern and southern boundary of Bosphorus. Ocean Engineering, 186(1), 106097. https://doi.org/10.1016/j.oceaneng.2019.06.002 [Google Scholar] [CrossRef]
60. Xie, Z., Liu, Q., Cao, Y. (2021). Hybrid deep learning modeling for water level prediction in Yangtze River. Intelligent Automation & Soft Computing, 28(1), 153–166. https://doi.org/10.32604/iasc.2021.016246 [Google Scholar] [CrossRef]
61. Zhao, X., Lv, H., Lv, S., Sang, Y., Wei, Y. et al. (2021b). Enhancing robustness of monthly streamflow forecasting model using gated recurrent unit based on improved grey wolf optimiser. Journal of Hydrology, 601(6), 126607. https://doi.org/10.1016/j.jhydrol.2021.126607 [Google Scholar] [CrossRef]
62. Al-Bugharbee, H., Trendafilova, I. (2016). A fault diagnosis methodology for rolling element bearings based on advanced signal pretreatment and autoregressive modelling. Journal of Sound and Vibration, 369, 246–265. https://doi.org/10.1016/j.jsv.2015.12.052 [Google Scholar] [CrossRef]
63. Liu, H., Mi, X., Li, Y. (2018). Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LSTM network and ELM. Energy Conversion and Management, 159(December 2016), 54–64. https://doi.org/10.1016/j.enconman.2018.01.010 [Google Scholar] [CrossRef]
64. Ma, X., Jin, Y., Dong, Q. (2017). A generalised dynamic fuzzy neural network based on singular spectrum analysis optimised by brain storm optimisation for short-term wind speed forecasting. Applied Soft Computing, 54, 296–312. https://doi.org/10.1016/j.asoc.2017.01.033 [Google Scholar] [CrossRef]
65. Ouyang, Q., Lu, W. (2017). Monthly rainfall forecasting using echo state networks coupled with data preprocessing methods. Water Resources Management, 32(2), 659–674. https://doi.org/10.1007/s11269-017-1832-1 [Google Scholar] [CrossRef]
66. Polomčić, D., Gligorić, Z., Bajić, D., Cvijović, Č. (2017). A hybrid model for forecasting groundwater levels based on fuzzy C-mean clustering and singular spectrum analysis. Water, 9(7), 541. https://doi.org/10.3390/w9070541 [Google Scholar] [CrossRef]
67. Unnikrishnan, P., Jothiprakash, V. (2018). Daily rainfall forecasting for one year in a single run using singular spectrum analysis. Journal of Hydrology, 561, 609–621. https://doi.org/10.1016/j.jhydrol.2018.04.032 [Google Scholar] [CrossRef]
68. Abdourahamane, Z. S., Acar, R., Serkan, Ş. (2019). Wavelet-copula-based mutual information for rainfall forecasting applications. Hydrological Processes, 33(7), 1127–1142. https://doi.org/10.1002/hyp.13391 [Google Scholar] [CrossRef]
69. Bouzgou, H., Gueymard, C. A. (2019). Fast short-term global solar irradiance forecasting with wrapper mutual information. Renewable Energy, 133, 1055–1065. https://doi.org/10.1016/j.renene.2018.10.096 [Google Scholar] [CrossRef]
70. Lv, N., Liang, X., Chen, C., Zhou, Y., Li, J. et al. (2020). A long short-term memory cyclic model with mutual information for hydrology forecasting: A case study in the Xixian Basin. Advances in Water Resources, 141(1–2), 103622. https://doi.org/10.1016/j.advwatres.2020.103622 [Google Scholar] [CrossRef]
71. Mehr, A. D., Gandomi, A. H. (2021). MSGP-LASSO: An improved multi-stage genetic programming model for streamflow prediction. Information Sciences, 561(15), 181–195. https://doi.org/10.1016/j.ins.2021.02.011 [Google Scholar] [CrossRef]
72. Khoojine, S. A., Shadabfar, M., Tabriz, E. Y. (2022). A mutual information-based network autoregressive model for crude oil price forecasting using open-high-low-close prices. Mathematics, 10(17), 3172. https://doi.org/10.3390/math10173172 [Google Scholar] [CrossRef]
73. Belvederesi, C., Zaghloul, M. S., Achari, G., Gupta, A., Hassan, Q. K. (2022). Modelling river flow in cold and ungauged regions: A review of the purposes, methods, and challenges. Environmental Reviews, 30(1), 159–173. https://doi.org/10.1139/er-2021-0043 [Google Scholar] [CrossRef]
74. Ibrahim, K. S. M. H., Huang, Y. F., Ahmed, A. N., Koo, C. H., El-Shafie, A. (2021). A review of the hybrid artificial intelligence and optimisation modelling of hydrological streamflow forecasting. Alexandria Engineering Journal, 61(1), 279–303. https://doi.org/10.1016/j.aej.2021.04.100 [Google Scholar] [CrossRef]
75. Troin, M. R. A., Andrew, W. W., François, B., Martel, J. L. (2021). Generating ensemble streamflow forecasts: A review of methods and approaches over the past 40 years. Water Resources Research, 57(7). https://doi.org/10.1029/2020WR028392 [Google Scholar] [CrossRef]
76. Terrier, M., Perrin, C., de Lavenne, A., Andréassian, V., Lerat, J. et al. (2020). Streamflow naturalisation methods: A review. Hydrological Sciences Journal, 66(1), 12–36. https://doi.org/10.1080/02626667.2020.1839080 [Google Scholar] [CrossRef]
77. Khudhair, Z. S., Zubaidi, S. L., Martorell, O. S., Al-Ansari, N., Ethaib, S. et al. (2022). A review of hybrid soft computing and data pre-processing techniques to forecast freshwater quality’s parameters: Current trends and future directions. Environments, 9(7), 85. https://doi.org/10.3390/environments9070085 [Google Scholar] [CrossRef]
78. Sundararajan, K., Garg, L., Srinivasan, K., Bashir, K. A., Kaliappan, J. et al. (2021). A contemporary review on drought modeling using machine learning approaches. Computer Modeling in Engineering & Sciences, 128(2), 447–487. https://doi.org/10.32604/cmes.2021.015528 [Google Scholar] [CrossRef]
79. Anusree, K., Varghese, K. O. (2016). Streamflow prediction of Karuvannur river basin using ANFIS, ANN and MNLR models. Procedia Technology, 24, 101–108. https://doi.org/10.1016/j.protcy.2016.05.015 [Google Scholar] [CrossRef]
80. Edossa, D. C., Babel, M. S. (2011). Application of ANN-based streamflow forecasting model for agricultural water management in the Awash River Basin, Ethiopia. Water Resources Management, 25(6), 1759–1773. https://doi.org/10.1007/s11269-010-9773-y [Google Scholar] [CrossRef]
81. Freire, P. K. D. M. M., Santos, C. A. G., Silva, G. B. L. D. (2019). Analysis of the use of discrete wavelet transforms coupled with ANN for short-term streamflow forecasting. Applied Soft Computing, 80(2), 494–505. https://doi.org/10.1016/j.asoc.2019.04.024 [Google Scholar] [CrossRef]
82. Noori, N., Kalin, L. (2016). Coupling SWAT and ANN models for enhanced daily streamflow prediction. Journal of Hydrology, 533(1), 141–151. https://doi.org/10.1016/j.jhydrol.2015.11.050 [Google Scholar] [CrossRef]
83. Taormina, R., Chau, K. W. (2015). ANN-based interval forecasting of streamflow discharges using the LUBE method and MOFIPS. Engineering Applications of Artificial Intelligence, 45, 429–440. https://doi.org/10.1016/j.engappai.2015.07.019 [Google Scholar] [CrossRef]
84. Tiu, E. S. K., Huang, Y. F., Ng, J. L., AlDahoul, N., Ahmed, A. N. et al. (2021). An evaluation of various data pre-processing techniques with machine learning models for water level prediction. Natural Hazards, 110(1), 121–153. https://doi.org/10.1007/s11069-021-04939-8 [Google Scholar] [CrossRef]
85. Dariane, A. B., Azimi, S. (2016). Forecasting streamflow by combination of a genetic input selection algorithm and wavelet transforms using ANFIS models. Hydrological Sciences Journal, 61(3), 585–600. https://doi.org/10.1080/02626667.2014.988155 [Google Scholar] [CrossRef]
86. Hashimi, S. A., Dalkiliç, H. Y. (2020). Prediction of daily streamflow using artificial neural networks (ANNswavelet neural networks (WNNsand adaptive neuro-fuzzy inference system (ANFIS) models. Water Supply, 20(4), 1396–1408. https://doi.org/10.2166/ws.2020.062 [Google Scholar] [CrossRef]
87. Sharma, S., Srivastava, P., Fang, X., Kalin, L. (2015). Performance comparison of adoptive neuro fuzzy inference system (ANFIS) with loading simulation program C++ (LSPC) model for streamflow simulation in el niño southern oscillation (ENSO)-affected watershed. Expert Systems with Applications, 42(4), 2213–2223. https://doi.org/10.1016/j.eswa.2014.09.062 [Google Scholar] [CrossRef]
88. Wang, Z. L., Li, Y. M, Sha, J., Li, X. (2018). Comparison of hybrid models for daily streamflow prediction in a forested basin. Journal of Hydroinformatics, 20(1), 191–205. https://doi.org/10.2166/hydro.2017.189 [Google Scholar] [CrossRef]
89. Yaseen, Z. M., Ebtehaj, I., Bonakdari, H., Deo, R. C., Mehr, D. A. et al. (2017). Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. Journal of Hydrology, 554(2), 263–276. https://doi.org/10.1016/j.jhydrol.2017.09.007 [Google Scholar] [CrossRef]
90. Erdal, H. I., Karakurt, O. (2013). Advancing monthly streamflow prediction accuracy of CART models using ensemble learning paradigms. Journal of Hydrology, 477(5), 119–128. https://doi.org/10.1016/j.jhydrol.2012.11.015 [Google Scholar] [CrossRef]
91. Liu, Z., Zhou, P., Chen, G., Guo, L. (2014). Evaluating a coupled discrete wavelet transform and support vector regression for daily and monthly streamflow forecasting. Journal of Hydrology, 519(3–4), 2822–2831. https://doi.org/10.1016/j.jhydrol.2014.06.050 [Google Scholar] [CrossRef]
92. Maity, R., Bhagwat, P. P., Bhatnagar, A. (2010). Potential of support vector regression for prediction of monthly streamflow using endogenous property. Hydrological Processes, 24(7), 917–923. https://doi.org/10.1002/hyp.7535 [Google Scholar] [CrossRef]
93. Malik, A., Tikhamarine, Y., Souag-Gamane, D., Kisi, O., Pham, Q. B. (2020). Support vector regression optimized by meta-heuristic algorithms for daily streamflow prediction. Stochastic Environmental Research and Risk Assessment, 34(11), 1755–1773. https://doi.org/10.1007/s00477-020-01874-1 [Google Scholar] [CrossRef]
94. Costa, A. C., Estacio, A. B. S., de Souza, F. D. A., Lima, I. E. (2021). Monthly and seasonal streamflow forecasting of large dryland catchments in Brazil. Journal of Arid Land, 13(3), 205–223. https://doi.org/10.1007/s40333-021-0097-y [Google Scholar] [CrossRef]
95. Nowak, K., Prairie, J., Rajagopalan, B., Lall, U. (2010). A nonparametric stochastic approach for multisite disaggregation of annual to daily streamflow. Water Resources Research, 46(8). https://doi.org/10.1029/2009WR008530 [Google Scholar] [CrossRef]
96. Tongal, H. (2020). Comparison of local and global approximators in multivariate chaotic forecasting of daily streamflow. Hydrological Sciences Journal, 65(7), 1129–1144. https://doi.org/10.1080/02626667.2020.1732983 [Google Scholar] [CrossRef]
97. Tongal, H., Berndtsson, R. (2016). Impact of complexity on daily and multi-step forecasting of streamflow with chaotic, stochastic, and black-box models. Stochastic Environmental Research and Risk Assessment, 31(3), 661–682. https://doi.org/10.1007/s00477-016-1236-4 [Google Scholar] [CrossRef]
98. Tongal, H., Booij, M. J. (2016). A comparison of nonlinear stochastic self-exciting threshold autoregressive and chaotic k-nearest neighbour models in daily streamflow forecasting. Water Resources Management, 30(4), 1515–1531. https://doi.org/10.1007/s11269-016-1237-6 [Google Scholar] [CrossRef]
99. de Lima, D. B., Lima, M. D. C. E., Saigado, R. M. (2011). An empirical analysis of MLP neural networks applied to streamflow forecasting. IEEE Latin America Transactions, 9, 295–301. https://doi.org/10.1109/TLA.2011.5893775 [Google Scholar] [CrossRef]
100. Onyari, E. K., Ilunga, F. M. (2013). Application of MLP neural network and M5P model tree in predicting streamflow: A case study of luvuvhu catchment, South Africa. International Journal of Innovation, Management and Technology, 4, 11–15. https://doi.org/10.7763/IJIMT.2013.V4.347 [Google Scholar] [CrossRef]
101. Nacar, S., Hınıs, M. A., Kankal, M. (2017). Forecasting daily streamflow discharges using various neural network models and training algorithms. KSCE Journal of Civil Engineering, 22(9), 3676–3685. https://doi.org/10.1007/s12205-017-1933-7 [Google Scholar] [CrossRef]
102. Wang, W., Gelder, P. H. A. J. M. V., Vrijling, J. K., Ma, J. (2006). Forecasting daily streamflow using hybrid ANN models. Journal of Hydrology, 324(1–4), 383–399. https://doi.org/10.1016/j.jhydrol.2005.09.032 [Google Scholar] [CrossRef]
103. Samanataray, S., Sahoo, A. (2021). A comparative study on prediction of monthly streamflow using hybrid ANFIS-PSO approaches. KSCE Journal of Civil Engineering, 25(10), 4032–4043. https://doi.org/10.1007/s12205-021-2223-y [Google Scholar] [CrossRef]
104. Thapa, S., Zhao, Z., Li, B., Lu, L., Fu, D. et al. (2020). Snowmelt-driven streamflow prediction using machine learning techniques (LSTM, NARX, GPR, and SVR). Water, 12(6), 1734. https://doi.org/10.3390/w12061734 [Google Scholar] [CrossRef]
105. Espejo, P. G., Ventura, S., Herrera, F. (2010). A survey on the application of genetic programming to classification. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 40(2), 121–144. https://doi.org/10.1109/TSMCC.2009.2033566 [Google Scholar] [CrossRef]
106. Hebbalaguppae, P., Balasangameshwara, J., Sreeman, S., Desai, S., Bengaluru, K. A. (2021). Cognitive computing models for estimation of reference evapotranspiration: A review. Cognitive Systems Research, 70(3), 109–116. https://doi.org/10.1016/j.cogsys.2021.07.012 [Google Scholar] [CrossRef]
107. Zubaidi, S. L., Dooley, J., Alkhaddar, R. M., Abdellatif, M., Al-Bugharbee, H. et al. (2018). A Novel approach for predicting monthly water demand by combining singular spectrum analysis with neural networks. Journal of Hydrology, 561, 136–145. https://doi.org/10.1016/j.jhydrol.2018.03.047 [Google Scholar] [CrossRef]
108. Zubaidi, S., Al-Bugharbee, H., Ortega-Martorell, S., Gharghan, S., Olier, I. et al. (2020). A novel methodology for prediction urban water demand by wavelet denoising and adaptive neuro-fuzzy inference system approach. Water, 12(3), 1628. https://doi.org/10.3390/w12061628 [Google Scholar] [CrossRef]
109. Zhang, J., Li, H., Shi, X., Hong, Y. (2019). Wavelet-nonlinear cointegration prediction of irrigation water in the irrigation district. Water Resources Management, 33(8), 2941–2954. https://doi.org/10.1007/s11269-019-02270-3 [Google Scholar] [CrossRef]
110. So, J. M., Lee, J. H., Bae, D. H. (2020). Development of a hydrological drought forecasting model using weather forecasting data from GloSea5. Water, 12(10), 2785. https://doi.org/10.3390/w12102785 [Google Scholar] [CrossRef]
111. Zubaidi, S. L., Ortega-Martorell, S., Kot, P., Alkhaddar, R. M., Abdellatif, M. et al. (2020). A method for predicting long-term municipal water demands under climate change. Water Resources Management, 34(3), 1265–1279. https://doi.org/10.1007/s11269-020-02500-z [Google Scholar] [CrossRef]
112. Behboudian, S., Tabesh, M., Falahnezhad, M., Ghavanini, F. A. (2014). A long-term prediction of domestic water demand using preprocessing in artificial neural network. Journal of Water Supply: Research and Technology-Aqua, 63(1), 31–42. https://doi.org/10.2166/aqua.2013.085 [Google Scholar] [CrossRef]
113. Zubaidi, S. L., Kot, P., Alkhaddar, R. M., Abdellatif, M., Al-Bugharbee, H. (2018). Short-term water demand prediction in residential complexes: Case study in Columbia city, USA. Proceedings of 2018 11th International Conference on Developments in eSystems Engineering (DeSE), pp. 31–35. Cambridge, UK. [Google Scholar]
114. Hui, X., Pandey, G., Steinbach, M., Kumar, V. (2006). Enhancing data analysis with noise removal. IEEE Transactions on Knowledge and Data Engineering, 18(3), 304– 319. https://doi.org/10.1109/TKDE.2006.46 [Google Scholar] [CrossRef]
115. Tabachnick, B. G., Fidell, L. S., Ullman, J. B. (2007). Using multivariate statistics. Boston, MA, USA: Pearson. [Google Scholar]
116. Pallant, J. (2013). SPSS survival manual: A step by step guide to data analysis using IBM SPSS. Australian and New Zealand Journal of Public Health, 37(6), 597–598. https://doi.org/10.1111/1753-6405.12166 [Google Scholar] [CrossRef]
117. Zhanga, J., Song, R., Bhaskar, N. R., French, M. N. (2006). Short-term water demand forecasting: A case study. 8th Annual Water Distribution Systems Analysis Symposium, pp. 1–14. Cincinnati, Ohio, USA, United States. [Google Scholar]
118. Ghorbani, M. A., Kisi, O., Aalinezhad, M. (2010). A probe into the chaotic nature of daily streamflow time series by correlation dimension and largest Lyapunov methods. Applied Mathematical Modelling, 34(12), 4050–4057. https://doi.org/10.1016/j.apm.2010.03.036 [Google Scholar] [CrossRef]
119. Peng, F., Wen, J., Zhang, Y., Jin, J. (2020). Monthly streamflow prediction based on random forest algorithm and phase space reconstruction theory. 8th Annual International Conference on Material Science and Engineering (ICMSE2020), pp. 1637. Guiyang, Guizhou, China. https://dx.doi.org/10.1088/1742-6596/1637/1/012091 [Google Scholar] [CrossRef]
120. Azad, A., Farzin, S., Kashi, H., Sanikhani, H., Karami, H. et al. (2018). Prediction of river flow using hybrid neuro-fuzzy models. Arabian Journal of Geosciences, 11(22), 718. https://doi.org/10.1007/s12517-018-4079-0 [Google Scholar] [CrossRef]
121. Danandeh, M. A. (2018). An improved gene expression programming model for streamflow forecasting in intermittent streams. Journal of Hydrology, 563(4), 669–678. https://doi.org/10.1016/j.jhydrol.2018.06.049 [Google Scholar] [CrossRef]
122. Yaseen, Z. M., Mohtar, W. H. M. W., Ameen, A. M. S., Ebtehaj, I., Razali, S. F. M. et al. (2019). Implementation of univariate paradigm for streamflow simulation using hybrid data-driven model: Case study in tropical region. IEEE Access, 7, 74471–74481. https://doi.org/10.1109/ACCESS.2019.2920916 [Google Scholar] [CrossRef]
123. Niu, W. J., Feng, Z. K., Yang, W. F., Zhang, J. (2020). Short-term streamflow time series prediction model by machine learning tool based on data preprocessing technique and swarm intelligence algorithm. Hydrological Sciences Journal, 65(15), 2590–2603. https://doi.org/10.1080/02626667.2020.1828889 [Google Scholar] [CrossRef]
124. Tripura, J., Roy, P., Barbhuiya, A. K. (2020). Simultaneous streamflow forecasting based on hybridized neuro-fuzzy method for a river system. Neural Computing and Applications, 33(8), 3221–3233. https://doi.org/10.1007/s00521-020-05194-x [Google Scholar] [CrossRef]
125. Kilinc, H. C. (2022c). Daily streamflow forecasting based on the hybrid particle swarm optimisation and long short-term memory model in the Orontes Basin. Water, 14(3), 490. https://doi.org/10.3390/w14030490 [Google Scholar] [CrossRef]
126. Meshram, S. G., Ghorbani, M. A., Shamshirband, S., Karimi, V., Meshram, C. (2018). River flow prediction using hybrid PSOGSA algorithm based on feed-forward neural network. Soft Computing, 23(20), 10429–10438. https://doi.org/10.1007/s00500-018-3598-7 [Google Scholar] [CrossRef]
127. Mohammadi, B., Ahmadi, F., Mehdizadeh, S., Guan, Y., Pham, Q. B. et al. (2020). Developing novel robust models to improve the accuracy of daily streamflow modeling. Water Resources Management, 34(10), 3387–3409. https://doi.org/10.1007/s11269-020-02619-z [Google Scholar] [CrossRef]
128. Zakhrouf, M., Hamid, B., Kim, S., Madani, S. (2021). Novel insights for streamflow forecasting based on deep learning models combined the evolutionary optimisation algorithm. Physical Geography, 44(1), 1–24. https://doi.org/10.1080/02723646.2021.1943126 [Google Scholar] [CrossRef]
129. Zakhrouf, M., Bouchelkia, H., Stamboul, M., Kim, S., Heddam, S. (2018). Time series forecasting of river flow using an integrated approach of wavelet multi-resolution analysis and evolutionary data-driven models. A case study: Sebaou River (Algeria). Physical Geography, 39(5), 506–522. https://doi.org/10.1080/02723646.2018.1429245 [Google Scholar] [CrossRef]
130. Samui, P., Yesilyurt, S. N., Dalkilic, H. Y., Yaseen, Z. M., Roy, S. S. et al. (2022). Comparison of different optimized machine learning algorithms for daily river flow forecasting. Earth Science Informatics, 16(1), 533–548. https://doi.org/10.1007/s12145-022-00896-3 [Google Scholar] [CrossRef]
131. Abdul Kareem, B., Zubaidi, S. L., Hussein, M. R., Al-Ansari, N., Nabeel, S. S. (2022). Applicability of ANN model and CPSOCGSA algorithm for multi-time step ahead river streamflow forecasting. Hydrology, 9(10), 171. https://doi.org/10.3390/hydrology9100171 [Google Scholar] [CrossRef]
132. Nguyen, D. H., Le, X. H., Anh, D. T., Kim, S. H., Bae, D. H. (2022). Hourly streamflow forecasting using a Bayesian additive regression tree model hybridized with a genetic algorithm. Journal of Hydrology, 606(3–4), 127445. https://doi.org/10.1016/j.jhydrol.2022.127445 [Google Scholar] [CrossRef]
133. Ikram, R. M. A., Ewees, A. A., Parmar, K. S., Yaseen, Z. M., Shahid, S. et al. (2022). The viability of extended marine predators algorithm-based artificial neural networks for streamflow prediction. Applied Soft Computing, 131(182), 109739. https://doi.org/10.1016/j.asoc.2022.109739 [Google Scholar] [CrossRef]
134. Adnan, R. M., Mostafa, R. R., Elbeltagi, A., Yaseen, Z. M., Shahid, S. et al. (2022). Development of new machine learning model for streamflow prediction: Case studies in Pakistan. Stochastic Environmental Research and Risk Assessment, 36(4), 999–1033. https://doi.org/10.1007/s00477-021-02111-z [Google Scholar] [CrossRef]
135. Ahmadi, F., Mehdizadeh, S., Mohammadi, B. (2021). Development of bio-inspired- and wavelet-based hybrid models for reconnaissance drought index modeling. Water Resources Management, 35(12), 4127–4147. https://doi.org/10.1007/s11269-021-02934-z [Google Scholar] [CrossRef]
136. Aria, M., Cuccurullo, C. (2017). Bibliometrix: An R-tool for comprehensive science mapping analysis. Journal of Informetrics, 11(4), 959–975. https://doi.org/10.1016/j.joi.2017.08.007 [Google Scholar] [CrossRef]
137. Donkor, E. A., Mazzuchi, T. A., Soyer, R., Alan Roberson, J. (2014). Urban water demand forecasting: Review of methods and models. Journal of Water Resources Planning and Management, 140(2), 146–159. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000314 [Google Scholar] [CrossRef]
138. Elavarasan, D., Vincent, D. R., Sharma, V., Zomaya, A. Y., Srinivasan, K. (2018). Forecasting yield by integrating agrarian factors and machine learning models: A survey. Computers and Electronics in Agriculture, 155(2), 257–282. https://doi.org/10.1016/j.compag.2018.10.024 [Google Scholar] [CrossRef]
139. Heo, K. Y., Ha, K. J., Yun, K. S., Lee, S. S., Kim, H. J. et al. (2014). Methods for uncertainty assessment of climate models and model predictions over East Asia. International Journal of Climatology, 34(2), 377–390. https://doi.org/10.1002/joc.3692 [Google Scholar] [CrossRef]
140. Touchette P. E., MacDonald R. F., Langer S. N. (1985). A scatter plot for identifying stimulus control of problem behavior. Journal of Applied Behavior Analysis, 189(4), 343–351. https://doi.org/10.1901/jaba.1985.18-343 [Google Scholar] [PubMed] [CrossRef]
141. Wang, Y., Han, F., Zhu, L., Deussen, O., Chen, B. (2017). Line graph or scatter plot? Automatic selection of methods for visualizing trends in time series. IEEE Transactions on Visualization and Computer Graphics, 24(2), 1141–1154. https://doi.org/10.1109/TVCG.2017.2653106 [Google Scholar] [PubMed] [CrossRef]
142. Rahman, M. M., Shakeri, M., Tiong, S., Khatun, F., Amin, N. et al. (2021). Prospective methodologies in hybrid renewable energy systems for energy prediction using artificial neural networks. Sustainability, 13(4), 2393. https://doi.org/10.3390/su13042393 [Google Scholar] [CrossRef]
143. Myttenaere, A., Golden, B., Le Grand, B., Rossi, F. (2016). Mean absolute percentage error for regression models. Neurocomputing, 192(1), 38–48. https://doi.org/10.1016/j.neucom.2015.12.114 [Google Scholar] [CrossRef]
144. Afan, H. A., Allawi, M. F., El-Shafie, A., Yaseen, Z. M., Ahmed, A. N. et al. (2020). Input attributes optimisation using the feasibility of genetic nature inspired algorithm: Application of river flow forecasting. Scientific Reports, 10(1), 4684. https://doi.org/10.1038/s41598-020-61355-x [Google Scholar] [PubMed] [CrossRef]
145. Dawson, C. W., Abrahart, R. J., See, L. M. (2007). HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environmental Modelling & Software, 22(7), 1034–1052. https://doi.org/10.1016/j.envsoft.2006.06.008 [Google Scholar] [CrossRef]
146. Mohammed, S. J., Zubaidi, S. L., Al-Ansari, N., Ridha, H. M., Al-Bdairi, N. S. S. et al. (2022). Hybrid technique to improve the river water level forecasting using artificial neural network-based marine predators algorithm. Advances in Civil Engineering, 2022(5267), 1–14. https://doi.org/10.1155/2022/6955271 [Google Scholar] [CrossRef]
147. Nash, J. E., Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I—A discussion of principles. Journal of Hydrology, 10(3), 282–290. https://doi.org/10.1016/0022-1694(70)90255-6 [Google Scholar] [CrossRef]
148. Ren, T., Liu, X., Niu, J., Lei, X., Zhang, Z. (2020). Real-time water level prediction of cascaded channels based on multilayer perception and recurrent neural network. Journal of Hydrology, 585(1), 124783. https://doi.org/10.1016/j.jhydrol.2020.124783 [Google Scholar] [CrossRef]
149. Okkan, U., Ali Serbes, Z. (2013). The combined use of wavelet transform and black box models in reservoir inflow modeling. Journal of Hydrology and Hydromechanics, 61(2), 112–119. https://doi.org/10.2478/johh-2013-0015 [Google Scholar] [CrossRef]
150. Shiri, J., Kişi, Ö. (2011). Comparison of genetic programming with neuro-fuzzy systems for predicting short-term water table depth fluctuations. Computers & Geosciences, 37(10), 1692–1701. https://doi.org/10.1016/j.cageo.2010.11.010 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF


 Downloads
Downloads
 Citation Tools
Citation Tools