Federated Learning Model for Auto Insurance Rate Setting Based on Tweedie Distribution

1  Introduction

In recent years, there has been a growing interest in the analysis of vehicle insurance data. Currently, many property and casualty insurance companies face a high combined cost ratio, with motor insurance accounting for a significant portion of the overall costs. In this context, usage-based insurance (UBI) for vehicles has emerged as a competitive product in the commercial vehicle insurance market. UBI premiums are determined based on specific vehicle usage behavior and the corresponding level of risk. Insurers collect data during the underwriting cycle to extract appropriate risk type parameters for different driving behaviors and habits of insured vehicles. These parameters are then used to adjust the traditional commercial vehicle insurance premiums for the next cycle, ultimately determining differentiated premiums for the insured vehicles. However, there is currently no clear standard for the differentiated premium adjustment mechanism of vehicle UBI products. It can only judge the risk type for a specific type of driving parameter (e.g., mileage, driving speed), or use multiple driving parameters to determine the comprehensive risk type [1].

In the motor insurance industry, there are numerous individual risks that require classification according to their characteristics and determining rates for each risk category based on the classification. The development of risk-based rate setting models for motor insurance can be divided into three stages: Initial rate setting models, the popularity of generalized linear models (GLM), and the emergence of extended classes. Early actuarial models for motor insurance rate setting used additive and multiplicative models, with the former assuming an additive relationship between rate factors and the latter assuming a multiplicative relationship. Since the late 20th century, GLMs [2] have become the industry standard for categorical rate setting in some countries, establishing a relationship between the mathematical expectations of response variables and predictor variables through a linkage function [3–5]. While GLMs have contributed to the development of non-life rate setting techniques, they have limitations when dealing with increasingly complex data with certain correlation structures, such as clustered, repeated, or stratified data, and when reflecting non-parametric effects of explanatory variables. Hastie et al. [6,7] proposed a generalized additive model (GAM) to analyse the semi-parametric and non-parametric relationships between variables, which was further applied to the analysis of factors influencing the modelling of auto insurance claim frequency. For correlated structural data, random effects models based on GLMs have been introduced to improve data analysis accuracy and validity, with examples including linear mixed models (LME) and generalized linear mixed models (GLMM) [8–10].

The applications of GLMs in the car insurance field include risk assessment, claims prediction, premium pricing, and loss fitting. These applications can help car insurance companies better manage and control risks, improve business efficiency, and profitability. Therefore, the development of GLMs in the car insurance field provides more accurate and reliable modeling tools for insurance companies.

Traditional motor insurance pricing is only related to fixed factors such as age, gender, mileage and price of the vehicle. In practice, however, there are also dynamic data on users and vehicles that affect motor insurance pricing. In the auto insurance claims process, insurance companies have an urgent need for external data due to the low understanding of personnel information and the low quality of information collection. Insurers are therefore beginning to work with external data vendors to fuse internal and external data and develop motor insurance risk control models using machine learning algorithms.

Risk control models are statistical models that are used to estimate the risk associated with an event or situation. In the context of car insurance, risk control models can be used to predict the likelihood of a claim and determine an appropriate premium. These models are often based on various factors such as driver age, driving record, vehicle make and model, and geographical location.

In auto insurance risk control scenario, joint modelling refers to a modelling project in which an insurer and an external data vendor collaborate to provide samples with risk performance to the data vendor, match the feature data to develop a model, and then access the model to make a risk strategy. With the tightening of regulations on personal data privacy and the increasing reliance of insurers on external data, joint modelling is also gaining importance.

However, in recent years, countries around the world have increasingly attached importance to data privacy protection, and laws and regulations for privacy protection have been introduced successively [11]. Original data from different institutions or individuals cannot be collected and used at will. The constraints of these laws and regulations have led to the emergence of data islands, where data sources cannot exchange data, making the traditional learning method of regression model training through data concentration impractical.

To overcome the challenges brought by data privacy protection, many new technologies and algorithms have emerged, such as federated learning and homomorphic encryption. Federated learning (FL) [12] can perform model training between multiple data sources without leaking personal data, allowing different institutions to share and aggregate data without revealing sensitive data. Homomorphic encryption [13] technology allows certain specific calculations, such as addition and multiplication, to be performed while keeping the data encrypted, making data sharing more secure.

Federated learning is widely used in scenarios that require data privacy protection, such as healthcare, financial services, and military fields. In regression problems, federated learning can be used to predict numerical target variables, such as predicting stock prices or disease incidence rates [14,15].

To address the above issues, a Tweedie generalized linear regression-based joint modelling scheme for federal learning car insurance rate setting is proposed. The scheme considers the joint modelling of car insurance rate setting while taking into account the privacy protection of user and vehicle data. All sensitive data is stored in the local institution to which the data belongs, and encryption-based user ID alignment is used to ensure that the participants align the common user sample without the flow of raw data. The experimental results show that the scheme has good results for the quantitative analysis of car insurance pricing variables and user risks.

2  Preliminaries

2.1 Federated Learning

Federated learning is essentially a cryptographic distributed machine learning framework that enables data sharing and joint modelling on the basis of data privacy and security and legal compliance. The core idea is that when multiple data sources participate in model training, only the intermediate parameters of the model are interacted with for joint model training without the need for raw data flow, and the raw data can be kept local. This approach achieves a balance between data privacy protection and data sharing and analysis, i.e., a “data available but not visible” data application model.

Vertical federated learning, i.e., sample-aligned federated learning, is suitable for scenarios where there is a large overlap in user space between participants and little or no overlap in feature space,as shown in Fig. 1. The training process of vertical federated learning generally consists of two parts, first aligning entities with the same ID but distributed across different participants, and then training a cryptographic model based on these aligned entities.

Figure 1: Vertical federated learning

2.2 Federated Learning Framework

The mainstream federal learning frameworks currently available include FATE (Federated AI Technology Enabler) by WeBank, PySyft by OpenMined, PaddleFL (Paddle Federated Learning) by Baidu, FedMl by USC, and TFF (TensorFlow Federated) by Google [16–21].

PySyft separates private data from model training using federation learning, differential privacy and cryptographic computation in major deep learning frameworks such as PyTorch and TensorFlow. PaddleFL is an open source federal learning framework based on PaddleFL, offering many federal learning strategies and their applications in computer vision, natural language processing, recommendation. FedML is an open research library and benchmark that facilitates the development of new federated learning algorithms and fair performance comparisons, supporting three computational paradigms (distributed training, mobile training and standalone simulation) for users to experiment in different system environments. TFF is mainly used for horizontal federal learning scenarios, especially for Android mobile devices. With TFF, developers are able to train shared global models across multiple participating clients.

FATE is an open source project initiated by the AI division of WeBank, the world’s first industrial-grade federation learning framework, providing a reliable and secure computing framework for the federation learning ecosystem. By the end of 2021, more than 1,000 companies and 200 research institutions have participated in the FATE open source ecosystem, with a large number of mainstream participants, contributors and major community contributors. the FATE project uses multiparty secure computing (MPC) [22] and homomorphic encryption technologies to build an underlying secure computing protocol that supports different types of secure machine learning. The FATE technical architecture is underpinned by Tensorflow/Pytorch (deep learning), EggRoll/Spark (distributed computing framework) and a multi-party federated communication network, with a federated security protocol on top, and a library of federated learning algorithms built on top of the security protocol. Around practical scenarios, FATE has built a federated blockchain, federated multi-cloud management, federated model visualisation platform, federated modelling pipeline scheduling, and federated online reasoning at the top of the technical architecture.

2.3 Tweedie Distribution

Tweedie-like distributions were first introduced in 1984 by Tweedie, a statistician at the University of Liverpool, UK, and later named by Smyth et al. [23]. In probability theory and statistics, the Tweedie distribution is a family of probability distributions that includes the purely continuous normal, gamma and inverse Gaussian distributions, the purely discrete scalar Poisson distribution, and the class of compound Poisson-gamma distributions that have positive mass at zero but are otherwise continuous. The Tweedie distribution is a special case of the exponential dispersion model and is often used as the distribution for generalized linear models.

The Tweedie distribution is a special case of an exponential dispersion model (EDM) with a power parameter p characterized by the following power relationship between the mean and variance of the distribution, where μ and ϕ are the mean and dispersion parameters, respectively.

Var(x)=ϕμp(1)

The power parameter p determines the subclass of distributions in the family. For example, p=1 links to the Poisson distribution, p=2 links to the Gamma distribution, p=3 links to the inverse Gaussian distribution, links to the Compound Poisson-Gamma distribution, which can be shown in Table 1.

Explanation of parameters: p is the exponential parameter, V(μ) is the variance function, κ(θ) is the cumulative function, θ is the typical parameter, ϕ is the dispersion, d(y,μ) is the deviation, α(y,ϕ) is the normalisation constant, S is the support, Ω is the mean and Θ is the respective parameter space of the natural parameters.

Given that it is a composite distribution, a random variable can be described as:

X={0M=0∑i=1MCiM>0(2)

where MPoisson(λ) and CiGamma(n,ζ), M independently of Ci. The probability density function of X is:

f(x∣μ,ϕ,p)=a(x,ϕ,p)⋅exp⁡{1ϕ(x⋅μ1−p1−p−μ2−p2−p)}(3)

where α(x,ϕ,p) is a normalisation constant to ensure that this is a valid probability density function.

2.4 Generalized Linear Model

The generalized linear model (GLM), first proposed by McCulloch [24] and Nelder et al. [25], is one of the most established models for car insurance pricing it is a model that analyses and treats the correlation between multiple rate factors and the explanatory variables with the help of an exponential family distribution due to the introduction of a link function. As the GLM is not limited to normal distributions, but extends to exponential family distributions, it is more suitable for modelling data with special structures such as biased and dichotomous data. At the same time, the GLM relaxes the assumptions required of its traditional linear regression model, expanding the range of applications of the model. The model generally consists of three components: the stochastic component, the systematic component and the link function.

Stochastic component: The probability distribution of the random component, error term or dependent variable Y is known as the random. The samples of the dependent variable Y, y1, y2, ..., yn, are independent of each other and obey any of the exponential distribution families distribution. These include the zero-truncated Poisson distribution, the normal distribution, the gamma distribution, the inverse Gaussian distribution, etc. The probability density of the family of exponential distributions is:

f(y∣θ,φ)=exp⁡{yθ−b(θ)a(φ)+c(y,φ)}(4)

Systematic component: System components, i.e., linear combinations of independent variables. There is a correlation between the system components and the independent variables and this relationship can be assumed to be linearly correlated. The system components can be expressed as follows:

ηi=β0+β1X1i+⋯+βrXri(5)

Link function: It is a function that expresses the relationship between the stochastic component and the system component. In traditional linear regression models, the link function is a unit function of 1. However, in generalized linear models, the link function is specified as strictly monotonic and differentiable, and is used to link the mean of the explanatory variable Y to the system components.

2.5 Homomorphic Encryption

Homomorphic encryption was first proposed by Rivest et al. [26]. The use of homomorphic encryption ensures that the result of algebraic operations on the ciphertext is the same as the result of encryption after performing the same algebraic operations on the plaintext. That is, for any valid operation f and plaintext m, there is the property f(Enc(m))=Enc(f(m)). This special property allows third parties to perform algebraic operations on the ciphertext, without the need for decryption operations throughout the process. According to the supported operations, homomorphic encryption can be classified into fully homomorphic encryption (FHE) [27,28], leveled fully homomorphic encryption (LFHE) [29], additional homomorphic encryption (AHE) [30] and multiplicative homomorphic encryption (MHE) [31].

This work is concerned with additive semi-homomomorphic encryption, e.g., the Paillier encryption algorithm is a classical additive semi-homomomorphic encryption algorithm and has been used in common federated learning algorithms. During the initialisation phase, the Paillier encryption algorithm generates the key pair <pk,sk>.The public key pk is used for encryption and can be disclosed to the other participants, the private key sk is used for decryption and cannot be disclosed. Given integers x,y, the Paillier encryption algorithm supports the following operations:

•   Encryption: Enc(x,pk)→[[x]].

•   Decryption: Dec([[x]],sk)→x.

•   Homomorphic addition: HAdd([[x]],[[y]])→[[z]], where [[z]] satisfies Dec([[z]],sk)→x+y.

•   Scalar addition: SAdd([[x]],y)→[[z]], where [[z]] satisfies Dec([[z]],sk)→x+y.

•   Scalar multiplication: SMul([[x]],y)→[[z]], where [[z]] satisfies Dec([[z]],sk)→x∗y.

3  Car Insurance Rate Setting Federated Learning Modelling Scheme

3.1 General Architecture

Through analysis of the data, this modelling applies to vertical federal learning, for which a system oriented towards vertical federal learning was created between the insurance company (generally referred to as Company A) and the data company (generally referred to as Company B), with the system architecture shown in Fig. 2.

Figure 2: Vertical federated learning for car insurance rate setting

The training process for vertical federation learning generally consists of two parts. The first part is cryptographic entity alignment, where the data of Company A and Company B are stored in their respective systems and the original data are not exchanged. The system uses an encryption-based user ID alignment technique to ensure that Parties A and B can align common users without exposing their respective original data. During entity alignment, the system does not expose users belonging to a particular company. The second part is the cryptographic model training phase, where the parties can use the data from these shared entities to collaboratively train a machine learning model after the shared entities have been identified.

3.2 Tweedie Distribution Generalised Linear Regression Federated Learning Model

3.2.1 System Initialisation

The proposed model consists of two participants, A and B, and one collaborator, C, working together to train the machine learning model, with each participant having a sample size of n. The work consists of the following main components:

1.    Participant A, with a certain number of specific samples, each with a corresponding feature value Xai=(xai1,xai2,...,xain), Xai∈DA. Participant B, with a certain number of samples, each with corresponding feature value Xbi=(xbi1,xbi2,...,xbin) and labels Ybi, (Xbi,Ybi)∈DB. DA and DB have partial overlap samples DC. This scheme assumes that A, B know the overlapping sample IDs in advance, otherwise, the sample IDs can be blinded using the RSA encryption mechanism, and then the samples can be aligned. Assume that the learning rate is η and the regularization parameter is α. Additive homomorphic encryption is represented using the notation [[•]].

2.    A and B each have their own machine learning model training servers, S1 and S2, which are controlled by A and B respectively and cannot carry out a conspiracy attack. This server is only responsible for the computation of machine learning models, such as eigenvalue computation, gradient computation and loss function computation.

3.2.2 Calculating Model Training Loss Function

Train1(WA,WB,DA,DB,DC)→L:

According to Table 2 the training objective function can be obtained as:

minWA,WBL=∑2‖d(yi,y^i)‖+α2(‖WA‖2+‖WB‖2)(6)

(a)   A and B input each sample i into the model to calculate the eigenvalues: uiA←NetA(WA,DA), uiB←NetB(WB,DB). The sample eigenvalue set matrix is uA, uB.

(b)   For the calculation of the loss function of the generalized linear regression of the Tweedie distribution, according to Eq. (6), we have:

[[L]]=‖∑i∣Dc∣2{−ybie(1−p)(uiA+uiB)1−p+e(2−p)(uiA+uiB)2−p}+α2(‖WA‖2+‖WB‖2)‖(7)

(c)   The servers S1, S2 compute the losses of A, B and use homomorphic encryption to obtain:

[[LA]]=‖α2(‖WA‖2)‖,[[LB]]=‖α2(‖WB‖2)‖,

[[LAB]]=‖∑i|DC|2{−ybie(1−p)([[uiA]]+[[uiB]])1−p+e(2−p)([[uiA]]+[[uiB]])2−p}‖.

(d)   Server S2 receives the parameters from S1 and calculates the overall loss, then we have:

L=[[LA]]+[[LB]]+[[LAB]](8)

Convergence or non-convergence based on L, if the model converges, the training is finished and the relevant parameters WA, WB are output.

3.2.3 Calculating Model Training Gradients

Train2(uA,uB,L)→(δLδWA,δLδWB):

Assuming that the loss function values L do not converge, the corresponding gradient values need to be calculated, let [[di]]=[[e(2−p)(uiA+uiB)]]−[[ybie(1−p)(uiA+uiB)]], according to Eq. (7):

[[δLδWA]]=∑i|DC|[[di]]xiA+[[αWA]](9)

[[δLδWB]]=∑i|DC|[[di]]xiB+[[αWB]](10)

A and B are computed jointly by homomorphic encryption to obtain the respective δLδWA and δLδWB, update the gradient and recalculate the loss function.

The steps of model training are summarized in four steps, the following are shown in Table 2.

Step 1: The coordinator C creates the key and sends the public key to both Party A and Party B.

Step 2: The intermediate results are encrypted and exchanged between side A and side B. The intermediate results are then used to help calculate the gradient and loss values.

Step 3: Parties A and B calculate the encryption gradient and add the additional mask respectively, and Parties A and B send the encryption result to Party C.

Step 4: Party C decrypts the gradient and loss information and sends the results back to Parties A and B. Parties A and B unmask the gradient information and update the model parameters based on the gradient information.

3.3 Security Analysis

The training protocol shown in Table 2 does not reveal any information to C because C is given only the parameters of the masked gradient, and the randomness and confidentiality of the masked matrix are guaranteed. In the above protocol, Party A learns its gradient at each step, but this is not sufficient for A to learn any information from B according to Eq. (9), since the security of the scalar product protocol is based on n equations with more than n unknowns that cannot be solved [20,21]. Here, it is assumed that the number of samples NA is much larger than the number of features nA. Similarly, B cannot obtain any information from A.

Proof of protocol security: This work assumes that both parties are semi-honest. If one party is malicious and tricks the system by falsifying its input, e.g., if Party A submits only a non-zero input and a non-zero feature, it can determine the value of uiB for that sample feature but has no way of knowing the value of xiB or WB, and this bias will distort the results of the next iteration, alerting the other party, which will terminate the learning process. At the end of the training process, each party (A or B) has no knowledge of the other party’s data structure and is only given the model parameters associated with its own features. During the inference process, both parties need to collaborate to settle the predictions through the steps shown in Table 3, which still does not lead to information leakage.

4  Experiment

In this Section, we evaluate the convergence value of our solution for different values of power and the time overhead for different size quantities through experiments. We also experimentally compare the evaluation results of our solution with those of the stand-alone solution.

4.1 Experimental Environments

The experiments are executed in a LAN environment based on the FATE vertical federated learning framework, running on an AMD Ryzen 7 5800H 3.20 Ghz CPU processor with 8 cores and 16 threads and 32 G DDR 4 RAM, in a 64-bit CentOS 7.3 environment with FATE version 1.8. The Tweedie regression model was trained using Python language and the Numpy library.

4.2 Experimental Datasets

We evaluated the performance of the Tweedie regression federated learning model using two datasets from the financial insurance field.

The freMTPL2freq dataset is a French automobile third-party liability claims dataset, containing 677,991 samples of third-party liability insurance policies, each sample consisting of 10-dimensional attribute features and one label. The attribute features include policy holder characteristics (age, gender, etc.), vehicle characteristics (make, model, etc.), and claim-related information (time, location, etc.).

The CarData dataset comes from a publicly available set of insurance policy claims data on car insurance in de Jong et al. [3]. This dataset provides 65,536 insurance samples from 2004–2005, each sample consisting of 7-dimensional attribute features and one label. The attribute features include policy holder characteristics (age, gender, etc.), vehicle characteristics (make, model, etc.), and other relevant information related to the insurance policy. The label represents the total amount of claims made by the policy holder during the policy period. It is widely used in machine learning research to develop models for predicting the total amount of claims made by policy holders based on their demographic and policy information.

4.3 Experimental Result

To verify the effectiveness of the FL-TRM (Tweedie Regression Federated Learning Model) method proposed experimental comparisons will be conducted with three other methods.

The experimental settings for LocalA-TRM and LocalB-TRM involve training the Tweedie regression model only on the local data of participant A and participant B, respectively. The purpose of this is to test the effectiveness of the Tweedie regression model under non-federated settings and verify the effectiveness of federated learning. The NoFL-TRM experimental setting involves training the model on the entire dataset after aggregating all the attribute features, which represents the traditional Tweedie regression method. The purpose of this is to compare its performance with the federated learning framework and evaluate the accuracy loss of the models trained under federated settings.

The freMTPL2freq dataset is partitioned into attribute features of 10 dimensions, which are split between participant A and participant B according to the ratios of 2:8, 3:7, 4:6, and 5:5. The label feature y is assigned to participant A, who serves as the active participant, while participant B serves as the collaborative participant. The FL-TRM model will be trained using vertical federated learning with the joint participation of both participants A and B.

The experiments are conducted with L1 regularization and a penalty factor of α = 0.1, using a batch size of 2000 for batch gradient descent, a learning rate of η = 0.1, and a power value of p = 1.8. The experimental results for different feature partition ratios are shown in Table 4.

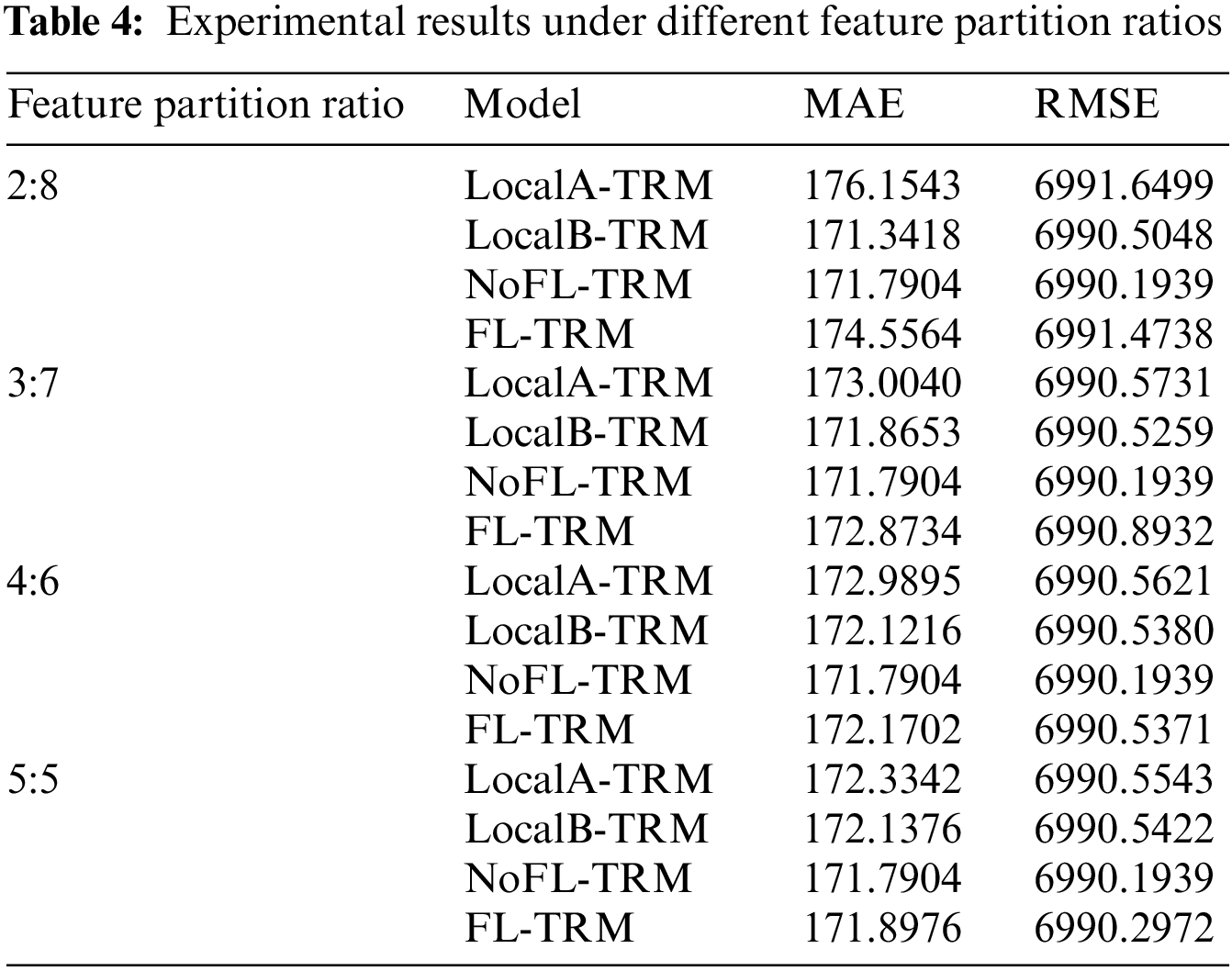
MAE (Mean Absolute Error) and RMSE (Root Mean Squared Error) are two evaluation metrics for regression models where lower values indicate better performance. Table 4 shows that for LocalA-TRM, as the number of features increases, both MAE and RMSE decrease, indicating an improvement in model performance. On the other hand, for LocalB-TRM, as the number of features decreases, both MAE and RMSE increase, indicating a deterioration in model performance. Both are weaker than NoFL-TRM, which utilizes all features to learn, demonstrating that the more features used, the better the trained model’s performance. This also proves that the model training performance in a single participant scenario is proportional to the number of features.

From Table 4, it can be observed that the difference in the number of features between the participating parties has an impact on the performance of FL-TRM. As the difference in the number of features between the two parties decreases, the performance of FL-TRM improves. However, when the feature segmentation ratio is 2:8, the performance of FL-TRM is worse than that of LocalB-TRM. This is because LocalB-TRM is trained by a single party and has 80% of the features, which makes it easier to find features that are beneficial for improving model performance.

In general, models trained on more data tend to perform better than models trained on less data. However, the contribution of participants’ models to evaluation results depends not only on the amount of data they have but also on many other factors such as data quality, model and hyperparameter selection, and how well their data represents the overall sample.

FL-TRM failed to learn effectively due to the extremely unbalanced feature segmentation ratio. This experiment also suggests that the difference in the number of features between the participating parties in federated learning should not be too large.

On the CarData dataset, we conducted experiments with two participating parties. The feature split ratio of the dataset was 4:3, which means that for each sample in the dataset, 4 out of 7 attributes were allocated to participating Party A as the collaborator, while the remaining 3 attributes and the label y were allocated to Party B as the active party. The FL-TRM model was trained through vertical federated learning with the joint participation of Parties A and B. The experimental results are shown in Table 5.

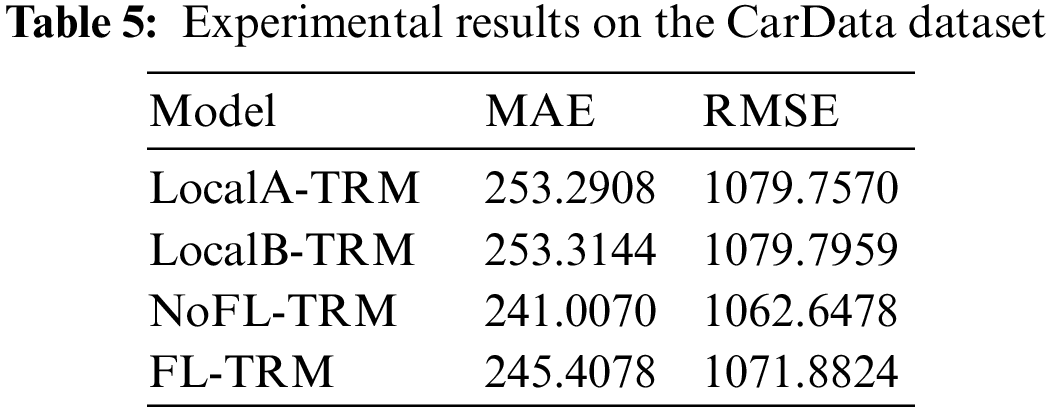
Based on Table 5, it can be seen that the model performance of FL-TRM on the CarData dataset is better than that of LocalA-TRM and LocalB-TRM, indicating that the model obtained through federated learning is better than the model trained by a single party.

In addition to evaluating the model using MAE and RMSE, the risk coefficient Ri=e(Intercept+ui) is calculated for each sample vehicle based on the model parameters; the risk coefficients for all samples in the CarData dataset are then cut into 10 quartiles of 0%, 10%, 20%, 30%, 45%, 65%, 80%, 85%, 90%, 95% and 100% to generate a risk score of “1 to 10”. Finally, the mean of the sample size and payout rates under each score were counted, as shown in Table 6.

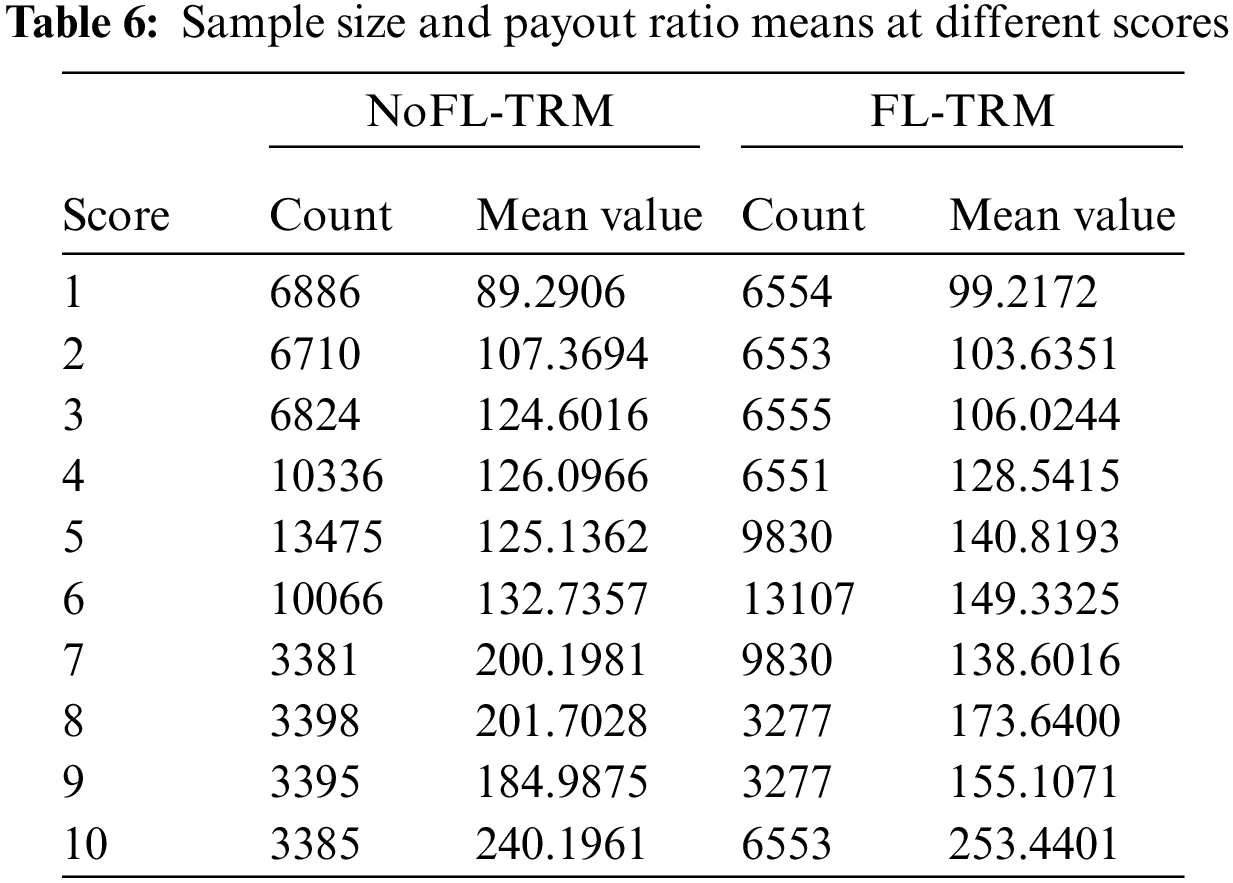
Fig. 3 shows a comparison of the grouped sample sizes obtained by the scheme after risk assessment of the data samples in the NoFL-TRM model and FL-TRM model, respectively, and it can be seen that the differences are very small and the distribution pattern is consistent, with the highest number of samples with a risk score of 6, the lowest number with a score of 1, and the second highest number of samples with scores of 5 and 7. Also, by averaging the sample payout rates under each score as shown in Fig. 4, the average payout rate of the samples was highest for a risk score of 10 and lowest for a risk score of 0 in both the stand-alone and federated learning environments, which is consistent with the actual payout data from the insurers.

Figure 3: Sample size at different scores

Figure 4: Sample payout means at different scores

Fig. 5 shows the relationship between the loss values and iteration rounds during the training of the FL-TRM model. It can be observed from the figure that under the aforementioned hyperparameter conditions, the proposed federated Tweedie regression model parameter update method can stably update the parameters in the direction of gradient descent, resulting in a stable decrease in the loss function. The model can converge after approximately 200 iterations.

Figure 5: Relationship between rounds and losses

Fig. 6 shows the variation of the convergence time of this scheme for different sizes of datasets. It can be seen that the time overhead of this scheme grows linearly and steadily with constant feature dimension and increasing dataset size, possessing better performance stability. The federal learning model has a longer training time compared to traditional Tweedie regression. The reasons for this performance degradation are the complexity of the federation learning algorithm itself and the performance drain of the data network transmission experiments in a distributed environment, especially the encryption and decryption based on the homomorphic encryption algorithm.

Figure 6: Time overhead at different data sizes

5  Conclusion

In this work, we propose a federated learning-based Tweedie regression algorithm for constructing a joint assessment model for multi-party auto insurance rate setting in data silos. The algorithm derives the logarithmic natural formula of the vertical federated Tweedie regression model using an iterative method and constructs the gradient updating strategy of the parameters based on the loss function, introducing homomorphic encryption algorithm to achieve fusion updates of parameters from all parties and obtain the federated Tweedie regression model. The experiments on two datasets demonstrate that federated learning can be used for model training using the datasets of all parties while protecting data privacy. Furthermore, the model testing results prove that the federated learning model performs better than the single-party trained models. In the auto insurance dataset with tag features following Tweedie distribution, the proposed model achieves good results in setting auto insurance rates. Future work will investigate the extension of the scheme to correlation structure data analysis and improve the accuracy and validity of data analysis by introducing random effects based on GLM.

Acknowledgement: I would like to express my heartfelt gratitude to all those who have contributed to the successful completion of this research work. First and foremost, I am deeply grateful to my supervisor, Professor Changgen Peng, whose guidance, support, and encouragement throughout the research process have been invaluable. Second, I would like to express my heartfelt gratitude to Professor Weijie Tan, whose expertise and insightful feedback have significantly improved the quality of this paper. I am also thankful to the members of my research committee, State Key Laboratory of Public Big Data, for their valuable suggestions and constructive criticism, which helped shape the direction of this study. I extend my appreciation to my colleagues and friends for their continuous support and for being a source of motivation during challenging times.

Funding Statement: This research was funded by the National Natural Science Foundation of China (No. 62272124), the National Key Research and Development Program of China (No. 2022YFB2701401), Guizhou Province Science and Technology Plan Project (Grant Nos. Qiankehe Paltform Talent [2020]5017). The Research Project of Guizhou University for Talent Introduction (No. [2020]61), the Cultivation Project of Guizhou University (No. [2019]56), and the Open Fund of Key Laboratory of Advanced Manufacturing Technology, Ministry of Education (GZUAMT2021KF [01]).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tao Yin, Changgen Peng; data collection: Tao Yin, Hanlin Tang; analysis and interpretation of results: Tao Yin, Weijie Tan; draft manuscript preparation: Dequan Xu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials used in this study are available upon request. Researchers and interested parties can obtain access to the datasets and any supplementary materials by contacting the corresponding author at cgpeng@gzu.edu.cn. We are committed to promoting open science and transparency, and we will do our best to provide the necessary information to facilitate reproducibility and further research. Please note that certain datasets or materials might be subject to restrictions due to confidentiality or copyright considerations. In such cases, we will strive to provide relevant information or point to publicly available resources that align with the research findings. We encourage the scientific community to engage in collaboration and exchange of ideas. If you have any inquiries or wish to access the data and materials for non-commercial research purposes, kindly reach out to us, and we will be glad to assist you.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Samarasinghe, H. T. D., Herath, N. M., Dabare, H. S., Gamaarachchi, Y. R., Pulasinghe, K. et al. (2021). Vehicle insurance policy document summarizer, AI insurance agent and on-the-spot claimer. 2021 6th International Conference for Convergence in Technology (I2CT), Piscataway, IEEE. [Google Scholar]

2. Cellamare, M., van Gestel, A. J., Alradhi, H., Martin, F., Moncada-Torres, A. (2022). A federated generalized linear model for privacy-preserving analysis. Algorithms, 15(7), 243. [Google Scholar]

3. de Jong, P., Heller, G. Z. (2008). Generalized linear models for insurance data. Cambridge Books. [Google Scholar]

4. Ohlsson, E. (2008). Combining generalized linear models and credibility models in practice. Scandinavian Actuarial Journal, 2008(4), 301–314. [Google Scholar]

5. Ohlsson, E., Johansson, B. (2010). Non-life insurance pricing with generalized linear models, vol. 2. Germany: Springer. [Google Scholar]

6. Hastie, T. J. (2017). Generalized additive models. In: Statistical models in S, pp. 249–307. England, UK: Routledge. [Google Scholar]

7. Hastie, T., Tibshirani, R. (1987). Generalized additive models: Some applications. Journal of the American Statistical Association, 82(398), 371–386. [Google Scholar]

8. Anjum, M. M., Mohammed, N., Li, W., Jiang, X. (2022). Privacy preserving collaborative learning of generalized linear mixed model. Journal of Biomedical Informatics, 127(5), 104008. [Google Scholar] [PubMed]

9. Gabrielli, A. (2020). A neural network boosted double overdispersed poisson claims reserving model. ASTIN Bulletin: The Journal of the IAA, 50(1), 25–60. [Google Scholar]

10. Frees, E. W., Valdez, E. A. (2008). Hierarchical insurance claims modeling. Journal of the American Statistical Association, 103(484), 1457–1469. [Google Scholar]

11. Zhang, C., Xie, Y., Bai, H., Yu, B., Li, W. et al. (2021). A survey on federated learning. Knowledge-Based Systems, 216(1), 106775. [Google Scholar]

12. Yang, Q., Liu, Y., Chen, T., Tong, Y. (2019). Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology, 10(2), 1–19. [Google Scholar]

13. Wood, A., Najarian, K., Kahrobaei, D. (2020). Homomorphic encryption for machine learning in medicine and bioinformatics. ACM Computing Surveys, 53(4), 1–35. [Google Scholar]

14. Byrd, D., Polychroniadou, A. (2021). Differentially private secure multi-party computation for federated learning in financial applications. Proceedings of the First ACM International Conference on AI in Finance ICAIF’20, New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/3383455.3422562 [Google Scholar] [CrossRef]

15. Wang, F., Zhu, H., Lu, R., Zheng, Y., Li, H. (2021). A privacy-preserving and non-interactive federated learning scheme for regression training with gradient descent. Information Sciences, 552, 183–200. [Google Scholar]

16. Li, L., Fan, Y., Tse, M., Lin, K. Y. (2020). A review of applications in federated learning. Computers & Industrial Engineering, 149(5), 106854. [Google Scholar]

17. Webank (2019). Federated AI technology enabler. https://www.fedai.org/cn/ [Google Scholar]

18. Yin, X., Zhu, Y., Hu, J. (2021). A comprehensive survey of privacy-preserving federated learning: A taxonomy, review, and future directions. ACM Computing Surveys, 54(6), 1–36. [Google Scholar]

19. Ma, Y., Yu, D., Wu, T., Wang, H. (2019). PaddlePaddle: An open-source deep learning platform from industrial practice. Frontiers of Data and Domputing, 1(1), 105–115. [Google Scholar]

20. He, C., Li, S., So, J., Zeng, X., Zhang, M. et al. (2020). FedML: A research library and benchmark for federated machine learning. arXiv preprint arXiv:2007.13518. [Google Scholar]

21. Google (2019). TensorFlow federated. https://www.tensorflow.org/federated [Google Scholar]

22. Zhu, Z. W., Huang, R. W. (2021). Efficient SMC protocol based on multi-bit fully homomorphic encryption. Applied Sciences, 11(21), 10332. [Google Scholar]

23. Smyth, G. K., Jørgensen, B. (2002). Fitting Tweedie’s compound poisson model to insurance claims data: Dispersion modelling. ASTIN Bulletin: The Journal of the IAA, 32(1), 143–157. [Google Scholar]

24. McCulloch, C. E. (2000). Generalized linear models. Journal of the American Statistical Association, 95(452), 1320–1324. [Google Scholar]

25. Nelder, J. A., Wedderburn, R. W. (1972). Generalized linear models. Journal of the Royal Statistical Society: Series A (General), 135(3), 370–384. [Google Scholar]

26. Rivest, R. L., Adleman, L., Dertouzos, M. L. (1978). On data banks and privacy homomorphisms. Foundations of Secure Computation, 4(11), 169–180. [Google Scholar]

27. Yang, A., Xu, J., Weng, J., Zhou, J., Wong, D. S. (2018). Lightweight and privacy-preserving delegatable proofs of storage with data dynamics in cloud storage. IEEE Transactions on Cloud Computing, 9(1), 212–225. [Google Scholar]

28. Mahato, G. K., Chakraborty, S. K. (2021). A comparative review on homomorphic encryption for cloud security. IETE Journal of Research, 117(15), 1–10. [Google Scholar]

29. Li, M. (2020). Leveled certificateless fully homomorphic encryption schemes from learning with errors. IEEE Access, 8, 26749–26763. [Google Scholar]

30. Paillier, P. (1999). Public-key cryptosystems based on composite degree residuosity classes. International Conference on the Theory and Applications of Cryptographic Techniques, Germany, Springer. [Google Scholar]

31. Li, L., Abd El-Latif, A. A., Niu, X. (2012). Elliptic curve ElGamal based homomorphic image encryption scheme for sharing secret images. Signal Processing, 92(4), 1069–1078. [Google Scholar]