A Hybrid Parallel Strategy for Isogeometric Topology Optimization via CPU/GPU Heterogeneous Computing

1  Introduction

Developing advanced manufacturing techniques [1,2] puts forward new requirements for design tools. Among design approaches, topology optimization (TO) is considered one of the most prospects for generating product prototypes during the conceptual design stage. Over the past few decades, TO has been improved significantly [3] and applied to various complex problems such as fluid-structure interaction [4], and thermos-elastic behavior [5]. Bendsøe et al. [6] proposed a homogenization method, laying a foundation for developing TO methods. According to the model expression, TO is roughly divided into two categories. One is geometric boundary representation-based methods [7–9]. The other is material representation-based methods [10–12], in which structural topology is defined by 0–1 distribution of material and evolved by making a material trade-off. Among them, the solid isotropic material with penalization (SIMP) is the most classic method based on variable density theory with the advantages of simple program implementation and stable solution. The SIMP is widely applied to various fields including multiscale and multi-material [13]. Doan et al. [14] presented a new computational design optimization method that finds the optimal multi-material design by considering structure strain energy and material cost. In most TOs, the finite element method (FEM) is employed to analyze displacement field and sensitivity. However, due to the disconnection between the geometric model and analysis [15], there are some errors in the calculation. Moreover, the Lagrange basis function continuity between adjacent elements is low, reducing the analysis accuracy [16].

To improve the accuracy of optimization, isogeometric analysis (IGA) was introduced [17–19] by using unified Non-Uniform Rational B-splines (NURBS) basis functions for the geometric and computational models. With the merits of high accuracy and efficiency, IGA-based TOs have been intensively studied [20]. Dedè et al. [21] utilized a phase field model for the formulation and solution, and encapsulated the exactness of the design domain in TO by the IGA-based spatial approximation. In the optimization of the lattice structure, the IGA is used to analyze the effective property for either isotropic or an-isotropic cellular microstructures [22–24]. However, the computational cost of TO is expensive for the complex large-scale model, since the number and order of elements need to be large enough for high accuracy. Especially for the IGA-based TO, the optimization analysis with the high-order NURBS elements leads to a further rise in computational complexity and memory usage [24,25]. Furthermore, TO is an iterative computing process and the computational cost will rise significantly with the increasing scale and complexity. Parallel computing technology has been investigated to accelerate the process of TO. In earlier work, Kim et al. [26] made use of parallel topology optimization to solve large-scale eigenvalue-related structural design problems. Subsequently, Vemaganti et al. [27] presented a parallel algorithm for 2D structure topology optimization based on the solid isotropic material with the penalization (SIMP) method and the optimality criteria (OC). Aage et al. [28] presented how to use PETSc for parallel computing and successfully applied it to solving large-scale topology optimization in parallel. A minimum weight formulation with parallelization techniques was used to accelerate the solving of the topology optimization problem in [29]. Since graphics processing units (GPUs) have an architecture that supports the large number of threads required for parallel computing, they can be applied for high-performance solutions to large-scale complex scientific problems [30,31]. Wadbro et al. [32] first exploited the parallel computing capabilities and programmability of GPUs to accelerate topological optimization methods. Schmidt et al. [33] used GPU to accelerate the SIMP method, and experimental results demonstrate that the parallel algorithm on the GeForce GTX280 runs faster than a 48-core shared memory central processing units (CPUs) system with a speed-up ratio of up to 60. Ratnakar et al. [34] presented an implementation of topology optimization on the GPU for a 3D unstructured mesh by developing efficient and optimized GPU kernel functions. Karatarakis et al. [35] proposed the interaction-wise approach for the parallel assembly of the stiffness matrix in IGA, which enables the efficient use of GPUs to substantially accelerate the computation. There are rare research papers focusing on the parallel strategy for isogeometric topology optimization (ITO). Xia et al. [25] proposed a GPU parallel strategy for level set-based ITO and obtained a speedup of two orders of magnitude. Wu et al. [36] used an efficient geometric multigrid solver and GPU parallelization in the FEM analysis session to accelerate the topology optimization iterations on a desktop.

However, the above-mentioned studies focus on the efficient utilization of GPU, while the computational capacity of the CPU was ignored. The open multi-processing (OpenMP) based CPU parallel and compute unified device architecture (CUDA) based GPU parallel [37] have been incorporated into optimization algorithms to accelerate their process. Lu et al. [38] first exploited the computational capacities of both CPUs and GPUs in the Tianhe-1A super-computer to perform a long-wave radiation simulation, while the ways to distribute the workload between CPU and GPU to achieve high computational efficiency were discussed. Subsequently, Cao et al. [39] took into account the cost of communication between GPU and CPU and developed a formula method for workload allocation. However, there are rare research papers focusing on parallel strategy both with CPU and GPU for ITO. The challenge in designing ITO heterogeneous parallel algorithms is to achieve workload balancing on the CPU/GPU to ensure computational efficiency. Meanwhile, the minimum mapping range of GPU to host memory is determined to improve the efficiency of memory resource usage and reduce the data transfer time from CPU to GPU.

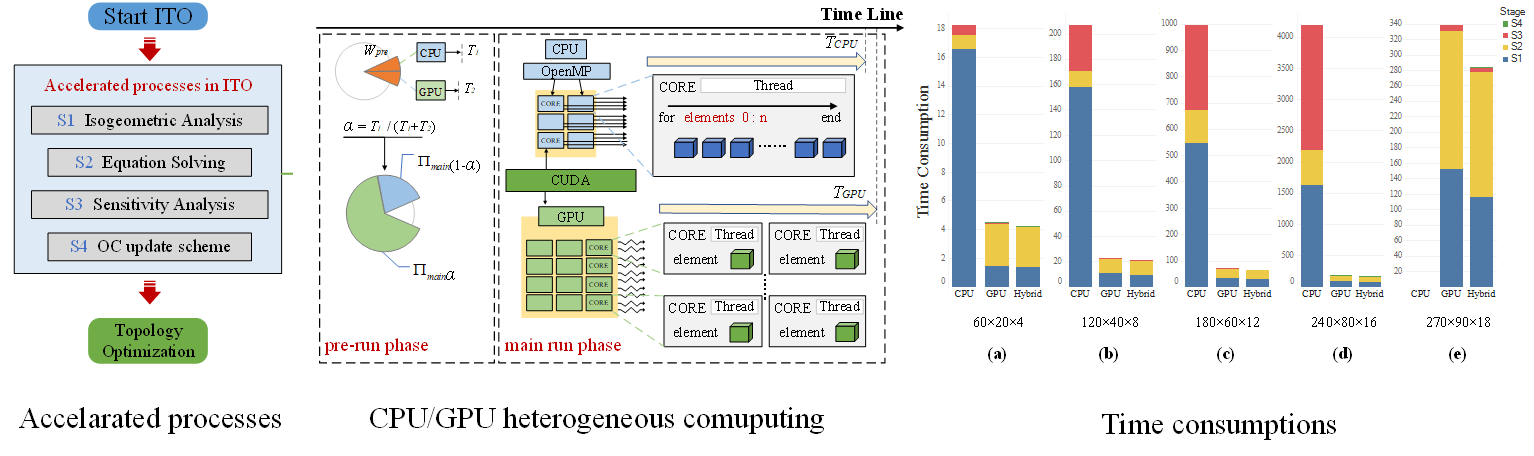
There are few literatures on ITO with heterogeneous parallelism acceleration. In this paper, a hybrid parallel strategy for ITO with CPU/GPU heterogeneous computing is proposed to accelerate the main time-consuming aspects of the computational processes. The hybrid parallel strategy for stiffness assembly based on control point pair is achieved by CPU/GPU hybrid computing for the first time, contributing to efficiency improvements. A dynamic workload balancing method is presented for its efficiency and versatility. The tasks are assigned according to the real-time local computing power measured by the pre-run phase. The rest of the paper is structured as follows: NURBS-based IGA and CPU/GPU heterogeneous parallel computing are briefly reviewed in Section 2. Section 3 illustrates the hybrid parallel strategy for ITO processes, including stiffness matrix assembly, equation solving, sensitivity analysis, and update scheme. A dynamic workload balancing method is proposed in Section 4. The advantages and correctness of the hybrid parallel strategy are demonstrated with several benchmark cases in Section 5. Finally, Section 6 concludes the paper and presents an outlook on future research.

2  Basic Theory

The theoretical foundations including IGA, ITO-SIMP and CPU/GPU heterogeneous computing [40,41] are summarized in this section.

2.1 NURBS Basic Theory

In IGA, NURBS is commonly used to discretize the design domain [42]. A knot vector Ξ, representing parametric coordinates, is a sequence of non-decreasing real numbers:

Ξ={ξ1,ξ2,…,ξn+p+1}(1)

where n is the number of control points, and p denotes the order of the B-spline. By the Cox-de Boor formula, the B-spline basis functions Bip(ξ) can be derived recursively from the given parameter vector [43]:

Bi0(ξ)={1, if ξi≤ξ≤ξi+10, otherwise(2)

Bip(ξ)=ξ−ξiξi+p−ξiBip−1(ξ)+ξi+p+1−ξξi+p+1−ξiBi+1p−1(ξ)(3)

NURBS basis function Nip(ξ) can be obtained by introducing a positive weight wi to each B-spline basis function [44]:

Nip(ξ)=Bip(ξ)wi∑j=1nBjp(ξ)wj(4)

Based on the tensor property, three-dimensional NURBS basis functions Ni⋅j,kp,q,r(ξ,η,ζ) are produced from the following formula [18]:

Ni⋅j,kp,q,r(ξ,η,ζ)=Bip(ξ)Bjq(η)Bkτ(ζ)wi,j,kΣi=1nΣj=1mΣk=1lBip(ξ)Bjq(η)Bkτ(ζ)wi,j,k(5)

where wi,j,k is the weight value of the tensor product Bip(ξ)Bjq(η)Bkτ(ζ).

2.2 SIMP-Based ITO

SIMP material model is implemented to search for the optimized solution in ITO. The design variable is the density x, which enables the distribution of the material under control [45]. ITO-SIMP aims to maximize the structural stiffness, which can be converted to minimize compliance. In ITO-SIMP, the density variables are stored at the control points, and the element density xe can be illustrated with the control point density as [46]:

xe=xn(ec)=∑i∈mNi(ec)xi(6)

where the density of element e is equivalent to the element center xn(ec). m is the set of control points related to element e. Ni denotes the NURBS basis function of the ith control point, and the corresponding density is written as xi.

Based on the SIMP material model, Young’s modulus Eexe of the element can be represented as [47]:

Ee(xe)=xn(ec)tE0,t>1(7)

where E0 is Young’s modulus of the base material. Penalty coefficient t is greater than 1, which penalizes the material’s stiffness.

The SIMP-based topology optimization is to find the distribution of material for the minimum compliance, which can be mathematically illustrated as follows [48]:

{min:C=UTkU=∑e=1NxetE0ueTkeues.t:{KU=FV(x)V0=θ0<xm<xe≤1,e=1,…,N(8)

where C is the compliance, K represents the global stiffness matrix, F denotes the load vector, and U is the global displacement field. ke denotes the element stiffness matrix calculated from unit Young’s modulus when ue is the element displacement vector. θ is the volume fraction, while V0 and V(x) denote the volume of the design domain and material, respectively. xe values from 0 to 1 to avoid the singularity of the stiffness matrix.

2.3 CPU/GPU Heterogeneous Computing

2.3.1 GPU Parallel Architecture

GPUs are computer graphics processors which can compute extensive data in parallel [49]. Since NVIDIA released CUDA in 2007, many researchers have been using GPUs to accomplish large-scale scientific computing problems [50]. The CUDA programming model provides a heterogeneous computing platform consisting of CPU and GPU architectures. Their applications are divided into CPU host-side and GPU device-side code, while the information is exchanged via the peripheral component interconnect express (PCIe) bus. Host-side code is responsible for controlling device and data transfer, while device-side code defines operational functions to perform the corresponding kernel functions. Thread is the smallest execution unit, while GPU uses many threads to execute kernel functions during parallel computing. Logically, all threads are grouped into blocks by a certain number. The threads in the block will run in warps (set of 32 threads) on the CUDA core processor, as shown in Fig. 1. Warp is the execution unit of streaming multiprocessor (SM), while SM supports concurrent execution of a large number of threads and threads are managed in a single-instruction-multiple-threads (SIMT) fashion.

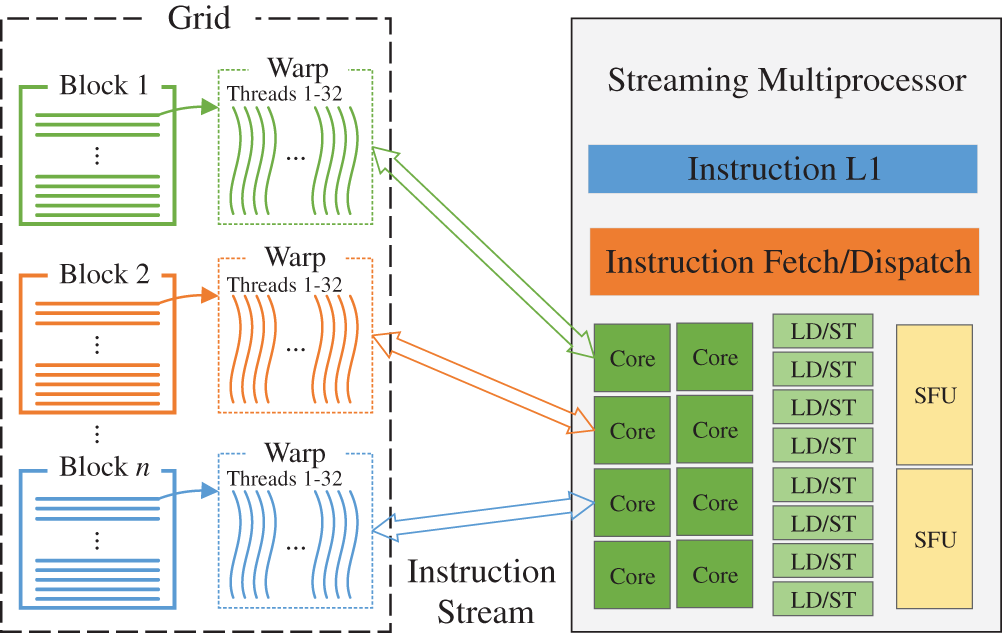
Figure 1: Warps in the block for thread scheduling

2.3.2 CPU/GPU Heterogeneous Parallel Architecture

Multi-core CPUs compute in parallel with fewer cores and have more arithmetic power per core than GPUs [51]. CPU/GPU heterogeneous parallel programming model is based on a heterogeneous computing platform where computing power involving both GPUs and CPUs is considered [52]. OpenMP supports multi-threaded concurrent execution of tasks on multi-core CPUs [53]. The independence of CPU cores allows different tasks to be performed simultaneously among different OpenMP threads. Typically, the CPU is involved in controlling GPU (e.g., the transfer of data and the launching of kernel functions) but not computing tasks. Indeed OpenMP is used in CPU/GPU heterogeneous parallel programming to enable multi-threading of the CPU, where one of the OpenMP threads is responsible for interaction with the GPU and others for computation [54]. Hence, the CPU and GPU work concurrently and cooperatively for the particular workload. As shown in Fig. 2, the total workload is divided into CPU and GPU parts. The CPU runs in “one-thread-multi-node” mode while each thread iterates through multiple tasks in a loop. Moreover, for the GPU, it operates in “one-thread-one-node” mode, while each thread performs only one task.

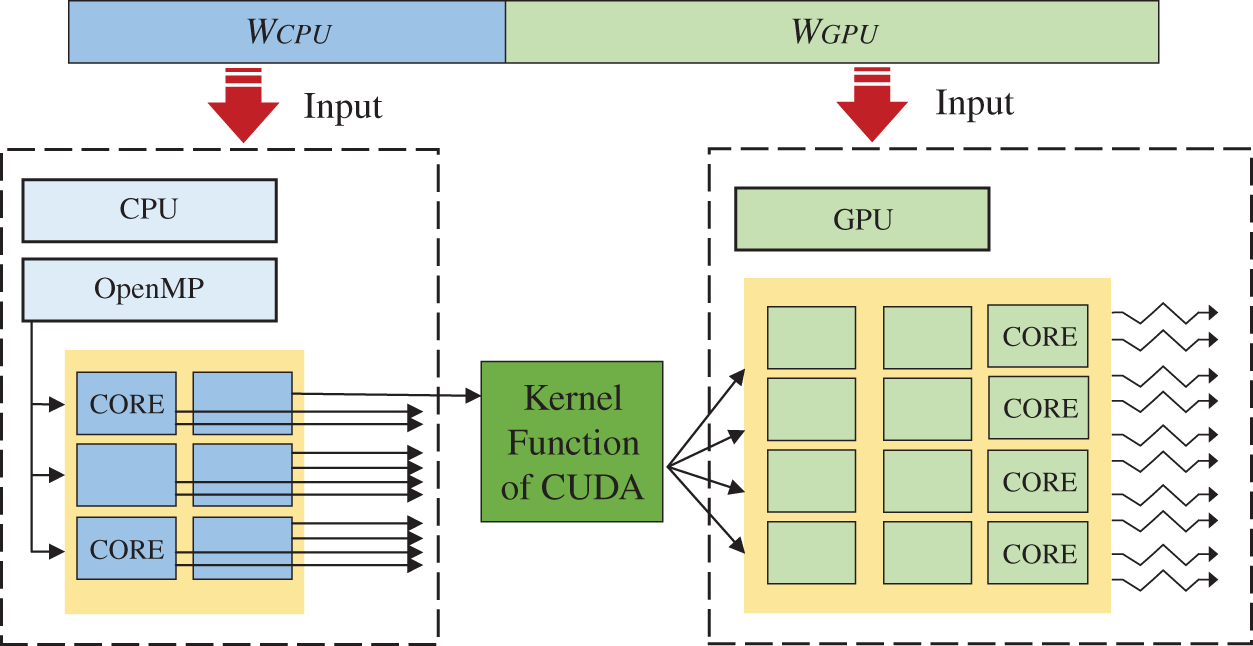
Figure 2: Schematic diagram for OpenMP/CUDA parallel programming model

3  CPU/GPU Hybrid Parallel Strategy for ITO

The CPU/GPU heterogeneous parallel computing is expected to accelerate the ITO computational processes. The proposed CPU/GPU hybrid parallel strategy for ITO consists of stiffness matrix assembly, equation solving, sensitivity analysis, and design variable update.

3.1 Strategy for Stiffness Matrix Assembly

The global stiffness matrix assembly consumes substantial computational resources. A parallel strategy is to calculate the local stiffness matrix among threads, where the contributions of Gaussian points in each element are summed up [55]:

Ke=∑GwGBGTDBG(9)

where BG is the deformation matrix calculated on Gaussian points and wG is the weight factor. Each local stiffness matrix is appended to the global stiffness matrix K in the corresponding locations:

K=∑Ke(10)

3.1.1 Thread Race Condition in Heterogeneous Parallelism

Theoretically, assembling a global stiffness matrix among elements can be directly executed [56]. However, due to shared control points among elements, a memory address may be written by multiple threads when the element-wise heterogeneous parallel strategy shown in Fig. 3 is employed. Such a conflict, called a thread race condition, will lead to incorrect updates on the stiffness coefficients.

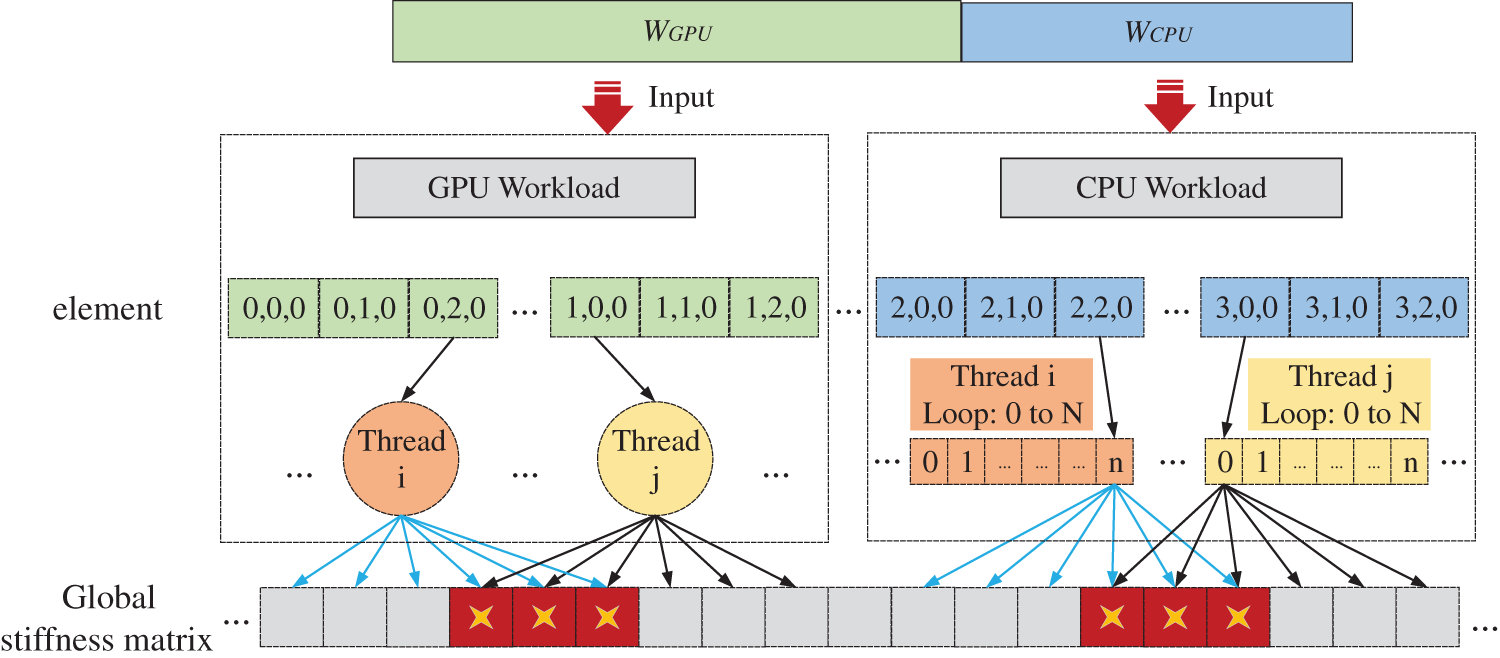
Figure 3: Element-wise heterogeneous parallel approach of assembling stiffness matrix

Although atomic operations can avoid race conditions, the efficiency of heterogeneous parallelism would be significantly reduced [57], and the assembly process would be critically degraded to serialization. To fundamentally avoid race conditions and maintain the efficiency of parallel computation, a hybrid parallel strategy for stiffness matrix assembly based on the control point pair is proposed herein. The workload is appropriately assigned between the host CPU and device GPU, while the heterogeneous parallel threads are divided by interacting i-j control point pair as shown in Fig. 4. Considering the control point pair shared by elements, as shown in Fig. 5, the local stiffness matrix ke of each element is discretized into a series of submatrices Hij defined at the control point pair [35]:

Hij=BiTDBj(11)

where Bi, Bj are the deformation matrix corresponding to the i-j control point pair, and D is the elasticity matrix. The submatrices Hij on all shared Gaussian points are calculated and multiplied by the weight factors, then summed to generate the final coefficients Kij of the global matrix K:

Kij=∑GwGHij(12)

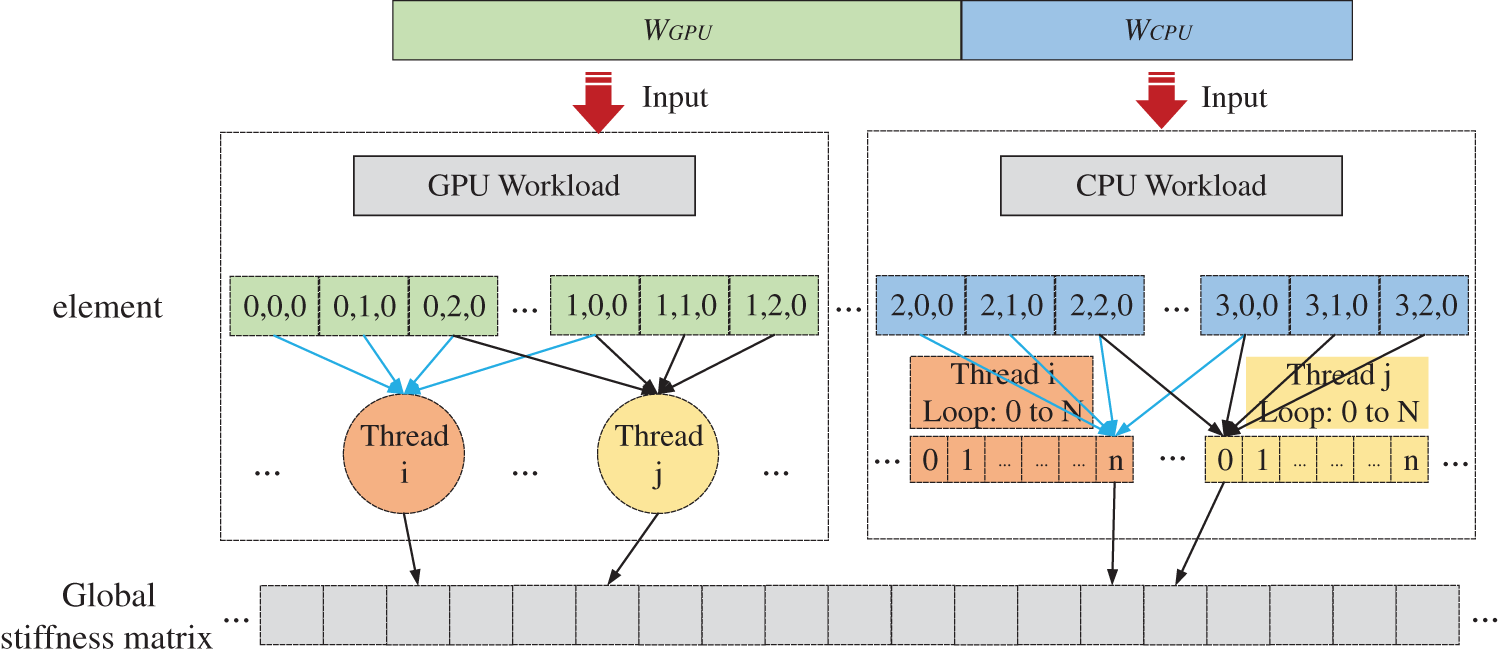
Figure 4: Interaction-wise heterogeneous parallel approach of assembling stiffness matrix

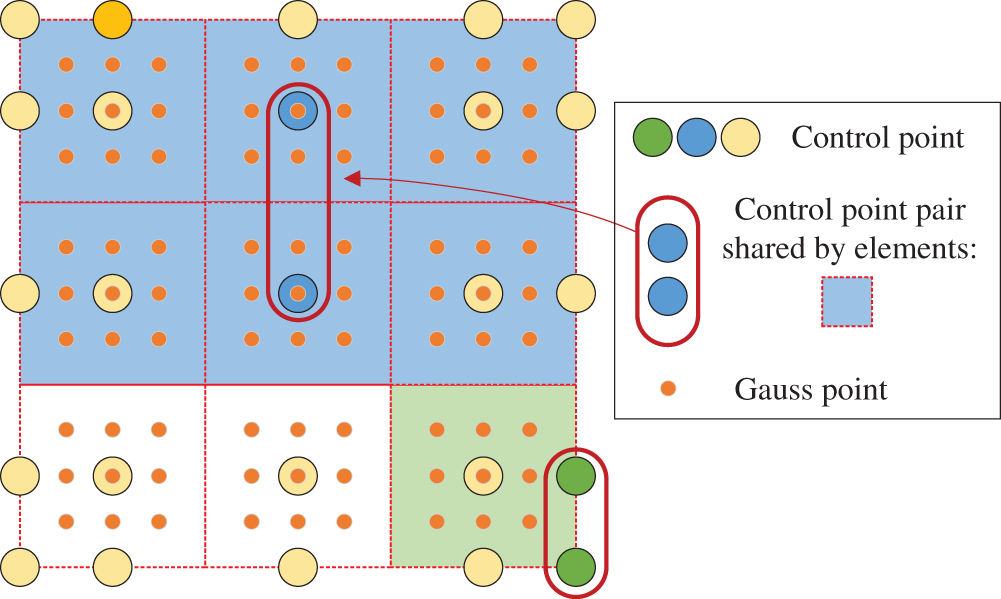
Figure 5: Shared control point pair between elements

3.1.2 Hybrid Parallel Strategy and Data Structure for Stiffness Matrix Assembly

The proposed hybrid parallel strategy for stiffness matrix assembly is based on interacting control point pair. Synchronized operations between threads on GPU and CPU can be avoided to make the algorithm applicable for efficient hybrid parallel computing. There are two phases: (1) the derivatives of the shape functions are calculated for all influenced Gaussian points. The computational workload is divided by element, in which a set of Gaussian points are calculated for shape function derivatives. (2) each heterogeneous parallel thread calculates derivatives in each element, as shown in Fig. 6, which increases the flexibility for calculating the global stiffness coefficient.

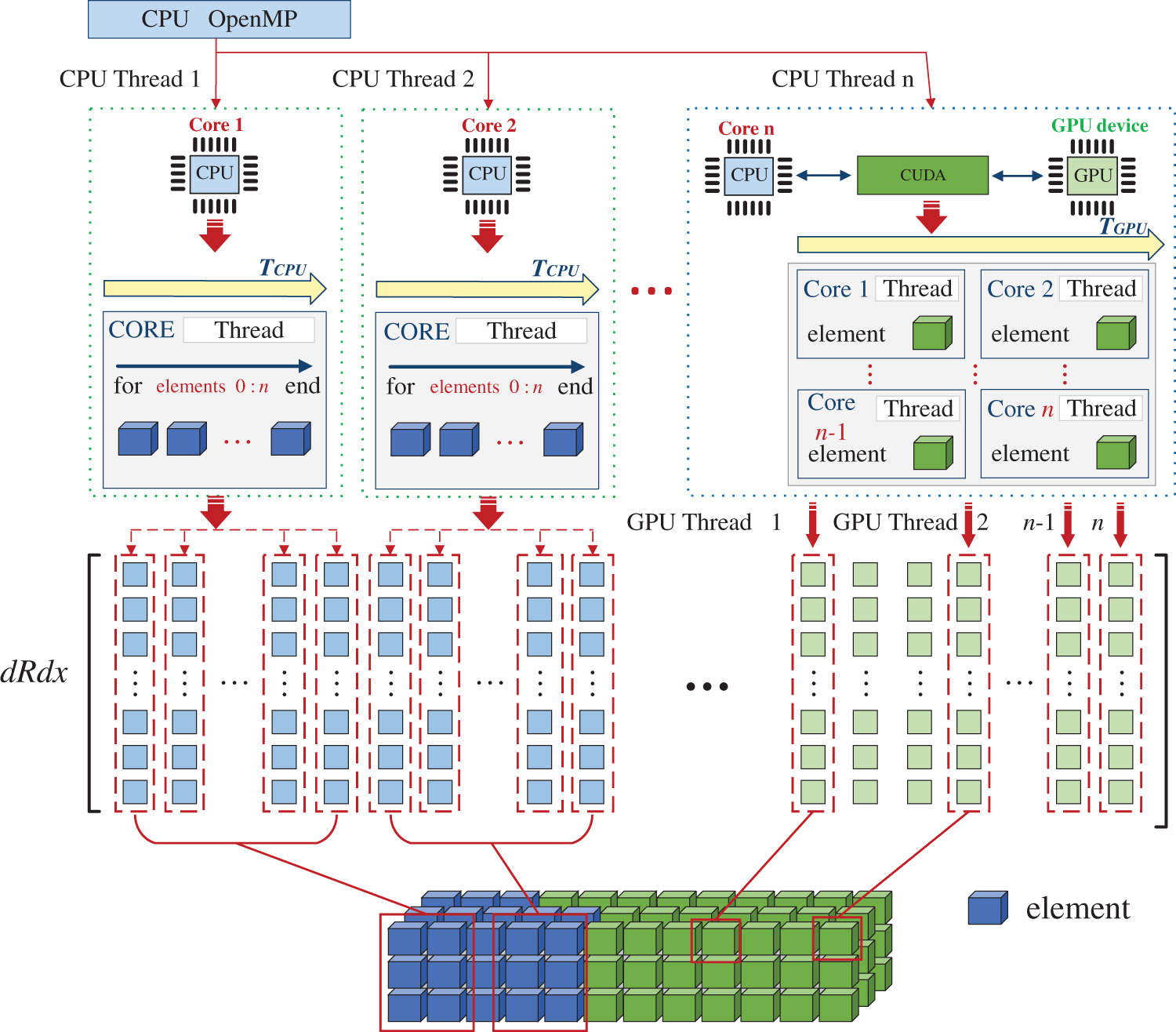
Figure 6: First phase in heterogeneous parallel computing of assembling stiffness matrix

The shape function derivatives are stored in GPU global memory and CPU shared memory in the second phase. As shown in Fig. 7, the threads can access the random memory addresses and concurrently access the same memory address among threads. The computational workload is divided by control point pairs. Each thread completes the numerical integration process for shared Gaussian points of the pair, and then calculates wGHij submatrices as Eq. (12). Finally, the parallel threads will fill stiffness coefficients into the corresponding unique positions of matrix K. Race condition will be eliminated by the hybrid parallel strategy, a precondition for efficient parallel computing. In addition, the total computation task can be divided into multiple fine-grained subtasks between CPU and GPU, which will contribute to efficiency improvements.

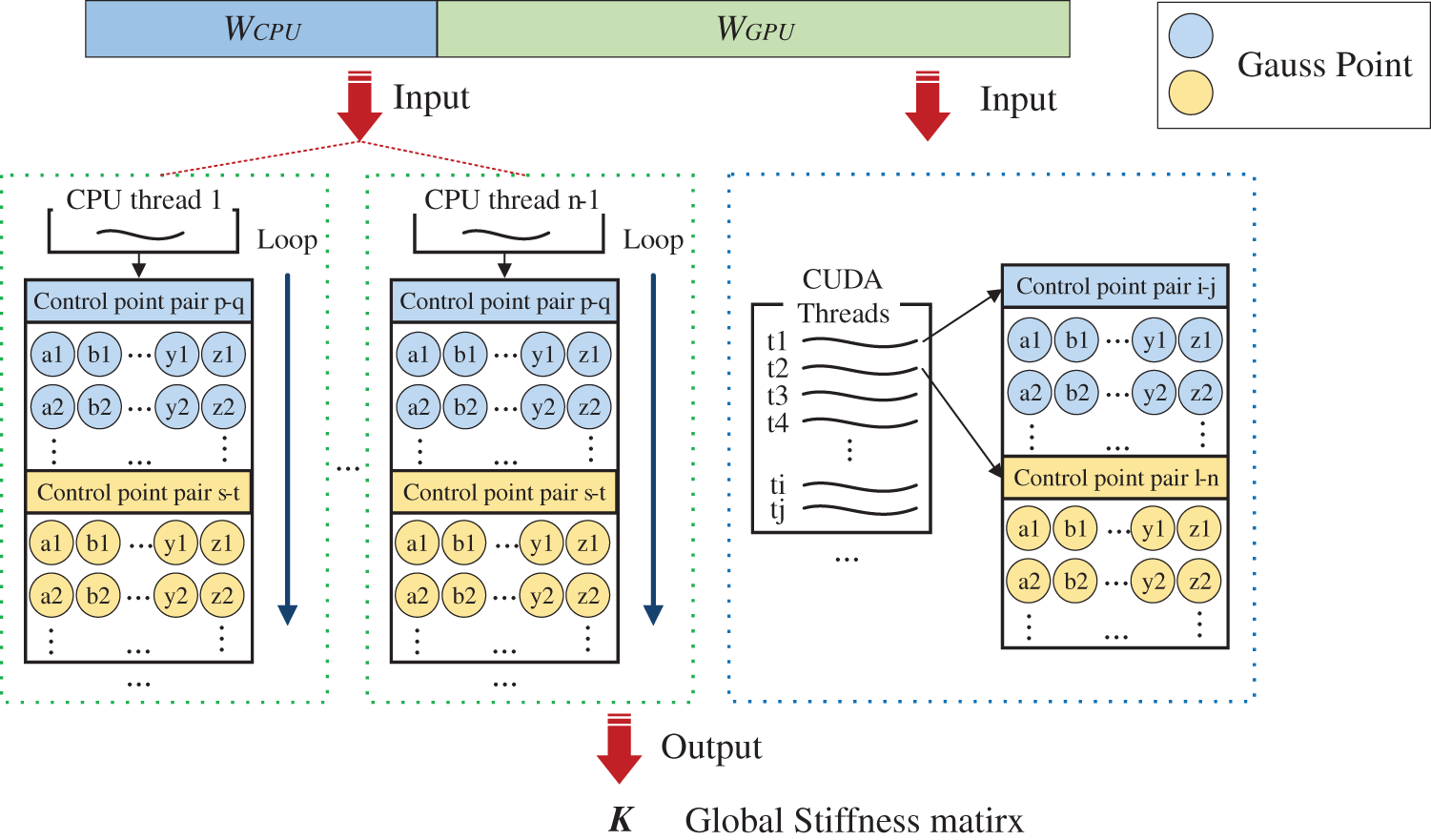
Figure 7: Second phase in the heterogeneous parallel strategy of assembling stiffness matrix

The simplified heterogeneous parallel algorithm for stiffness matrix assembly is stated in Table 1. “One-thread-one-stiffness matrix” mode in GPU and “one-thread-multi-stiffness matrix” mode in CPU are adopted in the hybrid parallel strategy. The symbol ← indicates variable assignment operations in local memory, and the double-linear arrow ⇒/⇐ indicates global memory read/write operations. Table 1 shows the first phase of the heterogeneous parallel strategy for the stiffness matrix assembly. The sensitivityFilter() function is a filtering scheme for smoothing free design boundaries in narrow-band regions. By using a window function to filter the pseudo-density of the element, the smoothness of the strain energy density is improved. The spaceConverter() function is for calculating the coordinates of the control points in parameter space. The JacobianMapping() function is used to transform Jacobian matrix. The Nurbs3Dders() function calculates the partial derivative values of the shape function in parameter space and then multiplies them by Jacobian inverse matrix. The results will be stored in matrix d_dRdx as information for the second stage of the calculation.

In the second phase, the DOFs of the control point pairs are calculated by CalcPairDOF() function as listed in Table 2. The DOFs indicate the locations of the stiffness coefficients in matrix K. Each thread iterates through the elements shared by the control point pairs. The shape function derivatives of node pairs are obtained according to the local indices of control points in the element, while the stiffness coefficients Kij can be calculated by integrating overall shared Gaussian points.

The sparse matrix K is compressed and stored in COO format to save memory, which only records non-zero element information. Arrays of the C/C++ structure store three vectors: the row and column index vectors (iK, jK) and the non-zero value vectors (vK). Unlike adding the contribution of local stiffness ke to assemble the matrix K, the final stiffness coefficient can be directly generated in the hybrid parallel strategy. Therefore, there are no repeated combinations of row and column indices. Non-zero values in matrix K are specified by the unique combinations of row and column as shown in Fig. 8.

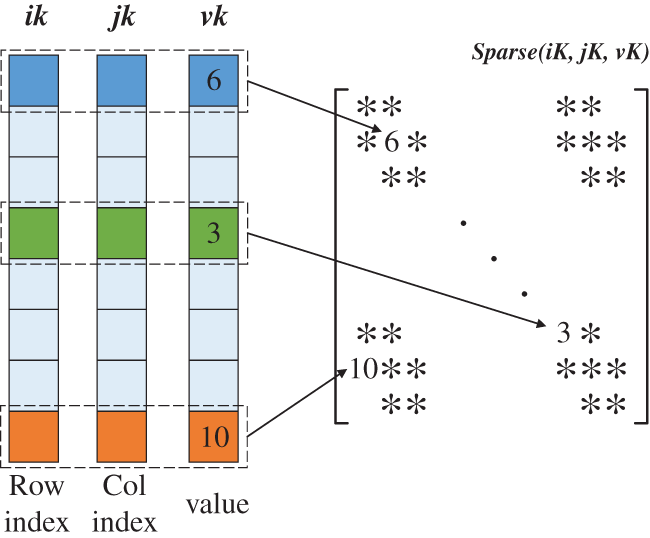
Figure 8: Storage of sparse matrix in COO format

3.2 Strategy for Equation Solving

A fast solving of equilibrium equations can significantly accelerate optimization iteration [58]. A hybrid parallel strategy of PCG (preconditioned conjugate-gradient method) is studied herein to improve equation-solving efficiency.

3.2.1 Preconditioned Conjugate-Gradient Method

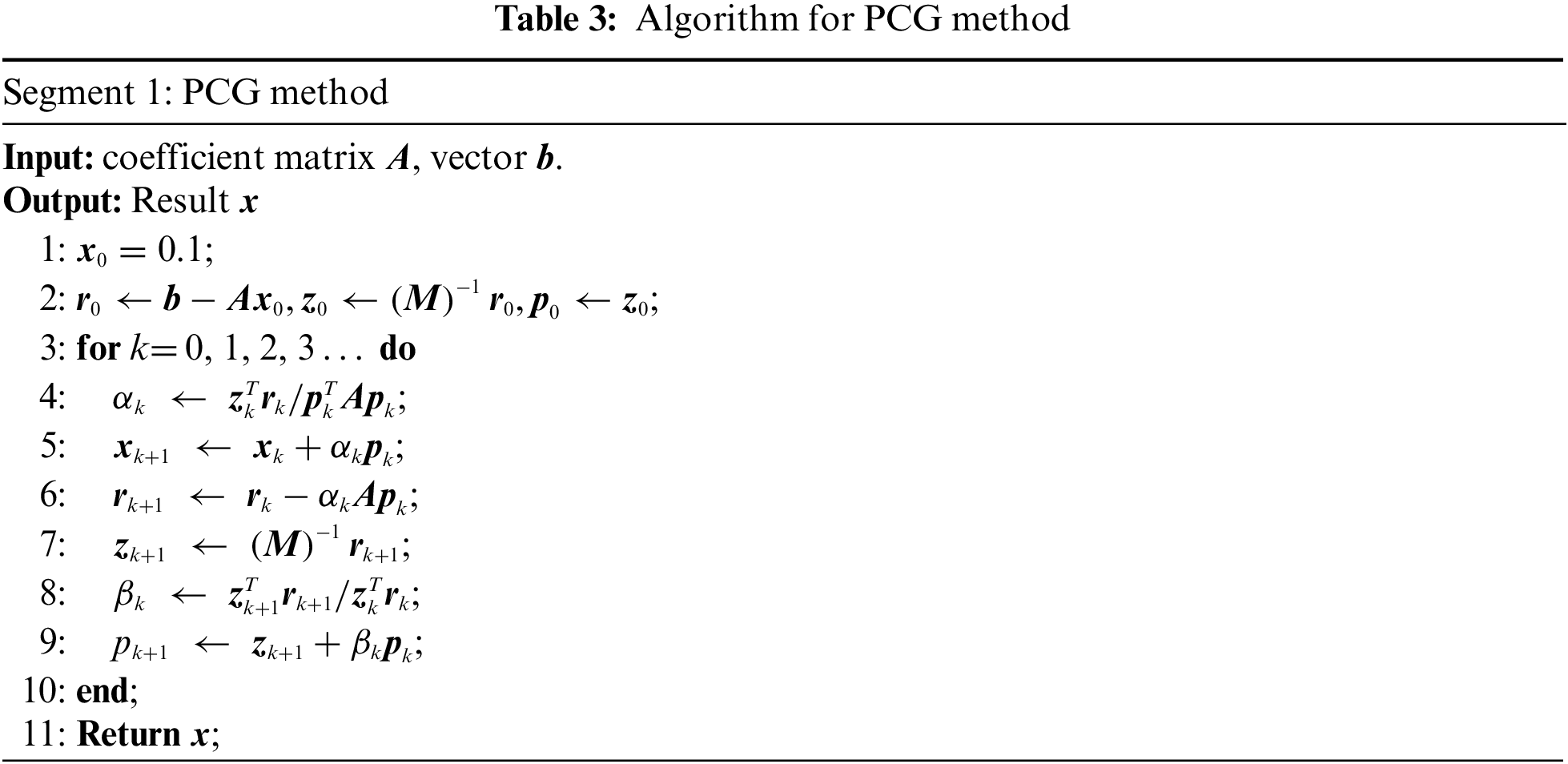
Conjugate-gradient method (CG) is an iterative method for solving systems of linear algebraic equations, preconditioned conjugate-gradient method (PCG) adopts a preconditioner to adjust the coefficient matrix in the equation to increase the convergence [59]. A series of approximate solutions are obtained during the iterations, and the iteration finally ends once the error reaches the given tolerance. Applying PCG to solve the equation Kx = f in ITO, the algorithm can be described as:

where M denotes the preconditioning matrix, and rk is the error between approximate and accurate solutions. In the PCG method, the matrix M should make the condition number of (M−1K) close to 1 according to the convergence rate [60]:

||x−xi||k−1≤||x−x0||k−1(c−1c+1)i(13)

where c is the condition number of the coefficient matrix K. When the c(M−1K) is closer to 1 than c(K), the convergence will be accelerated considerably.

An incomplete Cholesky factorization method is utilized to obtain a well-performing preconditioning matrix M, which will be factorized as follows:

M=LLT(14)

where L is a lower triangular matrix. To accelerate the convergence, condition number c((LL)TK) is closer to 1 than c(K).

From Table 3, the computation of the vector dot product zk+1Trk+1, while zkTrk are independent during the iteration. Overlapping the independent computations will reduce the time of equation solving.

3.2.2 Hybrid Parallel Strategy of PCG

The CUDA stream, a kind of logical queue, is utilized for the hybrid parallel strategy of PCG. Different streams can execute multiple commands concurrently on NVIDIA GPU [61,62], while the sequence of operations is performed serially in order. Independent computations are executed in different CUDA streams, making the original serial process parallel. As shown in Fig. 9, the same number of CPU threads as the CUDA streams are adopted. Each CUDA stream executes different parallel operations concurrently, and OpenMP threads can update data before or after the stream launching.

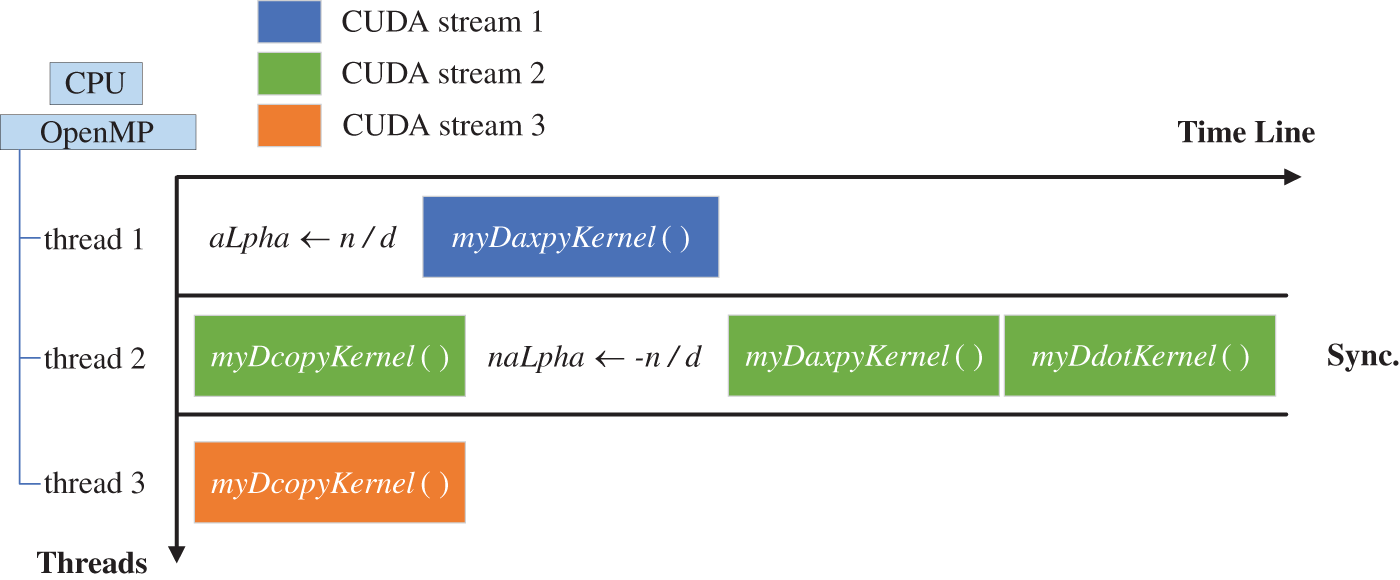
Figure 9: Overlapping computations in OpenMP threads

The CPU threads launch kernel functions concurrently and complete related calculations of kernel functions. Based on OpenMP, the total delay time for launching kernel functions in the serial is reduced, and the data processing for different kernel functions is executed in respective threads. It is beneficial to avoid synchronizing streams to update data in the master thread. The simplified heterogeneous parallel algorithm of PCG is shown in Table 4. In each iteration, the cuSPARSE library function cusparseSpSV_solve() is applied to solve the sparse triangular linear system d_zm1 ⇐ (LT)−1*L−1*d_r1, i.e., zk+1=M−1rk+1, which is a key to achieve an efficient PCG solution. The multiplication of a sparse matrix matA and a dense vector d_p is performed by cuSPARSE library function cusparseSpMV(). The sparse matrix is compressed and stored in CSR format. Kernel functions myDcopyKernel() and myDdotKernel() are designed to perform copying and dot product of dense vectors. The kernel function myDscalKernel() is used to calculate a vector and scalar multiplication. Function myDaxpyKernel() computes d_x ⇐ alpha*d_p + d_x, which multiplies the vector d_p by the scalar alpha and adds it to the vector d_x. The OpenMP compile command #pragma omp parallel sections initially create the threads (forks), and the command #pragma omp section is followed by independent phases executed concurrently in each CPU worker thread.

3.3 Strategy for Sensitivity Analysis and Update Scheme

3.3.1 Hybrid Parallel Strategy for Sensitivity Analysis

According to Eq. (4), the material properties of the element in SIMP model are represented by Young’s modulus, and compliance C can be formulated as a summation of the element strain energy multiplied by Young’s modulus [63]. Therefore, the element strain energy with unit Young’s modulus Se is calculated as:

Se=ueTKeue(15)

then the compliance C can be described as:

C=∑e=1NEe(xe)Se(16)

Therefore, the compliance sensitivity term ∂C∂xe can be described as:

∂C∂xe=−t(xe)t−1Se=−t(xe)t−1ueTKeue(17)

In the process of sensitivity analysis, the calculation of strain energy is parallelized as the main time-consuming part [64]. The heterogeneous parallel strategy for sensitivity analysis is illustrated in Table 5. The task set is divided by element, as the strain energy of an element is calculated in a task. In the hybrid parallel strategy, the “one-thread-one-strain energy” mode in GPU and the “one-thread-multi-strain energy” mode in CPU are adopted.

3.3.2 Hybrid Parallel Strategy for Update Scheme

For discrete optimization problems with many design variables, iterative optimization techniques such as the moving asymptote method and optimality criterion (OC) method are usually adopted [65]. The OC method is chosen herein due to its efficiency with a few constraints. A heuristic scheme in OC iteration updates the design variables. Following the optimality condition, Be can be written as:

Be=−∂C∂xeΛ∂V∂xe(18)

where V is the material volume, Λ is the Lagrange multiplier for the constraint. Finally, the update method can be illustrated as:

xenew={max(0,xe−m) if xeBeη≤max(0,xe−m)xeBeη if max(0,xe−m)≤xeBeη≤min(0,xe+m)min(1,xe+m) if xeBeη≥min(0,xe+m)(19)

where m is the move limit and η is the damping factor set to 0.3.

Here, the design variable x is updated in heterogeneous parallel during each OC iteration. The workload is divided by element. Table 6 shows the procedure of the update method, and the strategy is “one-thread-one-design variable” mode in GPU and “one-thread-multi-design variable” mode in CPU.

3.4 Strategy for CPU-GPU Data Transfer

A large amount of data transfer between CPU and GPU in the hybrid parallel strategy implementation is required, which is time-consuming. Therefore, achieving efficient data transfer is crucial for CPU/GPU hybrid computing. To obtain high performance in CPU/GPU heterogeneous parallel computing, an efficient data transfer method is adopted.

3.4.1 Data Flow between CPU and GPU

In the CPU/GPU-based heterogeneous computing system, the architecture and memory system of the CPU are different from the GPU, so the GPU cannot directly access the memory of the CPU for computation. When performing heterogeneous parallel computation, the computational data will be transferred from the CPU to GPU side. Depending on the specific hardware and software, the data flow process between the CPU host side and GPU device side is shown in Fig. 10:

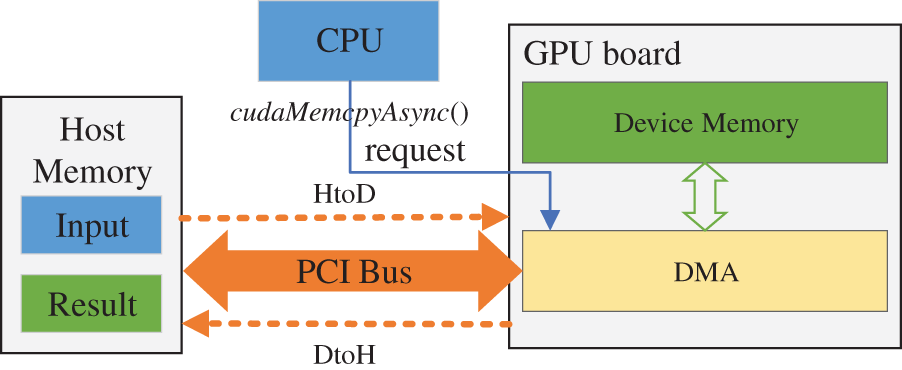
Figure 10: Data flow process between CPU host side to GPU

In the hybrid parallel strategy, the data is written to system memory first by the CPU. Then, a direct memory access (DMA) request to start the data transfer will be sent to the GPU by the CPU. With DMA, a data transfer execution is initiated by the CPU, then the dedicated DMA controller on the system bus will perform the transfer between the CPU and GPU. Thus, the involvement in the data transfer of the CPU is avoided, which frees it up to perform other tasks.

3.4.2 CPU-GPU Data Transfer Method for Hybrid Parallel Strategy

In the hybrid parallel strategy, the CPU memory is set as page-locked memory to ensure highly efficient data transfer between the CPU and GPU. The page-locked memory offers several advantages, while the bandwidth between the CPU and GPU memory will be higher, and the transfer speed will be faster. Page-locked memory allows the GPU to perform data transfer tasks directly through DMA engine without CPU involvement, reducing overall latency and decreasing transfer time. In addition, some asynchronous concurrent execution based on the page-locked memory is allowed in CUDA. Many researchers have explored overlapping data transfer and kernel execution with speed-up results when utilizing CUDA [65]. This approach is challenged in its direct application to ITO hybrid parallel strategy and will be integrated into future work, as the data set is hard to divide into chunks of suitable size for each kernel execution.

Several functions are provided by CUDA runtime for locked-page memory. One is cudaHostAlloc(), allocating new locked-page host memory; the other, cudaHostRegister(), can fix the allocated unlocked-page memory into being locked-page. The latter is adopted in the data transfer method. Then, cudaMemcpyAsync() is applied to transfer data asynchronously from the CPU to GPU. The process of data transfer will be completed by the GPU and signaled to the CPU, which allows the CPU to overlap data transfers with other computations, improving performance and reducing overall execution time.

In the hybrid parallel strategies proposed in this paper, the whole workload is split into two parts and the tasks will be allocated to the CPU and GPU. The GPU’s task set only corresponds to a portion of the resource data in the host, which provides an opportunity to reduce data transfer time by minimizing communication between the CPU and GPU. To minimize the communication, the corresponding range for vectors of GPU should be figured out first. For example, in the process of sensitivity analysis, the workload is divided by elements, where the corresponding range for vectors such as indices of elements can be easily determined. When transferring data from the CPU to the GPU, only related data are transferred, which saves communication time.

4  Loading Balance Strategy for CPU/GPU Heterogeneous Computing

In heterogeneous parallel computing, the loading balance strategy is key to ensuring computation efficiency. Thus a dynamic workload balancing method is proposed in this section.

4.1 CPU/GPU Computing for ITO

Computing resources in heterogeneous clusters include one multi-core CPU and one many-core GPU. In some GPU parallel studies, the CPU is responsible for data preparation and transfer, while GPU performs arithmetic operations [66,67]. However, some CPU cores are idle when preparing and transferring data for GPU, resulting in a waste of computational resources [68]. Therefore, cooperative computation for a particular workload is researched herein.

As described in Section 3.1, the workload for the first phase of stiffness matrix assembly can be subdivided into Nx * Ny * Nz independent tasks (Nx, Ny, Nz denote the mesh size in X, Y, Z axis directions). Moreover, the workload for the second phase is subdivided into NP independent tasks, where NP is the number of control point pairs. Therefore, the workload can be flexibly distributed between CPU and GPU, as shown in Fig. 11. The workload Π represents the total number of tasks and is divided into two parts: one core in CPU is reserved for data interaction, and (n−1) CPU cores are to handle the workload Π(1−α), where α denotes the workload balancing ratio between CPU and GPU.

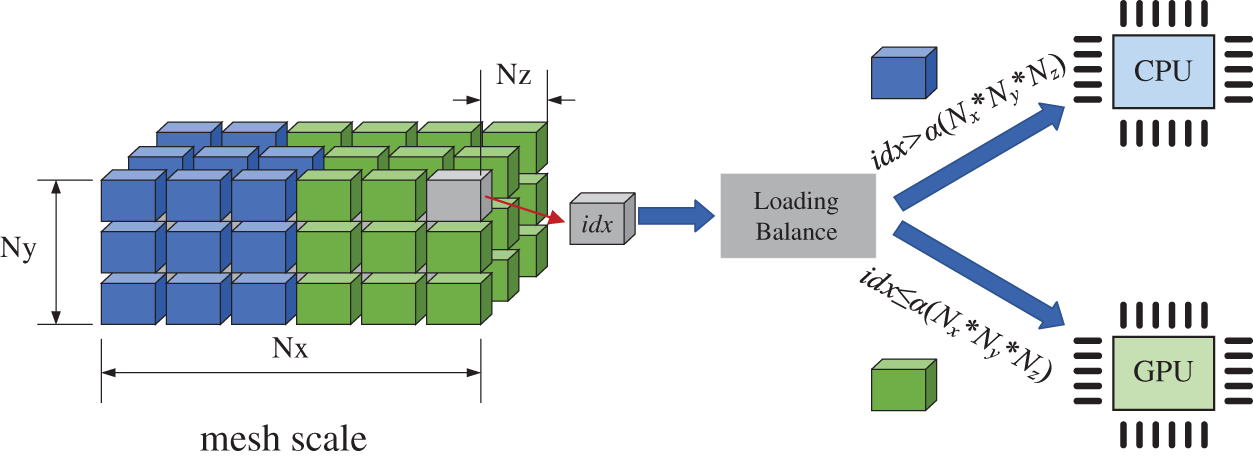
Figure 11: Workload balancing between the CPU and GPU by loading balance strategy

4.2 Dynamic Workload Balancing

For heterogeneous parallelism, balancing the workload between the CPU and GPU with different arithmetic capabilities for efficient computing is critical [69,70]. There are three main methods to evaluate the best workload balancing ratio α: the enumeration method, the formula method, and the pre-run method [71,72]. In the enumeration method, all possible workload balancing strategies are executed, and then the best workload balancing ratio α with the shortest time is chosen. The formula method requires quantifying the computing power of hardware devices. δCPU and δGPU denote the computing power of one CPU core and all GPU cores, respectively, while the computing power of the whole CPU is (n−1)δCPU. Then the wall-clock time τ for CPU/GPU computing can be expressed as:

{τ=max(τCPU,τGPU)τGPU=ΠGPU/δGPUτCPU=ΠCPU/(n−1)δCPU(20)

where τCPU is the wall-clock time for CPU computing and τGPU is for GPU. The total computing time τ is determined by the greater one of τCPU and τGPU. Therefore, when τCPU equals τGPU, the total computing time is minimized to avoid the mutual waiting between CPU and GPU. Thereby, the best workload balancing ratio α and workload ΠCPU, ΠGPU can be expressed as:

{α=1/(1+(n−1)(δCPU/δGPU))ΠGPU=αΠΠCPU=(1−α)Π(21)

The formula method requires accurate quantification of hardware computing power. Although this can be obtained directly from the APIs, the actual computational efficiency is affected by the parallel algorithm and hardware running. Therefore, a dynamic workload balancing method combining the formula and pre-run method is proposed in this paper, while the pre-run method is utilized to amend the formula method (theoretical value) for the main parameters of workload balancing. Assuming that there are Nx × Ny × Nz independent tasks, τCPU can be written as:

τCPU=(1−α)(Nx×Ny×Nz)tCPU(22)

where τCPU is the computation time to execute one task for the CPU. Taking into account the time consumed by the CPU and GPU data transfer, τGPU can be written as:

τGPU=τDT+τG(23)

{τDT=α×k(Nx×Ny×Nz)×Svalν,tdt=k×SvalντG=α(Nx×Ny×Nz)tGPU(24)

(1−α)(Nx×Ny×Nz)tCPU=α(Nx×Ny×Nz)(tdt+tGPU)(25)

α=tCPUtCPU+tdt+tGPU(26)

In the dynamic method, the pre-run phase aims to get the actual data transfer time tdt and the computation time tGPU and tCPU as shown in Fig. 12. The workload Πpre of the pre-run phase is greater than (n−1), ensuring that each CPU core is loaded. After the pre-run phase, the execution times Γ1 and Γ2 for CPU and GPU are tailed. The formula has a pre-run part, making the load balancing in real-time. Hence the data transfer time and the computation time can be evaluated:

{Γ1=ΠpreτCPUΓ2=Πpre(τdt+τGPU)(27)

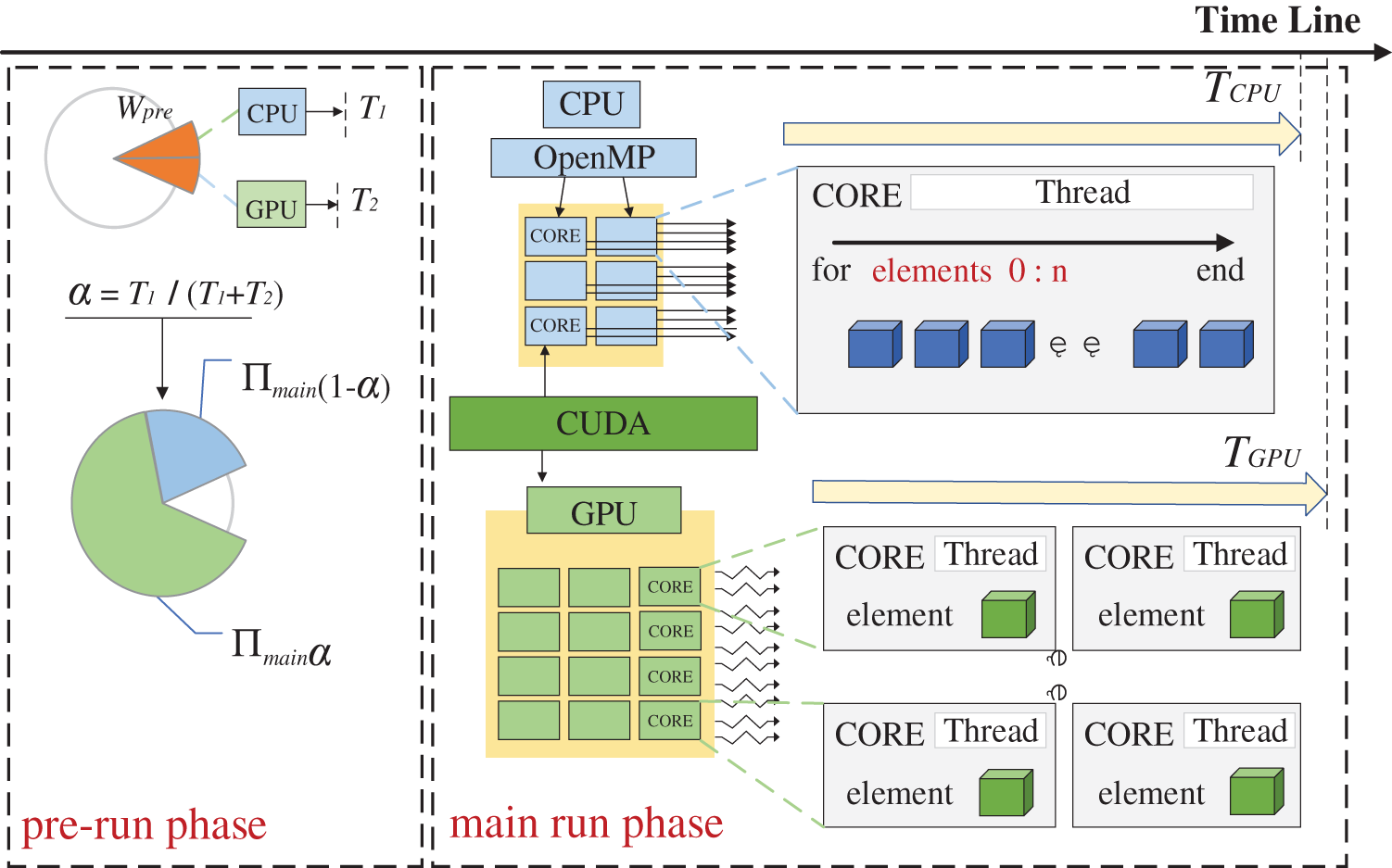
Figure 12: Dynamic workload balancing for CPU/GPU heterogeneous computing

Finally, the workload balancing ratio α can be expressed by Γ1 and Γ2 as follows:

α=Γ1Γ1+Γ2(28)

The time consumed for the data transfer and the computation per task does not change as the workload increases. The dynamic workload balancing algorithm is illustrated in Table 7. The total computational tasks in ITO hybrid parallel strategies can be divided by control point pairs or elements. For independence, the tasks are quite suitable for the workload balancing method based on a task set division. Through the balancing, the tasks are assigned according to the real-time local computing power measured by the pre-run phase. Therefore, the proposed dynamic workload balancing algorithm is reliable and versatile.

5  Numerical Experiments

There are three benchmarks examined to verify the performance of the heterogeneous parallel ITO algorithm. Poisson’s ratio v = −εl/ε is set to 0.3, where εl is the strain in the vertical direction, ε is the strain in the load direction. The modulus of elasticity E0 is 1.0 for solid materials and 0.0001 for weak materials, and the convergence criterion r = (Ci-1 – Ci)/Ci is set to 0.01, where Ci is the compliance in the ith OC iteration. When displaying the topology structure, the element density xe has a threshold value of 0.5, which means that the density of elements below 0.5 is not displayed. The filter radius fr is empirically set to 0.04 times the maximum length of the mesh in the axial direction. All examples are running on a desktop. The Intel Xeon Gold 5218 2.3 GHz CPU contains 16 CPU cores, and the RAM is DDR4 SDRAM (128 GB). The GPU is NVIDIA GeForce RTX 3090, which contains 5888 streaming multiprocessors and 10496 CUDA cores. The desktop OS is Windows 10.1 64-bit. As for the compilation, the CPU code is compiled by Mathworks MATLAB 2019 or Visual Studio 2019, while the GPU code is compiled by NVIDIA CUDA 11.6. The heterogeneous parallel algorithms are implemented by the programming language C using CUDA and OpenMP, allowing developed modules can be used in software written in C++. Fig. 13 shows the interface of efficient parallel software, where parallel computing is used to solve the ITO problems:

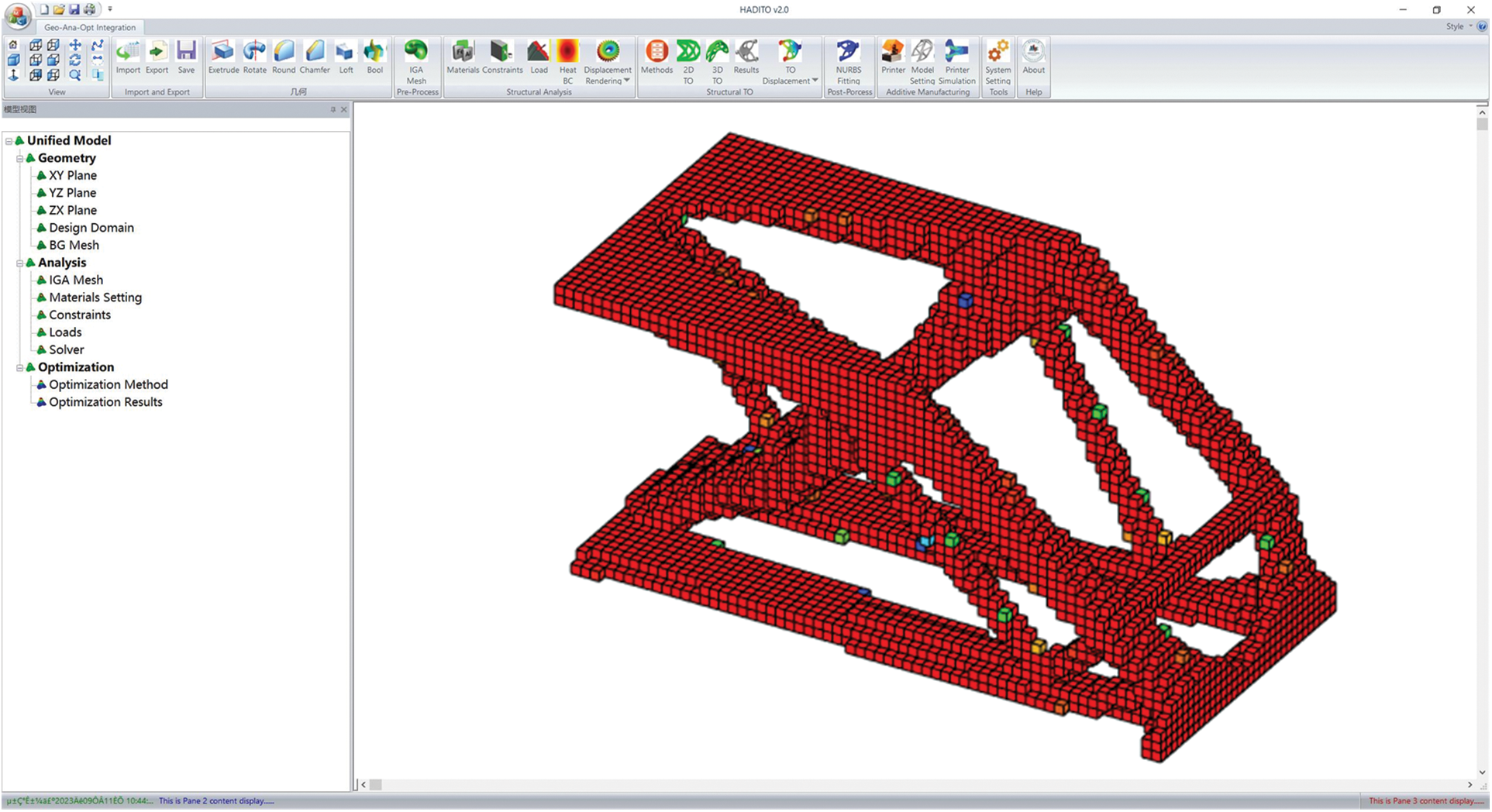
Figure 13: Interface of an efficient parallel software

5.1 Cantilever Beam

The cantilever beam is examined in this section to demonstrate the accelerated efficiency of the hybrid parallel strategy for ITO. The hybrid parallel strategy can be proved when the acceleration efficiency is higher than that of GPU. Fig. 14 shows the design domain of the 3D cantilever beam. The beam length, width, and height are set to 3 L, 0.2 L and L, respectively. The height L is set to 1, which follows the dimensionless quantity calculation rules. A unit-distributed vertical load F is applied downwards to the lower edge of the right end face while the left face is constrained.

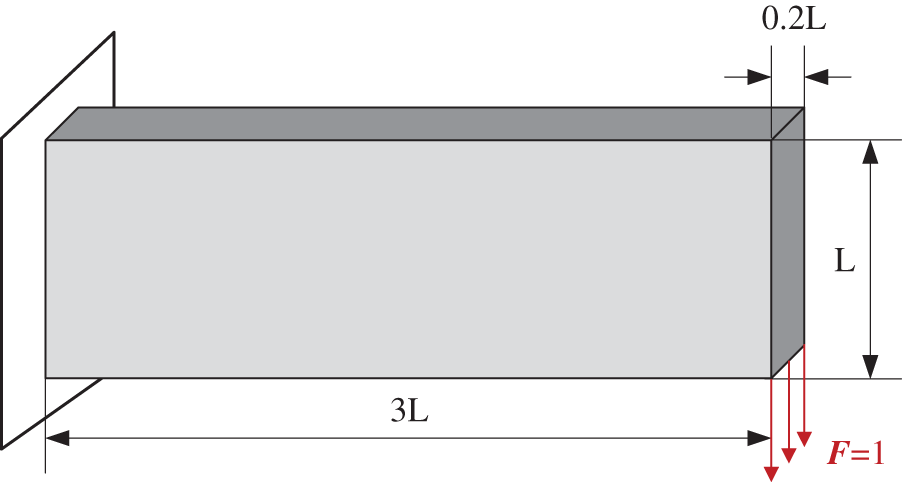
Figure 14: Design domain and boundary conditions of 3D cantilever beam

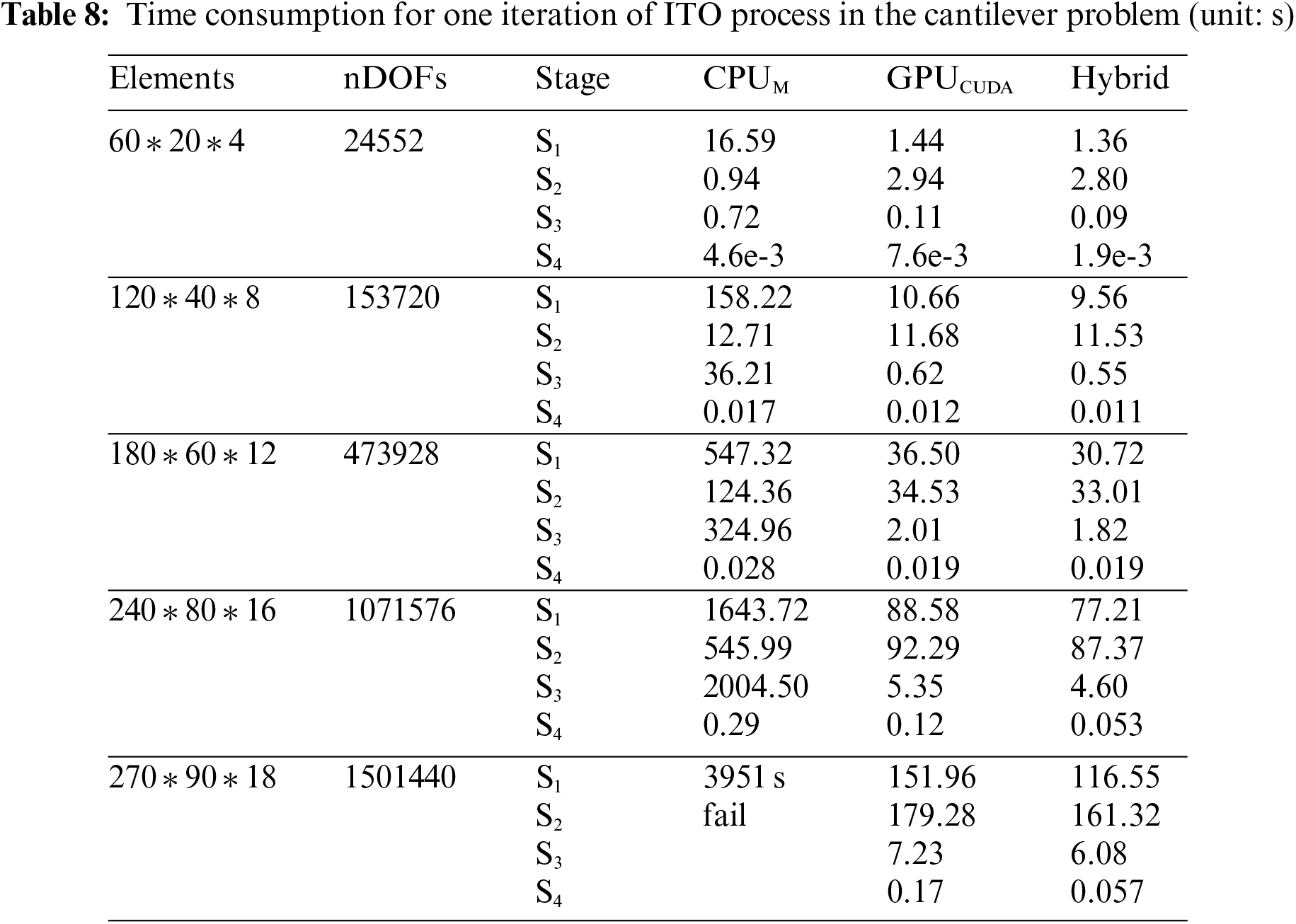
Fig. 15 shows the three different environments to compare efficiency, i.e., CPU with MATLAB, GPU with CUDA and the hybrid CPU/GPU with both C and CUDA. The original implementation of ITO is based on MATLAB. C and CUDA are used to allow for parallelized acceleration due to low-level access to computer hardware. To illustrate the speed-up of the CPU/GPU heterogeneous parallel strategy, several sets of the cantilever beam problem with different levels of quadratic NURBS elements are examined. The computational time of the ITO processes is shown in Table 8. The stiffness matrix assembly and the sensitivity analysis are executed in iterations of the solving processes, which shows that the parallel algorithm is more efficient than MATLAB. For the course mesh, the advantage of the hybrid over CUDA is not apparent enough. However, when the DOFs are up to 1.5 million, each step for the heterogeneous calculation takes tens of seconds faster than CUDA and thousands of seconds faster than MATLAB.

Figure 15: Different environments for ITO implementing

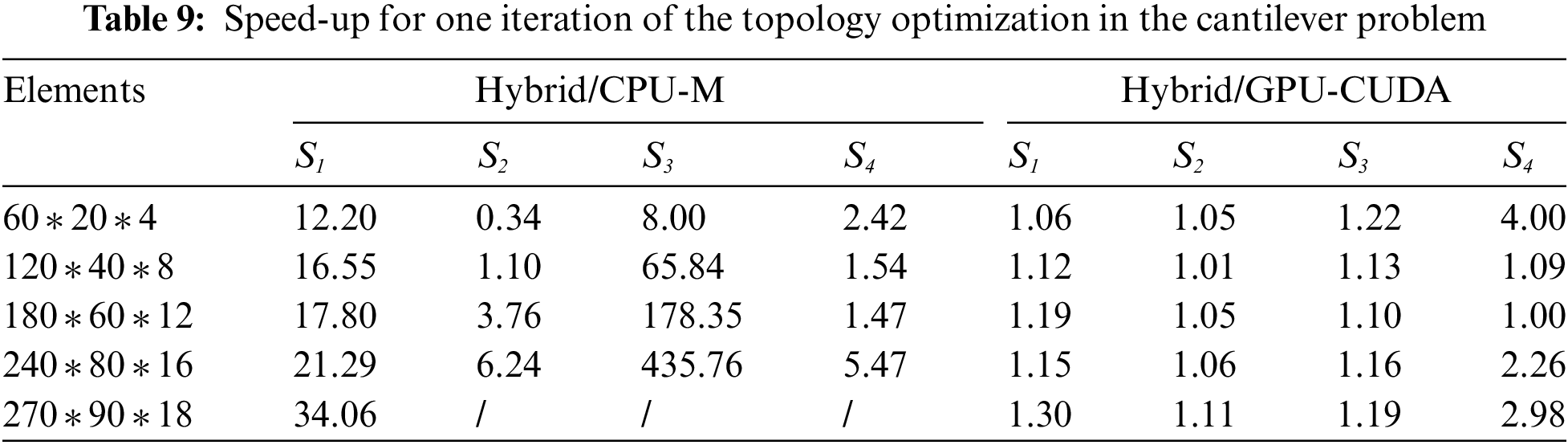
The speed-up ratio is obtained by comparing the hybrid computational time to others. As listed in Table 9, taking S1 as an example, the speed-ups of the hybrid to MATLAB vary from 12.20 to 34.06, while the hybrid to CUDA are from 1.06 to 1.30. The CPU parallel computing capability is poorer than the GPU, and it is difficult for the hybrid CPU/GPU to get a large acceleration ratio compared to the single GPU. From the table, the speed-up ratio is up to 2.96 in S4. Note that under the current hardware conditions, MATLAB cannot solve the equations x = K/f at the mesh size of 270 * 90 * 18. The time consumption of GPU contains data transfer time and computation time. When the scale reaches a certain level and the computation time is larger than the data transfer time, the increasing computation makes GPU’s parallel computing power fully utilized, which results in better acceleration. The GPU acceleration effect peaks with increasing scale, which causes the speed-up ratio in the table not to increase monotonically. Overall, from the data in the table, the speed-up ratio increases with the larger scale. The remarkable speed-up ratio proves the efficiency of the hybrid parallel algorithm, especially compared to MATLAB (achieving a speed-up ratio of 435.76 times). The ITO process based on the hybrid parallel strategy with the dynamic load balancing method can be further accelerated by utilizing the CPU and GPU parallel computing power.

The time consumption and speed-up ratios for the stiffness matrix assembly, equation solving, sensitivity analysis and the update scheme are shown in Fig. 16. The advantage of the hybrid strategy is not apparent on a small scale, but the hybrid strategy efficiency increases with the increasing scale. The optimized results of the cantilever beam problem with different mesh scales are shown in Fig. 17, while all the cases yield consistent, optimized results. The color mapping reflects the value of the element density, increasing from blue to red in order. When the number of elements is small, the boundary part of the structure appears jagged, and the continuity between element densities is low. With the number of elements increasing, the boundary of the structure gradually becomes smooth, and no large color gaps appear, indicating a high numerical continuity between adjacent element densities, consistent with the characteristics of realistic material manufacturing.

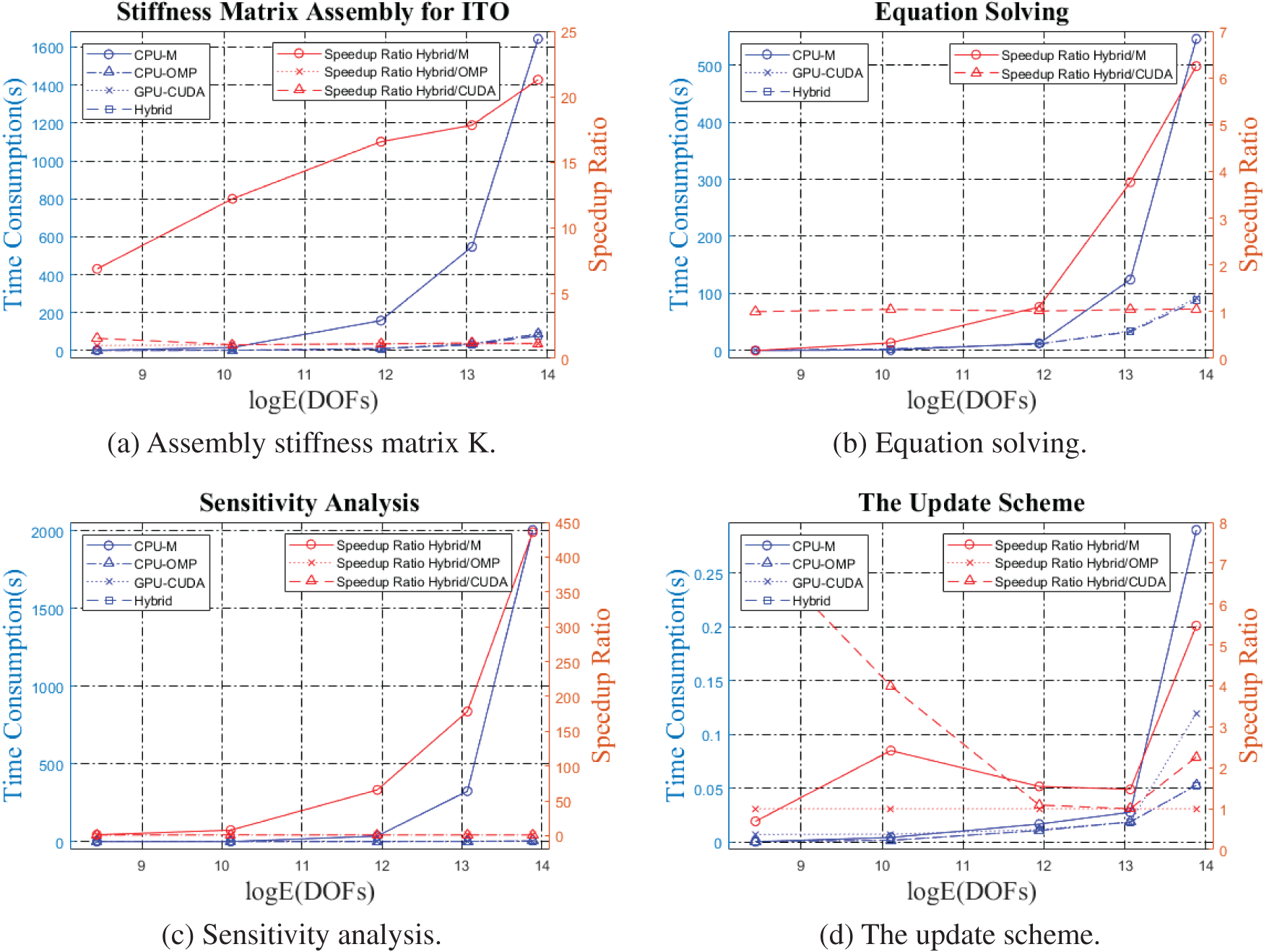
Figure 16: Time consumption and speed-up ration in ITO processes

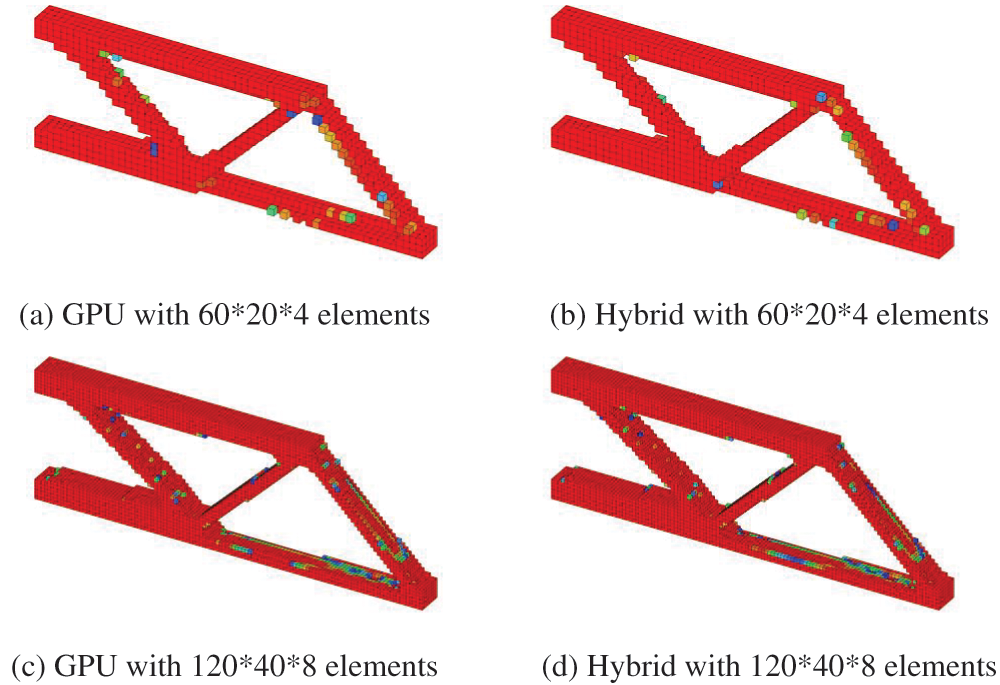
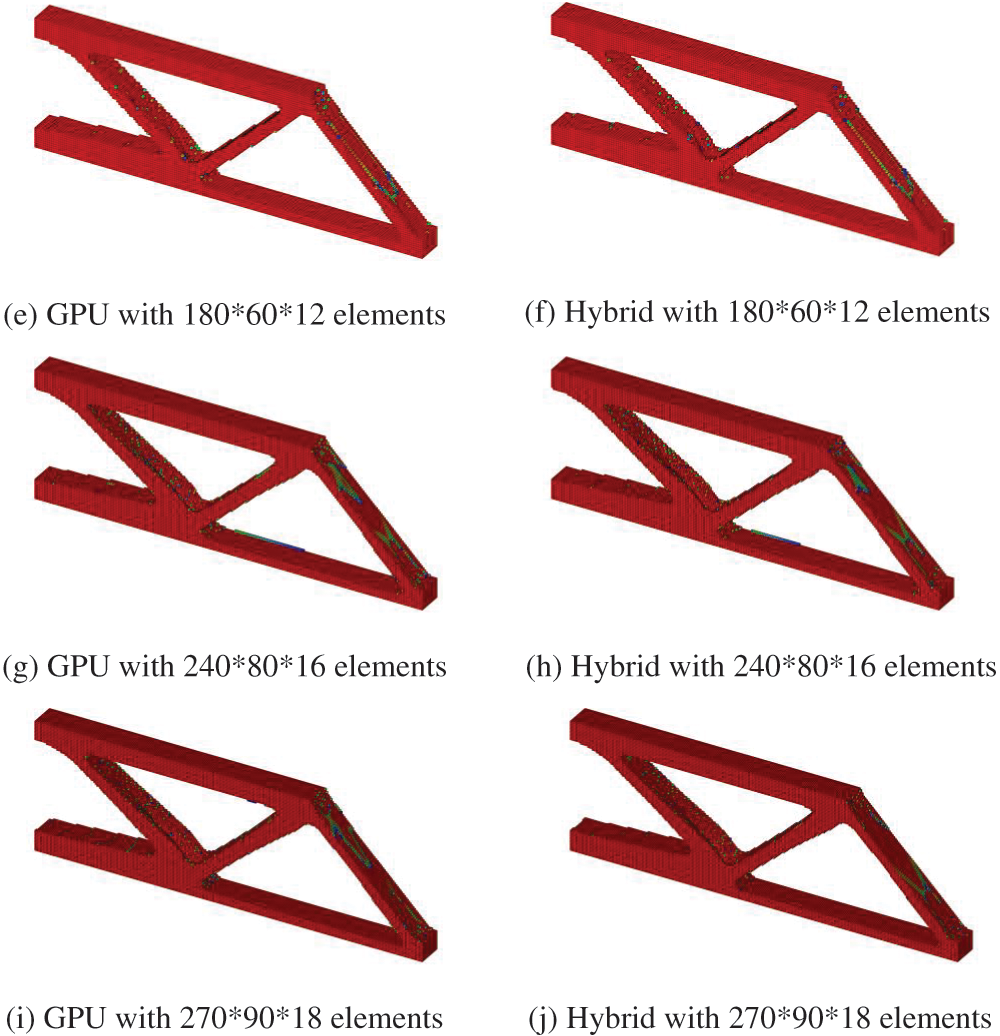
Figure 17: ITO results of cantilever beam problem with different NURBS elements

The time consumption of each process in the ITO iterations is shown in Fig. 18. In the CPU implementation with MATLAB, stiffness matrix assembly and sensitivity analysis are far more time-consuming than equation solving. However, in the hybrid, with the scale increasing, the time consumption ratios of stiffness matrix assembly decrease and become less than the equation solving. Compared to GPU, the hybrid main reduces time in stiffness matrix assembly and will achieve more significant results when the scale is larger. Thus, the efficiency of the hybrid parallel strategy for ITO is demonstrated. Then, equation solving will be the main time-consuming section in ITO.

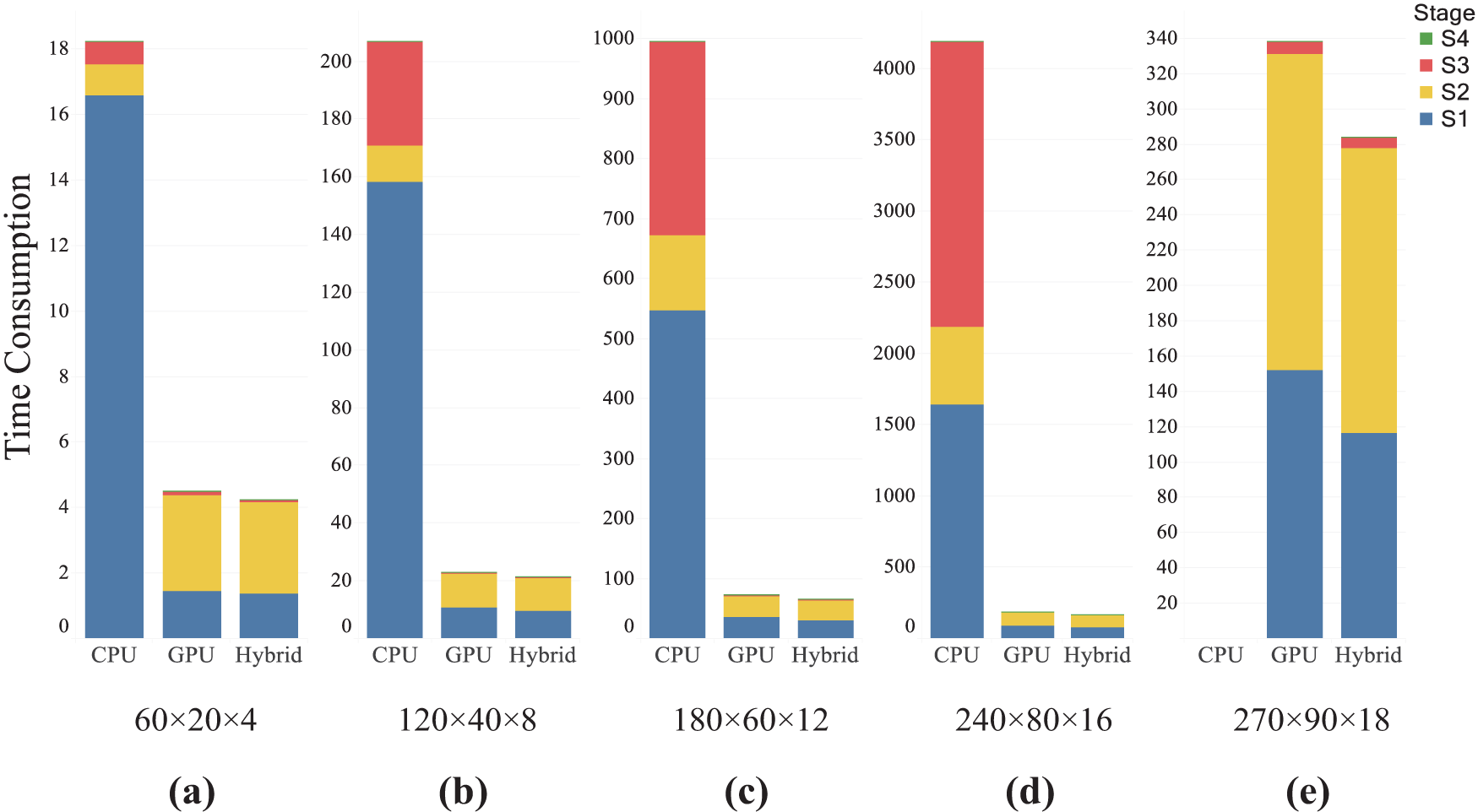
Figure 18: Time consumptions of IGA processes with different number of elements

5.2 MBB Beam

The MBB beam problem is to demonstrate the robust adaptability of the hybrid parallel strategy. Compared to the FEM-based TO, the IGA-based TO performs optimization analysis with higher-order NURBS elements, resulting in a significant increase in computational complexity and memory usage [24]. Considering the time cost, the maximum DOFs of the cases are set to two million, which exceeds the handling capacity of the GPU. The design domain of MBB beam is shown in Fig. 19, where the length is 6 L, width and height are both L. A unit load F is applied downwards to the center of the upper-end face. The four corners of the lower end face of the MBB beam are constrained while one side is free in the horizontal direction.

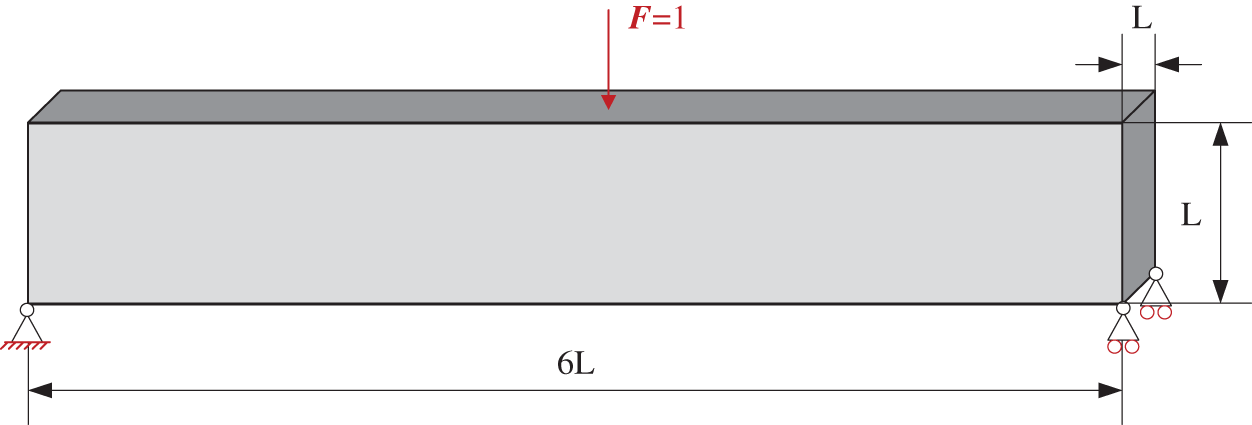
Figure 19: Design domain and boundary conditions of 3D MBB beam

Here the ITO problems require enormous memory resources. Three 3D cases with meshes of 120 * 20 * 20, 210 * 35 * 35, and 270 * 45 * 45 are tested, while the memory usage is listed in Table 10. When the scale reaches a critical level, it will lead to the failure of the CUDA parallel method since the memory resources are consumed beyond the limitation of GPU. The NVIDIA GeForce RTX 3090 used in this paper has 24 GB memory, which has a large gap to the 120 GB CPU memory. Limited memory is a performance bottleneck when using GPU to accelerate solving large-scale problems. In this paper, the tasks can be appropriately assigned to CPU/GPU via the dynamic workload balancing strategy. The management and efficient use of GPU memory can be achieved based on determining the minimum corresponding dataset for GPU’s tasks, which reduces the demand on GPU’s memory.

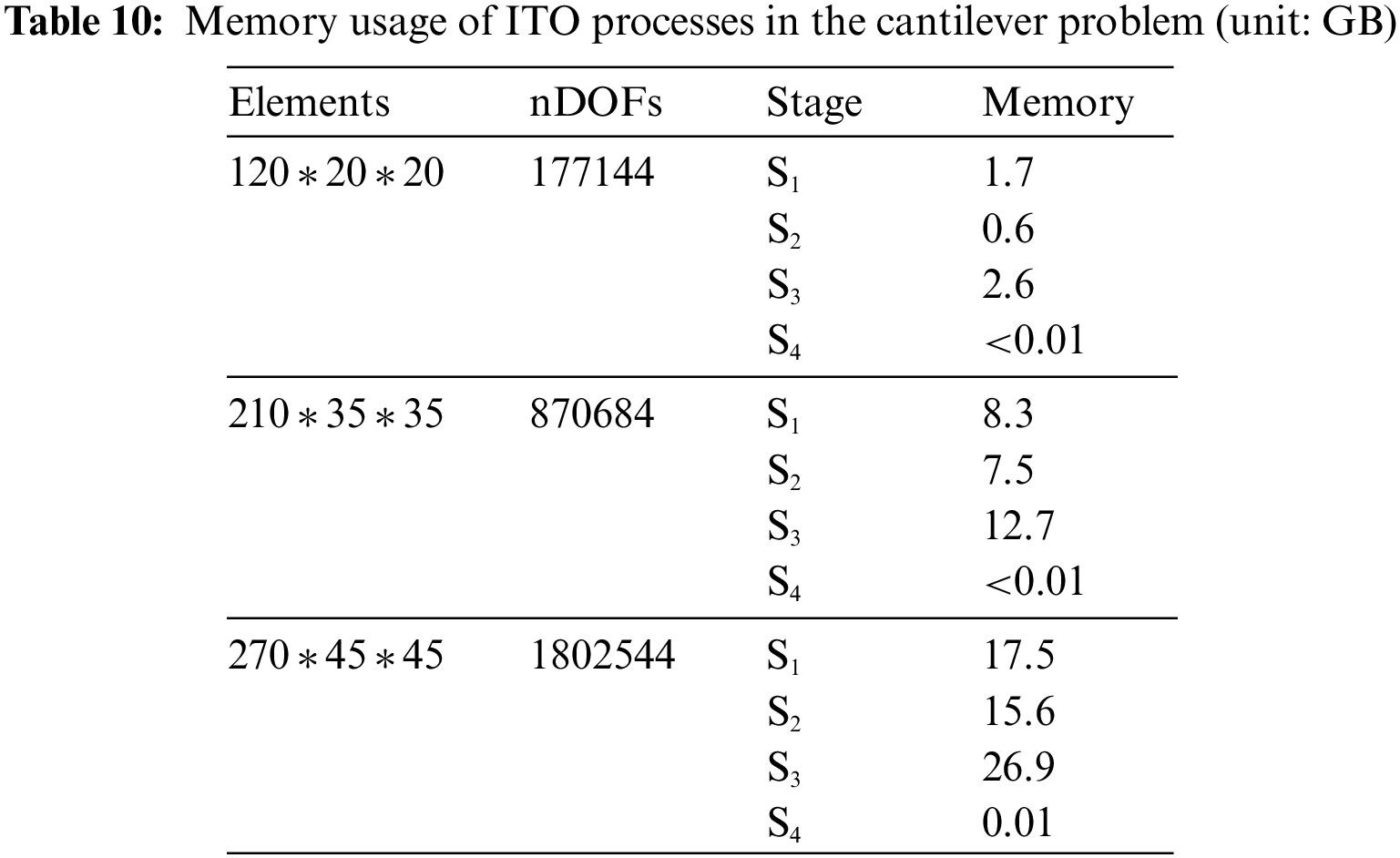
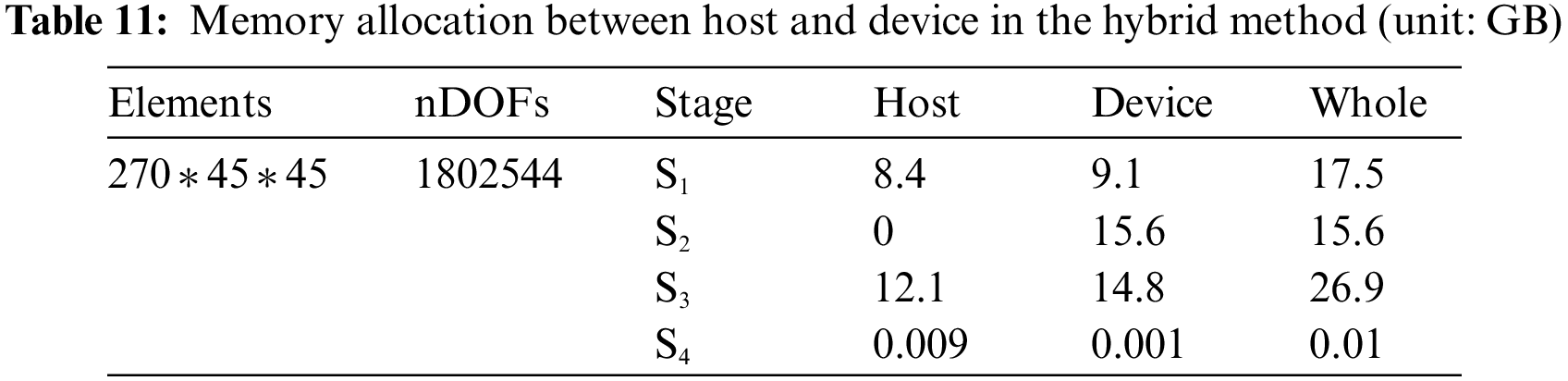
The optimized results of the 3D MBB beam problem are shown in Fig. 20. The 3D case with the mesh of 270 * 45 * 45 can only be solved by the hybrid method, while the memory allocation between CPU and GPU in each ITO process is shown in Table 11. The required memory in stages S1, S2, and S4 is lower than the GPU memory. However, S3 costs 26.9 GB, which exceeds the GPU’s limitation. In comparison, the hybrid method can allocate memory properly between CPU and GPU, and maximize the utilization of local computing resources.

Figure 20: ITO results of MBB beam problem with different NURBS elements

5.3 Wheel Beam

To demonstrate the accuracy of the proposed method, a 3D wheel beam problem is examined. The design domain is shown in Fig. 21. A unit external load F is applied to the center of the upper-end face, and the four corners of the wheel beam’s lower-end face are constrained.

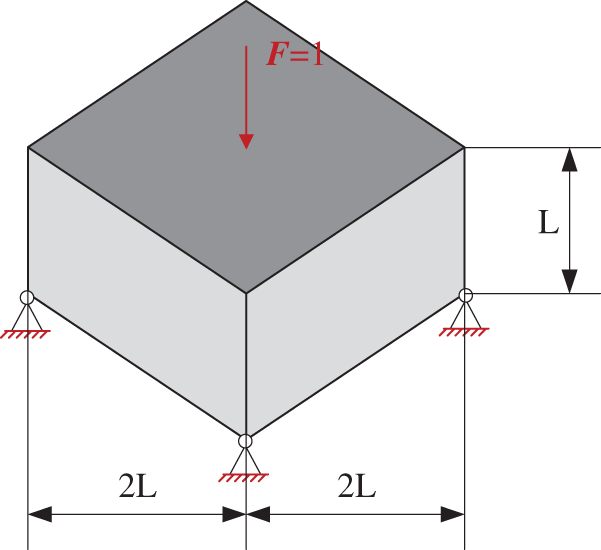
Figure 21: Design domain and boundary conditions of 3D wheel beam

The objective function values in ITO iteration are recorded in Table 12, and Fig. 22 shows the history of convergence for the CPU and the hybrid. The objective function values, i.e., compliance, decrease sharply in the beginning and smoothly converge over the iterations. The ITO process stops in the 132th iteration for the CPU, and 132th iteration for the hybrid. The iteration numbers are similar, while the results are illustrated in Fig. 23, which shows an identical structural topology.

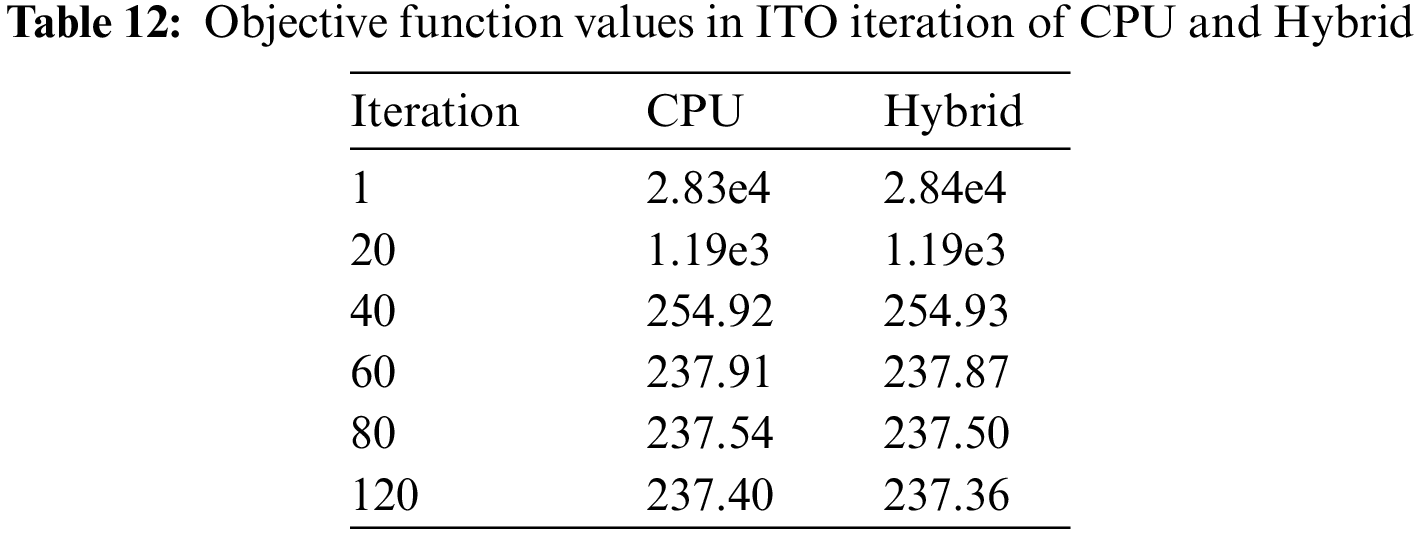
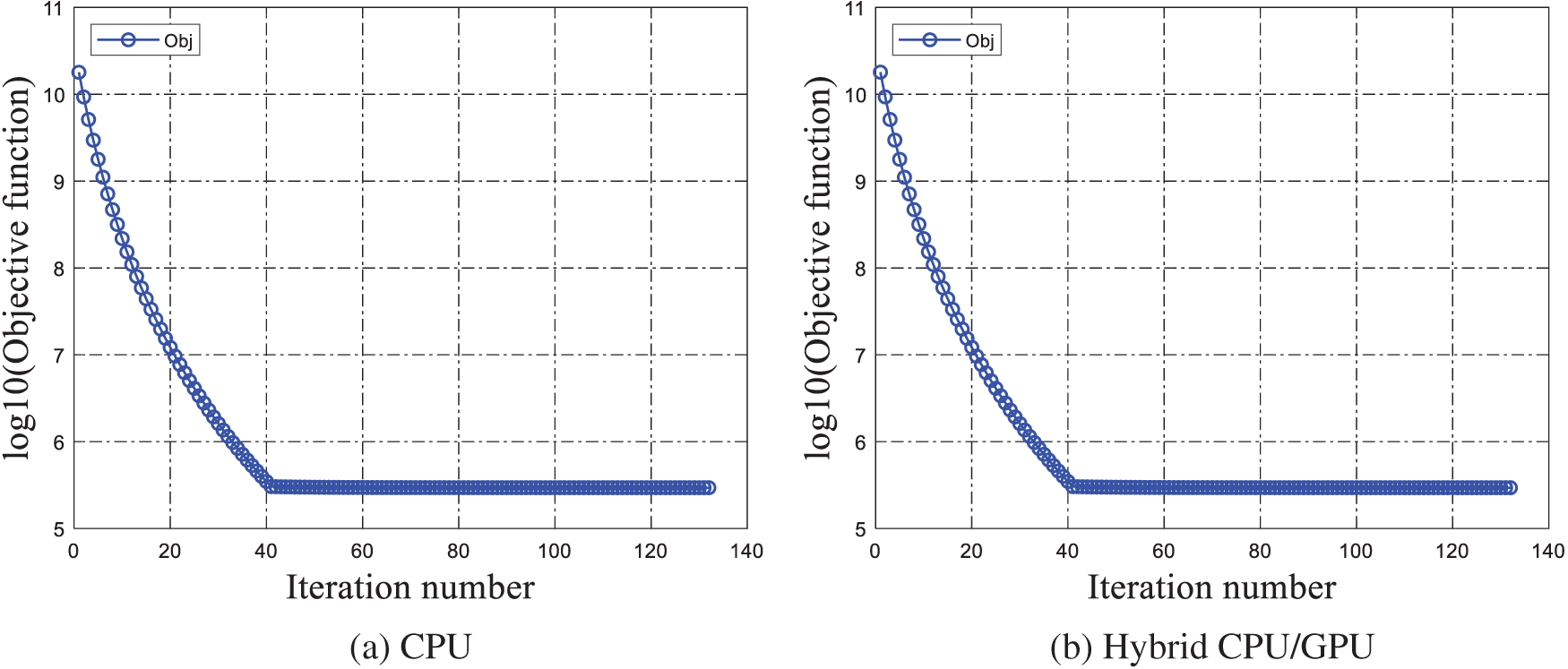
Figure 22: Convergent histories of the wheel beam

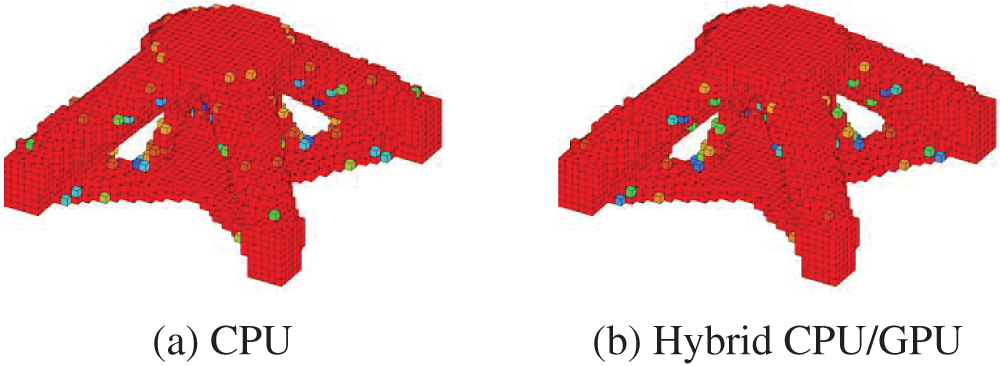
Figure 23: Optimization results of the wheel beam

The relative error of the objective function value between the CPU and the hybrid is calculated for each iteration:

ε=|OCPU−OHy||OCPU|(29)

where ε is the relative error. OCPU and OHy are the objective function values obtained from the CPU and the hybrid computing in an iteration.

Table 13 records the relative errors between CPU and hybrid computing, while the history of relative error is shown in Fig. 24. In the 1–40 iterations, there is a significant fluctuation since double precision is utilized in the CPU method, while both double and single are used in the hybrid strategy to reduce memory consumption. After the 40th iteration, the relative error gradually becomes stable and stays below 0.0002.

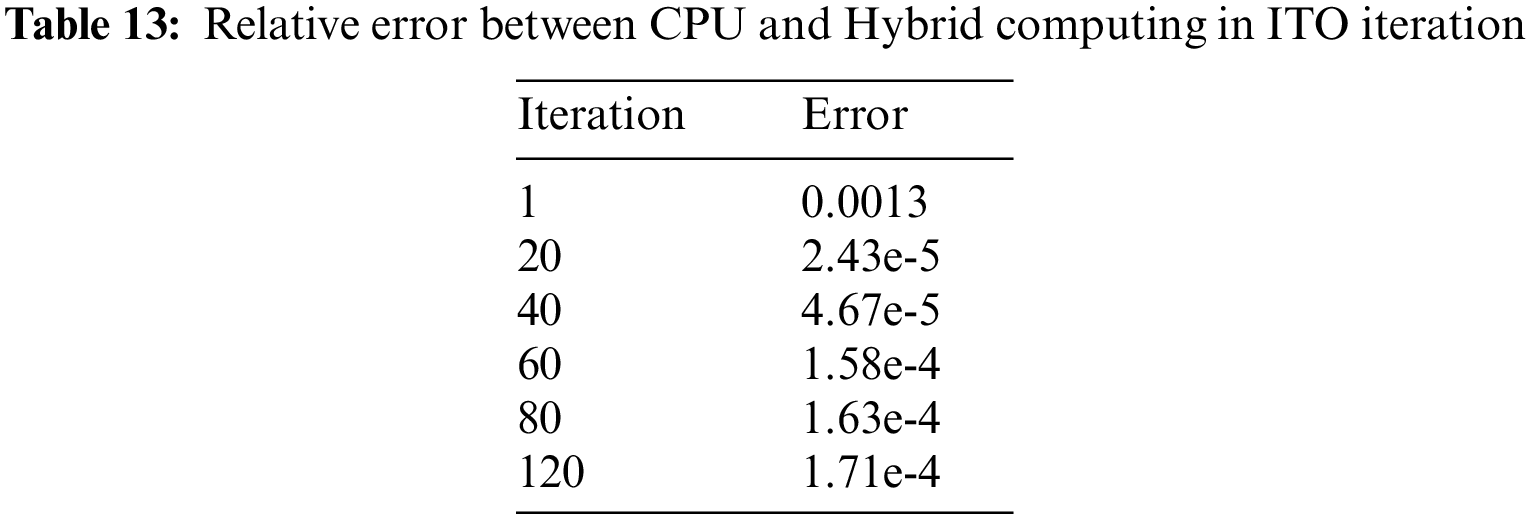
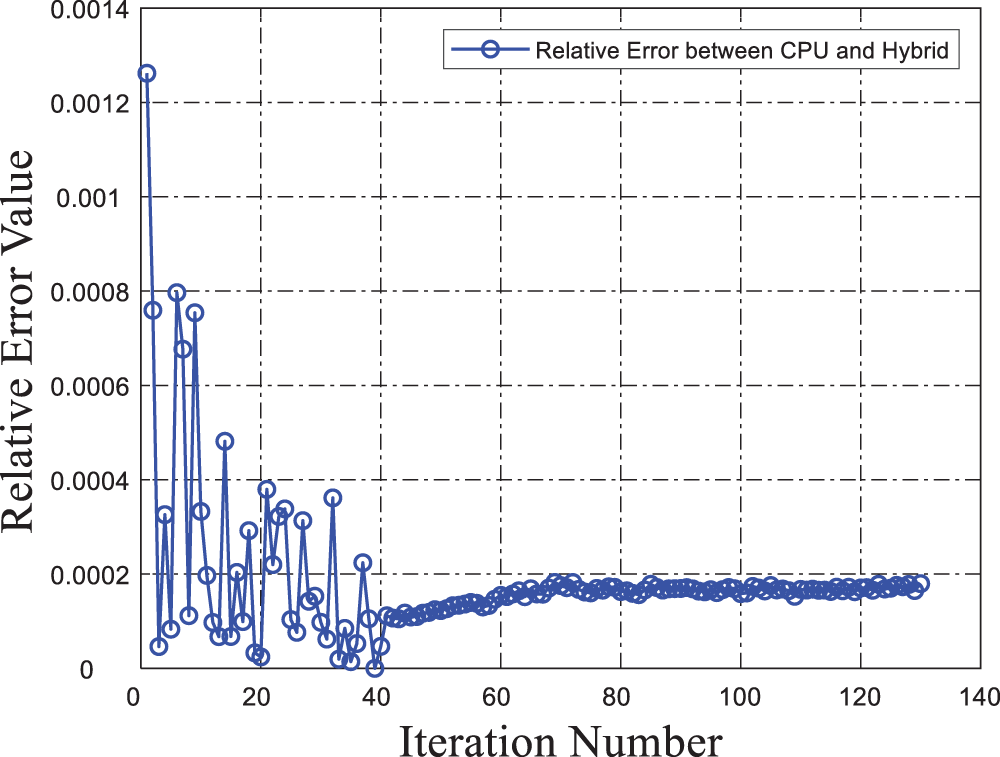
Figure 24: History of relative error between CPU and Hybrid computing

6  Conclusion

A hybrid parallel strategy for isogeometric topology optimization is proposed in this paper. Compared with the general GPU parallel strategy, the proposed method can improve computational efficiency while enhancing the ability for large cases. In the hybrid method, the tasks can be assigned to the GPU via the workload balancing strategy. Therefore, the local hardware resources can be fully utilized to improve the ability to solve large ITO problems. Four parts of ITO: stiffness matrix assembly, equation solving, sensitivity analysis, and update scheme, are accelerated by the hybrid parallel strategy, which shows significant speed-ups.

Three benchmark examples are tested to verify the proposed strategy. The 3D cantilever beam example demonstrates the high computational efficiency via the significant speed-up ratio over the CPU and GPU at different discrete levels. In the 3D MBB beam example, the method while only using the device GPU cannot afford the amount of memory when it ups to a specified mesh scale. It shows the advantages of the hybrid parallel strategy in solving large ITO problems. Furthermore, the 3D wheel beam example demonstrates the accuracy of the hybrid parallel strategy.

Although the SIMP method is utilized in this paper, the proposed hybrid parallel strategy is highly general and equally applicable to other TO methods. In the future, distributed CPU/GPU heterogeneous parallel computing with multiple computing nodes will be researched based on the current work.

Acknowledgement: Thank all the authors for their contributions to the paper.

Funding Statement: This work was supported by the National Key R&D Program of China (2020YFB1708300), the National Natural Science Foundation of China (52005192), and the Project of Ministry of Industry and Information Technology (TC210804R-3).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Zhaohui Xia; data collection: Haotian Han, Haobo Zhang; analysis and interpretation of results: Zhaohui Xia, Baichuan Gao, Shuting Wang; manuscript writing: Zhaohui Xia, Baichuan Gao; manuscript review and editing: Chen Yu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors do not have permission to share data.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Thompson, M. K., Moroni, G., Vaneker, T., Fadel, G., Campbell, R. I. et al. (2016). Design for additive manufacturing: Trends, opportunities, considerations, and constraints. CIRP Annals, 65(2), 737–760. https://doi.org/10.1016/j.cirp.2016.05.004 [Google Scholar] [CrossRef]

2. Wang, Y., Li, X., Long, K., Wei, P. (2023). Open-source codes of topology optimization: A summary for beginners to start their research. Computer Modeling in Engineering & Sciences, 137(1), 1–34. https://doi.org/10.32604/cmes.2023.027603 [Google Scholar] [PubMed] [CrossRef]

3. Sigmund, O., Maute, K. (2013). Topology optimization approaches. Structural and Multidisciplinary Optimization, 48(6), 1031–1055. https://doi.org/10.1007/s00158-013-0978-6 [Google Scholar] [CrossRef]

4. Lundgaard, C., Alexandersen, J., Zhou, M., Andreasen, C. S., Sigmund, O. (2018). Revisiting density-based topology optimization for fluid-structure-interaction problems. Structural and Multidisciplinary Optimization, 58(3), 969–995. https://doi.org/10.1007/s00158-018-1940-4 [Google Scholar] [CrossRef]

5. Meng, Q., Xu, B., Wang, C., Zhao, L. (2021). Thermo-elastic topology optimization with stress and temperature constraints. International Journal for Numerical Methods in Engineering, 122(12), 2919–2944. https://doi.org/10.1002/nme.6646 [Google Scholar] [CrossRef]

6. Bendsøe, M. P., Kikuchi, N. (1988). Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering, 71(2), 197–224. https://doi.org/10.1016/0045-7825(88)90086-2 [Google Scholar] [CrossRef]

7. Wang, M. Y., Wang, X., Guo, D. (2003). A level set method for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 192(1), 227–246. https://doi.org/10.1016/S0045-7825(02)00559-5 [Google Scholar] [CrossRef]

8. Zhang, S., Da, D., Wang, Y. (2022). TPMS-infill MMC-based topology optimization considering overlapped component property. International Journal of Mechanical Sciences, 235, 107713. https://doi.org/10.1016/j.ijmecsci.2022.107713 [Google Scholar] [CrossRef]

9. Xiao, M., Liu, X., Zhang, Y., Gao, L., Gao, J. et al. (2021). Design of graded lattice sandwich structures by multiscale topology optimization. Computer Methods in Applied Mechanics and Engineering, 384, 113949. https://doi.org/10.1016/j.cma.2021.113949 [Google Scholar] [CrossRef]

10. Bendsøe, M. P., Sigmund, O. (1999). Material interpolation schemes in topology optimization. Archive of Applied Mechanics, 69(9), 635–654. https://doi.org/10.1007/s004190050248 [Google Scholar] [CrossRef]

11. Huang, X., Xie, Y. M., Jia, B., Li, Q., Zhou, S. W. (2012). Evolutionary topology optimization of periodic composites for extremal magnetic permeability and electrical permittivity. Structural and Multidisciplinary Optimization, 46(3), 385–398. https://doi.org/10.1007/s00158-012-0766-8 [Google Scholar] [CrossRef]

12. Wang, Q., Han, H., Wang, C., Liu, Z. (2022). Topological control for 2D minimum compliance topology optimization using SIMP method. Structural and Multidisciplinary Optimization, 65(1), 38. https://doi.org/10.1007/s00158-021-03124-6 [Google Scholar] [CrossRef]

13. Doan, Q. H., Lee, D., Lee, J., Kang, J. (2019). Design of buckling constrained multiphase material structures using continuum topology optimization. Meccanica, 54(8), 1179–1201. https://doi.org/10.1007/s11012-019-01009-z [Google Scholar] [CrossRef]

14. Doan, Q. H., Lee, D., Lee, J., Kang, J. (2020). Multi-material structural topology optimization with decision making of stiffness design criteria. Advanced Engineering Informatics, 45, 101098. https://doi.org/10.1016/j.aei.2020.101098 [Google Scholar] [CrossRef]

15. Rodriguez, T., Montemurro, M., Le Texier, P., Pailhès, J. (2020). Structural displacement requirement in a topology optimization algorithm based on isogeometric entities. Journal of Optimization Theory and Applications, 184(1), 250–276. https://doi.org/10.1007/s10957-019-01622-8 [Google Scholar] [CrossRef]

16. Wang, Y., Wang, Z., Xia, Z., Poh, L. H. (2018). Structural design optimization using isogeometric analysis: A comprehensive review. Computer Modeling in Engineering & Sciences, 117(3), 455–507. https://doi.org/10.31614/cmes.2018.04603 [Google Scholar] [CrossRef]

17. Seo, Y. D., Kim, H. J., Youn, S. K. (2010). Isogeometric topology optimization using trimmed spline surfaces. Computer Methods in Applied Mechanics and Engineering, 199(49), 3270–3296. https://doi.org/10.1016/j.cma.2010.06.033 [Google Scholar] [CrossRef]

18. Wang, Y., Benson, D. J. (2016). Isogeometric analysis for parameterized LSM-based structural topology optimization. Computational Mechanics, 57(1), 19–35. https://doi.org/10.1007/s00466-015-1219-1 [Google Scholar] [CrossRef]

19. Qiu, W., Wang, Q., Gao, L., Xia, Z. (2022). Evolutionary topology optimization for continuum structures using isogeometric analysis. Structural and Multidisciplinary Optimization, 65(4), 121. https://doi.org/10.1007/s00158-022-03215-y [Google Scholar] [CrossRef]

20. Lieu, Q. X., Lee, J. (2017). A multi-resolution approach for multi-material topology optimization based on isogeometric analysis. Computer Methods in Applied Mechanics and Engineering, 323, 272–302. https://doi.org/10.1016/j.cma.2017.05.009 [Google Scholar] [CrossRef]

21. Dedè, L., Borden, M. J., Hughes, T. J. R. (2012). Isogeometric analysis for topology optimization with a phase field model. Archives of Computational Methods in Engineering, 19(3), 427–465. https://doi.org/10.1007/s11831-012-9075-z [Google Scholar] [CrossRef]

22. Wang, Y., Xu, H., Pasini, D. (2017). Multiscale isogeometric topology optimization for lattice materials. Computer Methods in Applied Mechanics and Engineering, 316, 568–585. https://doi.org/10.1016/j.cma.2016.08.015 [Google Scholar] [CrossRef]

23. Yu, C., Wang, Q., Mei, C., Xia, Z. (2020). Multiscale isogeometric topology optimization with unified structural skeleton. Computer Modeling in Engineering & Sciences, 122(3), 779–804. https://doi.org/10.32604/cmes.2020.09363 [Google Scholar] [PubMed] [CrossRef]

24. Yang, A., Wang, S., Luo, N., Xie, X., Xiong, T. (2022). Adaptive isogeometric multi-material topology optimization based on suitably graded truncated hierarchical B-spline. Composite Structures, 294, 115773. https://doi.org/10.1016/j.compstruct.2022.115773 [Google Scholar] [CrossRef]

25. Xia, Z., Wang, Y., Wang, Q., Mei, C. (2017). GPU parallel strategy for parameterized LSM-based topology optimization using isogeometric analysis. Structural and Multidisciplinary Optimization, 56(2), 413–434. https://doi.org/10.1007/s00158-017-1672-x [Google Scholar] [CrossRef]

26. Kim, T. S., Kim, J. E., Kim, Y. Y. (2004). Parallelized structural topology optimization for eigenvalue problems. International Journal of Solids and Structures, 41(9), 2623–2641. https://doi.org/10.1016/j.ijsolstr.2003.11.027 [Google Scholar] [CrossRef]

27. Vemaganti, K., Lawrence, W. E. (2005). Parallel methods for optimality criteria-based topology optimization. Computer Methods in Applied Mechanics and Engineering, 194(34), 3637–3667. https://doi.org/10.1016/j.cma.2004.08.008 [Google Scholar] [CrossRef]

28. Aage, N., Andreassen, E., Lazarov, B. S. (2015). Topology optimization using PETSc: An easy-to-use, fully parallel, open source topology optimization framework. Structural and Multidisciplinary Optimization, 51(3), 565–572. https://doi.org/10.1007/s00158-014-1157-0 [Google Scholar] [CrossRef]

29. París, J., Colominas, I., Navarrina, F., Casteleiro, M. (2013). Parallel computing in topology optimization of structures with stress constraints. Computers & Structures, 125, 62–73. https://doi.org/10.1016/j.compstruc.2013.04.016 [Google Scholar] [CrossRef]

30. Baji, T. (2018). Evolution of the GPU device widely used in AI and massive parallel processing. 2018 IEEE 2nd Electron Devices Technology and Manufacturing Conference (EDTM), pp. 7–9.Kobe, Japan. https://doi.org/10.1109/EDTM.2018.8421507 [Google Scholar] [CrossRef]

31. Zhang, W., Zhong, Z., Peng, C., Yuan, W., Wu, W. (2021). GPU-accelerated smoothed particle finite element method for large deformation analysis in geomechanics. Computers and Geotechnics, 129, 103856. https://doi.org/10.1016/j.compgeo.2020.103856 [Google Scholar] [CrossRef]

32. Wadbro, E., Berggren, M. (2009). Megapixel topology optimization on a graphics processing unit. SIAM Review, 51(4), 707–721. https://doi.org/10.1137/070699822 [Google Scholar] [CrossRef]

33. Schmidt, S., Schulz, V. (2011). T31 A 2589 line topology optimization code written for the graphics card. Computing and Visualization in Science, 14(6), 249–256. https://doi.org/10.1007/s00791-012-0180-1 [Google Scholar] [CrossRef]

34. Ratnakar, S. K., Sanfui, S., Sharma, D. (2021). SIMP-based structural topology optimization using unstructured mesh on GPU. In: Kumar, N., Tibor, S., Sindhwani, R., Lee, J., Srivastava, P. (Eds.Advances in interdisciplinary engineering, pp. 1–10. Singapore: Springer. https://doi.org/10.1007/978-981-15-9956-9_1 [Google Scholar] [CrossRef]

35. Karatarakis, A., Karakitsios, P., Papadrakakis, M. (2014). GPU accelerated computation of the isogeometric analysis stiffness matrix. Computer Methods in Applied Mechanics and Engineering, 269, 334–355. https://doi.org/10.1016/j.cma.2013.11.008 [Google Scholar] [CrossRef]

36. Wu, J., Aage, N., Westermann, R., Sigmund, O. (2018). Infill optimization for additive manufacturing—approaching bone-like porous structures. IEEE Transactions on Visualization and Computer Graphics, 24(2), 1127–1140. https://doi.org/10.1109/TVCG.2017.2655523 [Google Scholar] [PubMed] [CrossRef]

37. Ram, L., Sharma, D. (2017). Evolutionary and GPU computing for topology optimization of structures. Swarm and Evolutionary Computation, 35, 1–13. https://doi.org/10.1016/j.swevo.2016.08.004 [Google Scholar] [CrossRef]

38. Lu, F., Song, J., Cao, X., Zhu, X. (2012). CPU/GPU computing for long-wave radiation physics on large GPU clusters. Computers & Geosciences, 41, 47–55. https://doi.org/10.1016/j.cageo.2011.08.007 [Google Scholar] [CrossRef]

39. Cao, W., Xu, C., Wang, Z., Yao, L., Liu, H. (2014). CPU/GPU computing for a multi-block structured grid based high-order flow solver on a large heterogeneous system. Cluster Computing, 17(2), 255–270. https://doi.org/10.1007/s10586-013-0332-1 [Google Scholar] [CrossRef]

40. Sigmund, O. (2001). A 99 line topology optimization code written in Matlab. Structural and Multidisciplinary Optimization, 21(2), 120–127. https://doi.org/10.1007/s001580050176 [Google Scholar] [CrossRef]

41. Song, P., Zhang, Z., Zhang, Q., Liang, L., Zhao, Q. (2020). Implementation of the CPU/GPU hybrid parallel method of characteristics neutron transport calculation using the heterogeneous cluster with dynamic workload assignment. Annals of Nuclear Energy, 135, 106957. https://doi.org/10.1016/j.anucene.2019.106957 [Google Scholar] [CrossRef]

42. Liao, Z., Wang, Y., Gao, L., Wang, Z. P. (2022). Deep-learning-based isogeometric inverse design for tetra-chiral auxetics. Composite Structures, 280, 114808. https://doi.org/10.1016/j.compstruct.2021.114808 [Google Scholar] [CrossRef]

43. Liu, G., Gao, F., Liao, W. H. (2022). Design and optimization of a magnetorheological damper based on B-spline curves. Mechanical Systems and Signal Processing, 178, 109279. https://doi.org/10.1016/j.ymssp.2022.109279 [Google Scholar] [CrossRef]

44. Hughes, T. J. R., Cottrell, J. A., Bazilevs, Y. (2005). Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39), 4135–4195. https://doi.org/10.1016/j.cma.2004.10.008 [Google Scholar] [CrossRef]

45. Gao, J., Gao, L., Luo, Z., Li, P. (2019). Isogeometric topology optimization for continuum structures using density distribution function. International Journal for Numerical Methods in Engineering, 119(10), 991–1017. https://doi.org/10.1002/nme.6081 [Google Scholar] [CrossRef]

46. Wang, Y., Liao, Z., Ye, M., Zhang, Y., Li, W. et al. (2020). An efficient isogeometric topology optimization using multilevel mesh, MGCG and local-update strategy. Advances in Engineering Software, 139, 102733. https://doi.org/10.1016/j.advengsoft.2019.102733 [Google Scholar] [CrossRef]

47. Sigmund, O. (2022). On benchmarking and good scientific practise in topology optimization. Structural and Multidisciplinary Optimization, 65(11), 315. https://doi.org/10.1007/s00158-022-03427-2 [Google Scholar] [CrossRef]

48. Herrero-Pérez, D., Martínez Castejón, P. J. (2021). Multi-GPU acceleration of large-scale density-based topology optimization. Advances in Engineering Software, 157–158, 103006. https://doi.org/10.1016/j.advengsoft.2021.103006 [Google Scholar] [CrossRef]

49. Kiran, U., Sharma, D., Gautam, S. S. (2019). GPU-warp based finite element matrices generation and assembly using coloring method. Journal of Computational Design and Engineering, 6(4), 705–718. https://doi.org/10.1016/j.jcde.2018.11.001 [Google Scholar] [CrossRef]

50. Martínez-Frutos, J., Herrero-Pérez, D. (2017). GPU acceleration for evolutionary topology optimization of continuum structures using isosurfaces. Computers & Structures, 182, 119–136. https://doi.org/10.1016/j.compstruc.2016.10.018 [Google Scholar] [CrossRef]

51. Ahn, J. M., Kim, H., Cho, J. G., Kang, T., Kim, Y. et al. (2021). Parallelization of a 3-Dimensional hydrodynamics model using a hybrid method with MPI and OpenMP. Processes, 9(9), 1548. https://doi.org/10.3390/pr9091548 [Google Scholar] [CrossRef]

52. Poljak, M., Glavan, M., Kuzmić, S. (2019). Accelerating simulation of nanodevices based on 2D materials by hybrid CPU-GPU parallel computing. 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), pp. 47–52. Opatija, Croatia. https://doi.org/10.23919/MIPRO.2019.8756964 [Google Scholar] [CrossRef]

53. Lim, R., Lee, Y., Kim, R., Choi, J. (2018). OpenMP-based parallel implementation of matrix-matrix multiplication on the intel knights landing. Proceedings of Workshops of HPC Asia, 63–66. New York, NY, USA. https://doi.org/10.1145/3176364.3176374 [Google Scholar] [CrossRef]

54. Yang, W., Li, K., Li, K. (2017). A hybrid computing method of SpMV on CPU-GPU heterogeneous computing systems. Journal of Parallel and Distributed Computing, 104, 49–60. https://doi.org/10.1016/j.jpdc.2016.12.023 [Google Scholar] [CrossRef]

55. Karatarakis, A., Metsis, P., Manolis, P. (2013). GPU-acceleration of stiffness matrix calculation and efficient initialization of EFG meshless methods. Computer Methods in Applied Mechanics and Engineering, 258, 63–80. https://doi.org/10.1016/j.cma.2013.02.011 [Google Scholar] [CrossRef]

56. Bartoň, M., Puzyrev, V., Deng, Q., Calo, V. (2020). Efficient mass and stiffness matrix assembly via weighted Gaussian quadrature rules for B-splines. Journal of Computational and Applied Mathematics, 371, 112626. https://doi.org/10.1016/j.cam.2019.112626 [Google Scholar] [CrossRef]

57. Liu, H., Tian, Y., Zong, H., Ma, Q., Wang, M. Y. et al. (2019). Fully parallel level set method for large-scale structural topology optimization. Computers & Structures, 221, 13–27. https://doi.org/10.1016/j.compstruc.2019.05.010 [Google Scholar] [CrossRef]

58. Mukherjee, S., Lu, D., Raghavan, B., Breitkopf, P., Dutta, S. et al. (2021). Accelerating large-scale topology optimization: State-of-the-art and challenges. Archives of Computational Methods in Engineering, 28(7), 4549–4571. https://doi.org/10.1007/s11831-021-09544-3 [Google Scholar] [CrossRef]

59. Liao, Z., Zhang, Y., Wang, Y., Li, W. (2019). A triple acceleration method for topology optimization. Structural and Multidisciplinary Optimization, 60(2), 727–744. https://doi.org/10.1007/s00158-019-02234-6 [Google Scholar] [CrossRef]

60. Amir, O., Aage, N., Lazarov, B. S. (2014). On multigrid-CG for efficient topology optimization. Structural and Multidisciplinary Optimization, 49(5), 815–829. https://doi.org/10.1007/s00158-013-1015-5 [Google Scholar] [CrossRef]

61. Grubov, V. V., Nedaivozov, V. O. (2018). Stream processing of multichannel EEG data using parallel computing technology with NVIDIA CUDA graphics processors. Technical Physics Letters, 44(5), 453–455. https://doi.org/10.1134/S1063785018050188 [Google Scholar] [CrossRef]

62. Wang, R., Gu, T., Li, M. (2017). Performance prediction based on statistics of sparse matrix-vector multiplication on GPUs. Journal of Computer and Communications, 5(6), 65–83. https://doi.org/10.4236/jcc.2017.56005 [Google Scholar] [CrossRef]

63. Weng, L., Huang, L., Taheri, A., Li, X. (2017). Rockburst characteristics and numerical simulation based on a strain energy density index: A case study of a roadway in Linglong gold mine, China. Tunnelling and Underground Space Technology, 69, 223–232. https://doi.org/10.1016/j.tust.2017.05.011 [Google Scholar] [CrossRef]

64. Xie, X., Yang, A., Wang, Y., Jiang, N., Wang, S. (2021). Fully adaptive isogeometric topology optimization using MMC based on truncated hierarchical B-splines. Structural and Multidisciplinary Optimization, 63(6), 2869–2887. https://doi.org/10.1007/s00158-021-02850-1 [Google Scholar] [CrossRef]

65. Knap, M., Czarnul, P. (2019). Performance evaluation of unified memory with prefetching and oversubscription for selected parallel CUDA applications on NVIDIA pascal and volta GPUs. The Journal of Supercomputing, 75(11), 7625–7645. https://doi.org/10.1007/s11227-019-02966-8 [Google Scholar] [CrossRef]

66. Yang, W., Li, K., Li, K. (2018). A parallel computing method using blocked format with optimal partitioning for SpMV on GPU. Journal of Computer and System Sciences, 92, 152–170. https://doi.org/10.1016/j.jcss.2017.09.010 [Google Scholar] [CrossRef]

67. Martínez-Frutos, J., Martínez-Castejón, P. J., Herrero-Pérez, D. (2017). Efficient topology optimization using GPU computing with multilevel granularity. Advances in Engineering Software, 106, 47–62. https://doi.org/10.1016/j.advengsoft.2017.01.009 [Google Scholar] [CrossRef]

68. Xue, W., Roy, C. J. (2020). Heterogeneous computing of CFD applications on CPU-GPU platforms using OpenACC directives. AIAA Scitech 2020 Forum, Orlando, FL, USA, American Institute of Aeronautics and Astronautics. https://doi.org/10.2514/6.2020-1046 [Google Scholar] [CrossRef]

69. Zamani, Y., Huang, T. W. (2021). A High-performance heterogeneous critical path analysis framework. 2021 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA. https://doi.org/10.1109/HPEC49654.2021.9622872 [Google Scholar] [CrossRef]

70. Padhi, A. P., Chakraborty, S., Chakrabarti, A., Chowdhury, R. (2022). Efficient hybrid topology optimization using GPU and homogenization based multigrid approach. arXiv:2201.12931. https://doi.org/10.48550/arXiv.2201.12931 [Google Scholar] [CrossRef]

71. Mittal, S., Vetter, J. S. (2015). A survey of CPU-GPU heterogeneous computing techniques. ACM Computing Surveys, 47(4), 69:1–69:35. https://doi.org/10.1145/2788396 [Google Scholar] [CrossRef]

72. Wang, Y., Xiao, M., Xia, Z., Li, P., Gao, L. (2023). From computer-aided design (CAD) toward human-aided design (HADAn isogeometric topology optimization approach. Engineering, 22, 94–105. [Google Scholar]