 Open Access
Open Access
ARTICLE
Flow Breakdown of Hybrid Nanofluid on a Rigid Surface with Power Law Fluid as Lubricated Layers
1 Instituite of Mathematics, Khwaja Fareed University of Engineering and Information Technology, Rahim yar Khan, 64200, Pakistan
2 Department of Mathematics, Quaid-I-Azam University, Islamabad, 44000, Pakistan
3 Department of Mathematics, Wenzhou University, Wenzhou, 325035, China
4 College of Engineering, Department of Mechanical Engineering, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, 11564, Saudi Arabia
5 Research Laboratory of Ionized Backgrounds and Reagents Studies (EMIR), Preparatory Institute for Engineering Studies of Monastir (IPEIM), University of Monastir, Monastir, 5060, Tunisia
6 Higher School of Sciences and Technology of Hammam Sousse, Department of Physics, Jazan, 82511, Kingdom of Saudia Arabia
7 Department of Mechanical Engineering, Faculty of engineering, Jazan University, P. O. Box 45124, Jazan, Kingdom of Saudia Arabia
8 Center of Research, Faculty of Engineering, Future University in Egypt, New Cairo, 11835, Egypt
9 Department of Mechanical Engineering, College of Engineering, Prince Sattam bin Abdulaziz University, Alkharj, 16436, Saudi Arabia
* Corresponding Author: Sohail Nadeem. Email:
(This article belongs to the Special Issue: Numerical Modeling and Simulations on Non-Newtonian Flow Problems)
Computer Modeling in Engineering & Sciences 2024, 138(2), 1485-1499. https://doi.org/10.32604/cmes.2023.029351
Received 14 February 2023; Accepted 14 June 2023; Issue published 17 November 2023
Abstract
This work investigates an oblique stagnation point flow of hybrid nanofluid over a rigid surface with power law fluid as lubricated layers. Copper (Cu) and Silver (Ag) solid particles are used as hybrid particles acting in water H2O as a base fluid. The mathematical formulation of flow configuration is presented in terms of differential system that is nonlinear in nature. The thermal aspects of the flow field are also investigated by assuming the surface is a heated surface with a constant temperature T. Numerical solutions to the governing mathematical model are calculated by the RK45 algorithm. The results based on the numerical solution against various flow and thermal controlling parameters are presented in terms of line graphs. The specific results depict that the heat flux increases over the lubricated-indexed parameter.Keywords

Nanofluids are believed to be an integral part of nanotechnology. In many industrial sectors and manufacturing procedures, exchangers for heat are used because of the nanofluid’s ability to exceed the same degree of heat transfer and thermal conductivity as typical fluids such as water, kerosene and ethylene glycol. They are utilized as underlying fluids since they have a low viscosity level, density, and thermal conductivity. In many engineering fields and manufacturing processes, efficient heat transfer is required. This includes polymer extraction procedures, paper production, residential cooling, nuclear reactors, the polymer sector, lubricant manufacturing, and food processing. Employing ultrafine nanometer particles in manufacturing (base) solutions may boost thermal properties. The kinds of nanoparticles comprise metals (Cu, Al, Fe, Ag), metal oxides, carbides (Silicon carbide, Titanium carbide), and nonometals (SWCNT and MWCNT). The thermal conductivity of a great deal of industrial fluids (base fluids), such as kerosene oil, grease, motor oil, propylene glycol and ethylene glycol etc., is incredibly low. Masuda et al. supplied the initial proposal for dispersing nanomaterials in the base liquid [1]. Choi et al. [2] later came up with the phrase “nanofluid.” Systems based on nanofluids have applications in a wide range of industries, including heat exchangers, solar collectors, automotive cooling, nuclear reactor cooling, and electronic cooling. Hybrid nanofluid, a mixture of two different types of nanoparticles, has been the focus of several experiments [3,4]. But these types of hybrid nanoparticles are used to increase thermal conductivity as compared to nanofluid. Riaz et al. [5] executed the computational study for hybrid nanofluids with heat exchangers. Khan et al. [6] studied fundamental aspects of hybrid nanomaterial-confined yaw cylinders. For a hybrid nanofluid issue induced by a slanted spinning disc, Acharya [7] used spectral quasi-linearization numerical methods. In contrast with nanoparticles, hybrid nanofluids improved the rate of transmission of heat at the surface, according to Suresh et al.’s [8] research. The contact of fluid with solid objects creates stagnation points. Near the point of stagnation, the flow manifests maximal levels of heat transmission, static push, and mass discharge. Stagnation flows are essential for friction reduction, transpiration cooling (such as cooling a nuclear activator), some hydraulic and industrial operations. Weidman [9] thoroughly explored the hybrid nanofluid non-axisymmetric thermal potential. The flow and heat transfer examinations of nanofluid at the stagnation point on an exponentially surface affected by a magnetic field were covered by Ur Rehman et al. [10]. When a fluid strikes a surface obliquely at any angle of occurrence, oblique stagnation point flow occurs. An aircraft wing or blood flow at the intersection of the anterior cerebral artery (ACA) and the anterior communicating artery are both instances of such flows. Yuan et al. [11] scrutinised the effect of mixed convection on the flow of viscous fluid near an oblique stagnation point. The slip boundary circumstance for rotating fluid stagnation point flow via power law lubricant was identified by Andersson [12]. Recently, scientists conducted research into heat transmission in non-Newtonian stagnation point flow via lubricant sheets. The benefits of lubricated surface over oblique stagnation point flow of second-grade fluid with mass and heat flux have been investigated by Abbasi et al. [13] for hydraulic systems. Nadeem et al. [14] discovered the effects of a lubricated surface on a micropolar fluid’s oblique stagnation point flow. The unique type of flow was initially developed by Wang [15] by extending the sheet. Analysing MHD has fundamental significance for manufacturing, structure, and material investigations. It is greatest significance during the period related to drug discontinuation, asthma cure, cancer treatments, and generator intensity. Some recent research articles that address the topic of MHD flow inside a porous medium with irreversibility analysis and the influence of unsteadiness and Brownian flux on boundary extent are referred to as [16–18]. The above literature exhibits the study of nanofluids and orthogonal stagnation flows under various configurations. There is still no solution for the oblique stagnation flow using Casson fluid with MHD over the lubricant surface. We will find solutions. A hybrid nanofluid studied over a lubricated surface is considered in this evaluation, influenced by the magnetic effect. BVP [mid-rich] on the Maple platform is used to address numerically the simulated flow problem. Graphs and tables are used to demonstrate the results for each of the parameters without dimensions and to provide an appropriate explanation. By comparing our results to previous publications, we were able to figure out that all our findings were in excellent agreement, proving the accuracy of our research.
2 Problem Formulation and Governing Equations
Fig. 1 considers an incompressible, non-Newtonian Casson hybrid nanofluid flowing steadily as it orthogonally impacts an endless number of lubricated surfaces in the xy-plane. The fluid is placed in the upper half of plan y ≥ 0. Casson fluid tensor stress is as follows [19]:
where
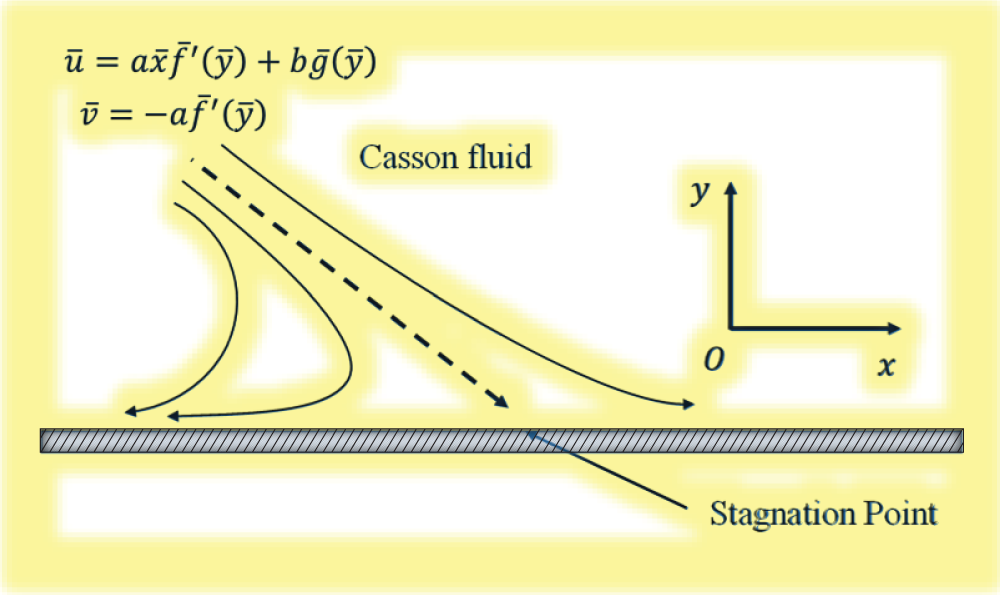
Figure 1: Geometrical description of the issue
A 2-D Oblique stagnation point flow is investigated past a power law fluid lubricated surface with magnetohydrodynamic (MHD) effects. Under this assumption the governing equation are as follows [20]:
The boundary condition are
The impinging velocity will not distribute owing to power law fluid their vertical velocity is always zero.
where
Suppose that
where
Let be velocity components which is given below is used to convert PDEs into ODEs:
Here some constant values are
using above velocity component, we got these results which are below:
After taking integration of Eqs. (11) and (12), we get
Boundary condition of above Eqs. (13) and (14) becomes (15) below here:
With the help of similarty transformation, we changed into a dimensionless equation:
We got these Diemensional ODE’s (17−19) from above using similarty trasnformation:
Boundary conditions are as follows:
The formulas for
where
by using Eq. (8), the dimensionless values of
3 Numerical Method Explanation
Employing the Maple BVP [mid-rich] command with the option numeric, the set of nonlinear ordinary differential Eqs. (17)–(19) combining boundary Eqs. (20)–(23) has been solved numerically. The 4,5 order Rung-Kutta Fehlberg approach for solving issues with boundary values was automatically found by this software.
The RK 45 uses 4th and 5th order Rung-kutta scheme. The used algorithm is as follows:
In this portion, we used excellent Maple packages and BVP [mid-rich] tackles for examining the system of nonlinear differential Eqs. (17) to (19). The BVP [mid-rich] methodology uses mathematics to tackle boundary value constraints. To explain how physical, non-dimensional characteristics like the Casson parameter
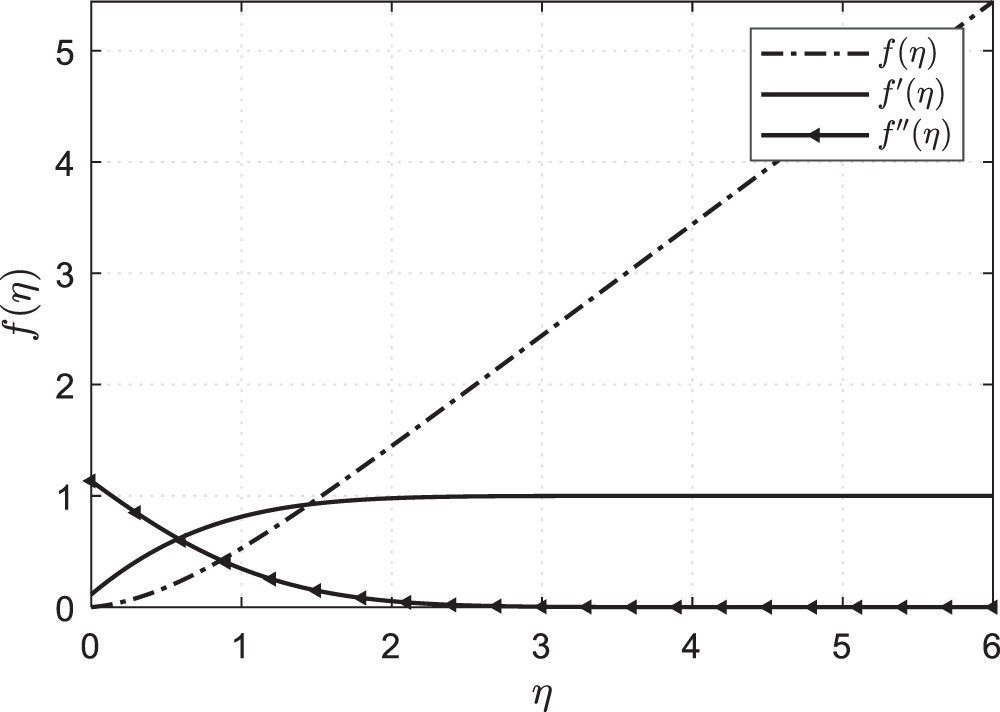
Figure 2:
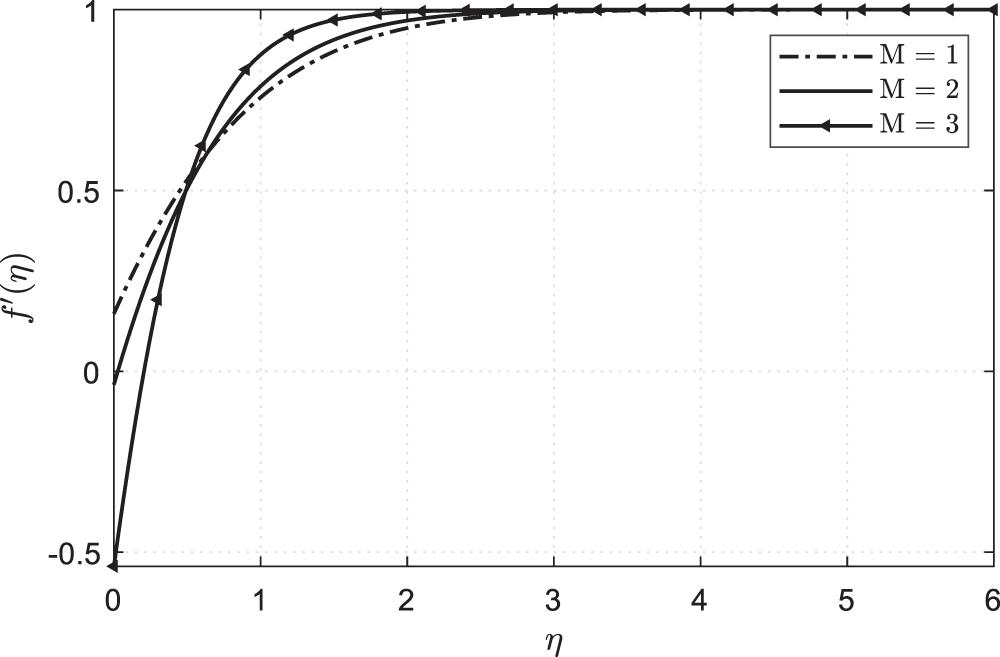
Figure 3:
In Fig. 4, when the value of Hartmann number M increases and

Figure 4: Plots showing

Figure 5: Plots showing
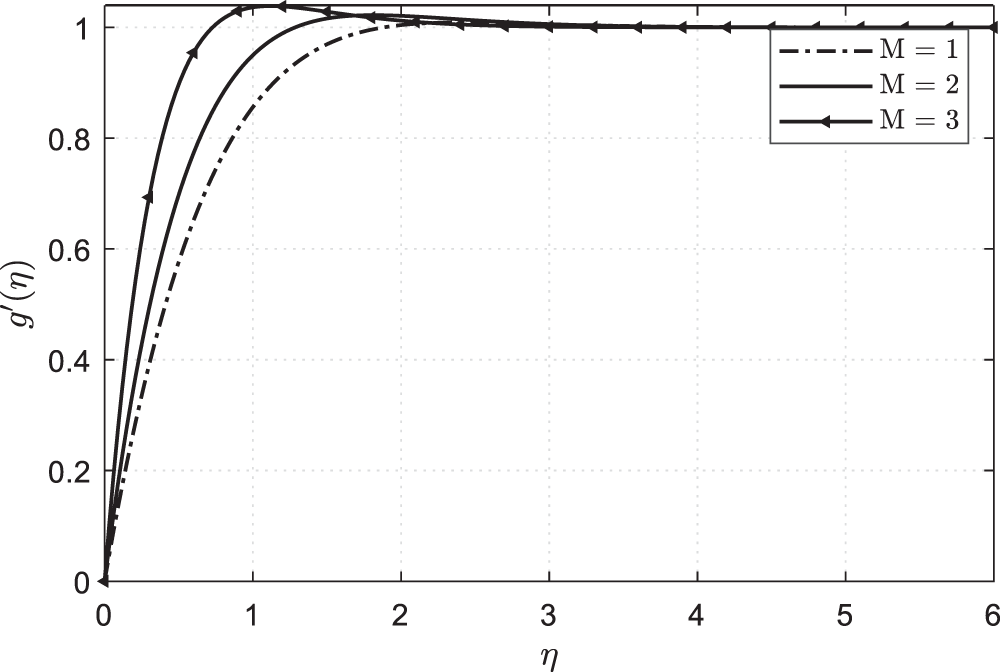
Figure 6: Plots showing

Figure 7: Plots showing
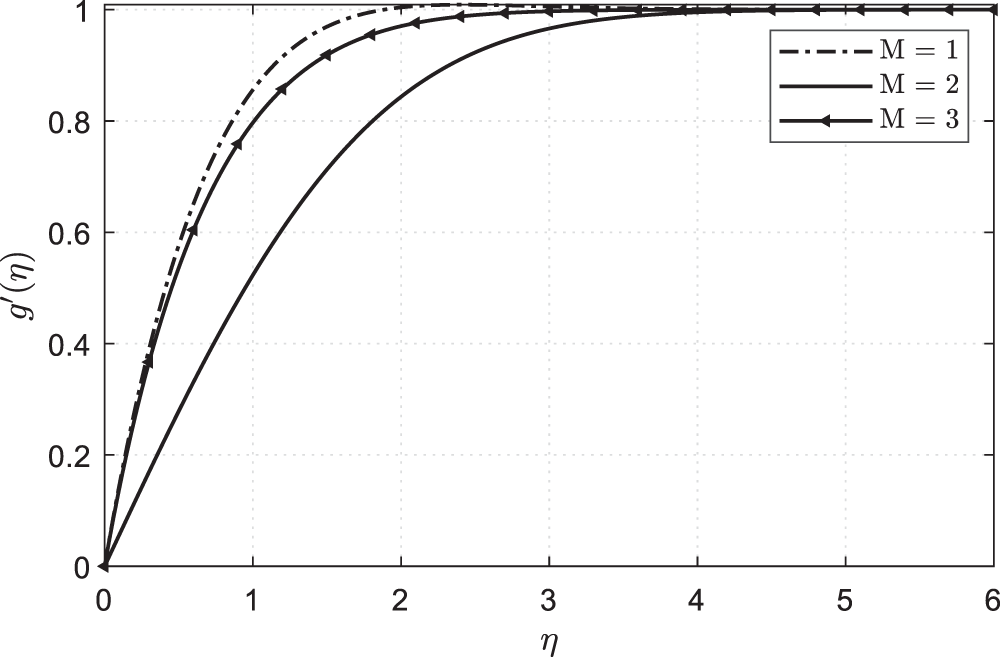
Figure 8: Plots showing
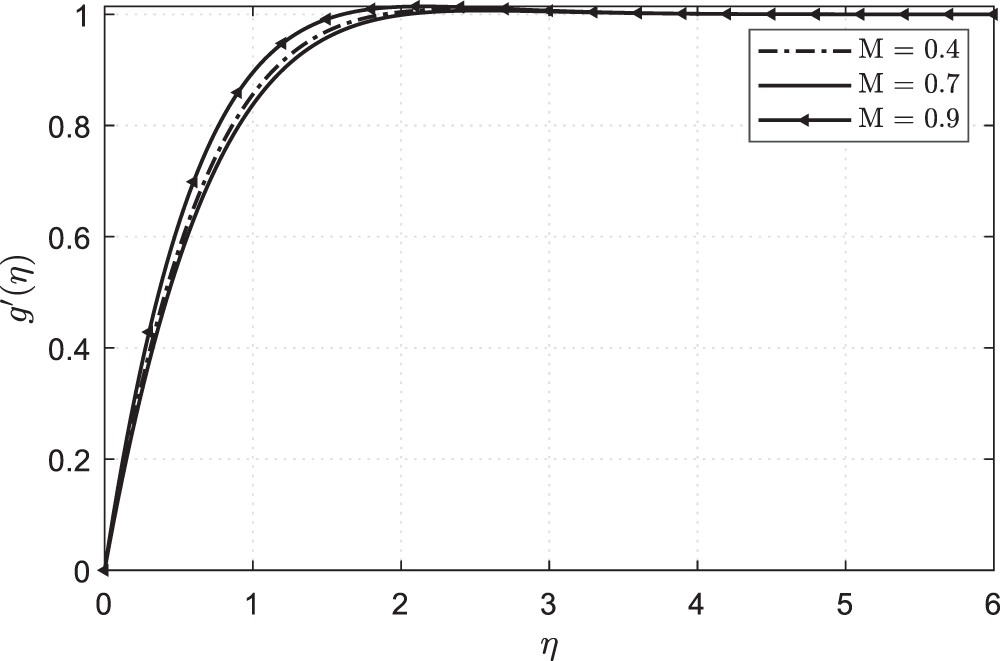
Figure 9: Plots showing

Figure 10: Plots showing

Figure 11: Plots showing

Figure 12: Plots showing
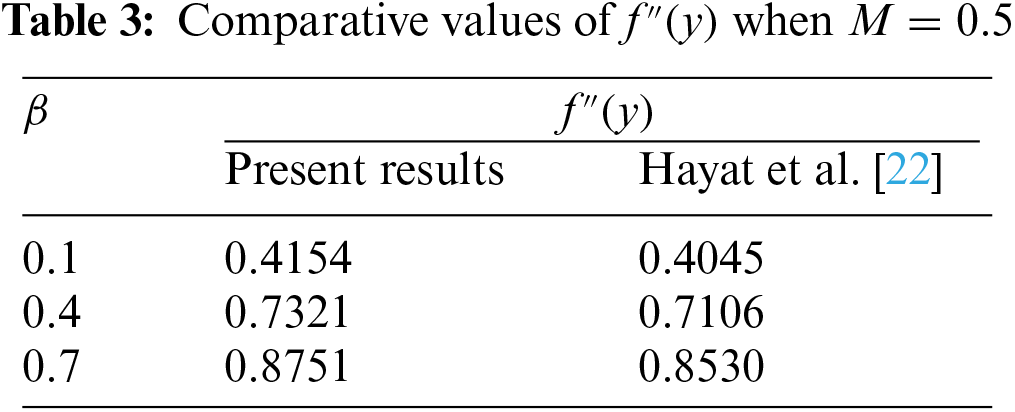
In the present investigation, water served as the acting base fluid, and we explored the MHD oblique-stagnation flow of a hybrid nanofluid into an oscillatory surface containing metal nanoparticles (Cu and Ag). Temperature T and the influence of the velocity distribution are additionally taken into account. Numerical solutions of the governing equations are carried out utilising BVP [mid-rich] in Maple. After recognising the problem category (BVP) by itself. The velocity and temperature distributions of nanofluids are tested against various variables. Table 4 presents numerical data for skin friction and heat transfer efficiency. The significant results from our inquiry have been outlined below:

• Hartman number M is discussed in the graphs.
•
• Skin friction will decrease when it increases M.
The index of the parameter n will increase when we increase it M.
Acknowledgement: Authors Most respected Professor Dr. Sohail Nadeem and Dr. Nadeem Salamat are thankful to endless support.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors claim to have given the article their all throughout research. The PhD scholar Mirza Naveed Jahangeer Baig evaluated the piece of writing; all other authors, working under the direction of Professor Sohail Nadeem, checked and wrote it.
Availability of Data and Materials: No data was used for the research described in this article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Masuda, H., Ebata, A., Teramae, K. (1993). Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Netsu Bussei, 7, 227–233. [Google Scholar]
2. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). Argonne, USA: Argonne National Lab (ANL). [Google Scholar]
3. Turgut, A., Elbasan, E. (2014). Nanofluids for electronics cooling. 2014 IEEE 20th International Symposium for Design and Technology in Electronic Packaging (SIITME), pp. 35–37. Bucharest, Romania. https://doi.org/10.1109/SIITME.2014.6966989 [Google Scholar] [CrossRef]
4. Hsieh, S. S., Leu, H. Y., Liu, H. H. (2015). Spray cooling characteristics of nanofluids for electronic power devices. Nanoscale Research Letters, 10(1), 1–16. [Google Scholar]
5. Riaz, A., Hassan, Q. M. U., Abbas, T., Ghachem, K., Majeed, A. et al. (2022). A study on effectiveness of the variational theory in fluid dynamics applications. Alexandria Engineering Journal, 61(12), 10779–10789. [Google Scholar]
6. Khan, U., Zaib, A., Ishak, A. (2021). Non-similarity solutions of radiative stagnation point flow of a hybrid nanofluid through a yawed cylinder with mixed convection. Alexandria Engineering Journal, 60(6), 5297–5309. [Google Scholar]
7. Acharya, N. (2021). Spectral quasi linearization simulation on the hydrothermal behavior of hybrid nanofluid spraying on an inclined spinning disk. Partial Differential Equations in Applied Mathematics, 4, 100094. [Google Scholar]
8. Suresh, S., Venkitaraj, K. P., Selvakumar, P., Chandrasekar, M. (2012). Effect of Al2O3-Cu/water hybrid nanofluid in heat transfer. Experimental Thermal and Fluid Science, 38, 54–60. [Google Scholar]
9. Weidman, P. D. (2012). Non-axisymmetric Homann stagnation-point flows. Journal of Fluid Mechanics, 702, 460–469. [Google Scholar]
10. Ur Rehman, F., Nadeem, S. (2018). Heat transfer analysis for three-dimensional stagnation-point flow of water-based nanofluid over an exponentially stretching surface. Journal of Heat Transfer, 140(5), 052401. [Google Scholar]
11. Yuan, B., Moghanloo, R. G. (2018). Nanofluid pre-treatment, an effective strategy to improve the performance of low salinity waterflooding. Journal of Petroleum Science and Engineering, 165, 978–991. [Google Scholar]
12. Anderson, J. L. (1989). Colloid transport by interfacial forces. Annual Review of Fluid Mechanics, 21(1), 61–99. [Google Scholar]
13. Abbasi, A., Farooq, W., Khan, S. U., Riaz, I. (2023). Lubricated surface oblique stagnation point flow of second-grade fluid with heat and mass transfer phenomenon: Applications to hydraulic systems. Waves in Random and Complex Media, 1–20. https://doi.org/10.1080/17455030.2022.2157513 [Google Scholar] [CrossRef]
14. Nadeem, S., Mehmood, R., Akbar, N. S. (2013). Non-orthogonal stagnation points flow of a nano non-Newtonian fluid towards a stretching surface with heat transfer. International Journal of Heat and Mass Transfer, 57(2), 679–689. [Google Scholar]
15. Wang, C. Y. (1990). Liquid film on an unsteady stretching surface. Quarterly of Applied Mathematics, 48(4), 601–610. [Google Scholar]
16. Zahor, F. A., Jain, R., Ali, A. O., Masanja, V. G. (2023). Modeling entropy generation of magnetohydrodynamics flow of nanofluid in a porous medium: A review. International Journal of Numerical Methods for Heat & Fluid Flow, 33(2), 751–771. [Google Scholar]
17. Kalpana, G., Madhura, K. R., Kudenatti, R. B. (2022). Numerical study on the combined effects of Brownian motion and thermophoresis on an unsteady magnetohydrodynamics nanofluid boundary layer flow. Mathematics and Computers in Simulation, 200, 78–96. [Google Scholar]
18. Sepehrnia, M., Khorasanizadeh, H., Shafii, M. B. (2021). Effect of transverse and parallel magnetic fields on thermal and thermo-hydraulic performances of ferro-nanofluid flow in trapezoidal microchannel heat sink. International Journal of Numerical Methods for Heat & Fluid Flow, 31(7), 2089–2111. [Google Scholar]
19. Khan, H., Ali, F., Khan, N., Khan, I., Mohamed, A. (2022). Electromagnetic flow of Casson nanofluid over a vertical riga plate with ramped wall conditions. Frontiers in Physics, 10, 1005447. https://doi.org/10.3389/fphy.2022.1005447 [Google Scholar] [CrossRef]
20. Rana, S., Mehmood, R., Akbar, N. S. (2016). Mixed convective oblique flow of a Casson fluid with partial slip, internal heating and homogeneous-heterogeneous reactions. Journal of Molecular Liquids, 222, 1010–1019. [Google Scholar]
21. Hayat, T., Nadeem, S., Khan, A. U. (2018). Rotating flow of Ag-CuO/H2O hybrid nanofluid with radiation and partial slip boundary effects. The European Physical Journal E, 41, 1–9. [Google Scholar]
22. Hayat, T., Nadeem, S. (2017). Heat transfer enhancement with Ag-CuO/water hybrid nanofluid. Results in Physics, 7, 2317–2324. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF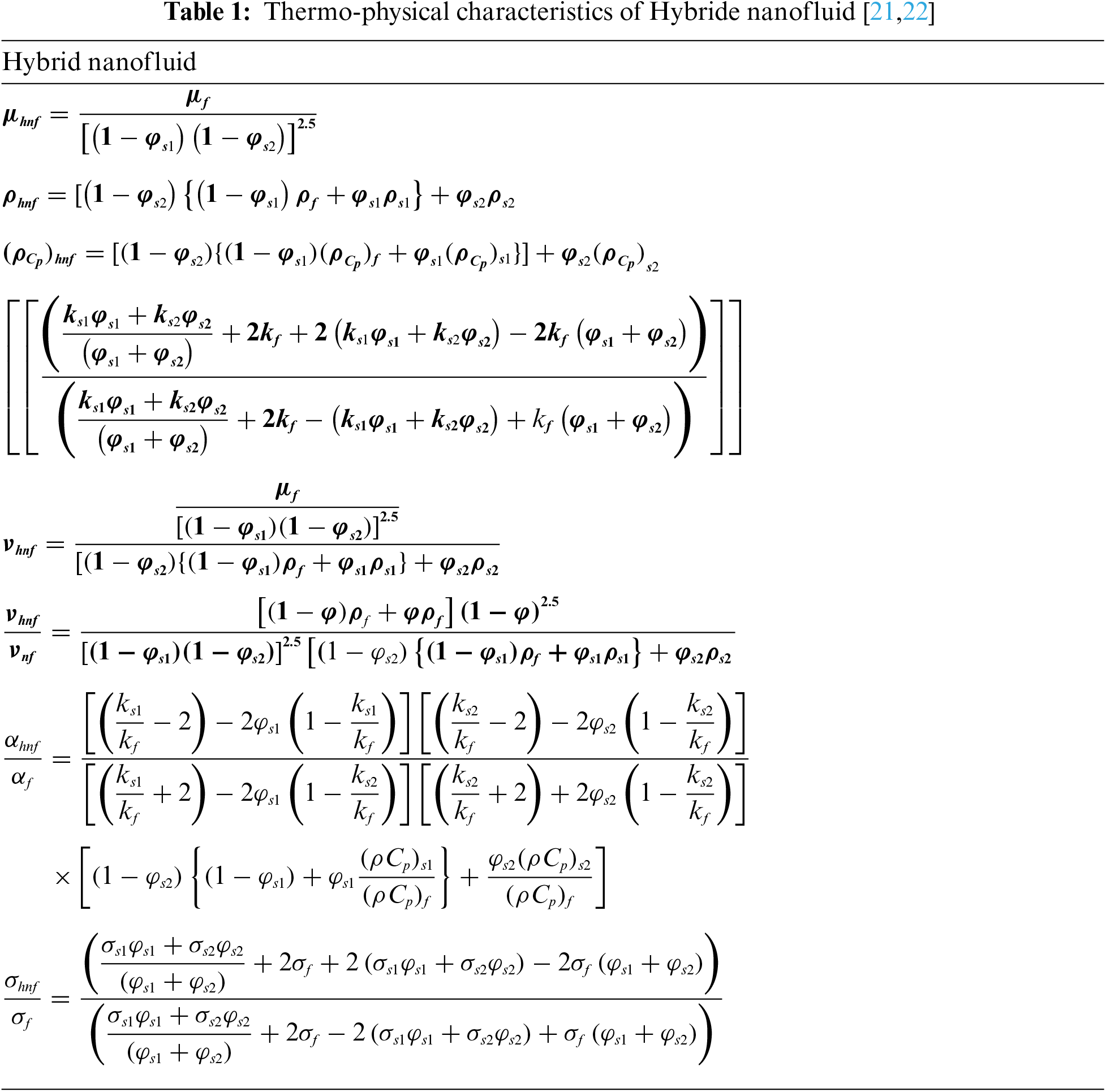
 Downloads
Downloads
 Citation Tools
Citation Tools