Open Access

ARTICLE

Euler’s First-Order Explicit Method–Peridynamic Differential Operator for Solving Population Balance Equations of the Crystallization Process

Chunlei Ruan^1,2,*, Cengceng Dong¹, Kunfeng Liang³, Zhijun Liu¹, Xinru Bao¹

1 Mathematics & Statistics School, Henan University of Science & Technology, Luoyang, 471023, China
2 Longmen Laboratory, Luoyang, 471023, China
3 College of Vehicle and Traffic Engineering, Henan University of Science & Technology, Luoyang, 471023, China

* Corresponding Author: Chunlei Ruan. Email:

(This article belongs to the Special Issue: Peridynamics and its Current Progress)

Computer Modeling in Engineering & Sciences 2024, 138(3), 3033-3049. https://doi.org/10.32604/cmes.2023.030607

Received 14 April 2023; Accepted 18 August 2023; Issue published 15 December 2023

Abstract

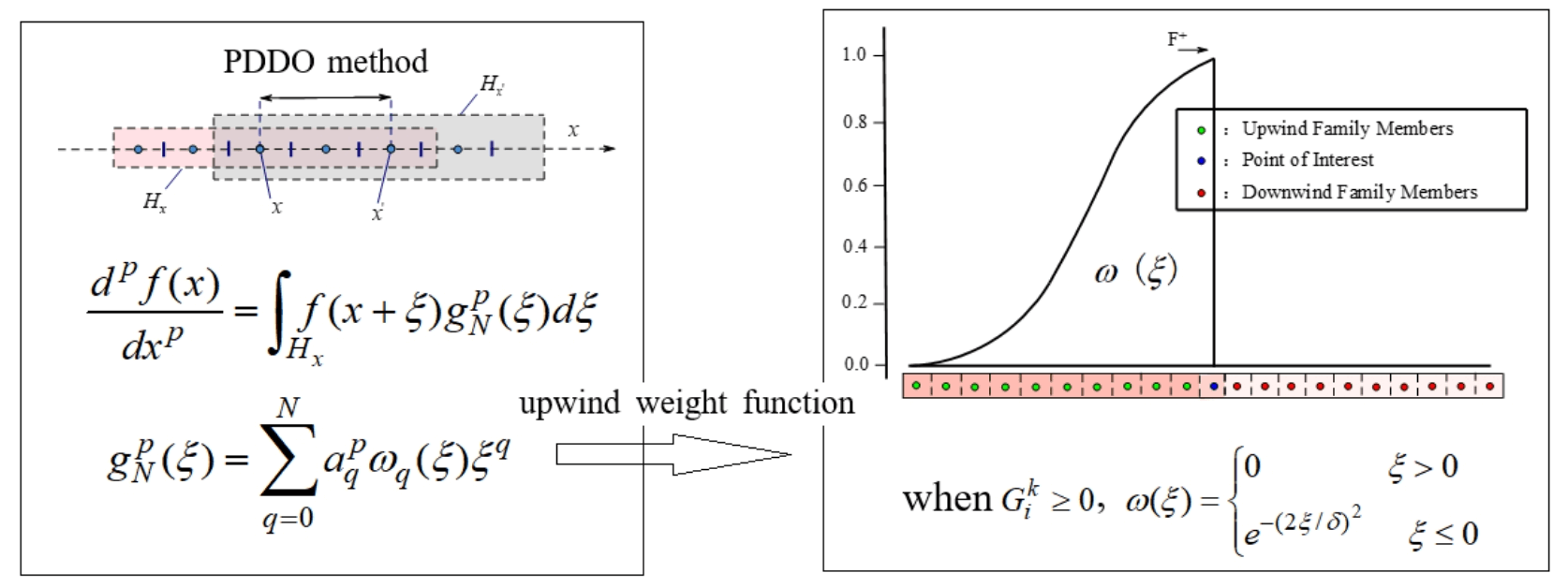
Using Euler’s first-order explicit (EE) method and the peridynamic differential operator (PDDO) to discretize the time and internal crystal-size derivatives, respectively, the Euler’s first-order explicit method–peridynamic differential operator (EE–PDDO) was obtained for solving the one-dimensional population balance equation in crystallization. Four different conditions during crystallization were studied: size-independent growth, size-dependent growth in a batch process, nucleation and size-independent growth, and nucleation and size-dependent growth in a continuous process. The high accuracy of the EE–PDDO method was confirmed by comparing it with the numerical results obtained using the second-order upwind and HR-van methods. The method is characterized by non-oscillation and high accuracy, especially in the discontinuous and sharp crystal size distribution. The stability of the EE–PDDO method, choice of weight function in the PDDO method, and optimal time step are also discussed.

---

Graphic Abstract

---

Keywords

---