A Comparative Study of Metaheuristic Optimization Algorithms for Solving Real-World Engineering Design Problems

1  Introduction

Experts involved in the design, manufacturing, and repair processes of an engineering system must make managerial and technological decisions about the system under certain constraints. Optimization is an attempt to achieve the best result under existing constraints. The most important aim of the optimization process is to minimize the effort and time spent on a system or to obtain maximum efficiency. So, if the design cost of the system is expressed as a function, optimization can be defined as the attempts to reach the minimum or maximum value of this function under certain conditions [1].

Constraint optimization is a critical component of any engineering or industrial problem. Most real-world optimization problems include a variety of constraints that affect the overall search space. Over the last few decades, a diverse spectrum of metaheuristic approaches for solving constrained optimization problems have been developed and applied. Constrained optimization problems provide more challenges in comparison to unconstrained optimization problems, primarily because they include the association of many constraints from different types (such as equalities or inequalities) and the interdependence between the objective functions. Nonlinear objective functions and nonlinear constraints in such problem instances may exhibit characteristics of being continuous, mixed, or discrete. There are two general categories of optimization techniques for such problems or functions: mathematical programming and metaheuristic methods. To solve such problems, various mathematical programming methods have been used, such as linear programming, homogeneous linear programming, dynamic, integer, and nonlinear programming. These algorithms use gradient information to explore the solution space in the vicinity of an initial beginning point. Gradient-based algorithms converge more quickly and generate more accurate results than stochastic approaches while performing local searches. However, for these methods to be effective, the generators’ variables and cost functions must be continuous. Furthermore, for these methods to be successful, a good starting point is required. Many optimization problems require the consideration of prohibited zones, non-smooth, and side limits or non-convex cost functions. As a result, traditional mathematical programming methods are unable to solve these non-convex optimization problems. Although mixed-integer nonlinear programming or dynamic programming as well as its variants provide a limited number of possibilities for solving non-convex problems, they are computationally expensive [2].

Metaheuristic optimization approaches have been used as a viable alternative to conventional mathematical procedures in order to achieve global or near-global optimal solutions [3]. The aforementioned approaches are very suitable for conducting global searches, as they possess the capability to effectively explore and identify potential places within the search space with a high accuracy degree and efficiency value. Additionally, these techniques eliminate the necessity for continuous cost functions and variables, which are frequently utilized in mathematical optimization. Although these are approximation approaches, their solutions are acceptable but not necessarily be optimal. They do not necessitate the objective function’s derivatives or constraints, and they employ probabilistic rather than deterministic transition rules. As a result, the searchers concentrate on metaheuristic strategies that seek a good constructive answer in a reasonable amount of time [4]. Classic algorithms, on the other hand, desire derivatives for all nonlinear constraint functions to evaluate system performance. However, due to the system’s high computational complexity, it is difficult to derive a real-world problem. These disadvantages of classical methods have prompted researchers to employ nature-inspired metaheuristic methods according to simulations to clarify engineering design problems. Metaheuristic optimization algorithms are well recognized as a prominent global optimization approach used to address complex search and optimization problems of significant size. They are frequently utilized to solve optimization problems of a broad variety [5]. Metaheuristic methods often work by combining rules and randomness to mimic events in nature and the behavior of animals. Due to their inherent inflexibility, these algorithms provide superior performance in optimization problems and several other problem domains compared to conventional approaches. Numerous studies have provided evidence to support the notion that nature-inspired algorithms, consisting of genetic algorithms (GA), particle swarm optimization (PSO), differential evaluation (DE), and evolution strategies (ES), possess inherent advantages due to their lack of reliance on mathematical assumptions in addressing optimization problems. Moreover, these algorithms exhibit superior global search capabilities compared to conventional optimization algorithms. These metaheuristic techniques have been widely used to accomplish constrained optimization problems in different fields, including structural design problems, engineering problems, decision-making, reliability optimization, and so on.

Even though there are several optimization techniques in the academic literature, no one method has been shown to universally provide the optimal answer for all optimization issues. The assertion is rationally substantiated by the “no free lunch theorem”. The aforementioned theorem has inspired by several scholars by prompting them to develop novel algorithms. Therefore, several methodologies have been lately suggested. However, there are not many studies on which of these suggested methods perform well in which areas. In this study, seventeen recently proposed and popular methods are employed to twelve constrained design problems in engineering with different constraints, objective functions, and decision variables, and performance analysis has been performed. For the problems; speed reducer, tension-compression spring, pressure vessel design, welded beam design, three-bar truss design, multiple disc clutch brake design, himmelblau’s function, cantilever beam, tubular column design, piston lever, robot gripper, and corrugated bulkhead design are investigated. The types of the problems differ considering the problem domains. The reason for this is to obtain better comparison results by comparing the optimization algorithms with each other according to their distinct capabilities in several types of problems. The algorithms used to solve these problems can be stated as; transient search optimization (TSO), equilibrium optimizer (EO), grey wolf optimizer (GWO), moth-flame optimization (MFO), whale optimization algorithm (WOA), slime mold algorithm (SMA), harris hawks optimization (HHO), chimp optimization algorithm (COA), coot optimization algorithm (COOT), multi verse optimization (MVO), arithmetic optimization algorithm (AOA), aquila optimizer (AO), sine cosine algorithm (SCA), smell agent optimization (SAO), and seagull optimization algorithm (SOA), pelican optimization algorithm (POA), and coati optimization algorithm (CA). Each algorithm’s performance is evaluated in terms of solution quality, robustness, and convergence speed.

The subsequent sections in the paper are structured in the following manner. Section 2 introduces a comprehensive review of the optimization approaches used in the study to address the complex challenges faced. Section 3 of this paper describes and examines the practical engineering design challenges and experimental findings that were encountered. In conclusion, Section 4 provides a comprehensive overview of the obtained results and offers suggestions for further investigations.

2  Literature Review

Metaheuristic optimization methods can be examined in five general groups: physics-based, swarm-based, game-based, evolutionary-based, and human-based. Optimization algorithms based on swarm intelligence are the methods that emerged from examining the movements of animals living in swarms. Numerous methodologies grounded in swarm intelligence have been put forward. Some of these are Red fox optimization algorithm [6], Cat and mouse based optimizer [7], Siberian tiger optimization [8], Dwarf mongoose optimization algorithm [9], Chimp optimization algorithm [10], Dingo optimizer [11], Flamingo search algorithm [12], and Orca predation algorithm [13].

Evolutionary-based metaheuristic optimization approaches have been generated by using modeling ideas in genetics, the law of natural selection, biological concepts, and random operators. GA and DE are widely utilized evolutionary algorithms that simulate the reproductive process, natural selection, and Darwin’s theory of evolution. These algorithms employ randomly selection, crossover, and mutation operators to optimize solutions. Physics-based metaheuristic optimization approaches draw inspiration from the fundamental principles of physics. Some of these are Henry gas solubility optimization [14], Archimedes optimization method [15], Multi verse optimization [16], Equilibrium optimizer [17], Transient search algorithm [18].

Game-based metaheuristic optimization methods have been created by mimicking the rules and circumstances that govern different games, as well as the behavior of the participants. Some of these are World cup optimization [19], League championship algorithm [20], Ring toss game based optimization algorithm [21], Darts game optimizer [22]. Human-based metaheuristic optimization methods have been created using mathematical models of human activities, behaviors, and interactions in both individual and societal settings. Some of these are Forensic-based investigation optimization [23], Political optimizer [24], Human urbanization algorithm [25], Teamwork optimization algorithm [26].

There are many algorithms that solve engineering problems with metaheuristic optimization algorithms. Table 1 presents a comprehensive overview of the methods used throughout the last decade. As seen in the literature, different optimization techniques have been effectively used in a variety of constrained optimization situations. When obtaining an ideal or near-optimal solution, the performance obtained, on the other hand, reveals a statistically significant difference. Due to this rationale, despite the existence of several optimization algorithms documented in scholarly literature, a single algorithm capable of finding the best solution to every optimization problem has yet to be discovered.

3  Metaheuristic Optimization Algorithms

This section provides a brief description of each algorithm that is employed in this study. Only the most significant parts are described; accordingly, interested readers can get all of the information they need in the cited papers.

3.1 Transient Search Algorithm

As a physics-based metaheuristic approach, Qais et al. introduced the transient search algorithm (TSO) in 2020. The source of motivation for this study is derived from the transient dynamics seen in switched electrical circuits having storage components, i.e., capacitance and inductance [18].

Electrical circuits consist of many components capable of storing energy. The components in question may be classified as inductors (L), capacitors (C), or a hybrid configuration consisting of both (LC). Typically, an electrical circuit that incorporates a resistor (R), capacitor (C), or inductor (L) exhibits a transient response as well as a steady-state response. Circuits that include both an energy storage device and a resistor are categorized as first-order circuits. When two energy storage devices are positioned next to a resistor inside a circuit, the resulting configuration is referred to as a second-order circuit. The TSO method is introduced, drawing inspiration from the transient response shown by these circuits in the vicinity of 0.

3.2 Equilibrium Optimizer (EO)

In the year 2020, Faramarzi et al. developed an equilibrium optimizer (EO), a metaheuristic algorithm that simulates the fundamental well-mixed dynamic mass balance in a control volume [17]. It is used in this method to describe the concentration of the non-reactive component in a control volume as a result of different source and sink components, based on the mass balance equation. When the dynamic mass balance against the control volume is compared, this comparison serves as the motivation for the balance optimization process. The equation of mass balance is utilized for characterizing the concentration of a non-reactive component inside the control volume, taking into account the numerous sources and leakage mechanisms that exist within the control volume. The conservation of mass principle is satisfied in a control volume due to the positive nature of the mass balance equation.

3.3 Grey Wolf Optimizer (GWO)

Mirjalili et al. introduced the grey wolf algorithm (GWO) in 2014, which is an optimization algorithm influenced by the population of grey wolves, their natural leading capabilities, and hunting habits [29]. Grey wolves are classified into four major classes based on their social hierarchy as well as the abilities of each wolf in the group: Alpha, Beta, Delta, and Omega. The leader of the group is called as the alpha wolf and is in charge of making critical decisions such as sleeping location, hunting, waking time, and so on. The tracking, the encircling, and the attacking are the three steps in the grey wolf hunting technique.

3.4 Moth-Flame Optimization (MFO)

The moth-flame optimization (MFO) is a metaheuristic method affected by the population of moths and offered by Mirjalili in 2015. The MFO is based upon a simulation of a distinctive nocturnal navigation system used by moths. It begins the optimization procedure, like other meta-heuristics. In other words, it randomly generates a set of candidate solutions. When traveling at night, the moth uses a mechanism known as transverse orientation to navigate. In the MFO method, candidate solutions are postulated as moths, while the variables of a given issue are postulated as the locations of these moths inside the search space [48].

3.5 Whale Optimization Algorithm (WOA)

Mirjalili et al. [30] developed the whale optimization algorithm (WOA), another nature-inspired metaheuristic optimization algorithm that replicates the social behavior of humpback whales to tackle complicated optimization problems. Predators are able to recognize the location of humpback whales and cover them fully when they approach. During iterations of WOA, target prey is presumed to be the greatest available search tool, and humpback whales update their position by considering the best search tool as they progress through the game. However, despite their enormous size, these creatures are distinguished by their intellect and sophisticated methods of collaborative work throughout the hunting process. In addition to the initiation stage, the WOA consists of the surrounding hunt, the bubble-net hunting method, and the hunt for prey, among other activities.

3.6 Slime Mould Algorithm (SMA)

Li et al. proposed a new optimization algorithm inspired by the behavior of slime mould in obtaining the optimal way to bind foods [40]. Slime mould is a type of eukaryote that thrives in cold, moist environments. Plasmodium, in its active and dynamic phase, is the primary source of sustenance for the parasite. Additionally, this stage serves as the foundation for the SMA. Slime mould is on the lookout for food that contains an organic substance in this phase. After the slime mould has finished its hunt, it wraps itself around the meal and secretes enzymes to break it down. The front end enhances into a fan-shaped mesh during the migration phase. It then spreads into a network of interconnecting veins, allowing blood to flow in. Due to its distinctive patterns and structure, it is capable of forming a venous network for multiple foods at the same time. By grouping these negative vs. positive responses, the slime mould can construct the optimal food route to add food in a more meaningful way. Thus, SMA was modeled mathematically and applied to solve engineering problems [49].

3.7 Harris Hawks Optimization (HHO)

Heidari et al. [36] proposed a population-based metaheuristic optimization algorithm inspired by the behavior and hunting model of Harris hawks. Harris hawks optimization (HHO) is a stochastic algorithm that can be used to search for optimal solutions in large search spaces. The fundamental steps of HHO can be achieved at a variety of energy levels. The exploration phase replicates the technique by which the Harris hawk loses track of prey. Hawks take a break in this situation to trace and locate new prey. At each step of the HHO process, possible solutions are referred to as hawks, and the optimal solution is determined by hunting. Hawks randomly settle into different sites and wait for prey using two probability-based operators [36].

3.8 Chimp Optimization Algorithm (COA)

The chimp optimization algorithm (COA) was designed by Khishe et al. as a biology-based optimization algorithm originated by the individual intellect and sexual motives of chimps during group hunts [10]. There are some differences between it and other social carnivores. Four different stages are employed to model various intelligence in this methodology. The chaser, the driver, the attacker, and the barrier are all believed to be more familiar with the first option in this case. The four optimal solutions produced in the previous step are kept, and the other chimps are urged to change placements to the chimp’s optimal locations.

3.9 Coot Optimization Algorithm (COOT)

The metaheuristic technique presented by Naruei et al. (2021) draws inspiration from the behavioral patterns shown by birds navigating on the surface of water. The behavior of the coot swarm on water includes three major movements [50]. These are irregular activity movement, synchronized movement, and chain movements on the water surface. Coots have different collective behaviors. There are four different water paddle movements on the water surface. These include acting randomly, chain movement, adjusting the position relative to the group leaders, and directing the group to the optimal area by the leaders. As in all optimization algorithms, the initial population is created first. After the initial population is created, the fitness value of the solution is calculated using the objective function.

3.10 Multi-Verse Optimization (MVO)

The notion of multi-verse optimization (MVO) was presented as a metaheuristic approach by Mirjalili et al. (2016), drawing inspiration from the field of cosmology. MVO explores search spaces with the concepts of black and white holes while exploiting search spaces with wormholes. Similar to other evolutionary algorithms, this method commences the optimization procedure by generating an initial population and endeavors to enhance these solutions via a predetermined number of iterations. Enhancement of individual performance inside each population may be attained via the utilization of this algorithm, which is grounded in one of the postulations about the presence of many universes. In the context of these theories, it is conceptualized that every solution to an optimization issue represents a distinct universe, whereby each constituent item is considered a variable within the specific problem at hand. In addition, they assign to each solution an inflation rate proportional to the value of the fitness function to which the solution corresponds [16].

3.11 Arithmetic Optimization Algorithm (AOA)

The arithmetic optimization algorithm (AOA), as presented by Abualigah et al. [42], is a metaheuristic approach that leverages the distribution characteristics of fundamental arithmetic operators in mathematics, such as division, multiplication, addition, and subtraction. Four traditional arithmetic operators are modeled into the position update equations to search for the global optimization solution, as the name implies. Division and multiplication are employed for the exploration search, producing enormous steps in the search space due to the varied impacts of these four arithmetic operators. It is applied to execute exploitation searches, which can create small step sizes in the addition and subtraction search space [42].

3.12 Aquila Optimizer (AO)

The aquila optimizer (AO) is a population-based metaheuristic approach developed by Abualigah et al. [43]. It draws inspiration from the natural behavior of the Aquila bird while hunting its prey. The Aquila employs four distinct hunting techniques. The first technique used by the Aquila is vertically inclined high-flying, which enables the bird to capture avian prey while soaring at significant altitudes above the Earth’s surface. The second method, known as contour flying with a brief glide attack, involves the Aquila ascending at a relatively low level from the surface. The third method involves using flying movement characterized by a gradual fall in order to execute an assault. This approach involves the Aquila descending to the ground and engaging in a slow pursuit of its prey. Additionally, the fourth way has the Aquila strolling on land and using tactics to capture its victim [43].

3.13 Sine Cosine Algorithm (SCA)

The sine cosine algorithm (SCA) is a recently developed meta-heuristic algorithm that is based on the properties of trigonometric sine and cosine functions [51]. SCA has gained a lot of attention from researchers since its debut by Mirjalili in 2016, and it is been extensively employed to achieve various optimization solutions of various fields. SCA employs a mathematical model depending on sine and cosine functions to create several beginning populations and afterwards select the optimal answer. A large number of random and adaptive variables are incorporated into the algorithm to ensure exploration and exploitation of the search space at various phases of the optimization process. The SCA optimization method begins with a random solution set, which is then refined. According to the method, the best solution produced is saved and assigned to a specific target point, after which all other solutions are updated in accordance with this solution. Meanwhile, as the number of iterations increases, the range of sine and cosine functions is updated to guarantee that they are exploitation. As a default, when the number of optimization iterations exceeds the maximum number of iterations, the optimization process is terminated by the algorithm [52].

3.14 Smell Agent Optimization (SAO)

The smell agent optimization (SAO) is a metaheuristic method responsible for implementing the relationships that exist between a smell agent and an object that evaporates a smell molecule [53]. The sniffing, trailing, and random modes are used to describe these relationships, and each mode has its own set of parameters. The sniffing mode simulates the capacity of an agent to perceive smells by causing the scent molecules to diffuse from a smell source toward the agent throughout the sniffing process. Using the trailing mode, the agent can simulate the ability to trace a portion of the scent molecules until the source of the smell molecules is determined. In contrast, the agent uses the random mode as a strategy to avoid becoming stuck in local minima.

3.15 Seagull Optimization Algorithm (SOA)

The seagull optimization algorithm (SOA) is an algorithm that pulls inspiration from the natural behavior of seagulls while migrating and attacking prey [37]. In this regard, these behaviors may be defined in a manner that is closely linked to the objective function that is to be improved. SOA, an optimization algorithm inspired by biology, starts the study with a randomly generated population. During position duplication operations, search agents are able to update their positions according to the best search agent. Migration represents exploration behavior and shows how a group of seagulls move from one location to another. There are three conditions that a seagull must meet at this stage. These are avoiding the collisions, moving towards best neighbor’s direction, and remaining close to the best search agent. The attacking phase represents exploitation behavior. Hunting for seagulls aims to take advantage of all the experience and experience gained from the search processes in the past. During migration, seagulls can also change their attack angle from time to time, apart from their speed. However, they take advantage of their long wingspan and body weight to maintain their high altitude. Seagulls exhibit spiraling behavior in the air when attacking prey, they have identified.

3.16 Pelican Optimization Algorithm (POA)

The pelican optimization algorithm (POA) is a swarm-based optimization technique that draws inspiration from the hunting behavior and methods shown by pelicans. In POA, exploration agents are represented by pelicans that look for sustenance sources. POA is made up of two stages that are carried out consecutively in each iteration. In the first phase, there is a global objective to which all pelicans will migrate. This global target is chosen at random inside the issue space at the start of each cycle. The pelican has two options for mobility. If this goal is more desirable than the pelican’s present position, the pelican will migrate toward it. Otherwise, the pelican will flee from this location. POA employs an acceptance-rejection method. The pelican will only relocate if the new place is superior to its present location. The pelican circles its present location throughout the second phase. Although this phrase is not always applicable, it might be thought of as a local or neighborhood search. During this step, a new location is chosen at random inside the local problem space of the pelican. With each iteration, the diameter of this local issue space rapidly decreases. It indicates that the local issue space is sufficiently large to begin with, and it may be seen as an exploration. This inquiry, on the other hand, progresses from investigation to exploitation with each repetition. In addition to the process of iteration, the current location of the agent has an impact on the problem space at a local level. In its initial form, the current positioning close to zero restricts the range of the local problem domain. Similar to the first phase, the pelican only advances toward the new location if the new location is superior to its current location [46].

3.17 Coati Optimization Algorithm (CA)

The coati optimization algorithm (CA) is a new metaheuristic method that imitates the coati’s natural behavior when it encounters and flees from predators. The process of modifying the positions of candidate solutions in the CA is derived from the emulation of two distinct behaviors shown by coatis in nature. These behaviors include: (i) coatis’ assault method on iguanas, and (ii) coatis’ predator escape strategy. As a result, the CA population is updated in two stages. The first phase of enhancing the coati population in the designated region is shown via a simulation that models their strategies for targeting iguanas. In this particular strategy, a considerable number of coatis ascend the tree in order to closely approach an iguana and elicit a startled response. A group of coatis congregates under a tree, observing the descent of an iguana to the ground. Upon the iguana’s descent, the coatis engage in aggressive behavior by launching an assault and pursuing the iguana. By using this approach, coatis demonstrate their ability to travel to different regions within the search area, hence highlighting the worldwide search capabilities of the COA within the realm of problem-solving. The subsequent phase of updating the locations of coatis inside the search space is formulated using mathematical modeling techniques, which take into account the coatis’ inherent behavior while encountering and evading predators. When a predator initiates an attack on a coati, the coati promptly vacates its position. Coati’s actions in this approach place it in a secure position near to its present location, indicating the CA’s exploitation ability to utilize local search. The iteration of a CA concludes when all coordinates of the coatis in the solution space have been modified according to the results of the first and second phases. The best solution discovered across all rounds of the method is provided as the result after CA has finished running [47].

4  Engineering Design Problems and Experimental Results

In this section, the most prevalent design challenges in engineering are stated. To make the problems more understandable, the mathematical form and definition are provided. The following are the problems investigated in the study:

•   Speed reducer problem

•   Tension-compression spring design problem

•   Pressure vessel design problem

•   Welded beam design problem

•   Three-bar truss design problem

•   Multiple disk clutch brake design problem

•   Himmelblau’s function

•   Cantilever beam problem

•   Tubular column design problem

•   Piston lever

•   Robot gripper

•   Corrugated bulkhead design problem

These engineering design issues are well recognized in practical applications. In order to identify the most favorable design, it is often necessary to use an active approach for determining the ideal parameters. In order to address each issue, some settings (variables) need adjustment. Furthermore, some limitations are included to guarantee that the variables’ values stay within the designated range. The specifics of the optimization issue are presented below.

The evaluation of optimization approaches often involves selecting bound-constrained and common-constrained optimization problems. Each design vector must consistently provide a constrained solution to any engineering or optimization problem [54,55]:

lb(j)≤x(i,j)≤ub(j), j=1,2,3,…,n(1)

where lb(j) and ub(j) are the lower and upper bounds of the problem defined for position x(i,j), respectively, and n is vector size. In addition, the real-world constrained optimization problem is typically given as follows [56]:

Minimize,f(x),x=(x1,x2,…,xn)(2)

Subjectto:gi(x)≤0, i=1,…,n

hj(x)=0,j=n+1,…,m

The bound-constrained structure incorporates the cost function into the assessment of the selected optimization process to describe all the stated constrained issues in Eq. (2). The cost function associated with each infeasible option may be included into the goal function that is being employed. The determination of the cost function arises from its property of situational homogeneity. The use of a single helper cost function renders this approach applicable to a diverse array of challenges.

The above-mentioned real-world constrained problems are used to create a benchmark suite. The benchmark suite includes a total of 12 problems designed from the problems listed above. Table 2 summarizes the specifics of these issues. D denotes the entire decision variables in the problem, h indicates the number of equality constraints, g denotes the total of inequality constraints, and fmin represents the best known optimal objective function value.

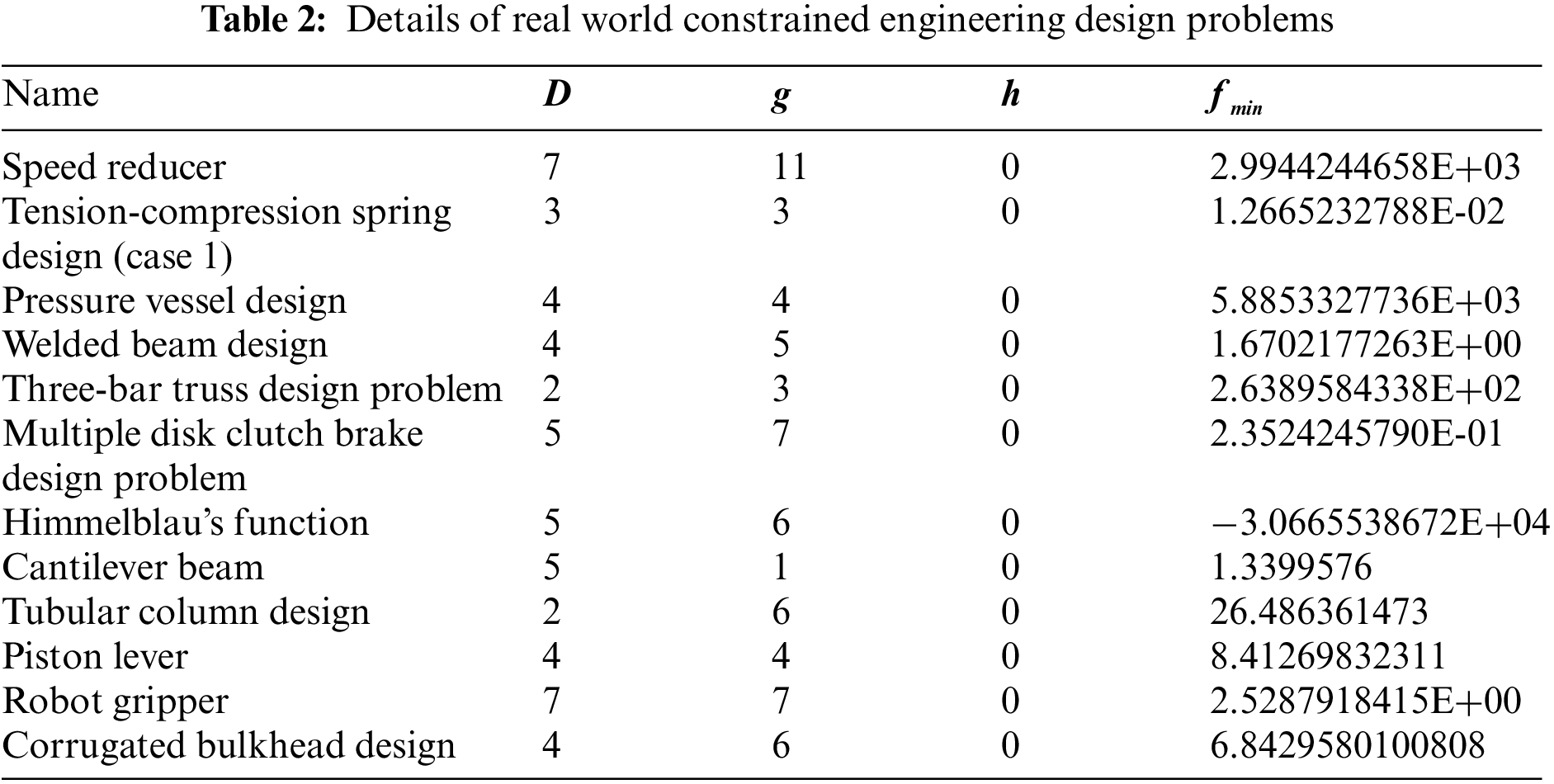
The experiments are conducted using a computing system equipped with the Windows 11 operating system, 16 GB of RAM, and an Intel (R) Core (TM) i7-10750H CPU (2.60 GHz). The comparison methods are coded using MATLAB R2021a. The aforementioned issues are inherently constrained, therefore necessitating the implementation of an external penalty approach mechanism in order to address them. The maximum number of iterations for all problems is 1000, the number of populations is 30, and the number of evaluations is chosen as 30000. Algorithm parameters are default values found in the literature and are shown in Table 3. To facilitate the analysis of the convergence behavior of the algorithms under study, the convergence curves, which represent the best fitness values achieved for each issue, are graphically shown. Each algorithm is subjected to 30 separate experimental runs. This study compares the best, mean, worst, standard deviation (SD), and Friedman mean rank (FMR) values. The method that yields the best answer is emphasized in bold to enhance readability.

4.1 Speed Reducer Problem

This problem is simply a gearbox problem that allows the aircraft engine to rotate at maximum efficiency [57]. In this problem, the minimum values of the seven decision variables must be optimized by finding the face width b (x1), the tooth modulus m (x2), the number of teeth on the pinion z (x3), the length of the first shaft between the bearings l1(x4), the length of the second shaft between the bearings l2(x5), the diameter of the first shaft d1(x6), and the diameter of the second shaft d2(x7). The schematic representation of the speed reducer is given in Fig. 1. The aim of the design issue is discovering the speed reducer with the lowest cost weight. The issue is mathematically represented in the following manner:

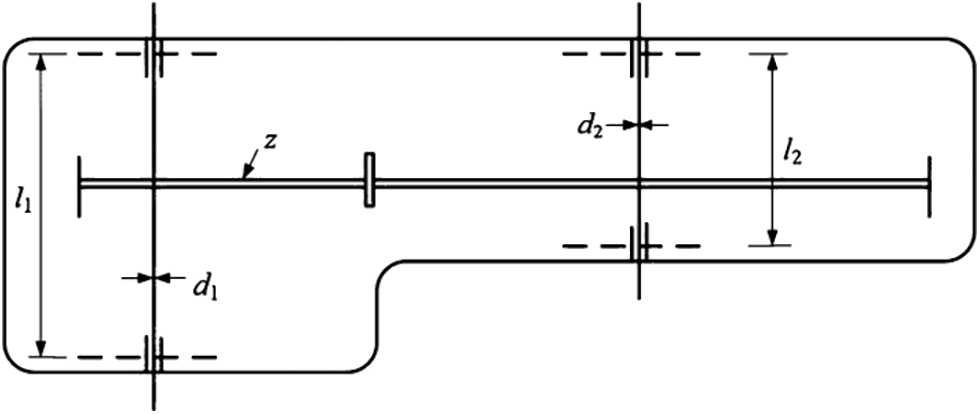
Figure 1: Speed reducer problem

Minimize:

f(x)=0.7854x22x1(14.9334x3−43.0934+3.3333x32)+0.7854(x5x72+x4x62)−1.508x1(x72+x62)+7.477(x73+x63)(3)

Subject to:

g1(x)=−x1x22x3+27≤0(4)

g2(x)=−x1x22x32+397.5≤0(5)

g3(x)=−x2x64x3x4−3+1.93≤0(6)

g4(x)=−x2x74x3x5−3+1.93≤0(7)

g5(x)=10x6−316.91×106+(745x4x2−1x3−1)2−1100≤0(8)

g6(x)=10x7−3157.5×106+(745x5x2−1x3−1)2−850≤0(9)

g7(x)=x2x3−40≤0(10)

g8(x)=−x1x2−1+5≤0(11)

g9(x)=x1x2−1−12≤0(12)

g10(x)=1.5x6−x4+1.9≤0(13)

g11(x)=1.1x7−x5+1.9≤0(14)

with bounds:

0.7≤x2≤0.8,17≤x3≤28,2.6≤x1≤3.6,5≤x7≤5.5,7.3≤x5,x4≤8.3,2.9≤x6≤3.9

Table 4 presents the comparative performance values of several approaches, including TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the speed reducer issue. Table 4 displays the optimal, mean, suboptimal, and standard deviation measurements of the used methodologies. Furthermore, Table 5 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 4, it becomes apparent that both EO and MFO exhibit superiority over other approaches in terms of the greatest value. Furthermore, when considering the average value, EO demonstrates greater success. Furthermore, Fig. 2 displays the convergence curve of the strategies used for the speed reducer issue.

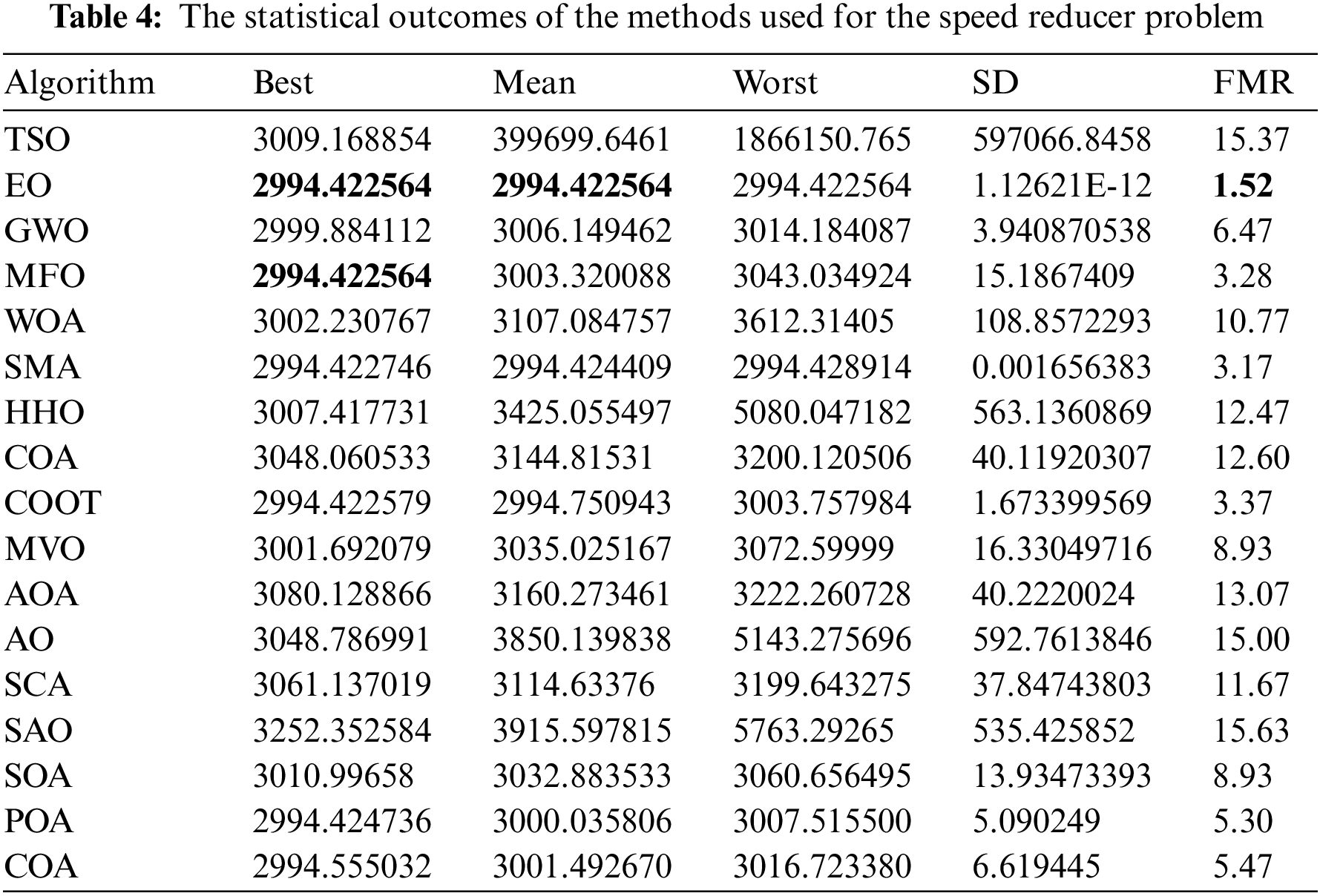
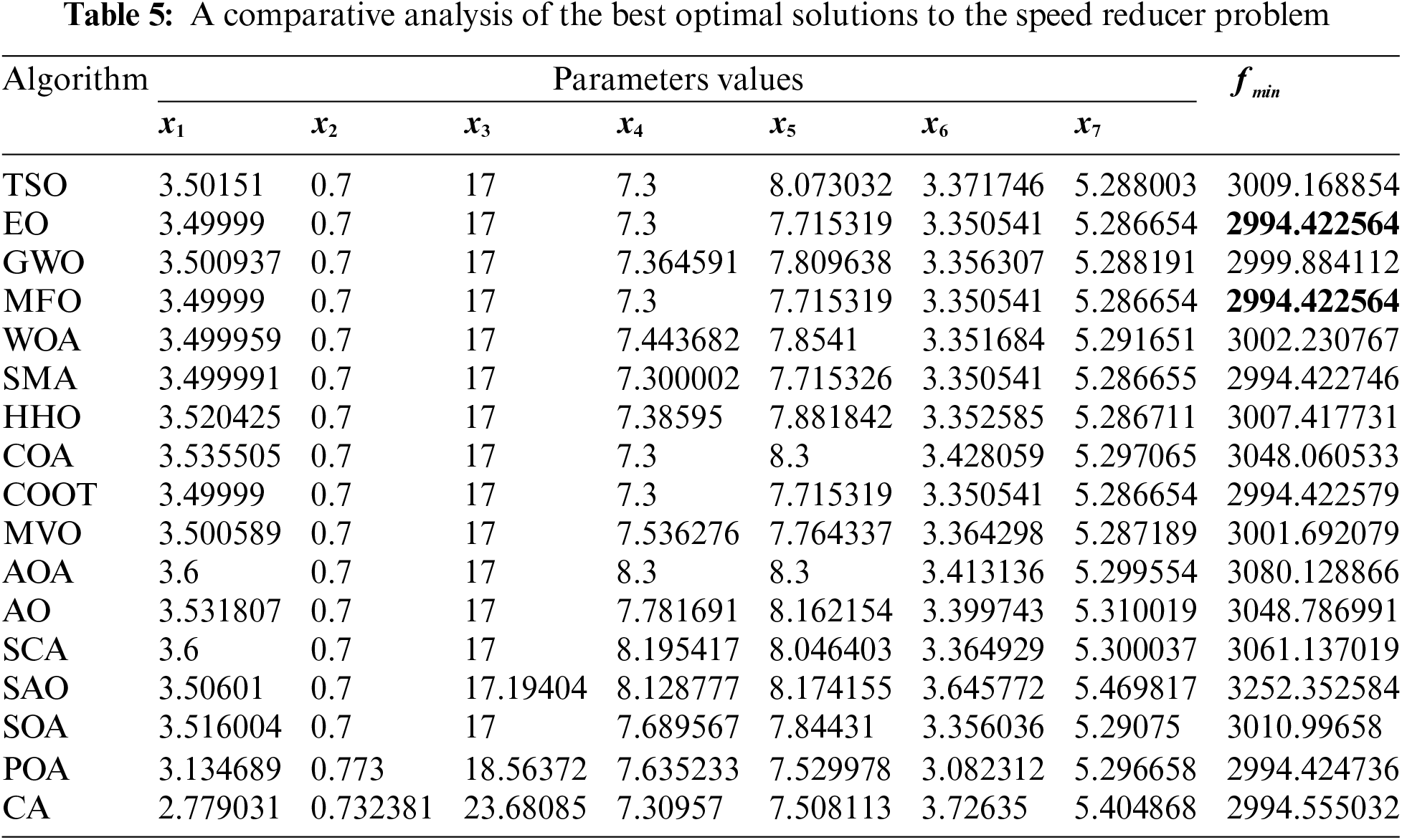
Figure 2: Convergence curve of the methods used on the speed reducer problem

4.2 Tension-Compression Spring Design Problem (Case 1)

The tension-compression spring design problem is a problem defined by Arora [58] which aims to create a spring design with the least amount of weight possible. This minimization problem, schematically illustrated in Fig. 3, has certain limitations such as cut-off voltage, ripple frequency and minimum deviation. The tension-compression spring problem has three decision variables: wire diameter d (x1), average coil diameter D (x2), and number of active coils N (x3). This problem is mathematically represented as follows:

Figure 3: Tension-compression spring design problem

Minimize:

f(x)=(x3+2)x12x2(15)

Subject to:

g1(x)=1−x23x371785x14≤0(16)

g2(x)=4x22−x1x212566(x2x1−3x14)+15108x12≤0(17)

g3(x)=1−140.45x1x23x3≤0(18)

g4(x)=x1+x21.5−1≤0(19)

with bounds:

0.05≤x1≤2.00,0.25≤x2≤1.30,2.00≤x3≤15.0

Table 6 presents the comparative values of the performance results of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the tension-compression issue. Table 6 displays the optimal, mean, suboptimal, and standard deviation values of the used methodologies. Furthermore, Table 7 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 6, it becomes evident that CA outperforms other approaches in terms of the highest value, but POA has more performance when evaluated based on the average value. Furthermore, Fig. 4 illustrates the convergence graph of the approaches used for the tension-compression issue.

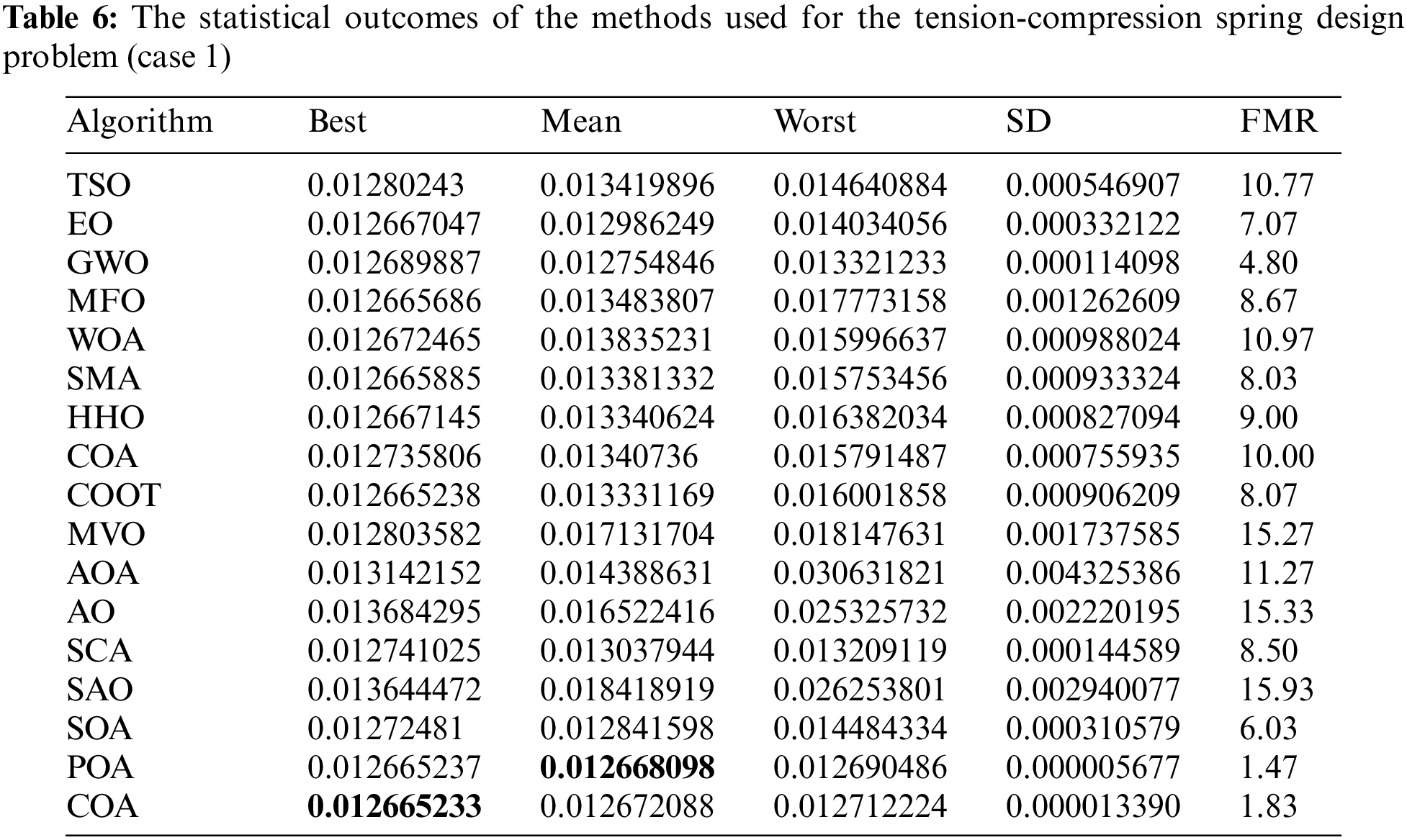
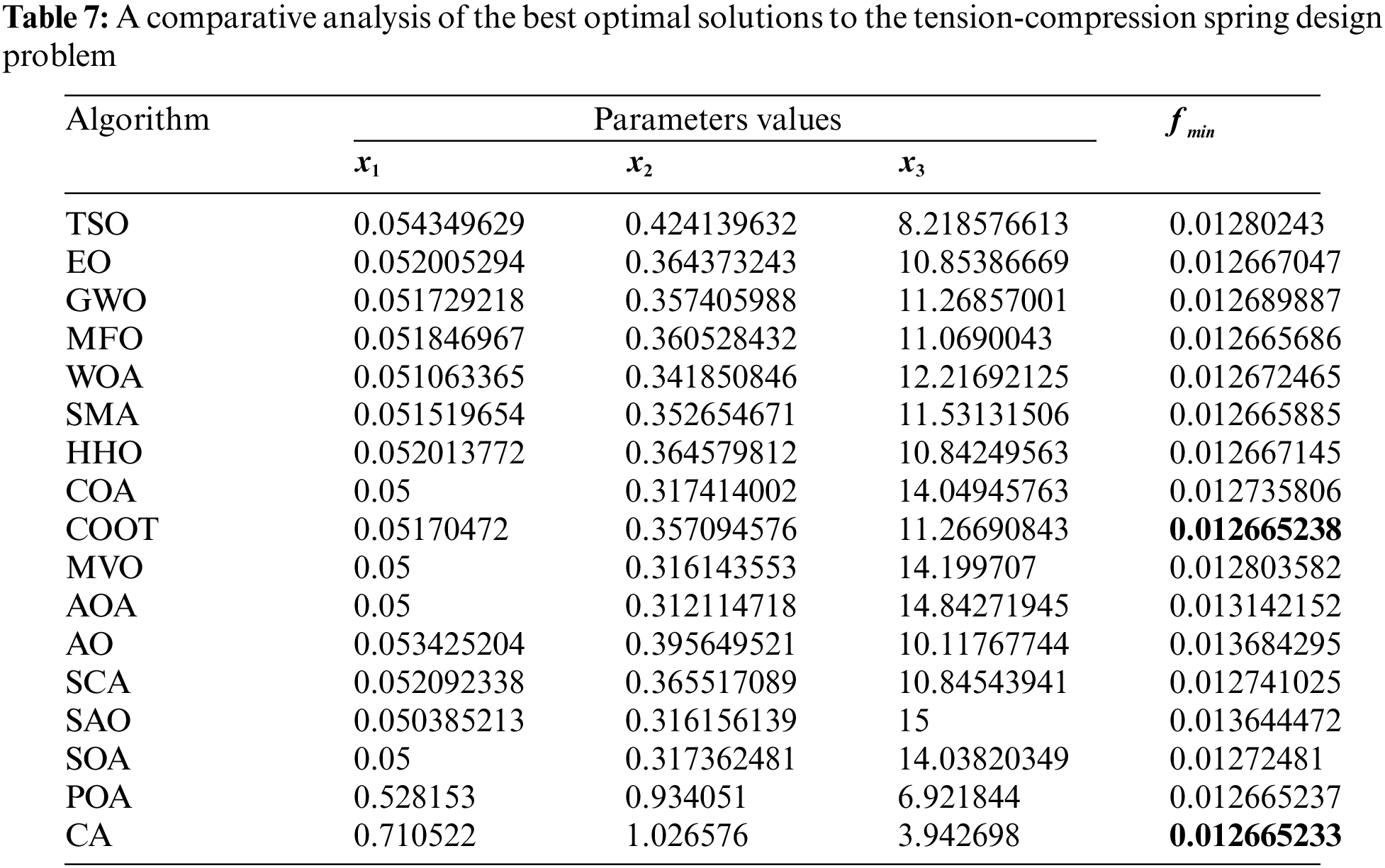
Figure 4: Convergence curve of the methods used on the tension-compression spring design problem

4.3 Pressure Vessel Design Problem

The primary aim of this challenge is to optimize the cost associated with welding, as well as the expenses related to materials and the creation process of a vessel [59]. This problem has four constraints that must be satisfied, and the objective function is calculated with respect to four variables: shell thickness (x1), head thickness (x2), inner radius (x3), and length (x4) without including vessel height. The schematic structure of the pressure vessel design problem is shown in Fig. 5. This problem is mathematically represented as follows:

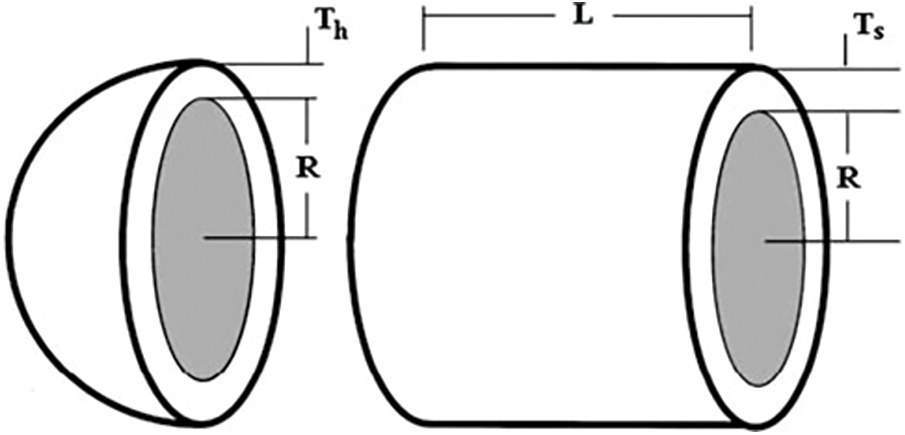
Figure 5: Pressure vessel

Minimize:

f(x)=0.6224x1x3x4+1.7781x2x32+3.1661x12x4+19.84x12x3(20)

Subject to:

g1(x)=−x1+0.0193x3≤0(21)

g2(x)=−x2+0.00954x3≤0(22)

g3(x)=−πx32x4−43πx33+1296000≤0(23)

g4(x)=x4−240≤0(24)

with bounds:

0.51≤x1,x2≤99.49,10≤x3,x4≤200

Table 8 presents the comparative values of the performances of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the pressure vessel design issue. Table 8 displays the optimal, mean, suboptimal, and standard deviation of the methodologies used. Furthermore, Table 9 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 8, it becomes evident that EO, POA, and CA exhibit superiority over other approaches in terms of the greatest value. Conversely, GWO has more success when evaluated based on the average value. Furthermore, Fig. 6 displays the convergence graph of the approaches used for the pressure vessel issue.

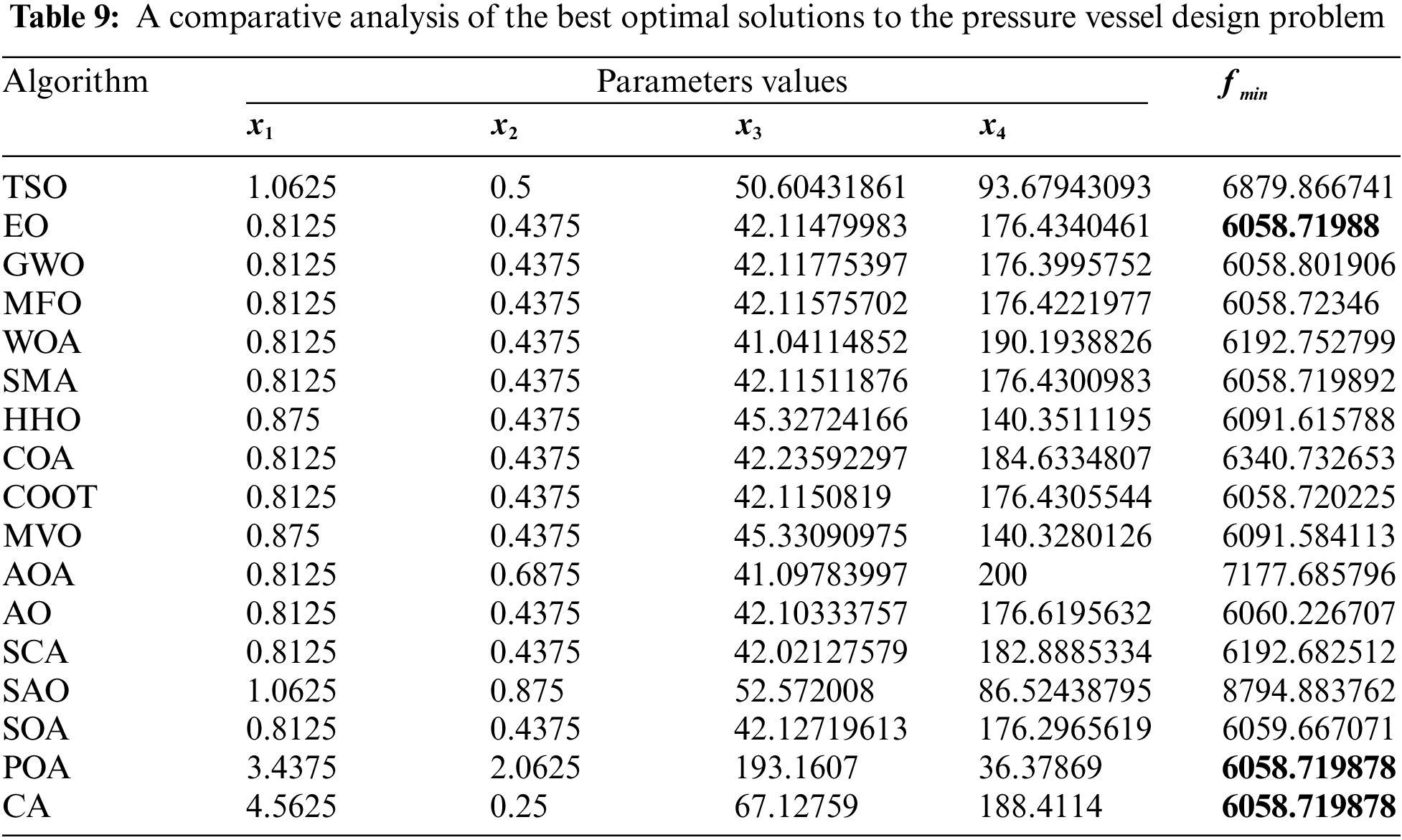
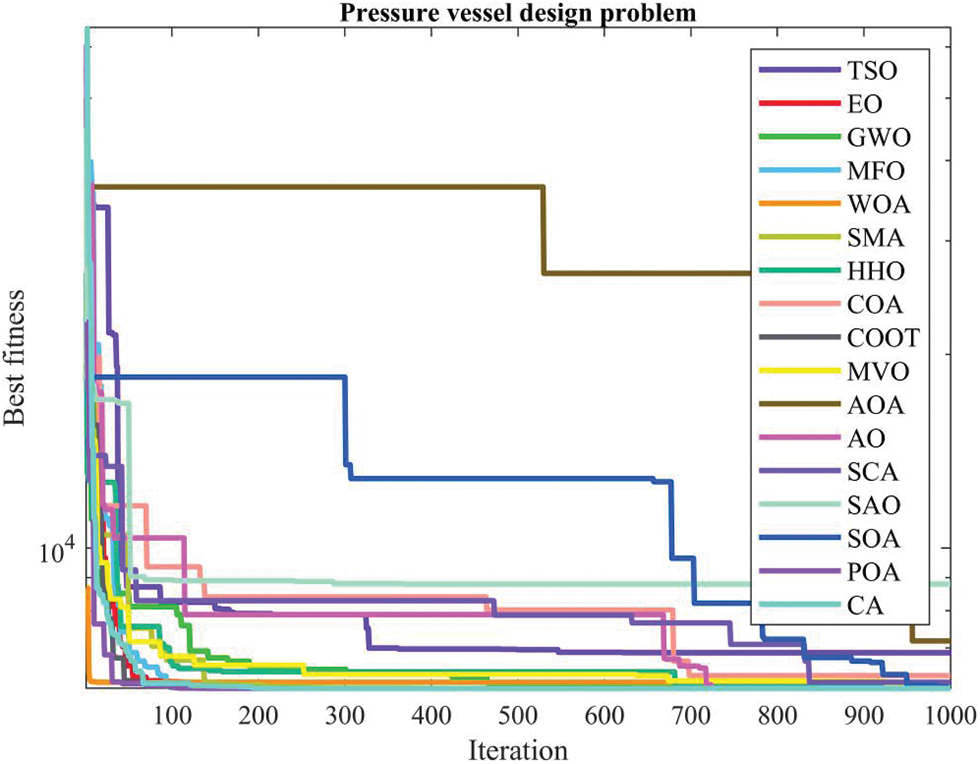
Figure 6: Convergence curve of the methods used on the pressure vessel design problem

4.4 Welded Beam Design Problem

The primary aim of the welded beam design challenge is to optimize the cost of producing a beam while adhering to certain limitations [5]. Fig. 7 depicts a welded beam structure comprised of beam A and the requisite weld to join this beam to object B. The problem includes four decision variables and five nonlinear inequality constraints. These design parameters are h (x1), l (x2), t (x3) and b (x4) representing the weld thickness, weld joint length, element width and element thickness, respectively. This problem is mathematically represented as follows:

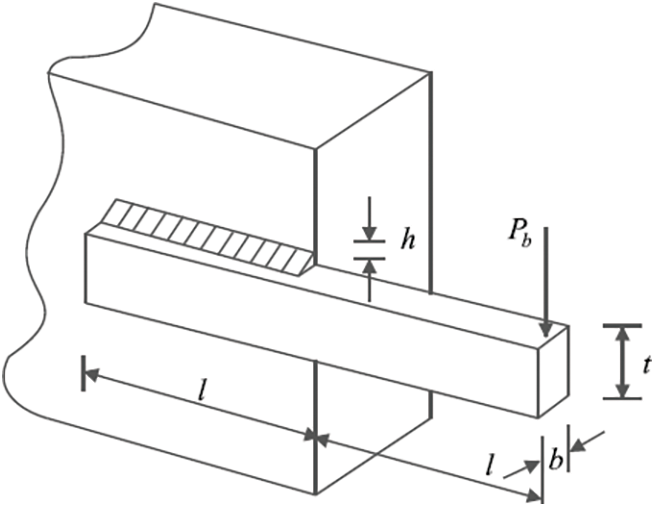
Figure 7: Schematic representation of welded beam

Minimize:

f(x)=1.10471x12x2+0.04811x3x4(14.0+x2)(25)

Subject to:

g1(x)=τ(x)−τmax≤0(26)

g2(x)=σ(x)−σmax≤0(27)

g3(x)=x1−x4≤0(28)

g4(x)=1.10471x12+0.04811x3x4(14.0+x2)−5.0≤0(29)

g5(x)=0.125−x1≤0(30)

g6(x)=δ(x)−δmax≤0(31)

g7(x)=P−Pc(x)≤0(32)

τ(x)=(τ′)2+(2τ′τ″)x22R+(τ″)2,τ′=60002x1x2,τ″=MRJ,M=6000(14.0+x22),R=x224+(x1+x32)2

J={x1x22[x2212+(x1+x32)2]},σ(x)=504000x4x32,δ(x)=2.1952x4x33,Pc(x)=4.013Ex32x4636196(1−E4Gx328)

Pc(x)=4.013Ex32x4636196(1−E4Gx328)

τmax=13600 psi,σmax=30000 psi,δmax=0.25 in,E=30×106 psi,G=12×106 psi

with bounds:

0.125 ≤ x1 ≤ 2, 0.1 ≤ x4 ≤ 2 ve 0.1 ≤ x2, x3 ≤ 10

Table 10 presents the comparative values of the performances of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the welded beam design issue. Furthermore, Table 11 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 10, it becomes evident that EO and CA exhibit superiority over other ways in terms of greatest value, whereas POA demonstrates superiority over other methods in terms of average value. Furthermore, Fig. 8 illustrates the convergence graph of the approaches used for the welded beam design issue.

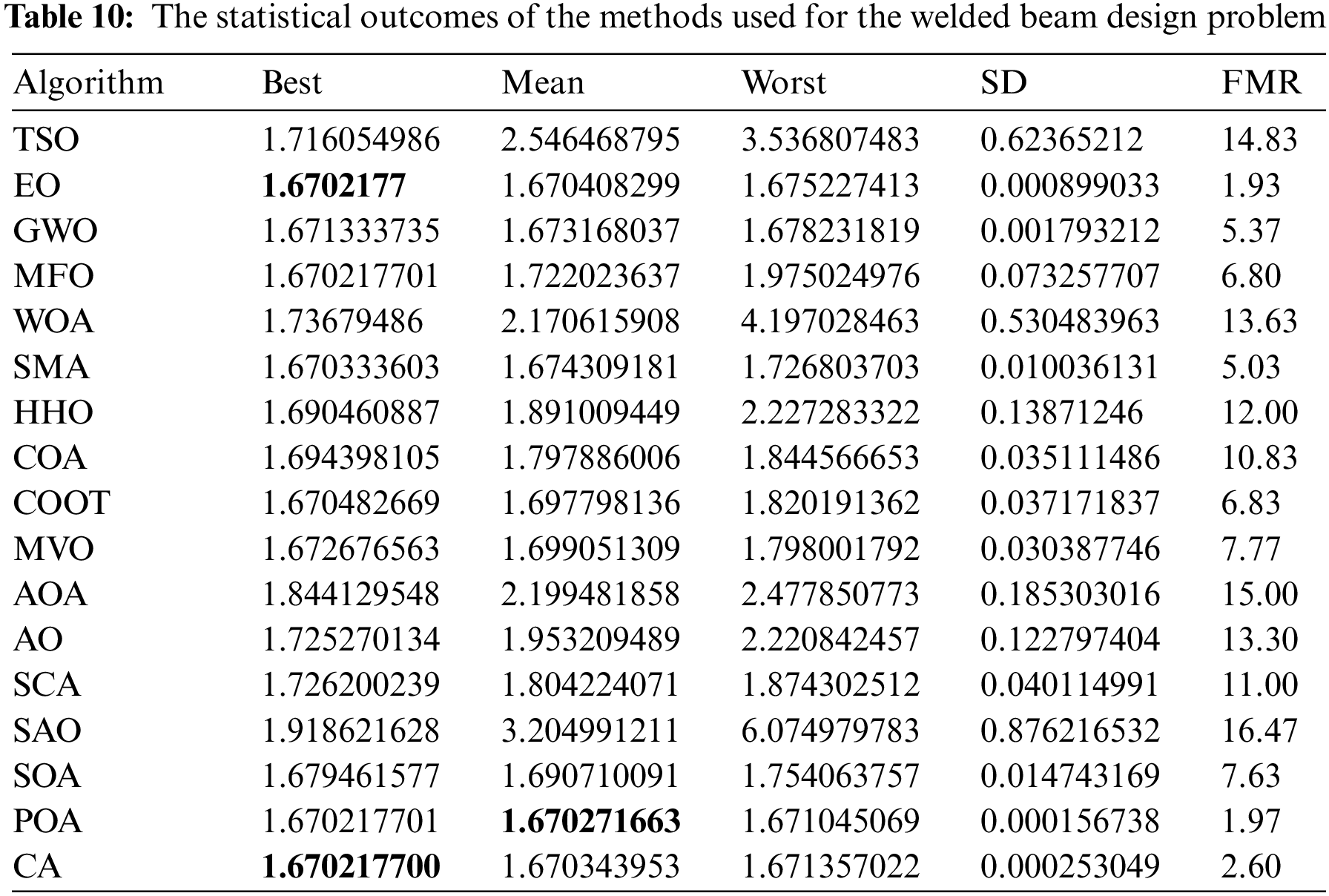
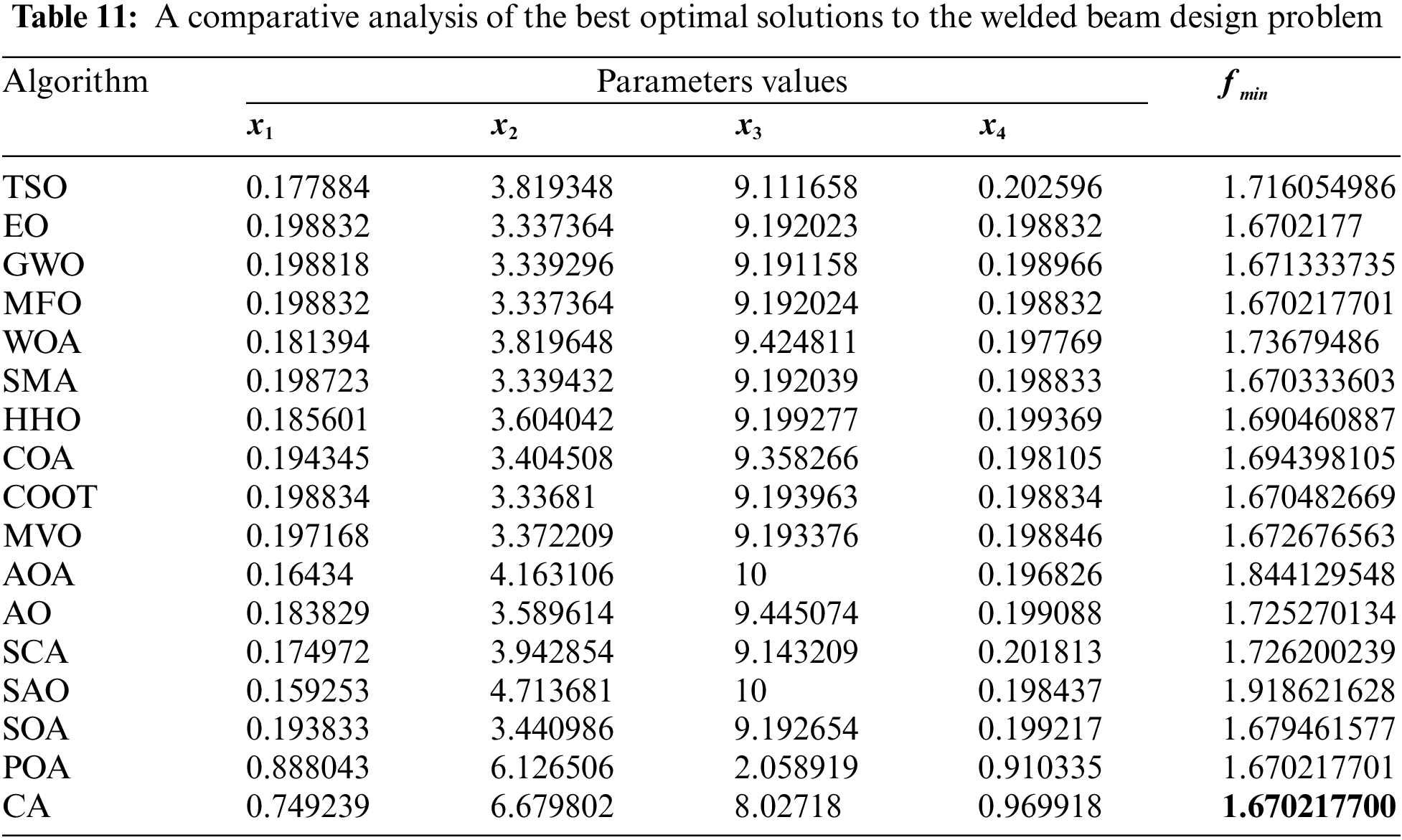
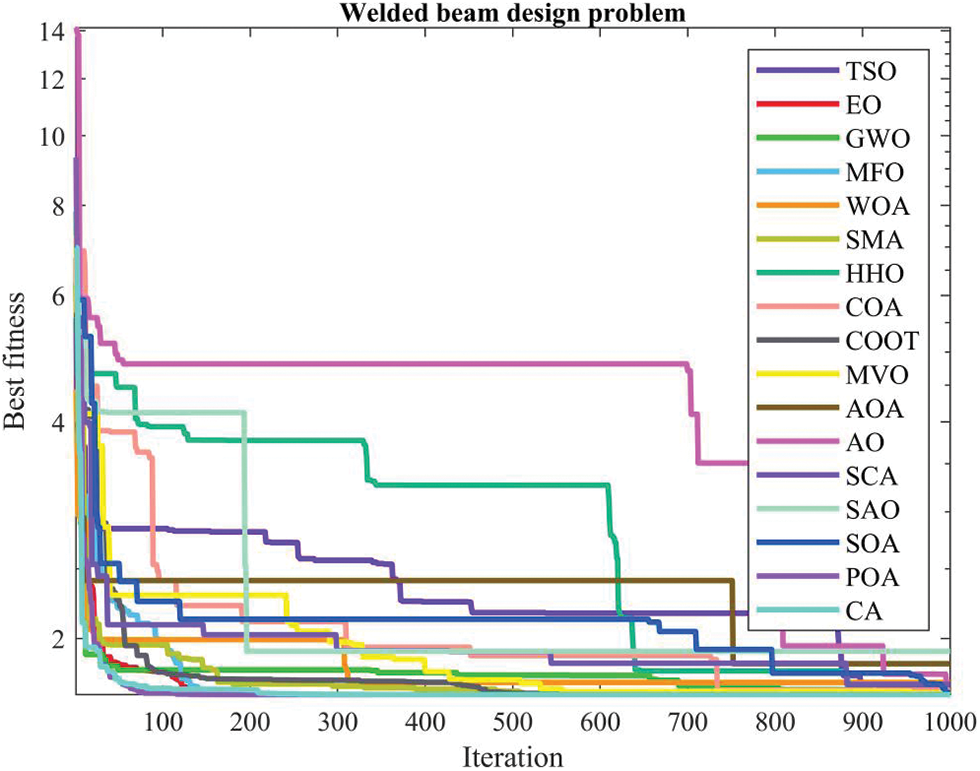
Figure 8: Convergence curve of the methods used on the welded beam design problem

4.5 Three-Bar Truss Design Problem

This problem is a structural optimization problem in civil engineering. The main objective of this problem introduced by Nowacki is to minimize the volume of the three-bar truss by adjusting the cross-sectional areas (x1 and x2), taking into account the stress (σ) on each of the truss members [27]. The value ranges that these values can take are 0≤x1,x2≤1. The mathematical definition of this problem, whose schematic representation is given in Fig. 9. This problem is mathematically represented as follows:

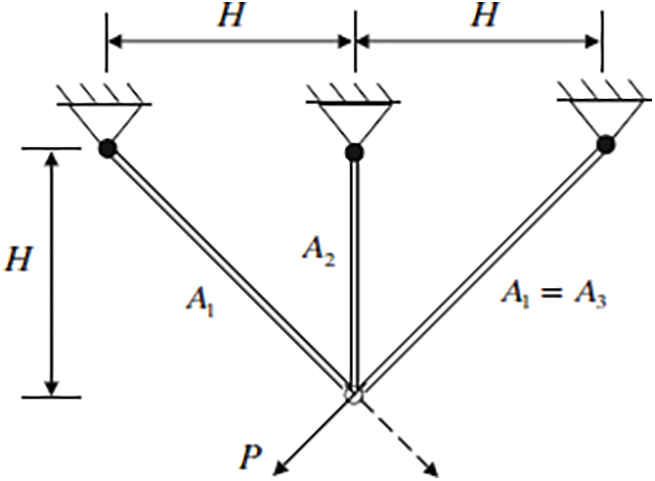
Figure 9: Three-bar truss design

Minimize:

f(x)=l(x2+22x1)(33)

Subject to:

g1(x)=x22x2x1+2x12P−σ≤0(34)

g2(x)=x2+2x12x2x1+2x12P−σ≤0(35)

g3(x)=1x1+2x2P−σ≤0(36)

where,

l=100,P=2,andσ=2

with bounds:

0≤x1,x2≤1

Table 12 presents the comparative values of the performances of several approaches, including TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the three-bar truss design issue. Furthermore, Table 13 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 12, it becomes evident that EO, COOT, POA, and CA exhibit superiority over other approaches in terms of the greatest value. Furthermore, when considering the average value, POA and CA demonstrate greater success. Furthermore, Fig. 10 illustrates the convergence graph of the methodologies used in addressing the three-bar truss design issue.

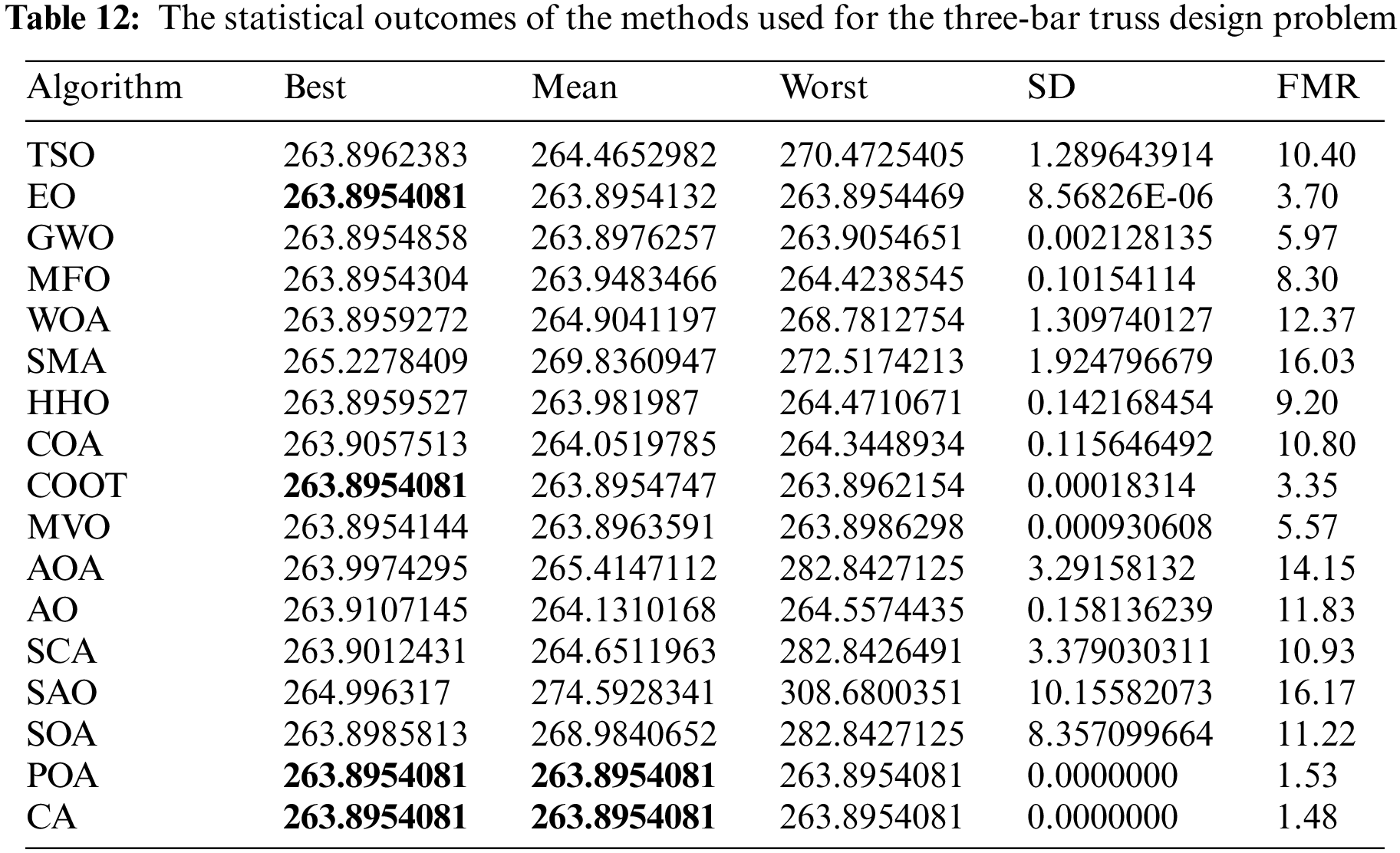
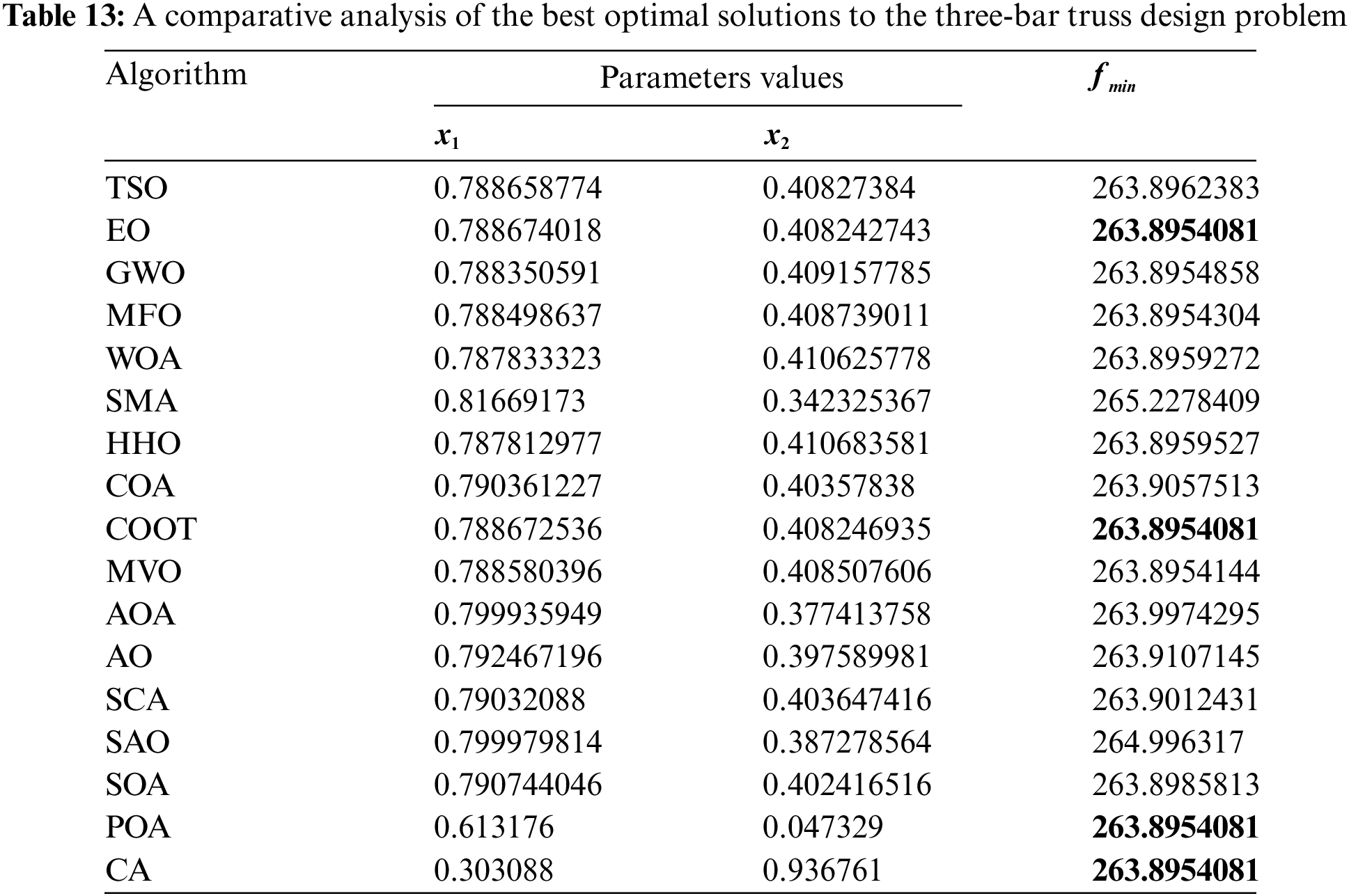
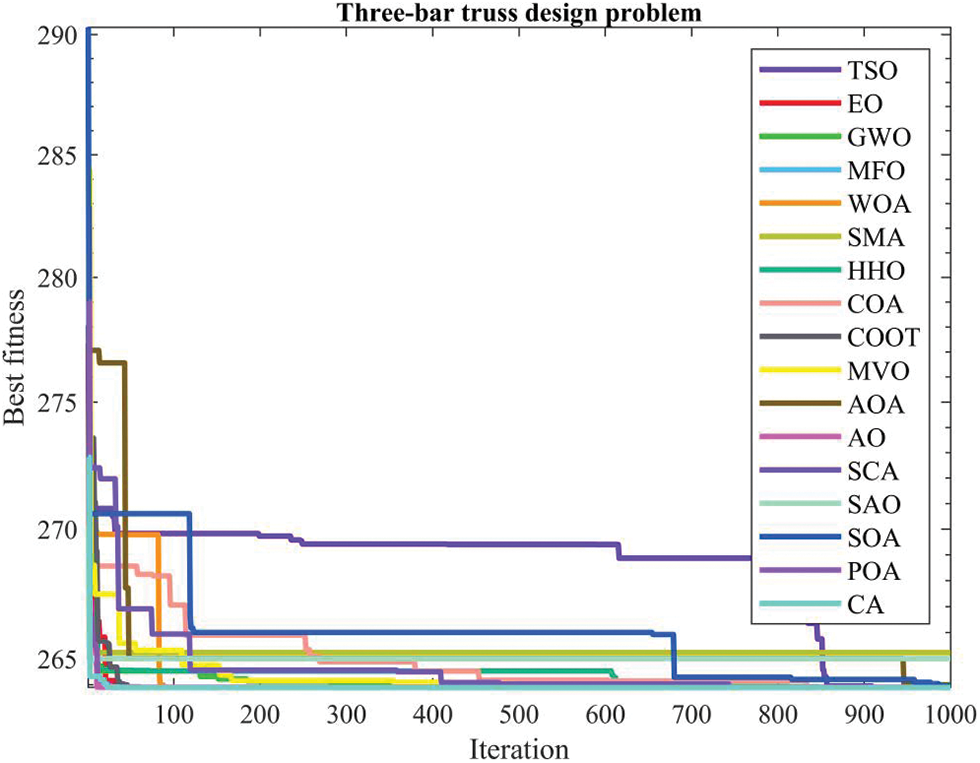
Figure 10: Convergence curve of the methods used on the three-bar truss design problem

4.6 Multiple Disk Clutch Brake Design Problem

The primary aim of this topic is to decrease the bulk of a clutch braking system consisting of numerous disks. Inner radius (x1), outer radius (x2), disk thickness (x3), force of actuators (x4), and number of frictional surfaces (x5) are the five integer choice variables employed in this problem [27]. There are nine nonlinear constraints in this problem. Fig. 11 depicts a schematic depiction of the issue. The issue is mathematically represented in the following manner:

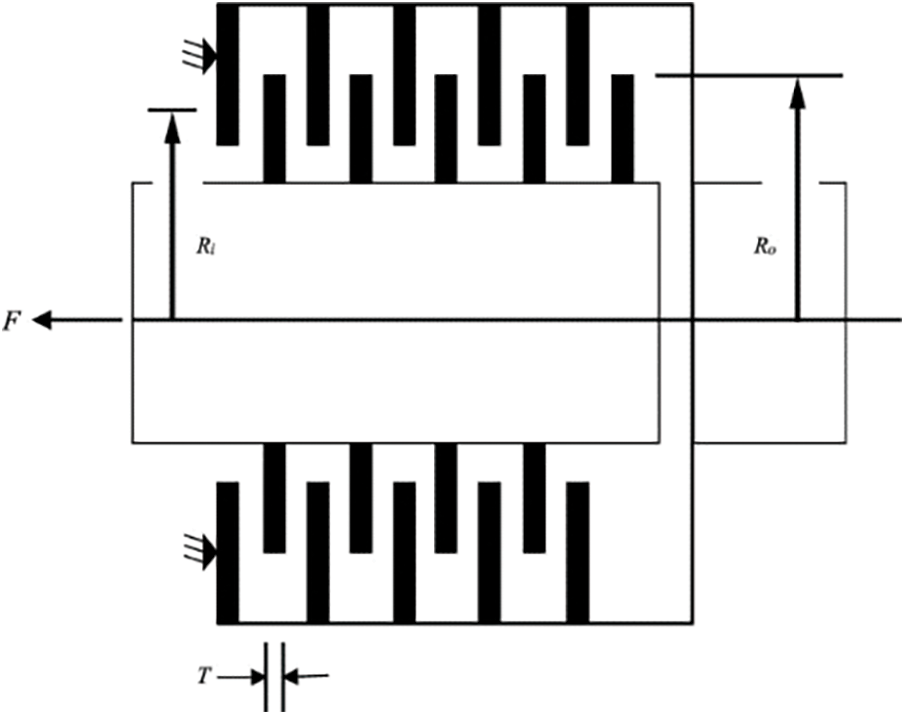
Figure 11: Multiple disk clutch brake design problem

Minimize:

f(x)=π∗(x22−x12)∗x3(x5+1)ρ(37)

Subject to:

g1(x)=−Pmax−Prz≤0(38)

g2(x)=PrzVsr−Vsr,maxPmax≤0(39)

g3(x)=ΔR+x1−x2≤0(40)

g4(x)=−Lmax+(x5+1)(x3+δ≤0(41)

g5(x)=sMs−Mh≤0(42)

g6(x)=T≥0(43)

g7(x)=−Vsr,max+Vsr≤0(44)

g8(x)=T−Tmax≤0(45)

where,

Mh=23μx4x5x23−x13x22−x12N.mm,ω=πn30rads,A=π(x22−x12)mm2,Prz=x4ANmm2,Vsr=πRsrn30mms,Rsr=23x23−x13x22x12mm,T=IzωMh+Mf

ΔR=20mm,Lmax=30mm,μ=0.6,Vsr,max=10m/s,δ=0.5mm,s=1.5,Tmax=15s,n=250rpm,Iz=55kg.m2,Ms=40Nm,Mf=3Nm,andPmax=1

with bounds:

60≤x1≤80,90≤x2≤110,1≤x3≤3,0≤x4≤1000,2≤x5≤9

Table 14 presents the comparative values of the performances of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the multiple disc clutch brake design issue. Furthermore, Table 15 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 14, it becomes evident that EO, MFO, WOA, SMA, HHO, COOT, POA, and CA exhibit superiority over other approaches in terms of the best value. Furthermore, when considering the average value, EO, HHO, POA, and CA demonstrate greater success. Furthermore, Fig. 12 displays the convergence graph of the strategies used for the multiple disc clutch brake design issue.

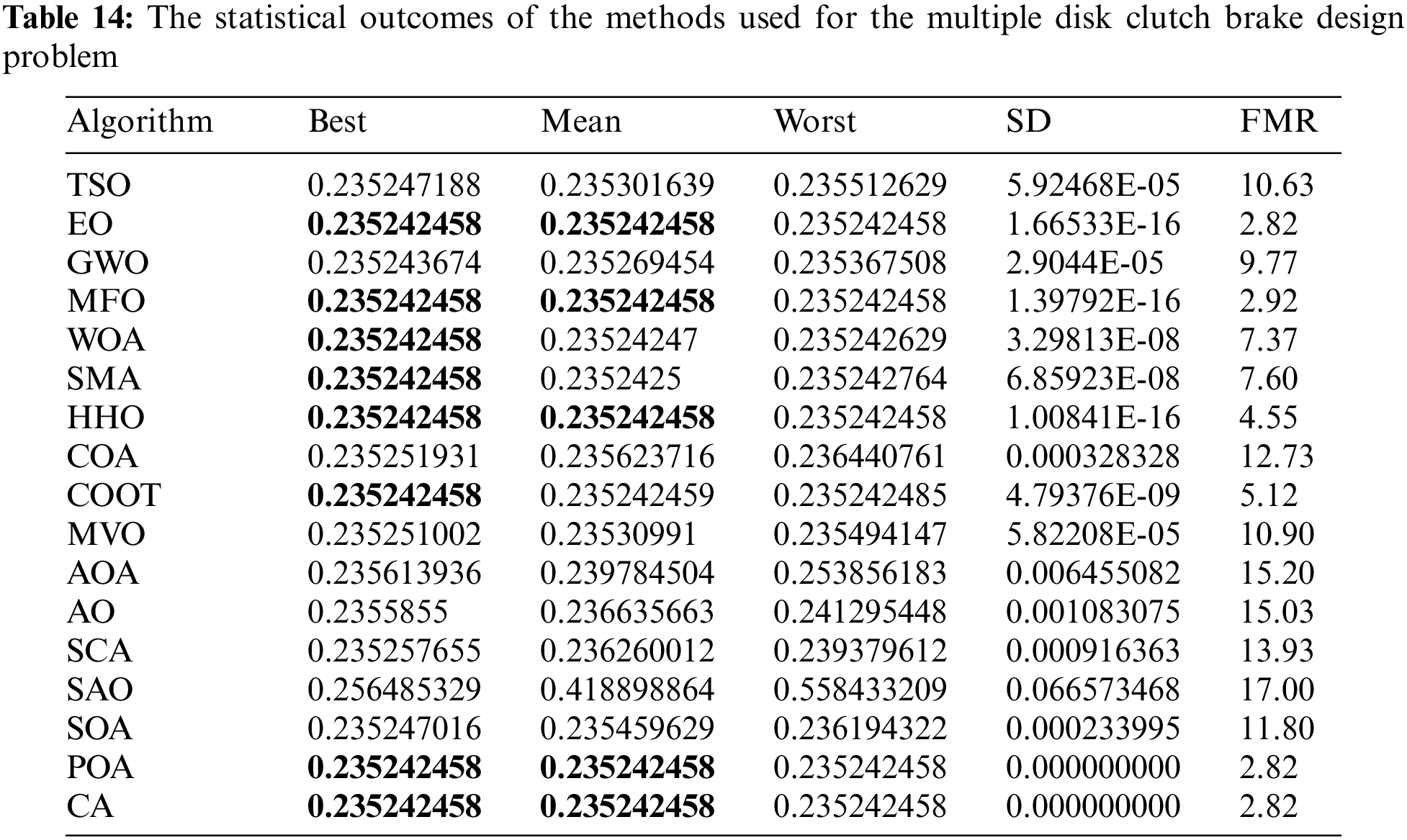
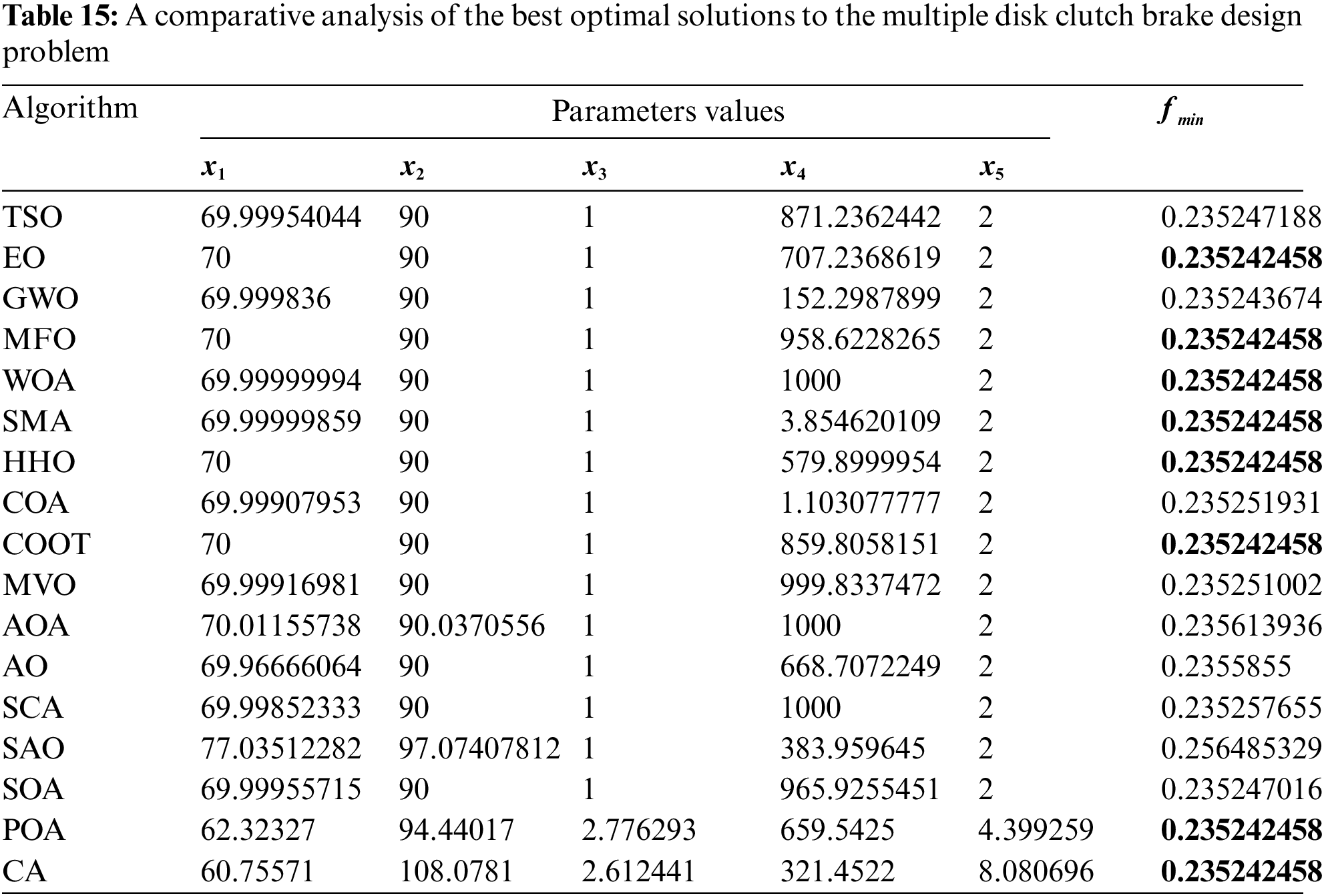
Figure 12: Convergence curve of the methods used on the multiple disk clutch design problem

4.7 Himmelblau’s Function

The issue proposed by Himmelblau serves as a widely used benchmark problem for the analysis of nonlinear constrained optimization methods. This issue consists of a set of five variables and six nonlinear constraints. The issue is mathematically represented in the following manner.

Minimize:

f(x)=5.3578547x32+0.8356891x1x5+37.293239x1−40792.141(46)

Subject to:

g1(x)=−G1≤0(47)

g2(x)=G1−92≤0(48)

g3(x)=90−G2≤0(49)

g4(x)=G2−110≤0(50)

g5(x)=20−G3≤0(51)

g6(x)=G3−25≤0(52)

where,

G1=85.334407+0.0056858x2x5+0.0006262x1x4−0.0022053x3x5

G2=80.51249+0.0071317x2x5+0.0029955x1x2−0:0021813x32

G1=9.300961+0.0047026x3x5+0.00125447x1x3−0.0019085x3x4

with bounds:

78≤x1≤102,33≤x2≤45,27≤x3,x4,x5≤45

Table 16 presents the comparative values of the performances of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on Himmelblau’s function issue. Furthermore, Table 17 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 16, it becomes apparent that EO, MFO, SMA, COOT, POA, and CA exhibit superiority over other approaches in terms of the greatest value. Additionally, SMA demonstrates greater success when evaluated based on the average value. Furthermore, Fig. 13 displays the convergence graph of the strategies used for solving Himmelblau’s function issue.

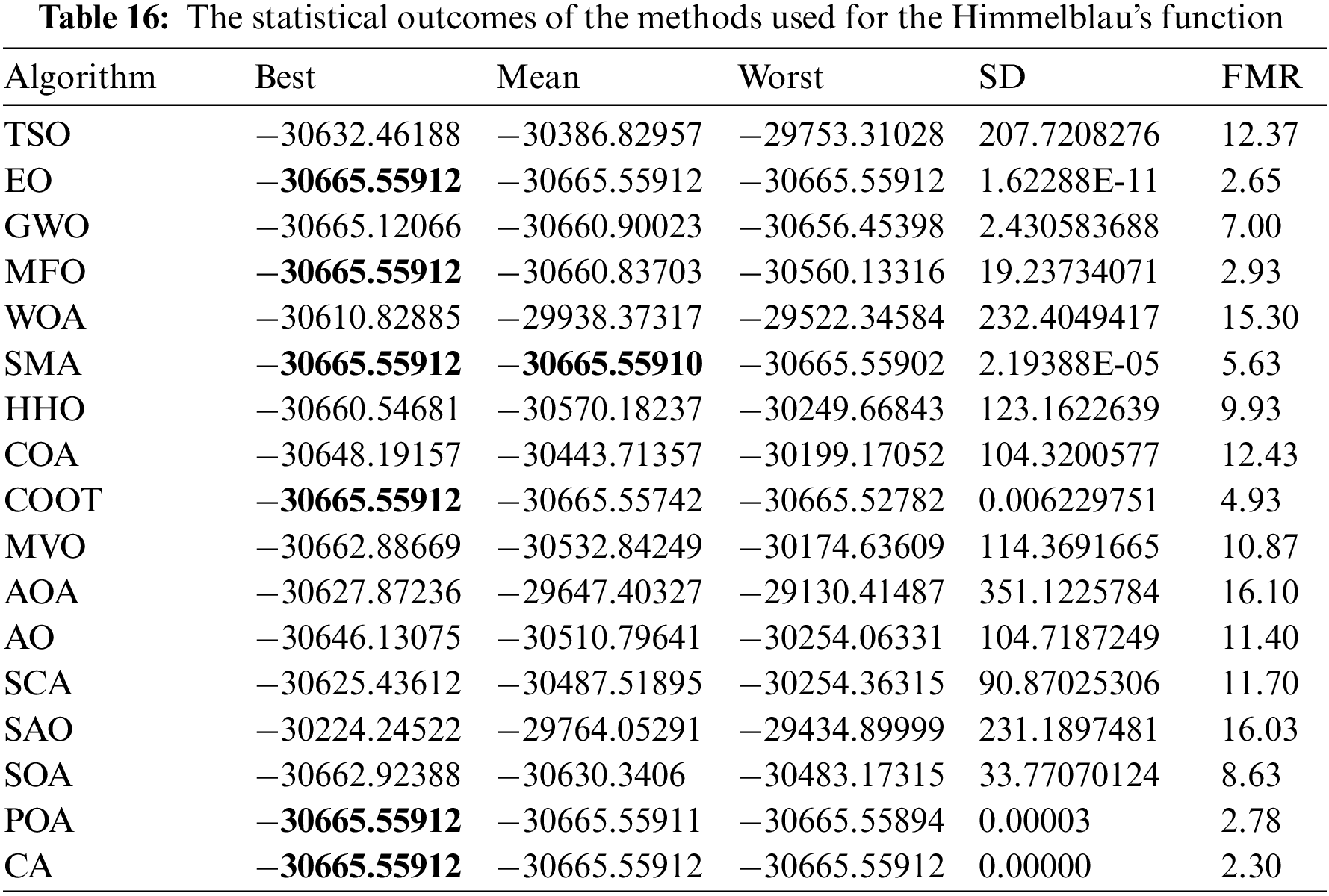
Figure 13: Convergence curve of the methods used on the Himmelblau’s Function

4.8 Cantilever Beam Problem

A cantilever beam design problem is a common optimization problem faced in the area of engineering. In this problem, the minimum values of five choice variables x1, x2, x3, x4, x5 must be found [28]. All variables provided are positive integers that belong to predetermined intervals. The schematic representation of the cantilever beam design problem is shown in Fig. 14. This design problem aims to find the minimum cost weight of the cantilever beam. The issue is mathematically represented in the following manner.

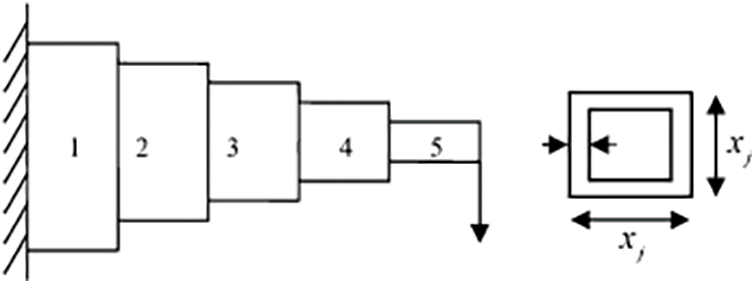
Figure 14: Cantilever beam

Minimize:

f(x)=0.6224(x1+x2+x3+x4+x5)(53)

Subject to:

g(x)=60x13+27x23+19x33+7x43+1x53−1≤0(54)

with bounds:

0.01≤x1,x2,x3,x4,x5≤100

Table 18 presents the comparative values of the performances of several approaches, including TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the cantilever beam design issue. Furthermore, Table 19 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 18, it becomes evident that the CA technique exhibits superiority over other ways in terms of greatest value, while the POA approach demonstrates superiority over other methods in terms of average value. Furthermore, Fig. 15 displays the convergence curve of the strategies used in the cantilever beam design issue.

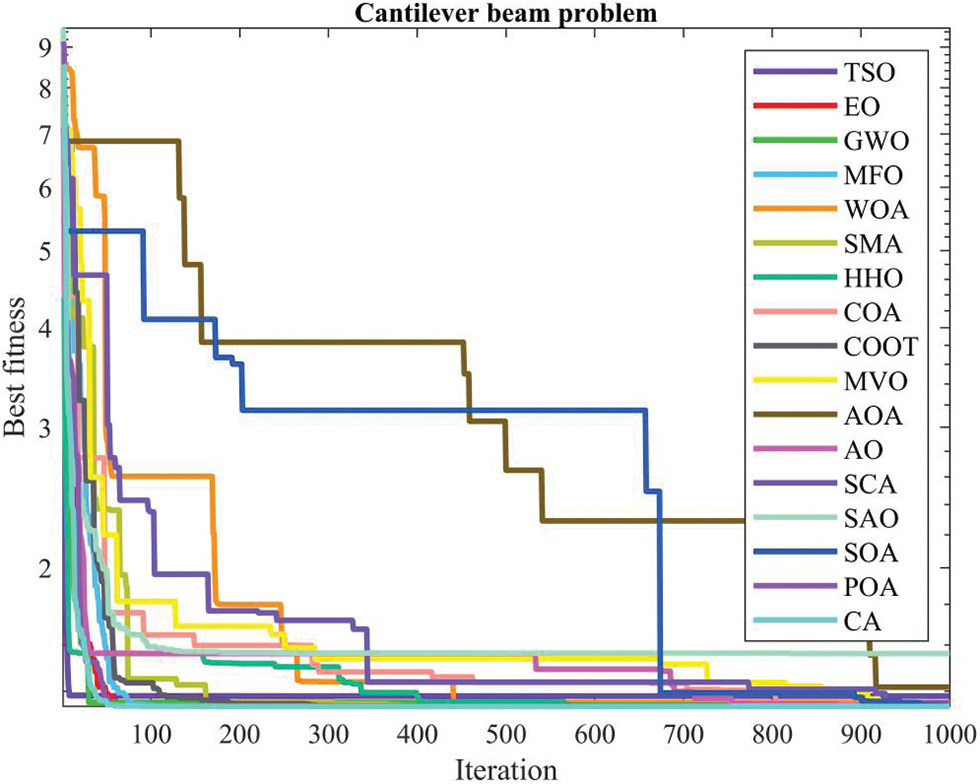
Figure 15: Convergence curve of the methods used on the cantilever beam problem

4.9 Tubular Column Design Problem

Fig. 16 shows an example of how to construct a uniform tubular column to handle a compressive load of P=2.500 for the lowest possible cost. The material used in the column has an elasticity modulus (E) of 0.85×106, a yield stress (σy) of 500 kgf/cm2, and a density (ρ) of 0.0025 kgf/cm3. The column’s length (L) is 250 cm. The stress in the column should be smaller than the yield stress (constraint g1) and the buckling stress (constraint g2). The column’s mean diameter is limited between 2 and 14 cm (constraints g3 and g4), because thicknesses greater than 0.2–0.8 cm are not commercially accessible (constraint g5 and g6). The column’s cost includes both construction costs and material [28]. It is assumed to be the objective function. The following is the optimization model for this problem:

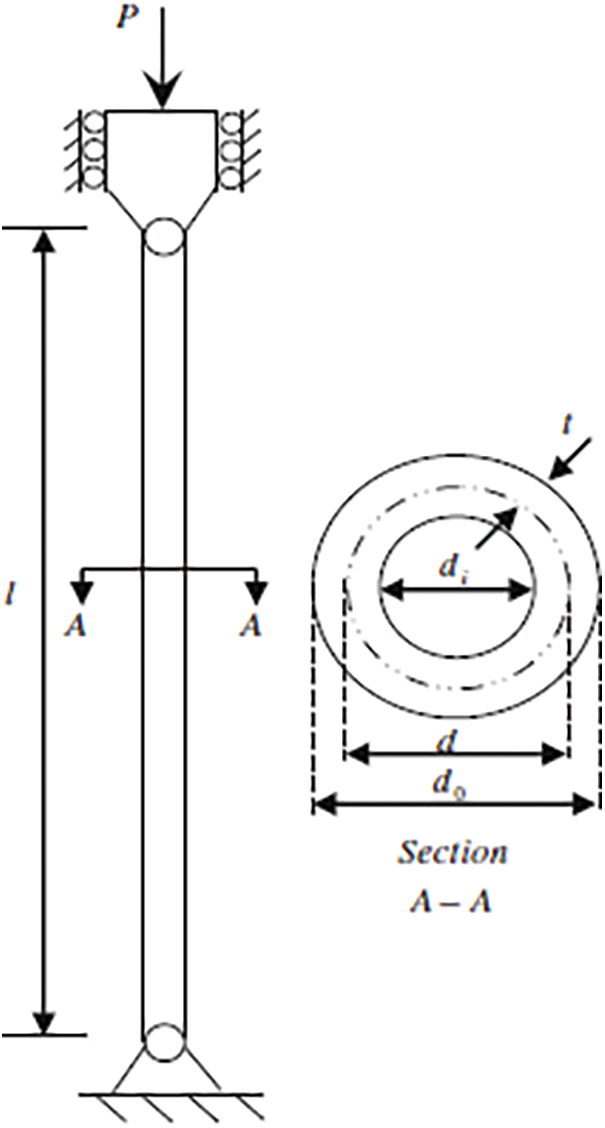
Figure 16: Tubular column design

Minimize:

f(d,t)=9.8dt+2d(55)

Subject to:

g1=Pπdtσy−1≤0(56)

g2=8PL2π3Edt(d2+t2)−1≤0(57)

g3=2.0d−1≤0(58)

g4=d14−1≤0(59)

g5=0.2t−1≤0(60)

g6=t0.8−1≤0(61)

Table 20 presents the comparative values of the performances of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, in relation to the tubular column design issue. Furthermore, Table 21 presents the choice factors that are contingent upon the optimal value obtained from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 20, it becomes evident that EO, MFO, COOT, POA, and CA exhibit superiority over other ways in terms of the best value. Furthermore, when evaluated based on the average value, EO, MFO, POA, and CA demonstrate greater success. Furthermore, Fig. 17 displays the convergence graph of the strategies used in solving the tubular column design issue.

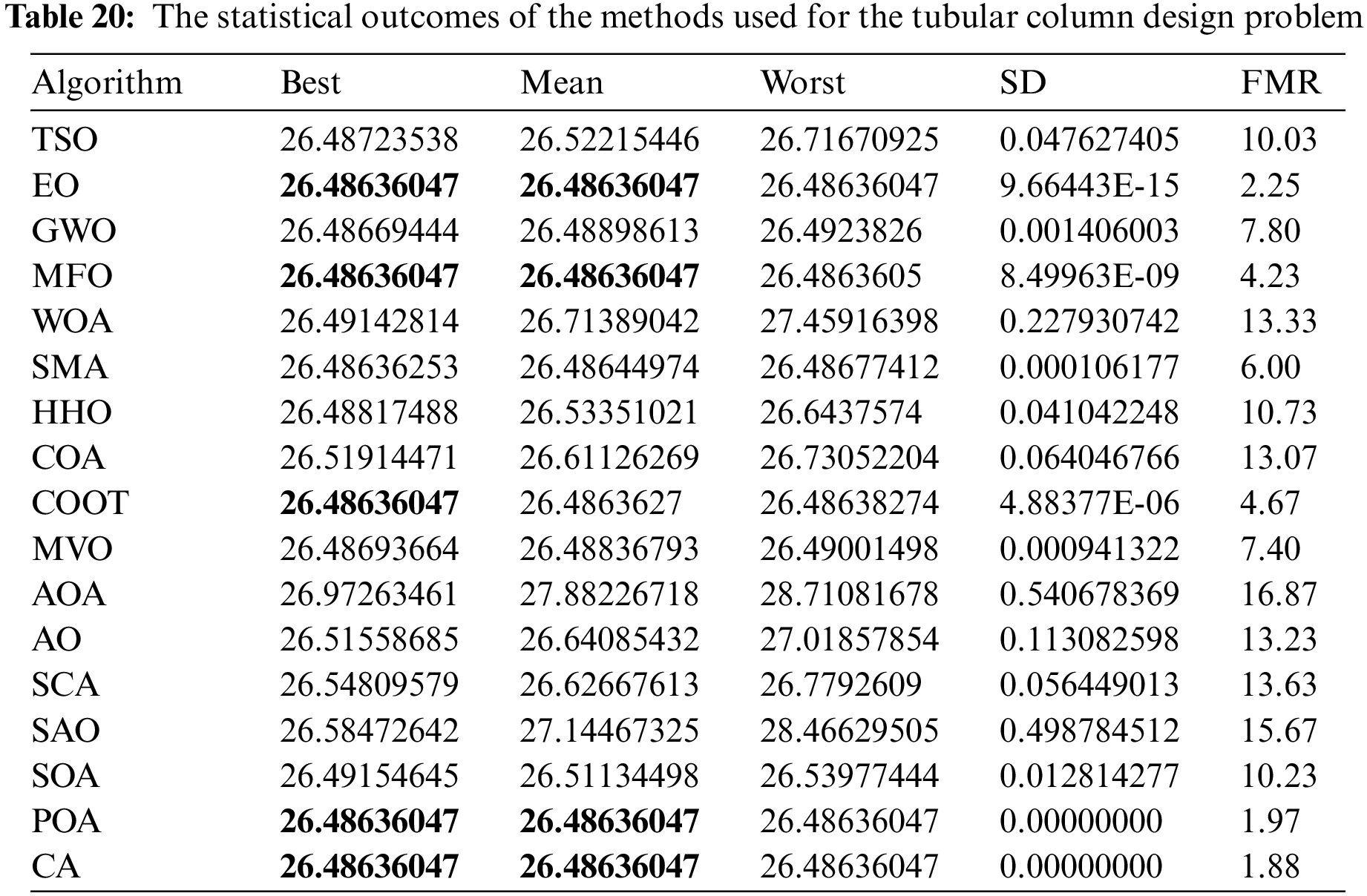
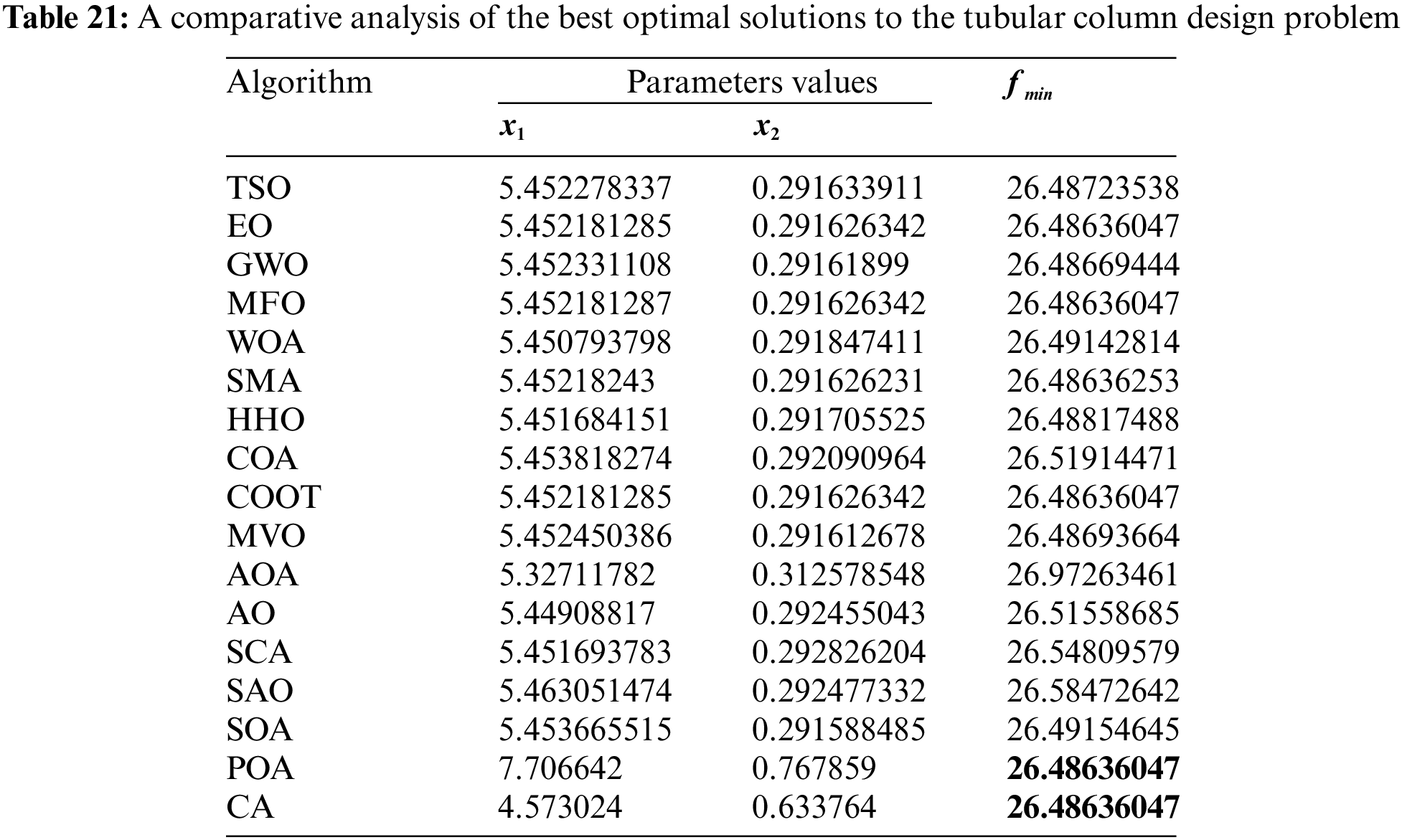
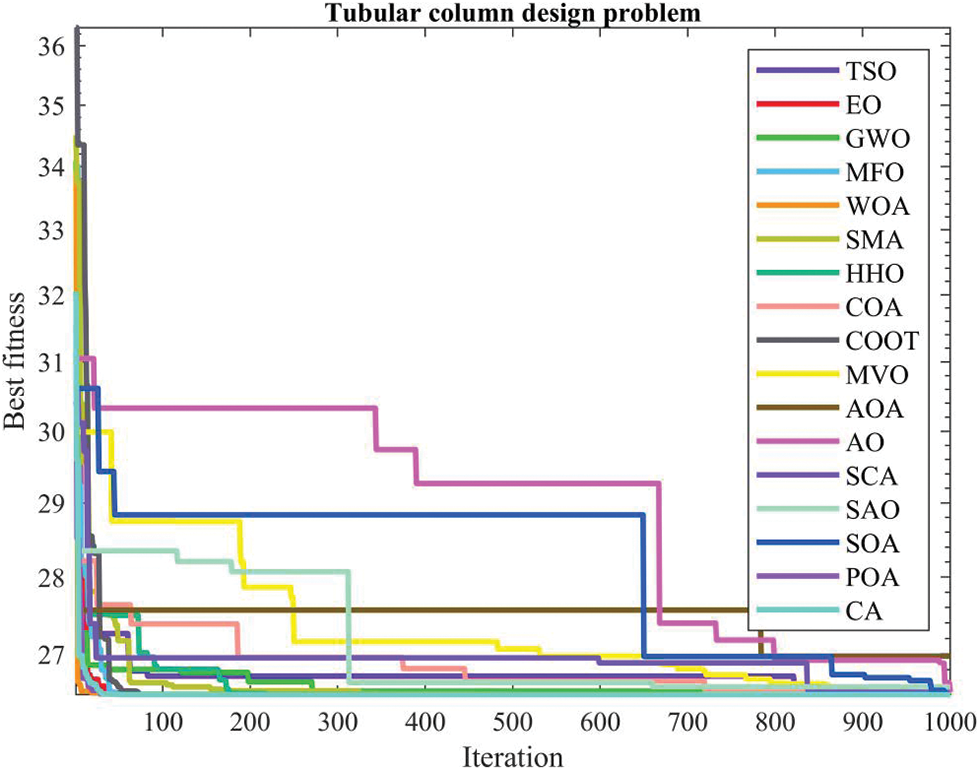
Figure 17: Convergence curve of the methods used on the tubular column design problem

4.10 Piston Lever

Piston lever problem was first raised by Vanderplaats [60]. When the piston lever is raised from 0 to 45 degrees, the main objective is to position the piston components H(x1), B(x2), D(x3), and X(x4) by limiting the oil volume, as shown in Fig. 18. The mathematical representation of this problem is as follows:

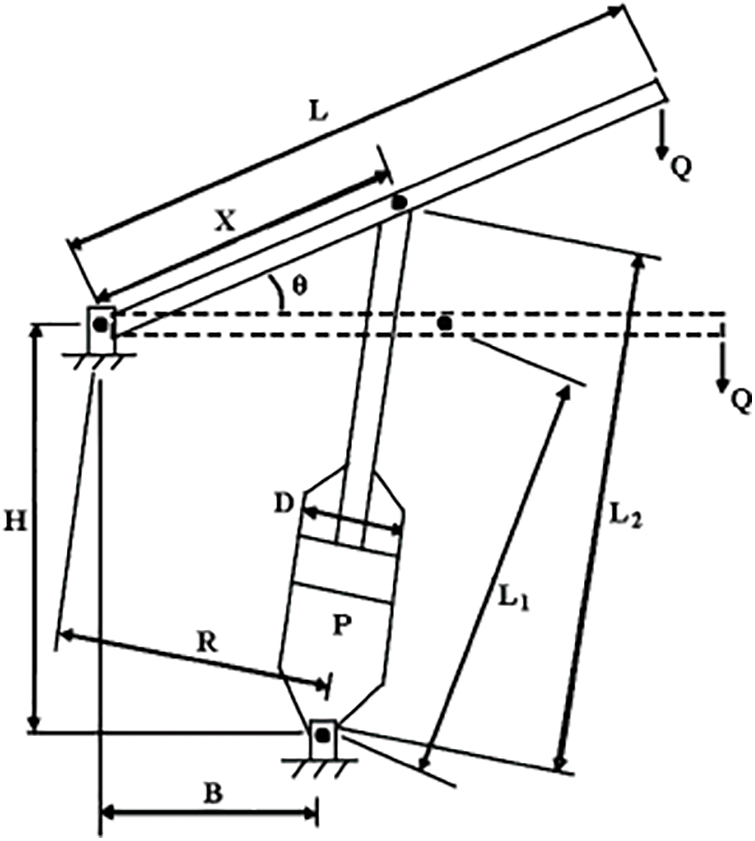
Figure 18: Piston lever

Minimize:

f(H,B,D,X)=14πD2(L2−L1)(62)

Subject to:

g1=QLcosθ−RF≤0 at θ=45∘(63)

g2=Q(L−X)−Mmax≤0(64)

g1=1.2(L2−L1)−L1≤0(65)

g1=D2−B≤0(66)

where,

R=|−X(Xsinθ+H)+H(B−Xcosθ)|(X−B)2+H2,F=πPD2/4,L1=(X−B)2+H2,L2=(Xsin45+H)2+(B−Xcos45)2

The payload is given as P=10.000 lbs, the lever is given as L=240 in, the maximum allowable bending moment of the lever is given as 6 max M=1.8×10 lbs.in, and the oil pressure is given as 1500 psi. Inequality limitations are enforced in a number of ways. Maximum bending moment of the lever, force equilibrium, geometrical conditions, and minimum piston stroke are all taken into account.

Table 22 presents the comparative performance values of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the piston lever issue. Furthermore, Table 23 presents the choice factors that are contingent upon the optimal value derived from the outcomes of 30 iterations conducted on this particular issue using the employed methodologies. Upon examination of Table 22, it becomes evident that EO, MFO, POA, and CA exhibit superiority over other approaches in terms of the greatest value. Conversely, COA demonstrates more success when evaluated based on the average value. Furthermore, Fig. 19 illustrates the convergence graph of the approaches used for the piston lever issue.

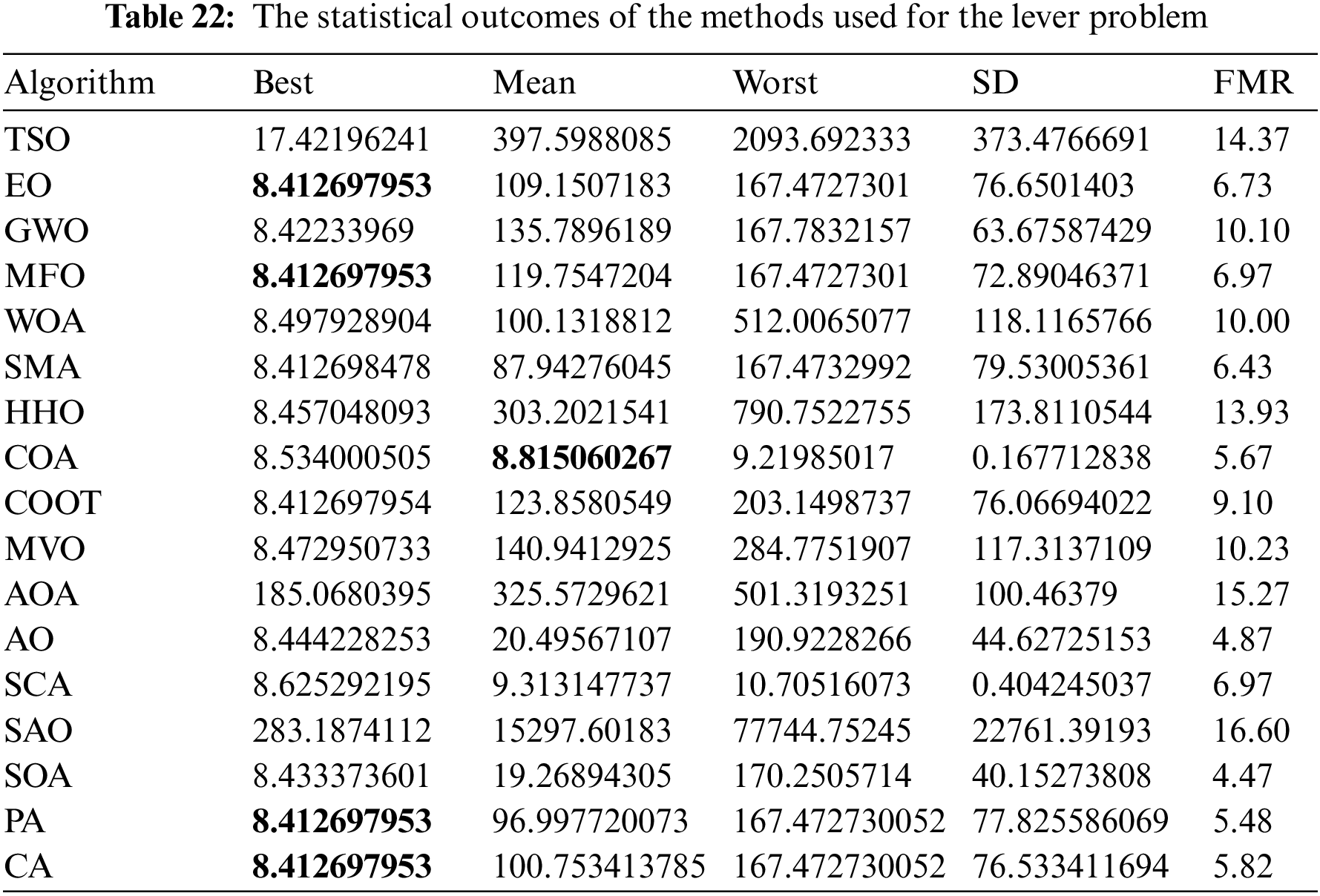
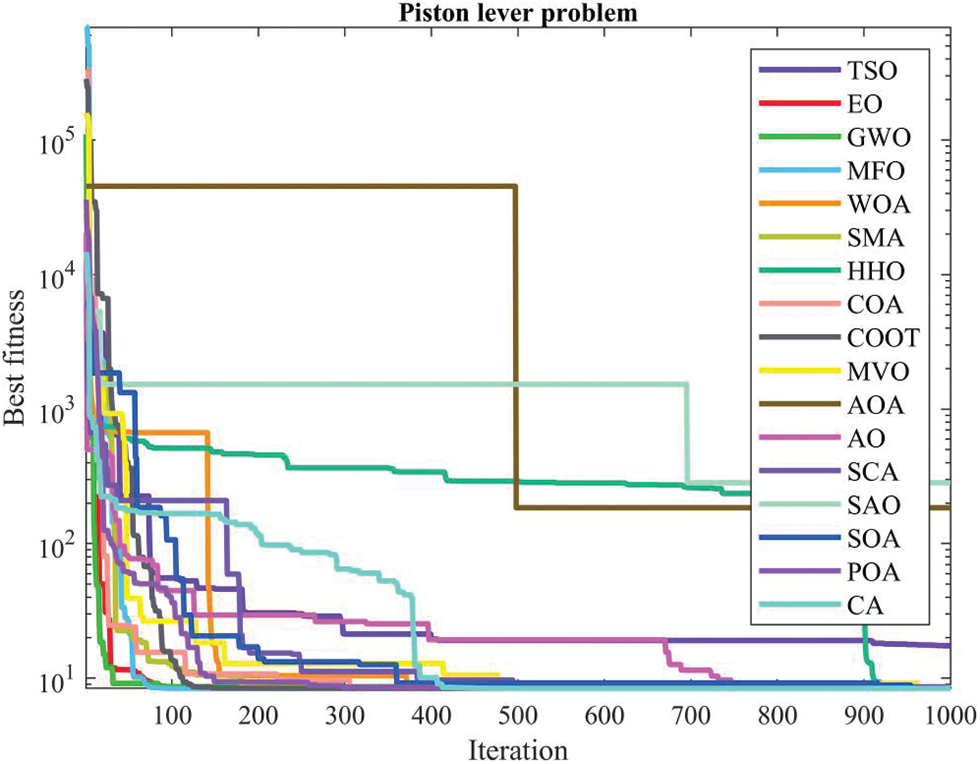
Figure 19: Convergence curve of the methods used on the piston lever

4.11 Robot Gripper

The difference between the robot gripper’s minimum and maximum force is used as an objective function in this challenge. The robot is involved in this challenge, which has six nonlinear design constraints and seven design variables [41]. The schematic representation of the problem is shown in Fig. 20. This problem is mathematically defined as follows:

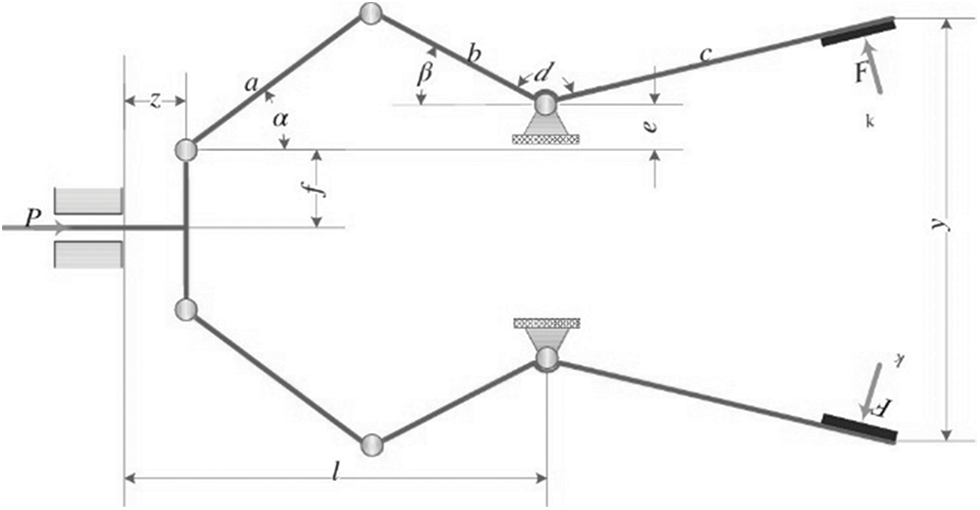
Figure 20: Robot gripper

Minimize:

f(x)=|maxFk(x,z)−minFk(x,z)|(67)

Subject to:

g1(x)=y(x,zmax)−Ymin≤0(68)

g2(x)=−y(x,zmax)≤0(69)

g3(x)=Ymax−y(x,0)≤0(70)

g4(x)=y(x,0)−YG≤0(71)

g5(x)=l2+e2−(a+b)2≤0(72)

g6(x)=b2−(a−e)2−(l−zmax)2≤0(73)

g7(x)=zmax−l≤0

where,

a=cos−1(a2+g2−b22a×g)+θ,g=e2+(z−l)2,θ=tan−1(el−z),

β=cos−1(b2+g2−a22b×g)−θ,y(x,z)=2(f+e+c×sin⁡(β+δ))

Fk=(b×p×sin⁡(a+β)2c×cos⁡(a)),Ymin=50,Ymax=100,YG=150,zmax=100,P=100

with bounds:

10≤f,a,b≤150,0≤e≤50,100≤c≤200,100≤l≤300,1≤β≤3.14

Table 24 presents the comparative values of the performances of several approaches, namely TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA, on the robot gripper issue. Furthermore, Table 25 presents the decision variables associated with the optimal values obtained from the outcomes of 30 iterations conducted on this particular topic. Upon examination of Table 25, it becomes evident that the Simple Moving Average (SMA) approach outperforms other methods in terms of both the best value and the average value. Furthermore, Fig. 21 illustrates the convergence graph of the strategies used in addressing the robot gripper issue.

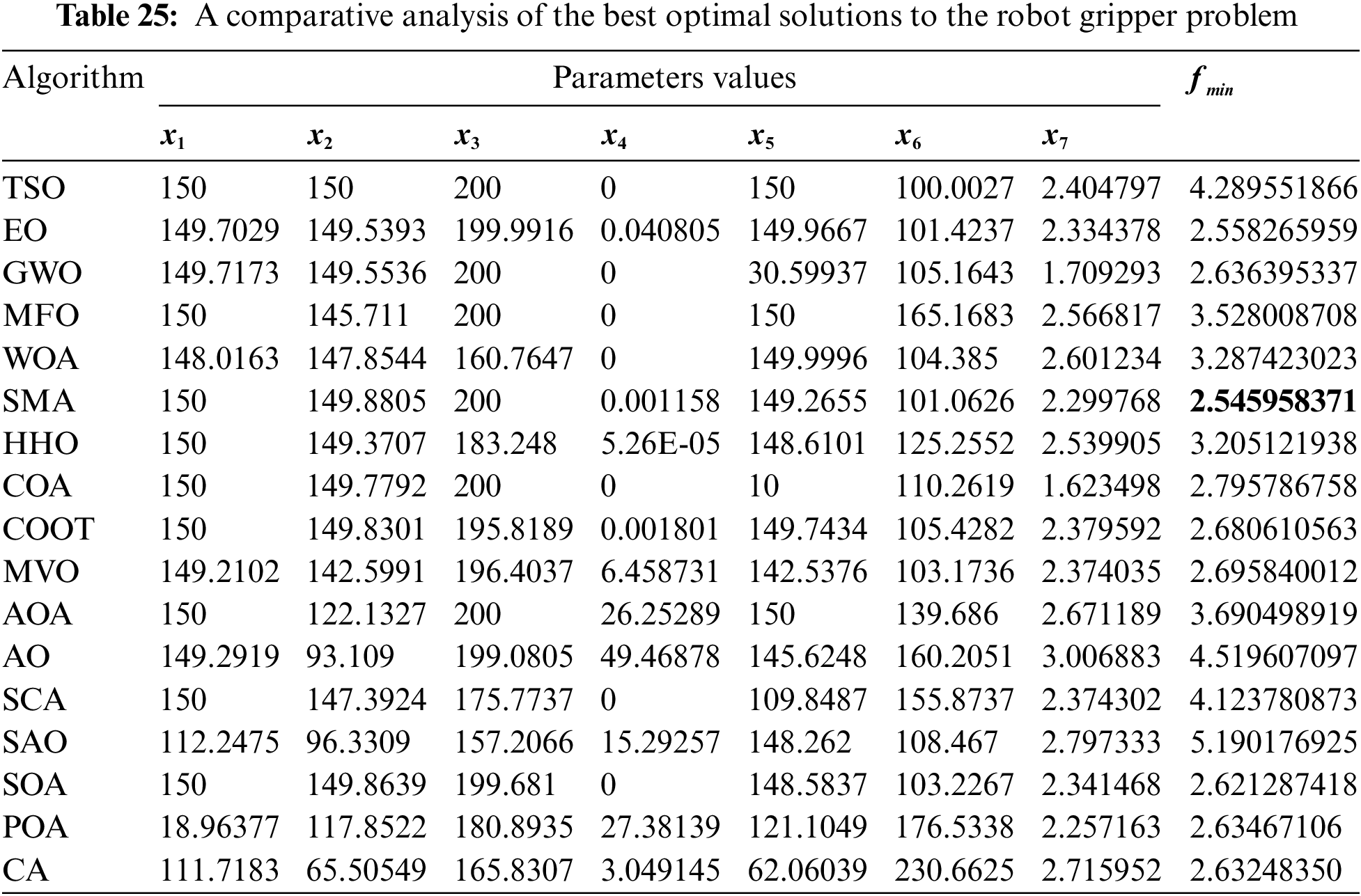
Figure 21: Convergence curve of the methods used on the robot gripper problem

4.12 Corrugated Bulkhead Design Problem

Corrugated bulkhead designs are frequently employed in chemical tankers and product tankers in order to aid in the efficient cleaning of cargo tanks at the loading dock [61]. This problem serves as an illustration of how to construct corrugated bulkheads for a tanker to be as light as possible while maintaining structural integrity. A tanker’s corrugated bulkheads are designed to be as light as possible while maintaining their structural integrity. The problem has four design variables: width b (x1), depth h (x2), length l (x3), and plate thickness t (x4). The mathematical formula for the optimization problem is as follows:

Minimize:

f(b,h,l,t)=5.885t(b+l)b+(l2−h2)(74)

Subject to:

g1=th(0.4b+16)−8.94(b+(l2−h2))≥0(75)

g2=th2(0.2b+112)−2.2(8.94(b+(l2−h2)))43≥0(76)

g3=t−0.0156b−0.15≥0(77)

g4=t−0.0156l−0.15≥0(78)

g5=t−1.15≥0(79)

g6=l−h≥0(80)

with bounds:

0≤b,h,l≤100and0≤t≤5

Table 26 presents the comparative values of the performances of several approaches (TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA) on the corrugated bulkhead design issue. Furthermore, Table 27 presents the decision variables associated with the optimal values obtained from the outcomes of 30 iterations conducted on this particular topic. Upon examination of Table 26, it becomes evident that EO, MFO, and CA exhibit superiority over other ways in terms of the best value. Additionally, when considering the average value, EO emerges as the more effective approach. Furthermore, Fig. 22 illustrates the convergence graph of the strategies used in addressing the corrugated bulkhead design issue.

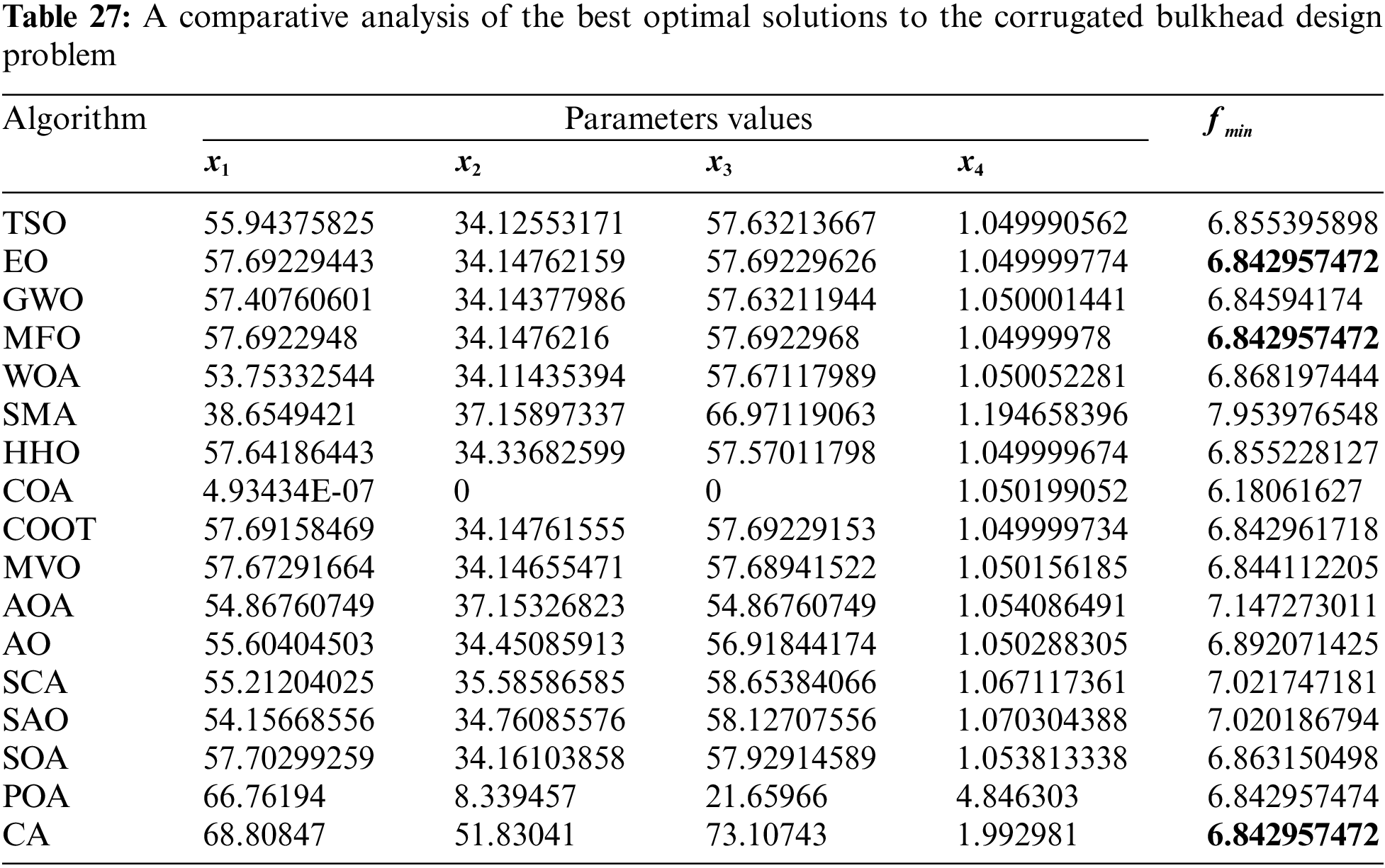
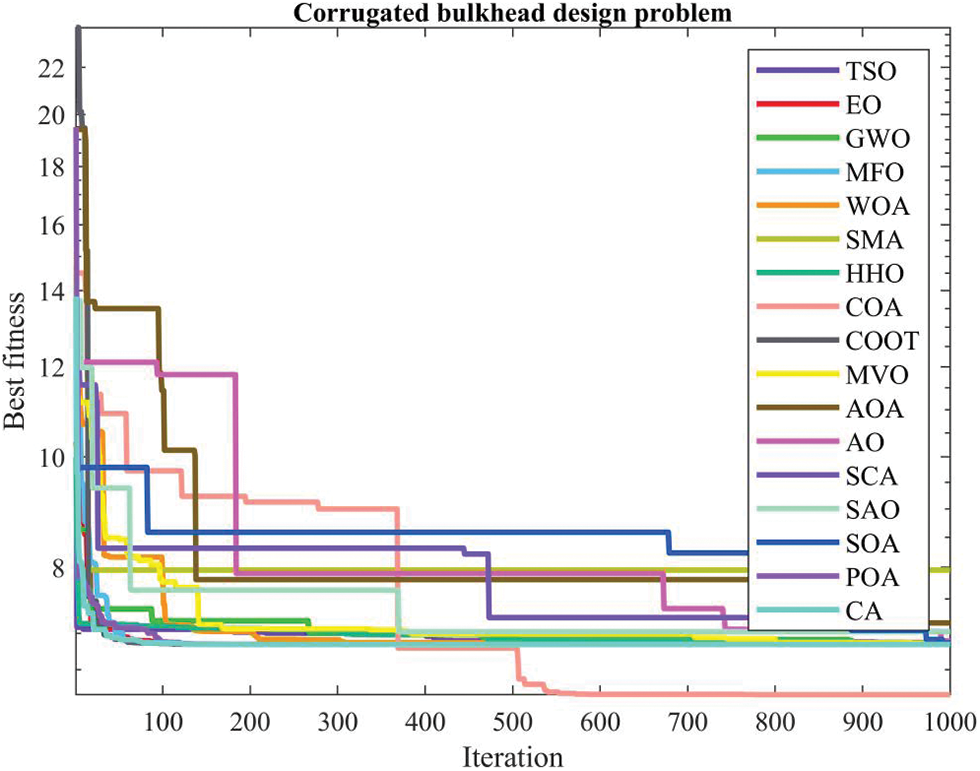
Figure 22: Convergence curve of the methods used on the corrugated bulkhead design problem

5  Discussions

This study introduces the investigation of 17 different metaheuristic optimization algorithms, which have been proposed in recent years and are popular in the literature, on 12 real-world engineering problems. In this study, an external penalty is imposed on algorithms that are used to cope with inequality and equality constraints when they are implemented. Although the use of such a method is relatively straightforward, determining the optimal values of penalty terms, particularly for optimization problems with a high number of constraints, proves to be a challenging optimization issue in and of itself.

According to the experimental results, CA produced the best optimum value in 10 problems, EO in 9 problems, and POA and MFO in 6 problems. Following these, COOT managed to produce the best optimum value in 4 problems and WOA in 3 problems. Although GWO could not find the best optimum value in any of the 12 different engineering problems, statistically, it showed the sixth-best performance among the methods. Furthermore, COOT could not find the mean value in any of the 12 different engineering problems; statistically, it showed the fourth-best performance among the methods. It is thought that statistical analysis has great importance, especially in the comprehensive examination of the performance of metaheuristic optimization methods.

Friedman statistical analysis is performed, and mean ranks are calculated to analyze the results of the investigation. According to these calculated values, the performances of metaheuristic optimization methods in all problems are presented in Table 28 by taking the average value. It is clear from the comparative results presented in the subheadings of Section 3 that the POA technique exhibits a distinct advantage over other algorithms. When the obtained results are examined in more detail, EO performed better in 5 of the 12 problems, CA in 4, and POA in 3 of them. It is also seen that the POA method is significantly superior to other methods statistically when Table 28 is examined. POA is followed by CA, EO, and COOT. SAO, AOA, and TSO are the methods with the worst performance among the methods compared. In light of the results obtained, it can be said that CA has the fastest convergence rate among the 17 different metaheuristic optimization methods used in the study and also has the best balance between exploration and exploitation stages.

The research conducted a rigorous analysis by using the Wilcoxon signed-rank test, a non-parametric statistical test, to provide a robust comparison between the suggested and competing algorithms and to provide statistical validation for the findings obtained. The statistical analyses at a significance level of 5% are shown in Table 29 using the Wilcoxon signed-rank test and the objective function values. While performing the Wilcoxon signed rank test, statistical analyses were performed based on the method that was found to be the best according to the Friedman mean rank value. According to the FMR value, out of 12 different problems, EO in 4, POA in 3, CA in 3, SMA in 1, and SOA in 1 problem achieved the best results. In light of these results, the results obtained in real-world engineering problems according to the Wilcoxon signed rank test are given in Table 29. △ indicates that the first method, based on the FMR value, is substantially superior to the other competitive methods, whereas ≈ indicates that its performance is negligible. - indicates the method that gives the best result according to the FMR value.

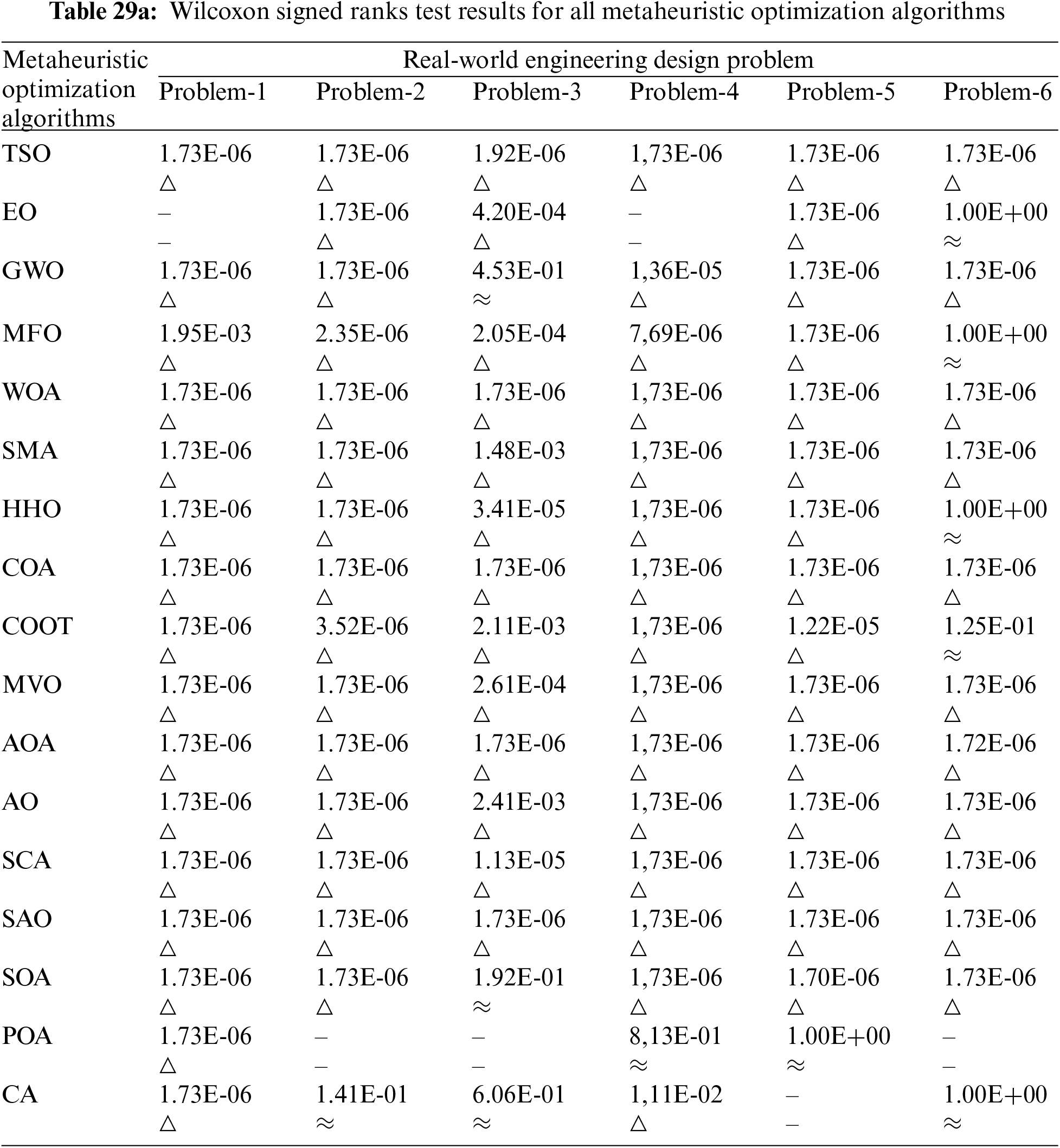
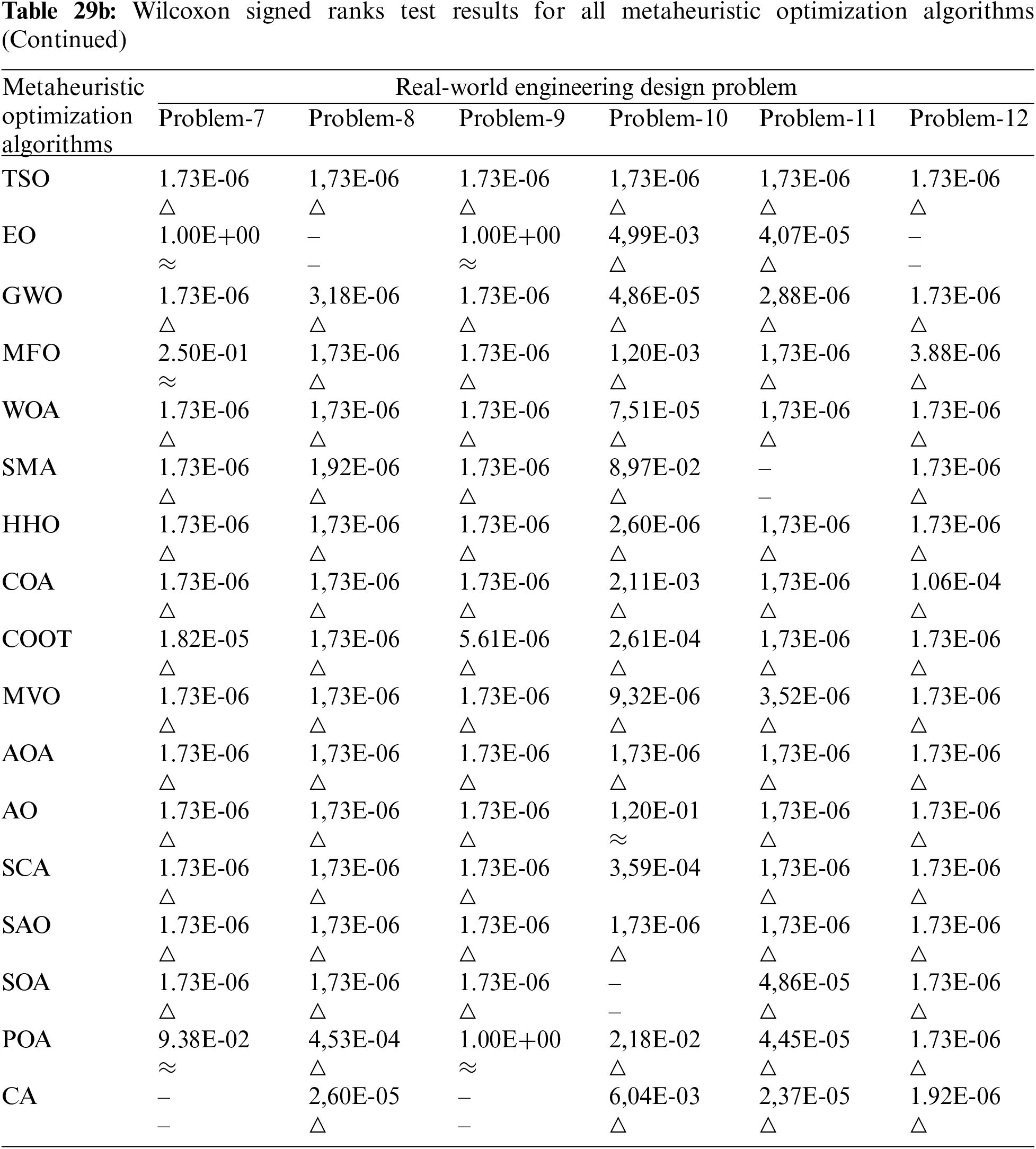
When Table 29 is examined, the EO method, which achieved the best result according to the FMR value in the speed reducer problem (Problem-1), provided a significant superiority to all methods compared to the Wilcoxon signed rank test. POA, which gave the best result according to the FMR value in the tension-compression spring design problem (Problem-2), could not provide a significant superiority to the CA method compared to the Wilcoxon signed rank test, but it outperformed all other methods. The POA method, which gave the best result according to the FMR value in the pressure vessel design problem (Problem-3), provided a significant superiority over the Wilcoxon signed rank test for all methods except GWO, SOA, and CA. The EO method, which gave the best result according to the FMR value in the welded beam design problem (Problem-4), provided a significant superiority to all other methods except POA compared to the Wilcoxon signed rank test. In the three-bar truss design problem (Problem-5), the CA method, which gave the best result according to the FMR value, provided a significant superiority to all other methods except POA compared to the Wilcoxon signed rank test. The POA method, which gives the best result according to FMR value in the multiple disc clutch brake design problem (Problem-6), provides a significant superiority over the Wilcoxon signed rank test over all other methods except EO, MFO, HHO, COOT, and CA. The CA method, which gave the best result according to the FMR value in Himmelblau’s Function (Problem-7), provided a significant superiority over the Wilcoxon signed rank test over all other methods except EO, MFO, and POA. In the cantilever beam problem (Problem-8), the EO method, which gave the best result according to the FMR value, provided a significant superiority to all methods compared to the Wilcoxon signed rank test. In the tubular column design problem (Problem-9), the CA method, which gave the best result according to the FMR value, provided a significant superiority to all other methods except EO and POA compared to the Wilcoxon signed rank test. The SOA method, which gave the best result according to the FMR value in the piston lever (Problem-10), provided a significant superiority to all other methods except AO compared to the Wilcoxon signed rank test. The SMA method, which gave the best result according to the FMR value in the robot gripper (Problem-11), provided a significant superiority to all methods compared to the Wilcoxon signed rank test. The EO method, which gave the best result according to the FMR value in the corrugated bulkhead design problem (Problem-12), provided a significant superiority to all methods compared to the Wilcoxon signed rank test.

As a result, in the study conducted, EO and POA in 7 different problems, CA in 6 different problems, SOA and MFO in 2 different problems, and GWO, HHO, COOT, and SMA in 1 different problem showed the most successful results, or the method showing the most successful results could not provide a significant superiority to these methods.

6  Conclusion

The efficient resolution of real-world engineering design optimization issues is widely acknowledged as a significant difficulty for any new metaheuristic algorithm presented to the market. Moreover, these issues include several goals and diverse variables, including integers, continuous values, and discrete elements. Additionally, they involve a range of nonlinear restrictions related to kinematic conditions, performance parameters, operational situations, and manufacturing specifications, among others. The TSO, EO, GWO, MFO, WOA, SMA, HHO, COA, COOT, MVO, AOA, AO, SCA, SAO, SOA, POA, and CA algorithms are used to address design optimization of twelve real-world engineering issues. Accordingly, their performances are compared considering the quality of solution, robustness, and convergence speed of the solutions obtained by various approaches. The outcomes reveal that EO and POA produce better optimized results against other available techniques. However, the results of statistical comparisons show that EO and POA achieve more competitive and better performance outcomes among most of the constraint problems investigated. In addition, as a consequence of the statistical examination, it was reported that the CA approach is at a level that can compete with these two methods.

This study discusses the most important subjects in engineering and artificial intelligence disciplines. Future research confidently relies on this review to investigate metaheuristic optimization approaches and engineering design challenges in greater depth in the near future. Moreover, by examining the studies in question, the researchers can more easily identify a beginning point for future researchers.

Acknowledgement: The authors thank Manisa Celal Bayar University for the use of the laboratories in the Department of Software Engineering. Especially, the devices in the laboratory established by Manisa Celal Bayar University—Scientific Research Projects Coordination Unit (MCBU–SRPCU) with Project Code 2022-134 were utilized in the study.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Elif Varol Altay, Osman Altay; data collection: Elif Varol Altay; analysis and interpretation of results: Elif Varol Altay, Osman Altay, Yusuf Özçevik; draft manuscript preparation: Osman Altay, Yusuf Özçevik. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated and analyzed throughout the research process are given in the published article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Rao, S. S. (2019). Engineering optimization: Theory and practice. USA: John Wiley & Sons. [Google Scholar]

2. Garg, H. (2016). A hybrid PSO-GA algorithm for constrained optimization problems. Applied Mathematics and Computation, 274(5), 292–305. https://doi.org/10.1016/j.amc.2015.11.001 [Google Scholar] [CrossRef]

3. Varol Altay, E., Altay, O. (2021). Güncel metasezgisel optimizasyon algoritmalarının CEC2020 test fonksiyonları ile karşılaştırılması. Dicle Üniversitesi Mühendislik Fakültesi Mühendislik Dergisi, 5, 729–741. https://doi.org/10.24012/dumf.1051338 [Google Scholar] [CrossRef]

4. Sra, S., Nowozin, S., Wright, S. J. (2012). Optimization for machine learning. England: Mit Press. [Google Scholar]

5. Varol Altay, E., Alatas, B. (2020). Bird swarm algorithms with chaotic mapping. Artificial Intelligence Review, 53(2), 1373–1414. https://doi.org/10.1007/s10462-019-09704-9 [Google Scholar] [CrossRef]

6. Połap, D., Woźniak, M. (2021). Red fox optimization algorithm. Expert Systems with Applications, 166(10), 114107. https://doi.org/10.1016/j.eswa.2020.114107 [Google Scholar] [CrossRef]

7. Dehghani, M., Hubálovský, Š., Trojovský, P. (2021). Cat and mouse based optimizer: A new nature-inspired optimization algorithm. Sensors, 21(15), 1–30. https://doi.org/10.3390/s21155214 [Google Scholar] [PubMed] [CrossRef]

8. Trojovský, P., Dehghani, M., Hanuš, P. (2022). Siberian tiger optimization: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. IEEE Access, 10, 132396–132431. https://doi.org/10.1109/ACCESS.2022.3229964 [Google Scholar] [CrossRef]

9. Agushaka, J. O., Ezugwu, A. E., Abualigah, L. (2022). Dwarf mongoose optimization algorithm. Computer Methods in Applied Mechanics and Engineering, 391(10), 114570. https://doi.org/10.1016/j.cma.2022.114570 [Google Scholar] [CrossRef]

10. Khishe, M., Mosavi, M. R. (2020). Chimp optimization algorithm. Expert Systems with Applications, 149(1), 113338. https://doi.org/10.1016/j.eswa.2020.113338 [Google Scholar] [CrossRef]

11. Bairwa, A. K., Joshi, S., Singh, D. (2021). Dingo optimizer: A nature-inspired metaheuristic approach for engineering problems. Mathematical Problems in Engineering, 1–12. https://doi.org/10.1155/2021/2571863 [Google Scholar] [CrossRef]

12. Wang, Z. H., Liu, J. H. (2021). Flamingo search algorithm: A new swarm intelligence optimization algorithm. IEEE Access, 9, 88564–88582. https://doi.org/10.1109/ACCESS.2021.3090512 [Google Scholar] [CrossRef]

13. Jiang, Y., Wu, Q., Zhu, S., Zhang, L. (2022). Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems. Expert Systems with Applications, 188(4), 116026. https://doi.org/10.1016/j.eswa.2021.116026 [Google Scholar] [CrossRef]

14. Hashim, F. A., Houssein, E. H., Mabrouk, M. S., Al-Atabany, W., Mirjalili, S. (2019). Henry gas solubility optimization: A novel physics-based algorithm. Future Generation Computer Systems, 101(4), 646–667. https://doi.org/10.1016/j.future.2019.07.015 [Google Scholar] [CrossRef]

15. Hashim, F. A., Hussain, K., Houssein, E. H., Mabrouk, M. S., Al-Atabany, W. (2021). Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Applied Intelligence, 51(3), 1531–1551. https://doi.org/10.1007/s10489-020-01893-z [Google Scholar] [CrossRef]

16. Mirjalili, S., Mirjalili, S. M., Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495–513. https://doi.org/10.1007/s00521-015-1870-7 [Google Scholar] [CrossRef]

17. Faramarzi, A., Heidarinejad, M., Stephens, B., Mirjalili, S. (2020). Equilibrium optimizer: A novel optimization algorithm. Knowledge-Based Systems, 191, 105190. https://doi.org/10.1016/j.knosys.2019.105190 [Google Scholar] [CrossRef]

18. Qais, M. H., Hasanien, H. M., Alghuwainem, S. (2020). Transient search optimization: A new meta-heuristic optimization algorithm. Applied Intelligence, 50, 3926–3941. https://doi.org/10.1007/s10489-020-01727-y [Google Scholar] [CrossRef]

19. Razmjooy, N., Khalilpour, M., Ramezani, M. (2016). A new meta-heuristic optimization algorithm inspired by FIFA world cup competitions: Theory and its application in PID designing for AVR system. Journal of Control, Automation and Electrical Systems, 27, 419–440. https://doi.org/10.1007/s40313-016-0242-6 [Google Scholar] [CrossRef]

20. Husseinzadeh Kashan, A. (2014). League championship algorithm (LCAAn algorithm for global optimization inspired by sport championships. Applied Soft Computing, 16, 171–200. https://doi.org/10.1016/j.asoc.2013.12.005 [Google Scholar] [CrossRef]

21. Doumari, S. A., Givi, H., Dehghani, M., Malik, O. P. (2021). Ring toss game-based optimization algorithm for solving various optimization problems. International Journal of Intelligent Engineering & Systems, 14(3), 545–554. https://doi.org/10.22266/ijies2021.0630.46 [Google Scholar] [CrossRef]

22. Dehghani, M., Montazeri, Z., Givi, H., Guerrero, J. M., Dhiman, G. (2020). Darts game optimizer: A new optimization technique based on darts game. International Journal of Intelligent Engineering and Systems, 13(5), 286–294. https://doi.org/10.22266/ijies2020.1031.26 [Google Scholar] [CrossRef]

23. Chou, J. S., Nguyen, N. M. (2020). FBI inspired meta-optimization. Applied Soft Computing, 93, 106339. https://doi.org/10.1016/j.asoc.2020.106339 [Google Scholar] [CrossRef]

24. Askari, Q., Younas, I., Saeed, M. (2020). Political optimizer: A novel socio-inspired meta-heuristic for global optimization. Knowledge-Based Systems, 195(5), 105709. https://doi.org/10.1016/j.knosys.2020.105709 [Google Scholar] [CrossRef]

25. Ghasemian, H., Ghasemian, F., Vahdat-Nejad, H. (2020). Human urbanization algorithm: A novel metaheuristic approach. Mathematics and Computers in Simulation, 178(1), 1–15. https://doi.org/10.1016/j.matcom.2020.05.023 [Google Scholar] [CrossRef]

26. Dehghani, M., Trojovský, P. (2021). Teamwork optimization algorithm: A new optimization approach for function minimization/maximization. Sensors, 21(13), 4567. https://doi.org/10.3390/s21134567 [Google Scholar] [PubMed] [CrossRef]

27. Eskandar, H., Sadollah, A., Bahreininejad, A., Hamdi, M. (2012). Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Computers & Structures, 110(1), 151–166. https://doi.org/10.1016/j.compstruc.2012.07.010 [Google Scholar] [CrossRef]

28. Gandomi, A. H., Yang, X. S., Alavi, A. H. (2013). Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Engineering with Computers, 29(1), 17–35. https://doi.org/10.1007/s00366-011-0241-y [Google Scholar] [CrossRef]

29. Mirjalili, S., Mirjalili, S. M., Lewis, A. (2014). Grey wolf optimizer. Advances in Engineering Software, 69, 46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007 [Google Scholar] [CrossRef]

30. Mirjalili, S., Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95(12), 51–67. https://doi.org/10.1016/j.advengsoft.2016.01.008 [Google Scholar] [CrossRef]

31. Askarzadeh, A. (2016). A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Computers & Structures, 169(2), 1–12. https://doi.org/10.1016/j.compstruc.2016.03.001 [Google Scholar] [CrossRef]

32. Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H. et al. (2017). Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software, 114, 163–191. https://doi.org/10.1016/j.advengsoft.2017.07.002 [Google Scholar] [CrossRef]

33. Dhiman, G., Kaur, A. (2017). Spotted hyena optimizer for solving engineering design problems. Proceedings of 2017 International Conference on Machine Learning and Data Science (MLDS), pp. 114–119. Noida, India. https://doi.org/10.1109/MLDS.2017.5 [Google Scholar] [CrossRef]

34. Ferreira, M. P., Rocha, M. L., Silva Neto, A. J., Sacco, W. F. (2018). A constrained ITGO heuristic applied to engineering optimization. Expert Systems with Applications, 110(1), 106–124. https://doi.org/10.1016/j.eswa.2018.05.027 [Google Scholar] [CrossRef]

35. Tawhid, M. A., Savsani, V. (2018). A novel multi-objective optimization algorithm based on artificial algae for multi-objective engineering design problems. Applied Intelligence, 48(10), 3762–3781. https://doi.org/10.1007/s10489-018-1170-x [Google Scholar] [CrossRef]

36. Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M. et al. (2019). Harris hawks optimization: Algorithm and applications. Future Generation Computer Systems, 97, 849–872. https://doi.org/10.1016/j.future.2019.02.028 [Google Scholar] [CrossRef]

37. Dhiman, G., Kumar, V. (2019). Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowledge-Based Systems, 165(25), 169–196. https://doi.org/10.1016/j.knosys.2018.11.024 [Google Scholar] [CrossRef]

38. Arora, S., Singh, S. (2019). Butterfly optimization algorithm: A novel approach for global optimization. Soft Computing, 23(3), 715–734. https://doi.org/10.1007/s00500-018-3102-4 [Google Scholar] [CrossRef]

39. Faramarzi, A., Heidarinejad, M., Mirjalili, S., Gandomi, A. H. (2020). Marine predators algorithm: A nature-inspired metaheuristic. Expert Systems with Applications, 152(4), 113377. https://doi.org/10.1016/j.eswa.2020.113377 [Google Scholar] [CrossRef]

40. Li, S., Chen, H., Wang, M., Heidari, A. A., Mirjalili, S. (2020). Slime mould algorithm: A new method for stochastic optimization. Future Generation Computer Systems, 111, 300–323. https://doi.org/10.1016/j.future.2020.03.055 [Google Scholar] [CrossRef]

41. Yildiz, B. S., Pholdee, N., Bureerat, S., Yildiz, A. R., Sait, S. M. (2021). Robust design of a robot gripper mechanism using new hybrid grasshopper optimization algorithm. Expert Systems, 38(3), e12666. https://doi.org/10.1111/exsy.12666 [Google Scholar] [CrossRef]

42. Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., Gandomi, A. H. (2021). The arithmetic optimization algorithm. Computer Methods in Applied Mechanics and Engineering, 376(2), 113609. https://doi.org/10.1016/j.cma.2020.113609 [Google Scholar] [CrossRef]

43. Abualigah, L., Yousri, D., Abd Elaziz, M., Ewees, A. A., Al-Qaness, M. A. et al. (2021). Aquila optimizer: A novel meta-heuristic optimization algorithm. Computers & Industrial Engineering, 157(11), 107250. https://doi.org/10.1016/j.cie.2021.107250 [Google Scholar] [CrossRef]

44. Yildiz, B. S., Pholdee, N., Bureerat, S., Yildiz, A. R., Sait, S. M. (2022). Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems. Engineering with Computers, 38(5), 4207–4219. https://doi.org/10.1007/s00366-021-01368-w [Google Scholar] [CrossRef]

45. Yıldız, B. S., Kumar, S., Pholdee, N., Bureerat, S., Sait, S. M. et al. (2022). A new chaotic Lévy flight distribution optimization algorithm for solving constrained engineering problems. Expert Systems, 39(8), e12992. https://doi.org/10.1111/exsy.12992 [Google Scholar] [CrossRef]

46. Trojovský, P., Dehghani, M. (2022). Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors, 22(3), 855. https://doi.org/10.3390/s22030855 [Google Scholar] [PubMed] [CrossRef]

47. Dehghani, M., Montazeri, Z., Trojovská, E., Trojovský, P. (2023). Coati optimization algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowledge-Based Systems, 259(1), 110011. https://doi.org/10.1016/j.knosys.2022.110011 [Google Scholar] [CrossRef]

48. Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Systems, 89, 228–249. https://doi.org/10.1016/j.knosys.2015.07.006 [Google Scholar] [CrossRef]

49. Altay, O. (2022). Chaotic slime mould optimization algorithm for global optimization. Artificial Intelligence Review, 55(5), 3979–4040. https://doi.org/10.1007/s10462-021-10100-5 [Google Scholar] [CrossRef]

50. Naruei, I., Keynia, F. (2021). A new optimization method based on COOT bird natural life model. Expert Systems with Applications, 183(2), 115352. https://doi.org/10.1016/j.eswa.2021.115352 [Google Scholar] [CrossRef]

51. Mirjalili, S. (2016). SCA: A sine cosine algorithm for solving optimization problems. Knowledge-Based Systems, 96(63), 120–133. https://doi.org/10.1016/j.knosys.2015.12.022 [Google Scholar] [CrossRef]

52. Varol Altay, E., Alatas, B. (2021). Differential evolution and sine cosine algorithm based novel hybrid multi-objective approaches for numerical association rule mining. Information Sciences, 554(10), 198–221. https://doi.org/10.1016/j.ins.2020.12.055 [Google Scholar] [CrossRef]

53. Salawudeen, A. T., Mu’azu, M. B., Yusuf, A., Adedokun, A. E. (2021). A novel smell agent optimization (SAOAn extensive CEC study and engineering application. Knowledge-Based Systems, 232(4), 107486. https://doi.org/10.1016/j.knosys.2021.107486 [Google Scholar] [CrossRef]

54. Gandomi, A. H., Deb, K. (2020). Implicit constraints handling for efficient search of feasible solutions. Computer Methods in Applied Mechanics and Engineering, 363(30–33), 112917. https://doi.org/10.1016/j.cma.2020.112917 [Google Scholar] [CrossRef]

55. Zamani, H., Nadimi-Shahraki, M. H., Gandomi, A. H. (2021). QANA: Quantum-based avian navigation optimizer algorithm. Engineering Applications of Artificial Intelligence, 104(989), 104314. https://doi.org/10.1016/j.engappai.2021.104314 [Google Scholar] [CrossRef]

56. Abualigah, L., Elaziz, M. A., Khasawneh, A. M., Alshinwan, M., Ibrahim, R. A. et al. (2022). Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: A comprehensive survey, applications, comparative analysis, and results. Neural Computing and Applications, 1–30. https://doi.org/10.1007/s00521-021-06747-4 [Google Scholar] [CrossRef]

57. Dhiman, G. (2021). ESA: A hybrid bio-inspired metaheuristic optimization approach for engineering problems. Engineering with Computers, 37(1), 323–353. https://doi.org/10.1007/s00366-019-00826-w [Google Scholar] [CrossRef]

58. Arora, J. (2004). Introduction to optimum design. USA: Elsevier. [Google Scholar]

59. He, X., Zhou, Y. (2018). Enhancing the performance of differential evolution with covariance matrix self-adaptation. Applied Soft Computing, 64, 227–243. https://doi.org/10.1016/j.asoc.2017.11.050 [Google Scholar] [CrossRef]

60. Vanderplaats, G. N. (1995). Design optimization tools (DOT) users manual, Version 4.20. Colorado: VR&D. [Google Scholar]

61. Abdel-Baset, M., Hezam, I. (2016). A hybrid flower pollination algorithm for engineering optimization problems. International Journal of Computer Applications, 140(12), 10–23. https://doi.org/10.5120/ijca2016909119 [Google Scholar] [CrossRef]