 Open Access
Open Access
ARTICLE
Einstein Hybrid Structure of q-Rung Orthopair Fuzzy Soft Set and Its Application for Diagnosis of Waterborne Infectious Disease
1 School of Mathematical Sciences, Zhejiang Normal University, Jinhua, 321004, China
2 Department of Mathematics, Government College University, Faisalabad, 38000, Pakistan
3 Department of Mathematics, University of Sargodha, Sargodha, 40100, Pakistan
4 Section of Mathematics, International Telematic University Uninettuno, Corso Vittorio Emanuele II, Roma, 3900186, Italy
5 Near East University, Operational Research Center in Healthcare, Near East Boulevard, Nicosia/Mersin 10, 99138, Turkey
6 Department of Statistics and Operations Research, College of Science, King Saud University, PO Box 2455, Riyadh, 11451, Saudi Arabia
* Corresponding Author: Shahid Hussain Gurmani. Email:
(This article belongs to the Special Issue: Advances in Ambient Intelligence and Social Computing under uncertainty and indeterminacy: From Theory to Applications)
Computer Modeling in Engineering & Sciences 2024, 139(2), 1863-1892. https://doi.org/10.32604/cmes.2023.031480
Received 20 June 2023; Accepted 12 September 2023; Issue published 29 January 2024
Abstract
This research is devoted to diagnosing water-borne infectious diseases caused by floods employing a novel diagnosis approach, the Einstein hybrid structure of q-rung orthopair fuzzy soft set. This approach integrates parts of fuzzy logic and soft set theory to develop a robust alternative for disease detection in stressful situations, especially in areas affected by floods. Compared to the traditional intuitionistic fuzzy soft set and Pythagorean fuzzy soft set, the q-rung orthopair fuzzy soft set (q-ROFSS) adequately incorporates unclear and indeterminate facts. The major objective of this investigation is to formulate the q-rung orthopair fuzzy soft Einstein hybrid weighted average (q-ROFSEHWA) operator and its specific characteristics. Moreover, our stated operator is implementing intelligent multi-criteria group decision-making (MCGDM) methodology. Floods are severe natural catastrophes that raise the risk of diseases and epidemics, particularly those caused by contaminants in the water, such as gastrointestinal diseases, respiratory infections, vector-borne diseases, skin infections, and water-borne parasites. The designed MCGDM strategy tackles the prevalence of certain conditions in flood-affected patients. A comparative investigation determined that the suggested method for detecting water-borne infectious disease due to floods is more effective and productive than conventional methods because of its logical structure.Keywords
Flood is a natural disaster when water overflows its natural or artificial boundaries, such as rivers, lakes, or coastal areas. Floods can cause significant damage to human settlements, infrastructure, and agriculture and can also result in loss of life. Floods can be caused by many factors, including heavy rainfall, melting snow, hurricanes, and storm surges. Flooding can have far-reaching impacts on communities and the environment, including displacement of people, destruction of homes and businesses, loss of crops and livestock, contamination of drinking water, and damage to infrastructure, such as roads, bridges, and utilities. Floods can also lead to long-term economic, social, and environmental impacts, including reduced property values, loss of tourism, and degradation of ecosystems. It is important to be prepared for a flood and take measures to minimize its impacts, such as building flood-resistant structures, having evacuation plans, and being aware of flood warnings and alerts. It is also important to reduce the risk of flooding, such as preserving natural floodplains and wetlands, managing land use, and implementing effective drainage and stormwater management systems. Every nation has systems and infrastructure to direct rainfall into the appropriate basins and reservoirs. When it rains heavily, the water does not drain as rapidly as it should because those systems get overloaded, and water periodically surges into homes, resulting in a flood. Deforestation, lake loss, climate change, and sea level rise are the main aspects of how humans constantly damage the environment, increasing flood intensity and frequency.
Floods can increase the risk of water-borne infections and diseases. Floodwaters containing contaminated water from sewage, agricultural runoff, or hazardous waste sites can pose a significant health risk to those who come into contact with it. Some common water-borne infections and diseases associated with floods include Gastrointestinal infections: Floodwaters can contain bacteria such as Escherichia coli and Salmonella, which can cause stomach cramps, diarrhea, and other gastrointestinal symptoms. Skin infections: Floodwaters can contain bacteria such as Staphylococcus aureus and Streptococcus pyogenes, which can cause skin infections such as impetigo and cellulitis. Vector-borne diseases: Floods can increase the populations of mosquitoes, ticks, and other vectors that can transmit diseases such as the West Nile virus, dengue fever, and Lyme disease. Water-borne diseases: Floodwaters can contain parasites and bacteria such as Giardia lamblia and Cryptosporidium, which can cause water-borne diseases such as giardiasis and cryptosporidiosis. It is important to take precautions to reduce the risk of infection and disease during and after a flood. This includes avoiding contact with floodwaters whenever possible, washing hands frequently with soap and water, and wearing protective clothing and footwear when working in contaminated areas. If you suspect you have been infected with a water-borne disease, seeking medical attention as soon as possible is important. Ahmad et al. [1] described flood-associated risks with the agriculture department in flood-affected Punjab, Pakistan. Ochani et al. [2] illustrated the destruction in different areas of Pakistan after a severe attack flood in 2022 and elaborated on the health-related challenges caused by a flood. Ochani et al. [3] discussed the consequences caused by the flood in Pakistan in 2022 and argued about the effects of the flood on the feed of newborn children and their survival in a humid region.
Multi-criteria group decision-making (MCGDM) can be applied to flood-related infections and diseases to make informed decisions about the severity of certain conditions in patients affected by floods. For example, a group of experts could be assembled to evaluate a patient’s disease severity based on multiple criteria, such as the patient’s symptoms, medical history, and test results. The experts would provide their evaluations of the patient based on these criteria. The results would then be combined using an aggregation operator, such as the q-rung orthopair fuzzy soft Einstein hybrid weighted average (q-ROFSEHWA) operator, to arrive at a final decision about the severity of the disease. In this context, MCGDM can be a useful tool for improving the accuracy and reliability of disease severity assessments. By combining the opinions of multiple experts, MCGDM can account for uncertainty and imprecision in the evaluations and provide a more robust and comprehensive assessment of the disease severity. Furthermore, the use of MCGDM can improve the transparency and fairness of disease severity assessments, as the results of the assessments are based on a systematic and documented process that considers the perspectives and expertise of multiple experts. This can help ensure that decisions are based on the best available information and are made relatively and impartial.
MCGDM is a technique used to determine the best alternative to a decision-making (DM) problem by considering the opinions of a team of experts. This process is based on multiple attributes of the alternatives being considered. The uncertainty and imprecision of information can present challenges in evaluating DM problems. A traditional crisp set, which assigns binary membership values of 0 or 1 to elements, is unsuitable for dealing with such uncertainty. To address this issue, Zadeh [4] introduced the concept of fuzzy sets (FS), which assigns membership values in the range of [0,1] to elements based on their properties. Ulucay [5] developed a novel similarity measure for trapezoidal fuzzy multi-numbers to resolve multi-criteria DM complications. FS allows for considering values between 0 and 1, providing a more flexible and comprehensive approach to evaluating DM problems that involve ambiguous information. There were limitations to the original concept of FS, as they only described elements’ membership degree (MD). To address these limitations, Atanassov [6] proposed the intuitionistic fuzzy set (IFS), which considers both MD and non-membership degrees (NMD). The linear relationship between MD and NMD ensures that the sum of the two does not exceed 1, and both belong to the range of [0,1]. Xu [7] introduced aggregation operators (AOs) for IFS and explored their fundamental properties. Wang et al. [8] extended this work by applying Einstein operational laws to IFS and developing Einstein AOs and weighted AOs for IFS. Similarly, Xu et al. [9] further expanded upon this by introducing geometric AOs for IFS and using them in evaluating DM problems. Zhao et al. [10] used the Einstein operational laws to develop Einstein hybrid AOs and applied them to multi-attribute decision-making (MADM) problems. Zeng et al. [11] applied these hybrid AOs in the digitalization of the manufacturing industry.
Pythagorean fuzzy sets (PFS) were introduced by Yager [12] to address the limitations of both FS and IFS. PFS is a generalization of IFS and can capture more complex and nuanced relationships between MD and NMD. One of the key differences between PFS and IFS is that PFS allows for a non-zero value for the square root of the product of the MD and NMD. This results in a more flexible and nuanced representation of uncertainty, simultaneously allowing elements to have uncertain degrees of membership and non-membership. In addition, PFS can also effectively handle conflicting information and attributes, making them well-suited for DM problems with multiple inconsistent criteria. Therefore, introducing PFS has expanded the scope of FS in DM and allowed for more accurate and robust representations of uncertainty and complexity. Ejegwa [13] explored the use of necessity and possibility operators in PFS, and Joshi [14] derived generalized average AOs for use in a PFS environment. Rahman et al. [15] introduced the Pythagorean fuzzy weighted averaging operator, which was applied to MCGDM problems. The Max-average approach in Fermatean fuzzy composite relations was implemented by Ejegwa et al. [16] to improve the validity of Fermatean fuzzy sets in machine learning using a soft computing technique. Zeng et al. [17] presented a multi-criteria decision-making (MCDM) model based on social networking to evaluate the efficiency of robotic vehicles. Rahman et al. [18] introduced a weighted ordered aggregation operator for PFS and a weighted geometric aggregation operator. Garg [19] proposed the Einstein operational laws for PFS, developed AOs, and ordered AOs for PFS. Rahman et al. [20] demonstrated the applicability of the Einstein-weighted geometric aggregation operator for solving DM problems. Yang et al. [21] presented a DM model constructed on the Fermatean fuzzy setting that employed a combination of weighted distance and the TOPSIS method to evaluate green low-carbon ports. Yager [22] proposed a new type of FS called the q-rung orthopair fuzzy set (q-ROFS) that encompasses FS, IFS, and PFS, where the sum of the
Molodtsov [27] introduced the theory of soft sets (SS), which provides a way to describe the values of alternatives using parameters. Maji et al. [28] extended the concept by creating a hybrid structure called fuzzy soft set (FSS), which combines SS and FS to address inaccuracies in DM techniques. Maji et al. [29] developed an intuitionistic fuzzy soft set (IFSS), an SS and IFS hybrid with the same constraint as IFS. IFSS offers a broader range of options for dealing with vague information about alternatives in DM problems. Arora et al. [30] discussed the AOs for IFSS and highlighted their different properties. Peng et al. [31] introduced the Pythagorean fuzzy soft set (PFSS) by extending the idea of SS to PFS and defined various operations such as addition, multiplication, union, intersection, complement, etc. Zulqarnain et al. [32] introduced the AOs for PFSS and proposed a DM methodology, which they applied to green supplier chain management. Zulqarnain et al. [33] presented interaction AOs in the context of PFSS and demonstrated a DM approach using the developed operators and their properties. Athira et al. [34] introduced a DM technique that uses entropy and distance measures in the PFSS environment, highlighting the limitations of existing DM models. Athira et al. [35] defined new entropy measures for PFSS and showed their superiority over the existing entropy measures of IFSS. Zulqarnain et al. [36] presented the TOPSIS technique based on correlation coefficients and weighted correlation coefficients for PFSS, demonstrating its effectiveness in DM problems for green supply chain management. Siddique et al. [37] explained the basic operations in the PFSS environment and highlighted the superiority and significance of the proposed model. Riaz et al. [38] discussed cosine similarity measures, weighted cosine similarity measures, and Frobenius inner product spaces of matrices for PFSS and applied these models to evaluate DM problems. Naeem et al. [39] proposed extended models of TOPSIS and VIKOR for PFS and demonstrated their application in stock exchange investment through comparative analysis with existing methods. Zulqarnain et al. [40–42] introduced the operational laws of Einstein and proposed Pythagorean fuzzy soft Einstein weighted average and geometric operators. They further extended this idea and formulated Einstein-ordered weighted AOs for PFSS, which they used to address multiple attribute group decision-making (MAGDM) problems.
Hussain et al. [43] figured out the hybrid formation of SS and q-ROFS by demonstrating a q-rung orthopair fuzzy soft set (q-ROFSS), a more efficient and competent model to deal with uncertainties in a broader format than IFSS and PFSS. Chinram et al. [44] carried the AOs concept in q-ROFSS, established AOs for q-ROFSS, and presented algorithms based on these operators to evaluate DM problems. They discussed their importance and rationality by comparative analysis. Zulqarnain et al. [45] carried the idea of AOs in q-ROFSS, introduced different interactive AOs, and argued their characteristics, such as idempotency, boundedness, and homogeneity. There is still a need to explore more work under q-ROFSS as there is no contribution for hybrid AOs, especially based on Einstein operational laws.
1.1 Motivation and Drawback of Existing Approaches
The hybrid weighted aggregation operator represents a sophisticated and all-encompassing evolution of the traditional weighted average and ordered weighted operators. While the conventional weighted average operator solely encapsulates experts’ viewpoints, the ordered weighted operator focuses solely on the prioritized position of each expert’s opinion based on a scoring mechanism. In stark contrast, the hybrid variant seamlessly merges the substance of experts’ arguments and their relative ranking, yielding a remarkably adaptable framework for grappling with the intricate intricacies of modelling ambiguous and uncertain data within decision-making problems. There is an assumption that this study might answer some of the following research questions: How is the simulation of unpredictability in the q-ROFSS context enhanced by combining the weighted average operator and ordered weighted average operator using Einstein’s operational laws? How are the developed hybrid model’s comparative advantages over existing aggregation operators in solving MCGDM concerns? How well does the suggested model handle confusing and inaccurate information in the decision-making process when diagnosing waterborne infectious diseases brought on by floods? Compared to other well-established methodologies, which is the suggested method to assess the extent of diseases in flood-affected patients employing the q-ROFSS structure? How can the advocated hybrid model handle the drawbacks of current approaches for addressing uncertainty and conflicts in MCGDM challenges? The model presented in [43,45] utilizes an aggregation and interactive aggregation framework to handle MCGDM problems within the q-ROFSS environment, where MD and NMD are represented as q-rung orthopair fuzzy soft numbers (q-ROFSNs), reflecting the experts’ perspectives on specific alternatives based on specific criteria. If we construct a matrix containing q-ROFSNs for evaluating the MCGDM problem where
Using Einstein’s operational laws in AOs has become increasingly important in dealing with uncertainty and vague data in DM problems. These operators consider all experts’ opinions, even if some score zero. Developing Einstein hybridized models is crucial in this context, as they offer a wider range of solutions than traditional models. The article is distributed on the following objectives:
• We are presenting Einstein norms-based operational laws within the q-ROFSS environment.
• It introduces the q-ROFSEHWA operator, an extended version of the AO based on the Einstein operational laws and its basic principles.
• An algorithm is presented using a deduced operator to cope with fuzziness and inappropriate data while evaluating DM problems.
• MCGDM approach is based on a protracted algorithm to determine the nature of water-borne infections in different patients affected by the flood.
• A comparative analysis of the latest MCGDM technique is conducted over prevalent MCGDM techniques for its validation and significance.
The article has been structured comprehensively to present the various aspects of the developed model. Section 1 discusses the basic definitions and concepts to understand the work’s background clearly. The concept of AOs based on Einstein’s operational laws is explained in detail in Section 2, where the properties and examples of the proposed model are also provided. The algorithm of the proposed model and its application to different DM problems are discussed in Section 4. The comparative study of the proposed model with existing methods is presented in a separate section, and the conclusion of the work is given in the final section. This structure provides a clear picture of the development and implementation of the proposed model and its comparison with existing methods.
This manuscript comprises fundamental definitions of fuzzy set theory, including FS, IFS, PFS, q-ROFS, SS, FSS, IFSS, PFSS, and q-ROFSS. Familiarity with these concepts can aid readers in comprehending the paper’s framework.
2.1 Definition [4]
FS
where
2.2 Definition [6]
IFS
where
2.3 Definition [12]
PFS
where
2.4 Definition [22]
q-ROFS over a universal set
where
2.5 Definition [27]
Let
2.6 Definition [28]
Let
where
2.7 Definition [29]
Let
where
2.8 Definition [31]
Let
where
2.9 Definition [43]
Let
where
2.10 Definition [43]
The score function signifies the comparison of two q-ROFSNs, which help to decide the optimal outcome from aggregated values. If
where
a) If
b)
c) If
i) If
ii) If
3 q-Rung Orthopair Fuzzy Soft Einstein Hybrid Weighted Average Operator
The hybrid weighted average AO based on Einstein operational laws, named the q-ROFSEHWA operator, is introduced in this section. Moreover, the properties of the proposed operator are also discussed.
Let
1.
2.
3.
4.
These operational laws will be used to develop the q-ROFSEHWA operator.
Let
where
Let
where
Proof: Using mathematical induction
Let
From Eq. (2), we have
Let
From Eq. (2), we have
Hence, the Eq. (2) is true for
Suppose that the statement is true for
Then, we have
and
Need to prove Eq. (2) for
Hence, it is true for
1. If
2. If
3. If
4. If
5. If
3.5 Properties of q-ROFSEHWA Operator
If
Proof: We know that
Since
we have
Hence
Proof: We know that
Now, by using theorem (1), we have
Let
Proof: We know that
Now by theorem (1), we have
4 Multi-Criteria Group Decision-Making Approach for q-ROFSEHWA Operator
In this section, we establish an algorithm on the functionality of the proposed operator to evaluate MCGDM problems and present its application in diagnosing water-born infections in different patients affected by the flood.
Suppose that a group of experts
Step 1: Arrange the decision matrices containing an evaluation of each expert in the form of q-ROFSNs based on the given criteria about the alternatives as follows:
Step 2: Convert cost type parameters into benefit type parameters by normalization process [46] using the following result:
Step 3: Update q-ROFSNs
Step 4: Arrange all updated q-ROFSNs
Step 5: Apply q-ROFSEHWA operator to upgraded matrices to obtain aggregated values
Step 6: Obtain score values of aggregated q-ROFSNs
Step 7: Compare the score values, and any aggregated q-ROFSN having the best score value will be the best optimal outcome.
The flowchart of the proposed technique is given in the following Fig. 1.

Figure 1: Flowchart of the proposed model
4.2 Application of the Proposed MCGDM Model
Every country’s infrastructure and systems are designed to manage the flow of rainwater into designated basins and reservoirs. When it rains, the infrastructure typically ensures that the water flows smoothly and does not flood homes or other areas. However, the systems can become overwhelmed when it rains heavily, causing clogged drainage and floods. There are various ways that human activities, such as deforestation, the destruction of lakes, climate change, and sea level rise, can impact the environment and exacerbate the severity and frequency of floods. Additionally, increased rainfall and extreme weather conditions contribute to more severe flooding. Floods significantly impact individuals, communities, and the environment, affecting social, economic, and health aspects. The effects of floods can vary greatly depending on the location and extent of the flooding. The image of damaged houses is presented in the following Fig. 2.
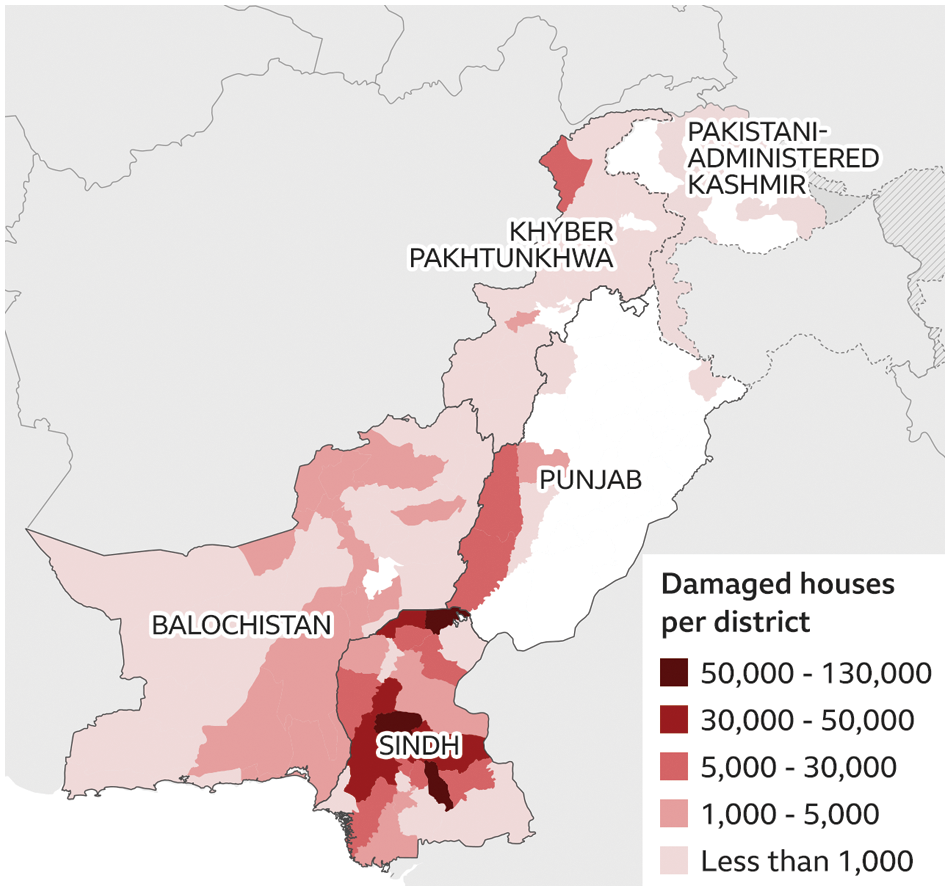
Figure 2: Damaged house per district in 2022 flood Pakistan
Floods can be particularly problematic in agriculture, civil engineering, and public health, resulting from excess water, and can cause widespread damage, destroying homes (see Fig. 3), trees, vehicles, roads, buildings, and more. Flooding can also have serious health consequences, forcing individuals to evacuate their homes, interrupting daily life, and damaging communication lines and critical infrastructure such as power plants, highways, and bridges. Overall, flooding is devastating, causing property damage, loss of life, and far-reaching health impacts.

Figure 3: Baluchistan province on august 29 (https://www.vox.com/science-and-health/2022/8/30/23327341/pakistan-flooding-monsoon-melting-glaciers-climate-c)
The aftermath of floods can significantly impact an affected individual’s mental and physical health. People may suffer from anxiety, depression, sleep disturbances, and post-traumatic stress disorder. The warmer environment and the increasing frequency of floods have made it a significant public health issue. Floods can cause water-borne diseases and outbreaks of various illnesses, such as typhoid fever, cholera, diarrhea, and leptospirosis. The stagnant water caused by floods can also create ideal breeding grounds for mosquitoes, pose chemical hazards, and increase the drinking water contamination risk. All these factors contribute to the significant health risks posed by floods and highlight the need for effective measures to minimize their impact on communities. Recently, in 2022, Pakistan was hit by an extreme flood, and it is observed that one-third population of Pakistan was affected by the flood. According to the Pakistan government’s source, more than 33 million individuals have suffered from floods, including 1,739 deaths and around 8.2 million people who needed medical care and humanitarian aid. According to the report of United Nations International Children’s Emergency Fund (UNICEF), as many as 4 million children were still close to toxic and stagnant flood water by the beginning of January 2023, putting their survival and safety in danger. The losses reported in the 2022 flood in Pakistan included Property damage: Many houses and buildings were destroyed, leading to the displacement of many families. Crop loss: A large amount of agricultural land was submerged, resulting in significant losses in the production of crops such as cotton, sugarcane, and rice. Livestock loss: Many livestock, such as cattle and buffalo, were drowned, resulting in a substantial financial loss for farmers. Infrastructure damage: Roads, bridges, and other infrastructure were severely damaged, making it difficult for relief and rescue teams to access affected areas. Economic loss: The flood caused significant disruptions to businesses and the economy, with many people losing their livelihoods due to the disaster. These are some of the major losses reported in the 2022 flood in Pakistan. The actual scale of the disaster was likely much larger, with many losses going unrecorded. The biggest danger associated with the flood is Health issues: The floodwaters resulted in a rise in water-borne diseases such as cholera and typhoid, leading to a public health crisis in affected areas. The loss reported in the 2022 flood in Pakistan is shown in Fig. 4.
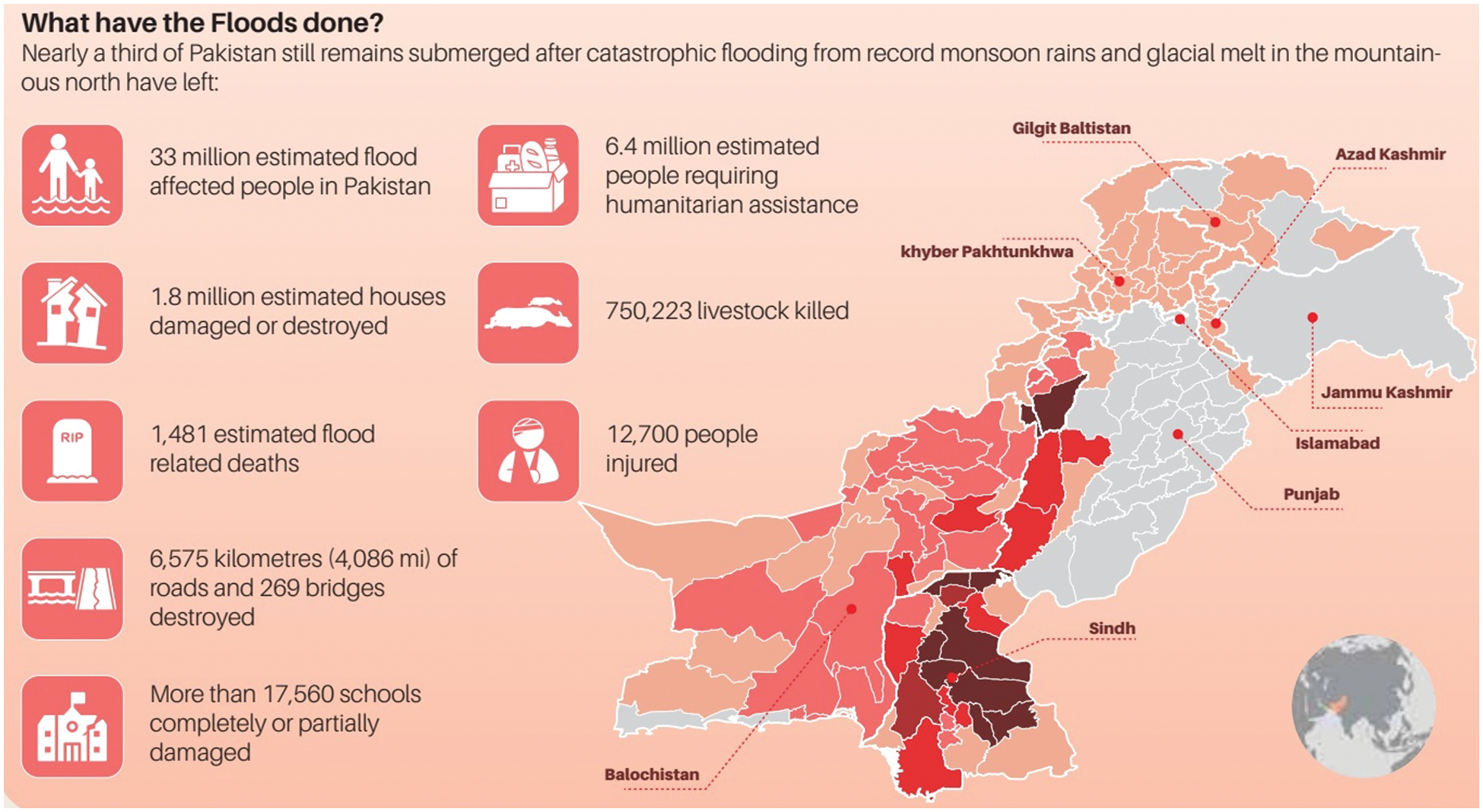
Figure 4: Loss reported in 2022 flood in Pakistan (https://communityworldservice.asia/pakistan-floods-2022-a-third-of-pakistan-still-underwater/)
During a flood, many types of water-borne diseases can be reported, including:
a) Gastrointestinal diseases
Gastrointestinal diseases are a common health risk associated with flooding. Flood water can contain bacteria, viruses, and other pathogens that can cause illnesses if ingested or come into contact with the skin. Common gastrointestinal diseases associated with floods include typhoid fever, cholera, diarrhea, and food poisoning caused by contaminated food and water. Additionally, standing water can provide a breeding ground for mosquitoes, which can transmit diseases such as dengue fever, yellow fever, and malaria. It is important for individuals and communities affected by floods to take precautions to prevent the spread of gastrointestinal diseases, such as using safe drinking water and proper hygiene practices.
b) Respiratory infections
Respiratory infections are another common health issue faced by individuals affected by floods. Exposure to stagnant water and damp conditions can create a breeding ground for mould and bacteria, triggering respiratory infections such as pneumonia, bronchitis, and asthma. Additionally, inhaling contaminated air from floodwaters can also cause respiratory problems. It is important for individuals to take necessary precautions and to seek medical attention if they experience any symptoms of respiratory infections after a flood.
c) Vector-borne diseases
Vector-borne diseases are illnesses transmitted to humans by vectors, such as mosquitoes, ticks, and fleas. Some of the most common vector-borne diseases include malaria, dengue, Lyme, and yellow fever. In areas affected by floods, the increase in standing water provides an ideal breeding ground for mosquitoes, which can lead to a rise in the transmission of vector-borne diseases. It is important to take precautions and implement measures to control the populations of vectors to reduce the risk of infection.
d) Skin infections
Flooding can also lead to skin infections, as people are more susceptible to skin problems such as cuts, scrapes, and abrasions when in contact with contaminated floodwater. Exposure to dirty water and bacteria, viruses, and parasites in the water can increase the risk of skin infections. In addition, exposure to moisture for prolonged periods can lead to skin rashes and fungal infections. To prevent skin infections, flood-affected individuals must take appropriate precautions, such as washing their hands frequently and avoiding direct contact with contaminated water. In case of any skin injury, cleaning the wound and seeking medical attention promptly is recommended.
d) Water-borne parasites
Water-borne parasites are diseases caused by ingesting contaminated water or direct contact with contaminated water. Some of the common water-borne parasites include Giardia, Cryptosporidium, and Cyclospora. These parasites can cause various symptoms, including diarrhea, nausea, vomiting, stomach cramps, and dehydration. It is important to properly treat and filter water before drinking or using it to avoid exposure to water-borne parasites.
It is important to take appropriate measures to prevent and control these diseases, such as practicing good hygiene, using clean water sources, and controlling mosquito populations. Children suffering from malnourishment and weakness face a difficult battle against various health issues, such as acute respiratory infections, severe starvation, malaria, and painful skin disorders. To effectively respond to these health risks, it is important to establish medical camps (see Fig. 5) in flood-affected areas to provide appropriate medical care and facilities to those in need. These camps should be equipped with adequate resources, including medical supplies, clean water, and sanitation facilities, to ensure the health and safety of those affected by floods. Furthermore, efforts should be made to educate communities on the health risks associated with floods and to implement measures to minimize the spread of diseases. Hussain et al. [43] presented an algorithm based on AOs to diagnose certain diseases in the environment of q-ROFSS. The authors propose a model based on the q-ROFSS environment to determine the severity of diseases in flood-affected patients.

Figure 5: Medical relief camps were established in the flood-affected area of Pakistan (source: daily times, 2022)
Suppose that a team of healthcare experts
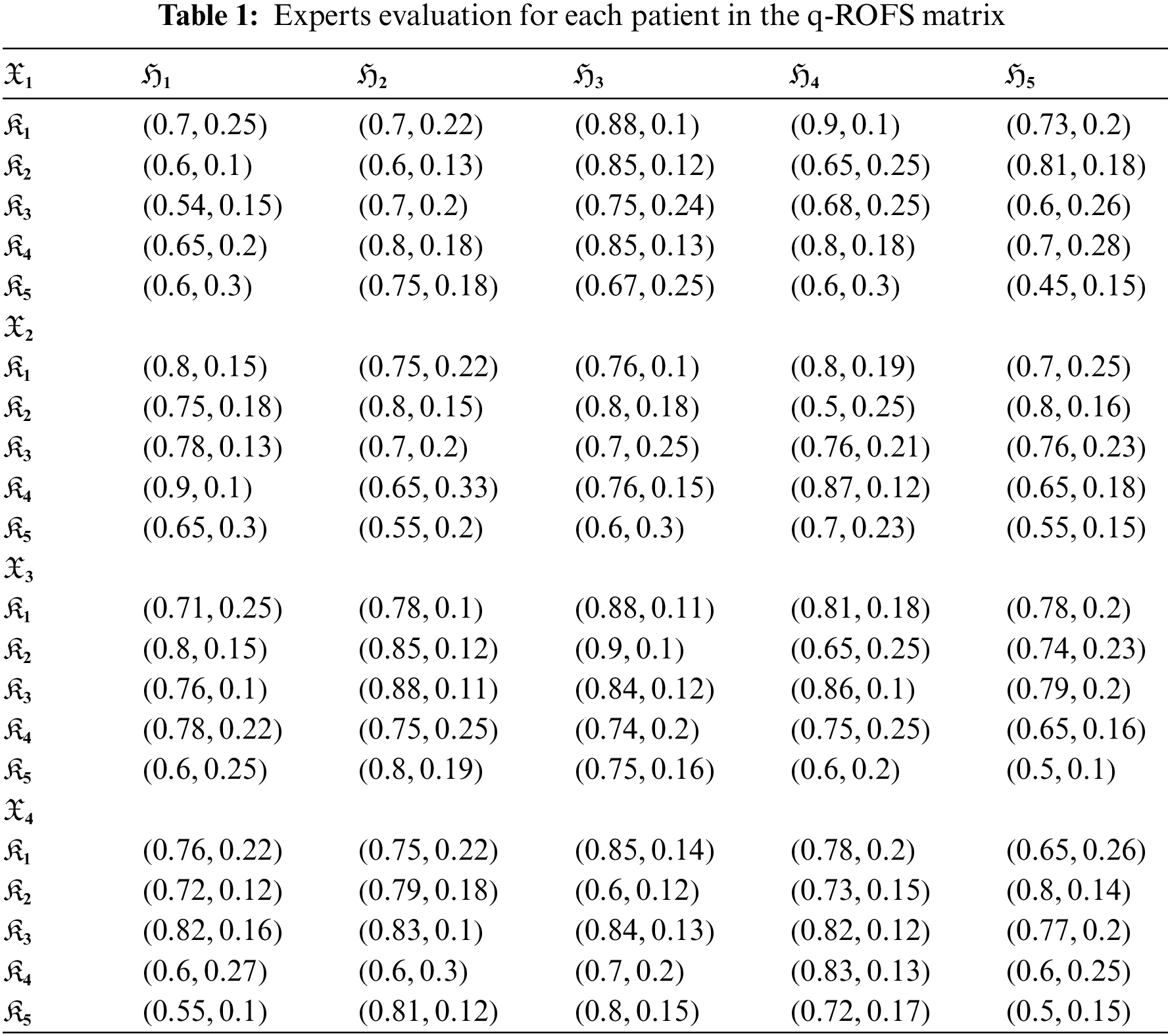
Step 1: The expert’s evaluation for each patient is given in Table 1.
Step 2: The considered parameters are the same type, so there is no need to be normalized.
Step 3: Update q-ROFSNs
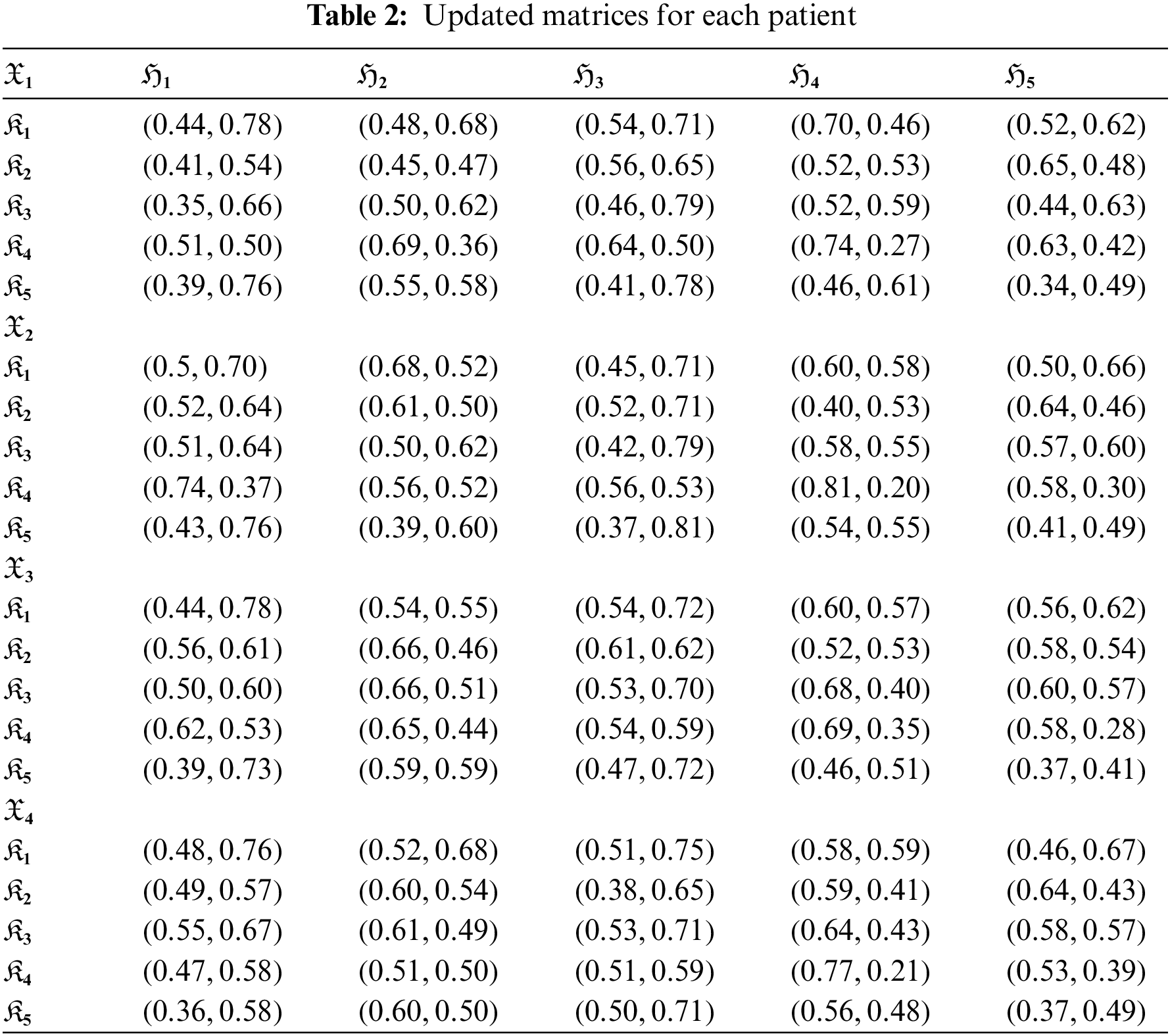
Step 4: Obtain the ordered matrices for each alternative using the score function from the updated matrices in Table 3.
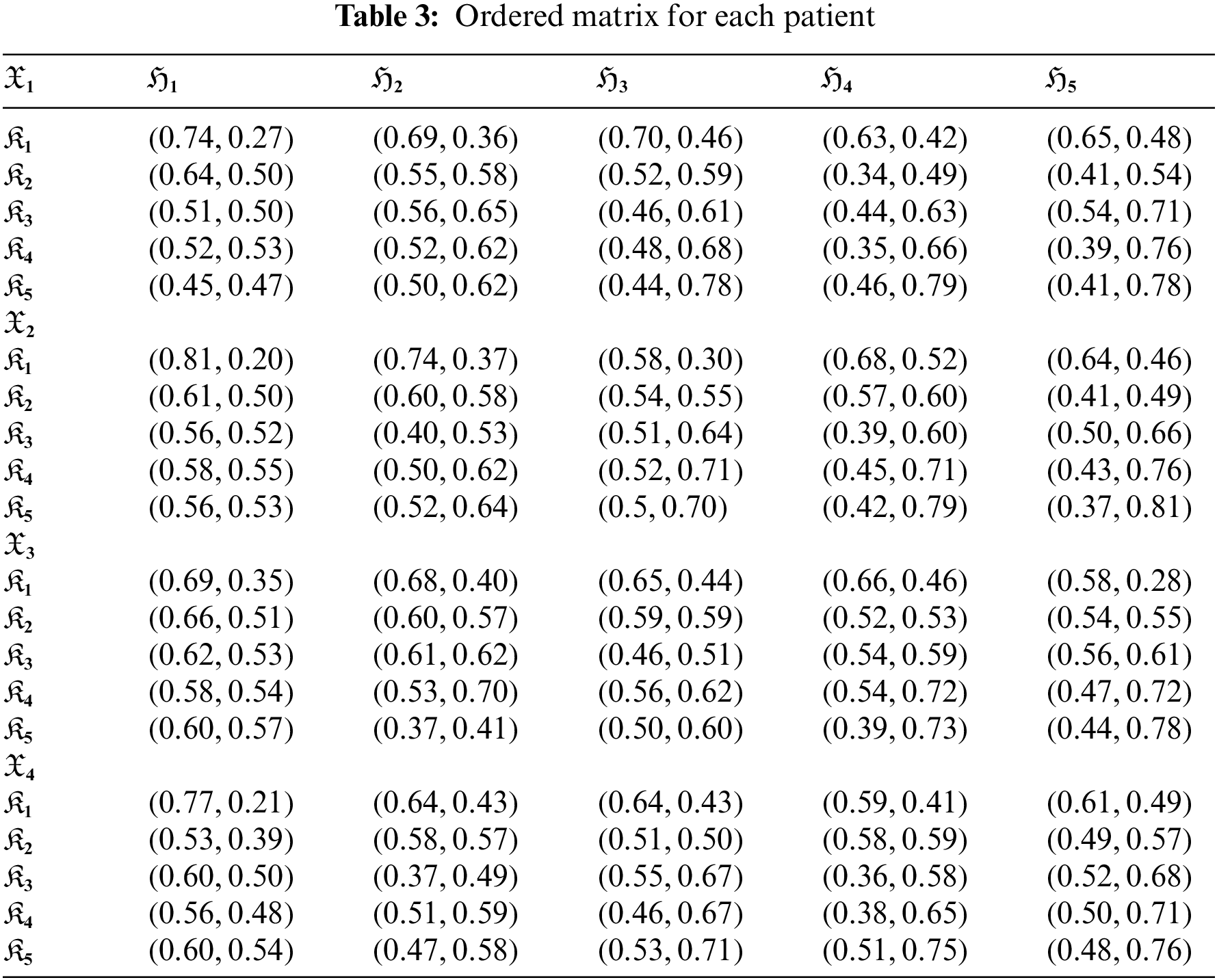
Step 5: Now we apply the anticipated q-ROFSEHWA operator on Table 3 respectively for
Step 6: Find the score values of aggregated q-ROFSNs by applying the score function. So, we have,
Step 7: Compute the ranking of the patients; the following pattern shows the severe condition of patients.
This shows that the patient
5 Comparative Analysis and Discussion
This section analyzes the comparative study of the proposed MCGDM technique over existing MCGDM techniques and discusses the superiority and efficiency of the developed approach.
5.1 Supremacy and Validity of the Proposed Model
The developed hybrid model combines the weighted average operator and ordered weighted average operator based on Einstein’s operational laws in the q-ROFSS environment. The model uses expert opinions expressed in q-ROFSNs and their ordered position to evaluate and determine the severity of diseases in patients affected by floods. Because of this hybridized structure, the proposed model based on the q-ROFSEHWA operator tackles MCGDM problems more effectively and produces better results while handling uncertainty and vagueness. The protracted approach is more flexible, delicate, and vigorous than the prevailing approaches. Existing methodologies based on rough observations have inconsistent rankings, but the developed model addresses this issue. Based on Einstein’s operational laws, the model can handle situations where experts propose NMD zero about the alternatives. The presented technique results are unpredictable compared to current hybrid structures of fuzzy sets, as concluded from this factual study and scientific evaluation. Additionally, the q-ROFSS is rarely coupled to the hybrid FS systems, such as IFSS and PFSS, due to some favorable circumstances in DM challenges; dealing with unclear, imprecise, and unsecured information requires a special method. As a result, our proposed model is more effective than prevalent FS structures. In addition, Fig. 6 and Table 4 provide a graphical and numerical comparison of the coined model’s characteristics and score values with those of other models.
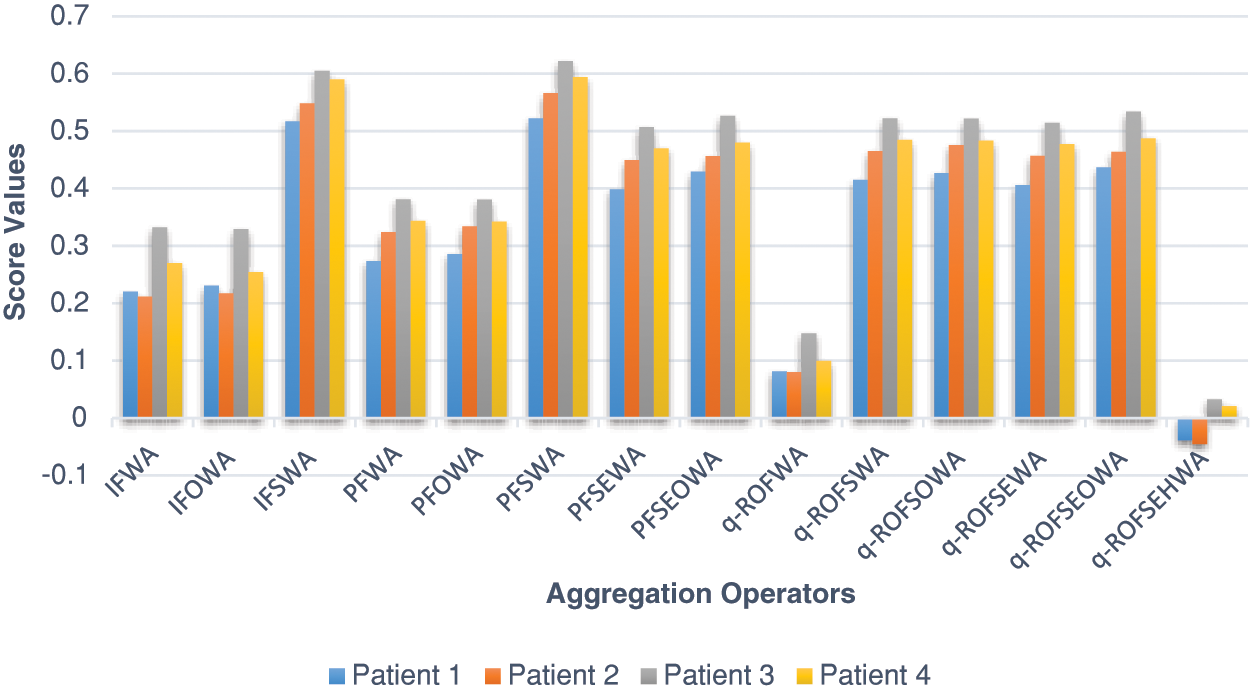
Figure 6: Graphical comparison of existing and proposed aggregation operators

To demonstrate the superiority and prominence of proposed AOs, a contrasting strategy has been suggested between anticipated and certain existent operators. If we use the IFWA operator [7] to solve DM problems, restrictions and specific conditions prevent us from analyzing fuzzy and vague data. Under the restrictive limitation that the sum of MD and NMD cannot exceed unity, the uncertainty cannot be measured If MD = 0.6 and NMD = 0.5, and it also fails to tackle parameterized problems. IFOWA operator [7] provides superior outcomes than IFWA due to q-ROPFSNs’ ordered position by evaluating the score values. The IFSWA [30] model can handle MCGDM problems with alternate attributes, but it has limitations and is ineffective when MD and NMD values exceed 1. As a generalization of IFS, PFS encompasses a wide range of ambiguity detection in DM situations with the restriction that the sum of the squares of MD and NMD must be less than or equal to 1. The technique in question can evaluate the degree of fuzziness in a given problem but cannot handle MCGDM models that involve multiple attributes of alternatives. The PFSWA operator [36] cannot deal with the data with the constraint of PFS if MD = 0.9 and NMD = 0.7. The article discusses the limitations of different models in handling MCGDM problems with uncertain information. While q-ROFWA [23] covers a wider range of uncertain information than PFWA [15] and PFOWA [18], it fails to operate with parametric axioms. Aggregated q-ROPFSNs through q-ROFSWA and q-ROFSOWA [43] are invalidated if any expert assigns an NMD of 0, which affects the opinions of all other experts and results in an aggregated NMD of 0. Our developed model cannot affect the opinions of other experts as our model can handle them. The comparison with different operators is listed in Table 5.
The proposed approach addresses MCGDM challenges with more data and decodes ambiguous and imprecise information under q-ROFSS. The developed operator outperforms prevailing operators in dealing with DM problems. A comparative study of the operator’s significant role is presented in Table 5, illustrating the score values of alternatives under various AOs. The proposed model and related measurements can avoid such judgments based on unfavorable factors in contrast to existing MCGDM methodologies. Therefore, combining ambiguous and uncertain data in the DM process is essential. Fig. 6 compares the intimated operator with many current operators through graphical representation.
5.3 Advantages of the Proposed Approach
The suggested technique, which integrates the Einstein hybrid aggregation operator with q-rung orthopair fuzzy soft sets (q-ROFSS), has multiple particular advantages which assist DM throughout a wide range of areas. Here are the benefits in further detail:
• The q-ROFSS structure integrally apprehensions hesitation more expansively, concurrently cooperative MD and NMD. This permits a more precise depiction of inexact and imprecise data often faced in real-world consequences.
• The q-ROFSS structure is proficient at conducting MCGDM states. Integrating expert estimations and their imports over the hybrid AO permits the method to assess alternatives based on numerous measures, consequential in more conversant and stable judgments.
• Distinct from some models, the q-ROFSS method can effectually handle states where professionals allocate zero NMD to convinced alternatives. This feature certifies that expert views are quartered even when alternatives are omitted.
• The planned q-ROFSS method and the hybrid AO are useful and flexible. It can be pragmatic to several domains and decision perspectives, making it an appreciated device for decision-makers in numerous areas.
The benefits of the projected q-ROFSS methodology with the Einstein hybrid AO lie in its inclusive dealing of hesitation, tractability in participating proficient ideas, efficiency in multi-criteria consequences, and applicability in real-world DM perspectives. Its capability to handle vagueness, deliberation of zero NMD, systematic developments, and applied confirmation further emphasize its implication in improving DM practices.
5.4 Social and Managerial Implications
The proposed strategy of combining the Einstein hybrid AO with q-ROFSS presents significant promise to deal with organizational and communal impacts in decision-making circumstances. It will be how the method chosen can influence the following characteristics:
• The technique encourages an inclusive approach to DM by incorporating expert perspectives while considering the advantages of various positions. Ensuring all perspectives have been taken seriously through the course of DM may result in enhanced involvement of stakeholders and involvement.
• Transparency in DM is promoted due to the method’s enhanced comprehension of unpredictability and confusion. It creates an impression of transparency and confidence in the decision’s finalization whenever stakeholders are apprised that their opinions have been taken seriously and assessed.
• The strategy’s versatility to adjust to multiple factors and the sensitive handling of inconsistency may deliver consequences that are better aligned with the demands and desires of societies in cases where outcomes impact communities. Improved satisfaction among communities can come through an approach.
• It is important to distribute resources properly while executing decisions regarding management. Administrators may benefit from this method’s capability to cope with numerous factors and inconsistencies by employing it for making instructed allocations of resource selections.
• The technique’s capability to cope with complexity and unreliable data can result in higher-quality managerial assessments for activities with a long-term impact. It is particularly significant for establishing objectives and long-term planning.
The proposed strategy can positively affect social outcomes by fostering stakeholder engagement, transparency, equity, and societal satisfaction. It can help with better communication, bias reduction, strategy adaptation, decision quality, dispute resolution, and resource allocation on the executive front. Due to these integrated impacts, this method is useful for resolving managing and communal implications in decision-making.
MCGDM is a technique for selecting appropriate options from a set of alternatives based on certain criteria. Our daily life includes DM, and we face various DM situations. Making the optimal pick from the available options is difficult for decision-makers. Decision-makers occasionally need to act quickly and precisely because the outcomes are time-sensitive. The decision-makers do not have much time to consider their alternatives. Therefore, they must be quick-witted and conscious of the implications. The q-ROFSS is a mathematical foundation that can address incomplete information about alternatives and set restrictions, avoiding incorrect DM. Unlike other fuzzy sets such as FS, IFS, and PFSS, q-ROFSS has a more general and profound mathematical background in the field of DM. This new methodology provides a framework for choosing wisely among alternatives with multiple attributes in a q-ROFSS context. The q-ROFSEHWA operator is proposed in this work in light of Einstein’s operational laws for q-ROFSNs together with fundamental properties. An algorithm based on these suggested models is developed for the MCGDM problems. An application of the MCGDM is presented to depict a diagnostic procedure in flood-affected areas to confirm the predicted methodology’s suitability and reliability. Under the q-ROFSS context, a comprehensive analysis of the dominant model relative to current models is offered. The findings indicate that the more optimal strategies can be inferred from this presented technique, and the suggested approach is more reliable and useful for MCGDM problems than existing techniques. Future studies will elaborate on the established model by considering its application to various aggregation operators such as q-rung orthopair fuzzy soft Einstein hybrid weighted geometric (q-ROFSEHWG) operator, q-rung orthopair fuzzy soft Einstein interactive hybrid weighted average (q-ROPFSEIHWA) operator, and q-rung orthopair fuzzy soft Einstein interactive hybrid weighted geometric (q-ROPFSEIHWG) operator. It can be extended to a q-rung orthopair fuzzy hypersoft environment with several AOs and their decision-making methodologies. These models can be used in operations research, social networking, supply chain management, healthcare DM, environmental impact assessment, investment portfolio management, disaster management, educational DM, project selection, energy planning, urban planning, risk assessment, and other fields.
Acknowledgement: The authors acknowledge the King Saud University, Riyadh, Saudi Arabia.
Funding Statement: This project is funded by King Saud University, Research Supporting Project Number (RSP2024R167), Riyadh, Saudi Arabia.
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: R. M. Z, H. K. ur R; data collection: I. S, S. A; analysis and interpretation of results: I. S, H. A, S. H. G; draft manuscript preparation: R. M. Z, H. K. ur R, S. H. G. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All the data used and analyzed is available in the manuscript.
Conflicts of Interest: The authors declare no competing interests.
References
1. Ahmad, D., Afzal, M. (2022). Flood hazards and agricultural production risks management practices in flood-prone areas of Punjab, Pakistan. Environmental Science and Pollution Research, 29(14), 20768–20783. [Google Scholar] [PubMed]
2. Ochani, S., Aaqil, S. I., Nazir, A., Athar, F. B., Ochani, K. et al. (2022). Various health-related challenges amidst recent floods in Pakistan; Strategies for future prevention and control. Annals of Medicine and Surgery, 82, 104667. [Google Scholar] [PubMed]
3. Ochani, S., Aaqil, S. I., Nazir, A., Athar, F. B., Ullah, K. (2022). Neonatal and child health crises due to recent floods in Pakistan. Annals of Medicine and Surgery, 84, 104837. [Google Scholar] [PubMed]
4. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8, 338–353. [Google Scholar]
5. Ulucay, V. (2020). A new similarity function of trapezoidal fuzzy multi-numbers based on multi-criteria decision making. Journal of Institute of Science and Technology, 10(2), 1233–1246. [Google Scholar]
6. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20, 87–96. [Google Scholar]
7. Xu, Z. (2007). Intuitionistic fuzzy aggregation operators. IEEE Transactions on Fuzzy Systems, 15(6), 1179–1187. [Google Scholar]
8. Wang, W., Liu, X. (2012). Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Transactions on Fuzzy Systems, 20(5), 923–938. [Google Scholar]
9. Xu, Z., Yager, R. R. (2006). Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems, 35(4), 417–433. [Google Scholar]
10. Zhao, X., Wei, G. (2013). Some intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute decision making. Knowledge-Based Systems, 37, 472–479. [Google Scholar]
11. Zeng, S., Zhou, J., Zhang, C., Merigó, J. M. (2022). Intuitionistic fuzzy social network hybrid MCDM model for an assessment of digital reforms of manufacturing industry in China. Technological Forecasting and Social Change, 176, 121435. [Google Scholar]
12. Yager, R. R. (2013). Pythagorean fuzzy subsets. 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), pp. 57–61. New York, USA, IEEE. [Google Scholar]
13. Ejegwa, P. A. (2019). Modal operators on Pythagorean fuzzy sets and some of their properties. The Journal of Fuzzy Mathematics, 27(4), 939–956. [Google Scholar]
14. Joshi, B. P. (2019). Pythagorean fuzzy average aggregation operators based on generalized and group-generalized parameter with application in MCDM problems. International Journal of Intelligent Systems, 34(5), 895–919. [Google Scholar]
15. Rahman, K., Ali, A., Shakeel, M., Khan, M. A., Ullah, M. (2017). Pythagorean fuzzy weighted averaging aggregation operator and its application to decision making theory. The Nucleus, 54(3), 190–196. [Google Scholar]
16. Ejegwa, P. A., Zuakwagh, D. (2022). Fermatean fuzzy modified composite relation and its application in pattern recognition. Journal of Fuzzy Extension and Applications, 3(2), 140–151. [Google Scholar]
17. Zeng, S., Zhang, N., Zhang, C., Su, W., Carlos, L. A. (2022). Social network multiple-criteria decision-making approach for evaluating unmanned ground delivery vehicles under the Pythagorean fuzzy environment. Technological Forecasting and Social Change, 175, 121414. [Google Scholar]
18. Rahman, K., Abdullah, S., Ali, A., Amin, F. (2020). Pythagorean fuzzy ordered weighted averaging aggregation operator and their application to multiple attribute group decision-making. EURO Journal on Decision Processes, 8, 61–77. [Google Scholar]
19. Garg, H. (2016). A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. International Journal of Intelligent Systems, 31(9), 886–920. [Google Scholar]
20. Rahman, K., Abdullah, S., Ahmed, R., Ullah, M. (2017). Pythagorean fuzzy Einstein weighted geometric aggregation operator and their application to multiple attribute group decision making. Journal of Intelligent & Fuzzy Systems, 33(1), 635–647. [Google Scholar]
21. Yang, S., Pan, Y., Zeng, S. (2022). Decision making framework based Fermatean fuzzy integrated weighted distance and TOPSIS for green low-carbon port evaluation. Engineering Applications of Artificial Intelligence, 114, 105048. [Google Scholar]
22. Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems, 25(5), 1222–1230. [Google Scholar]
23. Liu, P., Wang, P. (2018). Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. International Journal of Intelligent Systems, 33(2), 259–280. [Google Scholar]
24. Riaz, M., Sałabun, W., Athar Farid, H. M., Ali, N., Wątróbski, J. (2020). A robust q-rung orthopair fuzzy information aggregation using Einstein operations with application to sustainable energy planning decision management. Energies, 13(9), 2155. [Google Scholar]
25. Limboo, B., Dutta, P. (2022). A q-rung orthopair basic probability assignment and its application in medical diagnosis. Decision Making: Applications in Management and Engineering, 5(1), 290–308. [Google Scholar]
26. Khan, M. R., Ullah, K., Khan, Q. (2023). Multi-attribute decision-making using Archimedean aggregation operator in T-spherical fuzzy environment. Reports in Mechanical Engineering, 4(1), 18–38. [Google Scholar]
27. Molodtsov, D. (1999). Soft set theory—First results. Computers & Mathematics with Applications, 37(4–5), 19–31. [Google Scholar]
28. Maji, P. K., Biswas, R., Roy, A. R. (2001). Fuzzy soft sets. Journal of Fuzzy Mathematics, 9(3), 589–602. [Google Scholar]
29. Maji, P. K., Biswas, R., Roy, A. R. (2001). Intuitionistic fuzzy soft sets. Journal of Fuzzy Mathematics, 9(3), 677–692. [Google Scholar]
30. Arora, R., Garg, H. (2018). A robust aggregation operators for multi-criteria decision-making with intuitionistic fuzzy soft set environment. Scientia Iranica, 25(2), 931–942. [Google Scholar]
31. Peng, X. D., Yang, Y., Song, J., Jiang, Y. (2015). Pythagorean fuzzy soft set and its application. Computer Engineering, 41(7), 224–229. [Google Scholar]
32. Zulqarnain, R. M., Xin, X. L., Siddique, I., Asghar Khan, W., Yousif, M. A. (2021). TOPSIS method based on correlation coefficient under pythagorean fuzzy soft environment and its application towards green supply chain management. Sustainability, 13(4), 1642. [Google Scholar]
33. Zulqarnain, R. M., Xin, X. L., Garg, H., Ali, R. (2021). Interaction aggregation operators to solve multi criteria decision making problem under pythagorean fuzzy soft environment. Journal of Intelligent & Fuzzy Systems, 41(1), 1151–1171. https://doi.org/10.3233/JIFS-210098 [Google Scholar] [CrossRef]
34. Athira, T. M., John, S. J., Garg, H. (2019). Entropy and distance measures of pythagorean fuzzy soft sets and their applications. Journal of Intelligent & Fuzzy Systems, 37(3), 4071–4084. [Google Scholar]
35. Athira, T. M., John, S. J., Garg, H. (2020). A novel entropy measure of Pythagorean fuzzy soft sets. AIMS Mathematics, 5(2), 1050–1061. [Google Scholar]
36. Zulqarnain, R. M., Xin, X. L., Garg, H., Khan, W. A. (2021). Aggregation operators of pythagorean fuzzy soft sets with their application for green supplier chain management. Journal of Intelligent & Fuzzy Systems, 40(3), 5545–5563. [Google Scholar]
37. Siddique, I., Zulqarnain, R. M., Ali, R., Alburaikan, A., Iampan, A. et al. (2021). A decision-making approach based on score matrix for pythagorean fuzzy soft set. Computational Intelligence and Neuroscience, 2021, 5447422. https://doi.org/10.1155/2021/5447422 [Google Scholar] [PubMed] [CrossRef]
38. Riaz, M., Naeem, K., Afzal, D. (2020). A similarity measure under pythagorean fuzzy soft environment with applications. Computational and Applied Mathematics, 39(4), 1–17. [Google Scholar]
39. Naeem, K., Riaz, M., Peng, X., Afzal, D. (2019). Pythagorean fuzzy soft MCGDM methods based on TOPSIS, VIKOR and aggregation operators. Journal of Intelligent & Fuzzy Systems, 37(5), 6937–6957. [Google Scholar]
40. Zulqarnain, R. M., Siddique, I., Jarad, F., Hamed, Y. S., Abualnaja, K. M. et al. (2022). Einstein aggregation operators for pythagorean fuzzy soft sets with their application in multiattribute group decision-making. Journal of Function Spaces, 2022, 1–21. https://doi.org/10.1155/2022/1358675 [Google Scholar] [CrossRef]
41. Zulqarnain, R. M., Siddique, I., Ahmad, S., Iampan, A., Jovanov, G. et al. (2021). Pythagorean fuzzy soft Einstein ordered weighted average operator in sustainable supplier selection problem. Mathematical Problems in Engineering, 2021, 1–16. https://doi.org/10.1155/2021/2559979 [Google Scholar] [CrossRef]
42. Zulqarnain, R. M., Siddique, I., EI-Morsy, S. (2022). Einstein-ordered weighted geometric operator for Pythagorean fuzzy soft set with its application to solve MAGDM problem. Mathematical Problems in Engineering, 2022, 1–14. https://doi.org/10.1155/2022/5199427 [Google Scholar] [CrossRef]
43. Hussain, A., Ali, M. I., Mahmood, T., Munir, M. (2020). q-rung orthopair fuzzy soft average aggregation operators and their application in multi-criteria decision-making. International Journal of Intelligent Systems, 35(4), 571–599. [Google Scholar]
44. Chinram, R., Hussain, A., Ali, M. I., Mahmood, T. (2021). Some geometric aggregation operators under q-rung orthopair fuzzy soft information with their applications in multi-criteria decision making. IEEE Access, 9, 31975–31993. [Google Scholar]
45. Zulqarnain, R. M., Siddique, I., Iampan, A., Awrejcewicz, J., Bednarek, M. et al. (2022). Novel multi criteria decision making approach for interactive aggregation operators of q-rung orthopair fuzzy soft set. IEEE Access, 10, 59640–59660. https://doi.org/10.1109/ACCESS.2022.3178595 [Google Scholar] [CrossRef]
46. Arora, R. (2020). Intuitionistic fuzzy soft aggregation operator based on Einstein norms and its applications in decision-making. Intelligent Systems Design and Applications, pp. 998–1008. Cham, Springer International Publishing. https://doi.org/10.1007/978-3-030-16657-1_93 [Google Scholar] [CrossRef]
47. Rahman, K., Abdullah, S., Ali, A., Amin, F. (2020). Pythagorean fuzzy Einstein hybrid averaging aggregation operator and its application to multiple-attribute group decision making. Journal of Intelligent Systems, 29(1), 736–752. [Google Scholar]
48. Zulqarnain, R. M., Rehman, H. K. U., Awrejcewicz, J., Ali, R., Siddique, I. et al. (2022). Extension of Einstein average aggregation operators to medical diagnostic approach under q-rung orthopair fuzzy soft set. IEEE Access, 10, 87923–87949. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools