Open Access

ARTICLE

Fast and Accurate Predictor-Corrector Methods Using Feedback-Accelerated Picard Iteration for Strongly Nonlinear Problems

Xuechuan Wang¹, Wei He^1,*, Haoyang Feng¹, Satya N. Atluri²

1 School of Astronautics, Northwestern Polytechnical University, Xi’an, 710072, China
2 Department of Mechanical Engineering, Texas Tech University, Lubbock, 79409, USA

* Corresponding Author: Wei He. Email:

Computer Modeling in Engineering & Sciences 2024, 139(2), 1263-1294. https://doi.org/10.32604/cmes.2023.043068

Received 20 June 2023; Accepted 27 October 2023; Issue published 29 January 2024

Abstract

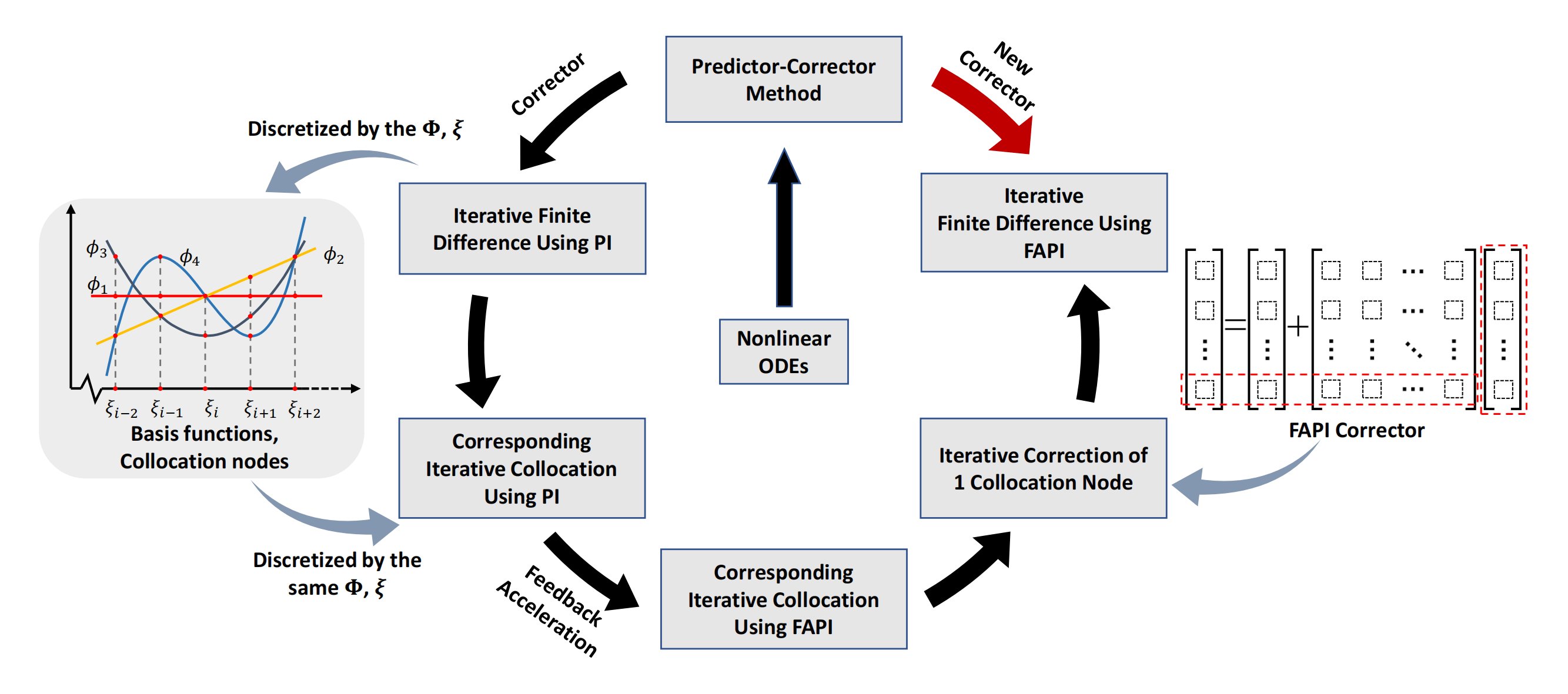
Although predictor-corrector methods have been extensively applied, they might not meet the requirements of practical applications and engineering tasks, particularly when high accuracy and efficiency are necessary. A novel class of correctors based on feedback-accelerated Picard iteration (FAPI) is proposed to further enhance computational performance. With optimal feedback terms that do not require inversion of matrices, significantly faster convergence speed and higher numerical accuracy are achieved by these correctors compared with their counterparts; however, the computational complexities are comparably low. These advantages enable nonlinear engineering problems to be solved quickly and accurately, even with rough initial guesses from elementary predictors. The proposed method offers flexibility, enabling the use of the generated correctors for either bulk processing of collocation nodes in a domain or successive corrections of a single node in a finite difference approach. In our method, the functional formulas of FAPI are discretized into numerical forms using the collocation approach. These collocated iteration formulas can directly solve nonlinear problems, but they may require significant computational resources because of the manipulation of high-dimensional matrices. To address this, the collocated iteration formulas are further converted into finite difference forms, enabling the design of lightweight predictor-corrector algorithms for real-time computation. The generality of the proposed method is illustrated by deriving new correctors for three commonly employed finite-difference approaches: the modified Euler approach, the Adams-Bashforth-Moulton approach, and the implicit Runge-Kutta approach. Subsequently, the updated approaches are tested in solving strongly nonlinear problems, including the Matthieu equation, the Duffing equation, and the low-earth-orbit tracking problem. The numerical findings confirm the computational accuracy and efficiency of the derived predictor-corrector algorithms.

---

Graphic Abstract

---

Keywords

---