C-CORE: Clustering by Code Representation to Prioritize Test Cases in Compiler Testing

1  Introduction

Edge AI [1,2] is a technique that has emerged with the rise of the Internet of Things [3–5] and is used in more and more scenarios like smart home, industrial automation and intelligent transportation that require high security. Therefore, it is becoming more and more important to ensure the security and reliability of this application. Edge AI operates on edge devices, executing both training and inference tasks. Nonetheless, these edge devices typically grapple with limited storage and computational resources, necessitating the intervention of traditional compilers and deep learning compilers to optimize code and models. Traditional compilers can convert the front-end high-level language code of the learning framework into an intermediate representation. They excel at optimizing for common computing tasks and hardware architectures, employing techniques such as loop unrolling, constant propagation, memory layout optimization, and memory reuse to curtail computational requirements and reduce storage access overhead. Then, the intermediate representation is handed over to the deep learning compiler for more model-specific optimizations, such as model pruning and operator fusion. As a result, the effectiveness of edge AI security is intricately tied to the reliable operation of these compilers. However, these optimization processes are prone to faults, emphasizing the need for extensive compiler testing to ensure reliability.

Currently, the most popular technique of compiler testing is fuzzing. Fuzzing explores a target program’s input space by automatically generating test cases to uncover hidden faults. One of the main fuzzing techniques is generation-based fuzzing, which generates inputs from scratch based on grammar or valid corpus [6]. Following the generation of a new test case, differential testing techniques are employed to ascertain the presence of compiler bugs. The main problem with this approach is that the process of differential testing will take a long testing time and resources while only detecting a relatively small number of compiler bugs [7]. For instance, the authors of Csmith [8] spent three years detecting 325 C compiler bugs, and the authors of Yet Another Random Program Generator (YARPGen) [9] spent two years detecting about 220 C and C++ compiler bugs. Most codes generated by these fuzzers do not reveal compiler bugs, and we categorize such codes as normal codes. Conversely, the remaining codes that can reveal compiler bugs are referred to as bug codes.

Some studies aim to enhance the efficiency of fuzzers by prioritizing the generated test cases. They suggest that certain characteristics in bug codes may be capable of triggering compiler bugs. For example, in the state-of-the-art (SOTA) approach, COP [7] proposes to use machine learning methods to predict code coverage of test cases. Then, they arrange the original test cases in order of priority, favoring those with distinct code coverage, to expedite the detection of new bugs. In software testing, increasing the code coverage of the test cases for the target software is often considered a substitute for expanding the scope of testing. Codes with similar testing capabilities can assess similar compiler functionalities. Consequently, they can minimize testing redundancy by categorizing test cases based on their predicted coverage.

However, these methods face several problems. The first problem is the model’s prediction accuracy. Some methods require bug codes as training samples and traditional machine learning algorithms demand substantial training data to yield satisfactory results. Usually, the proportion of bug codes within the overall codes is quite small. Gathering sufficient training samples is time-consuming, especially for higher compiler versions. This scarcity of training data hinders the model’s ability to acquire comprehensive insights from the target programs, let alone predict the code coverage of the target compiler. The second problem is the utilization of coverage. In traditional software testing, many researchers have tried to improve the bug detection rate of software by pursuing maximum coverage [10]. However, maximum coverage does not always ensure that all faults will be covered [11]. Coverage is only a proxy indicator of testing capabilities. Some researchers [8,9] tested coverage when analyzing the fuzzers’ performance, but the results were not ideal. Compared to GCC’s own test suite, the incremental coverage due to Csmith is so small as to be a negative result [8]. And this also happened in the research of YARPGen [9]. They believe that a reasonable takeaway from their results is that none of the function, line, or region coverage is very good at capturing the kind of stress testing that is generated by a random code generator [9]. The third problem is labeling coverage data. When measuring the code coverage of the compiler, it is necessary to fix it at a specific optimization level, which does not fully reflect all the compiler’s optimization processes. When using coverage to analyze codes related to compiler optimization-related bugs, codes with similar coverage should imply similar testing capabilities. However, these codes may undergo entirely different optimization processes within the compiler, potentially leading to the detection of entirely unrelated bugs.

One way to address the problem with models is through the use of the scaled pre-trained language model (PLM). The PLMs typically use unsupervised learning to uncover latent patterns and features from the extensive unlabeled data, thereby reducing the amount of labeled data required to train the model from scratch. However, these common PLMs have limited capacity to handle complex tasks due to their current size. According to [12], when PLMs are scaled while maintaining similar architectures and pre-training tasks, these large-sized PLMs can display different behaviors from smaller PLMs and show surprising abilities in solving a series of complex tasks. This finding motivates us to enhance the performance of pre-trained language models in code-related tasks by increasing their size. The pre-trained model needs to be trained on a large amount of unlabeled data, and the scaled model has a huge amount of parameters and calculation requirements, which can significantly prolong both the training and inference phases. Therefore, it becomes imperative to employ distributed training techniques [13–15] to speed up the training process. Distributed training refers to assigning the training tasks of machine learning or deep learning models to multiple computing resources for parallel computing. This method can significantly improve the training speed and ability to handle large-scale data. Distributed training can also use distributed storage and communication mechanisms to efficiently process large-scale datasets. When it is necessary to process many test codes, distributed computing can distribute inference tasks to multiple computing nodes and process input data in parallel, thereby improving processing speed and efficiency.

As the model size increases, its ability to learn semantic and structural information from the code becomes stronger. Distributed training can help us process test cases in a relatively short period of time, which provides us with a fresh perspective on prioritizing test cases for compiler testing. Information about the semantics and structure of the codes are highly related to the function of the compiler. Given our capability to accurately discern the deep features within different codes, it prompts the question of why we continue to rely on coverage—a less precise metric—to assess code testing capabilities. Instead, we can extract code representations that can effectively represent the structure and semantics information of source code from deep learning models as surrogate indicators of the testing capabilities. Compared with using coverage, the utilization of code representations allows for the direct inference of testing capabilities based on source code information. Some models like CodeBERT [16], C-BERT [17], and GraphcodeBERT [18] obtain the code representations by analyzing the codes’ abstract syntax tree (AST). Since the compiler optimizes two codes with the same AST in a consistent manner, the code representations obtained from the AST remain consistent in such cases. By identifying the differences in the code representations among different codes, we can effectively discern the variations in their compiler testing capabilities. The key insight here is that codes with similar semantic and structural information should have similar testing capabilities, and code representations are obtained from semantic and structural information. In other words, codes with similar code representations should have similar testing capabilities.

Driven by this idea, we propose the first way to optimize compiler testing by clustering test cases in the code representation space. First, we select a programming language model and pre-train the model on a large number of random codes generated by the target fuzzer to learn some basic features in advance. Subsequently, we assemble a set of codes known to trigger compiler bugs. With this data in hand, we proceed to train two models: a binary classification model designed to predict bug-revealing scores and a multi-classification model aimed at deriving code representations. These code representations enable us to categorize test codes into different groups through the application of an automatic clustering algorithm. Then, we sequentially select the code with the highest bug-revealing score from each group to include in the final sequence.

To evaluate the effectiveness of Clustering by Code Representation (C-Core), we choose GCC and LLVM as the subjects of our study. We generate all the training and testing sets for prioritization by Csmith, which is a famous generative fuzzer. The experiments are conducted in two application scenarios: utilizing historical data of a lower-version compiler to test the lower-version compiler and applying the same approach to a higher-version compiler. We employ the commonly used metric average percentage of faults detected (APFD) [19] and saved time in testing to measure the effectiveness of C-CORE. The experimental results demonstrate that, in comparison to the state-of-the-art methods, C-CORE enhances the average APFD values from 0.868 to 0.933 and reduces overall test time from 77.7% to 42.8% of original time across multiple scenarios. The higher APFD reflects that C-CORE excels in distinguishing the testing capabilities of test codes compared to previous methods, effectively discerning valuable test cases from random ones. At the same time, the lower overall time consumption shows that C-CORE attains these improvements in effectiveness without sacrificing time efficiency. To summarize, C-CORE makes the following contributions:

•   To the best of our knowledge, we are the first to employ code representations obtained from large language models as the alternative indicator of code testing capabilities.

•   We design C-CORE, a novel framework for prioritizing test cases of compilers based on the code representations. We implement this framework based on several different configurations and discuss their respective performance.

•   We conduct extensive experiments to evaluate the effectiveness of code representation. The result outperforms the approaches using predicted coverage by 1.1% to 12.3% in terms of APFD value and achieving a remarkable 159.1% overall reduction in testing time. C-CORE excels in distinguishing compiler functions and accelerates the detection of new bugs.

2  Related Work

Compilers fuzzers. Automatically generated random codes are the main source of compiler test cases. The fuzzers can generate many random codes that conform to the language rules in a short time. Csmith [8] can generate well-formed codes with a single meaning according to the C standard. They use complex heuristics to avoid generating C programs with undefined behavior. During generation, Csmith also performs certain safety checks and creates a code fragment only if all safety checks pass. In [20], they modify Csmith to generate programs with additional language features. Their method can support mutexes and atomic variables, as well as system calls to loads from and stores to memory and read-modify-writes of memory locations. Furthermore, YARPGen [9] can generate expressive programs that avoid undefined behavior without using dynamic checks and wrapper functions, thus improving generation efficiency. Another development direction is to restrict the set of language features available in fuzzers for generating a specific program. HiCOND [21] utilizes historical data to increase configuration diversification of fuzzer. They infer the range of each option in a test configuration from historical data, then use particle swarm optimization (PSO) to search for some sets of configurations that can lead to diverse test programs. The codes generated on these configurations are more likely to trigger new compiler bugs. In addition to tuning the fuzzer itself, program mutation [22,23] can construct new programs to expand the search space by adding, deleting, and modifying the original program from the fuzzer. Hermes [22] leverages the values of all variables at run-time w.r.t. the program inputs and proposes a bottom-up expression-building algorithm that safely avoids undefined behaviors to support mutation in the program’s live and dead regions. Their technique significantly increases the variant space by removing the restriction of mutating only the dead regions. MTFuzz [24] uses different tasks to predict the relationship between program inputs and different aspects of program behavior, like different types of edge coverage. Then, the model can learn a compact embedding of high-dimensional program input spaces. After the model is trained, they use the salience score of the embedding layer to guide the subsequent program generation. DIPROM [23] proposes a novel diversity-guided program mutation to generate test programs for compiler testing. They remove the dead code regions in given programs and construct a set of variants from seed programs by selecting mutation operators to prune or insert code snippets in the live code testing. NNSmith [25] generates a model framework through the constraints between the solved operators. Then, they use the gradient search algorithm to search for appropriate model weights by constraining the data gradient in the back-propagation on the model to generate a whole test model for deep learning compilers. Different from them, C-CORE does not affect the test case generation process. Our approach can be used as an additional strategy for the above generative fuzzers. After the fuzzers generate many test cases, our approach can prioritize the test cases to improve test efficiency further.

Test case prioritization. Test case prioritization [26–28] is a technique to accelerate software regression testing. It speeds up software testing by rearranging the sequence of test cases so that those test cases that can reveal software bugs are detected earlier. Then, the bugs can be repaired earlier. In [29], they significantly reduced the required pair-wise comparisons in AHP-based prioritization by clustering test cases based on their dynamic runtime behavior. Their study shows that the resulting prioritization is more effective than existing coverage-based prioritization techniques in terms of fault detection rate. The authors in [30] first transformed each test code to a vector by extracting the fault-relevant token features regarding programs as text and then rank them according to their Manhattan distances. LET [31] first identifies a set of features of test codes and trains two models to predict the bug-revealing score and execution time of each test program, then ranks them according to the bug-revealing score per unit time. COP [7] continue the work of LET [31]. They use the same code features to train a new model for predicting code coverage statically. Then, they cluster test codes by predicted coverage to cluster codes with similar testing capabilities. The authors in [32] used the historical bugs of the software to build a defect prediction neural network model. They use the model to estimate the fault-proneness of each area of the source code and then improve the coverage-based TCP methods by incorporating estimations into it. In [33], the authors adopted a unique approach by selecting a specific layer within the deep learning model as a breakpoint. They subsequently arrange all test cases by evaluating the distribution difference in the output across this breakpoint layer. Test cases exhibiting more substantial disparities in neuron output distribution are deemed more likely to reveal bugs during metamorphic tests. The authors in [34] used a combination of text embedding, text similarity, and clustering techniques to identify similar test cases specified in natural language. The method can reduce the redundant test cases that might exist in the test suite and decrease the cost of test execution. Unlike them, C-CORE uses the scaled pre-trained model to learn semantic and structural features from source code instead of text features and manually designing code features. And we no longer use coverage but code representations to represent the testing capabilities of the codes. The code representations are obtained from a multi-classification model.

3  Preliminaries

3.1 Differential Testing Techniques

Before embarking on compiler testing, it is imperative to address the oracle problem, which entails determining whether a given test case effectively triggers a bug. In the context of compiler testing, it is important to note that beyond compiler crashes, certain bug codes may not be readily identifiable, such as the output of wrong results. An efficient solution is combining generative fuzzers with differential testing techniques to determine whether these codes indeed trigger compiler bugs. These randomly generated codes can produce a checksum of the code’s non-pointer global variables at the end of execution. If the output checksum varies across different scenarios for the same code, it indicates the presence of a compiler bug. Several differential testing techniques are available, including Randomized Differential Testing (RDT) [35], Different Optimization Levels (DOL) [36], and Equivalence Modulo Inputs (EMI) [37].

•   RDT requires more than two different compilers. The same code is executed on each compiler, adhering to identical specifications. If discrepancies emerge in the outcomes, it indicates the presence of bugs in at least one of the compilers.

•   DOL is a variant of RDT, which only requires one compiler with an adjustable optimization level. Compiler bugs can be discerned if variations in results occur when the same code is executed under different optimization levels.

•   EMI generates some equivalent variants from a seed program each iteration. These variants alter the seed program while preserving its semantics. The identification of compiler bugs transpires when differences emerge in the outcomes between the original seed program and any of its variants.

Among these three methods, DOL stands out as the swiftest, and hence, we choose it as our preferred approach for bug detection.

3.2 Source of Code Representation

Deep learning (DL) models [38,39] are composed of multiple layers. They can learn data representations with multiple higher levels of abstraction [40]. We need a DL model that can apply the AST or the variant of the AST. In the study of [41], they use AST probes to evaluate five pre-trained models about their understanding of programming languages syntax, and the results show that GraphcodeBERT [18] performs best. GraphcodeBERT [18] is a pre-trained model for the task of programming language and natural language. GraphcodeBERT uses a multi-layer bidirectional transformer architecture. Unlike the previous PL models, GraphcodeBERT is the first PL model that leverages data flow graph (DFG) to learn code representation. DFG is obtained from AST but is smaller and more efficient. We can scale GraphcodeBERT by augmenting the number and dimensions of the hidden layers within the model. Importantly, the fundamental transformer architecture and the pre-training task design remain unaltered. To enhance the model’s capacity for understanding the semantic structure of code, GraphcodeBERT incorporates two novel structure-aware pre-training tasks in addition to the conventional masked language model (MLM) for self-learning. These tasks include edge prediction and node alignment.

•   Masked Language Modeling is a pre-training task proposed by BERT [42]. GraphCodeBERT first sample randomly 15% of the tokens from the source code and paired comment, and then replace them with a [MASK] token 80% of the time, with a random token 10% of the time, and leaves them unchanged 10% of the time.

•   Edge Prediction is designed to learn the relation of “where-the-value-comes-from” among variables from data flow. The researchers randomly sample 20% of nodes in the data flow and mask direct edges connecting these sampled nodes by adding an infinitely negative value in the mask matrix, then predict these masked edges.

•   Node Alignment is designed to align representation between source code and data flow. The researchers randomly sample 20% nodes in the graph, mask edges between code tokens and sampled nodes, and then predict masked edges.

3.3 Clustering Algorithm

The clustering algorithms can be classified into hard clustering [43,44] and fuzzy clustering [45,46]. The latter is more adversarial to noise, but our approach necessitates the explicit classification of each test case into a specific class. Furthermore, our choice of clustering algorithm presents two notable limitations. Firstly, the required number of clusters for the test cases is not known in advance, thus demanding algorithms capable of automatically determining the optimal cluster count. Secondly, considering the substantial volume of test codes requiring clustering, computational efficiency becomes a crucial factor in our approach. Considering the factors mentioned above, our approach adopts the X-means algorithm [47], which is an extension of the K-means algorithm [48]. Specifically, the algorithm requires users to specify the range of K before its initiation. Once initiated, the X-mean algorithm proceeds by employing the smallest k for the K-mean algorithm and utilizes a kd-tree to expedite computation. Subsequently, on each of the resulting classes, the X-mean algorithm conducts 2-mean clustering, known for its insensitivity to local optima, and computes Bayesian Information Criterion (BIC) scores for the data within each cluster before and after the 2-means clustering. This evaluation determines whether a specific cluster should be split into two new clusters. In other words, if the BIC score of the latter is higher, the division is retained, and the algorithm continues; otherwise, it is not retained. This iterative process continues until the number of clusters reaches the predefined maximum value or each cluster no longer meets the criteria for further division based on BIC scores.

4  Approaches

Fig. 1 provides an overview of our approach. In this section, we present a novel framework to prioritize test cases and explain its details. Our approach is divided into two stages: the learning stage and the scheduling stage.

Figure 1: Overview of C-CORE. All of our data is generated through Csmith. C-CORE comprises two key stages. In the learning stage, we employ GraphcodeBERT as our base model for pre-training. By incorporating various classification tasks, we derive two downstream models. In the scheduling stage, the codes are clustered according to their code representation. Then, we select the codes with the highest bug-revealing scores from each cluster. This ranking process continues until all codes are included in the final test sequence

4.1 Learning Stage

The primary objective of the learning stage is to prepare models that have gained a deep understanding of the semantic and structural intricacies of the target language and to derive the bug-revealing scores and code representations of the test cases. Given the considerable number of model parameters, training data, and testing data, this stage necessitates the utilization of a distributed learning framework to expedite the process.

4.1.1 Pre-Training and Base Model

When utilizing machine learning methods to detect compiler bugs, the issue of data shortage cannot be overlooked. Collecting a sufficient amount of bug codes can be a time-consuming task. Furthermore, extracting features related to compiler bugs from a limited number of historical bug codes is also challenging. Therefore, we propose to use a scaled language pre-training model to facilitate unsupervised learning on extensive collections of unlabeled random code snippets. The base model in our approach is GraphcodeBERT, which has proven effective in pre-training source code and other related tasks. We scale its size while keeping its internal structure and the pre-training tasks unchanged. This can give it a better ability to learn the common features of the code, thereby enhancing the model’s generalization ability and improving the accuracy of downstream classification tasks.

4.1.2 Downstream Model

In our method, we need two downstream models after the base model. Taking into consideration that a bug may manifest in a specific section of the compiler due to the complexity of its implementation or its high correlation with the entire compiler. Furthermore, considering that the original bug may have undergone partial modifications, regions with a history of bugs are more prone to generating new bugs compared to regions where no bugs have been previously identified. To address this, we opt for a binary classification model to predict the bug-revealing score for each test case. Following training on both normal codes and bug codes, we can estimate the likelihood of revealing bugs by examining the sigmoid value outputted by the binary classification model during inference.

However, certain compiler regions may have more relevant training test cases compared to others. Focusing solely on bug-revealing scores may result in consistently ranking codes associated with these regions higher. These codes might repeatedly trigger existing bugs, potentially delaying or preventing the discovery of new bugs. To mitigate this issue, we employ a multi-classification model to derive code representations that incorporate diverse bug information from different regions, thereby enhancing the efficiency of our approach.

Build. To facilitate a fair comparison of different sources of code representations and to consider the challenge of collecting bug-triggering codes, we adopt the same historical data batch for training both the binary classification model and the multi-classification model in each experiment, using different tags for distinct tasks. For GCC and LLVM, which we employ in our experiments, we gather bug codes along with an equal number of normal codes. In the binary classification task, bug codes are designated as positive samples and normal codes as negative samples. In the multi-classification task, we aim to identify the compiler bugs triggered by the bug codes and utilize the corresponding bugs as labels. However, if we want to know precisely which compiler bug each bug code corresponds to, we need to submit many reports and wait for the developer to reply. This process will take too long to test. Therefore, we use the method correcting commits [36] to classify the bugs. Authors in [36] proposed that when a test code fails on an early version of the compiler, we can check subsequent compiler commits and determine which commits correct the bugs. By treating bugs corrected in the same commit as identical, we can approximate the labels for each bug code. We construct our classification models based on the pre-trained model to inherit its parameters. Given the limited data available for classification, we employ ten-fold cross-validation to select the optimal model configuration.

Extract. After training, we need to extract different data from the two models in the inference phase of the test case. Since this part is very time-consuming, we use a distributed framework to reduce the processing time of test cases. In the binary classification model, we take the predicted value (the sigmoid value output by the binary classification model) of the positive sample as the test case’s bug-revealing score. In the multi-classification model, we utilize one of the hidden layers as the code representation of the test cases. According to our subsequent experiments, the effectiveness of choosing the penultimate layer (11th layer) is the best, and that is our final choice. More specifically, let us denote each model as

M={In,L1,L2,…L12,FCs,Out}(1)

where In is the data processing part, Li is the i-th hidden layer, FCs are some fully connected layers used for downstream tasks, and Out is the final output of the model.

For the binary classification model, the Out is the score of a positive sample, and we use the Out as the bug trigger score for each test case. For the multi-classification model, we take out Lk (1≤k≤12) as the code representation, and Lk is the layer most relevant to compiler bugs among all hidden layers. To evaluate the impact of the sources of code representation, we also collect Lk from both the binary classification model and the pre-trained model.

4.2 Scheduling Stage

The purpose of the scheduling stage is to cluster the test cases based on the similarity of their code representations. Subsequently, we select the test cases, one at a time, that are most likely to trigger compiler bugs and add them to the final sequence.

4.2.1 Cluster

After obtaining the code representations of test cases, we cluster them into different groups based on their distance in the code representation space. The code representation space consists of the vectors from the hidden layer Lk, and each point in the space represents a test code. Within this space, the points that belong to the same group are expected to possess similar testing capabilities. Assuming that the code representations encapsulate sufficient information, the test codes represented by points within the same group should share similar language characteristics. Consequently, they are more prone to evaluating similar compiler functions and potentially triggering similar bugs.

In clustering, we need to find the optimal number of clusters by X-mean algorithm [47]. It can automatically search for the most suitable value of k within the specified range [kmin,kmax]. And we measure the distance between code representations to decide the groups of the test cases. Depending on the distance metric used and the maximum number of clusters, we express the test result after clustering as (Lk,Metric,Max_N). Because clustering is a time-consuming task, we choose Manhattan Distance, a widely used and efficient implementation of distance metric as Metric. For any two vectors vi=(xi1,xi2,...,xim) and vj=(xj1,xj2,...,xjm), the distance metric implemented based on Manhattan distance is calculated as formula (2).

Man(vi,vj)=∑k=1m|xik−xjk|(2)

Another challenge we must address is determining the appropriate upper limit, denoted as Max_N, for automatic clustering. A small upper limit restricts the search range, while an excessively large upper limit introduces significant time overhead. The X-mean algorithm, which we have implemented, increases the total number of clusters exponentially as long as it continues running. Based on our preliminary testing, we have observed that the X-mean algorithm typically yields results exceeding 64 clusters in most cases. When the upper limit for clustering is set at 64 or below, the algorithm can only generate final cluster numbers that are powers of 2, specifically 2, 4, 8, 16, 32, and 64. Considering that the actual number of unique commits is not substantial and considering the associated time consumption, setting clustering upper limits beyond 64 does not provide significant value. Therefore, we decide to set the upper limits for evaluation at 4, 8, 16, 32, 64, and 128 while utilizing multiples of 8 (such as 24 and 40) to bridge the gaps.

4.2.2 Prioritization

Prior to prioritization, two sets of data need to be prepared: the bug-revealing score and the code representation for each test code. Subsequently, we proceed to cluster the test codes into groups based on their code representations. Following this, we check each non-empty group in turn and select the test code with the largest bug-revealing score from the group when we check it. At the end of each iteration, we arrange these selected test codes in order and incorporate them into the final sequence, repeating this process until all test codes have been included.

Algorithm 4.1 formally depicts the main procedure and prioritization algorithm of C-CORE. The input is a set of test codes as C={c1,c2,…,cN}, N is the number of test codes. Lines 1 to 11 show the primary process of C-CORE. Lines 2 to 3 extract semantic and structural information from the source code text. Lines 4 to 9 cluster C to G={g1,g2,…,gM}, and M is the number of clusters, gi contains the serial number and the bug-revealing scores of the codes in it. Line 10 sends G to the function “Prioritize”, which can get the final sequence of test codes. Lines 19 to 20 select the case with the highest bug-revealing score in the current group and add it to the sequence waiting to be sorted. Then, Line 21 removes the case from that group. Lines 24 to 25 sort the cases selected in this round and add their serial numbers to the final sequence.

5  Experiments and Analysis

5.1 Subjects

In the study, we choose GCC and LLVM, which are the two most popular C compilers, as our subjects. They are chosen as the subject in most research about C compilers testing [7–9]. In order to verify that C-CORE is more advantageous than predicted coverage to measure code capabilities on various occasions, in addition to testing the acceleration effect between the same version, we also tested the acceleration effect across versions. For the experiment in GCC, we choose GCC-4.4.3 as the source of training data and GCC-4.4.3 and GCC-6.1.0 as the target of the acceleration. For the experiment in LLVM, we choose LLVM-3.0.0 as the source of training data and LLVM-3.0.0 and LLVM-4.0.0 as the target of the acceleration.

5.2 Datasets

As for pre-training, we use Csmith to generate about 300,000 C programs. In the scenario of testing GCC, we detect 1000 bug codes and 1000 normal codes by testing GCC-4.4.3 and directly use these 2000 codes as the training set of the binary classification model. At the same time, we use the method of “correcting commit” to detect these 1000 bug codes for their first version to be fixed and use these versions as their unique label. Then, we put them together with the same 1000 normal codes used in binary classification models as the training set of the representation model. When generating the test cases for GCC-4.4.3 and GCC-6.1.0, we first generate a large number of random codes. According to our investigation, there will be large fluctuations in code execution time even if the code is run in the same environment. Therefore, the difference will have a relatively large impact if the execution time is short. And for those codes that have a long execution time, we are not sure whether there is a problem with the codes or the codes just take so long to run. Therefore, we select the codes whose running time is in the middle interval in a batch of randomly generated codes to make test cases. Since the number of bugs of GCC-6.1.0 is too small, we merge the bugs found in several batches of randomly generated codes to observe obvious differences between prioritization approaches. Each batch of randomly generated codes contains 300,000 cases. In the scenario of testing LLVM, the process is the same. We put the specific information of the test cases in Table 1.

5.3 Tools and Implementations

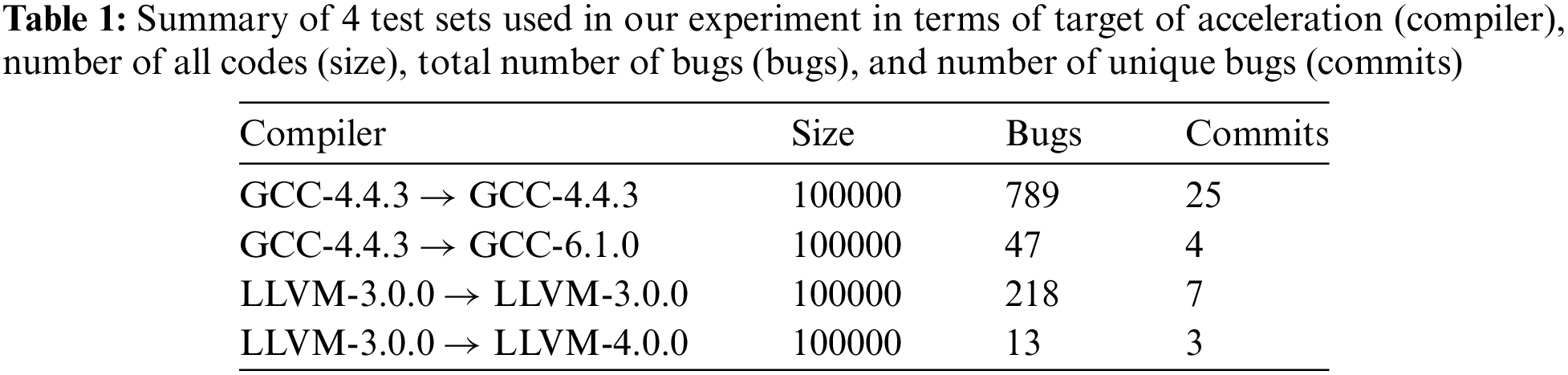
In our study, we choose Csmith [8] as the fuzzer for generating test cases. The version of Csmith we use is Csmith-2.3.0. In this version, users can adjust the configuration parameters to make the generated code more inclined to contain certain language features. In order to facilitate the reproduction of our results by other researchers, we choose to use only the default configuration to generate all experimental data.

In our approach, each test code can produce six results: compilation hang, compilation crash, execution hang, execution crash, mismatch of checksum, and pass. Compilation hang means the test code times out when compiling, and execution hang means the test code times out when executing. Among these five situations, compilation hang, compilation crash, execution crash, and mismatch of checksum would be considered to find a bug, and execution hangs and pass would be considered normal in testing. But for the sake of caution, when counting the final results, we do not count the timeout codes into any case and will exclude them from the discussion.

We use the DOL [36] technique to test compilers for that DOL is the fastest among the DOL, RDT, and EMI. The optimization levels of GCC can be adjusted to 5 levels: −O0, −O1, −O2, −Os, and −O3. The degree of optimization is gradually increasing in this order, and the O0 level is almost not optimized. With this in mind, we set the order of the optimization levels to test as −O0, −O3, −Os, −O2 and −O1. Because if a code can trigger compiler bugs, then the test process between −O0 and −O3 with the largest difference in optimization level is the most likely to find the bugs. Once the bugs are found, we can return the result immediately to save time for detection.

The original input size for GraphCodeBERT is 256. To maximize the utilization of code input information, we expand the input size to 1024. Due to GPU memory constraints, we do not scale other aspects of the model. Our distributed learning framework is implemented in PyTorch, and the environment runs on a single machine equipped with eight GPUs. The experiments are conducted on a workstation featuring a twelve-core Intel Xeon E5-2685 CPU, 120 GB of memory, a GeForce RTX 2080 Ti with 10GB VRAM, and an Ubuntu 16.04 operating system. When applying the X-mean algorithm to cluster the initial test cases, we set the lower limit at 2, the upper limit at 32, and the maximum iterations at 1000. To assess the influence of various upper limits, we vary the upper limit, ranging from 4 to 128 at specified intervals.

5.4 Evaluation Approaches

To measure the effectiveness of C-CORE, we compare it with various approaches. We test each one 20 times with the same 20 random seeds and calculate the average results to mitigate the error caused by randomness.

(a)   Random order. This means that the test cases are executed in the original order without using any acceleration approach, and it serves as the baseline of overall effectiveness in our experiments.

(b)   Text-vector based algorithm. The method comes from [30]. We extract the text features from source codes according to the method in the paper and sort the text vectors using the adaptive search algorithm.

(c)   Greedy algorithm. The method means only the binary classification model is used to predict the bug-revealing score, but no clustering method is used. We directly move the test case with the highest bug-revealing score in the remaining test cases to the final sequence. Therefore, comparing it with other approaches that use clustering can show the effectiveness of their clustering component.

(d)   Predicted code coverage from GBDT(Gradient Boosting Decision Tree). The method comes from COP [7]. We keep the same settings for gradient boosting and maintain the file alignment when predicting coverage between different versions of compilers. We conduct experiments on the branch coverage (measure whether each branch point in the program has been executed), which has better effectiveness than line coverage.

(e)   Predicted code coverage from GraphcodeBERT. Since the GBDT method is quite different from our method, we use the same model structure of C-CORE to train a regression model to predict coverage. And we keep the same way in COP to obtain all coverage data.

The specific way to compare the effectiveness of acceleration among these ways is as follows. After getting the final sequence, we test it with a bug hunter and record the number of used cases and the time spent every time a bug is first detected. That is, the times of recording are equal to the number of unique bugs. According to this record, we can calculate the APFD and time-saving. APFD can reflect the difference in the ability of different strategies to identify code testing capabilities. There are analogous indicators within the realm of software testing. For instance, the cost-sensitive weighted average percentage of faults detected (APFDc) takes into account both the expense and gravity of distinct defects. Additionally, the normalized average fault detection percentage (NAPFD) addresses scenarios wherein test cases might not be able to be completely executed due to resource limitations. However, in our testing scenario, we only have information about the type of each defect, and nothing else distinguishes them. Furthermore, all test cases can be executed in their entirety. Therefore, APFD is our ultimate choice. Time-saving can display the overall acceleration effectiveness after considering the time consumption of the strategies. The overall time includes the inference time of the score prediction model, the inference time of the model used to obtain code representation or coverage, and the time used by clustering. The inference time is greatly reduced through the distributed training learning framework. Since the training phase is one-time, we do not count the time of this part but mainly focus on the acceleration effectiveness in the inference phase. We calculate the average time spent generating test case vectors under the eight-core and single-core multiple times. The result shows that the speedup of eight-core to single-core is about 2.25 times.

APFD for a test case prioritization can be calculated by the formula (3). TFj refers to the first test code in prioritized test cases that detects the ith bug, n refers to the total number of test cases, and m refers to the number of unique bugs detected by the test cases.

APFD=1−∑i=0mTFinm+12n(3)

Time-saving on detecting r bugs can be calculated according to the method form formula (4). TRO(r) refers to the time spent on detecting r bugs with method RO, and TACC(r) refers to the time spent on detecting r bugs with one acceleration approach.

Time-saving(r)=TRO(r)−TACC(r)TRO(r)(4)

5.5 Analysis

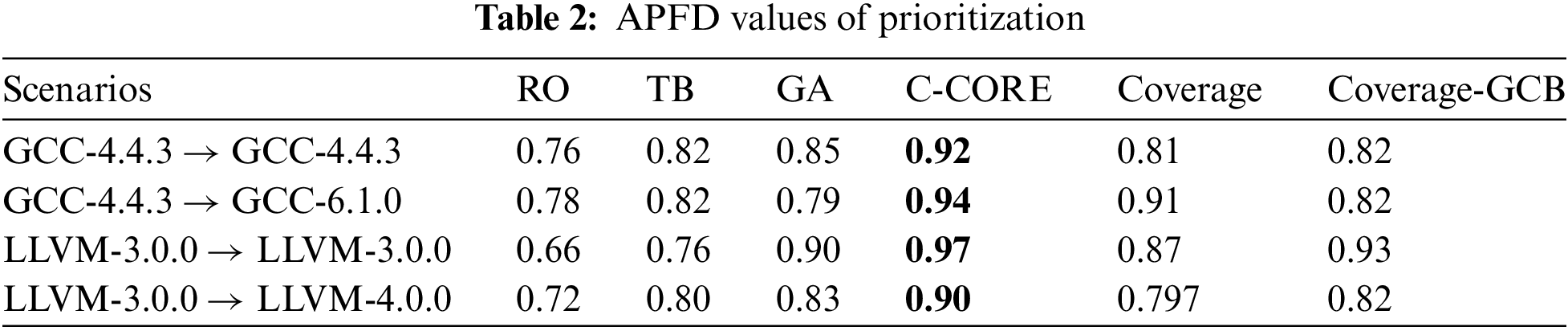
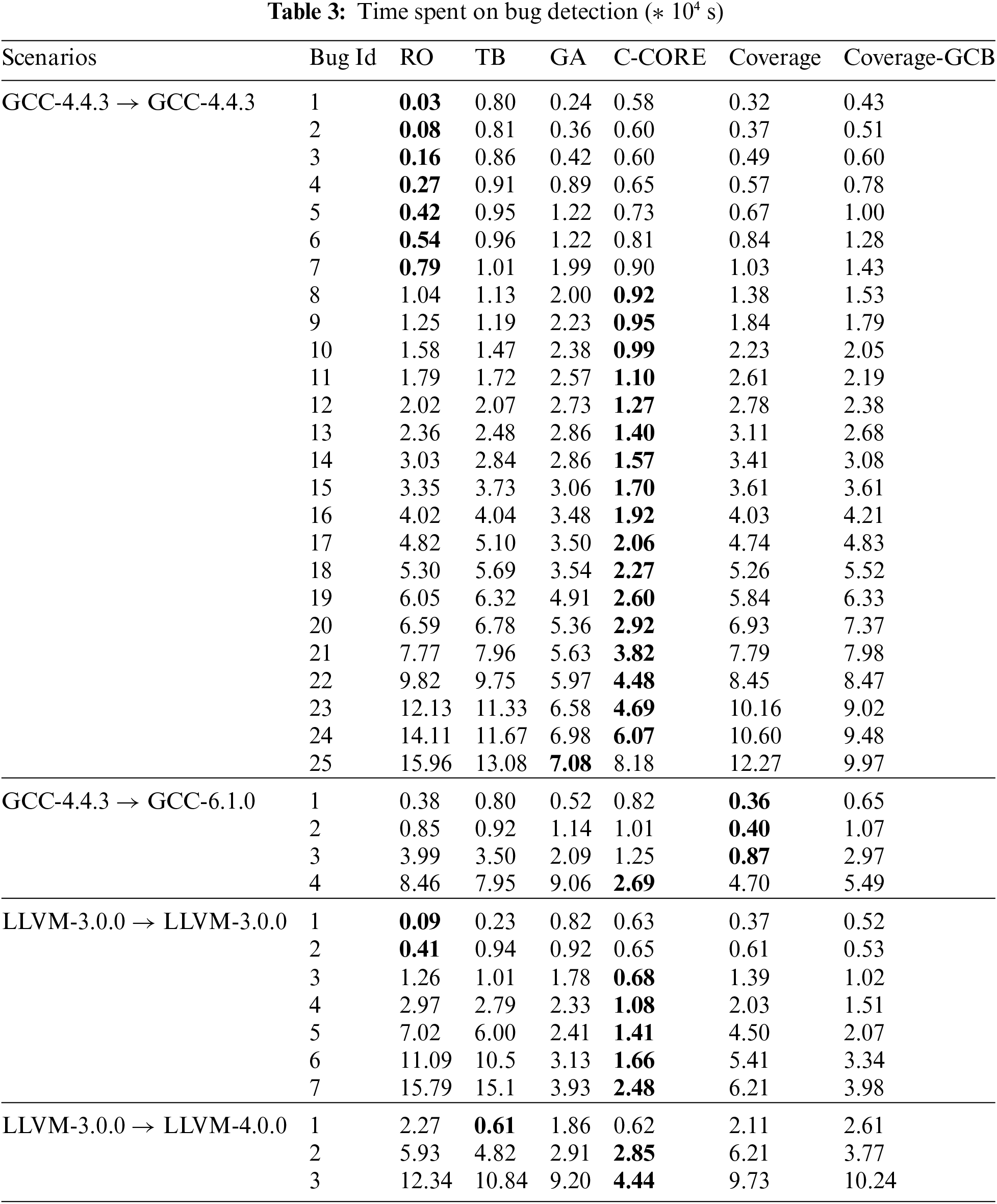
We will present the results in two formats: a line chart illustrating detected bugs and total test cases consumed and tables containing data on APFD and the time spent on detecting each bug. In the line chart, as shown in Fig. 2, the x-axis displays unique detected bugs, while the y-axis represents the number of checked test cases. The legend includes the following categories: “RO” (Random Order), “TB” (Sorting by Text-Based Vector), “GA” (Greedy Algorithm utilizing only bug-revealing scores), “C-CORE” (Clustering by Code Representation), “Coverage” (Clustering by predicted branch coverage from COP [7]) and “Coverage-GCB” (Clustering by predicted branch coverage from GraphCodeBERT-based method). In Tables 2 and 3, the “Scenarios” column indicates the source of training data and the target of acceleration. The remaining columns correspond to the categories mentioned in the line chart legend. In Table 3, “Bug” refers to the count of unique detected bugs.

Figure 2: The results of testing the same version of the compiler

5.5.1 The Ability of Distinguishing Test Capability

First, we want to discuss whether C-CORE is superior in distinguishing code with varying test capabilities compared to approaches utilizing predicted coverage. Specifically, we compare their performances based on their APFD values and the line chart depicting test case consumption during bug detection. In the line chart, both RO and GA serve as the baseline. GA and other approaches with clustering use the same bug-revealing score, so the effectiveness of clustering can be seen by comparing them with GA. We cluster the test cases according to code representation or coverage and select them in turn. This strategy enables us to, to some extent, mitigate the repetitive testing of codes with similar testing capabilities. Generally, in software testing, methods that employ more detailed coverage information tend to exhibit greater proficiency in distinguishing testing capabilities. This experience can also be used to compare code representation and predicted coverage. Enhanced separation reduces the likelihood of continuous testing of codes with similar testing capabilities, thereby increasing the chances of uncovering new bugs. The degree of separation is related to the information relied on when clustering.

By observing Fig. 2, we can find that when testing in the same version, the C-CORE line (in red) consistently resides at the bottom, and the gaps between C-CORE and other approaches are very obvious. The findings from cross-version testing, depicted in Fig. 3, reveal a similar trend. In the previous segment of the line chart, the C-CORE line is slightly lower than the lines representing strategies utilizing coverage and text vectors. However, it consistently returns to the bottom in the latter segment. The line chart results indicate that C-CORE performs at least as well as strategies employing predicted coverage and significantly outperforms them when a sufficient number of cases are available. Notably, the text-based strategy (TB), which relies solely on textual information, is evidently less effective than methods incorporating additional information. For a quantitative assessment, refer to the APFD values presented in Table 2. In the context of testing within the same version, APFD significantly outperforms others, aligning with the trends observed in the line chart. In the context of cross-version testing, C-CORE still maintains a clear advantage.

Figure 3: The results of testing the higher version of the compile

At the same time, by observing the strategies using predicted coverage obtained by GBDT and scaling GraphCodeBERT, we can find that the results obtained by these two models are relatively close. They are all inferior to the results of C-CORE, indicating that differences in coverage prediction models do not account for the observed variations in results. Instead, the key distinction lies in code representation vs. predicted coverage. Code representation proves superior in discerning the testing capabilities of code segments as it inherently factors in the code’s self-determined characteristics. When the compiler processes two codes with similar semantics and structures, their functions to be tested are also similar. Moreover, while coverage can distinguish compiler functions, obtaining the necessary training data for fine-grained coverage testing is laborious and resource-intensive. In contrast, pre-training on a substantial dataset of readily available random codes allows us to acquire a vast array of code features. Furthermore, larger language models can extract more information from source codes than their smaller counterparts, rendering code representation more precise and enhancing its ability to distinguish testing capabilities.

5.5.2 Overall Effectiveness of Acceleration

More detailed information can enhance our ability to distinguish between different testing capabilities. However, it is essential to acknowledge that acquiring this additional information will inevitably consume more time. Once we have established that code representation offers a notable advantage in distinguishing code testing capabilities, our next step is to evaluate its practical acceleration effectiveness. In Table 3, we present the overall effectiveness results, with the shortest time spent on detecting each unique bug highlighted.

In the case of GCC-4.4.3 and LLVM-3.0.0, which involve a sufficient number of bug cases, it is evident that RO consistently identifies new bugs at the outset. However, after a few initial bugs, almost all new bugs are first discovered by C-CORE. In the case of GCC-6.1.0 and LLVM-4.0.0, which have a limited number of bug cases, the situation is a little different from before. In GCC-6.1.0, Coverage is the first to identify the initial three new bugs, but C-CORE continues to excel in identifying subsequent new bugs. Other approaches take roughly twice as long as C-CORE to discover all new bugs. In LLVM-4.0.0, GA is the first to identify the first two bugs, but C-CORE closely trails them. Again, other approaches require more than twice the time of C-CORE to uncover all new bugs. Considering the data from Table 3, C-CORE reduces testing time by more than 30% in 66% of cases and by more than 50% in 46% of cases. We calculate the overall time savings for TB, GA, C-CORE, Coverage, and Coverage-GCB in comparison to RO, which amount to 7%, 32%, 57%, 17%, and 22%, respectively. Notably, C-CORE achieves the highest reduction of 57%, showcasing its acceleration effectiveness. On the other hand, C-CORE accelerates the discovery of 72% of new bugs compared to RO and 82% of new bugs compared to GA. The best-performing method using coverage only accelerates the discovery of 46% of the bugs compared to RO and 41% of the bugs compared to GA. This demonstrates that C-CORE, when compared to approaches utilizing predicted coverage, significantly speeds up a more substantial number of test cases.

The result is determined by the composition of the overall time, which includes two parts: the preparation time and the time required to find unique bugs in the prioritized sequence. We set the preparation time of RO to zero. For all approaches except RO, the source of bug-revealing scores is the same model, so the preparation time difference among these approaches to obtain scores is negligible. As for C-CORE and predicted coverage from GBDT, the preparation time disparity arises from model inference. Scaled GraphCodeBERT possesses a complex neural network architecture with a higher number of parameters than GBDT. Additionally, the clustering process contributes to the time difference. Since we do not reduce the dimension of the original code representation vector, clustering incurs a relatively high time cost. We process coverage data using the method from COP (that is, to remove those compiler files with coverage differences of less than 5% from the mean tested coverage in 99% of test cases). This leads to a lower dimension for the coverage vector, resulting in differences in clustering costs. As for the predicted coverage from scaled GraphCodeBERT, compared with C-CORE, the inference time is almost the same. So, the preparation time gap between them mainly comes from clustering. Therefore, when the number of bugs is large enough, the probability of RO bumping into several new bugs is not low. At the same time, because no preparation time is required, the time to discover the first few new bugs of RO is very low. On the contrary, C-CORE has the lengthiest preparation time, making its overall time to discover the initial new bugs the longest. However, the time spent detecting additional new bugs is primarily influenced by the approach’s effectiveness in test case prioritization. C-CORE excels in distinguishing code testing capabilities, allowing it to catch up with and surpass other approaches. In summary, the advantages of using code representation effectively offset the additional time overhead, and C-CORE demonstrates significantly superior overall effectiveness compared to strategies relying on predicted coverage.

5.5.3 Impact on the Pre-Training Process

One of our primary concerns revolves around the necessity of employing a scaled pre-trained model, specifically, whether pre-training the base model on unlabeled random codes can enhance the efficacy of C-CORE. Specifically, we compare C-CORE in the following four cases. The first is that neither the binary classification model nor the multi-classification model is pre-trained before training. The second is that only the binary classification model is pre-trained. The third is that only the multi-classification model is pre-trained. The fourth is that both models are pre-trained, which is the final version of C-CORE. The results are shown in Fig. 4. To simplify the notation, we use “NN”, “YN”, “NY”, and “YY” to denote these four cases, with the first “Y” or “N” indicating whether the binary classification model is pre-trained, and the second “Y” or “N” indicating whether the multi-classification model is pre-trained. Fig. 4 illustrates that, among these four scenarios, the “YY” curve lies closest to the bottom, indicating superior performance compared to both “YN” and “NY”. Conversely, the “NN” curve is situated closer to the top than both “YN” and “NY”. This observation underscores the significance of pre-training. Pre-training the base model with random codes from the same fuzzer unequivocally enhances C-CORE’s effectiveness. This is primarily because the amount of data available for training both the binary classification model and the multi-classification model is insufficient. And the modes will be greatly affected by the randomness of the code. Pre-training enables the models to proactively acquire certain shared code features, a task that might be challenging with limited dataset sizes.

Figure 4: Results of four cases about pre-training process

5.5.4 Impact on the Code Representation Model and the Location of the Hidden Layer

We choose the multi-classification model as our final code representations model because it leverages extra labels, allowing it to extract more information from source codes. Now, we need to confirm whether the extra information is useful for prioritization by comparing the use of the pre-trained model, binary classification model, and multi-classification model. However, the extracted information is scattered in each hidden layer. We need to find out which layer is the best to obtain code representation first. Due to the large amount of data and the slight difference in time overhead between them, we choose to employ the APFD value, presented in the form of a histogram, to assess the effectiveness of each layer in prioritization. The results are shown in Fig. 5. Among them, the two classification models have two extra layers than the pre-trained model. Among these results, it is evident that the 11th hidden layer consistently delivers the best performance across all three scenarios. This may be attributed to its position as the second deepest hidden layer, inheriting valuable features from the base model while remaining less influenced by downstream tasks compared to the final layer. Therefore, the 11th layer can keep the most in-depth information. Then, we use the data from the 11th layer to compare the three code representations. The results are presented in Fig. 6. As we expected, the line corresponding to the multi-classification model is closest to the bottom, signifying its superior capability to distinguish test cases. We believe this superiority stems from the additional bug information introduced, which assists the model in identifying functions with historical bugs. Regions previously affected by bugs tend to have a higher likelihood of harboring new bugs in the future compared to bug-free areas. Therefore, the inclusion of more bug-related information accelerates the detection of new bugs.

Figure 5: Impact of the hidden layers

Figure 6: Impact of the source of code representation on prioritization

5.5.5 Impact on the Clustering Upper Limit

We choose automatic clustering because it is impossible to determine an optimal number of clusters in advance. In theory, setting a higher exploration limit increases the likelihood of discovering an optimal solution. However, this approach does not account for time costs. A larger exploration space entails greater time overhead, potentially diminishing the overall effectiveness of clustering with a high upper limit compared to a lower one. To explore this, we do an experiment with automatic cluster numbers set at 4, 8, 16, 32, 64, and 128, as outlined in the Approaches section. In order to fill the vacancy, we use K-mean to conduct the experiments with the multiples of 8 as the number of clusters. The final result is shown in the Fig. 7. The blue curve represents the APFD value. The number above the blue curve represents the actual number of clusters. Since we take the average value of multiple experimental results, the results are expressed in decimal form. First of all, we need to determine whether raising the upper limit of exploration within the set search range can improve the discrimination of code testing capabilities. Observing the blue line in Fig. 7, it is evident that the values for “32”, “64” and “128” are relatively close to each other, which means their abilities to distinguish test capability of codes is similar. And when the number of clusters is greater than “32”, it is obvious that automatic clustering outperforms fixed-cluster methods. Next, we can consider the overall effectiveness. It can be seen from the red line in Fig. 7 that when the upper limit increases after “32”, the time-saving dramatically decreases for the increasing additional time overhead spent exploring in space. This phenomenon shows that a higher upper limit does not consistently yield substantial improvements in the ability to differentiate test capabilities. Instead, it may result in a significant decrease in overall effectiveness. This outcome can be attributed to the limited variety of bugs present. A slight increase in the number of clusters may not necessarily enhance effectiveness, and the substantial increase in cluster numbers significantly increases time consumption. Although a higher cluster count can improve code discrimination, the accompanying time overhead renders it impractical. Therefore, it is more reasonable to take a lower upper limit.

Figure 7: Impact of the clustering upper limit

6  Conclusion

This work proposes a novel test case prioritization framework for compiler testing named C-CORE. To address the challenge of data shortage, we introduce the scaled pre-trained model. This model facilitates the learning of common code features from a code generator, reducing the reliance on historical bug code for classification tasks. Furthermore, we propose a method for discriminating the testing capabilities of codes based on their code representations. Clustering test cases using these code representations substantially reduces the redundancy of detecting the same bugs repeatedly. To mitigate the time overhead associated with large models, we implement a distributed learning framework, significantly reducing training and inference times. We evaluate our approach using four sets of test cases, with the random order strategy serving as the baseline. In comparison to the baseline, C-CORE improves average APFD values from 0.730 to 0.933 and achieves a 57% reduction in total test time. Additionally, when compared to the best-performing coverage-based approach, C-CORE outperforms it with a 1.1% to 12.3% increase in APFD value and a remarkable 159.1% overall time-saving. These findings suggest the significant potential of code representation in replacing predicted coverage for discriminating test capabilities and accelerating test case prioritization in compilers.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions, which greatly improved the presentation of this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Wei Zhou, Xincong Jiang; data collection: Wei Zhou, Chuan Qin; analysis and interpretation of results: Wei Zhou; draft manuscript preparation: Wei Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Readers can access the test codes used in this study from https://drive.google.com/file/d/1FUU0zPL9kpIBZIG4fQh0bQQOf3sF7UZM/view?usp=drive_link.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Gao, H., Huang, W., Duan, Y. (2021). The cloud-edge-based dynamic reconfiguration to service workflow for mobile ecommerce environments: A QoS prediction perspective. ACM Transactions on Internet Technology, 21(1), 1–23. [Google Scholar]

2. Ding, A. Y., Peltonen, E., Meuser, T., Aral, A., Becker, C. et al. (2022). Roadmap for edge AI: A dagstuhl perspective. ACM SIGCOMM Computer Communication Review, 52(1), 28–33. [Google Scholar]

3. Gao, H., Duan, Y., Shao, L., Sun, X. (2021). Transformation-based processing of typed resources for multimedia sources in the IoT environment. Wireless Networks, 27, 3377–3393. [Google Scholar]

4. Zhang, R., Chu, X., Ma, R., Zhang, M., Lin, L. et al. (2022). OSTTD: Offloading of splittable tasks with topological dependence in multi-tier computing networks. IEEE Journal on Selected Areas in Communications, 41(2), 555–568. [Google Scholar]

5. Gao, H., Qin, X., Barroso, R. J. D., Hussain, W., Xu, Y. et al. (2020). Collaborative learning-based industrial IoT API recommendation for software-defined devices: The implicit knowledge discovery perspective. IEEE Transactions on Emerging Topics in Computational Intelligence, 6(1), 66–76. [Google Scholar]

6. Zhu, X., Wen, S., Camtepe, S., Xiang, Y. (2022). Fuzzing: A survey for roadmap. ACM Computing Surveys, 54(11s), 1–36. [Google Scholar]

7. Chen, J., Wang, G., Hao, D., Xiong, Y., Zhang, H. et al. (2018). Coverage prediction for accelerating compiler testing. IEEE Transactions on Software Engineering, 47(2), 261–278. [Google Scholar]

8. Yang, X., Chen, Y., Eide, E., Regehr, J. (2011). Finding and understanding bugs in c compilers. Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, San Jose, CA, USA. [Google Scholar]

9. Livinskii, V., Babokin, D., Regehr, J. (2020). Random testing for c and c++ compilers with yarpgen. Proceedings of the ACM on Programming Languages, 4(OOPSLA), 1–25. [Google Scholar]

10. Wong, W. E., Gao, R., Li, Y., Abreu, R., Wotawa, F. (2016). A survey on software fault localization. IEEE Transactions on Software Engineering, 42(8), 707–740. [Google Scholar]

11. Mukherjee, R., Patnaik, K. S. (2021). A survey on different approaches for software test case prioritization. Journal of King Saud University-Computer and Information Sciences, 33(9), 1041–1054. [Google Scholar]

12. Zhao, W. X., Zhou, K., Li, J., Tang, T., Wang, X. et al. (2023). A survey of large language models. arXiv preprint arXiv:2303.18223. [Google Scholar]

13. Shi, H., Wang, H., Ma, R., Hua, Y., Song, T. et al. (2022). Robust searching-based gradient collaborative management in intelligent transportation system. ACM Transactions on Multimedia Computing, Communications, and Applications, 20(2), 1–23. [Google Scholar]

14. Cai, Z., Ren, B., Ma, R., Guan, H., Tian, M. et al. (2023). GUARDIAN: A hardware-assisted distributed framework to enhance deep learning security. IEEE Transactions on Computational Social Systems, 10(6), 3012–3020. [Google Scholar]

15. Guo, H., Yang, Q., Wang, H., Hua, Y., Song, T. et al. (2021). Spacedml: Enabling distributed machine learning in space information networks. IEEE Network, 35(4), 82–87. [Google Scholar]

16. Feng, Z., Guo, D., Tang, D., Duan, N., Feng, X. et al. (2020). CodeBERT: A pre-trained model for programming and natural languages. arXiv preprint arXiv:2002.08155. [Google Scholar]

17. Buratti, L., Pujar, S., Bornea, M., McCarley, S., Zheng, Y. et al. (2020). Exploring software naturalness through neural language models. arXiv preprint arXiv:2006.12641. [Google Scholar]

18. Guo, D., Ren, S., Lu, S., Feng, Z., Tang, D. et al. (2020). Graphcodebert: Pre-training code representations with data flow. arXiv preprint arXiv:2009.08366. [Google Scholar]

19. Rothermel, G., Untch, R. H., Chu, C., Harrold, M. J. (2001). Prioritizing test cases for regression testing. IEEE Transactions on Software Engineering, 27(10), 929–948. [Google Scholar]

20. Morisset, R., Pawan, P., Zappa Nardelli, F. (2013). Compiler testing via a theory of sound optimisations in the C11/C++11 memory model. ACM SIGPLAN Notices, 48(6), 187–196. [Google Scholar]

21. Chen, J., Wang, G., Hao, D., Xiong, Y., Zhang, H. et al. (2019). History-guided configuration diversification for compiler test-program generation. Proceedings of the IEEE/ACM International Conference on Automated Software Engineering (ASE), San Diego, CA, USA, IEEE. [Google Scholar]

22. Sun, C., Le, V., Su, Z. (2016). Finding compiler bugs via live code mutation. Proceedings of the 2016 ACM SIGPLAN International Conference on Object-Oriented Programming, Systems, Languages, and Applications, pp. 849–863. Amsterdam, Netherlands. [Google Scholar]

23. Tang, Y., Jiang, H., Zhou, Z., Li, X., Ren, Z. et al. (2021). Detecting compiler warning defects via diversity-guided program mutation. IEEE Transactions on Software Engineering, 48(11), 4411–4432. [Google Scholar]

24. She, D., Krishna, R., Yan, L., Jana, S., Ray, B. (2020). MTFuzz: Fuzzing with a multi-task neural network. Proceedings of the 28th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, pp. 737–749. USA. [Google Scholar]

25. Liu, J., Lin, J., Ruffy, F., Tan, C., Li, J. et al. (2023). Nnsmith: Generating diverse and valid test cases for deep learning compilers. Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, vol. 2. New York, NY, USA. [Google Scholar]

26. Lou, Y., Chen, J., Zhang, L., Hao, D. (2019). A survey on regression test-case prioritization. In: Advances in Computers, vol. 113. pp. 1–46. Amsterdam, Netherland: Elsevier. [Google Scholar]

27. Rothermel, G., Harrold, M. J., Von Ronne, J., Hong, C. (2002). Empirical studies of test-suite reduction. Software Testing, Verification and Reliability, 12(4), 219–249. [Google Scholar]

28. Miller, C. (2008). Fuzz by number: More data about fuzzing than you ever wanted to know. Proceedings of the CanSecWest, Vancouver, Canada. [Google Scholar]

29. Yoo, S., Harman, M., Tonella, P., Susi, A. (2009). Clustering test cases to achieve effective and scalable prioritisation incorporating expert knowledge. Proceedings of the Eighteenth International Symposium on Software Testing and Analysis, Chicago, IL, USA. [Google Scholar]

30. Chen, J., Bai, Y., Hao, D., Xiong, Y., Zhang, H. et al. (2016). Test case prioritization for compilers: A text-vector based approach. Proceedings of the IEEE International Conference on Software Testing, Verification and Validation (ICST), Chicago, IL, USA, IEEE. [Google Scholar]

31. Chen, J., Bai, Y., Hao, D., Xiong, Y., Zhang, H. et al. (2017). Learning to prioritize test programs for compiler testing. Proceedings of the IEEE/ACM 39th International Conference on Software Engineering (ICSE), Buenos Aires, Argentin, IEEE. [Google Scholar]

32. Mahdieh, M., Mirian-Hosseinabadi, S. H., Etemadi, K., Nosrati, A., Jalali, S. (2020). Incorporating fault-proneness estimations into coverage-based test case prioritization methods. Information and Software Technology, 121, 106269. [Google Scholar]

33. Xie, X., Yin, P., Chen, S. (2022). Boosting the revealing of detected violations in deep learning testing: A diversity-guided method. Proceedings of the 37th IEEE/ACM International Conference on Automated Software Engineering, Rochester, MI, USA. [Google Scholar]

34. Viggiato, M., Paas, D., Buzon, C., Bezemer, C. P. (2022). Identifying similar test cases that are specified in natural language. IEEE Transactions on Software Engineering, 49(3), 1027–1043. [Google Scholar]

35. McKeeman, W. M. (1998). Differential testing for software. Digital Technical Journal, 10(1), 100–107. [Google Scholar]

36. Chen, J., Hu, W., Hao, D., Xiong, Y., Zhang, H. et al. (2016). An empirical comparison of compiler testing techniques. Proceedings of the International Conference on Software Engineering (ICSE), Austin, TX, USA. [Google Scholar]

37. Le, V., Afshari, M., Su, Z. (2014). Compiler validation via equivalence modulo inputs. ACM Sigplan Notices, 49(6), 216–226. [Google Scholar]

38. LeCun, Y., Bengio, Y., Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444. [Google Scholar] [PubMed]

39. Zhang, J., Hua, Y., Song, T., Wang, H., Xue, Z. et al. (2022). Improving bayesian neural networks by adversarial sampling. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 36, no. 9, pp. 10110–10117. USA. [Google Scholar]

40. Bengio, Y. (2009). Learning deep architectures for ai. Foundations and Trends® in Machine Learning, 2(1), 1–127. [Google Scholar]

41. Hernández López, J. A., Weyssow, M., Cuadrado, J. S., Sahraoui, H. (2022). AST-Probe: Recovering abstract syntax trees from hidden representations of pre-trained language models. 37th IEEE/ACM International Conference on Automated Software Engineering, Rochester, MI, USA. [Google Scholar]

42. Devlin, J., Chang, M. W., Lee, K., Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805. [Google Scholar]

43. Yadav, J., Sharma, M. (2013). A review of k-mean algorithm. International Journal of Engineering Trends and Technology, 4(7), 2972–2976. [Google Scholar]

44. Murtagh, F., Contreras, P. (2012). Algorithms for hierarchical clustering: An overview. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2(1), 86–97. [Google Scholar]

45. Yang, M. S. (1993). A survey of fuzzy clustering. Mathematical and Computer Modelling, 18(11), 1–16. [Google Scholar]

46. Gao, H., Xu, Y., Yin, Y., Zhang, W., Li, R. et al. (2019). Context-aware QoS prediction with neural collaborative filtering for Internet-of-Things services. IEEE Internet of Things Journal, 7(5), 4532–4542. [Google Scholar]

47. Pelleg, D., Moore, A. W. et al. (2000). X-means: Extending k-means with efficient estimation of the number of clusters. Proceedings of the Seventeenth International Conference on Machine Learning, pp. 727–734. San Francisco, CA, USA. [Google Scholar]

48. Hartigan, J. A., Wong, M. A. (1979). Algorithm as 136: A k-means clustering algorithm. Journal of the Royal Statistical Society Series C (Applied Statistics), 28(1), 100–108. [Google Scholar]