Open Access

ARTICLE

Complex Decision Modeling Framework with Fairly Operators and Quaternion Numbers under Intuitionistic Fuzzy Rough Context

Nadeem Salamat¹, Muhammad Kamran^1,2,*, Shahzaib Ashraf¹, Manal Elzain Mohammed Abdulla³, Rashad Ismail³, Mohammed M. Al-Shamiri³

1 Institute of Mathematics, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
2 Department of Mathematics, Thal University Bhakkar, Punjab, 30000, Pakistan
3 Department of Mathematics, Faculty of Science and Arts, King Khalid University, Muhayl Assir, 61913, Saudi Arabia

* Corresponding Author: Muhammad Kamran. Email:

(This article belongs to the Special Issue: Advances in Ambient Intelligence and Social Computing under uncertainty and indeterminacy: From Theory to Applications)

Computer Modeling in Engineering & Sciences 2024, 139(2), 1893-1933. https://doi.org/10.32604/cmes.2023.044697

Received 06 August 2023; Accepted 09 November 2023; Issue published 29 January 2024

Abstract

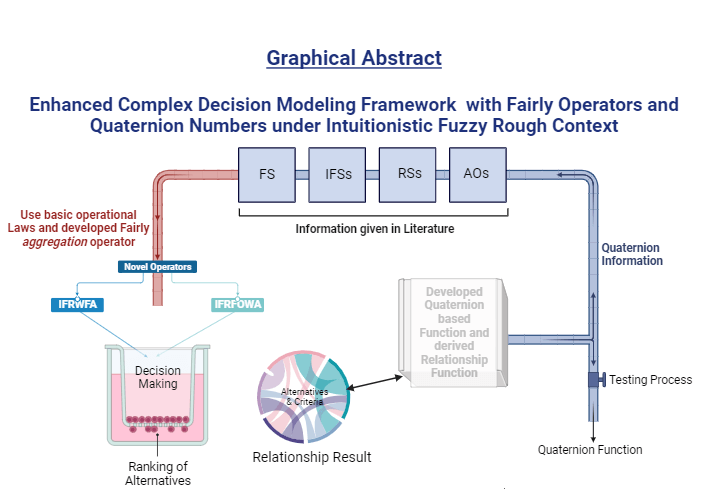
The main goal of informal computing is to overcome the limitations of hypersensitivity to defects and uncertainty while maintaining a balance between high accuracy, accessibility, and cost-effectiveness. This paper investigates the potential applications of intuitionistic fuzzy sets (IFS) with rough sets in the context of sparse data. When it comes to capture uncertain information emanating from both upper and lower approximations, these intuitionistic fuzzy rough numbers (IFRNs) are superior to intuitionistic fuzzy sets and pythagorean fuzzy sets, respectively. We use rough sets in conjunction with IFSs to develop several fairly aggregation operators and analyze their underlying properties. We present numerous impartial laws that incorporate the idea of proportionate dispersion in order to ensure that the membership and non-membership activities of IFRNs are treated equally within these principles. These operations lead to the development of the intuitionistic fuzzy rough weighted fairly aggregation operator (IFRWFA) and intuitionistic fuzzy rough ordered weighted fairly aggregation operator (IFRFOWA). These operators successfully adjust to membership and non-membership categories with fairness and subtlety. We highlight the unique qualities of these suggested aggregation operators and investigate their use in the multi-attribute decision-making field. We use the intuitionistic fuzzy rough environment’s architecture to create a novel strategy in situation involving several decision-makers and non-weighted data. Additionally, we developed a novel technique by combining the IFSs with quaternion numbers. We establish a unique connection between alternatives and qualities by using intuitionistic fuzzy quaternion numbers (IFQNs). With the help of this framework, we can simulate uncertainty in real-world situations and address a number of decision-making problems. Using the examples we have released, we offer a sophisticated and systematically constructed illustrative scenario that is intricately woven with the complexity of medical evaluation in order to thoroughly assess the relevance and efficacy of the suggested methodology.

---

Graphic Abstract

---

Keywords

---