 Open Access
Open Access
ARTICLE
Complex Decision Modeling Framework with Fairly Operators and Quaternion Numbers under Intuitionistic Fuzzy Rough Context
1 Institute of Mathematics, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
2 Department of Mathematics, Thal University Bhakkar, Punjab, 30000, Pakistan
3 Department of Mathematics, Faculty of Science and Arts, King Khalid University, Muhayl Assir, 61913, Saudi Arabia
* Corresponding Author: Muhammad Kamran. Email:
(This article belongs to the Special Issue: Advances in Ambient Intelligence and Social Computing under uncertainty and indeterminacy: From Theory to Applications)
Computer Modeling in Engineering & Sciences 2024, 139(2), 1893-1933. https://doi.org/10.32604/cmes.2023.044697
Received 06 August 2023; Accepted 09 November 2023; Issue published 29 January 2024
Abstract
The main goal of informal computing is to overcome the limitations of hypersensitivity to defects and uncertainty while maintaining a balance between high accuracy, accessibility, and cost-effectiveness. This paper investigates the potential applications of intuitionistic fuzzy sets (IFS) with rough sets in the context of sparse data. When it comes to capture uncertain information emanating from both upper and lower approximations, these intuitionistic fuzzy rough numbers (IFRNs) are superior to intuitionistic fuzzy sets and pythagorean fuzzy sets, respectively. We use rough sets in conjunction with IFSs to develop several fairly aggregation operators and analyze their underlying properties. We present numerous impartial laws that incorporate the idea of proportionate dispersion in order to ensure that the membership and non-membership activities of IFRNs are treated equally within these principles. These operations lead to the development of the intuitionistic fuzzy rough weighted fairly aggregation operator (IFRWFA) and intuitionistic fuzzy rough ordered weighted fairly aggregation operator (IFRFOWA). These operators successfully adjust to membership and non-membership categories with fairness and subtlety. We highlight the unique qualities of these suggested aggregation operators and investigate their use in the multi-attribute decision-making field. We use the intuitionistic fuzzy rough environment’s architecture to create a novel strategy in situation involving several decision-makers and non-weighted data. Additionally, we developed a novel technique by combining the IFSs with quaternion numbers. We establish a unique connection between alternatives and qualities by using intuitionistic fuzzy quaternion numbers (IFQNs). With the help of this framework, we can simulate uncertainty in real-world situations and address a number of decision-making problems. Using the examples we have released, we offer a sophisticated and systematically constructed illustrative scenario that is intricately woven with the complexity of medical evaluation in order to thoroughly assess the relevance and efficacy of the suggested methodology.Graphic Abstract
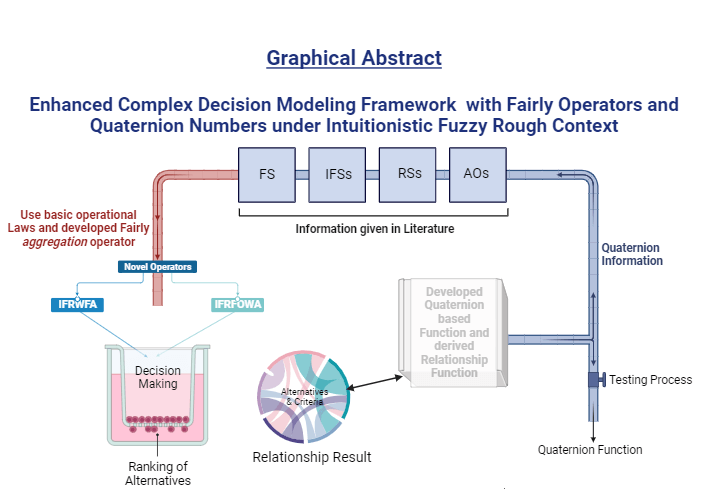
Keywords
The main notion of the multi-attribute decision-making (MADM) method, which is a modified form of the simple decision-making scenario, is a fantastic and dominant strategy for illuminating the valuable opinion from a collection of preferences. We analyze or encounter several decision-making issues in daily life, and one of the most important things we can do is acquire knowledge of how to make good, excellent, or outstanding decisions [1,2]. Typically, the expert presents conventional knowledge without assessing its level of ambiguity and uncertainty. While a logical method uses data and facts to reach conclusions that are in line with science. Although emotional intelligence is an excellent technique to make choices, it frequently functions best when the option is straightforward, private, or urgent [3,4]. A more formal, systematic approach that involves both intuition and logical reasoning is fuzzy set theory, which is often required for more complex judgments. The theory of fuzzy set (FS) processing was introduced by Zadeh [5] in 1965 as a solution to such issues. For resolving difficult and ambiguous information in many real-life scenarios, fuzzy information is one of the most useful and realistic variations of classical data. Each component of a set is given a membership degree (MD) in the real standard
Researchers have also developed a number of novel theory that focuses on IFSs, including similarity measures and aggregation operators (AOs). On the basis of IFSs, many authors [19] developed multiple geometric AOs. Additionally, Naz et al. [20] introduced several average AOs built on IFSs. Double domination on intuitionistic fuzzy (IF) graphs was first proposed by Nagoorgani et al. [21]. Xu was the pioneer in introducing weighted arithmetic (WA) operators based on intuitionistic fuzzy numbers (IFNs) [22]. Subsequently, Xu and Yager [23,24] proposed the extended Bonferroni mean (BM) operators and weighted geometric (WG) operators, both based on IFNs. Qin and Liu [25] developed the weighted Maclaurin symmetric mean operator using IFNs. Additionally, Liu and Liu [26] presented partitioned BM operators for intuitionistic uncertain language variables. Furthermore, the extended MADM (Multiple Attribute Decision Making) method has been extensively discussed with detailed illustrations of useful approaches such as the TOPSIS method for IFNs [27,28], the triangular intuitionistic fuzzy-TODIM method [29,30], and the intuitionistic fuzzy PROMETHE II method [31]. However, the restriction that the sum of membership degree (MD) and non-membership degree (NMD) cannot exceed one limit of the applicability of IFS (Intuitionistic Fuzzy Sets). Decision-makers and experts prefer more complex decision-making situations, making this condition less valid. Due to its effectiveness as a general formal framework, IFS has received significant attention from academics. Nguyen et al. [32] developed the exponentially similarity matrix for Pythagorean fuzzy sets (PFSs) and demonstrated their application in pattern identification and decision-making. However, PFSs can only be implemented when the sum of the squares representing MD and NMD falls within the range [0,1]. To address this challenge, it becomes necessary to define information expression differently when the sum falls outside this range.
Smarandache first proposed the neutrosophic set (NS), an analytical framework and quantitative tool for comprehending the origin, nature, and extent of neutralities [33]. It is a spiritual practice that focuses on neutralities’ origins, nature, and scope as well as how they interact with other ideational spectrums. The NS generalizes the ideas behind the classical set, fuzzy set, interval valued fuzzy set, interval-valued IFS, paraconsistent set, dialetheist set, paradoxist set, and tautological set. A NS is characterized by a truth membership function, indeterminacy membership function, and falsity membership function where all functions are real standard or nonstandard elements from
Previous AOs [40–44] have been proposed to handle MADM problems under fuzzy environments, but few have addressed the unbiased treatment of MD and NMD. Consolidated values reported in the literature [45–48] cannot be differentiated when a decision-maker compares both MD and NMD, indicating favoritism in the verdict. Therefore, new neutral procedures for IFRSs (Intuitionistic Fuzzy Rough Sets) are required to ensure equal treatment of information about members and non-members. Through the idea of ”intuitionistic” membership functions, IFRN expands the traditional fuzzy-rough framework. The IFRN contains two membership functions, one for a level of belongingness and a separate function for the degree of non-belongingness, in contrast to standard fuzzy sets. A more accurate portrayal of the ambiguity in real-world data is made possible by this dual perspective. To achieve this, the concept of proportional distribution rules of MD and NMD is used to establish two neutral or fair operations, enabling the evaluation of MD and NMD with true satisfaction in the decision-making process. A thorough understanding of the human decision-making process is essential to build a realistic model. This calls for the incorporation of fairness operators and a hybrid idea, such as intuitionistic fuzzy rough set, into the decision-making paradigm. Normally, decision-making involves weighing a range of options and standards. By placing a strong emphasis on the relationship between these options and the specified criteria, we provide a fresh strategy in this work. We use the quaternion function, that’s a key component of our technique, to clarify and codify the relationship between options and criteria. This novel strategy provides a more organized and thorough framework for decision-making, improving our capacity to make wise and effective decisions. Complex numbers and non-commutative four-dimensional algebra are both generalized by quaternion numbers. The concept of quaternion numbers and its applications to rotations were first published in 1840 by Olinde Rodrigues et al. [49]. However, an Irish mathematician by the name of Sir William Rowan Hamilton [50] independently made the discovery in 1843 and utilized it to research three-dimensional mechanics. A quaternion can be used to store each rotation in a 4-D coordinate system. The union of three complex components and one real element is known as a quaternion. It also applies to a lot more than just rotations. Rotations are better performed with quaternions than Euler angles, and the gamble lock problem is resolved. In computer animation, quaternions are frequently used to represent changes in the orientation of graphical elements. They offer a creative fix for issues like convenient interpolation, gimbal lock, and instability that plagued early animated systems. In order to express 4-dimensional complex information, we apply the intuitionistic fuzzy information to establish the relationship between intuitionistic fuzzy numbers and quaternion numbers. To assess the applicability of the suggested strategy, an example of a medical diagnosis based on the suggested representations is given. We can establish a connection between attributes and alternatives through this relationship.
Following the discussion above, we described the objectives of this study as follows:
• Although IFS and RS are merged, IFRS anticipates giving decision-makers additional space.
• IFS lacks the positive and negative approximation spaces that IFRS utilizes.
• The advance requirement that the sum (MD, NMD) must belong to
• To establish a few new neutral or fair functions that handle membership and non-membership functions equally using the connectivity coefficient.
• Understanding the characteristics of weighted aggregation operators like intuitionistic fuzzy rough fairly weighted aggregation (IFRFWA) and intuitionistic fuzzy rough fairly ordered weighted aggregation (IFRFOWA). The level of expertise with evaluated substances that IFRFWA and IFRFOWA AOs can incorporate for first evaluation is a quality that is lacking in IFWA and IFWG aggregation operators.
• To design a decision-making process that uses the weighted aggregation operators stated above to address multi-attribute decision-making issues with IFR data.
• We also use intuitionistic fuzzy data to determine how quaternion numbers and intuitionistic fuzzy numbers relate to one another.
• An example of a medical diagnosis based on the suggested representations is provided to demonstrate the strategy’s usefulness. Through this relationship, we can construct a link between attributes and possibilities.
According to the following, this paper is structured:
Section 2 focuses exclusively on the evaluation of a few preliminary documents. In Section 3, we describe the operators of the IF context and elucidate their fundamental characteristics. Section 4 provides a definition of the IFRFWA and IFRFOWA operators. Section 5 is intended to facilitate multi-attribute group decision-making (MAGDM). In accordance with the suggested methodology, which depicts the rating values of options on the characteristic in terms of IFR numbers, the best/most acceptable option is determined by ranking the alternatives based on their IFR score values. A case study with numerical examples for decision making is explained in Section 6. Relationship Model between Alternatives and Attributes is given in Section 7. In Section 8, Discussion and Comparison Analysis and positive aspects of the model are given. The conclusion can be found in Section 9.
We have discussed some of the key ideas related to IFSs in this section of the article. We will also go over the fundamental concepts of FSs, IFSs, scoring functions (SFs), accuracy functions (AFs), quaternion numbers (QNs), and IFQNs.
Definition 2.1. (See [5]) A fuzzy set (FS) Z in
for each
Definition 2.2. (See [6]) An intuitionistic fuzzy set (IFS) A in
here
Definition 2.3. (See [51]) Assume that
The element’s successor neighborhood with respect to the relation
The pair
Definition 2.4. (See [52]) Assume that
Definition 2.5. Assume
•
•
•
•
•
•
If
Consequently, none of the procedures
deemed to be impartial or equitable in reality. Therefore, developing some fair operations between IFRNs must be the focus of our attention in the outset.
Example 1. For the Definition 2.5, we prove it by the following example. A generalization of conventional fuzzy sets, intuitionistic fuzzy sets (IFS) involve both membership and non-membership degrees. To merge two IFSs into only one IFS, utilize the bounded operations of an IFS.
Assume that
•
•
•
•
•
•
It can compute
Definition 2.6. (See [53]) Assume that,
Here
Definition 2.7. (See [54]) Assume that,
Similarly, the pure complex NMD was added to the concept of complex fuzzy class to create the concept of complex intuitionistic fuzzy class.
Definition 2.8. (See [49,50]) A quaternion q is a four dimensional complex number also called a hyper complex number, introduced by Hamilton in 1843. Let
•
•
Definition 2.9. (See [49,50]) A fuzzy quaternion number is given by
for some
Definition 2.10. A intuitionistic fuzzy quaternion set (IFQS) is given by the complex function
In other hands, we can defined as:
Definition 2.11. Assume
mathematically represented as:
the values
3 Devolpment Fairly Operators of IFR Context
In this part, we combined RSs with IFS to develop some aggregation operators and examine their fundamental characteristics.
Definition 3.1. Assume that
It is simple to validate that
Theorem 3.1. Assume that
1.
2.
Proof. As given
1.
consequently,
2.
consequently,
if
The processes revealed by this theorem
Theorem 3.2. consider
1.
2.
3.
1. This one is trivial.
2.
Hence
3.
Hence,
4 Fairly Aggregation Operators for IFRNs
This part examines fairly AOs for IFRSs along with their characteristics.
4.1 Intuitionistic Fuzzy Rough Fairly Weighted Averaging (IFRFWA) Aggregation Operator
Definition 4.1. Assume that
then the mapping IFRFWA is called ”intuitionistic fuzzy rough fairly weighted averaging
Theorem 4.1. Assume that
where
Proof. We will use mathematical induction to present this proof.
For
Theorem is true at
Now we will proof at
The conclusion is valid for
The following theorems list a few particular attributes that the proposed AO fulfills.
Theorem 4.2. Assume that
Proof. Given that
Theorem 4.3. Let
we have
Proof. We begin with
By the above theorem, we obtained
This is how we learn
Consequently,
Theorem 4.4. Assume that
and
Then,
Proof. By using the theorem on the two groups of IFRNs, namely,
By this, if
4.2 Intuitionistic Fuzzy Rough Fairly Orderd Weighted Averaging (IFRFOWA) Aggregation Operator
Definition 4.2. Assume that
then the arrangement IFRFOWA is known “intuitionistic fuzzy rough fairly ordered weighted averaging
Theorem 4.5. Let
where
Proof. Validation is identical to the previous argument.
Theorem 4.6. Let
Proof. Validation is identical to the previous argument.
Theorem 4.7. Assume that
Proof. Validation is identical to the previous argument.
Theorem 4.8. Assume that
and
Then,
Proof. Validation is identical to the previous argument.
5 Multi Attribute Group Decisions-Making (MAGDM) Methodology
We visualized an MAGDM issue where there are n different alternatives, and each alternative is assessed employing a set of
In this section, we devolved the decision algorithm for n-by-m matrix.
Step 1. Based on the applicability of the DMs mentioned in IFRNs, determine the weights of the DMs.
Step 2. A decision-matrix in terms of IFRNs was constructed based on the expertise of professionals. It is denoted by
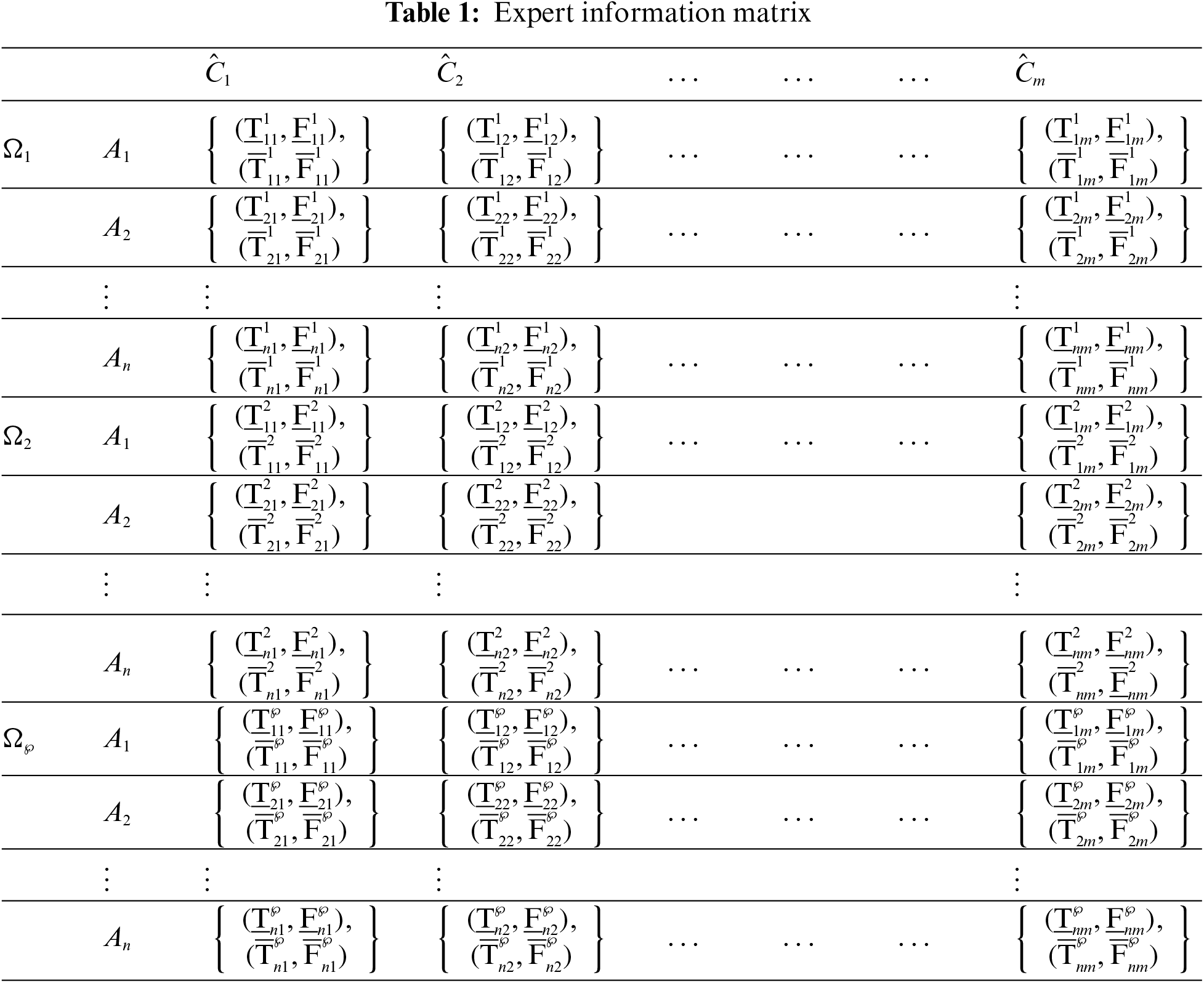
Step 3. To create a combined IFR evaluation matrix and subsequently generate an aggregated IFR decision matrix, it is imperative to consider that in a group decision-making process, the individual opinions must be carefully accumulated and integrated to form a cohesive and representative group opinion.
Step 4. Normalize the decision matrix if the attributes are of the cost type; otherwise, there is no need for normalization.
Step 5. Develop the score matrix using the IFRNs’ scoring function.
Step 6. Utilizing the normalized decision matrix, evaluate the weighted IFR decision matrix as a whole by appyling the suggested AOs.
Step 7. Obtain a score value for the total weighted aggregated value using SF. Determine the order in which the options should be ranked based on the SF, and then decide the option you think is the best.
The science learning objectives of experimentation include improving subject-matter mastery, developing scientific reasoning skills, raising awareness of the variety and uncertainty associated with empirical work, establishing practical skills, raising awareness of the nature of science, fostering enthusiasm for the sciences and scientific learning, and enhancing teamwork skills. According to the research, laboratory experiences are more likely to succeed in achieving these objectives if they are planned with definite learning objectives in mind, meticulously organized into the flow of educational settings science instruction, integrated with acquiring about science topics and procedures, and include continuing learner discussion and reflection. Large scientific databases and virtual representations of natural phenomena are more likely to be useful if they are incorporated within a well-planned arrangement of classroom science training that also incorporates laboratory activities.
For efficient patient care in the field of healthcare, medical disorders must be accurately and promptly diagnosed. Healthcare professionals and medical facilities frequently depend on outside laboratories for medical testing to do this. However, choosing the best laboratory for testing can be challenging as it involves weighing criteria like price, reliability, turnaround time, and others. This case study attempts to investigate the selection procedure for the best medical testing laboratory. A medical testing laboratory is seeking to collaborate with Healthcare Institution, a large local health care institution, to provide a variety of diagnostic services. The hospital’s management thinks that by combining their testing requirements with a single laboratory, operations might be made more efficient and expenses could perhaps be decreased. Currently, they send their samples to multiple outside labs. However, they want to be sure the chosen laboratory gives top-notch services and satisfies their particular needs. The management staff of the hospital must take into account a number of things while selecting the best laboratory. Here are some important factors to think about:
Assurance of quality: To make sure the laboratory complies with industry standards, look into its licenses and accreditations, including ISO 15189 or CAP. Examine the lab’s track record for consistency and dependability in test results. Inquire about the laboratory’s quality assurance procedures and error prevention strategies.
Testing menu: Make sure the laboratory’s diagnostic menu has the necessary range of examinations that the hospital requires. As the hospital grows its offerings, ascertain if the laboratory is capable of handling upcoming testing requirements.
Reaction time: Examine the lab’s turnaround times for various test types. Think about how turnaround time affects patient care and hospital operations.
Cost and price: Ask for comprehensive price information, which should include test-specific expenses, volume reductions, and any other fees. Be sure to factor in any possible cost savings from combining testing services under one laboratory.
Transportation and sample handling: To guarantee sample integrity, assess the laboratory’s sample collecting, transportation, and handling procedures. With the laboratory, go over details including specimen pick-up and delivery schedules.
Customer service: Evaluate the customer service provided by the lab, paying particular attention to adaptability, communication, and the presence of an assigned account manager. Find out how the laboratory handles problems or inconsistencies in test results.
Integration of data: For effective data sharing, ascertain whether the laboratory can easily interface to the hospital’s electronic health record, or EHR, system.
Security and conformity: Make sure the lab adheres to data protection laws and maintains strict security procedures for patient data.
Reputation and references: Look for references and learn about the laboratory’s standing in the medical community.
The healthcare organization can make an informed choice that supports its objectives of delivering excellent care to patients while maximizing operational efficiency by carefully weighing these variables and thoroughly evaluating possible laboratory partners. The case study serves as an excellent example of the value of making well-structured decisions when choosing a medical screening laboratory. This strategy can be used as a guide for other providers of healthcare that are faced with comparable choices in the constantly changing field of medical diagnostics.
During a surgical procedure, surgical technologists also known as operating room technicians assist surgeons, nurses, and other members of the medical staff. The surgical technologist’s job is crucial because they maintain a clean and ordered environment. Assume someone is interested in learning about the best laboratory out of a list of four options
Step 1 The weights values are
Step 2 The expert data that was acquired from the survey are presented in Tables 2–5.
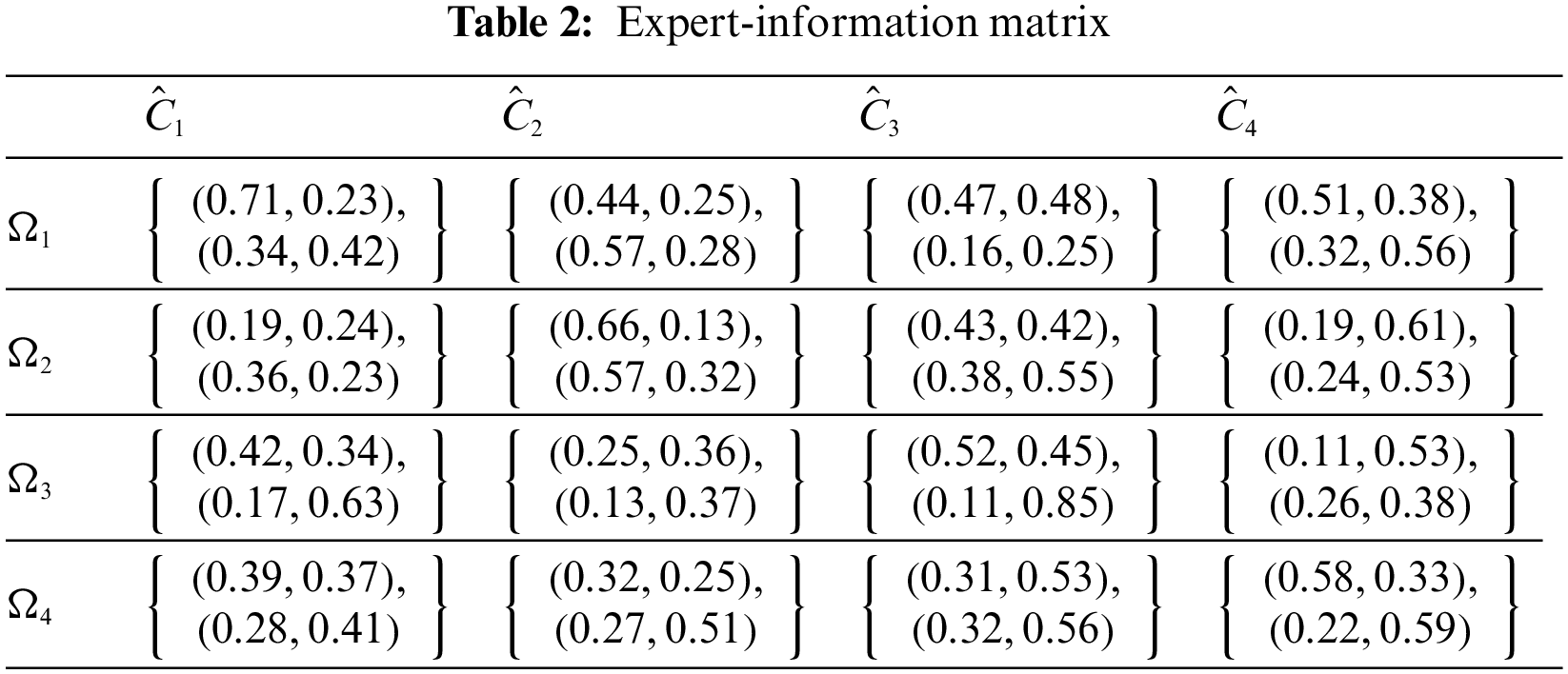
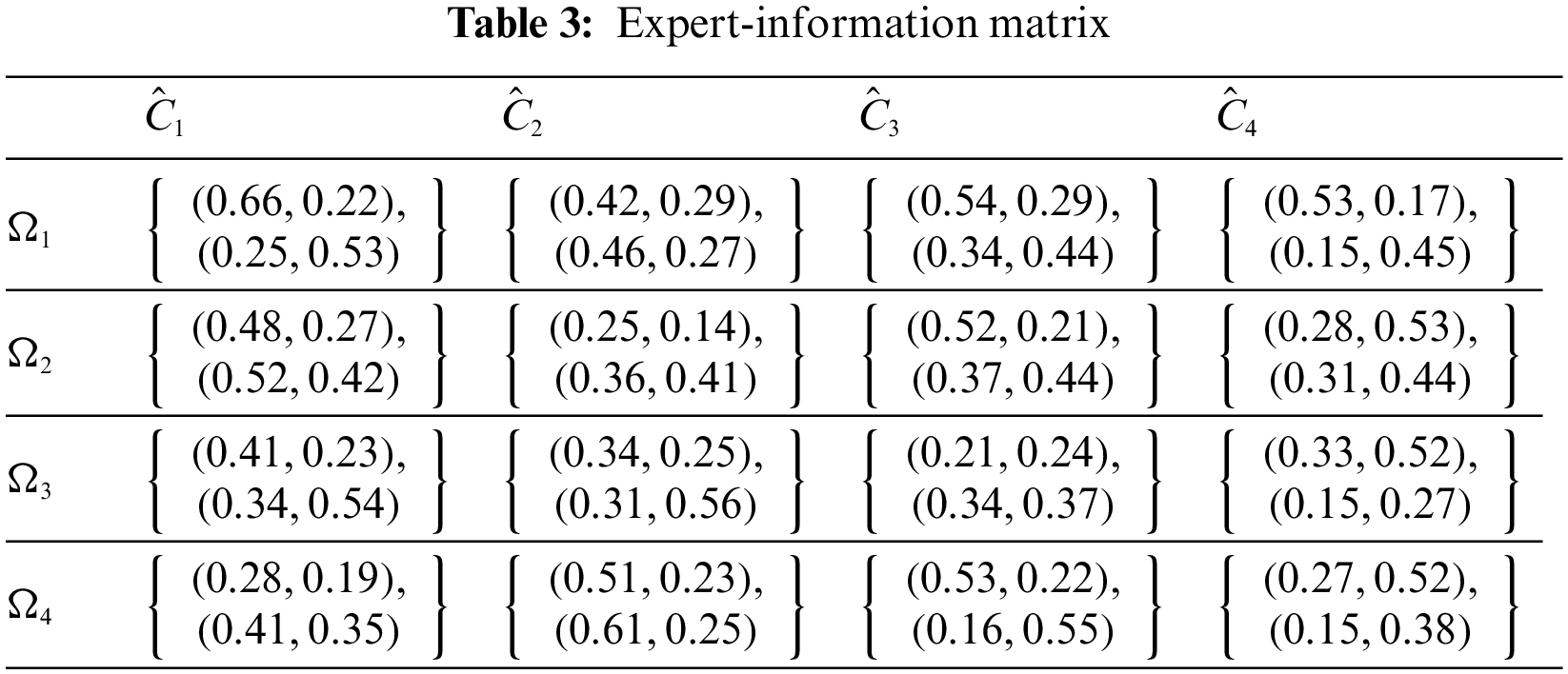
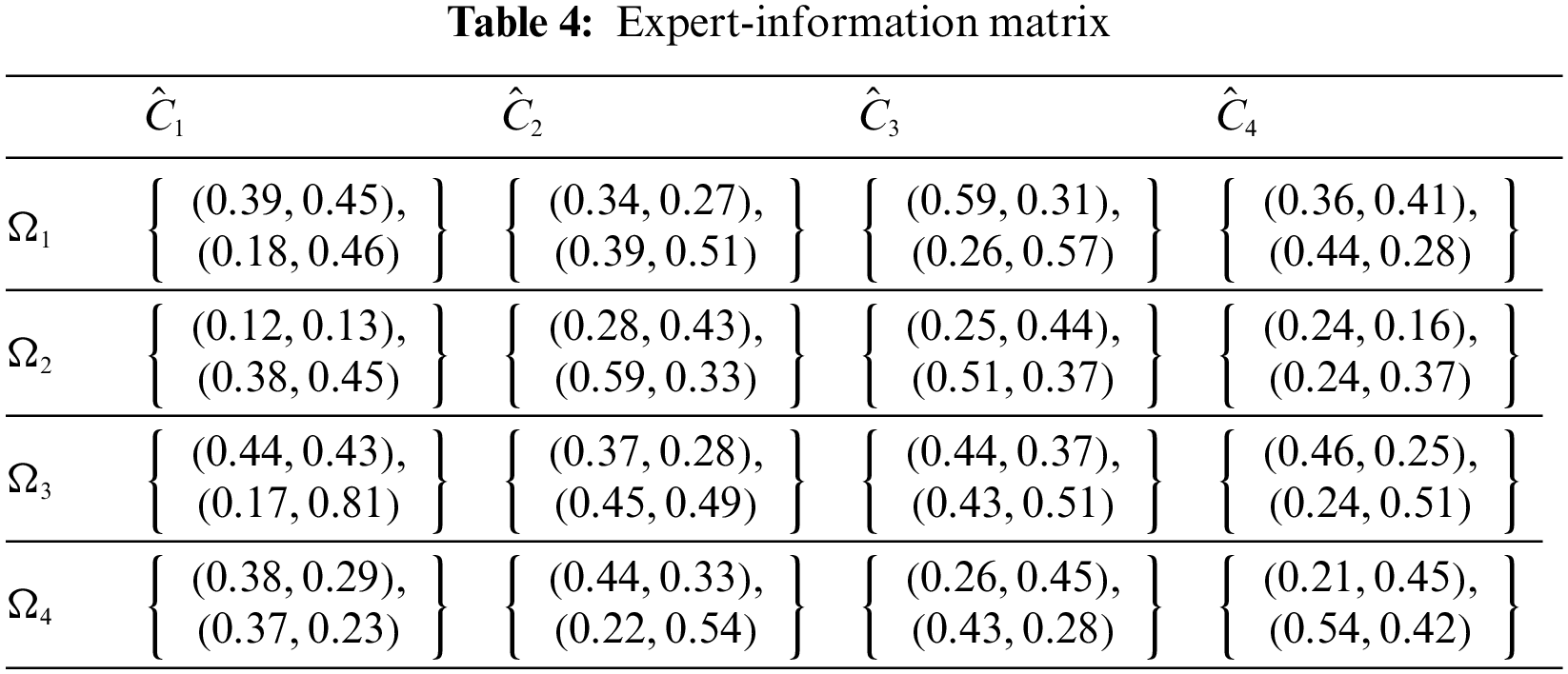
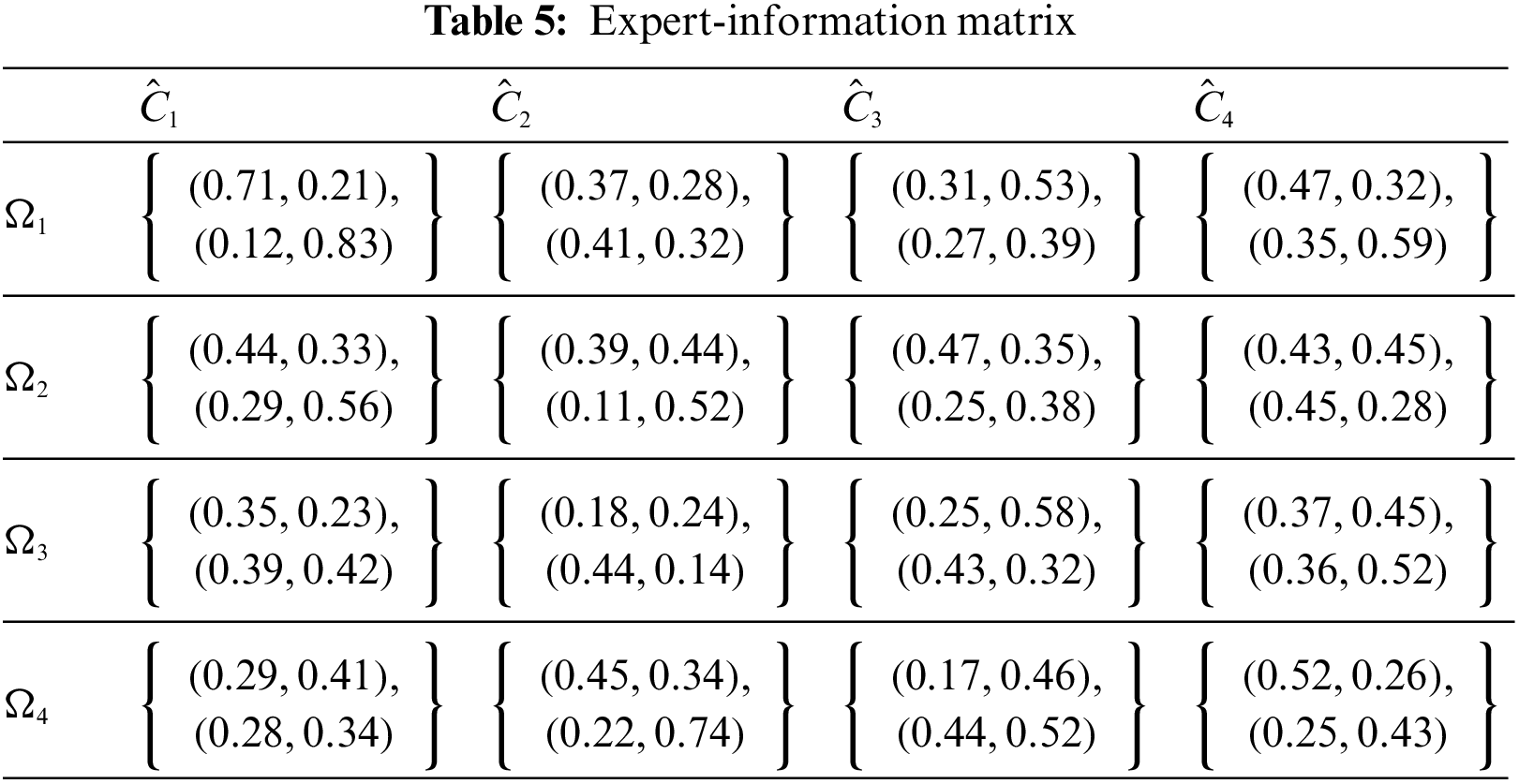
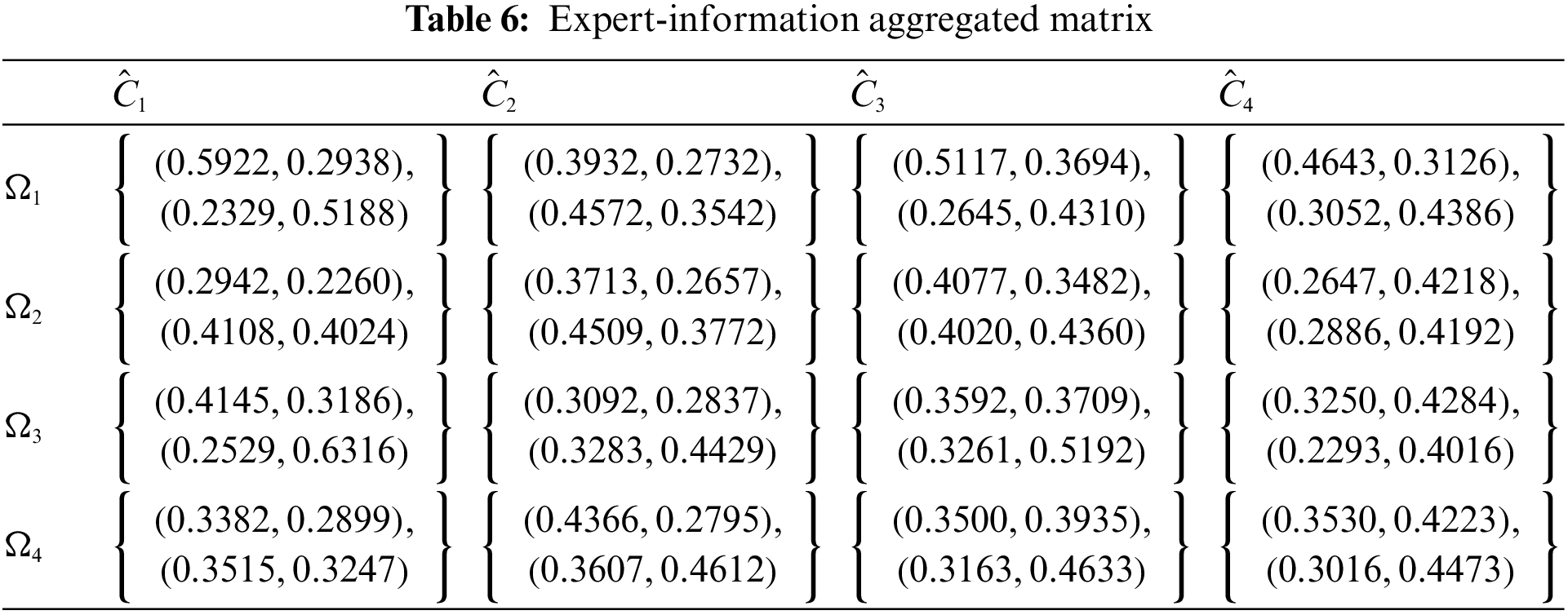
Step 3 In Table 6, develop a combined IFR evaluation matrix.
Step 4 All the information is beneficent, so there is no need to normalize it.
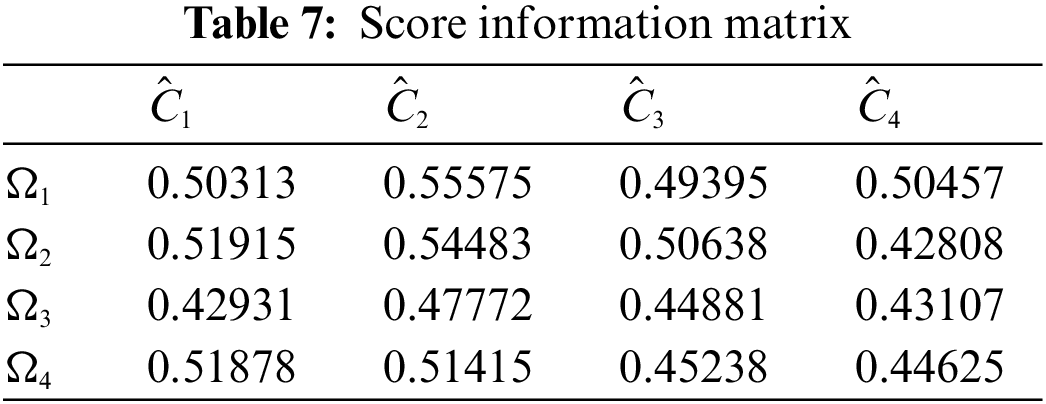
Step 5 Develop the score matrix in Table 7 with the help of Table 6, using the IFRNs’ scoring function.
Step 6 Utilizing the normalized decision matrix, evaluate the weighted IFR decision matrix using weight values are 0.2314, 0.3312, 0.3161, 0.1213 as a whole by applying the suggested AOs given in Table 8.
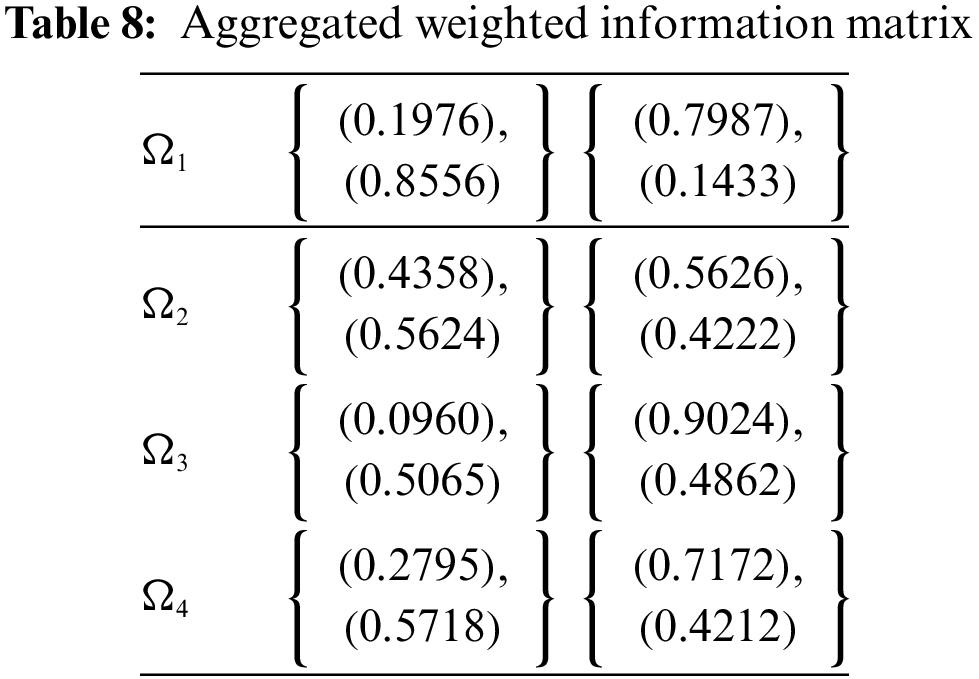
Step 7 Obtain a score value for the total weighted aggregated value using SF in Table 9.
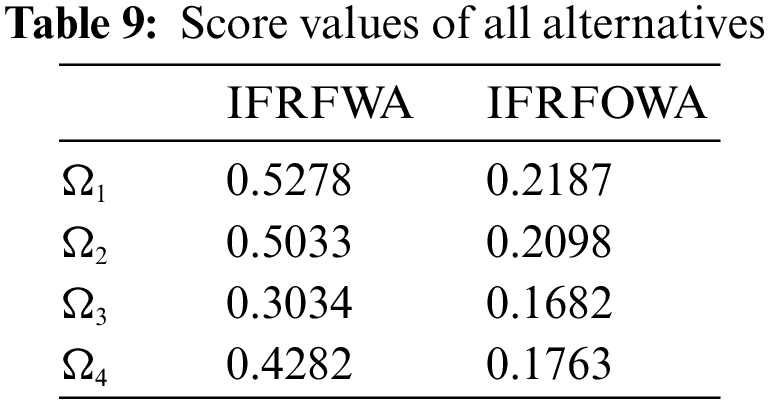
Step 8 Ranking of the alternative is described in Table 10.

The ranking in graphical is shown in Fig. 1.

Figure 1: Graphical representation of ranking
7 Relationship Model between Alternatives and Attributes
In this specific section, we have built a thorough model that makes it easier for researchers to draw associations and connections between various options and the evaluation criteria. We can properly express and evaluate the information in this model by using quaternion numbers, which work in four-dimensional spaces. Let us examine the main points of this model in greater detail in order to give a clearer understanding. In 1840, Olinde Rodrigues introduced the concept of quaternion numbers and their applications to rotations. However, in 1843, Irish mathematician Sir William Rowan Hamilton independently made the discovery and applied it to the study of three-dimensional mechanics. A quaternion can store every rotation in a three-dimensional coordinate system. A quaternion is the combination of three complex components and one real element. Furthermore, it pertains to much more than just rotations. For rotations, quaternions are favoured over Euler angles, and the wager lock issue is eliminated. In computer animation, quaternions are frequently used to demonstrate how the orientations of graphical objects vary. Early animated systems were beset by issues such as convenient interpolation, gimbal lock, and instability. They provide a creative solution to these problems.
To determine the relationship between a patient’s disease and their symptoms, we first provided an example medical diagnosis. We can use this methodology to determine the relationship between alternatives and attributes based on this instance.
Numerical Example Based on IFQNs: See Table 11 for our consideration of four Patient-referenced documents. Label
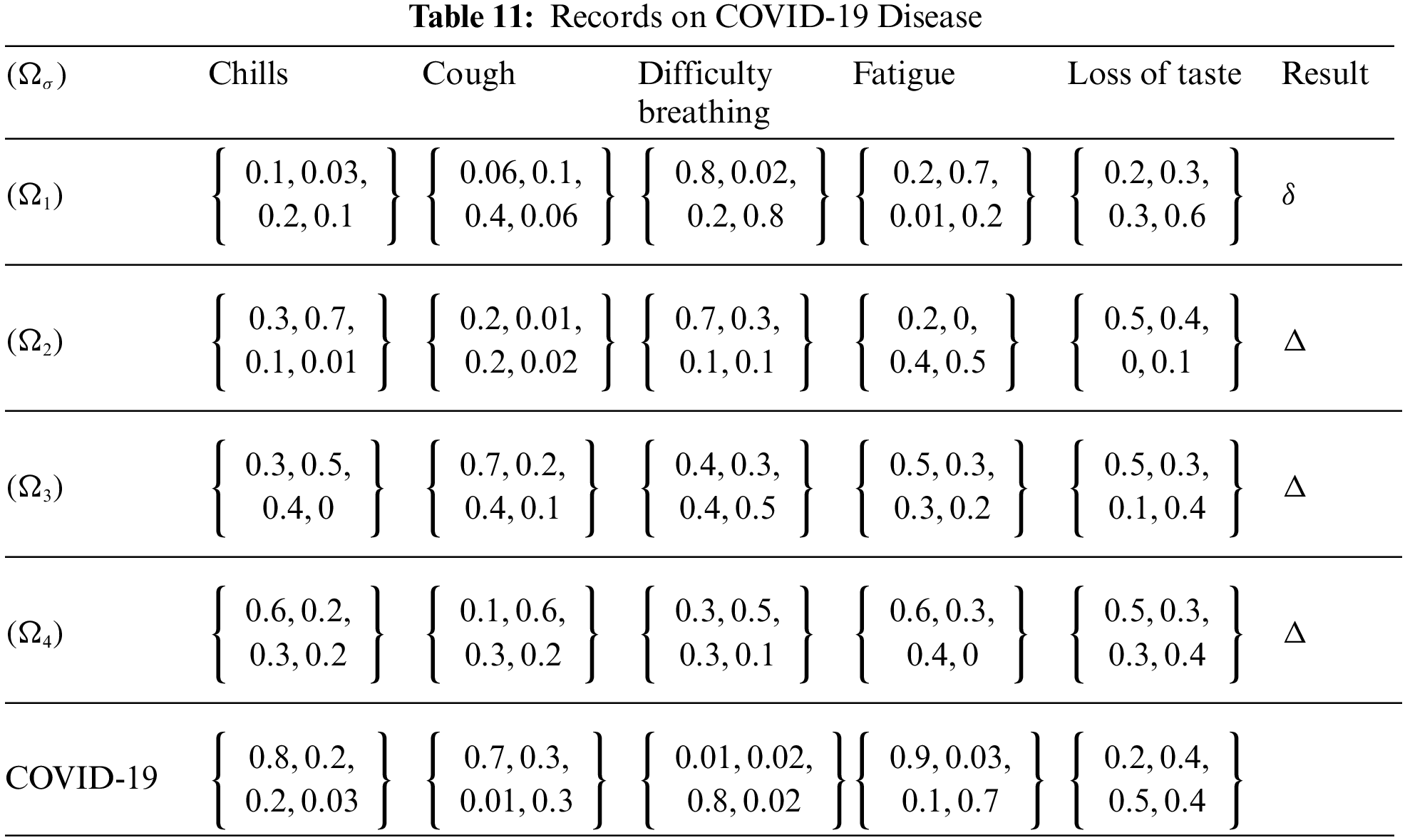
Here if
Testing Process: The formula
Assume
From the Table 11, we find that
8 Discussion and Comparison Analysis
The approach has applications in many different industries where decision-makers must cope with erroneous or incomplete data, including financial markets, engineering, health care diagnosis, and risk assessment. Making more trustworthy and solid judgements in these areas is made feasible by utilizing IFRSs and fairness operators. One of the main benefits of this approach is its capacity to acquire and process complicated, hesitant, and uncertain data, resulting in more accurate and realistic decision-making. The model can be highly computational despite its benefits, especially when working with enormous data sets. The additional complexity associated with IFRSs and fairness operators can make it difficult for non-experts to grasp and evaluate the model’s conclusions. Occasionally, decision-makers lack knowledge of each intuitionistic fuzzy component, for instance. In light of this, an IFRS theory is defined as the combination of positive and negative information within a framework that is intuitively ambiguous. However, this theory does not adequately replicate the situation in which both positive and negative information in the IFS component must be considered. After making the necessary adjustments, we redesigned the concept of IFRS. In addition, we present new algebraic properties for the proposed operators and a brand-new aggregation operator. Based on the IFRFWA and IFRFOWA data proposed in this research, we utilized the expanded MAGDM method. Table 12 compares our proposed model to the intuitionistic fuzzy rough weighted geometric (IFRWG), intuitionistic fuzzy rough ordered weighted geometric (IFROWG) and intuitionistic fuzzy rough hybrid geometric (IFRHG) aggregation operators [55], intuitionistic fuzzy hybrid weighted arithmetic and geometric aggregation operators (IFHWAGA) [56], intuitionistic fuzzy power weighted average (IFPWA) operator, intuitionistic fuzzy Heronian mean (AIFHM) aggregation operator [57], IFRWAA, and IFRWGA AOs and intuitionistic fuzzy rough Yager (IFRY) weighted averaging (IFRYWA), IFRY ordered weighted averaging (IFRYOWA), IFRY hybrid averaging (IFRYHA) aggregation operators [58]. The graphical view of the comparison analysis is given in Fig. 2.
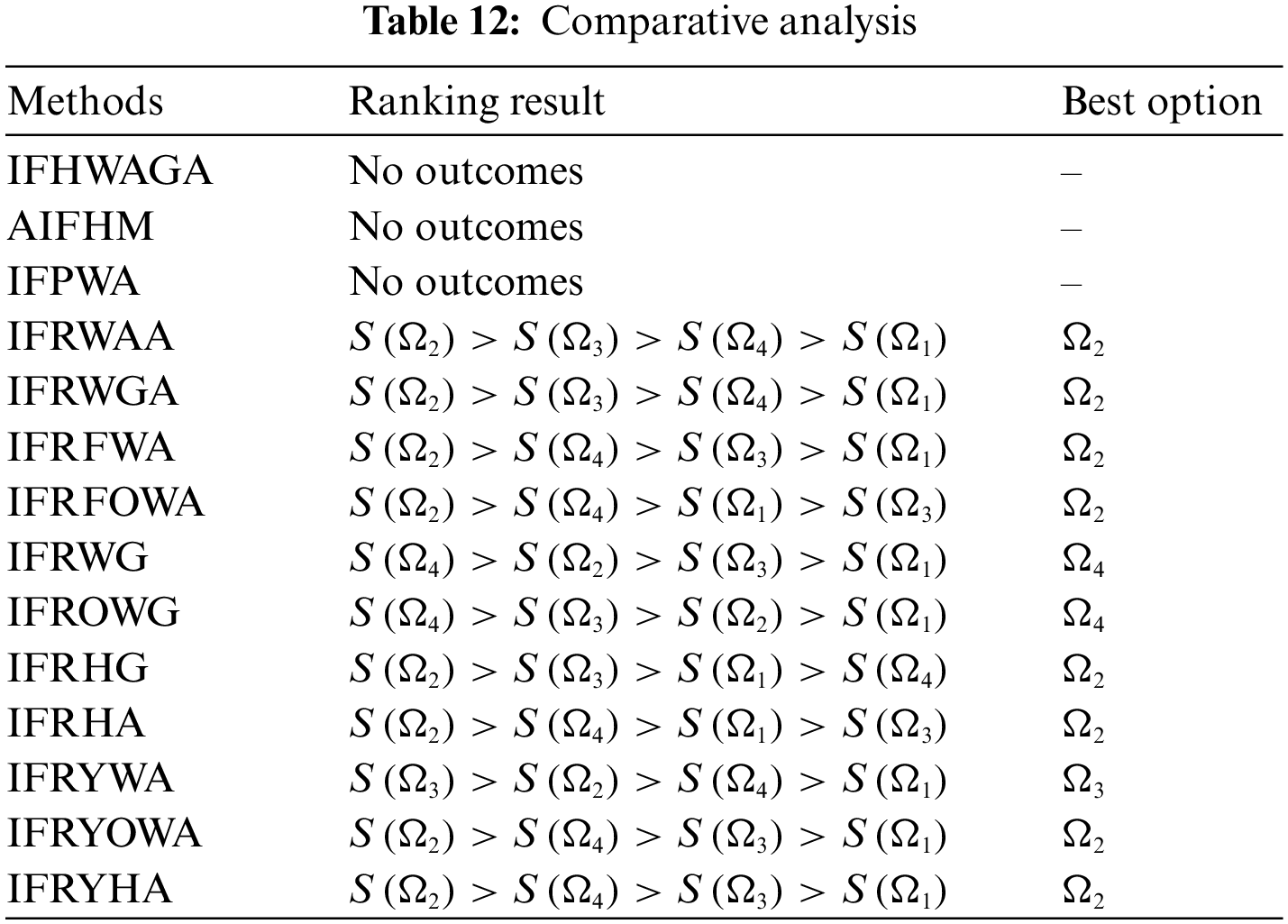

Figure 2: Graphical representation of comparison analysis
Positive aspects of the suggested technique and AOs: It is clear that practically all factors are given similar weight through the process in real decision-making challenges. For instance, in some specific situations, the reliability of the thing is prioritized over its price and speed of manufacturing. As a result, choosing the right weight for the attributes requires careful consideration. The ranking order of alternatives is impacted since the researchers in the existing approaches [59–62] select attribute weights at random. We applied a method of optimization based on limited weight input of the attributes in our devised approach to satisfy the attribute weights. Our suggested method for determining characteristic weight is more accurate and effective. Former academics studied decision-makers (DMs) using weights that were arbitrarily chosen without a sound justification. As a result, dealing with risk-preference judgement issues will be challenging because of this. However, according to the real decision demands, DMs were given priority in our proposed system. As a result, as shown in our suggested approach, the weighting mechanism is more appropriate and workable.
To summarize, in this study, we developed a variety of unique operational principles for IFRNs that ensure neutrality or fairness while interacting with the MD and NMD of the associated IFRSs. According to a recent study, DMs’ associated aggregate evaluations are unfair if they produce an equal amount of MD and NMD while assessing objects. With an emphasis on correctness and relevance during decision-making that is influenced by the DM’s thinking, we proposed a number of original fairness or neutrality frameworks that focus on IFRSs and the proportionality allocation laws of MD and NMD. The linkages between the IFQNs were also inferred and evaluated, and a practical decision-making scenario was defined and handled using relationships. It was chosen to create a potent combination of an IFS using quaternion numbers for scenarios where each item has a range of possible values that are determined by quaternion membership and non-membership. A fresh approach to decision-making was also suggested based on the IF-QNs. The benefits of these strategies are further described below:
• A DM should designate the same level of truthfulness and falsity when evaluating items; otherwise, the accompanying aggregate rankings are unethical. We examined how well the supplied AOs adapted to the previous AOs and demonstrated that our proposed operators are more adaptable than the previous operators.
• When compared to other currently available solutions for MADM tasks in an IFR environment, the IFRFWFA and IFRFOWFA operators’ findings are accurate and dependable, highlighting their practical applications.
• Quaternion-based decision-making models were also offered and assessed. Medical diagnostics, a recently created application for addressing the symptoms and characteristics of diseases in patients, provide experimental support for the proposed paradigm.
• On the basis of the intuitionistic fuzzy quaternion model, the relationship between alternatives and attributes can be determined.
• When compared to current methodologies, which fail to take into account the interrelationships of attributes in practical applications, the MAGDM strategies recommended by this study are more accurate and have a larger setpoint due to their increased ability to recognize connections between attribute values and alternatives. This illustrates that more links between traits may be discovered using the MAGDM methods discussed in this study.
• The application of the proposed AOs (Arithmetic Operators) could significantly contribute to the advancement of research in various areas, such as two-sided perfectly matched decision-making involving multi-granular and insufficient requirement weight information. Furthermore, these AOs can be utilized for personalized individual continuity and regulation of consensus. When evaluating the constraints imposed by the proposed AOs, there is no need to consider the levels of participation, abstention, and non-membership. The anticipated AOs have been developed with an innovative hybrid design that incorporates prioritized and collaborative AOs, making them cutting-edge and versatile in addressing complex decision-making scenarios.
• In future work, we will explore the theoretical foundation of Intuitionistic Fuzzy Rough Sets (IFRSs) for Einstein functions, utilizing state-of-the-art decision-making approaches such as AHP, TOPSIS, GRA, and EDAS. Our research will delve into the application of these methods in various domains, including soft computing, robotics, horticulture, smart systems, the humanities, economics, and human resource management. By investigating the intersection of IFRSs and cutting-edge decision-making techniques, we aim to enhance our understanding of these hybrid methodologies and their potential impact across diverse fields of study.
• In future research, the proposed methods can be applied to address various issues, including two-sided matching decision-making involving multi-granular and incomplete criterion weight information. Additionally, these methods can be extended to handle personalized individual consistency control consensus problems and tackle consensus reaching with non-cooperative behavior management decision-making problems.
Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large group research project under Grant Number R.G.P.2/449/44.
Funding Statement: This research work is funded by King Khalid University through a large group research project under Grant Number R.G.P.2/449/44.
Author Contributions: Each author made an equal contribution. The manuscript has been read by all authors, and they have all agreed that it should be published.
Availability of Data and Materials: The manuscript includes all the data that were used to support this study.
Ethics Approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Mahmud, H., Islam, A. N., Ahmed, S. I., Smolander, K. (2022). What influences algorithmic decision-making? A systematic literature review on algorithm aversion. Technological Forecasting and Social Change, 175, 121390. [Google Scholar]
2. Alsalem, M. A., Mohammed, R., Albahri, O. S., Zaidan, A. A., Alamoodi, A. H. et al. (2022). Rise of multiattribute decision-making in combating COVID-19: A systematic review of the state-of-the-art literature. International Journal of Intelligent Systems, 37(6), 3514–3624. [Google Scholar]
3. Xie, D., Xiao, F., Pedrycz, W. (2022). Information quality for intuitionistic fuzzy values with its application in decision making. Engineering Applications of Artificial Intelligence, 109, 104568. [Google Scholar]
4. Soltani, M., Edalatpanah, S., Sobhani, F. M. (2020). A novel two-stage dea model in fuzzy environment: Application to industrial workshops performance measurement. International Journal of Computational Intelligence Systems, 13(1), 1134–1152. [Google Scholar]
5. Goguen, J. A. (1973). La zadeh. fuzzy sets. information and control, vol. 8 (1965pp. 338–353.-la zadeh. similarity relations and fuzzy orderings. information sciences, vol. 3 (1971pp. 177–200. The Journal of Symbolic Logic, 38(4), 338–353. [Google Scholar]
6. Atanassov, K. T. (1999). Intuitionistic fuzzy sets. In: Studies in fuzziness and soft computing, vol. 35. Heidelberg: Physica. https://doi.org/10.1007/978-3-7908-1870-3_1 [Google Scholar] [CrossRef]
7. Song, J., Jiang, L., Liu, Z., Leng, X., He, Z. (2022). Selection of third-party reverse logistics service provider based on intuitionistic fuzzy multi-criteria decision making. Systems, 10(5), 188. [Google Scholar]
8. Mohammadi, S. S., Azar, A., Ghatari, A. R., Alimohammadlou, M. (2022). A model for selecting green suppliers through interval-valued intuitionistic fuzzy multi criteria decision making models. Journal of Management Analytics, 9(1), 60–85. [Google Scholar]
9. Pawlak, Z., Pawlak, Z. (1991). Imprecise categories, approximations and rough sets. In: Theory and decision library, vol. 9. Dordrecht: Springer. https://doi.org/10.1007/978-94-011-3534-4_2 [Google Scholar] [CrossRef]
10. Polkowski, L. (2002). Rough sets. Heidelberg: Physica-Verlag. Springer. [Google Scholar]
11. Moheimani, A., Sheikh, R., Hosseini, S. M. H., Sana, S. S. (2022). Assessing the preparedness of hospitals facing disasters using the rough set theory: Guidelines for more preparedness to cope with the COVID-19. International Journal of Systems Science: Operations & Logistics, 9(3), 339–354. [Google Scholar]
12. Forghani, E., Sheikh, R., Hosseini, S. M. H., Sana, S. S. (2022). The impact of digital marketing strategies on customers buying behavior in online shopping using the rough set theory. International Journal of System Assurance Engineering and Management, 13, 625–640. https://doi.org/10.1007/s13198-021-01315-4 [Google Scholar] [CrossRef]
13. Alnoor, A., Zaidan, A., Qahtan, S., Alsattar, H. A., Mohammed, R. et al. (2022). Toward a sustainable transportation industry: Oil company benchmarking based on the extension of linear diophantine fuzzy rough sets and multicriteria decision-making methods. IEEE Transactions on Fuzzy Systems, 31(2), 449–459. [Google Scholar]
14. Ayub, S., Shabir, M., Riaz, M., Mahmood, W., Bozanic, D. et al. (2022). Linear diophantine fuzzy rough sets: A new rough set approach with decision making. Symmetry, 14(3), 525. [Google Scholar]
15. Ghosh, S. K., Ghosh, A., Bhattacharyya, S. (2022). Recognition of cancer mediating biomarkers using rough approximations enabled intuitionistic fuzzy soft sets based similarity measure. Applied Soft Computing, 124, 109052. [Google Scholar]
16. Anwar, M. Z., Al-Kenani, A. N., Bashir, S., Shabir, M. (2022). Pessimistic multigranulation rough set of intuitionistic fuzzy sets based on soft relations. Mathematics, 10(5), 685. [Google Scholar]
17. Gohain, B., Chutia, R., Dutta, P. (2023). A distance measure for optimistic viewpoint of the information in interval-valued intuitionistic fuzzy sets and its applications. Engineering Applications of Artificial Intelligence, 119, 105747. [Google Scholar]
18. Tiwari, A., Lohani, Q. D. (2023). Interval-valued intuitionistic fuzzy rough set system over a novel conflict distance measure with application to decision-making. MethodsX, 10, 102012. [Google Scholar] [PubMed]
19. Khan, M. J., Kumam, W., Alreshidi, N. A. (2022). Divergence measures for circular intuitionistic fuzzy sets and their applications. Engineering Applications of Artificial Intelligence, 116, 105455. [Google Scholar]
20. Naz, S., Akram, M., Muzammal, M. (2023). Group decision-making based on 2-tuple linguistic t-spherical fuzzy copras method. Soft Computing, 27(6), 2873–2902. [Google Scholar]
21. Hameed, S., Ahmad, U., Batool, Z. (2023). Total perfect and total efficient domination in intuitionistic fuzzy graphs. International Journal of Applied and Computational Mathematics, 9(5), 60. [Google Scholar]
22. Xu, Z. (2007). Intuitionistic fuzzy aggregation operators. IEEE Transactions on Fuzzy Systems, 15(6), 1179–1187. [Google Scholar]
23. Xu, Z., Yager, R. R. (2006). Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems, 35(4), 417–433. [Google Scholar]
24. Xu, Z., Yager, R. R. (2010). Intuitionistic fuzzy bonferroni means. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 41(2), 568–578. [Google Scholar]
25. Qin, J., Liu, X. (2014). An approach to intuitionistic fuzzy multiple attribute decision making based on maclaurin symmetric mean operators. Journal of Intelligent & Fuzzy Systems, 27(5), 2177–2190. [Google Scholar]
26. Liu, Z., Liu, P. (2017). Intuitionistic uncertain linguistic partitioned bonferroni means and their application to multiple attribute decision-making. International Journal of Systems Science, 48(5), 1092–1105. [Google Scholar]
27. Liu, S. (2021). Research on the teaching quality evaluation of physical education with intuitionistic fuzzy topsis method. Journal of Intelligent & Fuzzy Systems, 40(5), 9227–9236. [Google Scholar]
28. Gupta, P., Mehlawat, M. K., Grover, N. (2019). A generalized topsis method for intuitionistic fuzzy multiple attribute group decision making considering different scenarios of attributes weight information. International Journal of Fuzzy Systems, 21, 369–387. [Google Scholar]
29. Yang, J., Xu, Z. (2022). Matrix game-based approach for madm with probabilistic triangular intuitionistic hesitant fuzzy information and its application. Computers & Industrial Engineering, 163, 107787. [Google Scholar]
30. Babatunde, O. M., Munda, J. L., Hamam, Y. (2022). Triangular intuitionistic fuzzy aggregating and ranking function approach for the rating of battery end-of-life handling alternatives. Energies, 15(6), 2248. [Google Scholar]
31. Zhu, H., Zhao, J. (2022). 2DLIF-PROMETHEE based on the hybrid distance of 2-dimension linguistic intuitionistic fuzzy sets for multiple attribute decision making. Expert Systems with Applications, 202, 117219. [Google Scholar]
32. Nguyen, X. T., Nguyen, V. D., Nguyen, V. H., Garg, H. (2019). Exponential similarity measures for pythagorean fuzzy sets and their applications to pattern recognition and decision-making process. Complex & Intelligent Systems, 5, 217–228. [Google Scholar]
33. Smarandache, F. (1999). A unifying field in logics: Neutrosophic logic. Neutrosophy, neutrosophic set, neutrosophic probability. Rehoboth, DE, USA: American Research Press. [Google Scholar]
34. Wang, H., Smarandache, F., Zhang, Y., Sunderraman, R. (2012). Single-valued neutrosophic sets. Australia: Hurstville. [Google Scholar]
35. Broumi, S., Sundareswaran, R., Shanmugapriya, M., Nordo, G., Talea, M. et al. (2022). Interval-valued fermatean neutrosophic graphs. Decision Making: Applications in Management and Engineering, 5(2), 176–200. https://doi.org/10.31181/dmame0311072022b [Google Scholar] [CrossRef]
36. Kamran, M., Ismail, R., Al-Sabri, E. H. A., Salamat, N., Farman, M. et al. (2023). An optimization strategy for madm framework with confidence level aggregation operators under probabilistic neutrosophic hesitant fuzzy rough environment. Symmetry, 15(3), 578. [Google Scholar]
37. Martin, N., Edalatpanah, S. (2023). Application of extended fuzzy isocov methodology in nanomaterial selection based on performance measures. Journal of Operational and Strategic Analytics, 1(2), 55–61. [Google Scholar]
38. Jiao, L., Yang, H. L., Li, S. G. (2020). Three-way decision based on decision-theoretic rough sets with single-valued neutrosophic information. International Journal of Machine Learning and Cybernetics, 11, 657–665. [Google Scholar]
39. Kamran, M., Ashraf, S., Salamat, N., Naeem, M., Botmart, T. (2023). Cyber security control selection based decision support algorithm under single valued neutrosophic hesitant fuzzy einstein aggregation information. AIMS Mathematics, 8(3), 5551–5573. [Google Scholar]
40. Palanikumar, M., Arulmozhi, K., Jana, C. (2022). Multiple attribute decision-making approach for pythagorean neutrosophic normal interval-valued fuzzy aggregation operators. Computational and Applied Mathematics, 41(3), 90. [Google Scholar]
41. Zhang, C., Hu, Q., Zeng, S., Su, W. (2021). Iowlad-based mcdm model for the site assessment of a household waste processing plant under a pythagorean fuzzy environment. Environmental Impact Assessment Review, 89, 106579. [Google Scholar]
42. Farid, H. M. A., Riaz, M. (2022). Single-valued neutrosophic einstein interactive aggregation operators with applications for material selection in engineering design: Case study of cryogenic storage tank. Complex & Intelligent Systems, 8(3), 2131–2149. [Google Scholar]
43. Kamran, M., Ashraf, S., Naeem, M. (2023). A promising approach for decision modeling with single-valued neutrosophic probabilistic hesitant fuzzy dombi operators. Yugoslav Journal of Operations Research, 1, 1–26. [Google Scholar]
44. Ashraf, S., Ahmad, S., Naeem, M., Riaz, M., Alam, M. A. (2022). Novel edas methodology based on single-valued neutrosophic aczel-alsina aggregation information and their application in complex decision-making. Complexity, 2022, 1–18. [Google Scholar]
45. Gao, H., Zhang, H., Liu, P. (2019). Multi-attribute decision making based on intuitionistic fuzzy power maclaurin symmetric mean operators in the framework of dempster-shafer theory. Symmetry, 11(6), 807. [Google Scholar]
46. Sivaprakasam, P., Angamuthu, M. (2023). Generalized z-fuzzy soft β-covering based rough matrices and its application to magdm problem based on ahp method. Decision Making: Applications in Management and Engineering, 6(1), 134–152. [Google Scholar]
47. Li, Y. M., Khan, M., Khurshid, A., Gulistan, M., Ur Rehman, A., et al. (2023). Designing pentapartitioned neutrosophic cubic set aggregation operator-based air pollution decision-making model. Complex Intell. Syst., 9, 4765–4782. https://doi.org/10.1007/s40747-023-00971-2 [Google Scholar] [CrossRef]
48. Tamilarasi, G., Paulraj, S. (2023). A new aggregation operator for single-valued triangular neutrosophic number in decision-making. In: Mathematics and computing, pp. 37–49. Vellore, India, Springer. [Google Scholar]
49. Gray, J. J. (1980). Olinde Rodrigues' paper of 1840 on transformation groups. Archive for History of Exact Sciences, 21, 375–385. https://doi.org/10.1007/BF00595376 [Google Scholar] [CrossRef]
50. Altmann, S. L. (1989). Hamilton, rodrigues, and the quaternion scandal. Mathematics Magazine, 62(5), 291–308. [Google Scholar]
51. Tan, A., Wu, W. Z., Qian, Y., Liang, J., Chen, J. et al. (2018). Intuitionistic fuzzy rough set-based granular structures and attribute subset selection. IEEE Transactions on Fuzzy Systems, 27(3), 527–539. [Google Scholar]
52. Kamran, M., Ismail, R., Ashraf, S., Salamat, N., Ozon, S. (2023). Decision support algorithm under SV-neutrosophic hesitant fuzzy rough information with confidence level aggregation operators. AIMS Mathematics, 8(5), 11973–12008. [Google Scholar]
53. Yazdanbakhsh, O., Dick, S. (2018). A systematic review of complex fuzzy sets and logic. Fuzzy Sets and Systems, 338, 1–22. [Google Scholar]
54. Garg, H., Vimala, J., Rajareega, S., Preethi, D., Perez-Dominguez, L. (2022). Complex intuitionistic fuzzy soft swara-copras approach: An application of erp software selection. AIMS Math, 7(4), 5895–5909. [Google Scholar]
55. Chinram, R., Hussain, A., Mahmood, T., Ali, M. I. (2021). Edas method for multi-criteria group decision making based on intuitionistic fuzzy rough aggregation operators. IEEE Access, 9, 10199–10216. [Google Scholar]
56. Nguyen, H. (2020). Some new operations on atanassovs intuitionistic fuzzy sets in decision-making problems. Journal of Intelligent & Fuzzy Systems, 38(1), 639–651. [Google Scholar]
57. Kumar, K., Chen, S. M. (2022). Group decision making based on advanced intuitionistic fuzzy weighted heronian mean aggregation operator of intuitionistic fuzzy values. Information Sciences, 601, 306–322. [Google Scholar]
58. Mahmood, T., Ahmmad, J., Rehman, U. U., Bilal Khan, M. (2023). Analysis and prioritization of the factors of the robotic industry with the assistance of edas technique based on intuitionistic fuzzy rough yager aggregation operators. IEEE Access, 11, 50462–50479. https://doi.org/10.1109/ACCESS.2023.3272388 [Google Scholar] [CrossRef]
59. Saha, A., Reddy, J., Kumar, R. (2022). A fuzzy similarity based classification with archimedean-dombi aggregation operator. Journal of Intelligent Management Decision, 1(2), 118–127. [Google Scholar]
60. Rasoulzadeh, M., Edalatpanah, S. A., Fallah, M., Najafi, S. E. (2022). A multi-objective approach based on markowitz and dea cross-efficiency models for the intuitionistic fuzzy portfolio selection problem. Decision Making: Applications in Management and Engineering, 5(2), 241–259. [Google Scholar]
61. Ahmmad, J., Mahmood, T., Mehmood, N., Urawong, K., Chinram, R. (2022). Intuitionistic fuzzy rough aczel-alsina average aggregation operators and their applications in medical diagnoses. Symmetry, 14(12), 2537. [Google Scholar]
62. Ali, A., Ullah, K., Hussain, A. (2023). An approach to multi-attribute decision-making based on intuitionistic fuzzy soft information and Aczel-Alsina operational laws. Journal of Decision Analytics and Intelligent Computing, 3(1), 80–89. https://doi.org/10.31181/jdaic10006062023a [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools