A Hybrid SIR-Fuzzy Model for Epidemic Dynamics: A Numerical Study

1  Introduction

The creation of reliable computational models for comprehending and forecasting the transmission of infectious illnesses is more important than ever in the wake of significant global health disasters like the COVID-19 pandemic. The Susceptible-Infectious-Recovered (SIR) epidemic model is useful for understanding how diseases spread. Traditional SIR models are based on several simplifying assumptions often invalidated by the complexity of disease transmission in the actual world.

Quantities associated with the spread of disease, like vulnerability, exposure, infectious state, isolation, and recovery, are uncertain due to variable degrees. The difference can be achieved by considering other factors like custom, age, habits of a given population, and their ability to resist a particular change. To account for this, more realistic models can be needed. Considering the work done by Mishra et al. [1], one can see that the epidemic models peculiar to infectious spread require cautious dealing due to uncertainty. The prevalence of an infectious disease depends on both the number of susceptible and infected nodes, making it difficult to predict. Sensitivity and infectivity are through uncertain quantities but innately are fuzzy terminology. Therefore, they can be described in terms of fuzzy logic. Nowadays, biological systems are accurately modelled using fuzzy logic, which cures all the uncertainty of parameters due to variable degrees, specifically in epidemics.

Uncertainty about the Epidemic model arises due to various factors like a different degree of confusion, escape, and recovery between individual cyber consumers, which was fixed by Zadeh in 1965 [2] in his fuzzy theory. The author describes the methods to eliminate chaos and uncertainty produced in mathematical models in this theory. That is why several researchers focus on building models based on fuzzy theory instead of classical models devoid of this theory. Implementing this theory to epidemic modelling reduces time expense. Therefore, many researchers applied this theory to cash the currency of time. Taking imprecise parameters [3] and discussing the presence and stability of equilibrium, Das and Pal’s works are particularly important in this context since they examine the SIR (Susceptible Infected and Recovered) model. Facts were supported thoroughly by numerical evidence. Sadhukhan et al. used Pontryagin’s maximal principle [4] to create a fuzzy theory-based harvesting model.

In 1965 [2], Zadeh induced the fuzzy theory, which was later implemented by Barros et al. in the form of an SI model to elaborate the transmission coefficient as a fuzzy set [5]. In this model, the mean of infectious individuals was compared to the average virus mutation, and reproduction values were analyzed. Mondal et al. worked similarly on the plague model and created a fuzzy coefficient-based SIS model [6]. The threshold condition and the rate of pathogen reproduction were calculated. Additionally, a fuzzy SIR model was developed by Verma et al. [7]. They compared equilibrium points in the classical model to those in the fuzzy model, and they also looked at how susceptible different people were to the virus. Ortega et al. [8] designed a fuzzy-based epidemiological model of rabies in which the average of vaccinated dogs was calculated along with the comparative analysis of fuzzy linguistic rules and the classical differential equation. Verma et al. [9] plotted this theory to construct SEIR and SEIRHD models for the Ebola epidemic. The equilibrium presence and stability were reckoned through fuzzy triangular numbers, and the whole process was related to the primary producing amount of the virus. This amount was observed using a unique methodology known as the next-generation matrix, whereas numerical simulation was followed to maintain the accuracy of theoretical results. Das formed the SIR model for the implicit calculation of biological parameters and Das et al. [3]; however, numerical simulation and theoretical work were provided to support the facts and figures. A unique study regarding the movement of energy in a linear way (food chain) to understand the presence of bio-economic balance in fuzzy logic using the Lyapunov function was done by Sadhukhan et al. [4].

Jafelice et al. studied variable stages involved in the transmission of HIV among individuals and modelled the progressive stages of AIDS [10]. This study proves uncertainty in the transfer rate of HIV, which can be resolved using a fuzzy set of virus loads. Another relatable research was done by Lefevr et al., who modelled HIV among the individuals administering the drugs against the pathogen. The fuzzy number theory was applied to reduce the uncertainty among the parameters and calculated the number of viruses in the number of individuals practicing the drugs [11]. El Allaoui et al. [12] created a different fuzzy theory-based smoking model, and a comparative analysis was done with traditional cases. Authors believed that fuzzy numbers could be used to picture the exact position of skin aberration. They formulated a specific technique called dermoscopy to produce and slide such images. A significant merit of using this technique was that it reduced the artwork and minimized the noise effects, ultimately improving the vision and detection of the wound [13]. A scientific study by Alamin et al. based on edge detection in grayscale proved the suitability of pixels to an area homogeneous around the image. Fuzzy number theory was used to lessen the uncertainty produced due to shades of grey that formulate the image; however, edge pixels are referred to as pixels that do not belong to the region [14].

Using fuzzy theory, Mishra et al. sort out how to control virus transmission in the computer network [15]. Lefevr et al. investigated the spread of HIV (Human Immunodeficiency Virus) using a fuzzy environment [13]. Many fractional models have been developed since the development of fuzzy theory, which intrigued scientists like Akgül [16] to develop a method like the Atangana-Baleanu operator to solve initial valued fractional problems. Another example of the fuzzy fractional model is [17], in which Dandapani et al. studied the alteration in the death rate of a specific population. In [17], the Laplace-Adomian decomposition method (LADM) and a differential transformation method (DTM) were employed. Fourth-order Runge-Kutta (RKM-4) was used to evaluate the results. Taking into account the studies [18–20], the authors revealed the use of fuzzy theory in contemporary style, and his extreme focus was to determine fraction dispersive PDE in fuzzy senses. Subsequently, he created a fuzzy fractional model employing Caputo’s operator to characterize human liver dynamics after studying the fuzzy fractional Fisher equation via the Laplace-Adomian decomposition technique (LADM). Ullah et al. [21] investigated the Volterra integral equation in a fuzzy setting utilizing Laplace transformation and LADM.

Micken developed the NSFD scheme [22]; however, Cresson et al. [23] introduced a two-dimensional differential equation to the NSFD scheme and several other population dynamics models. The major aims of the study [23] were to observe different properties like convergence and stability of the NSFD numerical scheme, including comparison with the Euler, Runge Kutta (RK) method of orders 2 and 4. A significant amount of work involving the NSFD numerical scheme can be seen thoroughly in references [24–26]. Alternatively, Mangongo et al. [27] developed a fuzzy-based malarial model to determine fuzzy global stability. The ambiguity of COVID-19 was calculated using the SEIQR model in a fuzzy environment by Dayan et al. [28].

Alterations in biological parameters are due to the gradual and successive evolution of the ecosystem, which is why the mathematical models are not always fixed [29]. One of the major causes of ecosystem destruction is global warming, which raises the earth’s surface temperature, hence dwindling the virus transmission rate among individuals. Prata et al. calculated the relationship between mean environment temperature and confirmed cases of COVID-19 in Brazil [30]. The results showed a negative linear association between temperature and the total number of verified cases. Irfan et al. [31] looked into how weather conditions and the spread of COVID 19 varied between provinces. Areas with low temperatures revealed an increased transmission of the virus. Studies based on temperature and epidemics should exclusively use fuzzy theory instead of a crisp model to reduce uncertain events. The authors pay close attention to this detail in [32] by developing a model that accounts for two kinds of interactions: one with asymptomatic people and another with infected people who are showing symptoms.

Additionally, they enhance the initial model to incorporate population interactions through complex networks, specifically the Watts-Strogatz model—the optimal fit for social networks—and extend it accordingly. The authors in [33] introduced a new delayed fractional-order susceptible-infected-recovered-susceptible (SIRS) reaction-diffusion model that operates on a network. This model is commonly employed to simulate disease transmission, but it may also be used to represent the spread of rumours in social settings.

Research Gap: The standard Susceptible-Infectious-Recovered (SIR) model is one example of a deterministic model that is heavily used in existing disease modelling research. These models do a good job of shedding light on the topic, but they cannot always account for the fuzziness and uncertainty of actual pandemic situations. The main obstacles are oversimplifying complicated transmission dynamics, failing to account for uncertainty in parameter values, and failing to reflect the impact of imprecise or missing data on disease transmission.

Challenges of Existing Studies: When dealing with situations with inadequate data or unclear model parameters, the limits of current studies become apparent. Predictions made using deterministic models may be inaccurate because they fail to account for the complexities of real-world dynamics. These models may have limited use in many epidemiological settings due to their inflexible structure, which does not allow them to capture the complex and unpredictable nature of disease transmission.

Justification for the Study: This research fills a significant need in the current literature by presenting a Hybrid SIR-Fuzzy Model. We plan to integrate fuzzy logic into the conventional SIR framework to tackle the problems caused by imprecision and uncertainty in illness modelling. An adaptable framework for data and parameter uncertainty, fuzzy logic, is available. A more accurate depiction of the complexity and diversity in epidemic dynamics can be achieved by including a transmission rate parameter that is based on fuzzy logic.

Significance of the Study: This study is important because it may provide a more realistic picture of the dynamics of disease spread than deterministic models, which have their limits. Fuzzy analysis captures the impact of ambiguity on epidemic outcomes and enables a more flexible and refined analysis. We hope that publishing this extensive numerical study may help public health decision-makers with their work and further our theoretical knowledge of epidemic dynamics.

The current study presents a revolutionary Hybrid SIR-Fuzzy Model that combines conventional SIR modeling with fuzzy logic to fill important gaps in disease modelling. Deterministic models frequently fail to account for uncertainty in data and model parameters; however, a strong foundation for handling these uncertainties is provided by incorporating fuzzy logic. The article adds to the continuing conversation in epidemiology by recognizing and resolving these issues. In addition, the suggested model provides a flexible tool for navigating difficult settings, which has practical significance for public health decision-making. This research makes a substantial and timely addition to improving disease modelling methodologies with its extensive numerical investigation that confirms the proposed methodology and adds to the increasing body of knowledge in the field.

Motivation: The motivation for this research arises from the acknowledged constraints of current disease modelling methodologies, specifically deterministic models like the traditional SIR model. The idea stems from the urgent requirement for advanced tools capable of successfully managing uncertainties and imprecisions inherent in epidemiology data and model parameters. Conventional models sometimes have difficulties accurately representing the intricate dynamics of disease transmission, particularly when confronted with inadequate or ambiguous data. The objective of the Hybrid SIR-Fuzzy Model suggested in this paper is to close this disparity by incorporating fuzzy logic into the modelling framework. This unique methodology revolutionizes disease modelling and addresses the urgent demand for more flexible and authentic techniques. The research aims to enhance decision-making in public health by overcoming these limitations and providing a more detailed comprehension of epidemic dynamics. This will ultimately reinforce the importance of infectious disease modelling in a larger context.

Implications: This work has significant implications, contributions, and innovative aspects in disease modelling. The advent of the Hybrid SIR-Fuzzy Model is a notable divergence from conventional deterministic models as it incorporates fuzzy logic. This innovation enables a more comprehensive depiction of the inherent errors and inaccuracies in epidemiological data and model parameters, filling a crucial void in current techniques. The suggested model’s capacity to adjust to unpredictable situations has tangible consequences for making public health decisions, offering a valuable instrument for policymakers. The extensive quantitative analysis confirms the approach and enhances the current understanding by providing valuable insights into the intricate dynamics of disease transmission. The uniqueness of this work stems from its comprehensive approach, integrating theoretical developments with practical applications, thus pushing forward the field of infectious disease modelling.

This work begins a numerical investigation to build a complex computational scheme by introducing the principles of fuzzy logic into the traditional SIR model. By combining these disparate ideas in novel ways, we hope to improve the model’s prediction power and flexibility to account for the complex dynamics of infectious diseases. This study’s primary goal is to answer several pressing concerns. How can we make epidemic models more accurate predictors when faced with ambiguity and missing data? How can we more accurately model infectious disease’s complex, situation-specific dynamics? Combining fuzzy logic and the SIR model is a potent tactic for overcoming these obstacles.

In this paper, a fuzzy epidemic disease model is proposed. The model consists of three types of individuals: those who are susceptible, infected, and recovered. A fuzzy transmission rate parameter is taken into account. The effect of linear incident rate is also incorporated into the model. In addition to this, a fuzzy numerical scheme is constructed. The scheme is first-order accurate and can provide positive solutions under some constraints or conditions. The Taylor series expansions are used to construct a scheme for three cases. The three cases depend on the fuzzy parameter. Also, the convergence of the numerical scheme is given to find conditions when the scheme will converge.

2  Fuzzy Epidemic Model

Before constructing a fuzzy-based epidemic model, some basic definitions and preliminaries are given:

2.1 Fuzzy Subset

A fuzzy subset f of the universe set X is expressed by the function μf(x):X→[0,1], which is called a membership function where μf(x) indicates the degree of membership of x in the fuzzy set A.

2.2 Triangular Fuzzy Number

A number f=(a,b,c) is called a Triangular fuzzy number if its membership function is

μf(x)={0,x≤ax−ab−a,a<x≤bx−cb−c,b<x≤c0,c≤x(1)

where a≤b≤c.

2.3 Trapezoidal Fuzzy Number

The number f=(a,b,c,d) is called a trapezoidal fuzzy number if its membership function is defined as

μf(x)={x−ab−a,a≤x≤b1,b≤x≤cd−xd−c,c<x≤d0,otherwise(2)

where a≤b≤c≤d.

2.4 Expected Value

The expected value of a triangular fuzzy number is given as

E(f)=p+2q+r4(3)

2.5 Fuzzy Basic Reproductive Number

The fuzzy basic reproductive number of a triangular fuzzy number R0(v) is given by

R0f=E[R0(v)](4)

For an existing mathematical model, SIR with linear incidence rate is expressed as [34]

dSdt=A−d1S−βSI1+αI(5)

dIdt=βSI1+αI−(d1+γ1)I(6)

dRdt=γ1I−d1R(7)

N(t)=S(t)+I(t)+R(t)(8)

where S(t) denotes the density of susceptible, I(t) denotes the density of infective and R(t) denotes the density of recovered individuals, d1 is the natural mortality rate, β denotes the transmission rate, A denotes the flux into S-population, γ represents the recovery rate and Holling type rate α. S,I and R number of people in million and rates are number of people per day.

This study considers the fuzzy epidemic model of the form

dSdt=A−d1(v)S−β(v)SI1+αI(9)

dIdt=β(v)SI1+αI−(d1(v)+γ1)I(10)

where A,d1,β(v),d1(v),γ and α are positive constants.

The chance of transmission of susceptible individuals to infective ones is denoted by β(v). The β(v) is defined as

β(v)={0,v≤vmv−vmv0−vm,vm≤v≤v∘1,v0<v<vm(11)

The transmission of disease from infective to susceptible will be ignorable if v is less than vm. The rate of transmission will be maximum if v is greater than v∘. The recovery rate d1=d1(v) is given by

d1(v)=d0−1vMv+1,0≤v≤vM(12)

where d0>0 denotes the recovery rate.

3  Mathematical Analysis

This section is concerned with the equilibrium points of the fuzzy model (9)–(10).

3.1 Fuzzy Equilibrium Analysis

Since β(v) is divided into three parts, the whole model will be split into three models.

Case I: If v<vm, then equilibrium points E0(S0,I0) can be found in the equations

0=A−d1S(13)

0=−(d1(v)+γ1)I(14)

Solving Eqs. (13) and (14) gives the equilibrium points for this case. The equilibrium point can be expressed as

E∘(S∘,I∘)=(Ad1(v),0)(15)

Case II: For this case consider, vm≤v≤v∘, so solving the equations

0=A−d1(v)S−(v−vmv∘−vm)SI1+αI(16)

0=(v−vmv∘−vm)SI1+αI−(d1(v)+γ1)I(17)

E∘(S∘,I∘)=(Ad1(v),0) and S∗=d1(v)+αA+γ1αd1(v)+β(v)I∗=−d2+Aβ−dγ1(αd1(v)+β(v))(d1(v)+γ1)}(18)

Case III: For this case, consider v0≤v≤vM, then equilibrium points can be found from the equations

0=A−d1(v)S−SI1+αI(19)

0=SI1+αI−(d1+γ1)I(20)

The equilibrium points are expressed as

E∘(S∘,I∘)=(Ad1(v),0)S∗∗=d1(v)+γ1I∗∗=A−d12(v)−d1(v)γ1d1+γ1}(21)

3.2 Fuzzy Basic Reproductive Number

Since the basic reproductive number for the deterministic model has already been given in [34]. For converting deterministic basic reproductive numbers to fuzzy basic reproductive numbers, only “β” and “d1” will be converted to fuzzy β(v) and d1(v). Therefore, the fuzzy basic reproductive number can be expressed as

R∘SIR=Aβ(v)d1(v)(d1(v)+γ1)(22)

Since the fuzzy parameter β(v) can be divided into three parts, three cases will be discussed.

Case I. For this case, let v<vm then β(v)=0 so R0SIR can be given by

R0SIR=0(23)

Case II: For this case, let vm≤v≤v0, then β(v)=v−vmv∘−vm, then R0SIR can be expressed as

R0SIR=A(v−vm)(v0−vm)d1(v)(d1(v)+γ1)(24)

Case III: This case considers v≥v0, so β(v)=1, and R0SIR can be expressed as

R0SIR=Ad1(v)(d1(v)+γ1)(25)

The fuzzy reproductive number can be expressed as

R0(v)=(0,Aβ(v)d1(v)(d1(v)+γ1),Ad1(v)(d1(v)+γ1))

Using the definition of expected value, R0f is expressed as

R∘f=E[R0(v)]=A(β(v)+1)d1(v)(d1(v)+γ1)(26)

3.3 Sensitivity Analysis

For this study, the normalized forward sensitivity index of a parameter s is given as

Ψ(s)=sR∘f∂R∘f∂s(27)

Using Eq. (27), the sensitivity of all parameters in Eqs. (9) and (10) are expressed by

Ψ(β(v))=β(v)R∘f∂∂β(v)(A(β(v)+1)d1(v)(d1(v)+γ1))=β(v)A(β(v)+1)d1(v)(d1(v)+γ1)Ad1(v)(d1(v)+γ1)=Aβ(v)A(β(v)+1)>0(28)

Ψ(A)=AR∘f∂∂A(A(β(v)+1)d1(v)(d1(v)+γ1))=Aβ(v)A(β(v)+γ1)>0(29)

Ψ(d1(v))=d1(v)R∘f∂∂d1(v)(A(β(v)+1)d1(v)(d1(v)+γ1))=−d1(v)A(1+β(v))(2d1(v)+γ1)A(β(v)+γ1)d1(v)(d1(v)+γ1)<0(30)

Ψ(γ1)=γ1R∘f∂∂γ1(A(β(v)+1)d1(v)(d1(v)+γ1))=−γ1A(1+β(v))A(β(v)+1)(d1(v)+γ1)<0(31)

From the calculated results, it can be concluded that β(v) and A are sensitive parameters. It means that the R∘fwill increase by increasing sensitive parameters and vice versa.

4  Proposed Numerical Scheme

For solving Eqs. (9) and (10) a numerical scheme is presented. The numerical scheme will be first-order accurate. To do so, consider the difference equations

Sn+1=Sn+a1h[A−d1(v)Sn+1−β(v)Sn+1In1+αIn](32)

In+1=In+a2h[β(v)SnIn1+αIn−(d1(v)+γ1)In+1](33)

Expand Sn+1 and In+1 using the Taylor series, it is obtained

Sn+1=Sn+h(dSdt)in+O(h2)(34)

In+1=In+h(dIdt)in+O(h2)(35)

Substituting Eqs. (34) and (35) into Eqs. (32) and (33), respectively, it is obtained

Sn+h(dSdt)n+O(h2)=Sn+a1h[A−d1(v)Sn−h(dSdt)nd1(v)−β(v)SnIn1+αIn−hβ(v)In1+αIn(dSdt)n](36)

In+h(dSdt)n+O(h2)=In+a2h[β(v)SnIn1+αIn−(d1(v)+γ1)In−h(d1(v)+γ1)(dSdt)n](37)

Eqs. (36) and (37) can be re-written as

Sn+h(dSdt)n+O(h2)=Sn+a1h[(dSdt)n−d1(v)h(dSdt)in−hβ(v)In1+αIn(dSdt)n](38)

In+h(dIdt)in+O(h2)=In+a2h[(dIdt)in−h(d1(v)+γ1)(dIdt)in](39)

Comparing coefficients of Sn,In,h(dSdt)in and h(dIdt)in on both sides of Eqs. (38) and (39) it yields

1=a1(1−hd1(v)−hβ(v)In1+αIn)(40)

1=a2(1−h(d1(v)+γ1))(41)

Solving Eqs. (40) and (41) yield the expression for a1 and a2

a1=11−hd1(v)−hβ(v)In1+αIn(42)

a2=1−h(d1(v)+γ1)(43)

Now, three different cases will be discussed.

Case I: when v<vm then β(v)=0, so the presented numerical scheme is

Sn+1=Sn+a1h[A−d1(v)Sn+1](44)

In+1=In+a2h[−(d1(v)+γ1)In](45)

a1=11−hd1(v) and a2=11−h(d1(v)+γ1)(46)

Case II: When vm≤v≤v∘, then β(v)=v−vmv∘−vm. So, the numerical scheme for this case is mentioned in Eqs. (32) and (33), with a1 and a2 are given in Eqs. (43) and (43), respectively.

Case III: When v>v0 then β(v)=1, so the numerical scheme for this case can be expressed as

Sn+1=Sn+a1h[A−d1(v)Sn+1−Sn+1In1+αIn](47)

In+1=In+a2h[SnIn1+αIn−(d1(v)+γ1)In](48)

a1=11−hd1(v)−hIn1+αIna2=11−h(d1(v)+γ1)}(49)

4.1 Convergence Analysis

Theorem 1: The scheme (44)–(49) is conditionally convergent.

Proof: Three cases will be discussed to prove the scheme to be conditionally convergent.

Case I: When v<vm then β(v)=0 and consider

F=S−hA1−hd1(v)1+d1(v)h1−hd1(v)(50)

G=I(1−h(d1+γ1))1+h(d1+γ1)(51)

The Jacobian J∘ at equilibrium point E∘(s∘,I∘) can be expressed as

[1−hd1(v)001−h(d1(v)+γ1)1+h(d1(v)+γ1)](52)

The scheme will converge if |1−hd1(v)|<1 and |1−hd1(v)−hγ11+hd1(v)+hγ1|<1

Case II: When v0>v≥vm then β(v)=v−v0v0−vm and consider

F=S(1−hd1(v)−hβ(v)I1+αI)+hA(1−hd1(v)−hβ(v)I1+αI)(1+a1hd1(v))+βIn(53)

G=I(1−h(d1+γ1))+hβ(v)SI1+αI(1−h(d1+γ1))+h(d1+γ1)In(54)

The Jacobian J0 at equilibrium point E0(s0,I0) can be expressed as

[1−hd1β(v)(−Ad1+A(h−1)h+A(1−h))01+Aβ(v)hd1(v)−hd1−hγ11−hd1−hγ1](55)

The conditions for convergence are expressed as

|1−hd1(v)|<1(56)

|−Aβ(v)h−d1(v)+hd12(v)+hd1(v)γ1h(Aβ(v)+d12(v)−hd13(v)−hd12(v)γ1)|≤1(57)

Case III: When v>v0 then β(v)=1, so stability conditions are expressed as

|−Ah−d1(v)+hd12(v)+hd1(v)γ1h(A+d12(v)−hd13(v)−hd12(v)γ1)|<1(58)

5  Results and Discussions

The scheme is presented for solving differential equations having fuzzy parameters. The scheme is first-order accurate, which can be verified by looking at the scheme’s construction procedure. Since the scheme achieves first-order accuracy and is thus conditionally convergent, it is also consistent. It is also an explicit scheme. The conditional positivity of the suggested scheme is its primary benefit. The scheme provides a positive solution to the epidemic model under some conditions. The scheme will provide a positive solution if the unknown parameters used in difference equations are positive and the initial condition is positive. So, the expressions for parameters (whose expressions are found using Taylor series expansions) can be used to check positivity. An existing forward Euler scheme cannot provide the conditions to check a positive solution. Also, some forms of existing nonstandard finite difference methods are not first-order accurate.

Figs. 1–7 are drawn by employing the proposed scheme on the considered fuzzy model. Fig. 1 compares the proposed scheme with the existing forward Euler method. Both schemes provide accurate solutions. The absolute error is drawn in Fig. 1. This absolute error is obtained by finding the difference between Euler/proposed and Matlab solver ode45. The Matlab solver ode45 can be considered to solve initial value problems. For boundary value problems, the solver can be used with the Newton-Raphson method to find solutions. The Matlab solver’s solution is considered in place of the exact solution. Fig. 2 shows the impact of the mortality coefficient on susceptible and infective people.

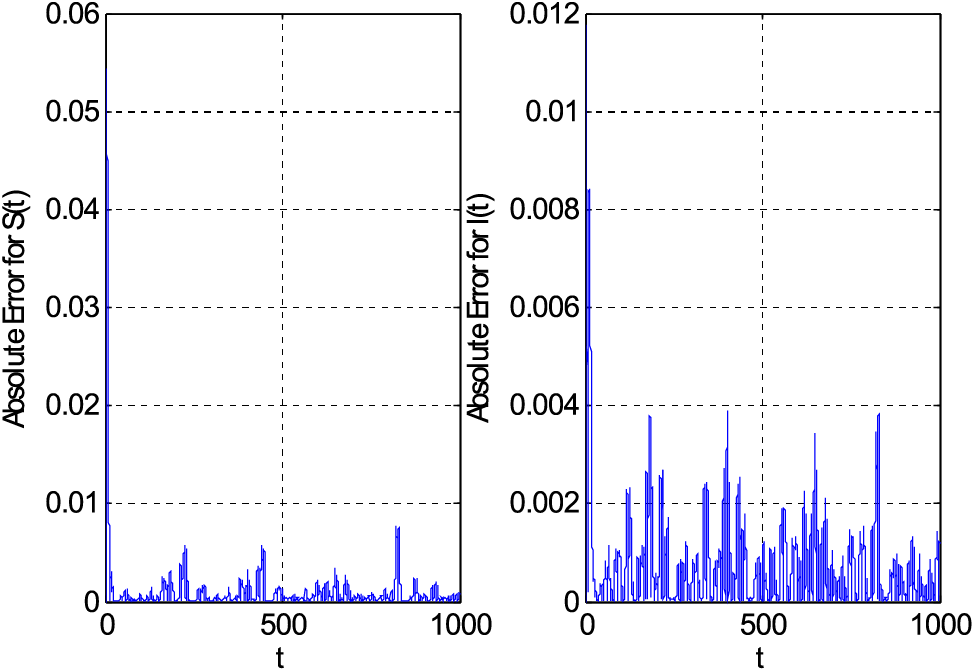
Figure 1: Comparison of the proposed scheme with forward Euler method using A=3.9,β=0.1,d1=0.3,α=0.5,r1=0.1,N=50,S0=4.4,I0=1

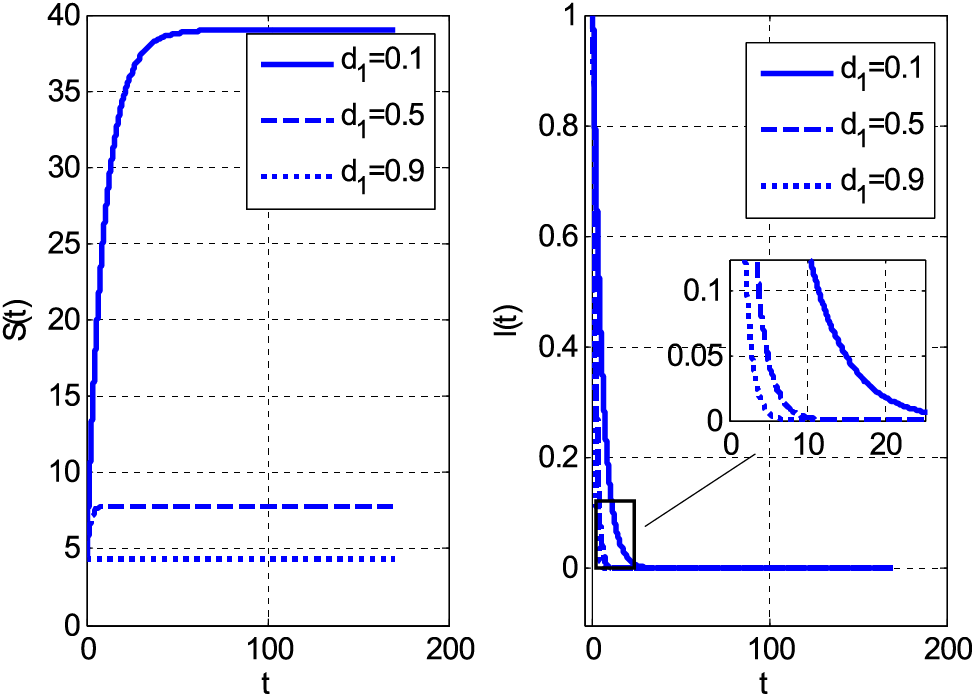
Figure 2: Impact of mortality coefficient on susceptible and infective individuals using A=3.9,β=0,α=0.5,r1=0.1,N=50,S0=4.4,I0=1

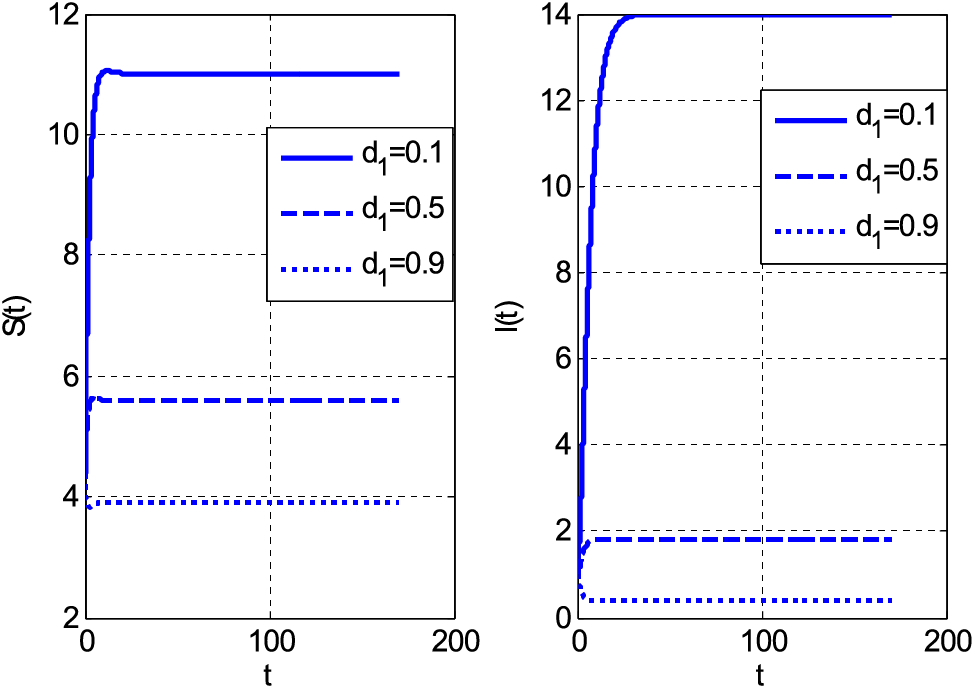
Figure 3: Impact of mortality coefficient on susceptible and infective people using A=3.9,β=0.4,α=1.5,r1=0.1,N=50,S0=4.4,I0=1

Figure 4: Impact of Holling type rate on susceptible and infective individuals using A=3.9,d1=0.3,β=0.1,r1=0.1,N=50,S0=4.4,I0=1

Figure 5: Impact of Holling type rate on susceptible and infective individuals using A=1,d1=0.9,β=1,r1=0.1,N=50,S0=4.4,I0=1

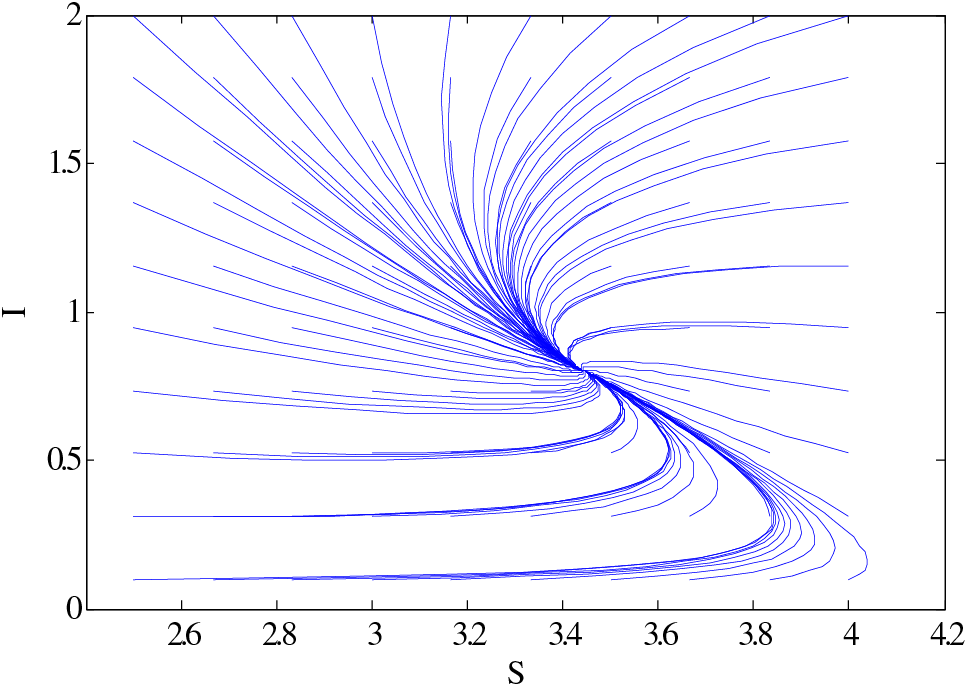
Figure 6: Relationship between susceptible and infective using A=3.9,d1=0.9,β=0.5,α=0.9,r1=0.1,N=100,2.5≤S0≤4,0.1≤I0≤2

Figure 7: Relationship between susceptible and infective individuals using A=3.9,d1=0.9,β=1,α=0.9,r1=0.1,N=100,2≤S0≤3,1≤I0≤2.5

Both categories of people decrease by increasing the mortality coefficient. The decay of people is the consequence of the increasing number of deaths. If both susceptible and infective people die, the graphs should decay. The same decreasing behaviour with rising values of mortality coefficient can be seen in Fig. 3. Fig. 3 shows susceptible and infective people by the growth of mortality parameter for case 2. Fig. 4 shows the Holling type rate α on susceptible and infective people. The susceptible people increase, and infective people decay by rising Holling type rate. The increase in the Holling-type rate leads to decay in the interaction of susceptible and infective people. If the interaction decreases, the number of susceptible people has to be increased while infective people should decrease.

Similarly, the same people’s behaviour can be seen in Fig. 5 for case 3. Figs. 6 and 7 show the curves that converge to equilibrium points for cases 2 and 3 using different initial conditions. Figs. 5 and 7 show the relationship between susceptible and infected people.

The analysis of the results will be improved to offer a more scientifically rigorous examination, clarifying the assertions and results of the study. We will thoroughly analyze the numerical findings, establishing explicit links between the model’s parameters and the observed patterns in epidemiological dynamics. This will require a systematic investigation of how factors such as the uncertain transmission rate and mortality coefficient affect the number of individuals vulnerable to the disease and those afflicted. Furthermore, we will examine the Holling-type rate’s consequences on persons capable of being infected and those sensitive to infection. The revised explanation will employ a systematic and scientific method to provide a thorough interpretation of the results. This will ensure that the insights obtained from the Hybrid SIR-Fuzzy Model are conveyed with clarity and transparency.

6  Conclusion

This research developed and investigated a unique approach, the Fuzzy Computational Scheme for the SIR Epidemic Model, to better comprehend infectious disease dynamics and a more solid foundation for public health decision-making. This computational paradigm combined the traditional SIR model with fuzzy logic to tackle the unknowns and complexities of disease spread. Our comprehensive numerical study of this novel approach revealed some interesting findings. First, we showed that fuzzy logic improves SIR model adaptation to real-world settings. It incorporates imprecise data to better account for disease parameter uncertainty. Our Fuzzy Computational Scheme can make more accurate and adaptable predictions, making it a valuable epidemiological tool. Second, our work showed that infectious illness modelling requires context. The fuzzy logic framework considers population density, healthcare infrastructure, and behavioural patterns, which can affect disease spread. Public health initiatives must be contextually sensitive to work in specific places and conditions. As a result of our studies, we also stress the ever-changing character of infectious disease dynamics. Our Fuzzy Computational Scheme can account for the dynamic nature of epidemics across time. It gives a more complete picture of the fight against infectious illnesses by automatically adjusting to new data as it becomes available. A fuzzy-based epidemic SIR model has been presented. The model used the fuzzy transferring rate parameter. The sensitivity analysis was given, and the sensitivity of parameters and a condition for the sensitivity of a parameter were found. The main concluding points are given as

•   The susceptible and infected people decayed by increasing values of the mortality coefficient.

•   The susceptible people increased, and infective was escalated by increasing values of Holling type rate for case 2 and case 3.

•   The constructed scheme provided approximately the same accuracy as the forward Euler method for a particular step size value.

•   The scheme provided the conditional positive solution.

In this study, we will evaluate the proposed Fuzzy Computational Scheme using numerical data to assess its ability to capture various facets of disease transmission effectively. We hope that our efforts will add to the growing body of literature devoted to improving our knowledge of epidemic dynamics. Our ultimate objective is to provide public health workers and policymakers with a more accurate and versatile tool for deliberating over health emergencies. We hope that by bringing together the fields of mathematics, epidemiology, and computer science, we might better understand the dynamics of infectious diseases and develop more efficient prevention and control methods.

Limitations of the research: This study acknowledges the significance of resolving research limitations and recognizes specific constraints in the suggested Hybrid SIR-Fuzzy Model. Firstly, using fuzzy logic improves the model’s ability to handle uncertainty, but it also adds complexity, potentially impacting computational efficiency. To address this issue, the numerical scheme utilized is optimized for efficiency. However, additional investigation into computational techniques could potentially improve performance. In addition, the model impliles that all population interactions are homogeneous, which may oversimplify real-world situations. Subsequent versions should consider spatial heterogeneity for a more detailed and sophisticated depiction.

Moreover, the study’s dependence on numerical simulations may restrict analytical observations. There were attempts to authenticate the numerical scheme thoroughly to tackle this issue. Nevertheless, conducting analytical examinations on the model’s behaviour presents a promising path for further inquiry. The explicit recognition of these constraints emphasizes the dedication to enhancing the model’s trustworthiness, relevance, and influence in future versions of the study.

Acknowledgement: The authors wish to express their gratitude to Prince Sultan University for facilitating the publication of this article through the Theoretical and Applied Sciences Lab.

Funding Statement: The authors would like to acknowledge the support of Prince Sultan University for paying the article processing charges (APC) of this publication.

Author Contributions: Conceptualization, methodology, and analysis, writing—review and editing, Y.N.; funding acquisition, K.A.; investigation, Y.N.; methodology, M.S.A.; project administration, K.A.; resources, K.A.; supervision, M.S.A.; visualization, K.A.; writing—review and editing, M.S.A.; proofreading and editing, M.S.A. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: The manuscript included all required data and implementing information.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Mishra, B. K., Prajapati, A. (2013). Spread of malicious objects in computer network: A fuzzy approach. Applications and Applied Mathematics: An International Journal (AAM), 8(2), 22. [Google Scholar]

2. Zadeh, L. A. (1965). Fuzzy sets, information and control. Information and Control, 8(3), 338–353. [Google Scholar]

3. Das, A., Pal, M. (2018). A mathematical study of an imprecise SIR epidemic model with treatment control. Journal of Applied Mathematics and Computing, 56, 477–500. [Google Scholar]

4. Sadhukhan, D., Sahoo, L. N., Mondal, B., Maiti, M. (2010). Food chain model with optimal harvesting in fuzzy environment. Journal of Applied Mathematics and Computing, 34, 1–18. [Google Scholar]

5. Barros, L. D., Leite, M. F., Bassanezi, R. C. (2003). The SI epidemiological models with a fuzzy transmission parameter. Computers Mathematics with Applications, 45(10–11), 1619–1628. [Google Scholar]

6. Mondal, P. K., Jana, S., Haldar, P., Kar, T. K. (2015). Dynamical behavior of an epidemic model in a fuzzy transmission. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 23(5), 651–665. [Google Scholar]

7. Verma, R., Tiwari, S. P., Upadhyay, R. K. (2017). Dynamical behaviors of fuzzy SIR epidemic model. Proceedings of the Conference of the European Society for Fuzzy Logic and Technology, pp. 482–492. Cham, Springer International Publishing. [Google Scholar]

8. Ortega, N. R. S., Sallum, P. C., Massad, E. (2000). Fuzzy dynamical systems in epidemic modelling. Kybernetes, 29(2), 201–218. [Google Scholar]

9. Verma, R., Tiwari, S. P., Upadhyay, R. K. (2019). Transmission dynamics of epidemic spread and outbreak of Ebola in West Africa: Fuzzy modeling and simulation. Journal of Applied Mathematics and Computing, 60, 637–671. [Google Scholar]

10. Jafelice, R. M., de Barros, L. C., Bassanezi, R. C., Gomide, F. (2004). Fuzzy modeling in symptomatic HIV virus infected population. Bulletin of Mathematical Biology, 66, 1597–1620. [Google Scholar] [PubMed]

11. Lefevr, N., Kanavos, A., Gerogiannis, V. C., Iliadis, L., Pintelas, P. (2021). Employing fuzzy logic to analyze the structure of complex biological and epidemic spreading models. Mathematics, 9(9), 977. [Google Scholar]

12. El Allaoui, A., Melliani, S., Chadli, L. S. (2020). A mathematical fuzzy model to giving up smoking. 2020 IEEE 6th International Conference on Optimization and Applications (ICOA), pp. 1–6. IEEE. https://doi.org/10.1109/ICOA49421.2020.9094470 [Google Scholar] [CrossRef]

13. Diniz, J. B., Cordeiro, F. R. (2017). Automatic segmentation of melanoma in dermoscopy images using fuzzy numbers. 2017 IEEE 30th International Symposium on Computer-Based Medical Systems (CBMS), pp. 150–155. IEEE. https://doi.org/10.1109/CBMS.2017.39 [Google Scholar] [CrossRef]

14. Alamin, A., Mondal, S. P., Alam, S., Goswami, A. (2020). Solution and stability analysis of non-homogeneous difference equation followed by real life application in fuzzy environment. Sādhanā, 45, 1–20. [Google Scholar]

15. Mishra, B. K., Pandey, S. K. (2010). Fuzzy epidemic model for the transmission of worms in computer network. Nonlinear Analysis: Real World Applications, 11(5), 4335–4341. [Google Scholar]

16. Akgül, A. (2018). A novel method for a fractional derivative with non-local and non-singular kernel. Chaos, Solitons Fractals, 114, 478–482. [Google Scholar]

17. Dhandapani, P. B., Baleanu, D., Thippan, J., Sivakumar, V. (2021). New fuzzy fractional epidemic model involving death population. Computer Systems Science & Engineering, 37(3), 331–346. https://doi.org/10.32604/csse.2021.015619 [Google Scholar] [CrossRef]

18. Ahmad, S., Ullah, A., Akgül, A., Abdeljawad, T. (2021). Semi-analytical solutions of the 3rd order fuzzy dispersive partial differential equations under fractional operators. Alexandria Engineering Journal, 60(6), 5861–5878. [Google Scholar]

19. Ahmad, S., Ullah, A., Ullah, A., Akgül, A., Abdeljawad, T. (2021). Computational analysis of fuzzy fractional order non-dimensional Fisher equation. Physica Scripta, 96(8), 084004. [Google Scholar]

20. Ahmad, S., Ullah, A., Akgül, A., Abdeljawad, T. (2021). Numerical analysis of fractional human liver model in fuzzy environment. Journal of Taibah University for Science, 15(1), 840–851. [Google Scholar]

21. Ullah, Z., Ahmad, S., Ullah, A., Akgül, A. (2021). On solution of fuzzy Volterra integro-differential equations. Arab Journal of Basic and Applied Sciences, 28(1), 330–339. [Google Scholar]

22. Mickens, R. E. (2005). Advances in the applications of nonstandard finite difference schemes. World Scientific. https://doi.org/10.1142/5884 [Google Scholar] [CrossRef]

23. Cresson, J., Pierret, F. (2016). Non standard finite difference scheme preserving dynamical properties. Journal of Computational and Applied Mathematics, 303, 15–30. [Google Scholar]

24. Saleem, N., Javed, K., Uddin, F., Ishtiaq, U., Ahmed, K. et al. (2023). Unique solution of integral equations via intuitionistic extended fuzzy b-metric-like spaces. Computer Modeling in Engineering & Sciences, 135(1). https://doi.org/10.32604/cmes.2022.021031 [Google Scholar] [CrossRef]

25. Alqudah, M. A., Ashraf, R., Rashid, S., Singh, J., Hammouch, Z. et al. (2021). Novel numerical investigations of fuzzy Cauchy reaction-diffusion models via generalized fuzzy fractional derivative operators. Fractal and Fractional, 5(4), 151. [Google Scholar]

26. Mjahed, S., Bouzaachane, K., Taher Azar, A., El Hadaj, S., Raghay, S. (2020). Hybridization of fuzzy and hard semi-supervised clustering algorithms tuned with ant lion optimizer applied to Higgs boson search. Computer Modeling in Engineering & Sciences, 125(2), 459–494. https://doi.org/10.32604/cmes.2020.010791 [Google Scholar] [CrossRef]

27. Mangongo, Y. T., Bukweli, J. D. K., Kampempe, J. D. B. (2021). Fuzzy global stability analysis of the dynamics of malaria with fuzzy transmission and recovery rates. American Journal of Operations Research, 11(6), 257–282. [Google Scholar]

28. Dayan, F., Ahmed, N., Rafiq, M., Akgül, A., Raza, A. et al. (2022). Construction and numerical analysis of a fuzzy non-standard computational method for the solution of an SEIQR model of COVID-19 dynamics. AIMS Math, 7(5), 8449–8470. [Google Scholar]

29. Panja, P., Mondal, S. K., Chattopadhyay, J. (2017). Dynamical study in fuzzy threshold dynamics of a cholera epidemic model. Fuzzy Information and Engineering, 9(3), 381–401. [Google Scholar]

30. Prata, D. N., Rodrigues, W., Bermejo, P. H. (2020). Temperature significantly changes COVID-19 transmission in (sub) tropical cities of Brazil. Science of the Total Environment, 729, 138862. [Google Scholar] [PubMed]

31. Irfan, M., Ikram, M., Ahmad, M., Wu, H., Hao, Y. (2021). Does temperature matter for COVID-19 transmissibility? Evidence across Pakistani provinces. Environmental Science and Pollution Research, 28(42), 59705–59719. [Google Scholar] [PubMed]

32. Stella, L., Martínez, A. P., Bauso, D., Colaneri, P. (2022). The role of asymptomatic infections in the COVID-19 epidemic via complex networks and stability analysis. SIAM Journal on Control and Optimization, 60(2), S119–S144. [Google Scholar]

33. Zhou, J., Ye, Y., Arenas, A., Gómez, S., Zhao, Y. (2023). Pattern formation and bifurcation analysis of delay induced fractional-order epidemic spreading on networks. Chaos, Solitons Fractals, 174, 113805. [Google Scholar]

34. George, R., Gul, N., Zeb, A., Avazzadeh, Z., Djilali, S. et al. (2022). Bifurcations analysis of a discrete time SIR epidemic model with nonlinear incidence function. Results in Physics, 38, 105580. [Google Scholar]