 Open Access
Open Access
REVIEW
Stochastic Fractal Search: A Decade Comprehensive Review on Its Theory, Variants, and Applications
1 Department of Mathematics, College of Science and Humanities in Al-Kharj, Prince Sattam bin Abdulaziz University, Al-Kharj, 11942, Saudi Arabia
2 Faculty of Science and Technology, Hassan II University of Casablanca, Mohammedia, 28806, Morocco
3 School of Engineering and Technology, Sunway University Malaysia, Petaling Jaya, 27500, Malaysia
4 Centre for Research Impact & Outcome, Chitkara University Institute of Engineering and Technology, Chitkara University, Rajpura, 140401, Punjab, India
5 Faculty of Engineering, Helwan University, Cairo, 11792, Egypt
6 Applied Science Research Center, Applied Science Private University, Amman, 11937, Jordan
* Corresponding Author: Anas Bouaouda. Email:
(This article belongs to the Special Issue: Swarm and Metaheuristic Optimization for Applied Engineering Application)
Computer Modeling in Engineering & Sciences 2025, 142(3), 2339-2404. https://doi.org/10.32604/cmes.2025.061028
Received 15 November 2024; Accepted 10 February 2025; Issue published 03 March 2025
Abstract
With the rapid advancements in technology and science, optimization theory and algorithms have become increasingly important. A wide range of real-world problems is classified as optimization challenges, and meta-heuristic algorithms have shown remarkable effectiveness in solving these challenges across diverse domains, such as machine learning, process control, and engineering design, showcasing their capability to address complex optimization problems. The Stochastic Fractal Search (SFS) algorithm is one of the most popular meta-heuristic optimization methods inspired by the fractal growth patterns of natural materials. Since its introduction by Hamid Salimi in 2015, SFS has garnered significant attention from researchers and has been applied to diverse optimization problems across multiple disciplines. Its popularity can be attributed to several factors, including its simplicity, practical computational efficiency, ease of implementation, rapid convergence, high effectiveness, and ability to address single- and multi-objective optimization problems, often outperforming other established algorithms. This review paper offers a comprehensive and detailed analysis of the SFS algorithm, covering its standard version, modifications, hybridization, and multi-objective implementations. The paper also examines several SFS applications across diverse domains, including power and energy systems, image processing, machine learning, wireless sensor networks, environmental modeling, economics and finance, and numerous engineering challenges. Furthermore, the paper critically evaluates the SFS algorithm’s performance, benchmarking its effectiveness against recently published meta-heuristic algorithms. In conclusion, the review highlights key findings and suggests potential directions for future developments and modifications of the SFS algorithm.Keywords
Nomenclature
| ANN | Artificial Neural Network |
| CSFS | Chaotic Stochastic Fractal Search |
| DE | Differential Evolution |
| FDB | Fitness-Distance Balance |
| FS | Fractal Search |
| GA | Genetic Algorithm |
| GWO | Grey Wolf Optimizer |
| MAE | Mean Absolute Error |
| ORPD | Optimal Reactive Power Dispatch |
| PID | Proportional-Integral-Derivative |
| PSO | Particle Swarm Optimization |
| RESs | Renewable Energy Sources |
| RMSE | Root Mean Square Error |
| SFS | Stochastic Fractal Search |
| WOA | Whale Optimization Algorithm |
| WSN | Wireless Sensor Networks |
Optimization aims to determine the optimal values for decision variables that minimize or maximize objective functions while satisfying specific constraints. Numerous real-world optimization problems present significant challenges, such as high computational costs, nonlinear constraints, non-convex search spaces, dynamic or noisy objective functions, and extensive solution spaces [1]. These factors influence the choice between exact and approximate methods for addressing complex problems. While exact methods can accurately identify the global optimum, their computational time typically increases exponentially with the number of variables [2]. In contrast, stochastic optimization algorithms can effectively find near-optimal or optimal solutions within a practical timeframe. Heuristic and meta-heuristic methods are among the most effective approximate algorithms for solving complex optimization problems [3].
Heuristic algorithms are techniques employed to find near-optimal solutions efficiently. They generate feasible solutions within a predefined number of iterations, demonstrating adaptability to the problem being addressed. Heuristics typically employ a trial-and-error approach to explore potential solutions, aiming to do so within reasonable computational time and resource constraints. However, their inherent tendency towards local exploration can lead to convergence at local optima, which may prevent the attainment of the global optimum [3].
On the other hand, meta-heuristic algorithms were developed to address the limitations of heuristic algorithms. Each meta-heuristic employs distinct strategies to guide the search process, aiming for a comprehensive search space exploration to identify near-optimal solutions. These algorithms encompass diverse techniques, ranging from simple local exploration to sophisticated learning methods [4]. Meta-heuristics are often considered problem-independent as they do not rely on the specific characteristics of the problem being solved. Furthermore, their non-greedy approach enables a comprehensive search space exploration, potentially resulting in improved solutions that may sometimes align with global optima [5]. Consequently, meta-heuristic algorithms can uncover superior solutions for many optimization problems while avoiding local optima. These robust and adaptable algorithms tackle many challenges, including path planning, feature selection, wireless sensor networks, image processing, and neural network optimization [6].
Several vital attributes contribute to the appeal of meta-heuristic algorithms, such as simplicity, flexibility, black-box nature, and the capability to avoid local optima traps [6]. Unlike heuristic algorithms, meta-heuristics effectively manage the balance between exploration and exploitation, two essential components of the optimization process [7]. Exploration focuses on discovering solutions in unexplored regions of the search space, while exploitation aims to identify optimal solutions among the current candidate solutions. By employing iterative and efficient processes that effectively balance these components, meta-heuristic algorithms guide the search towards optimal or near-optimal solutions [7].
Numerous meta-heuristic algorithms have been developed over the past few decades [8]. Fig. 1 illustrates the five primary categories of meta-heuristic algorithms, which include evolutionary-based, swarm-based, human-inspired, chemistry/physics-based, and mathematics-based methods.
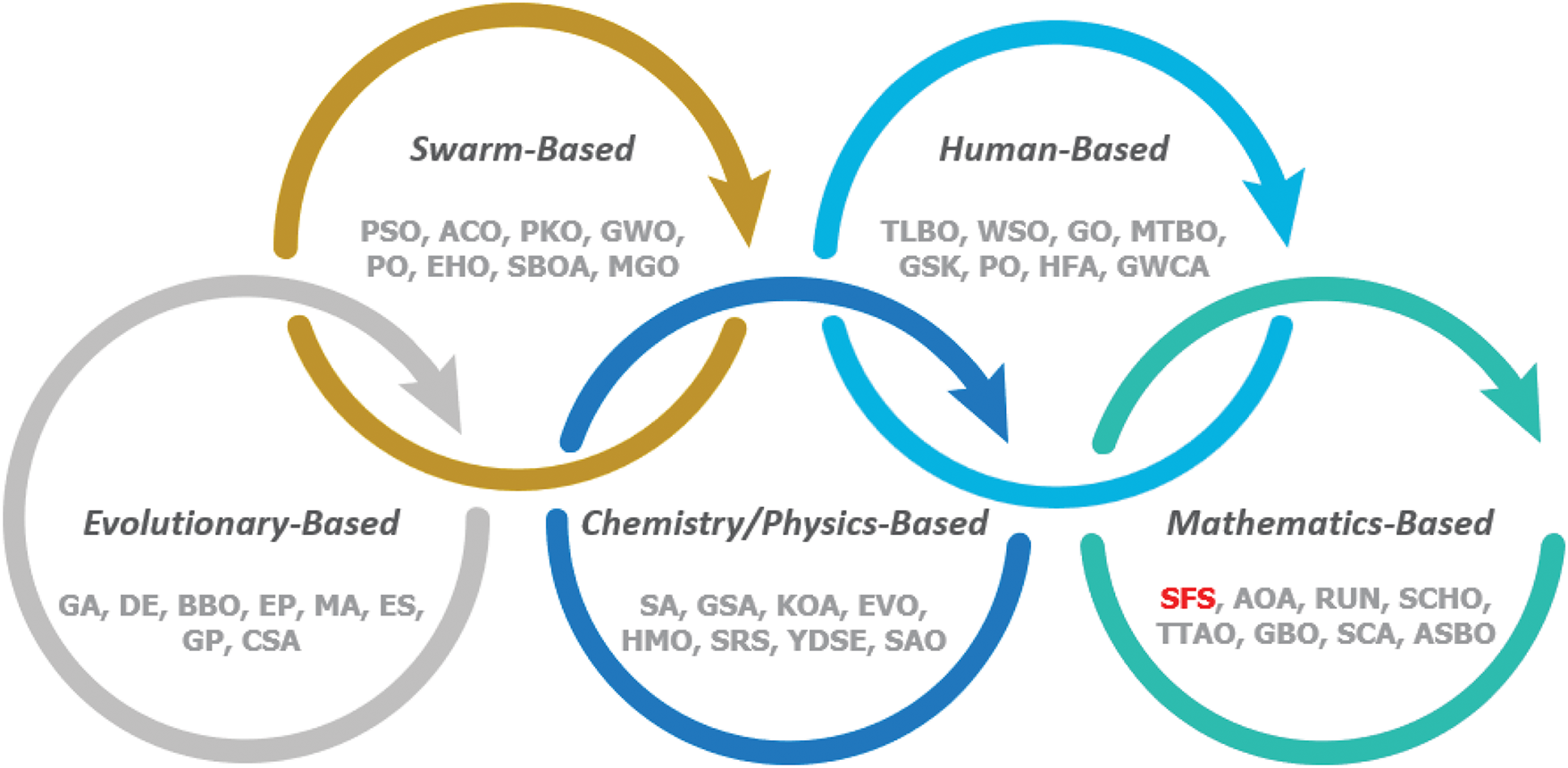
Figure 1: A brief classification of meta-heuristic techniques
The first class encompasses evolutionary techniques inspired by the biological principle of survival of the fittest [9]. The most well-known evolutionary algorithm is the Genetic Algorithm (GA), developed by Holland [10]. GA emulates Darwin’s theory of evolution by generating improved solutions through mating the fittest parents using the crossover mechanism, which enhances exploitation by producing offspring similar to the parents. On the other hand, the mutation operator helps maintain diversity by introducing new genetic material into the population, facilitating the exploration of different regions in the search space. Another notable evolutionary algorithm is Differential Evolution (DE) [11], introduced by Storn and Price. DE addresses optimization problems by refining candidate solutions through an effective evolutionary process that includes mutation, crossover, and selection. Other developed evolutionary algorithms, such as Biogeography Based Optimization (BBO) [12], Evolutionary Programming (EP) [13], Memetic Algorithm (MA) [14], Genetic Programming (GP) [15], Clonal Selection Algorithm (CSA) [16], Evolution Strategy (ES) [17], have demonstrated significant effectiveness in addressing several optimization challenges.
The second class comprises swarm intelligence techniques inspired by the collective behaviors observed in natural swarms, such as those of social animals. Group intelligence emerges from the interactions among simple individuals within the group, allowing the emergence of specific intelligent traits without centralized control [9]. A prominent example is Particle Swarm Optimization (PSO) [18], which simulates the foraging behavior of birds to guide the search process. PSO effectively utilizes individual and collective information during the search, typically achieving optimal solutions through collaboration and information sharing among individuals within the population. Another noteworthy algorithm is Ant Colony Optimization (ACO) [19], which mimics how ants find the shortest paths while foraging. In ACO, ants deposit pheromones as they traverse paths, leading to a positive feedback mechanism where more ants gradually favor shorter routes over time. This process allows the ant colony to determine the shortest paths. Other significant swarm-based algorithms include the Pied Kingfisher Optimizer (PKO) [20], Grey Wolf Optimizer (GWO) [21], Puma Optimizer (PO) [22], Elk Herd Optimizer (EHO) [23], Secretary Bird Optimization Algorithm (SBOA) [24], Mountain Gazelle Optimizer (MGO) [25], White Shark Optimizer (WSO) [26], and others.
The third class encompasses chemistry/physics-based algorithms replicating physical or chemical phenomena. These algorithms simulate the interactions among search agents based on fundamental principles from physics or chemistry [9]. The most popular physics-based approach is Simulated Annealing (SA) [27], inspired by the annealing process of metals. In SA, the metal is initially heated to a molten state and then gradually cooled, allowing it to form an optimal crystal structure. Another notable algorithm is the Gravitational Search Algorithm (GSA) [28], which models Newton’s laws of gravity by treating search agents as a group of masses that interact according to the laws of gravity and motion, facilitating the search for an optimal solution. Several other chemistry/physics-based algorithms have been introduced, including Kepler Optimization Algorithm (KOA) [29], Energy Valley Optimizer (EVO) [30], Homonuclear Molecules Optimization (HMO) [31], Special Relativity Search (SRS) [32], Young’s Double-Slit Experiment (YDSE) optimizer [33], Snow Ablation Optimizer (SAO) [34], Artificial Chemical Reaction Optimization Algorithm (ACROA) [35], Chemical Reaction Optimization (CRO) [36], and so on.
The fourth class includes human-inspired techniques inspired by human societal activities [9]. An example is Teaching-Learning-Based Optimization (TLBO) [37], which draws inspiration from the interaction between teachers and learners. TLBO mimics the traditional classroom teaching method, encompassing teacher and learner phases. In the teacher phase, each student learns from the highest-performing individuals, while in the learner phase, students acquire knowledge randomly from their peers. Other notable examples of human-inspired algorithms include War Strategy Optimization (WSO) [38], Growth Optimizer (GO) [39], Mountaineering Team-Based Optimization (MTBO) [40], Gaining Sharing Knowledge based algorithm (GSK) [41], Political Optimizer (PO) [42], Human Felicity Algorithm (HFA) [43], Great Wall Construction Algorithm (GWCA) [44], Coronavirus herd immunity optimizer (CHIO) [45], and more.
Finally, mathematics-based algorithms represent a contemporary category of meta-heuristic algorithms that do not imitate specific phenomena or behaviors but instead rely on mathematical formulations. A well-known example is the Sine Cosine Algorithm (SCA) [46], inspired by the properties of the transcendental functions sine and cosine. Another notable algorithm, the Arithmetic Optimization Algorithm (AOA) [47], utilizes the distribution behavior of the four basic arithmetic operators. Recently developed mathematics-based algorithms include the Average and Subtraction-Based Optimizer (ASBO) [48], RUNge Kutta optimizer (RUN) [49], Geometric Mean Optimizer (GMO) [50], Sinh Cosh Optimizer (SCHO) [51], Topology Aggregation Optimizer (TTAO) [52], and Gradient-Based Optimizer (GBO) [53], among others. Although mathematics-based algorithms are less prevalent than the previously mentioned categories, their significance in the optimization process should not be underestimated. These algorithms offer an innovative perspective for developing effective search strategies, distinguishing themselves from conventional metaphor-based approaches through their unique mathematical formulations.
The Stochastic Fractal Search (SFS) algorithm is an example of a robust mathematics-based meta-heuristic method developed by Salimi [54] in 2015 based on the mathematical concept of fractals. SFS leverages the diffusion properties observed in random fractals, enabling its particles to navigate the search space more effectively. The SFS algorithm process involves two main stages: diffusion and updating [54]. Each particle disperses from its initial position during diffusion, promoting local exploitation. In the updating stage, SFS utilizes statistical techniques to refine the position of each agent, enabling the exploration of more promising areas within the search space. This dynamic allows for efficient information sharing among particles, facilitating rapid convergence towards optimal solutions [54].
The SFS algorithm has effectively addressed many complex optimization problems, including engineering design, machine learning, deep learning, energy optimization, feature selection, and image segmentation. The exceptional performance of SFS has garnered significant attention from researchers, leading to the development of numerous advanced variants. These variants can effectively tackle single- and multi-objective problems across discrete and continuous search spaces, addressing challenges associated with unknown and potentially complex landscapes. Despite the sustained interest and ongoing research in SFS, a comprehensive literature review is still lacking. We believe that such a review is crucial for several reasons. First, it would offer researchers a clear and concise summary of the latest advancements in SFS. Second, it would provide valuable insights and inspiration for exploring future research directions in this domain.
Therefore, this paper provides a comprehensive review of the existing literature on the SFS algorithm, aiming to identify the most commonly studied problems, significant modifications to its framework, and prevalent hybridization techniques. Our objective is to assess the current state of SFS research, highlighting its strengths and weaknesses across diverse problem variants while offering an extensive overview of its applications. In summary, the primary contributions of this review paper are as follows:
• A detailed overview of SFS, including its mathematical foundations and research trends;
• An examination of all SFS variants to demonstrate the algorithm’s adaptability across several contexts;
• A presentation of SFS applications in diverse optimization scenarios, as well as its integration with other optimization algorithms;
• A discussion of the challenges associated with the SFS algorithm, aiding researchers in recognizing key issues;
• A roadmap of future research directions aimed at guiding subsequent studies toward critical gaps and emerging trends.
The subsequent sections of the paper are organized as follows: Section 2 provides a concise overview of the classical SFS algorithm and its core concepts. Section 3 explores the evolution of the SFS algorithm and its spread in the literature, highlighting the volume of relevant papers and citations published over the past decade. Section 4 focuses on analyzing and evaluating diverse SFS variants. Section 5 presents a selection of studies that apply the SFS algorithm across diverse domains. Section 6 introduces open-source software and online resources related to SFS. Section 7 offers a comparative performance analysis of SFS against the latest published meta-heuristic algorithms using the CEC’2022 benchmark test. Section 8 identifies ongoing challenges and potential future research directions for users of the SFS algorithm. Finally, Section 9 concludes the review paper by summarizing the study and its key findings.
2 Fundamentals of the SFS Algorithm
This section discusses the origins, core theoretical foundations, fundamental structure, shared characteristics, computational complexity, advantages, and limitations of the SFS algorithm.
The SFS algorithm is a mathematics-based meta-heuristic algorithm inspired by the fractal growth patterns observed in natural materials, introduced by Salimi in 2015 [54]. Unlike most existing meta-heuristic algorithms, which often rely on the collective behavior of organisms such as ACO or PSO, SFS’s optimization principle is based on the mathematical concept of fractals. Fractals are complex geometric shapes exhibiting self-similarity across different scales, a concept first introduced by Benoît Mandelbrot in 1975 [55]. Common methods for generating fractal shapes include Random fractals [56], Finite subdivision rules [57], L-systems [58], Strange attractors [59], and Iterated function systems [60]. Among these, Diffusion Limited Aggregation (DLA) [61] is a widely used method. Salimi was the first to apply DLA to the Fractal Search (FS) algorithm by modeling DLA growth using Lévy flights and Gaussian walks [54]. Fig. 2 illustrates a random fractal generated using the DLA method.

Figure 2: Diffusion-limited aggregation fractal
The SFS algorithm comprises two primary processes: diffusion and updating [54]. Inspired by the FS algorithm, the diffusion process aims to intensify or exploit the search space by allowing each particle to diffuse around its current position. This characteristic is crucial for enhancing the likelihood of locating the global optimum while minimizing the risk of being trapped in local optima. Unlike the basic FS algorithm, the diffusion process in SFS remains static, preventing a significant increase in active particles [54]. Only the best-generated particle during the diffusion phase is retained, while the others are discarded. In contrast, the updating process serves as an exploration phase, during which each particle modifies its position based on the locations of other chosen particles within the group [54].
The mathematical model of the SFS algorithm comprises three main procedures: initialization, diffusion, and updating, as illustrated in Fig. 3. Initially, a group of particles is generated, each assigned a predetermined level of electrical potential energy. The diffusion process focuses on exploiting the search within promising areas, while the updating process prioritizes exploring new regions of the solution space. These procedures are mathematically defined as follows:
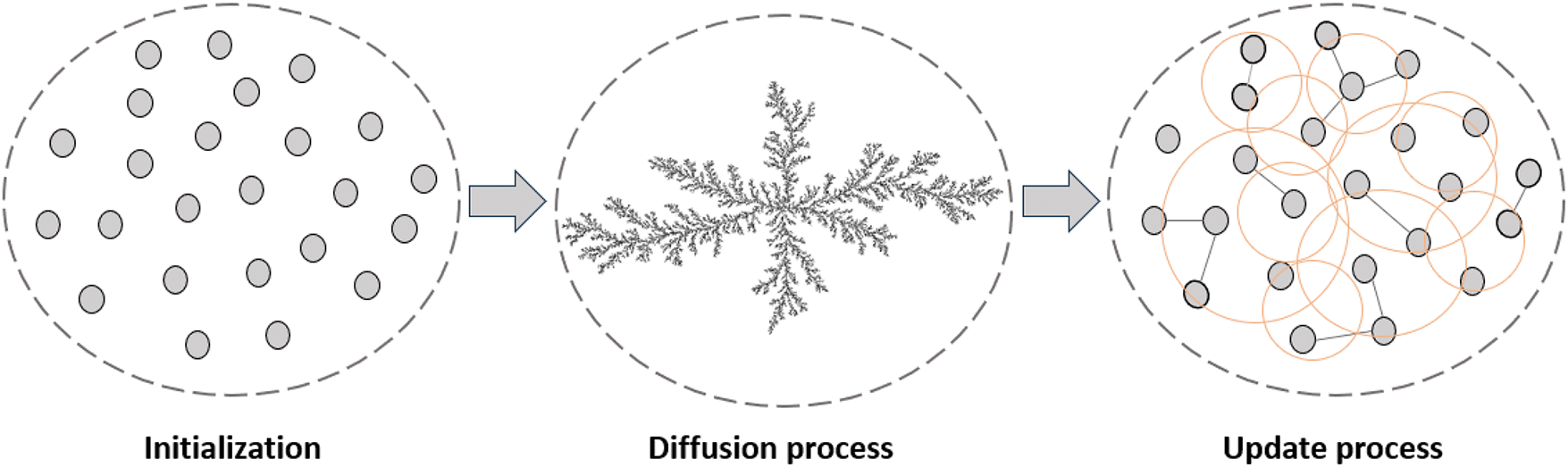
Figure 3: Main processes of the SFS algorithm
Like other optimization algorithms, the SFS begins by initializing a set of particles representing a collection of initial solutions. The population size, denoted as N, defines the number of particles in the system. Each particle is described as a
where
During this process, each particle diffuses around its current location to exploit the search space, increasing the likelihood of discovering better solutions and avoiding local minima. This is achieved by generating new points using the Gaussian walk, which is mathematically represented by the following equations [54]:
where
where
This process involves two statistical procedures designed to explore the search space effectively. In the initial procedure, all points are ranked based on their fitness values, and a probability value,
where
where
where
2.3 Framework of the SFS Algorithm
Fig. 4 illustrates the flowchart of SFS, which comprises four distinct stages: initialization, diffusion, and two update processes. Each stage plays a critical role in the overall search process. The initialization phase randomly establishes the initial population, while the diffusion process focuses on local exploitation. In contrast, the two update processes prioritize global exploration, enhancing solution accuracy and robustness. The steps for implementing the SFS are detailed as follows:
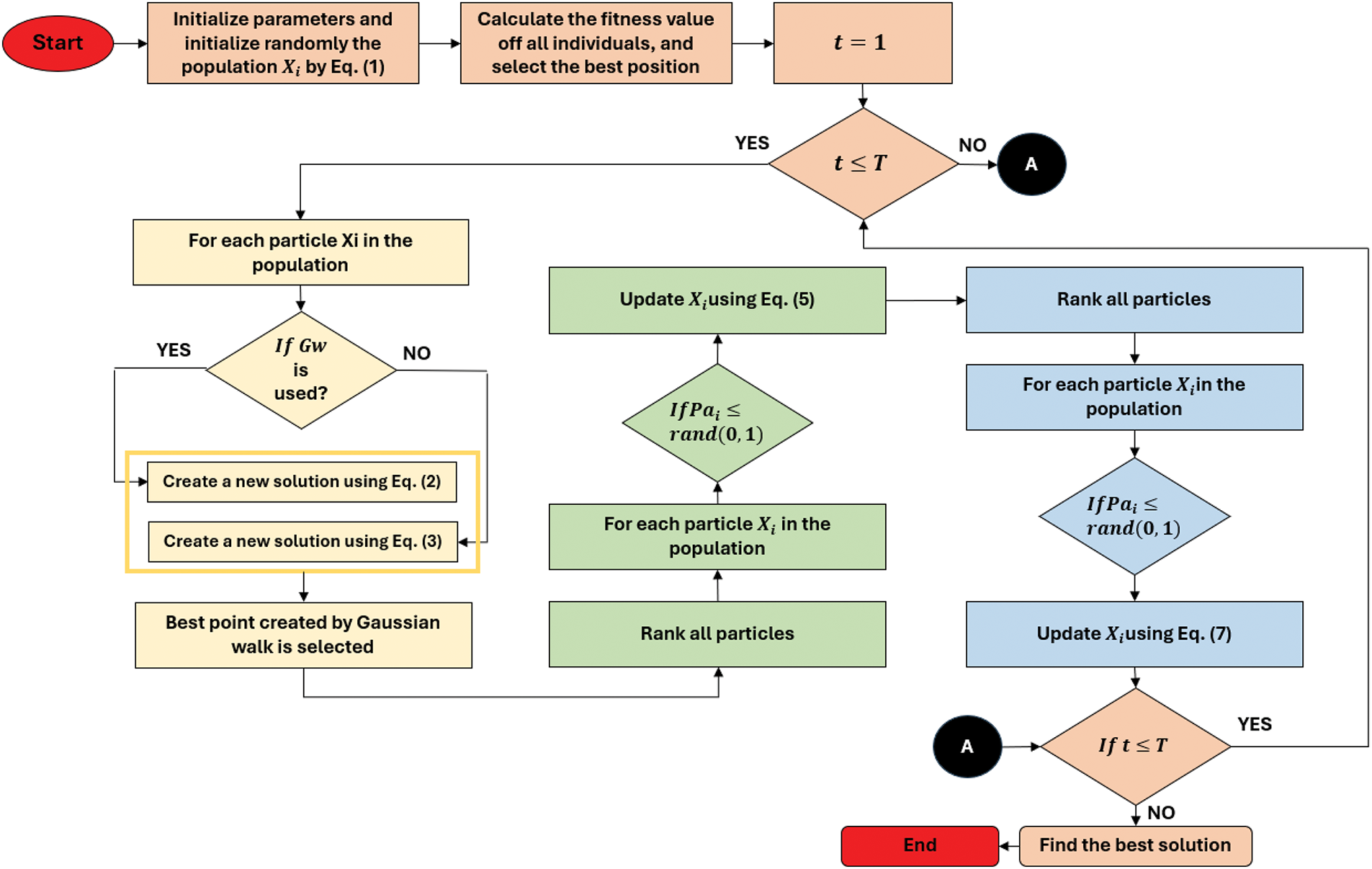
Figure 4: Flowchart of the SFS algorithm
Step 1: Define the relevant parameters and initialize the population using Eq. (1).
Step 2: Compute and evaluate the fitness values of all individuals in the population, then record the optimal individual.
Step 3: Each individual disperses around its current position. Eqs. (2) and (3) represent the diffusion equations.
Step 4: Determine the updated probability for all individuals in the population using Eq. (6). If
Step 5: The updated probability for the new individual is recalculated using Eq. (6). Likewise, if
Step 6: Continue repeating steps 2 to 5 until the loop’s termination condition is met.
Understanding algorithmic complexity is crucial for researchers to demonstrate an algorithm’s practicality and effectiveness. While some algorithms may achieve minimal error rates, extended computation times limit their applicability. High computational complexity often diminishes an algorithm’s appeal, impacting its usability and efficiency. Therefore, an algorithm’s effectiveness is not solely defined by error or convergence metrics; convergence speed and computational efficiency are equally vital considerations. In the SFS algorithm, computational complexity is primarily influenced by the initialization phase, the diffusion process, and the first and second update stages. The total computational complexity of SFS can be represented as follows:
where T denotes the maximum number of generations, D represents the dimensionality of the problem, N denotes the population size, and MDN represents the maximum diffusion number.
Algorithm 1 gives the pseudo-code of the SFS algorithm.

The effectiveness of meta-heuristic algorithms in addressing optimization challenges is significantly influenced by the strategies employed for generating new solutions and the associated parameter settings. An adaptive approach to parameter tuning is crucial for optimizing algorithm performance, especially when dealing with complex problems characterized by non-separability, poor conditioning, multimodality, or high dimensionality. While the SFS algorithm reduces the number of parameters inherent in basic FS, it still relies on fixed parameter values throughout generations. This reliance on static values can limit the algorithm’s adaptability, as optimal parameter settings can vary significantly across different problem types [62]. Furthermore, knowledge sharing between stages within the SFS algorithm remains limited. An adaptive scheme, leveraging optimal values from high-performing individuals, could enhance the generation of new solutions and improve the algorithm’s overall performance [63].
Additionally, the update process facilitates exploration, while the diffusion process focuses on exploitation. Achieving an optimal balance between these two stages in terms of function evaluations remains challenging. Specifically, the diffusion phase requires
3 The Popularity and Growth of the SFS Algorithm in the Literature
The SFS algorithm has garnered considerable attention in recent years due to its simplicity and versatility. This growing interest is reflected in a noticeable increase in published research and citations related to the SFS algorithm. To explore this trend, we conducted a comprehensive literature review using the Scopus1 database. Scopus offers advanced search capabilities, including regular expressions and complex query design, allowing for precise searches based on authors, article titles, and publication dates. The following criteria guided the search in the Scopus database:
• The search query was “Stochastic Fractal Search”.
• Only papers published in English were considered for inclusion.
• The timeframe for the search was restricted to articles published between 2015 and 2024.
• The data were collected on 01 October 2024.
In summary, the comprehensive search query executed in the Scopus database is as follows: (TITLE-ABS-KEY(“Stochastic Fractal Search”) AND PUBYEAR > 2014 AND PUBYEAR < 2025 AND (LIMIT-TO (LANGUAGE,“English”))). The results of this search are discussed below:
Based on statistical analysis of data from the Scopus database, Fig. 5 illustrates the cumulative citations of the foundational SFS paper from 2015 to 2024. The citation count commenced at 2 in 2015 and increased steadily to 23 in 2016, followed by a sharp rise in subsequent years. By 2019, the cumulative total had reached 52, reflecting the growing recognition and application of the SFS algorithm across numerous domains. The peak citation count was observed in 2023, with 86 citations, highlighting the algorithm’s significant impact on research. While the cumulative citation count is projected to exceed 68 in 2024, the overall trend indicates sustained interest and ongoing research into the algorithm’s applications.
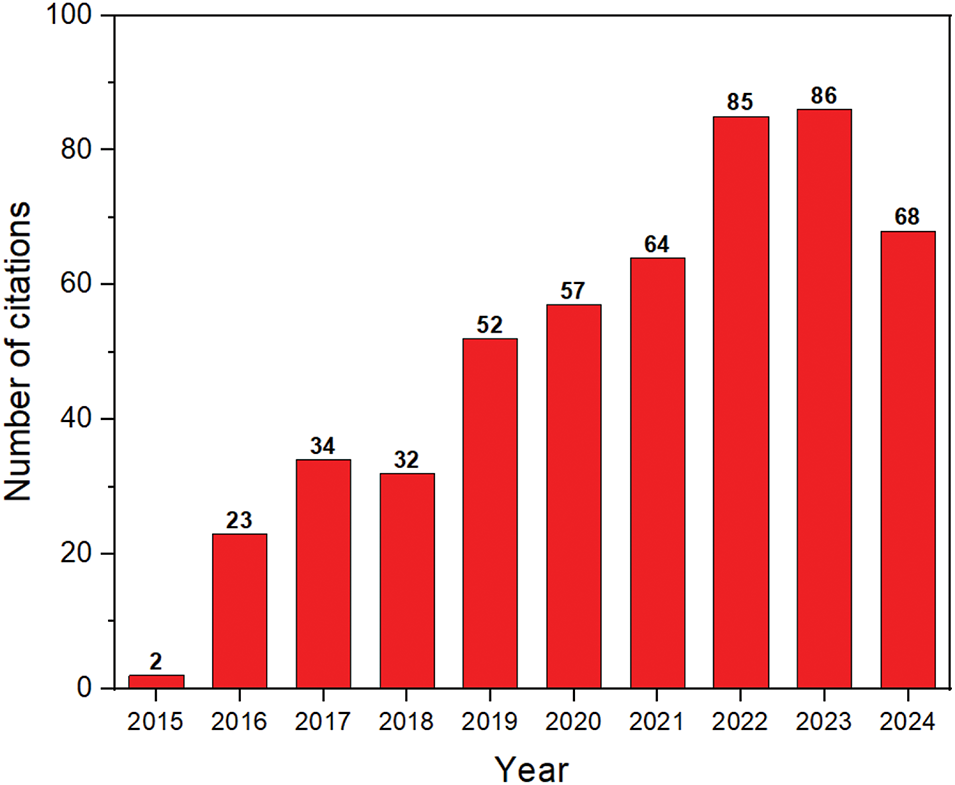
Figure 5: Number of citations of SFS algorithm per year
Fig. 6 illustrates the significant increase in publications related to the SFS algorithm from 2015 to 2024. Throughout this period, the SFS algorithm has experienced a notable surge in popularity across diverse research domains. Starting with only one publication in 2015, the number of SFS-related publications steadily increased to 12 in 2016 and doubled to 24 by 2019, reflecting growing acceptance within the scientific community. In subsequent years, the SFS algorithm continued to gain momentum, reaching 40 publications in 2022 and peaking at 45 by the end of 2023. This substantial growth underscores the algorithm’s extensive applicability across diverse fields, solidifying its position as a robust optimization method. The projected publication count for 2024 remains strong at 25, indicating sustained interest and ongoing research into the SFS algorithm among researchers.
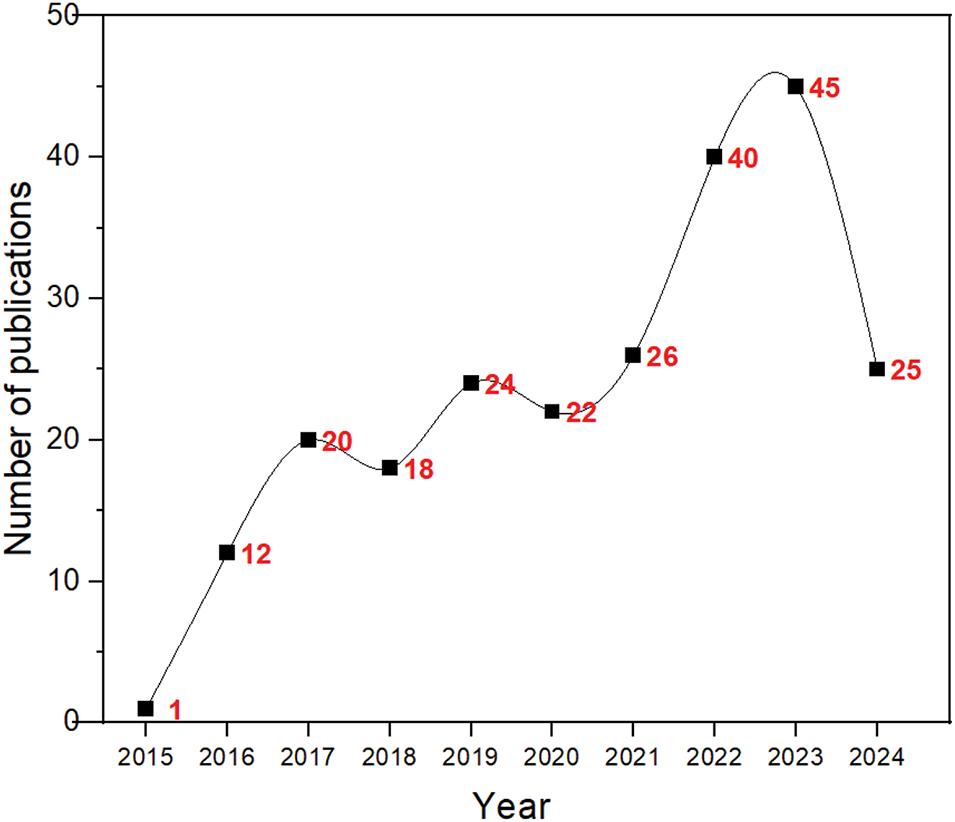
Figure 6: Number of publication of SFS algorithm per year
Fig. 7 graphically illustrates the leading publishers who have published studies on the SFS algorithm in several journals. Elsevier leads the list with 52 published articles, followed by IEEE with 34 and Springer with 31. MDPI has contributed 14 papers, while the remaining publications are distributed among diverse other publishers, as depicted in Fig. 7. The prominent presence of SFS research in reputable publishing outlets such as Elsevier, IEEE, and Springer underscores the algorithm’s strong theoretical foundation and notable attributes.
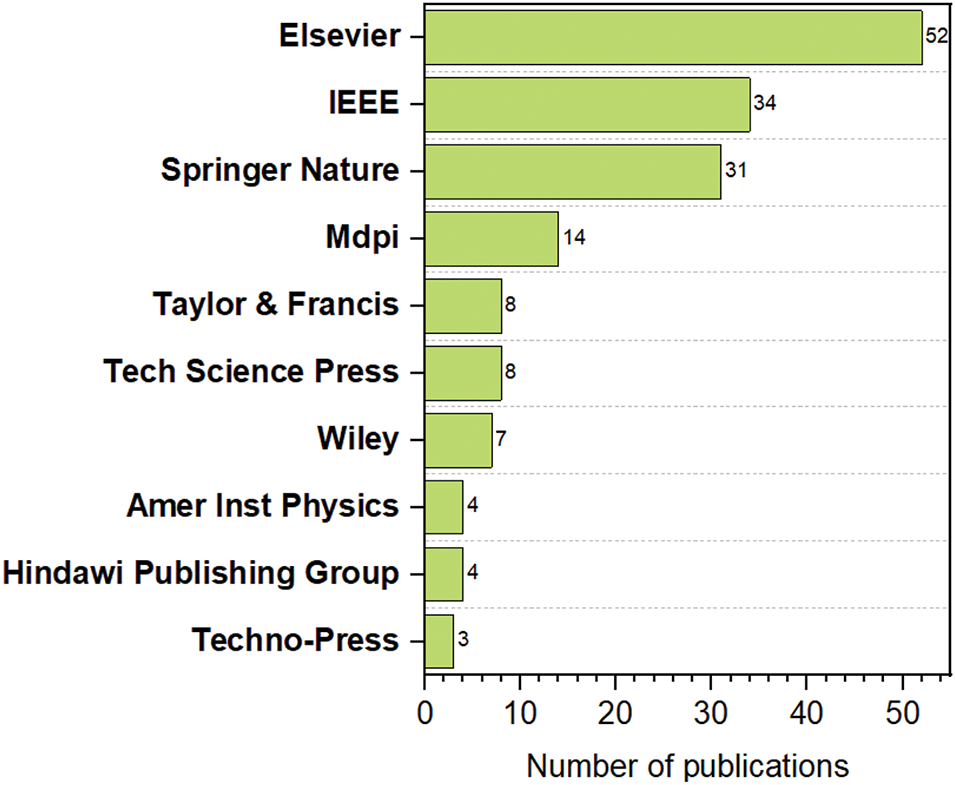
Figure 7: Number of publication of SFS algorithm per publisher
Among the journals, the “Computers Materials and Continua” journal has published the most SFS-related articles, totaling six publications. Meanwhile, the “Swarm and Evolutionary Computation”, “Neural Computing and Applications”, and “Energies” journals each have five articles, as depicted in Fig. 8. Additionally, the “Knowledge Based Systems”, “IEEE Access”, “Engineering Applications of Artificial Intelligence”, “Complexity”, and “Canadian Conference on Electrical and Computer Engineering” journals have each contributed four articles focused on applying the SFS algorithm to numerous optimization problems. On the other hand, the “Soft Computing” journal has published three articles.
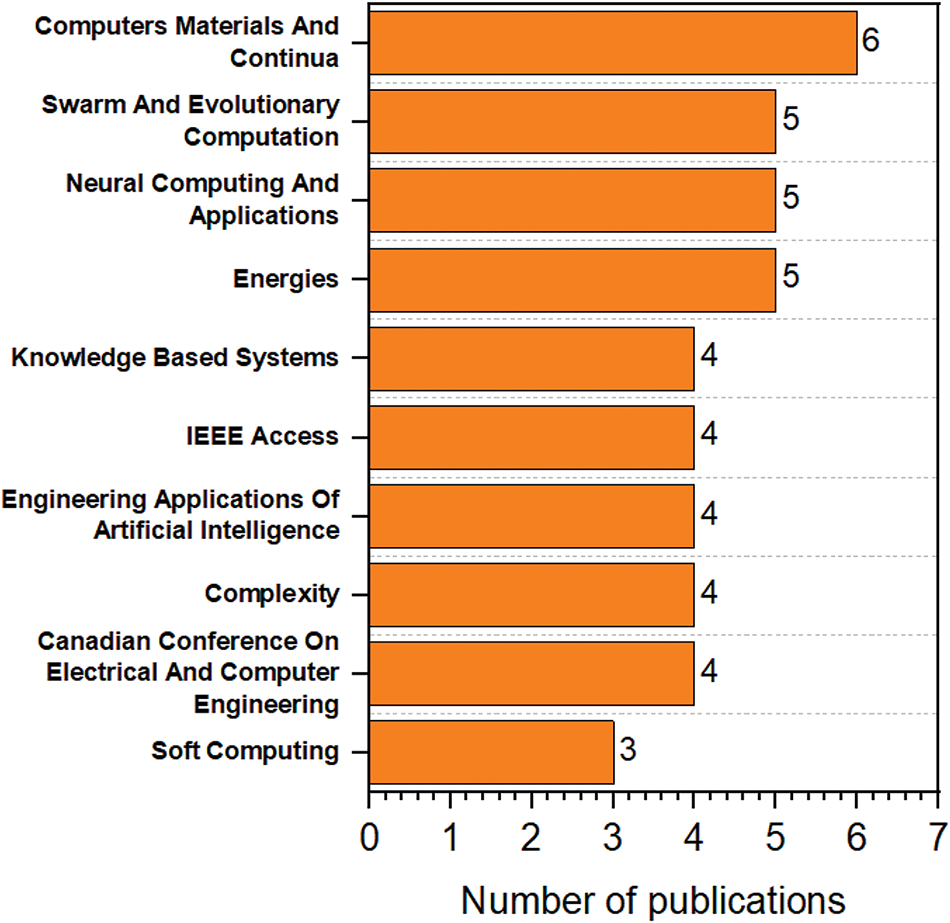
Figure 8: Number of publication of SFS algorithm per journal
Chinese researchers are the most prolific contributors to the SFS algorithm literature, with 47 published articles. They are closely followed by Indian researchers with 43 publications and Vietnamese researchers with 35 articles. Egyptian researchers have published 29 articles, while Iranian and Saudi Arabian researchers have 25 and 23 publications, respectively. Furthermore, Turkish, Malaysian, and Jordanian researchers have published 19, 16, and 14 articles, respectively, with Algerian researchers contributing 12, as illustrated in Fig. 9.
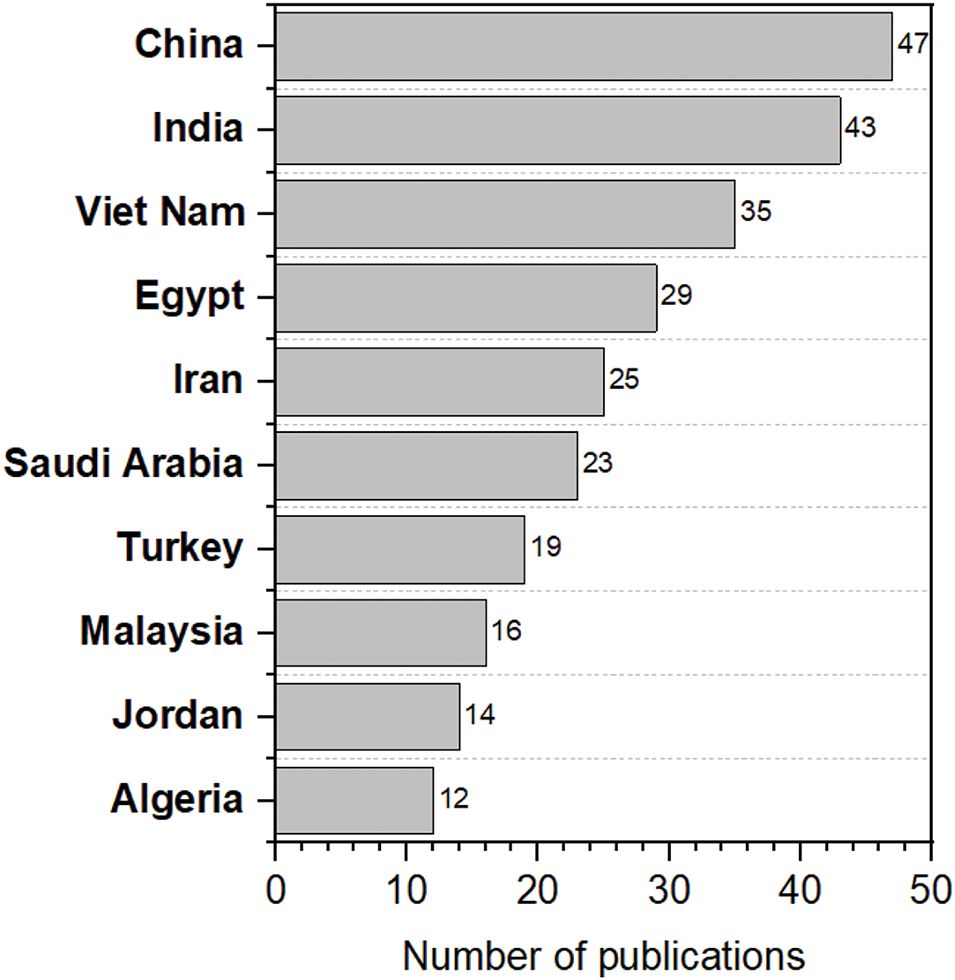
Figure 9: Number of publication of SFS algorithm per country
Regarding SFS publications by affiliation, researchers from the “Delta Higher Institute of Engineering and Technology” have published over 16 studies related to the SFS algorithm, as illustrated in Fig. 10. Researchers from “Mansoura University,” “Duy Tan University,” and the “Faculty of Engineering” have each published more than 13 research papers on SFS. Researchers from “Delta University for Science and Technology” and “Ain Shams University” have contributed 12 and 11 SFS-related studies, respectively. In contrast, the remaining affiliations listed in Fig. 10 have each published ten or fewer articles.
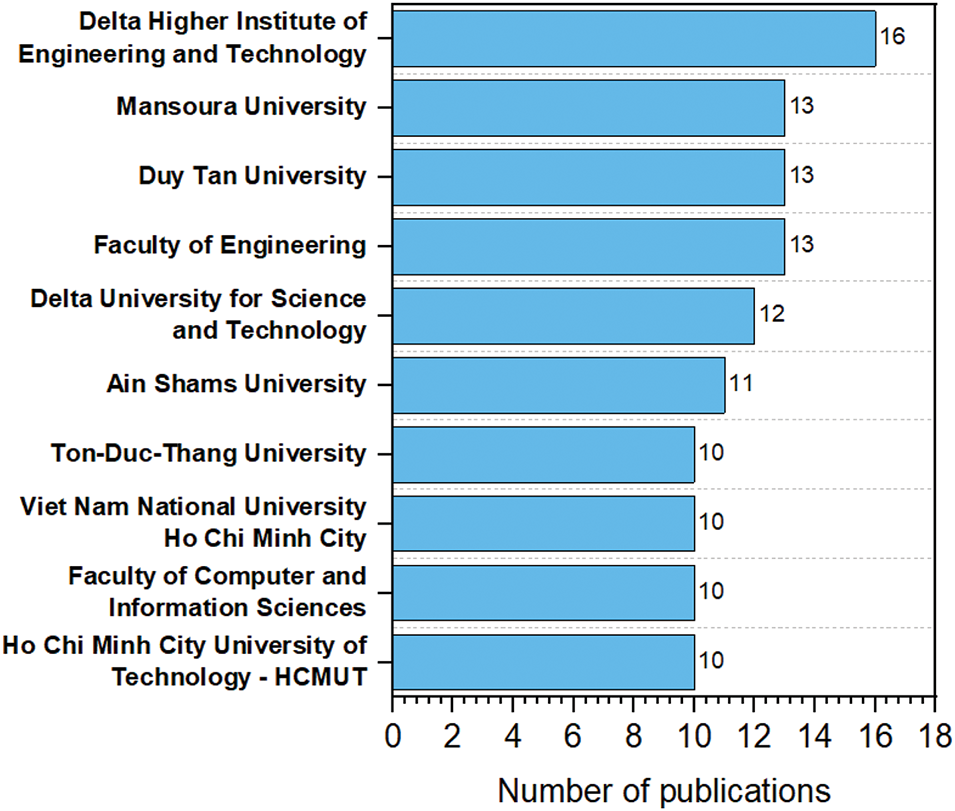
Figure 10: Number of publication of SFS algorithm per affiliation
Fig. 11 presents the top 10 most prolific researchers applying the SFS algorithm and its variants to optimization problems. “Ibrahim, A.” and “El-Kenawy, E.S.M.” are the leading contributors, each with 14 publications. They are followed by “Eid, M.M.”, “Abdelhamid, A.A.”, and “Rahman, T.A.Z.”, each of whom has contributed 10 articles. The remaining authors listed in the figure have published nine or fewer articles.
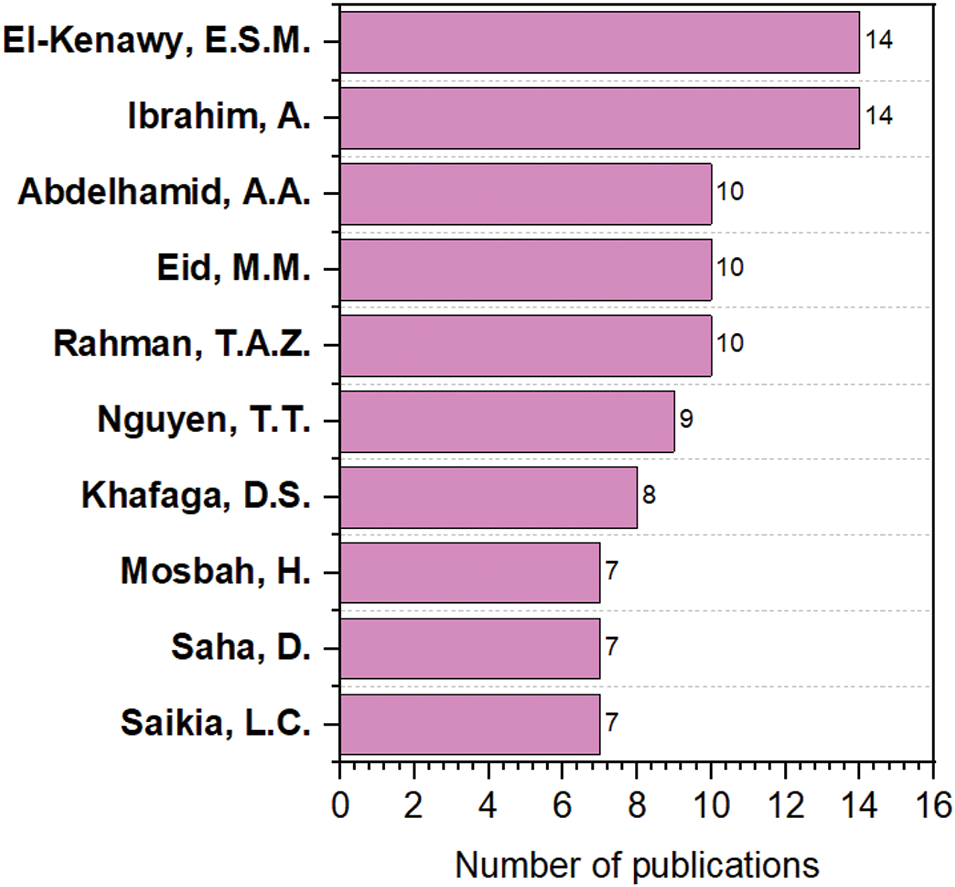
Figure 11: Number of SFS algorithm publication per author
Finally, the SFS algorithm has been successfully applied to diverse optimization problems. Fig. 12 categorizes these applications into ten primary research areas. According to the Scopus dataset, over 50% of SFS-related articles are concentrated in engineering and computer science, with the algorithm employed 135 times for computer science challenges and 129 times for engineering-related issues. Furthermore, the SFS algorithm has been applied 76 times to mathematical problems and 41 times to energy-related challenges. Other research domains, including chemical engineering, environmental science, decision sciences, materials science, physics and astronomy, and multidisciplinary studies, have fewer than 30 publications each.
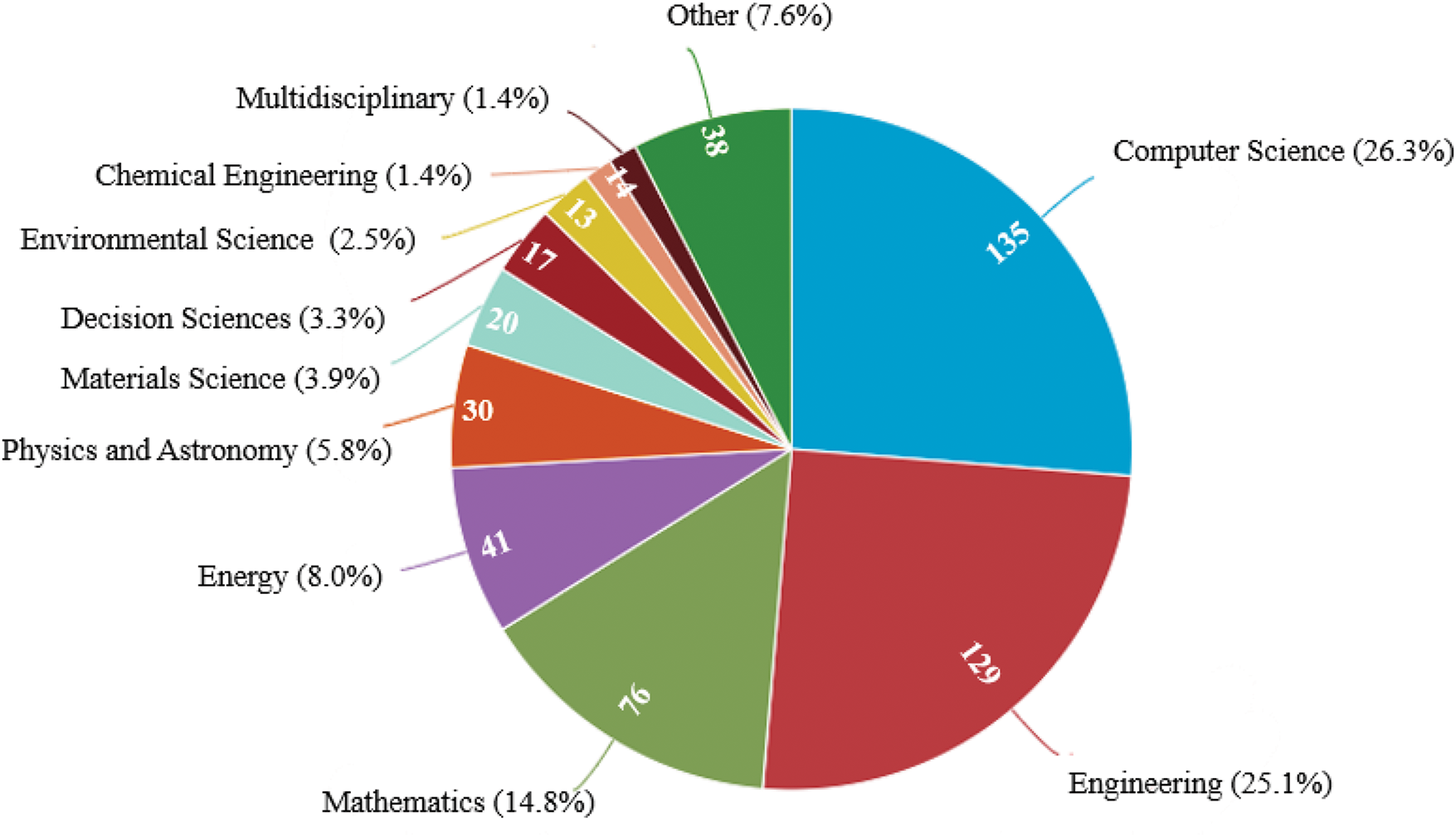
Figure 12: Distribution of SFS algorithm application per domain
4 Variants of the SFS Algorithm
The original SFS algorithm was developed to tackle numerical optimization problems, with its performance evaluated on standard benchmark functions, similar to other meta-heuristic approaches. Several enhancements have been introduced to adapt SFS for problems with distinct characteristics or complex structures, including modified, hybridized, and multi-objective versions. A concise summary of each version and relevant examples from the literature are provided below.
4.1 Modified Versions of the SFS Algorithm
The effectiveness and robustness of the SFS algorithm in addressing diverse optimization problems depend significantly on the complexity and intricacies of the search space. To navigate these challenges, researchers have introduced modifications to the fundamental framework of the SFS algorithm. Table 1 summarizes these modification approaches, which are discussed in detail in the subsequent sections.
Rahman et al. [65] proposed several modifications to the SFS algorithm to improve its convergence speed and accuracy for diverse optimization problems. The authors enhanced the localized search through Gaussian jump adjustments by integrating five chaotic maps, particularly the Gauss/Mouse map. Later, Rahman et al. [66] introduced the Chaotic SFS (CSFS) algorithm to optimize an AutoRegressive exogenous (ARX) model for a Twin Rotor System (TRS) operating in hovering mode. The CSFS algorithm outperformed other SFS variants primarily due to its enhanced diffusion and update processes.
The CSFS algorithm was further employed by Rahman et al. [67] to optimize the parameters of Support Vector Machines (SVM) for diagnosing ball-bearing conditions. Utilizing vibration data from the Case Western Reserve University Bearing Data Center, their approach significantly improved the classifier’s convergence speed and accuracy.
Expanding their research, Rahman et al. [68] applied the CSFS algorithm to active vibration control of flexible beam structures. The CSFS algorithm achieved substantial vibration suppression when integrated with a PID controller. Furthermore, it demonstrated enhanced optimization capabilities for PID and Proportional-Derivative (PD) fuzzy logic controllers in a twin-rotor system [69].
In 2019, Rahman et al. [70] utilized the CSFS algorithm to model a flexible beam structure with Feedforward Neural Networks (FNNs) for active vibration control. This method achieved superior convergence rates and accuracy compared to other meta-heuristic algorithms. They also explored the application of the CSFS algorithm for training FNNs in the Structural Health Monitoring (SHM) of aircraft structures [71], employing experimental spectral testing and Principal Component Analysis (PCA) to enhance vibration data analysis.
Furthermore, Rahman et al. [72] introduced the CSFS algorithm to optimize an ANN’s weight and bias parameters for predicting glove transmissibility to the human hand. Through experimental data collection, their method achieved an impressive average accuracy of 97.67% in estimating the human hand’s apparent mass.
In another study, Çelik et al. [73] introduced an improved SFS (ISFS) that integrates chaos-based search mechanisms and a modified cost function to address automatic generation control (AGC) challenges in power systems. The study optimizes the gains of a PID controller for models such as a two-area non-reheat thermal system and a three-area hydro-thermal power plant, minimizing a cost function that includes integral time absolute error (ITAE) along with frequency and tie-line power deviations. The results show that the ISFS-tuned PID controller outperforms the traditional SFS in terms of settling times and oscillations, demonstrating improved tuning capabilities and convergence speed, marking a significant advancement in power system optimization.
Moreover, Bingöl et al. [74] enhanced the SFS algorithm by integrating chaotic map values to improve accuracy and convergence speed. The authors evaluated the improved SFS against the original using seven classical mathematical benchmark functions. The main improvement involved modifying the Gaussian walk function in the diffusion process by adding chaotic map values to optimize the step length for a better local search. Simulation results showed that seven of the ten chaotic maps tested significantly enhanced the performance of the original SFS, demonstrating superior convergence and accuracy.
Following this, Nguyen et al. [75] developed the CSFS algorithm to optimize the sizing, placement, and quantity of distributed generation (DG) units in electrical distribution systems. The method aims to minimize power losses while meeting constraints such as power balance and voltage limits. By incorporating chaotic maps into the traditional SFS, the CSFS improves solution accuracy and convergence speed, using ten chaotic variants to determine the best strategy. Validation on the IEEE 33/69/118-bus systems demonstrated that CSFS outperformed the original SFS and other optimization methods, showcasing its effectiveness for optimal DG placement.
Additionally, Tran et al. [76] introduced the CSFS algorithm to address the reconfiguration problem in distribution systems, focusing on minimizing power loss and enhancing voltage profiles. This method improves the traditional SFS algorithm by using a Gaussian walk for point generation and an update mechanism to refine particle positions. The CSFS enhances diffusion efficiency by incorporating chaos theory, accelerating convergence and solution discovery. Validation on several test systems, including the 33/84/119/136-bus networks, demonstrated that CSFS outperforms existing optimization methods, establishing it as a promising approach for solving the reconfiguration problem in electrical distribution systems.
Finally, Duong et al. [77] proposed the Chaotic Maps Integrated SFS (CMSFS) algorithm to address the optimal distributed generation placement (ODGP) problem in radial distribution networks. The primary objective was to minimize real power losses while adhering to the operational constraints of distributed generations (DGs) and the network. CMSFS significantly improved solution quality and convergence rates by enhancing the standard SFS with chaotic maps. Experimental validations on the IEEE 33/69/118-bus networks demonstrated power loss reductions of 99.21%, 99.43%, and 92.36%, respectively, with optimally placed DGs having non-unity power factors. The results indicate that CMSFS outperforms several existing optimization methods, positioning it as a promising solution for ODGP challenges in radial distribution networks.
4.1.2 Fitness-Distance Balance-Based SFS Algorithm
Aras et al. [62] introduced the Fitness-Distance Balance SFS (FDBSFS), an enhanced version of the SFS algorithm designed to improve the balance between exploration and exploitation. By integrating a novel diversity operator based on the Fitness-Distance Balance method, FDBSFS effectively addresses the diversity issues present in the original SFS. Experimental evaluations involving thirty-nine meta-heuristic algorithms and several test functions demonstrated that FDBSFS significantly mitigated premature convergence and outperformed other algorithms, showcasing its superior capabilities in solving complex optimization problems.
Furthermore, Dalcali et al. [78] developed a hybrid model combining multiple linear regression with a feedforward artificial neural network (MLR-FFANN) to enhance electricity consumption forecasting in Bursa, Turkey, particularly during the COVID-19 pandemic. The model optimizes polynomial coefficients and neural network parameters using multiple algorithms, including the SFS-based Fitness Distance Balance (SFSFDB), slime mold algorithm, equilibrium optimizer, and adaptive guided differential evolution. The optimized MLR-FFANN model was evaluated using metrics such as root mean square error (RMSE) and mean absolute error (MAE), showing that the SFSFDB-optimized model outperformed others, effectively forecasting energy demand during the pandemic and improving resource management in the energy sector.
In another work, Ramezani et al. [79] introduced a Markovian process-based method to enhance the Reliability-Redundancy Allocation Problem (RRAP), focusing on the reliability of cold-standby systems with imperfect switching mechanisms. The authors adapted the Fitness-Distance Balance SFS (FDBSFS) algorithm to address this NP-hard optimization problem. Numerical experiments on benchmark problems demonstrated the algorithm’s effectiveness, and a practical case study involving a pump system in a chemical plant further highlighted its applicability in real-world scenarios.
Moreover, Duman et al. [80] introduced the Adaptive Fitness-Distance Balance Selection-based SFS (AFDB-SFS) algorithm to optimize the complex optimal power flow (OPF) problem in power systems with renewable energy resources (RESs). Evaluated under diverse scenarios involving tidal, small hydro, solar, wind, and thermal systems, the AFDB-SFS algorithm effectively addressed load demand uncertainties. Statistical comparisons showed that AFDB-SFS achieved cost optimization improvements ranging from 0.0954% to 7.6244% over other algorithms. It also offered faster convergence to optimal solutions, highlighting its effectiveness in enhancing efficiency and reliability in modern power systems.
Following this, Bakir et al. [81] introduced the Fitness-Distance Balance-based SFS (FDB-SFS) algorithm to improve solar PV system performance by accurately estimating the electrical parameters of solar cells. Compared with PSO, SPBO, and AGDE, the FDB-SFS achieved the lowest RMSE values, demonstrating superior accuracy. This study highlights FDB-SFS as an effective method for parameter extraction, enhancing efficiency in solar energy applications.
In a related study, Bakir et al. [82] introduced an optimized power flow (OPF) model that integrates renewable energy sources with voltage source converter-based multiterminal direct current (VSC-MTDC) transmission lines. To tackle the OPF problem, the authors utilized several meta-heuristic algorithms, including atom search optimization, marine predators algorithm, adaptive guided differential evolution, SFS algorithm, and FDB-SFS. Their study on a modified IEEE 30-bus power network revealed that FDB-SFS outperformed SFS and other algorithms in minimizing fuel costs, emissions, voltage deviation, and power loss. Statistical tests validated FDB-SFS’s superior performance and robustness for OPF optimization.
Finally, Kahraman et al. [83] introduced an enhanced SFS algorithm with a dynamic fitness-distance balance (dFDB) selection method to improve optimization capabilities. Six dFDB-SFS variants were developed to balance exploration and exploitation, replicating natural selection processes. Tested on CEC 2020 benchmark functions, the best-performing variant was identified and applied to parameter estimation for PV modules. The dFDB-SFS outperformed existing algorithms in accuracy and robustness for single and double-diode models, demonstrating its potential in PV system design and engineering applications.
Nguyen et al. [84] proposed a modified SFS algorithm (MSFS) to optimize reactive power dispatch (ORPD) by minimizing the L-index, voltage deviation, and power loss. Key enhancements include simplifying the diffusion process and refining solution updates, resulting in fewer solutions per iteration and improved execution time and solution quality. Tests on IEEE 30/118-bus systems demonstrated that MSFS outperformed other optimization methods, such as PSO and GA, confirming its robustness and efficiency in solving ORPD problems.
Furthermore, Pham et al. [85] introduced the MSFS to tackle the economic load dispatch (ELD) problem, addressing complexities such as prohibited operating zones and valve-point effects. Key modifications include a new strategy for generating solutions and an update mechanism prioritizing the worst solutions first. Testing on 3/6/10/20-unit configurations showed that MSFS outperformed conventional SFS and other methods in terms of solution quality, stability, and convergence speed, highlighting its potential as a robust optimization technique for ELD and related electrical engineering applications.
In another work, Nguyen et al. [86] introduced an improved version of the SFS algorithm (ISFSA) to optimize the optimal power flow (OPF) problem by addressing five single objectives while satisfying key system constraints. ISFSA improves upon the original SFS by refining its diffusion and update processes, enhancing the algorithm’s ability to find optimal solutions. Tested on three standard IEEE power systems, ISFSA outperformed conventional SFS and other existing methods in terms of solution quality, speed, and success rate. The results indicate that ISFSA effectively reduces fuel costs, power losses, and emissions while improving voltage profiles, making it a recommended approach for high-voltage power systems.
Following this, Van et al. [87] introduced an improved SFS optimization algorithm (ISFSOA) to tackle the ORPD problem, minimizing total voltage deviation and total power loss while enhancing voltage stability. By improving the diffusion process of the original SFS algorithm, ISFSOA achieves more effective exploration of large search spaces and better exploitation of local zones. Comparative analysis using the IEEE 30-bus system demonstrated that ISFSOA outperforms standard SFSOA and other methods in terms of solution quality, stability, and robustness, making it highly suitable for complex engineering optimization tasks.
Finally, Xu et al. [88] developed a modified SFS algorithm to accurately estimate the unknown parameters of solar cell models, including single- and double-diode models. Key enhancements include adjustments to the diffusion and update processes and a mechanism to reduce population size, thereby improving implementation and performance. The modified algorithm was tested on three benchmark cases and compared with seven advanced algorithms, demonstrating superior accuracy, faster convergence, and enhanced stability. It consistently achieved optimal solutions with low root mean square error (RMSE) values across several photovoltaic modules, highlighting its effectiveness for parameter estimation in solar energy applications.
4.1.4 Multi-Surrogate-Assisted SFS Algorithm
Cheng et al. [89] introduced a multi-surrogate-assisted SFS (MSASFS) algorithm to address high-dimensional, computationally intensive problems. Key enhancements include an improved surrogate-assisted differential evolution (SDE) updating mechanism combining coordinate systems for better exploration and a pre-screening strategy using a Gaussian process model to identify promising solutions. Additionally, two surrogate models are employed to enhance robustness. Numerical experiments demonstrated that MSASFS outperforms other surrogate-assisted algorithms, particularly in high-dimensional problems and chaotic system parameter estimation.
In another study, Cheng et al. [90] introduced the scale-free network-based multi-surrogate-assisted SFS (SF-MSASFS) algorithm. This variant integrates multiple surrogate models, such as Radial Basis Function (RBF) and Kriging, to boost robustness and efficiency. Leveraging a scale-free network topology, SF-MSASFS enhances particle interaction and offspring generation. An adaptive mechanism with three update strategies based on reward values further increases adaptability. Tested against advanced surrogate-assisted meta-heuristic algorithms, SF-MSASFS demonstrated superior performance on high-dimensional expensive optimization problems.
4.1.5 Fuzzy Logic Controller-Based SFS Algorithm
Lagunes et al. [91] developed the Stochastic Fractal Dynamic Search (SFDS) algorithm that incorporates a fuzzy inference system for the dynamic adjustment of the diffusion parameter within the SFS algorithm. This innovation enhances SFS’s adaptability and performance, as shown in tests against the CEC 2017 benchmark functions. The results demonstrated that SFDS significantly improved SFS’s optimization capabilities, highlighting its robustness and versatility for complex optimization tasks.
Similarly, Lagunes et al. [92] introduced the Dynamic SFS (DSFS), an enhanced version of the SFS algorithm that uses fuzzy logic to manage the diffusion parameter adaptively. The DSFS incorporates chaotic stochastic diffusion and type-1 and type-2 fuzzy inference models to dynamically adjust the diffusion parameter based on particle diversity and iteration. Tested on multimodal, hybrid, and composite benchmark functions, DSFS demonstrated improved adaptability and performance, effectively generating new fractal particles for complex optimization tasks.
4.1.6 Penalty-Guided SFS Algorithm
Mellal et al. [93] introduced the penalty-guided SFS algorithm for reliability optimization problems, tested on ten case studies, including redundancy and reliability allocation. The results showed that this approach outperformed previous methods in terms of solution accuracy, robustness, and computational efficiency. With smaller standard deviations and fewer function evaluations, the penalty-guided SFS proved highly effective in optimizing system reliability across diverse scenarios.
In another work, Mellal et al. [94] introduced the penalty-guided SFS (PSFS) algorithm to address the reliability-redundancy allocation problem. Compared to GA and cuckoo optimization with penalty functions (PFCOA), PSFS demonstrated superior performance in system reliability and execution efficiency. The use of dynamic penalty factors in PSFS was a key advantage, enhancing its effectiveness for this optimization problem, particularly in systems with ten and thirty subsystems in series.
Hosny et al. [95] introduced an algorithm for classifying galaxy images that leverages quaternion polar complex exponential transform moments (QPCET) to capture color information. The authors used a binary SFS algorithm combined with Extreme Machine Learning (EML) to optimize feature selection, enhancing classification accuracy. Testing on the EFIGI galaxy dataset demonstrated that this method outperformed existing approaches, achieving high accuracy.
4.1.8 Eagle Strategy-Based SFS Algorithm
Das et al. [96] introduced a fuzzy clustering methodology that integrates a two-stage Eagle Strategy with SFS for better segmentation of white blood cells (WBC) in Acute Lymphoblastic Leukemia (ALL) images. This method overcomes the limitations of classical clustering techniques, such as Fuzzy C-means and K-means, which are sensitive to noise and local optima. By incorporating morphological reconstruction, the approach enhances noise immunity and cluster robustness. Comparative experiments demonstrated that the ES-SFS-based method outperformed traditional clustering techniques in terms of accuracy, computational efficiency, and robustness.
4.1.9 Disruption Operator-Based SFS Algorithm
Xu et al. [97] introduced an Improved SFS algorithm (ISFS) for optimizing the joint operation of cascade reservoirs, aiming to improve flood control and maximize hydropower generation. ISFS effectively manages the complex, high-dimensional challenges of long-term hydropower operations by incorporating a disruption operator. Tested on 13 benchmark functions, ISFS demonstrated superior optimization capabilities, and simulations on the Yangtze River cascade reservoirs showed faster convergence and higher solution quality, enhancing overall power generation.
4.1.10 Opposition-Based Learning SFS Algorithm
Gonzalez et al. [98] introduced a hybrid optimization technique that combines the SFS algorithm with an opposition-based learning strategy to design high-quality substitution boxes (S-boxes) for cryptographic systems. The method uses a sequential model algorithm configuration for parameter tuning, focusing on maximizing nonlinearity. Validated against cryptographic criteria such as bijectivity and the strict avalanche criterion, the designed S-boxes demonstrated superior performance, enhancing cryptographic security and robustness.
4.1.11 Random Walk Mechanism-Based SFS Algorithm
Pham et al. [99] introduced the SFS algorithm to address the economic load dispatch (ELD) problem, proposing two variants: SFS-Gauss, which uses a Gaussian random walk, and SFS-Lévy, which employs a Lévy flight random walk. Tested on three systems with varying units, both variants outperformed standard, modified, and hybrid optimization methods, delivering high solution quality and faster convergence for the ELD problem.
Najmi et al. [100] introduced the parallel SFS algorithm to solve the reliability-redundancy allocation problem (RRAP) within a realistic framework that accommodates heterogeneous components and tailored redundancy strategies for each subsystem. Using an exact Markov model to calculate subsystem reliability, the approach was tested on three benchmark cases, demonstrating significant improvements over existing models and proving effective in enhancing system reliability through stochastic fractal search.
4.1.13 Multi-Strategy SFS Algorithm
Lin et al. [101] proposed a hybrid SFS (HSFS) algorithm for parameter identification in fractional-order chaotic systems. This algorithm integrates several advanced techniques to enhance optimization performance, such as the opposition-based learning method to improve population diversity and accelerate convergence, and the differential evolution algorithm for better exploitation in the search process. Additionally, a re-initialization mechanism is employed to avoid local optima. The HSFS was tested on three fractional-order chaotic systems, and numerical simulations showed that it outperforms existing methods in global optimization.
Furthermore, Pang et al. [102] developed an adaptive decision-making framework to optimize conflict resolution strategies for unmanned aircraft systems (UAS) in urban environments. The framework addresses low-altitude air traffic management through a double-layer problem incorporating rerouting, speed adjustment, and scheduling. It enhances the SFS algorithm with a conflict penalty-guided fitness function that prioritizes solutions with fewer flight conflicts. It also incorporates an exploration and exploitation balance strategy to improve search diversity. Simulation results demonstrate significant optimization of 4D flight routes, reducing operational costs, flight conflicts, and delays while showcasing the effectiveness of the improved SFS algorithm across varying traffic densities.
In another study, Zhou et al. [103] developed an improved Stochastic Fractal Search algorithm (ISFS) to solve the protein structure prediction (PSP) problem, which is crucial for biological research and drug development. By transforming the prediction into a non-linear programming problem using an AB off-lattice model, ISFS addresses the limitations of traditional SFS by incorporating Lévy flight strategies and internal feedback mechanisms to enhance search efficiency. Simulations on Fibonacci and real peptide sequences showed that ISFS significantly improved performance, demonstrating greater robustness in finding global minima while avoiding local traps, highlighting its potential for complex optimization challenges in biology.
Moreover, Mosbah et al. [104] developed a modified SFS (M-SFS) technique to enhance accuracy and computational efficiency in power system state estimation (PSSE). Key modifications include replacing the logarithmic function in the diffusion process with benchmark functions and incorporating chaotic maps instead of uniform distribution parameters during the diffusion and updating phases. These enhancements significantly improved algorithm performance. Validated on IEEE 30/57/118-bus systems, M-SFS demonstrated superior accuracy and faster computational times than the original SFS technique.
Following this, Lin et al. [105] introduced an improved SFS (ISFS) algorithm to address the complex multi-area economic dispatch (MAED) problem, characterized by high non-linearity and non-convexity. The ISFS enhances the exploration-exploitation balance through opposition-based learning for population initialization and generation jumping. It incorporates a hybrid diffusion process using differential evolution to improve local search capabilities. A repair-based penalty approach is also integrated to generate feasible solutions efficiently. Tested on systems with 16 to 120 generating units, ISFS outperformed state-of-the-art algorithms in solving MAED problems effectively and robustly.
Additionally, Chen et al. [106] proposed the perturbed SFS (pSFS) algorithm to improve parameter estimation in PV systems, addressing challenges related to non-linearity and multi-modality. This innovative meta-heuristic integrates unique searching operators to balance global exploration with local exploitation. Furthermore, pSFS employs a chaotic elitist perturbation strategy to enhance search performance. Demonstrated across three PV estimation scenarios, experimental results showed that pSFS significantly outperformed several recent algorithms, achieving higher estimation accuracy and robustness in solar PV modeling.
In other research, Nguyen et al. [107] introduced the Improved SFS (ISFS) algorithm, incorporating Chaotic Local Search (CLS) and Quasi-opposition-Based Learning (QOBL) mechanisms to tackle the optimal capacitor placement (OCP) problem in radial distribution networks (RDNs). This approach minimizes the total annual cost while meeting operational constraints. Tested on IEEE 69/119/152-bus RDNs, ISFS outperformed the original SFS and other methods, particularly in large-scale, complex networks, demonstrating high-quality solutions and robust performance.
Similarly, Kien et al. [108] introduced a modified SFS (MSFS) algorithm to optimize capacitor bank placement and sizing in distribution systems comprising 33/69/85 buses. To minimize power loss and total costs, MSFS incorporates three enhancements, including an innovative diffusion approach and two update strategies to improve the standard SFS. The results showed that MSFS achieved up to a 3.98% reduction in power loss and more significant cost savings, converging to global optima faster than SFS and other methods, underscoring its effectiveness in capacitor optimization for power distribution systems.
In another study, Huynh et al. [109] proposed an Improved SFS (ISFS) algorithm to enhance PV power generation by accurately estimating key PV module parameters. This method frames parameter estimation as an RMSE minimization problem. It incorporates two modifications to improve SF,S including replacing the logarithmic function with an exponential function to enhance exploration and using a sine map instead of a uniform distribution for optimized diffusion and update processes. The results show that ISFS outperforms traditional meta-heuristic algorithms, including the original SFS and PSO, in achieving accurate model parameters and maximum power points (MPPs) for PV optimization.
Besides that, Alkayem et al. [110] introduced the SA-QSFS algorithm for structural health monitoring and damage identification. This approach combines a triple modal-based objective function and an improved self-adaptive framework to enhance damage detection accuracy, alongside quasi-oppositional learning to strengthen exploration at diverse stages. The SA-QSFS algorithm showed superior performance in diverse damage scenarios under noisy conditions and proved effective for continuous optimization in structural damage assessment.
Finally, Isen et al. [111] introduced the FDB-NSM-SFS-OBL algorithm, which enhances parameter extraction for renewable energy sources by incorporating Opposite-Based Learning (OBL), Fitness Distance Balance (FDB), and Natural Survivor updating Mechanism (NSM) within the SFS framework. Experimental results demonstrated improved accuracy in optimizing parameters for photovoltaic cells, PEMFCs, and Li-Ion batteries.
4.2 Hybrid Versions of the SFS Algorithm
A hybrid algorithm combines two or more algorithms to solve a given problem, aiming to mitigate weaknesses and enhance computational speed and accuracy. Researchers have improved the performance of SFS by integrating it with other established heuristics and meta-heuristic algorithms. Table 2 provides an overview of hybridized SFS variants, with the following sections offering detailed insights into integrating SFS with diverse meta-heuristic and local search algorithms.
Awad et al. [64] introduced a hybrid approach that combines Differential Evolution (DE) with the SFS algorithm to enhance optimization performance. This method leverages the diffusion properties of fractal search and incorporates two innovative update processes to improve exploration. The algorithm enhances exploration by replacing random fractals with a DE-based diffusion process while reducing computational costs. Validated against 30 benchmark functions from the IEEE CEC2014 competition, the hybrid algorithm outperformed the original SFS and other contemporary techniques, particularly in hybrid and composite test functions.
In another study, Awad et al. [112] introduced an enhanced evolutionary algorithm that combines DE algorithm with the SFS framework, termed SFS-DPDE-GW, to tackle complex optimization challenges. This approach improves the traditional SFS diffusion process by integrating DE and Gaussian Walks, enhancing search efficiency. Evaluated using 30 functions from the CEC’2014 test suite, SFS-DPDE-GW outperformed the standard SFS and other well-known algorithms, demonstrating its potential for solving diverse optimization problems.
Furthermore, Ashraf et al. [113] developed a hybrid biogeography-based optimization (BBO) algorithm enhanced with SFS to tackle vendor-managed inventory (VMI) systems with various supplier-retailer configurations, aiming to minimize total costs. The algorithm significantly improved search and exploitation capabilities by integrating SFS’s diffusion process into BBO. The hybrid algorithm outperformed conventional methods in multiple VMI configurations, effectively addressing this complex nonlinear optimization problem.
Moreover, Sivalingam et al. [114] introduced a hybrid optimization technique that combines the SFS algorithm with Local Unimodal Sampling (LUS) for tuning a multistage Proportional Integral Derivative (PID) controller to improve Automatic Generation Control (AGC) in power systems. Initially, SFS optimized parameters for a single-area, multi-source system, outperforming methods like DE and TLBO. The addition of LUS further enhanced performance. When extended to complex multi-area systems, the approach demonstrated the superiority of the hybrid SFS-LUS algorithm in managing nonlinearities such as generation rate constraints and time delays.
Following this, Mosbah et al. [115] introduced a hybrid approach that combines the SFS algorithm with Simulated Annealing (SA) to solve distributed multi-area state estimation (SE) problems. The method operates at two levels: local SE using SFS for individual area data, and coordination SE using SA to exchange boundary information for overall state estimation. Tested on the IEEE 118-bus system divided into four areas, the approach significantly reduced computational time, demonstrating its efficiency in distributed SE.
Additionally, Yu et al. [116] proposed a hybrid approach for path planning in autonomous unmanned vehicles by integrating the A* algorithm with the SFS algorithm. This method considers the vehicle’s front-wheel-drive model and mechanical constraints to enhance path calculation. The A* algorithm identifies the shortest path on a raster map, which SFS then refines to generate the vehicle’s trajectory based on status information. Simulation results in MATLAB R2012a show that this composite algorithm effectively addresses path-planning challenges in complex urban environments.
In other research, El-Kenawy et al. [117] introduced a Modified Binary Grey Wolf Optimizer (MbGWO) that integrates the SFS algorithm to enhance feature selection by balancing exploration and exploitation. MbGWO features an exponential iteration scheme to expand the search space and incorporates crossover and mutation operations to increase population diversity. SFS’s diffusion mechanism employs a Gaussian distribution for random walks to refine the solutions, converting continuous values into binary for feature selection. Tested on nineteen UCI machine learning datasets using K-Nearest Neighbor (KNN), the MbGWO-SFS algorithm outperformed several state-of-the-art optimization techniques, with results found to be statistically significant at the 0.05 level.
Similarly, Chen et al. [118] proposed a novel method for task allocation in heterogeneous multi-UAV systems by integrating an enhanced SFS mechanism into a modified Wolf Pack Algorithm (WPA). The authors categorized complex combat tasks into reconnaissance, strike, and evaluation, enabling a tailored task allocation model based on UAV load capacities. The chaotic Wolf Pack Algorithm with enhanced SFS (MSFS-CWPA) employs Gaussian walking optimized through chaos to improve adaptive task assignment. Performance evaluations show that MSFS-CWPA outperforms the standard WPA and other variants in convergence accuracy, highlighting the robustness of SFS in multi-UAV task allocation strategies.
In another study, Alsawadi et al. [119] introduced an advanced method for skeleton-based action recognition using the BlazePose system, which models human body skeletons as spatiotemporal graphs. They enhanced the Spatial-Temporal Graph Convolutional Network (STGCN) by integrating the SFS-Guided Whale Optimization Algorithm (GWOA), leveraging SFS’s diffusion process for optimization. This approach achieved accuracies of 93.14% on X-View and 96.74% on X-Sub using the Kinetics and NTU-RGB+D datasets, surpassing existing techniques.
Additionally, Bharani et al. [120] proposed a novel method for exoplanet detection using the Kepler dataset, combining the Grey Wolf Optimizer (GWO) with an Enhanced SFS Algorithm (ESFSA) for feature selection. This hybrid approach reduced input features and classified exoplanets into False Positive, Not Detected, and Candidate categories using a Random Forest (RF) model. The GWO-ESFSA method outperformed existing techniques, achieving high performance across recall, specificity, accuracy, sensitivity, precision, and F1-score.
In addition, El-Kenawy et al. [121] proposed a novel digital image watermarking method that combines the SFS algorithm, Dipper-Throated Optimization (DTO), Discrete Wavelet Transform (DWT), and Discrete Cosine Transform (DCT). The technique uses DWT to decompose the cover image, followed by DCT for frequency-domain transformation. To optimize the scale factor for embedding, they introduced the DTOSFS algorithm. Rigorous evaluations using metrics like Image Fidelity (IF), Peak Signal-to-Noise Ratio (PSNR), and Normalized Cross-Correlation (NCC) demonstrated the method’s robustness against attacks and its superiority over traditional watermarking techniques, improving watermark quality and resilience.
In related research, El-Kenawy et al. [122] proposed a novel method for diagnosing COVID-19 using chest CT scans that integrates the SFS algorithm within a feature selection framework. The approach consists of three phases: extracting features from CT scans using the AlexNet Convolutional Neural Network (CNN), selecting relevant features with an enhanced Guided Whale Optimization Algorithm (Guided WOA) integrated with SFS, and balancing the features. A voting classifier, utilizing a PSO-based method, aggregates predictions from classifiers such as Decision Trees (DT), k-Nearest Neighbor (KNN), Neural Networks (NN), and Support Vector Machines (SVM). The framework achieved an area under the curve (AUC) of 0.995 on COVID-19 datasets, demonstrating the effectiveness of the SFS-Guided WOA in enhancing diagnostic processes.
Likewise, Zhang et al. [123] introduced a hybrid algorithm named GBSFSSSA, which combines the Gaussian Barebone SFS algorithm with the Salp Swarm Algorithm (SSA) to enhance image segmentation. This approach improves the balance between local and global search capabilities, addressing the limitations of the basic SSA. Tested on the CEC2017 dataset and applied to COVID-19 CT image segmentation, GBSFSSSA outperformed other algorithms in PSNR, SSIM, and FSIM metrics, making it a reliable solution for multi-threshold image segmentation in medical imaging.
Furthermore, Xu et al. [124] introduced an improved SFS (ISFS) algorithm to optimize cascade reservoir operations in the Yalong River, considering the complexities of the Lianghekou Reservoir’s multiyear regulation capacity. Inspired by PSO, the ISFS algorithm integrates global and individual best points and employs an adaptive variation rate (Fw) to enhance convergence. The study evaluated power generation and water abandonment across three operational modes using inflow data from five years. Results indicated that ISFS outperformed traditional SFS and PSO in both speed and accuracy, with the global joint operation mode being most effective in high-inflow scenarios, highlighting the significance of operational strategies in reservoir management.
In another study, Salamai et al. [125] developed a hybrid algorithm combining the SFS algorithm and the Guided Whale Optimization Algorithm (WOA) to optimize e-commerce sales forecasting. This method fine-tunes the parameter weights of Bidirectional Recurrent Neural Networks (BRNN) for time series demand forecasting. The hybrid algorithm outperformed other techniques, including PSO, WOA, and GA, achieving significantly lower RMSE, with results validated through ANOVA analyses.
Moreover, Eid et al. [126] introduced an innovative hybrid method combining the SFS algorithm and Guided WOA to optimize electroencephalography (EEG) channel selection for motor imagery classification and seizure detection. The SFS-Guided WOA effectively identifies relevant features, enhancing Brain-Computer Interface (BCI) systems by reducing dataset complexity and improving machine learning performance. The algorithm outperformed others in statistical tests, including ANOVA and the Wilcoxon rank-sum test.
Following this, Saini et al. [127] proposed a hybrid optimization approach that combines the SFS algorithm with Pattern Search (PS) to optimize PID controller parameters for DC motor speed control. Using ITAE as the objective function, the method leverages SFS’s diffusion property alongside PS’s derivative-free technique to enhance local search while maintaining robust global exploration. Simulation results demonstrated that the hybrid SFS-PID controller outperformed recent techniques, providing faster, smoother dynamic responses with reduced oscillations.
Additionally, Eid et al. [128] proposed a weighted average ensemble model for predicting hemoglobin levels from blood samples, which is critical for diagnosing conditions like anemia. The authors used a sine cosine algorithm combined with SFS (SCSFS) to optimize the ensemble weights. This hybrid method effectively fine-tuned model parameters, and comparisons with traditional machine learning techniques such as Decision Trees, MLP, SVR, and Random Forest, demonstrated that the SCSFS model significantly outperformed existing models, providing accurate hemoglobin level estimates and highlighting the effectiveness of SFS in optimizing ensemble learning for medical applications.
In other research, Cheraghalipour et al. [129] proposed optimizing a closed-loop agricultural supply chain with an eight-echelon logistics network, including suppliers, farms, and biogas centers. The authors developed a bi-level programming model to minimize costs and maximize profits from biogas and compost sales. To address the NP-hard nature of the problem, they used meta-heuristic algorithms, specifically SFS and GA, along with hybrid approaches (GA-SFS and SFS-GA). The SFS-GA hybrid outperformed other methods, demonstrating its effectiveness in supply chain optimization. The study highlights the benefits of incorporating biogas and compost production, reducing pollution while enhancing profitability in agricultural-dependent countries.
Similarly, Abdelhamid et al. [130] enhanced speech emotion recognition by augmenting datasets with noise and optimizing a CNN-LSTM deep learning model’s hyperparameters using a hybrid method that combines the SFS algorithm and Whale Optimization Algorithm (WOA). This approach improved recognition accuracy on four datasets such as IEMOCAP, Emo-DB, RAVDESS, and SAVEE, to 98.13%, 99.76%, 99.47%, and 99.50%, respectively, outperforming existing methods.
In another study, Abdel-Nabi et al. [131] developed eMpSDE, a hybrid optimization framework combining the SFS algorithm with Success-History based Adaptive Differential Evolution (SHADE) to address local minima and premature convergence issues. The three-phase structure includes a local search to enhance solution quality and convergence speed. Evaluations across several optimization problems showed that eMpSDE is competitive with contemporary algorithms, demonstrating the effectiveness of integrating SFS with adaptive techniques for improved optimization performance.
Additionally, Saini et al. [132] introduced a hybrid SFS (HSFS) algorithm that combines pattern search optimization with a fractional-order proportional-integral-derivative (FOPID) controller to improve DC motor speed control. The HSFS algorithm optimizes the FOPID controller parameters by minimizing the integral time multiplied by the absolute error (ITAE). The HSFS-FOPID approach demonstrates enhanced performance in motor control, outperforming existing methods in metrics such as rise time, settling time, overshoot, and overall ITAE, highlighting its effectiveness in this application.
In related research, El-Kenawy et al. [133] proposed a hybrid model integrating Grey Wolf Optimization and SFS (GWO-SFS) with a Random Forest regressor to predict sunshine duration accurately. Using meteorological data and a pre-feature selection process, the model reduced prediction errors by over 20% and achieved correlation coefficients above 0.999, outperforming previous models in accuracy and precision.
In addition, Tarek et al. [134] developed an optimization method combining the SFS algorithm and PSO to enhance wind power generation predictions using an optimized Long Short-Term Memory (LSTM) network. The authors constructed several regression models and utilized a dataset of 50,530 instances. The SFS-PSO optimized LSTM model achieved a coefficient of determination (
Likewise, Zhang et al. [135] developed the SFS-HGSO algorithm, an enhanced version of Henry’s Gas Solubility Optimization (HGSO), to improve feature selection and engineering optimization. It incorporates SFS strategies, such as Lévy flight and Gaussian walk, to enhance search diversity and local search capabilities. The algorithm effectively addresses slow convergence issues and was validated on 20 UCI benchmark datasets, outperforming other algorithms such as Whale Optimization and Harris Hawks Optimization.
Furthermore, Khafaga et al. [136] introduced a hybrid approach that combines Long Short-Term Memory (LSTM) units with the SFS algorithm and Dipper-Throated Optimization (DTO) to improve energy consumption forecasting. The dynamic DTO-SFS algorithm optimizes LSTM parameters, resulting in enhanced accuracy. Comparative analyses with five benchmark algorithms showed that the proposed model achieved an RMSE of 0.00013, indicating its effectiveness in energy prediction, further supported by statistical validation of its performance.
In another study, Abdel-Nabi et al. [137] introduced a hybrid algorithm called 3-sCHSL, which integrates the SFS algorithm with L-SHADE to tackle real-parameter, single-objective numerical optimization. This approach enhances diversity and reduces stagnation through a guided initialization strategy. Tested on the CEC 2021 benchmark suite, 3-sCHSL demonstrated superior performance in handling complex transformations and achieved competitive results in two engineering design problems, surpassing well-known optimization algorithms.
Moreover, Rahman et al. [138] developed the Chaotic SFS-GTO (CSGO) algorithm to solve flow-shop scheduling problems (FSP). Combining features from the SFS algorithm, the Artificial Gorilla Troops Optimizer (GTO), and the Marine Predators Algorithm (MPA) with chaotic operators, the algorithm aims to minimize processing costs on non-identical parallel machines. Tested on ten benchmark FSPs, CSGO demonstrated strong performance in lower-dimensional problems but faced challenges in scalability as problem dimensions increased, showing reduced accuracy compared to earlier algorithms.
Following this, Abdel-Nabi et al. [139] developed the Iterative Cyclic Tri-strategy with an adaptive Differential Stochastic Fractal Evolutionary Algorithm (Ic3-aDSF-EA) to solve numerical optimization problems. This novel evolutionary algorithm combines SFS with a DE variant to improve exploration and exploitation. Operating in iterative cycles, it focuses on the best-performing strategies while incorporating diverse contributions. The algorithm was tested on 43 benchmark problems, demonstrating high-quality solutions, scalability, and potential for addressing real-world optimization challenges.
Additionally, Zhang et al. [140] developed a framework for diagnosing Alzheimer’s disease (AD) and mild cognitive impairment (MCI) using MRI data. The authors enhanced a Fuzzy k-nearest neighbor (FKNN) model with a hybrid algorithm, SSFSHHO, which combines the Sobol sequence, Harris Hawks Optimizer (HHO), and SFS algorithm. This approach improves initial population diversity and helps avoid local optima. The SSFSHHO-FKNN model achieved high accuracy on the ADNI dataset, surpassing other algorithms and demonstrating its potential for early diagnosis.
In other research, Zaki et al. [141] developed a hybrid optimization method combining SFS and PSO to improve the K-Nearest Neighbors (KNN) algorithm in wireless sensor networks. This approach optimizes KNN by adjusting particle positions and velocities, significantly reducing the RMSE to 0.00894 and the mean MAE. The results highlight the effectiveness of SFS-PSO in enhancing KNN’s predictive performance for data collection applications.
In another study, Xu et al. [142] proposed an enhanced SFS algorithm to improve energy efficiency and security in clustering for mission-critical IoT-enabled WSNs. The authors introduced a multitrust fusion model using an entropy weight method (EWM) to evaluate sensor trustworthiness. The improved SFS algorithm employs differential and adaptive mutation factors to select optimal cluster heads based on residual energy, integrated trust, and distance to the base station. Experimental results show that this model significantly outperforms existing clustering protocols in energy efficiency and security.
Besides that, Alsawadi et al. [143] developed an action recognition method integrating BlazePose skeletal data with a hybrid optimization technique combining the SFS algorithm and WOA. This approach optimizes the graph structure used in spatial-temporal graph convolutional networks, enhancing action recognition performance. The method was tested on the NTU-RGB+D and Kinetics datasets, showing competitive results compared to traditional techniques.
In another study, Bandong et al. [144] introduced a method to optimize gantry crane automation control by integrating the SFS algorithm with the Flower Pollination Algorithm (FPA) for PID controllers. The approach focused on enhancing position control and minimizing sway angle during crane operation, which is crucial for reducing damage and safety risks in port and construction settings. Results showed that the SFS-FPA method outperformed the PSO-based PID controller in terms of speed response and positional accuracy, although there were trade-offs in settling time.
Finally, Alhussan et al. [145] proposed a diabetes classification model combining the Waterwheel Plant Algorithm with SFS (WWPASFS) to optimize Long Short-Term Memory (LSTM) networks. Using clinical data from the Pima Indians Diabetes Database, the model achieved 98.2% accuracy, outperforming various machine learning techniques. The approach also utilized binary WWPASFS for feature extraction, enhancing classification performance. Statistical analyses validated the model’s effectiveness, highlighting the role of the SFS algorithm in healthcare diagnostics.
4.3 Multi-Objective Versions of the SFS Algorithm
In contrast to single-objective optimization, multi-objective optimization involves addressing multiple conflicting objectives. Achieving a single optimal solution is often impractical, as improving one objective compromises others. Instead, a balance or trade-off among objectives is achieved to identify the most satisfactory solution. This complexity makes multi-objective optimization a particularly challenging area in optimization. Given the strong performance of the SFS algorithm in single-objective tasks, numerous studies have investigated its potential for solving multi-objective problems.
Dubey et al. [146] introduced the SFS algorithm to address the multi-objective economic and emission dispatch (MOEED) problem. By leveraging self-repeating patterns from nature, SFS explores the problem space for optimal solutions, generating fractals that guide particles through random diffusion. The Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS) is employed to evaluate the fitness of multiple Pareto-optimal solutions. Validation on 10- and 13-unit generating systems demonstrated that the SFS algorithm combined with TOPSIS (SFS_TOP) significantly outperforms the weighted sum method (SFS_WS), highlighting its effectiveness in solving MOEED problems.
Furthermore, Labato et al. [147] investigated using the SFS algorithm within a multi-objective optimization framework to solve inverse problems related to the COVID-19 pandemic. The authors employed the SIDR model to simulate virus dynamics, focusing on parameter estimation under uncertainty. The study minimized uncertainties and enhanced robustness by integrating the Multi-objective SFS algorithm with the Effective Mean concept. This approach yielded reliable results using real-world epidemic data from China, demonstrating the effectiveness of SFS in addressing complex models.
In another study, Khalilpourazari et al. [148] introduced the Multi-Objective SFS (MOSFS) algorithm for tackling complex multi-objective problems. The algorithm utilizes an external archive to store Pareto-optimal solutions and incorporates dominance rules and grid mechanisms to approximate the Pareto front. Testing on nine benchmark functions demonstrated superior convergence and coverage compared to other algorithms. Additionally, MOSFS effectively addressed a real-world engineering problem, with statistical validation at a 95% confidence level confirming its efficiency in delivering optimal solutions.
Similarly, Khalilpourazari et al. [149] introduced the SFS algorithm to optimize grinding processes by addressing multiple objectives and constraints to enhance surface quality and production rates while minimizing costs. They combined the Taguchi method for parameter tuning with advanced constraint-handling techniques. Experimental results showed that SFS outperformed traditional methods and contemporary algorithms like MPEDE and HCLPSO, demonstrating its effectiveness in grinding optimization.
Moreover, Tran et al. [150] developed the Non-dominated Sorting SFS (NSSFS), a multi-objective algorithm tailored for distributed network reconfiguration (DNR) and the optimal placement of distributed generation (DG) in radial distribution networks (RDNs). This enhanced SFS algorithm incorporates advanced non-dominated sorting and selection strategies to identify optimal solutions efficiently. Following validation on eight benchmark functions, NSSFS was employed to optimize real power loss and voltage stability in DNR-DG scenarios. It outperformed other techniques, demonstrating significant improvements in system performance.
Subsequently, Ghasemi et al. [151] proposed a two-stage optimization model for distribution center location, vehicle routing, and inventory management in earthquake scenarios. The first stage addresses the location of distribution centers and inventory management, while the second stage optimizes vehicle routing using a multi-objective SFS algorithm. Inspired by fractal growth and incorporating cooperative game theory, the model aims to enhance transportation efficiency and reduce relief time. Validation through a real case study in Tehran demonstrated its effectiveness in capturing real-world performance during disaster scenarios.
Additionally, Xu et al. [152] proposed a multi-objective SFS algorithm for Neural Architecture Search (NAS) to optimize classification accuracy and network complexity. The approach minimizes classification error and network parameters using a decomposition-based SFS method, which enhances local and global search capabilities. Experimental results demonstrated competitive performance across six benchmark datasets, providing a parameter-efficient solution for deep network architecture design.
In another study, Hajghani et al. [153] proposed a multi-objective mixed-integer linear programming model for the location-routing problem in supply chain management, addressing economic, environmental, and social objectives. To tackle this NP-hard problem, they employed the Non-dominated Sorting Genetic Algorithm (NSGA-II) and the Multi-Objective SFS (MOSFS) algorithm. Validation using the Augmented Epsilon Constraint method and CPLEX revealed that MOSFS outperformed NSGA-II in terms of solution diversity and spacing, demonstrating its effectiveness for medium- to large-scale optimization problems.
Similarly, Darvish et al. [154] proposed an innovative method for generating staircase sinusoidal voltage in a Dynamic Voltage Restorer (DVR) using a DC-DC boost converter and a DC-AC multilevel inverter. Designed to improve power quality by mitigating voltage disturbances, the system employs a photovoltaic-powered boost converter for high-gain voltage and a multilevel inverter for producing a high-step sinusoidal output with minimal switches. An interval type-2 fuzzy controller, fine-tuned using a multi-objective SFS algorithm, enhances control precision. Simulation results confirm the system’s effectiveness in compensating for asymmetrical voltage disturbances.
Finally, Xu et al. [63] proposed a reference vector-guided SFS (RVSFS) algorithm for multi-objective optimization. The algorithm enhances exploration and convergence by integrating decomposition strategies with Gaussian walks and Lévy flights. An adaptive mechanism further accelerates convergence while maintaining solution diversity. Testing on 45 benchmark problems demonstrated that RVSFS outperformed several state-of-the-art algorithms.
5 Applications of the SFS Algorithm
The SFS algorithm has been successfully applied to a wide range of real-world challenges in both science and engineering. Effectively addressing these applications requires the careful formulation of objective functions and the selection of relevant variables. This review categorizes SFS applications into key areas, including power and energy, engineering, machine learning, medical and bioinformatics, image processing, environmental modeling, and economics and finance, among others. Table 3 provides an overview of these diverse applications, while the subsequent sections offer detailed discussions on specific uses of the SFS algorithm.
5.1 Power and Energy Applications
Mosbah et al. [155] introduced the SFS algorithm for tracking state estimation in power systems to improve security contingency predictions. The study evaluated SFS on various IEEE bus systems, demonstrating its superior accuracy in state estimation compared to traditional methods like GA and PSO, particularly under measurement uncertainty conditions.
Furthermore, Saha et al. [156] applied the SFS algorithm to optimize an integral-minus-proportional-derivative (I-PDF) controller for automatic generation control in a complex three-area power system. The SFS-optimized controller outperformed conventional methods, and integrating FACTS devices and energy storage systems further enhanced system stability and response, especially in damping frequency oscillations.
In another study, El-Fergany et al. [157] applied the SFS algorithm to optimize relay coordination in meshed power networks. The objective was to minimize the total operating time of primary and backup relays while adhering to coordination constraints across three design variables. Testing on various power systems demonstrated that SFS efficiently produced competitive optimal relay settings within a reasonable timeframe.
Additionally, Saha et al. [158] employed the SFS algorithm to optimize automatic generation control in a three-area system comprising thermal, wind, and combined-cycle gas turbine units. The study showed that two-degrees-of-freedom PID controllers outperformed conventional PID controllers. SFS successfully managed system parameters despite communication delays and generation constraints, demonstrating robustness under varying conditions without recalibration.
Subsequently, Khadanga et al. [159] proposed an SFS-optimized PID controller for frequency regulation in an islanded AC microgrid with diverse distributed energy resources. The SFS-based controller effectively mitigated frequency instability caused by load variations and fluctuations in renewable energy generation, significantly outperforming a traditional PI controller in maintaining frequency stability.
Furthermore, Saha et al. [160] introduced a method for Automatic Generation Control (AGC) in a combined-cycle gas turbine (CCGT) system operating within a complex thermal framework. Using the SFS algorithm, they optimized an integral-minus-proportional-derivative (I-PDF) controller with a first-order filter. The findings revealed that the SFS-optimized controller efficiently handled system dynamics and demonstrated robustness under varying loading conditions, emphasizing its potential for enhancing AGC performance in intricate power systems.
In other research, Saha et al. [161] introduced the SFS-optimized integral-minus-proportional-derivative with first-order filter (I-PDF) controller to improve automatic generation control (AGC) in a combined cycle gas turbine (CCGT)–hydro-thermal power system. The study highlighted the integration of redox flow batteries (RFB) and capacitive energy storage (CES), demonstrating that the I-PDF controller outperformed other controller types. Additionally, RFB placement significantly enhanced oscillation damping, underscoring the controller’s effectiveness in improving system stability.
Similarly, Çelik et al. [162] employed the SFS algorithm to optimize PID parameters in automatic voltage regulator (AVR) systems, achieving enhanced efficiency, accuracy, and convergence speed. The SFS method outperformed other algorithms in tuning gains (Kp, Ki, Kd) and demonstrated improved system stability and voltage regulation, confirming its robustness in AVR applications.
In another study, Nguyen et al. [163] proposed the SFS algorithm for the optimal allocation of distributed generators (OADG) in radial distribution systems (RDSs). This approach improves voltage profiles and stability while adhering to operational constraints. The SFS algorithm is efficient and easy to implement, requiring few control parameters. Evaluations on the IEEE 33-bus, 69-bus, and 118-bus systems showed superior performance compared to other optimization methods, demonstrating its effectiveness for the OADG problem.
In related research, Saha et al. [164] proposed an SFS-optimized control strategy for load frequency regulation in combined cycle gas turbine (CCGT) systems within a three-area interconnected power model. The approach integrates air flow and temperature controllers to minimize control errors and manage system dynamics during load disturbances. The SFS algorithm optimized control parameters, including PI and PID gains. Simulations demonstrated that the SFS-optimized PID controller significantly improved system stability and robustness while offering a cost-effective solution for governor control.
In addition, Mosbah et al. [165] developed a KF-MLP-based SFS method that integrates Kalman filtering with SFS-optimized neural network parameters for state estimation in power systems. This approach enhances the Kalman filter by improving accuracy and reducing divergence through optimized multilayer perceptron (MLP) parameters. It effectively detects anomalies and data errors during fluctuating loads. The method outperformed traditional Kalman filtering techniques when applied to the IEEE 57-bus system, highlighting its potential in complex power system state estimation.
Besides that, Saha et al. [166] proposed an automatic generation control method for a two-area interconnected system, optimizing gains and parameters using the SFS algorithm. Area 1 includes two thermal units with distributed energy generation (DG), while Area 2 has one hydro and one thermal unit. The study addresses nonlinear dynamics and employs classical controllers to mitigate control errors from intermittent DG sources. The SFS-optimized Proportional-Integral-Derivative with first-order filter (PIDN) controller outperformed standard PID controllers, effectively managing frequency and tie-power deviations in response to random inputs.
Likewise, Duong et al. [167] used the SFS method to address the Optimal Reactive Power Flow (ORPF) problem, focusing on minimizing power losses, voltage deviation, and stability index. The SFS algorithm efficiently handled constraints in ORPF. Tested on IEEE 30/118-bus systems, SFS provided rapid, practical solutions, showcasing its potential for solving ORPF issues and suggesting further improvement opportunities.
Furthermore, Saini et al. [168] used the SFS algorithm to optimize parameters in two Proportional-Integral (PI) controllers for Automatic Generation Control (AGC) in thermal power systems. Their approach minimized the Integral of Time-weighted Absolute Error (ITAE), resulting in significantly improved performance, including reduced settling times and smoother dynamic responses compared to established optimization techniques.
In another study, Alomoush et al. [169] applied the SFS algorithm to optimize the Combined Heat and Power Economic Dispatch (CHPED) problem, aiming to minimize operational costs while addressing various constraints. The SFS algorithm demonstrated superior performance in handling non-convexities and achieving near-global solutions more efficiently than other methods.
Moreover, Tran et al. [170] used the SFS algorithm to optimize distribution network reconfiguration (DNR) with distributed generations (DGs). The authors first employed the loss sensitivity factor (LSF) to find optimal DG placements and then applied SFS to determine the best DG sizes and network configurations. The method outperformed other techniques across various bus distribution networks, highlighting the effectiveness of SFS in solving DNR problems.
Following this, Rezk et al. [171] applied the SFS algorithm to improve the performance of PV systems under partial shading. SFS effectively tracked the global maximum power point (MPP) of triple-junction solar cells, outperforming traditional maximum power point tracking (MPPT) methods that struggle with multiple peaks. The algorithm showed fast convergence and superior performance compared to other optimization techniques, demonstrating its robustness in optimizing PV system performance.
To minimize power loss, Nguyen et al. [172] used the SFS algorithm to optimize capacitor and PV system installations in distribution networks. Their study, involving simulations on 33-node and 69-node networks, found that the SFS algorithm outperformed existing methods in determining optimal sizes and locations for these components. The results emphasized the effectiveness of integrating capacitors and PV systems to enhance voltage profiles and reduce active power losses.
Additionally, Alomoush et al. [173] used the SFS algorithm to optimize the bi-objective combined heat and power economic dispatch (CHPED) problem, which involves balancing thermal and electrical energy production from CHP systems. By employing a compromise programming method to address non-convex outputs and constraints, SFS achieved superior near-global solutions compared to traditional optimization techniques, showcasing its effectiveness in complex energy optimization scenarios.
In other research, Rezk et al. [174] introduced a robust method for estimating solar PV parameters using the SFS algorithm. This approach enhances the modeling of PV cells by fitting parameters based on measured current-voltage (I-V) data. Testing various PV models, such as single-diode, double-diode, and PV module models, across different case studies showed that the SFS method outperformed other techniques in accuracy and reliability, underscoring its potential to improve the efficiency and control of PV systems.
Similarly, Elrachid et al. [175] introduced a method for optimizing the dual-input Power System Stabilizer (PSS) using the SFS algorithm within a nonlinear Single Machine Infinite Bus (SMIB) system. This study involved fine-tuning stabilizer parameters and evaluating system performance under different conditions, particularly during three-phase ground faults. The results showed improved system stability, demonstrating the effectiveness of the SFS algorithm in optimizing PSS parameters and enhancing overall performance.
In another study, Van et al. [176] developed the SFS algorithm to optimize environmental and economic dispatch in power systems, focusing on fuel cost, emissions, and economic emissions while meeting load and generation constraints. Testing on various configurations, including the IEEE 30-bus system with wind turbines, showed that the SFS algorithm effectively balanced environmental optimization and operational stability, outperforming established algorithms.
In related research, Saeed et al. [177] proposed the BERSFS algorithm, which combines the al-Biruni Earth radius (BER) algorithm with the SFS algorithm to enhance wind power forecasting. The BERSFS approach was utilized for feature selection and optimization within an ensemble model. Evaluations against various optimization methods and machine learning models, such as LSTM and k-nearest neighbors, showed that the BERSFS model significantly outperformed others, proving its effectiveness and robustness in improving prediction accuracy.
In addition, Darvish et al. [178] introduced a Dynamic Voltage Restorer (DVR) to improve power quality in distribution systems. Key innovations include an Upside-Down Asymmetrical Multi-Level Inverter (UDAMLI) for efficient voltage generation, a Fractional Order Interval Type-2 Fuzzy System (FOIT2FS) for control, and SFS algorithm. These enhancements allow the DVR to effectively address voltage disturbances like sags and swells, achieving superior performance and reduced Total Harmonic Distortion (THD) compared to traditional solutions.
Besides that, Van et al. [179] developed an SFS algorithm to optimize energy resource allocation in electricity production, aiming to maximize profits from power plants. Applied to systems with 10 and 40 elements, the SFS algorithm outperformed other optimization methods, demonstrating its effectiveness in addressing complex energy management challenges in power systems.
Likewise, Huynh et al. [180] introduced a method for accurately estimating solar photovoltaic (SPV) cell model parameters, including single-diode, double-diode, and triple-diode configurations. The authors transformed the estimation into an optimization problem solved by the SFS algorithm, known for its ability to find global optima. Unlike PSO and Chaos PSO, SFS demonstrated superior performance, achieving more accurate parameter estimations for SPV cell models in various applications.
Furthermore, Kumar et al. [181] proposed an innovative hybrid SFS Network (SFSN) for energy management in all-electric ships, utilizing fuel cells and batteries for optimized power distribution. The system combines Deep Neural Networks with SFS optimization to predict fuel cell output and adjust energy usage based on demand. Simulation results indicate improved efficiency and reliability in managing energy for marine applications.
Finally, Bacha et al. [182] developed a model to optimize a stand-alone hybrid energy system with photovoltaic sources, wind turbines, storage systems, and diesel generators for isolated rural areas. Utilizing actual weather data from Biskra, Algeria, they analyzed various configurations to minimize electricity costs. The SFS algorithm, alongside SOS and PSO, was employed for optimization. The results indicated that SFS significantly reduced the levelized cost of energy (LCOE) across all scenarios, demonstrating its effectiveness in optimizing hybrid energy systems for rural applications.
Khanam et al. [183] applied the SFS algorithm to tune PID controller parameters for DC motor control systems. Using the integration of time multiplied by absolute error (ITAE) as the objective function, the SFS-optimized PID controller achieved zero overshoot and improved settling and rise times compared to existing methods. The robustness analysis demonstrated the effectiveness of the SFS/PID approach under varying motor parameters, highlighting its adaptability and efficiency.
Furthermore, Khanam et al. [184] employed the SFS algorithm for order reduction in large-scale single-input single-output (SISO) linear time-invariant (LTI) systems. The algorithm minimizes the integral square error (ISE) between the original reduced-order and higher-order systems. The study compares both systems’ step and frequency responses, demonstrating that SFS outperforms existing techniques in effectively reducing system order.
Moreover, Li et al. [185] applied the SFS algorithm to unmanned aerial vehicle (UAV) path planning, addressing complex optimization tasks with specific constraints. The study showcased SFS’s superior search accuracy and convergence speed in continuous function optimization. Experimental results indicated that SFS effectively identified feasible paths between start and end points, demonstrating robust real-time performance under various environmental conditions.
Following this, Liu et al. [186] developed a hierarchical optimization framework to enhance UAV aerial photography route planning amidst real-world uncertainties. The framework accounts for interval uncertainties affecting flight quality, leading to varying potential outcomes. A criterion was established to evaluate and rank candidate flight routes based on efficiency and robustness. The SFS algorithm was utilized to navigate the optimization landscape effectively. This approach improves the reliability of UAV route planning, contributing to better data collection and photography quality across various applications.
Additionally, Bhatt et al. [187] applied the SFS algorithm to approximate and control linear time-invariant (LTI) systems. They derived low-order systems from higher-order counterparts and optimized DC motor speed control using PID controllers. SFS effectively explored the search space, achieving minimal overshoot and improved performance metrics. The results demonstrated that SFS maintained system characteristics while outperforming traditional system approximation and motor control methods.
In other research, Çelik et al. [188] developed the PI + DF controller, enhancing PID control by integrating a derivative path with a low-pass filter. The authors optimized the controller’s gains using the SFS algorithm, demonstrating superior performance in simulations and experiments on a DC servo system. The SFS-tuned controller outperformed traditional methods, highlighting its effectiveness in refining PID controller design for advanced control applications.
Similarly, Huang et al. [189] addressed reliability-redundancy allocation problems using survival signature theory to optimize system reliability while meeting constraints. They introduced an adaptive penalty function to convert the constrained problem into an unconstrained one, which was then solved using the SFS algorithm. This method also evaluates component importance for effective redundancy allocation. It simplifies the optimization process by requiring only one survival signature calculation, enhancing the understanding of reliability-redundancy allocation in systems.
In another study, Zafrane et al. [190] developed a multidisciplinary design optimization strategy for launch vehicle satellites using a three-stage liquid propellant system. The approach enhances solution quality and convergence speed by integrating heuristic algorithms like GSA and SFS. This strategy addresses complex design challenges and emphasizes using virtual reality tools to streamline the design process, ultimately reducing analysis time and costs in aerospace development.
In related research, Mandala et al. [191] proposed the SFS algorithm to optimize the parameters of a two-degree-of-freedom PID controller, aiming to enhance control actions in complex quadrotor systems. In their study, the performance of the SFS algorithm was compared with that of the PSO algorithm for parameter tuning. The results demonstrated that the SFS algorithm outperformed PSO, showcasing its effectiveness as an optimization tool for this specific control application.
In addition, Juybari et al. [192] introduced the SFS algorithm to address the reliability-redundancy allocation problem, aiming to maximize system reliability by optimizing redundancy levels and component reliability. Focusing on a cold-standby strategy, the SFS algorithm was applied to various benchmark problems, yielding improved configurations with enhanced reliability values. The results demonstrated the algorithm’s superior solution quality and robustness in cold-standby redundancy scenarios compared to previous methods.
Besides that, Dobani et al. [193] developed a new approach to the reliability-redundancy allocation problem (RRAP) by incorporating component mixing and treating reliability as a decision variable within a heterogeneous framework. The authors applied the SFS algorithm to solve the mixed-integer nonlinear programming (MINLP) models, achieving superior reliability structures and significantly improved reliability values in benchmark tests compared to prior studies.
Likewise, Lagunes et al. [194] introduced a multi-meta-heuristic optimization model that combines various algorithms, including the SFS algorithm, to optimize fuzzy system membership functions for autonomous mobile robot navigation. The approach outperformed existing techniques, demonstrating its effectiveness in solving complex control challenges.
Furthermore, Li et al. [195] enhanced a multi-support vector regression (SVR) model for predicting the remaining useful life (RUL) of rolling bearings by using the SFS algorithm to optimize SVR parameters. This method improved prediction accuracy by extracting time-domain features, reducing noise with a Butterworth filter, and applying principal component analysis for dimensionality reduction. Validated on IMS experimental datasets, the approach demonstrated strong alignment with actual RUL values and outperformed other prediction techniques in terms of accuracy and convergence.
Moreover, Jing et al. [196] developed a method to optimize the parameters of the Adaptive Neuro-Fuzzy Inference System (ANFIS) using the SFS algorithm for predicting uniaxial compressive strength (UCS) in geotechnical projects. Evaluated with data from the Pahang–Selangor freshwater tunnel in Malaysia, the SFS-ANFIS model achieved a high coefficient of determination (
Bendaoud et al. [197] introduced a method for identifying nonlinear synchronous generator parameters using the SFS algorithm, which minimizes a quadratic criterion based on the differences between simulated and actual outputs. Compared to PSO, the SFS algorithm demonstrated better stability, robustness, estimation accuracy, and convergence speed, proving its effectiveness for this application.
Following this, Mai et al. [198] introduced an optimization method for Fuzzy PD controllers in a two-link robot manipulator system, utilizing the SFS algorithm to enhance control performance. The system’s dynamics were modeled using the Lagrangian method, and simulations in MATLAB showed that SFS outperformed GA and the modified Neural Network Algorithm, achieving superior accuracy, responsiveness, and stability.
Additionally, Sasmito et al. [199] addressed the permutation flow shop scheduling problem by using the SFS algorithm to optimize job sequences and minimize makespan. Their rigorous testing against Taillard’s benchmark problems showed that SFS consistently outperformed other optimization algorithms, delivering near-optimal solutions and effectively solving complex scheduling challenges.
In other research, Hasan et al. [200] introduced a load-balanced workflow allocation method using the SFS algorithm to optimize resource utilization in an Infrastructure-as-a-Service (IaaS) cloud environment. This approach effectively addresses the NP-hard workflow allocation problem by minimizing load imbalance on virtual machines. Performance analysis in MATLAB showed that the SFS strategy outperformed PSO, providing more efficient solutions for balancing workflows and enhancing resource utilization in cloud computing.
Similarly, Ye et al. [201] proposed a hybrid evolutionary model that integrates an adaptive neuro-fuzzy inference system (ANFIS) with the SFS algorithm to predict air overpressure (AOp) caused by rock blasting. The study compares the ANFIS-SFS model with the ANFIS-PSO and ANFIS-GA models using data from four granite quarry sites. The results show that the ANFIS-SFS model, with the lowest root mean square error (1.223 dB), outperforms the other models, demonstrating SFS’s superior ability to predict AOp and improve accuracy in open-pit mining applications.
In another study, Meredef et al. [202] developed a method to stabilize Takagi-Sugeno fuzzy systems using an integral Lyapunov fuzzy candidate (ILF) and solved linear matrix inequalities (LMIs) with the SFS algorithm. This approach reduces conservatism and enables broader stability conditions compared to traditional methods. A numerical example demonstrated that the ILF method offers improved feasibility for stabilization over other Lyapunov-based techniques.
In related research, Houili et al. [203] compared six meta-heuristic algorithms, including the SFS algorithm, for estimating induction motor parameters. The performance was measured using the sum of absolute differences (SAD) between actual and predicted outputs. CGO outperformed the others with a SAD of 1.1045, while SFS achieved a competitive SAD of 1.1063, demonstrating its effectiveness in parameter estimation.
In addition, Liu et al. [204] developed a two-step method for accurately localizing low-velocity impacts in composite plate structures using wavelet packet energy characteristics. Using a fiber Bragg grating (FBG) sensing system, the method first identifies the impact area and then applies the SFS algorithm for precise localization. Experimental results demonstrated that integrating the SFS algorithm significantly enhanced localization accuracy for impacts on carbon fiber-reinforced plastic (CFRP) materials.
Besides that, Zheng et al. [205] enhanced the performance of permanent magnet synchronous linear motors (PMSLM) by developing a high-accuracy inductance model using analytic kernel-embedded elastic-net regression (AKER). The authors optimized the motor’s performance with the SFS algorithm, which iteratively solved the optimization function. The AKER model was shown to be more accurate and faster than finite element methods, demonstrating the effectiveness of SFS in PMSLM optimization.
Likewise, Chengquan et al. [206] introduced the SFS algorithm to predict the compressive strength of concrete (CSC) using a dataset of 1030 specimens. The authors optimized parameters such as fly ash, cement, and water content. Their results showed that the SFS-enhanced multi-layer perceptron (SFS-MLP) outperformed the MVO and VSA algorithms, achieving high accuracy (R2 of 0.99942) and low error rates (RMSE of 0.24922).
Furthermore, Zhou et al. [207] introduced the SFS-enhanced multi-layer perceptron neural network (SFS-NN-MLP) for predicting concrete slumps. This model improves upon traditional measurement methods by utilizing machine learning techniques, accurately predicting slump based on ingredient proportions and curing age. It outperformed other optimization algorithms, demonstrating superior mean square error and Pearson correlation coefficient accuracy. The SFS-NN-MLP model shows promise for cost-effective slump prediction in concrete applications.
Finally, Wang et al. [208] developed an artificial neural network (ANN) model enhanced by integrating the SFS algorithm with vortex search (VS) and multi-verse optimizer (MVO) techniques to predict cooling load requirements in eco-friendly buildings. The study addressed the complexities of estimating non-linear heat loss in sustainable structures. The SFS-ANN model outperformed the VS-ANN and MVO-ANN models, achieving an R2 value of 0.99827 and an RMSE of 0.00619. These results demonstrate the effectiveness of SFS in optimizing neural network performance, enhancing prediction accuracy, and improving energy efficiency in building design and operation.
5.3 Machine Learning Applications
Mosavi et al. [209] proposed using the SFS algorithm to train Radial Basis Function Neural Networks (RBF NNs), enhancing convergence speed and mitigating issues related to local minima. SFS improves search space exploration through its fractal diffusion properties. Evaluations on benchmark and sonar datasets showed that SFS-trained RBF networks achieved better classification accuracy and faster convergence than traditional training methods.
Furthermore, Mosbah et al. [210] developed the SFS algorithm to optimize the parameters of multilayer perceptron (MLP) neural networks for dynamic state estimation (DSE). The SFS method effectively identifies optimal weights and thresholds, enhancing accuracy and preventing local minimum traps. Results showed significant precision and computational efficiency improvements compared to GA and PSO, highlighting its effectiveness for real-time power system monitoring and forecasting.
Besides that, Khishe et al. [211] applied the SFS algorithm to train multilayer perceptron neural networks, introducing the Chaotic Fractal Walk Trainer (CFWT) to enhance convergence speed and avoid local minima. Their classifier outperformed four established meta-heuristic trainers on benchmark and sonar datasets, and FPGA implementation demonstrated effective real-time processing for complex problems.
In addition, Mosbah et al. [212] developed a hybrid method combining Multilayer Perceptron Neural Networks (MLP) with the SFS algorithm to improve state estimation in power grids using phasor measurement units (PMUs). The approach utilizes MLP for initial state calculations and SFS for refining estimates. Testing on IEEE 14, 30, and 57-bus systems showed enhanced accuracy with adding more PMUs, demonstrating the effectiveness of the hybrid MLP-SFS method over standalone approaches.
In another work, Moayedi et al. [213] proposed an innovative hybrid model combining artificial neural networks (ANN) with the SFS algorithm to enhance cooling load predictions in residential buildings. Compared to the GOA and FA, the SFS-ANN model achieved over 90% correlation in optimizing predictions, significantly reducing prediction error by 36%, while GOA and FA achieved reductions of 23% and 18%, respectively. This study demonstrates the superior effectiveness of the SFS-ANN model for early cooling load predictions.
Similarly, Neelakandan et al. [214] proposed combining the SFS algorithm with a modified deep learning neural network (DLMNN) to enhance e-commerce sales forecasting. The SFS algorithm optimized the DLMNN parameters, improving prediction accuracy across product categories. Evaluations on a time series dataset showed that the SFS-optimized DLMNN outperformed traditional non-deep learning methods in terms of RMSE and other metrics, highlighting its effectiveness for online sales forecasting.
Finally, Yang et al. [215] used the SFS algorithm for hyperparameter tuning in predictive modeling of membrane distillation processes. Analyzing a dataset with over 5,000 data points from computational fluid dynamics, they evaluated three regression models: SVM, DNN, and KRR. SFS effectively optimized the model parameters, achieving a high R2 score of 0.99839 for SVM and a low RMSE of 0.77001 for DNN, demonstrating its potential to enhance predictive accuracy in complex systems.
5.4 Medical and Bioinformatics Applications
Hinojosa et al. [216] applied the SFS algorithm to image thresholding in breast histology imagery to enhance segmentation for early breast cancer diagnosis. The SFS algorithm was evaluated using three entropy-based objective functions, Kapur, Minimum Cross Entropy, and Tsallis, and it was compared to ABC and DE. The results demonstrated that combining SFS with Minimum Cross Entropy achieved the highest-quality segmentation, highlighting SFS’s potential in medical image analysis.
Furthermore, Bingöl et al. [217] utilized the SFS algorithm to optimize threshold values for improving skin cancer lesion detection from dermoscopic images. The study applied five entropy-based methods to achieve accurate lesion delineation, including Minimum Cross, Renyi, Charvat, Havrda, Tsallis, and Kapur. SFS significantly improved threshold optimization for each method, resulting in enhanced detection accuracy. The approach was validated on the PH2 dataset of skin lesion images, showcasing the potential of SFS in dermatological medical imaging.
Similarly, Dhal et al. [218] applied the SFS algorithm to improve blood image segmentation for leukemia detection. Unlike conventional clustering techniques, which are sensitive to initial positions and prone to false positives, SFS effectively addressed segmentation complexities. Experimental results demonstrated that SFS outperformed other methods’ accuracy, efficiency, and segmentation quality, highlighting its potential to advance early leukemia diagnosis through automated pathology systems.
In addition, Khafaga et al. [219] developed a computer-aided diagnosis framework for monkeypox, addressing challenges related to the low visual resolution of images. This hybrid approach combines convolutional neural networks (CNNs) with an optimization technique called the Al-Biruni Earth Radius Optimization-based SFS algorithm (BERSFS). The framework first employs CNNs to extract image features, followed by an optimized classification model utilizing a triplet loss function to differentiate monkeypox cases. Tested on skin disease images from an African hospital, the BERSFS framework significantly outperformed existing methods in effectiveness and stability, as validated by statistical tests such as Wilcoxon and ANOVA. This research highlights the potential of SFS variants in advancing medical image classification.
In related research, Abdellatif et al. [220] investigated dynamic systems for diabetes control and its socio-economic impacts by implementing various local search AI methods, particularly meta-heuristic algorithms. The SFS algorithm generated continuous and cost-effective control strategies among the tested algorithms, including BA, FA, and GA. The study highlights the effectiveness of SFS in producing efficient solutions that alleviate socio-economic burdens while adhering to budget constraints, offering valuable insights into diabetes management.
Finally, Khalilpourazari et al. [221] proposed the SFS algorithm integrated with a mathematical model to forecast COVID-19 trajectories, aiding policymakers in developing effective containment strategies. Applied to public datasets, the model predicted symptomatic and asymptomatic infections, recoveries, and fatalities in Canada. The findings highlighted the significant impact of asymptomatic cases on transmission dynamics and underscored the importance of enhanced testing capacity. Sensitivity analyses evaluated the influence of transmission rate variations on pandemic growth, offering valuable insights for future case projections and practical recommendations to reduce community transmission.
5.5 Image Processing Applications
Luo et al. [222] developed LI-SFS, a hybrid approach combining the SFS algorithm and lateral inhibition (LI) for template matching in image processing. By leveraging the strengths of both methods, LI-SFS improves accuracy and robustness, demonstrating superior performance over other LI-based algorithms in simulations.
Furthermore, Li et al. [223] proposed a target-matching approach using edge features and the SFS algorithm to optimize geometric transformations inspired by particle interactions. By treating pixels as groups of atoms, the method seeks optimal matches through numerical optimization. Comparative simulations demonstrated the SFS algorithm’s effectiveness in identifying multiple correct targets in test images, with theoretical analyses suggesting its alignment with existing image enhancement techniques, such as lateral inhibition, thus laying a foundation for more efficient target-matching methods.
In another study, Betka et al. [224] introduced a block-matching algorithm using the SFS technique to enhance motion estimation in video processing. By addressing the long computation times of traditional algorithms, the authors implemented a parallel processing approach with a multi-population model of SFS. Key enhancements included fixed-pattern initialization, a new fitness function combining two matching criteria, and an adaptive window size strategy. Evaluated across nine video sequences, the algorithm demonstrated significant improvements in estimation accuracy and computational efficiency compared to established methods, establishing its superiority in the field.
Moreover, Dhal et al. [225] integrated the SFS algorithm with a fuzzy entropy-based multi-level thresholding model to improve the segmentation of color satellite images. The authors addressed the computational challenges of traditional thresholding techniques, demonstrating that SFS outperformed four established algorithms such as PSO, CS, HS, and ABC, in terms of image quality, fitness value, and efficiency. Specifically, SFS was 2.5% faster than CS and significantly quicker than the others for the same number of function evaluations, underscoring its effectiveness in image segmentation.
Following this, Charef et al. [226] proposed the SFS algorithm for visual tracking, addressing the challenges of local minimum convergence in existing methods. By leveraging SFS for localization, the algorithm explores the search space to find candidates that match a predefined template, using a kernel-based spatial color histogram and Bhattacharyya distance for the fitness function. Evaluated on 20 video sequences from the OTB-100 dataset and compared to 11 advanced tracking algorithms, the SFS tracker demonstrated superior quantitative and qualitative performance, showcasing its robustness and effectiveness in visual tracking tasks.
Finally, Das et al. [227] developed a Histogram-based Fast and Robust Crisp Image Clustering (HFRCIC) technique enhanced by the SFS algorithm. This method addresses noise sensitivity and local optima issues in conventional K-means clustering by integrating morphological reconstruction and clustering based on gray levels. The use of SFS to optimize cluster centers boosts performance. Experimental results on synthetic and real-world images, including white blood cell segmentation, showed that HFRCIC-SFS outperforms other segmentation and clustering algorithms.
5.6 Environmental Modeling Applications
Alomoush et al. [236] applied the SFS algorithm to solve the environmental-economic dispatch problem in power systems, addressing generator constraints, emissions, and transmission losses. Benchmarking against eight optimization methods, including GA and PSO, demonstrated that the SFS algorithm achieves lower production costs and outperforms traditional techniques in finding global optimal solutions efficiently.
Furthermore, Van et al. [237] utilized the SFS algorithm for the economic emission dispatch (EED) problem, balancing environmental and economic goals amid limited fossil fuel resources. Tested on a 6-generator system and the IEEE 30-bus system, the SFS algorithm demonstrated competitive performance, enhancing both profitability and emissions reduction for power plants.
In another study, Xu et al. [238] developed a runoff forecasting model using the SFS algorithm, Gated Recurrent Unit (GRU), and Variational Mode Decomposition (VMD) within a DIP framework. Tested on runoff data from the Upper Yangtze River Basin, the model showed improved prediction accuracy and training efficiency, outperforming other hybrid models.
Similarly, Zhang et al. [239] developed neuro meta-heuristic models integrating the Sunflower Optimization Algorithm, Vortex Search Algorithm, and SFS algorithm with neural networks to improve pan evaporation predictions. Tested with climate data, the SFS-MLPNN model achieved the best results, with a mean absolute error of 0.0997 and a Pearson correlation of 0.9957, demonstrating significant promise for environmental modeling.
Finally, Ahmadi et al. [240] compared optimization techniques, including the SFS algorithm, to improve ANN models for predicting landslide susceptibility. Using data from eastern Azerbaijan and Iran, the SFS-MLP model achieved the highest accuracy, outperforming other models and demonstrating the effectiveness of SFS for environmental risk mapping.
5.7 Economic and Financial Applications
Khalilpourazari et al. [228] proposed a constrained multi-product economic production quantity model to minimize total inventory costs while allowing for shortages and partial backordering. The model incorporates various constraints, including a stochastic budget constraint. The authors utilized several solution methods, including the SFS algorithm, which performed well in optimizing objective values and minimizing CPU time. Sensitivity analyses highlighted the significant impact of production rates on the objective function, demonstrating the effectiveness of the SFS algorithm in complex inventory management.
In another study, Dinh et al. [229] analyzed factors affecting undergraduate employability for business and economics students in Ho Chi Minh City, Vietnam, considering Industry 4.0. The authors identified key determinants such as human capital, social capital, and identity, through in-depth interviews and used the SFS algorithm for ranking. The study highlighted the critical role of human capital, particularly attitude, and emphasized the significance of social capital while noting the emerging relevance of identity. The findings inform strategies to enhance employability in a changing job market.
Similarly, Shahid et al. [230] introduced a risk-budgeted portfolio selection strategy using the SFS algorithm to optimize investment decisions in capital markets. The SFS algorithm utilizes a fractal search mechanism to maximize the Sharpe ratio while managing risk for risk-averse investors. An experimental study using data from the S&P BSE Sensex of the Indian stock exchange demonstrated the superior performance of the SFS strategy compared to GA, highlighting its potential in financial decision-making and risk management.
In related research, Shahid et al. [231] proposed a portfolio selection model using the SFS algorithm to optimize investments in capital markets. The model focuses on maximizing the Sharpe ratio while managing risk constraints. Evaluated against traditional methods like GA and PSO using real datasets from Indian and global stock exchanges, the SFS approach significantly outperformed its counterparts, marking a pioneering contribution to portfolio optimization, validated through statistical analysis.
Finally, Shahid et al. [232] proposed a portfolio selection model using the SFS algorithm to enhance the Sharpe ratio. The model addresses challenges in portfolio optimization, including constraints like cardinality and transaction costs, and outperforms traditional methods such as Markowitz’s mean-variance optimization. Tested against GA and SA with data from the Bombay Stock Exchange, the SFS model demonstrated superior performance, proving its effectiveness in optimizing portfolio selection in complex financial environments.
5.8.1 Wireless Sensor Network Applications
Hriez et al. [233] proposed a clustering protocol for Wireless Sensor Networks (WSNs) that integrates a trust model to enhance data reliability in IoT applications. The protocol uses the SFS optimization method to identify trusted nodes by evaluating parameters such as remaining energy and node density while promoting balanced cluster formation. Experimental results indicate that it significantly outperforms existing energy efficiency and trustworthiness models, particularly in mission-critical scenarios.
Similarly, Yang et al. [234] developed a radar task scheduling method using the SFS algorithm within the Q-RAM framework to improve mission effectiveness in radar resource management. Their approach achieves near-optimal scheduling with reduced computation time compared to traditional methods, showcasing the potential of SFS in complex radar scheduling tasks.
5.8.2 Cybersecurity Applications
Duhayyim et al. [235] developed the SFSA-DLIDS, a cybersecurity model that combines the SFS algorithm with deep learning to enhance intrusion detection in cloud-based cyber-physical systems. By optimizing feature selection and classification using the SFS algorithm and chicken swarm optimization, respectively, the model achieved superior detection accuracy compared to recent alternatives, thereby improving CPS network security.
6 Open Source Software for the SFS Algorithm and Online Lectures
To provide a comprehensive review that serves both theoretical and practical purposes for researchers, we present the open-source code for the SFS algorithm, developed by its founder and subsequent contributors, as follows:
• The original implementation of the SFS algorithm, written in MATLAB, can be found at the following URL: https://www.mathworks.com/matlabcentral/fileexchange/47565-stochastic-fractal-search-sfs (accessed on 20 October 2024).
• The original implementation of the SFS algorithm, written in Python, can be found at the following URL: https://github.com/mohammed-elkomy/stochastic-fractal-search-python (accessed on 20 October 2024).
• The SFS algorithm for economic dispatch, implemented in MATLAB, is available at the following URL: https://www.mathworks.com/matlabcentral/fileexchange/159431-stochastic-fractal-search-for-economic-dispatch (accessed on 20 October 2024).
• The Dynamic Fitness-Distance Balance-based SFS, implemented in MATLAB, can be found at the following URL: https://www.mathworks.com/matlabcentral/fileexchange/156762-an-improved-stochastic-fractal-search-algorithm-dfdb-sfs (accessed on 20 October 2024).
• The Adaptive Fitness-Distance Balance-based SFS algorithm, implemented in MATLAB, can be found at the following URL: https://www.mathworks.com/matlabcentral/fileexchange/118485-afdb-sfs (accessed on 20 October 2024).
• The Natural Survivor Method-based SFS algorithm (NSM_SFS), developed using MATLAB, is accessible at the following URL: https://www.mathworks.com/matlabcentral/fileexchange/125920-nsm_sfs (accessed on 20 October 2024).
• The Multi-Surrogate-Assisted SFS algorithm, implemented in MATLAB, can be found at the following URL: https://github.com/xiaodi-Cheng/SF-MSASFS (accessed on 20 October 2024).
Furthermore, several publicly available lectures provide detailed explanations of the procedure of the original SFS algorithm, as outlined below:
• Lecture 1: Presented by Simulation Tutor, this lecture examines the SFS algorithm code and its application in load flow analysis. It is available at the following URL: https://www.youtube.com/watch?v=0nGLqydECRI (accessed on 20 October 2024).
• Lecture 2: Presented by Logsig Solutions, this lecture investigates the application of distributed generation and capacitor placement using the Chaotic SFS algorithm. It can be accessed at the following URL: https://www.youtube.com/watch?v=dmb8n79SmCU (accessed on 20 October 2024).
7 Performance Evaluation of the SFS Algorithm
Since its introduction in 2015, numerous meta-heuristic algorithms have been developed to tackle real-world optimization challenges. To provide a comprehensive assessment of the SFS algorithm’s performance compared to recently proposed meta-heuristic algorithms, this section analyzes optimization outcomes using a diverse set of benchmark functions from the CEC’2022 benchmark test, including unimodal, multimodal, composite, and hybrid functions. Table 4 provides an overview of the CEC’2022 benchmark functions and their optimal solutions. Additional detailed information about these functions can be found in the literature [241]. This set of functions is designed to evaluate various aspects of optimization algorithms: unimodal functions test exploitation ability, multimodal functions assess global exploration proficiency, and composite and hybrid functions offer a comprehensive evaluation of algorithm performance.
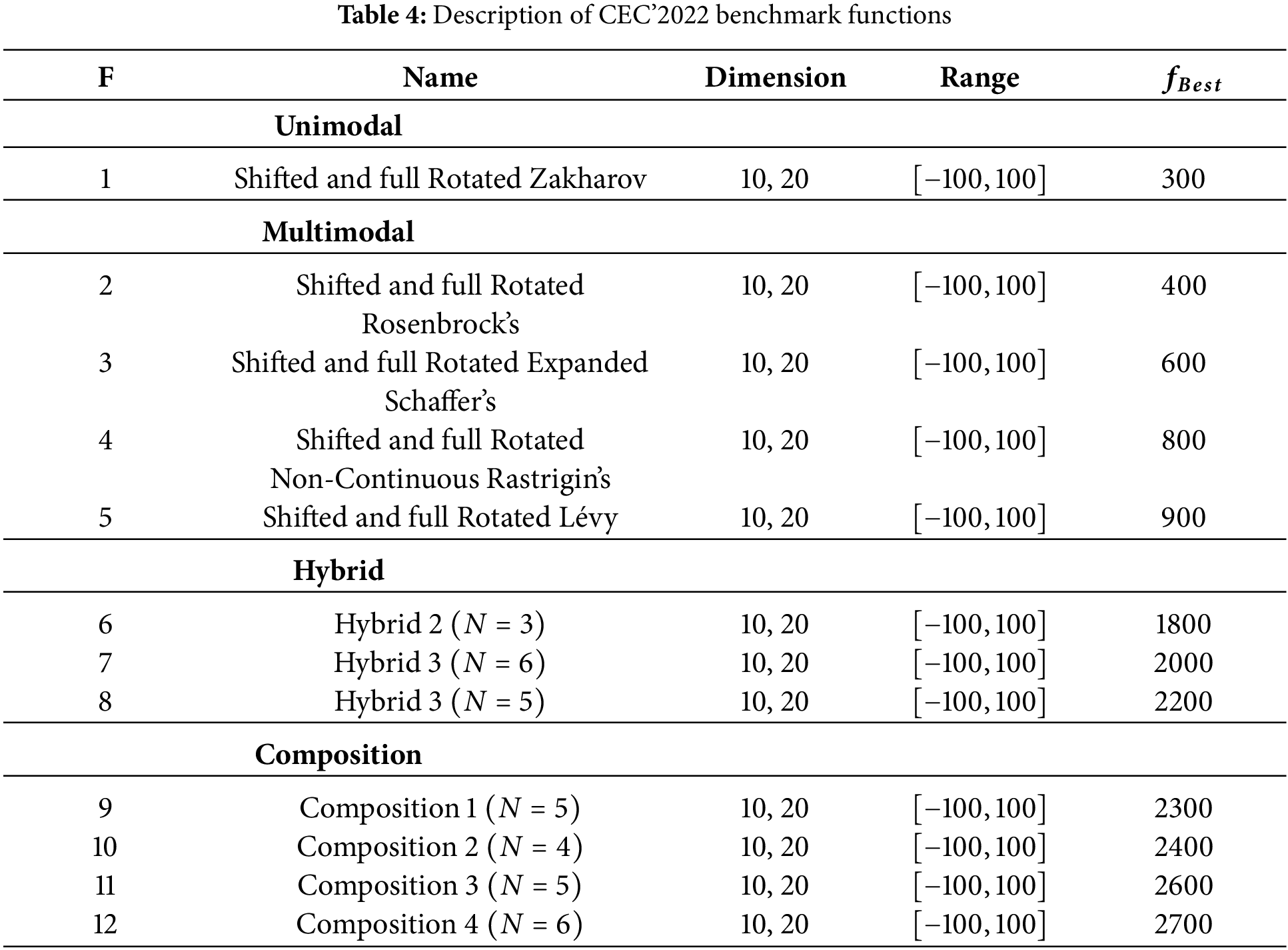
This section compares the SFS algorithm with eight recently introduced optimization algorithms published within the last three years. These algorithms include: the Elk Herd Optimizer (EHO) 2024 [23], White Shark Optimizer (WSO) 2022 [26], Dream Optimization Algorithm (DOA) 2025 [242], Newton Raphson Based Optimizer (NRBO) 2024 [243], Optical Microscope Algorithm (OMA) 2023 [244], Chernobyl Disaster Optimizer (CDO) 2023 [245], Artificial Lemming Algorithm (ALA) 2025 [246], and the Memory, evolutionary operator, and local search-based improved Grey Wolf Optimizer (MELGWO) 2023 [247]. These algorithms’ parameters and corresponding values were sourced directly from their original publications.
To ensure a fair comparison, all algorithms are executed under the same initial conditions. The solution space is set to a dimensionality of
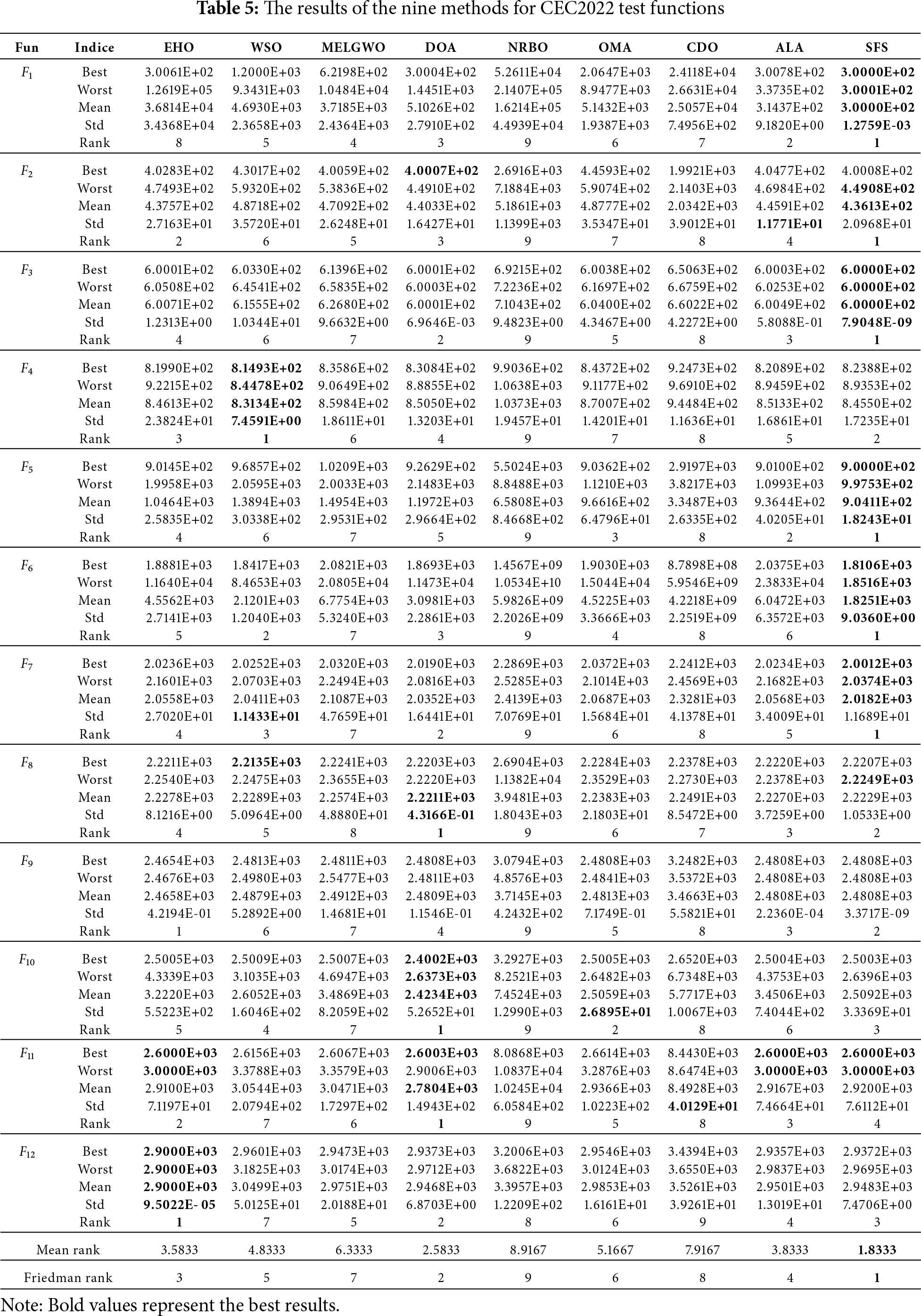
Table 5 presents detailed statistics on the best, worst, mean, standard deviation, and rank metrics based on analyzing thirty fitness values generated by each algorithm across thirty independent runs on the CEC’2022 benchmark. The table shows that SFS achieves the lowest mean value on six functions (F1, F2, F3, F5, F6, and F7) and ranks second on three functions (F4, F8, and F9). In contrast, the DOA algorithm secures the top rank on three functions (F8, F10, and F11). Similarly, the EHO algorithm ranks first on two functions (F9 and F12), while the WSO algorithm achieves the top rank on the F4 function.
Furthermore, to validate the effectiveness and reliability of the SFS algorithm, the Friedman rank test was conducted for each benchmark function, with the results presented in the final row of Table 5. The Friedman rank compares algorithm performance across all functions, whereas a lower rank indicates better overall performance. The table shows that the SFS algorithm achieves the lowest Friedman rank, reflecting its superior average performance, followed by DOA in second place. In contrast, NRBO records the highest Friedman rank, indicating weaker overall performance. The SFS algorithm consistently delivers competitive results, achieving low mean values and favorable rankings across multiple functions, outperforming or matching the performance of other algorithms in most cases. These findings highlight the efficiency and dominance of the SFS algorithm in solving optimization challenges.
The Wilcoxon rank test was applied to assess the statistical significance of differences between the SFS algorithm and its competing algorithms. The results for the CEC’2022 test set are summarized in Table 6, where the p-values comparing SFS with each method are reported. A p-value below 5% indicates a statistically significant difference between SFS and the other methods. As shown in Table 6, SFS demonstrates statistically substantial differences from most competitors across most functions. For instance, SFS significantly differs from WSO, MELGWO, NRBO, OMA, and CDO across all functions. Additionally, SFS differs from DOA on all functions except F4, F9, and F12 and from EHO on all functions except F4, F8, F11, and F12, based on the results for the CEC’2022 benchmark suite. Furthermore, some p-values equal
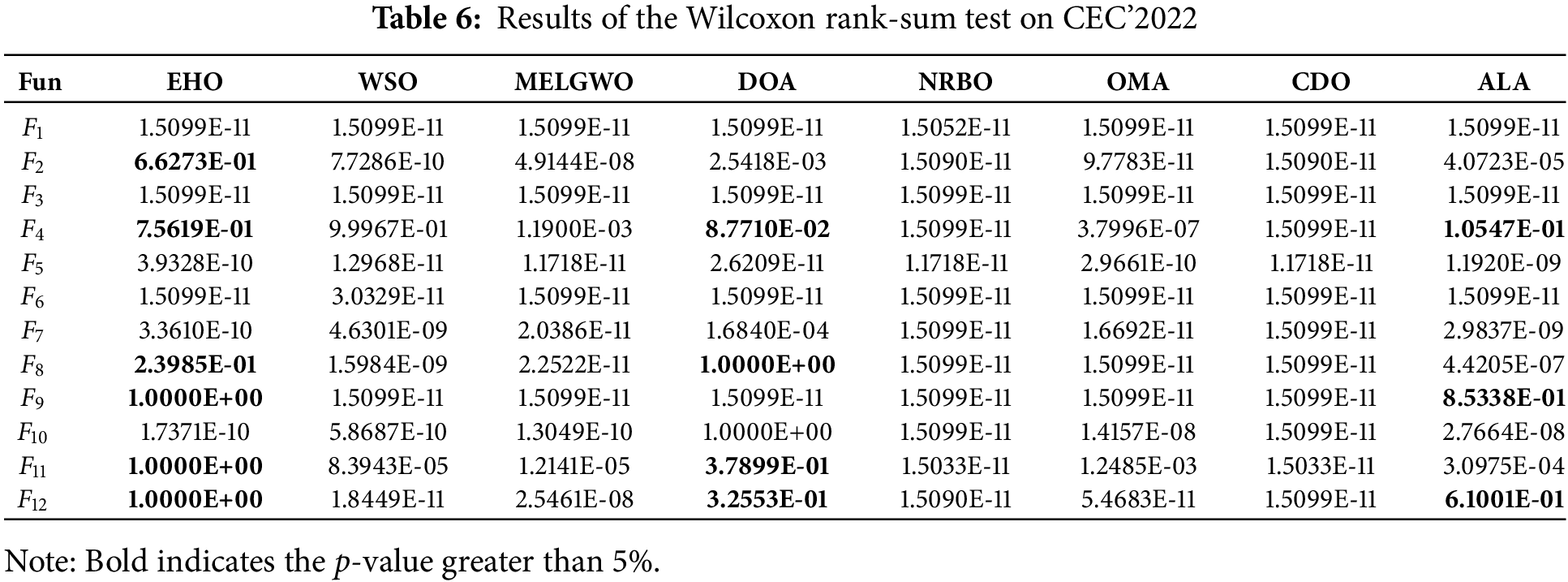
On the other hand, Fig. 13 illustrates the convergence curves of the nine algorithms applied to the CEC’2022 benchmark suite, providing a visual representation of their convergence behavior. The SFS convergence curves are highlighted in red to facilitate performance evaluation. As shown in Fig. 13, SFS exhibits rapid convergence during the early iterations. It consistently progresses toward the optimal solution, demonstrating its ability to explore the search space and approach the global optimum efficiently. The convergence curves of the other algorithms are also displayed, allowing for a comprehensive comparison of their convergence patterns. This analysis provides valuable insights into the relative performance of each algorithm on the CEC’2022 benchmark suite. Overall, the convergence analysis highlights SFS’s ability to converge quickly and achieve near-optimal solutions, with the convergence curves offering a detailed evaluation of its performance relative to the other algorithms.
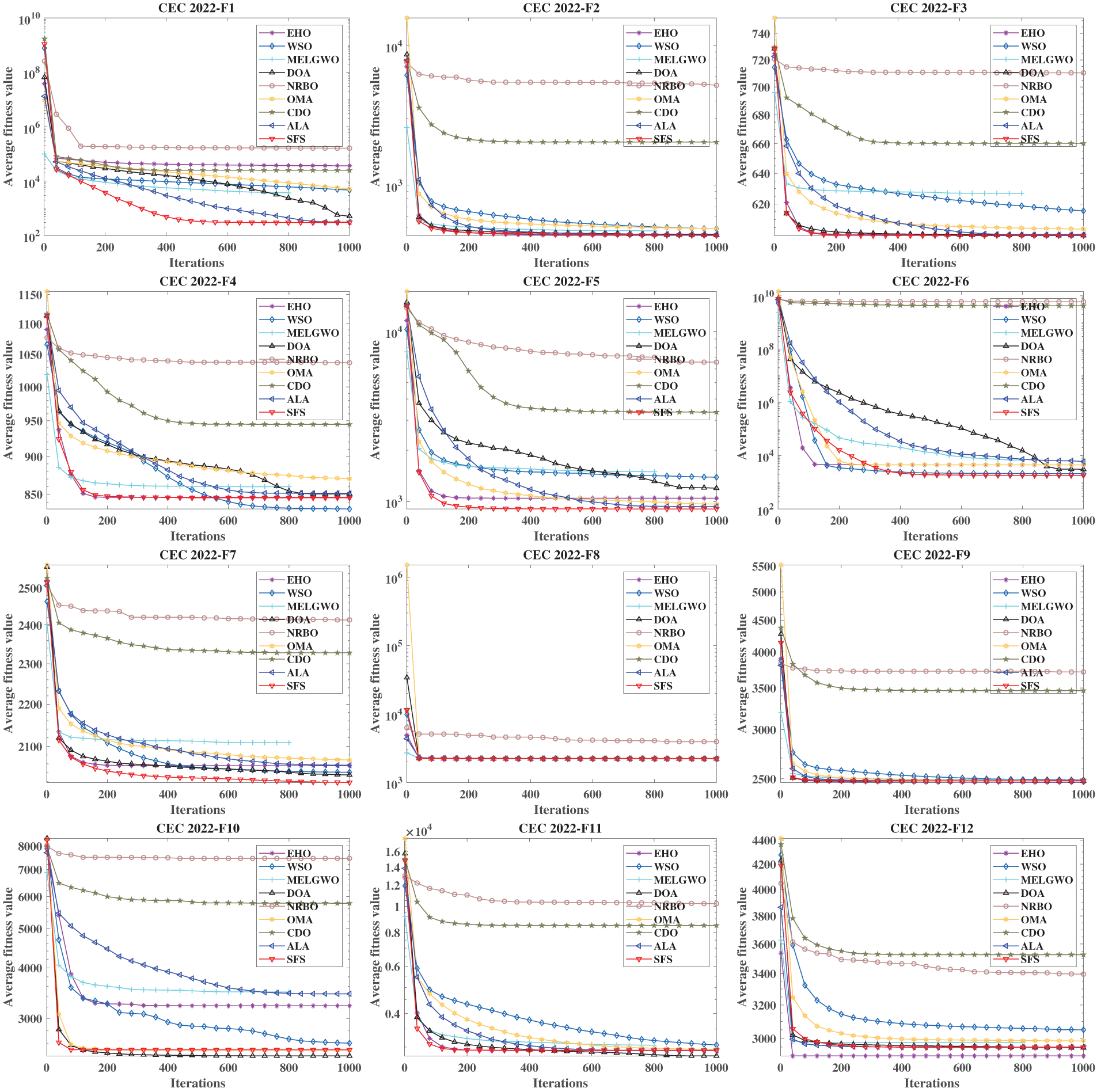
Figure 13: Convergence curves of the nine algorithms for solving CEC’2022
Finally, Fig. 14 depicts the boxplot results of the nine algorithms on the CEC’2022 test set. The central line within each box represents the data median, while the upper and lower edges correspond to the upper and lower quartiles, respectively. The height of each box reflects the variability within the sample data. The lines extending beyond the box indicate the maximum and minimum values in the dataset, with any points outside these lines considered outliers. These boxplots provide an intuitive view of data variability and concentration trends, enabling an assessment of the algorithms’ solution stability. As shown in Fig. 14, the SFS boxplots are generally narrower and positioned lower for most functions, indicating that the SFS algorithm demonstrates strong stability and high solution accuracy.
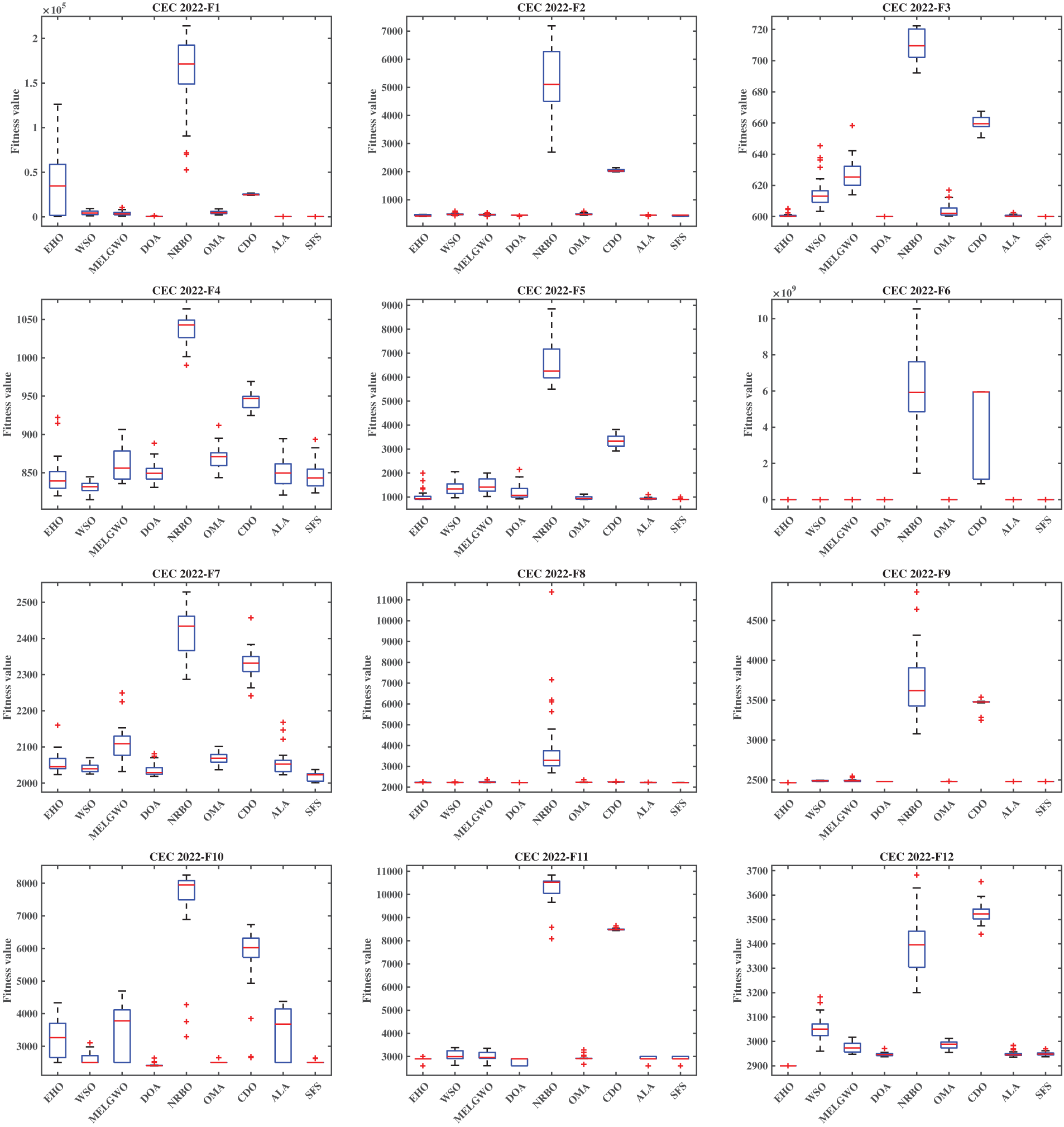
Figure 14: Boxplots of the nine algorithms for solving CEC’2022
While the SFS algorithm has been successfully applied across diverse domains, it faces several challenges and presents significant opportunities for further exploration. Despite its growing popularity and practical applications, critical issues need additional attention. Researchers and scholars are encouraged to invest further effort in addressing these challenges and developing innovative SFS methodologies to enhance its performance and expand its applicability. Drawing from the reviewed literature, Section 8.1 summarizes the key findings of this review paper. In contrast, Section 8.2 highlights critical issues and related topics within the SFS field that require further exploration by the research community. Furthermore, Section 8.3 suggests potential research directions, such as developing new SFS variants and applications.
• Researchers have successfully applied the SFS algorithm across diverse domains. As illustrated in Fig. 15, the distribution of SFS-based studies reveals that power and energy applications and engineering each constitute the largest share at 33%. Other significant application areas include machine learning (8%), medical and bioinformatics (7%), image processing (7%), environmental modeling (6%), and economic and financial applications (6%). This distribution underscores the broad applicability of the SFS algorithm and its potential to effectively address complex optimization challenges in established and emerging research fields.
• Fig. 16 illustrates the distribution of various SFS algorithm variants employed in different optimization challenges. The data reveals that the standard version of SFS remains the most prevalent, accounting for 49% of applications. This indicates that classical SFS remains the preferred choice among researchers and practitioners. Additionally, 27% of applications utilized modified SFS versions, highlighting a strong interest in tailoring the algorithm to address specific problem requirements. Hybrid variants of SFS, which integrate the algorithm with other optimization techniques, were employed in 18% of cases. Lastly, 6% of studies focused on multi-objective versions of SFS, specifically designed to optimize multiple objectives simultaneously. These results underscore the diversity of approaches and preferences within the research community, emphasizing the significant adoption of SFS’s modified, hybridized, and multi-objective variants, reflecting the algorithm’s ongoing evolution in addressing the complexities of various optimization problems.
• Section 4 of this review on SFS variants underscores the pivotal role of various enhancement techniques in advancing SFS performance. These techniques encompass chaotic maps, fitness-distance balance methods, multi-surrogate-assisted approaches, fuzzy logic controllers, penalty-guided methods, binary adaptations, eagle strategies, disruption operators, opposition-based learning, random walk mechanisms, parallel implementations, and multi-strategy integrations. Additionally, SFS has been effectively combined with other meta-heuristic algorithms from evolutionary and swarm intelligence categories. Modified and hybrid approaches tackle key challenges in SFS, such as overcoming local optima, enhancing population diversity, and balancing exploration and exploitation. These advanced SFS variants frequently demonstrate superior performance due to the strategic implementation of these optimization techniques.
• A review of various SFS variants reveals that chaotic maps, fitness-distance balance method, and multi-strategy integrations are among the most frequently employed enhancements. These techniques significantly improve the algorithm’s balance between exploitation and exploration, making it well-suited for complex optimization challenges. Additionally, GWO, WOA, and DE are commonly used as hybridization algorithms. Combining SFS with evolutionary and swarm-based meta-heuristic algorithms leverages the strengths of both algorithms, leading to enhanced convergence rates and solution accuracy, especially in cases requiring advanced search strategies.
• Based on the performance evaluation updates of the SFS algorithm presented in Section 7, it can be concluded that, after a decade of continuous development and refinement, the SFS algorithm still consistently outperforms many recently published meta-heuristic algorithms across various categories. The comparative analysis, using the CEC’2022 benchmark test suite, confirms the superiority of SFS in terms of convergence speed, solution quality, and robustness.
• Despite its advantages, this comprehensive review has several limitations. First, the study is limited to peer-reviewed journal articles, excluding unpublished research, such as preprints, which may contain valuable insights. Second, language restrictions were imposed, excluding studies published in languages other than English, which could introduce language bias. Furthermore, the quality and limitations of the included studies varied, potentially impacting the reliability of the overall conclusions. Additionally, the authors’ subjective decisions influenced the study inclusion and exclusion criteria, as well as data extraction and quality assessments.
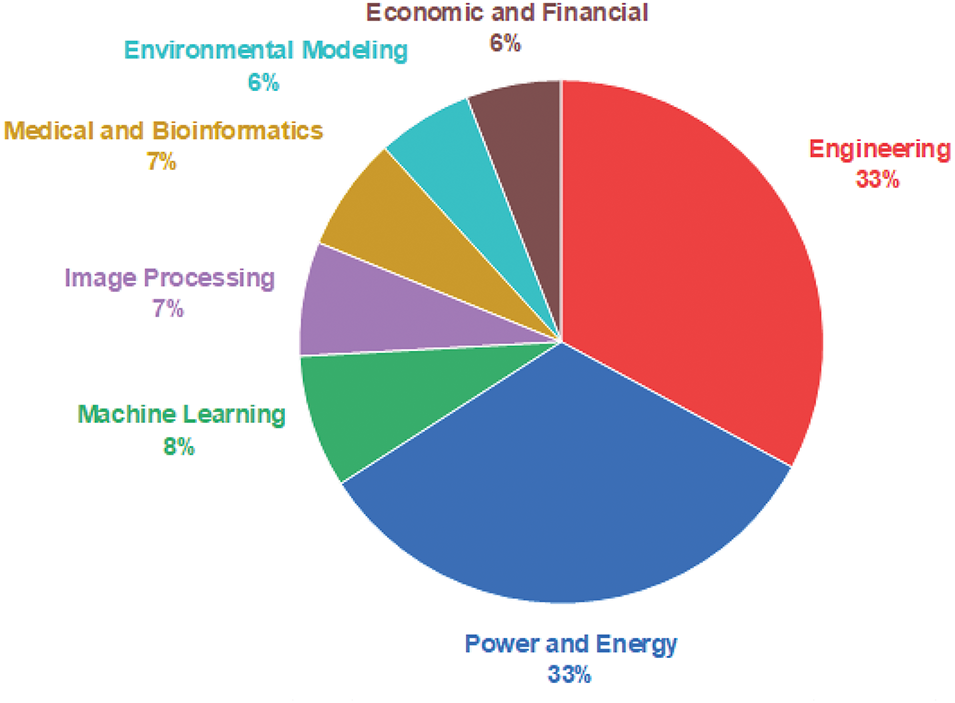
Figure 15: Proportional distribution of SFS applications across different domains
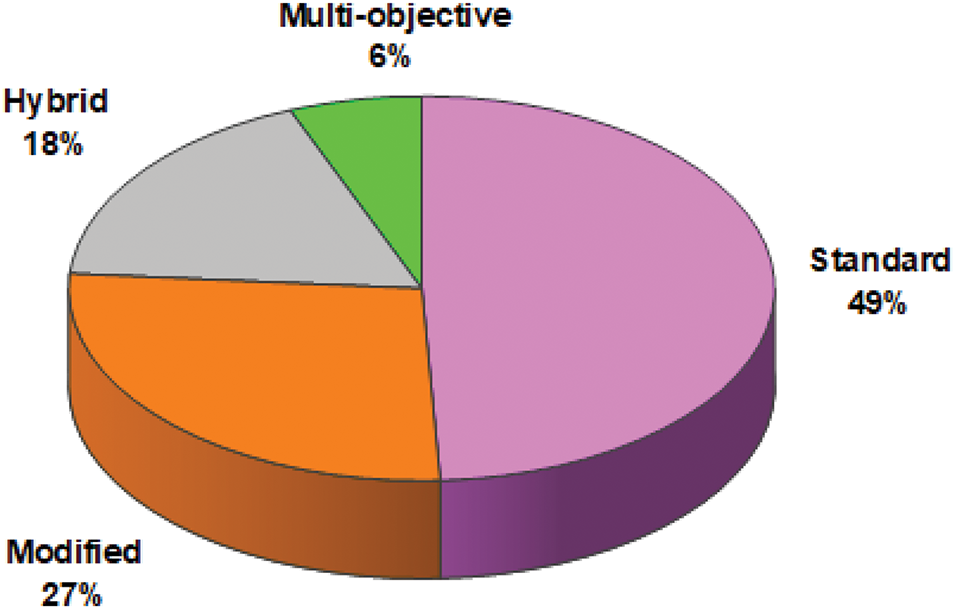
Figure 16: Distribution of SFS variants in various optimization problems
• The literature review reveals a growing trend in the volume of publications and citations related to the SFS algorithm. Future research on SFS is anticipated to increasingly emphasize its applications across diverse domains, shifting the focus away from its foundational principles. However, several fundamental challenges within existing SFS techniques still require in-depth examination. Researchers prioritize two key areas: the automation of techniques and the generalization of SFS-based algorithms. Addressing these areas is crucial for overcoming the challenges faced by optimization methods.
• The majority of SFS algorithm modifications documented in the literature predominantly evaluate their effectiveness and efficiency on relatively small datasets. This approach overlooks the complexities inherent in contemporary big data scenarios. While modified SFS variants have exhibited promising performance on smaller datasets, their ability to effectively handle large-scale datasets remains largely unproven.
• The increasing demand for statistically validated results has garnered significant attention within the knowledge engineering community, primarily driven by the widespread practical applications of optimization algorithms. However, researchers proposing modifications to the SFS often neglect to employ inferential statistics to ascertain significant differences between the modified SFS and the original version. Typically, comparisons are based solely on error rates and convergence times, with the algorithm exhibiting the lowest error and fastest convergence deemed superior. However, estimation errors can substantially influence these observed differences. Therefore, conducting rigorous statistical tests with appropriate confidence intervals is crucial to determine whether the modified SFS outperforms the original SFS accurately. This ensures that observed differences are not merely artifacts of the estimation process.
• A fundamental limitation inherent in the SFS algorithm, shared with other optimization algorithms, is related to the No Free Lunch theorem [248]. This theorem suggests that no single optimization algorithm can consistently outperform all others across all possible optimization problems. Consequently, the convergence behavior of SFS is significantly influenced by the specific characteristics of the search space associated with a particular problem. In scenarios involving unknown or highly complex search spaces, it becomes crucial to adapt SFS or integrate it with complementary techniques to address the optimization task at hand effectively.
• The diffusion process in the SFS algorithm requires
• Achieving an effective balance between exploration and exploitation in the SFS algorithm remains a significant challenge, as no systematic approach has yet been established to manage these components effectively. Despite numerous modifications to SFS, researchers have not proposed a coherent strategy to optimize this balance. While SFS is recognized as a nature-inspired algorithm that attempts to balance exploration and exploitation, there is still substantial potential for improvement in this area.
• While the SFS algorithm is generally less sensitive to parameter settings than many other meta-heuristic algorithms, the challenge of parameter tuning remains. This is primarily due to the user-defined nature of these parameters, as there is no guarantee that specific configurations will yield optimal performance across all problem types. Consequently, the effectiveness of SFS is still dependent on the chosen parameter settings, which may limit its overall efficiency and performance.
• As discussed in Section 4.2, SFS has proven effective in solving various real-world applications. However, significant potential remains for expanding SFS to address a wider range of optimization challenges, including applications in the traveling salesman problem, drone swarm technology, smart homes, work scheduling, robotics, and chemical engineering.
• Recent research suggests that adjusting population size can enhance algorithm performance [249]. A larger population size is generally advantageous in the early stages, promoting extensive search space exploration. Conversely, smaller populations are more effective in later stages, enabling finer tuning near the optimal region. The linear population reduction [250] has shown promising results. Further investigation into adaptive population sizing is essential to assess its potential benefits across various optimization contexts, particularly for single-objective problems.
• The challenges associated with high-dimensionality in optimization problems have raised concerns about the effectiveness of SFS in handling large datasets and computationally intensive tasks. While SFS has shown promise in feature selection, applying it to datasets with tens of thousands of features remains challenging due to the vast search space. Consequently, innovative strategies such as Principal Component Analysis (PCA) [251] are required to effectively minimize the number of selected features while maximizing classification accuracy.
• Over the past decade, numerous innovative meta-heuristic algorithms have been developed. This review reveals that most hybrid versions of SFS have focused on combining SFS with evolutionary and swarm-based approaches. Exploring the hybridization of SFS with other mathematics-based or human-based meta-heuristic algorithms could present promising research opportunities. Additionally, leveraging the potential of a knowledge space to provide multiple information sources could enhance SFS performance when integrated with other meta-heuristic techniques.
• A promising avenue for future research in the SFS algorithm involves investigating alternative population structures. While SFS has demonstrated strong performance, refining its population dynamics could significantly enhance its efficiency. Implementing structured population techniques, such as the island model, hierarchical model, and cellular automata models, which have proven successful in other evolutionary algorithms [252], could potentially improve the diversity and convergence behavior of the SFS algorithm, leading to more robust and practical solutions.
• As discussed in Section 4.3, SFS has been successfully applied to multi-objective optimization problems, demonstrating impressive results. However, many real-world optimization problems involve more than three objective functions. Therefore, extending multi-objective variants of SFS to address many-objective problems effectively represents a challenging and valuable direction for future research.
• Numerous real-world problems are dynamic, involving changes in search and/or objective space variables over time. As a result, optimization algorithms must rapidly and efficiently track moving optima or Pareto fronts in these dynamic environments. Integrating incremental learning techniques or predictive strategies into SFS to address dynamic optimization problems with time-varying objective functions presents a promising avenue for future research.
• In the field of meta-heuristic optimization, there is a notable lack of guidelines for selecting the most suitable optimization algorithm based on problem characteristics. This challenge is particularly relevant for real-world optimization issues. A systematic investigation is needed to understand how decision variables should interact and identify which problem features make SFS applicable to specific objective functions. Unfortunately, such comprehensive studies have not been adequately conducted to assist in selecting appropriate SFS variants based on problem characteristics. The diverse nature of real-world problems within the search space further complicates this challenge.
This review paper presents a comprehensive analysis of SFS-related articles since the algorithm’s inception, systematically synthesizing advancements, trends, and innovations to establish a robust framework for future research. By evaluating publications spanning from 2015 through the latter half of 2024, this study highlights the SFS algorithm’s expansive applicability and versatility across diverse fields, including power and energy, engineering, machine learning, medical and bioinformatics, image processing, environmental modeling, and economics and finance. These findings demonstrate the widespread adoption of SFS, driven by its advantageous characteristics. On the other hand, numerous modifications have been proposed to enhance its performance in addressing diverse optimization problems, including improved initialization strategies, adaptation of control parameters, and exploration of diverse neighborhood topologies. Furthermore, hybridizations with other algorithms and multi-objective implementations have significantly expanded their applicability to complex and conflicting optimization tasks. The performance of SFS was also evaluated against recently published meta-heuristic algorithms using the CEC’2022 benchmark test, where results highlighted its outstanding performance, establishing it as a top-performing algorithm among the eight meta-heuristics evaluated.
Looking ahead, the SFS algorithm is expected to continue evolving through ongoing adaptations and hybridizations designed to enhance its efficiency in addressing optimization problems. This trend is driven by the growing interest among researchers and the algorithm’s demonstrated performance in tackling engineering challenges. The increasing number of SFS adaptations indicates a promising future for the algorithm. This review aims to assist experienced and novice researchers in developing future SFS modifications by providing valuable insights and inspiration.
Acknowledgement: The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (2024/RV/06).
Funding Statement: This study was supported by Prince Sattam bin Abdulaziz University for funding this research work through the project number (2024/RV/06).
Author Contributions: Mohammed A. El-Shorbagy: Writing—review & editing, Writing—original draft, Visualization, Validation, Project administration, Methodology, Investigation, Formal analysis, Conceptualization. Anas Bouaouda: Writing—review & editing, Writing—original draft, Visualization, Methodology, Investigation, Formal analysis, Conceptualization. Laith Abualigah: Writing—review & editing, Writing—original draft, Visualization, Validation. Fatma A. Hashim: Writing—review & editing, Writing—original draft, Visualization, Validation. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: No data is attached to this work.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
1https://www.scopus.com (accessed on 09 February 2025).
References
1. Liu J, Sarker R, Elsayed S, Essam D, Siswanto N. Large-scale evolutionary optimization: a review and comparative study. Swarm Evol Comput. 2024;85(8):101466. doi:10.1016/j.swevo.2023.101466. [Google Scholar] [CrossRef]
2. Velasco L, Guerrero H, Hospitaler A. A literature review and critical analysis of metaheuristics recently developed. Arch Computat Meth Eng. 2024;31(1):125–46. doi:10.1007/s11831-023-09975-0. [Google Scholar] [CrossRef]
3. Juan AA, Keenan P, Martí R, McGarraghy S, Panadero J, Carroll P, et al. A review of the role of heuristics in stochastic optimisation: from metaheuristics to learnheuristics. Ann Operat Res. 2023;320(2):831–61. doi:10.1007/s10479-021-04142-9. [Google Scholar] [CrossRef]
4. Ngoo CM, Goh SL, Sze SN, Sabar NR, Hijazi MHA, Kendall G, et al. A survey of mat-heuristics for combinatorial optimisation problems: variants, trends and opportunities. Appl Soft Comput. 2024;164(3):111947. doi:10.1016/j.asoc.2024.111947. [Google Scholar] [CrossRef]
5. Bouaouda A, Sayouti Y. Hybrid meta-heuristic algorithms for optimal sizing of hybrid renewable energy system: a review of the state-of-the-art. Arch Computat Meth Eng. 2022;29(6):4049–83. doi:10.1007/s11831-022-09730-x. [Google Scholar] [PubMed] [CrossRef]
6. Rajwar K, Deep K, Das S. An exhaustive review of the metaheuristic algorithms for search and optimization: taxonomy, applications, and open challenges. Artif Intell Rev. 2023;56(11):13187–257. doi:10.1007/s10462-023-10470-y. [Google Scholar] [PubMed] [CrossRef]
7. Morales-Castañeda B, Zaldivar D, Cuevas E, Fausto F, Rodríguez A. A better balance in metaheuristic algorithms: does it exist? Swarm Evol Comput. 2020;54(1):100671. doi:10.1016/j.swevo.2020.100671. [Google Scholar] [CrossRef]
8. Li G, Zhang T, Tsai CY, Yao L, Lu Y, Tang J. Review of the metaheuristic algorithms in applications: visual analysis based on bibliometrics (1994–2023). Expert Syst Appl. 2024;255(7):124857. doi:10.1016/j.eswa.2024.124857. [Google Scholar] [CrossRef]
9. Salgotra R, Sharma P, Raju S, gandomi AH. A Contemporary systematic review on meta-heuristic optimization algorithms with Their MATLAB and python code reference. Arch Computat Meth Eng. 2024;31(3):1749–822. doi:10.1007/s11831-023-10030-1. [Google Scholar] [CrossRef]
10. Holland JH. Genetic algorithms. Scient American. 1992;267(1):66–73. doi:10.1038/scientificamerican0792-66. [Google Scholar] [CrossRef]
11. Das S, Suganthan PN. Differential evolution: a survey of the state-of-the-art. IEEE Transact Evolution Computat. 2010;15(1):4–31. doi:10.1109/TEVC.2010.2059031. [Google Scholar] [CrossRef]
12. Simon D. Biogeography-based optimization. IEEE Transact Evolution Computat. 2008;12(6):702–13. doi:10.1109/TEVC.2008.919004. [Google Scholar] [CrossRef]
13. Zhang JH, Xu XH. An efficient evolutionary programming algorithm. Comput Operati Res. 1999;26(7):645–63. doi:10.1016/S0305-0548(98)00084-7. [Google Scholar] [CrossRef]
14. Moscato P. On evolution, search, optimization, genetic algorithms and martial arts: towards memetic algorithms. In: Caltech concurrent computation program, C3P report. Pasadena: California Institute of Technology; 1989. [Google Scholar]
15. Koza JR, Bennett FH, Andre D, Keane MA, Dunlap F. Automated synthesis of analog electrical circuits by means of genetic programming. IEEE Transact Evolution Computat. 1997;1(2):109–28. doi:10.1109/4235.687879. [Google Scholar] [CrossRef]
16. De Castro LN, Von Zuben FJ. The clonal selection algorithm with engineering applications. Proc GECCO. 2000;2000:36–9. [Google Scholar]
17. Bäck T. Evolution strategies: an alternative evolutionary algorithm. In: European Conference on Artificial Evolution; 1995; Springer. p. 1–20. doi:10.1007/3-540-61108-8_27. [Google Scholar] [CrossRef]
18. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks; 1995; IEEE. Vol. 4, p. 1942–8. doi:10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]
19. Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents. IEEE Transact Syst Man Cybernet Part B (cybernet). 1996;26(1):29–41. doi:10.1109/3477.484436. [Google Scholar] [PubMed] [CrossRef]
20. Bouaouda A, Hashim FA, Sayouti Y, Hussien AG. Pied kingfisher optimizer: a new bio-inspired algorithm for solving numerical optimization and industrial engineering problems. Neural Comput Appl. 2024;80(1):1–59. doi:10.1007/s00521-024-09879-5. [Google Scholar] [CrossRef]
21. Makhadmeh SN, Al-Betar MA, Doush IA, Awadallah MA, Kassaymeh S, Mirjalili S, et al. Recent advances in Grey Wolf Optimizer, its versions and applications. IEEE Access. 2023;12(3):22991–3028. doi:10.1109/ACCESS.2023.3304889. [Google Scholar] [CrossRef]
22. Abdollahzadeh B, Khodadadi N, Barshandeh S, Trojovskỳ P, Gharehchopogh FS, El-kenawy ESM, et al. Puma optimizer (POa novel metaheuristic optimization algorithm and its application in machine learning. Cluster Comput. 2024;27(4):5235–83. doi:10.1007/s10586-023-04221-5. [Google Scholar] [CrossRef]
23. Al-Betar MA, Awadallah MA, Braik MS, Makhadmeh S, Doush IA. Elk herd optimizer: a novel nature-inspired metaheuristic algorithm. Artif Intell Rev. 2024;57(3):48. doi:10.1007/s10462-023-10680-4. [Google Scholar] [CrossRef]
24. Fu Y, Liu D, Chen J, He L. Secretary bird optimization algorithm: a new metaheuristic for solving global optimization problems. Artif Intell Rev. 2024;57(5):1–102. doi:10.1007/s10462-024-10729-y. [Google Scholar] [CrossRef]
25. Abdollahzadeh B, Gharehchopogh FS, Khodadadi N, Mirjalili S. Mountain gazelle optimizer: a new nature-inspired metaheuristic algorithm for global optimization problems. Adv Eng Softw. 2022;174(3):103282. doi:10.1016/j.advengsoft.2022.103282. [Google Scholar] [CrossRef]
26. Braik M, Hammouri A, Atwan J, Al-Betar MA, Awadallah MA. White Shark Optimizer: a novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl Based Syst. 2022;243(7):108457. doi:10.1016/j.knosys.2022.108457. [Google Scholar] [CrossRef]
27. Van Laarhoven PJ, Aarts EH, van Laarhoven PJ, Aarts EH. Simulated annealing. Dordrecht: Springer; 1987. doi:10.1007/978-94-015-7744-1_2. [Google Scholar] [CrossRef]
28. Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Inform Sci. 2009;179(13):2232–48. doi:10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]
29. Abdel-Basset M, Mohamed R, Azeem SAA, Jameel M, Abouhawwash M. Kepler optimization algorithm: a new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl Based Syst. 2023;268(3):110454. doi:10.1016/j.knosys.2023.110454. [Google Scholar] [CrossRef]
30. Azizi M, Aickelin U, Khorshidi H, Baghalzadeh Shishehgarkhaneh M. Energy valley optimizer: a novel metaheuristic algorithm for global and engineering optimization. Sci Rep. 2023;13(1):226. doi:10.1038/s41598-022-27344-y. [Google Scholar] [PubMed] [CrossRef]
31. Mahdavi-Meymand A, Zounemat-Kermani M. Homonuclear molecules optimization (HMO) meta-heuristic algorithm. Knowl Based Syst. 2022;258(3):110032. doi:10.1016/j.knosys.2022.110032. [Google Scholar] [CrossRef]
32. Goodarzimehr V, Shojaee S, Hamzehei-Javaran S, Talatahari S. Special relativity search: a novel metaheuristic method based on special relativity physics. Knowl Based Syst. 2022;257(1):109484. doi:10.1016/j.knosys.2022.109484. [Google Scholar] [CrossRef]
33. Abdel-Basset M, El-Shahat D, Jameel M, Abouhawwash M. Young’s double-slit experiment optimizer: a novel metaheuristic optimization algorithm for global and constraint optimization problems. Comput Methods Appl Mech Eng. 2023;403(9):115652. doi:10.1016/j.cma.2022.115652. [Google Scholar] [CrossRef]
34. Deng L, Liu S. Snow ablation optimizer: a novel metaheuristic technique for numerical optimization and engineering design. Expert Syst Appl. 2023;225(1):120069. doi:10.1016/j.eswa.2023.120069. [Google Scholar] [CrossRef]
35. Alatas B. ACROA: artificial chemical reaction optimization algorithm for global optimization. Expert Syst Appl. 2011;38(10):13170–80. doi:10.1016/j.eswa.2011.04.126. [Google Scholar] [CrossRef]
36. Lam AY, Li VO. Chemical reaction optimization: a tutorial. Memetic Comput. 2012;4(1):3–17. doi:10.1007/s12293-012-0075-1. [Google Scholar] [CrossRef]
37. Rao RV, Savsani VJ, Vakharia DP. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput-Aid Des. 2011;43(3):303–15. doi:10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]
38. Ayyarao TS, Ramakrishna N, Elavarasan RM, Polumahanthi N, Rambabu M, Saini G, et al. War strategy optimization algorithm: a new effective metaheuristic algorithm for global optimization. IEEE Access. 2022;10(4):25073–105. doi:10.1109/ACCESS.2022.3153493. [Google Scholar] [CrossRef]
39. Zhang Q, Gao H, Zhan ZH, Li J, Zhang H. Growth Optimizer: a powerful metaheuristic algorithm for solving continuous and discrete global optimization problems. Knowl Based Syst. 2023;261(3):110206. doi:10.1016/j.knosys.2022.110206. [Google Scholar] [CrossRef]
40. Faridmehr I, Nehdi ML, Davoudkhani IF, Poolad A. Mountaineering team-based optimization: a novel human-based metaheuristic algorithm. Mathematics. 2023;11(5):1273. doi:10.3390/math11051273. [Google Scholar] [CrossRef]
41. Mohamed AW, Hadi AA, Mohamed AK. Gaining-sharing knowledge based algorithm for solving optimization problems: a novel nature-inspired algorithm. Int J Mach Learn Cybernet. 2020;11(7):1501–29. doi:10.1007/s13042-019-01053-x. [Google Scholar] [CrossRef]
42. Askari Q, Younas I, Saeed M. Political Optimizer: a novel socio-inspired meta-heuristic for global optimization. Knowl Based Syst. 2020;195(5):105709. doi:10.1016/j.knosys.2020.105709. [Google Scholar] [CrossRef]
43. Verij kazemi M, Fazeli Veysari E. A new optimization algorithm inspired by the quest for the evolution of human society: human felicity algorithm. Expert Syst Appl. 2022;193(1):116468. doi:10.1016/j.eswa.2021.116468. [Google Scholar] [CrossRef]
44. Guan Z, Ren C, Niu J, Wang P, Shang Y. Great Wall Construction Algorithm: a novel meta-heuristic algorithm for engineer problems. Expert Syst Appl. 2023;233(10):120905. doi:10.1016/j.eswa.2023.120905. [Google Scholar] [CrossRef]
45. Al-Betar MA, Alyasseri ZAA, Awadallah MA, Abu Doush I. Coronavirus herd immunity optimizer (CHIO). Neur Comput Applicat. 2021;33(10):5011–42. doi:10.1007/s00521-020-05296-6. [Google Scholar] [PubMed] [CrossRef]
46. Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]
47. Abualigah L, Diabat A, Mirjalili S, Abd Elaziz M, Gandomi AH. The arithmetic optimization algorithm. Comput Meth Appl Mech Eng. 2021;376:113609. doi:10.1016/j.cma.2020.113609. [Google Scholar] [CrossRef]
48. Trojovskỳ P, Dehghani M. Subtraction-average-based optimizer: a new swarm-inspired metaheuristic algorithm for solving optimization problems. Biomimetics. 2023;8(2):149. doi:10.3390/biomimetics8020149. [Google Scholar] [PubMed] [CrossRef]
49. Ahmadianfar I, Heidari AA, Gandomi AH, Chu X, Chen H. RUN beyond the metaphor: an efficient optimization algorithm based on Runge Kutta method. Expert Syst Appl. 2021;181(21):115079. doi:10.1016/j.eswa.2021.115079. [Google Scholar] [CrossRef]
50. Rezaei F, Safavi HR, Abd Elaziz M, Mirjalili S. GMO: geometric mean optimizer for solving engineering problems. Soft Comput. 2023;27(15):10571–606. doi:10.1007/s00500-023-08202-z. [Google Scholar] [CrossRef]
51. Bai J, Li Y, Zheng M, Khatir S, Benaissa B, Abualigah L, et al. A sinh cosh optimizer. Knowl Based Syst. 2023;282(1):111081. doi:10.1016/j.knosys.2023.111081. [Google Scholar] [CrossRef]
52. Zhao S, Zhang T, Cai L, Yang R. Triangulation topology aggregation optimizer: a novel mathematics-based meta-heuristic algorithm for continuous optimization and engineering applications. Expert Syst Appl. 2024;238(1):121744. doi:10.1016/j.eswa.2023.121744. [Google Scholar] [CrossRef]
53. Ahmadianfar I, Bozorg-Haddad O, Chu X. Gradient-based optimizer: a new metaheuristic optimization algorithm. Inform Sci. 2020;540:131–59. doi:10.1016/j.ins.2020.06.037. [Google Scholar] [CrossRef]
54. Salimi H. Stochastic fractal search: a powerful metaheuristic algorithm. Knowl Based Syst. 2015;75(4):1–18. doi:10.1016/j.knosys.2014.07.025. [Google Scholar] [CrossRef]
55. Mandelbrot BB. The fractal geometry of nature. New York: Revised and Enlarged Edition; 1983. [Google Scholar]
56. Falconer KJ. Random fractals. Math Proc Camb Philos Soc. 1986;100(3):559–82. doi:10.1017/S0305004100066299. [Google Scholar] [CrossRef]
57. Cannon J, Floyd W, Parry W. Finite subdivision rules. Confor Geom Dynam American Mathem Soc. 2001;5(8):153–96. doi:10.1090/S1088-4173-01-00055-8. [Google Scholar] [CrossRef]
58. Prusinkiewicz P. Graphical applications of L-systems. Proc Graph Interf. 1986;86:247–53. [Google Scholar]
59. Grassberger P, Procaccia I. Characterization of strange attractors. Phys Rev Lett. 1983;50(5):346. doi:10.1103/PhysRevLett.50.346. [Google Scholar] [CrossRef]
60. Barnsley MF, Demko S. Iterated function systems and the global construction of fractals. Proc Royal Soc London A Mathem Phys Sci. 1985;399(1817):243–75. doi:10.1098/rspa.1985.0057. [Google Scholar] [CrossRef]
61. Witten TA, Sander LM. Diffusion-limited aggregation. Phys Rev B. 1983;27(9):5686. [Google Scholar]
62. Aras S, Gedikli E, Kahraman HT. A novel stochastic fractal search algorithm with fitness-distance balance for global numerical optimization. Swarm Evol Comput. 2021;61(4):100821. doi:10.1016/j.swevo.2020.100821. [Google Scholar] [CrossRef]
63. Xu H, Dong B, Liu X, Lei M, Wu X. Adaptive stochastic fractal search algorithm for multi-objective optimization. Swarm Evol Comput. 2023;83(5):101392. doi:10.1016/j.swevo.2023.101392. [Google Scholar] [CrossRef]
64. Awad NH, Ali MZ, Suganthan PN, Jaser E. A decremental stochastic fractal differential evolution for global numerical optimization. Inform Sci. 2016;372(43):470–91. doi:10.1016/j.ins.2016.08.032. [Google Scholar] [CrossRef]
65. Rahman TA, Tokhi MO. Enhanced stochastic fractal search algorithm with chaos. In: 2016 7th IEEE Control and System Graduate Research Colloquium (ICSGRC); 2016; IEEE. p. 22–7. doi:10.1109/ICSGRC.2016.7813295. [Google Scholar] [CrossRef]
66. Rahman TA. Parametric modelling of twin rotor system using chaotic fractal search algorithm. In: 2016 7th IEEE Control and System Graduate Research Colloquium (ICSGRC); 2016; IEEE. p. 34–9. doi:10.1109/ICSGRC.2016.7813297. [Google Scholar] [CrossRef]
67. Rahman TA, Jalil NA, As’Arry A, Ahmad RR. Chaos-enhanced stochastic fractal search algorithm for global optimization with application to fault diagnosis. IOP Conf Ser: Mat Sci Eng. 2017;210:012060. doi:10.1088/1757-899X/210/1/012060. [Google Scholar] [CrossRef]
68. Rahman TA, As’arry A, Jalil NAA. Active vibration control of a flexible beam structure using chaotic fractal search algorithm. Procedia Eng. 2017;170(6):299–306. doi:10.1016/j.proeng.2017.03.033. [Google Scholar] [CrossRef]
69. Rahman TA, As’ Arry A, Jalil NAA, Ahmad RMKR. Chaotic fractal search algorithm for global optimization with application to control design. In: 2017 IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE); 2017; IEEE. p. 111–6. doi:10.1109/ISCAIE.2017.8074960. [Google Scholar] [CrossRef]
70. Rahman TA, As’arry A, Jalil NA, Kamil R. Dynamic modelling of a flexible beam structure using feedforward neural networks for active vibration control. Int J Automot Mech Eng. 2019;16(1):6263–80. doi:10.15282/ijame.16.1.2019.13.0475. [Google Scholar] [CrossRef]
71. Rahman TA, Rezali KAM, Jalil NA, As’arry A, Kamil R. Training feedforward neural networks for structural health monitoring of an aircraft structure. J Phy: Conf Ser. 2019;1262:012031. doi:10.1088/1742-6596/1262/1/012031 IOP Publishing. [Google Scholar] [CrossRef]
72. Rahman TA, Rezali K, As’arry A, Jalil N. Biodynamic modelling of hand for glove transmissibility prediction using artificial neural networks. J Phy: Conf Ser. 2019;1262:012032. doi:10.1088/1742-6596/1262/1/012032 IOP Publishing. [Google Scholar] [CrossRef]
73. Çelik E. Improved stochastic fractal search algorithm and modified cost function for automatic generation control of interconnected electric power systems. Eng Appl Artif Intell. 2020;88(1):103407. doi:10.1016/j.engappai.2019.103407. [Google Scholar] [CrossRef]
74. Bingöl O, Güvenç U, Duman S, Paçaci S. Stochastic fractal search with chaos. In: 2017 International Artificial Intelligence and Data Processing Symposium (IDAP); 2017; IEEE. p. 1–6. doi:10.1109/IDAP.2017.8090231. [Google Scholar] [CrossRef]
75. Nguyen TP, Tran TT, Vo DN. Improved stochastic fractal search algorithm with chaos for optimal determination of location, size, and quantity of distributed generators in distribution systems. Neural Comput Appl. 2019;31(11):7707–32. doi:10.1007/s00521-018-3603-1. [Google Scholar] [CrossRef]
76. Tran The T, Vo Ngoc D, Tran Anh N. Distribution network reconfiguration for power loss reduction and voltage profile improvement using chaotic stochastic fractal search algorithm. Complexity. 2020;2020(1):2353901. doi:10.1155/2020/2353901. [Google Scholar] [CrossRef]
77. Duong TL, Nguyen PT, Vo ND, Le MP. A newly effective method to maximize power loss reduction in distribution networks with highly penetrated distributed generations. Ain Shams Eng J. 2021;12(2):1787–808. doi:10.1016/j.asej.2020.11.003. [Google Scholar] [CrossRef]
78. Dalcali A, Özbay H, Duman S. Prediction of electricity energy consumption including COVID-19 precautions using the hybrid MLR-FFANN optimized with the stochastic fractal search with fitness distance balance algorithm. Concurr Comput. 2022;34(15):e6947. doi:10.1002/cpe.6947. [Google Scholar] [PubMed] [CrossRef]
79. Ramezani Dobani E, Juybari MN, Abouei Ardakan M. System reliability-redundancy optimization with cold-standby strategy by fitness-distance balance stochastic fractal search algorithm. J Statist Computat Simulat. 2022;92(10):2156–83. doi:10.1080/00949655.2021.2022151. [Google Scholar] [CrossRef]
80. Duman S, Kahraman HT, Kati M. Economical operation of modern power grids incorporating uncertainties of renewable energy sources and load demand using the adaptive fitness-distance balance-based stochastic fractal search algorithm. Eng Appl Artif Intell. 2023;117(3):105501. doi:10.1016/j.engappai.2022.105501. [Google Scholar] [CrossRef]
81. Bakır H. Comparative performance analysis of metaheuristic search algorithms in parameter extraction for various solar cell models. Environ Chall. 2023;11(2):100720. doi:10.1016/j.envc.2023.100720. [Google Scholar] [CrossRef]
82. Bakır H, Guvenc U, Duman S, Kahraman HT. Optimal power flow for hybrid AC/DC electrical networks configured with VSC-MTDC transmission lines and renewable energy sources. IEEE Syst J. 2023;17(3):3938–49. doi:10.1109/JSYST.2023.3248658. [Google Scholar] [CrossRef]
83. Kahraman HT, Hassan MH, Katı M, Tostado-Véliz M, Duman S, Kamel S. Dynamic-fitness-distance-balance stochastic fractal search (dFDB-SFS algorithman effective metaheuristic for global optimization and accurate photovoltaic modeling. Soft Comput. 2024;28(9):6447–74. doi:10.1007/s00500-023-09505-x. [Google Scholar] [CrossRef]
84. Nguyen TT, Vo DN, Van Tran H, Van Dai L. Optimal dispatch of reactive power using modified stochastic fractal search algorithm. Complexity. 2019;2019(1):4670820. doi:10.1155/2019/4670820. [Google Scholar] [CrossRef]
85. Pham LH, Duong MQ, Phan VD, Nguyen TT, Nguyen HN. A high-performance stochastic fractal search algorithm for optimal generation dispatch problem. Energies. 2019;12(9):1796. doi:10.3390/en12091796. [Google Scholar] [CrossRef]
86. Nguyen TT, Nguyen TT, Duong MQ, Doan AT. Optimal operation of transmission power networks by using improved stochastic fractal search algorithm. Neural Comput Applicat. 2020;32(13):9129–64. doi:10.1007/s00521-019-04425-0. [Google Scholar] [CrossRef]
87. Van Tran H, Van Pham T, Pham LH, Le NT, Nguyen TT. Finding optimal reactive power dispatch solutions by using a novel improved stochastic fractal search optimization algorithm. TELKOMNIKA (Telecommun Comput Elect Cont). 2019;17(5):2517–26. doi:10.12928/telkomnika.v17i5.10767. [Google Scholar] [CrossRef]
88. Xu S, Qiu H. A modified stochastic fractal search algorithm for parameter estimation of solar cells and PV modules. Energy Rep. 2022;8(11):1853–66. doi:10.1016/j.egyr.2022.01.008. [Google Scholar] [CrossRef]
89. Cheng X, Yu Y, Hu W. Multi-surrogate-assisted stochastic fractal search algorithm for high-dimensional expensive problems. Inf Sci. 2023;640(24):119035. doi:10.1016/j.ins.2023.119035. [Google Scholar] [CrossRef]
90. Cheng X, Hu W, Yu Y, Rahmani A. Multi-surrogate-assisted stochastic fractal search based on scale-free network for high-dimensional expensive optimization. Expert Syst Appl. 2024;249(5439):123517. doi:10.1016/j.eswa.2024.123517. [Google Scholar] [CrossRef]
91. Lagunes ML, Castillo O, Valdez F, Soria J. Stochastic fractal dynamic search for the optimization of CEC’2017 benchmark functions. In: International Conference on Hybrid Intelligent Systems; 2020; Springer. p. 349–57. doi:10.1007/978-3-030-73050-5_35. [Google Scholar] [CrossRef]
92. Lagunes ML, Castillo O, Valdez F, Soria J, Melin P. A new approach for dynamic stochastic fractal search with fuzzy logic for parameter adaptation. Fract Fractio. 2021;5(2):33. doi:10.3390/fractalfract5020033. [Google Scholar] [CrossRef]
93. Mellal MA, Zio E. A penalty guided stochastic fractal search approach for system reliability optimization. Reliab Eng Syst Saf. 2016;152(3):213–27. doi:10.1016/j.ress.2016.03.019. [Google Scholar] [CrossRef]
94. Mellal MA, Zio E. System reliability-redundancy allocation by evolutionary computation. In: 2017 2nd International Conference on System Reliability and Safety (ICSRS); 2017; IEEE. p. 15–9. doi:10.1109/ICSRS.2017.8272790. [Google Scholar] [CrossRef]
95. Hosny KM, Elaziz M, Selim I, Darwish MM. Classification of galaxy color images using quaternion polar complex exponential transform and binary Stochastic Fractal Search. Astron Comput. 2020;31(1):100383. doi:10.1016/j.ascom.2020.100383. [Google Scholar] [CrossRef]
96. Das A, Namtirtha A, Dutta A. Fuzzy clustering of Acute Lymphoblastic Leukemia images assisted by Eagle strategy and morphological reconstruction. Knowl Based Syst. 2022;239(3):108008. doi:10.1016/j.knosys.2021.108008. [Google Scholar] [CrossRef]
97. Xu Z, Zhou J, Yang Y, Qin Z. Improved stochastic fractal search algorithm for joint optimal operation of cascade hydropower stations. In: Sustainable Development of Water and Environment: Proceedings of the ICSDWE2022; 2022; Springer. p. 11–26. doi:10.1007/978-3-031-07500-1_2. [Google Scholar] [CrossRef]
98. Gonzalez F, Soto R, Crawford B. Stochastic fractal search algorithm improved with opposition-based learning for solving the substitution box design problem. Mathematics. 2022;10(13):2172. doi:10.3390/math10132172. [Google Scholar] [CrossRef]
99. Pham LH, Nguyen TT, Pham LD, Nguyen NH. Stochastic fractal search based method for economic load dispatch. TELKOMNIKA (Telecommun Comput Elect Cont). 2019;17(5):2535–46. doi:10.12928/telkomnika.v17i5.12539. [Google Scholar] [CrossRef]
100. Najmi A, Abouei Ardakan M, Javid Y. Optimization of reliability redundancy allocation problem with component mixing and strategy selection for subsystems. J Statist Comput Simulat. 2021;91(10):1935–59. doi:10.1080/00949655.2021.1879080. [Google Scholar] [CrossRef]
101. Lin J, Wang ZJ. Parameter identification for fractional-order chaotic systems using a hybrid stochastic fractal search algorithm. Nonlinear Dynamics. 2017;90(2):1243–55. doi:10.1007/s11071-017-3723-7. [Google Scholar] [CrossRef]
102. Pang B, Low KH, Lv C. Adaptive conflict resolution for multi-UAV 4D routes optimization using stochastic fractal search algorithm. Transport Res Part C: Emerg Technol. 2022;139(1):103666. doi:10.1016/j.trc.2022.103666. [Google Scholar] [CrossRef]
103. Zhou C, Sun C, Wang B, Wang X. An improved stochastic fractal search algorithm for 3D protein structure prediction. J Molecu Model. 2018;24(6):1–11. doi:10.1007/s00894-018-3644-5. [Google Scholar] [PubMed] [CrossRef]
104. Mosbah H, El-Hawary M. Power system static state estimation using modified stochastic fractal search technique. In: 2018 IEEE Canadian Conference on Electrical & Computer Engineering (CCECE); 2018; IEEE. p. 1–4. doi:10.1109/CCECE.2018.8447826. [Google Scholar] [CrossRef]
105. Lin J, Wang ZJ. Multi-area economic dispatch using an improved stochastic fractal search algorithm. Energy. 2019;166(1):47–58. doi:10.1016/j.energy.2018.10.065. [Google Scholar] [CrossRef]
106. Chen X, Yue H, Yu K. Perturbed stochastic fractal search for solar PV parameter estimation. Energy. 2019;189:116247. doi:10.1016/j.energy.2019.116247. [Google Scholar] [CrossRef]
107. Nguyen PT, Nguyen Anh T, Vo Ngoc D, Le Thanh T. A cost-benefit analysis of capacitor allocation problem in radial distribution networks using an improved stochastic fractal search algorithm. Complexity. 2020;2020(1):8811674. doi:10.1155/2020/8811674. [Google Scholar] [CrossRef]
108. Kien LC, Nguyen TT, Dinh BH, Nguyen TT. Optimal reactive power generation for radial distribution systems using a highly effective proposed algorithm. Complexity. 2021;2021(1):2486531. doi:10.1155/2021/2486531. [Google Scholar] [CrossRef]
109. Huynh DC, Dunnigan MW, Barbalata C. Estimation for model parameters and maximum power points of photovoltaic modules using stochastic fractal search algorithms. IEEE Access. 2022;10(2):104408–28. doi:10.1109/ACCESS.2022.3210687. [Google Scholar] [CrossRef]
110. Alkayem NF, Shen L, Asteris PG, Sokol M, Xin Z, Cao M. A new self-adaptive quasi-oppositional stochastic fractal search for the inverse problem of structural damage assessment. Alexandria Eng J. 2022;61(3):1922–36. doi:10.1016/j.aej.2021.06.094. [Google Scholar] [CrossRef]
111. Isen E, Duman S. Improved stochastic fractal search algorithm involving design operators for solving parameter extraction problems in real-world engineering optimization problems. Appl Energy. 2024;365(1):123297. doi:10.1016/j.apenergy.2024.123297. [Google Scholar] [CrossRef]
112. Awad NH, Ali MZ, Suganthan PN, Jaser E. Differential evolution with stochastic fractal search algorithm for global numerical optimization. In: 2016 IEEE Congress on Evolutionary Computation (CEC); 2016; IEEE. p. 3154–61. doi:10.1109/CEC.2016.7744188. [Google Scholar] [CrossRef]
113. Ashraf Z, Malhotra D, Muhuri PK, Lohani QD. Hybrid biogeography-based optimization for solving vendor managed inventory system. In: 2017 IEEE Congress on Evolutionary Computation (CEC); 2017; IEEE. p. 2598–605. doi:10.1109/CEC.2017.7969621. [Google Scholar] [CrossRef]
114. Sivalingam R, Chinnamuthu S, Dash SS. A hybrid stochastic fractal search and local unimodal sampling based multistage PDF plus (1+PI) controller for automatic generation control of power systems. J Franklin Instit. 2017;354(12):4762–83. doi:10.1016/j.jfranklin.2017.05.038. [Google Scholar] [CrossRef]
115. Mosbah H, El-Hawary M. A Distributed Multiarea State Estimation. In: 2018 IEEE Canadian Conference on Electrical & Computer Engineering (CCECE); 2018; IEEE. p. 1–5. doi:10.1109/CCECE.2018.8447821. [Google Scholar] [CrossRef]
116. Yu RX, Zhu B, Cao M, Zhao X, Wang JW. Research on path planning method of an unmanned vehicle in urban road environments. In: Smart Multimedia: First International Conference, ICSM 2018; 2018 Aug 24–26; Toulon, France: Springer. p. 235–47. [Google Scholar]
117. El-Kenawy E-SM, Eid MM, Saber M, Ibrahim A. MbGWO-SFS: modified binary grey wolf optimizer based on stochastic fractal search for feature selection. IEEE Access. 2020;8:107635–49. doi:10.1109/ACCESS.2020.3001151. [Google Scholar] [CrossRef]
118. Chen H, Xu J, Wu C. Multi-UAV task assignment based on improved Wolf Pack Algorithm. In: Proceedings of the 2020 International Conference on Cyberspace Innovation of Advanced Technologies; 2020. p. 109–15. doi:10.1145/3444370.3444556. [Google Scholar] [CrossRef]
119. S.Alsawadi M, M.El-kenawy ES, Rio M. Advanced guided whale optimization algorithm for feature selection in blazepose action recognition. Intell Automat Soft Comput. 2023;37(3):2767–82. doi:10.32604/iasc.2023.039440. [Google Scholar] [CrossRef]
120. Bharani B, Murtugudde G, Sreenivasa B, Verma A, Al-Yarimi FA, Khan MI, et al. Grey wolf optimization and enhanced stochastic fractal search algorithm for exoplanet detection. Eur Phys J Plus. 2023;138(5):1–11. doi:10.1140/epjp/s13360-023-04024-y. [Google Scholar] [CrossRef]
121. El-Kenawy ESM, Khodadadi N, Khoshnaw A, Mirjalili S, Alhussan AA, Khafaga DS, et al. Advanced dipper-throated meta-heuristic optimization algorithm for digital image watermarking. Appl Sci. 2022;12(20):10642. doi:10.3390/app122010642. [Google Scholar] [CrossRef]
122. El-Kenawy ESM, Ibrahim A, Mirjalili S, Eid MM, Hussein SE. Novel feature selection and voting classifier algorithms for COVID-19 classification in CT images. IEEE Access. 2020;8(1):179317–35. doi:10.1109/ACCESS.2020.3028012. [Google Scholar] [PubMed] [CrossRef]
123. Zhang Q, Wang Z, Heidari AA, Gui W, Shao Q, Chen H, et al. Gaussian barebone salp swarm algorithm with stochastic fractal search for medical image segmentation: a COVID-19 case study. Comput Biol Med. 2021;139(10):104941. doi:10.1016/j.compbiomed.2021.104941. [Google Scholar] [PubMed] [CrossRef]
124. Xu A, Mo L, Wang Q. Research on operation mode of the yalong river cascade reservoirs based on improved stochastic fractal search algorithm. Energies. 2022;15(20):7779. doi:10.3390/en15207779. [Google Scholar] [CrossRef]
125. Salamai AA, Ageeli AA, El-Kenawy E. Forecasting e-commerce adoption based on bidirectional recurrent neural networks. Comput Mater Contin. 2022;70(3):5091–106. doi:10.32604/cmc.2022.021268. [Google Scholar] [CrossRef]
126. Eid MM, Alassery F, Ibrahim A, Saber M. Metaheuristic optimization algorithm for signals classification of electroencephalography channels. Comput Mater Contin. 2022;71(3):4627–41. doi:10.32604/cmc.2022.024043. [Google Scholar] [CrossRef]
127. Saini R, Parmar G, Gupta R, Sikander A. An enhanced tuning of PID controller via hybrid stochastic fractal search algorithm for control of DC motor. In: Advanced Energy and Control Systems: Select Proceedings of 3rd International Conference, ESDA 2020; 2022; Springer. p. 185–94. doi:10.1007/978-981-16-7274-3_16. [Google Scholar] [CrossRef]
128. Eid MM, Alassery F, Ibrahim A, Aloyaydi BA, Ali HA, El-Mashad SY. Hybrid sine cosine and stochastic fractal search for hemoglobin estimation. Comput Mater Contin. 2022;72(2):2467–82. doi:10.32604/cmc.2022.025220. [Google Scholar] [CrossRef]
129. Cheraghalipour A, Roghanian E. A bi-level model for a closed-loop agricultural supply chain considering biogas and compost. Environ, Develop Sustain. 2022;6(3):1–47. doi:10.1007/s10668-022-02397-1. [Google Scholar] [CrossRef]
130. Abdelhamid AA, El-Kenawy ESM, Alotaibi B, Amer GM, Abdelkader MY, Ibrahim A, et al. Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm. IEEE Access. 2022;10:49265–84. doi:10.1109/ACCESS.2022.3172954. [Google Scholar] [CrossRef]
131. Abdel-Nabi H, Ali M, Daoud M, Alazrai R, Awajan A, Reynolds R, et al. An enhanced multi-phase stochastic differential evolution framework for numerical optimization. In: 2022 IEEE Congress on Evolutionary Computation (CEC); 2022; IEEE. p. 1–8. doi:10.1109/CEC55065.2022.9870438. [Google Scholar] [CrossRef]
132. Saini R, Parmar G, Gupta R. An enhanced hybrid stochastic fractal search FOPID for speed control of DC motor. In: Fractional order systems and applications in engineering. USA: Academic Press; 2023. p. 51–67. doi:10.1016/B978-0-32-390953-2.00011-6. [Google Scholar] [CrossRef]
133. El-kenawy ESM, Ibrahim A, Bailek N, Bouchouicha K, Hassan MA, Jamei M, et al. Sunshine duration measurements and predictions in Saharan Algeria region: an improved ensemble learning approach. Theor Appl Climatol. 2022;147(3–4):1–17. doi:10.1007/s00704-021-03843-2. [Google Scholar] [CrossRef]
134. Tarek Z, Shams MY, Elshewey AM, El-kenawy ESM, Ibrahim A, Abdelhamid AA, et al. Wind power prediction based on machine learning and deep learning models. Comput Mater Contin. 2023;75(1):715–32. doi:10.32604/cmc.2023.032533. [Google Scholar] [CrossRef]
135. Zhang M, Wang JS, Liu Y, Wang M, Li XD, Guo FJ. Feature selection method based on stochastic fractal search henry gas solubility optimization algorithm. J Intell Fuzzy Syst. 2023;44(3):5377–406. doi:10.3233/JIFS-221036. [Google Scholar] [CrossRef]
136. Khafaga DS, El-kenawy ESM, Alhussan AA, Eid MM. Forecasting energy consumption using a novel hybrid dipper throated optimization and stochastic fractal search algorithm. Intell Automat Soft Comput. 2023;37(2):2117–32. doi:10.32604/iasc.2023.038811. [Google Scholar] [CrossRef]
137. Abdel-Nabi H, Ali MZ, Awajan A, Alazrai R, Daoud MI, Suganthan PN, et al. 3-sCHSL: three-stage cyclic hybrid SFS and L-SHADE algorithm for single objective optimization. In: 2023 IEEE Congress on Evolutionary Computation (CEC); 2023; IEEE. p. 1–8. doi:10.1109/CEC53210.2023.10254143. [Google Scholar] [CrossRef]
138. Rahman TA, Chek LW. Chaotic SFS-GTO optimizer algorithm for flowshop scheduling problems. In: 2023 IEEE Industrial Electronics and Applications Conference (IEACon); 2023; IEEE. p. 1–6. doi:10.1109/IEACon57683.2023.10370112. [Google Scholar] [CrossRef]
139. Abdel-Nabi H, Ali MZ, Awajan A, Alazrai R, Daoud MI, Suganthan PN. An iterative cyclic tri-strategy hybrid stochastic fractal with adaptive differential algorithm for global numerical optimization. Inform Sci. 2023;628:92–133. doi:10.1016/j.ins.2023.01.065. [Google Scholar] [CrossRef]
140. Zhang Q, Sheng J, Zhang Q, Wang L, Yang Z, Xin Y. Enhanced Harris hawks optimization-based fuzzy k-nearest neighbor algorithm for diagnosis of Alzheimer’s disease. Comput Biol Med. 2023;165(1):107392. doi:10.1016/j.compbiomed.2023.107392. [Google Scholar] [PubMed] [CrossRef]
141. Zaki AM, Abdelhamid AA, Ibrahim A, Eid MM, El-Kenawy ESM. Enhancing K-nearest neighbors algorithm in wireless sensor networks through stochastic fractal search and particle swarm optimization. J Cybersecur Inform Manag. 2024;13(1):76–84. doi:10.54216/JCIM.130108. [Google Scholar] [CrossRef]
142. Xu C, Su S, Wang Y. An improved stochastic fractal search based on entropy multi-trust fusion model for IoT-enabled WSNs clustering. IEEE Sens J. 2023;23:29694–704. doi:10.1109/JSEN.2023.3324013. [Google Scholar] [CrossRef]
143. Alsawadi MS, Sandoval-Gastelum M, Danish I, Rio M. BlazePose-Based action recognition with feature selection using stochastic fractal search guided whale optimization. In: 2023 International Conference on Control, Automation and Diagnosis (ICCAD); 2023; IEEE. p. 1–5. doi:10.1109/ICCAD57653.2023.10152320. [Google Scholar] [CrossRef]
144. Bandong S, Miransyahputra MR, Setiaji Y, Nazaruddin YY, Siregar PI, Joelianto E. Optimization of gantry crane PID controller based on PSO, SFS, and FPA. In: 2021 60th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE); 2021; IEEE. p. 338–43. doi:10.1109/SICE54164.2021.00027. [Google Scholar] [CrossRef]
145. Alhussan AA, Khafaga DS, El-kenawy ESM, Eid MM, Abdelhamid AA. Hybrid waterwheel plant and stochastic fractal search optimization for robust diabetes classification. AIP Adv. 2024;14(6):S73. doi:10.1063/5.0208862. [Google Scholar] [CrossRef]
146. Dubey HM, Pandit M, Panigrahi BK, Tyagi T. Multi-objective Power dispatch using Stochastic fractal search algorithm and Topsis. In: Swarm, Evolutionary, and Memetic Computing: 6th International Conference, SEMCCO 2015; 2015 Dec 18–19; Hyderabad, India: Springer. p. 154–66. [Google Scholar]
147. Lobato FS, Libotte GB, Platt GM. Identification of an epidemiological model to simulate the COVID-19 epidemic using robust multiobjective optimization and stochastic fractal search. Comput Math Methods Med. 2020;2020(1):9214159. doi:10.1155/2020/9214159. [Google Scholar] [PubMed] [CrossRef]
148. Khalilpourazari S, Naderi B, Khalilpourazary S. Multi-objective stochastic fractal search: a powerful algorithm for solving complex multi-objective optimization problems. Soft Comput. 2020;24(4):3037–66. doi:10.1007/s00500-019-04080-6. [Google Scholar] [CrossRef]
149. Khalilpourazari S, Khalilpourazary S. A Robust Stochastic Fractal Search approach for optimization of the surface grinding process. Swarm Evolut Computat. 2018;38(1–3):173–86. doi:10.1016/j.swevo.2017.07.008. [Google Scholar] [CrossRef]
150. Tran The T, Truong BH, Dang Tuan K, Vo Ngoc D. A nondominated sorting stochastic fractal search algorithm for multiobjective distribution network reconfiguration with distributed generations. Math Probl Eng. 2021;2021(1):6638559. doi:10.1155/2021/6638559. [Google Scholar] [CrossRef]
151. Ghasemi P, Goodarzian F, Muñuzuri J, Abraham A. A cooperative game theory approach for location-routing-inventory decisions in humanitarian relief chain incorporating stochastic planning. Appl Mathem Modell. 2022;104(1):750–81. doi:10.1016/j.apm.2021.12.023. [Google Scholar] [CrossRef]
152. Xu H, Dong B, Liu X, Wu X. Deep neural network architecture search via decomposition-based multi-objective stochastic fractal search. Intell Automat Soft Comput. 2023;38(2):185–202. doi:10.32604/iasc.2023.041177. [Google Scholar] [CrossRef]
153. Hajghani M, Forghani MA, Heidari A, Khalilzadeh M, Kebriyaii O. A two-echelon location routing problem considering sustainability and hybrid open and closed routes under uncertainty. Heliyon. 2023;9(3):e14258. doi:10.1016/j.heliyon.2023.e14258. [Google Scholar] [PubMed] [CrossRef]
154. Darvish Falehi A, Torkaman H. New staircase sinusoidal voltage synthesizer and optimal interval type-2 fuzzy controller for dynamic voltage restorer to compensate voltage disturbances. Artif Intell Rev. 2023;56(Suppl 2):2125–50. doi:10.1007/s10462-023-10572-7. [Google Scholar] [CrossRef]
155. Mosbah H, El-Hawary M. Power system tracking state estimation based on stochastic fractal search technique under sudden load changing conditions. In: 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE); 2016; IEEE. p. 1–6. doi:10.1109/CCECE.2016.7726788. [Google Scholar] [CrossRef]
156. Saha D, Saikia L. Performance of FACTS and energy storage devices in a multi area wind-hydro-thermal system employed with SFS optimized I-PDF controller. J Renew Sustain Energy. 2017;9(2):434. doi:10.1063/1.4980160. [Google Scholar] [CrossRef]
157. El-Fergany AA, Hasanien HM. Optimized settings of directional overcurrent relays in meshed power networks using stochastic fractal search algorithm. Int Trans Electr Energy Syst. 2017;27(11):e2395. doi:10.1002/etep.2395. [Google Scholar] [CrossRef]
158. Saha D, Saikia L. Impact of phase-locked loop on system dynamics of a CCGT incorporated diverse source system employed with AC/DC interconnection. J Renew Sustain Energy. 2017;9(4):318. doi:10.1063/1.5000254. [Google Scholar] [CrossRef]
159. Khadanga RK, Kumar V, Kumar A, Padhy S. Robust frequency control in an islanded microgrid: a novel stochastic fractal search algorithm approach. In: 2017 14th IEEE India Council International Conference (INDICON); 2017; IEEE. p. 1–6. doi:10.1109/INDICON.2017.8487578. [Google Scholar] [CrossRef]
160. Saha D, Saikia LC. Automatic generation control of a multi-area CCGT-thermal power system using stochastic search optimised integral minus proportional derivative controller under restructured environment. IET Generat Transm Distrib. 2017;11(15):3801–13. doi:10.1049/iet-gtd.2016.1737. [Google Scholar] [CrossRef]
161. Saha D, Saikia L, Rajbongshi R. Impact of redox flow battery and capacitive energy storage devices in performance enhancement of restructured AGC of a CCGT incorporated hydro-thermal system. In: 2017 7th International Conference on Power Systems (ICPS); 2017; IEEE. p. 127–32. doi:10.1109/ICPES.2017.8387280. [Google Scholar] [CrossRef]
162. Çelik E. Incorporation of stochastic fractal search algorithm into efficient design of PID controller for an automatic voltage regulator system. Neural Comput Applicat. 2018;30(6):1991–2002. doi:10.1007/s00521-017-3335-7. [Google Scholar] [CrossRef]
163. Nguyen TP, Vo DN. A novel stochastic fractal search algorithm for optimal allocation of distributed generators in radial distribution systems. Appl Soft Comput. 2018;70(3):773–96. doi:10.1016/j.asoc.2018.06.020. [Google Scholar] [CrossRef]
164. Saha D, Saikia LC. Automatic generation control of an interconnected CCGT-thermal system using stochastic fractal search optimized classical controllers. Int Trans Electr Energy Syst. 2018;28(5):e2533. doi:10.1002/etep.2533. [Google Scholar] [CrossRef]
165. Mosbah H, El-Hawary ME. Optimized neural network parameters using stochastic fractal technique to compensate Kalman filter for power system-tracking-state estimation. IEEE Transact Neural Netw Learn Syst. 2018;30(2):379–88. doi:10.1109/TNNLS.2018.2839101. [Google Scholar] [PubMed] [CrossRef]
166. Saha D, Saikia LC, Talukdar BK. Classical controller based AGC of a hybrid multisource power system incorporating distributed generation. In: AIP Conference Proceedings; 2019; AIP Publishing. Vol. 2091. doi:10.1063/1.5096493. [Google Scholar] [CrossRef]
167. Duong TL, Duong MQ, Phan VD, Nguyen TT. Optimal reactive power flow for large-scale power systems using an effective metaheuristic algorithm. J Electr Comput Eng. 2020;2020(1):6382507. doi:10.1155/2020/6382507. [Google Scholar] [CrossRef]
168. Saini R, Parmar G, Gupta R, Sikander A. SFS/PI approach for AGC of two area interconnected thermal power system. In: Energy Systems, Drives and Automations: Proceedings of ESDA 2019; 2020; Springer. p. 91–102. doi:10.1007/978-981-15-5089-8_9. [Google Scholar] [CrossRef]
169. Alomoush MI. Optimal combined heat and power economic dispatch using stochastic fractal search algorithm. J Modern Pow Syst Clean Energy. 2020;8(2):276–86. doi:10.35833/MPCE.2018.000753. [Google Scholar] [CrossRef]
170. Tran TT, Truong KH, Vo DN. Stochastic fractal search algorithm for reconfiguration of distribution networks with distributed generations. Ain Shams Eng J. 2020;11(2):389–407. doi:10.1016/j.asej.2019.08.015. [Google Scholar] [CrossRef]
171. Rezk H, Fathy A. Stochastic fractal search optimization algorithm based global MPPT for triple-junction photovoltaic solar system. Energies. 2020;13(18):4971. doi:10.3390/en13184971. [Google Scholar] [CrossRef]
172. Nguyen TT, Dinh BH, Pham TD, Nguyen TT. Active power loss reduction for radial distribution systems by placing capacitors and PV systems with geography location constraints. Sustainability. 2020;12(18):7806. doi:10.3390/su12187806. [Google Scholar] [CrossRef]
173. Alomoush MI. Application of the stochastic fractal search algorithm and compromise programming to combined heat and power economic-emission dispatch. Eng Optimizat. 2020;52(11):1992–2010. doi:10.1080/0305215X.2019.1690650. [Google Scholar] [CrossRef]
174. Rezk H, Babu TS, Al-Dhaifallah M, Ziedan HA. A robust parameter estimation approach based on stochastic fractal search optimization algorithm applied to solar PV parameters. Energy Rep. 2021;7(5):620–40. doi:10.1016/j.egyr.2021.01.024. [Google Scholar] [CrossRef]
175. Elrachid B, Hammoud R, Oussama B, Meriem H. Parameter tuning of power systems stabilizer using stochastic fractal search optimisation. In: 2022 19th International Multi-Conference on Systems, Signals & Devices (SSD); 2022; IEEE. p. 1853–7. doi:10.1109/SSD54932.2022.9955763. [Google Scholar] [CrossRef]
176. Van Hong TP, Tuan KD, Ngoc DV. Applied stochastic fractal search algorithm to solve economic emission dispatch problems. In: 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST); 2022; IEEE. p. 1–5. doi:10.1109/GECOST55694.2022.10010664. [Google Scholar] [CrossRef]
177. Saeed MA, Ibrahim A, El-Kenawy ESM, Abdelhamid AA, El-Said M, Abualigah L, et al. Forecasting wind power based on an improved al-Biruni Earth radius metaheuristic optimization algorithm. Front Energy Res. 2023;11:1220085. doi:10.3389/fenrg.2023.1220085. [Google Scholar] [CrossRef]
178. Darvish Falehi A, Torkaman H. Optimal fractional order interval type-2 fuzzy controller for upside-down asymmetric multilevel inverter based dynamic voltage restorer to accurately compensate faulty network voltage. J Ambient Intell Human Comput. 2023;14(12):16683–701. doi:10.1007/s12652-023-04673-y. [Google Scholar] [CrossRef]
179. Van Hong TP, Khanh DT. Applying stochastic fractal search algorithm for solving non-convex economic dispatch problems. In: 2023 International Conference on Smart-Green Technology in Electrical and Information Systems (ICSGTEIS); 2023; IEEE. p. 190–5. doi:10.1109/ICSGTEIS60500.2023.10424332. [Google Scholar] [CrossRef]
180. Huynh DC, Ho LD, Dunnigan MW. Modelling and determining parameters of a solar photovoltaic cell based on voltage and current measurements. Convergence. 2024;3:23. [Google Scholar]
181. Kumar PS, Kanimozhi T. A smart and effective energy management system for shipboard applications using a stochastic fractal search network (SFSN) controlling model. Int J Intell Syst Applicat Eng. 2024;12(2s):529–39. [Google Scholar]
182. Bacha B, Ghodbane H, Dahmani H, Betka A, Toumi A, Chouder A. Optimal sizing of a hybrid microgrid system using solar, wind, diesel, and battery energy storage to alleviate energy poverty in a rural area of Biskra. Algeria J Energy Storage. 2024;84(3):110651. doi:10.1016/j.est.2024.110651. [Google Scholar] [CrossRef]
183. Khanam I, Parmar G. Application of SFS algorithm in control of DC motor and comparative analysis. In: 2017 4th IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics (UPCON); 2017; IEEE. p. 256–61. doi:10.1109/UPCON.2017.8251057. [Google Scholar] [CrossRef]
184. Khanam I, Parmar G. Application of stochastic fractal search in order reduction of large scale LTI systems. In: 2017 International Conference on Computer, Communications and Electronics (Comptelix); 2017; IEEE. p. 190–4. doi:10.1109/COMPTELIX.2017.8003962. [Google Scholar] [CrossRef]
185. Li W, Sun S, Li J, Hu Y. Stochastic fractal search algorithm and its application in path planning. In: 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC); 2018; IEEE. p. 1–5. doi:10.1109/GNCC42960.2018.9018694. [Google Scholar] [CrossRef]
186. Liu H, Lin M, Deng L. UAV route planning for aerial photography under interval uncertainties. Optik. 2016;127(20):9695–700. doi:10.1016/j.ijleo.2016.06.117. [Google Scholar] [CrossRef]
187. Bhatt R, Parmar G, Gupta R, Sikander A. Application of stochastic fractal search in approximation and control of LTI systems. Microsyst Technol. 2019;25(1):105–14. doi:10.1007/s00542-018-3939-6. [Google Scholar] [CrossRef]
188. Çelik E, Gör H. Enhanced speed control of a DC servo system using PI+DF controller tuned by stochastic fractal search technique. J Franklin Instit. 2019;356(3):1333–59. doi:10.1016/j.jfranklin.2018.11.020. [Google Scholar] [CrossRef]
189. Huang X, Coolen FP, Coolen-Maturi T. A heuristic survival signature based approach for reliability-redundancy allocation. Reliab Eng Syst Saf. 2019;185(2):511–7. doi:10.1016/j.ress.2019.02.010. [Google Scholar] [CrossRef]
190. Zafrane MA, Boudjemai A, Boughanmi N. Interactive design of space manufacturing systems, optimality and opportunity. Int J Interact Des Manufact. 2019;13(2):773–96. doi:10.1007/s12008-018-0515-3. [Google Scholar] [CrossRef]
191. Mandala II, Nazaruddin YY. Optimization of two degree of freedom PID controller for quadrotor with stochastic fractal search algorithm. In: 2019 IEEE Conference on Control Technology and Applications (CCTA); 2019; IEEE. p. 1062–7. doi:10.1109/CCTA.2019.8920540. [Google Scholar] [CrossRef]
192. Juybari MN, Abouei Ardakan M, Davari-Ardakani H. A penalty-guided fractal search algorithm for reliability-redundancy allocation problems with cold-standby strategy. Proc Instit Mech Eng Part O: J Risk Reliab. 2019;233(5):775–90. doi:10.1177/1748006X19825707. [Google Scholar] [CrossRef]
193. Dobani ER, Ardakan MA, Davari-Ardakani H, Juybari MN. RRAP-CM: a new reliability-redundancy allocation problem with heterogeneous components. Reliab Eng Syst Saf. 2019;191(6):106563. doi:10.1016/j.ress.2019.106563. [Google Scholar] [CrossRef]
194. Lagunes ML, Castillo O, Soria J, Valdez F. Optimization of a fuzzy controller for autonomous robot navigation using a new competitive multi-metaheuristic model. Soft Comput. 2021;25(17):11653–72. doi:10.1007/s00500-021-06036-1. [Google Scholar] [CrossRef]
195. Li Y, Huang X, Zhao C, Ding P. Stochastic fractal search-optimized multi-support vector regression for remaining useful life prediction of bearings. J Brazilian Soc Mech Sci Eng. 2021;43(9):1–18. doi:10.1007/s40430-021-03138-7. [Google Scholar] [CrossRef]
196. Jing H, Nikafshan Rad H, Hasanipanah M, Jahed Armaghani D, Qasem SN. Design and implementation of a new tuned hybrid intelligent model to predict the uniaxial compressive strength of the rock using SFS-ANFIS. Eng Comput. 2021;37(4):2717–34. doi:10.1007/s00366-020-00977-1. [Google Scholar] [CrossRef]
197. Bendaoud E, Radjeai H, Boutalbi O. Identification of nonlinear synchronous generator parameters using stochastic fractal search algorithm. J Cont Automat Elect Syst. 2021;32(6):1639–51. doi:10.1007/s40313-021-00804-y. [Google Scholar] [CrossRef]
198. Mai TA, Dang TS. Optimal fuzzy PD control for a two-link robot manipulator based on stochastic fractal search. Euro Phy J Spec Topics. 2021;230(21):3935–45. doi:10.1140/epjs/s11734-021-00339-y. [Google Scholar] [CrossRef]
199. Sasmito A, Pratiwi AB. Stochastic fractal search algorithm in permutation flowshop scheduling problem. In: AIP Conference Proceedings; 2021; AIP Publishing. Vol. 2329. doi:10.1063/5.0042196. [Google Scholar] [CrossRef]
200. Hasan F, Imran M, Shahid M, Ahmad F, Sajid M. Load balancing strategy for workflow tasks using stochastic fractal search (SFS) in Cloud Computing. Procedia Comput Sci. 2022;215(1):815–23. doi:10.1016/j.procs.2022.12.084. [Google Scholar] [CrossRef]
201. Ye J, Dalle J, Nezami R, Hasanipanah M, Armaghani DJ. Stochastic fractal search-tuned ANFIS model to predict blast-induced air overpressure. Eng Comput. 2022;38(1):1–15. doi:10.1007/s00366-020-01085-w. [Google Scholar] [CrossRef]
202. Ie M, Hammoudi MY, Betka A, Hamiane M, Mimoune K. Stability and stabilization of TS fuzzy systems via line integral Lyapunov fuzzy function. Electronics. 2022;11(19):3136. doi:10.3390/electronics11193136. [Google Scholar] [CrossRef]
203. Houili R, Hammoudi MY, Betka A, Titaouine A. Stochastic optimization algorithms for parameter identification of three phase induction motors with experimental verification. In: 2023 International Conference on Advances in Electronics, Control and Communication Systems (ICAECCS); 2023; IEEE. p. 1–6. doi:10.1109/ICAECCS56710.2023.10104526. [Google Scholar] [CrossRef]
204. Liu Q, Wang F, Liu M, Xiao W. A two-step localization method using wavelet packet energy characteristics for low-velocity impacts on composite plate structures. Mech Syst Signal Process. 2023;188(9):110061. doi:10.1016/j.ymssp.2022.110061. [Google Scholar] [CrossRef]
205. Zheng Z, Zhao J, Wang L, Yu Z. Thrust bandwidth modeling and optimization of PMSLM based on analytic kernel-embedded elastic-net regression. IEEE Transact Indust Inform. 2022;19(8):9005–18. doi:10.1109/TII.2022.3224976. [Google Scholar] [CrossRef]
206. Chengquan Z, Aghajanirefah H, Zykova KI, Moayedi H, Le BN. Predicting concrete’s compressive strength through three hybrid swarm intelligent methods. Comput Conc. 2023;32(2):149–63. doi:10.12989/cac.2023.32.2.149. [Google Scholar] [CrossRef]
207. Zhou Y, Jiang Z, Zhu X. Predictive analysis of concrete slump using a stochastic search-consolidated neural network. Heliyon. 2024;10(10):e30677. doi:10.1016/j.heliyon.2024.e30677. [Google Scholar] [PubMed] [CrossRef]
208. Wang W, Foong LK, Le BN. The impact of thermal insulating materials in heat loss control in smart green buildings using experimental and swarm intelligent analysis. Environ Sci Pollut Res. 2024;31(27):38553–72. doi:10.1007/s11356-023-30118-2. [Google Scholar] [PubMed] [CrossRef]
209. Mosavi M, Khishe M, Hatam Khani Y, Shabani M. Training radial basis function neural network using stochastic fractal search algorithm to classify sonar dataset. Iran J Electr Electron Eng. 2017;13(1):100–11. [Google Scholar]
210. Mosbah H, El-Hawary M. Optimization of neural network parameters by Stochastic Fractal Search for dynamic state estimation under communication failure. Elect Power Syst Res. 2017;147(12):288–301. doi:10.1016/j.epsr.2017.03.002. [Google Scholar] [CrossRef]
211. Khishe M, Mosavi M, Moridi A. Chaotic fractal walk trainer for sonar data set classification using multi-layer perceptron neural network and its hardware implementation. Appl Acoust. 2018;137(1):121–39. doi:10.1016/j.apacoust.2018.03.012. [Google Scholar] [CrossRef]
212. Mosbah H, El-Hawary M. Evaluating the impact of phasor measurement units on the accuracy of state estimation. In: 2018 IEEE Canadian Conference on Electrical & Computer Engineering (CCECE); 2018; IEEE. p. 1–5. doi:10.1109/CCECE.2018.8447640. [Google Scholar] [CrossRef]
213. Moayedi H, Mosavi A. Suggesting a stochastic fractal search paradigm in combination with artificial neural network for early prediction of cooling load in residential buildings. Energies. 2021;14(6):1649. doi:10.3390/en14061649. [Google Scholar] [CrossRef]
214. Neelakandan S, Prakash V, PranavKumar M, Balasubramaniam R. Forecasting of E-commerce system for sale prediction using deep learning modified neural networks. In: 2023 International Conference on Applied Intelligence and Sustainable Computing (ICAISC); 2023; IEEE. p. 1–5. doi:10.1109/ICAISC58445.2023.10199817. [Google Scholar] [CrossRef]
215. Yang Y, Espín CGS, AL-Khafaji MO, Kumar A, Velasco N, Abdulameer SF, et al. Development of a mathematical model for investigation of hollow-fiber membrane contactor for membrane distillation desalination. J Mol Liq. 2024;404(1):124907. doi:10.1016/j.molliq.2024.124907. [Google Scholar] [CrossRef]
216. Hinojosa S, Dhal KG, Abd Elaziz M, Oliva D, Cuevas E. Entropy-based imagery segmentation for breast histology using the stochastic fractal search. Neurocomputing. 2018;321(1):201–15. doi:10.1016/j.neucom.2018.09.034. [Google Scholar] [CrossRef]
217. Bingöl O, Paçacı S, Güvenç U. Entropy-based skin lesion segmentation using stochastic fractal search algorithm. In: Artificial Intelligence and Applied Mathematics in Engineering Problems: Proceedings of the International Conference on Artificial Intelligence and Applied Mathematics in Engineering (ICAIAME 2019); 2020; Springer. p. 801–11. doi:10.1007/978-3-030-36178-5_69. [Google Scholar] [CrossRef]
218. Dhal KG, Gálvez J, Ray S, Das A, Das S. Acute lymphoblastic leukemia image segmentation driven by stochastic fractal search. Multim Tools Applicat. 2020;79(17):12227–55. doi:10.1007/s11042-019-08417-z. [Google Scholar] [CrossRef]
219. Khafaga DS, Ibrahim A, El-Kenawy ESM, Abdelhamid AA, Karim FK, Mirjalili S, et al. An Al-Biruni earth radius optimization-based deep convolutional neural network for classifying monkeypox disease. Diagnostics. 2022;12(11):2892. doi:10.3390/diagnostics12112892. [Google Scholar] [PubMed] [CrossRef]
220. Abdellatif EO, Karim EM, Hicham B, Saliha C. Intelligent local search for an optimal control of diabetic population dynamics. Mathem Mod Comput Simulat. 2022;14(6):1051–71. doi:10.1134/S2070048222060047. [Google Scholar] [CrossRef]
221. Khalilpourazari S, Hashemi Doulabi H. Robust modelling and prediction of the COVID-19 pandemic in Canada. Int J Product Res. 2023;61(24):8367–83. doi:10.1080/00207543.2021.1936261. [Google Scholar] [CrossRef]
222. Luo Q, Zhang S, Zhou Y. Stochastic fractal search algorithm for template matching with lateral inhibition. Sci Program. 2017;2017(1):1803934. doi:10.1155/2017/1803934. [Google Scholar] [CrossRef]
223. Li B. Atomic potential matching: an evolutionary target recognition approach based on edge features. Optik. 2016;127(5):3162–8. doi:10.1016/j.ijleo.2015.11.186. [Google Scholar] [CrossRef]
224. Betka A, Terki N, Toumi A, Hamiane M, Ourchani A. A new block matching algorithm based on stochastic fractal search. Appl Intell. 2019;49(3):1146–60. doi:10.1007/s10489-018-1312-1. [Google Scholar] [CrossRef]
225. Dhal KG, Ray S, Das A, Gálvez J, Das S. Fuzzy multi-level color satellite image segmentation using nature-inspired optimizers: a comparative study. J Indian Soc Remote Sens. 2019;47(8):1391–415. doi:10.1007/s12524-019-01005-6. [Google Scholar] [CrossRef]
226. Charef-Khodja D, Toumi A, Medouakh S, Sbaa S. A novel visual tracking method using stochastic fractal search algorithm. Signal Image Video Process. 2021;15(2):331–9. doi:10.1007/s11760-020-01748-7. [Google Scholar] [CrossRef]
227. Das A, Dhal KG, Ray S, Gálvez J. Histogram-based fast and robust image clustering using stochastic fractal search and morphological reconstruction. Neural Comput Applicat. 2022;34(6):4531–54. doi:10.1007/s00521-021-06610-6. [Google Scholar] [CrossRef]
228. Khalilpourazari S, Pasandideh SHR, Niaki STA. Optimization of multi-product economic production quantity model with partial backordering and physical constraints: SQP, SFS, SA, and WCA. Appl Soft Comput. 2016;49(19):770–91. doi:10.1016/j.asoc.2016.08.054. [Google Scholar] [CrossRef]
229. Dinh HTT, Chu NNM, Tran VH, Nguyen DV, Nguyen QLHTT. Applying Stochastic Fractal Search Algorithm (SFSA) in ranking the determinants of undergraduates employability: evidence from Vietnam. J Asian Fin, Econ Busi. 2020;7(12):583–91. doi:10.13106/jafeb.2020.vol7.no12.583. [Google Scholar] [CrossRef]
230. Shahid M, Ansari MS, Shamim M, Ashraf Z. A stochastic fractal search based approach to solve portfolio selection problem. In: Proceedings of the 2nd International Conference on Recent Trends in Machine Learning, IoT, Smart Cities and Applications: ICMISC 2021; 2022; Springer. p. 453–61. doi:10.1007/978-981-16-6407-6_41. [Google Scholar] [CrossRef]
231. Shahid M, Ashraf Z, Shamim M, Ansari MS. Solving constrained portfolio optimization model using stochastic fractal search approach. Int J Intell Comput Cybernet. 2022;16(2):223–49. doi:10.1108/IJICC-03-2022-0086. [Google Scholar] [CrossRef]
232. Shahid M, Shamim M, Ashraf Z, Ansari MS. A novel evolutionary optimization algorithm based solution approach for portfolio selection problem. IAES Int J Artif Intell. 2022;11(3):843. doi:10.11591/ijai.v11.i3.pp843-850. [Google Scholar] [CrossRef]
233. Hriez S, Almajali S, Elgala H, Ayyash M, Salameh HB. A novel trust-aware and energy-aware clustering method that uses stochastic fractal search in IoT-enabled wireless sensor networks. IEEE Syst J. 2021;16(2):2693–704. doi:10.1109/JSYST.2021.3065323. [Google Scholar] [CrossRef]
234. Yang J, Sun J, Yang Y. Radar task scheduling based on stochastic fractal search. In: 2023 7th International Conference on Electrical, Mechanical and Computer Engineering (ICEMCE); 2023; IEEE. p. 222–7. doi:10.1109/ICEMCE60359.2023.10490993. [Google Scholar] [CrossRef]
235. Duhayyim MA, Alissa KA, Alrayes FS, Alotaibi SS, Tag El Din EM, Abdelmageed AA, et al. Evolutionary-based deep stacked autoencoder for intrusion detection in a cloud-based cyber-physical system. Appl Sci. 2022;12(14):6875. doi:10.3390/app12146875. [Google Scholar] [CrossRef]
236. Alomoush MI, Oweis ZB. Environmental-economic dispatch using stochastic fractal search algorithm. Int Trans Electr Energy Syst. 2018;28(5):e2530. doi:10.1002/etep.2530. [Google Scholar] [CrossRef]
237. Van Hong TP, Ngoc DV, Tuan KD. Environmental economic dispatch using stochastic fractal search algorithm. In: 2021 International Symposium on Electrical and Electronics Engineering (ISEE); 2021; IEEE. p. 214–9. doi:10.1002/etep.2530. [Google Scholar] [CrossRef]
238. Xu Z, Zhou J, Mo L, Jia B, Yang Y, Fang W, et al. A novel runoff forecasting model based on the decomposition-integration-prediction framework. Water. 2021;13(23):3390. doi:10.3390/w13233390. [Google Scholar] [CrossRef]
239. Zhang Y, Liu L, Zhu Y, Wang P, Foong LK. Novel integrative soft computing for daily pan evaporation modeling. Smart Struct Syst. 2022;30(4):421–32. doi:10.12989/sss.2022.30.4.421. [Google Scholar] [CrossRef]
240. Ahmadi Dehrashid A, Dong H, Fatahizadeh M, Gholizadeh Touchaei H, Gör M, Moayedi H, et al. A new procedure for optimizing neural network using stochastic algorithms in predicting and assessing landslide risk in East Azerbaijan. Stoch Environ Res Risk Assess. 2024;448(2):1–30. doi:10.1007/s00477-024-02690-7. [Google Scholar] [CrossRef]
241. Ahrari A, Elsayed S, Sarker R, Essam D, Coello CAC. Problem definition and evaluation criteria for the cec’2022 competition on dynamic multimodal optimization. In: Proceedings of the IEEE World Congress on Computational Intelligence (IEEE WCCI 2022); 2022; Padua, Italy. p. 18–23. [Google Scholar]
242. Lang Y, Gao Y. Dream Optimization Algorithm (DOAa novel metaheuristic optimization algorithm inspired by human dreams and its applications to real-world engineering problems. Comput Methods Appl Mech Eng. 2025;436(2):117718. doi:10.1016/j.cma.2024.117718. [Google Scholar] [CrossRef]
243. Sowmya R, Premkumar M, Jangir P. Newton-Raphson-based optimizer: a new population-based metaheuristic algorithm for continuous optimization problems. Eng Appl Artif Intell. 2024;128:107532. doi:10.1016/j.engappai.2023.107532. [Google Scholar] [CrossRef]
244. Cheng MY, Sholeh MN. Optical microscope algorithm: a new metaheuristic inspired by microscope magnification for solving engineering optimization problems. Knowl Based Syst. 2023;279(4):110939. doi:10.1016/j.knosys.2023.110939. [Google Scholar] [CrossRef]
245. Shehadeh HA. Chernobyl disaster optimizer (CDOa novel meta-heuristic method for global optimization. Neural Comput Applicat. 2023;35(15):10733–49. doi:10.1007/s00521-023-08261-1. [Google Scholar] [CrossRef]
246. Xiao Y, Cui H, Khurma RA, Castillo PA. Artificial lemming algorithm: a novel bionic meta-heuristic technique for solving real-world engineering optimization problems. Artif Intell Rev. 2025;58(3):84. doi:10.1007/s10462-024-11023-7. [Google Scholar] [CrossRef]
247. Ahmed R, Rangaiah GP, Mahadzir S, Mirjalili S, Hassan MH, Kamel S. Memory, evolutionary operator, and local search based improved Grey Wolf Optimizer with linear population size reduction technique. Knowl Based Syst. 2023;264:110297. doi:10.1016/j.knosys.2023.110297. [Google Scholar] [CrossRef]
248. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Transact Evolution Computat. 1997;1(1):67–82. doi:10.1109/4235.585893. [Google Scholar] [CrossRef]
249. Brest J, Sepesy Maučec M. Population size reduction for the differential evolution algorithm. Appl Intell. 2008;29(3):228–47. doi:10.1007/s10489-007-0091-x. [Google Scholar] [CrossRef]
250. Tanabe R, Fukunaga AS. Improving the search performance of SHADE using linear population size reduction. In: 2014 IEEE Congress on Evolutionary Computation (CEC); 2014; IEEE. p. 1658–65. doi:10.1109/CEC.2014.6900380. [Google Scholar] [CrossRef]
251. Alomari OA, Elnagar A, Afyouni I, Shahin I, Nassif AB, Hashem IA, et al. Hybrid feature selection based on principal component analysis and grey wolf optimizer algorithm for Arabic news article classification. IEEE Access. 2022;10:121816–30. doi:10.1109/ACCESS.2022.3222516. [Google Scholar] [CrossRef]
252. Awadallah MA, Al-Betar MA, Doush IA, Makhadmeh SN, Alyasseri ZAA, Abasi AK, et al. CCSA: cellular crow search algorithm with topological neighborhood shapes for optimization. Expert Syst Appl. 2022;194(8):116431. doi:10.1016/j.eswa.2021.116431. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF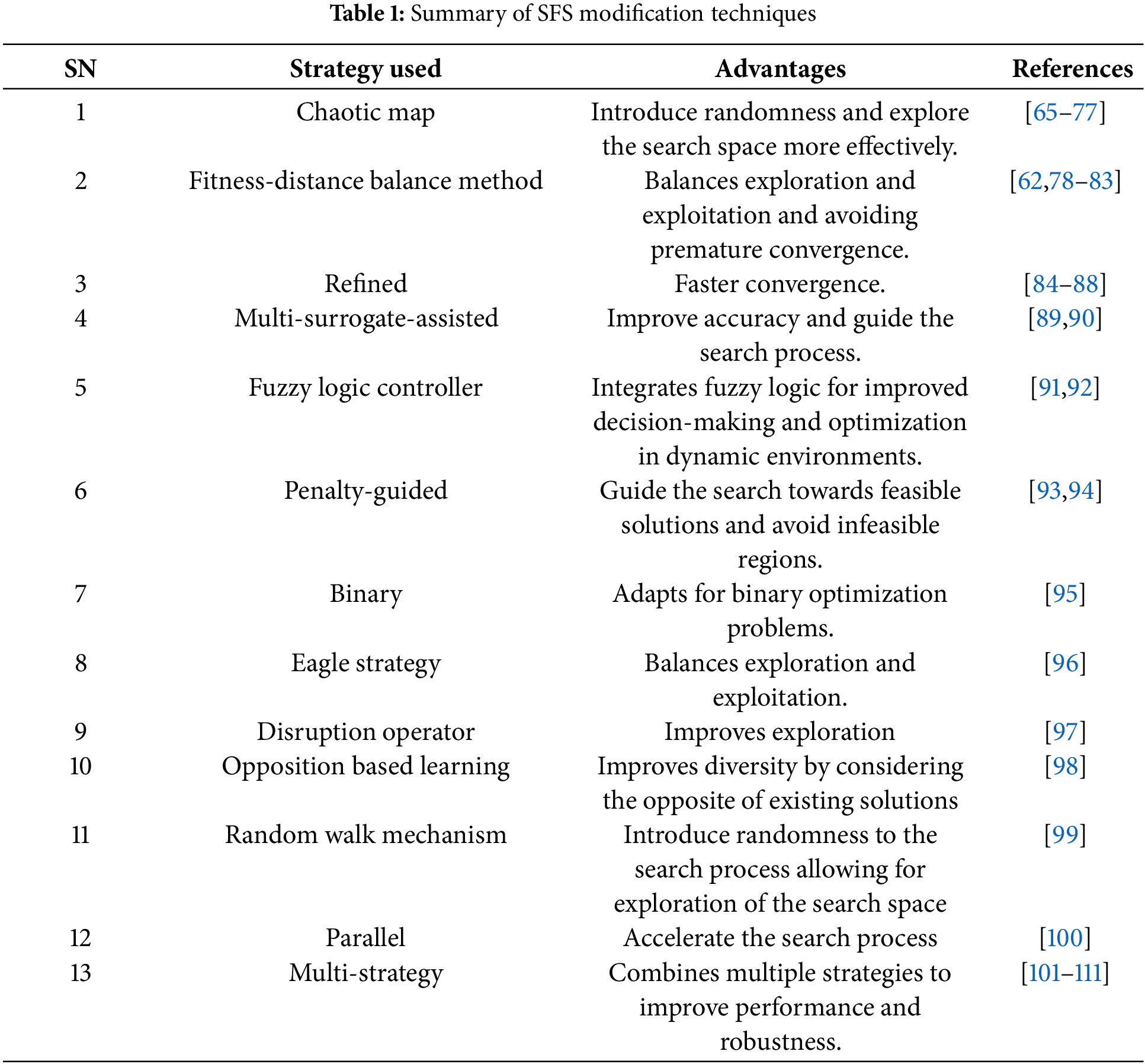
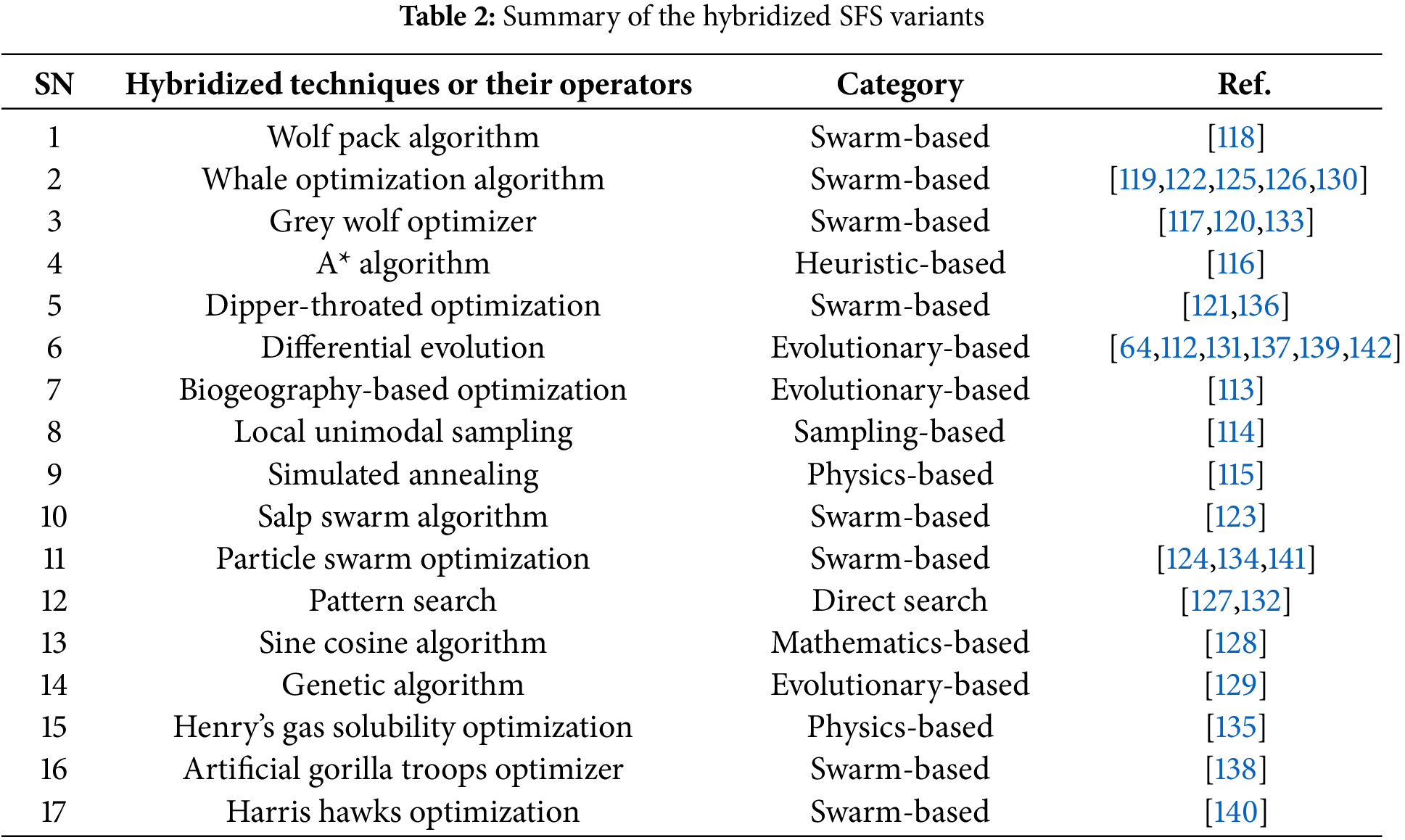

 Downloads
Downloads
 Citation Tools
Citation Tools