Dynamic Response of a Nonlocal Multiferroic Laminated Composite with Interface Stress Imperfections

1  Introduction

The ongoing trends of device miniaturization has driven significant interest in the magneto-electro-elastic (MEE) nanostructures comprising piezoelectric and piezomagnetic phases. The MEE heterostructures exhibit novel electrical, magnetic, and mechanical properties, offering promising applications in intelligent adaptive systems, including memory devices and energy harvesting [1,2]. Since MEE nanostructures exist at the nanoscale, their behavior and overall properties differ significantly from those of bulk composites. Long-range interatomic and intermolecular cohesive forces play a more significant role in determining the properties of MEE nanostructures [3]. Consequently, size effects must be accounted for in both theoretical and experimental studies [4,5]. While classical continuum mechanics remains a valuable tool, its scale-independent nature may lead to inaccurate results when analyzing nanostructures.

The nonlocal elasticity theory proposed by Eringen [6,7], which accounts for scale effects, offers a computationally efficient alternative to direct atomistic or molecular dynamics simulations [8]. For example, Wu and Li [9] effectively implemented this theory in free vibration analyses of embedded single-layered nanoplates and graphene sheets. Wu and Yu [10] investigated its application to nanobeams and carbon nanotubes (CNT), incorporating nonlocal effects. The application of the theory has been further extended to MEE plates [11–14], and MEE fibrous composites [15–17].

Dynamic responses of MEE composites, such as wave propagation and free vibration, have attracted significant research attention in recent years. Fundamental to the design process is determining natural frequencies and corresponding vibration modes-an analysis that has become a focal point in several studies. For example, Liu et al. [18] developed a dynamic analysis method for three-phase MEE structures using overlapping triangular finite elements. Jiang et al. [19] created a coupled MEE edge-based smoothed finite element method to evaluate the dynamic behavior of MEE solids. Kuo et al. [20] systematically compared wave propagation characteristics in MEE laminated composites with varying layering directions. Ly et al. [21] introduced a numerical approach for nonlinear analysis and smart damping control in functionally graded CNT reinforced MEE plate.

Most studies assume perfectly bonded interfaces between different phases-an idealized condition that may not reflect real-world scenarios. However, interfaces often exhibit imperfections due to cracking, dislocations, aging, or manufacturing defects. Additionally, these interfacial imperfections significantly affect magneto-electric coupling effects. Several studies have addressed interfacial imperfections in MEE composites, including [22–24] for static cases and [25,26] for dynamic cases.

Therefore, this study aims to investigate MEE laminates using the nonlocal theory proposed by Eringen, with a particular focus on extended interface stress-type contact condition. The paper is organized as follows. Section 2 presents the formulation of the multifield boundary-value problem, including considerations of extended interface stress imperfections. Section 3 presents the derivation of the field solutions for each homogeneous layer using the pseudo-Stroh formulation. A recursive framework that incorporates both propagation and interface matrices is developed to account for imperfect interface characteristics and determine exact solutions throughout the laminate. Section 4 discusses particular numerical cases analyzing the effect of the interface stress and nonlocal length parameters. Section 5 provides conclusions remarks.

2  Basic Formulations

2.1 Nonlocal Theory for MEE Materials

We consider a three-dimensional N−bonded orthotropic and rectangular MEE plate with nonlocal effect as shown in Fig. 1. A global Cartesian coordinate system (x,y,z) is attached to the laminate such that the bottom surfaces of the plate is set as the horizontal coordinate plane x−z. The plate is horizontally infinite but vertically finite in the y−direction with the total thickness H. The lower and upper interfaces of the jth layer are defined as yj−1+ and yj−, respectively, with the thickness hj=yj−−yj−1+. The internal interfaces between the adjacent plates are imperfectly connected, which will be discussed later on. The fabrication of the type of MEE laminated composites can be referred to the work by Dong et al. [27], Wang et al. [28], and Zhai et al. [29].

Figure 1: Geometry and coordinate system of an N-bonded orthotropic, nonlocal rectangular linearly MEE plate. The laminated plate is horizontally infinite but vertically finite in the y-direction with total thickness H. The jth layer is bonded by its lower interface yj−1+ and upper interface yj−. The interfaces between the plates are imperfectly connected

Following Pan and Waksmanski [13], the constitutive relations of a nonlocal linear anisotropic MEE within the context of nonlocal model proposed by Eringen can be expressed as

σijg−l2∇2σijg=σijc=cijklεkl−ekijEk−qkijHk,Dig−l2∇2Dig=Dic=eijkεjk+κijEj+λjiHj,Big−l2∇2Big=Bic=qijkεjk+λijEj+μijHj,(1)

where ∇2 is the 3D Laplace operator; l is the nonlocal length parameter. σij, εij, Di, Ei,Bi and Hi are the stress, strain, electric displacement, electric field, magnetic flux density, and magnetic field. cijkl, eijk, qijk, κij, μij, and λij are elastic stiffness constant, piezoelectric coefficient, piezomagnetic coefficient, dielectric permittivity, magnetic permeability, and magnetoelectric coupling coefficient. The upper index g denotes the nonlocal field quantities, while the upper index c denotes the classical field quantities.

The infinitesimal strain εij, electric field Ei, and magnetic field Hi can be derived from the gradient of the elastic displacement ui, electric potential ϕ, and magnetic potential ψ as follows:

εij=12(ui,j+uj,i), Ei=−ϕ,i, Hi=−ψ,i,(2)

for which comma followed by lowercase subscript i denotes partial derivative.

For each individual plate, the equilibrium equations for the stress, electric displacement, and magnetic flux in the absence of body forces and electric sources are defined by

σij,jg=ρ∂2ui∂t2, Di,ig=0, Bi,ig=0.(3)

Here ρ is the mass density and t is time.

3  Free Vibration Analysis of the MEE Laminate

3.1 Field Solutions for Each Nonlocal Plate

We consider the material is orthotropic symmetry. The polarization and magnetization directions are along the z−axis. The involved material coefficients with the three orthogonal planes of symmetry along the x−,  y−,  z−directions can be expressed in the matrix form as

C=[C11C12C13000C22C23000C33000C4400symmC550C66],eT=[00e3100e3200e330e240e1500000], qT=[00q3100q3200q330q240q1500000],κ=[κ11000κ22000κ33], μ=[μ11000μ22000μ33], λ=[λ11000λ22000λ33].(4)

Here CIJ, eiJ, and qiJ (i=1−3, I,J=1−6) are elastic stiffness constant, piezoelectric coefficient and piezomagnetic coefficient in the Voigt notation.

Assuming time-harmonic vibration motion, the field solutions are sought in the form of

Φ=(u1u2u3ϕψ)=∑m, nei(k1x+k2y+k3z−ωt)a, a=(a1a2a3a4a5),Σng=(σ21gσ22gσ23gD2gB2g)=∑m, nei(k1x+k2y+k3z−ωt)b, b=(b1b2b3b4b5), Σnc=(σ21cσ22cσ23cD2cB2c)=∑m, nei(k1x+k2y+k3z−ωt)d, d=(d1d2d3d4d5),(5)

where ω is the angular vibration frequency of the excitation, and i=−1.  k1,  k3 are the components of the wave vector depending on the angle of the wavenumber along the propagating direction in the x−z plane. k2 is an unknown to be determined. a,~b,~d are unknown amplitudes to be determined.

Substituting Eqs. (4) and (5) into Eqs. (1) and (2), the nonlocal constitutive relation yields

[1+l2(k12+k22+k32)]b=i(RT+k2T)a,(6)

where matrices R and T are given by

R=[0C12k1000C66k10C44k3e24k3q24k30C23k30000e32k30000q32k3000], T=[C660000C22000C44e24q24symm−κ22−λ22−μ22].(7)

Furthermore, inserting Eq. (5) into the governing Eq. (3) leads to a quadratic eigenequation, as follows:

[Qn+k2(R+RT)+k22Tn]a=0.(8)

Finally, the above equation with the help of Eq. (6) can further be converted into the linear eigensystem of equations

[−Tn−1RT−iTn−1−i(Qn−RTn−1RT)−RTn−1][ad]=k2[ad].(9)

Here

Qn≡Q−[1+l2(k12+k32)]ρω2I3, Tn≡T−ρω2l2I3,

Q=[C11k12+C55k320k1k3(C13+C55)k1k3(e15+e31)k1k3(q15+q31)C66k12+C44k32000C55k12+C33k32e15k12+e33k32q15k12+q33k32symm−(κ11k12+κ33k32)−(d11k12+d33k32)−(μ11k12+μ33k32)],

I3 is a 3×3 unit matrix, and the 5×1 constant column matrix d is related to a by

d=i(RT+k2T)a,(10)

from the constitutive law (1).

Without the proportional position term eei(k1x+k3z) and the time-dependent factor eiωt in (5) for clarity, the general y− dependent solution for the extended displacement and traction expansion coefficient vectors can be expressed as

[Φ~(y)Σ~ng(y)]=[A∣A∥B∣B∥]⟨eiky⟩[K∣K∥],(11)

with

Φ~(y)=eik2ya, Σ~n(y)=eik2yb,(12)

⟨eiky⟩=diag(eik2(1)y,eik2(2)y,eik2(3)y,eik2(4)y,eik2(5)y,eik2(6)y,eik2(7)y,eik2(8)y,eik2(9)y,eik2(10)y),

and A∣, A∥, B∣, B∥ being the eigenvector matrices defined by

A∣=(a1,a2,a3,a4,a5), A∥=(a6,a7,a8,a9,a10),B∣=(b1,b2,b3,b4,b5), B∥=(b6,b7,b8,b9,b10),

here K∣ and K∥ are two 5×1 constant column matrices to be determined from the internal and external boundary conditions of the plate; k2 and {ai,di} are the eigenvalue and corresponding eigenvectors of Eq. (9), and bi can be calculated from (6).

By eliminating the involved undetermined coefficients constants K1 and K2 in Eq. (11), the extended displacement and traction on the top and bottom of the jth layer can be related as

[Φ~(yj−)Σ~ng(yj−)]=Pj(hj)[Φ~(yj−1+)Σ~ng(yj−1+)],(13)

where

Pj(y)=[A1A2B1B2]⟨eik(y−yj)⟩[A1A2B1B2]−1,(14)

is the propagation matrix of the jth layer.

In order to complete the total field solutions, the remaining in-plane stress, electric displacement, and magnetic flux density are organized as follows:

Σtg=[σ11σ33σ13D1D3B1B3]=∑m, nei(k1x+k2y+k3z−ωt)c, c=(c1c2c3c4c5c6c7).(15)

Substituting the extended displacement expansion in Eq. (5) and Eq. (15) into the constitutive relation (1), additional relations between the associated expansion coefficients are derived as

[1+l2(k12+k22+k32)]c=i[C11k1C12k2C13k3e31k3q31k3C13k1C23k2C33k3e33k3q33k3C55k30C55k1e15k1q15k1e15k30e15k1−κ11k1−λ11k1e31k1e32k2e33k3−κ33k3−λ33k3q15k30q15k1−λ11k1−μ11k1q31k1q32k2q33k3−λ33k3−μ33k3]a.(16)

3.2 Interface Stress-Type Imperfect Interface

To find the exact solutions, we need the interfacial conditions. We consider the extended interface stress interfacial conditions [30]:

[[Φ]]yj=0, [[σ2αc]]=−fαβγμuγ,μβ,[[σ22c]]=0, [[D2c]]=καβfϕ,αβ, [[B2c]]=μαβfψ,αβ,α,β,γ,μ=1,3,(17)

where [[⋅]] denotes that the corresponding physical quantity has a jump across the interface. fαβγμ, καβf, μαβf denote the interface elastic modulus, interface electric permittivity, and interface magnetic permeability, respectively. Next, we rearrange the above extended interface stress-type interfacial condition as

[Φ~(yj+)Σ~nc(yj+)]=Mj[Φ~(yj−)Σ~nc(yj−)],(18)

where the interface matrix Mj at the interface y=yj is defined as

Mj=[I50LjI5].(19)

Here I5 is a 5×5 unit matrix and

Lj=[k12f1111+k32f13130k1k3(f1133+f1313)000000k12f1313+k32f333300symm−k12κ11f−k32κ33f0−k12μ11f−k32μ33f].(20)

3.3 Recursive Field Solutions in the Laminate

Transferring the general field solution from the jth layer to the next j+1th layer with an imperfect interface yj in between, we need to combine Eqs. (13) and (18). However, the former is related to the nonlocal extended traction while the latter is related to the classical extended traction. To connect the nonlocal and classical extended traction fields, we notice that

[Φ~(y)Σ~nc(y)]=[A∣A∥D∣D∥]⟨eiky⟩[K∣K∥],(21)

where

D∣=(d1,d2,d3,d4,d5), D∥=(d6,d7,d8,d9,d10).

Combining (11) and (21) and then substituting the result into (18) yields

[Φ~(yj+)Σ~ng(yj+)]=Mjg[Φ~(yj−)Σ~ng(yj−)],(22)

where

Mjg=[A∣A∥B∣B∥][A∣A∥D∣D∥]−1Mj[A∣A∥D∣D∥][A∣A∥B∣B∥]−1.

Therefore, when transferring the solution from the jth layer to the next j+1th layer with an imperfect interface yj in between, we only need to multiply the interface matrix between the two layer matrices Pj(hj) and Pj+1(hj+1) to obtain

[Φ~(yj+1−)Σ~ng(yj+1−)]=Pj+1(hj+1)MjgPj(hj)[Φ~(yj−1+)Σ~ng(yj−1+)].(23)

Here the propagator matrix Pj(y) is defined in Eq. (14). A similar recursive relation for the field quantities as Eq. (23) from the bottom surface to any field point y in the kth layer ( yk−1≤y≤yk) can be expressed as follows:

[Φ~(y)Σ~ng(y)]=Pk(y−yk−1)Mk−1Pk−1(hk−1)⋯P2(h2)M1P1(h1)[Φ~(0)Σ~ng(0)].(24)

The prescribed boundary conditions on both bottom y=0 and top y=H surfaces are traction free and magneto-electric circuit open. That is

Σ~ng(0)=Σ~ng(H)=0.(25)

By means of the above boundary conditions, the recursive field

[Φ~(H)Σ~ng(H)]=[S11S12S21S22][Φ~(0)Σ~ng(0)](26)

[S11S12S21S22]=PN(hN)MN−1g⋯M2gP2(h2)M1gP1(h1),

yields the dispersion equation

detS21=0.(27)

4  Numerical Results and Discussion

To investigate the behavior of nonlocal effects and interface stresses, the proposed solution was applied to a sandwich plate composed of piezoelectric barium titanate (BaTiO3, BTO) and piezomagnetic cobalt ferrite (CoFe2O4, CFO). Two laminate configurations were examined: (1) a BTO/CFO/BTO layered structure and (2) a CFO/BTO/CFO layered structure. All three layers were assumed to have equal thickness, while the materials were transversely isotropic. The material properties used in the numerical analysis were as follows: C11=166GPa, C12=77GPa, C13=78GPa, C33=162GPa, C44=43GPa, e15=11.6C/m2, e31=−4.4C/m2, e33=18.6C/m2, κ11=11.2nC2/Nm2, κ33=12.6nC2/Nm2, μ11=5μNs2/C2, μ33=10μNs2/C2, ρ=5800kg/m3 for BTO, and C11=286GPa, C12=173GPa, C13=170.5GPa, C33=269.5GPa, C44=45.3GPa, q15=550N/Am, q31=580.3N/Am, q33=699.7N/Am, κ11=0.08nC2/Nm2, κ33=0.093nC2/Nm2, μ11=590μNs2/C2, μ33=157μNs2/C2, ρ=5300kg/m3 for CFO [31].

The imperfect interface was modeled as a thin interphase layer c with thickness δ and distinct material properties. The interphase properties were characterized by [30]

f1111=f3333=λf+2Gf, f1133=λf, f1313=Gf, καβf=κf, μαβf=μf.(28)

where

λf=2Gcλcδλc+2Gc,Gf=δGc, κf=δκc, μf=δμc,

here λc represents the Lamé constant, Gc indicates the shear modulus, κc is the dielectric permittivity, and μc represents the magnetic permeability. For the analysis, the following assumptions were made

Cc=ΓmCmax/δ, Gc=ΓmGmax/δ, κc=Γmκmax/δ, μc=Γmμmax/δ,(29)

where Γm represents the relative scaling parameter, and Cmax, Gmax, κmax,  and μmax denote the maximum values of the elastic constant, dielectric permittivity, and magnetic permeability from the BTO and CFO constituents, respectively. Different interface conditions were investigated: perfect contact, Γm=10−1 and Γm=100. The perfect contact condition maintained continuity in both extended displacement and traction vectors across the interface. The relative scaling parameter Γm directly correlated with interfacial stiffness and electromagnetic properties-higher values indicated stiffer interfaces with stronger dielectric constant and magnetic permeability. We analyzed three different nonlocal length-to-thickeness ratios (l/H=0,0.06,0.12). For modeling simplicity, identical nonlocal lengths were maintained across all material layers in each analysis case.

For numerical analysis, the wave was assumed to propagate exclusively along the x−axis (k=k1, k3=0). The wave was decoupled into a Lamb wave (u3=0) and a Love wave (u1=0 and u2=0). Dimensionless frequency Ω=ωHρmax/Cmax and dimensionless wavenumber kH were used, where Cmax and ρmax represent the maximum elastic modulus and density of the constituents, respectively. An efficient root-finding algorithm developed by Zhu et al. [32] was employed to obtain the accurate solutions.

4.1 Lamb Wave

Figs. 2 and 3 illustrate the dispersion curves for the first three Lamb wave modes of nonlocal BTO/CFO/BTO and CFO/BTO/CFO sandwich plates. The results showed that the dispersion curves for the classical case (i.e., l/H=0) of the BTO/CFO/BTO configuration are consistent with those of a previous study [26]. Furthermore, significant influence of the nonlocal effect was observed. The dispersion curves associated with the same branches differed significantly between the classical and nonlocal modes. Specifically, the inclusion of the nonlocal length reduced the dispersion curve values, particularly in the high-frequency regimes (i.e., at high wavenumbers and short wavelengths). Additionally, the nonlocal effect altered the overall trends of the dispersion behavior; as the nonlocal length increased, the curves exhibited faster convergence. The slope of the dispersion curves in the nonlocal plate decreased as the wavenumber increased. The nonlocal length indicated the spatial range over which a material point could exert an instantaneous effect. As the nonlocal length increased-indicating a broader interaction domain [6,7]-the slope of the dispersion curves decreased further in high-frequency regions. These findings demonstrate that nonlocal effects become critically significant for high-frequency device operation.

Figure 2: Dispersion curves for Lamb waves in a BTO/CFO/BTO sandwich plate with different interface contacts: perfect contact, imperfect contact with the relative scaling parameter Γm=10−1, Γm=100. Dimensionless nonlocal length parameter (a) l/H = 0, (c) l/H = 0.06, (c) l/H = 0.12

Figure 3: Dispersion curves for Lamb waves in a CFO/BTO/CFO sandwich plate with different interface contacts: perfect contact, imperfect contact with the relative scaling parameter Γm=10−1, Γm=100. Dimensionless nonlocal length parameter (a) l/H = 0, (b) l/H = 0.06, (c) l/H = 0.12

Furthermore, the dispersion curves exhibited distinct discontinuities at specific wavenumber values kH ≈ 6, 6.5, and 6.8 (Fig. 2c) and kH≈ 6.8, 7.5, and 8.1 (Fig. 3c). Analysis revealed that these discontinuities represented fundamentally different phenomena-the discontinuities at kH≈ 6, 6.5 (Fig. 2c) and 7.5, 8.1 (Fig. 3c) corresponded to abrupt phase velocity jumps. In contrast, the discontinuity at kH≈6.8 manifested as a rapid phase velocity variation. These discontinuities appeared in both perfect and imperfect interface conditions when the normalized nonlocal length reached l/H=0.12. This indicates their origin is nonlocal effects rather than the interface imperfections.

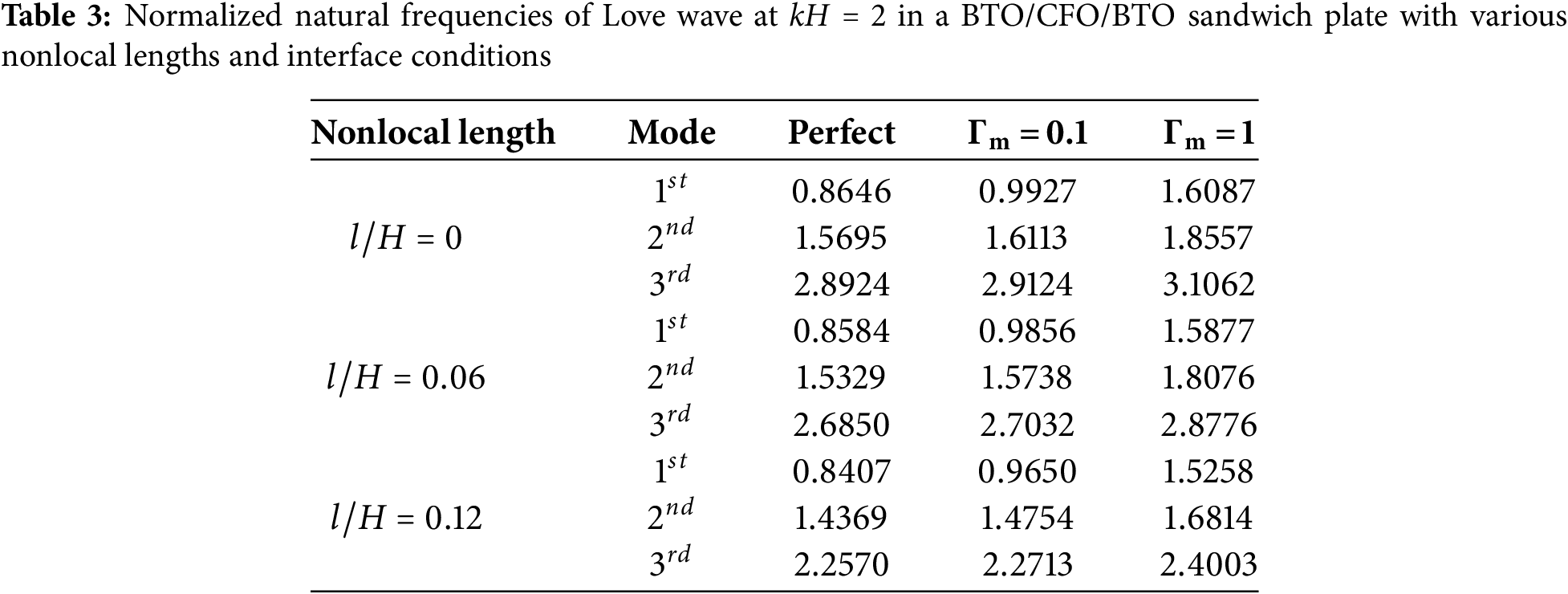
We further investigated the modal natural frequencies associated with different nonlocal lengths and interface imperfections at a given wavenumber. Tables 1 and 2 present the first three modal natural frequencies at wavenumber kH=2 for nonlocal BTO/CFO/BTO and CFO/BTO/CFO sandwich plate configurations. The results demonstrated significant interface effects-imperfect contact consistently produced higher frequencies at the examined wavenumber. This frequency elevation correlated directly with increasing interphase stiffness and strength, confirming that dimensionless natural frequencies increase with enhanced interfacial properties.

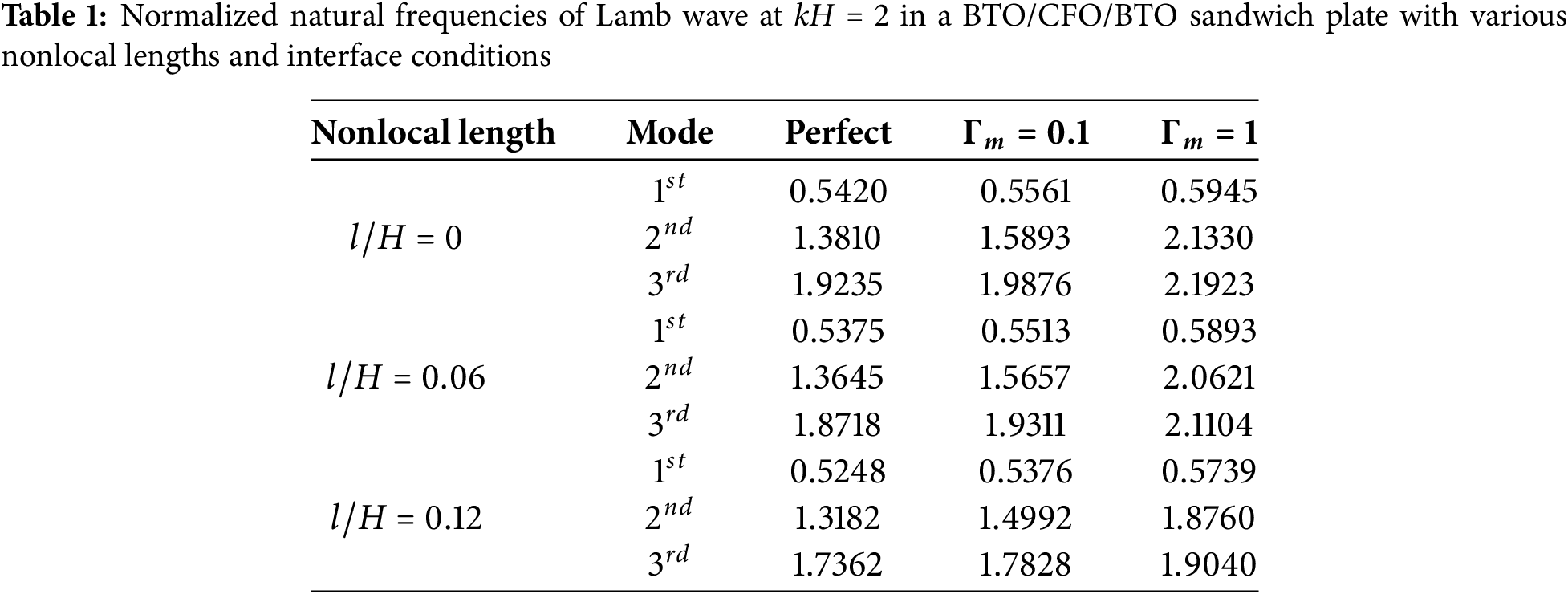
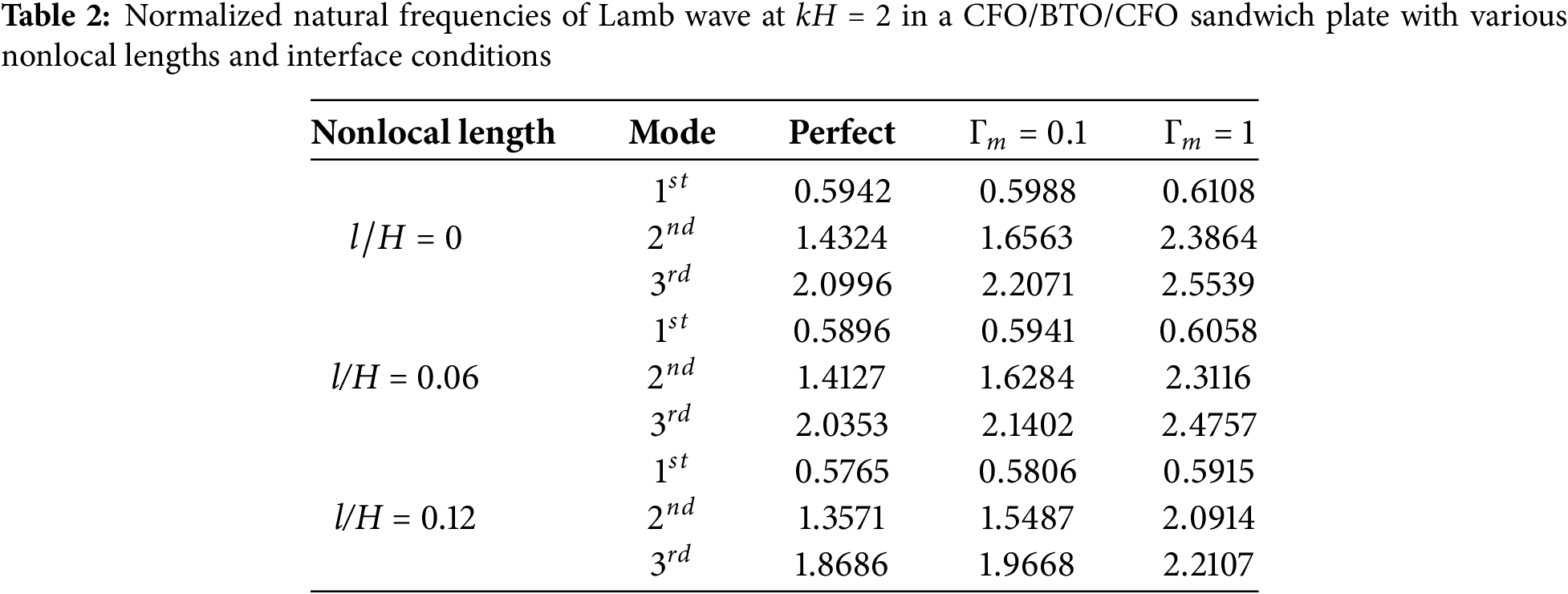
Figs. 4 and 5 show the first-order (Ω=Ω1) and second-order mode (Ω=Ω2) shapes along the thickness direction (y-axis) of the BTO/CFO/BTO plate at the given wavenumber kH=2, evaluated at the fixed horizontal coordinate (x,z)=(π/4,0). Panels (a, b) show the elastic displacements u1 and u2; panels (c–f) illustrate the tractions σ21,σ22 and the stresses σ11,σ33; and panels (g–h) show the electric displacement D3 and magnetic flux density B3. Figs. 6 and 7 illustrate the first-order and second-order mode shapes for the CFO/BTO/CFO plate configuration. The classical case results for the BTO/CFO/BTO plate configurations are consistent with those reported in a previous study [26]. The analysis confirmed two key interfacial behaviors: (1) continuous displacements u1 and u2 across all interfaces and (2) discontinuous traction σ21 due to the extended interface stress imperfections. Further observations from the first-order mode shapes (Figs. 4 and 6) revealed the following features. First, the displacement u1, traction σ22, stresses σ11 and σ33, electric displacement D3, and magnetic flux density B3 exhibited anti-symmetric distributions about the midplane, while the displacement u2 and traction σ21 showed symmetric distributions. These patterns reflect both the symmetry of the sandwich plate and the extended traction free boundary conditions. Second, the displacement u1 and stresses σ11,σ33 reached maximum magnitudes at the top and bottom surfaces, while the traction σ21 peaked at the midplane. The electric displacement D3 (magnetic flux density B3) reached maximum conditions at both the top and bottom surfaces (Figs. 4 and 6, respectively), while the magnetic flux density B3 (electric displacement D3) peaked at the material interfaces (Figs. 4 and 6, respectively). Third, an increase in the relative scaling parameter Γm resulted in an increase in the displacement u2, an increase in the discontinuities traction σ21 across the interfaces, and a decrease in the discontinuities in electric displacement D3 and magnetic flux density B3. As the nonlocal length l increased, the values of u2, σ21 increased, and the discontinuity of σ21 across the interface became more pronounced. Fourth, the nonlocal length l exhibited a negligible effect on u1, σ11, σ22, σ33, D3 and B3, as indicated by their clustered mode shapes and parameter insensitivity. Fifth, comparative analysis revealed that imperfect contacts exhibited significantly greater influence on mode shapes than nonlocal effects.

Figure 4: Variations for the first-order mode shapes of the Lamb wave in a BTO/CFO/BTO plate along the thickness direction (dimensionless wavenumber kH = 2): (a, b) displacements u1 and u2, (c, d) tractions σ21 and σ22, (e–h) stresses σ11 and σ33, electric displacement D3, and magnetic flux density B3. The plate is with nonlocal effect and extended interface stress imperfect interfaces

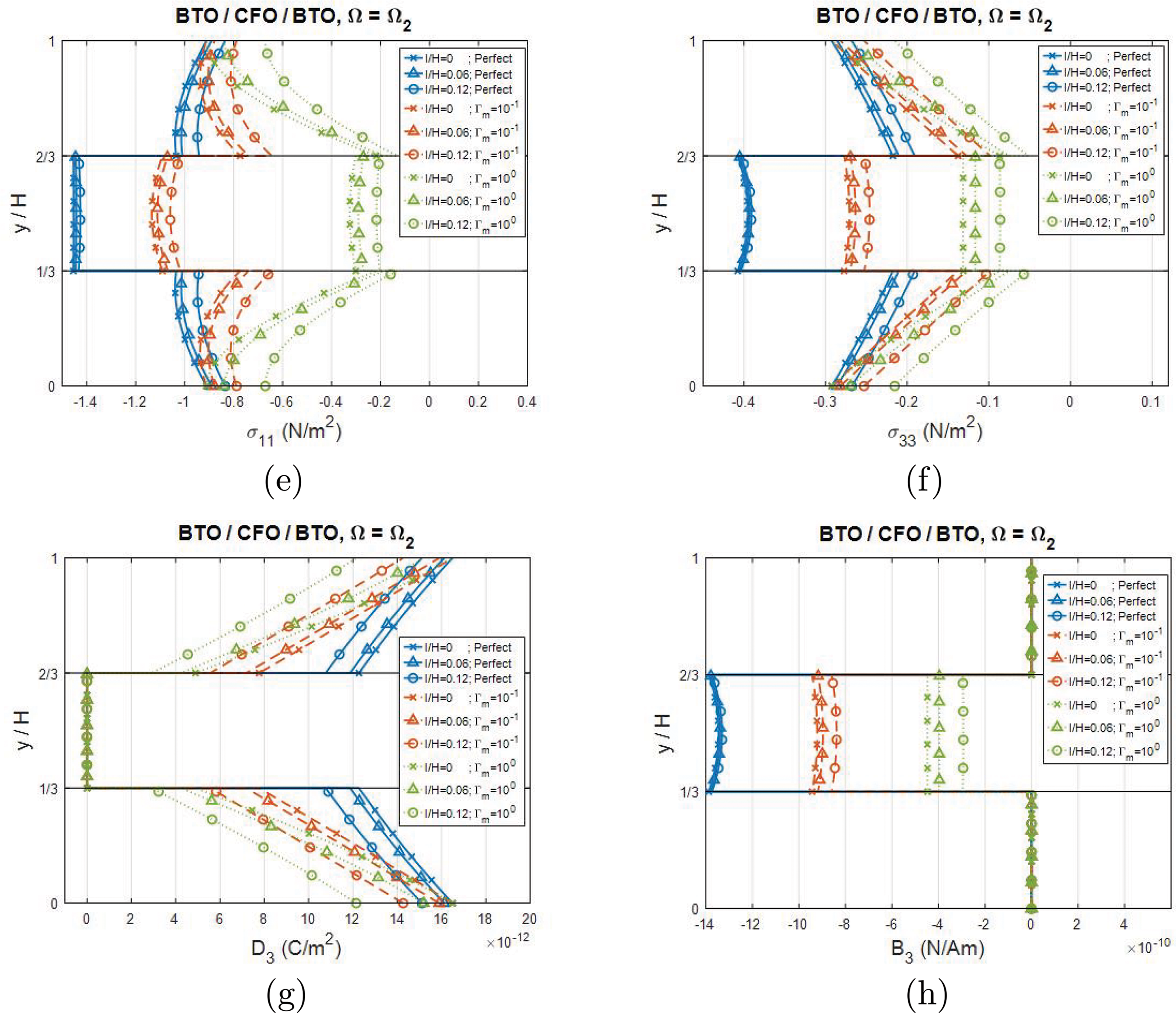
Figure 5: Variations for the second-order mode shapes of the Lamb wave in a BTO/CFO/BTO plate along the thickness direction (dimensionless wavenumber kH = 2): (a, b) displacements u1 and u2, (c, d) tractions σ21 and σ22, (e–h) stresses σ11 and σ33, electric displacement D3, and magnetic flux density B3. The plate is with nonlocal effect and extended interface stress imperfect interfaces

Figure 6: Variations for the first-order mode shapes of the Lamb wave in a CFO/BTO/CFO plate along the thickness direction (dimensionless wavenumber kH = 2): (a, b) displacements u1 and u2, (c, d) tractions σ21 and σ22, (e–h) stresses σ11 and σ33, electric displacement D3, and magnetic flux density B3. The plate is with nonlocal effect and extended interface stress imperfect interfaces

Figure 7: Variations for the second-order mode shapes of the Lamb wave in a CFO/BTO/CFO plate along the thickness direction (dimensionless wavenumber kH = 2): (a, b) displacements u1 and u2, (c, d) tractions σ21 and σ22, (e–h) stresses σ11 and σ33, electric displacement D3, and magnetic flux density B3. The plate is with nonlocal effect and extended interface stress imperfect interfaces

Analysis of the corresponding second-order mode shapes (Figs. 5 and 7), revealed consistent pattern for both configurations: (1) The displacement u1,  stresses σ11, σ22,  σ33, electric displacement D3, and magnetic flux density B3 exhibited symmetric distributions about the midplane, while the displacement u2 and traction σ21 showed anti-symmetric behavior. (2) The displacement u2 reached maximum magnitudes at both the top and bottom surfaces of the plate, while the traction σ21,stress σ33, and magnetic flux density B3 peaked at material interfaces. For the BTO/CFO/BTO plate configuration, we observed the following: (1) The relative scaling parameter Γm inversely affected interfacial discontinuities: increasing Γm decreased jumps in σ11,σ33, D3 and B3, while increasing the σ21 discontinuity. (2) Increasing the nonlocal lengths l decreased σ21,σ11, σ33, along with the interface discontinuities in D3 and B3. (3) The displacement u2 and traction σ22 showed minimal sensitivity to nonlocal effects, as indicated by clustered mode shapes in the parameter space. (4) Imperfect contacts dominated over the nonlocal effects in modifying mode shapes. (5) The extended interface stress conditions induced polarity reversal in traction σ21 and σ22 fields. In contrast, the nonlocal length showed no polarity-reversal effects. For the CFO/BTO/CFO plate configuration, except the stress σ11, all the remaining field components underwent directional reversal when both conditions were met: relative scaling parameter Γm=100 and nonlocal length l=0.12.

4.2 Love Wave

Figs. 8 and 9 show the variation of the first three dispersion curves for the Love wave in the BTO/CFO/BTO and CFO/BTO/CFO sandwich plate configurations under different nonlocal lengths and interfacial contact conditions. The analysis revealed that nonlocal effects significantly reduced dispersion values, particularly in high-frequency regimes (characterized by large wavenumbers and short wavelengths). Additionally, the nonlocal length modifications significantly altered the overall trend of the dispersion curves. The dispersion curves converged more rapidly as the nonlocal length increased. An increase in the nonlocal length resulted in a decrease in the slope of the curves. Furthermore, the effect of the interfacial imperfection was significant (Tables 3 and 4) for selected points at a wavenumber of kH=2 in the BTO/CFO/BTO and CFO/BTO/CFO sandwich plates, respectively. The identical response patterns observed for both Love and Lamb waves indicated that the nonlocal constitutive law (1), rather than wave vibration type, primarily regulated dispersion characteristics.

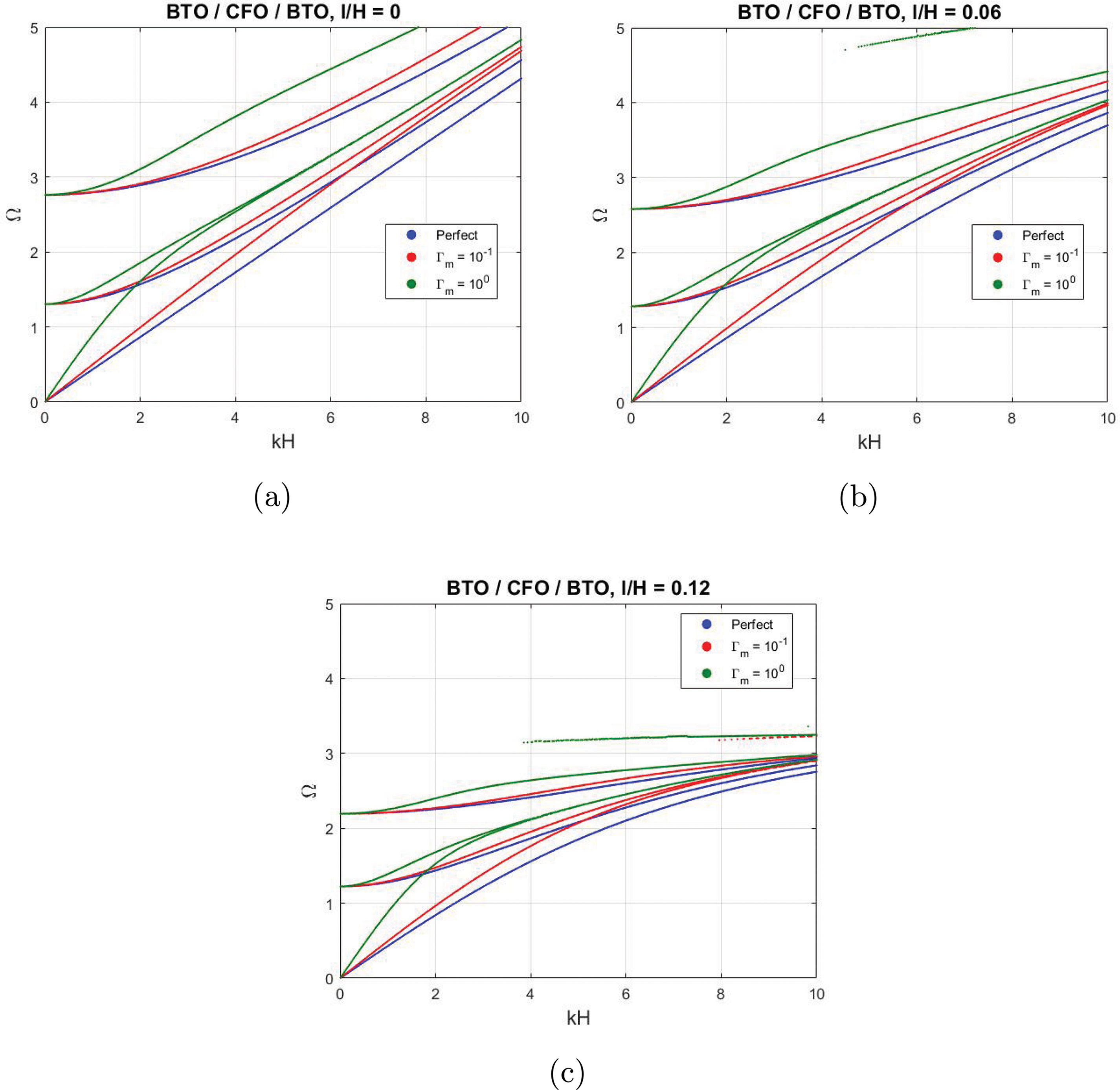
Figure 8: Dispersion curves for Love waves in a BTO/CFO/BTO sandwich plate with different interface contacts: perfect contact, imperfect contact with the relative scaling parameter Γm=10−1, Γm=100. Dimensionless nonlocal length parameter (a) l/H = 0, (b) l/H = 0.06, (c) l/H = 0.12

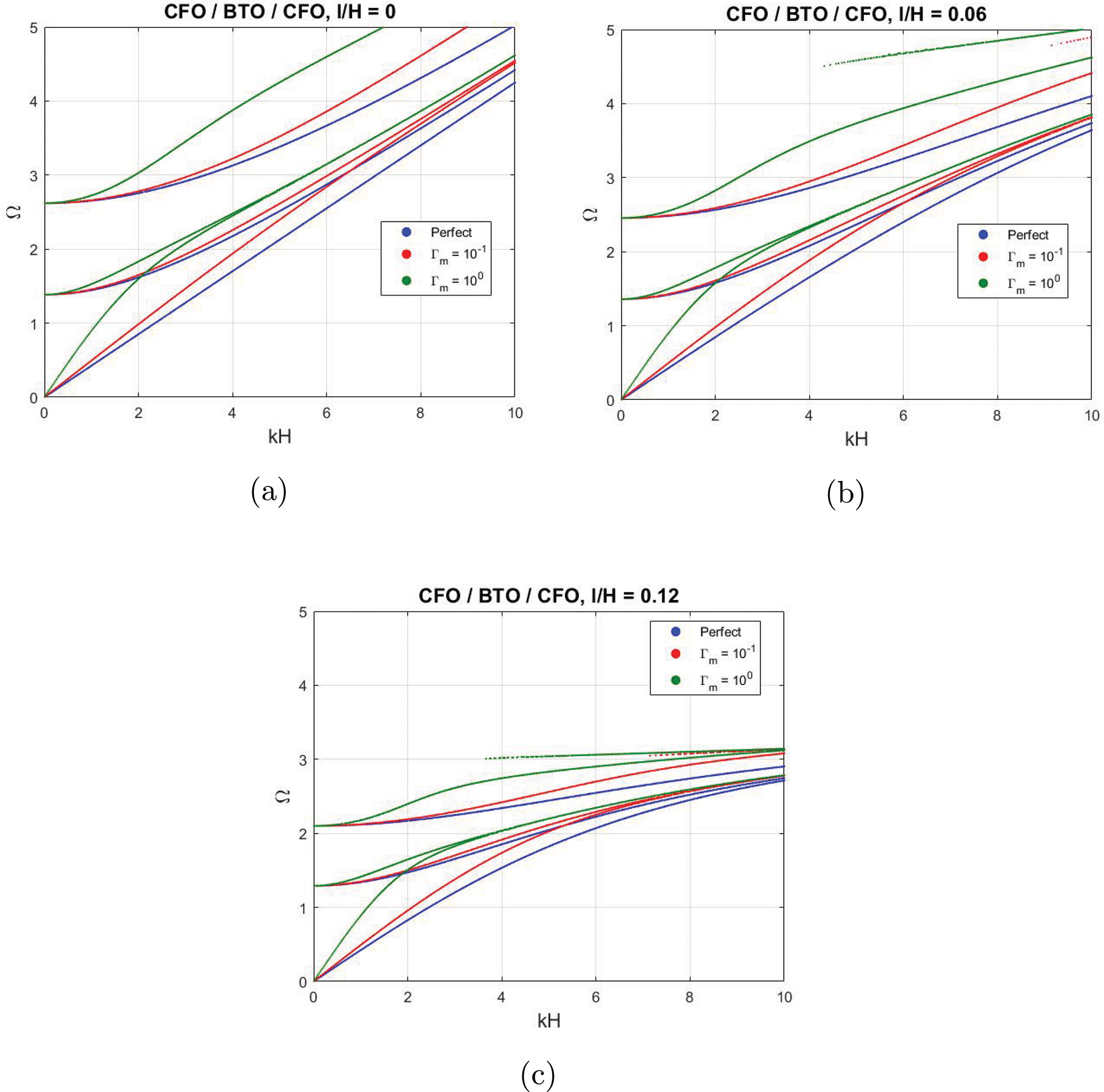
Figure 9: Dispersion curves for Love waves in a CFO/BTO/CFO sandwich plate with different interface contacts: perfect contact, imperfect contact with the relative scaling parameter Γm=10−1, Γm=100. Dimensionless nonlocal length parameter (a) l/H= 0, (b) l/H = 0.06, (c) l/H = 0.12

Figs. 10 and 11 illustrate thickness-wise distributions of the first-order and second-order mode shapes of the BTO/CFO/BTO plate at a wavenumber kH=2, respectively. Panels (a–c) show the elastic displacement u3, electric potential ϕ, and magnetic potential ψ. Panels (d–f) show the shear stresses σ13, σ23, electric displacements D1, D2 and magnetic flux densities B1,B2, respectively. Figs. 12 and 13 illustrate the corresponding mode shapes for the CFO/BTO/CFO plate. Analysis of first-order mode shapes (Figs. 10 and 12) revealed seven key characteristics: (1) The displacement u3, electric potential ϕ, and magnetic potential ψ remained continuous across the imperfect interfaces, while the traction σ23, normal electric displacement D2, and magnetic flux density B2 exhibited discontinuities. (2) The distributions of u3,ϕ, ψ, σ13, D1, and B1 were symmetric about the midplane, while σ23, D2, and B2 showed anti-symmetric behavior. (3) The traction σ23, electric displacement D1, D2, magnetic flux density B1 and B2 reached their maximum values at the interfaces. (4) An increase in the relative scaling parameter Γm resulted in an increase of σ23, D2 and B2. This occurred due to the increasing the interface stiffness (or equivalently, the relative scaling parameter Γm) enhanced the discontinuity in σ23, D2 and B2 across the interface under the interface stress model. (5) An increase in the nonlocal length l resulted in a decrease in u3, σ13, σ23, D1, D2, B1, and B2. (6) The nonlocal length l exhibited a minimal effect on the distribution of ϕ and ψ. The corresponding mode shapes were clustered, indicating insensitivity to the nonlocal length. (7) Compared to the effect of imperfect conditions, the influence of the nonlocal length on the mode shape distributions was less significant.

Figure 10: Variations for the first-order mode shapes of the Love wave in a BTO/CFO/BTO plate along the thickness direction (dimensionless wavenumber kH = 2): (a–c) displacement u3, electric potential ϕ, and magnetic potential ψ, (d,e) stresses σ13 and σ23, (f,g) electric displacements D1 and D2, (h,i) magnetic flux density B1 and B2. The plate is with nonlocal effect and extended interface stress imperfect interfaces

Figure 11: Variations for the second-order mode shapes of the Love wave in a BTO/CFO/BTO plate along the thickness direction (dimensionless wavenumber kH = 2): (a–c) displacement u3, electric potential ϕ, and magnetic potential ψ, (d,e) stresses σ13 and σ23, (f,g) electric displacements D1 and D2, (h,i) magnetic flux density B1 and B2. The plate is with nonlocal effect and extended interface stress imperfect interfaces

Figure 12: Variations for the first-order mode shapes of the Love wave in a CFO/BTO/CFO plate along the thickness direction (dimensionless wavenumber kH = 2): (a–c) displacement u3, electric potential ϕ, and magnetic potential ψ, (d,e) stresses σ13 and σ23, (f,g) electric displacements D1 and D2, (h,i) magnetic flux density B1 and B2. The plate is with nonlocal effect and extended interface stress imperfect interfaces

Figure 13: Variations for the second-order mode shapes of the Love wave in a CFO/BTO/CFO plate along the thickness direction (dimensionless wavenumber kH = 2): (a–c) displacement u3, electric potential ϕ, and magnetic potential ψ, (d,e) stresses σ13 and σ23, (f,g) electric displacements D1 and D2, (h,i) magnetic flux density B1 and B2. The plate is with nonlocal effect and extended interface stress imperfect interfaces

For the second-order mode shapes (Figs. 11 and 13), the following features were observed for both plate configurations: (1) The distributions of u3,ϕ, ψ, σ13, D1 and B1 were anti-symmetric about the midplane, while the extended tractions σ23, D2, and B2 were symmetric about the midplane. (2) The fields of u3, σ13 reached their maximum values at both the top and bottom surfaces, while the fields of D1, D2, B1 and B2 peaked at the interfaces. (3) An increase in the relative scaling parameter Γm resulted in a decrease of u3, ϕ, ψ, and σ13 and an increase of the discontinuities of σ23, D1, D2, B1 and B2 across the interfaces. (4) An increase in the nonlocal length l resulted in a decrease in σ13 and σ23. (5) The nonlocal length l had negligible effects on u3, ϕ, and ψ. The mode shapes of these field quantities were clustered, suggesting insensitivity to the nonlocal length parameter. (6) Compared to the extended interface stress conditions, the effects of the nonlocal length on the mode shape distributions were less significant.

5  Conclusions

In this study, a comprehensive analytical framework was developed for predicting three-dimensional field distributions in nonlocal MEE laminates with interface stress imperfections. The methodology was used to generalize four key components: the pseudo-Stroh formulation, transfer matrix method, interface matrix method, and the nonlocal constitutive equation proposed by Eringen, which were collectively facilitate recursive field solutions. The key theoretical advancement involved the constructive relationship between the nonlocal and classical extended tractions fields. The analytical framework was illustrated through its application to BTO/CFO/BTO and CFO/BTO/CFO sandwich plates. The study revealed the following key findings: (1) both the nonlocal effect and interface stress-type imperfections significantly influenced the dispersion curves; (2) increasing the nonlocal length reduced the natural frequency, particularly in high-frequency regions; (3) increasing the severity of interface stress-type imperfections increases the natural frequency; (4) compared to the interface imperfections, the nonlocal effect has a less significant influence on the mode shapes of most field quantities; (5) the mode shapes of some field quantities exhibit similar behavior and appear insensitive to variations in the nonlocal length parameter; (6) interface stress-type imperfections reverses the direction and enhances the magnitude of the mode shapes, with the nonlocal effect further amplifying these changes.

While the current model effectively captures the local behavior of the investigated plate, its applicability to more complex laminated nanostructures may be limited. Specifically, the formulation may require an extension to address piezomagnetic facesheet configurations or a CNT composite layer with piezoelectric surface layers (common in energy harvesting applications). Future studies should focus on extending this framework to investigate these advanced MEE plate configurations, incorporate higher-fidelity plate theories (e.g., layer-wise or zigzag models), and improve local field distribution predictions in composite architecture [33].

Acknowledgement: The author is grateful to the editor and anonymous referees for their insightful comments and suggestions, which helped to improve the paper’s presentation.

Funding Statement: The study is supported by the Ministry of Science and Technology Taiwan under Grant No. MOST 109-2628-E-009-002-MY3.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Hsin-Yi Kuo; analysis and interpretation of results: Li-Huan Yang, Hsin-Yi Kuo; draft manuscript preparation: Li-Huan Yang, Hsin-Yi Kuo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data that support the findings of this study are included within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Eerenstein W, Mathur ND, Scott JF. Multiferroic and magnetoelectric materials. Nature. 2006;442(7104):759–65. doi:10.1038/nature05023. [Google Scholar] [PubMed] [CrossRef]

2. Vinyas M. Computational analysis of smart magneto-electro-elastic materials and structures: review and classification. Arch Comput Method Eng. 2021;28(3):1205–48. doi:10.1007/s11831-020-09406-4. [Google Scholar] [CrossRef]

3. Shetty S, Palkar VR, Pinto R. Size effect study in magnetoelectric BiFeO3 system. J Phys. 2002;58(5–6):1027–30. doi:10.1007/s12043-002-0211-4. [Google Scholar] [CrossRef]

4. Bühlmann S, Dwir B, Baborowski J, Muralt P. Size effect in mesoscopic epitaxial ferroelectric structures: increase of piezoelectric response with decreasing feature size. Appl Phys Lett. 2002;80(17):3195–7. doi:10.1063/1.1475369. [Google Scholar] [CrossRef]

5. Yoo K, Jeon BG, Chun SH, Patil DR, Lim YJ, Noh SH, et al. Quantitative measurements of size-dependent magnetoelectric coupling in Fe3O4 nanoparticles. Nano Lett. 2016;16(12):7408–13. doi:10.1021/acs.nanolett.6b02978. [Google Scholar] [PubMed] [CrossRef]

6. Eringen AC. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys. 1983;54(9):4703–10. doi:10.1063/1.332803. [Google Scholar] [CrossRef]

7. Eringen AC. Nonlocal continuum field theories. New York, NY, USA: Springer; 2002. [Google Scholar]

8. Di Paola M, Failla G, Pirrotta A, Zingales M. The mechanically based non-local elasticity: an overview of main results and future challenges. Philos Trans A. 2013;371(1993):20120433. doi:10.1098/rsta.2012.0433. [Google Scholar] [PubMed] [CrossRef]

9. Wu C-P, Li W-C. Free vibration analysis of embedded single-layered nanoplates and graphene sheets by using the multiple time scale method. Computer Math Appl. 2017;73(5):838–54. doi:10.1016/j.camwa.2017.01.014. [Google Scholar] [CrossRef]

10. Wu C-P, Yu J-Y. A review of mechanical analyses of rectangular nanobeams and single-, double-, and multi-walled carbon nanotubes using Eringen’s nonlocal elasticity theory. Arch Appl Mech. 2019;89(9):1761–92. doi:10.1007/s00419-019-01542-z. [Google Scholar] [CrossRef]

11. Ke L-L, Wang Y-S, Yang J, Kitipornchai S. Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory. Acta Mech Sinica. 2014;30(4):516–25. doi:10.1007/s10409-014-0072-3. [Google Scholar] [CrossRef]

12. Amiri A, Fakhari SM, Pournaki IJ, Rezazadeh G, Shabani R. Vibration analysis of circular magneto-electro-elastic nano-plates based on Eringen’s nonlocal theory. Int J Eng Trans. 2015;C 28:1808–17. [Google Scholar]

13. Pan E, Waksmanski N. Deformation of a layered magnetoelectroelastic simply-supported plate with nonlocal effect, an analytical three-dimensional solution. Smart Mater Struct. 2016;25(9):095013. doi:10.1088/0964-1726/25/9/095013. [Google Scholar] [CrossRef]

14. Waksmanski N, Pan E. An analytical three-dimensional solution for free vibration of a magneto-electro-elastic plate considering the nonlocal effect. J Intel Mater Syst Struct. 2017;28(11):1501–13. doi:10.1177/1045389x16672734. [Google Scholar] [CrossRef]

15. Ke L-L, Wang Y-S, Yang J, Kitipornchai S. The size-dependent vibration of embedded magneto-electro-elastic cylindrical nanoshells. Smart Mater Struct. 2014;23(12):125036. doi:10.1088/0964-1726/23/12/125036. [Google Scholar] [CrossRef]

16. Kuo H-Y. Effective moduli of multiferroic fibrous composites with strain gradient and electromagnetic field gradient effects. Int J Solids Struct. 2021;222–223:111007. doi:10.1016/j.ijsolstr.2021.02.018. [Google Scholar] [CrossRef]

17. Li G-E, Kuo H-Y. Effects of strain gradient and electromagnetic field gradient on potential and field distributions of multiferroic fibrous composites. Acta Mech. 2021;232(4):1353–78. doi:10.1007/s00707-020-02910-5. [Google Scholar] [CrossRef]

18. Liu C, Li. K, Min S, Chai Y. Dynamic analysis of the three-phase magneto-electro-elastic (MEE) structures with the overlapping triangular finite elements. Comput Math Appl. 2025;179:148–177.2. doi:10.1016/j.camwa.2024.11.025. [Google Scholar] [CrossRef]

19. Jiang Z, Gui Q, Li W, Chai Y. Assessment of the edge-based smoothed finite element method for dynamic analysis of the multi-phase magneto-electro-elastic structures. Eng Anal Bound Elem. 2024;163(3):94–107. doi:10.1016/j.enganabound.2024.02.021. [Google Scholar] [CrossRef]

20. Kuo H-Y, Yang L-H, Huang P-C, Pan E. Comparisons of wave characteristics in magneto-electro-elastic laminated composites with different layering directions. Acta Mech. 2023;234(9):4467–85. doi:10.1007/s00707-023-03611-5. [Google Scholar] [CrossRef]

21. Ly D-K, Vu H-N, Thongchom C, Nguyen-Thoi T. A multi-physical coupling isogeometric formulation for nonlinear analysis and smart control of laminated CNT-MEE plates. Eng Anal Bound Elem. 2024;159(13):36–57. doi:10.1016/j.enganabound.2023.11.023. [Google Scholar] [CrossRef]

22. Bichurin MI, Petrov VM, Srinivasan G. Theory of low-frequency magnetoelectric coupling in magnetostrictive-piezoelectric bilayers. Phys Rev B. 2003;68(5):054402. doi:10.1103/physrevb.68.054402. [Google Scholar] [CrossRef]

23. Wang Y, Su Y, Li J, Weng GJ. A theory of magnetoelectric coupling with interface effects and aspect-ratio dependence in piezoelectric-piezomagnetic composites. J Appl Phys. 2015;117(16):164106. doi:10.1063/1.4919016. [Google Scholar] [CrossRef]

24. Kuo H-Y, Chung C-Y. Multiferroic laminated composites with interfacial imperfections and the nonlocal effect. Compos Struct. 2022;287:115235. doi:10.1016/j.compstruct.2022.115235. [Google Scholar] [CrossRef]

25. Kuo H-Y, Wang Y-H. Wave motion of magneto-electro-elastic laminated plates with membrane-type interfacial imperfections. Compos Struct. 2022;293:115661. doi:10.1016/j.compstruct.2022.115661. [Google Scholar] [CrossRef]

26. Kuo H-Y, Huang P-C. Nonlocal free vibration of magneto-electro-elastic nanoplates with imperfect contacts. Mech Adv Mater Struct. 2024;31(30):12759–73. doi:10.1080/15376494.2024.2328753. [Google Scholar] [CrossRef]

27. Dong S, Li J-F, Viehland D. Longitudinal and transverse magnetoelectric voltage coefficients of magnetostrictive/piezoelectric laminate composite: experiments. IEEE Trans Ultras, Ferroelectr Frequ Control. 2004;51(7):794–9. doi:10.1109/tuffc.2004.1320738. [Google Scholar] [PubMed] [CrossRef]

28. Wang Y, Or SW, Chan HLW, Zhao Z, Luo H. Enhanced magnetoelectric effect in longitudinal-transverse mode Terfenol-D/Pb(Mg1/3Nb2/3)O3-PbTiO3 laminate composites with optimal crystal cut. J Appl Phys. 2008;103(12):124511. doi:10.1063/1.2943267. [Google Scholar] [CrossRef]

29. Zhai J, Xing Z, Dong S, Li J, Viehland D. Magnetoelectric laminate composites: an overview. J Am Ceram Soc. 2008;91(2):351–8. doi:10.1111/j.1551-2916.2008.02259.x. [Google Scholar] [CrossRef]

30. Benveniste Y, Miloh T. Imperfect soft and stiff interfaces in two dimensional elasticity. Mech Mater. 2001;33(6):309–23. doi:10.1016/s0167-6636(01)00055-2. [Google Scholar] [CrossRef]

31. Chen J, Guo J, Pan E. Wave propagation in magneto-electro-elastic multilayered plates with nonlocal effect. J Sound Vibrat. 2017;440:550–63. doi:10.1016/j.jsv.2017.04.001. [Google Scholar] [CrossRef]

32. Zhu F, Wang B, Qian ZH. A numerical algorithm to solve multivariate transcendental equation sets in complex domain and its application in wave dispersion curve characterization. Acta Mech. 2019;230(4):1303–21. doi:10.1007/s00707-017-2025-y. [Google Scholar] [CrossRef]

33. Ly D-K, Vu-Do H-C, Thongchom C, Nguyen-Thoi T. A multiscale and multiphysical numerical approach for sandwich multiphasehybrid fiber plates with smart composite facesheets. Eng Anal Bound Elem. 2025;173(03):106134. doi:10.1016/j.enganabound.2025.106134. [Google Scholar] [CrossRef]