 Open Access
Open Access
ARTICLE
Computational Design of Interval Type-2 Fuzzy Control for Formation and Containment of Multi-Agent Systems with Collision Avoidance Capability
1 Department of Marine Engineering, National Taiwan Ocean University, Keelung, 202, Taiwan
2 Department of Information Management, National Sun Yat-Sen University, Kaohsiung, 804, Taiwan
3 Artificial Intelligence Research Institute, China University of Mining and Technology, Xuzhou, 2211106, China
4 Department of Marine Engineering, National Kaohsiung University of Science and Technology, Kaohsiung, 811, Taiwan
* Corresponding Authors: Wen-Jer Chang. Email: ; Yi-Chen Lee. Email:
(This article belongs to the Special Issue: Computational Models and Applications of Multi-Agent Systems in Control Engineering and Information Science)
Computer Modeling in Engineering & Sciences 2025, 144(2), 2231-2262. https://doi.org/10.32604/cmes.2025.067464
Received 04 May 2025; Accepted 01 August 2025; Issue published 31 August 2025
Abstract
An Interval Type-2 (IT-2) fuzzy controller design approach is proposed in this research to simultaneously achieve multiple control objectives in Nonlinear Multi-Agent Systems (NMASs), including formation, containment, and collision avoidance. However, inherent nonlinearities and uncertainties present in practical control systems contribute to the challenge of achieving precise control performance. Based on the IT-2 Takagi-Sugeno Fuzzy Model (T-SFM), the fuzzy control approach can offer a more effective solution for NMASs facing uncertainties. Unlike existing control methods for NMASs, the Formation and Containment (F-and-C) control problem with collision avoidance capability under uncertainties based on the IT-2 T-SFM is discussed for the first time. Moreover, an IT-2 fuzzy tracking control approach is proposed to solve the formation task for leaders in NMASs without requiring communication. This control scheme makes the design process of the IT-2 fuzzy Formation Controller (FC) more straightforward and effective. According to the communication interaction protocol, the IT-2 Containment Controller (CC) design approach is proposed for followers to ensure convergence into the region defined by the leaders. Leveraging the IT-2 T-SFM representation, the analysis methods developed for linear Multi-Agent Systems (MASs) are successfully extended to perform containment analysis without requiring the additional assumptions imposed in existing research. Notably, the IT-2 fuzzy tracking controller can also be applied in collision avoidance situations to track the desired trajectories calculated by the avoidance algorithm under the Artificial Potential Field (APF). Benefiting from the combination of vortex and source APFs, the leaders can properly adjust the system dynamics to prevent potential collision risk. Integrating the fuzzy theory and APFs avoidance algorithm, an IT-2 fuzzy controller design approach is proposed to achieve the F-and-C purpose while ensuring collision avoidance capability. Finally, a multi-ship simulation is conducted to validate the feasibility and effectiveness of the designed IT-2 fuzzy controller.Keywords
Prompted by the rapid development of intelligent equipment, control problems under the Multi-Agent System (MAS) framework have proliferated in recent decades [1]. Since the agents can achieve common goals through their own communication, these control issues have become an important milestone for the cooperative control of multiple autonomous vehicles [2]. In various control scenarios, the cooperation of multiple autonomous devices offers a faster and more efficient solution than using only one device. More importantly, multiple autonomous devices equipped with low-cost onboard systems can serve as a substitute for a single device that relies on high-end equipment [3]. This advantage significantly reduces the cost when the devices require maintenance and are even destroyed. In the broader context of control issues in MASs, cooperative behaviors are primarily discussed in terms of consensus, formation, and containment [4–6]. Consensus control serves as a foundational application for multiple agents to coordinate and reach a common state. Under the leader-follower control framework, consensus means that all follower agents reach the same state as the leader [4]. When there is more than one leader, the consensus problem escalates to the containment problem. Containment control is commonly found in control scenarios where agents with lower capabilities need to be protected by those with higher capabilities and guided into a specific region [5]. Usually, this specific region is defined through the formation control of leaders. Formation control refers to making the agents adhere to a predetermined order to achieve the formation [6]. This feature makes formation control a dominant topic in the research of MASs.
The Formation and Containment (F-and-C) issues have contributed to more efficient achievement of common objectives and broadened the application scope of multi-device control. An increasing number of researchers have also developed composite applications of the Formation Controller (FC) and Containment Controller (CC) using the leader-follower framework [7–9]. However, the safety of agents, especially the leaders, in MASs remains a critical concern due to the dynamic and ever-changing working environments in which autonomous devices operate. Given this consideration, an increasing number of researchers have placed emphasis on the issue of collision avoidance in the control of MASs. Several researchers have also incorporated the collision avoidance mechanism into the design of FC and CC [10,11]. It should be noted that the path planning algorithm plays a crucial role in collision-avoidance methods. Over the past decades, various motion or path planning algorithms have been developed and remained active research topics in collision avoidance scenarios, such as the A* algorithm [12], the dynamic window approach [13], the velocity obstacle method [14], and the Artificial Potential Field (APF) [15]. The collision avoidance mechanisms based on the APF offers advantages such as an intuitive design process, low computational complexity, and reliance on local environmental information. These features make APF particularly suitable for scenarios involving multiple unit encounters and situations requiring rapid emergency responses. For the design of FC and CC, the APF method has also been employed to achieve control objectives while maintaining the capability to avoid collisions between agents [10,11]. Up to now, only a few studies have investigated the collision avoidance issue using the APF in the F-and-C control of MASs.
However, the inherent nonlinearities in system dynamics must be considered due to the complex working environments and the control precision requirements of autonomous devices. With consideration of the interaction protocol, it can be observed that nonlinear dynamic behaviors in Nonlinear MASs (NMASs) significantly complicate the controller design process [4–9]. It is further worth noting that the complexities and challenges are exacerbated when multiple control objectives are required, such as incorporating the collision avoidance issue into F-and-C [10,11]. Solving the control and analysis challenges of systems with nonlinearities, the Takagi-Sugeno Fuzzy Model (T-SFM) has been proposed as an efficient method to convert nonlinear control problems into linear [16–19]. In this manner, nonlinear systems can be linearized into multiple linear subsystems based on a set of fuzzy rules by appropriately selecting premise variables and operating ranges. This characterization enables the design of fuzzy controllers within the linear framework and efficiently reduces the design complexity associated with nonlinear control methods. According to [20], the kinematic components of the mathematical model for the mobile robot exhibit clear nonlinear characteristics. The researchers used the T-SFM to achieve trajectory tracking along with obstacle avoidance capability. Since fuzzy logic and fuzzy inference systems serve as a powerful approach in decision making, fuzzy theory has gradually been integrated into various obstacle avoidance methods [21,22]. Researchers have also extended the fuzzy-based obstacle avoidance mechanism into the FC design using the APF method [23,24]. However, the collision avoidance using fuzzy logic for the F-and-C control of MASs remains an open issue, especially when considering the integration of APF.
Nevertheless, the so-called type-1 T-SFM used in previous studies [16–20] is insufficient for comprehensively characterizing uncertainties in nonlinear systems. This limitation also results in the corresponding fuzzy controller design methods being unable to handle uncertainties. In widely adopted applications of NMASs, such as unmanned vehicles, uncertainty problem becomes even more critical. These uncertainties may be attributed to discrepancies in the design of membership grades from a linguistic perspective, and structural changes from an application perspective [25,26]. As a result, Type-2 (T-2) fuzzy sets and fuzzy systems have been developed to more comprehensively incorporate uncertain factors into system modeling [27]. A typical T-2 MF consists of primary and secondary membership grades, which results in a three-dimensional structure. However, this structure significantly increases the computational complexity and burden compared to the two-dimensional type-1 MFs [28]. To improve practicality, Interval Type-2 (IT-2) MFs were introduced by setting all secondary membership grades to the maximum value of 1 [29], which reduces computational burden and still maintains a reasonable level of descriptive capability. The IT-2 T-SFM offers better capability for modeling nonlinear systems with uncertainties than type-1 T-SFM, while requiring lower computational resources than the general T-2 T-SFM. Since computational efficiency remains a key concern in real-world control systems, especially in autonomous devices with dynamic uncertainty, this advantage makes IT-2 fuzzy systems a widely adopted solution [30]. Furthermore, due to the close relationship between collision avoidance and decision-making, IT-2 fuzzy logic controllers have been successfully applied to address uncertainties in practical avoidance scenarios [31]. In addition, IT-2 fuzzy control theory provides a powerful framework for NMASs, which involve high computational demands, to mitigate the effects of dynamic uncertainties [32,33].
Although the F-and-C controllers for NMASs have been proposed by some researchers [34,35], the nonlinear frameworks reduce practical applicability and cost-effectiveness. Leveraging the IT-2 T-SFM representation [36], nonlinear control design problems can be recast as the linear problems, while uncertainties are also better handled. As the pioneering work applying IT-2 T-SFM to UNMASs, the researchers in [37] have solved the containment problem of UNMASs under the leader-follower framework. Nevertheless, the leaders are considered as the open-loop systems, which lead to the divergence of the entire UNMAS since the leaders are unstable even though the followers achieve containment. In [38,39], the authors developed the IT-2 fuzzy F-and-C controller design method, which not only guarantees leaders’ stability but also achieves the formation objective. In contrast to the existing formation-containment literatures, the design concept of the IT-2 fuzzy FC for leaders is proposed by developing the individual tracking controller. This FC design strategy eliminates the need for communication between the leaders that are farthest apart from each other in the F-and-C problem and enables specifying the entire UNMAS dynamics and time-varying formation without the additional control term in the FC framework. The detailed advantages of the IT-2 F-and-C design method can be found in [39]. However, the safety of agents in UNMASs can only be ensured if the agents possess collision avoidance capabilities. It can be inferred that, since the IT-2 fuzzy F-and-C controller design method for UNMASs was first proposed in [38,39], the collision avoidance issue under this framework has not yet been investigated. Moreover, a novel collision avoidance algorithm is proposed in this research by combining the fuzzy logic and the APF method. Extending the application of fuzzy theory, very few studies have used fuzzy logic to allocate control efforts between modes [40], and research using fuzzy logic to allocate between different APF types remains limited. However, combining different types of APF is a common practice in collision avoidance. Moreover, these studies on the fuzzy APF method still focus on single control systems. Based on the above statements, the contributions of this research can be summarized as follows:
(1) Building upon the advantages of the IT-2 fuzzy FC design concept in [38,39], an IT-2 fuzzy F-and-C controller design approach combined with a collision avoidance method is first proposed for UNMASs.
(2) A new collision avoidance algorithm is developed by combining the APF method and fuzzy theory, and integrated into the IT-2 fuzzy FC design under the IT-2 T-SFM framework.
(3) Fuzzy logic is used to manage the switching between different APF types, including the vortex APF and the source APF, as well as between the trajectory tracking mode and the collision avoidance mode. In addition, the Distance at Closest Point of Approach (DCPA), commonly applied in avoidance scenarios, is selected to serve as the criterion within the fuzzy logic for determining the switching between modes.
Following the discussion of contributions, the design procedure for this research is presented as follows. First, the IT-2 T-SFM is constructed to more comprehensively represent UNMASs by extending the results in [36]. Leveraging the IT-2 T-SFM and the Imperfect Premise Matching (IPM) concept, the IT-2 fuzzy FC is designed with the tracking control approach, and the IT-2 fuzzy CC is designed with the interaction protocol. Most importantly, the collision avoidance algorithm is proposed by combining fuzzy theory and the APF method into the FC design for the leaders. Since the followers all comply with the dynamics of the leaders, the entire UNMAS can avoid potential collision and obstacle risks if the leaders have the avoidance capability. In this research, a vortex flow serves to steer the agents toward the right-hand side, whereas a source flow serves to repel the agents away from collision points. For the closed-loop IT-2 T-SFM, the IT-2 MF-dependent stability analysis methods are proposed to achieve F-and-C for leaders and followers according to Lyapunov theory. It is worth noting that the desired trajectories calculated by the APF-based method must also be tracked in the avoidance mode, which can efficiently be solved by the IT-2 tracking controller designed for the formation purpose. Finally, the stability conditions are converted into a Linear Matrix Inequality (LMI) problem for the IT-2 fuzzy F-and-C controller design. To verify the feasibility and applicability, a simulation considering multiple ships under the UNMAS structure is conducted.
The organization of this research is as follows. In Section 2, the IT-2 T-SFM and IPM-based fuzzy F-and-C controller are presented for UNMASs. The vortex and source flows are also introduced for the APF method. In Section 3, the stability criteria and IT-2 fuzzy F-and-C controller design with the collision avoidance algorithm are proposed. In Section 4, the simulation results of a multi-ship UNMAS are presented to verify the formation, containment, and collision avoidance performances. In Section 5, some conclusions are presented for the proposed IT-2 fuzzy F-and-C control method.
2 System Description and Problem Statements
In this section, the T-SFM is established for UNMASs based on interval type-2 fuzzy sets. To achieve the tracking objective, an IT-2 T-SFM is also constructed for the target trajectory of UNMASs. By dividing the IT-2 T-SFM into leader and follower models, the IT-2 fuzzy F-and-C controller are respectively developed according to the IPM concept. Subsequently, the definitions of vortex and source flows are introduced to aid the APF-based collision avoidance design. First, the IT-2 T-SFM is presented as follows.
where
where
For the formation of leaders under the tracking control framework, the IT-2 T-SFM of the target trajectory is constructed in a similar manner to (1).
For the followers in UNMASs, the interaction protocol is considered through communication between agents to achieve the containment purpose. Because of this reason, the definition of the interaction relationship for the followers in IT-2 T-SFM (1) is provided based on graph theory as follows.
Definition 1: For an undirected graph
Based on Definition 1, the agents in UNMASs are denoted as nodes while the interaction relationships are denoted as edges. In most leader-follower structures, the leaders serve as units to detect environmental changes and potential dangers, subsequently commanding the followers for control purposes. That is to say, the leaders do not acquire information from other agents. As a result, the Laplacian matrix
where
Referring to [37], the properties of the Laplacian matrix (4) are presented in Lemma 1.
Lemma 1 [37]: All eigenvalues of matrix
In this research, it is assumed that there is at least one interaction from each leader to the followers. Then, dividing the IT2 T-SFM (1) into the leader and follower parts, the following tracking error model for the leader is obtained by subtracting (3) from the leader’s T-SFM.
where
Therefore, the tracking objective can be achieved by designing the control input
For the error model (5) of leaders and the followers in the IT-2 T-SFM (1), the IT-2 fuzzy controller is designed as follows to achieve the F-and-C objectives.
where
where
It is worth noting that the MFs as well as the fuzzy rules of FC and CC in (6) and (7) can be designed differently due to the IPM concept. This feature makes the fuzzy controller design process more flexible and helps reduce application complexity by using fewer rules in the controller. Accordingly, the closed-loop error model for leaders can be obtained by substituting (6) into (5) as follows.
From (9), it can be observed that if the tracking error converges through the design of gain
To achieve the containment objective for followers, the closed-loop IT-2 T-SFM is obtained as follows by substituting (7) into (1).
where
Nevertheless, the analysis process for fuzzy CC design may become increasingly conservative as both the number of agents and the fuzzy rules escalate due to the growing number of stability conditions. To solve the problem, an analysis approach for the containment analysis of the IT-2 T-SFM (10) as follows.
Lemma 2 [41]: Let
where
Owing to the representation of IT-2 T-SFM, Lemma 2 can be utilized for the followers in UNMASs. From Lemma 2, it can be seen that the conditions in (11) are presented in LMI form. Moreover, the condition (11) indicates that only four LMI conditions need to be solved during the containment analysis process, regardless of how many followers are present in the UNMASs. This reduction in the number of stability conditions significantly benefits the controller design method based on the T-SFM, since the number of conditions tends to increase with the number of rules.
After the F-and-C objectives are ensured for leaders and followers, the collision avoidance requirement must also be considered for the safety improvement of UNMASs. By combining the fuzzy theory with the APF method, the collision avoidance algorithm is incorporated into the IT-2 fuzzy F-and-C controller design process. However, one of the most critical issues in the APF method is the deadlock problem. Based on the results in [42], a velocity potential field design approach is presented to efficiently avoid deadlock in collision avoidance situations.
Remark 1: Referring to [42], no deadlock exists within the region if the velocity potential function
Since the prerequisite information required by the APF method is difficult to be directly provided based on the state vector of the IT-2 T-SFM (9) and (10), the states of the leader agents are preliminarily assumed as follows for the application. Specifically, the X and Y positions, yaw angle on the earth-fixed frame, as well as the longitudinal and lateral velocities and yaw angular velocity on the body-fixed frame, are typically considered in trajectory tracking problems. Therefore, the states are set as
Definition 2: The vortex potential field and the corresponding gradient are given as follows.
Definition 3: The source potential field and the corresponding gradient are given as follows.
where
Note that the vortex potential field is defined with a counterclockwise direction to adjust the agents toward the right-hand side in this research. Moreover, the source potential field serves as an APF to repulse the agents away from the collision events. According to the theory of APF method, it is known that if only the source APF is applied in the collision avoidance mechanism, the agent may become stuck at a point in front of the obstacle when the target is located directly behind the obstacle. In addition, if only the vortex APF is applied, the agent may keep circling around the obstacle without reaching the target. Based on the definitions in (12) and (13), these undesired behaviors become more significant as the agent gets closer to the obstacle, which corresponds to the center of the APFs. To overcome these problems, a combined application of the source APF and the vortex APF is proposed in this research through the use of fuzzy logic. The key function of fuzzy logic is that the abrupt changes caused by the switching between different APFs can be reduced, and smoother avoidance behavior can be realized.
In addition to the APF method, the Time to Closest Point of Approach (TCPA) and Distance at Closest Point of Approach (DCPA) are commonly used for the assessment of collision situations and risks. The concepts of TCPA and DCPA have been widely applied in collision avoidance for autonomous vehicles. Incorporating these factors into the development of collision avoidance algorithms enables agents to achieve more precise avoidance performance. Based on the above setting for the system states, the TCPA and DCPA are presented in Definition 4.
Definition 4: The TCPA and DCPA for all potential collisions are defined using the positions
TCPAσ:
DCPAσ:
where the vectors
Within the collision avoidance framework, the TCPA and DCPA parameters are utilized to assess whether a potential collision event is imminent within the detection range. Specifically, when the conditions based on TCPA and DCPA are satisfied, the leaders transition into collision avoidance mode; otherwise, the leaders maintain tracking mode. Upon entering collision avoidance mode, the target trajectories used in the IT-2 fuzzy formation controller (6) are generated by combining the vortex APF in Definition 2 and the source APF in Definition 3. Moreover, fuzzy logic is applied in this research to achieve smoother adjustment between the two APFs.
Therefore, an IT-2 fuzzy F-and-C controller design approach combined with the collision avoidance algorithm is proposed for UNMASs based on the IT-2 T-SFMs (9) and (10) and the APF method from Definitions 2–4. Moreover, Lemma 2 is also applied to obtain a more relaxed containment analysis process for followers.
3 Interval Type-2 Fuzzy Controller Design for Multiple Objectives
According to the IT-2 T-SFM (9) of tracking error, a more convenient stability criterion is proposed to achieve FC design objectives in this section. By virtue of this design scheme, a collision avoidance algorithm combining the APF method with fuzzy theory is also proposed for the leaders in UNMASs. After the collision-free formation controller has been designed, the IT-2 fuzzy CC design approach can be proposed for followers based on the interaction relationship among all agents. Therefore, the entire UNMAS can avoid potential collisions through the IT-2 fuzzy FC design and the control commands of leaders. Since the followers are ensured to converge into the leaders’ formation, their safety is certainly guaranteed by IT-2 fuzzy CC. First, a stability criterion for the IT-2 fuzzy FC design is proposed as follows based on the Lyapunov theory and the IPM concept.
Theorem 1: If there exist the positive definite matrices
where
Proof of Theorem 1: In this research, the formation control objective is achieved through individual trajectory tracking controllers for each leader. That is, due to the homogeneity among UNMASs, the stability analysis is only required to be developed for one leader. Accordingly, the Lyapunov function is defined as follows for the stability analysis.
where
It is known that the Lyapunov function (19) is defined for the tracking errors from an energy perspective. That is, if the derivative (20) of the Lyapunov function, which denotes the rate of energy change, is ensured to be negative, then the energy of the tracking error dynamics will converge to zero. This also implies that the leader dynamics can approach the desired target dynamics.
To simplify the IT-2 MF-dependent analysis method,
where
Subsequently, the upper and lower bound MFs in (21) can be defined as follows.
where
Then, the parameter
In relation to the IT-2 MFs, the slack matrices are introduced as follows.
Based on the properties of the IT-2 MFs, it can be readily verified that equality (25) and inequality (26) hold. These slack matrices are combined into the stability analysis and stability conditions as additional variables to be solved using LMI techniques. It is known that increasing the number of variables in the stability conditions can reduce conservatism when solving the control problem under stability criteria. With the combination of (25) and (26), the relationship for (24) is derived as follows.
Consequently, the following results can be obtained by extracting the cross term from the right-hand side of inequality (27).
It is obvious that the negative definiteness of (28) can be achieved if the stability conditions (16)–(18) are satisfied by Theorem 1. This implies that the asymptotic stability of the error dynamics for Leader 1 is ensured based on the relationship in (27). In conclusion, the states of Leader 1 in the UNMAS are capable of tracking the desired state trajectory. □
By Theorem 1, the IT-2 fuzzy controller (6) can be designed for Leader 1. It is worth noting that the designed fuzzy controller can be directly extended to all other leaders in view of the homogeneity. In other words, the design approach of Theorem 1 enables the leaders to complete the formation task merely by properly assigning different target trajectories to each leader. However, the leaders are still required to provide a collision avoidance capability to lead the entire UNMAS away from potential dangers. Therefore, a collision avoidance algorithm combining the APF method with fuzzy theory is presented as follows.
Theorem 2: Based on the IT-2 fuzzy FC designed in Theorem 1, the controller (6) is formulated as follows to simultaneously achieve the trajectory tracking and collision avoidance objectives.
where the desired state trajectories

In Algorithm 1, the conditions
The advantage of fuzzy logic lies in its ability to make the collision avoidance behavior of agents smoother and more reasonable. In Fig. 1a, the MF is designed to combine two different APFs using fuzzy logic. It is observed that when the distance to the potential collision event is less than
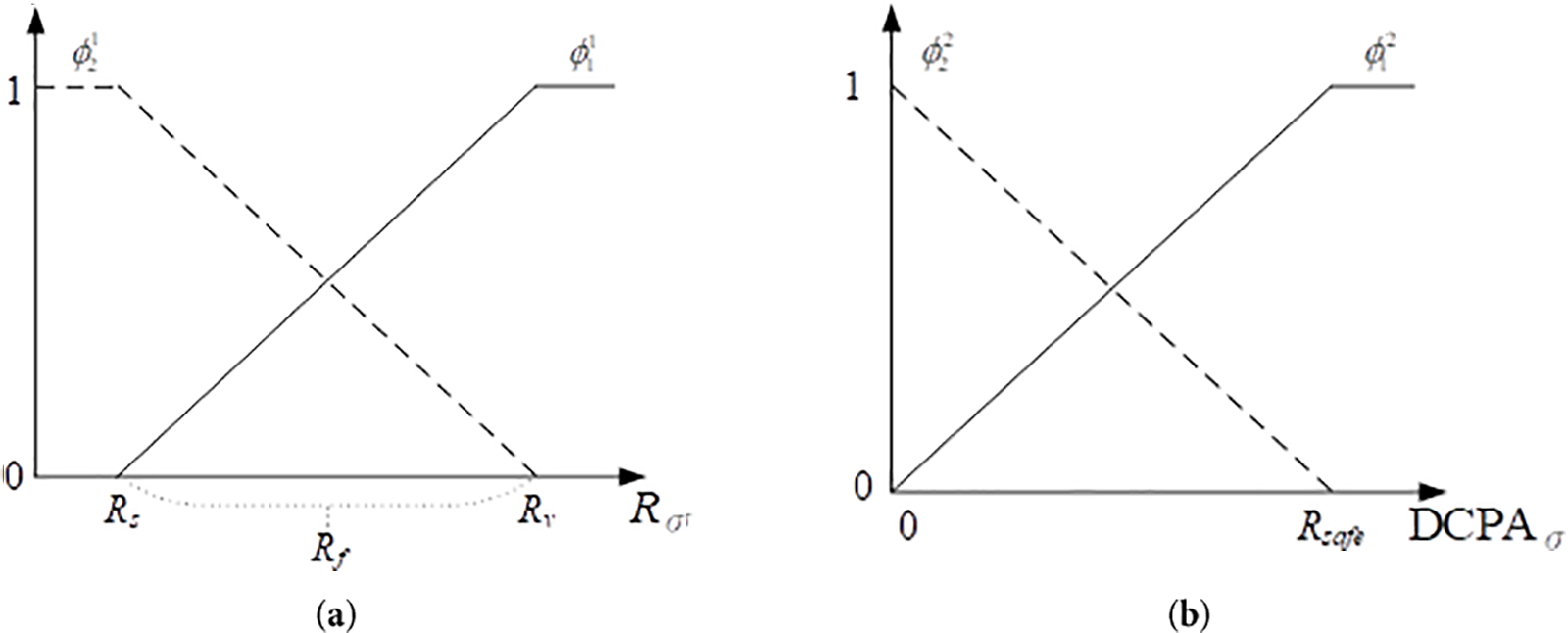
Figure 1: (a) MF associated with different APF strategies; (b) MF associated with different control modes
Similar to this concept, the fuzzy logic is applied in Step 6 when at least one collision event is detected, but no condition triggers the avoidance conditions, which prevents abrupt switching between the tracking mode and collision avoidance mode. Based on Theorem 2 and Algorithm 1, an IT-2 fuzzy FC design approach with the collision avoidance capability is proposed for leaders to lead the entire UNMAS away from potential risks.
Then, based on the control command for the leaders given in (29), the IT-2 fuzzy CC design approach is presented in the following theorem.
Theorem 3. If there exist the positive definite matrices
where
Proof of Theorem 3: To carry out the containment analysis, the containment error is first defined as follows for the IT-2 T-SFM (10).
Based on the definition of the containment error in (54), the followers’ dynamics can converge within the leaders’ dynamics based on the properties of the Laplacian matrix in Lemma 2 if the error dynamics are stabilized. Then, the following derivative is obtained from (53).
where
However, the control input of leaders
According to properties of Laplacian matrix in Lemma 1, the item associated with the vector
where
Then, the upper bound condition can be derived for (56) using the inequality
Consequently, the fact
where
In order to reduce the conservativeness of the containment analysis using Lemma 2, the nonsingular matrix
where
By expressing the variable in terms of the real part and the imaginary part, the error dynamic system (60) is reformulated in the following form.
where
Notably, the containment problem of system (59) with interaction among agents can be efficiently reduced to the analysis of individual follower agents by the expression of (61). To analysis the stability of dynamic system (61), the corresponding Lyapunov function is given as follows.
where
Following the analysis concept in [44], an ellipsoid is defined for the containment error dynamics.
Accordingly, the ellipsoid (63) can be ensured as an attractive invariant set if the following condition is satisfied.
Substituting (61), the following inequality can be obtained from (64).
By following a similar analytical procedure as in (20)–(28), (65) is derived as the following inequality based on the IT-2 MF-dependent parameters.
It can be observed that inequality (66) is satisfied based on the relation (11) in Lemma 2 if the conditions (50)–(52) can be ensured by Theorem 3. Note that analyzing the stability of (60) is equivalent to analyzing the stability of (55).
After the ellipsoid is ensured as an attractive invariant set by satisfying (64), derived through (64)–(66), the minimization problem to ensure containment performance is solved as follows. From the condition (53) in Theorem 3, the following relationship can be derived by multiplying
The relationship (67) implies that
By applying the IT-2 fuzzy F-and-C controller design approach from Theorems 1–3, the simulation of a multi-ship system is conducted in the next section to demonstrate the efficiency in formation, containment, and collision avoidance objectives.
4 Simulation of Multi-Ship System
In research [45,46], the authors developed a detailed method for mathematical modeling of ship steering using the kinematic and dynamic equations. Therefore, the following nonlinear multi-ship systems can be established by extending the results from [45–47].
where
From Fig. 2, it can also be observed that the sway and surge motions differ from the velocities along the x and y axes. These velocities, used in the collision avoidance algorithm, can be calculated from the sway and surge motions based on the yaw angle. Specifically, the surge motion
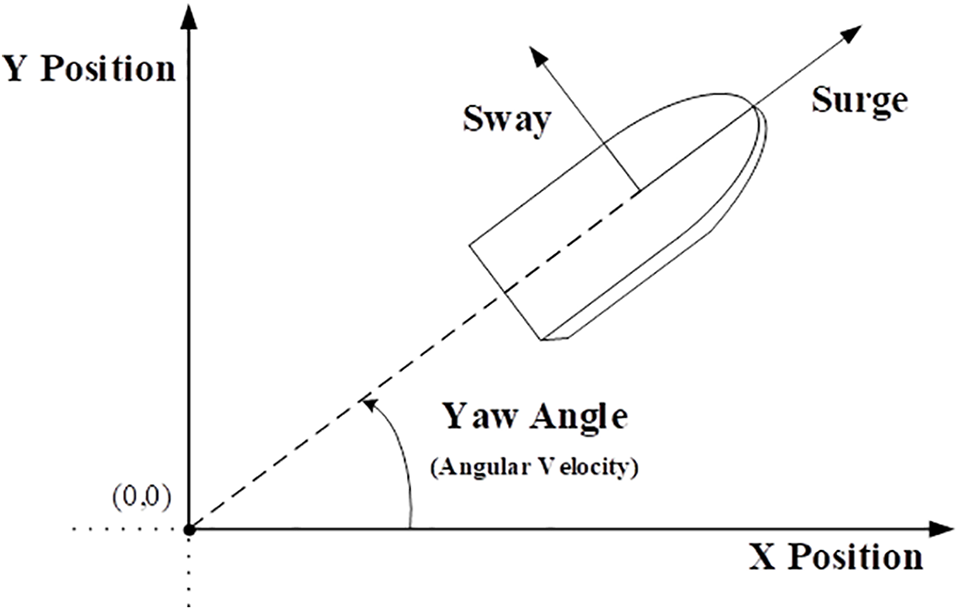
Figure 2: Diagram of a ship dynamic system
Considering the uncertain factors
where
It should be noted that the operating points for the linearization of subsystem in the IT-2 T-SFM (76) are chosen as
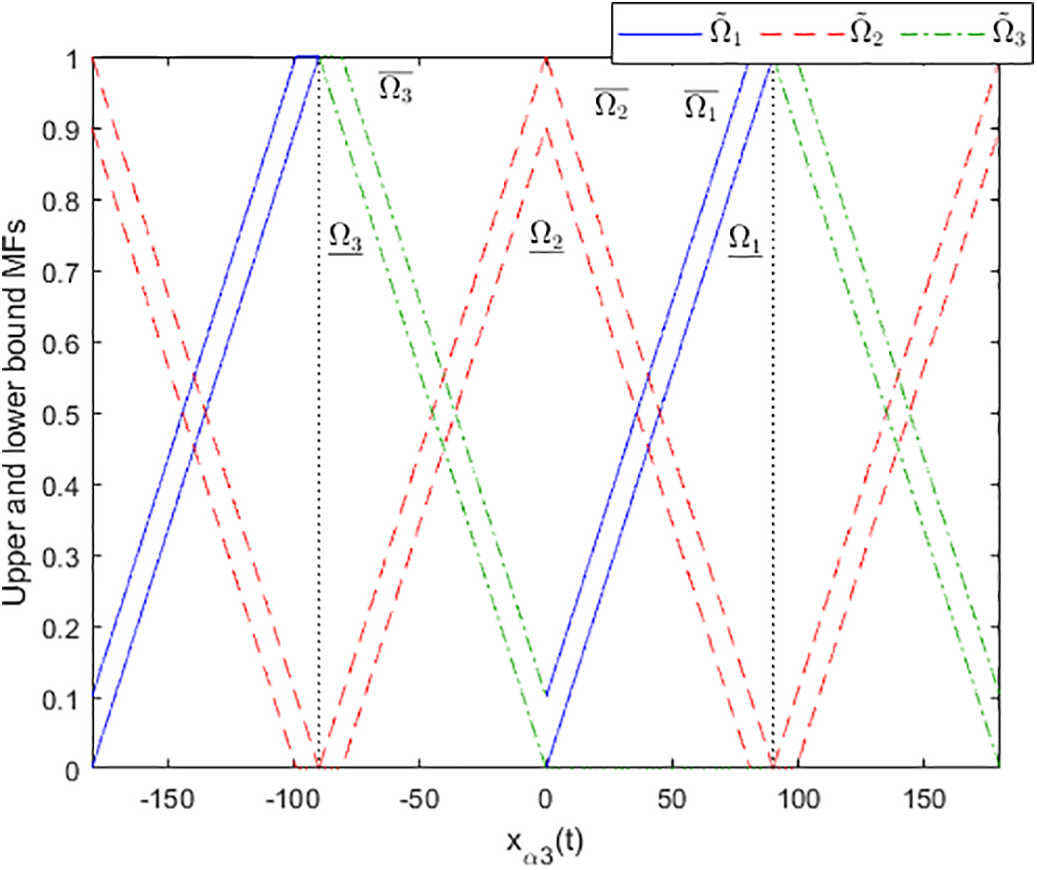
Figure 3: MF of nonlinear multi-ship system
Since the uncertain factors are considered with the value of 0.1 times of system parameters in the UNMAS (68)–(73), the range of interval in the IT-2 MF is also considered with 0.1 times of the original operating value. Since the uncertainties in the UNMAS (68)–(73) are considered as 10% of the system parameters, the interval width of the IT-2 MF is also set to 10% of the original operating range.
It is worth noting that the x position, y position, and yaw angle are selected as the tracking states in the trajectory tracking problem of this simulation. Therefore, the leader ships can reach the desired positions to complete the formation and maintain the correct course. However, the existing research on T-SFM modeling concerning the nonlinear ship system established in [45–47] has been primarily conducted within the yaw angle range of −90 to 90 degrees. These T-SFMs are not applicable and reasonable for yaw angle tracking. Therefore, the IT-2 MF originally defined over the range of −90 to 90 degrees is extended to cover a broader operating range, as illustrated in Fig. 3 so that all possible yaw angles in the x-y plane are included.
Based on the IT-2 T-SFM (76), the control problem verifying the formation, containment, and collision avoidance objectives is stated for the UNMASs (68)–(73) in Fig. 4.

Figure 4: Control problem of multiple objectives
In the simulation of this research, “LDR” is used to denote leader ships numbered 1 to 4, and “FLR” is used to denote follower ships numbered 5 to 10. From the F-and-C control problem shown in Fig. 4, the initial and destination conditions are listed in the following Table 1. In addition, the position of Obstacle 2 is provided.
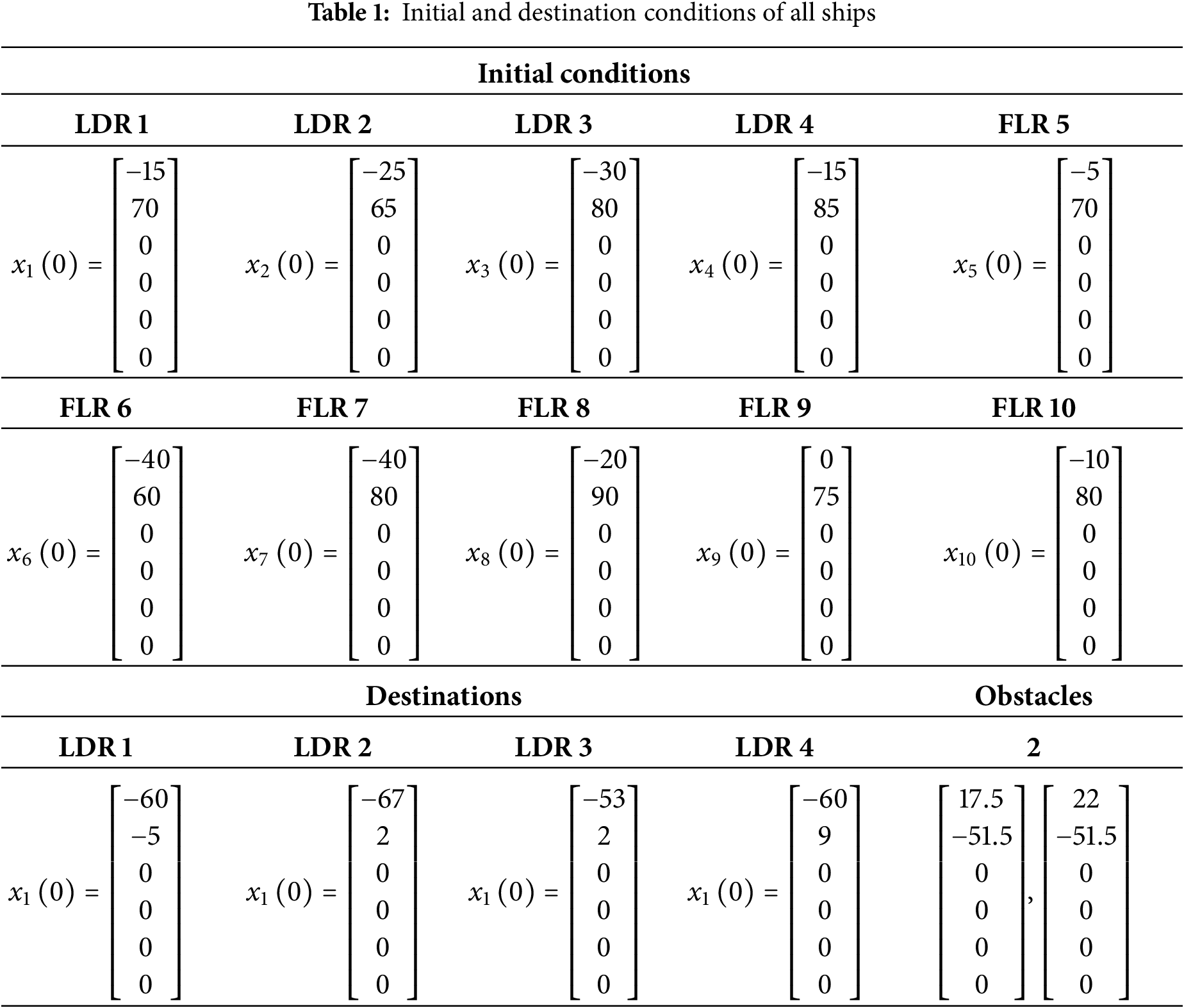
As shown in Fig. 4, the formation objective is to control the leader ships in maintaining a square formation until reaching the destination. Moreover, a known obstacle referred to as Obstacle 1 is located between the initial positions and the destination. The leader ships should bypass this obstacle through the design of the IT-2 fuzzy FC. In addition, unknown obstacles referred to as Obstacle 2 may emerge unpredictably in the ocean. The leader ships are expected to avoid both the unknown obstacles and collisions with other ships, including the followers, then return to the target trajectories. For the follower ships, the IT-2 fuzzy CC is designed to ensure that they remain within the square region formed by the leaders.
Based on the initial positions of all ships, the interaction topology is illustrated in Fig. 5, and the corresponding Laplacian matrix is constructed accordingly.

Figure 5: Interaction topology of multi-ship system
Thus, the elements in the adjacency matrix can be easily inferred from the Laplacian matrix (77). Subsequently, the IT-2 fuzzy formation-and-containment controller is designed based on the forms of (29) and (7) as follows.
where the IT-2 MF is designed in Fig. 6.

Figure 6: MF of IT-2 fuzzy F-and-C controller
It is worth noting that the number of rules and the shape of the IT-2 MF for the fuzzy controller can be designed independently from the IT-2 T-SFM (76) since the IPM concept. This flexibility allows the use of fewer fuzzy rules than required by the model, which effectively reduces the complexity and implementation cost of fuzzy controller. Without loss of generality, the IT-2 MF in Fig. 6 is also designed based on the operating points of 90 and −90 degrees. Moreover, the IT-2 MF designed between −90 and 90 degrees is further extended to a wider operating range to cover all the possible yaw angles.
Based on the IT-2 membership functions in Figs. 3 and 6, the following control gains are derived by solving the design problems stated in Theorems 1 and 3 using MATLAB, where the required parameters are set as
After the control gains for the leader ships are determined, the following parameters are selected for the IT-2 fuzzy FC design in Theorem 2 and Algorithm 1 to achieve formation and collision avoidance simultaneously.
By using MATLAB tools, including S-functions and Simulink, the simulation results and state response plots can be obtained as follows. Then, the following simulation results for the UNMASs (68)–(73) are obtained based on the conditions in Table 1 by applying the IT-2 fuzzy F-and-C controller (78), (79) with parameters (82).
From Figs. 7–9, it is evident that the state trajectories of leaders are effectively controlled to follow the target trajectories by the IT-2 fuzzy FC (78). That is, the x position and y position can achieve the assigned positions to complete the formation task. The desired yaw angle is also tracked to ensure the correctness of the ship course. Moreover, the state trajectories can also be adjusted to track the target trajectories computed by the collision avoidance algorithm. It is important to note that, regardless of whether in tracking or collision avoidance mode, the state trajectories of all followers remain within the leaders by the IT-2 fuzzy CC (79). Therefore, the followers can effectively avoid potential dangers by complying with the control commands of the leaders. In this research, the primary focus is on directly tracking the ships’ positions and yaw angles. In other words, the surge motion, sway motion, and yaw angular velocity in Figs. 10–12 are automatically regulated by the ship to achieve this tracking objective. Nevertheless, the trajectories of these states for the followers can also be constrained within the interval defined by the leaders. To clearly present the simulation results, the ship trajectories corresponding to the control problem in Fig. 4 are shown in the following figure.

Figure 7: Responses of the x positions of all ships
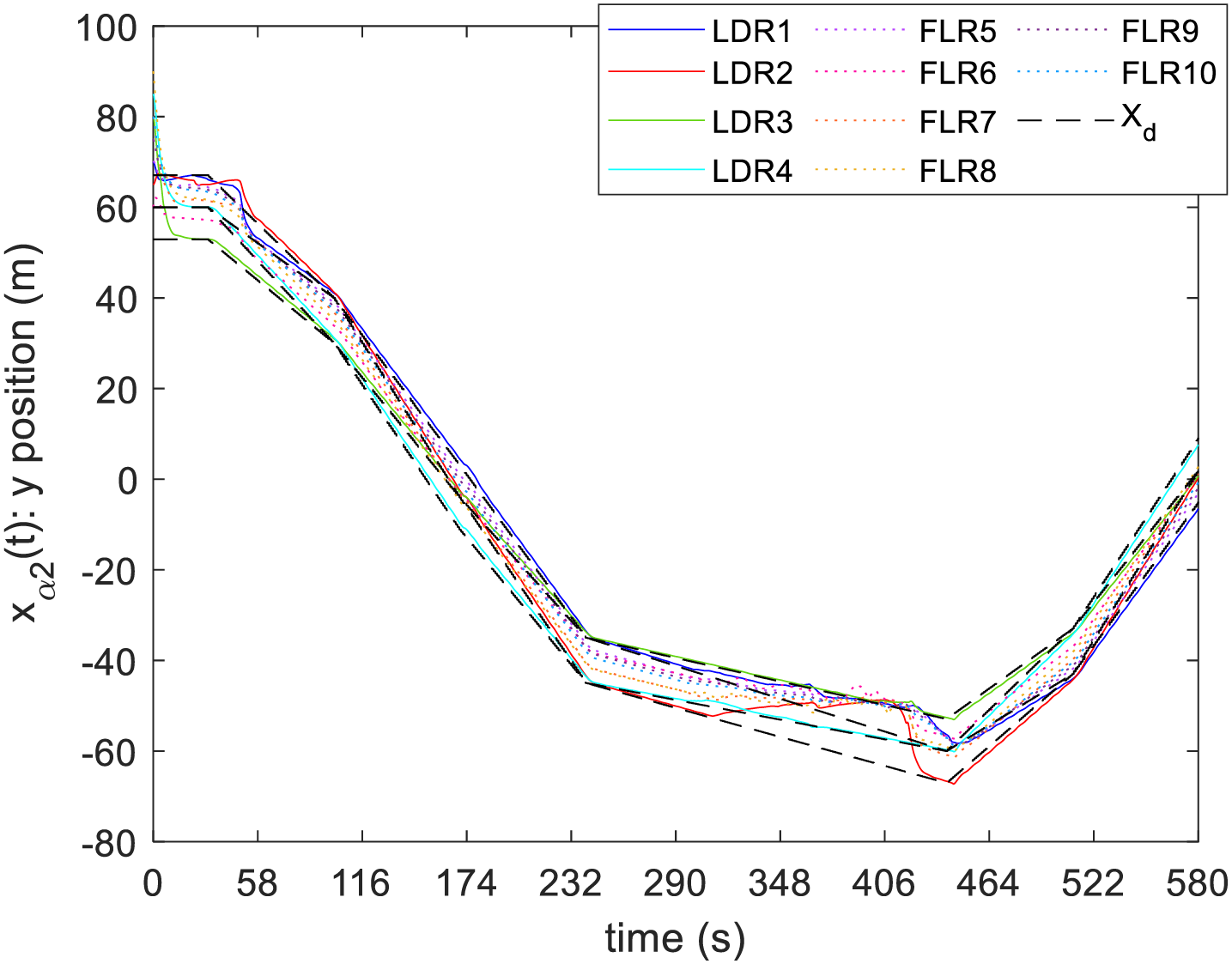
Figure 8: Responses of the y positions of all ships

Figure 9: Responses of the yaw angles of all ships

Figure 10: Responses of the surge motions of all ships

Figure 11: Responses of the sway motions of all ships
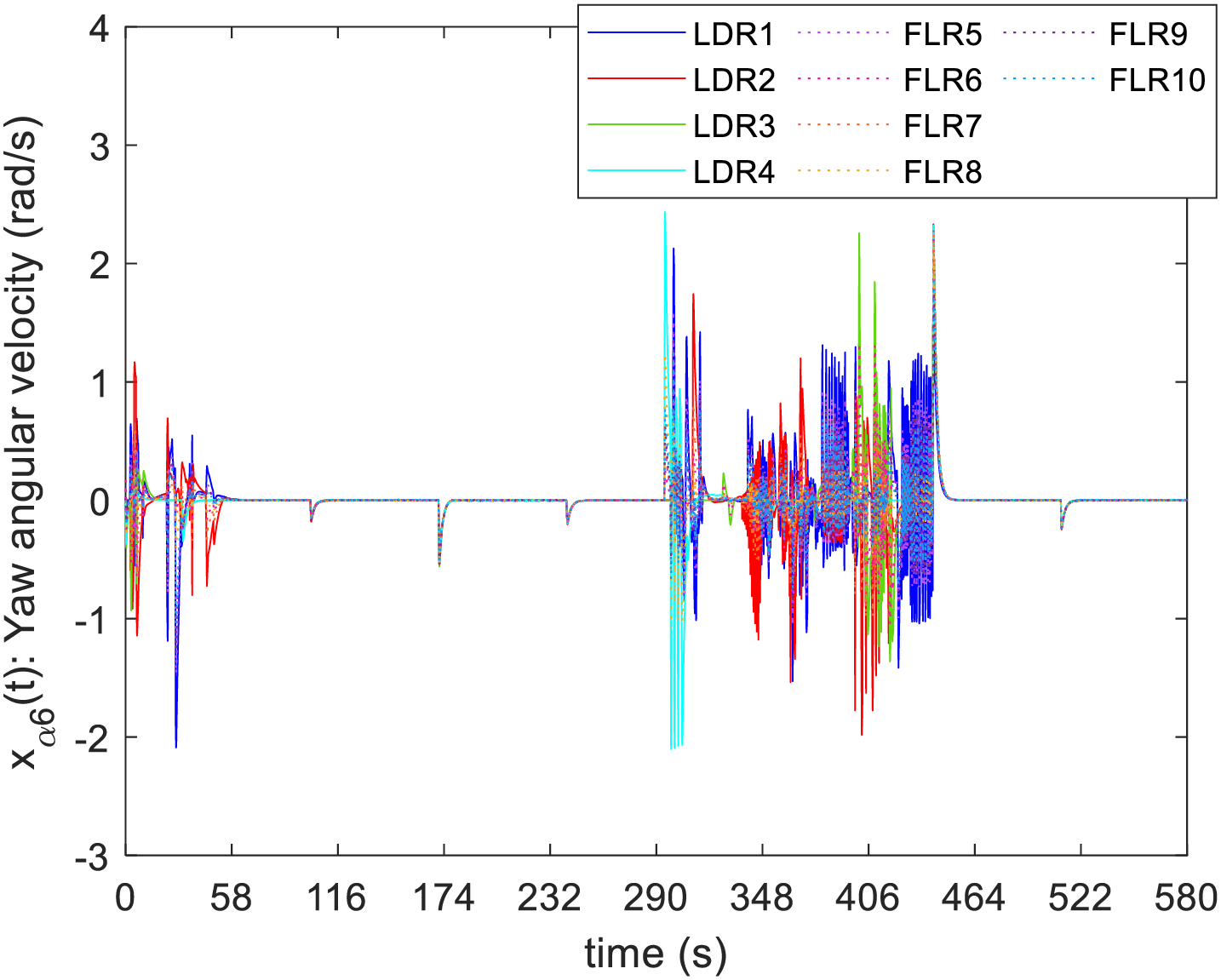
Figure 12: Responses of the yaw angular velocities of all ships
According to Fig. 13, it is demonstrated that the formation of the leaders and the dynamic behavior of this formation can be effectively achieved through the design of the IT-2 fuzzy FC (78) using the tracking technique individually. In addition, the leaders can bypass Obstacle 1 with just the proper design of the target trajectories and successfully arrive the destination. With the application of Algorithm 1, the leaders can also avoid collisions with other ships, including the followers, as shown in Fig. 14. It is worth noting that the followers are forced within the formation region defined by the leaders, using the IT-2 fuzzy CC (79), before the formation is fully completed.

Figure 13: Trajectories of multi-ship system

Figure 14: Zoomed-in view of initial trajectories
When the unpredictable Obstacle 2 occurs, the leaders can also adjust the positions and courses to effectively avoid the obstacle, which is seen in Fig. 15. In Fig. 15, the outer yellow dashed circle represents the effective range of the vortex APF, while the inner circle corresponds to the effective range of the source APF. It is observed that the leaders can guide the entire multi-ship system to successfully avoid collisions and subsequently return to the desired trajectory after the avoidance maneuver by the IT-2 fuzzy FC (78) based on Algorithm 1. By the IT-2 fuzzy CC, the safety of all followers is ensured by maintaining within the formation throughout the entire period.

Figure 15: Zoomed-in view of trajectories during collision avoidance
From the simulation results in Figs. 7–9, it is observed that the tracking objective for all leaders is achieved at approximately 60 s. Moreover, the collision avoidance behavior is activated between 290 and 445 s. To verify the tracking error of the leaders, the periods before formation achievement and during collision avoidance should be excluded. Additionally, the most important states for the formation objective are the first two states, namely the x and y positions of the ships. Hence, the variance values of the tracking errors for all leaders are presented below to verify the effectiveness of the IT-2 fuzzy FC controller.
where
Based on the variance values presented in (83), it is observed that the tracking error variances for all leaders are within the units digit, which is relatively small compared to the overall range in the F-and-C problem of Fig. 4. These results verify the tracking accuracy under uncertainties using the proposed IT-2 fuzzy FC controller. For the followers in the multi-ship system, the containment objectives are demonstrated in Figs. 7–9 and Figs. 13–15. To further clarify the containment performance, the following results present the minimum and maximum distances from the followers to the convex hull, which is a square region formed by the leaders.
From the simulation results in (84), it is verified that all the followers have remained within a certain distance from the convex hull formed by the leaders. This indicates that the followers are successfully contained within the square region. It can be concluded that a feasible and effective control method is provided by the IT-2 fuzzy F-and-C controller proposed in Theorems 1–3 of this research for the formation, containment and collision objectives.
Nevertheless, some visible fluctuations still occur in the collision avoidance scenarios shown in the above simulation results. These fluctuations are caused by abrupt switches between different APFs, as well as transitions between tracking and avoidance modes. To further reduce these fluctuations, effective methods such as the hybrid feedback proposed in [48] can be integrated into the collision avoidance algorithm to achieve smoother switching performance. Although this study validates the proposed IT-2 fuzzy F-and-C controller with collision avoidance on a multi-ship system, the approach is applicable to a wide range of NMASs, including unmanned aerial vehicles, ground vehicles, and surface vehicles. It should be noted that formation, containment, and collision avoidance are primarily considered in systems where the control of positions and trajectories is essential, such as unmanned vehicles. The fuzzy controller based on the IT-2 T-SFM also effectively solve the uncertainty problem, which are critical and unavoidable in these vehicles. Therefore, the proposed IT-2 fuzzy F-and-C controller design can be extended beyond maritime applications to enhance the cooperative control performance and safety of other unmanned vehicles. However, this research still establishes the first successful integration of the IT-2 fuzzy formation-and-containment controller design with a collision avoidance capability.
An IT-2 F-and-C design approach with collision avoidance capability is proposed in this research for UNMASs based on the combination of the APF method and fuzzy theory. First, the IT-2 T-SFM is adopted to provide a more comprehensive representation for UNMASs under uncertain factors. Based on the modeling process, the IT-2 T-SFM for the target trajectory is also constructed for the formation objective. Unlike the existing F-and-C works, the IT-2 fuzzy FC for the leaders is individually designed using a tracking control approach. This scheme simplifies the formation controller design process and reduces implementation complexity. Notably, since the tracking controller is originally designed to achieve the formation objective, it can also be naturally applied to track the desired trajectories generated by the APF method in the avoidance mode. Through the combined application of the source and vortex APFs, the leaders are repelled from the obstacle and guided to turn right to bypass the collision. In this research, fuzzy logic is applied to enable smoother adjustments between these two APFs and enhance the avoidance behavior. By extending the analysis methods for linear MASs, the analysis problem for the IT-2 fuzzy CC design approach can still be solved, even when the leaders’ control inputs involve both tracking and avoidance modes. In other words, the containment objective can be maintained in both scenarios, which allows the followers to remain within the leaders’ formation and avoid potential collisions. Finally, the simulation results of a multi-ship system are presented to verify the control performance of multiple objectives. According to the results, it is observed that the integration of the collision avoidance algorithm successfully turns the leaders’ course to avoid potential dangers. Moreover, the followers can avoid collisions by adhering to the leaders’ formation and trajectories. It can be proven that the safety of the entire multi-ship system is enhanced when the collision avoidance capability of the leaders is ensured. In conclusion, the proposed IT-2 fuzzy F-and-C controller design approach provides a feasible and effective control scheme for UNMASs to simultaneously accomplish formation, containment, and collision avoidance tasks. In this research, the leaders achieve the formation purpose without using communication. However, the containment purpose of followers heavily depends on the dynamics of other agents, which means that communication is unavoidable. Therefore, fault and attack problems constitute promising directions for future work within the proposed design framework. Moreover, considering the practical application of multi-ship systems, issues such as measurement noise, communication delays, and environmental disturbances should also be discussed in future work.
Acknowledgement: Not applicable.
Funding Statement: This research was founded by the National Science and Technology Council of the Republic of China under contract NSTC113-2221-E-019-032.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Yann-Horng Lin, Wen-Jer Chang and Yi-Chen Lee; methodology, Yann-Horng Lin, Yi-Chen Lee and Wen-Jer Chang; software, Yann-Horng Lin, Cheung-Chieh Ku and Muhammad Shamrooz Aslam; validation, Wen-Jer Chang, Muhammad Shamrooz Aslam and Cheung-Chieh Ku; formal analysis, Yi-Chen Lee and Muhammad Shamrooz Aslam; investigation, Yann-Horng Lin, Muhammad Shamrooz Aslam and Wen-Jer Chang; resources, Wen-Jer Chang, Yi-Chen Lee and Cheung-Chieh Ku; data curation, Yann-Horng Lin and Cheung-Chieh Ku; writing—original draft preparation, Yann-Horng Lin; writing—review and editing, Wen-Jer Chang, Yi-Chen Lee and Cheung-Chieh Ku; visualization, Yann-Horng Lin, Muhammad Shamrooz Aslam and Cheung-Chieh Ku; supervision, Wen-Jer Chang and Cheung-Chieh Ku; project administration, Wen-Jer Chang and Yi-Chen Lee; funding acquisition, Wen-Jer Chang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Abbreviations
| IT-2 | Interval Type-2 |
| MAS | Multi-Agent System |
| NMAS | Nonlinear MAS |
| UNMAS | Uncertain NMAS |
| T-SFM | Takagi-Sugeno Fuzzy Model |
| FC | Formation Controller |
| CC | Containment Controller |
| F-and-C | Formation and Containment |
| IPM | Imperfect Premise Matching |
| APF | Artificial Potential Field |
| MF | Membership Function |
| LMI | Linear Matrix Inequality |
References
1. Zhu Z, Du Q, Wang Z, Li G. A survey of multi-agent cross domain cooperative perception. Electronics. 2022;11(7):1091. doi:10.3390/electronics11071091. [Google Scholar] [CrossRef]
2. Lizzio FF, Capello E, Guglieri G. A review of consensus-based multi-agent UAV implementations. J Intell Robot Syst. 2022;106(2):43. doi:10.1007/s10846-022-01743-9. [Google Scholar] [CrossRef]
3. Kwon JW. Cooperative environment scans based on a multi-robot system. Sensors. 2015;15(3):6483–96. doi:10.3390/s150306483. [Google Scholar] [PubMed] [CrossRef]
4. Li Z, Mazouchi M, Modares H, Wang X, Sun J. Finite-time adaptive output synchronization of uncertain nonlinear heterogeneous multi-agent systems. Int J Robust Nonlinear Control. 2021;31(18):9416–35. doi:10.1002/rnc.5779. [Google Scholar] [CrossRef]
5. Tang L, Zhang L, Xu N. Optimized backstepping-based finite-time containment control for nonlinear multi-agent systems with prescribed performance. Optim Control Appl Methods. 2024;45(5):2364–82. doi:10.1002/oca.3160. [Google Scholar] [CrossRef]
6. Shamrooz Aslam M, Bilal H, Chang WJ, Yahya A, Anjum Badruddin I, Kamangar S, et al. Formation control of heterogeneous multi-agent systems under fixed and switching hierarchies. IEEE Access. 2024;12:97868–82. doi:10.1109/access.2024.3419815. [Google Scholar] [CrossRef]
7. Li D, Ge SS, Ma G, He W. Layered formation-containment control of multi-agent systems in constrained space. Int J Control Autom Syst. 2020;18(3):768–79. doi:10.1007/s12555-019-0172-8. [Google Scholar] [CrossRef]
8. Zhou Y, Liu Y, Zhao Y, Wen G. Appointed-time formation-containment control for nonlinear multi-agent networks using sample-data feedback. Int J Robust Nonlinear Control. 2023;33(8):4616–35. doi:10.1002/rnc.6635. [Google Scholar] [CrossRef]
9. Alsinai A, Ali Al-Shamiri MM, Ul Hassan W, Rehman S, Niazi AUK. Fuzzy adaptive approaches for robust containment control in nonlinear multi-agent systems under false data injection attacks. Fractal Fract. 2024;8(9):506. doi:10.3390/fractalfract8090506. [Google Scholar] [CrossRef]
10. Wang Y, Zhong Y, Zhang Y, Shi Y, Chen H. Unmanned aerial vehicle formation control method based on improved artificial potential field and consensus. IET Control Theory Appl. 2024;18(18):2555–67. doi:10.1049/cth2.12772. [Google Scholar] [CrossRef]
11. Tang C, Ji L, Yang S, Guo X, Li H. Prescribed-time containment control of multi-agent systems subject to collision avoidance and connectivity maintenance. ISA Trans. 2024;148:156–68. doi:10.1016/j.isatra.2024.03.002. [Google Scholar] [PubMed] [CrossRef]
12. He Z, Liu C, Chu X, Negenborn RR, Wu Q. Dynamic anti-collision A-star algorithm for multi-ship encounter situations. Appl Ocean Res. 2022;118:102995. doi:10.1016/j.apor.2021.102995. [Google Scholar] [CrossRef]
13. Pandav P, Ren J. A data-driven approach to motion planning and optimal control of medical nanorobots with dynamic window approach. IFAC-PapersOnLine. 2023;56(3):583–8. doi:10.1016/j.ifacol.2023.12.087. [Google Scholar] [CrossRef]
14. Tang W, Zhou Y, Zhang T, Liu Y, Liu J, Ding Z. Cooperative collision avoidance in multirobot systems using fuzzy rules and velocity obstacles. Robotica. 2023;41(2):668–89. doi:10.1017/s0263574722001515. [Google Scholar] [CrossRef]
15. Xi Z, Han H, Cheng J, Lv M. Reducing oscillations for obstacle avoidance in a dense environment using deep reinforcement learning and time-derivative of an artificial potential field. Drones. 2024;8(3):85. doi:10.3390/drones8030085. [Google Scholar] [CrossRef]
16. Wang HO, Tanaka K, Griffin MF. An approach to fuzzy control of nonlinear systems: stability and design issues. IEEE Trans Fuzzy Syst. 1996;4(1):14–23. doi:10.1109/91.481841. [Google Scholar] [CrossRef]
17. Chang CW, Tao CW. A novel approach to implement Takagi-sugeno fuzzy models. IEEE Trans Cybern. 2017;47(9):2353–61. doi:10.1109/TCYB.2017.2701900. [Google Scholar] [PubMed] [CrossRef]
18. Su CL, Lee YC, Chang WJ, Ku CC. Decentralized optimal passive control for discrete-time Takagi-Sugeno interconnected descriptor systems with uncertainties. Int J Fuzzy Syst. 2024;26(4):1175–90. doi:10.1007/s40815-023-01659-y. [Google Scholar] [CrossRef]
19. Lee YC, Lin YH, Chang WJ, Aslam MS, Lin ZY. Optimal fuzzy tracking synthesis for nonlinear discrete-time descriptor systems with T-S fuzzy modeling approach. Comput Model Eng Sci. 2025;143(2):1433–61. doi:10.32604/cmes.2025.064717. [Google Scholar] [CrossRef]
20. Akka K, Khaber F. Optimal fuzzy tracking control with obstacles avoidance for a mobile robot based on Takagi-Sugeno fuzzy model. Trans Inst Meas Control. 2019;41(10):2772–81. doi:10.1177/0142331218811462. [Google Scholar] [CrossRef]
21. Wang X, Ma H, Kang H. Fuzzy adaptive group obstacle avoidance control for second-order multi-agent systems under fixed and switching topologies. IEEE Trans Netw Sci Eng. 2023;10(2):619–30. doi:10.1109/TNSE.2022.3213342. [Google Scholar] [CrossRef]
22. Ebrahimi A, Farrokhi M. Multi-agent flocking with obstacle avoidance and safety distance preservation: a fuzzy potential-based approach. Intell Serv Robot. 2024;17(2):181–95. doi:10.1007/s11370-023-00500-7. [Google Scholar] [CrossRef]
23. Tsai CC, Wu HL, Tai FC, Chen YS. Distributed consensus formation control with collision and obstacle avoidance for uncertain networked omnidirectional multi-robot systems using fuzzy wavelet neural networks. Int J Fuzzy Syst. 2017;19(5):1375–91. doi:10.1007/s40815-016-0239-0. [Google Scholar] [CrossRef]
24. Chang Z, Zong G, Song S, Zhao X. Fast finite-time bipartite formation with obstacle avoidance for time-delay multiagent systems: application in mobile robot swarm. IEEE Trans Ind Inform. 2025;21(6):4586–94. doi:10.1109/TII.2025.3545050. [Google Scholar] [CrossRef]
25. Keshavarz-Ghorabaee M. Sustainable supplier selection and order allocation using an integrated ROG-based type-2 fuzzy decision-making approach. Mathematics. 2023;11(9):2014. doi:10.3390/math11092014. [Google Scholar] [CrossRef]
26. Men J, Zhao C. A Type-2 fuzzy hybrid preference optimization methodology for electric vehicle charging station location. Energy. 2024;293:130701. doi:10.1016/j.energy.2024.130701. [Google Scholar] [CrossRef]
27. Mendel JM. Type-2 fuzzy sets and systems: an overview. IEEE Comput Intell Mag. 2007;2(1):20–9. doi:10.1109/MCI.2007.380672. [Google Scholar] [CrossRef]
28. Karnik NN, Mendel JM. Operations on type-2 fuzzy sets. Fuzzy Sets Syst. 2001;122(2):327–48. doi:10.1016/S0165-0114(00)00079-8. [Google Scholar] [CrossRef]
29. Mendel JM, John RI, Liu F. Interval type-2 fuzzy logic systems made simple. IEEE Trans Fuzzy Syst. 2006;14(6):808–21. doi:10.1109/TFUZZ.2006.879986. [Google Scholar] [CrossRef]
30. Wang JC, Wang FH, He R, Lv LF. Anti-lock braking control using an interval type-2 fuzzy neural network scheme for electric vehicles. Proc Inst Mech Eng Part D J Automob Eng. 2024;238(14):4534–50. doi:10.1177/09544070231197856. [Google Scholar] [CrossRef]
31. Al-Mallah M, Ali M, Al-Khawaldeh M. Obstacles avoidance for mobile robot using type-2 fuzzy logic controller. Robotics. 2022;11(6):130. doi:10.3390/robotics11060130. [Google Scholar] [CrossRef]
32. Lin YH, Chang WJ, Ku CC. Solving the formation and containment control problem of nonlinear multi-boiler systems based on interval type-2 Takagi-Sugeno fuzzy models. Processes. 2022;10(6):1216. doi:10.3390/pr10061216. [Google Scholar] [CrossRef]
33. Afaghi A, Ghaemi S, Ghiasi AR, Ali Badamchizadeh M. Type-2 fuzzy consensus control of nonlinear multi-agent systems: an LMI approach. J Frankl Inst. 2021;358(8):4326–47. doi:10.1016/j.jfranklin.2021.03.024. [Google Scholar] [CrossRef]
34. Hua M, Ding H, Yao XY, Zhang X. Distributed fixed-time formation-containment control for multiple Euler-Lagrange systems with directed graphs. Int J Control Autom Syst. 2021;19(2):837–49. doi:10.1007/s12555-020-0106-5. [Google Scholar] [CrossRef]
35. Li C, Chen L, Guo Y, Ma G. Formation-containment control for networked Euler-Lagrange systems with input saturation. Nonlinear Dyn. 2018;91(2):1307–20. doi:10.1007/s11071-017-3946-7. [Google Scholar] [CrossRef]
36. Lam HK, Li H, Deters C, Secco EL, Wurdemann HA, Althoefer K. Control design for interval type-2 fuzzy systems under imperfect premise matching. IEEE Trans Ind Electron. 2014;61(2):956–68. doi:10.1109/TIE.2013.2253064. [Google Scholar] [CrossRef]
37. Zhang Z, Dong J. Containment control of interval type-2 fuzzy multi-agent systems with multiple intermittent packet dropouts and actuator failure. J Frankl Inst. 2020;357(10):6096–120. doi:10.1016/j.jfranklin.2020.04.003. [Google Scholar] [CrossRef]
38. Chang WJ, Lin YH, Ku CC. Passive formation and containment control of multiple nonlinear autonomous ship systems with external disturbances based on interval type-2T-S fuzzy model. Int J Fuzzy Syst. 2024;26(8):2505–17. doi:10.1007/s40815-024-01742-y. [Google Scholar] [CrossRef]
39. Chang WJ, Lin YH, Lee YC, Ku CC. Investigating formation and containment problem for nonlinear multiagent systems by interval type-2 fuzzy sliding mode tracking approach. IEEE Trans Fuzzy Syst. 2024;32(7):4163–77. doi:10.1109/tfuzz.2024.3387045. [Google Scholar] [CrossRef]
40. Tanakitkorn K. Fuzzy-based potential field collision avoidance technique for unmanned surface vehicles. IOP Conf Ser Mater Sci Eng. 2021;1137(1):012017. doi:10.1088/1757-899x/1137/1/012017. [Google Scholar] [CrossRef]
41. Xi J, Shi Z, Zhong Y. Consensus analysis and design for high-order linear swarm systems with time-varying delays. Phys A Stat Mech Its Appl. 2011;390(23–24):4114–23. doi:10.1016/j.physa.2011.06.045. [Google Scholar] [CrossRef]
42. Shibata N, Sugiyama S, Wada T. Collision avoidance control with steering using velocity potential field. In: 2014 IEEE Intelligent Vehicles Symposium Proceedings; 2014 Jun 8–11; Dearborn, MI, USA. p. 438–43. doi:10.1109/IVS.2014.6856469. [Google Scholar] [CrossRef]
43. Lee MC, Nieh CY, Kuo HC, Huang JC. A collision avoidance method for multi-ship encounter situations. J Mar Sci Technol. 2020;25(3):925–42. doi:10.1007/s00773-019-00691-8. [Google Scholar] [CrossRef]
44. Li P, Jabbari F, Sun XM. Containment control of multi-agent systems with input saturation and unknown leader inputs. Automatica. 2021;130:109677. doi:10.1016/j.automatica.2021.109677. [Google Scholar] [CrossRef]
45. Fossen TI. Guidance and control of ocean vehicles. Chichester, UK: John Wiley & Sons; 1994. [Google Scholar]
46. Fossen TI, Grovlen A. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping. IEEE Trans Control Syst Technol. 1998;6(1):121–8. doi:10.1109/87.654882. [Google Scholar] [CrossRef]
47. Lin YH, Chang WJ, Pen CL. Fuzzy steering control for TS fuzzy model-based multiple ship systems subject to formation and containment. Int J Fuzzy Syst. 2023;25(5):1782–94. doi:10.1007/s40815-023-01479-0. [Google Scholar] [CrossRef]
48. Berkane S, Bisoffi A, Dimarogonas DV. Obstacle avoidance via hybrid feedback. IEEE Trans Autom Control. 2021;67(1):512–9. doi:10.1109/TAC.2021.3086329. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools