 Open Access
Open Access
ARTICLE
An Analytical Approach for Simulating the Bending of Nanobeams in Thermal Environments Considering the Flexomagnetic Effect
1 Faculty of Mechanical Engineering, Le Quy Don Technical University, No. 236 Hoang Quoc Viet Street, Hanoi, 100000, Vietnam
2 Hanoi University of Industry, No. 298 Cau Dien Street, Tay Tuu Ward, Hanoi, 100000, Vietnam
* Corresponding Author: Do Van Thom. Email:
Computer Modeling in Engineering & Sciences 2025, 145(2), 1711-1734. https://doi.org/10.32604/cmes.2025.071187
Received 01 August 2025; Accepted 14 October 2025; Issue published 26 November 2025
Abstract
This research utilizes analytical solutions to investigate the issue of nonlinear static bending in nanobeams affected by the flexomagnetic effect. The nanobeams are exposed to mechanical loads and put in a temperature environment. The equilibrium equation of the beam is formulated based on the newly developed higher-order shear deformation theory. The flexomagnetic effect is explained by the presence of the strain gradient component, which also takes into consideration the impact of small-size effects. This study has used a flexible transformation to derive the equilibrium equation for a single variable, which significantly simplifies the process of determining the precise solution to the bending issue. This highlights the originality and significance of the present study, which is based on a newly developed shear deformation theory to clarify the distinctions between the nonlinear and linear problems. This study also presents the findings of numerical simulations that investigate the impact of various geometric, material, and temperature parameters on the nonlinear behavior of nanobeams. These discoveries are significant for designers to develop nanobeams that can function efficiently in many physical conditions, including mechanical, thermal, and magnetic mediums.Keywords
Currently, smart materials are widely used in several significant sectors such as aerospace, medical, military industry, and others. Common examples of smart materials include materials that exhibit varying mechanical characteristics, piezoelectric materials, magnetic materials, materials with flexoelectric effects, materials with flexomagnetic effects, and so on. Therefore, the investigation into the mechanical behavior of structures composed of this intelligent material has taken a substantial leap ahead. Zhang et al. [1] performed research on the bending characteristics of piezoelectric material plates that have a bidirectional functionally graded (FG) structure inside the plane. Jing et al. [2] conducted an oscillation evaluation of piezoelectric cantilever beams with bimodular FG characteristics. Khiem et al. [3,4] completed a study on the vibration response of a cracked beam made of functionally graded material (FGM) with a piezoelectric section, subjected to a moving load. Li and collaborators [5] conducted a study on the electro-mechanical vibration and stress distribution of a piezoelectric nanobeam with a symmetrical FGM core when subjected to a low-velocity reaction. Binh et al. [6] demonstrated the use of analytical modeling to analyze the mechanical properties of piezoelectric nanobeams, focusing on the inclusion of flexoelectric influences. Son and coworkers [7] proposed a theoretical framework called the novel shear deformation theory. This theory aims to accurately model the behavior of nanoplates under dynamic conditions. Doan et al. [8] investigated the impact of the flexoelectric effect on the free oscillation characteristics of cracked nanoplates using the phase-field theory. Askari and colleagues [9] presented a study of the vibrations in beams that are both transversely and sheared linked and made of piezoelectric functionally graded porous materials. The analysis was conducted using higher-order theories. Duc and Phuc [10] presented a thorough investigation of the mechanical behavior of piezoelectric nanoplates with varying thicknesses, including the influence of the flexoelectric effect.
Small-scale electronics, such as nanosensors, transistors, nanogenerators, and actuators, frequently consist of beam or nanoplate structures that experience various forms of stress. Research has successfully shown their mechanical reactions. Jankowski et al. [11] discussed the piezoelectric influence on the bifurcation buckling of a symmetric FGM porous nanobeam. This was done using a higher-order nonlocal elasticity and strain gradient theory, together with Reddy’s third-order shear deformation beam theory. Sator et al. [12] delivered a presentation on the analysis of FG piezoelectric micro/nano plates using the moving finite element method (FEM). Kammoun and coworkers [13] researched the study of thermo-electro-mechanical dynamics and free vibrations of a nanobeam made of functionally graded piezoelectric material, taking into account the effects of initial stress. Van Thom and colleagues [14] conducted a study on the mechanical reactions of nanoplates when placed on viscoelastic foundations in settings with multiple physical properties. Hoan et al. [15] demonstrated nonlinear vibration nanobeam analysis sustaining thermal environment with flexomagnetic effect consideration. Selvamani and collaborators [16] examined the propagation of nonlocal state-space strain gradient waves in an FG magnetothermoelectric nanobeam. Ebrahimi et al. [17] scrutinized the Influence of temporal nonlocality on the wave propagation characteristics of viscoelastic FGM nanoshells. Li and his team [18] explored the dynamic behaviors of imperfect functionally graded piezoelectric sandwich microplates with thermal-electric properties. The study was based on the modified couple stress theory. Wang and coworkers [19] delivered a study on the examination of wave propagation in porous FG piezoelectric nanoshells that are supported by a viscoelastic foundation. Fang et al. [20] and Tien et al. [21] presented an application of the nonlocal hypothesis to analyze the free and forced oscillation of multilayer nanoplates. Phung [22] delivered a presentation on the static bending analysis of nanoplates on a discontinuous elastic foundation, focusing specifically on the inclusion of the flexoelectric effect. Sun et al. [23] conducted a study on the characteristics of nonlinear dynamical instability in FG piezoelectric microshells. The study included the effects of nonlocality and strain gradient size dependencies. The most recent related studies can be found in these documents [24–30]. Lan et al. [24] combined nonlocal elasticity with the Galerkin method, Tho et al. [25] adopted nonlocal elasticity within an analytical framework, and Dehsaraji et al. [26] integrated higher-order shear deformation theory with nonlocal theory. Yademellat et al. [27] employed both classical beam theory and the nonlocal strain gradient theory, while Cong et al. [28] utilized a phase-field approach to examine the influence of size effects on crack propagation in structural components. In addition, for structures at the nanoscale, the surface effect is one of the key factors significantly influencing their mechanical responses [31–33]. However, when analyzing nanoscale structures, various theoretical models have been proposed, among which Eringen’s model [34] is one of the most widely used. However, this model can lead to inaccuracies under certain special boundary conditions. Therefore, researchers have developed more advanced and effective models for solving nanoscale structural mechanics problems [35–39]. Romano et al. [35] examined the linear problem, Ussorio et al. [37] investigated the nonlinear case, while Vaccaro et al. [38,39] developed higher-order theories to improve the accuracy of the analysis. In this work, the proposed Eringen model [34] is adopted, as it is simple, computationally convenient, and still widely accepted and employed by many scholars [21,24,25,31,32].
Beam constructions can endure several sorts of loads, including mechanical loads and thermal stresses. Due to this factor, beams can experience significant deformations. In addition, the presence of the flexomagnetic effect further complicates the beam’s reaction, resulting in an entirely distinct behavior compared to situations involving just minor deformations. There are various methods available for beam analysis. For example, Mahboubi Nasrekani and Eipakchi [40], Chandel and Talha [41] employed the perturbation approach, Wu [42] applied the Meshless method, Useche and Alvarez [43] adopted the Boundary Element Method, while Pereira et al. [44] and Liu et al. [45] utilized approximate solution techniques. Unlike other approximate methods [40,46,47], the objective of this research is to develop an innovative approach based on analytical methodologies. The presented findings will undoubtedly provide designers with a foundation for developing efficient structures that fulfill the specified criteria.
This paper is organized into the following primary sections: The equilibrium equation and solution for the issue of nonlinear bending of nanobeams are described in Section 2. Section 3 presents some instances to show the dependability of the solution in this study. Section 4 presents the outcomes of numerical computations and the subsequent examination of these results. Section 5 provides a concise overview of the primary findings that have been examined in this study.
2 Nano Beams Subjected to Bending, Considering Geometric Nonlinearity and Flexoemagnetic Effects
Fig. 1 illustrates the nanobeam model constructed from materials exhibiting flexomagnetic properties. Align the x-axis parallel to the beam axis, and position the z-axis perpendicular to the beam axis. The beam has a length denoted as L, a height represented by h, and is situated inside an environment that experiences mechanical stress Fz and temperature variations.

Figure 1: Model of a nanobeam with flexomagnetic effect in a temperature environment
There are several theories available for calculating beams. However, when it comes to nonlinear issues, most projects have relied on classical beam theory. This is due to the simplicity and convenience of its structure, which facilitates calculations. However, the drawback of the classical theory lies in its limited applicability to slender beams. When dealing with beams that have a significant thickness, using this theory for calculations will result in substantial inaccuracies since it fails to account for the impact of shear deformation. This study employs the novel third-order shear deformation theory to provide a solution to the bending issue of nanobeams affected by the flexomagnetic effect. The two displacement components are expressed in the following manner [48]:
where
When employing the function gz as expressed in Eq. (2), although the thickness integration becomes more complex compared to other functions, the use of this gz function ensures that the shear stresses vanish at the beam surfaces without the need for any shear correction factors, while accurately capturing the mechanical response of the structure.
After the displacement field derivative, the strains consider the large deformation:
in which the axial strain takes into account the influence of temperature:
where
This study examines the effects of significant deformation and thermal deformation caused by temperature changes. This augments the intricacy and unwieldiness of the computation formulae provided below. However, addressing the issue of nonlinear bending in nanobeams using this theory will be more significant since the theoretical calculation model closely aligns with real-world conditions.
Continuing to differentiate the strain, one derives the strain gradient:
where
This study considers only the size-dependent effect based on nonlocal theory, without accounting for the influence of the surface effect. The flexomagnetic effect and the size effect make the relationship between stress and strain as [20,28]:
in which
with
The following can be obtained by applying Gauss’s law:
Using the condition
Vertical force (Nx), bending moment (Mx), higher order moment (Sx), and shear force (Qxz) are calculated as follows:
with the coefficients provided in the Appendix A.
Presently, the work principle is applicable to nanobeams:
where is the virtual work of the internal force of the nanobeam:
in which
with the coefficients ATb, ATs, AYb, AYs provided in the Appendix A.
Virtual work of the mechanical force acting on the beam:
Therefore, Eq. (18) is implemented into three equations as follows:
The vertical force (14) now has the following form:
Integrating the above expression once, one derives:
Suppose the beam is simply supported at both ends:
Hence, significant deformation and temperature variations have a direct impact on the stress and longitudinal force of the beam, resulting in a much more complex mathematical expression. The second derivative of the moment is obtained from Eq. (24):
On the other hand, based on (15), the following can be calculated:
The following equation is derived by transforming Eqs. (24) and (30):
The second derivative of Sx is calculated from (25):
On the other hand, Eq. (16) gives:
Finally, Eq. (25) is rewritten in the following form:
Therefore, the system of equilibrium equations for the beam has the following form:
The above system of equations is written more specifically as follows:
The beam’s equilibrium equation system includes nonlocal coefficients, which represent the influence of the flexomagnetic effect, the influence of temperature, and the influence of large strain. These equations are very complicated and cumbersome because they involve two variables vb and vs.
Assuming the nanobeam is subjected to a single support boundary at both ends and it is simply supported at both ends, this condition requires that the displacements
in which X0b, X0s, and P0v are the amplitudes of the respective components. In addition, the beam can also be subjected to other boundary conditions such as clamped-clamped, clamped-free, or clamped-simply supported. For these cases, the boundary constraints at both ends differ from those of the simply supported beam, and the selection of displacement functions becomes more complex.
Taking the difference between (37) and (38) yields:
Eq. (40) is rewritten as follows:
If
Systems (40) and (41) are solved as follows:
where the coefficients Yb, Ys are provided in the Appendix A.
The system of Eqs. (37) and (38) becomes:
Multiply the systems (45) and (46) by
The above system of equations leads to a more reduced form of the equation as:
with the following descriptive coefficients are:
In the case of uniformly distributed load (
Thus, the nonlinear Eq. (51) includes coefficients containing components related to temperature, flexomagnetic and size effects, the solution
3 Comparison and Validation of the Proposed Approach
Example 1: Consider a beam with h = L/10 and L/20, where the length is L = 10 nm. Material parameters are E = 30 GPa and
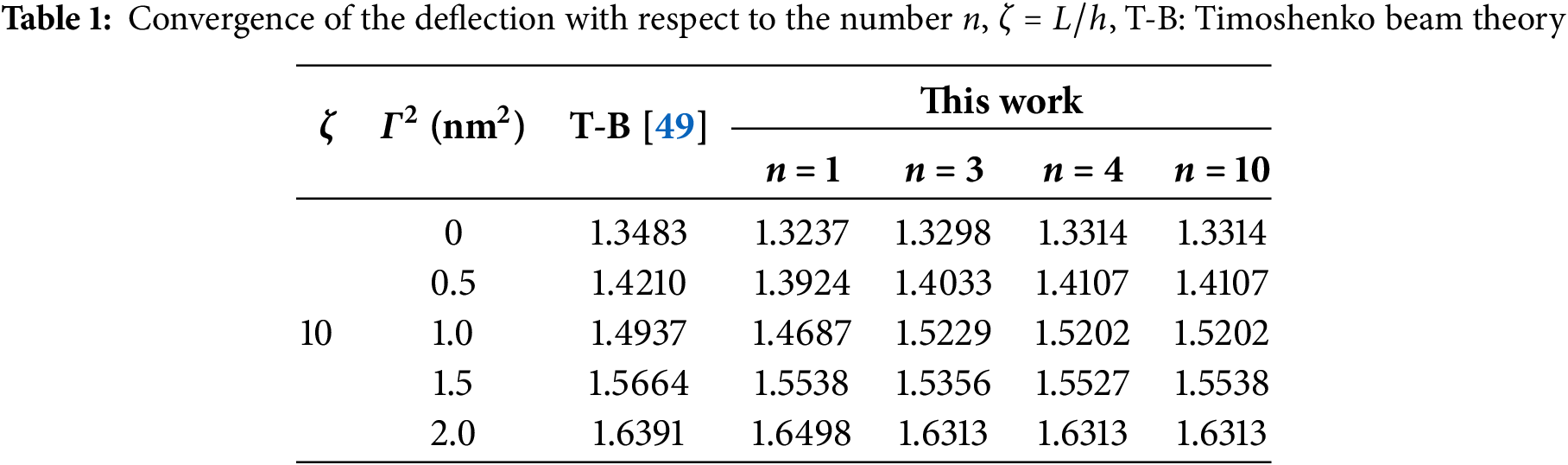
The convergence of the computational results with respect to the number n is listed in Table 1. For n = 4, the results achieve the required accuracy, and this work adopts this value for further calculations. Table 2 details the outcomes of computing the maximum deflection of the beam using various beam theories and methodologies. Specifically, Ref. [49] employed exact solutions combined with various beam theories ranging from the classical theory to higher-order beam theories, whereas Ref. [50] adopted the Timoshenko beam theory along with numerical approaches. The outcomes of this work exhibit minor discrepancies in comparison to the published findings. The disparity in beam theory used in these structures accounts for the comprehensibility of this phenomenon.

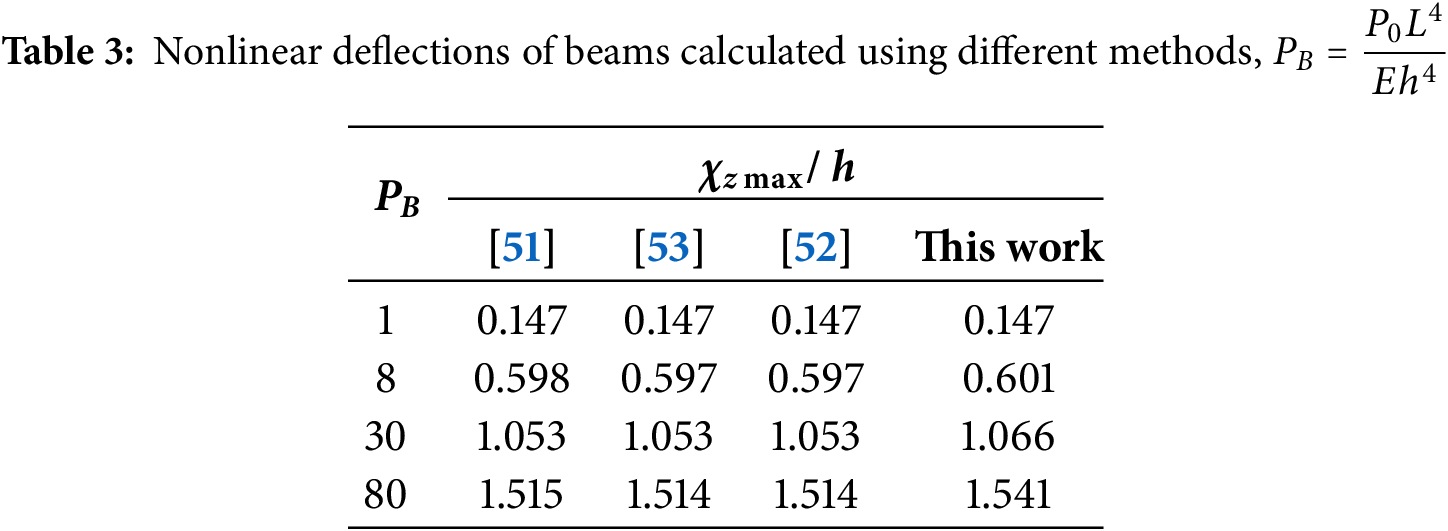
Example 2: Let us analyze a beam with a cross-sectional height of 1 m (h = 1 m), a length of 20 times its height (L = 20h), an elastic modulus of 70 GPa (E = 70 GPa), a Poisson’s ratio of 0.3, and a uniformly distributed load intensity denoted as P0. Table 3 lists the correlation between the deflection of the beam and the applied load. In addition, the computational results of this study show only minor deviations from the values reported in the reference papers, where Refs. [51,52] employed higher-order beam theories combined with the Ritz method, while Ref. [53] adopted the first-order beam theory with analytical approaches. This provides evidence of the accuracy of this study in addressing the issue of nonlinear bending of beams.
Given the confirmed dependability of this study, presented below are numerical findings that demonstrate the impact of material characteristics, temperature, and load on the nonlinear behavior of nano beams. The beam’s starting parameters are L = 10 nm and h = L/10. The material characteristics are as follows: c11 = 286 GPa,
where Q0v is the load intensity, E0 = 70 GPa, h0 = L/10. The linear (
where PN = 3 × 103 N/m2.
The results of calculating the bending deflections of beams, both linear and nonlinear, based on nonlocal parameters for the scenario where L/h = 10, are shown in Fig. 2. Fig. 3 displays the computation result for the scenario when L/h is equal to 30. The following remarks can be made based on the figure:

Figure 2: Result of calculating the maximum deflection when the parameter
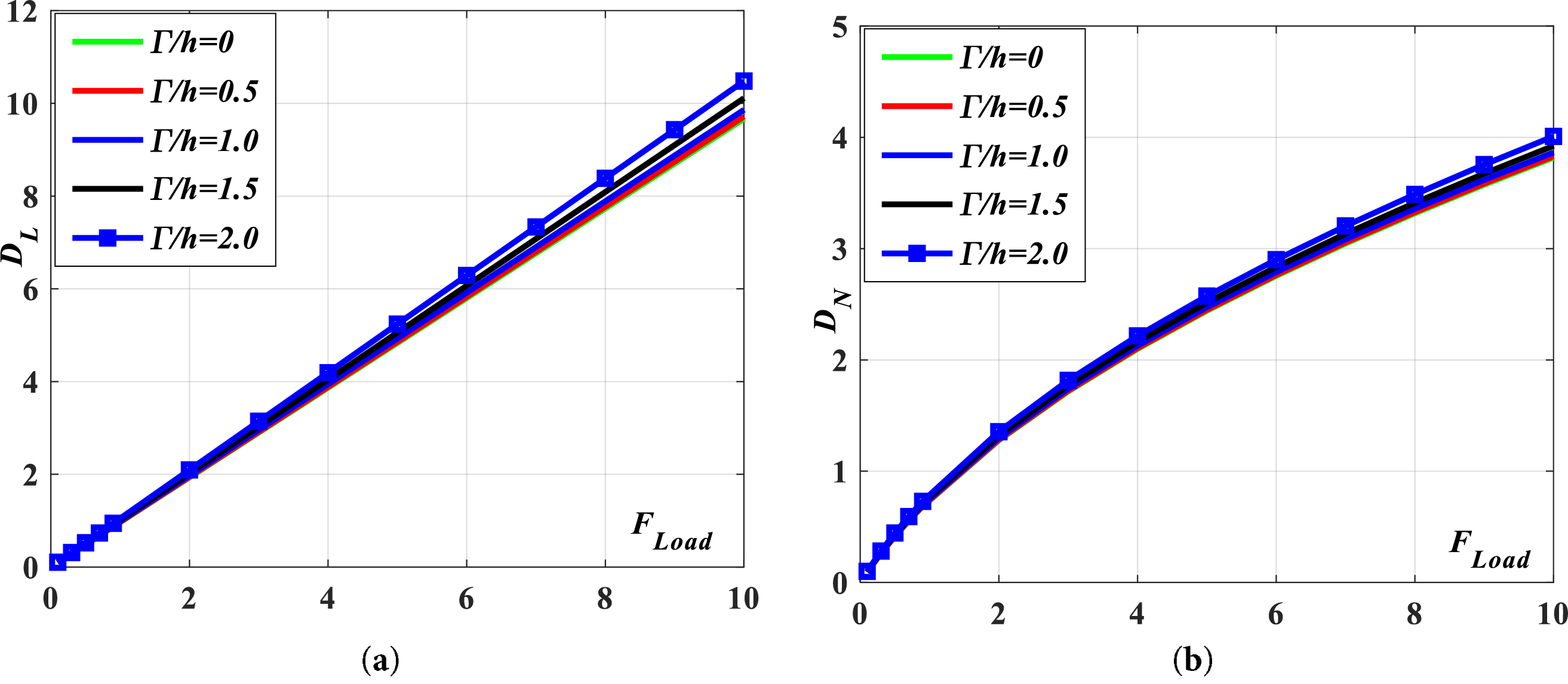
Figure 3: Result of calculating the maximum deflection when the parameter
+As the load rises, the deflection in the linear issue similarly increases proportionally, but the deflection calculation results in the nonlinear problem vary based on the nonlinear curve.
+The deflection of the beam increases as the nonlocal parameter value increases, indicating an inverse relationship between the stiffness of the beam and the magnitude of this parameter.
+For a beam with a thickness h equal to one-tenth of its length (h = L/10), the deflection of the beam is obviously influenced by the nonlocal parameter. In other words, the stiffness of the beam is clearly affected by the nonlocal parameter. When considering a beam with a thickness of h = L/30, the impact of the nonlocal parameter is not readily apparent. This demonstrates that the nonlocal parameter significantly affects the bending response of beams with substantial thickness.
Figs. 4 and 5 show the outcomes of computing the maximum deflection of the beam concerning the L/h ratio for various values of the nonlocal parameter. The presented data indicates: Decreasing the width of the beam (h): Decreasing the thickness h of the beam results in a reduction in the beam’s stiffness, which in turn causes an increase in beam deflection. When the nonlocal parameter changes, the deflection difference becomes considerable for a beam with an L/h ratio of 10. However, for L/h values equal to or greater than 40, the beam deflection remains relatively constant despite changes in the nonlocal parameter. This confirms that the nonlocal parameter has a negligible influence on the stiffness of slender beams, which is also consistent with the findings in [20].

Figure 4: Calculation results of maximum deflection when the thickness of the beam changes for each case of

Figure 5: Calculation results of maximum deflection when the thickness of the beam changes for each case of
Fig. 6 demonstrates the correlation between beam deflection and the t14 parameter. Significantly, when the t14 value grows, the maximum deflection of the beam falls. A higher t14 value indicates a stronger flexomagnetic effect, leading to greater beam stiffness. Increasing the applied stresses on the beam further enhances the flexomagnetic effect.

Figure 6: Calculation results of nonlinear deflection when t14 changes corresponding to the case of
Figs. 7–9 depict the relationship between beam deflection and temperature fluctuations. The figures demonstrate that when the temperature applied to the beam rises, the maximum deflection of the beam likewise increases. Temperature directly affects the load placed on the beam, causing it to increase. In addition, the effect of temperature on nonlinear deflection is more significant than its effect on linear deflection. The nonlocal parameter and L/h ratio have an impact on the beam. Increasing the nonlocal parameter and L/h ratio leads to a considerable impact of temperature fluctuations on the computation results.

Figure 7: Calculation results of maximum deflection when temperature changes,

Figure 8: Calculation results of maximum deflection when

Figure 9: Calculation results of maximum deflection when L/h changes,
This research uses a combination of novel order shear deformation theory and nonlocal theory to investigate the nonlinear bending characteristics of nanobeams under both mechanical and thermal stresses. The novelty and significance of this work lie in the derivation of an accurate and reliable analytical formulation for establishing the nonlinear static equation of nanobeams. The analysis also considers the impact of flexomagnetic phenomena. The main discoveries consist of calculations involving large deflections that exhibit substantial differences compared to issues involving modest deflections. The numerical results demonstrate that the displacement-load response curves of the beam diverge further as the applied load increases. Therefore, it is essential to account for geometric nonlinearity when dealing with cases of high loading. This factor is also the key contribution that this work aims to highlight for nanobeams with the flexomagnetic effect. Reducing the nonlocal parameter values leads to decreased beam deflections, and the influence of size effects on beam bending response decreases as the beam’s thickness decreases. The temperature is a factor that leads to an increase in deflection in nanobeams.
However, this study is limited to the case of simply supported beams and does not address beams with other boundary conditions, which represents a limitation of this work. At the same time, the present study provides a foundation for further investigations into more complex problems in mechanics, such as the nonlinear dynamic behavior of nanobeams, heat conduction in beams, and the responses of nanobeams containing crack-like defects.
Additional studies can investigate the mechanical reactions of different beam and nanoplate configurations when subjected to various kinds of loads and in multi-physics situations.
Acknowledgement: The authors gratefully thank Le Quy Don Technical University and Hanoi University of Industry for helping the authors complete this research.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Do Van Thom: Writing—original draft, Visualization, Validation, Supervision, Software. Pham Van Hoan: Writing—review & editing, Methodology, Conceptualization, Software, Funding acquisition. Nguyen Huu Phan: Visualization, Project administration, Funding acquisition, Conceptualization. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data used to support the findings of this study are included in the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Zhang P, Qi C, Sun X, Fang H, Huang Y. Bending behaviors of the in-plane bidirectional functionally graded piezoelectric material plates. Mech Adv Mater Struct. 2022;29(13):1925–45. doi:10.1080/15376494.2020.1846100. [Google Scholar] [CrossRef]
2. Jing HX, He XT, Du DW, Peng DD, Sun JY. Vibration analysis of piezoelectric cantilever beams with bimodular functionally-graded properties. Appl Sci. 2020;10(16):5557. doi:10.3390/app10165557. [Google Scholar] [CrossRef]
3. Khiem NT, Hai TT, Huong LQ. Modal analysis of cracked FGM beam with piezoelectric layer. Mech Based Des Struct Mach. 2023;51(9):5120–40. doi:10.1080/15397734.2021.1992775. [Google Scholar] [CrossRef]
4. Khiem NT, Huan DT, Hieu TT. Vibration of cracked FGM beam with piezoelectric layer under moving load. J Vib Eng Technol. 2023;11(2):755–69. doi:10.1007/s42417-022-00607-8. [Google Scholar] [CrossRef]
5. Li L, Ren Y, Jin Q. Electro-mechanical vibration and stress field of piezoelectric nanobeam with symmetrical FGM core under the low-velocity impact. Eur Phys J Plus. 2022;137(6):751. doi:10.1140/epjp/s13360-022-02934-x. [Google Scholar] [CrossRef]
6. Binh VH, Khien PB, Van Tuyen B. Bending, free, and forced vibration responses of nanobeams taking flexoelectricity and temperature into account. J Vib Eng Technol. 2025;13(7):506. doi:10.1007/s42417-025-02062-7. [Google Scholar] [CrossRef]
7. Son LT, Chinh VM, Tounsi A, Thom DV, Minh PV. Effect of flexomagneticity on the dynamic response of nanoplates using FEM. Comput Concr. 2025;35(5):527–36. doi:10.12989/cac.2025.35.5.527. [Google Scholar] [CrossRef]
8. Doan DH, Zenkour AM, Van Thom D. Finite element modeling of free vibration of cracked nanoplates with flexoelectric effects. Eur Phys J Plus. 2022;137(4):447. doi:10.1140/epjp/s13360-022-02631-9. [Google Scholar] [CrossRef]
9. Askari M, Brusa E, Delprete C. On the vibration analysis of coupled transverse and shear piezoelectric functionally graded porous beams with higher-order theories. J Strain Anal Eng Des. 2021;56(1):29–49. doi:10.1177/0309324720922085. [Google Scholar] [CrossRef]
10. Duc DH, Phuc PM. Buckling analysis of variable thickness cracked nanoplatesconsiderting the flexoelectric effect. Transp Commun Sci J. 2022;73(5):470–85. doi:10.47869/tcsj.73.5.3. [Google Scholar] [CrossRef]
11. Jankowski P, Żur KK, Kim J, Lim CW, Reddy JN. On the piezoelectric effect on stability of symmetric FGM porous nanobeams. Compos Struct. 2021;267(10):113880. doi:10.1016/j.compstruct.2021.113880. [Google Scholar] [CrossRef]
12. Sator L, Sladek V, Sladek J. Analysis of functionally graded piezoelectric micro/nano plates by moving finite element method. AIP Conf Proc. 2023;2950:020001. doi:10.1063/5.0180781. [Google Scholar] [CrossRef]
13. Kammoun N, Feki N, Hentati H, Bouaziz S, Amar MB, Soula M, et al. Thermo-electro-mechanical dynamic and free vibration analysis of FGPM nanobeam with initial stress. Proc Inst Mech Eng Part E J Process Mech Eng. 2024;238(3):1313–29. doi:10.1177/09544089231169568. [Google Scholar] [CrossRef]
14. Van Thom D, Chinh VM, Van Minh P, Anh Vu ND. Mechanical responses of nanoplates resting on viscoelastic foundations in multi-physical environments. Eur J Mech A/Solids. 2024;106(3):105309. doi:10.1016/j.euromechsol.2024.105309. [Google Scholar] [CrossRef]
15. Hoan PV, Anh ND, Thom DV, Minh PV. Nonlinear vibration of nanobeams in thermal environment. Mech Based Des Struct Mach. 2025;53(8):5690–716. doi:10.1080/15397734.2025.2472253. [Google Scholar] [CrossRef]
16. Selvamani R, Loganathan R, Dimitri R, Tornabene F. Nonlocal state-space strain gradient wave propagation of magneto thermo piezoelectric functionally graded nanobeam. Curved Layer Struct. 2023;10(1):20220192. doi:10.1515/cls-2022-0192. [Google Scholar] [CrossRef]
17. Ebrahimi F, Ghazali M, Dabbagh A. Effect of temporal nonlocality on wave propagation behaviors of viscoelastic FGM nanoshells. J Braz Soc Mech Sci Eng. 2024;46(3):126. doi:10.1007/s40430-024-04701-8. [Google Scholar] [CrossRef]
18. Li FL, Fan SJ, Hao YX, Yang L, Lv M. Dynamic behaviors of thermal-electric imperfect functionally graded piezoelectric sandwich microplates based on modified couple stress theory. J Vib Eng Technol. 2023;11(5):2387–401. doi:10.1007/s42417-022-00709-3. [Google Scholar] [CrossRef]
19. Wang X, Liu J, Hu B, Li Z, Zhang B. Wave propagation in porous functionally graded piezoelectric nanoshells resting on a viscoelastic foundation. Phys E Low Dimension Syst Nanostruct. 2023;151:115615. doi:10.1016/j.physe.2022.115615. [Google Scholar] [CrossRef]
20. Fang XQ, Zou YH, He QL. Nonlinear vibration of five-layered functionally graded piezoelectric semiconductor nano-plate on Pasternak foundation. Mech Based Des Struct Mach. 2024;52(12):10761–82. doi:10.1080/15397734.2024.2362913. [Google Scholar] [CrossRef]
21. Tien DM, Hai Van NT, Tounsi A, Van Minh P, Mai DN. Buckling and forced oscillation of organic nanoplates taking the structural drag coefficient into account. Comput Concr. 2023;32(6):553–65. doi:10.12989/cac.2023.32.6.553. [Google Scholar] [CrossRef]
22. Phung VM. Static bending analysis of nanoplates on discontinuous elastic foundation with flexoelectric effect. J Sci Tech. 2022;17(5):47–57. doi:10.56651/lqdtu.jst.v17.n05.529. [Google Scholar] [CrossRef]
23. Sun J, Sahmani S, Safaei B. Nonlinear dynamical instability characteristics of FG piezoelectric microshells incorporating nonlocality and strain gradient size dependencies. Int J Str Stab Dyn. 2023;23(7):2350074. doi:10.1142/s0219455423500748. [Google Scholar] [CrossRef]
24. Lan DM, Anh ND, Dong PV, Thom DV, Civalek Ö, Minh PV. A new Galerkin method for buckling of sandwich nanobeams. Proc Inst Mech Eng Part C J Mech Eng Sci. 2025;239(8):3034–51. doi:10.1177/09544062241304233. [Google Scholar] [CrossRef]
25. Tho NC, Tien DM, Thom DV, Minh PV, Doan DV. A new approach to the static bending problem of organic nanoplates. Proc Inst Mech Eng Part C J Mech Eng Sci. 2025;239(8):3052–64. doi:10.1177/09544062241306986. [Google Scholar] [CrossRef]
26. Dehsaraji ML, Arefi M, Loghman A. Thermo-electro-mechanical buckling of FGP nano shell with considering thickness stretching effect based on size dependent analysis. Mech Based Des Struct Mach. 2023;51(3):1521–42. doi:10.1080/15397734.2021.1873146. [Google Scholar] [CrossRef]
27. Yademellat H, Ansari R, Darvizeh A, Torabi J, Zabihi A. Nonlinear electromechanical analysis of micro/nanobeams based on the nonlocal strain gradient theory tuned by flexoelectric and piezoelectric effects. Mech Based Des Struct Mach. 2023;51(1):179–98. doi:10.1080/15397734.2020.1836970. [Google Scholar] [CrossRef]
28. Cong PH, Van Thom D, Duc DH. Phase field model for fracture based on modified couple stress. Eng Fract Mech. 2022;269(2):108534. doi:10.1016/j.engfracmech.2022.108534. [Google Scholar] [CrossRef]
29. Dao Minh T, Do Van T, Phung Van M, Pham Huy H. Bending and buckling responses of organic nanoplates considering the size effect. Transp Commun Sci J. 2024;75(7):2015–29. doi:10.47869/tcsj.75.7.1. [Google Scholar] [CrossRef]
30. Zheng YF, Liu BW, Wang F, Chen CP. Nonlinear bending study of size-dependent magneto-electro-elastic laminated nanobeams under flexomagnetoelectric effect. Mech Solids. 2025;60(2):1087–104. doi:10.1134/s0025654425600072. [Google Scholar] [CrossRef]
31. Nguyen TB, Reddy JN, Rungamornrat J, Lawongkerd J, Senjuntichai T, Luong VH. Nonlinear analysis for bending, buckling and post-buckling of nano-beams with nonlocal and surface energy effects. Int J Str Stab Dyn. 2019;19(11):1950130. doi:10.1142/s021945541950130x. [Google Scholar] [CrossRef]
32. Juntarasaid C, Pulngern T, Chucheepsakul S. Bending and buckling of nanowires including the effects of surface stress and nonlocal elasticity. Phys E Low Dimension Syst Nanostruct. 2012;46:68–76. doi:10.1016/j.physe.2012.08.005. [Google Scholar] [CrossRef]
33. Li JL, Li XF. Bending and free vibration of piezomagnetic Timoshenko beams with the flexomagnetic and surface effects. Acta Mech. 2024;132(5):665. doi:10.1007/s00707-024-04135-2. [Google Scholar] [CrossRef]
34. Eringen AC. Nonlocal polar elastic continua. Int J Eng Sci. 1972;10(1):0020722572900705. doi:10.1016/0020-7225(72)90070-5. [Google Scholar] [CrossRef]
35. Romano G, Barretta R, Diaco M, Marotti de Sciarra F. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int J Mech Sci. 2017;121(3–5):151–6. doi:10.1016/j.ijmecsci.2016.10.036. [Google Scholar] [CrossRef]
36. Barretta R, Diaco M, Feo L, Luciano R, de Sciarra FM, Penna R. Stress-driven integral elastic theory for torsion of nano-beams. Mech Res Commun. 2018;87(1):35–41. doi:10.1016/j.mechrescom.2017.11.004. [Google Scholar] [CrossRef]
37. Ussorio D, Vaccaro MS, Barretta R, Luciano R, Marotti de Sciarra F. Large deflection of a nonlocal gradient cantilever beam. Int J Eng Sci. 2025;206(11):104172. doi:10.1016/j.ijengsci.2024.104172. [Google Scholar] [CrossRef]
38. Vaccaro MS, Luciano R, Marotti de Sciarra F. Size-dependent stress-driven behaviour of nanobeams based on higher-order theories. Meccanica. 2025;244(5):111453. doi:10.1007/s11012-025-02004-3. [Google Scholar] [CrossRef]
39. Vaccaro MS, Barretta R, Marotti de Sciarra F, Reddy JN. Nonlocal integral elasticity for third-order small-scale beams. Acta Mech. 2022;233(6):2393–403. doi:10.1007/s00707-022-03210-w. [Google Scholar] [CrossRef]
40. Mahboubi Nasrekani F, Eipakchi H. Geometrically nonlinear effect on forced vibrational behavior of superlight composite beams with auxetic core layer under harmonic excitation based on FSDT. Mech Based Des Struct Mach. 2024;52(8):5435–56. doi:10.1080/15397734.2023.2255262. [Google Scholar] [CrossRef]
41. Chandel VS, Talha M. The random thermo-elastic nonlinear vibration analysis of porous FGM nano-beams using the first order perturbation theory. Proc Inst Mech Eng Part C J Mech Eng Sci. 2024;238(11):5241–57. doi:10.1177/09544062231212324. [Google Scholar] [CrossRef]
42. Wu CP. A Hermitian C differential reproducing kernel interpolation meshless method for the 3D microstructure-dependent static flexural analysis of simply supported and functionally graded microplates. Comput Model Eng Sci. 2024;141(1):917–49. doi:10.32604/cmes.2024.052307. [Google Scholar] [CrossRef]
43. Useche J, Alvarez H. Elastodynamic analysis of thick multilayer composite plates by the boundary element method. Comput Model Eng Sci. 2015;107(4):277–96. doi:10.3970/cmes.2015.107.277. [Google Scholar] [CrossRef]
44. Pereira W, Karam V, Carrer J, Monteiro C, Mansur W. Numerical solutions for free vibration analysis of thick square plates by the BEM. Comput Model Eng Sci. 2013;96(2):117–30. doi:10.3970/cmes.2013.096.117. [Google Scholar] [CrossRef]
45. Liu D, Tu C, Chung C. Coupled PIEM/FEM algorithm based on Mindlin-Reissner Plate Theory for bending analysis of plates with through-thickness hole. Comput Model Eng Sci. 2013;92(6):573–94. doi:10.3970/cmes.2013.092.573. [Google Scholar] [CrossRef]
46. Nguyen HN, Canh TN, Thanh TT, Ke TV, Phan VD, Thom DV. Finite element modelling of a composite shell with shear connectors. Symmetry. 2019;11(4):527. doi:10.3390/sym11040527. [Google Scholar] [CrossRef]
47. Dat PT, Binh LP. Dynamic buckling analysis of reinforced composite plate subjected to harmonic loads. Vietnam J Mech. 2023;45(1):60–74. doi:10.15625/0866-7136/17938. [Google Scholar] [CrossRef]
48. Van Vinh P, Dung NT, Tho NC, Van Thom D, Hoa LK. Modified single variable shear deformation plate theory for free vibration analysis of rectangular FGM plates. Structures. 2021;29(4):1435–44. doi:10.1016/j.istruc.2020.12.027. [Google Scholar] [CrossRef]
49. Reddy JN. Buckling and vibration of beams. Int J Eng Sci. 2007;45(2–8):288–307. doi:10.1016/j.ijengsci.2007.04.004. [Google Scholar] [CrossRef]
50. Pradhan SC. Nonlocal finite element analysis and small scale effects of CNTs with Timoshenko beam theory. Finite Elem Anal Des. 2012;50(part 2):8–20. doi:10.1016/j.finel.2011.08.008. [Google Scholar] [CrossRef]
51. Zhang DG. Nonlinear bending analysis of FGM beams based on physical neutral surface and high order shear deformation theory. Compos Struct. 2013;100:121–6. doi:10.1016/j.compstruct.2012.12.024. [Google Scholar] [CrossRef]
52. Dang XH. Nonlinear bending analysis of FGM beams under various boundary conditions by ritz method. Int J GEOMATE. 2023;25(109):1–8. doi:10.21660/2023.109.3947. [Google Scholar] [CrossRef]
53. Van Long N, Nguyen VL, Tran MT, Thai DK. Exact solution for nonlinear static behaviors of functionally graded beams with porosities resting on elastic foundation using neutral surface concept. Proc Inst Mech Eng Part C J Mech Eng Sci. 2022;236(1):481–95. doi:10.1177/09544062211021112. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools