Grey Wolf Optimizer for Cluster-Based Routing in Wireless Sensor Networks: A Methodological Survey

1  Introduction

Wireless Sensor Networks (WSNs) are increasingly recognized as fundamental components of modern technology [1,2]. WSNs facilitate a diverse array of applications, including environmental monitoring, healthcare, industrial automation, and the development of smart cities [3–5]. These networks are comprised of distributed Sensor Nodes (SNs) that wirelessly collect and transmit data, often functioning in environments with limited resources [6–9]. Despite their considerable potential, WSNs encounter significant challenges, such as energy efficiency, scalability, adaptability with dynamic environments, and robustness, which demand innovative solutions [10–14].

Clustering is a crucial technique within WSNs that organizes SNs into groups or clusters to enhance both energy efficiency and network scalability [15–19]. By designating specific nodes as Cluster Heads (CHs) responsible for collecting and transmitting data to Base Station (BS), clustering effectively reduces overall energy consumption and prolongs the network’s operational lifespan [20–24]. This strategic organization not only optimizes data transmission but also facilitates better resource management across the network [25–28]. Multi-hop cluster-based routing strategies further enhance energy efficiency by allowing data to traverse multiple hops while utilizing the established clustering structure [29]. In this routing paradigm, data is relayed between CHs, which minimizes transmission distances and alleviates the energy burden on individual nodes [30]. This process involves the careful selection of paths for data transmission from SNs to the BS [31].

Given the inherent energy constraints of SNs, routing protocols must be meticulously designed to minimize energy consumption and maximize the network’s longevity [32]. Generally, routing methods can be classified into four categories: data-centric routing, hierarchical routing, location-based routing, and quality-of-service-based routing [33]. This classification is particularly beneficial in large-scale WSNs, where direct communication with the BS may be impractical.

In recent years, metaheuristic algorithms have gained significant traction for solving various complex optimization problems in wireless networks [34–37]. Among these, the Grey Wolf Optimizer (GWO) [38] has emerged as an effective algorithm inspired by the social hierarchy and hunting behavior of grey wolves. GWO is noted for its simplicity, rapid convergence, and ability to avoid local optima, making it well-suited for addressing various challenges WSNs. Recent studies have demonstrated GWO’s effectiveness in optimizing clustering, routing, and cluster-based routing in WSNs.

This survey offers a comprehensive exploration of the applications of GWO in WSNs, focusing on the data transmission issues in terms of clustering, multi-hop routing, and co-designed cluster-based routing techniques. Unlike prior surveys [39–43] that provide generic performance summaries, this study is the first comprehensive review that focuses exclusively on GWO-based clustering and routing approaches in WSNs. GWO has emerged as the most widely used metaheuristic algorithm in this domain, and its extensive application justifies the need for a focused methodological survey. This work emphasizes the methodological aspects of GWO variants to show how they model WSN routing and clustering challenges, formulate objective functions, and integrate hybrid techniques. This fills the existing gap between algorithmic design understanding and practical WSN deployment frameworks. This dedicated focus enables a methodological analysis rather than a performance-ranking comparison, providing a deeper understanding of how GWO and its variants formulate objective functions, encode decision variables, and incorporate hybrid mechanisms.

This survey systematically reviewed and collected relevant research articles from several major digital scientific databases, including IEEE Xplore, ScienceDirect, SpringerLink, and MDPI, covering the entire publication period from 2018 to 2025. To ensure comprehensive coverage, the search strategy employed a combination of specific keywords, including “Grey Wolf Optimizer”, “Clustering,” “Routing,” and “Wireless Sensor Networks”. Only studies that explicitly focused on GWO-based optimization applied to clustering or routing in WSNs were considered relevant and retained for further analysis. Conversely, studies that did not involve the GWO algorithm, did not address WSN applications, or were unrelated to clustering or routing optimization were excluded from the survey. This filtering approach ensured that the review remained highly targeted and relevant, allowing for a detailed examination of the state-of-the-art applications and trends of GWO in WSN optimization.

This survey begins with an introduction to each of the aforementioned WSN domains, summarizing their mechanisms, methods, and features. The characteristics of each method are analyzed and categorized based on solution-based and network-based parameters, presented in tabular form. Following this, a detailed discussion on GWO and its applications in each identified domain will be provided. Through this exploration, we aspire to contribute to the growing body of knowledge on the application of metaheuristic algorithms, particularly GWO, in WSNs, offering valuable insights for researchers and practitioners in the field.

2  Taxonomy and Evaluation Parameters

This section provides a comprehensive overview and classification of the applications of GWO and its variants for cluster-based routing in WSNs.

2.1 Classification of Existing Techniques

Fig. 1 presents the overall taxonomy of GWO-based clustering and routing methods in WSNs. As shown, the reviewed approaches are organized into three primary categories: (1) Clustering approaches, where GWO is employed to select CHs and form clusters; (2) Routing approaches, which utilize GWO to determine optimal inter-cluster communication paths; and (3) Co-designed clustering/routing approaches, which simultaneously optimize both clustering and routing mechanisms. This taxonomy helps illustrate that although all methods are GWO-driven, their objectives and modeling frameworks vary depending on the optimization layer they target. The classification in Fig. 1 emphasizes the diverse applications of GWO in improving energy efficiency, data transmission reliability, and scalability in WSNs.

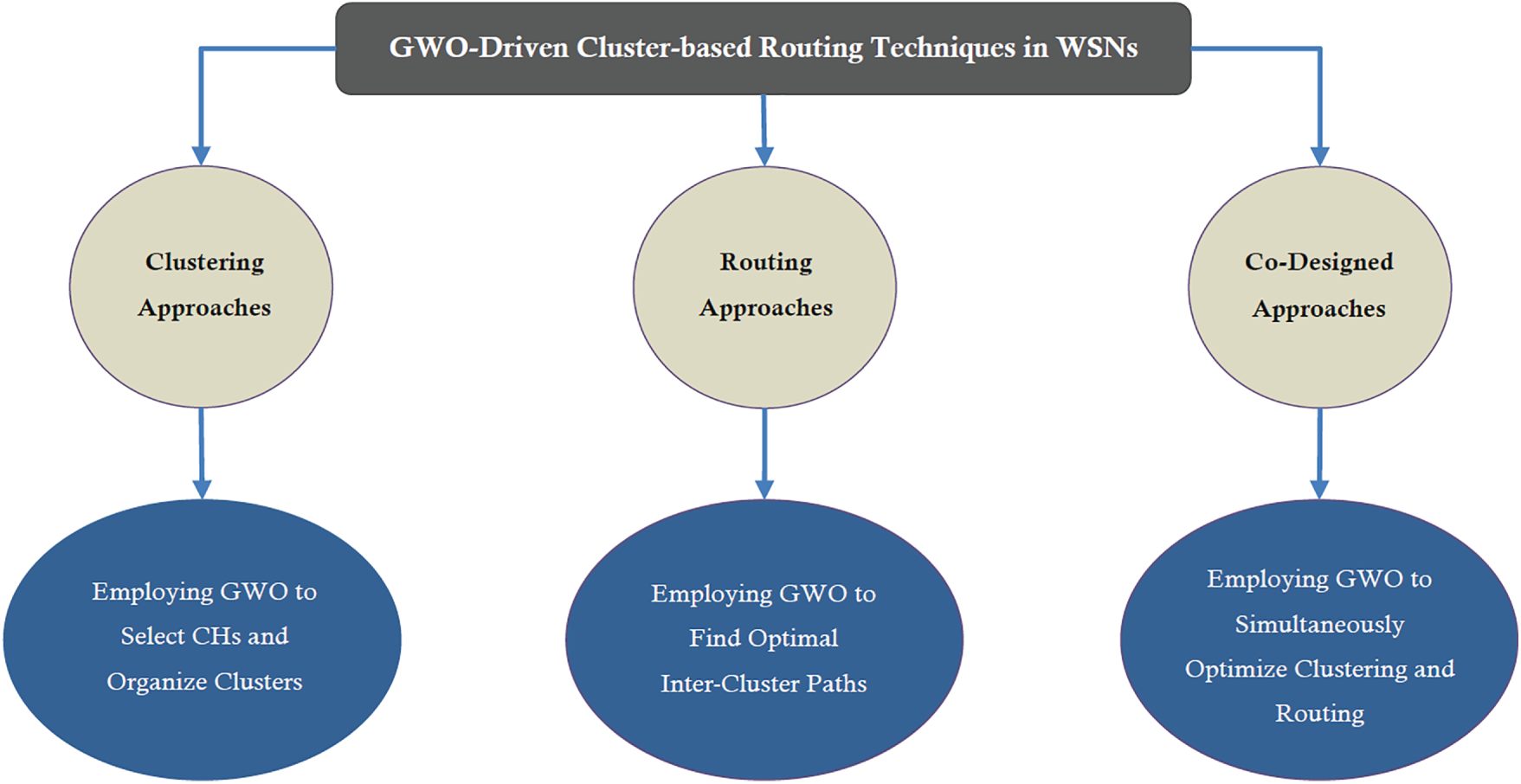
Figure 1: Classification of the existing GWO-driven cluster-based routing techniques in WSNs

Furthermore, Figs. 2–4 outline the key capabilities and limitations associated with each category provided in Fig. 1 (clustering, routing, and co-designed methods), respectively. Fig. 2 shows the classification of the existing clustering-oriented methods, which typically focus on CH selection and load balancing among sensor nodes. These models exploit GWO’s exploration–exploitation capability to minimize intra-cluster energy consumption while maintaining network coverage. Furthermore, Fig. 3 depicts the routing-based approaches, emphasizing how GWO optimizes multi-hop path construction and relay node selection under constraints such as residual energy, link distance, and latency. Fig. 4 illustrates co-designed clustering–routing techniques, where GWO simultaneously optimizes both stages, capturing interdependencies between cluster formation and data transmission. This integrated structure demonstrates the trend toward holistic optimization, where routing and clustering decisions are modeled as a joint objective to enhance overall energy efficiency. Together, Figs. 1–4 provide a complete methodological landscape of GWO-based methods, emphasizing not only the classification of algorithms but also the reasoning behind these distinctions. This structured taxonomy supports the survey’s methodological perspective, bridging algorithmic characteristics with their practical optimization purposes.

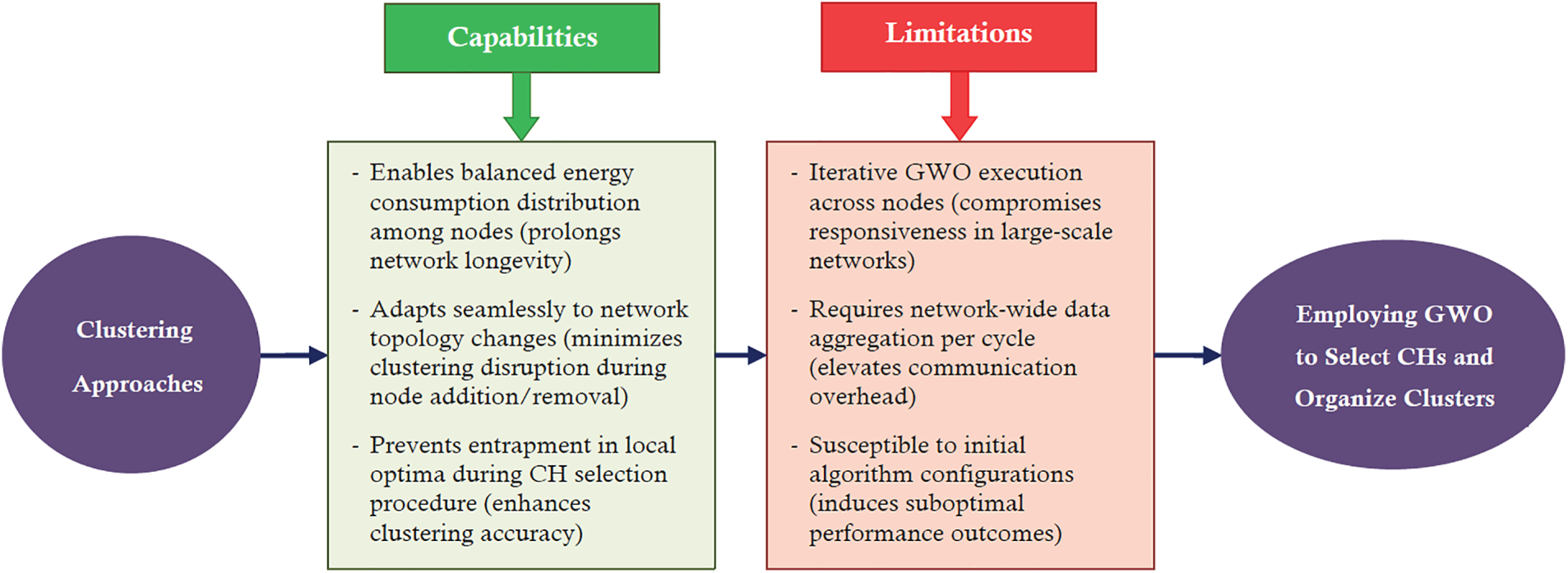
Figure 2: Capabilities and limitations of the GWO-driven clustering techniques

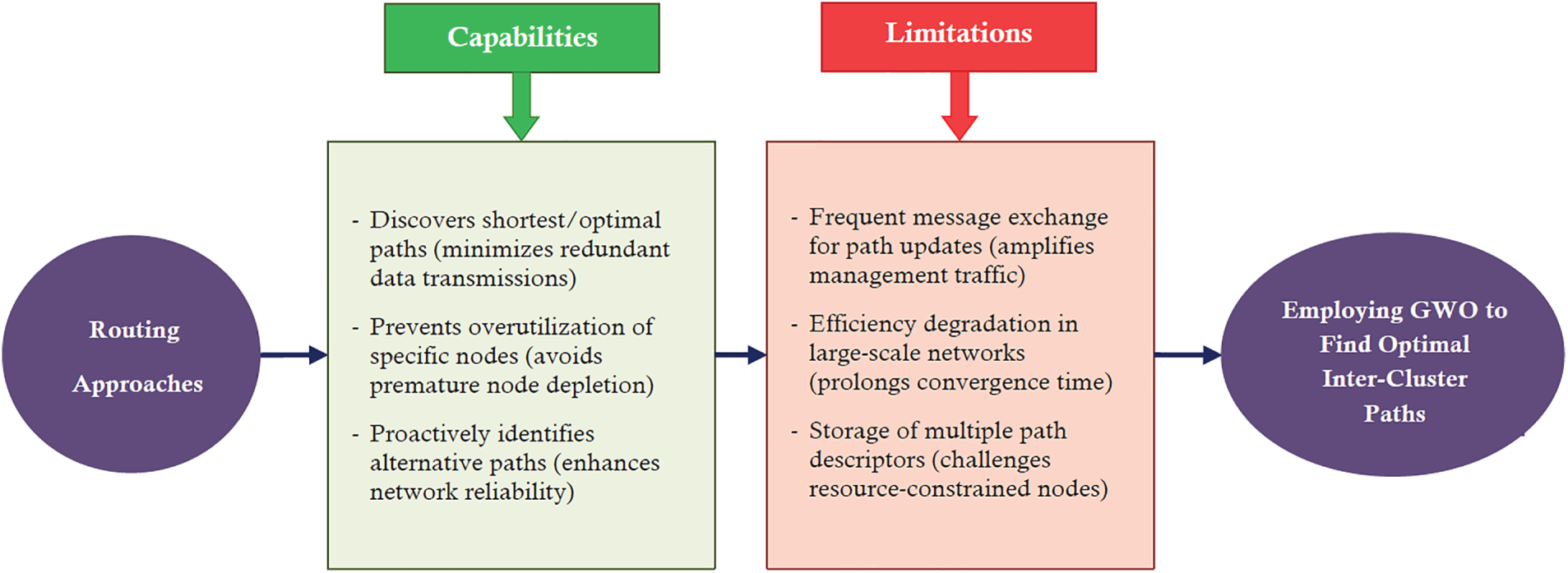
Figure 3: Capabilities and limitations of the GWO-driven routing techniques

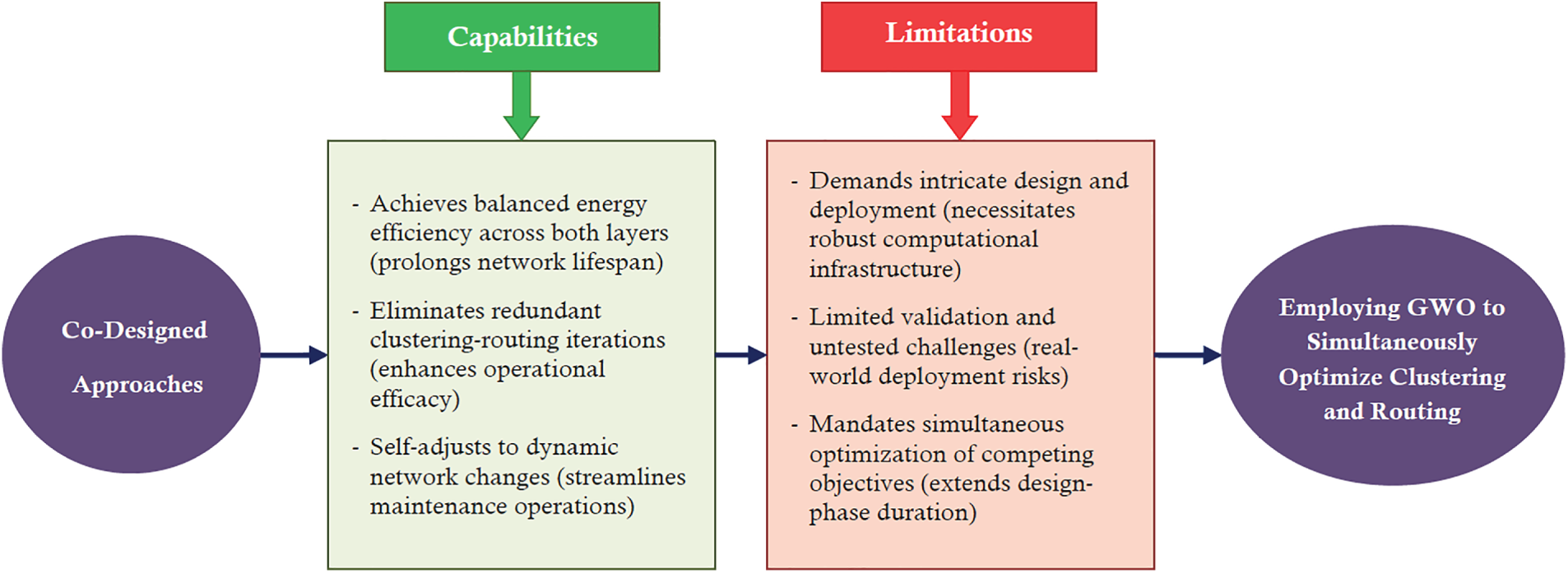
Figure 4: Capabilities and limitations of the GWO-driven co-designed techniques

2.2 Evaluation Parameters

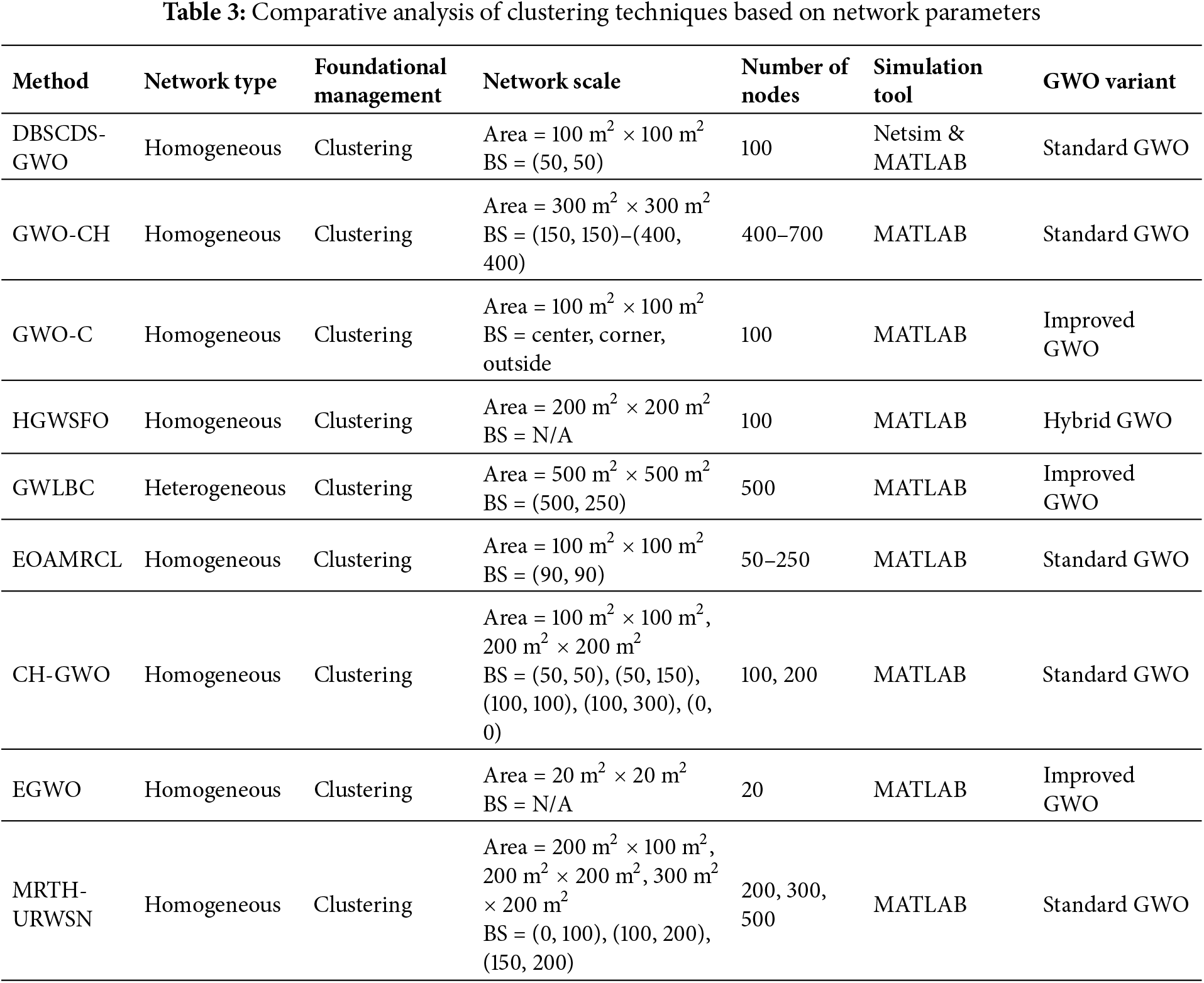
Existing approaches within each category are analyzed based on network parameters and solution parameters, considering different types of GWO such as standard GWO, multi-objective GWO, and its hybridization with other AI-based techniques. Each GWO-based technique is evaluated considering the specific decision variables of the problem and its objective function(s). Solution parameters include operational mode, operational state, modeling approach, objective(s), and key objective factors, while network parameters focus on method, network type, foundational management approach, network scale, number of nodes, simulation tool, and GWO variant.

Figs. 5 and 6 introduce a hierarchical framework for evaluating the performance of the existing GWO-driven techniques using solution- and network- parameters, respectively. This parameter hierarchy spans multiple levels, starting from broad operational modes and states, down to specific solution parameters and objectives. The top layers define the modeling approach and operational state, followed by network parameters such as node types, network scale, and the number of deployed nodes. It also includes practical aspects like the simulation tool and the specific GWO variant being utilized. At the core of the hierarchy are the solution parameters and key objective factors, which guide the optimization process toward targeted performance goals such as prolonging lifespan, minimizing energy usage, and improving communication efficiency. Figs. 5 and 6 serve as foundational references to develop or evaluate GWO-based clustering and routing protocols, offering a clear breakdown of the essential elements that influence performance outcomes in simulation or real-world scenarios.

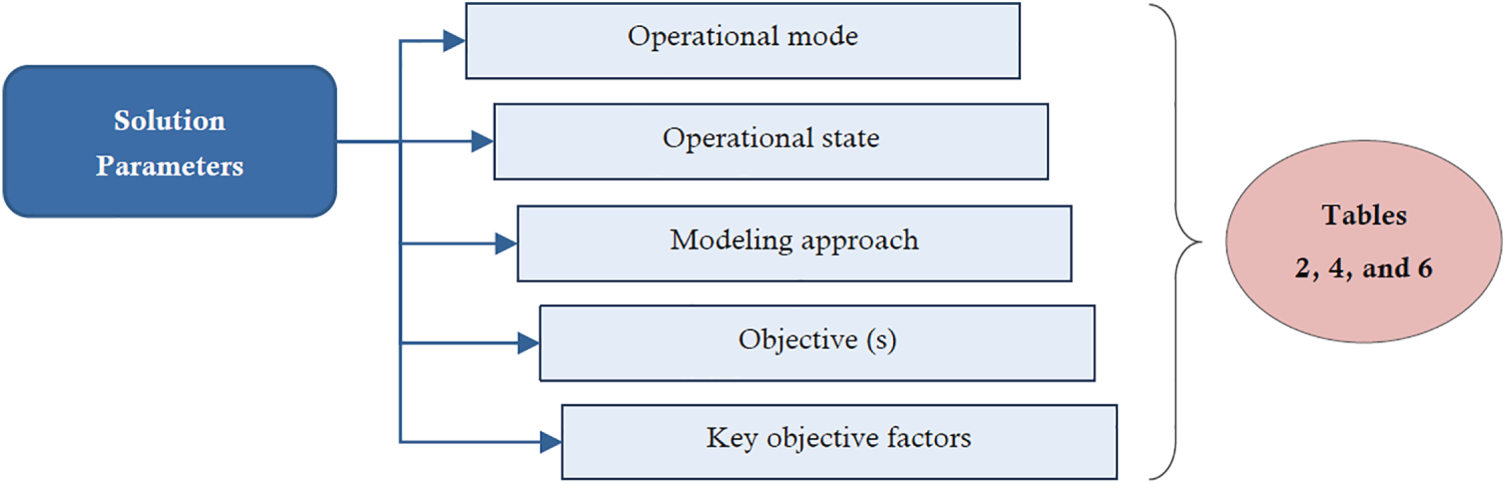
Figure 5: Solution parameters for performance evaluation of GWO-driven cluster-based routing techniques

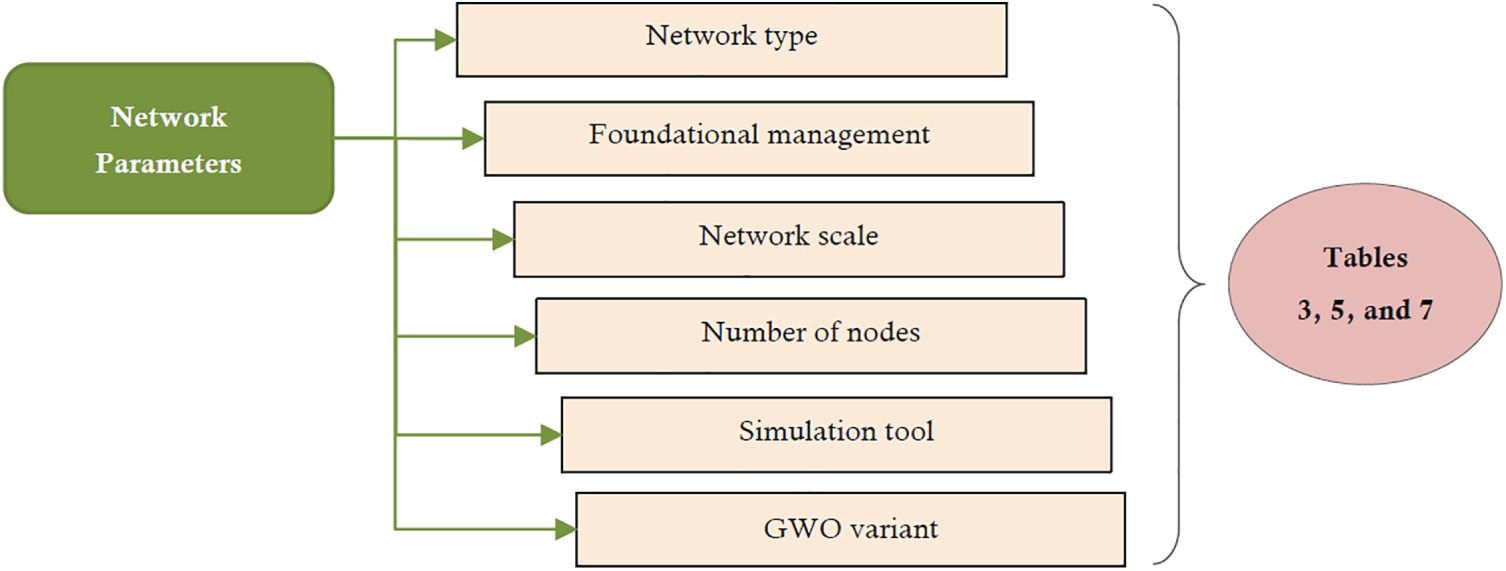
Figure 6: Network parameters for performance evaluation of GWO-driven cluster-based routing techniques

Although Figs. 1–4 classify GWO applications by their operational objectives, Figs. 5 and 6 complement the functional taxonomy shown earlier by shifting focus from what is optimized to how and under which conditions optimizations are evaluated. Fig. 5 maps the solution parameters used across GWO-based methods (e.g., operational mode, modeling approach, objectives, and key objective factors). Furthermore, Fig. 6 organizes the network parameters (e.g., network type, management approach, scale, node count, and simulation tools) that define each study’s experimental context. Together, these two figures (Figs. 5 and 6) provide a compact methodological snapshot: Fig. 5 shows what methods optimize and why, while Fig. 6 shows where and under which conditions those optimizations were tested.

3  Overview of GWO Algorithm

The GWO algorithm was introduced by Mirjalili et al. [38]. It emulates the leadership hierarchy and hunting strategies of grey wolves in nature. Known for their cooperative pack dynamics, grey wolves exhibit behaviors such as tracking, encircling, and attacking prey. These behaviors are mathematically modeled in GWO to solve complex optimization problems in diverse applications in communication networks [44–48].

In GWO, the population of wolves is divided into four groups based on their fitness [49]. The alpha (α) represents the best solution and acts as the leader of the pack. The beta (β) is the second-best solution and assists the alpha in decision-making. The delta (δ) is the third-best solution and is responsible for scouting and protecting the pack. The remaining wolves, known as omega (ω), follow the alpha, beta, and delta. The hunting process is guided by α, β, and δ wolves, while the omega wolves follow their lead [50]. Below is a summary of the key steps and mechanisms of the GWO algorithm. The overall steps of the GWO algorithm are as follows:

1.   Initialize the population of wolves (candidate solutions) randomly.

2.   Evaluate the fitness of each solution.

3.   Identify the α, β, and δ wolves based on fitness.

4.   Update positions using Eqs. (10)–(18).

5.   Decrease a→ linearly over iterations to shift from exploration to exploitation.

6.   Repeat steps 2–5 until a stopping criterion (e.g., maximum number of iterations) is met.

3.1 Encircling Prey

Grey wolves encircle their prey during the hunt, and this behavior is mathematically modeled using specific equations [51]. The distance between a wolf and the prey is calculated as follows:

D→=|C→⋅Xp→(t)−X→(t)|(1)

where Xp→(t) is the position vector of the prey (global best solution found so far), and X→(t) is the current position vector of a grey wolf. The wolves then update their positions as X→(t+1)=Xp→(t)−A→⋅D→, which can be calculated as follows:

X→(t+1)=Xp→(t)−A→⋅|C→⋅Xp→(t)−X→(t)|(2)

Here, A→ and C→ are coefficient vectors calculated as A→=2a→⋅r1→−a→ and C→=2⋅r2→, where a→ decreases linearly from 2 to 0 over iterations, and r1→ and r2→ are random vectors in [0, 1]. These equations allow the grey wolves to adjust their positions around the prey, simulating the encircling behavior.

3.2 Hunting Process

The hunting process is guided by the alpha, beta, and delta wolves, which are assumed to have better knowledge of the prey’s location [52]. The positions of the omega wolves are updated based on the positions of these leaders. To achieve this purpose, first, the distances between the current wolf and the alpha, beta, and delta are calculated as:

Dα→=|C1→⋅Xα→−X→|(3)

Dβ→=|C2→⋅Xβ→−X→|(4)

Dδ→=|C3→⋅Xδ→−X→|(5)

Then, the new associated positions can be expressed as:

X1→=Xα→−A1→⋅Dα→(6)

X2→=Xβ→−A2→⋅Dβ→(7)

X3→=Xδ→−A3→⋅Dδ→(8)

Accordingly, the final position of the grey wolf can be updated as follows:

X→(t+1)=X1→+X2→+X3→3(9)

This averaging mechanism ensures that wolves update their positions by considering the guidance of the top three solutions, improving convergence toward the global optimum.

3.3 Exploration-Exploitation Mechanisms

The exploitation and exploration phases of the GWO algorithm are controlled by the coefficient vector A→, which is influenced by the parameter a→ that linearly decreases from 2 to 0 over iterations. When |A→| < 1, the wolves converge towards the best-known positions, thereby intensifying the exploitation phase and focusing the search around promising areas in the solution space. Conversely, when |A→| > 1, the wolves are encouraged to diverge away from the current leaders, promoting exploration and allowing the algorithm to discover new regions, thus avoiding premature convergence to local optima. The stochastic nature of the coefficient vectors A→ and C→, derived from random numbers r1→ and r2→, plays a major role in balancing exploration and exploitation throughout the optimization process [53–55].

4  System Modeling for GWO-Based Clustering and Routing in WSNs

This section presents the fundamental system framework underlying the GWO-based clustering and routing techniques reviewed in this survey. It provides a unified description of the operational workflow of cluster-based and multi-hop routing communications in WSNs, followed by an analytical energy consumption model that forms the basis of most objective functions used in GWO-driven optimization.

4.1 Operational Workflow of the Clustering and Routing Framework

This section delineates the operational workflow of clustering and routing techniques. As illustrated in Fig. 7, this framework encompasses multiple phases, including cluster formation, relay selection, and final routing toward the BS. By elucidating the workflow of the techniques examined in this study, this section enables a better understanding of the interactions among these components and how each is optimized by the GWO algorithm. As illustrated in Fig. 7, the overall operational workflow of the cluster-based routing optimization suing GWO typically follows a multi-phase process, including initialization, CH selection, routing path construction, and steady-state communication. Each phase interacts dynamically, where the positions of grey wolves represent candidate solutions (e.g., CH sets or routing configurations), and their fitness reflects energy efficiency and coverage quality. This schematic provides a unified conceptual view of how GWO is adapted to handle WSN clustering and routing problems through iterative exploration and exploitation of the solution space.

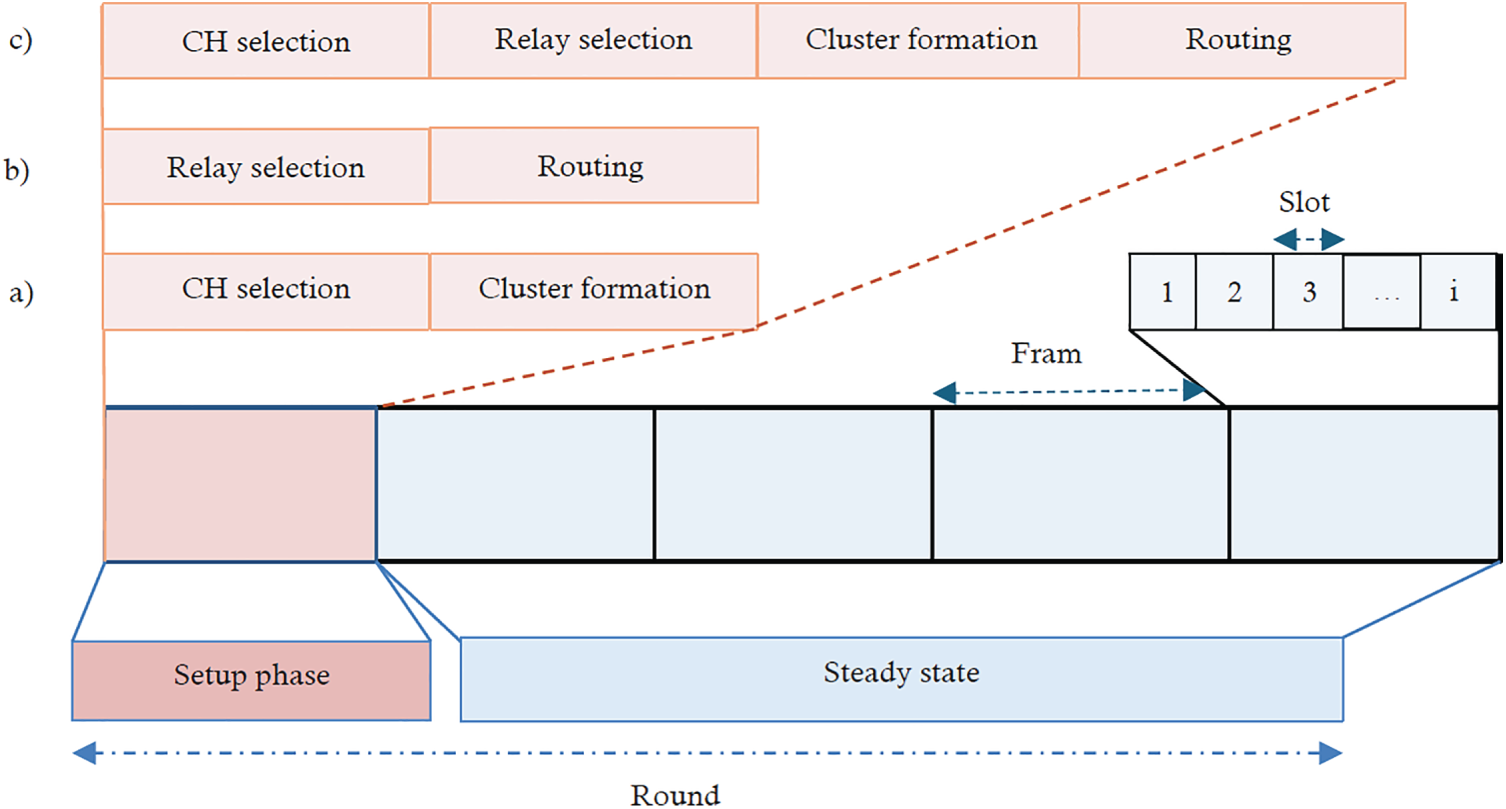
Figure 7: Operational workflow, (a) clustering, (b) routing, (c) co-designed clustering/routing

Setup phase: The setup phase involves several sub-phases, including CH selection, cluster formation, relay selection, and routing [56–60].

•   CH selection: In the CH selection phase, cluster heads are typically chosen based on the positional and status information of nodes, either autonomously and in a distributed manner or centrally at the BS. If the technique’s mechanism relies on rotating the CH role in each round, CHs are selected in each round according to the strategies and design criteria adopted in that technique [61]. It is worth noting that in GWO-based techniques, this process is often modeled as part of the algorithm’s fitness function.

•   Cluster formation: After the CHs are determined in the previous step, the BS sends a message to all nodes selected as CHs in the current round [62]. Based on node identifiers, each node that has been chosen as a CH becomes aware of its role. The final selected CHs then broadcast a message containing their own ID. Non-CH nodes, based on the received signal strength of the CH messages, join the CH with the least distance to them. They confirm their cluster membership by sending a JOIN-CH message to the CH. Subsequently, the CHs create a TDMA scheduling table according to the number of member nodes in their cluster [63]. Each member node is assigned a dedicated time slot, and this scheduling table is generated only once per round [64–67]. All network nodes are clustered using this approach based on the selected CHs, as illustrated in part (a) of Fig. 7.

•   Relay selection: After the cluster formation process is completed, CH nodes may require one or more intermediate nodes as relays to deliver their data to the base station (BS), which may be located at a considerable distance. This phase is emphasized in some methods because it is essential, especially in large-scale networks, to prevent excessive energy dissipation of cluster head nodes due to long-distance data transmission. Selecting an optimal relay node plays a vital role in enhancing energy efficiency and network lifetime [68–70]. In GWO-based techniques, this process is often modeled as part of the algorithm’s fitness function, and relay node selection is performed according to the criteria and objectives defined by network designers.

–   Routing: The routing process refers to the overall strategy of transmitting data from CH nodes to the BS, often through multi-hop paths. While “relay selection” focuses on choosing the best next single-hop node, “routing” deals with designing and optimizing the entire path from source to destination [71–73]. After clusters are formed and relay nodes are selected, the step of establishing a global optimal path follows. The GWO algorithm can be applied at this level to find the shortest and most efficient possible path among the pre-identified cluster heads and relay nodes to deliver data to the BS. For example, the BS uses the GWO algorithm to calculate the most optimal multi-hop paths, while the fitness function considers minimizing total energy consumption, balancing the load among nodes, and reducing delay. After computation, the BS communicates these optimal paths to all CH and/or relay nodes. Thus, each CH operates not only based on proximity (as in the cluster formation phase) but also according to a pre-calculated and optimized path for transmitting its data toward the BS.

Steady state phase: During this phase, each non-CH node sends its data only during the time slot (slot) allocated by its CH (as shown in Fig. 7, each CH is assigned a frame, which the CH divides into slots according to its number of members). Member nodes are awake only in this phase and return to sleep mode after sending data to the CH. However, the CH node remains awake to receive data from its member nodes. Each node sends only one data packet per round to its CH. The CHs transmit the received data, either after aggregation or directly, to the BS. Once this phase is completed, the current round terminates and the next round begins [74–78].

4.2 Mathematical Model for Data Transmission

Energy consumption is widely recognized as the most important performance metric and a central component of the objective function in metaheuristic-based clustering and routing applications for WSNs, as it directly influences network lifetime [79–82]. To ensure a common understanding of this key objective across the GWO-based methods reviewed in this paper, a basic mathematical model of data communication and energy dissipation is presented. All symbols, parameters, and variables used in the first-order radio energy model, along with their definitions and units, are summarized in Table 1 for clarity and consistent reference throughout the manuscript.

This section introduces the first-order radio energy model [83], which provides the necessary analytical framework for calculating the energy cost during data transmission and reception. The equations in this section represent the foundational energy model used in most GWO-based clustering and routing studies. GWO utilizes this energy model by encoding energy cost components directly into the fitness function, ensuring that CH selection and routing decisions minimize overall transmission energy and maximize network lifetime.

This model enables a fair and quantitative understanding of energy consumption in different GWO-based clustering and routing approaches, which will be discussed in subsequent sections. The fundamental principles of the mathematical model for SN communications are as follows:

ETx(l,d)={l×Eelec+l×εfs×d2  for   d<dol×Eelec+l×εmp×d4for  d≥do(10)

The transmitter node expends energy both to power its electronic radio circuitry (to modulate data onto the channel) and to operate its radio frequency amplifier. In contrast, the receiver node only consumes energy to power its electronic radio circuitry (to demodulate data from the channel). Consequently, to calculate the energy required to transmit l bits over a distance d, ETx(l,d) is computed using Eq. (10): the first case applies to free-space models where the distance is less than a threshold d0, while the second case is used for distances greater than do, where do=εfsεmp.

On the other hand, the energy required to receive l bits of a data packet can be calculated as follows:

ERx(l)=l×Eelec(11)

–   Energy consumption using aggregation strategy: One of the duties of CH nodes in the network, corresponding to the nature and essence of the sensor network application, is aggregation. This process can be considered in various forms in clustering or multi-hop routing methods. For example, an aggregation strategy for CHs can be expressed as follows [84]:

Scomp=Srec×Ragg×(TCLUSTER−1)(12)

Sagg=Srec×Scomp(13)

where (TCLUSTER−1) denotes the number of member nodes in the cluster excluding the CH.

–   Total energy consumption of member nodes and CHs (ECH) in an operational round (without aggregation): The energy consumption of member nodes for communicating with the CH as well as the energy consumption of the CH (without aggregation) for communicating with the BS can be readily calculated using Eqs. (10) and (11), respectively. Thus, it can be expressed as follows [85]:

Emember=l×Eelec+l×εfs×d2(14)

ECH=(l×Eelec×(TCLUSTER−1))+TCLUSTER×(l×Eelec+{l×εfs× d2l×εmp× d4)(15)

Therefore, Emember can be expressed in Eq. (14), while the total energy consumption of CHs for receiving and transmitting data without aggregation can be calculated according to Eq. (15).

–   Total energy consumption of a cluster in an operational round (without aggregation): ECLUSTER, the energy consumption of a cluster in one round, includes Emember (the energy consumed by nodes for collecting and transmitting data to the CH) as well as the energy consumed by the cluster head ECH for transmitting data packets to the BS. This is calculated as follows:

ECLUSTER=Emember×(TCLUSTER;−1)+ECH(16)

–   Total energy consumption of member nodes and CHs in an operational round (with aggregation): The energy consumption of the nodes, given that aggregation is performed solely at the CHs, can be readily calculated using Eqs. (10)–(13). Meanwhile, the energy consumption of the CHs considering the aggregation rate for distances less than d0, is expressed as follows:

ECH-agg=(l×Eelec×(TCLUSTER−1))+(l×Eelec+{l×εfs× d2l×εmp× d4)(1+TCLUSTER−1/Ragg)(17)

For distances greater than do to the BS, only d4 is used instead of d2. Eq. (17) indicates that the energy consumption for data transmission is calculated in full for the CH itself, while for cluster members undergoing data aggregation at rate Ragg, the transmission energy consumption is computed as 1/Ragg. For reception, energy consumption is calculated only for cluster members excluding the CH itself.

–   Total energy consumption of a cluster in an operational round (with aggregation): The energy consumption of a cluster in one round using data aggregation at rate Ragg includes the energy consumption of all cluster nodes Emember along with the energy consumption of the CH under aggregation conditions ECH−agg, expressed as follows:

ECLUSTER−agg=Emember×(TCLUSTER−1)+ECH−agg(18)

Numerical Example: Consider a typical network with 100 nodes deployed in a 100 m × 100 m area, where the packet size l = 400 bits, Eelec = 50 nJ/bit, εfs=10pJ/bit/m2, εmp = p.0013 J/bit/m4, and Ragg = 0.6. This simple example illustrates how the energy model is used to calculate transmission and reception costs for both cluster members and CHs, and how the energy values can be encoded into the fitness functions of GWO-based methods to optimize network lifetime. The energy consumptions for member nodes and CH nodes can be calculated as follows:

•   Cluster Member Transmission Energy Consumption: For a member node at distance d = 10 m from its CH node, the energy consumption is ETx=l⋅Eelec+l⋅εfs⋅d2=4000⋅50 nJ+4000⋅10 pJ⋅102, which results in a dissipated energy of ETx≈ 204 µJ.

•   Cluster Head Reception Energy Consumption: Assuming TCLUSTER = 10 member nodes, the CH receives 9 data packets from its member nodes: ERx=9⋅l⋅Eelec=9⋅4000⋅50 nJ, which results in a total energy consumption of ERx = 1.8 mJ.

•   Cluster Head Transmission Energy Consumption: Considering a distance d=50 m (<d0) from the CH node to BS, and that the aggregated data size is calculated as Sagg=l⋅Ragg=4000⋅0.6=2400 bits, the total dissipated energy from the CH node (due to data transmission to BS) can be expressed as ECH−Tx=Sagg⋅Eelec+Sagg⋅εfs⋅d2=2400⋅50 nJ+2400⋅10 pJ⋅2500, which results in a total dissipated energy of ECH−Tx≈ 180 mJ.

4.3 Connection between Energy Model and Performance Metrics

In a typical GWO-driven clustering and/or routing framework, the network operation proceeds in discrete rounds, each consisting of two main phases: (i) a setup phase, where cluster heads and/or routing paths are optimized using GWO, and (ii) a steady-state phase, where actual data transmissions take place. During the setup phase, each sensor node is assigned a specific role (CH or member node), and routing paths are established based on the optimized GWO solution vectors. Accordingly, in each operational round:

•   GWO selects CHs and/or routes in the setup phase.

•   Roles of nodes are assigned (CH or member).

•   During the steady-state phase, Eqs. (1)–(9) compute the transmission and reception energies.

•   Node energies are updated using Ei(r+1) according to Eq. (19).

Subsequently, during the steady-state phase, all nodes transmit, receive, and possibly aggregate data, and their energy levels are updated using the first-order radio energy model defined in Section 4.2. Let Ei(r) denote the residual energy of node i at the beginning of round r. After data transmission and reception in that round, the updated residual energy of node i can be computed as follows:

Ei(r+1)=Ei(r)−EiTx(r)−EiRx(r)(19)

where EiTx and EiRx are computed using Eqs. (10)–(18), depending on whether node i operates as a cluster member or a cluster head in the current round and on whether data aggregation is performed.

This round-by-round energy updating process continues until nodes exhaust their available energy. Based on the above round-based energy evolution, the standard network lifetime performance indicators include First Node Death (FND), Half Node Death (HND), and Last Node Death (LND), which are the ultimate objective of most GWO-based optimization strategies reviewed in this survey, and can be mathematically defined as follows:

FND=min{r∣∃i∈{1,…,N}:Ei(r)=0(20)

HND=min{r∣∑i=1NI(Ei(r)=0)≥N2}(21)

LND=min{r∣∑i=1NI(Ei(r)=0)=N}(22)

where I(⋅) is the indicator function.

The optimized clustering and routing decisions, in turn, determine the residual energy evolution Ei(r), which directly governs the lifetime metrics FND, HND, and LND. In Eq. (20), FND is defined as the first round in which the residual energy of at least one sensor node becomes zero. This metric reflects the initial stability period of the network. Furthermore, HND in Eq. (21) corresponds to the first round in which at least half of the sensor nodes have depleted their energy. This metric reflects the functional sustainability of the network. Finally, LND in Eq. (22) represents the final round in which the last remaining active node depletes its energy.

In most GWO-based clustering and routing methods surveyed in Sections 5–7, the fitness function is constructed based on one or several metrics including FND, HND, LND, and other metrics such as the total residual energy or the total dissipated energy by all nodes per round r, which can be respectively expressed as follows:

Eresidual(r)=∑i=1NEi(r)(23)

Econsumed(r)=∑i=1N(EiTx(r)+EiRx(r))(24)

This successive round-based process continues until the FND, HND, and ultimately LND conditions are satisfied. It quantitatively links the analytical energy model to the performance metrics reported in Section 8.

5  GWO-Driven Clustering Techniques

This section delves into the application of GWO and its variants to enhance clustering techniques in WSNs. In clustering-based communication for WSNs, as illustrated in Fig. 8, SNs are grouped into localized clusters, each managed by a CH. SNs within a cluster send their sensed data directly to their respective CH, which then performs data aggregation and forwards the summarized information to the BS [86]. This hierarchical structure reduces redundant transmissions and significantly lowers the number of long-distance communications to the BS, conserving energy across the network [87]. Clustering enhances scalability and allows the system to adapt to node failures or additions more efficiently. The selection of CHs is typically rotated or optimized using algorithms to balance energy usage and prolong the overall network lifespan [88].

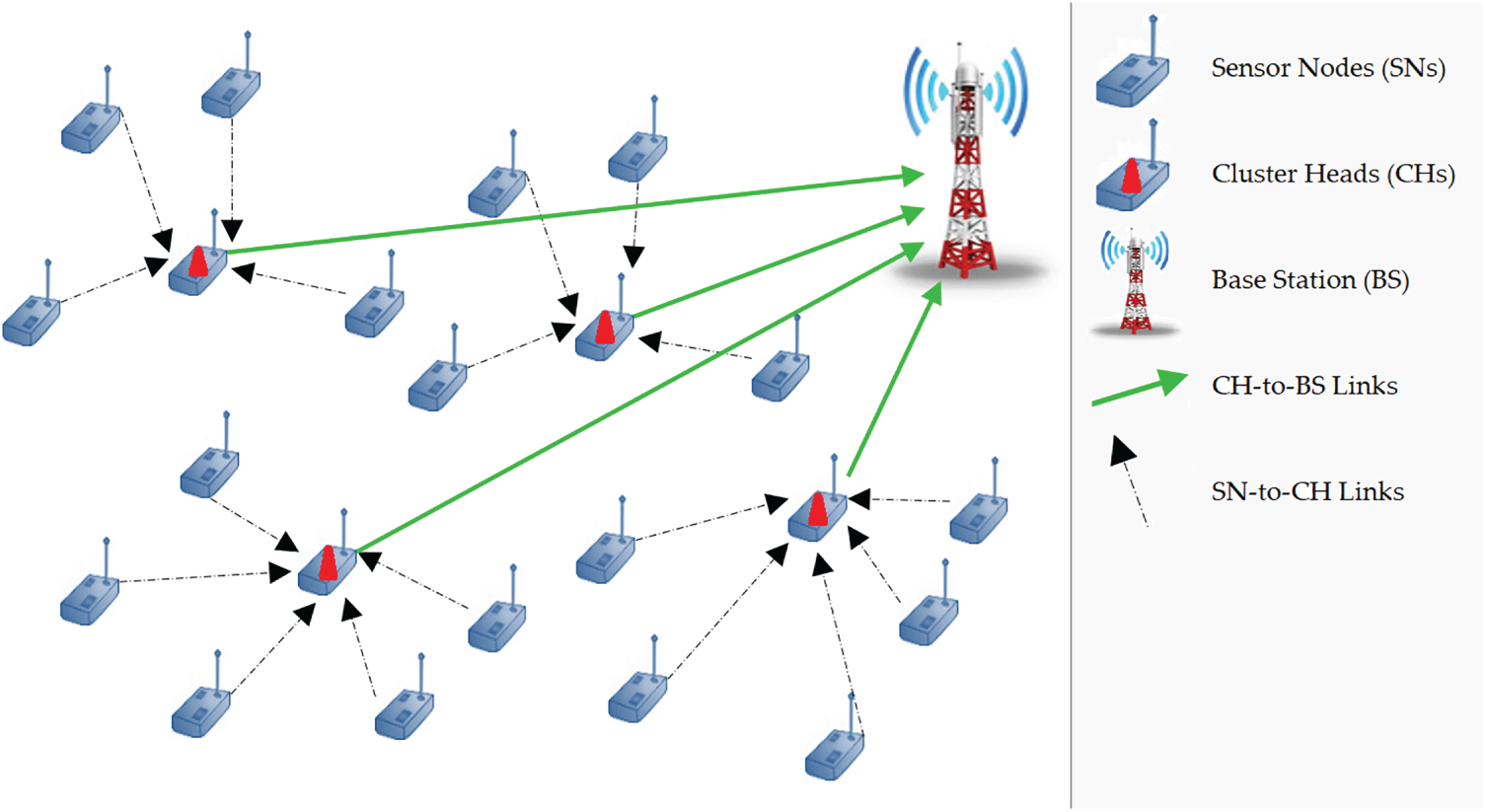
Figure 8: GWO-driven clustering techniques

Fig. 8 illustrates the hierarchical structure of GWO-based clustering in WSNs, where nodes are organized into multiple levels of abstraction from sensor nodes to base stations. This representation emphasizes how GWO optimizes the upper-level decision of CH placement while ensuring balanced energy consumption among lower-level sensor nodes. The hierarchical architecture facilitates scalability and distributed coordination, which are essential for large-scale WSN deployments.

Fig. 9 depicts a typical pseudocode and solution encoding structure for CH selection using GWO. Each grey wolf represents a potential CH configuration encoded as a position vector in the search space. This figure consists of two main parts. The first part includes the pseudocode of the GWO algorithm, which outlines the algorithm’s execution process step by step, and the second part presents a candidate solution, depicting the general framework and an example of solution encoding and representation (a wolf) in the algorithm. In this representation, each solution is typically modeled as a binary vector whose length is equal to the number of sensor nodes in the network. The value of each element in this vector (0 or 1) indicates the status of the corresponding node; where a value of 1 denotes that the node is selected as a CH, and a value of 0 represents an ordinary member node. The algorithm iteratively updates these positions based on the best α, β, and δ wolves, thereby guiding the search toward energy-efficient and well-balanced clustering layouts. This detailed illustration clarifies the underlying optimization mechanism that governs CH determination across most reviewed GWO-based clustering methods.

Figure 9: Pseudocode and a candidate solution of GWO applied to CH selection in GWO-driven clustering techniques

In the depicted candidate solution (first population member), 200 sensor nodes are represented, where a value of 1 indicates a CH node and a value of 0 denotes a regular member node. For instance, as shown in the figure, nodes 2, 3, and 6 function as CHs, while nodes 1, 4, 5, 7, and 200 are member nodes. Overall, this network configuration can support up to 15 cluster heads.

5.1 DBSCDS-GWO

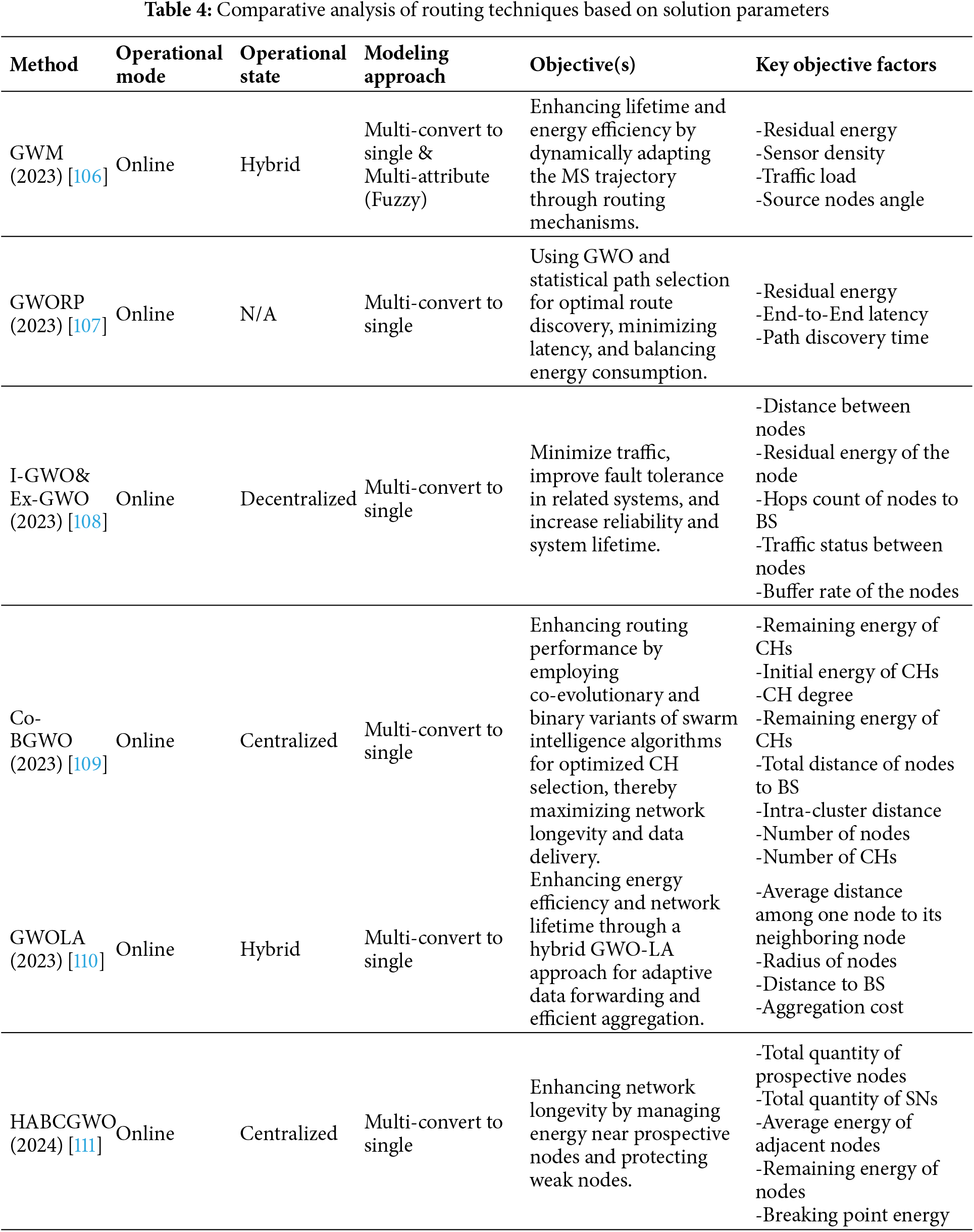
In [89], two methodologies are introduced to improve data delivery in WSNs: the Distance-Based Stable Connected Dominating Set using GWO (DBSCDS-GWO) and the Distance-Based Stable Clustering algorithm (DBSC-GWO). These approaches aim to create a stable and energy-efficient network by optimizing the selection and positioning of dominator nodes and CHs. DBSCDS-GWO utilizes a meta-heuristic optimization technique to determine the optimal locations of dominator nodes relative to the sink and dominate nodes. A key innovation in this method is the use of the Dominator Lifetime Index (DLI), which measures the approximate lifetime of dominator nodes and facilitates load balancing by minimizing the interquartile range of DLIs across the network. Similarly, DBSC-GWO introduces the CH Lifetime Index (CLI) to achieve balanced load allocation among CHs. Both algorithms focus on minimizing energy dissipation associated with data transmission distances, thereby enhancing the overall stability and lifespan of the WSN. The effective transmission distance parameter is utilized to evaluate and minimize energy consumption linked to data transmission. By ensuring uniform DLI and CLI values, these methods promote equitable energy usage among nodes, ultimately leading to reduced data transmission redundancy and communication delays.

5.2 GWO-CH

Further advancing the application of GWO in WSNs, [90] proposes the GWO-based CH (GWO-CH) selection method. This algorithm considers critical factors such as residual energy, intra-cluster distance, and the distance to the sink. An objective function and weight parameters are formulated to enhance the efficiency of CH selection and cluster formation. In this method, CHs are selected based on residual energy, neighborhood ratio, and their distance from the BS. The GWO algorithm represents search agents as m-dimensional CHs, each defined by its position (x-axis, y-axis) and sensor ID. Initially, the algorithm randomly selects CHs and calculates their objective values. It then identifies the top three search agents, denoted as α (the best), β (the second best), and δ (the third best), while the remaining agents are labeled as ω. Utilizing these three optimal solutions, the other search agents update their positions, leading to the identification of new CHs that satisfy the objective function. Subsequently, a weight function is employed to determine the appropriate cluster members that should join their respective CHs.

5.3 GWO-C

In [91], a modified GWO approach named GWO-C is introduced for CH election. This method aims to prolong the network’s lifespan by strategically selecting CHs based on multiple parameters, including average intra-cluster distance, sink distance, residual energy, and a newly introduced CH balancing factor. The GWO-C protocol initiates by enabling all SNs to relay their precise location and remaining energy to the BS. The BS subsequently executes the GWO-based clustering protocol, utilizing a fitness function that incorporates the aforementioned parameters to ensure optimal CH selection. Following the CH election, non-CH nodes identify and connect to the nearest CHs, facilitating effective cluster formation through a request and acceptance messaging system.

5.4 HGWSFO

Building on the principles of GWO, Ref. [92] presents a novel hybrid algorithm, the Hybrid GWO-based Sunflower Optimization (HGWSFO). This method is designed to optimize CH selection in WSNs while considering constraints such as energy consumption and separation distance. The HGWSFO algorithm enhances network longevity by balancing exploration and exploitation phases. The Sunflower Optimization (SFO) component conducts a broad search for global optima using a step-size parameter inspired by sunflowers’ pursuit of sunlight, thus improving exploration efficiency. Conversely, the GWO component focuses on a more targeted search, emphasizing exploitation through the use of coefficient vectors. In the implementation, 100 SNs are randomly deployed, with 5% acting as CHs. The CH selection process gains the strengths of both SFO and GWO through an index-based search mechanism, with a critical index value of 5 distinguishing their application: SFO is applied when the fitness index is below 5, while GWO is utilized for higher indices. This iterative process is repeated for each data transmission round, with GWO exploring potential solutions through a population of wolves and SFO managing a broader search via a population of plants oriented toward the sun.

5.5 GWLBC

In [93], the authors propose an energy-efficient load-balanced clustering approach for sustainable WSNs based on the Improved GWO (IGWO), referred to as GWO-based Load Balanced Clustering (GWLBC). This study develops a comprehensive performance matrix that accounts for critical factors such as the number of dead sensors, inactive CHs, overall energy consumption, network lifetime, and the convergence rate of the algorithm. The performance of various computational techniques for achieving energy-efficient load-balanced clustering in WSNs is compared against the proposed IGWO-based methodology. The enhancements made to traditional GWO focus on optimizing computational efficiency concerning energy consumption within WSNs deployed in smart city environments. The refined performance metrics not only facilitate improved communication among SNs but also enhance area coverage, thereby contributing to increased user satisfaction.

Furthermore, this research considers a heterogeneous model of WSNs, wherein disjoint sets of sensors are organized into clusters. Each cluster is associated with a CH responsible for transmitting data packets received from individual SNs. Following data collection at each CH, information is aggregated and relayed to a BS. Notably, this communication process incurs power consumption at both the receiver and transmitter ends due to factors such as free space loss and multipath fading channels. Consequently, these power demands significantly impact network longevity by necessitating effective load balancing among CHs. To systematically address these challenges, the problem of load balancing among CHs is formulated mathematically, using conventional symbols to represent their respective meanings.

5.6 EOAMRCL

In [94], a multi-layer protocol for efficient energy management in WSNs, referred to as the Energy Optimization Approach based on MAC/Routing Cross-Layer (EOAMRCL), is proposed. This protocol emphasizes the interaction between the Medium Access Control (MAC) and network layers to minimize unnecessary energy consumption. The EOAMRCL employs a centralized approach with a hierarchical architecture, partitioning the network into clusters and managing all processes at the BS. This multi-layer protocol enhances performance and addresses scalability issues by utilizing an objective function to identify optimal CHs based on residual energy levels and intra-cluster distances. During the handover phase, nodes alternate between active and sleep states using Network Allocation Vector (NAV) time slots, enabling the MAC layer to generate a duty cycle schedule informed by multi-layer routing information. Furthermore, the integration of a modified Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA) mechanism, along with sleep and active modes, significantly enhances the protocol’s energy efficiency by more effectively managing node activity. The protocol aims to prevent the premature depletion of nodes’ energy resources, thereby extending the overall lifetime of the network by ensuring that nodes are paired to alternate their active and sleep cycles.

5.7 CH-GWO

In [95], a CH selection protocol based on GWO (CH-GWO) was presented for WSNs, aimed at maximizing network lifetime. Recognizing power as a critical resource in battery-powered SNs, the study focuses on optimizing CH selection as a key strategy for energy conservation. The proposed approach employs a modified GWO algorithm, a metaheuristic optimization technique, to select optimal CHs. Unlike traditional CH selection methods that often rely on a single parameter, CH-GWO considers eleven attributes in its fitness function. These attributes encompass various network characteristics, including CH coverage, distance to the BS, residual energy of CHs and nodes, and average distances between nodes, CHs, and the BS. By incorporating both beneficiary (requiring higher values) and non-beneficiary (requiring lower values) attributes, the fitness function aims to balance competing factors influencing energy consumption. The weights assigned to these attributes are determined through experimentation, prioritizing beneficial attributes (72%) over non-beneficial ones (28%). The CH selection process is performed centrally at the BS, which receives location and energy information from all nodes. The GWO algorithm then operates on the defined fitness function to identify the optimal CH set. Following CH selection, member nodes associate with their nearest CH based on Euclidean distance, forming clusters. The protocol uses CSMA MAC for communication within clusters.

5.8 EGWO

Fauzan et al. [96] presented an Enhanced GWO (EGWO) algorithm aimed at optimizing transmission power in WSNs. The authors improved the original GWO by modifying the exploitation mechanism. While the conventional GWO employs a linearly decreasing control parameter to balance exploration and exploitation, the EGWO introduces a cosine-based concave decay function. This adjustment enables a smoother and more adaptive reduction in the exploitation rate, enhancing the algorithm’s ability to fine-tune solutions during later iterations. The proposed EGWO was evaluated through a series of simulations and benchmarked against several popular metaheuristic algorithms. The results demonstrated that EGWO consistently achieved lower transmission power consumption and prolonged network lifetime more effectively than its counterparts. The algorithm proved particularly robust in scenarios involving complex or non-uniform node topologies, making it a suitable candidate for deployment in real-world WSN applications with irregular spatial distributions.

5.9 MRTH-URWSN

Shokouhifar et al. [97] introduced a novel hybrid protocol, termed MRTH-URWSN (Metaheuristic-Real-Time Heuristic for UAV-assisted Rechargeable WSNs), specifically designed to enhance real-time clustering and energy-efficient routing in smart agriculture environments. The proposed framework integrates Wireless Power Transfer (WPT) via Unmanned Aerial Vehicles (UAVs) to recharge energy-depleted SNs, ensuring network sustainability and prolonging operational lifespan. The protocol features a two-phase structure: (i) an offline optimization phase, where a GWO-based metaheuristic fine-tunes the hyperparameters of the clustering and trajectory planning components according to farm-specific conditions; and (ii) an online heuristic phase, where two real-time algorithms manage cluster formation and UAV path planning to deliver energy and collect data. The model’s design allows for adaptive behavior across various deployment scenarios, addressing both data communication and energy replenishment through a UAV-assisted architecture. This study is notable for being one of the first to propose a fully integrated WPT-enabled UAV-assisted Rechargeable WSN system tailored for smart agriculture, combining the strengths of real-time decision-making with robust offline optimization to meet practical deployment needs.

5.10 Classification of GWO-Driven Clustering Techniques

Tables 2 and 3 present a comparative analysis of the examined methods, focusing on key solution-based and network-based parameters. Table 2 provides a detailed comparison of the solution parameters employed in the methods, while Table 3 focuses on the configuration, simulation, and network characteristics of each approach. It is evident from the reviewed studies that although all GWO-based clustering techniques aim to enhance energy efficiency and prolong network lifetime, their methodological distinctions lie mainly in the way they encode cluster head selection and manage energy balancing. Overall, clustering-oriented GWO approaches primarily differ in how they balance exploration and exploitation during CH selection. Adaptive variants tend to outperform basic GWO models in convergence stability and cluster distribution, while hybrid models achieve superior energy balancing at the cost of higher computational complexity. This comparison highlights that methodological innovation, rather than parameter tuning alone, plays a more decisive role in improving network performance.

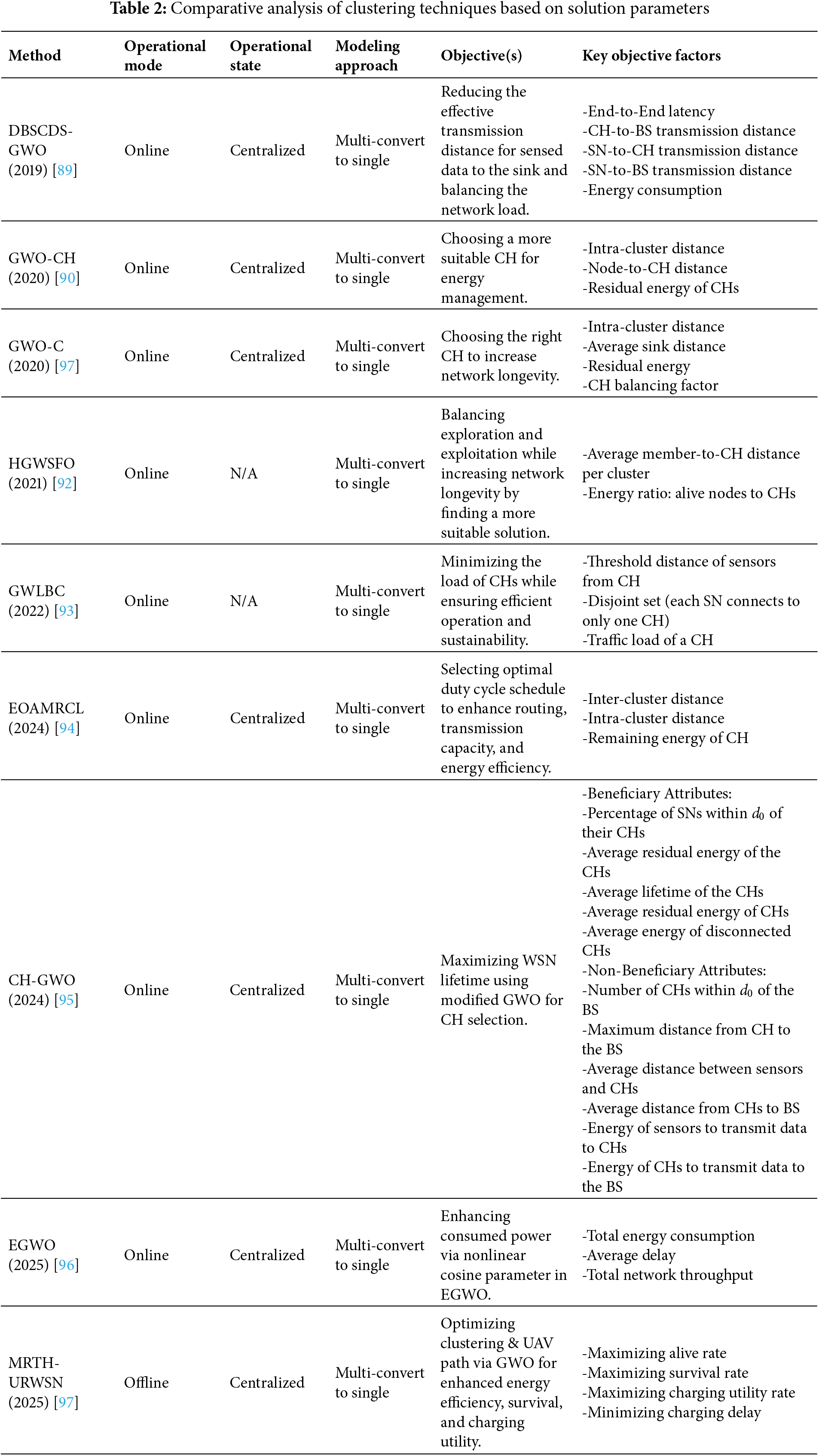
Several variations and enhancements of GWO have been proposed to improve its performance in clustering. For instance, DBSCDS-GWO introduces the DLI and CLI to balance energy consumption and extend network lifetime. HGWSFO combines GWO with SFO to enhance exploration and exploitation capabilities, thereby improving CH selection efficiency. GWO-CH focuses on residual energy, intra-cluster distance, and distance to the BS to optimize CH selection. GWO-C incorporates a CH balancing factor to ensure equitable energy usage among CHs. GWLBC employs IGWO to achieve energy-efficient load-balanced clustering, enhancing network sustainability. EOAMRCL combines GWO with an enhanced CSMA/CA mechanism to minimize energy consumption and extend network lifetime. Finally, CH-GWO utilizes a modified GWO algorithm with a comprehensive fitness function that considers eleven attributes, including residual energy, CH coverage, and distances to the BS, to maximize network lifetime. EGWO enhances the exploitation mechanism of standard GWO by replacing the linear control parameter with a cosine-based concave decay function, enabling finer solution tuning in later iterations and proving effective in reducing transmission power consumption for optimized clustering. Finally, MRTH-URWSN performs a GWO-based metaheuristic in its offline phase to optimize hyperparameters for clustering and UAV trajectory planning within a hybrid UAV-assisted rechargeable WSN framework.

6  GWO-Driven Routing Techniques

This section explores the application of GWO and its variants to enhance routing protocols in WSNs. Protocols implementing multi-hop routing aim to ensure load balancing and reduce latency by optimizing the number and length of hops by distributing energy usage more evenly across the network [98–101].

Fig. 10 demonstrates a typical multi-hop routing technique in which data is transmitted from one SN to another in a series of intermediate hops until it eventually reaches the BS. This approach is particularly beneficial in large-scale or sparse networks where direct communication with the BS is energy-intensive or physically unfeasible [102–104]. Each SN participates in forwarding data from its neighbors, which requires careful path selection to minimize energy consumption and avoid network congestion [105]. As shown in Fig. 10, GWO is further extended to optimize routing and relay node selection. The figure outlines how routing paths evolve iteratively as wolves update their positions based on multi-objective fitness functions considering distance, residual energy, and link quality. This depiction highlights GWO’s capacity to adaptively refine routing strategies under changing network conditions and energy constraints.

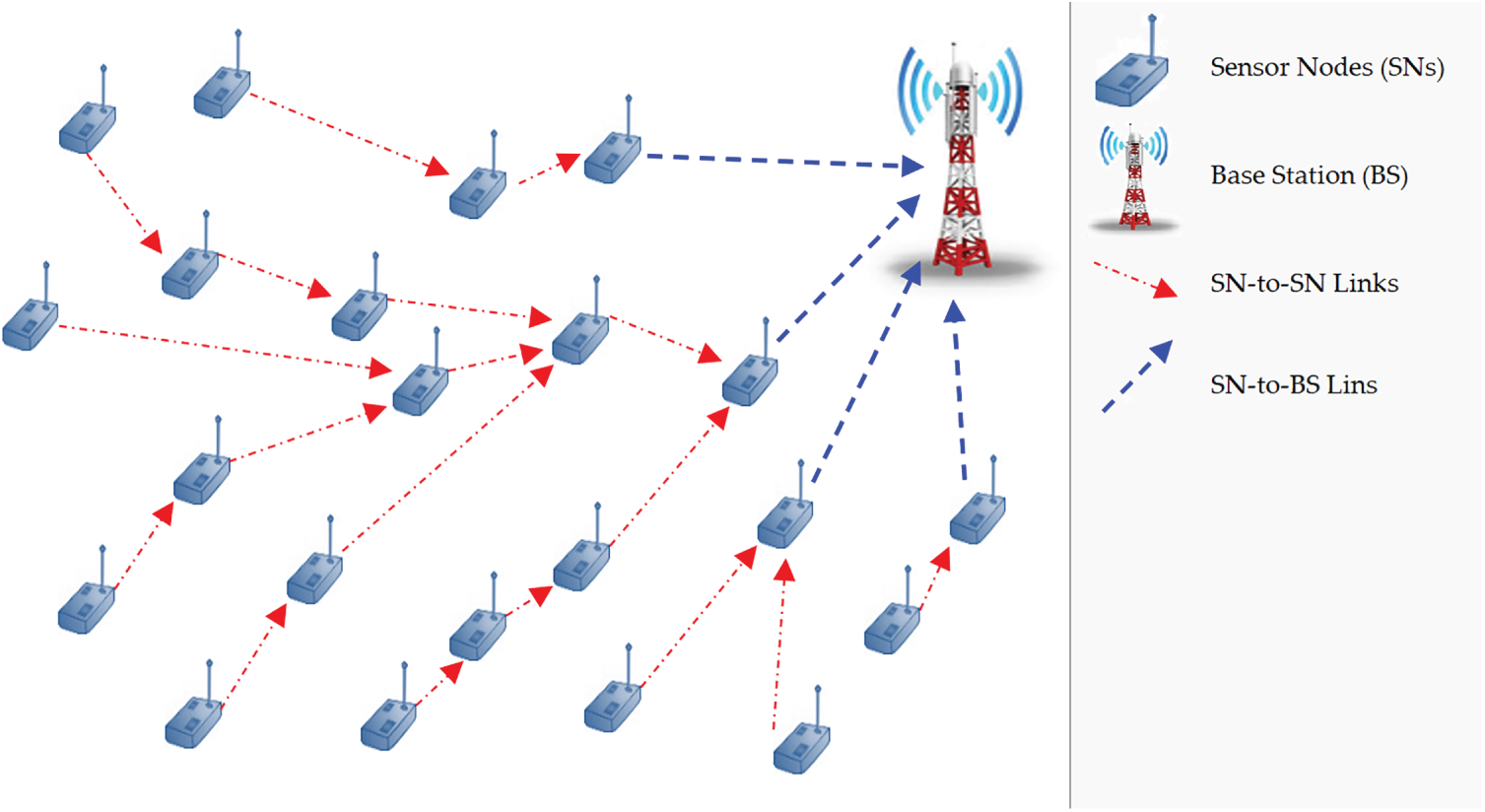
Figure 10: GWO-driven routing techniques

Fig. 11 illustrates the pseudocode flow and an example of a candidate solution generated by the GWO algorithm for relay and Cluster Head (CH) selection in routing optimization. As depicted, each grey wolf represents a possible routing configuration where sensor nodes determine their relay connections based on fitness evaluations. For instance, Node 1 transmits its data via Node 15, CH 2 forwards its packets through CH 1, and CH 3 also routes its information to the Base Station (BS) through CH 1, forming a multi-hop communication chain. Meanwhile, Node 4 selects Node 5 as its relay, and Node 15 directly transmits its data to the BS without intermediaries. The pseudocode highlights how GWO iteratively refines such routing paths, updating wolf positions according to both node-level and path-level parameters—such as residual energy, distance, and transmission cost. The process continues until convergence criteria are met, typically minimizing energy consumption or maximizing network lifetime. This example clearly demonstrates the flexibility and practicality of the GWO algorithm in dynamically constructing near-optimal multi-hop routes and selecting efficient relay nodes in WSNs.

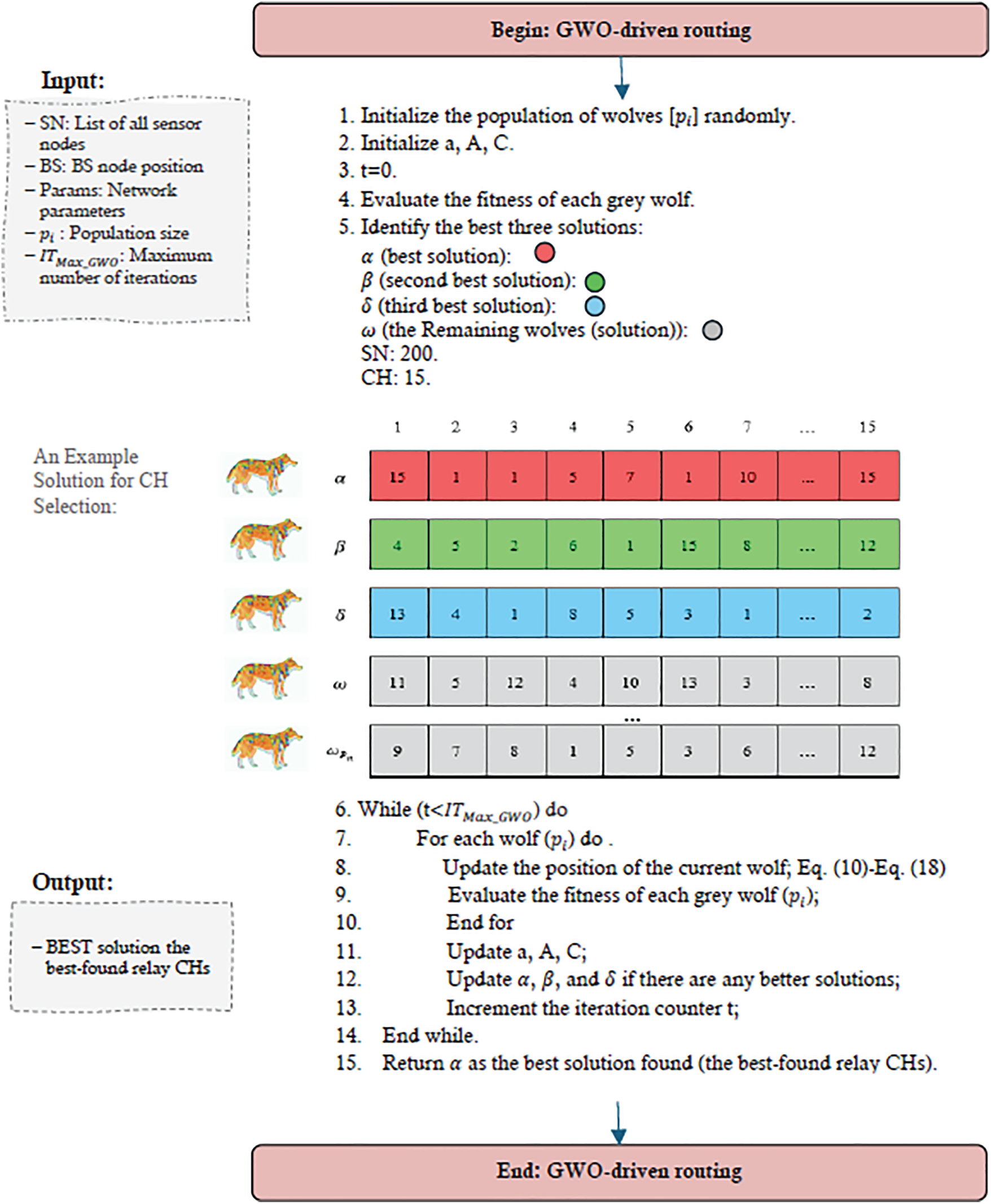
Figure 11: Pseudocode and a candidate solution of GWO applied to relay CH selection in GWO-driven routing techniques

6.1 GWM

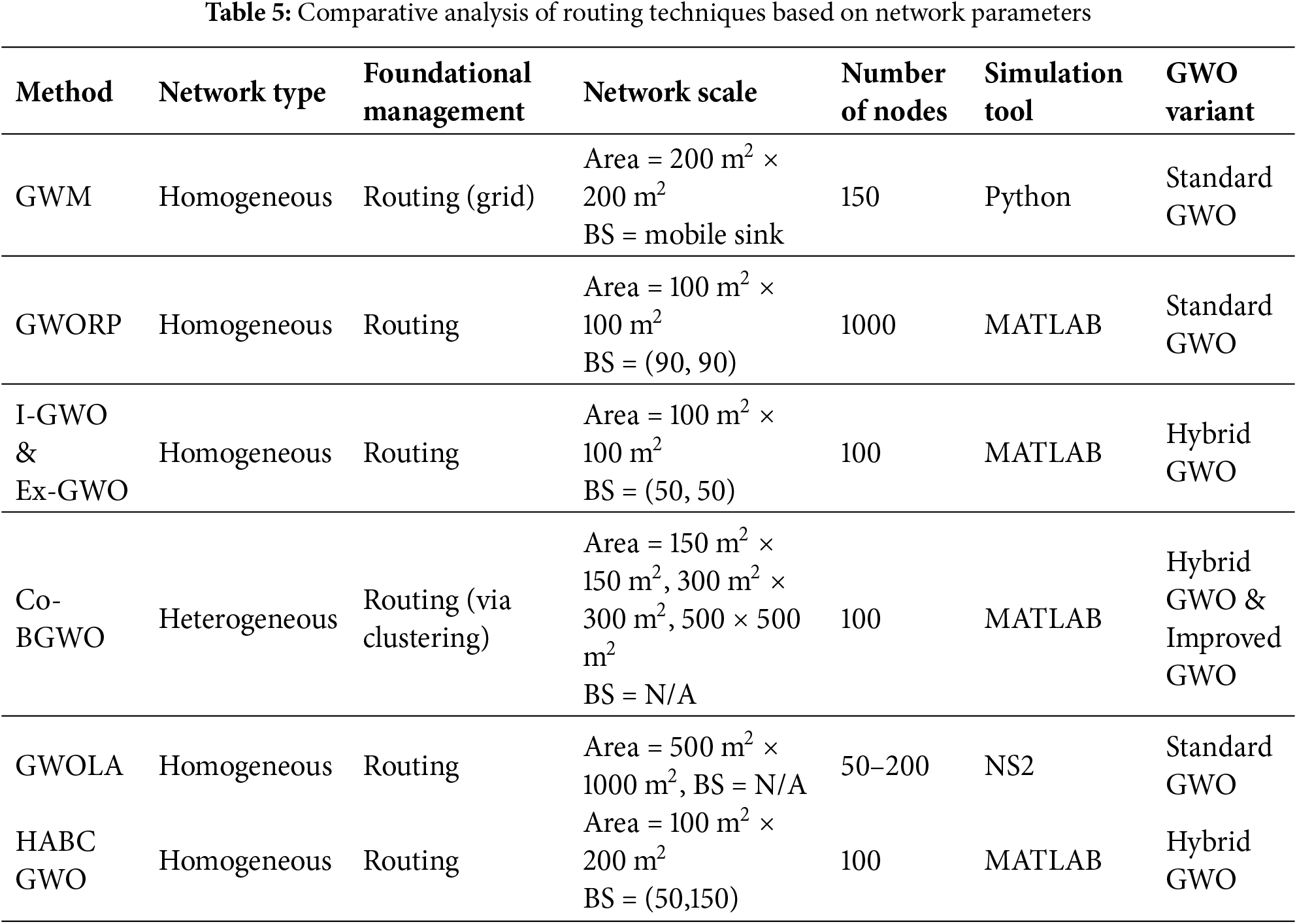
In [106], two novel Mobile Sink (MS) localization methods, Fuzzy A-star Sink Mobility (FASM) and Grey Wolf Mobility (GWM), are introduced to enhance energy efficiency and reduce data latency in WSNs. These methods address the limitations of predetermined MS trajectories, which often fail to adapt to dynamic changes in SN status. Both approaches aim to mitigate energy holes and minimize data latency by considering key parameters: residual energy, sensor density, source sensor angle, and traffic load. FASM employs a grid-based model combined with a fuzzy inference system. The network area is divided into equal-sized grids, and the MS moves to the center of the optimal grid. The fuzzy system evaluates neighboring grids based on the aforementioned parameters to select the next target grid. Furthermore, GWM utilizes the GWO to determine the optimal MS position within a defined search space outside potential energy hole areas. A fitness function, incorporating the same parameters as FASM (residual energy, sensor density, traffic load, and source sensor angle), guides the GWO algorithm to converge towards energy-rich areas while minimizing traffic load and transmission hops. This multi-hop routing technique minimizes buffer overflow and promotes balanced energy consumption across the network. The main focus is on the efficient movement of the MS by considering multiple network parameters and using intelligent algorithms for both sink mobility and data routing.

6.2 GWORP

In [107], the GWO Routing Protocol (GWORP) is introduced to maximize network lifespan. GWORP addresses the challenge of energy conservation by employing a statistically optimal path discovery method. GWORP’s core innovation lies in its ability to discover and reuse an ideal route from the source to the destination, ensuring balanced energy consumption across all WSN nodes. This method significantly reduces path discovery time compared to existing approaches like the Particle Swarm Optimization Routing Protocol (PSORP). The algorithm evaluates multiple paths simultaneously using a paired samples T-test to determine the statistically best path based on metrics such as residual energy. This statistical approach enhances the robustness of path selection and guarantees the selection of the optimal path. The network model employed in GWORP is heterogeneous, consisting of basic sensors (S-sensors) and CH sensors (CH-sensors). CH-sensors are strategically deployed to ensure connectivity and coverage for all S-sensors. While the text mentions clustering techniques, the primary focus of GWORP is on the routing mechanism and path optimization using GWO and the statistical evaluation.

6.3 I-GWO & Ex-GWO

In [108], two innovative energy-efficient routing methods, Incremental GWO (I-GWO) and Expanded GWO (Ex-GWO), are introduced. These methods are specifically designed to identify optimal paths in WSNs and Decentralized IoT (DIoT) systems. Central to these approaches is a newly developed fitness function that integrates critical parameters, including residual energy, traffic status, buffer size, and hop count, thereby improving the node selection process. The aforementioned metaheuristic algorithms are employed to determine optimal values for these parameters, enabling the identification of the best path of any length between source and destination nodes. The proposed architecture facilitates the adaptive operation of various metaheuristic algorithms, thereby enhancing efficient routing in complex network environments. Moreover, the proposed methods demonstrate particular proficiency in managing multi-hop scenarios, where intermediate nodes are essential for determining the most efficient routing paths. Both I-GWO and Ex-GWO utilize the distinctive capabilities of these algorithms to develop effective routing solutions in complex network structures. The search space is organized as a matrix representing search agents and coefficients, with iterative updates to these coefficients enhancing the adaptability of the algorithms. In the pathfinding mechanism, the algorithms compute the costs of potential paths, ultimately selecting the optimal route based on minimal cost across multiple hops.

6.4 Co-BGWO

In [109], a novel routing framework based on swarm intelligence is proposed to address the critical challenge of energy efficiency in heterogeneous WSNs. While the framework implicitly forms clusters through optimized CH selection, the primary focus is on enhancing routing performance rather than implementing explicit clustering mechanisms. The research aims to prolong network lifetime and improve data reliability by optimizing CH selection using a Co-evolutionary BGWO (Co-BGWO). The proposed method operates in two distinct phases: setup and communication. During the setup phase, the BS centrally selects CHs using the aforementioned algorithms, each evaluated against three distinct objective functions. These objective functions consider the following performance indicators: (1) the ratio of CHs’ remaining energy to their initial energy, aiming to prioritize energy-rich nodes; (2) a balance between CH degree (number of neighboring nodes) and remaining energy, promoting CHs with fewer neighbors and sufficient energy to manage intra-cluster communication; and (3) a trade-off between intra-cluster distance and CH-to-BS distance, minimizing both to reduce energy consumption during data transmission. Following CH selection, SNs associate with the nearest CH based on Received Signal Strength Indicator (RSSI), effectively forming clusters. In the subsequent communication phase, intra-cluster communication is managed using Time Division Multiple Access (TDMA), while inter-cluster communication from CHs to the BS utilizes Carrier Sense Multiple Access (CSMA). The Co-BGWO algorithm enhances the standard BGWO by employing Particle Swarm Optimization (PSO) to co-evolve and optimize the GWO parameters, thereby improving the search for optimal CH configurations and preventing premature convergence.

6.5 GWOLA

In [110], GWOLA, a novel approach for data aggregation and forwarding in WSNs, is proposed to minimize energy consumption and maximize network lifetime. Unlike traditional routing protocols, GWOLA combines the strengths of GWO and Learning Automata (LA) to achieve adaptive data forwarding and efficient aggregation. The method operates in two phases. Initially, GWO is employed to establish an initial neighbor list for each SN, prioritizing paths with fewer hops to the sink. The fitness function in GWO considers both the distance to the BS and the aggregation cost, which is defined as the average distance to neighboring nodes divided by the node’s radius. This pre-selection of neighbors helps reduce communication overhead. Subsequently, LA is utilized for adaptive data forwarding. Each node employs an LA to select the next hop towards the sink based on an Adaptive Forwarding (AF) factor. This factor is calculated using the load factor (LOF), which represents the ratio of transmitted/received packets, and the connectivity ratio (COR), which measures link breakage. By minimizing the AF factor, LA dynamically selects intermediate nodes for data transmission, facilitating efficient data aggregation. A reward-penalty mechanism is implemented within the LA framework to reinforce favorable routing decisions and discourage less efficient paths. This combined GWO-LA approach optimizes both path discovery (through GWO) and real-time path adaptation (through LA), leading to improved energy efficiency, reduced data delivery delays, and enhanced network longevity. The focus of GWOLA is primarily on efficient routing and data aggregation rather than explicit clustering.

6.6 HABCGWO

In [111], a novel hybrid metaheuristic framework based on the HABCGWO algorithm is proposed to address the critical challenge of energy optimization in IoT networks. Recognizing the limitations of the Artificial Bee Colony (ABC) algorithm such as its moderate convergence rate in high-dimensional search spaces, this method aims to enhance convergence speed and avoid local optima, ultimately improving network longevity. The HABCGWO algorithm utilizes the strengths of ABC, particularly its reduced number of adjustable parameters and particle interaction-based optimization, while mitigating its weaknesses through hybridization with GWO. The research focuses on optimizing several key performance indicators relevant to IoT network efficiency. These indicators, incorporated into the objective function, include energy utilization, network longevity, the number of active nodes, temperature, and throughput. By considering these multiple parameters, the HABCGWO algorithm aims to select the most suitable nodes for network operation, leading to improved overall performance.

6.7 Classification of GWO-Driven Routing Techniques

To demonstrate the efficacy of these GWO-based approaches, Tables 4 and 5 provide a comprehensive comparison of diverse routing techniques within WSNs, considering the solution-based and network-based parameters, respectively. While clustering optimization focuses on intra-cluster efficiency, routing-oriented GWO methods shift attention toward inter-cluster communication and relay path optimization. This shift reflects a methodological evolution from local energy balancing to global network optimization.

Several variations and enhancements of GWO have been proposed to improve its performance in routing. For instance, GWM combines GWO with fuzzy a-star sink mobility to enhance energy efficiency and reduce data latency, minimizing buffer overflow and promoting balanced energy consumption. GWORP maximizes network lifespan by employing a statistically optimal path discovery method. Utilizing the metaheuristic nature of GWO, GWORP discovers and reuses an ideal route from the source to the destination. The algorithm evaluates multiple paths using a paired samples T-test to determine the statistically best path based on metrics such as residual energy. This approach enhances the robustness of path selection and ensures the selection of the optimal path. I-GWO and Ex-GWO introduce incremental GWO and Ex-GWO to identify optimal paths in WSNs and decentralized IoT systems. These methods utilize a newly developed fitness function that integrates critical parameters, including residual energy, traffic status, buffer size, and hop count. The algorithms compute the costs of potential paths and select the optimal route based on minimal cost across multiple hops. Co-BGWO enhances routing performance in heterogeneous WSNs by employing co-evolutionary and binary variants of swarm intelligence algorithms for optimized CH selection. GWOLA combines GWO with LA to achieve adaptive data forwarding and efficient aggregation, minimizing energy consumption and maximizing network lifetime. Finally, HABCGWO integrates ABC with GWO to enhance convergence speed and avoid local optima, thereby improving network longevity.

7  GWO-Driven Co-Designed Clustering/Routing Techniques

This section investigates the application of the GWO algorithm in the co-design of clustering and routing protocols for WSNs. By utilizing the capabilities of GWO, researchers have developed innovative approaches to optimize CH selection, extend network lifetime, and enhance overall performance [112]. This section explores various techniques in this field, including hybrid algorithms that combine GWO with other AI-driven optimization methods, to address complex challenges in WSNs.

Fig. 12 summarizes the co-designed clustering and routing mechanism that integrates both processes within a single GWO framework. Here, each wolf encodes a joint decision vector representing CH positions and routing links simultaneously. This hybridization allows the optimizer to capture interdependencies between cluster formation and data transmission cost. The figure underscores the methodological advantage of joint optimization in reducing total energy expenditure and improving network stability compared to independently optimized stages.

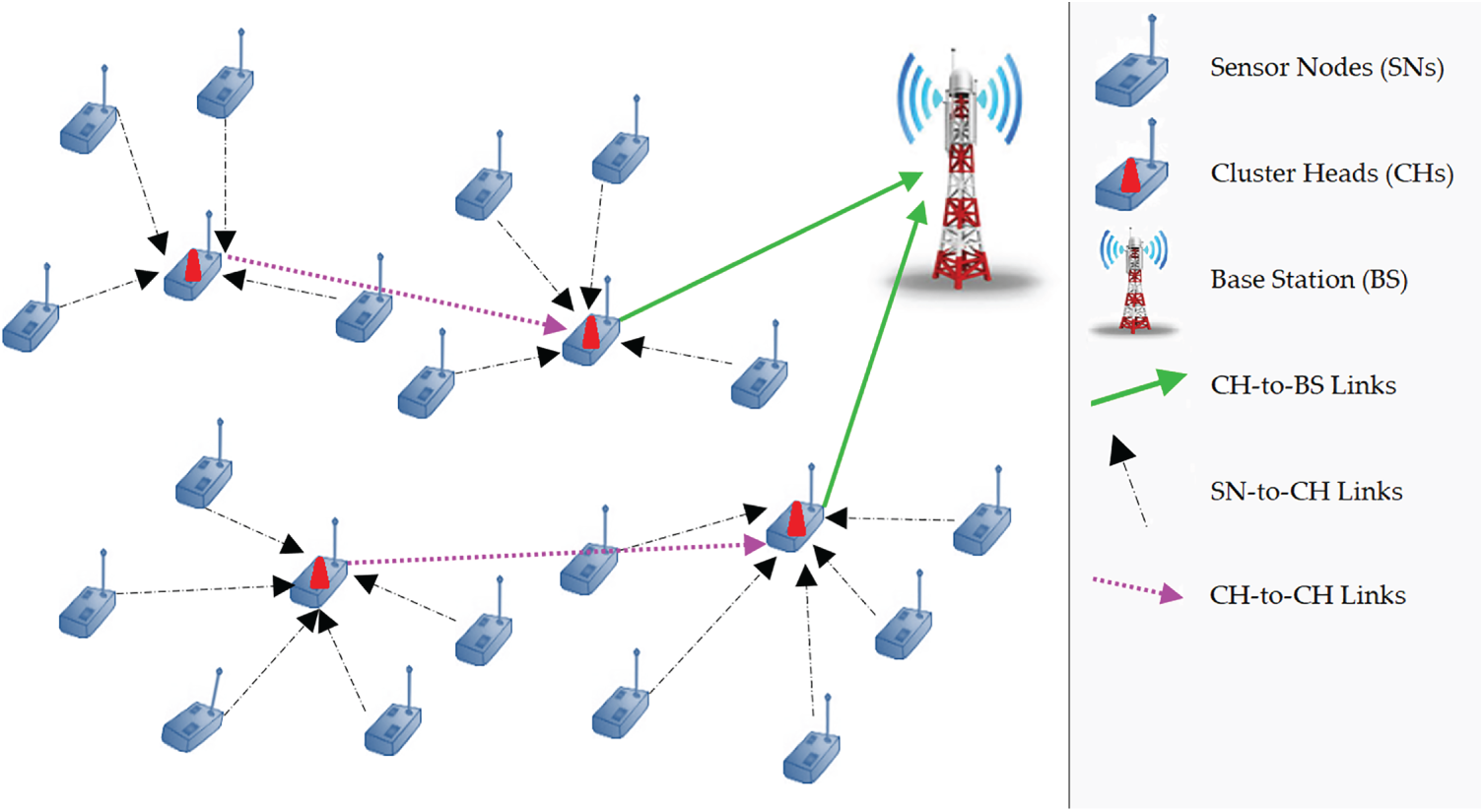
Figure 12: GWO-driven co-designed clustering/routing techniques

In the hybrid co-designed clustering/routing scheme, data is first transmitted from SNs to their local CHs, similar to basic clustering. However, instead of CHs sending data directly to the BS, the CHs form a secondary network and communicate with one another in a multi-hop fashion until the data reaches the BS [113]. This layered transmission strategy utilizes both the energy efficiency of clustering and the transmission flexibility of multi-hop routing [114]. By optimizing CH-to-CH communication paths, this method effectively reduces long-range transmissions and balances the energy load among CHs [115]. Such co-designed protocols often incorporate metaheuristic or adaptive algorithms to select optimal CHs and relay paths, ensuring robust and scalable network performance [116–120].

7.1 FIGWO

One such advancement is the Fitness value-based Improved GWO (FIGWO) algorithm proposed in [121]. FIGWO enhances the traditional GWO by incorporating a fitness value mechanism to improve CH selection, ensuring a balanced cluster structure and extended network lifetime. The protocol operates in two main phases: cluster building and data transmission. During the cluster building phase, initial CHs are selected based on fitness values that consider both the distance to the BS and the residual energy of the nodes. This approach favors energy-rich and strategically located nodes, optimizing the initial CH selection. In the data transmission phase, energy consumption is minimized by recalculating transmission distances. If a cluster member (CM) is closer to the BS than to its CH, it transmits data directly to the BS, reducing unnecessary hops and conserving energy.

7.2 CA-GWO

Building on this, the Cluster-based Approach via GWO (CA-GWO) introduced in [122] performs GWO for CH selection, evaluating nodes based on predicted energy consumption and residual energy. A key innovation of CA-GWO is its ability to reuse clustering configurations across multiple rounds, significantly reducing the energy expenditure associated with frequent re-clustering. This approach not only preserves energy but also enhances network longevity. Additionally, the protocol incorporates a dual-hop routing mechanism for CHs located far from the BS, ensuring balanced energy consumption while maintaining efficient communication through single-hop routes for other nodes. The simplified fitness function, directly related to energy consumption, streamlines the optimization process by reducing the number of parameters involved. Furthermore, by allowing the BS to predict the operational longevity of each node based on current clustering, the protocol can skip unnecessary setup phases in subsequent rounds, leading to further energy savings.

7.3 FGWSTERP

Addressing uncertainties in CH selection, the Fuzzy GWO-based Stable Threshold-sensitive Energy-efficient Routing Protocol (FGWSTERP) proposed in [123] integrates a Fuzzy Inference System (FIS) with an Extended GWO (EGWO). This protocol operates in rounds, comprising a setup phase for CH selection and a steady-state phase for data transmission. During the setup phase, the BS collects node data such as energy levels, locations, and types (advanced or normal). Each node computes a chance value using FIS, which considers parameters such as residual energy, node centrality, and distance to the BS. The BS then employs EGWO to elect CHs based on these chance values, favoring nodes with higher chance values. The initial population of potential CHs is represented as binary vectors, with each node’s status encoded within these vectors. The EGWO algorithm iteratively refines these solutions, ensuring optimal distribution of CHs across the network. In the steady-state phase, data communication is facilitated through intra-cluster and inter-cluster transmissions, which are strategically managed to minimize energy consumption. By employing event-based reactive short-range transmissions within clusters and multi-hop communications between clusters, FGWSTERP enhances overall network reliability and efficiency.

7.4 HMGWO

For heterogeneous WSNs, the Modified GWO (HMGWO) proposed in [124] introduces distinct fitness functions tailored to the varying energy levels of nodes. These fitness values serve as initial weights in the optimization process and are dynamically updated based on the proximity of the nodes to the BS and the coefficient vectors, thereby improving the optimization capabilities of GWO. The protocol employs Euclidean distance to finalize CH selection, ensuring a balanced distribution of CHs by considering both distance and residual energy. Additionally, HMGWO allows for the probabilistic acceptance of less optimal clusters in subsequent iterations, ultimately leading to a globally optimal cluster set. By centralizing the CH selection process at the BS and broadcasting the results, HMGWO minimizes randomness in cluster formation.

7.5 GWOC-QOS

In the context of Quality of Service (QoS) enhancement, the Gray Wolf-based Optimal Clustering Approach for QoS Improvement (GWOC-QOS) introduced in [125] employs GWO for efficient CH selection. This approach considers factors such as node energy levels, node degree, sink distance, and intra-cluster distance to improve the overall performance and lifetime of WSNs. The protocol classifies nodes into three types (normal, advanced, and super nodes), each with distinct energy constraints. A novel fitness function, designed using linear programming, optimizes CH selection and addresses the hot spot problem by introducing a priority factor during CH selection. This ensures fair opportunities for all nodes to become CHs, distributing energy consumption evenly across the network. The protocol operates through three phases: setup, steady state, and maintenance, repeated until the network collapses or all nodes exhaust their energy. The routing strategy incorporates a cost function that considers QoS parameters, ensuring reliable communication and efficient data transmission. By adopting a greedy approach, the algorithm selects relay nodes based on residual energy and distance criteria, facilitating multi-hop communication when necessary. The ultimate goal of this comprehensive strategy is to increase the network’s lifetime while maintaining optimal performance levels.

7.6 MOGWO-DRS

The Multi-objective GWO-based Data Routing Scheme (MOGWO-DRS) presented in [126] enhances network longevity and prevents premature node death by segmenting the network into optimally sized clusters and selecting optimal Rendezvous Points (RPs). A mobile sink (MS) collects data from RPs via an optimal path, significantly reducing energy consumption. The algorithm uses intermediate hop counts, transmission distances, and average intra-cluster distances as objectives within a multi-objective fitness function. Pareto dominance is employed to identify nondominated solutions, improving network lifetime and reducing transmission delays. A novel RP rotation mechanism balances energy consumption among SNs, ensuring that nodes closer to RPs consume less energy than those farther away. The methodology comprises two phases: a setup phase, where the MOGWO algorithm selects optimal RP positions and clusters nodes, and an intelligent data gathering phase, which establishes an optimal data path connecting the RPs.

7.7 QAMO-GWO

Further advancing QoS optimization, the multi-objective GWO (QAMO-GWO) algorithm proposed in [127] addresses the need for WSNs to manage overall network performance and ensure information transmission based on QoS parameters. Unlike single-objective GWO algorithms, QAMO-GWO employs a multi-objective fitness function that balances parameters such as data delay rate, data delivery rate, and node energy consumption. The algorithm categorizes nodes into three groups (alpha, beta, and delta/gamma), based on their optimality, with alpha nodes serving as CHs that forward aggregated data. The fitness function calculates a weighted score for each potential next hop, considering the distance to the next hop, the distance to the BS, and the residual node energy. This iterative local optimization, applied across the network, aims to achieve globally optimal routing.

7.8 PMR-GWO

To address energy efficiency and lifetime challenges in WSNs, the Probabilistic Multi-Tiered GWO-Based Routing (PMR-GWO) protocol introduced in [128] employs a modified GWO within a four-tiered network architecture. This tiered structure categorizes nodes based on their distance from the BS, assigning specific roles to each tier: leaders (CHs in tier 1), co-leaders (tier 2), standby co-leaders (tier 3), and cluster members (CMs in tier 4). The protocol’s objective function incorporates critical parameters such as residual energy, distance to the BS, node dormancy ratio, network coverage, balancing element, and interspace proportion between the BS and CH. By considering these parameters, PMR-GWO selects CHs with higher residual energy, closer proximity to the BS, and balanced coverage areas, ensuring balanced energy consumption across all network nodes and preventing early depletion of critical nodes. The protocol utilizes a two-level hybrid clustering algorithm, with the first level employing the Low-Energy Adaptive Clustering Hierarchy (LEACH) with Distance Degree Residual Index (DDRI) to pre-select candidate CHs and the second level applying a modified Multi-Tiered GWO (MGWO) algorithm to refine CH selection.

7.9 ML-AEFA

The energy-aware cluster-based routing protocol proposed in [129] addresses challenges related to fault tolerance, load balancing, and local optima. The protocol operates in two phases: optimal CH selection and efficient data transmission. For CH selection, a hybrid algorithm named Moth Levy adopted Artificial Electric Field Algorithm (ML-AEFA) combines the strengths of the Artificial Electric Field Algorithm (AEFA) and the Moth Search Algorithm (MSA), incorporating Levy flights to enhance convergence and avoid local optima. The CH selection process considers parameters such as residual energy, node degree, distance between SNs, distance to the BS, and time of death of the node. Data transmission is optimized using a Customized GWO (CGWO) algorithm, which addresses limitations of the standard GWO by improving convergence and local search capabilities. The CGWO algorithm optimizes data transmission paths from CHs to the BS, considering both distance and packet drop ratio to minimize energy consumption and maximize data delivery.

7.10 CMROCS

The Centralized Multi-Clustering with Relay Nodes and Optimized CH Selection (CMROCS) protocol proposed in [130] enhances network lifetime by addressing limitations such as repetitive CH selection, inappropriate CH selection, and unbalanced clusters. CMROCS employs GWO for optimal CH selection and introduces relay nodes to alleviate the communication burden on CHs. The protocol operates in two phases per round: cluster setup and data transmission. Three distinct clustering schemes are implemented: (1) First Clustering uses a cost function that considers residual energy and the number of neighbors; (2) Second Clustering retains the previous CHs, avoiding re-selection; and (3) Third Clustering uses a cost function based on residual energy and distance to the previous CH. Relay node selection is based on a cost function that considers residual energy and distance to the BS, creating balanced clusters and optimizing energy consumption.

7.11 EECHIGWO

The Energy-Efficient CH Improved GWO (EECHIGWO) algorithm introduced in [131] addresses challenges such as exploration-exploitation imbalance, limited population diversity, and premature convergence in CH selection. EECHIGWO selects CHs based on factors such as sink distance, residual energy, balancing factor, and average intra-cluster distance. The BS implements the algorithm, broadcasting the chosen CHs to all SNs via multi-hop communication. The SNs are divided into four subsets based on fitness values, with sixteen nodes fixed in location to support multi-hop paths. The algorithm operates in defined rounds, each comprising a CH formation stage followed by a data transmission stage.

7.12 EEC-GWO

In [132], the Energy-Efficient and Coverage-aware GWO (EEC-GWO) is introduced for Software-Defined WSNs (SDWSN). This approach employs a fitness function that maximizes coverage, minimizes blind spots, and conserves energy. The algorithm consists of three phases: neighbor discovery, setup, and communication. During the setup phase, the BS compiles control messages to create a network map, which the controller uses to elect CHs and assign normal nodes to their nearest CHs based on Euclidean distance and energy availability. The communication phase employs TDMA scheduling for organized data transmission, optimizing node coverage and reducing blind spots.

7.13 CBGWOA

The Clustering Based on GWO Algorithm (CBGWOA) introduced in [133] utilizes the GWO algorithm to enhance energy efficiency and overall network performance. The proposed method divides the network’s operational lifespan into distinct cycles, comprising two key stages: initialization and stabilization. During the initialization stage, the BS gathers information regarding the location and energy levels of nodes, subsequently selecting CHs based on this data and the GWO algorithm. This selection process aims to maximize the longevity of the network by ensuring that CHs possess sufficient residual energy to manage their respective clusters effectively. A significant innovation of this approach is the introduction of the Dead Time (TD) parameter, which quantifies the maximum number of iterations a node can sustain based on its remaining energy. By maximizing the average TD across all nodes, the method ensures that CHs can maintain communication without depleting their energy reserves prematurely. Additionally, to mitigate energy consumption, each CH is assigned a relay node, optimizing the data transmission route to the BS and balancing energy usage between CHs and their relays. The clustering process is initiated when nodes transmit their energy and location information to the BS, which then selects CHs and relays based on the GWO algorithm.

7.14 GWFPO

Addressing the challenges of energy-efficient communication with minimal delay, the Grey Wolf-Flower Pollination Optimization (GWFPO) hybrid model proposed in [134] introduces a novel two-phase approach. In the first phase, CHs are selected using Type 2 fuzzy logic, considering five input variables: node residual energy, BS and node distance, neighbor node distance, node degree, and node centrality. The output variables of the fuzzy logic system are selection probability and cluster size. Type 2 fuzzy logic is employed to effectively handle uncertainties and improve CH selection compared to Type 1 fuzzy logic. In the second phase, the GWFPO hybrid optimization algorithm, combining GWO and Flower Pollination Optimization (FPO), is utilized to determine the optimal data transmission path. The GWFPO hybrid algorithm considers several key parameters in its objective function: energy consumption (sum of remaining node energies), delay (based on nodes and hops), link lifetime (based on the lifetime of consecutive nodes), and intra- and inter-cluster distances. The integration of GWO’s hunting strategy and FPO’s pollination mechanisms enhances both exploration and exploitation capabilities, leading to improved routing performance. The focus on both efficient CH selection through fuzzy logic and optimized routing through the GWFPO hybrid metaheuristic algorithm contributes to enhanced network performance and QoS in WSNs.

7.15 MOGWO

The Multi-Objective Binary GWO (MOGWO) proposed in [135] identifies Pareto optimal clustering centers by optimizing five objectives: maximizing overall CH energy, minimizing compactness, reducing the number of CHs, decreasing energy consumption from non-CHs to CHs, and maximizing separation between CHs. The framework operates in two phases: CH election and CH association. During the election phase, binary-encoded wolf solutions are generated, and fitness functions evaluate these solutions based on the specified objectives. In the association phase, member nodes transmit sensory data to their designated CHs, implementing energy-saving measures during inactivity.

7.16 GWO-SMSLO

In [136], a hybrid approach combining the GWO and modified Sea Lion Optimization (SLO) is presented to improve energy efficiency and security in WSNs. This method uses GWO for effective clustering of SNs, addressing load balancing and hot spots, while SLO is utilized for optimal and secure data routing. The protocol features an uneven hierarchical clustering technique for selecting an optimal CH based on residual energy, distance, and trust factors. GWO’s meta-heuristic capabilities iteratively compute fitness values for CH selection. To bolster security, an Elliptic Curve Cryptography (ECC)-based Certificate-Less Aggregate Signature (CLAS) scheme is implemented, ensuring robust authentication and privacy against various attacks. The GWO-SMSLO protocol consists of four main modules: node initialization and distribution, optimal CH selection and cluster formation, trustworthy route selection, and secure authentication analysis. During initialization, parameters are set and unique identifiers are assigned. The clustering phase elects the CH via GWO, forming clusters with an unequal hierarchical approach. The routing phase employs SLO to find optimal communication paths, excluding malicious nodes based on trust factors. Secure data transmission is ensured through a comprehensive security analysis that includes key generation, anonymous ID creation, and signature verification.

7.17 CGA-GWO

The Chaotic Genetic Algorithm-GWO (CGA-GWO) method proposed in [137] minimizes overall energy consumption by combining energy-aware CH selection with the optimal creation of routing paths to the BS. The method employs chaotic dynamics during the initial population, crossover, and mutation stages, incorporating chaotic systems such as logistic and tent maps. This methodology generates a diverse set of solutions that are subsequently evaluated using a fitness function. For routing, GWO mimics the social structure and hunting behavior of gray wolves, assigning different roles to optimize the routing path to the BS. The CGA-GWO method operates within a hierarchical architecture, where SNs are organized into clusters, with CHs transmitting information to the BS via multi-hop communication.

7.18 PUAG

The Partitioned Uneven Cluster Routing Algorithm based on GWO (PUAG) presented in [138] increases energy efficiency by partitioning the network into regions and selecting CHs based on residual energy, distance to the BS, number of neighboring nodes, and spatial compactness. The algorithm introduces the Next CH (NCH) concept and a similarity judgment function to reduce re-clustering rounds. GWO determines optimal multi-hop paths for data communication, mimicking the natural predatory behavior of gray wolves by dynamically adjusting node positions based on relative distances and hierarchical roles within the network.

7.19 MOGWO-C

The Multi-Objective GWO-based Clustering (MOGWO-C) approach proposed in [139] enhances network performance by minimizing energy consumption, prolonging network lifespan, and reducing end-to-end delay. The multi-objective fitness function considers three key metrics: Maximum Average Transmission Distance, Maximum Average Hop Counts between nodes and CHs, and Maximum Average Distance between SNs within the same cluster. By minimizing these metrics concurrently, the algorithm seeks to optimize cluster formation for efficient data transmission. The MOGWO-C algorithm iteratively refines cluster formation and CH selection, exploring trade-offs between the defined objectives. After CH selection, cluster members are assigned, and a data transmission path to the BS is established. The BS uses HELLO and Acknowledgment (ACK) messages to coordinate data transmission within allocated time slots, further enhancing energy efficiency.

7.20 CRGA

Shang et al. [140] proposed a Cluster Routing algorithm based on an improved GWO algorithm (CRGA), specifically designed for inter-cluster routing in air-sea cross-domain wireless networks. Traditional routing protocols like LEACH and Distributed Energy-Efficient Clustering (DEEC) are inadequate for such heterogeneous and hierarchical environments because they overlook key domain-specific factors such as the types of nodes (aerial vs. underwater), inter-node communication mediums, and structural hierarchy. To address these limitations, the authors built on the DEEC protocol and introduced a modified GWO algorithm that integrates Differential Evolution (DE) mechanisms and a “survival of the fittest” strategy to enhance exploration and exploitation dynamics. The CRGA uses a multi-objective fitness function that simultaneously considers the distance between clusters, the residual energy of potential next-hop nodes, and overall energy balance across the network. By incorporating these factors, the algorithm aims to ensure stable and energy-efficient inter-cluster communication across diverse domains (e.g., air and sea).

7.21 MQAGWO-EECR

Xu et al. [141] proposed the Multi-Objective Quantum Adaptive GWO-based Energy-Efficient Clustering Routing (MQAGWO-EECR) algorithm. The MQAGWO-EECR algorithm incorporates two operators (quantum calculation and adaptive adjustment) within the GWO framework, enhancing solution quality and improving convergence rates. Additionally, a comprehensive energy-efficient clustering routing model is introduced, which includes sleep scheduling, CH selection, and QoS routing, effectively capturing the data transmission process. The EECR model includes a comprehensive system for CH selection, sleep scheduling, and multi-hop routing, all optimized concurrently using the multi-objective MQAGWO. Specifically, CH selection is based on multiple criteria including residual energy, node density, distance to BS, communication delay, and packet loss rate, ensuring energy-balanced and QoS-aware clustering decisions. Meanwhile, sleep scheduling allows SNs to alternate between active and dormant states, significantly reducing energy consumption from idle communication.

7.22 DC-GWO

Sun et al. [142] introduced DC-GWO, a hybrid energy-efficient routing algorithm that combines Dijkstra-based clustering with an enhanced GWO framework to address key challenges in WSNs, including uneven energy consumption, inefficient CH selection, and unbalanced spatial distribution. The proposed method operates in two main phases: cluster formation and energy-aware routing. In the first phase, Dijkstra’s algorithm is used to form spatially balanced clusters by analyzing node locations and density, helping mitigate the hotspot and energy-hole problems prevalent in traditional protocols like LEACH and K-Energy Adaptive Clustering (KEAC). In the second phase, an improved GWO selects CHs within each cluster by evaluating multiple criteria such as residual energy, neighborhood connectivity (node degree), and local energy dispersion. This ensures that CH selection aligns with both energy efficiency and topological considerations. For routing, the approach employs a hybrid communication model, using single-hop intra-cluster transmission and GWO-optimized multi-hop inter-cluster routing toward the sink. The enhanced GWO dynamically adapts path selection based on real-time assessments of node energy and depletion trends, thereby maintaining reliability while minimizing energy overhead. Simulation results confirmed that DC-GWO significantly extends the network lifetime and improves data delivery performance across different network scales.

7.23 GWFCCV

Rahmani et al. [143] proposed GWFCCV, a hybrid routing framework that integrates GWO and Fuzzy C-Means (FCM) clustering with multi-criteria decision-making techniques to enhance energy-efficient routing in WSN-IoT environments. Given the growing importance of reliable and scalable communication in sectors like healthcare, industry, and education, this work addresses the critical need for stable routing and energy-aware clustering in resource-constrained IoT networks. The GWFCCV algorithm operates in two stages. First, FCM is used to form initial clusters based on data similarity, and GWO is then applied to optimize these clusters by refining the initial cluster centers, reducing intra-cluster distances, and improving overall cluster quality. In this method, a dynamic weighting scheme is used to select CHs based on multiple decision criteria, such as residual energy, throughput, and memory availability. Then, to determine the most suitable nodes for routing, the candidates are ranked based on the same criteria, ensuring both optimal route selection and energy-efficient data transmission.

7.24 Classification of GWO-Driven Co-Designed Clustering/Routing Techniques

The efficacy of the investigated techniques in this section is evaluated through comprehensive simulations. To provide a more informative comparison, Tables 6 and 7 have been augmented with performance-metric columns aligned with their corresponding solution and network parameters, respectively.

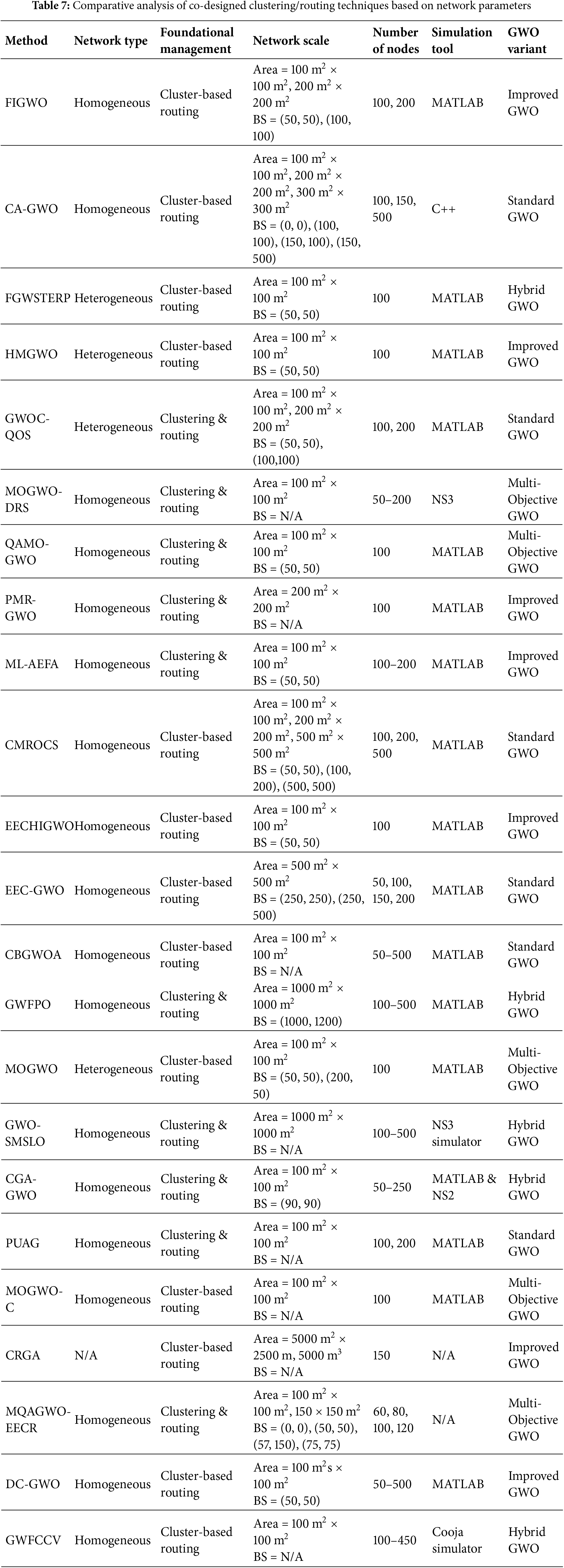
Table 6 presents a comparative analysis of the performance of the investigated methods in terms of solution-based parameters, while Table 7 explores the network specific parameters used in the simulations of the investigated methods. The existing co-designed clustering–routing frameworks represent the most integrated methodological trend in GWO-based WSN research. By jointly optimizing both phases, these approaches better capture the interdependencies between clustering and data transmission, resulting in improved network lifetime and energy efficiency under heterogeneous conditions.

Several variations and enhancements of GWO have been proposed to improve its performance in co-designing clustering and routing. FIGWO combines GWO with a fitness value mechanism to improve CH selection, ensuring a balanced cluster structure and extended network lifetime. CA-GWO applies GWO for CH selection and reuses clustering configurations across multiple rounds to reduce energy expenditure. FGWSTERP integrates a FIS with an EGWO to enhance CH selection and routing. HMGWO introduces distinct fitness functions tailored to the varying energy levels of nodes, improving optimization capabilities. GWOC-QOS employs GWO for efficient CH selection, considering factors such as node energy levels, node degree, and sink distance. QAMO-GWO uses a multi-objective fitness function to balance parameters such as data delay rate, data delivery rate, and node energy consumption. MOGWO-DRS segments the network into optimally sized clusters and selects optimal RPs for data collection, significantly reducing energy consumption. PMR-GWO employs a modified GWO within a multi-tiered network architecture to optimize CH selection and routing. ML-AEFA combines the strengths of the AEFA and the MSA for CH selection, while CGWO optimizes data transmission paths. CMROCS enhances network lifetime by addressing limitations such as repetitive CH selection and unbalanced clusters. EECHIGWO improves CH selection by addressing exploration-exploitation imbalance and premature convergence. EEC-GWO maximizes coverage, minimizes blind spots, and conserves energy. MOGWO identifies Pareto optimal clustering centers by optimizing multiple objectives. CRGA integrates differential evolution and a “survival of the fittest” strategy into GWO, utilizing a multi-objective fitness function to ensure stable and energy-efficient inter-cluster routing in heterogeneous air-sea networks. DC-GWO combines Dijkstra-based clustering with an enhanced GWO framework, using Dijkstra for balanced cluster formation and improved GWO for multi-criteria CH selection and adaptive multi-hop routing. GWFCCV integrates GWO with Fuzzy C-Means (FCM) clustering and the CRITIC weighting method, optimizing initial clusters with GWO and employing multi-criteria decision-making for energy-aware CH selection and routing in WSN-IoT. MQAGWO-EECR incorporates quantum calculation and adaptive adjustment within the GWO framework to enhance solution quality and convergence rates, co-optimizing CH selection, sleep scheduling, and multi-hop routing via a multi-objective approach. CBGWOA utilizes GWO to enhance energy efficiency and overall network performance. GWFPO combines GWO with FPO to determine the optimal data transmission path. GWO-SMSLO enhances energy efficiency and security in WSNs by combining GWO with modified SLO. CGA-GWO minimizes overall energy consumption by combining energy-aware CH selection with the optimal creation of routing paths. PUAG increases energy efficiency by selecting CHs based on residual energy and distance to the BS. Finally, MOGWO-C enhances network performance by minimizing energy consumption, prolonging network lifespan, and reducing end-to-end delay.

7.25 Multi-Objective GWO in WSNs

Multi-objective GWO algorithms are widely used in WSNs to optimize multiple, often conflicting objectives, such as energy efficiency, network lifetime, delay, and coverage. These techniques, including MOGWO-DRS, QAMO-GWO, MOGWO, MOGWO-C, and MQAGWO-EECR, demonstrate how multi-objective formulations can improve network performance while balancing trade-offs.

A common feature of these approaches is the use of Pareto dominance or related techniques to generate a set of nondominated solutions, forming the Pareto front. This allows network designers to select solutions that achieve an appropriate compromise between conflicting goals. For example, minimizing transmission distance or hop counts may improve energy efficiency but increase delay, whereas optimizing delivery rate may require higher energy consumption. Weighted-sum and ε-constraint strategies are often used to guide solution selection along the Pareto front according to design priorities. These frameworks often integrate additional mechanisms, such as adaptive routing, cluster-head rotation, and sleep scheduling, to enhance network performance while exploring trade-offs. Table 8 summarizes representative objectives, trade-offs, Pareto front approaches, and key mechanisms across the reviewed multi-objective GWO methods.

8  Discussion

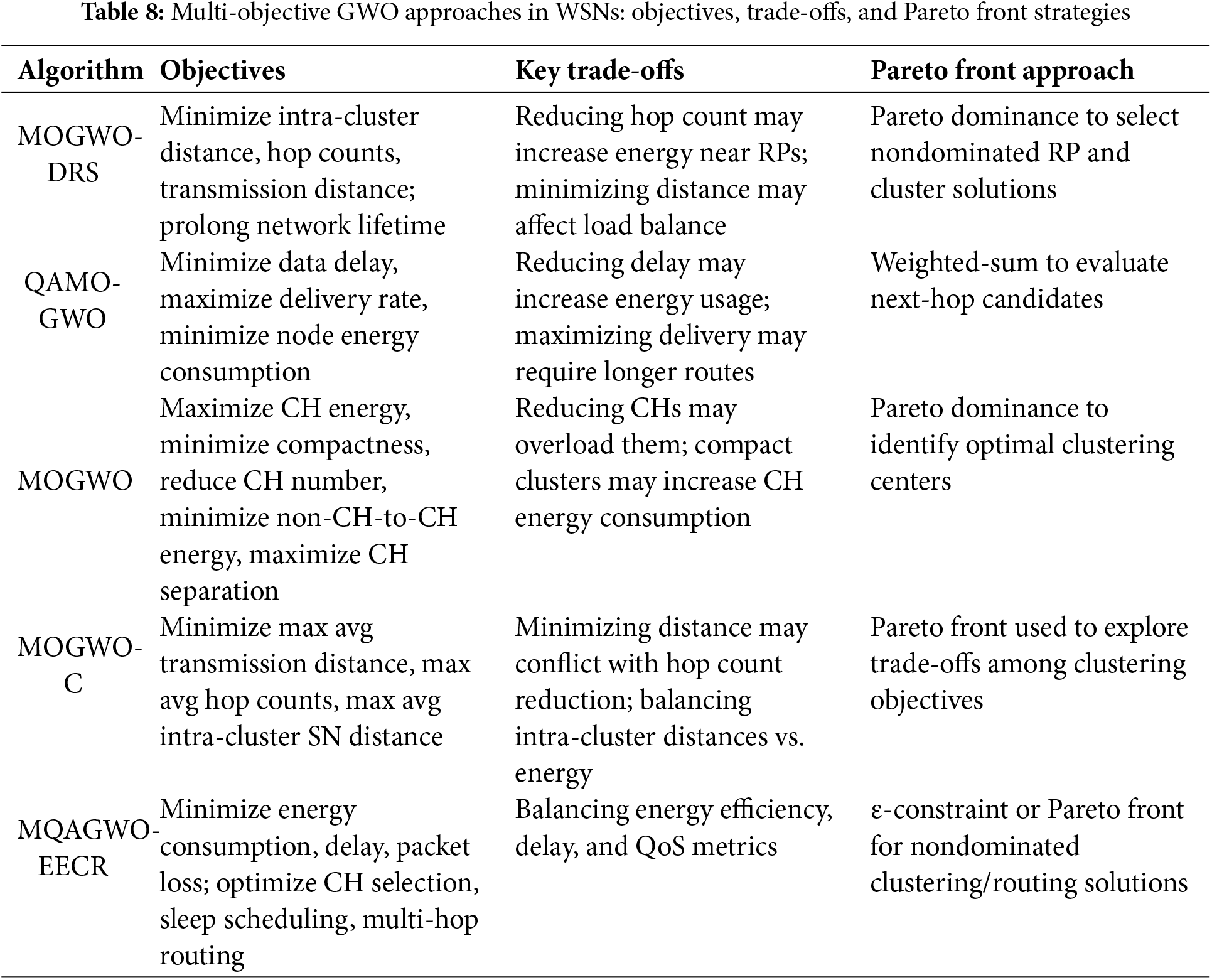
This section provides a comprehensive analysis of the diverse applications of the GWO across three critical domains within WSNs. The analysis systematically examines problem formulations and GWO implementations in each domain, as documented in Tables 2–7 and synthesized in Sections 5–7. It evaluates both the overarching objectives and specific goals of each methodology, alongside modifications and enhancements applied to the canonical GWO algorithm. Fig. 13 presents a taxonomy of GWO variants according to their algorithmic improvements, offering a consolidated perspective on the algorithm’s extensive utilization in WSN research. This classification facilitates deeper insight into GWO’s role in addressing heterogeneous and complex WSN challenges. Hybrid GWO variants integrate complementary strategies from PSO, ABC, or fuzzy inference systems to overcome GWO’s limited diversity and slow late-stage convergence. These hybridizations yield more adaptive fitness landscapes and higher-quality solutions for complex WSN scenarios.

Figure 13: Categorizes WSN-related methods reviewed in this survey based on the different variants of the GWO

Furthermore, Fig. 14 illustrates the temporal distribution of GWO-centric WSN publications reviewed in this survey, categorized by year of publication. Qualitative analysis of 38 pertinent peer-reviewed studies reveals a marked surge in scholarly interest regarding GWO applications to WSNs over the preceding triennium.

Figure 14: Percentage of WSN-related papers reviewed in this survey that employ GWO, broken down by publication year

Fig. 15 quantifies publication volume across the survey’s three focal research themes. Given the intrinsic significance of clustering and routing mechanisms, these domains demonstrably command greater research attention. Fig. 16 analyzes simulation environments employed in the evaluated studies, indicating a pronounced preference for MATLAB among GWO-based methodologies. Finally, Fig. 17 characterizes the node architectures adopted in experimental scenarios across the three research themes, revealing a predominance of homogeneous node configurations in simulations and performance evaluations.

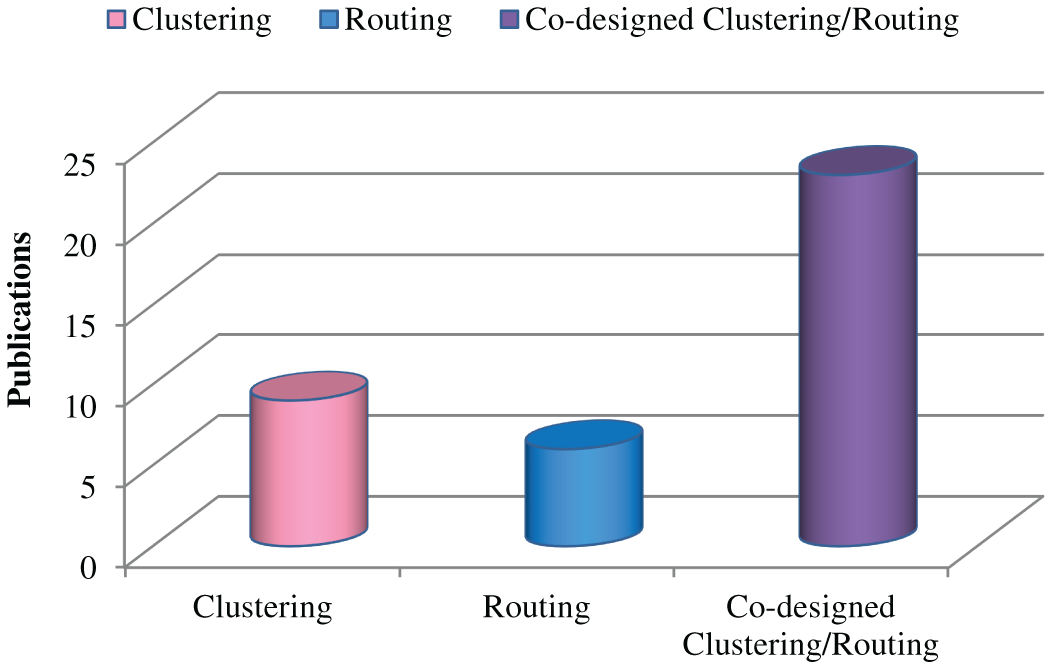
Figure 15: Number of GWO-driven papers, broken down by the routing mechanism

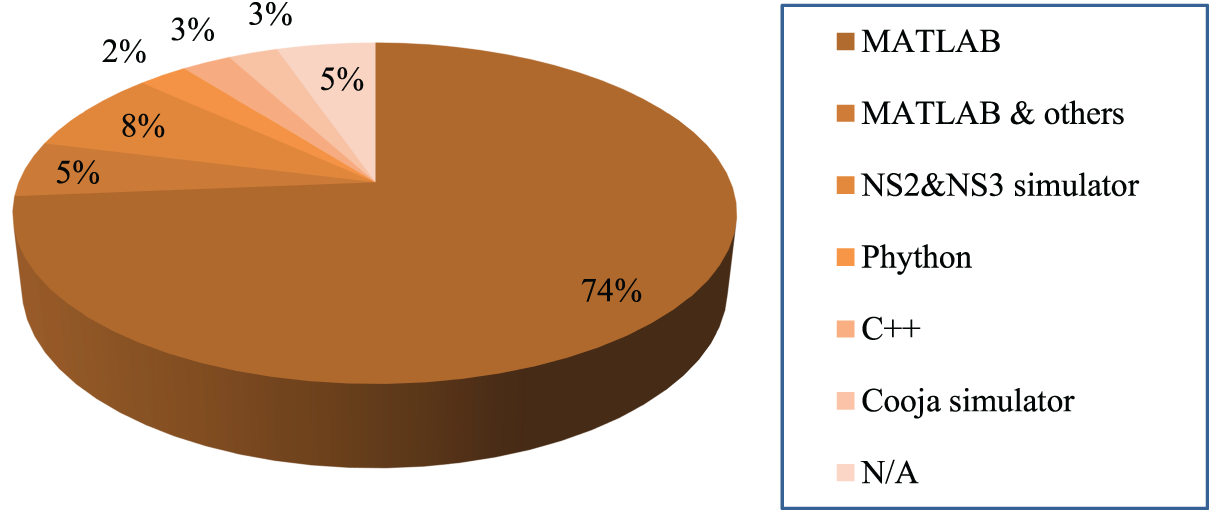
Figure 16: Percentage of reviewed WSN articles using GWO, by simulator

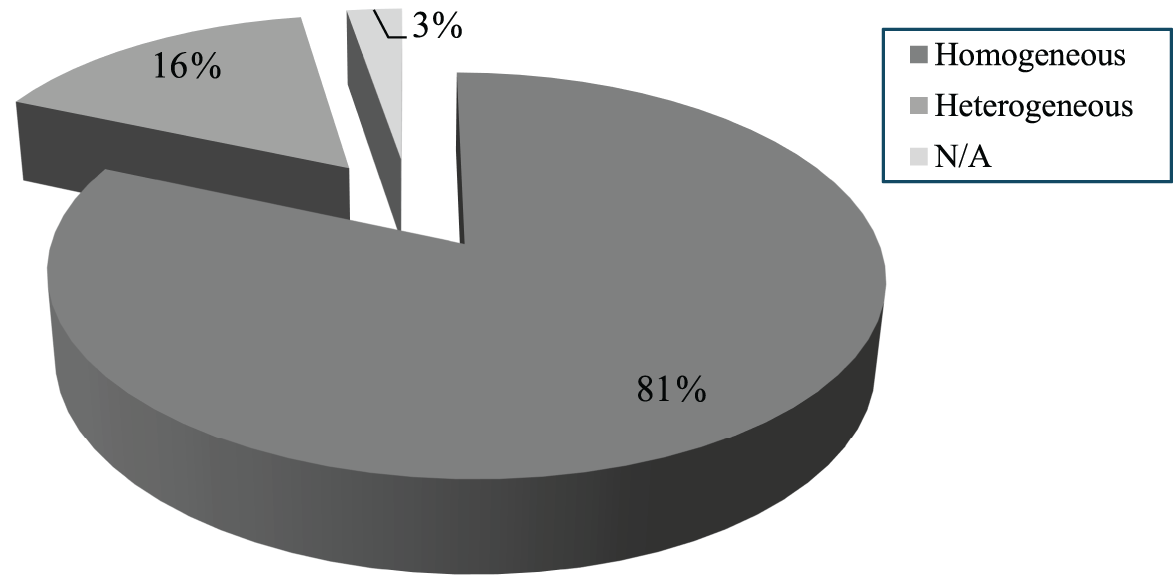
Figure 17: Percentage of reviewed WSN articles utilizing GWO, categorized by network type

This growing trend underscores the importance and effectiveness of GWO in tackling challenges related to optimization, energy management, network coverage, and other critical issues in WSNs. Finally, based on the findings of this study, several recommendations for future research are proposed. These recommendations aim to address existing limitations and expand the capabilities of the GWO algorithm in emerging WSN domains. They include the development of hybrid versions of GWO integrated with other optimization algorithms, enhancing its efficiency in dynamic and complex environments, and exploring its applications in cutting-edge technologies such as the IoT and next-generation networks.

8.1 Quantitative Performance Analysis

Tables 9–11 provide a quantitative performance analysis of the reviewed GWO-based clustering, routing, and co-designed clustering/routing approaches by extracting their reported numerical results from the original studies. These tables collectively report concrete performance metrics together with the corresponding network settings such as deployment area, node density, packet size, base station location, and initial energy. The reported performance metrics include:

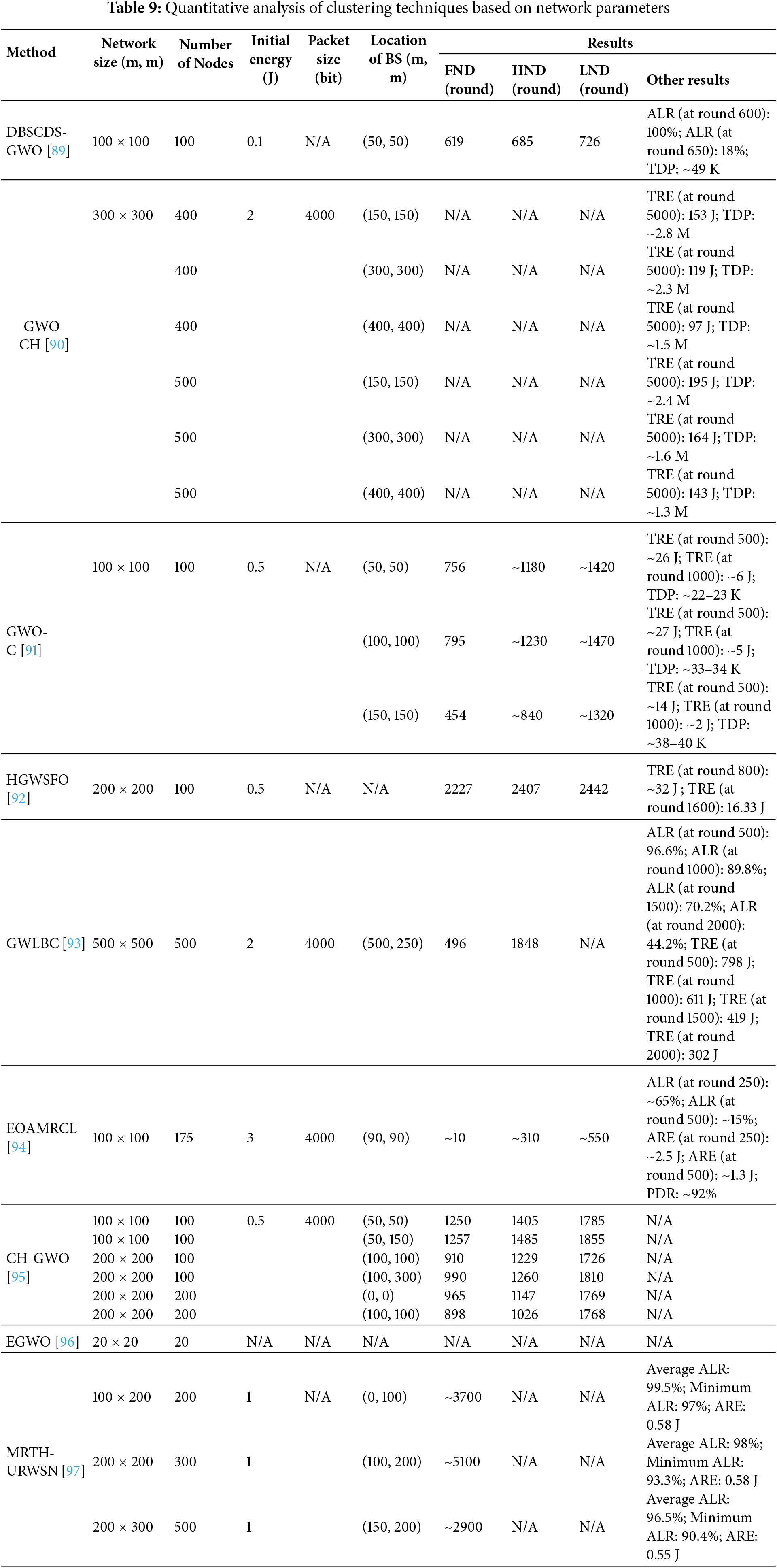
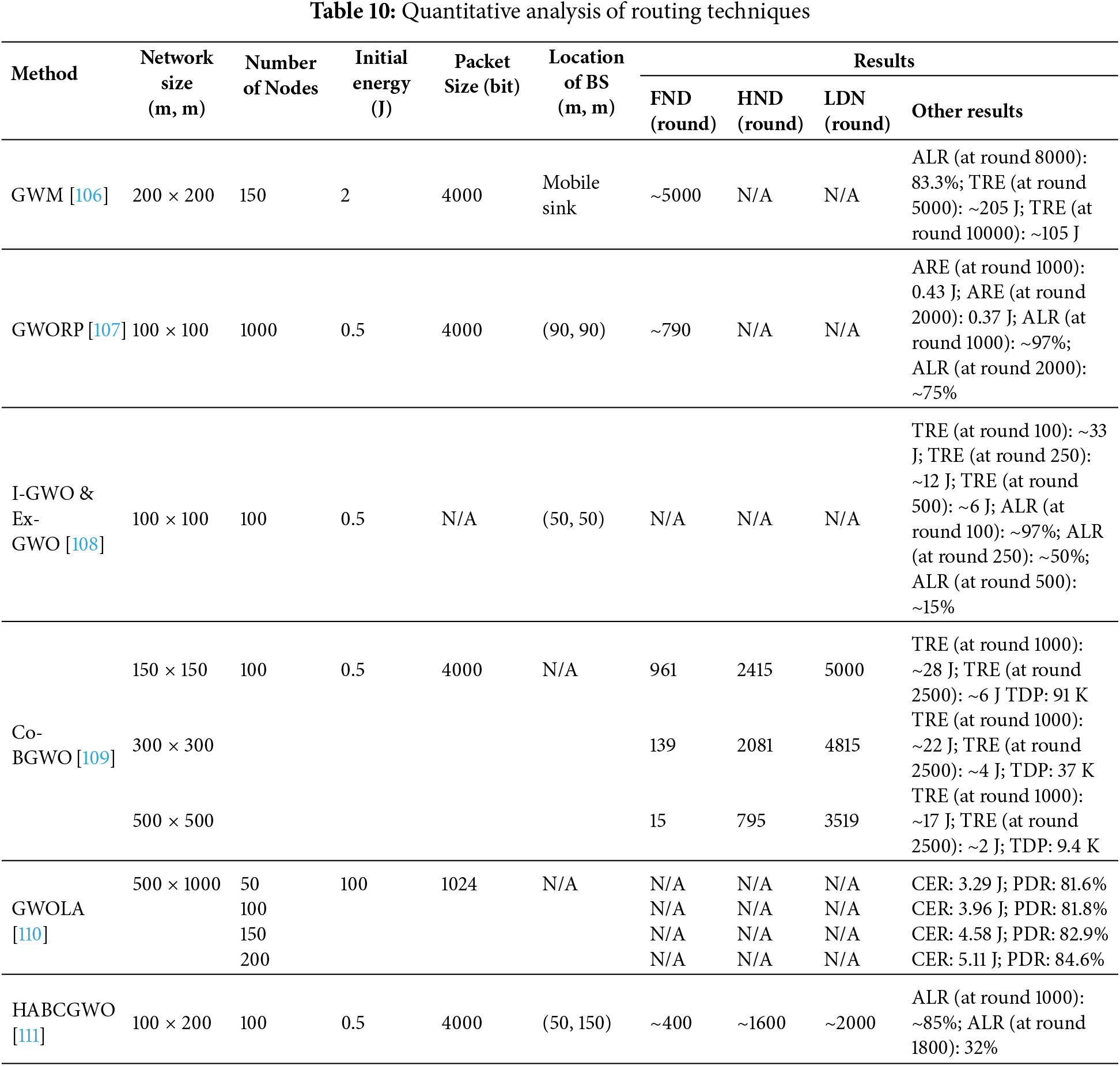
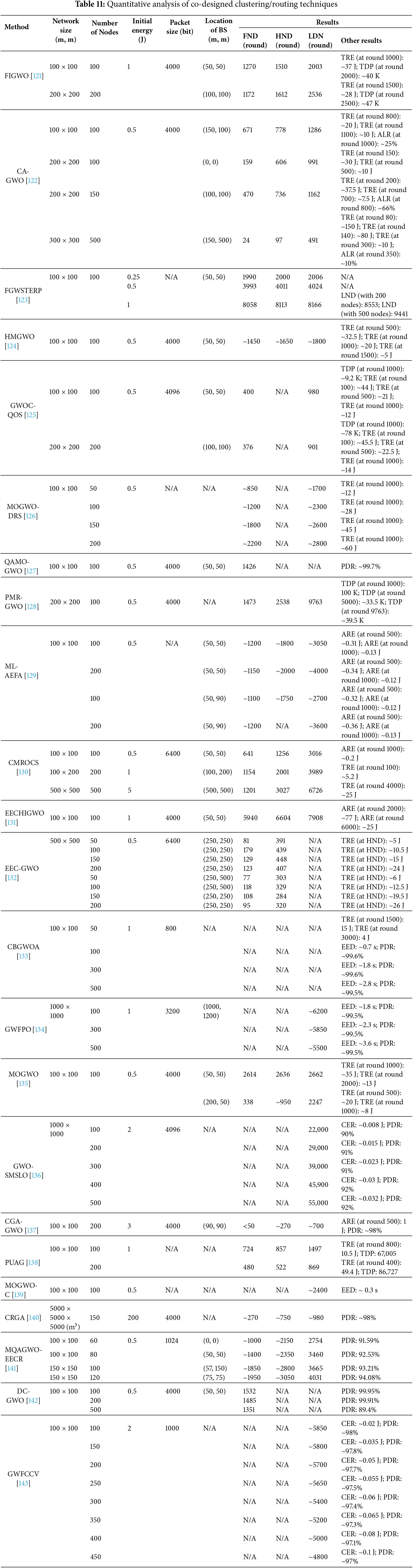
•   TRE: Total Residual Energy (J)

•   ARE: Average Residual Energy (J)

•   TDP: Total Delivery Packets (number of delivery packets)

•   PDR: Packet Delivery Ratio (%)

•   EED: End-to-End Delay (s: seconds)

•   CER: Consumed Energy per Round (J)

•   ALR: Alive Rate (%)

From Tables 9–11, several consistent performance trends can be observed across the three methodological categories. Clustering-based techniques (Table 9) generally exhibit extended stability periods (high FND values) and gradual node death patterns, particularly in small- and medium-scale networks (100–200 nodes), indicating their effectiveness in early-stage energy balancing. In contrast, routing-based methods (Table 10) demonstrate strong improvements in packet delivery and residual energy preservation over longer operational rounds, especially in scenarios with mobile sinks or large packet sizes. Finally, co-designed clustering/routing techniques (Table 11) consistently achieve the longest network lifetimes and the highest data delivery volumes, at the cost of increased algorithmic complexity, confirming the benefit of joint inter- and intra-cluster optimization. At the same time, the wide variation in node densities, deployment areas, and radio parameters across studies highlights the intrinsic heterogeneity of the reported results and explains why a direct numerical benchmarking across different works would be methodologically invalid without a unified simulation framework.

8.2 Functional Roles of GWO in Reviewed Categories

This section reviews how the GWO algorithm is utilized across the three optimization categories: clustering, routing, and co-designed clustering/routing approaches. Although these paradigms target different optimization scopes, they all exploit the hunting-inspired search mechanism of GWO to balance energy efficiency, network lifetime, and communication reliability.

8.2.1 Role of GWO in Clustering Techniques

Clustering is a key strategy for improving energy efficiency in WSNs by organizing sensor nodes into clusters managed by CHs. Since CH selection strongly affects energy consumption, load distribution, and lifetime, GWO has been widely adopted to optimize this process. In clustering-based methods, each wolf represents a candidate CH configuration, and the fitness function typically incorporates residual energy, distance to the BS, intra-cluster distance, and load balancing. Through iterative position updates guided by the α, β, and δ wolves, GWO searches for energy-efficient and well-distributed CHs. Nodes are then assigned to the nearest or most suitable CH based on distance or energy-aware criteria. This process enhances intra-cluster energy balancing and stabilizes cluster structures, although its responsiveness may decrease in large-scale or highly dynamic networks.

8.2.2 Role of GWO in Routing Techniques

In routing-oriented approaches, GWO is employed to discover energy-efficient and reliable multi-hop paths between sensor nodes and the BS. Each candidate solution represents a feasible routing path, and the fitness function commonly considers energy consumption, hop count, residual node energy, and link reliability. By iteratively updating routing candidates using the leadership hierarchy of grey wolves, GWO enables the selection of paths that reduce transmission energy and improve data delivery reliability. Once the optimal path is identified, data packets are forwarded along this route. Although GWO-based routing improves reliability and energy efficiency, it typically incurs higher control overhead due to continuous path discovery and maintenance. Minimizing the path length (hop count) reduces latency, while considering link reliability ensures that data packets reach the destination without loss. Once the optimal paths are identified, data is transmitted along these paths, ensuring efficient utilization of network resources.

8.2.3 Role of GWO in Co-Designed Clustering/Routing Techniques

Co-designed approaches jointly optimize clustering and routing within a unified GWO framework to achieve end-to-end energy efficiency. In this paradigm, each candidate solution simultaneously encodes CH selection and inter-cluster routing decisions. The fitness function integrates clustering-related metrics (e.g., residual energy, CH–BS distance, intra-cluster compactness) with routing metrics (e.g., hop count, energy consumption, and link reliability). GWO iteratively optimizes both decisions in a coupled manner, resulting in improved global energy balancing and reduced performance degradation caused by treating clustering and routing independently. After optimization, nodes are assigned to CHs and data is transmitted through optimized inter-cluster paths. While co-designed methods offer the highest performance gains, they also involve higher computational complexity, signaling overhead, and design complexity compared to single-stage approaches.

8.3 Computational Complexity Analysis

This subsection provides an overall analytical comparison of the computational complexity of the surveyed GWO-based methods across three major categories: (i) clustering-only, (ii) routing-only, and (iii) co-designed hybrid clustering-routing frameworks. For consistency, all analyses consider the standard GWO computational model per round with a time complexity of O(P × I × D), where P is the population size (number of wolves), I is the maximum number of iterations, and D is the dimensionality of the search space. Hybrid or multi-stage variants (e.g., HGWSFO and Co-BGWO) typically increase complexity by a factor proportional to the secondary optimizer, though the order remains linear in P and I. From a practical standpoint, the rather high complexity of the GWO-based techniques is feasible for BS-centric (centralized) implementations, where computation occurs at the BS rather than on low-power nodes. However, distributed GWO incurs higher control-message overhead since nodes must periodically exchange local state (residual energy, distances, neighbors). This limits scalability in dense or rapidly changing topologies.

In comparison, classical algorithms such as LEACH-based techniques exhibit substantially lower computational cost; for instance, LEACH performs cluster formation with a per-round complexity of O(N). However, traditional protocols lack adaptivity, often leading to suboptimal CH selection and accelerated energy depletion. While GWO-based methods introduce higher runtime overhead, they consistently achieve longer network lifetimes and improved FND/HND performance. Overall, GWO remains practically feasible for large-scale WSNs when computations are offloaded to the base station and control overhead is reduced through periodic or event-driven updates rather than continuous global information exchange.

8.3.1 Complexity of Clustering Techniques

Clustering-oriented approaches treat the CH selection or cluster formation process as the optimization objective. In typical WSN scenarios, the dimensionality D reflects the number of nodes (N). Therefore, the standard GWO-based clustering variants follow O(P × I × N), with modest overhead for local fitness evaluation (such as for distance and residual-energy computations). For techniques with evaluations per clusters, this complexity may be increased to O(P × I × N × C), where C is the number of CHs. Techniques such as HGWO, CGWO, and energy-aware GWO maintain this base complexity because they modify the fitness function without altering the core optimization structure. Furthermore, hybrid clustering methods (e.g., HABCGWO) add either a secondary update step or iterative refinement: O((P × I × N × C) + Chybrid), where Chybrid is the cost of the auxiliary optimizer.

8.3.2 Complexity of Routing Techniques

The GWO-based routing methods optimize next-hop selection, multi-hop path construction, or CH-to-BS routing. Compared to clustering, the dimensionality D often increases, because routing decisions involve multiple path components. Fitness evaluations may include path reliability, hop count, link quality, or delay, increasing per-iteration cost. The dimensionality factor D depends mainly on the number of nodes and average hop count (H). Therefore, standard routing variants retain the baseline complexity of O(P × I × N × H), with additional per-solution overhead for evaluating path metrics. This overhead does not change the order of complexity but may increase the constant factor. Hybrid routing techniques (e.g., GWO-LA) incorporate iterative local search or reinforcement, and thus, their complexity can be expressed as O((P × I × N × H) + Croute-eval), where Croute-eval accounts for computing multi-hop costs and performing local repairs. Although more expensive than clustering variants, the overall order remains linear, and feasibility is preserved for BS-level computation.

8.3.3 Complexity of Co-Designed Hybrid Clustering–Routing Techniques

Co-design frameworks jointly optimize clustering and routing within a unified solution representation, leading to a larger dimensionality D due to the combined parameters. In such techniques, fitness evaluation must consider both intra-cluster and inter-cluster computations, and hybrid variants commonly incorporate reinforcement mechanisms, multi-objective operators, or secondary metaheuristics. For standard (non-hybrid) co-designed GWO approaches, the complexity can be expressed as O((P × I × N) + (P × I × N × H)), but the dimensionality D may also scale with the number of clusters, making these methods more computationally intensive with an approximate complexity of O((P × I × N × C) + (P × I × N × H)). For hybrid co-designed models that integrate parallel optimizers or co-evolution mechanisms (e.g., MOGWO), the overall computational complexity further increases. However, these overheads increase the constant term but not the big-O order. Since computation is executed at the base station, the complexity remains acceptable even for networks of several hundred nodes.

8.4 Overall Comparison of Different Categories

To provide an integrated view of how different GWO-based methodologies operate across WSN optimization tasks, Table 12 presents a comprehensive cross-category comparison of the three major classes of techniques in terms of their primary optimization focus, dominant optimization terms, sources of computational cost, control signaling requirements, and communication overhead implications.

Clustering, routing, and co-designed GWO-based techniques differ significantly in their optimization scope, sources of computational burden, and communication requirements. Clustering-oriented approaches primarily optimize node-level and intra-cluster characteristics such as residual energy, distance to the base station, node density, and cluster compactness. The main computational effort in this category arises from repeated fitness evaluation during CH selection and subsequent cluster updates. Because these methods typically follow a centralized, BS-driven operational mode, their communication overhead remains relatively low and is mainly limited to periodic reporting of node energy and position information. Consequently, clustering techniques offer strong intra-cluster energy balancing and stable network organization, but their responsiveness may degrade in very large-scale or highly dynamic networks.

Routing-focused techniques operate on end-to-end multi-hop paths and therefore emphasize metrics such as hop count, link reliability, latency, packet loss rate, and residual energy along routes. Their computational burden stems primarily from evaluating candidate routes, performing neighbor discovery, and executing local path repairs when network conditions change. Unlike clustering, routing approaches impose moderate to high communication overhead due to frequent control packet exchanges for route discovery, monitoring, and maintenance. These methods provide reliable and energy-aware data delivery but may face scalability limitations in dense or highly mobile environments because of their continuous signaling requirements.

Co-designed clustering/routing techniques jointly optimize CH selection and inter-cluster routing within a unified solution model. Their computational cost is driven by the simultaneous evaluation of clustering and routing decisions, often combined with hybrid or multi-objective optimization operators. From a communication perspective, these techniques generate the highest overhead, since nodes must continuously report both clustering-related parameters and routing state, and CH-to-CH coordination requires multi-hop control exchanges. Despite this overhead, co-designed approaches achieve the highest level of global energy efficiency and eliminate the performance loss associated with treating clustering and routing as independent processes. Their main limitations lie in their higher design complexity, longer convergence behavior, and limited real-world deployment.

While clustering techniques incur complexity primarily during periodic CH reselection, routing methods require continuous multi-hop path evaluation and maintenance, and co-designed techniques introduce simultaneous inter- and intra-cluster optimization. Consequently, the superior energy balancing and adaptability of co-designed approaches come at the cost of increased computational burden and signaling traffic.

9  Limitations and Future Research Directions

While this survey has provided a methodological synthesis of GWO-based clustering and routing approaches, it also highlights several important limitations that warrant future investigation. Despite its effectiveness, GWO presents several limitations when deployed in highly resource-constrained WSN environments. First, GWO relies on iterative population-based optimization, which can introduce non-negligible computational cost and memory usage if executed on sensor nodes; thus, most practical implementations must remain BS-centric. Second, many GWO variants assume periodic global information exchange (such as residual energy, distances, or neighborhood updates), which can generate significant communication overhead, reducing the network lifetime they aim to optimize. Third, the algorithm’s performance can degrade in highly dynamic scenarios (node failures, mobility, irregular traffic patterns), as the static parameter settings and synchronous update mechanism may delay adaptation. Finally, hybrid and multi-objective GWO extensions often increase dimensionality and fitness-evaluation cost, making them less suitable for dense or rapidly changing networks unless carefully simplified. These limitations highlight the need for lightweight, event-driven, or distributed adaptations of GWO tailored specifically for constrained WSN deployments.

Future research should aim to establish standardized benchmark datasets and simulation frameworks that enable rigorous statistical assessment and reproducible evaluation across algorithms. Such benchmarks would make it possible to conduct numerical performance comparisons among GWO variants and also to examine their relative strengths against other metaheuristics under identical conditions. Developing these standardized testbeds and comparative analyses would not only address the current lack of cross-algorithm benchmarking but also advance methodological understanding of when and why GWO excels or underperforms relative to alternative optimization paradigms. Accordingly, this line of research is a key step toward turning methodological ideas into practical, performance-validated solutions for energy-efficient WSN design.

Based on the analysis of existing GWO-based approaches in WSNs, several promising research directions emerge to enhance GWO’s capabilities and address current limitations. Future studies could focus on hybrid GWO algorithms that integrate machine learning or deep learning for dynamic cluster-head selection, as well as multi-objective variants optimizing energy efficiency, load balancing, and network lifetime. Applying GWO to heterogeneous WSNs with diverse node capabilities can further improve scalability and robustness.

Developing GWO-based routing protocols that consider real-time conditions such as traffic load and link quality, or that combine GWO with reinforcement learning for adaptive routing, can enhance energy efficiency, reliability, and resilience to node failures and congestion. Co-optimizing clustering and routing with lightweight GWO frameworks could balance energy efficiency, coverage, and data delivery while maintaining computational efficiency, and integrating GWO with emerging technologies like Software-Defined Networking may enable more flexible network management.

Energy-aware strategies are another important avenue, including GWO-based energy harvesting, sleep scheduling, and data aggregation techniques to extend network lifetime and reduce redundant transmissions. Research should also explore decentralized and self-organizing GWO frameworks for large-scale WSNs to improve scalability, adaptability, and resilience under dynamic conditions.

Integration with advanced technologies such as 5G, edge computing, blockchain, federated learning, and quantum computing presents opportunities to boost WSN performance, security, and collaborative capabilities. Real-world validation in applications such as smart cities, industrial IoT, healthcare, and disaster management is essential to ensure practical reliability. Finally, enhancing convergence speed and accuracy through advanced initialization, adaptive parameter tuning, chaos theory, hybrid metaheuristics, and parallel or distributed computing offers further potential for optimizing GWO in large-scale, complex WSNs.

10  Conclusion

This survey has provided a comprehensive analysis of the applications of the Grey Wolf Optimizer (GWO) and its variants in addressing cluster-based routing challenges in WSNs. The study focused on three key domains: clustering, routing, and the co-design of clustering and routing. Each domain was examined in detail, highlighting the role of GWO in optimizing network performance, energy efficiency, and reliability. The analysis included a critical review of existing GWO-based approaches, their modifications, and their effectiveness in solving specific WSN problems. In the clustering domain, GWO was shown to enhance energy efficiency and network lifetime by optimizing cluster-head (CH) selection and balancing load across the network. For routing, GWO-based protocols demonstrated improvements in energy consumption, latency reduction, and reliability, particularly in dynamic and large-scale networks. The co-design of clustering and routing further emphasized the impact of simultaneously optimizing energy efficiency, coverage, and data delivery to improve overall network performance.

Despite these achievements, several limitations in current GWO-based approaches were identified, including scalability challenges, computational overhead, and limited adaptability to dynamic or heterogeneous network environments. Furthermore, most studies have relied heavily on simulations, with limited real-world validation, which restricts insights into practical deployment. To address these challenges, future research should focus on the development of hybrid GWO algorithms that combine metaheuristics or adaptive mechanisms to improve scalability and responsiveness. Integrating machine learning and reinforcement learning techniques could enhance decision-making and predictive optimization for both clustering and routing. Additionally, exploring GWO applications in emerging technologies such as 5G networks, edge/fog computing, IoT systems, and quantum computing could help address the needs of next-generation WSNs. Real-world validation in practical applications is also crucial to verify simulation results and assess feasibility. Future studies can develop standardized WSN benchmarks to enable a valid performance assessment and facilitate fair comparisons across different methods.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Mohammad Shokouhifar, Fakhrosadat Fanian, and Mehdi Hosseinzadeh; methodology, Mohammad Shokouhifar and Fakhrosadat Fanian; software, Fakhrosadat Fanian and Aseel Smerat; validation, Mohammad Shokouhifar and Mehdi Hosseinzadeh; investigation, Fakhrosadat Fanian, Aseel Smerat, Kamal M. Othman, Abdulfattah Noorwali and Esam Y. O. Zafar; resources, Mehdi Hosseinzadeh and Kamal M. Othman; data curation, Mohammad Shokouhifar and Fakhrosadat Fanian; writing—original draft preparation, Mohammad Shokouhifar, Fakhrosadat Fanian, Aseel Smerat and Kamal M. Othman; writing—review and editing, Mohammad Shokouhifar, Mehdi Hosseinzadeh, Kamal M. Othman, Abdulfattah Noorwali and Esam Y. O. Zafar; visualization, Fakhrosadat Fanian; supervision, Mohammad Shokouhifar and Mehdi Hosseinzadeh; project administration, Mohammad Shokouhifar. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data sharing not applicable to this review article as no datasets were generated or analyzed during the current study.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kandris D, Nakas C, Vomvas D, Koulouras G. Applications of wireless sensor networks: an up-to-date survey. Appl Syst Innov. 2020;3(1):14. doi:10.3390/asi3010014. [Google Scholar] [CrossRef]

2. Fanian F, Rafsanjani MK. Cluster-based routing protocols in wireless sensor networks: a survey based on methodology. J Netw Comput Appl. 2019;142(14):111–42. doi:10.1016/j.jnca.2019.04.021. [Google Scholar] [CrossRef]

3. Ojha A, Gupta B. Evolving landscape of wireless sensor networks: a survey of trends, timelines, and future perspectives. Discov Appl Sci. 2025;7(8):825. doi:10.1007/s42452-025-07070-6. [Google Scholar] [CrossRef]

4. Shokouhifar M, Jalali A. Optimized sugeno fuzzy clustering algorithm for wireless sensor networks. Eng Appl Artif Intell. 2017;60(4):16–25. doi:10.1016/j.engappai.2017.01.007. [Google Scholar] [CrossRef]

5. Moharamkhani E, Zadmehr B, Memarian S, Saber MJ, Shokouhifar M. Multiobjective fuzzy knowledge-based bacterial foraging optimization for congestion control in clustered wireless sensor networks. Int J Commun Syst. 2021;34(16):e4949. doi:10.1002/dac.4949. [Google Scholar] [CrossRef]

6. Lanzolla A, Spadavecchia M. Wireless sensor networks for environmental monitoring. Sensors. 2021;21(4):1172. doi:10.3390/s21041172. [Google Scholar] [PubMed] [CrossRef]

7. Luo J, Chen Y, Wu M, Yang Y. A survey of routing protocols for underwater wireless sensor networks. IEEE Commun Surv Tutor. 2021;23(1):137–60. doi:10.1109/comst.2020.3048190. [Google Scholar] [CrossRef]

8. Sharma H, Haque A, Blaabjerg F. Machine learning in wireless sensor networks for smart cities: a survey. Electron. 2021;10(9):1012. doi:10.3390/electronics10091012. [Google Scholar] [CrossRef]

9. Gulati K, Boddu RS, Kapila D, Bangare SL, Chandnani N, Saravanan G. A review paper on wireless sensor network techniques in Internet of Things (IoT). Mater Today Proc. 2022;51(1):161–5. doi:10.1016/j.matpr.2021.05.067. [Google Scholar] [CrossRef]

10. Subramani N, Mohan P, Alotaibi Y, Alghamdi S, Khalaf OI. An efficient metaheuristic-based clustering with routing protocol for underwater wireless sensor networks. Sensors. 2022;22(2):415. doi:10.3390/s22020415. [Google Scholar] [PubMed] [CrossRef]

11. Amutha J, Sharma S, Sharma SK. Strategies based on various aspects of clustering in wireless sensor networks using classical, optimization and machine learning techniques: review, taxonomy, research findings, challenges and future directions. Comput Sci Rev. 2021;40(4):100376. doi:10.1016/j.cosrev.2021.100376. [Google Scholar] [CrossRef]

12. Jamshed MA, Ali K, Abbasi QH, Imran MA, Ur-Rehman M. Challenges, applications, and future of wireless sensors in Internet of Things: a review. IEEE Sens J. 2022;22(6):5482–94. doi:10.1109/jsen.2022.3148128. [Google Scholar] [CrossRef]

13. Ahmad R, Wazirali R, Abu-Ain T. Machine learning for wireless sensor networks security: an overview of challenges and issues. Sensors. 2022;22(13):4730. doi:10.3390/s22134730. [Google Scholar] [PubMed] [CrossRef]

14. Lilhore UK, Khalaf OI, Simaiya S, Tavera Romero CA, Abdulsahib GM, Manoharan P, et al. A depth-controlled and energy-efficient routing protocol for underwater wireless sensor networks. Int J Distrib Sens Netw. 2022;18(9):15501329221117118. doi:10.1177/15501329221117118. [Google Scholar] [CrossRef]

15. Lakshmanna K, Subramani N, Alotaibi Y, Alghamdi S, Khalafand OI, Nanda AK. Improved metaheuristic-driven energy-aware cluster-based routing scheme for IoT-assisted wireless sensor networks. Sustainability. 2022;14(13):7712. doi:10.3390/su14137712. [Google Scholar] [CrossRef]

16. Sahoo L, Sen SS, Tiwary K, Moslem S, Senapati T. Improvement of wireless sensor network lifetime via intelligent clustering under uncertainty. IEEE Access. 2024;12(3):25018–33. doi:10.1109/access.2024.3365490. [Google Scholar] [CrossRef]

17. Shokouhifar M, Fanian F, Rafsanjani MK, Hosseinzadeh M, Mirjalili S. AI-driven cluster-based routing protocols in WSNs: a survey of fuzzy heuristics, metaheuristics, and machine learning models. Comput Sci Rev. 2024;54(4):100684. doi:10.1016/j.cosrev.2024.100684. [Google Scholar] [CrossRef]

18. Van Son N, Hanh NT, Minh TT, Binh HTT. Thang NX Heuristic and approximate Steiner tree algorithms for ensuring network connectivity in mobile wireless sensor networks. J Netw Comput Appl. 2025;238(4):104155. doi:10.1016/j.jnca.2025.104155. [Google Scholar] [CrossRef]

19. Sen S, Sahoo L, Ghosh SL. Lifetime extension of wireless sensor networks by perceptive selection of cluster head using K-means and Einstein weighted averaging aggregation operator under uncertainty. J Ind Intell. 2024;2(1):54–62. doi:10.56578/jii020105. [Google Scholar] [CrossRef]

20. Ashraf N, Viratikul R, Silawan T, Saivichit C. Maximizing the lifetime of wireless sensor networks: integrating K-means clustering with LEACH protocol to improve energy efficiency. In: Proceedings of the 2024 21st International Joint Conference on Computer Science and Software Engineering (JCSSE); 2024 Jun 9–12; Phuket, Thailand. p. 494–9. [Google Scholar]

21. Sulthana NN, Duraipandian M. EELCR: energy efficient lifetime aware cluster based routing technique for wireless sensor networks using optimal clustering and compression. Telecommun Syst. 2024;85(1):103–24. doi:10.1007/s11235-023-01068-4. [Google Scholar] [CrossRef]

22. Mishra SD, Verma D. Energy-efficient and reliable clustering with optimized scheduling and routing for wireless sensor networks. Multimed Tools Appl. 2024;83(26):68107–33. doi:10.1007/s11042-024-18623-z. [Google Scholar] [CrossRef]

23. Prince B, Kumar P, Singh SK. Multi-level clustering and Prediction based energy efficient routing protocol to eliminate Hotspot problem in wireless sensor networks. Sci Rep. 2025;15(1):1122. doi:10.1038/s41598-024-84596-6. [Google Scholar] [PubMed] [CrossRef]

24. Kumar S, Chinthaginjala R, Ahmad S, Kim T. Energy-efficient unequal multi-level clustering for underwater wireless sensor networks. Alex Eng J. 2025;111(7):33–46. doi:10.1016/j.aej.2024.10.026. [Google Scholar] [CrossRef]

25. Kaur S, Kour S, Singh M. Energy efficiency in wireless sensor networks: comparing traditional and advanced clustering protocols. Eng Res Express. 2025;7(1):015258. doi:10.1088/2631-8695/adb37b. [Google Scholar] [CrossRef]

26. Vijayaragavan P, Saravanan V, Suresh C, Maheshwari A, Vijayalakshmi K, Hrbac R, et al. FOAEAUC-SARP: a novel energy-efficient protocol integrating unequal clustering and intelligent routing for sustainable wireless sensor networks. Results Eng. 2025;25(3):103806. doi:10.1016/j.rineng.2024.103806. [Google Scholar] [CrossRef]

27. Juwaied A, Jackowska-Strumillo L, Sierszeń A. Enhancing clustering efficiency in heterogeneous wireless sensor network protocols using the K-nearest neighbours algorithm. Sensors. 2025;25(4):1029. doi:10.3390/s25041029. [Google Scholar] [PubMed] [CrossRef]

28. Vimalarani C, Selvi CT, Gopinathan B, Kalaivani T. Improving energy efficiency in WSN through adaptive memetic-based clustering and routing for resource management. Sustain Comput Inform Syst. 2025;45(6):101073. doi:10.1016/j.suscom.2024.101073. [Google Scholar] [CrossRef]

29. Alnawafa E, Allaymoun M. EDMR: an enhanced dynamic multi-hop routing protocol with a novel sleeping mechanism for wireless sensor networks. Sensors. 2025;25(14):4510. doi:10.3390/s25144510. [Google Scholar] [PubMed] [CrossRef]

30. Al-Karaki J. Routing techniques in wireless sensor networks: a survey. IEEE Commun Mag. 2004;2(6):6–28. doi:10.1109/mwc.2004.1368893. [Google Scholar] [CrossRef]

31. Min J, Wu Z. Research on stamping modeling based on multiobjective fusion and multistrategy improved grey wolf optimization algorithm. J Struct Des Constr Pract. 2026;31(1):04025135. doi:10.1061/jsdccc.sceng-1855. [Google Scholar] [CrossRef]

32. Zelani SK, Babu DN, Surendra D, Rahman MZ. Energy-efficient ant routing algorithm for optimized path selection network longevity in wireless sensor networks. Telecommun Radio Eng. 2025;84(2):21–42. doi:10.1615/telecomradeng.2024054002. [Google Scholar] [CrossRef]

33. Zagrouba R, Kardi A. Comparative study of energy efficient routing techniques in wireless sensor networks. Inf. 2021;12(1):42. doi:10.3390/info12010042. [Google Scholar] [CrossRef]

34. Xue X, Shanmugam R, Palanisamy S, Khalaf OI, Selvaraj D, Abdulsahib GM. A hybrid cross layer with Harris-Hawk-optimization-based efficient routing for wireless sensor networks. Symmetry. 2023;15(2):438. doi:10.3390/sym15020438. [Google Scholar] [CrossRef]

35. Del-Valle-Soto C, Rodríguez A, Ascencio-Piña CR. A survey of energy-efficient clustering routing protocols for wireless sensor networks based on metaheuristic approaches. Artif Intell Rev. 2023;56(9):9699–770. doi:10.1007/s10462-023-10402-w. [Google Scholar] [CrossRef]

36. Saranya VG, Karthik S. Bio-inspired intelligent routing in WSN: integrating mayfly optimization and enhanced ant colony optimization for energy-efficient cluster formation and maintenance. Comput Model Eng Sci. 2024;141(1):127. doi:10.32604/cmes.2024.053825. [Google Scholar] [CrossRef]

37. Houssein EH, Saad MR, Djenouri Y, Hu G, Ali AA, Shaban H. Metaheuristic algorithms and their applications in wireless sensor networks: review, open issues, and challenges. Clust Comput. 2024;27(10):13643–73. doi:10.1007/s10586-024-04619-9. [Google Scholar] [CrossRef]

38. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

39. Raj B, Ahmedy I, Idris MY, Md. Noor R. A survey on cluster head selection and cluster formation methods in wireless sensor networks. Wirel Commun Mob Comput. 2022;2022(1):5322649. doi:10.1155/2022/5322649. [Google Scholar] [CrossRef]

40. John J, Rodrigues P. A survey of energy-aware cluster head selection techniques in wireless sensor network. Evol Intell. 2022;15(2):1109–21. doi:10.1007/s12065-019-00308-4. [Google Scholar] [CrossRef]

41. Karpurasundharapondian P, Selvi M. A comprehensive survey on optimization techniques for efficient cluster based routing in WSN. Peer Peer Netw Appl. 2024;17(5):3080–93. doi:10.1007/s12083-024-01678-y. [Google Scholar] [CrossRef]

42. Kumar S, Agrawal R. A comprehensive survey on meta-heuristic-based energy minimization routing techniques for wireless sensor network: classification and challenges. J Supercomput. 2022;78(5):6612–63. doi:10.1007/s11227-021-04128-1. [Google Scholar] [CrossRef]

43. Hamim SI, Ab Rahman AB. Optimizing wireless sensor networks: a survey of clustering strategies and algorithms. Int J Comput Networks Appl. 2024;11(5):673–89. doi:10.22247/ijcna/2024/42. [Google Scholar] [CrossRef]

44. Isaac SR, Bibin CV, Joselin KM, Akhila TS. An energy aware secure three-level weighted trust evaluation and grey wolf optimization based routing in wireless ad hoc sensor network. Wirel Netw. 2022;28(4):1439–55. doi:10.1007/s11276-022-02917-x. [Google Scholar] [CrossRef]

45. Sumathi K, Kumar DV. Minimizing delay in mobile ad-hoc network using ingenious grey wolf optimization based routing protocol. Int J Comput Netw Appl. 2022;9(2):251–61. doi:10.22247/ijcna/2022/212340. [Google Scholar] [CrossRef]

46. Yu D, Yuan T, Qing H, Xie W, Zhu P. Gray wolf optimizer with communication strategy based on DV-Hop for nodes location of wireless sensor networks. IEEE Access. 2024;13:115307–20. doi:10.21203/rs.3.rs-2673198/v1. [Google Scholar] [CrossRef]

47. Umamahesh G, Senthurya S, Khatarkar P, Alsalami Z, Kaur J, Ramesh PS. Leveraging grey wolf optimizer for reliable data transmission in underwater wireless sensor networks. In: Proceedings of the 2024 IEEE International Conference on Communication, Computing and Signal Processing (IICCCS); 2024 Sep 19–20; Asansol, India. p. 1–5. [Google Scholar]

48. Aravindh G, Sridhar KP. Resilient and adaptive secure routing protocol for wireless sensor networks using a grey wolf optimizer and lightning search algorithm. J Internet Serv Inf Secur. 2024;14(4):331–46. doi:10.58346/jisis.2024.i4.020. [Google Scholar] [CrossRef]

49. Liu Y, As’ arry A, Hassan MK, Hairuddin AA, Mohamad H. Review of the grey wolf optimization algorithm: variants and applications. Neural Comput Appl. 2024;36(6):2713–35. doi:10.1007/s00521-023-09202-8. [Google Scholar] [CrossRef]

50. Das D, Sadiq AS, Mirjalili S. Grey wolf optimizer: foundations and mathematical models. In: Optimization algorithms in machine learning: a meta-heuristics perspective. Singapore: Springer Nature; 2025. p. 59–66. doi:10.1007/978-981-96-3849-9_6. [Google Scholar] [CrossRef]

51. Selvaraj S, Nanjappan M, Nagalingam M, Balasubramanian UM. Crossover boosted grey wolf optimizer-based framework for leader election and resource allocation in intrusion detection systems for MANETs. Trans Emerg Telecommun Technol. 2024;35(5):e4974. doi:10.1002/ett.4974. [Google Scholar] [CrossRef]

52. Patil M, Chawhan M, Umate R, Madankar A, Neole B. Energy efficient adaptive clustering with QoS-aware CBRP and grey wolf optimization clustering algorithm for mobile ad-hoc network (MANET). Discov Comput. 2025;28(1):1–44. doi:10.1007/s10791-025-09685-0. [Google Scholar] [CrossRef]

53. Singh H, Saxena S, Sharma H, Kamboj VK, Arora K, Joshi GP, et al. An integrative TLBO-driven hybrid grey wolf optimizer for the efficient resolution of multi-dimensional, nonlinear engineering problems. Sci Rep. 2025;15(1):11205. doi:10.1038/s41598-025-89458-3. [Google Scholar] [PubMed] [CrossRef]

54. Goswami C, Shieh CS, Chakrabarti P. Energy-aware power and rate control in MANETs using adaptive game theory and grey wolf optimization. Future Technol. 2025;4(3):29–44. doi:10.55670/fpll.futech.4.3.4. [Google Scholar] [CrossRef]

55. Jadhav S, Patil P, Kulkarni D. Gray Wolf-Based clustering for enhanced energy efficiency in wireless sensor networks. Int J Commun Syst. 2025;38(14):e70228. doi:10.1002/dac.70228. [Google Scholar] [CrossRef]

56. Kumar H. Wireless sensor networks in healthcare system: a systematic review. Wirel Pers Commun. 2024;134(2):1013–34. doi:10.1007/s11277-024-10954-2. [Google Scholar] [CrossRef]

57. Aldawsari H. A blockchain-based approach for secure energy-efficient IoT-based wireless sensor networks for smart cities. Alex Eng J. 2025;126(20):1–7. doi:10.1016/j.aej.2025.04.052. [Google Scholar] [CrossRef]

58. Zing Y, Zhao N. Routing revolution: strategic applications of meta-heuristic AI in wireless sensor networks—a comprehensive survey. Multimed Tools Appl. 2025;84(35):44605–46. doi:10.1007/s11042-025-20843-w. [Google Scholar] [CrossRef]

59. Mahmoud AA, Abdel Salam K, Ali AF, Elgohary R. Optimizing energy consumption in WSNs: an improved K-means clustering approach. In: International Conference on Advanced Machine Learning Technologies and Applications. Cham, Switzerland: Springer Nature; 2025. p. 85–94. [Google Scholar]

60. Mushtaq MU, Venter H, Singh A, Owais M. Advances in energy harvesting for Sustainable wireless sensor networks: challenges and opportunities. Hardware. 2025;3(1):1. doi:10.3390/hardware3010001. [Google Scholar] [CrossRef]

61. Yadav RK, Mahapatra RP. Hybrid metaheuristic algorithm for optimal cluster head selection in wireless sensor network. Pervasive Mob Comput. 2022;79(3):101504. doi:10.1016/j.pmcj.2021.101504. [Google Scholar] [CrossRef]

62. Jing D. Harris harks optimization based clustering with fuzzy routing for lifetime enhancing in wireless sensor networks. IEEE Access. 2024;12(3):12149–63. doi:10.1109/access.2024.3354276. [Google Scholar] [CrossRef]

63. Abdul-Rashid R, Rahman MA, Chan KT, Sangaiah AK. Adaptive time synchronization in time sensitive-wireless sensor networks based on stochastic gradient algorithms framework. Comput Model Eng Sci. 2025;142(3):2585–616. doi:10.32604/cmes.2025.060548. [Google Scholar] [CrossRef]

64. Guo H, Zhang J, Omidizadeh H. Adaptive and scalable energy aware clustering for mobile wireless sensor networks using a density driven approach. Sci Rep. 2025;15(1):40198. doi:10.1038/s41598-025-23992-y. [Google Scholar] [PubMed] [CrossRef]

65. Sinduja B, Yaashuwanth C, Prathibanandhi K, Ramesh S. An energy aware routing protocol using mayfly optimization (ERPMO) and TDMA scheduling in wireless sensor networks. Sci Rep. 2025;15(1):40492. doi:10.1038/s41598-025-24315-x. [Google Scholar] [PubMed] [CrossRef]

66. Harrouz F, Omari M, Kaddi M. Clustering in wireless sensor networks using K-means for cluster formation. In: International Conference on Data Engineering and Communication Technology. Singapore: Springer Nature; 2024. p. 329–42. [Google Scholar]

67. Ghasemi OA, Amirani MC, Azghani M. Resource and power allocation for sum-throughput maximization in RIS-assisted TDMA wireless sensor networks. IEEE Internet Things J. 2024;11(13):24123–33. doi:10.1109/jiot.2024.3390199. [Google Scholar] [CrossRef]

68. Rubavathy AH, Sundar S. Optimizing relay node selection in cooperative wireless body area networks with modified POA. Results Eng. 2024;24(3):103215. doi:10.1016/j.rineng.2024.103215. [Google Scholar] [CrossRef]

69. Bengheni A. Relay node selection scheme and deep sleep period for power management in energy-harvesting wireless sensor networks. Int J Commun Syst. 2024;37(8):e5742. doi:10.1002/dac.5742. [Google Scholar] [CrossRef]

70. Saqhib MN, Lakshmikanth S. Augmenting relay node selection for improved energy efficiency in non-hierarchical IoT-oriented wireless sensor networks using Q-learning and fuzzy logic. Comput Electr Eng. 2025;123(12):110068. doi:10.1016/j.compeleceng.2025.110068. [Google Scholar] [CrossRef]

71. Aryai P, Khademzadeh A, Jassbi SJ, Hosseinzadeh M, Hashemzadeh O, Shokouhifar M. Real-time health monitoring in WBANs using hybrid metaheuristic-driven machine learning routing protocol (MDML-RP). AEU-Int J Electron Commun. 2023;168(1):154723. doi:10.1016/j.aeue.2023.154723. [Google Scholar] [CrossRef]

72. Karunkuzhali D, Meenakshi B, Lingam K. A QoS-aware routing approach for Internet of Things-enabled wireless sensor networks in smart cities. Multimed Tools Appl. 2025;84(17):17951–77. doi:10.1007/s11042-024-18125-y. [Google Scholar] [CrossRef]

73. Yuebo L, Haitao Y, Hongyan L, Qingxue L. Fuzzy clustering and routing protocol with rules tuned by improved particle swarm optimization for wireless sensor networks. IEEE Access. 2023;11:128784–800. doi:10.1109/access.2023.3332914. [Google Scholar] [CrossRef]

74. Jeong H, Lee SW, Hussain Malik M, Yousefpoor E, Yousefpoor MS, Ahmed OH, et al. SecAODV: a secure healthcare routing scheme based on hybrid cryptography in wireless body sensor networks. Front Med. 2022;9:829055. doi:10.3389/fmed.2022.829055. [Google Scholar] [PubMed] [CrossRef]

75. Gou H, Zhang G, Calixto RR, Jagatheesaperumal SK, de Albuquerque VH. Reliable data collection model and transmission framework in large-scale wireless medical sensor networks. Comput Model Eng Sci. 2024;140(1):1077. doi:10.32604/cmes.2024.047806. [Google Scholar] [CrossRef]

76. Fanian F, Rafsanjani MK, Shokouhifar M. Combined fuzzy-metaheuristic framework for bridge health monitoring using UAV-enabled rechargeable wireless sensor networks. Appl Soft Comput. 2024;167(5_6):112429. doi:10.1016/j.asoc.2024.112429. [Google Scholar] [CrossRef]

77. Priyadarshi R. Energy-efficient routing in wireless sensor networks: a meta-heuristic and artificial intelligence-based approach: a comprehensive review. Arch Comput Methods Eng. 2024;31(4):2109. doi:10.1007/s11831-023-10039-6. [Google Scholar] [CrossRef]

78. Memarian S, Behmanesh-Fard N, Aryai P, Shokouhifar M, Mirjalili S, del Carmen Romero-Ternero M. TSFIS-GWO: metaheuristic-driven takagi-sugeno fuzzy system for adaptive real-time routing in WBANs. Appl Soft Comput. 2024;155(1):111427. doi:10.1016/j.asoc.2024.111427. [Google Scholar] [CrossRef]

79. Vellaichamy J, Basheer S, Bai PS, Khan M, Kumar Mathivanan S, Jayagopal P, et al. Wireless sensor networks based on multi-criteria clustering and optimal bio-inspired algorithm for energy-efficient routing. Appl Sci. 2023;13(5):2801. doi:10.3390/app13052801. [Google Scholar] [CrossRef]

80. Prakash V, Pandey S. Metaheuristic algorithm for energy efficient clustering scheme in wireless sensor networks. Microprocess Microsyst. 2023;101(4):104898. doi:10.1016/j.micpro.2023.104898. [Google Scholar] [CrossRef]

81. Behzadi M, Motameni H, Mohamadi H, Barzegar B. Multi-objective energy-efficient clustering protocol for wireless sensor networks: an approach based on metaheuristic algorithms. IET Wirel Sens Syst. 2025;15(1):e70011. doi:10.1049/wss2.70011. [Google Scholar] [CrossRef]

82. Rao C, Kan M, Zhou P, Lan Y. A novel multi objective energy efficient clustering optimization scheme based on heuristic intelligence for wireless sensor networks. Sci Rep. 2025;15(1):36988. doi:10.1038/s41598-025-21918-2. [Google Scholar] [PubMed] [CrossRef]

83. Heinzelman WB, Chandrakasan AP, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans Wirel Commun. 2002;1(4):660–70. doi:10.1109/twc.2002.804190. [Google Scholar] [CrossRef]

84. Sert SA, Bagci H, Yazici A. MOFCA: multi-objective fuzzy clustering algorithm for wireless sensor networks. Appl Soft Comput. 2015;30(6):151–65. doi:10.1016/j.asoc.2014.11.063. [Google Scholar] [CrossRef]

85. Fanian F, Kuchaki Rafsanjani M. Memetic fuzzy clustering protocol for wireless sensor networks: shuffled frog leaping algorithm. Appl Soft Comput. 2018;71:568–90. doi:10.1016/j.asoc.2018.07.012. [Google Scholar] [CrossRef]

86. Zeng W, Wang Z, Yang S, He D, Chan S. ICMH-CHR: an intra-cluster multi-hop based cluster head rotation protocol for wireless sensor networks. Ad Hoc Netw. 2025;173(4):103829. doi:10.1016/j.adhoc.2025.103829. [Google Scholar] [CrossRef]

87. Liu Y, Huang H, Zhou J. A dual cluster head hierarchical routing protocol for wireless sensor networks based on hybrid swarm intelligence optimization. IEEE Internet Things J. 2024;11(9):16710–21. doi:10.1109/jiot.2024.3355993. [Google Scholar] [CrossRef]

88. Kiani F, Seyyedabbasi A, Nematzadeh S. Improving the performance of hierarchical wireless sensor networks using the metaheuristic algorithms: efficient cluster head selection. Sens Rev. 2021;41(4):368–81. doi:10.1108/sr-03-2021-0094. [Google Scholar] [CrossRef]

89. Kaushik A, Indu S, Gupta D. A grey wolf optimization approach for improving the performance of wireless sensor networks. Wirel Pers Commun. 2019;106(3):1429–49. doi:10.1007/s11277-019-06223-2. [Google Scholar] [CrossRef]

90. Sekaran K, Rajakumar R, Dinesh K, Rajkumar Y, Latchoumi T, Kadry S, et al. An energy-efficient cluster head selection in wireless sensor network using grey wolf optimization algorithm. TELKOMNIKA. 2020;18(6):2822–33. doi:10.12928/telkomnika.v18i6.15199. [Google Scholar] [CrossRef]

91. Agrawal D, Qureshi MHW, Pincha P, Srivastava P, Agarwal S, Tiwari V, et al. Grey wolf optimizer-based clustering scheme for WSNs. Int J Commun Syst. 2020;33(8):e4344. doi:10.1002/dac.4344. [Google Scholar] [CrossRef]

92. Nagarajan L, Thangavelu S. Hybrid grey wolf sunflower optimisation algorithm for energy-efficient cluster head selection in wireless sensor networks for lifetime enhancement. IET Commun. 2021;15(3):384–96. doi:10.1049/cmu2.12072. [Google Scholar] [CrossRef]

93. Singh S, Nikolovski S, Chakrabarti P. Gray wolf optimization based load balanced clustering for sustainable WSNs in smart city environment. Sensors. 2022;22(19):7113. doi:10.3390/s22197113. [Google Scholar] [PubMed] [CrossRef]

94. Kaddi M, Omari M, Salameh K, Alnoman A. Energy-efficient clustering in wireless sensor networks using grey wolf optimization and enhanced CSMA/CA. Sensors. 2024;24(16):5234. doi:10.20944/preprints202407.2221.v1. [Google Scholar] [CrossRef]

95. Lekhraj Kumar A, Kumar A. Load balanced and optimal clustering in WSNs using grey wolf optimizer. Int J Syst Assur Eng Manag. 2024;15(7):1–15. doi:10.1007/s13198-024-02306-x. [Google Scholar] [CrossRef]

96. Fauzan MN, Munadi R, Sumaryo S, Nuha HH. Enhanced grey wolf optimization for efficient transmission power optimization in wireless sensor network. Appl Syst Innov. 2025;8(2):36. doi:10.3390/asi8020036. [Google Scholar] [CrossRef]

97. Shokouhifar M, Werner F, Almazyad AS, Mohamed AW. Combined heuristic-metaheuristic protocol for real-time clustering and routing in agricultural monitoring using UAV-assisted rechargeable WSNs. AEU Int J Electron Commun. 2025;200(21):155935. doi:10.1016/j.aeue.2025.155935. [Google Scholar] [CrossRef]

98. Jin R, Fan X, Sun T. Centralized multi-hop routing based on multi-start minimum spanning forest algorithm in the wireless sensor networks. Sensors. 2021;21(5):1775. doi:10.3390/s21051775. [Google Scholar] [PubMed] [CrossRef]

99. Pang S, Lu J, Pan R, Wang H, Wang X, Ye Z, et al. Optimizing routing protocol design for long-range distributed multi-hop networks. Electron. 2024;13(19):3957. doi:10.3724/sp.j.1087.2008.01844. [Google Scholar] [CrossRef]

100. Elmonser M, Alaerjan A, Jabeur R, Chikha HB, Attia R. Enhancing energy distribution through dynamic multi-hop for heterogeneous WSNs dedicated to IoT-enabled smart grids. Sci Rep. 2024;14(1):30690. doi:10.1038/s41598-024-76492-w. [Google Scholar] [PubMed] [CrossRef]

101. Ma L, Zhang N, Chen X, Chen P, Yao Y. A hierarchical traffic offloading mechanism for end-to-end reliability in a multi-hop multi-connection wireless sensor network. IEEE Sens J. 2025;25(4):7390–402. doi:10.1109/jsen.2024.3522394. [Google Scholar] [CrossRef]

102. Al Mazaideh M, Levendovszky J. A multi-hop routing algorithm for WSNs based on compressive sensing and multiple objective genetic algorithm. J Commun Netw. 2021;23(2):138–47. doi:10.23919/jcn.2021.000003. [Google Scholar] [CrossRef]

103. Balan S, Champla D, Pushpavalli M, Ahilan A. Energy efficient multi-hop routing scheme using Taylor based gravitational search algorithm in wireless sensor networks. Int J Electr Comput Eng Syst. 2023;14(3):333–43. doi:10.32985/ijeces.14.3.11. [Google Scholar] [CrossRef]

104. Tang Z, Liu H, Zhou L, Liu T, Chen X. Multi-hop routing algorithm in Lora Sparse monitoring network using backward equilibrium for ecological environment monitoring. [cited 2025 Jan 1]. Available from: https://ssrn.com/abstract=4691490. [Google Scholar]

105. Liu Y, Wen X, Xia C, Zhang H. Research on multi-chain multi-hop routing protocol for smart road chain distributed sensor networks. IEEE Sens J. 2025;25(7):11915–23. doi:10.1109/jsen.2025.3542140. [Google Scholar] [CrossRef]

106. Algubili MD, Alshawi IS. Employing grey wolf optimizer for energy sink holes avoidance in WSNs. Arab J Sci Eng. 2023;48(2):2297–311. doi:10.1007/s13369-022-07259-6. [Google Scholar] [CrossRef]

107. Hussein DM, Kheerallah YA, Alkenani J, Alshawi IS. Lifetime maximization using grey wolf optimization routing protocol with statistical technique in WSNs. Inform. 2023;47(5):75–82. [Google Scholar]

108. Seyyedabbasi A, Kiani F, Allahviranloo T, Fernandez-Gamiz U, Noeiaghdam S. Optimal data transmission and pathfinding for WSN and decentralized IoT systems using I-GWO and Ex-GWO algorithms. Alex Eng J. 2023;63(12):339–57. doi:10.1016/j.aej.2022.08.009. [Google Scholar] [CrossRef]

109. Nebti S, Redjimi M. A co-evolutionary algorithm-based enhanced grey wolf optimizer for the routing of wireless sensor networks. J Commun Softw Syst. 2023;19(4):230–43. doi:10.24138/jcomss-2023-0080. [Google Scholar] [CrossRef]

110. Karmakonda K, Guguloth R. Learning automata based grey wolf optimization algorithm for adaptive data forwarding and aggregation in wireless sensor networks. Preprint. 2023. doi:10.21203/rs.3.rs-3127042/v1. [Google Scholar] [CrossRef]

111. Digra M, Rajput P, Gupta S, Priyadharshini A. Hybrid artificial bee colony and grey wolf optimization technique for energy efficient framework in WSN. Evol Intell. 2024;17(5):4239–56. doi:10.1007/s12065-024-00981-0. [Google Scholar] [CrossRef]

112. Shaikh MS, Wang C, Xie S, Zheng G, Dong X, Qiu S, et al. Coverage and connectivity maximization for wireless sensor networks using improved chaotic grey wolf optimization. Sci Rep. 2025;15(1):15706. doi:10.1038/s41598-025-00184-2. [Google Scholar] [PubMed] [CrossRef]

113. Ramani KP, Badholia A. Cluster based routing protocols in WSN sensor. Inf Technol Ind. 2021;9(1):198–206. doi:10.17762/itii.v9i1.119. [Google Scholar] [CrossRef]

114. Rezaeipanah A, Amiri P, Nazari H, Mojarad M, Parvin H. An energy-aware hybrid approach for wireless sensor networks using re-clustering-based multi-hop routing. Wirel Pers Commun. 2021;120(4):3293–314. doi:10.1007/s11277-021-08614-w. [Google Scholar] [CrossRef]

115. Jagadeesh S, Muthulakshmi I. Hybrid metaheuristic algorithm-based clustering with multi-hop routing protocol for wireless sensor networks. In: Proceedings of Data Analytics and Management. Singapore: Springer; 2021. p. 843–55. [Google Scholar]

116. Saleem MM, Alabady SA. Improvement of the WMSNs lifetime using multi-hop clustering routing protocol. Wirel Netw. 2022;28(7):3173–83. doi:10.1007/s11276-022-03036-3. [Google Scholar] [CrossRef]

117. Chaurasia S, Kumar K, Kumar N. EEM-CRP: energy-efficient meta-heuristic cluster-based routing protocol for WSNs. IEEE Sens J. 2023;23(23):29679–93. doi:10.1109/jsen.2023.3322631. [Google Scholar] [CrossRef]

118. El Khediri S, Selmi A, Khan RU, Moulahi T, Lorenz P. Energy efficient cluster routing protocol for wireless sensor networks using hybrid metaheuristic approache’s. Ad Hoc Netw. 2024;158(8):103473. doi:10.1016/j.adhoc.2024.103473. [Google Scholar] [CrossRef]

119. Altuwairiqi M. An optimized multi-hop routing protocol for wireless sensor network using improved honey badger optimization algorithm for efficient and secure QoS. Comput Commun. 2024;214(12):244–59. doi:10.1016/j.comcom.2023.08.011. [Google Scholar] [CrossRef]

120. Mohammed BM, Alsaadi M, Khalaf M, Awad AS. Game theory-based multi-hop routing protocol with metaheuristic optimization-based clustering process in WSN for precision agriculture. J Eur Autom Syst. 2024;57(3):653. doi:10.18280/jesa.570302. [Google Scholar] [CrossRef]

121. Zhao X, Zhu H, Aleksic S, Gao Q. Energy-efficient routing protocol for wireless sensor networks based on improved grey wolf optimizer. KSII Trans Internet Inf Syst. 2018;12(6):2644–57. doi:10.3837/tiis.2018.06.011. [Google Scholar] [CrossRef]

122. Daneshvar SMH, Mohajer PAA, Mazinani SM. Energy-efficient routing in WSN: a centralized cluster-based approach via grey wolf optimizer. IEEE Access. 2019;7:170019–31. doi:10.1109/access.2019.2955993. [Google Scholar] [CrossRef]

123. Mittal N, Singh U, Salgotra R, Sohi BS. An energy efficient stable clustering approach using fuzzy extended grey wolf optimization algorithm for WSNs. Wirel Netw. 2019;25(8):5151–72. doi:10.1007/s11276-019-02123-2. [Google Scholar] [CrossRef]

124. Zhao X, Ren S, Quan H, Gao Q. Routing protocol for heterogeneous wireless sensor networks based on a modified grey wolf optimizer. Sensors. 2020;20(3):820. doi:10.3390/s20030820. [Google Scholar] [PubMed] [CrossRef]

125. Jaiswal K, Anand V. A grey-wolf based optimized clustering approach to improve QoS in wireless sensor networks for IoT applications. Peer Peer Netw Appl. 2021;14(4):1943–62. doi:10.1007/s12083-021-01099-1. [Google Scholar] [CrossRef]

126. Ojha A, Chanak P. Multiobjective gray-wolf-optimization-based data routing scheme for wireless sensor networks. IEEE Internet Things J. 2021;9(6):4615–23. doi:10.1109/jiot.2021.3105425. [Google Scholar] [CrossRef]

127. Nabavi SR, Eraghi NO, Torkestani JA. Intelligent optimization of QoS in wireless sensor networks using multiobjective grey wolf optimization algorithm. Wirel Commun Mob Comput. 2022; 2022;2022(1):5385502. doi:10.1155/2022/5385502. [Google Scholar] [CrossRef]

128. Bahl V, Kumar A. Probabilistic multi-tiered grey wolf optimizer-based routing for sustainable sensor networks. J Inf Commun Technol. 2022;21(4):627–63. doi:10.32890/jict2022.21.4.7. [Google Scholar] [CrossRef]

129. Malisetti N, Pamula VK. Energy efficient cluster based routing for wireless sensor networks using moth levy adopted artificial electric field algorithm and customized grey wolf optimization algorithm. Microprocess Microsyst. 2022;93(18):104593. doi:10.1016/j.micpro.2022.104593. [Google Scholar] [CrossRef]

130. Ghorbanvirdi M, Mazinani SM. Energy efficient multi-clustering using grey wolf optimizer in wireless sensor network. Int J Inf Commun Technol Res. 2022;14(1)1–12. [Google Scholar]

131. Reddy MR, Chandra MR, Venkatramana P, Dilli R. Energy-efficient cluster head selection in wireless sensor networks using an improved grey wolf optimization algorithm. Computers. 2023;12(2):35. doi:10.3390/computers12020035. [Google Scholar] [CrossRef]

132. Qabouche H, Sahel A, Badri A, Mourabit IE. Energy efficient and coverage aware grey wolf optimizer based clustering process for software-defined wireless sensor networks. Ad Hoc Netw. 2023;151(4):103288. doi:10.1016/j.adhoc.2023.103288. [Google Scholar] [CrossRef]

133. Chunfen H, Haifei Z, Shiyun L. Clustering based on gray wolf optimization algorithm for internet of things over wireless nodes. Int J Adv Comput Sci Appl. 2023;14(6):334–41. doi:10.14569/ijacsa.2023.0140637. [Google Scholar] [CrossRef]

134. Ramya R, Padmapriya K. Hybrid optimized using grey wolf-flower pollination for wireless sensor network routing. Int J Inf Technol. 2023;15(4):2263–71. doi:10.1007/s41870-023-01240-8. [Google Scholar] [CrossRef]

135. Pal R, Saraswat M, Kumar S, Nayyar A, Rajput PK. Energy efficient multi-criterion binary grey wolf optimizer based clustering for heterogeneous wireless sensor networks. Soft Comput. 2024;28(4):3251–65. doi:10.1007/s00500-023-09316-0. [Google Scholar] [CrossRef]

136. Dinesh K, Svn SK. Grey wolf optimization based clustering with secured modified sea lion optimization routing algorithm in wireless sensor networks. Peer Peer Netw Appl. 2024;17(2):585–611. doi:10.1007/s12083-023-01603-9. [Google Scholar] [CrossRef]

137. Khujamatov H, Pitchai M, Shamsiev A, Mukhamadiyev A, Cho J. Clustered routing using chaotic genetic algorithm with grey wolf optimization to enhance energy efficiency in sensor networks. Sensors. 2024;24(13):4406. doi:10.3390/s24134406. [Google Scholar] [PubMed] [CrossRef]

138. Zhou Y, Zhang L, Li W. Partitioned uneven cluster routing algorithm based on gray wolf optimization in WSNs. Ad Hoc Netw. 2024;163(3):103564. doi:10.1016/j.adhoc.2024.103564. [Google Scholar] [CrossRef]

139. Dhinnesh AN, Sabapathi T. Multi-objective grey wolf optimization based self configuring wireless sensor network. Wirel Netw. 2024;30(5):3149–60. doi:10.1007/s11276-024-03732-2. [Google Scholar] [CrossRef]

140. Shang Z, Yu H, Li M, Li H. Inter cluster routing algorithm for air sea cross domain clustering network based on improved grey wolf optimization algorithm. In: Proceedings of the 2025 8th World Conference on Computing and Communication Technologies (WCCCT); 2024 Jun 13; Shenzhen, China. p. 138–44. [Google Scholar]

141. Xu M, Zu Y, Zhou J. Energy-efficient clustering routing for WSNs based on multi-objective quantum adaptive grey wolf optimization. IEEE Sens J. 2025;25(8):14080–98. doi:10.2139/ssrn.4832897. [Google Scholar] [CrossRef]

142. Sun J, Xu Y, Zhou Q. Energy-efficient routing algorithm of dijkstra clustering and grey wolf optimization for wireless sensor networks. Eng Res Express. 2025;7(1):015381. doi:10.1088/2631-8695/adc077. [Google Scholar] [CrossRef]

143. Rahmani AM, Haider A, Ali S, Mohammadi M, Mehranzadeh A, Khoshvaght P, et al. A routing approach based on combination of gray wolf clustering and fuzzy clustering and using multi-criteria decision making approaches for WSN-IoT. Comput Electr Eng. 2025;122(3):109946. doi:10.1016/j.compeleceng.2024.109946. [Google Scholar] [CrossRef]