Inverse Design of Composite Materials Based on Latent Space and Bayesian Optimization

1  Introduction

Composite materials, renowned for their high strength, toughness, and multifunctionality, have found extensive applications across aerospace, new energy vehicles, and high-end manufacturing sectors [1–4]. As quintessential multiphase materials, their macroscopic properties, such as mechanical strength, thermal conductivity, and fatigue resistance, are governed not only by the intrinsic attributes of the matrix and reinforcement but also by microstructural features, including reinforcement distribution density, size distribution, and spatial orientation [5,6]. For instance, a regular arrangement of reinforcement within the matrix can significantly enhance the strain hardening rate and flow stress, while a gradient arrangement, particularly when aligned parallel to the applied load, effectively mitigates damage propagation. Conversely, clustered microstructures may induce stress concentrations and precipitate premature failure [7]. Consequently, the precise design of microstructures to achieve targeted performance constitutes a pivotal objective in advanced materials engineering [8].

Inverse design, a critical pathway bridging performance targets and microstructure, aims to infer optimal microstructural configurations from predefined macroscopic properties, with its efficiency and accuracy directly influencing the development cycle and engineering value of novel materials. Traditional inverse design methodologies rely on microstructure characterization techniques [9], employing physical descriptors [10], such as fiber volume fraction, average diameter, and spacing distribution [11–14], to reduce the high-dimensional microstructural space to a lower-dimensional representation for optimization. However, these descriptors are often constrained by empirically defined rules, exhibiting limitations such as restricted spatial dimensionality and incomplete information representation. For example, volume fraction alone fails to capture localized clustering features, resulting in the inability to perform precise microstructure inverse design. As material systems continue to increase in complexity, conventional inverse design methodologies face growing challenges in simultaneously capturing both global microstructural patterns and localized features, emerging as a significant bottleneck in enhancing inverse design precision.

In recent years, deep generative models have ushered in a transformative paradigm for the precise characterization and inverse design of microstructures [9]. The pixel-based representation of microstructures fundamentally constitutes a high-dimensional random field. Meanwhile, the core objective of generative models which is high-dimensional probability density estimation [15], aligns intrinsically with the representational needs of microstructures, enabling the capture of higher-order statistical properties thereby providing a more comprehensive depiction of their complex information. Among these models, the Variational Autoencoder (VAE) emerges as a classical approach [16], employing an encoder to map high-dimensional microstructures into a low-dimensional latent space and a decoder to reconstruct the structures, demonstrating robust dimensionality reduction and generative capabilities. VAE has been extensively applied in the microstructure reconstruction of composite materials, metallic alloys, sandstones, and other material systems [17–19], offering efficient tools for material characterization and design.

Leveraging the latent space of VAE for optimization design has emerged as a frontier strategy for inverse materials design. Recent studies have demonstrated its applicability across diverse material systems, aiming to generate materials with desired properties through latent space exploration and optimization. For instance, Wang et al. [20] demonstrated that VAE latent spaces provide a meaningful distance metric for assessing shape similarity, enabling vector operations to adjust mechanical properties and manipulate complex microstructures. Lew and Buehler [21] focused on compliance optimization of cantilever designs, encoding cantilever structures into a 2D latent space using a VAE and employing a Long Short-Term Memory (LSTM) network to learn optimization trajectories within that space. Kusampudi and Diehl [22] trained a VAE to identify descriptors from synthetic dual-phase steel microstructures, utilizing Bayesian optimization to determine optimal descriptor combinations that yield microstructures with specific yield strengths and reduced damage initiation sensitivity. Xue et al. [23] employed the VAE to compress the low-resolution (28×28) microstructures of composite materials into a 10-dimensional latent space. As this low-dimensional representation was sufficient to capture the essential features at this low resolution, it allowed for efficient integration with Bayesian optimization, thereby facilitating the inverse design of the macroscopic elastic modulus. Extending this approach to composite laminates, Sun et al. [24] developed a generative VAE framework that efficiently tackles the one-to-many mapping challenge in layup design. By structuring the latent space to separate stiffness-related features from sequence-style characteristics, their model enables rapid generation of numerous non-conventional laminates meeting target mechanical and manufacturing constraints. Park et al. [25] employed various optimization algorithms, such as the single-code modification algorithm, genetic algorithm, and stochastic algorithm, within the VAE latent space to enhance the local energy stability of spin configurations and optimize global physical quantities, including topological indices, magnetization strength, energy, and directional correlations.

Nevertheless, VAEs exhibit inherent limitations in microstructure generation. Their objective function primarily optimizes for latent distribution regularization and pixel-wise reconstruction error, which often leads to decoded microstructures with lost details, such as blurred edges [26]. Although increasing the dimensionality of the latent space can partially alleviate reconstruction inaccuracies, it does not fully eliminate the blurring effect, while substantially increasing computational cost and complicating downstream inverse design tasks. As noted by Peng et al. [27], selecting an appropriate latent dimension requires balancing reconstruction quality against the curse of dimensionality. An undersized latent space lacks sufficient representational capacity, resulting in high reconstruction loss, whereas an oversized space introduces diminishing returns in accuracy while exponentially expanding the search space. This trade-off is particularly consequential when VAEs are coupled with Bayesian optimization (BO). Since BO is typically applicable to dimensions below 20, the microstructures generated by VAEs within this range are often blurry and inadequate for precise design and manufacturing objectives. Therefore, maintaining a low latent space dimension without compromising microstructural fidelity is essential to fully leverage Bayesian optimization in VAE-based inverse design frameworks.

To overcome this bottleneck, our research group previously introduced a Variational Autoencoder guided Conditional Diffusion Generative Model (VAE-CDGM) tailored for material design [28], integrating the low-dimensional mapping capabilities of VAEs with the high-fidelity generative attributes of Denoising Diffusion Probabilistic Models (DDPM). This model uses the blurred image generated by the VAE as a conditional input to restructure the forward diffusion process of DDPM. It then employs multi-step denoising iterations to progressively refine the microstructural details. This approach thus achieves high-fidelity microstructure reconstruction while maintaining a continuous and controllable latent space.

For the inverse design of composite materials, this study builds upon the VAE-CDGM framework, balancing latent space manipulability with high-quality generation, and proposes a dual-strategy inverse design approach integrated with Bayesian optimization. When higher latent space dimensionality is required, SHapley Additive exPlanations (SHAP) sensitivity analysis is employed to identify the most impactful dimensions for performance, enabling Bayesian optimization within a reduced subspace. Conversely, for lower-dimensional spaces, direct Bayesian optimization is performed in VAE-CDGM’s latent space. Both strategies utilize VAE-CDGM to map optimized latent vectors back to the pixel space, generating high-quality microstructure images providing guidance for subsequent manufacturing processes. The material design framework proposed in the study is shown in Fig. 1. The subsequent sections are organized as follows: Section 2 elaborates the construction principles of the VAE-CDGM model; Section 3 validates the latent space properties and reconstruction quality of VAE-CDGM; Section 4 experimentally confirms the model’s generative performance and the efficacy of the inverse design strategy; Section 5 summarizes the findings, discusses the method’s advantages and future improvement directions.

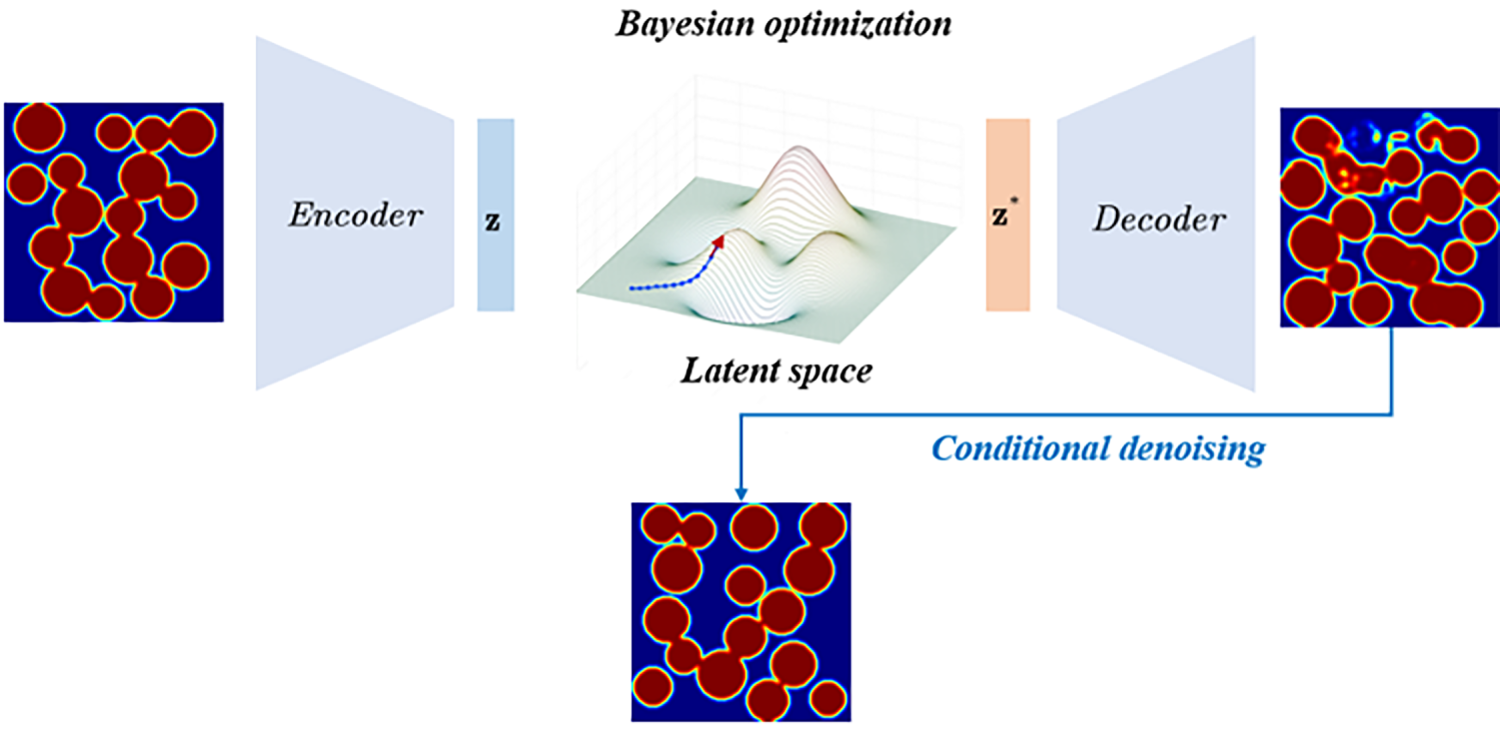
Figure 1: Material design framework based on VAE-CDGM and Bayesian optimization

2  VAE-CDGM Introduction

2.1 Introduction to VAE

The Variational Autoencoder, a generative model integrating probabilistic modeling with deep learning, was pioneered by Kingma and Welling [16]. Its core innovation lies in employing variational inference to establish a probabilistic mapping between high-dimensional data and a low-dimensional latent space, facilitating the representation, generation, and reconstruction of microstructure images. Distinct from traditional autoencoders [29], VAE introduces regularization in the latent space, endowing it with continuity and interpretability, which lays a theoretical foundation for interpolation-based generation and optimization-driven design in materials engineering.

The generative process assumes that observed data x is produced via pθ(x|z), where the latent variable z follows a prior distribution p(z), typically a standard normal distribution N(0,I). The objective is to learn the joint distribution p(x, z)=p(x|z)p(z) to approximate the true data distribution. However, directly maximizing the log-likelihood log⁡p(x)=log⁡∫p(x, z)dz in high-dimensional spaces is intractable due to the complex integral over the latent variables.

To address this, VAE employs variational inference and Jensen’s inequality to avoid direct integration. By introducing an approximate posterior distribution, the marginal log-likelihood can be expressed as:

log⁡p(x)=log⁡(∫zq(z|x)⋅p(x|z)p(z)q(z|x)dz),(1)

log⁡p(x)=log⁡(Eq(z|x)[p(x|z)p(z)q(z|x)]),(2)

here, since log⁡() is a strictly concave function, according to Jensen’s inequality, the above expression can be transformed into,

log⁡p(x)≥Eq(z|x)[log⁡p(x|z)p(z)q(z|x)].(3)

The expectation term on the right side of the above equation is the core of VAE, the Evidence Lower Bound (ELBO),

ELBO=Eq(z|x)[log⁡p(x|z)p(z)q(z|x)].(4)

By applying Jensen’s inequality, the intractable log-likelihood log⁡p(x) is transformed into a computationally tractable lower bound, the ELBO. Since log⁡p(x)≥ELBO, maximizing the ELBO indirectly approximates the maximization of log⁡p(x).

Splitting the logarithmic terms in Eq. (4) and substituting them into the expectation-based definition of the ELBO yields:

ELBO=Eq(z|x)[log⁡p(x|z)]+Eq(z|x)[log⁡p(z)−log⁡q(z|x)]=Eq(z|x)[log⁡p(x|z)]−DKL(q(z|x)‖p(z)).(5)

Since machine learning typically minimizes loss functions via gradient descent, while the objective of VAE is to maximize the ELBO, this is equivalent to minimizing the negative ELBO (−ELBO). The VAE optimization objective can ultimately be written in the following form,

LVAE=−ELBO=−Eqϕ(z|x)[logpθ(x|z)]+DKL(qϕ(z|x)‖p(z)),(6)

where pθ(x|z) is the conditional likelihood modeled by the decoder, qϕ(z|x) is the approximate posterior modeled by the encoder, and θ and ϕ denote the parameters of the decoder and encoder, respectively. The first term represents the reconstruction error, quantifying the similarity between generated and original data, while the second term serves as a regularization constraint, ensuring the approximate posterior aligns with the prior distribution. The schematic diagram of the VAE framework is shown in Fig. 2.

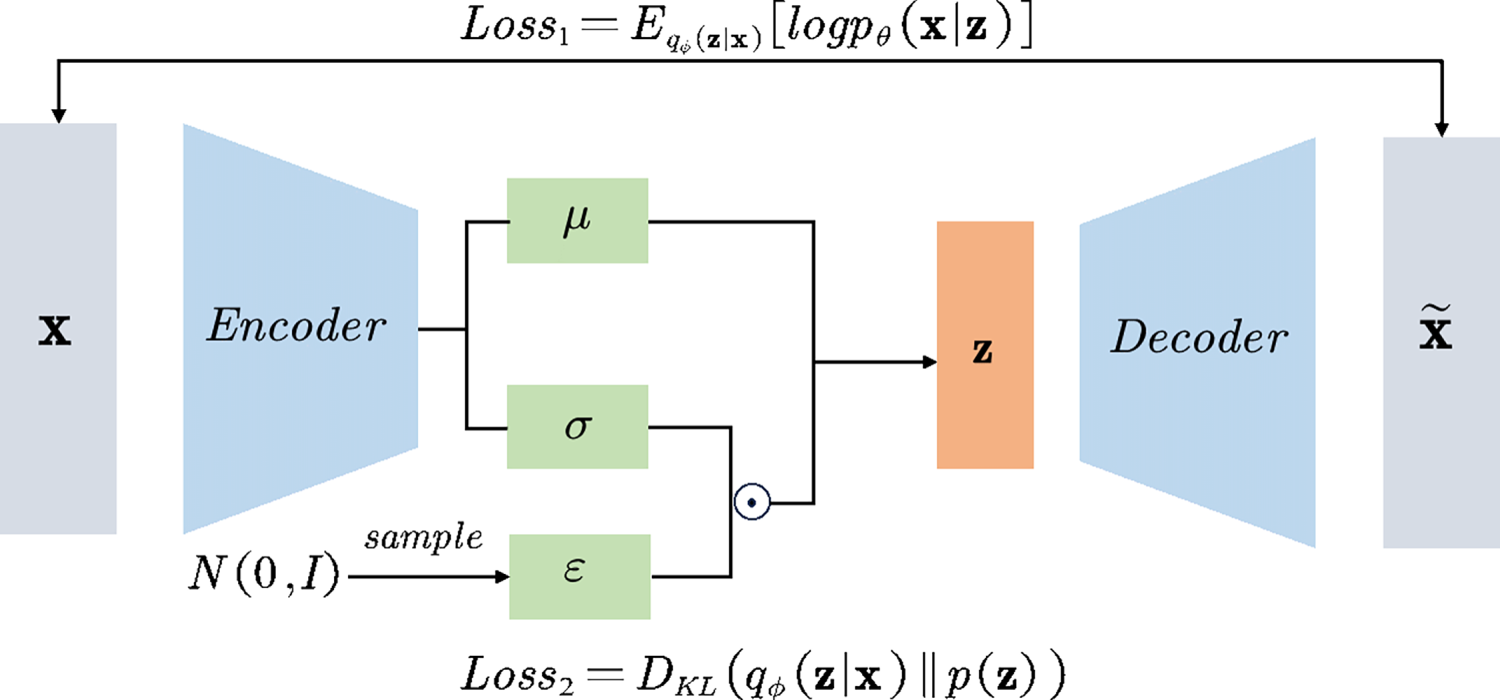
Figure 2: Schematic diagram of VAE architecture

In materials science, VAE’s robust non-linear dimensionality reduction and generative capabilities have been widely leveraged for microstructure characterization and reconstruction across diverse material systems. Its probabilistic framework enables interpolation and optimization operations within the continuous latent space, providing a foundation for target-oriented material design. Despite these advantages, VAE-generated outputs often suffer from blurriness due to the loss’s emphasis on mean-field approximations. Moreover, the choice of latent space dimensionality critically influences both generation quality and computational complexity. Low-dimensional spaces may result in the loss of essential microstructural features, whereas high-dimensional spaces, while potentially reducing blurriness, significantly increase the computational burden and optimization challenges in subsequent inverse design tasks.

2.2 Introduction to Denoising Diffusion Probabilistic Model (DDPM)

The Denoising Diffusion Probabilistic Model (DDPM), a deep learning framework rooted in probabilistic generative processes, was initially proposed by Sohl-Dickstein et al. in 2015 [30] and subsequently developed by Ho et al. in 2020 [31]. DDPM achieves high-precision modeling of complex high-dimensional data distributions by simulating a stepwise noising and denoising process. Compared to VAEs, DDPM excels in generating high-quality samples, demonstrating significant advantages in image generation and microstructure reconstruction [32–34].

The core concept of DDPM revolves around a forward diffusion process and a reverse denoising process to model the data probability distribution, as shown in Fig. 3. The forward process incrementally adds Gaussian noise to the original data x0∼p(x), transitioning it over T steps toward an isotropic Gaussian distribution. This process is defined as a Markov chain:

q(xt|xt−1)=N(xt;1−βtxt−1,βtI),(7)

where βt represents the noise scheduling parameter, controlling the intensity of noise addition. According to the properties of Gaussian distribution, the forward process can be directly expressed as:

q(xt∣x0)=N(xt;α¯tx0,(1−α¯t)I),(8)

where αt:=1−βt and α¯t:=∏i=0tαi.

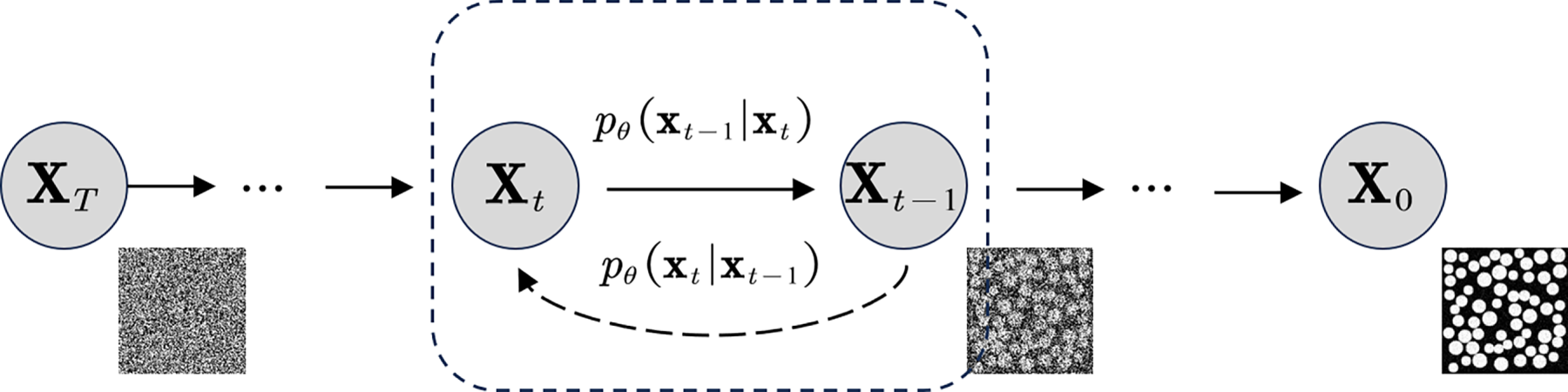
Figure 3: The forward and reverse processes of diffusion model

The reverse process aims to recover the original data from noise,

pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σt2I),(9)

where μθ(xt,t) is the mean and σt2 is a predefined or learned variance. According to Bayes’ theorem, the mean μθ can be derived as:

μθ(xt,t)=1αt(xt−βt1−α¯tϵθ(xt,t)).(10)

The objective of DDPM is to minimize the KL divergence between the true posterior distribution q(xt−1|xt,x0) and the model-predicted distribution pθ(xt−1| xt).

DKL(q(xt−1∣xt,x0)|pθ(xt−1∣xt))=12σt2‖μ~t(xt,x0)−μθ(xt,t)‖2.(11)

Moreover, since,

μ~t(xt,x0)=1αt(xt−βt1−α¯tϵ),(12)

μθ(xt,t)=1αt(xt−βt1−α¯tϵθ(xt,t)).(13)

Substituting the above equation into the optimization objective, the objective becomes:

L=Ex0,ϵ∼N(0,I)[βt22σt2αt(1−α¯t)‖ϵ−ϵθ(xt,t)‖2].(14)

Removing the coefficient yields the final loss function of DDPM,

Lsimple=Ex0,ϵ∼𝒩(0,I)‖ϵ−ϵθ(xt,t)‖2,(15)

where ϵ is the noise added during the forward process, and ϵθ(xt,t) is the noise predicted by the neural network.

Compared to the blurred images generated by VAEs, DDPM’s multi-step denoising process markedly enhances detail fidelity, providing reliable samples for material performance prediction and reverse design. However, the diffusion model does not undergo dimensionality reduction during implementation, resulting in its latent space and pixel space being the same dimensions, making it impossible to use it as a search space for target optimization.

2.3 Introduction to VAE-CDGM

The preceding analyses highlight that while VAEs offer a low-dimensional, continuous latent space conducive to optimization, they are prone to producing blurred reconstructions. Conversely, DDPM excels in high-quality image reconstruction but lacks a manipulable latent space for material optimization. To address these complementary limitations, the VAE-CDGM integrates the strengths of VAEs and DDPMs, ensuring the presence of a continuous latent space while enhancing microstructure reconstruction quality [28].

Unlike standard DDPM, VAE-CDGM incorporates a conditional diffusion process during the forward process:

q(xt∣x0,x~0(z))=N(α¯tx0+x~0(z),(1−α¯t)I),(16)

where z is the latent vector from the VAE, and x~0(z) is the blurred image obtained by mapping z through the VAE decoder. In contrast to Eq. (8), the VAE-CDGM diffusion process does not fully transition the clean image to pure Gaussian noise but applies a mean correction, shifting the zero-mean noise toward the blurred image’s mean, as illustrated in Fig. 4.

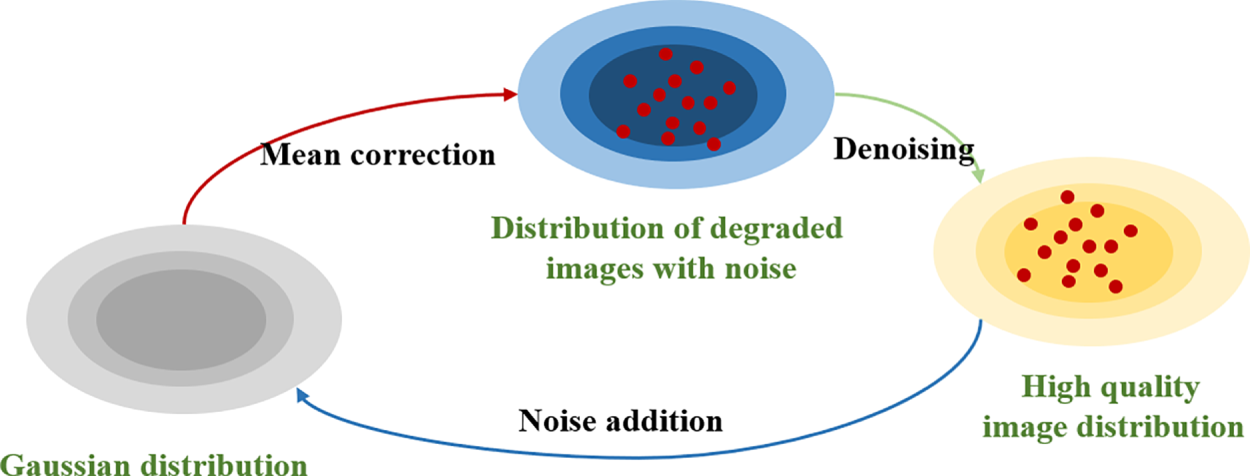
Figure 4: Mean correction process of VAE-CDGM

Subsequently, based on Bayesian inference, the reverse process can be expressed as:

q(xt−1∣xt,x0,x~0(z))=q(xt∣xt−1,x0,x~0(z))q(xt−1∣x0,x~0(z))q(xt∣x0,x~0(z)),(17)

with the posterior mean and variance derived from the forward process as:

μ~t(xt,x0,x~0(z))=βtα¯t−11−α¯tx0+(1−α¯t−1)αt1−α¯txt+(1−(1−α¯t−1)αt1−α¯t)x~0(z),(18)

β~t=(1−α¯t−1)1−α¯tβt,(19)

where x0=1α¯t(xt−x~0(z)−ϵ1−α¯t). The loss function for VAE-CDGM is thus formulated as:

|x0−μ~(xt)|2=1−α¯tα¯t|ϵ−ϵθ(α¯tx0+x~(z)+1−α¯tϵ,x~(z),t)|2.(20)

Traditional conditional diffusion models typically employ a standard diffusion process, incrementally adding Gaussian noise to images until they degenerate into pure noise, with conditional information (e.g., low-quality images) appended as input to the noise prediction network. In contrast, VAE-CDGM explicitly models the image degradation process, progressively degrading high-quality images x into low-quality images x~ with superimposed noise. The reverse process of traditional models initiates from pure noise, relying on conditional information to incrementally reconstruct content. However, the high initial randomness often leads to deviations from the true content. VAE-CDGM’s reverse process starts from the noisy low-quality image, directly optimizing the recovery path. This approach avoids expending model capacity to regenerate existing features from pure noise, initializing the reverse process closer to the target distribution and reducing generative bias.

2.4 Model Architecture Design

The VAE-CDGM model adopts a two-phase training strategy [35], fully decoupling the training parameters of its constituent components. In the first phase, the model focuses on training the VAE component, where the encoder network maps input microstructure images x into low-dimensional latent variables z, and the decoder network reconstructs these latent variables into blurred microstructure images x~. The primary optimization objective during this phase is to minimize the loss function LVAE. Upon completion of the VAE training, its parameters are fully frozen, and the model transitions to the second phase, concentrating on training the conditional diffusion model. This phase utilizes the blurred reconstructions from the first phase as conditional inputs, employing a meticulously designed Markov chain process. In the forward process, Gaussian noise is incrementally added to the original data, while the reverse process learns a complex denoising process to generate high-fidelity microstructure details. The primary optimization objective during this phase is to minimize the loss function LDDPM. The overall workflow is depicted in Fig. 5.

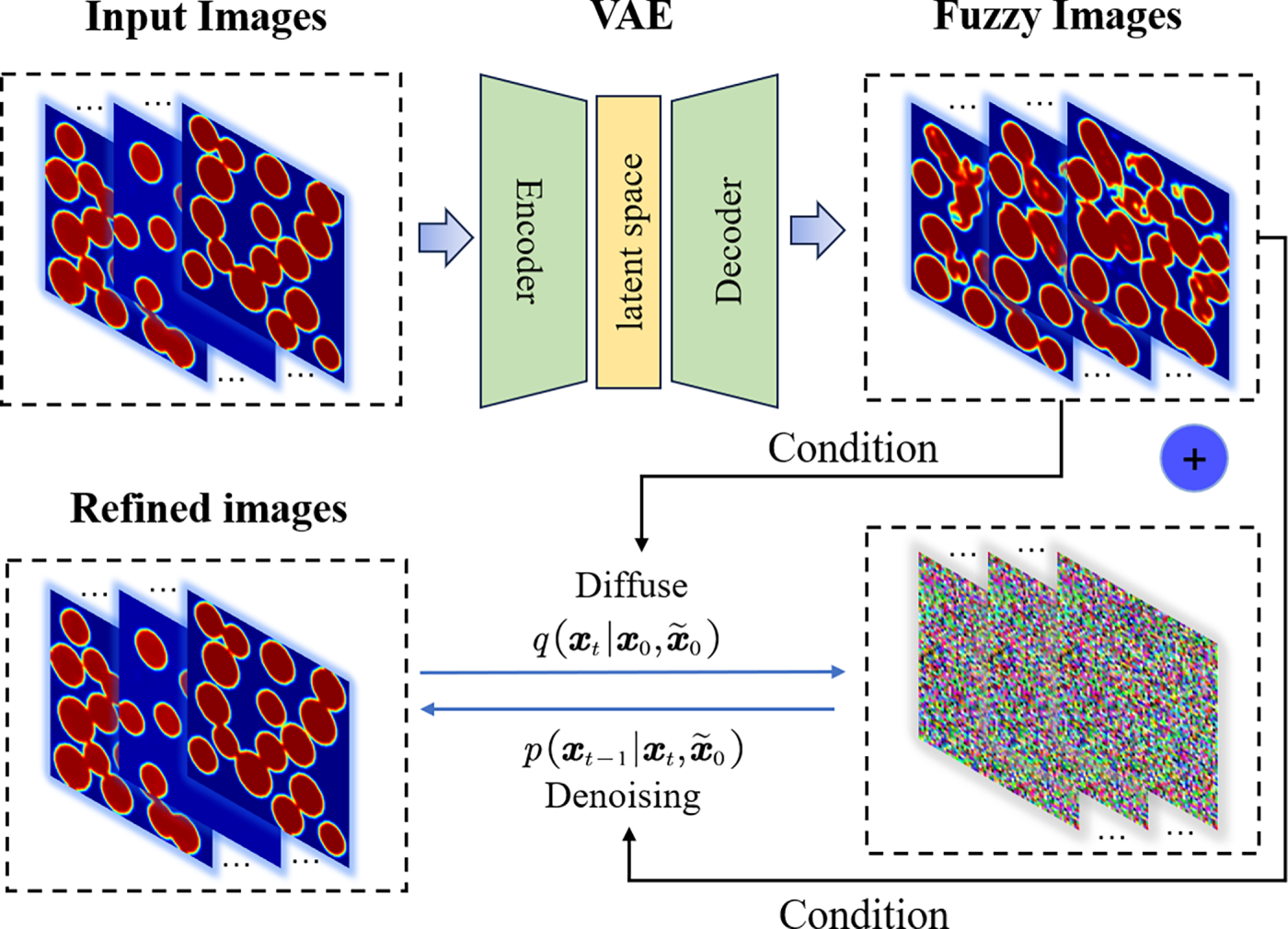
Figure 5: Schematic diagram of VAE-CDGM framework

The model’s first branch comprises a convolutional VAE network. The encoder employs a five-layer downsampling module, each consisting of a Conv2d, BatchNorm2d, and ReLU combination, compressing a 128×128 input image into a 4×4 feature map, which is subsequently mapped to a low-dimensional latent space. The corresponding decoder utilizes a symmetric five-layer transposed convolutional structure (ConvTranspose2d + BatchNorm2d + ReLU) to reconstruct the latent variables into blurred microstructure images. The second branch features a U-Net-based conditional diffusion model, incorporating 16 residual blocks and multiple attention layers. This branch takes the VAE-output blurred reconstructions as conditional inputs, employing downsampling and upsampling paths for feature extraction and fusion. The specific architectural configuration of the U-Net is detailed in Table 1. The model comprises approximately 20.1 million trainable parameters. Training was conducted for 100 epochs on an NVIDIA GeForce320 RTX 4070 Ti GPU, with a total training time of approximately 105,767 s.

3  Characterization and Reconstruction of Composites Based on VAE-CDGM

3.1 Dataset Generation

This study generates two-dimensional microstructure images of composite materials with randomly distributed circular inclusions to simulate diverse inclusion patterns. The images are synthesized at a resolution of 128×128 pixels, with inclusion radii varying randomly between 10 and 15 pixels, and 12 to 18 circular inclusions randomly placed per image. The center coordinates (x,y) are randomly sampled within the image bounds x∈[r,W−r] and y∈[r,H−r] to prevent edge truncation, where r is the radius, and W and H are the image width and height, respectively. A total of 11,893 composite microstructure images were generated for training the VAE-CDGM model. Both the VAE and DDPM components were configured with a batch size of 64, optimized using the Adam optimizer with a learning rate of 0.001.

3.2 Generation Quality Validation

In this study, we conducted a comparative analysis of the microstructure generation quality for composite materials with circular inclusions, using VAE and the proposed VAE-CDGM model at latent space dimensions of 256 and 16, as sown in Fig. 6. For the 256-dimensional latent space, the VAE generated microstructures with improved detail retention compared to its 16-dimensional counterpart, capturing finer geometric features such as inclusion boundaries and spatial distributions. However, the VAE outputs still exhibited noticeable blurriness, particularly in boundary regularity and inclusion size accuracy. In contrast, the VAE-CDGM model at 256 dimensions significantly enhanced generation quality, producing microstructures with sharper boundaries and higher fidelity. When reducing the latent space to 16 dimensions, the VAE suffered from substantial information loss, resulting in overly blurry microstructures with diminished topological accuracy. Conversely, the VAE-CDGM model maintained superior generation quality even at 16 dimensions, leveraging the iterative denoising process of DDPM to reconstruct detailed microstructures while preserving the low-dimensional latent representation of VAE. These results underscore the VAE-CDGM model’s ability to balance latent space dimensionality and high-fidelity microstructure generation, making it a robust tool for inverse design applications in composite materials.

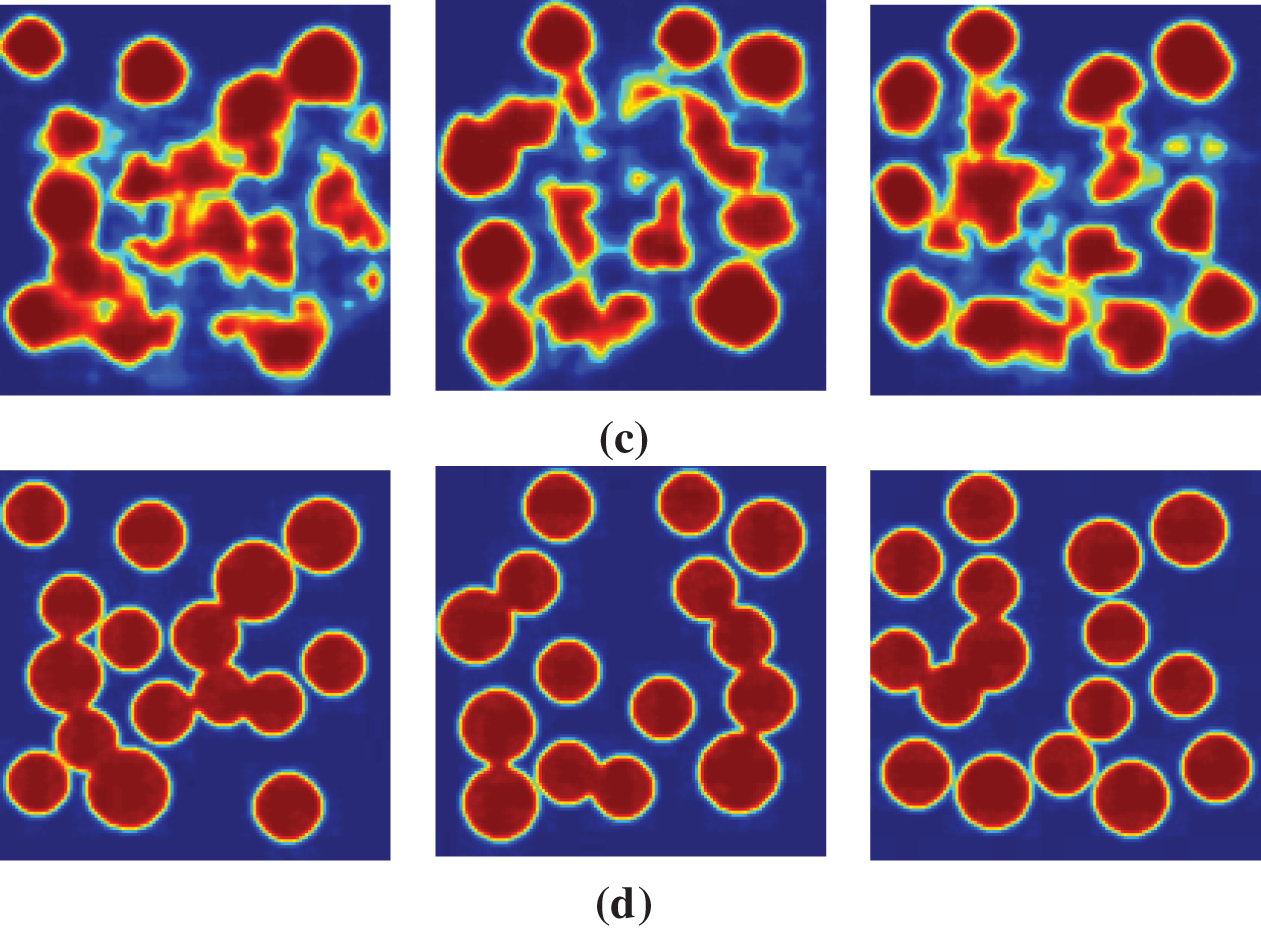
Figure 6: Comparison of VAE and VAE-CDGM generation quality under different latent spaces (a) VAE-256; (b) VAE-CDGM-256; (c) VAE-16; (d) VAE-CDGM-16

3.3 Latent Space Analysis

To gain deeper insights into the latent space properties of the VAE-CDGM model, we conducted a detailed analysis of the 16-dimensional latent space. To facilitate visualization, Principal Component Analysis (PCA) was employed to reduce the dimensionality to three principal components, enabling the projection of the latent space onto the first two principal components (PC1 and PC2). The label assigned to each data point represents the homogenized stress of the composite material under uniaxial compression. The finite element model configuration, including mesh discretization and boundary conditions, is depicted in Fig. 7. Each microstructure image was directly converted into a corresponding finite element model using the python script that maps pixel intensities to material properties, with each pixel corresponding to one CPS4R finite element. The model simulates the mechanical behavior of the composite using two linearly elastic materials: Material- matrix with a Young’s modulus E=73GPa and Poisson’s ratio ν=0.33, and Material- reinforcement with E=420GPa and ν=0.13. A vertical displacement load of 5 mm was applied, and the quasi-static response was solved using a static analysis step.

Figure 7: Microstructure image and finite element setup of composite material (a) Microstructure image of composite material; (b) Mesh discretization and boundary setting

The PCA visualization results, presented in Fig. 8a, reveal that the 16-dimensional latent space retains significant structural characteristics post-reduction. In stark contrast to the diffusion model’s latent space, which exhibits a disordered and unstructured distribution under identical PCA conditions (Fig. 8b), the homogenized stress exhibits a pronounced clustered distribution within the PC1-PC2 plane. Low-stress microstructures concentrated in the lower-left region and high-stress microstructures in the upper-right region, accompanied by a smooth gradient along the diagonal. This clustering in the PCA space indicates that the VAE-CDGM model successfully compresses high-dimensional microstructural information into a low-dimensional representation while preserving critical features correlated with mechanical performance. The smooth gradient further reflects the continuity of the latent space, enabling interpolation or optimization to explore performance variations, which is conducive to efficient inverse design. This structured latent space not only validates the superior representational capability of the VAE-CDGM model but also provides a reliable design space for target-oriented material optimization.

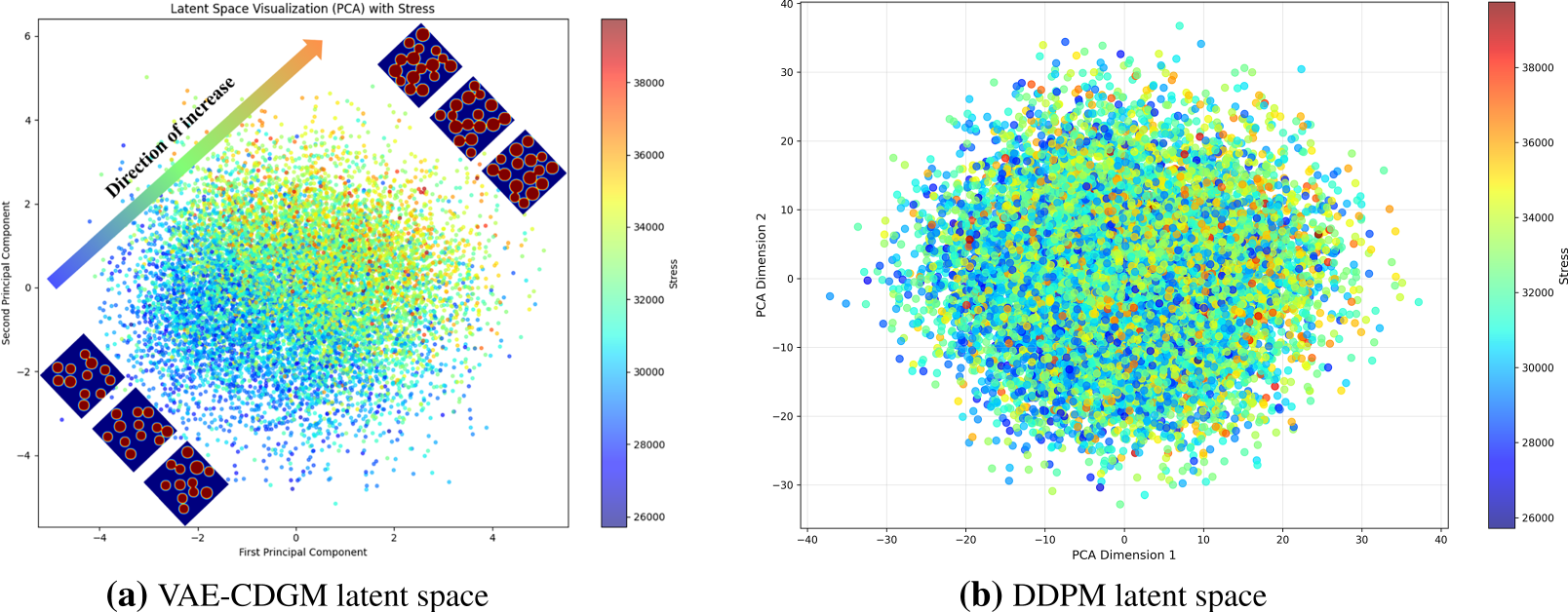
Figure 8: Distribution characteristics of composite materials in (a) VAE-CDGM latent space and (b) DDPM latent space

4  Inverse Design of Composites Based on Bayesian Optimization

4.1 Introduction to Bayesian Optimization

Bayesian Optimization (BO) represents an efficient global optimization methodology that constructs a probabilistic surrogate model of the target function and leverages an acquisition function to guide the search process, thereby significantly reducing the number of evaluations required for parameter optimization. In the realm of materials science, BO has been extensively adopted for inverse design applications [36–40].

The primary objective of Bayesian optimization is to identify the global optimum of a target function f(x) within its defined domain X, where f(x) typically represents a computationally expensive black-box function lacking an analytical form or gradient information [41]. This method iteratively proceeds through two fundamental steps to achieve efficient optimization. First, a probabilistic surrogate model is constructed based on existing observational data D={(xi,f(xi))}i=1n, with the Gaussian Process (GP) being the most commonly employed choice due to its ability to quantify uncertainty [42]. The GP assumes that the target function follows a multivariate normal distribution, where the kernel function governs the smoothness and correlation structure of the function across the domain. Given the observational data, the GP yields a posterior distribution over f(x), expressed as p(f(x)|D)∼N(μ(x),σ2(x)), where μ(x) and σ2(x) are the predictive mean and variance, respectively, computed from the kernel function and data, providing a comprehensive characterization of the function’s uncertainty and expected behavior. Second, an acquisition function α(x) is utilized to select the next evaluation point, strategically balancing exploration, sampling regions with high uncertainty, and exploitation, sampling regions with high predicted function values to accelerate convergence toward the optimum.

The Expected Improvement (EI) acquisition function stands as a widely adopted choice in Bayesian optimization, renowned for its effective balance between exploration and exploitation [43,44]. EI quantifies the anticipated improvement in the objective function f(x) at a given point x, defined as:

αEI(x)=E[max(0,f(x)−f(x∗))],(21)

where f(x∗) denotes the current best-known function value. Assuming a Gaussian Process (GP) posterior distribution f(x)∼N(μ(x),σ2(x)), EI can be computed analytically as:

αEI(x)=(μ(x)−f(x∗))Φ(z)+σ(x)ϕ(z),(22)

where z=μ(x)−f(x∗)σ(x) and Φ(z) and ϕ(z) represent the cumulative distribution function and probability density function of the standard normal distribution, respectively. The first term promotes exploitation by favoring points with high predicted values, while the second term encourages exploration by prioritizing regions with significant uncertainty. Each iteration of the Bayesian optimization loop selects the next point by maximizing the acquisition function:

xnext=argmaxx∈XαEI(x)(23)

This process iterates iteratively until the predetermined number of evaluations or convergence conditions are reached. However, the computational complexity of GP regression, coupled with the sparsity of data in high-dimensional spaces, poses significant challenges, typically constraining its effectiveness to low-dimensional problems (d≤20).

To address these limitations, the proposed VAE-CDGM model integrates the low-dimensional representation capabilities of VAE with the high-fidelity image generation prowess of DDPM, enabling the generation of detailed microstructures for composite materials while maintaining an efficient latent space. Theoretically, the model’s capacity to produce high-quality microstructure images from low-dimensional latent spaces (<20 dimensions) suggests that Bayesian optimization can be directly applied to such spaces to efficiently search for microstructures with target mechanical performance. Nevertheless, to reconcile the practical trade-offs among representational completeness, computational efficiency, and optimization robustness, we devised two tailored optimization strategies. For high-dimensional latent spaces (dimensionality > 20), we conducted SHAP analysis using a fully connected neural network (FCN) to quantify feature importance, subsequently selecting the top 16 most influential dimensions according to their mean absolute SHAP values. This dimension reduction ensures that Bayesian optimization, guided by the EI acquisition function, operates within a compact yet informative subspace, enhancing convergence speed and robustness. Conversely, for low-dimensional latent spaces (<20 dimensions), the VAE-CDGM model provides a concise representation, enabling direct Bayesian optimization without further reduction. By proposing this dual-strategy framework, we address the distinct computational and representational demands of high- and low-dimensional latent spaces, harnessing the VAE-CDGM to facilitate efficient and robust inverse design of composite microstructures.

4.2 Bayesian Optimization under 256 Dimensional Latent Space

The VAE-CDGM framework employs a decoupled training strategy for its VAE and DDPM components, which enhances compatibility with pre-trained VAE models across diverse tasks. This architecture offers significant flexibility by enabling the integration of existing VAEs without requiring computationally expensive retraining. However, when merging pre-trained VAEs for design tasks, especially those with high-dimensional latent spaces where retraining is prohibitively costly, a critical challenge is the efficient optimization of targets in such high-dimensional spaces. This challenge is further compounded by stringent requirements for reconstruction fidelity of VAE or the need to model intricate high-order statistical correlations. However, direct optimization in such high-dimensional spaces introduces substantial challenges. To mitigate these issues, we employed SHAP [45] sensitivity analysis to identify the 16 most influential dimensions based on mean absolute SHAP values, enabling Bayesian optimization to operate within a compact yet information-rich subspace that preserves critical features while significantly reducing computational overhead.

To perform sensitivity analysis and identify critical latent features governing mechanical properties, we first developed a surrogate mapping model between the latent space and material performance. This approach is fundamentally similar to CNN-based methods [46,47], which also operate by extracting abstract low-dimensional features from high-dimensional images and then mapping them to physical properties via a fully connected neural network. In the present study, the VAE encoder replaces the CNN as the feature extractor. Specifically, we constructed a FCN to predict homogenized stress from 256-dimensional latent vectors. The network architecture comprised an input layer (256 dimensions), followed by hidden layers with dimensions of 512, 256, 128, and 64, each employing ReLU activation functions, and a final single-output linear layer. The model was trained on a dataset of 11,893 samples, randomly partitioned into an 80% training set (9514 samples) and a 20% validation set (2379 samples). Training was performed using the Adam optimizer with a learning rate of 0.001 and mean squared error (MSE) loss. The selection of the above hyperparameters was determined through ablation experiments and trial and error. Meanwhile, we added dropout layers (p = 0.1) after each hidden layer. Early stopping was enforced with a patience of 10 epochs and a minimum validation improvement of Δ=0.001. Under this protocol, the model achieves R2=0.97 on the training set and R2=0.69 on the validation set after convergence, as shown in Fig. 9. The significant discrepancy between the training and validation performance indicates a degree of overfitting. Nonetheless, the model is still able to identify correlations between latent features and mechanical properties, which serves as a reasonable reference for subspace dimensionality reduction [22]. Therefore, in this study, we directly utilized the 16 relatively important features identified through SHAP analysis, without further expanding the dataset for training.

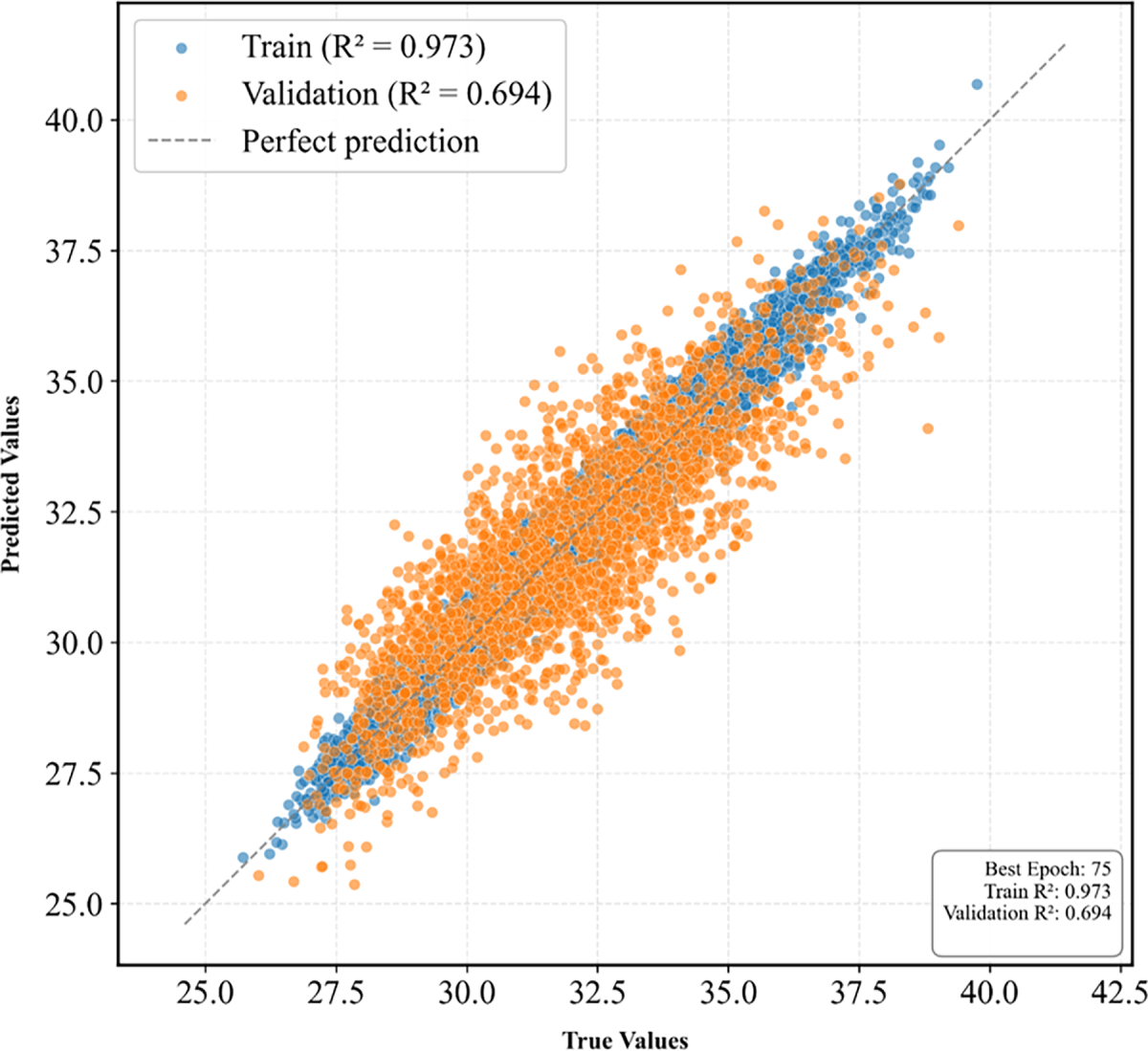
Figure 9: Performance of the surrogate model on the training and testing sets

To identify the latent dimensions most critical for homogenized stress prediction, we conducted a comprehensive sensitivity analysis using SHAP implemented through the DeepExplainer. SHAP is a framework rooted in cooperative game theory, specifically the Shapley Value, which aims to fairly allocate the prediction output for a single instance to each of its features. The SHAP value ϕi for a feature is calculated according to the following equation:

ϕi=∑S⊆N/{i}|S|!(|N|−|S|−1)!|N|![f(S∪{i})−f(S)],(24)

here, N is the set of all features, S is a subset of features excluding i, and f(S) is the model’s prediction using the subset of features S. This formula evaluates the marginal contribution of feature i across all possible subsets of features, weighted by the number of ways each subset can be formed.

This approach quantitatively evaluated the contribution of each latent dimension to the predictions generated by our FCN by computing SHAP values. The mean absolute SHAP values were ranked, and the top 16 dimensions were selected, as they captured the majority of the predictive influence. To ensure the stability and reliability of the SHAP analysis, this study performed multiple random splits of the dataset (3 splits × 2 repeats, resulting in 6 independent subdatasets) for comprehensive validation. The top 16 important features remained identical across all 6 independent analyses, as shown in Fig. 10. Furthermore, all 16 features exhibit coefficient of variation (CV) values below 0.1, confirming that each feature’s importance remains highly stable under data resampling. The most influential feature is Feature 34, as indicated by its highest mean SHAP value. Through SHAP dependency analysis, this study systematically investigated the influence mechanisms of different latent dimension features on the prediction of homogenized stress. Specifically, Fig. 11 presents dependency plots that reveal the relationships between the six most important latent variables and SHAP value. The results demonstrate that Feature 34 exhibits a significant negative correlation with homogenized stress. When this feature value is negative and decreases, its positive contribution to homogenized stress significantly enhances; whereas when the feature value is positive and increases, it demonstrates a substantial weakening effect on homogenized stress. Notably, Features 151, 7, 213, 47, and 38 display distinct U-shaped relationships with homogenized stress. When these feature values are below the critical value (zero), SHAP values decrease monotonically with increasing feature values, indicating a negative correlation with homogenized stress. When feature values exceed the critical threshold, SHAP values increase monotonically with feature values, transitioning to a positive correlation. Further analysis reveals that the overall influence of Features 34 and 151 is predominantly negative, while Features 213, 47, and 38 exhibit primarily positive characteristic responses. The corresponding microstructural variations resulting from systematic perturbations of these key latent dimensions are visualized in Appendix A (see Fig. A1). This quantitative feature-response relationship provides important insights for latent space-based optimization design: through targeted adjustment of specific latent dimension values, precise control of homogenized stress can be achieved, offering theoretical guidance for optimizing material performance design.

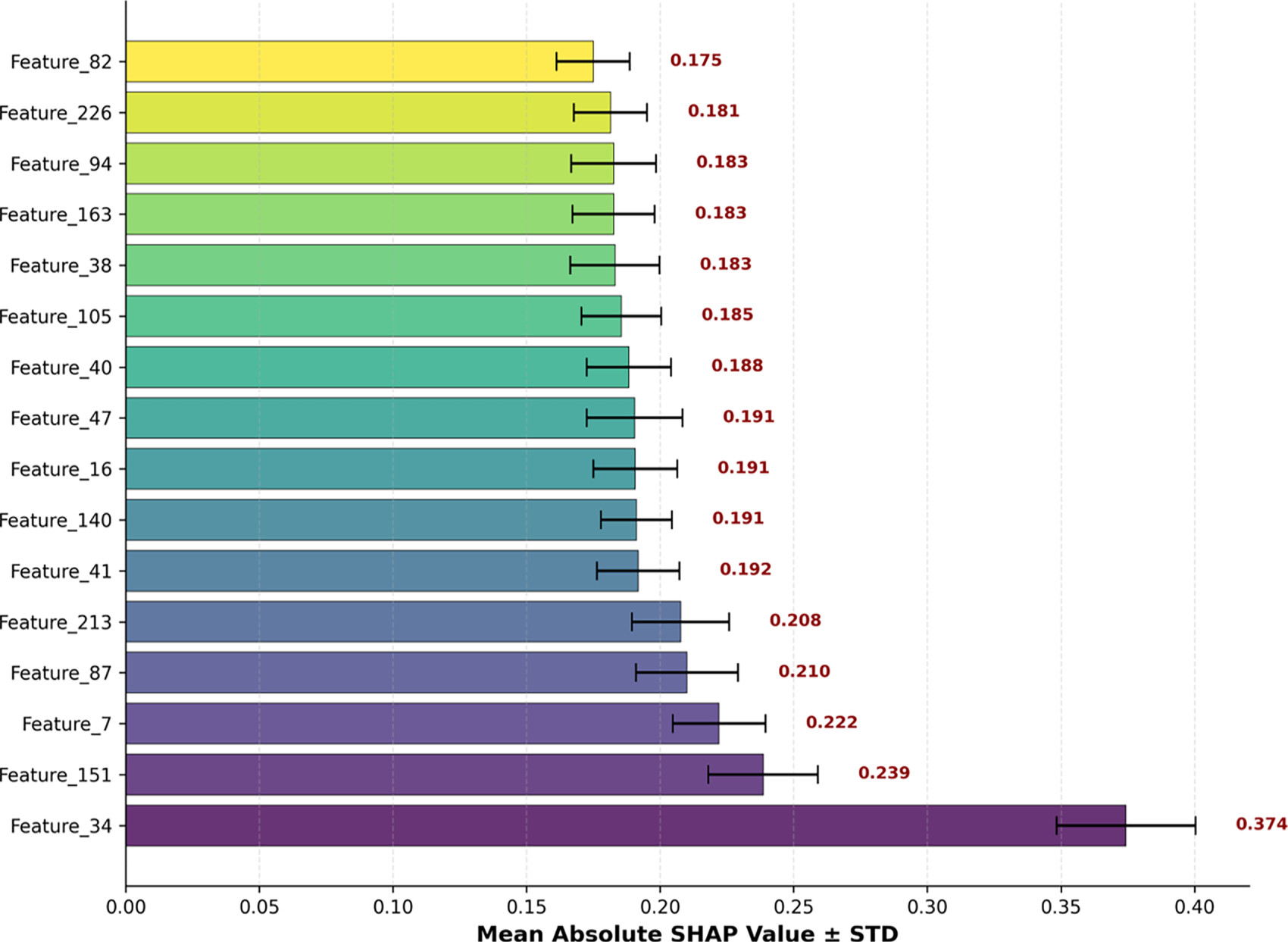
Figure 10: Top 16 feature importance ranking based on mean absolute SHAP values

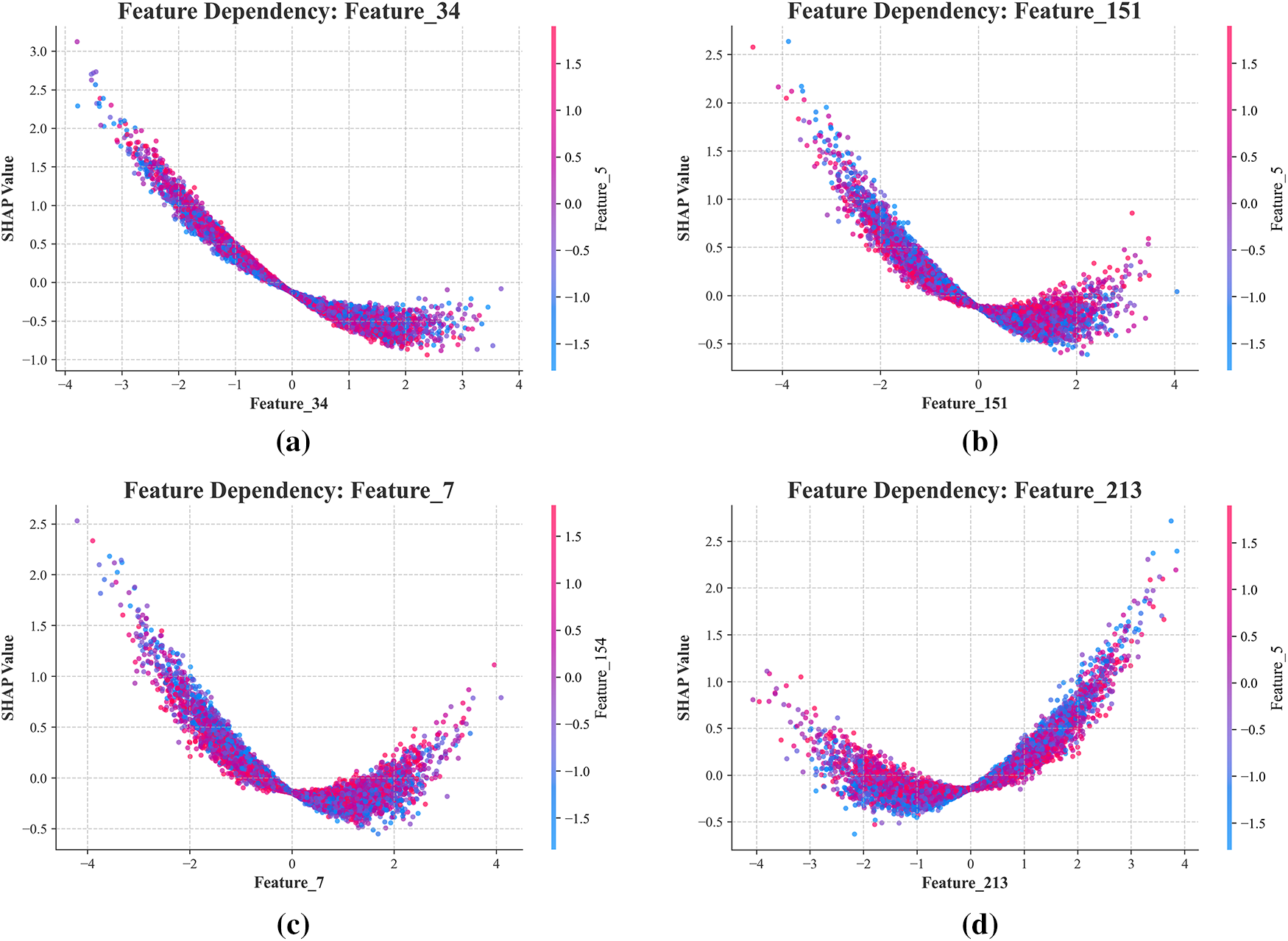
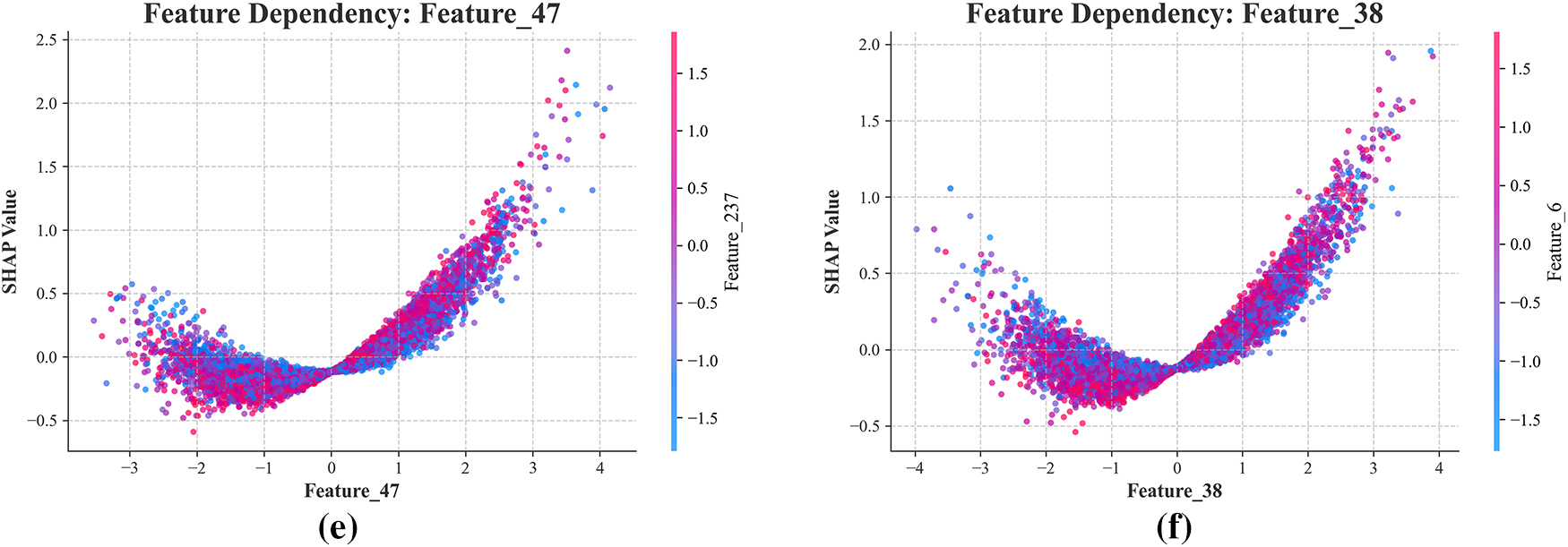
Figure 11: SHAP dependency plots for homogenized stress predictions (a) Feature 34; (b) Feature 151; (c) Feature 7; (d) Feature 213; (e) Feature 47; (f) Feature 38

Subsequently, Bayesian optimization was performed within the 16-dimensional subspace to identify latent vectors corresponding to a target homogenized stress of 4.2×104 MPa under uniaxial compression. It is noteworthy that this target value was deliberately set beyond the maximum homogenized stress of approximately 3.9×104 MPa observed in the dataset, explicitly testing the model’s capability to extrapolate beyond the known design space. Employing a Gaussian Process (GP) as the surrogate model and the EI acquisition function, the optimization iteratively navigated the subspace to maximize the likelihood of achieving the target homogenized stress. The GP was initialized with 6 random samples of latent vectors, and the EI function balanced exploration of regions with high uncertainty against exploitation of areas with elevated predicted performance. The optimization procedure maintained the remaining 240 latent dimensions as fixed parameters while actively exploring combinations within the critical 16-dimensional subspace. At each iteration, five candidate 16-dimensional vectors were generated and assembled with a fixed 240-dimensional vector to form complete latent representations, which were subsequently decoded into microstructure images by the VAE decoder. These microstructures were evaluated via finite element analysis (FEA) to determine their mechanical performance, with the results incorporated into the GP model to refine subsequent predictions. To validate the stability and reliability of the optimization process, three independent optimization trials were conducted for the same target. As depicted in Fig. 12a, the target function value, plotted as the mean homogenized stress per iteration, exhibited rapid convergence after only 4–6 iterations. During the final iteration and evaluation, the microstructure image that was blurry yet closest to the target was identified. It was then refined into a high-quality microstructure image using the VAE-CDGM model. Notably, to significantly reduce the computational cost associated with the diffusion sampling process, we employed the Denoising Diffusion Implicit Model (DDIM) during the denoising stage [48]. The microstructural changes during the iteration process are shown in Fig. 12b. Comparative analysis of the decoded microstructures presented in Fig. 13 revealed significant differences in generation quality. While VAE-produced images exhibited blurred inclusion boundaries and structural artifacts, VAE-CDGM generated microstructures with sharply defined, geometrically regular inclusions. FEA quantification of mechanical performance yielded homogenized stress of 4.19×104 MPa for VAE-generated structures and 4.10×104 MPa for VAE-CDGM-generated structures on average over three independent optimization processes, both approximating the target of 4.2×104 MPa. The slight discrepancy arises from the fundamental difference in structural fidelity. The marginally higher stress value in the VAE-generated structure is attributed to the numerous irregular, fine-scale inclusions inherent in its blurred output, which create localized stress concentrations and thereby inflate the homogenized stress. In contrast, the refinement process of VAE-CDGM eliminates these geometrical irregularities, resulting in a more uniform stress distribution and a slightly lower, yet potentially more physically realistic, homogenized stress value. Although the VAE-CDGM result showed a minor deviation, this was considered operationally acceptable given its superior microstructural fidelity, a critical factor for manufacturability. The demonstrated capability to maintain mechanical performance while significantly improving microstructure image quality highlights the practical advantage of the VAE-CDGM framework for materials design applications.

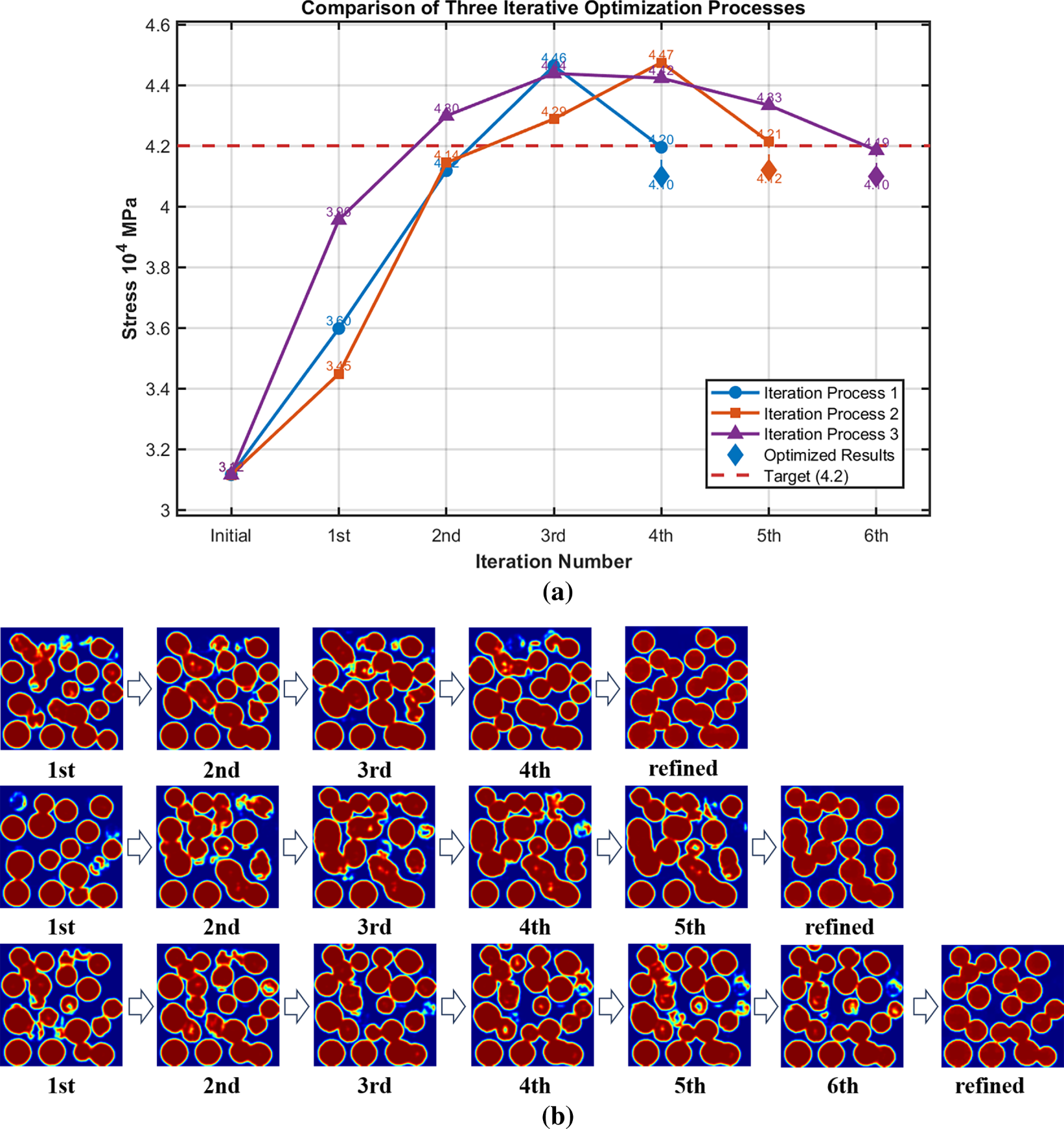
Figure 12: Bayesian optimization iteration process (a) Homogenized stress changes during the iteration process; (b) Microstructure changes during the iterative process

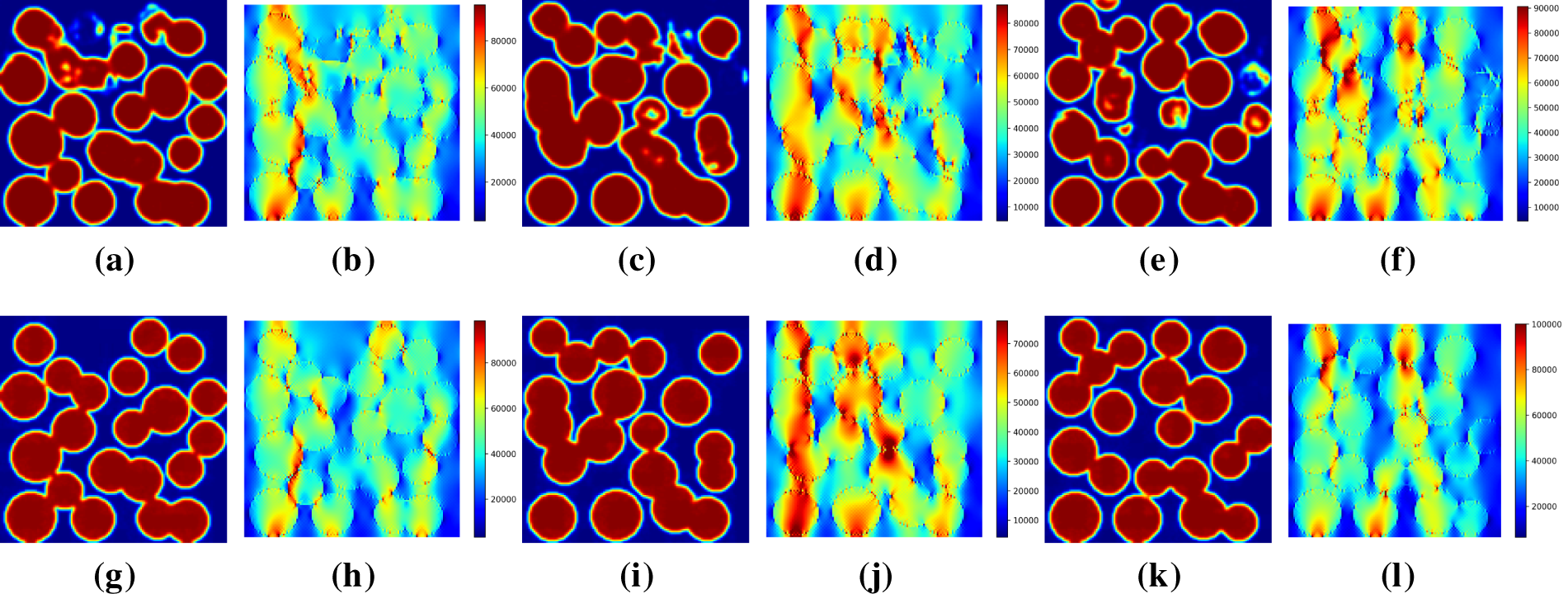
Figure 13: Bayesian optimization results: (a,c,e) VAE decoded microstructure; (b,d,f) FEM verification of VAE; (g,i,k) VAE-CDGM decoded microstructure; (h,j,l) FEM verification of VAE-CDGM

4.3 Bayesian Optimization under 16 Dimensional Latent Space

A 16-dimensional latent space is preferentially selected when computational efficiency and rapid optimization are prioritized, or when prior analyses demonstrate that a compact representation adequately captures the key microstructural features and statistical information. This latent space is derived from the VAE-CDGM model, where prior PCA visualization reveals a structured distribution characterized by distinct clusters of homogenized stress values along smooth gradients. This organized topology, coupled with the VAE-CDGM model’s capacity to generate high-fidelity microstructure images supports direct optimization without necessitating additional dimensionality reduction. A Gaussian Process (GP) surrogate model was initialized using a random sample of latent vectors from the 16-dimensional space, with the EI acquisition function guiding the search process. The EI function strategically balances exploration of regions with high predictive uncertainty and exploitation of areas with superior predicted performance, iteratively optimizing the latent vectors to achieve the target homogenized stress of 2.5×104 MPa, which was deliberately chosen to be lower than the minimum value in the dataset.

As illustrated in Fig. 14, Bayesian optimization achieved convergence to the target performance after merely 2 iterations, requiring only 10 finite element evaluations, demonstrating remarkable efficiency in the optimization process. The optimized 16-dimensional latent vector was subsequently decoded into realistic microstructure images using both the VAE and VAE-CDGM models, with the results presented in Fig. 15. The VAE-decoded images, constrained by significant information loss inherent to the 16-dimensional representation, exhibited blurred features with indistinct circular inclusions, limiting their fidelity to the target microstructure. In contrast, the VAE-CDGM-decoded images displayed enhanced clarity and detailed characteristics, including well-defined circular inclusions, reflecting its superior generative capacity. FEA quantification of mechanical performance yielded homogenized stress of 2.52×104 MPa for VAE-generated structures and 2.51×104 MPa for VAE-CDGM-generated structures on average over three independent optimization processes, both approximating the target of 2.5×104 MPa. These results underscore that, within a low-dimensional latent space (d < 20), the VAE-CDGM model not only facilitates rapid and effective Bayesian optimization but also ensures high-quality decoded microstructure images. This dual capability holds significant implications for guiding the design and manufacturing of advanced composite materials.

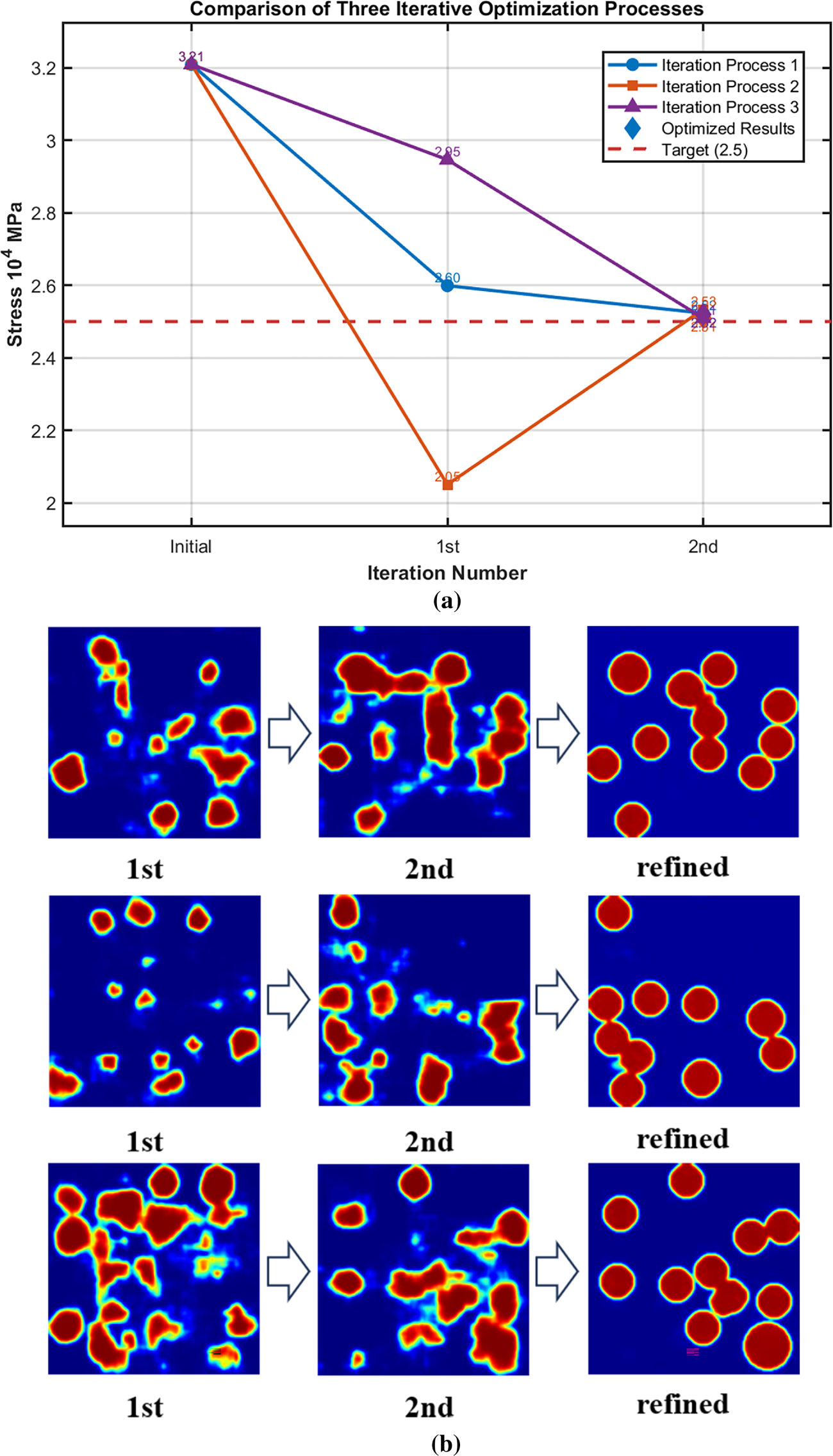
Figure 14: Bayesian optimization iteration process (a) Homogenized stress changes during the iteration process; (b) Microstructure changes during the iterative process

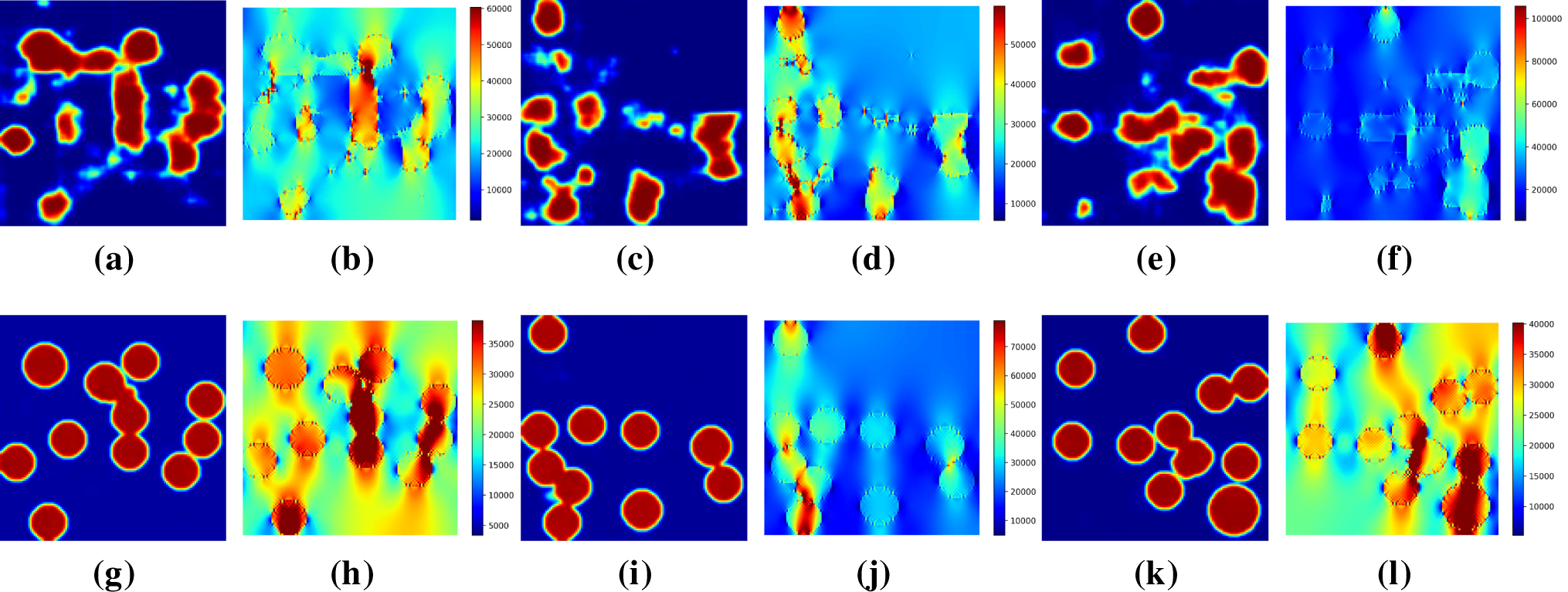
Figure 15: Bayesian optimization results: (a,c,e) VAE decoded microstructure; (b,d,f) FEM verification of VAE; (g,i,k) VAE-CDGM decoded microstructure; (h,j,l) FEM verification of VAE-CDGM

5  Conclusion

This study proposes a inverse design framework for composite materials that integrates the VAE-CDGM with Bayesian optimization. The VAE-CDGM model addresses the blurriness of VAE reconstructions while providing a continuous and differentiable latent space. Bayesian optimization, leveraging a probabilistic surrogate model and acquisition function, achieves convergence to target performance with minimal finite element evaluations. To accommodate varying dimensional requirements of the latent space, two distinct optimization strategies are introduced. For high-dimensional latent spaces, a fully connected neural network was developed to model the relationship between input features and target properties. Subsequently, SHapley Additive exPlanations (SHAP) analysis was employed to quantify the contribution of individual input features to the model’s predictions, identifying key factors influencing target performance, and Bayesian optimization was performed within the subspace defined by these critical features. For low-dimensional latent spaces, optimization was conducted directly within the design space provided by VAE-CDGM. In the case study targeting the mechanical property of composite materials, convergence to the target performance was achieved with only 2–6 iterations, corresponding to 10–30 finite element analyses, respectively. Notably, microstructures decoded by VAE-CDGM exhibited superior clarity and fidelity compared to those from VAE. Collectively, this inverse design framework achieves both high efficiency and precise microstructure reconstruction, offering an innovative and viable pathway for the inverse design of advanced materials.

It is noteworthy that in this study, while VAE-CDGM refines the blurred images generated by the VAE, it also tends to mitigate stress concentrations induced by fine inclusions present in the VAE-generated blurry images. As a result, the homogenized stress of the microstructures refined by VAE-CDGM may be slightly lower than the target stress. Although this outcome is both predictable and acceptable, future work could explore performing VAE-CDGM refinement on the decoded VAE images at each iteration to address this discrepancy. Meanwhile, while the selection of key latent dimensions through SHAP analysis enables effective integration with Bayesian optimization, it does entail a partial loss of the full latent space’s representational capacity for microstructures. Future work will explore hierarchical optimization strategies, commencing with preliminary exploration in low-dimensional spaces before progressively expanding to refined searches in higher dimensions. Additionally, the integration of Bayesian optimization with diffusion models within the latent space represents a promising direction for future research.

Acknowledgement: Not applicable.

Funding Statement: The financial support provided by National Natural Science Foundation of China (Grant No. 52478198) and Shanghai Municipal Commission of Science and Technology (Grant No. 24510711500) is greatly appreciated.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, methodology and writing—original draft preparation: Xianrui Lyu; supervision, funding acquisition and writing—review and editing: Xiaodan Ren. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A

To elucidate the physical significance of the SHAP-identified latent features, we conducted a systematic sensitivity analysis by perturbing individual dimensions while holding others constant. The procedure was as follows: a baseline latent vector was first randomly sampled from the latent space to serve as the origin. For each of the 16 SHAP-ranked dimensions, we generated a sequence of seven latent vectors by varying the target coordinate in increments of 0.5, spanning the range Δ=[−1.5,−1.0,−0.5,0,+0.5,+1.0,+1.5], while keeping all other coordinates fixed at their baseline values. These perturbed latent vectors were subsequently decoded using the trained VAE to reconstruct the corresponding microstructural images, thereby enabling a direct visualization of how variation in each latent dimension influences microstructural morphology.

The results demonstrate a remarkable consistency with the SHAP-based sensitivity analysis. As illustrated in Fig. A1a, an increase in the value of Feature 34 leads to a pronounced reduction in the volume fraction of circular inclusions, which also become more sparsely distributed. Conversely, a decrease in Feature 34 results in a substantial increase in inclusion volume fraction. It is worth noting that while variations in Feature 34 also induce other microstructural changes (e.g., inclusion arrangement), the alteration in volume fraction is the most visually salient effect. This visualization directly validates the negative correlation between Feature 34 identified by the SHAP analysis and homogenized stress.

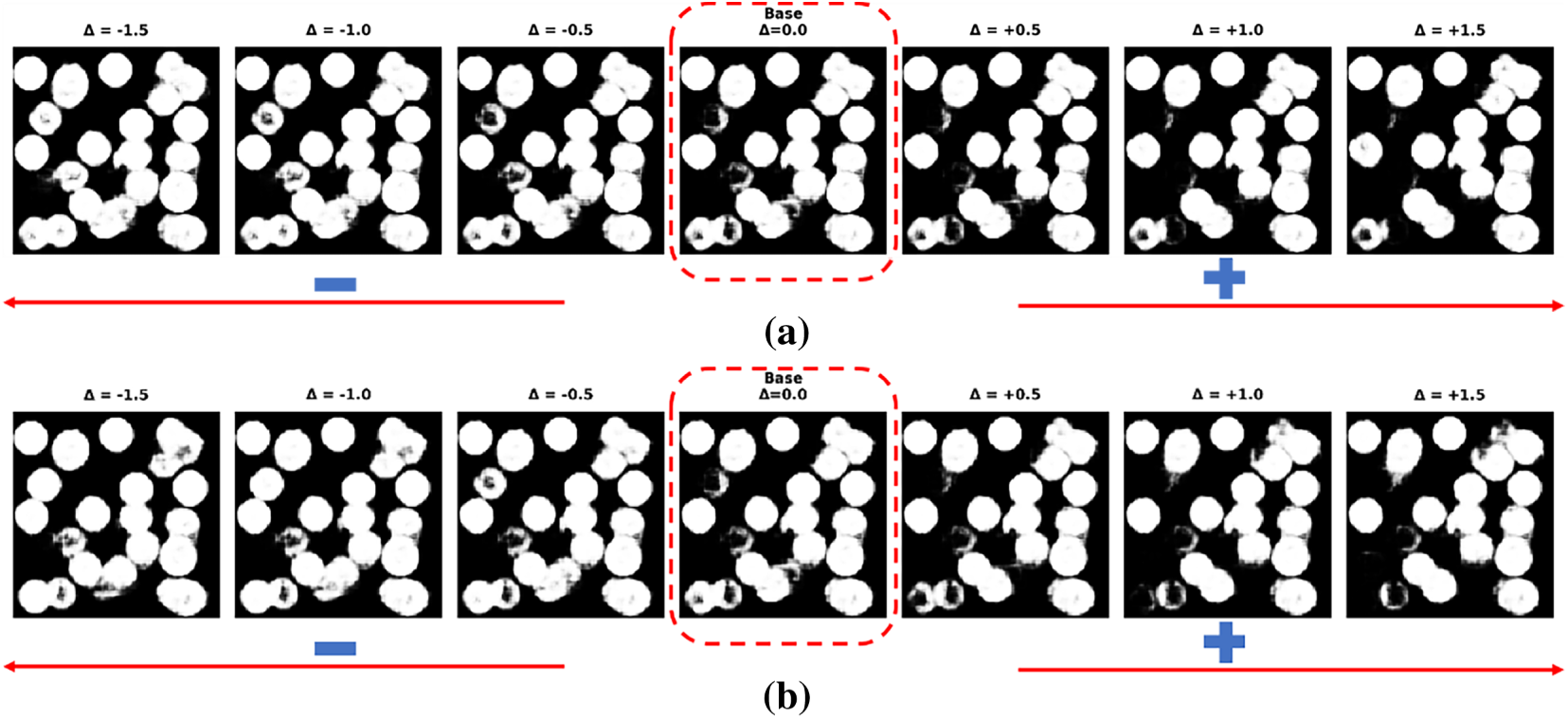
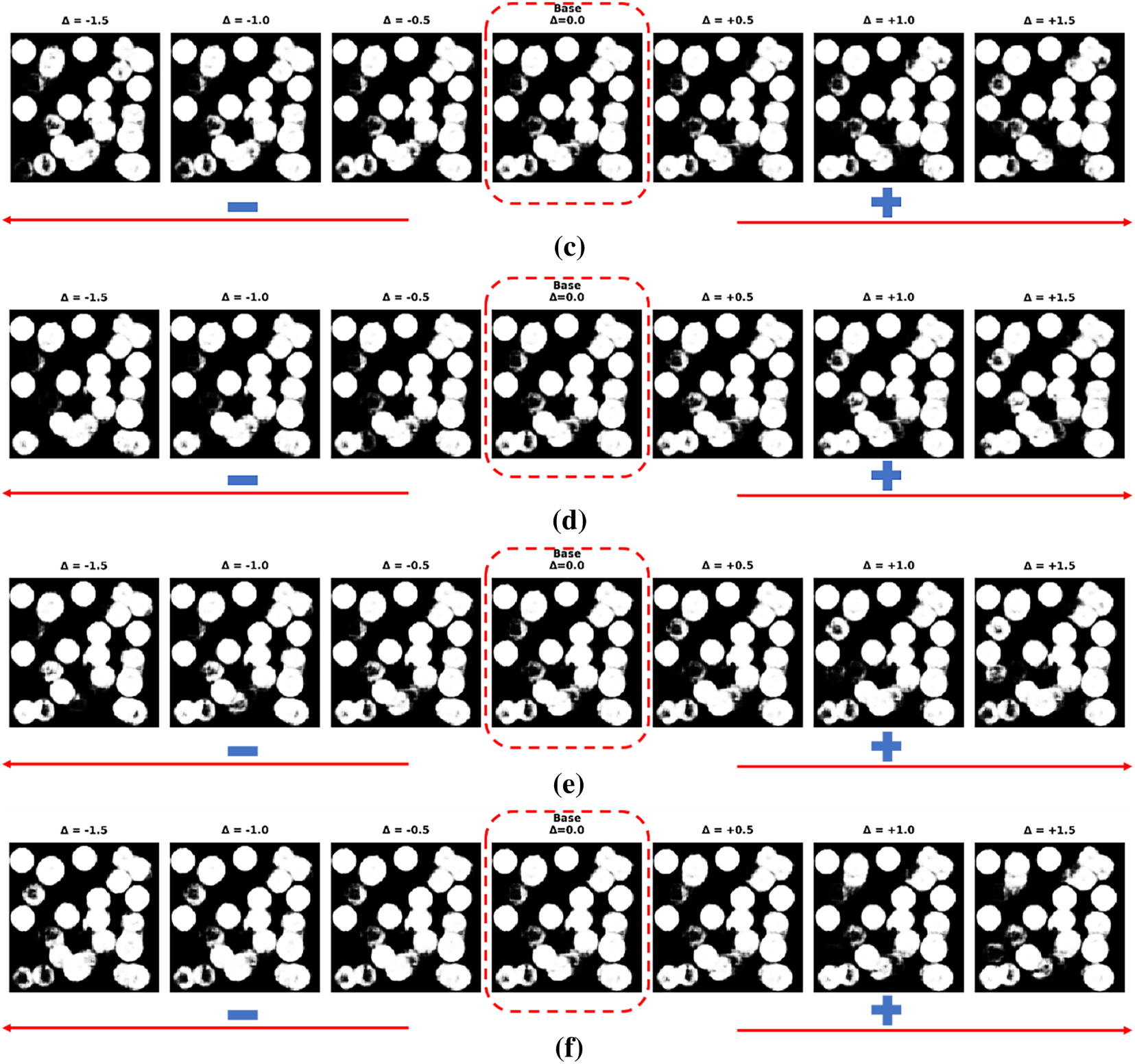
Figure A1: Microstructural evolution induced by variations in latent features identified through SHAP analysis (a) Effect of Features 34 variation on microstructure; (b) Effect of Features 151 variation on microstructure; (c) Effect of Features 7 variation on microstructure; (d) Effect of Features 213 variation on microstructure; (e) Effect of Features 47 variation on microstructure; (f) Effect of Features 38 variation on microstructure

Similarly, as shown in Fig. A1d, an increase in Feature 213 leads to a marked increase in the volume fraction of inclusions, which aligns perfectly with the positive correlation identified by the SHAP analysis. These findings confirm that the latent representations learned by the VAE encapsulate physically interpretable microstructural characteristics, and that the SHAP-identified dimensions correspond to meaningful geometric controls. The strong agreement between the perturbation-based visualizations and the SHAP dependency plots validates the reliability of the interpretability framework and underscores the utility of the latent space for guiding microstructure-sensitive design.

References

1. Barile C, Casavola C, De Cillis F. Mechanical comparison of new composite materials for aerospace applications. Compos Part B Eng. 2019;162:122–8. doi:10.1016/j.compositesb.2018.10.101. [Google Scholar] [CrossRef]

2. Cheng P, Peng Y, Li S, Rao Y, Le Duigou A, Wang K, et al. 3D printed continuous fiber reinforced composite lightweight structures: a review and outlook. Compos Part B Eng. 2023;250:110450. doi:10.1016/j.compositesb.2022.110450. [Google Scholar] [CrossRef]

3. Jiao JK, Cheng XY, Wang JL, Sheng LY, Zhang YM, Xu JH, et al. A review of research progress on machining carbon fiber-reinforced composites with lasers. Micromachines. 2023;14(1):24. doi:10.3390/mi14010024. [Google Scholar] [PubMed] [CrossRef]

4. Li J, Durandet Y, Huang X, Sun G, Ruan D. Additively manufactured fiber-reinforced composites: a review of mechanical behavior and opportunities. J Mater Sci Technol. 2022;119:219–44. doi:10.1016/j.jmst.2021.11.063. [Google Scholar] [CrossRef]

5. Brockenbrough JR, Suresh S, Wienecke HA. Deformation of metal-matrix composites with continuous fibers: geometrical effects of fiber distribution and shape. Acta Metall Mater. 1991;39(5):735–52. doi:10.1016/0956-7151(91)90274-5. [Google Scholar] [CrossRef]

6. Christman T, Needleman A, Suresh S. An experimental and numerical study of deformation in metal-ceramic composites. Acta Metall. 1989;37(11):3029–50. doi:10.1016/0001-6160(89)90339-8. [Google Scholar] [CrossRef]

7. Mishnaevsky JL. Computational mesomechanics of composites. Hoboken, NJ, USA: John Wiley & Sons, Ltd.; 2008. [Google Scholar]

8. Liu C, Zhang X, Liu X, Yang Q. Mechanical field guiding structure design strategy for meta-fiber reinforced hydrogel composites by deep learning. Adv Sci. 2024;11(22):2310141. doi:10.1002/advs.202310141. [Google Scholar] [PubMed] [CrossRef]

9. Bostanabad R, Zhang Y, Li X, Kearney T, Brinson LC, Apley DW, et al. Computational microstructure characterization and reconstruction: review of the state-of-the-art techniques. Prog Mater Sci. 2018;95(4):1–41. doi:10.1016/j.pmatsci.2018.01.005. [Google Scholar] [CrossRef]

10. Torquato SA, Haslach JHW. Random heterogeneous materials: microstructure and macroscopic properties. Appl Mech Rev. 2002;55(4):B62–3. doi:10.1115/1.1483342. [Google Scholar] [CrossRef]

11. Kenney B, Valdmanis M, Baker C, Pharoah JG, Karan K. Computation of TPB length, surface area and pore size from numerical reconstruction of composite solid oxide fuel cell electrodes. J Power Sources. 2009;189(2):1051–9. doi:10.1016/j.jpowsour.2008.12.145. [Google Scholar] [CrossRef]

12. Pattan PC, Mytri V, Hiremath P. Classification of cast iron based on graphite grain morphology using neural network approach. In: SPIE—the international society for optical engineering. Washington, DC, USA: SPIE; 2010. 75462S p. [Google Scholar]

13. Tewari A, Gokhale AM. Nearest-neighbor distances between particles of finite size in three-dimensional uniform random microstructures. Mater Sci Eng A. 2004;385(1–2):332–41. doi:10.1016/j.msea.2004.06.049. [Google Scholar] [CrossRef]

14. Xu H, Li Y, Brinson C, Chen W. A descriptor-based design methodology for developing heterogeneous microstructural materials system. J Mech Des. 2014;136(5):051007. doi:10.1115/1.4026649. [Google Scholar] [CrossRef]

15. Goodfellow IJ, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial networks. arXiv:1406.2661. 2014. [Google Scholar]

16. Kingma DP, Welling M. Auto-encoding variational bayes. arXiv:1312.6114. 2013. [Google Scholar]

17. Cang R, Li H, Yao H, Jiao Y, Ren Y. Improving direct physical properties prediction of heterogeneous materials from imaging data via convolutional neural network and a morphology-aware generative model. Comput Mater Sci. 2018;150(1):212–21. doi:10.1016/j.commatsci.2018.03.074. [Google Scholar] [CrossRef]

18. Sardeshmukh A, Reddy S, Gautham B, Bhattacharyya P. Material microstructure design using VAE-regression with multimodal prior. arXiv:2402.17806. 2024. [Google Scholar]

19. Zhang Y, Seibert P, Otto A, Raßloff A, Ambati M, Kästner M. DA-VEGAN: differentiably augmenting VAE-GAN for microstructure reconstruction from extremely small data sets. Comput Mater Sci. 2024;232(1):112661. doi:10.1016/j.commatsci.2023.112661. [Google Scholar] [CrossRef]

20. Wang L, Chan YC, Ahmed F, Liu Z, Zhu P, Chen W. Deep generative modeling for mechanistic-based learning and design of metamaterial systems. Comput Methods Appl Mech Eng. 2020;372:113377. doi:10.1016/j.cma.2020.113377. [Google Scholar] [CrossRef]

21. Lew AJ, Buehler MJ. Encoding and exploring latent design space of optimal material structures via a VAE-LSTM model. Forces Mech. 2021;5:100054. doi:10.1016/j.finmec.2021.100054. [Google Scholar] [CrossRef]

22. Kusampudi N, Diehl M. Inverse design of dual-phase steel microstructures using generative machine learning model and Bayesian optimization. Int J Plast. 2023;171:103776. doi:10.1016/j.ijplas.2023.103776. [Google Scholar] [CrossRef]

23. Xue T, Wallin TJ, Menguc Y, Adriaenssens S, Chiaramonte M. Machine learning generative models for automatic design of multi-material 3D printed composite solids. Extrem Mech Lett. 2020;41:100992. doi:10.1016/j.eml.2020.100992. [Google Scholar] [CrossRef]

24. Sun H, Wang X, Li J, Li Z, Guan Z. Efficient property-oriented design of composite layups via controllable latent features using generative VAE. Compos Sci Technol. 2025;259:110936. doi:10.1016/j.compscitech.2024.110936. [Google Scholar] [CrossRef]

25. Park SM, Yoon HG, Lee DB, Choi JW, Kwon HY, Won C. Optimization of physical quantities in the autoencoder latent space. Sci Rep. 2022;12(1):9003. doi:10.1038/s41598-022-13007-5. [Google Scholar] [PubMed] [CrossRef]

26. Prince SJD. Understanding deep learning. Cambridge, MA, USA: MIT Press; 2023. [Google Scholar]

27. Peng B, Wei Y, Qin Y, Dai J, Li Y, Liu A, et al. Machine learning-enabled constrained multi-objective design of architected materials. Nat Commun. 2023;14(1):6630. doi:10.1038/s41467-023-42415-y. [Google Scholar] [PubMed] [CrossRef]

28. Lyu X, Ren X. Variational autoencoder guided conditional diffusion generative model for material microstructure reconstruction and inverse design. Mater Today Commun. 2025;48(1):113087. doi:10.1016/j.mtcomm.2025.113087. [Google Scholar] [CrossRef]

29. Michelucci U. An introduction to autoencoders. arXiv:2201.03898. 2022. [Google Scholar]

30. Sohl-Dickstein J, Weiss EA, Maheswaranathan N, Ganguli S. Deep unsupervised learning using nonequilibrium thermodynamics. arXiv:1503.03585. 2015. [Google Scholar]

31. Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models. arXiv:2006.11239. 2020. [Google Scholar]

32. Düreth C, Seibert P, Rücker D, Handford S, Kästner M, Gude M. Conditional diffusion-based microstructure reconstruction. Mater Today Commun. 2023;35:105608. doi:10.1016/j.mtcomm.2023.105608. [Google Scholar] [CrossRef]

33. Lyu X, Ren X. Microstructure reconstruction of 2D/3D random materials via diffusion-based deep generative models. Sci Rep. 2024;14(1):5041. doi:10.1038/s41598-024-54861-9. [Google Scholar] [PubMed] [CrossRef]

34. Vlassis NN, Sun W. Denoising diffusion algorithm for inverse design of microstructures with fine-tuned nonlinear material properties. Comput Methods Appl Mech Eng. 2023;413(1):116126. doi:10.1016/j.cma.2023.116126. [Google Scholar] [CrossRef]

35. Pandey K, Mukherjee A, Rai P, Kumar A. DiffuseVAE: efficient, controllable and high-fidelity generation from low-dimensional latents. arXiv:2201.00308. 2022. [Google Scholar]

36. Honarmandi P, Attari V, Arroyave R. Accelerated materials design using batch Bayesian optimization: a case study for solving the inverse problem from materials microstructure to process specification. Comput Mater Sci. 2022;210(1):111417. doi:10.1016/j.commatsci.2022.111417. [Google Scholar] [CrossRef]

37. Matsuda Y, Ookawara S, Yasuda T, Yoshikawa S, Matsumoto H. Framework for discovering porous materials: structural hybridization and Bayesian optimization of conditional generative adversarial network. Digit Chem Eng. 2022;5:100058. doi:10.1016/j.dche.2022.100058. [Google Scholar] [CrossRef]

38. Shahriari B, Swersky K, Wang Z, Adams RP, de Freitas N. Taking the human out of the loop: a review of bayesian optimization. Proc IEEE. 2016;104(1):148–75. doi:10.1109/jproc.2015.2494218. [Google Scholar] [CrossRef]

39. Zhang W, Tang M, Mu H, Yang X, Zeng X, Tuo R, et al. Inverse design of nonlinear mechanics of bio-inspired materials through interface engineering and Bayesian optimization. Extrem Mech Lett. 2025;78:102359. doi:10.1016/j.eml.2025.102359. [Google Scholar] [CrossRef]

40. Zhao Y, Altschuh P, Santoki J, Griem L, Tosato G, Selzer M, et al. Characterization of porous membranes using artificial neural networks. Acta Mater. 2023;253:118922. doi:10.1016/j.actamat.2023.118922. [Google Scholar] [CrossRef]

41. Wang X, Jin Y, Schmitt S, Olhofer M. Recent advances in Bayesian optimization. arXiv:2206.03301. 2022. [Google Scholar]

42. Rasmussen CE. Gaussian processes in machine learning. In: Advanced lectures on machine learning. Berlin/Heidelberg, Germany: Springer; 2003. p. 63–71. doi:10.1007/978-3-540-28650-9_4. [Google Scholar] [CrossRef]

43. Močkus J. On Bayesian methods for seeking the extremum. In: IFIP technical conference on optimizationtechniques. Berlin/Heidelberg, Germany: Springer; 1974. p. 400–4. [Google Scholar]

44. Zhan D, Xing H. Expected improvement for expensive optimization: a review. J Glob Optim. 2020;78(3):507–44. doi:10.1007/s10898-020-00923-x. [Google Scholar] [CrossRef]

45. Lundberg S, Lee SI. A unified approach to interpreting model predictions. arXiv:1705.07874. 2017. [Google Scholar]

46. Kondo R, Yamakawa S, Masuoka Y, Tajima S, Asahi R. Microstructure recognition using convolutional neural networks for prediction of ionic conductivity in ceramics. Acta Mater. 2017;141:29–38. doi:10.1016/j.actamat.2017.09.004. [Google Scholar] [CrossRef]

47. Prifling B, Röding M, Townsend P, Neumann M, Schmidt V. Large-scale statistical learning for mass transport prediction in porous materials using 90,000 artificially generated microstructures. Front Mater. 2021;8:786502. doi:10.3389/fmats.2021.786502. [Google Scholar] [CrossRef]

48. Song J, Meng C, Ermon S. Denoising diffusion implicit models. arXiv:2010.02502. 2020. [Google Scholar]