Surface activity of cancer cells: The fusion of two cell aggregates

Introduction

Cancer invasion through the extracellular matrix (ECM) and the surrounding tissue is a key step in cancer progression (Clark and Vignjevic, 2015; Gandalovičová et al., 2016; Beunk et al., 2019; Kubitschke et al., 2021). Therefore, physical interactions between cells and their surroundings guide cell spreading. Cumulative effects of these interactions appear as the interplay between physical parameters such as: (1) solid stress accumulated within the aggregate core region (Kalli and Stylianopoulos, 2018), (2) tissue surface tension (Devanny et al., 2021), and (3) viscoelasticity caused by collective cell migration (CCM) (Pajic-Lijakovic and Milivojevic, 2019a; 2022). In this review, we have discussed the influence of these factors on cell rearrangement studied in the model systems such as the fusion of two cell aggregates by emphasizing the difference between epithelial and cancer cells. We have focused here on cell rearrangement caused by CCM occurring at a time scale of hours, while cell division is neglected at this time scale, because it occurs on a much longer time scale (i.e., days).

Cell migration generally involves four basic inter-connected steps: (a) protrusion, (b) adhesion, (c) contraction, and (d) retraction (Etienne-Manneville, 2013). The prerequisite of cell movement is the formation of leading-edge protrusions. Gupta and Yap (2021) revealed different ways by which adherens junctions promote the locomotion of cells within tissues: through protrusions and contraction of the junctions. Small G proteins of the Rho family regulate cell movement by promoting protrusion and stimulating adhesion (Etienne-Manneville, 2013). Cell movement is associated with the generation of the polarization flux caused by the rearrangement of already polymerized actin filaments driven by the ATP-consuming force (Yamada and Sixt, 2019). Microtubules and intermediate filaments also contribute to cell contractions and directional cell movement, besides actin rearrangement Cell contractions result in cytoskeleton deformation which provokes the response of nucleus by influencing gene expression and signaling (Barriga and Mayor, 2019). The coordinated movement of groups of cells with respect to the surrounding tissue is often guided by short- or long-range signaling (Blanchard et al., 2019). Gene expression induces a time delay in cell response to various mechanical and biochemical stimulus. This time delay might be relevant for cell coupling because what cells acquire in real-time is the information of surrounding cells some time ago. Often, in the gene regulatory network, one gene regulator controls another, and so on. Post-translational modification, such as phosphorylation and glycosylation of membrane proteins, may only require a few minutes, whereas the synthesis of proteins and their transport can take tens of minutes (Petrungaro et al., 2019). This time scale corresponds to CCM (Pajic-Lijakovic and Milivojevic, 2019a). Warmt et al. (2021) examined the contractility of various breast cells and pointed out that MCF-10A epithelial cells show higher cortical contractility in comparison with the MDA-MB-231 and MDA-MB-436 mesenchymal cells. The dominant mechanism of the contractility of mesenchymal cells corresponds to stress fiber-mediated contractility. Rac1 enhances the stress fiber activity in MDA-MB-231 and MDA-MB-436 cells (Warmt et al., 2021). In contrast to the mesenchymal cells, increased expression of RhoA is observed in contractile MCF-10A cells, while Rac1 and Rock2 expressions were lower than in epithelial cells. Cells are capable of adapting their movement depending on the surrounding conditions by changing the strength of cell-cell and cell-matrix adhesion contacts which exerts feedback on cell contractions and persistence of cell movement.

Under stress, cell rearrangement during the fusion of two cell aggregates occurs. Besides the solid stress accumulated in the core region of the two-aggregate system, cell movement can induce additional accumulation of the residual stress depending on the viscoelasticity caused by CCM (Pajic-Lijakovic and Milivojevic, 2019a, 2020b). Solid stress represents a consequence of cell growth and compression between cell aggregate and surrounding ECM, which represents the physiological environment for cancer cells. The order of magnitude of solid stress is a few kPa (Kalli and Stylianopoulos, 2018). The solid stress in the core region of CT26 cancer cell aggregate (diameter of 240 μm) is about eight times higher than the stress at the aggregate surface under externally applied osmotic stress of 5 kPa (Dolega et al., 2017). This osmotic stress corresponds to physiological compressive stress that occurs under in vivo conditions. The maximum cell residual stress accumulation during: (1) free expansion of epithelial monolayers is 100–150 Pa (Tambe et al., 2013) and (2) rearrangement of confluent epithelial monolayers is 300 Pa (Notbohm et al., 2016). However, the accumulated stress during 3-dimensional collective migration of epithelial cells could be higher. To understand the cell rearrangement during the aggregate fusion, it is necessary to point out the cell response under various stress conditions. The compressive stress of 773 Pa is enough to suppress the movement of epithelial MCF-10A cells and tumorigenic but not metastatic MCF-7 cells (Tse et al., 2012). However, this stress enhances the movement of highly invasive 4T1, MDA-MB-231, and 67NR cells (Tse et al., 2012). Riehl et al. (2020, 2021) revealed that shear stress of 1.5 Pa stimulates movement of the MDA-MB-231 cells and reduces movement of MCF-10A epithelial cells. The response of various cell types under stress has been discussed in the context of single-cell stiffness and the level of E-cadherin in cell-cell adhesion contacts (Tse et al., 2012; Rudzka et al., 2019; Mohammed et al., 2021). Stiff cancer cells are less invasive than relatively softer ones (Rudzka et al., 2019). Mohammed et al. (2021) indicated that E-cadherin-mediated cell-cell adhesion contacts are the main cause of the reduction in MCF-10A epithelial cell movement under compressive stress.

Tissue surface tension, as the specific energy of the surface, depends on the state of cell-cell adhesion contacts and the cell contractility (Stirbat et al., 2013). Beside multicellular systems, the surface tension represents a characteristic of various soft matter systems such as: liquids and amorphous solids (Mondal et al., 2015). While epithelial cells within the aggregate establish strong E-cadherin mediated adherens junctions (AJs), cancer cells frequently establish weak cell-cell adhesion contacts and β1 integrin mediated focal adhesions (FAs) between cells and ECM which are already present within the cell aggregates (Kenny et al., 2007; Devanny et al., 2021). Consequently, the resulted surface tension of epithelial aggregates is much higher than the one of the cancer aggregates. Cell contractility significantly influences the surface tension. Epithelial cell contractions enhance the strength of AJs and cause an increase in tissue surface tension (Lin et al., 2006; Devanny et al., 2021). Migrating clusters of epithelial cells have higher tissue surface tension in comparison with resting (non-contractile) epithelial cells. However, the contractility of cancer cells, which establish integrin-mediated adhesion contacts, induces an increase in cell-cell repulsions that reduce the tissue surface tension (Devanny et al., 2021).

Based on these findings, various scenarios of cell rearrangement during the aggregate fusion can be expected depending on: (1) cell response under solid stress and (2) the magnitude of tissue surface tension. These scenarios influence the surface and volume of the two-aggregate system. Cell rearrangement, occurring via CCM, has an impact on energy storage and dissipation within a two-aggregate system (Pajic-Lijakovic and Milivojevic, 2021a). Migrating collectives have been treated as viscoelastic liquids or viscoelastic solids depending on the state of cell-cell adhesion contacts. The coordinated movement of free or weakly connected cell streams corresponds to viscoelastic liquids, while the movement of strongly connected cell clusters corresponds to viscoelastic solids (Pajic-Lijakovic and Milivojevic, 2020c, 2021a). The first mode of cell migration corresponds to a movement of cancer cells (Friedl and Alexander, 2011; Clark and Vignjevic, 2015), while the second mode corresponds to the collective migration of epithelial cells (Shellard and Mayor, 2019; Pajic-Lijakovic and Milivojevic, 2019a; 2020c).

In this review, we will discuss the interplay between tissue surface tension, solid stress and viscoelasticity caused by CCM on the cell rearrangement during the aggregate fusion based on experimental data from the literature by pointing to the difference in the spread of cancer and epithelial cells.

The Fusion of Two Cell Aggregates

The fusion of two cell aggregates caused by CCM is influenced by the interplay between tissue surface tension and solid stress accumulated within the two-aggregate system, while the CCM itself induces additional energy storage or dissipation depending on the long-time viscoelasticity occurs at a time scale of hours. The surface of the two-aggregate system in contact is expressed as (Kosztin et al., 2012): A(τ)=4πR(τ)2(1+cosθ(τ)) while the total volume is (Dechristé et al., 2018): V(τ)=2π3R(τ)3(2+3cosθ(τ)−cos3θ(τ)) (where R(τ) is the aggregate radius and θ(τ) is the fusion angle). The geometry of the two-aggregate system is presented in Fig. 1.

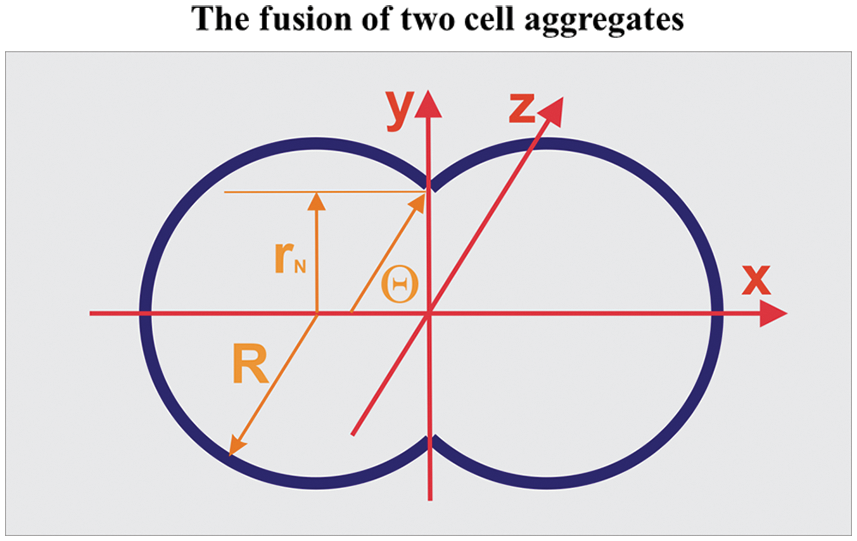
Figure 1: Geometrical characteristics of the two-aggregate systems during fusion.
The aspect ratio is equal to AR(τ) = d(τ)/2rN(τ) (where d(τ) is the longer axis equal to d(τ) = 2R(τ)(1 + cosθ) and 2r(τ) is the shorter axis of the multicellular system, while the neck radius is equal to rN(τ) = sinθ(τ)) (Dechristé et al., 2018). The two-aggregate systems during fusion are treated as canonical ensembles such that N ≈ const (where N is the total cell number), while the cell division is neglected in the time scale of hours.

The aspect ratio is equal to AR(τ)=d(τ)2rN(τ) (where d(τ) is the longer axis equal to d(τ)=2R(τ)(1+cosθ) and 2r(τ) is the shorter axis of the multicellular system, while the neck radius is equal to rN(τ)=R(τ)sinθ(τ) ) (Dechristé et al., 2018). The two-aggregate systems during fusion are treated as canonical ensembles such that N≈const (where N is the total cell number), while the cell division is neglected in the time scale of hours.

Various scenarios of cell rearrangement during the aggregate fusion

Two scenarios of cell rearrangement are possibly guided by the tissue surface tension on the one hand and the solid stress on the other asshown in Fig. 2.

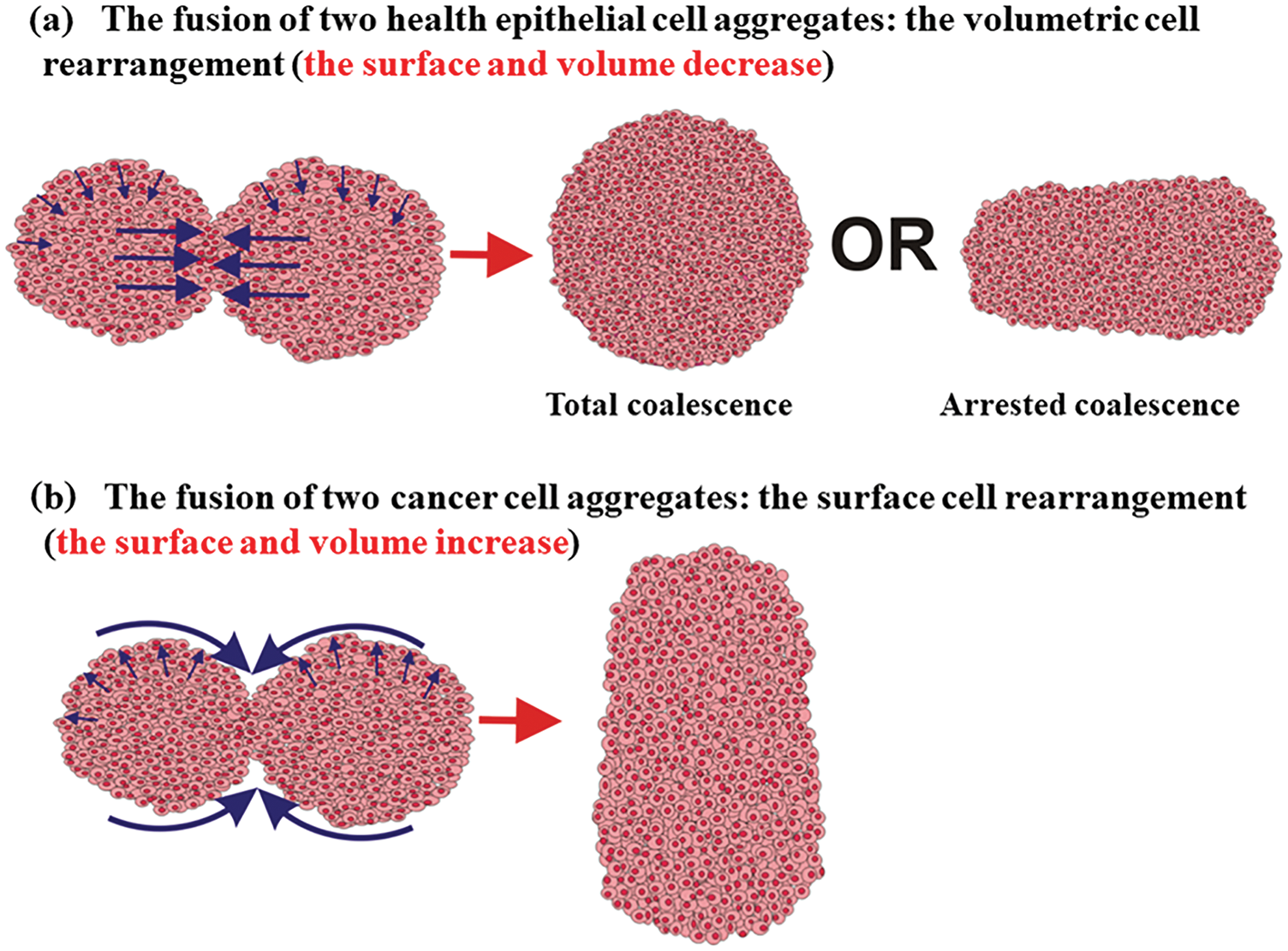
Figure 2: Two scenarios of the cell aggregate fusion were observed for epithelial and cancer mono-cultured multicellular systems.

The first scenario corresponds to a volumetric rearrangement, while the second can be treated as a surface rearrangement. Higher surface tension, which represents a characteristic of epithelial aggregates, induces cell movement from the surface to the core region of the two-aggregate system. The movement is intensive near the contact point between two cell aggregates (Fig. 2). Two volumetric velocity fronts with opposite directions are generated within a contact region to minimize the surface. Their collision induces an additional increase in the cell residual stress and can lead to the cell jamming state transition (Trepat et al., 2009; Nnetu et al., 2012, 2013; Pajic-Lijakovic and Milivojevic, 2019b; 2021a). If the cell jamming exists, it causes the arrested coalescence (Oriola et al., 2020; Grosser et al., 2021). In this case, cells perform the volumetric rearrangement which results in: (1) a decrease in surface and volume of the two-aggregate system, (2) an increase in the cell packing density accompanied by the cell residual stress accumulated in the core region of the two-aggregate system, and (3) an increase in the neck radius (Pajic-Lijakovic and Milivojevic, 2022). The corresponding cell volumetric rearrangement during the aggregate fusion can result in a total or arrested coalescence depending on the accumulated cell stress (Oriola et al., 2020; Grosser et al., 2021; Pajic-Lijakovic and Milivojevic, 2022).

Otherwise, reduced surface tension, which represents a characteristic of cancer aggregates, induces cell movement from the core region of the two-aggregate system toward its surface driven by the solid stress (Kalli and Stylianopoulos, 2018). Cell movement in this case results in: (1) an increase in the volume and surface of two-aggregate systems, (2) a decrease in the cell packing density accompanied by a decrease in the compressive residual stress in the core region of the two-aggregate system, and (3) an increase in the neck radius (Pajic-Lijakovic and Milivojevic, 2022). In contrast to the rearrangement of epithelial cells, cancer cells rather perform the surface rearrangement by avoiding the transition into a jamming state (Grosser et al., 2021).

Volumetric and surface cell rearrangement during the aggregate fusion: Various experimental systems

The rearrangement of cancer cells during the aggregate fusion has often been compared with the rearrangement of epithelial cells by considering various experimental systems (Kosztin et al., 2012; Shafiee et al., 2015; Dechristé et al., 2018; Grosser et al., 2021). Shafiee et al. (2015) considered the fusion of two confluent skin fibroblast cell aggregates and pointed 2.18 times decrease in the surface of the two-aggregate systems decreases 2.18 times, while and 2.38 times decrease in the volume within 140 h (Figs. 3a and 3b). Cells within these aggregates are in a confluent state. Consequently, the cell proliferation is neglected. The corresponding aspect ratio is AR ≈ 1.1 after 140 h which points out that the two-aggregate system reaches a nearly spherical shape.

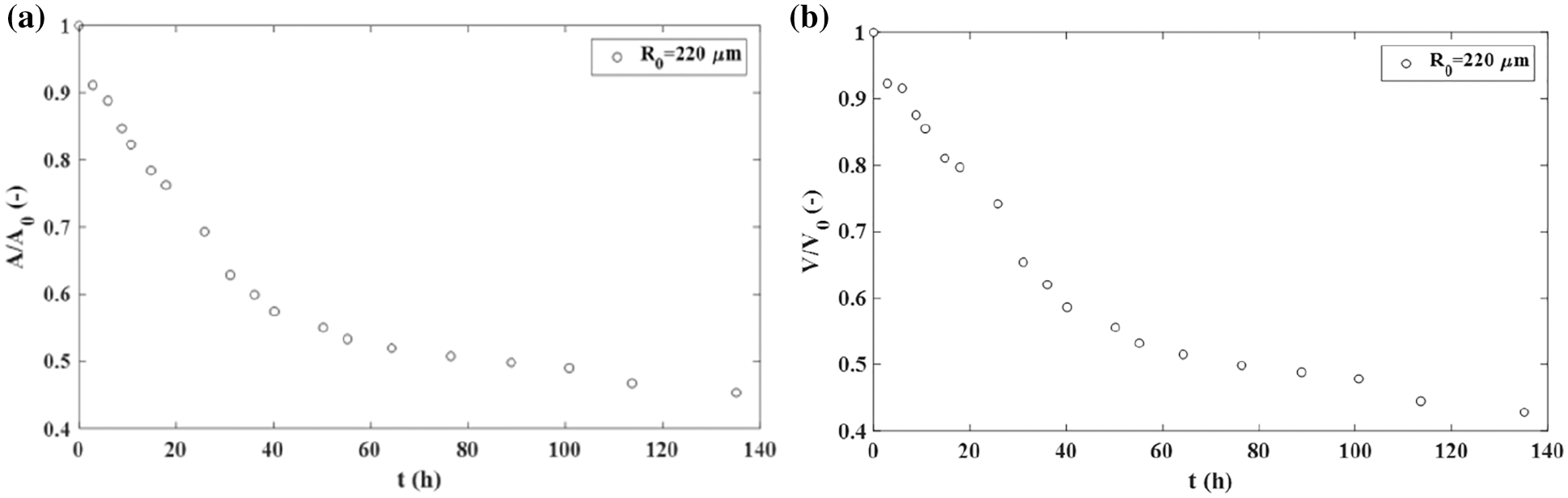
Figure 3: The fusion of two confluent skin fibroblast cell aggregates: (a) the surface of a two-aggregate system vs. time and (b) the volume of a two-aggregate system vs. time.

During the fusion process, the surface and volume relax and reach the equilibrium states. A similar result is obtained for the fusion of two MCF-10A epithelial cell aggregates (Grosser et al., 2021). The decrease in the surface of the two-aggregate system during the fusion is driven by the tissue surface tension.

However, the fusion of two cancer cell aggregates sometimes follows a quite different scenario, depending on the nature of cell-cell and cell-ECM adhesion contacts, as is shown in Fig. 2. The fusion also induces an increase in the neck radius while the surface and volume of the two-aggregate system increase by forming an irregular ellipsoidal shape. Dechristé et al. (2018) considered the fusion of two human carcinoma cell aggregates (HCT116 cell line) as a consequence of cell divisions within 70 h. The doubling time of HCT116 cells is 18 h (Gongora et al., 2008), however, the volume and surface of two-aggregate systems increase even during the first 5 h. Cancer cell divisions can be neglected within this time period, while the surface and volume changes occur primarily via CCM driven by solid stress accumulated in a core region of the two-aggregate systems (Pajic-Lijakovic and Milivojevic, 2022). The surface of two-aggregate systems increases: (1) 1.8 times for larger cancer cell aggregates (500 μm diameter) and (2) 2.3 times for smaller aggregates (300 μm diameter) within the first 5 h (Fig. 4a) (Dechristé et al., 2018). The corresponding increase in the volume of two-aggregate systems within 5 h is: (1) 1.24 times for larger aggregates and (2) 1.12 times for smaller aggregates (Fig. 4b) (Dechristé et al., 2018).

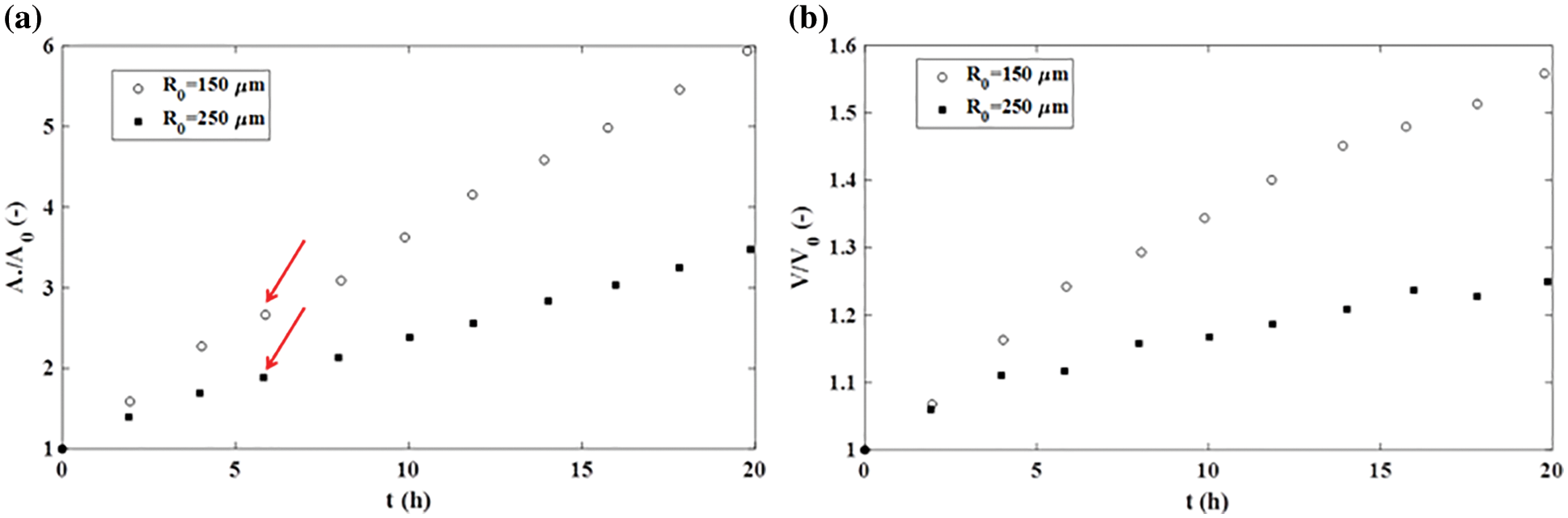
Figure 4: The fusion of HCT116 cell aggregates: (a) an increase in the surface of a two-aggregate system vs. time and (b) an increase in the volume of a two-aggregate system vs. time.

While the increase in volume is limited, an increase in the surface of two-aggregate systems is intensive and approximately linear (Fig. 4a). The aspect ratio is equal to AR ≈ 0.92 for smaller aggregates after 18 h, which corresponds to a new ellipsoidal shape. In contrast, the aspect ratio change is slower for larger aggregates and equal to AR ≈ 1.1 after 18 h (Dechristé et al., 2018). This AR is similarto the one obtained during the fusion of two confluent skin fibroblast cell aggregates which point to a similar shape of these multicellular systems. While the shapes of these systems are similar, underlying scenarios of cell rearrangement are quite different. This result revealed that the surface area of two-aggregate systems vs. time can be used as an indicator of various scenarios of cell rearrangement rather than the AR.

This result points to the surface rearrangement of cancer cells, as a dominant scenario (Pajic-Lijakovic and Milivojevic, 2022). This surface rearrangement becomes more intensive with an increase in the surface-to-volume ratio of the two-aggregate system, i.e., for smaller cell aggregates. Grosser et al. (2021) examined and compared the fusion of two breast cell aggregates such as: (1) epithelial MCF-10A cell lines and (2) cancerous mesenchymal MDA-MB-436 cells within 60 h. While MCF-10A cells underwent arrested coalescence and the average cell velocity dropped to zero, cancer cells kept their velocity approximately constant within this time period and avoided the jamming state transition. This result confirms the surface activity of cancer cells; instead of generating two opposite volumetric velocity fronts near the contact point between two aggregates, cancer cells rather undergo the surface cell rearrangement. The surface cell rearrangement occurs by generating the surface velocity fronts directed toward the contact point between the aggregates (Fig. 2).

Viscoelasticity Caused by Collective Cell Migration

Cell movement induces energy storage and energy dissipation within multicellular systems (Pajic-Lijakovic, 2021). Depending on the ratio between these two parts of energy, cell rearrangement caused by CCM has been treated as viscoelastic liquids or viscoelastic solids (Guevorkian et al., 2011; Notbohm et al., 2016; Pajic-Lijakovic and Milivojevic, 2019a; 2021a). Energy storage and dissipation depend primarily on the state of cell-cell adhesion contacts. Coordinated movement of weakly connected cell streams induces intensive energy dissipation and has been treated as viscoelastic liquids, while the movement of strongly connected cell clusters corresponds to viscoelastic solids (Pajic-Lijakovic and Milivojevic, 2020b; 2021a). Consequently, collective migration of cancer cells is treated as viscoelastic liquids, while collective migration of epithelial cells corresponds rather to viscoelastic solids. The main characteristics of viscoelasticity caused by CCM are: (1) multi-time nature and (2) inhomogeneity (Pajic-Lijakovic and Milivojevic, 2019a; 2021a). The strain and the rate of strain change due to cell migration, as well as, the cell residual stress accumulation, occur at a time scale of hours, τ (Marmottant et al., 2009; Serra-Picamal et al., 2012; Notbohm et al., 2016; Pajic-Lijakovic and Milivojevic, 2020c; 2021a). However, stress relaxation occurs on a time scale of minutes, t (Marmottant et al., 2009; Pajic-Lijakovic and Milivojevic, 2020c). Consequently, cell movement occurs within successive stress relaxation cycles of short time durations (Pajic-Lijakovic and Milivojevic, 2019a; 2020c). Inhomogeneous distributions of cell velocity and cell residual stress have been recognized during (1) free expansion of cell monolayers (Serra-Picamal et al., 2012), (2) rearrangement of confluent epithelial cell monolayers (Notbohm et al., 2016), and (3) cell aggregate rounding after uni-axial compression (Pajic-Lijakovic and Milivojevic, 2017). CCM induces the generation of stress (normal and shear). Normal stress is generated within migrating cell clusters during their movement through dense surroundings or during the collision of velocity fronts caused by uncorrelated motility (Pajic-Lijakovic and Milivojevic, 2019a; 2020b). Due to their viscoelastic nature, the shear flow of cancer cells also induces the generation of normal stress (Pajic-Lijakovic and Milivojevic, 2021a). Maximum normal and shear stresses generated during 2-dimensional CCM corresponds to 150–300 Pa (Tambe et al., 2013; Notbohm et al., 2016). Shear stress can be significant within the biointerface between migrating cell clusters and surrounding cells in the resting state (Pajic-Lijakovic and Milivojevic, 2020a).

The movement of cell streams has been modeled by the Maxwell model, suitable for viscoelastic liquids. Guevorkian et al. (2011) considered cell aggregate micropipette aspiration and experimentally confirmed the validity of this model. The forced movement of cells, in this case, induces intensive energy dissipation characteristics for the viscoelastic liquids. Otherwise, the Zener model, suitable for viscoelastic solid, has been recognized in various experimental systems such as: (1) free expansion of epithelial monolayers (Serra-Picamal et al., 2012; Pajic-Lijakovic and Milivojevic, 2020c), (2) rearrangement of confluent epithelial monolayers (Notbohm et al., 2016; Pajic-Lijakovic and Milivojevic, 2017), (3) cell aggregate uni-axial compression between parallel plates (Mombach et al., 2005; Marmottant et al., 2009; Pajic-Lijakovic and Milivojevic, 2019a; 2021a), and (4) the fusion of two epithelial cell aggregates (Pajic-Lijakovic and Milivojevic, 2022). The Zener model has been chosen based on the following findings:

Cell stress relaxes linearly under constant strain during the cell aggregate uni-axial compression between parallel plates (Marmottant et al., 2009; Pajic-Lijakovic and Milivojevic, 2019a; 2019b) and cell strain relaxes linearly under constant stress condition (Mombach et al., 2005). The stress relaxation time corresponds to a few minutes, while the strain relaxation time corresponds to a few hours (Mombach et al., 2005; Marmottant et al., 2009).

The strain rate is correlated with the rate of change in the residual stress in the cellular system during the free expansion of epithelial monolayers and the rearrangement of confluent epithelial monolayers (Serra-Picamal et al., 2012; Notbohm et al., 2016).

Volume and surface, as well as, the volumetric and surface strains can relax during the fusion of two epithelial cell aggregates (Shafiee et al., 2015; Pajic-Lijakovic and Milivojevic, 2022).

The main characteristics of the Maxwell and Zener models are shown in Table 1.

The main characteristic of the Maxwell model is that stress can relax under a constant strain rate, while the strain itself cannot relax (Pajic-Lijakovic, 2021). In contrast, to the Maxwell model, the Zener model describes strain relaxation under constant stress conditions and stress relaxation under constant strain conditions (Pajic-Lijakovic, 2021). The main characteristic of viscoelastic solids, which distinguishes them from viscoelastic liquids, is that strain can relax under constant stress (or zero stress) conditions. This condition has been satisfied for various epithelial model systems in vitro.

The Maxwell model describes elastic behavior at a short times and viscous behavior at long times (Pajic-Lijakovic, 2021). Consequently, the corresponding cell residual stress, accumulated at a long time scale, is purely dissipative (Table 1). However, the Zener model describes viscous behavior at short times and elastic behavior at long times (Pajic-Lijakovic, 2021). Consequently, the corresponding cell residual stress, accumulated at a long time scale, is reversible (elastic) (Table 1). This is the main difference between the CCM of cancer cells and the CCM of epithelial cells. In addition, while the CCM of cancer cells induces energy dissipation, the CCM of epithelial cells leads to the storage of strain energy within the two-aggregate system during the fusion process.

Accumulation of cell normal residual stress accompanied by the strain energy during CCM of epithelial cells results in an increase in cell packing density (Trepat et al., 2009). Such an increase leads to a decrease in cell mobility and can induce the jamming state transition which has been observed experimentally during the fusion of various epithelial cell aggregates (Oriola et al., 2020; Grosser et al., 2021). The corresponding reduction in cell mobility leads to a local change in the state of viscoelasticity (Nnetu et al., 2013; Pajic-Lijakovic and Milivojevic, 2021b). While the viscoelasticity caused by CCM shows linear behavior, the viscoelasticity becomes non-linear near the cell jamming (Pajic-Lijakovic, 2019b; 2021b). In contrast to epithelial cells, cancer cells perform surface rearrangement during the aggregate fusion and can avoid the jamming state transition (Grosser et al., 2021; Pajic-Lijakovic and Milivojevic, 2022).

Cell residual stress accumulation during movement of epithelial cells: The role of tissue surface tension

The tissue surface tension induces the volumetric rearrangement of epithelial cells which leads to an accumulation of cell normal residual stress, while the surface tension gradient influences the accumulation of cell shear residual stress (Pajic-Lijakovic and Milivojevic, 2021c). The normal residual stress of the epithelial cells σ~rReV is expressed as the sum of isotropic and deviatoric contributions:

σ~rReV=ΔpeI~+σ~eVd (1)

where Δpe=−γe(∇→⋅n→) is an isotropic part of the normal stress (formulated based on the Young-Laplace equation), γe is the epithelial surface tension, n→ is the normal vector to the surface and σ~eVd is the deviatoric part of the normal stress caused by the cell rearrangement, I~ is the unit tensor (Pajic-Lijakovic and Milivojevic, 2019b; 2021c). The shear residual stress σ~reS of the epithelial cells is generated by natural convection and forced convection. The natural convection is induced by the surface tension gradient established at the biointerface between migrating epithelial clusters and the surrounding epithelial cells found in a resting state, while the forced convection is caused by the CCM (Pajic-Lijakovic and Milivojevic, 2021c). This is supported by the fact that the surface tension of active (migrating) epithelial cells is larger than the surface tension of passive (resting) epithelial cells (Devanny et al., 2021). This gradient ∇→γe guides the shear flow from the regions of lower surface tension to the regions of higher surface tension, i.e., from the interface between migrating and resting epithelial cells toward the bulk of migrating epithelium. The phenomenon represents the Marangoni effect that influences the rearrangement of various soft matter systems in which the surface tension gradient is caused by a change in temperature or a change in the distribution of system constituents (Karbalaei et al., 2016). Consequently, the cell shear residual stress σ~ReS can be expressed as a sum of the natural convection contribution and forced convection contribution:

n→⋅σ~ReS⋅t→=∇→γe⋅t→+n→⋅σ~reSF⋅t→ (2)

where t→ is the tangent vector to the surface and σ~reSF is the shear stress that resulted from the forced convection, and ∇→γe is the gradient of epithelial surface tension. The generation of the shear residual stress is accompanied by the Marangoni flux expressed for the mono-cultured epithelial systems as: J→Me=kMne(r,τ)∇→γe (where kM is a parameter that measures cell mobility caused by the surface tension gradient between migrating cell clusters and surrounding cells in the resting state and ne is the packing density of epithelial cells) (Pajic-Lijakovic and Milivojevic, 2021c).

Accordingly, with the fact that the surface tension can be neglected for migrating cancer cells, the resulted cell normal stress in this case, represents only a deviatoric part. The cell shear residual stress of cancer cells arises as a product of forced convection.

The acceptable paper size is US A4 (21 cm × 29.7 cm). All margins–top (1.34 cm), bottom (0.49 cm), left (1.52 cm), and right (1.31 cm). The acceptable font is Minion Pro, 10 pt., except for writing special symbols and mathematical equations. Use 0.7 cm intend on the first line of the second paragraph.

Cell Rearrangement during the Aggregate Fusion: The Force Balance

The fusion of epithelial cell aggregates is driven by the competition between the surface tension force and the viscoelastic force, while the traction force is usually neglected. This is supported by the fact that epithelial cells within the aggregates do not establish FAs (Devanny et al., 2021). While the surface tension force tries to minimize the surface and thus induces CCM, the viscoelastic force acts to reduce the movement of the cells. The surface tension force is expressed as (Pajic-Lijakovic and Milivojevic, 2020c): neF→ste=neγeu→e (where γe is the surface tension of epithelial cells and ne is the packing density of epithelial cells). The viscoelastic force, in this case, is F→Tvee=∇→⋅(σ~eRT) (where σ~eRT is the total cell residual stress σ~eRT=σ~eRCCM+σ~eRSD , σ~eRCCM is the cell residual stress (shear σ~reS and normal σ~rReV ) accumulated during CCM (i.e., σ~eRCCM=σ~reS+σ~rReV ) and σ~eRSD is the solid stress already present in the core region of two-aggregate systems) (Murray et al., 1988; Pajic-Lijakovic and Milivojevic, 2022). The role of the viscoelastic force in reducing the movement of epithelial cells is supported by experimental findings (Tse et al., 2012; Fuhrmann et al., 2017; Riehl et al., 2020). It is necessary to emphasize that the tissue surface tension influences both forces, i.e., (1) the surface tension force and (2) the viscoelastic force by impacting the cell residual stress accumulation (see Eqs. (1) and (2)).

The competition between these two forces induces an oscillatory change in cell velocity and generated strains and stresses (normal and shear), which further leads to oscillatory changes in the neck radius between the aggregates (Pajic-Lijakovic and Milivojevic, 2022). The phenomenon represents the mechanical waves caused by CCM (Pajic-Lijakovic and Milivojevic, 2020c; 2022). The oscillatory changes in cell velocity and rheological parameters have also been observed experimentally during: (1) free expansion of epithelial cell monolayers (Serra-Picamal et al., 2012; Pajic-Lijakovic and Milivojevic, 2020c), (2) the fusion of two epithelial cell aggregates (Grosser et al., 2021; Pajic-Lijakovic and Milivojevic, 2022), and (3) the rounding of epithelial cell aggregates after uni-axial compression (Pajic-Lijakovic and Milivojevic, 2017; 2022). The corresponding force balance for the rearrangement of epithelial cells during the fusion of epithelial aggregates is expressed by modifying the model proposed by Pajic-Lijakovic and Milivojevic (2020c):

⟨m⟩ene(r,τ)Dv→e(r,τ)Dτ=neF→ste−F→Tvee (3)

where τ is the time scale of hours, ⟨m⟩e is the average mass of a single epithelial cell, v→e is the epithelial cell velocity equal to v→e(r,τ)=du→edτ , u→e is the epithelial cell displacement field, Dv→eDτ=∂v→e∂τ+(v→e⋅∇→)v→e is the material derivative (Bird et al., 1960).

While the rearrangement of epithelial cell aggregates occurs primarily through cadherin-mediated adhesion complexes, the rearrangement of cancer cell aggregates, in the majority of cases, occurs through β1 integrin-mediated adhesion complexes (Devanny et al., 2021). The volume fraction of ECM within cancer aggregates is less than 2.5% (Ivascu and Kubbies, 2006). Consequently, to account for the establishment of FAs, as the main mechanism of cancer cell rearrangement, it is necessary to include the traction force into the corresponding force balance equation. The traction force of cancer cells is equal to: ρF→trc=ρku→ECM (where k is an elastic constant of single FA, ρ is the number density of FAs, and u→ECM is the displacement field of ECM caused by the movement of cancer cells) (Murray et al., 1988). The traction force can reduce the movement of cancer cells depending on the strength of FAs (Fuhrmann et al., 2017). The surface tension force of cancer cells is much lower than the one for the epithelial cells and it can be neglected (Devanny et al., 2021). Consequently, the forces that balance the rearrangement of cancer cells during the fusion of cellular aggregates are viscoelastic force and traction force. The viscoelastic force represents a driving force of cancer cell migration and can be expressed as: F→Tvec=∇→⋅((σ~cRSD−σ~cRCCM)−σ~RECM) (where σ~cRSD is the cancer cell solid stress, while the cell residual stress caused by CCM, σ~cRCCM is the residual stress caused by the movement of cancer cells which is dissipated, and σ~RECM is the residual stress accumulated within the ECM) (Murray et al., 1988; Pajic-Lijakovic and Milivojevic, 2020c). It is in accordance with the fact that accumulated solid stress enhances the movement of cancer cells (Tse et al., 2012; Kalli and Stylianopoulos, 2018; Riehl et al., 2020). The competition between these two forces induces an oscillatory change in cell velocity and neck radius during the aggregate fusion, i.e., the mechanical waves (Grosser et al., 2021; Pajic-Lijakovic and Milivojevic, 2022). The force balance, in this case, is expressed based on the modified model proposed by Pajic-Lijakovic and Milivojevic (2020c):

⟨m⟩cnc(r,τ)Dv→c(r,τ)Dτ=F→Tvec−ρF→trc (4)

where ⟨m⟩c is the average mass of a single cancer cell, v→c is the cancer cell velocity equal to v→c(r,τ)=du→cdτ , u→c is the cancer cell displacement field, Dv→cDτ=∂v→c∂τ+(v→c⋅∇→)v→c is the material derivative (Bird et al., 1960), nc(r,τ) is the cancer cell packing density.

The change in the cell packing density occurs on a time-scale of hours, and has been expressed by Murray et al. (1988) as:

∂nk(r,τ)∂τ=−∇→⋅J→ (5)

where k≡c,e denotes the cancer and epithelium cells, J→=∑iJ→i is the flux of cells which accounts for convective and conductive contributions as well as for the haptotaxis, chemotaxis, durotaxis fluxes, as well as, the Marangoni flux (Pajic-Lijakovic and Milivojevic, 2021c) in the case of the fusion of epithelial aggregates that describe different types of cell-cell interactions (e.g., mechanical, electrostatic or chemical).

Surface Rearrangement of Cancer Cells: Modeling Consideration

The surface of a two-aggregate system of cancer cells A(τ) is equal to:

A(τ)=Ncs(τ)⟨ncs(τ)⟩−1 (6)

where Ncs(τ) is the number of cancer cells located at the surface of cell aggregate equal to Ncs(τ)=∫ncs(ℜ,τ)d2ℜ , ncs(ℜ,τ) is the local cell surface packing density, and ℜ=ℜ(x,y,z) is the coordinate of the surface. The ncs(ℜ,τ) changes during the fusion process as a product of two opposite tendencies. The tissue surface tension acts to reduce the surface. However, the cell contractility induces repulsion between cells which cannot be compensated by weak cell-cell adhesion contacts (Devanny et al., 2021). Consequently, this repulsion among cancer cells enhances cell contractility relative to the adhesion strength between cells which leads to a decrease in the surface tension of cancer cells. In order to quantify these changes, we formulated the effective surface activity of cancer cells a(ℜ,τ) , as the ratio between cell active-contractile energy and passive energy:

a(ℜ,τ)=⟨Ua⟩ℜ⟨Up⟩ℜ (7)

where ⟨Ua⟩ℜ is the local average cell active contractile energy and ⟨Up⟩ℜ is the local average cell passive energy which accounts for the single-cell elasticity and the state of cell-cell adhesion contacts. Both energetic contributions per single cell can be expressed based on the vertex model proposed by Koride et al. (2018). The average cell active contractile energy is equal to ⟨Ua⟩ℜ=1Nsℜ∑i=1NsTconi2Li2 (where Nsℜ is the number of cells within a mesoscopic surface domain, Tconi is the contractility coefficient, and Li is the perimeter of the i-th cell) (Koride et al., 2018). The average cell passive energy is equal to ⟨Up⟩ℜ=1Nsℜ[∑iNs12Ki(Ai−A0)+∑i,j⁡Λlij] (where Ki is an effective bulk modulus of the cell, A0 is the reference area of the cell while, Ai is the current area of the i-th cell, Λ is the adhesion energy per unit length, lij is the edge length between vertex i and j ) (Koride et al., 2018).

Accordingly, the change in the cell surface packing density ncs(ℜ,τ) can be expressed based on particularly formulated phase model:

dncs(ℜ,τ)dτ=Γ[δFs(ncs)δncs−kBTeffln(Xa(ℜ,τ))] (8)

where Γ is the kinetic constant and Fs is the Landau-Ginzburg surface free energy equal to Fs=∫γc(ncs)d2ℜ , γc is the surface tension of passive (non-contractile) cancer cells, kB is the Boltzmann constant, Teff is the effective temperature, and the derivative δFs(ncs)δncs is equal to δFs(ncs)δncs=limϵ→0Fs[ncs(ℜ′,τ)+ϵδ(ℜ′−ℜ)]−Fs[ncs(ℜ′,τ)]ϵ , ϵ is an increment of ℜ (Ala-Nissila et al., 2004). The concept of effective temperature has been applied for considering a rearrangement of various thermodynamic systems from glasses and sheared fluids to granular systems (Casas-Vazquez and Jou, 2003). Pajic-Lijakovic and Milivojevic (2019b; 2021a) applied this concept to a long-time rearrangement of dense cellular systems. The effective temperature, in this case, represents a product of cell mobility and is expressed as (kBTeff)1/2∼⟨|v→c|⟩ (where ⟨|v→c|⟩ is the cell average speed). The cell activity ratio is expressed as Xa(ℜ,t)=aaθ (where a is the cell activity that satisfies the condition that a≥aθ , while aθ is the activity of epithelial cells under physiological conditions). The first term of Eq. 8 accounts for the surface tension action to increase the cell surface packing density and decrease the surface (Eq. (6)), while the second term represents the result of repulsions among cancer cells caused by their contractility which lead to a decrease in the cell surface packing density and consequently, an increase in the surface.

The activity of cancer cells as well as their contractility depends on: (1) cell mobility expressed by the effective temperature, (2) cell surface packing density, and (3) the cumulative energy of AJs and FAs which is equal to FA=∑j⁡μjδ(ℜ−ℜj) (where μj is the chemical potential of the j-th adhesion contact). The change of Xa can be expressed as:

dXa(ℜ,t)dτ=(∂Xa∂Teff)ncs,FA∂Teff∂τ−(∂Xa∂ncs)Teff,FA∂ncs∂τ−(∂Xa∂FA)ncs,Teff∂FA∂τ (9)

The cell activity increases with an effective temperature, while an increase in the cell surface packing density and the strength of cell-cell adhesion contacts reduce the cell activity, as well as, the cancer cell invasiveness. An increase in ncs under a constant number of cells within the surface Ncs leads to a decrease in the surface of the two-aggregate system A(τ) during the fusion of cell aggregates (Eq. (6)).

Conclusion

The surface activity of cancer cells is estimated by considering simple model systems such as the fusion of two cell aggregates. While the fusion of epithelial cell aggregate, driven by the tissue surface tension, leads to a decrease in the surface and volume of two-aggregate systems, the fusion of cancer cell aggregates follows quite a different scenario. In this case, cell movement is induced by the solid stress accumulated within a core region of a two-aggregate system, while the surface tension can be neglected. The corresponding rearrangement of cancer cells leads to an increase in the surface and volume of two-aggregate systems. Consequently, epithelial cells perform volumetric cell rearrangement, while the cancer cells undergo surface rearrangement. CCM of cancer cells is purely dissipative and results in a decrease in the solid stress, while that of epithelial cells induces an increase in the solid stress accompanied by the strain energy density, which can lead to the cell jamming state transition within the core region of two-aggregate systems and at the contact between these aggregates. The origin of this interesting phenomenon lies in the ability of cancer cells to reduce the tissue surface tension and behave as surface active constituents.

The surface activity of cancer cells is closely connected with the crosstalk between cell-cell and cell-ECM adhesion complexes obtained for contractile cells. While epithelial cells establish stronger E-cadherin mediated cell-cell adhesion contacts, cancer cells form weak cell-cell adhesion contacts and β1 integrin-mediated cell-ECM adhesion contacts. Cellular contractions, significant in the aggregate surface region, generate repulsion among cancer cells which results in a decrease in the surface tension. In contrast, the contractility of epithelial cells leads to establishing stronger cell-cell adhesion contacts which lead to an increase in surface tension.

The surface activity of cancer cells depends on: (1) the mobility of cancer cells-modeled by the effective temperature, (2) the strength of cell-cell adhesion contacts–modeled by proper free energy functional, and (3) the cell surface packing density. These factors obtained at the supracellular level influence the single-cell contractility and on that basis the surface activity of single cells.

Additional experiments are necessary to: (1) estimate the underlying molecular mechanisms for the change in the state of cell-cell adhesion contacts influenced by cellular contractions (for cancer cells and epithelial cells), (2) assess the feedback impact of these changes on cellular contractility, and (3) correlate the collective effects of these changes with the tissue surface tension and invasiveness of cancer cells.

Author Contributions: Both authors contributed equally to this paper.

Ethics Approval:Not applicable.

Funding Statement: This work was supported by the Ministry of Education, Science and Technological Development of The Republic of Serbia (Contract No. 451-03-68/2022-14/200135).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

Ala-Nissila T, Majaniemi K, Elder K (2004). Phase-field modeling of dynamical interface phenomena in fluids. Lecture Notes in Physics 640: 357–388. DOI 10.1007/b95265. [Google Scholar] [CrossRef]

Barriga EH, Mayor R (2019). Adjustable viscoelasticity allows for efficient collective cell migration. Seminars in Cell and Developmental Biology 93: 55–68. DOI 10.1016/j.semcdb.2018.05.027. [Google Scholar] [CrossRef]

Blanchard GB, Fletcher AG, Schumacher LJ (2019). The devil is in the mesoscale: Mechanical and behavioural heterogeneity in collective cell movement. Seminars in Cell and Developmental Biology 93: 46–54. DOI 10.1016/j.semcdb.2018.06.003. [Google Scholar] [CrossRef]

Beunk L, Brown K, Nagtegaal I, Friedl P, Wolf K (2019). Cancer invasion into musculature: Mechanics, molecules and implications. Seminars in Cell and Developmental Biology 93: 36–45. DOI 10.1016/j.semcdb.2018.07.014. [Google Scholar] [CrossRef]

Bird RB, Stewart WE, Lightfoot EN (1960). Transport Phenomena, John Wiley & Sons INC. [Google Scholar]

Casas-Vazquez J, Jou D (2003). Temperature in non-equilibrium states: A review of open problems and current proposals. Report on Progress in Physics 66: 1937–2023. DOI 10.1088/0034-4885/66/11/R03. [Google Scholar] [CrossRef]

Clark AG, Vignjevic DM (2015). Models of cancer cell invasion and the rule of microenvironment. Current Opinion in Cell Biology 36: 13–22. DOI 10.1016/j.ceb.2015.06.004. [Google Scholar] [CrossRef]

Dechristé G, Fehrenbach J, Griseti E, Lobjois V, Poignard C (2018). Viscoelastic modeling of the fusion of multicellular tumor spheroids in growth phase. Journal of Theoretical Biology 454: 102–109. DOI 10.1016/j.jtbi.2018.05.005. [Google Scholar] [CrossRef]

Devanny AJ, Vancura MB, Kaufman LJ (2021). Exploiting differential effects of actomyosin contractility to control cell sorting among breast cancer cells. Molecular Biology of the Cell 32: 1–15. DOI 10.1091/mbc.E21-07-0357. [Google Scholar] [CrossRef]

Dolega ME, Delarue M, Ingremeau F, Prost J, Delon A, Cappello G (2017). Cell-like pressure sensors reveal increase of mechanical stress towards the core of multicellular spheroids under compression. Nature Communications 8: 14056. DOI 10.1038/ncomms14056. [Google Scholar] [CrossRef]

Etienne-Manneville S (2013). Microtubules in cell migration. Annual Review of Cell and Developmental Biology 29: 471–499. DOI 10.1146/annurev-cellbio-101011-155711. [Google Scholar] [CrossRef]

Friedl P, Alexander S (2011). Cancer invasion and the microenvironment: Plasticity and reciprocity. Cell 147: 992–1009. DOI 10.1016/j.cell.2011.11.016. [Google Scholar] [CrossRef]

Fuhrmann A, Banisadr A, Beri P, Tlsty TD, Engler AJ (2017). Metastatic state of cancer cells may be indicated by adhesion strength. Biophysical Journal 112: 736–745. DOI 10.1016/j.bpj.2016.12.038. [Google Scholar] [CrossRef]

Gandalovičová A, Vomastek T, Rosel D, Brábek J (2016). Cell polarity signaling in the plasticity of cancer cell invasiveness. Oncotarget 7: 25022–25049. DOI 10.18632/oncotarget.7214. [Google Scholar] [CrossRef]

Gongora C, Candeil L, Vezzio N, Copois V, Denis V et al. (2008). Altered expression of cell proliferation-related and interferon-stimulated genes in colon cancer cells resistant to SN38. Cancer Biology & Therapy 7: 822–832. DOI 10.4161/cbt.7.6.5838. [Google Scholar] [CrossRef]

Grosser S, Lippoldt J, Oswald L, Merkel M, Sussman DM et al. (2021). Cell and nucleus shape as an indicator of tissue fluidity in carcinoma. Physics Reviews X 11: 011033. DOI 10.1103/PhysRevX.11.011033. [Google Scholar] [CrossRef]

Guevorkian K, Gonzalez-Rodriguez D, Carlier C, Dufour S, Brochard-Wyart F (2011). Mechanosensitive shivering of model tissues under controlled aspiration. PNAS 108: 13387–13392. DOI 10.1073/pnas.1105741108. [Google Scholar] [CrossRef]

Gupta S, Yap AS (2021). How adherens junctions move cells during collective migration. Faculty Reviews 10: 1–10. DOI 10.12703/r/10-56. [Google Scholar] [CrossRef]

Ivascu A, Kubbies M (2006). Rapid generation of single-tumor spheroids for high-throughput cell function and toxicity analysis. Journal of Biomolecular Screening 11: 922–932. DOI 10.1177/1087057106292763. [Google Scholar] [CrossRef]

Kalli M, Stylianopoulos T (2018). Defining the Role of Solid Stress and Matrix Stiffness in Cancer Cell Proliferation and Metastasis. Frontiers in Oncology 8: 55. DOI 10.3389/fonc.2018.00055. [Google Scholar] [CrossRef]

Kenny PA, Lee GY, Myers CA, Neve RM, Semeiks JR et al. (2007). The morphologies of breast cancer cell lines in three-dimensional assays correlate with their profiles of gene expression. Molecular Oncology 1: 84–96. DOI 10.1016/j.molonc.2007.02.004. [Google Scholar] [CrossRef]

Karbalaei A, Kumar R, Cho HJ (2016). Thermocapillarity in microfluidics—A review. Micromachines 7: 13. DOI 10.3390/mi7010013. [Google Scholar] [CrossRef]

Koride S, Loza AJ, Sun SX (2018). Epithelial vertex models with active biochemical regulation of contractility can explain organized collective cell motility. APL Bioengineering 2: 031906. DOI 10.1063/1.5023410. [Google Scholar] [CrossRef]

Kosztin I, Vunjak-Novakovic G, Forgacs G (2012). Colloquium: Modeling the dynamics of multicellular systems: Application to tissue engineering. Review in Modern Physics 84: 1791–1805. DOI 10.1103/RevModPhys.84.1791. [Google Scholar] [CrossRef]

Kubitschke H, Blauth E, Gottheil P, Grosser S, Kaes J (2021). Jamming in embryogenesis and cancer progression. Frontiers in Physics 9: 666709. DOI 10.3389/fphy.2021.666709. [Google Scholar] [CrossRef]

Lin RZ, Chou LF, Chien CCM, Chang HY (2006). Dynamic analysis of hepatoma spheroid formation: Roles of E-cadherin and β1-integrin. Cell and Tissue Research 324: 411–422. DOI 10.1007/s00441-005-0148-2. [Google Scholar] [CrossRef]

Marmottant P, Mgharbel A, Kafer J, Audren B, Rieu JP, Vial JC, van der Sanden B, Maree AFM, Graner F, Delanoe-Ayari H (2009). The role of fluctuations and stress on the effective viscosity of cell aggregates. PNAS 106: 17271–17275. DOI 10.1073/pnas.0902085106. [Google Scholar] [CrossRef]

Mohammed D, Park CY, Fredberg JJ, Weitz DA (2021). Tumorigenic mesenchymal clusters are less sensitive to moderate osmotic stresses due to low amounts of junctional E‐cadherin. Scientific Reports 11: 16279. DOI 10.1038/s41598-021-95740-x. [Google Scholar] [CrossRef]

Mombach JCM, Robert D, Graner F, Gillet G, Thomas GL, Idiart M, Rieu JP (2005). Rounding of aggregates of biological cells: Experiments and simulations. Physica A: Statistical Mechanics and its Applications 352: 525–534. DOI 10.1016/j.physa.2005.02.008. [Google Scholar] [CrossRef]

Mondal S, Phukan M, Ghatak A (2015). Estimation of solid-liquid interfacial tension using curved surface of a soft solid. PNAS 112: 12563–12568. DOI 10.1073/pnas.1502642112. [Google Scholar] [CrossRef]

Murray JD, Maini PK, Tranquillo RT (1988). Mechanochemical models for generating biological pattern and form in development. Physics Report 171: 59–84. DOI 10.1016/0370-1573(88)90003-8. [Google Scholar] [CrossRef]

Nnetu KD, Knorr M, Kaes J, Zink M (2012). The impact of jamming on boundaries of collectively moving weak-interacting cells. New Journal of Physics 14: 115012. DOI 10.1088/1367-2630/14/11/115012. [Google Scholar] [CrossRef]

Nnetu KD, Knorr M, Pawlizak S, Fuhs T, Kaes J (2013). Slow and anomalous dynamics of an MCF-10A epithelial cell monolayer. Soft Matter 9: 9335–9341. DOI 10.1039/c3sm50806d. [Google Scholar] [CrossRef]

Notbohm J, Banerjee S, Utuje KJC, Gweon B, Jang H, Park Y, Shin J, Butler JP, Fredberg JJ, Marchetti MC (2016). Cellular contraction and polarization drive collective cellular motion. Biophysical Journal 110: 2729–2738. DOI 10.1016/j.bpj.2016.05.019. [Google Scholar] [CrossRef]

Oriola D, Marin-Riera M, Anlas K, Gritti N, Matsumiya M, Aalderink G, Ebisuya M, Sharpe J, Trivedi V (2020). Arrested coalescence of multicellular aggregates. https://arxiv.org/abs/2012.01455. [Google Scholar]

Pajic-Lijakovic I, Milivojevic M (2017). Successive relaxation cycles during long-time cell aggregate rounding after uni-axial compression. Journal of Biological Physics 43: 197–209. DOI 10.1007/s10867-017-9446-7. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2019a). Long-time viscoelasticity of multicellular surfaces caused by collective cell migration–multi-scale modeling considerations. Seminars in Cell and Developmental Biology 93: 87–96. DOI 10.1016/j.semcdb.2018.08.002. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2019b). Jamming state transition and collective cell migration. Journal of Biological Engineering 13: 73. DOI 10.1186/s13036-019-0201-4. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2020a). Viscoelasticity of multicellular systems caused by collective cell migration: Dynamics at the biointerface. European Biophysics Journal 49: 253–265. DOI 10.1007/s00249-020-01431-2. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2020b). Collective cell migration and residual stress accumulation: Rheological consideration. Journal of Biomechancis 108: 109898. DOI 10.1016/j.jbiomech.2020.109898. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2020c). Mechanical oscillations in 2D collective cell migration: The elastic turbulence. Frontiers in Physics 8: e551721. DOI 10.3389/fphy.2020.585681. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2021a). Multiscale nature of cell rearrangement caused by collective cell migration. European Biophysics Journal 50: 1–14. DOI 10.1007/s00249-021-01496-7. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2021b). Viscoelasticity and cell jamming state transition. European Physical Journal Plus 136: 750. DOI 10.1140/epjp/s13360-021-01730-3. [Google Scholar] [CrossRef]

Pajic-Lijakovic I (2021). Basic concept of viscoelasticity. In: Pajic-Lijakovic I, Barriga E (eds.Viscoelasticity and Collective Cell Migration, USA: Academic Press. [Google Scholar]

Pajic-Lijakovic I, Milivojevic M (2021c). Marangoni effect and cell spreading. European Biophysics Journal. DOI 10.1007/s00249-022-01612-1. [Google Scholar] [CrossRef]

Pajic-Lijakovic I, Milivojevic M (2022). Mechanical waves caused by collective cell migration: Generation. European Biophysics Journal 51: 1–13. DOI 10.1007/s00249-021-01581-x. [Google Scholar] [CrossRef]

Petrungaro G, Morelli L, Uriu K (2019). Information flow in the presence of cell mixing and signaling delays during embryonic development. Seminars in Cell and Developmental Biology 93: 26–35. DOI 10.1016/j.semcdb.2018.09.008. [Google Scholar] [CrossRef]

Rudzka DA, Spennati G, McGarry DJ, Chim YH, Neilson M et al. (2019). Migration through physical constraints is enabled by MAPK induced cell softening via actin cytoskeleton re-organization. Journal of Cell Science 132: jcs224071. DOI 10.1242/jcs.224071. [Google Scholar] [CrossRef]

Riehl BD, Kim E, Lee JS, Duan B, Yan R, Donahue HJ, Lim JY (2020). The role of fluid shear and metastatic potential in breast cancer cell migration. Journal of Biomechanical Engineering 142: 101001. DOI 10.1115/1.4047076. [Google Scholar] [CrossRef]

Riehl BD, Kim E, Bouzid T, Lim YJ (2021). The role of microenvironmental cues and mechanical loading milieus in breast cancer cell progression and metastasis. Frontiers in Bioengineering and Biotechnology 8: 608526. DOI 10.3389/fbioe.2020.608526. [Google Scholar] [CrossRef]

Serra-Picamal X, Conte V, Vincent R, Anon E, Tambe DT, Bazellieres E, Butler JP, Fredberg JJ, Trepat X (2012). Mechanical waves during tissue expansion. Nature Physics 8: 628–634. DOI 10.1038/nphys2355. [Google Scholar] [CrossRef]

Shafiee A, McCune M, Forgacs G, Kosztin I (2015). Post-deposition bioink self-assembly: A quantitative study. Biofabrication 7: 045005. DOI 10.1088/1758-5090/7/4/045005. [Google Scholar] [CrossRef]

Shellard A, Mayor R (2019). Supracellular migration–beyond collective cell migration. Journal of Cell Science 132: jcs226142. DOI 10.1242/jcs.226142. [Google Scholar] [CrossRef]

Stirbat TV, Mgharbel A, Bodennec S, Ferri K, Mertani HC, Rieu JP, Delanoe-Ayari H (2013). Fine tuning of tissues’ viscosity and surface tension through contractility suggests a new role for a-catenin. PLoS One 8: e52554. DOI 10.1371/journal.pone.0052554. [Google Scholar] [CrossRef]

Tambe DT, Croutelle U, Trepat X, Park CY, Kim JH, Millet E, Butler JP, Fredberg JJ (2013). Monolayer stress microscopy: Limitations, artifacts, and accuracy of recovered intercellular stresses. PLoS One 8: e55172. DOI 10.1371/journal.pone.0055172. [Google Scholar] [CrossRef]

Trepat X, Wasserman MR, Angelini TE, Millet E, Weitz DA, Butler JP, Fredberg JJ (2009). Physical forces during collective cell migration. Nature Physics 5: 426–430. DOI 10.1038/nphys1269. [Google Scholar] [CrossRef]

Tse JM, Cheng G, Tyrrell JA, Wilcox-Adelman SA, Boucher Y, Jain RK, Munn LL (2012). Mechanical compression drives cancer cells toward invasive phenotype. PNAS 109: 911–949. DOI 10.1073/pnas.1118910109. [Google Scholar] [CrossRef]

Warmt E, Grosser S, Blauth E, Xie X, Kubitschke H et al. (2021). Differences in cortical contractile properties between healthy epithelial and cancerous mesenchymal cells. New Journal of Physics 23: 103020. DOI 10.1088/1367-2630/ac254e. [Google Scholar] [CrossRef]

Yamada KM, Sixt M (2019). Mechanisms of 3D cell migration. Nature Reviews Molecular Cell Biology 20: 738–752. DOI 10.1038/s41580-019-0172-9. [Google Scholar] [CrossRef]