 Open Access
Open Access
ARTICLE
Dynamics along the epithelial-cancer biointerface: Hidden system complexities
Faculty of Technology and Metallurgy, Department of Chemical Engineering, University of Belgrade, Belgrade, Serbia
* Corresponding Author: Ivana Pajic-Lijakovic,
BIOCELL 2023, 47(11), 2321-2334. https://doi.org/10.32604/biocell.2023.043796
Received 14 July 2023; Accepted 08 September 2023; Issue published 27 November 2023
Abstract
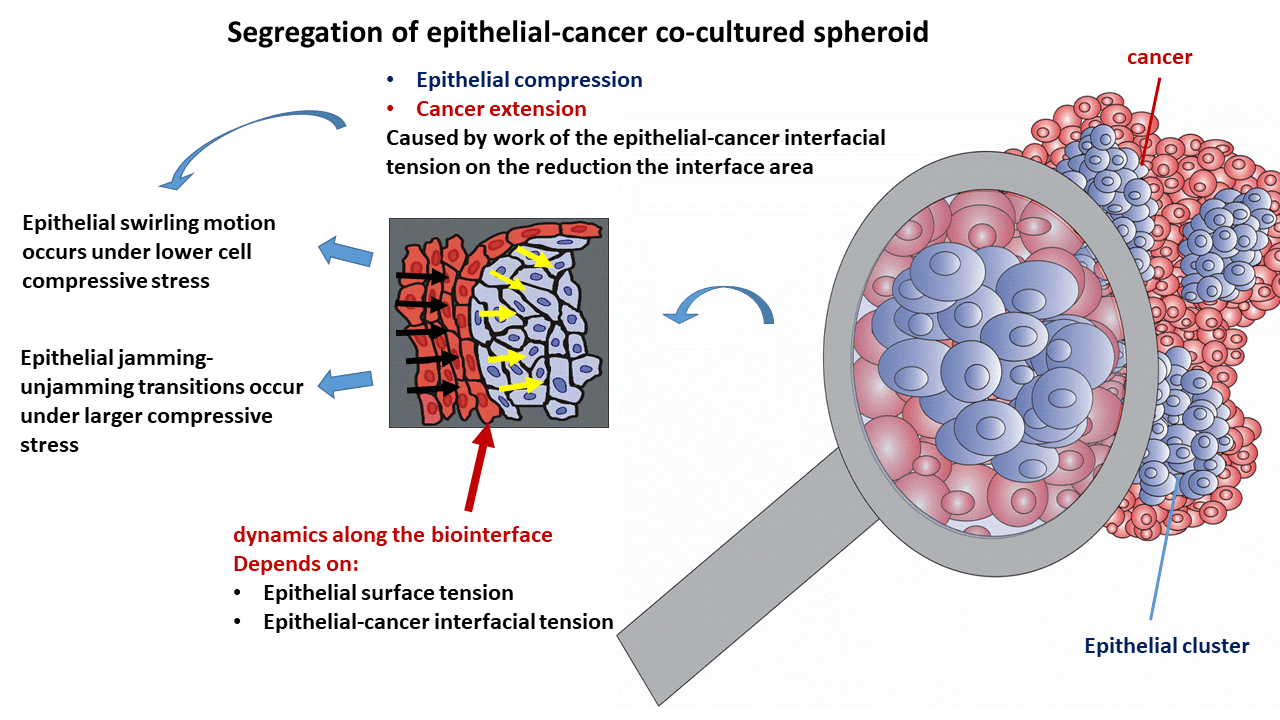
The biointerface dynamics influence any cancer spreading through the epithelium since it is documented in the early stages some malignancies (like epithelial cancer). The altered rearrangement of epithelial cells has an impact on the development of cancer. Therefore, it is necessary to comprehend the underlying biological and physical mechanisms of this biointerface dynamics for early suppression of cancer. While the biological mechanisms include cell signaling and gene expression, the physical mechanisms are several physical parameters such as the epithelial-cancer interfacial tension, epithelial surface tension, and compressive stress accumulated within the epithelium. Although the segregation of epithelia-cancer co-cultured systems was widely investigated, the role of these physical parameters in cell reorganization is still not fully recognized. Hence, this review is focused on clarifying the role that some physical parameters have during cell reorganization within the epithelial cell clusters and cancer spread within co-cultured spheroids. We have applied the developed biophysical model to point out the inter-relations among physical parameters that influence cell reorganization within epithelial-cancer co-cultured systems. The main results of this theoretical consideration have been assessed by integrating the biophysical model with biological and bio-mechanical experiments from the available literature. The epithelial-cancer interfacial tension leads to the reduction of the biointerface area, which leads to an increase in the compressive residual stress within the epithelial clusters depending on the viscoelasticity of the epithelial subpopulation. This stress impacts epithelial rearrangement and the dynamics along the biointerface by influencing the epithelial surface tension and epithelial-cancer interfacial tension. Further, the interrelation between the epithelial surface tension and epithelial-cancer interfacial tension influences the spread of cancer cells.Graphic Abstract
Keywords
Cancer development entails several successive steps. The initial step of epithelial cancer development is cancer cell migration throughout the epithelium (Lee et al., 2012; Millar et al., 2017; Campbell et al., 2019; Jo et al., 2021; Riehl et al., 2021; Pajic-Lijakovic et al., 2023a). This contact with cancer cells causes epithelium reorganization, which further influences cancer cell spreading (Lucia et al., 2022; Pajic-Lijakovic and Milivojevic, 2023d). This complex phenomenon has been assayed with model systems of co-cultured epithelial-cancer spheroids and studying the epithelial cell rearrangement within the dispersed epithelial clusters surrounded by the cancer subpopulation, which represents a continuum. Further, the spreading of a cancer subpopulation primarily depends on the dynamics along the biointerface (Batlle and Wilkinson, 2012; Lucia et al., 2022; Pajic-Lijakovic et al., 2023b). Biointerface dynamics is a product of homotypic and heterotypic interactions governed by the interplay among biological and physical mechanisms (Takeichi, 2023). The biological mechanisms include cell signaling and gene expression (Bateman et al., 2010; Lee et al., 2012; Leal-Orta et al., 2022), while the physical mechanisms include the inter-relation between surface and interfacial tensions present in epithelial-cancer cellular systems (Pajic-Lijakovic et al., 2023b).
The biological mechanisms that influence the rearrangement of epithelial and cancer cell subpopulations along the biointerface have been well elaborated using model systems such as MCF10A/ MDA-MB-231 co-cultured cellular systems. For example, Lee et al. (2012) revealed that the motility of MDA-MB-231 cancer cells is significantly increased when they are surrounded by the epithelial MCF10A cells. The release of macromolecules like fibronectin and laminin-5 by epithelial MCF10A cells facilitates the formation of focal adhesions (FAs) on MDA-MB-231 cells with these macromolecules (Bateman et al., 2010). Additionally, the MDA-MB-231 cells secrete vesicles that stimulate the epithelial-to-mesenchymal transition of the MCF10A cells (Leal-Orta et al., 2022). During the epithelial-to-mesenchymal transition of cells, several transformations occur. Cells lose their apicobasal polarity, obtain mesenchymal phenotypes, and the strength of cell-cell adhesion contacts and cell viscoelasticity are altered (Yang et al., 2020). Further, Heine et al. (2021) pointed to an intensive neighbor exchange along the MCF10A/ MDA-MB-231 biointerface. Other epithelial-cancer cell co-cultured systems show similar inter-connected cellular responses induced by cell signaling (Lucia et al., 2022).
While the biological mechanisms have been intensively studied, physical mechanisms are yet to be probed. In addition, while some physical parameters have been measured only under equilibrium conditions, other parameters have not been measured yet. It is well known that the tissue surface tension (also called “dynamic tissue surface tension”) is a space-time dependent dynamic parameter. This varies due to the change of generated strain caused by collective cell migration (CCM), alterations in the cell surface packing density, variations in the strength of cell-cell adhesion contacts, and cell contractility (Pajic-Lijakovic et al., 2023c). Although this parameter has a large impact on cell rearrangement and tissue shaping (Foty et al., 1996), only the static (equilibrium) value of the tissue surface tension has been determined up to now. This included using various measuring techniques like uni-axial compression of cell aggregates between parallel plates, micropipette aspiration of cell aggregates, and the magnetic force tensiometer (Mombach et al., 2005; Marmottant et al., 2009; Stirbat et al., 2013; Guevorkian et al., 2021; Nagle et al., 2022). In addition, the values of dynamic tissue surface tension have not been determined as of now (Pajic-Lijakovic et al., 2023c). Further, a systematic comparative analysis of the static tissue surface tension for the same cellular system using different experimental techniques has not been performed. Hence, we still do not know which technique is the best for such measurements. Further, the values of several important physical parameters for biointerface dynamics, like epithelial-cancer interfacial tension, have not been measured yet as per records (Pajic-Lijakovic et al., 2023b). Therefore, this review focuses on pointing out the role of the mentioned physical parameters in the segregation of the subpopulations and cancer spreading to inspire further biological experiments.
While the surface tension of cancer and epithelial subpopulations represent a product of the homotypic interactions, the epithelial-cancer interfacial tension is a product of the heterotypic interactions along the biointerface (Pajic-Lijakovic et al., 2023b). The inter-relation between these parameters, called the spreading factor of the subpopulation, regulates the wetting/de-wetting process of the subpopulations and the size of the biointerface accompanied by the efficiency of the segregation process (Pajic-Lijakovic et al., 2023a, 2023b). A minimum size of the biointerface is established for the case of complete segregation, while the size of the biointerface increases in the case of partial segregation. An increase in the biointerface area increases the number of epithelial cells that are in direct contact with the cancer cells (Pajic-Lijakovic and Milivojevic, 2023d). Epithelial-cancer interfacial tension exerts work to minimize the the biointerfacial area, due to which the compressive stress within the epithelium is increased. While the epithelial subpopulation undergoes de-wetting (compression), the cancer subpopulation undergoes wetting (extension) (Pajic-Lijakovic et al., 2023a). Extension of cancer subpopulation is directly influenced by epithelial cell rearrangement especially, within the clusters which are under compressive stress (Lucia et al., 2022). In spite of the extensive research examining the epithelial cancer segregation process, we still do not understand how this epithelial cell reorganization influences cancer spreading in light of introduced physical parameters. Therefore, this review is aimed to reveal the cause-consequence relations between (1) altered rearrangement of epithelium under compressive stress, (2) resulting change of the epithelial surface tension and epithelial-cancer interfacial tension, and (3) the influence of these changes on cancer spread. One of the main parameters that control epithelial cell rearrangement is the residual compressive stress accumulated within the epithelial clusters. Further, this stress is influenced by epithelial-cancer interfacial tension and epithelial viscoelasticity caused by collective cell migration (CCM). This complex cell segregation dynamics is discussed in this review using a developed biophysical model to emphasize the interplay among physical parameters.
The Segregation of Co-Cultured Cell Spheroids Due to Epithelial and Cancer-Mesenchymal Subpopulations
The segregation of co-cultured epithelial-cancer spheroids can undergo complete segregation or partial segregation (Kenny et al., 2007; Carey et al., 2013; Devanny et al., 2021). The efficiency of the segregation process depends on the inter-relations among the macroscopic surface tension of the epithelial subpopulation in contact with a liquid medium, the macroscopic surface tension of the cancer subpopulation in contact with a liquid medium, and the interfacial tension between the subpopulations (Pajic-Lijakovic et al., 2023b). These macroscopic quantities account for the cumulative effects of single-cell contributions along the biointerface. While the surface tension along the subpopulation biointerface is a measure of their cohesiveness, the epithelial-cancer interfacial tension reveals the level of adhesiveness between those subpopulations. A detailed discussion on the interrelation among these physical parameters and their impact on the segregation process itself is provided in the next section. The various model systems in the context of the segregation efficiency are now discussed.
The breast epithelial MCF-10A cells in co-cultured cellular systems perform partial or complete segregation depending on cancer-mesenchymal subpopulation surface tension and the epithelial-cancer interfacial tension. The surface tension of MCF-10A cells is very large; for instance, Nagle et al. (2022) reported that the static surface tension of MCF-10A cells determined using a magnetic force tensiometer had a value of
In order to recognize the complex dynamics of cell segregation and cancer spread, it is necessary to provide the biological and physical aspects of these complex phenomena.
The Biological Aspects of the Segregation of Epithelial-Cancer Co-Cultured Cell Spheroids
The epithelial and cancer subpopulation segregation depends primarily on heterotypic cell-cell collisions along the biointerface that are caused by the generation of shear stress (Lucia et al., 2022). These collisions lead to the alignment of the epithelial cytoskeletal bundles, which has an influence on the cell cortical tension and the strength of cell-cell adhesion contacts (Lucia et al., 2022). The strength of E-cadherin-mediated adhesion contacts is influenced by the number of cadherin molecules for a single contact and by inter-chain and intra-chain interactions (Sadhu et al., 2021). Actin has a double function: it provides a protrusive force that pushes the membrane outwards and traction forces that augment the growth of adhesion complexes (Sadhu et al., 2021). Consequently, cell-cell collisions have an impact on the traction forces (Lucia et al., 2022). Cell signaling, caused by collisions, can also influence actomyosin-mediated contractions. Myosin II activation coincides with cadherin downregulation, suggesting a functional relationship between these molecules (Takeichi, 2023). In some cases, cell signaling accompanied by the generated mechanical stress along the biointerface can lead to the epithelial-to-mesenchymal transition (Leal-Orta et al., 2022). Contrary to the epithelial cells, cancer-mesenchymal cells form weak cell-cell adhesion contacts and β1 integrin-mediated cell-matrix focal adhesions (Devanny et al., 2021). Luctuations of the cell membranes are caused by cell-cell collisions which, result in the activation of various membrane receptors to further impact cell segregation (Takeichi, 2023).
Hence, the cell contractility, along with the strength of cell-cell adhesion contacts, affect the tissue surface tension, the epithelial-cancer interfacial tension, and cell stress generation.
Physical Conditions for the Complete and Partial Segregation of Co-Cultured Cell Spheroids
In a recent publication, Pajic-Lijakovic et al. (2023a, 2023b) showed that the reorganization of epithelial cells within the clusters surrounded by cancer-mesenchymal cells depends on the interplay among epithelial surface tension, cancer surface tension, and epithelial-cancer interfacial tension in the form of the spreading factors of the subpopulations. These spreading factors represent the difference between adhesion energy and cohesion energy of the subpopulation per unit area of the biointerface. These physical parameters are space-time dependent. They are approximately constant within multicellular mesoscopic domains within the biointerface and change from the domain to the domain. The inter-relation between macroscopic and local parameters can be expressed as:

The surface tensions of the subpopulations, which are primarily determined by the strength of cell-cell adhesion contact, satisfy the condition that
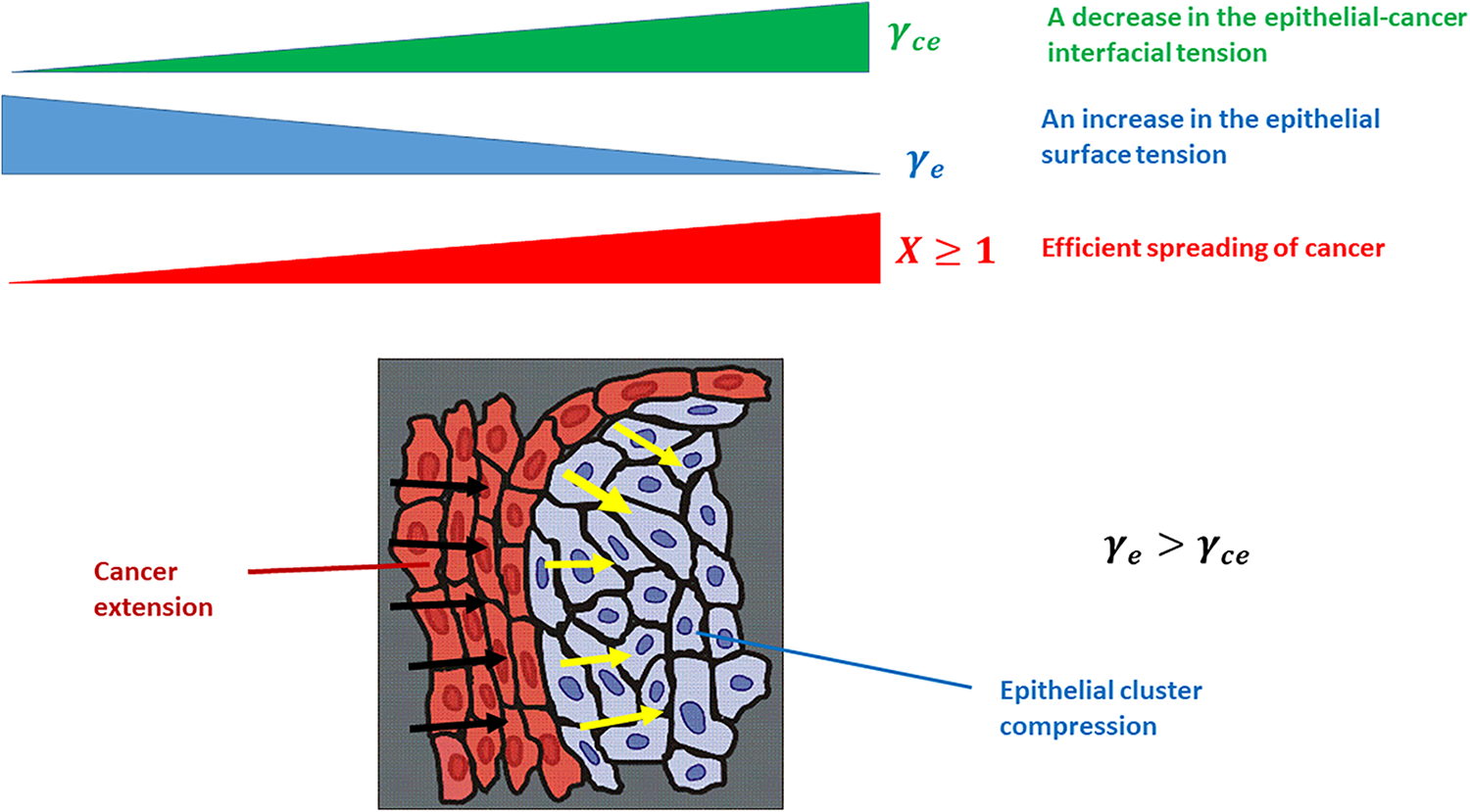
Figure 1: The efficiency of cancer spread depends on the epithelial surface tension and epithelial-cancer interfacial tension. Black arrows describe the spread of the cancer subpopulation, while yellow arrows describe the compression of the epithelial cluster. The physical parameters presented in the Fig. 1 are: γe is the epithelial surface tension, γce is the epithelial-cancer interfacial tension, and X is the efficiency of cancer spreading.
The ratio of the local epithelial surface tension and epithelial-cancer interfacial tension or
The Compression of Epithelial Clusters Caused by the Epithelial-Cancer Interfacial Tension Work
The macroscopic interfacial tension is given by the expression
where
Compressive Residual Stress Accumulation Inside the Migrating Epithelial Clusters
A local compressive stress inside the epithelial cell clusters depends on the effects along the biointerface and the CCM within the cell clusters. While the effects along the biointerface influence the isotropic part of compressive residual stress, the CCM within clusters influences the deviatoric part of the compressive residual stress. As a consequence, the compressive residual stress within the epithelial clusters has been expressed as given below (Pajic-Lijakovic et al., 2023b):
where
• Free expansion of epithelial monolayers (i.e., the expansion of epithelial monolayers toward the empty space) and swirling motion of confluent epithelial monolayers satisfy the condition that the cell’s normal residual stress (extensional and compressive) correlates with the corresponding strain, which points to the elastic nature of the cell residual stress (Serra-Picamal et al., 2012; Notbohm et al., 2016).
• Cell stress can relax under the constant strain caused by (a) the uni-axial compression between parallel plates (Marmottant et al., 2009) and (b) the external extension of cell monolayers (Khalilgharibi et al., 2019). The ability of stress to relax under constant strain represents one of the main characteristics of viscoelastic solids (Pajic-Lijakovic, 2021).
• Cell strain can relax under a constant externally induced compressive stress of cell spheroids between parallel plates (Marmottant et al., 2009). While the stress relaxation time is in a time scale of minutes, the strain relaxation time has a time scale of hours. These observations suggest that strain relaxation happens via CCM, and stress relaxation is caused by the remodeling of cell shapes and cell-cell adhesion contacts (Marmottant et al., 2009; Barriga and Mayor, 2019; Pajic-Lijakovic et al., 2023c).
• The accumulation of the cell residual stress also falls in the time scale of hours (Marmottant et al., 2009; Pajic-Lijakovic and Milivojevic, 2020b).
Consequently, experimental data on CCM of various epithelial-like model systems suggest the relevance of the Zener stress-strain model. The main characteristics of this constitutive model are: (1) a stress can relax under constant strain conditions, (2) a strain can relax under constant stress, (3) the cell residual stress is elastic. The Zener model is presented below (Pajic-Lijakovic and Milivojevic, 2022a):
where
The stress relaxation under constant strain
where
where
where
Cell Rearrangement within the Epithelial Clusters Caused by the Compressive Residual Stress
The response of epithelial cell clusters depends on the magnitude of the accumulated compressive cell residual stress:
• When the compressive stress is low enough (i.e., less than a few hundred Pa) and is not able to induce a contact inhibition of locomotion, epithelial cells can establish supracellular actin cable aligned circumferentially in the form of a network along the biointerface which was shown schematically in Fig. 2a (Röper, 2013). This supracellular actin network protects epithelial clusters against the cell shear stress generated along the biointerface as a consequence of CCM (Lucia et al., 2022).
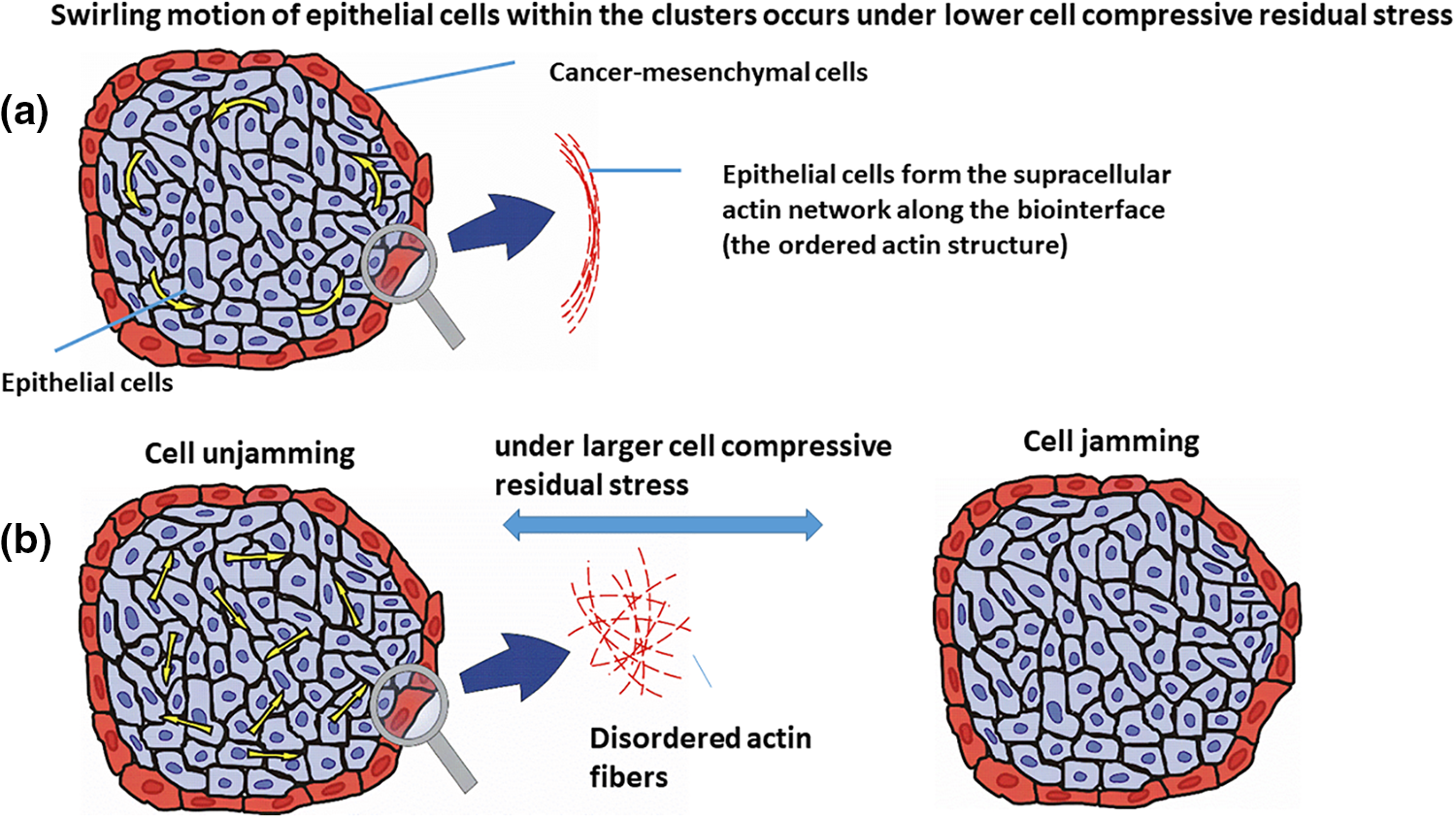
Figure 2: Epithelial cell rearrangement within the cell cluster under: (a) lower compressive residual stress, i.e., the cell swirling motion, and (b) larger compressive residual stress, which are the cell jamming/unjamming transitions. The velocity of epithelial cells within the cluster is presented by yellow arrows. The epithelial cells are shown in the blue color, surrounded by the cancer cells in red.
This network induces the stiffening of epithelial cells that are in direct contact with cancer cells along the biointerface and as a result, stabilizes the biointerface (Lucia et al., 2022). The contractility of this actin network can stimulate the cell swirling motion (Lucia et al., 2022). This cell swirling motion causes an oscillatory change of the speed, velocity, and the compressive stress of cells (Notbohm et al., 2016; Pajic-Lijakovic and Milivojevic, 2022c). Further, Peyret et al. (2019) pointed out at the cell swirling motion within the confluent HaCaT cell monolayers. Intensive cell-cell interactions cause an oscillatory mechanotransduction of yes-associated protein (YAP) in cells. The cell swirling motion depends on (1) the strength of cell-cell adhesion contacts and cell packing density, which influence the velocity correlation length, and (2) the size of the confinement (Doxzen et al., 2013; Chen et al., 2018; Wang and Xu, 2023). Various modes of the cell swirling motion have been considered depending on the interrelation between velocity correlation length and the size of the confinement (Wang and Xu, 2023). The overall rotation of the cellular system is characterized by a higher value of the velocity correlation length, while the appearance of local swirls points to more random cell movement characterized by a lower value of the velocity correlation length (Wang and Xu, 2023). An increased size of the confinement causes the induction of the local swirls for higher values of the velocity correlation length.
This oscillatory cell velocity change has been studied on the principles of mechanical standing waves in few reports (Notbohm et al., 2016; Pajic-Lijakovic and Milivojevic, 2022c). The generated oscillations represent a part of the low Reynolds turbulence that has been generated during a flow of different soft matter systems (Pajic-Lijakovic and Milivojevic, 2022c). The low Reynolds turbulence is connected with long-time inertial effects, which appears due to system viscoelasticity (Pajic-Lijakovic and Milivojevic, 2020b, 2022c).
• When compressive stress is large enough (i.e., of about one kPa) and able to suppress the cell movement within the clusters, successive jamming, and unjamming transitions can be expected as given in Fig. 2b (Pajic-Lijakovic and Milivojevic, 2021b). Epithelial jamming has been recognized in various cellular systems such as (1) the development of a chicken embryo (Spurlin et al., 2019), (2) the gastrulation of the developing fruit fly embryo (Bi et al., 2016; Atia et al., 2018, 2021), (3) the elongation of the body axis during the zebrafish development (Mongera et al., 2018) and many others.
The development of these transitions includes several steps: (a) large compressive stress, accompanied by an increase in the cell packing density, intensifies the contact inhibition of locomotion (Zimmermann et al., 2016; Roycroft and Mayor, 2016; Alert and Trepat, 2020), (b) the contact inhibition of locomotion reduces the cell movement and induces weakening of cell-cell adhesion contacts and consequently, cells undergo the jamming state transition such that the average cell speed tends to zero (Pajic-Lijakovic and Milivojevic, 2021b), i.e.,
Further, Lucia et al. (2022) studied the rearrangement of (1) Madin-Darby canine kidney type II (MDCK) epithelial cell clusters surrounded by mesenchymal C2C12 cells (i.e., immortalized mouse myoblast cell line) and (2) keratinocytes (HaCaT) epithelial cell clusters surrounded by mesenchymal C2C12 cells during the segregation process within spheroids. While both epithelial cell lines formed clusters surrounded by the same mesenchymal cells, their migration modes within the clusters were quite different, caused by compressive stress. The cell compressive stress was larger within the MDCK cell clusters in comparison to the HaCaT cell clusters. This is in agreement with the fact that the HaCaT cells provide larger resistance effects to the compression compared to MDCK cells. The MDCK cells performed random movement within the clusters, caused by the weakening of cell-cell adhesion contacts, while the HaCaT cells retained the strength of cell-cell adhesion contacts and underwent the swirling motion (Lucia et al., 2022). Additionally, the HaCaT cells established a supracellular actin structure along the biointerface with the mesenchymal cells. The actin fibers were aligned circumferentially, forming network-like structures along the biointerface (Lucia et al., 2022). Circumferential actomyosin cables are likely to result in a centripetal tension which is responsible for the swirling motion of cells (Röper, 2013). These cables also frequently appear along the biointerface between epithelium and adjust tissue and represent local force generators (Röper, 2013). The supracellular actin cable is a hallmark of non-adhesive dynamics along the biointerface and can be established when cells retain their cell-cell adhesion contacts (Wei et al., 2020). The appearance of the supracellular actin network along the biointerface causes an increase in the epithelial surface tension.
The MDCK cells can form the supracellular actin cable during 2D non-adhesive gap closure (Wei et al., 2020). However, within the 3D MDCK cell clusters, the cells successively lost their cell-cell adhesion contacts and recovered them through the jamming/unjamming transitions in an oscillatory manner.
Overall, the common features of both modes of cell movement within the epithelial clusters, i.e., (1) the cell swirling motion and (2) the successive jamming/unjamming transitions are the oscillatory change in the cell velocity will be examined using a developed biophysical model in the next section.
The biophysical model has been developed to describe the rearrangement of epithelial cells surrounded by cancer cells by focusing on the dynamics along the biointerface (Pajic-Lijakovic et al., 2023b). The rearrangement of epithelial cells within clusters is characterized by long-time changes in cell packing density and relative cell velocity between epithelial and cancer subpopulations (Pajic-Lijakovic et al., 2023a). The cumulative effects of epithelial-cancer interactions along the biointerface are characterized by epithelial-cancer interfacial tension, which causes the accumulation of compressive stress within the epithelial clusters. The accumulation of compressive stress has an effect on the epithelial surface tension that influences the rearrangement of epithelial cells and the spreading of cancer cells. The main goal of this modeling consideration is to describe the role of physical parameters in the segregation of epithelial-cancer co-cultured systems by observing the oscillatory trend of collective cell migration (Serra-Picamal et al., 2012; Notbohm et al., 2016; Pajic-Lijakovic and Milivojevic, 2022a). The model is created using the system of mass and force balances for the epithelial subpopulation. Additional calculations are not possible when we keep in mind that some parameters have not been measured yet, such as the epithelial-cancer interfacial tension, while others such as the epithelial surface tension have been measured under simplified conditions (i.e., in the form of the static epithelial surface tension). A detailed description of forces that influence the oscillatory change of the relative velocity between epithelial and cancer subpopulations will be listed first. After that, we will discuss the fluxes accompanied by physical mechanisms that influence long-time change of the epithelial packing density within the clusters.
The volumetric force balance accounts for the interplay among the inertial force

The force balance for the de-wetting of epithelial subpopulation along the biointerface has been given by a modified model put forth by Pajic-Lijakovic et al. (2023b).
The oscillatory change of the relative velocity of epithelial cells within the clusters is a product of the competition between the mixing force and interfacial tension force against the friction force and viscoelastic force. Cell movement increases the compressive stress followed by epithelial packing density increase within the clusters and overall affects the cell-cell interactions. There are different mechanisms for the oscillatory change of the epithelial velocity
• If the stress is large enough to reduce cell migration, the successive cell jamming/unjamming transitions (primarily caused by two processes such as the contact inhibition of locomotion and remodeling of E-cadherin adhesion contacts) are responsible for the oscillatory change of the epithelial velocity.
• If the stress is lower, cells retain their adhesion contacts and perform the swirling motion caused by contractions of the already established supracellular actin network distributed circumferentially along the biointerface. Cells inside a swirl start the rotational movement: (1) successive radial inward and outward flows and (2) azimuthal shear flow (Pajic-Lijakovic and Milivojevic, 2020b, 2022c). The radial inward flow and outward flow, caused by the action of centrifugal force, accompanied by the mixing force and interfacial tension force against viscoelastic force and frictional force, induce the 3D mechanical standing waves (Pajic-Lijakovic and Milivojevic, 2022c). The centrifugal force represents a part of the inertial force generated during the swirling motion of cells. The standing waves have also been obtained during the rearrangement of confluent epithelial MDCK monolayers (Notbohm et al., 2016). Consequently, in this case, an oscillatory change of cell velocity is induced by the action of the centrifugal force
In addition to the force balance, it is also required to calculate the mass balance for the movement of epithelial cells within the clusters. The mass balance of the epithelial subpopulation can be expressed as:
where the flux
The flux
The Impact of Epithelial Cell Rearrangement within the Clusters on the Spread of Cancer
The main physical parameters related to the reorganization of epithelial cells within the clusters, which are responsible for the spreading of cancer cells, include the epithelial surface tension, epithelial-cancer interfacial tension, and compressive residual stress accumulation within the epithelial clusters. The interrelations between these parameters and the physical mechanisms that drive the spread of cancer are shown in Fig. 3.
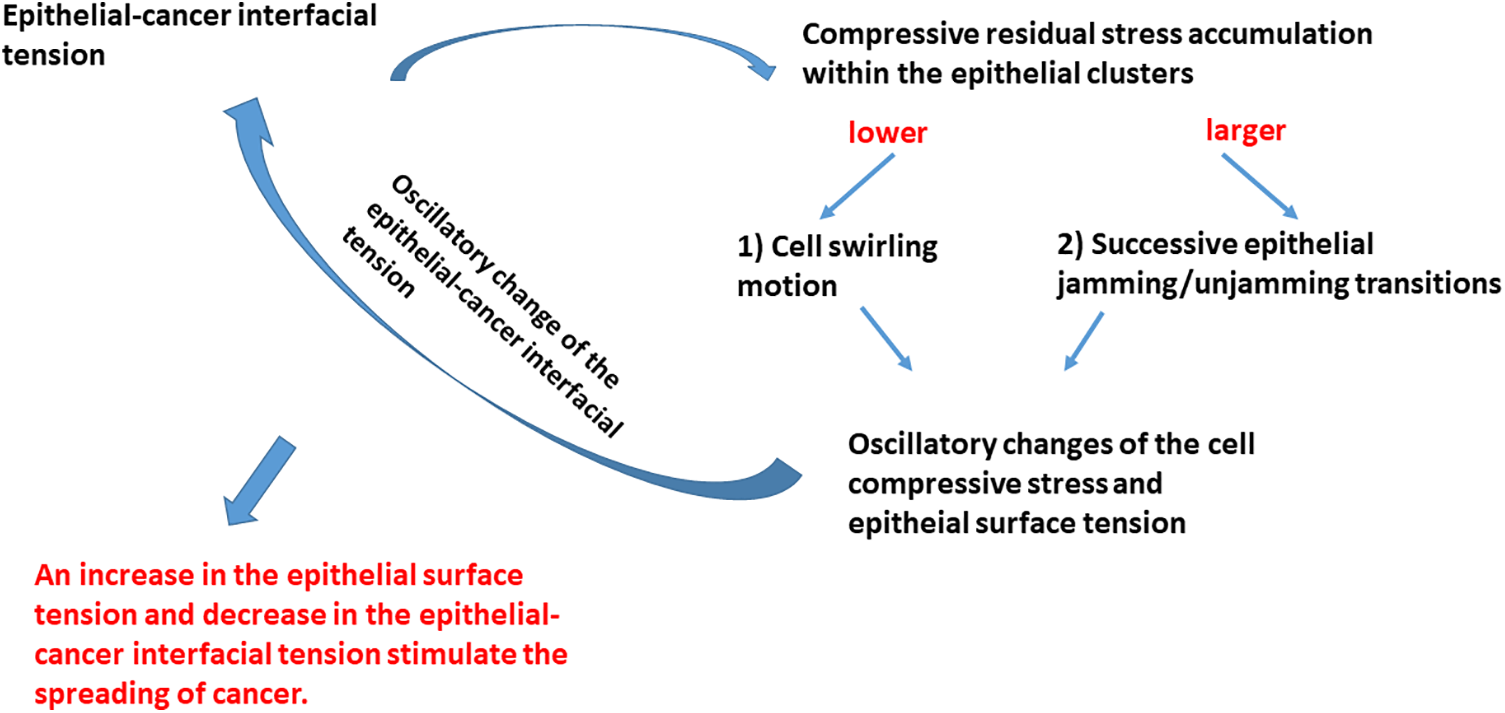
Figure 3: Schematic presentation of the impact that physical parameters have on the spreading of cancer cells.
The compressive residual stress accumulated within the epithelial clusters is one of the main parameters responsible for the rearrangement of epithelial cells within clusters. Two modes of the movement of epithelial cells are possible: (1) cell swirling motion occurring under lower values of the compressive stress and (2) cell jamming/unjamming transitions occurring under larger values of the compressive stress. Epithelial cells within the clusters can establish the supracellular actin network along the biointerface when two conditions are satisfied: (1) when epithelial cells do not establish heterotypic adhesion contacts and (2) the accumulated compressive stress is not high enough to induce the cell jamming. The establishment of the supracellular actin network along the biointerface results in an increase in the epithelial surface tension.
The common characteristics in both scenarios are oscillatory changes of the cell velocity, corresponding strain, and cell compressive stress. These oscillatory trends of the cell reorganization caused by cell movement, which represents an example of the low-Reynolds turbulence, have been obtained within various model systems. These include (1) the segregation of epithelial-cancer spheroids (Lucia et al., 2022), (2) the rearrangement of confluent epithelial monolayers (Notbohm et al., 2016), (3) free extension of epithelial monolayers (Serra-Picamal et al., 2012), (4) cell aggregate rounding after uni-axial compression between parallel plates (Mombach et al., 2005; Pajic-Lijakovic and Milivojevic, 2022a), and (5) fusion of two cell aggregates (Grosser et al., 2021; Pajic-Lijakovic and Milivojevic, 2022a, 2023e). The oscillatory change of the cell stress causes the oscillatory change of the cell packing density (Trepat et al., 2009), which leads to an oscillatory change of the strength of E-cadherin mediated cell-cell adhesion contacts along the biointerface followed by a change in the epithelial surface tension (Pajic-Lijakovic et al., 2023b). The compressive stress oscillatory change also induces an oscillatory change of epithelial-cancer interfacial tension, as expressed by Eq. (1).
This oscillatory rearrangement of epithelial cells within the clusters results in oscillatory extension of the cancer subpopulation. The inter-relation between the efficiency of the segregation which primarily depends on the dynamics along the biointerface and the spreading of cancer cells is presented in Fig. 4.
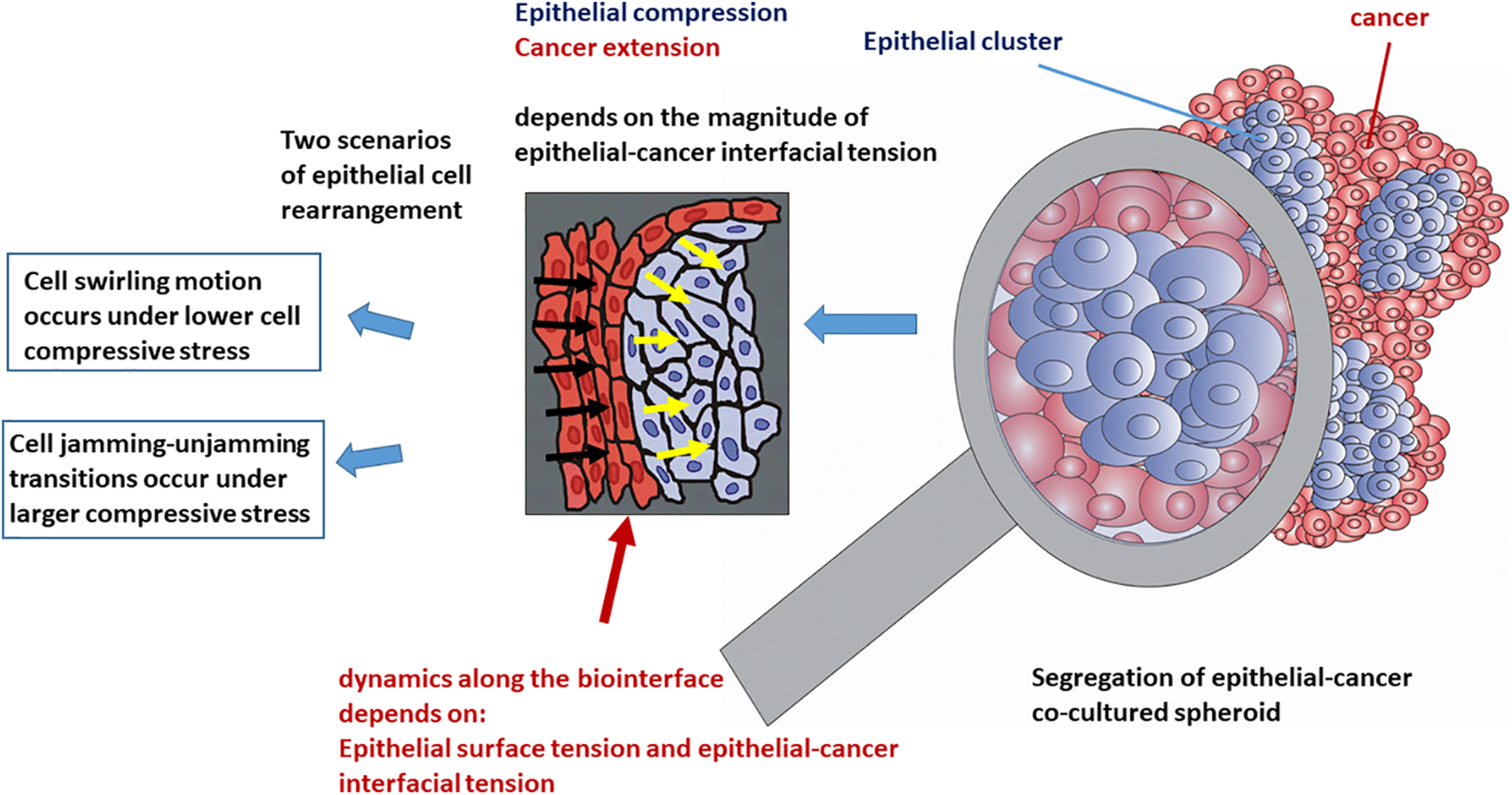
Figure 4: The efficiency of cell segregation and spreading of cancer depends on the dynamics along the epithelial-cancer biointerface.
The increase in the epithelial surface tension and decrease in the epithelial-cancer interfacial tension enhances the spreading of cancer. Based on all these findings, we can conclude that the spreading of cancer is more intensive when swirling motions of cells occur within the epithelial clusters under lower values of compressive stress.
This theoretical review is focused on the clarification of the role that physical parameters have on the segregation of co-cultured epithelial-cancer spheroids by highlighting the importance of the dynamics along the epithelial-cancer biointerface. These include the epithelial surface tension, the epithelial-cancer interfacial tension, and the generated stress caused by CCM, The main results were obtained by integrating the biophysical model with biological and bio-mechanical experiments from the literature, and we can summarize them as follows:
• The function of interfacial tension on the reduction of the biointerfacial area against the volumetric resistant effects of epithelial clusters is responsible for the generation of the compressive stress within the clusters. The volumetric resistance effects are connected with the viscoelasticity of epithelial clusters caused by CCM.
• The compressive stress, which depends on the system viscoelasticity, appears as one of the main control parameters, which influence the rearrangement of epithelial cells in the context of the mode of cell movement and the strength of cell-cell adhesion contacts. Lower compressive stress stimulates the epithelial cells to organize the supracellular actin network along the biointerface. This represents one of the factors responsible for the swirling motion of cells, where the cells retain the strong E-cadherin mediated cell-cell adhesion contacts. This actin network protects cells against the shear stress generated along the biointerface. However, larger compressive stress can also induce the cell jamming state transition. The cell jamming causes the weakening of cell-cell adhesion contacts, which causes a dissipation of energy and a decrease in the compressive stress and as a result cause the cell unjamming state transition. The swirling motion of cells, a characteristic of the lower compressive stress, and successive cell jamming/unjamming transition, a feature of the larger stress, cause an oscillatory change of the cell velocity, compressive stress, epithelial-cancer interfacial tension, and epithelial surface tension.
• Epithelial surface tension accompanied by the epithelial-cancer interfacial tension influences the compression (de-wetting) of the epithelial subpopulation and the extension (de-wetting) of the cancer subpopulation. The spreading of cancer is enhanced at lower values of the interfacial tension and larger values of the epithelial surface tension.
It is necessary to provide more experiments to measure an oscillatory change of these physical parameters and correlate the change of (1) the epithelial-cancer interfacial tension with the cell compressive residual stress, and (2) the epithelial-cancer interfacial tension with the epithelial surface tension.
Acknowledgement: None.
Funding Statement: This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia (Contract No. 451-03-68/2022-14/200135).
Author Contributions: The authors contributed equally to the paper.
Availability of Data and Materials: Data sharing does not apply to this article as no datasets were generated or analyzed during the current study.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
Alert R, Trepat X (2020). Physical models of collective cell migration. Annual Review of Condensed Matter Physics 11: 77–101. https://doi.org/10.1146/annurev-conmatphys-031218-013516 [Google Scholar] [CrossRef]
Atia L, Bi D, Sharma Y, Mitchel JA, Gweon B et al. (2018). Universal geometric constraints during epithelial jamming. Nature Physics. https://doi.org/10.1038/s41567-018-0089-9 [Google Scholar] [CrossRef]
Atia L, Fredberg JJ, Gov NS, Pegoraro AF (2021). Are cell jamming and unjamming essential in tissue development? Cells & Development 168: 203727. https://doi.org/10.1016/j.cdev.2021.203727 [Google Scholar] [PubMed] [CrossRef]
Barriga EH, Mayor R (2019). Adjustable viscoelasticity allows for efficient collective cell migration. Seminars in Cell and Developmental Biology 93: 55–68. https://doi.org/10.1016/j.semcdb.2018.05.027 [Google Scholar] [PubMed] [CrossRef]
Bateman NW, Sun M, Hood BL, Flint MWS, Conrads TP (2010). Defining central themes in breast cancer biology by differential proteomics: Conserved regulation of cell spreading and focal adhesion kinase. Journal of Proteome Research 9: 5311e24. https://doi.org/10.1021/pr100580e [Google Scholar] [PubMed] [CrossRef]
Batlle E, Wilkinson DG (2012). Molecular mechanisms of cell segregation and boundary formation in development and tumorigenesis. Cold Spring Harbor Perspectives in Biology 4: a008227. https://doi.org/10.1101/cshperspect.a008227 [Google Scholar] [PubMed] [CrossRef]
Bi D, Yang X, Marchetti MC, Manning LM (2016). Motility driven glass and jamming transitions in biological tissues. Physical Review X 6: 021011 1–13. https://doi.org/10.1103/PhysRevX.6.021011 [Google Scholar] [PubMed] [CrossRef]
Bird RB, Stewart WE, Lightfoot EN (1960). Transport phenomena, pp. 84. New York, London: John Wiley & Sons INC. [Google Scholar]
Cai G, Nguyen A, Bashirzadeh Y, Lin SS, Bi D, Liu AP (2022). Compressive stress drives adhesion-dependent unjamming transitions in breast cancer cell migration. Frontiers in Cell and Developmental Biology 10: 933042. https://doi.org/10.3389/fcell.2022.933042 [Google Scholar] [PubMed] [CrossRef]
Campbell K, Rossi F, Adams J, Pitsidianaki I, Barriga FM, Garcia-Gerique L, Batlle E, Casanova J, Casali A (2019). Collective cell migration and metastases induced by an epithelial-to-mesenchymal transition in Drosophila intestinal tumours. Nature Communications 10: 2311. https://doi.org/10.1038/s41467-019-10269-y [Google Scholar] [PubMed] [CrossRef]
Carey SP, Starchenko A, McGregor AL, Reinhart-King CA (2013). Leading malignant cells initiate collective epithelial cell invasion in a three-dimensional heterotypic tumor spheroid model. Clinical and Experimental Metastasis 30: 615–630. https://doi.org/10.1007/s10585-013-9565-x [Google Scholar] [PubMed] [CrossRef]
Casas-Vazquez J, Jou D (2003). Temperature in non-equilibrium states: A review of open problems and current proposals. Report on Progress in Physics 66: 1937–2023. [Google Scholar]
Chen T, Saw TB, Mège RM, Ladoux B (2018). Mechanical forces in cell monolayers. Journal of Cell Science 131: jcs218156. https://doi.org/10.1242/jcs.218156 [Google Scholar] [PubMed] [CrossRef]
Devanny AJ, Vancura MB, Kaufman LJ (2021). Exploiting differential effects of actomyosin contractility to control cell sorting among breast cancer cells. Molecular Biology of the Cell 32: 1–15. https://doi.org/10.1091/mbc.E21-07-0357 [Google Scholar] [PubMed] [CrossRef]
Doxzen K, Vedula SRK, Leong MC, Hirata H, Gov NS, Kabla AJ, Ladoux B, Lim CT (2013). Guidance of collective cell migration by substrate geometry. Integrative Biology 5: 1026. https://doi.org/10.1039/c3ib40054a [Google Scholar] [PubMed] [CrossRef]
Foty RA, Pfleger CM, Forgacs G, Steinberg MS (1996). Surface tensions of embryonic tissues predict their mutual envelopment behavior. Development 122: 1611–1620. https://doi.org/10.1242/dev.122.5.1611 [Google Scholar] [PubMed] [CrossRef]
Grosser S, Lippoldt J, Oswald L, Merkel M, Sussman DM et al. (2021). Cell and nucleus shape as an indicator of tissue fluidity in carcinoma. Physical Review X 11: 011033. https://doi.org/10.1103/PhysRevX.11.011033 [Google Scholar] [CrossRef]
Guevorkian K, Brochard-Wyart F, Gonzalez-Rodriguez D (2021). Flow dynamics of 3D multicellular systems into capillaries. In: Pajic-Lijakovic I, Barriga E (eds.Viscoelasticity and Collective Cell Migration, pp. 193. US: Academic Press. [Google Scholar]
Heine P, Lippoldt J, Reddy GA, Katira P, Kaes J (2021). Anomalous cell sorting behaviour in mixed monolayers discloses hidden system complexities. New Journal of Physics 23: 043034. https://doi.org/10.1088/1367-2630/abf273 [Google Scholar] [CrossRef]
Iyer KV, Gomez RP, Paijmans J, Julicher F, Eaton S (2019). Epithelial viscoelasticity is regulated by mechanosensitive E-cadherin turnover. Current Biology 29: 1–14. https://doi.org/10.1016/j.cub.2019.01.021 [Google Scholar] [PubMed] [CrossRef]
Jo SH, Heo WH, Son HY, Quan M, Hong BS et al. (2021). S100A8/A9 mediates the reprograming of normal mammary epithelial cells induced by dynamic cell-cell interactions with adjacent breast cancer cells. Scientific Reports 11: 1337. https://doi.org/10.1038/s41598-020-80625-2 [Google Scholar] [PubMed] [CrossRef]
Kalli M, Stylianopoulos T (2018). Defining the role of solid stress and matrix stiffness in cancer cell proliferation and metastasis. Frontiers in Oncology 8: 55. https://doi.org/10.3389/fonc.2018.00055 [Google Scholar] [PubMed] [CrossRef]
Karbalaei A, Kumar R, Cho HJ (2016). Thermocapillarity in microfluidics—A review. Micromachines 7: 13. https://doi.org/10.3390/mi7010013 [Google Scholar] [PubMed] [CrossRef]
Kenny PA, Lee GY, Myers CA, Neve RM, Semeiks JR et al. (2007). The morphologies of breast cancer cell lines in three-dimensional assays correlate with their profiles of gene expression. Molecular Oncology 1: 84–96. https://doi.org/10.1016/j.molonc.2007.02.004 [Google Scholar] [PubMed] [CrossRef]
Khalilgharibi N, Fouchard J, Asadipour N, Yonis A, Harris A et al. (2019). Stress relaxation in epithelial monolayers is controlled by actomyosin. Nature Physics 15: 839–847. https://doi.org/10.1038/s41567-019-0516-6 [Google Scholar] [PubMed] [CrossRef]
Leal‐Orta E, Ramirez‐Ricardo J, Garcia‐Hernandez A, Cortes‐Reynosa P, Salazar EP (2022). Extracellular vesicles from MDA‐MB‐231 breast cancer cells stimulated with insulin‐like growth factor 1 mediate an epithelial-mesenchymal transition process in MCF10A mammary epithelial cells. Journal of Cell Communication and Signaling 16: 531–546. https://doi.org/10.1007/s12079-021-00638-y [Google Scholar] [PubMed] [CrossRef]
Lee MH, Wu PH, Staunton JR, Ros R, Longmore GD, Wirtz D (2012). Mismatch in mechanical and adhesive properties induces pulsating cancer cell migration in epithelial monolayer. Biophysical Journal 102: 2731–2741. https://doi.org/10.1016/j.bpj.2012.05.005 [Google Scholar] [PubMed] [CrossRef]
Lucia SE, Jeong H, Shin JH (2022). Cell segregation via differential collision modes between heterotypic cell populations. Molecular Biology of the Cell 33: 1–12. https://doi.org/10.1091/mbc.E22-03-0097 [Google Scholar] [PubMed] [CrossRef]
Marmottant P, Mgharbel A, Kafer J, Audren B, Rieu JP, Vial JC, van der Sanden B, Maree AFM, Graner F, Delanoe-Ayari H (2009). The role of fluctuations and stress on the effective viscosity of cell aggregates. Proceedings of the National Academy of Sciences of the United States of America 106: 17271–17275. https://doi.org/10.1073/pnas.0902085106 [Google Scholar] [PubMed] [CrossRef]
Millar FR, Janes SM, Giangreco A (2017). Epithelial cell migration as a potential therapeutic target in early lung cancer. European Respiratory Review 26: 160069. https://doi.org/10.1183/16000617.0069-2016 [Google Scholar] [PubMed] [CrossRef]
Mombach JCM, Robert D, Graner F, Gillet G, Thomas GL, Idiart M, Rieu JP (2005). Rounding of aggregates of biological cells: Experiments and simulations. Physica A 352: 525–534. https://doi.org/10.1016/j.physa.2005.02.008 [Google Scholar] [CrossRef]
Mongera A, Rowghanian P, Gustafson HJ, Shelton E, Kealhofer DA, Carn EK, Serwane F, Lucio AA, Giammona J, Campàs O (2018). A fluid-to-solid jamming transition underlies vertebrate body axis elongation. Nature. https://doi.org/10.1038/s41586-018-0479-2 [Google Scholar] [PubMed] [CrossRef]
Murray JD, Maini PK, Tranquillo RT (1988). Mechanochemical models for generating biological pattern and form in development. Physics Reports 171: 59–84. [Google Scholar]
Nagle I, Richert A, Quinteros M, Janel S, Buysschaert E et al. (2022). Surface tension of model tissues during malignant transformation and epithelial-mesenchymal transition. Frontiers in Cell and Developmental Biology 10: 926322. https://doi.org/10.3389/fcell.2022.926322 [Google Scholar] [PubMed] [CrossRef]
Nnetu KD, Knorr M, Kaes J, Zink M (2012). The impact of jamming on boundaries of collectively moving weak-interacting cells. New Journal of Physics 14: 115012. https://doi.org/10.1088/1367-2630/14/11/115012 [Google Scholar] [CrossRef]
Nnetu KD, Knorr M, Pawlizak S, Fuhs T, Kaes J (2013). Slow and anomalous dynamics of an MCF-10A epithelial cell monolayer. Soft Matter 9: 9335–9341. https://doi.org/10.1039/c3sm50806d [Google Scholar] [CrossRef]
Notbohm J, Banerjee S, Utuje KJC, Gweon B, Jang H, Park Y, Shin J, Butler JP, Fredberg JJ, Marchetti MC (2016). Cellular contraction and polarization drive collective cellular motion. Biophysical Journal 110: 2729–2738. https://doi.org/10.1016/j.bpj.2016.05.019 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I (2021). Basic concept of viscoelasticity. In: Pajic-Lijakovic I, Barriga E (eds.Viscoelasticity and Collective Cell Migration, pp. 21. USA: Academic Press. [Google Scholar]
Pajic-Lijakovic I, Eftimie R, Milivojevic M, Bordas SPA (2023a). The rearrangement of co-cultured cellular model systems via collective cell migration. Seminars in Cell and Developmental Biology 147: 34–46. https://doi.org/10.1016/j.semcdb.2022.10.002 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Eftimie R, Milivojevic M, Bordas SPA (2023b). The dynamics along the biointerface between the epithelial and cancer mesenchymal cells: Modeling consideration. Seminars in Cell and Developmental Biology 147: 47–57. https://doi.org/10.1016/j.semcdb.2022.12.010 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Eftimie R, Milivojevic M, Bordas SPA (2023c). Multi-scale nature of the tissue surface tension: Theoretical consideration on tissue model systems. Advances in Colloid and Interface Science 315: 102902. https://doi.org/10.1016/j.cis.2023.102902 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2019). Long-time viscoelasticity of multicellular surfaces caused by collective cell migration—Multi-scale modeling considerations. Seminars in Cell and Developmental Biology 93: 87–96. https://doi.org/10.1016/j.semcdb.2018.08.002 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2020a). Collective cell migration and residual stress accumulation: Rheological consideration. Journal of Biomechanics 108: 109898. https://doi.org/10.1016/j.jbiomech.2020.109898 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2020b). Mechanical oscillations in 2D collective cell migration: The elastic turbulence. Frontiers in Physics 8: e551721. https://doi.org/10.3389/fphy.2020.585681 [Google Scholar] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2021a). Multiscale nature of cell rearrangement caused by collective cell migration. European Biophysics Journal 50: 1–14. https://doi.org/10.1007/s00249-021-01496-7 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2021b). Viscoelasticity and cell jamming state transition. The European Physical Journal Plus 136: 750. https://doi.org/10.1140/epjp/s13360-021-01730-3 [Google Scholar] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2022a). Mechanical waves caused by collective cell migration: Generation. European Biophysics Journal 51: 1–13. https://doi.org/10.1007/s00249-021-01581-x [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2022b). Marangoni effect and cell spreading. European Biophysics Journal 51: 419–429. https://doi.org/10.1007/s00249-022-01612-1 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2022c). Viscoelasticity and cell swirling motion. Advances in Applied Mechanics 55: 393–424. https://doi.org/10.1016/bs.aams.2022.05.002 [Google Scholar] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2022d). The role of viscoelasticity in long time cell rearrangement. Progress in Biophysics and Molecular Biology 173: 60–71. https://doi.org/10.1016/j.pbiomolbio.2022.05.005 [Google Scholar] [PubMed] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2023d). Morphological changes of epithelial cells and spreading of cancer: Theoretical consideration. Applied Physics A. https://doi.org/10.1007/s00339-023-06814-8 [Google Scholar] [CrossRef]
Pajic-Lijakovic I, Milivojevic M (2023e). Surface activity of cancer cells: The fusion of two cell aggregates. Biocell 47: 15–25. https://doi.org/10.32604/biocell.2023.023469 [Google Scholar] [CrossRef]
Peyret G, Mueller R, d’Alessandro J, Begnaud S, Marcq P, Mège RM, Yeomans JM, Doostmohammadi A, Ladoux B (2019). Sustained oscillations of epithelial cell sheets. Biophysical Journal 117: 464–478. https://doi.org/10.1016/j.bpj.2019.06.013 [Google Scholar] [PubMed] [CrossRef]
Podlubny I (1999). Fractional differential equations. In: Mathematics in Science and Engineering, vol. 198, pp. 78. London: London Academic Press. [Google Scholar]
Riehl BD, Kim E, Bouzid T, Lim YJ (2021). The role of microenvironmental cues and mechanical loading milieus in breast cancer cell progression and metastasis. Frontiers in Bioengineering and Biotechnology 8: 608526. https://doi.org/10.3389/fbioe.2020.608526 [Google Scholar] [PubMed] [CrossRef]
Roycroft A, Mayor R (2016). Molecular basis of contact inhibition of locomotion. Cellular and Molecular Life Sciences 73: 1119–1130. https://doi.org/10.1007/s00018-015-2090-0 [Google Scholar] [PubMed] [CrossRef]
Röper K (2013). Supracellular actomyosin assemblies during development. BioArchitecture 3: 45–49. https://doi.org/10.4161/bioarch.25243 [Google Scholar] [CrossRef]
Sadhu RK, Penic S, Iglic A, Gov NS (2021). Modelling cellular spreading and emergence of motility in the presence of curved membrane proteins and active cytoskeleton forces. The European Physical Journal Plus 136: 495. https://doi.org/10.1140/epjp/s13360-021-01433-9 [Google Scholar] [CrossRef]
Serra-Picamal X, Conte V, Vincent R, Anon E, Tambe DT, Bazellieres E, Butler JP, Fredberg JJ, Trepat X (2012). Mechanical waves during tissue expansion. Nature Physics 8: 628–634. https://doi.org/10.1038/nphys2355 [Google Scholar] [CrossRef]
Spurlin JW, Siedlik MJ, Nerger BA, Pang MF, Jayaraman S, Zhang R, Nelson CM (2019). Mesenchymal proteases and tissue fluidity remodel the extracellular matrix during airway epithelial branching in the embryonic avian lung. Development 146: dev175257. https://doi.org/10.1242/dev.175257 [Google Scholar] [PubMed] [CrossRef]
Stirbat TV, AMgharbel A, Bodennec S, Ferri K, Mertani HC, Rieu JP, Delanoë-Ayari H (2013). Fine tuning of tissues’ viscosity and surface tension through contractility suggests a new role for a-catenin. PLoS One 8: e52554. https://doi.org/10.1371/journal.pone.0052554 [Google Scholar] [PubMed] [CrossRef]
Takeichi M (2023). Cell sorting in vitro and in vivo: How are cadherins involved? Seminars in Cell and Developmental Biology 147: 2–11. https://doi.org/10.1016/j.semcdb.2022.11.004 [Google Scholar] [PubMed] [CrossRef]
Trepat X, Wasserman MR, Angelini TE, Millet E, Weitz DA, Butler JP, Fredberg JJ (2009). Physical forces during collective cell migration. Nature Physics 5: 426–430. https://doi.org/10.1038/nphys1269 [Google Scholar] [CrossRef]
Wang BC, Xu GK (2023). Collective migration of cells in geometric spaces: Intrinsic correlation length racing against extrinsic confinement size. Journal of the Mechanics and Physics of Solids 177: 105327. https://doi.org/10.1016/j.jmps.2023.105327 [Google Scholar] [CrossRef]
Wei Q, Shi X, Zhao T, Cai P, Chen T, Zhang Y, Huangd C, Yang J, Chen X, Zhang S (2020). Actin-ring segment switching drives nonadhesive gap closure. Proceedings of the National Academy of Sciences of the United States of America 117: 33263–33271. https://doi.org/10.1073/pnas.2010960117 [Google Scholar] [PubMed] [CrossRef]
Yang J, Antin P, Berx G, Blanpain C, Brabletz T et al. (2020). Guidelines and definitions for research on epithelial-mesenchymal transition. Nature Reviews Molecular Cell Biology 21: 341–352. https://doi.org/10.1038/s41580-020-0237-9 [Google Scholar] [PubMed] [CrossRef]
Zimmermann J, Camley BA, Rappel WJ, Herbert LH (2016). Contact inhibition of locomotion determines cell-cell and cell-substrate forces in tissues. Proceedings of the National Academy of Sciences of the United States of America 113: 2660–2665. https://doi.org/10.1073/pnas.1522330113 [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools