Optimization Scheme of Trusted Task Offloading in IIoT Scenario Based on DQN

1  Introduction

With the rapid development of fifth-generation (5G) communication technology and the Industrial Internet of Things (IIoT), a growing number of end devices (EDs) with sensing and monitoring capabilities are being connected at an unprecedented rate [1]. The connection of these EDs generates a large amount of information to be processed. However, IIoT EDs remain in a situation of constrained resources in terms of computational power and storage space. That hinders the execution of computationally intensive practices, such as smart homes, smart grids, intelligent diagnosis, and other intelligent decision-making scenarios. These applications usually require low latency, high bandwidth, high reliability, and high computing power.

Mobile edge computing (MEC) is a widely considered solution that can meet the above requirements by using offloading algorithms [2]. Instead of traditional centralized computing, by deploying MEC servers in the system, the computing and storage resources can be transferred from central nodes to MEC servers that are much closer to IIoT EDs. Consequently, fast response, low energy consumption, and high throughput services may be provided [3–5]. Terminals can offload large-scale local data to the MEC servers and then receive the computing results. Nevertheless, the offloading framework, which includes IIoT EDs, edge servers, and cloud servers, still faces significant issues and various challenges [6]. The most important one is data security because the data can be easily manipulated during the transmission from EDs to MEC servers, which may lead to unpredictable consequences. As the scale of offloading data increases sharply, the security of data attracts more attention than before. Traditional data protection methods are centralized, for example, with trusted third-party entities. However, the inherent heterogeneity of MEC systems (i.e., edge servers may be deployed by multiple vendors and have various mobile terminals) and single-point failure may both make the solutions inapplicable in MEC systems [7].

To resolve the security issues, researchers introduce blockchain to build a secure environment for data offloading in the IIoT systems with MEC [8–11]. As a well-known technology, blockchain includes distributed processing, data tamper-proof, and multi-party consensus features, which can establish decentralized trust. In this way, EDs and MEC servers can validate data consistency by checking records on the blockchain. However, challenges still exist in IIoT systems that integrated with MEC servers and blockchain [12–14]. For consistency validation, the data offloaded to MEC servers must be reached on the blockchain. As communication is the basis of consensus, a large number of communications are time-consuming and will cause low throughput, which negatively affects the efficiency of task offloading. So when it comes to data security and high efficiency, there is a tradeoff in the task-offloading framework with MEC and blockchain. On the one hand, the blockchain requires maintaining a distributed ledger among all validation nodes, which leads to low throughput and may affect integrated systems. On the other hand, data security, computation resources, transmission latency, computation power, and dynamic channel state must be considered in system design when using MEC. It is complex to balance the two parts and make use of MEC to safely solve as many computing tasks as possible.

Many applications are highly sensitive to time and data security in IIoT scenarios [15], for example, smart hospital and factory monitoring. So, our objective is to design a scheme to optimize it. In summary, this article makes the following contributions:

1)   We design a comprehensive scheme that integrates MEC servers, controllers, and blockchain into IIoT systems for efficiency and data security. At the same time, because the offloading action is related to blockchain, we also consider chain optimization.

2)   By fully considering the important features of IIoT, MEC servers, and blockchain, as well as the adjustable factors of the integrated systems, we define the optimal decision-making problem as a Markov decision process (MDP). To better handle computing tasks, we propose a novel reward function by taking task difficulty and scale into account.

3)   Due to the complexity of the issue, we adopt a deep Q-learning-based (DQN) approach to make offloading decisions dynamically, including validation node selection, block size adjustment, task-offloading server choice, and block interval adjustment. The aim is to optimize the overall performance of the task offloading systems combined with MEC and blockchain.

4)   The simulation demonstrates that the proposed scheme addresses more computing tasks than other schemes under security.

The remainder of this article is organized as follows. In Section 2, we present the related works about the integration of IIoT systems, MEC, and blockchain, as well as the related methods to solve optimization problems with deep reinforcement learning (DRL) algorithms. The system framework and formulation of the offloading model, as well as the DRL-based solution, are presented in Section 3. In Section 4, simulation results are exhibited and analyzed. Finally, Section 5 concludes this article with an overview of proposed future work.

2  Related Work

2.1 IIoT and IIoT with MEC

IIoT uses smart EDs, fast protocols, and efficient cybersecurity mechanisms to improve industrial processes and applications [15]. The achievements of communication, software, and hardware have greatly improved the manufacturing process in the industrial environment [16–18], which leads to the rapid increment of the number of interconnected devices in IIoT systems. Additionally, strong alliances and alignment of interests between stakeholders and emerging applications have attracted large companies around the world to invest in this emerging market [19]. However, the performance of intelligent applications in IIoT is closely related to the processing of big data. Neither EDs nor traditional cloud computing can meet the requirements of IIoT. Researchers propose a new network paradigm named task offloading to solve the challenge [20]. Mach et al. [21] propose metrics including energy consumption and latency to assess offloading methods. Liu et al. [22] take the queueing state, central processing unit (CPU) state, the execution state of EDs, and communication status into account to achieve more task offloading. However, both of them don’t take data security into account. By jointly considering the task topologies, dependency, heterogeneity of MEC servers, and resource of users, Shu et al. [23] propose a fine-grained offloading framework to reduce the completion time of the computation-intensive applications, but the framework ignores some limitations, e.g., buffer space of MEC, which makes optimization inapplicable. Xie et al. [24] research the observable computational offloading problem with imperfect fast time-varying channel state information and formulate the problem as a partially observable Markov decision process (POMDP), as well as minimize the average consumption of the EDs and latency. However, they don’t consider the impact of the capability of EDs and the complexity of tasks on the result. All of the cited works point out that data processing is a serious problem faced by the rapidly developing IIoT, and a framework with MEC or EDs only cannot fully take data security as well as the specific status of computing devices into account, which makes the framework not realistic.

2.2 Blockchain-Empowered IIoT with MEC

Data is vulnerable during transmission, and the information stored in MEC servers may result in leakage, theft, and breach. Miller [25] states that integration of the IIoT and blockchain would address problems of data regulation. BeCome, a blockchain-empowered computation offloading method was proposed by Xu et al. [7]. Blockchain and multi-criteria decision-making are used to ensure data integrity and generate resource allocation strategies. However, the method cannot make decisions dynamically because it is applied in a relatively static environment, with every smart device in IIoT only accommodating one task. To make efficient use of cloud computing and MEC resources, Wu et al. [26] adopt a dynamic algorithm to decide the optimal computing place, while the optimization is applied to trade-off limited computing consumption against high latency. Huang et al. [27] propose a task offloading and resource allocation framework based on fog computing networks (FCNs) to ensure fairness of transactions. However, the two methods pay more attention to optimizing the energy consumption of computing servers and ignore the impact of blockchain on system latency. In summary, the majority of these works utilize static optimization techniques and cannot consider the features of blockchain. As a result, the approaches cannot be applied in practical dynamic systems to make optimal decisions and fail to maximize long-term performance in a high-dimensional and complicated dynamic environment.

2.3 Blockchain-Empowered IIoT with DRL

DRL is one of the most suitable methods for optimizing decision-making policy and maximizing long-term rewards. So, it has attracted many researchers to make use of the algorithm to solve task offloading problems for IIoT systems with MEC and blockchain. Qiu et al. [28] design a trusted consensus protocol for blockchain to collect and synchronize various views between different software-defined networking (SDN) controllers. For better balanced computational capability and trust value of blockchain nodes and controllers, they choose the dueling DQN approach for view change, access decision, and resource allocation problems. However, they don’t consider block size and block interval into account, which makes limited optimization for blockchain. Nguyen et al. [29] propose a network that includes MEC and blockchain, where people act as miners to offload extensive tasks to a selected MEC server and formulate task offloading decisions, user privacy, and mining tasks profit as a joint optimization problem. They then propose a DRL-based offloading scheme to solve large state space and action space, but they ignore the optimization of blockchain. As mentioned above, few studies jointly consider blockchain and MEC systems in detail, only taking blockchain as an additional system beyond IIoT and MEC systems. So, the optimal performance of the system cannot be achieved.

3  Proposed Model

In this section, we introduce the system framework. Then, we express the offloading optimization problem in formulas. Finally, we present the DRL-based solution to the problem.

3.1 System Architecture

Generally, a MEC server only performs data computing in the task offloading framework. However, to verify the data consistency during the offloading process, we randomly select MEC servers to form the blockchain and perform data verification. Fig. 1 presents the system architecture, with three layers: 1) IIoT layer, 2) MEC layer, and 3) cloud layer.

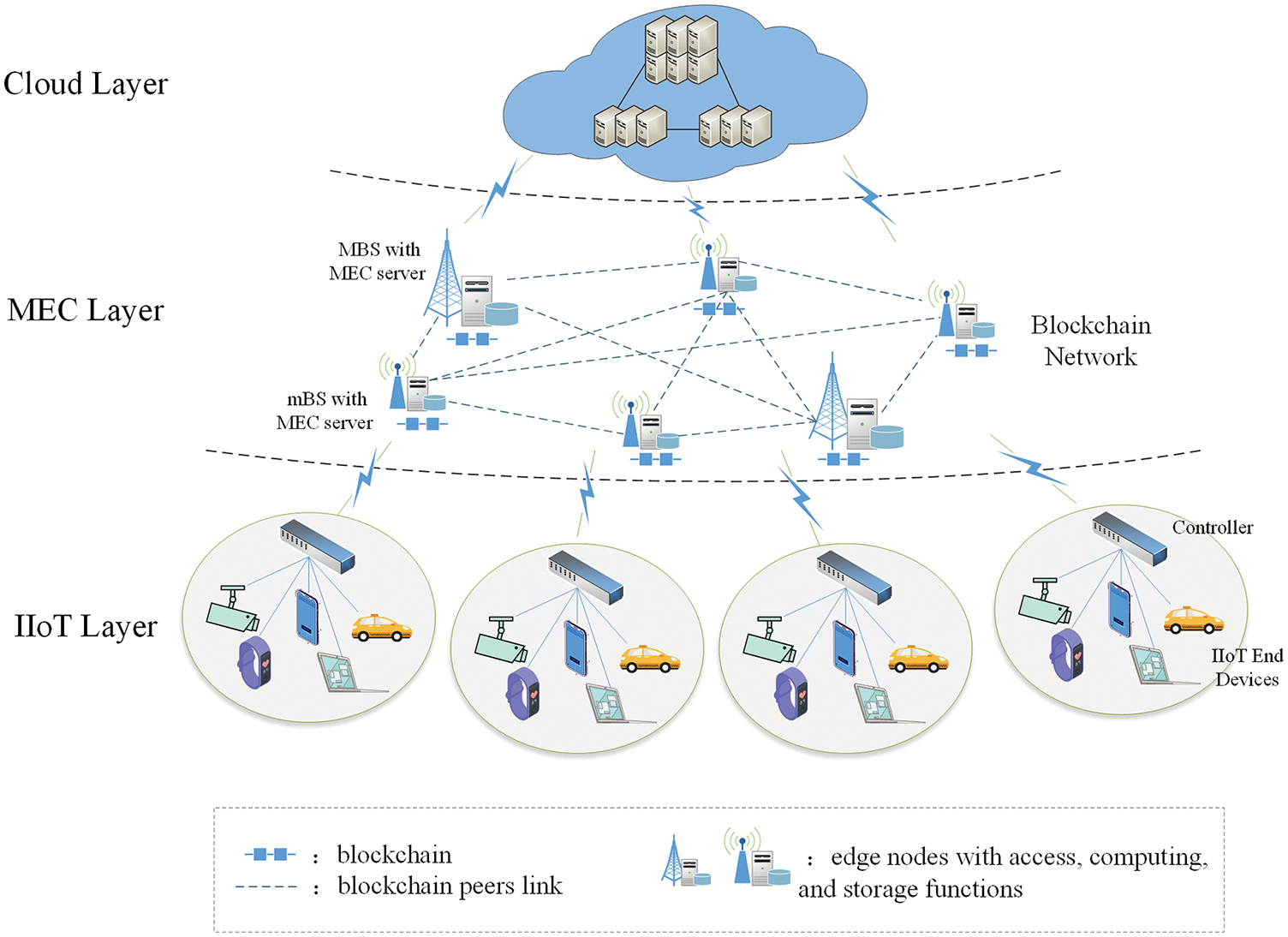
Figure 1: Architecture of the proposed system for task offloading in IIoT with blockchain

In the IIoT layer, we assume that IIoT EDs are divided into M cells [13] denoted by C = {c1, c2, …, cm, …, cM}. Each cell is managed by a local controller, so the set of controllers is denoted by Ccon = {c1con,c2con,…,cmcon,…,cMcon}. We also consider that each cell cm has Dm IIoT EDs, where Dm, j represents the j-th (j ∈ {1, 2, …, Dm}) ED of the m-th cell in the IIoT layer. EDs collect and generate massive data and produce a large number of tasks to be calculated. Similar to Feng et al. [30], time is slotted with each timeslot denoted by t. Most security and privacy problems do not occur in local computing but often happen during data transmission to the servers. In this paper, we only focus on the tasks that must be offloaded to MEC or cloud servers. If an IIoT ED cannot handle heavy computation tasks independently, these tasks may be offloaded to MEC or cloud computing servers with the assistance of the controller in the same cell. Therefore, let Km, j(t) = (dm, j(t), em, j(t), τm, j(t)) be the tasks that ED Dm, j decides to offload at timeslot t, where dm, j(t) is the data size of the offloading tasks; em, j(t) is the required number of CPU cycles to complete tasks; τm, j(t) is the maximum tolerable execution time. M controllers are very close to the corresponding IIoT EDs and receive data from EDs. The controllers make the offloading decisions and offload the information to the selected MEC server in real-time [31].

The MEC layer consists of N macro base stations (MBSs) and micro base stations (mBSs) with MEC servers. We consider that each MEC server has a data buffer to store some arrived offloading tasks, while the data buffer has its storage limits. The set of MEC servers is denoted as E = {E1, E2, …, En, …, EN}, and we let Mn(t)=(fn(t),anb(t),enb(t),en0(t)) be the state of MEC server En at timeslot t (n∈{1, 2, …, N}), where fn(t) denotes the computational power of the MEC server; anb(t) represents the number of tasks in the buffer; enb(t) denotes the required number of CPU cycles to complete all tasks in the buffer; eb0(t) is the required number of CPU cycles to complete the earliest task in the buffer. The offloading decision is denoted by Om, j(t) (Om, j(t)∈{1, 2, …, N, N + 1}), where Om, j(t) ∈{1, 2, …, N} means that controllers offload the tasks to MEC servers, and Om, j(t) = N + 1 denotes that the tasks are offloaded to cloud computing servers. To enhance the security of the offloading process, we embed a blockchain system in the MEC layer (i.e., some MEC servers act as blockchain node and form a blockchain system) [32–34].

There is a cloud computing server in the cloud layer. The state of the cloud computing server at timeslot t is denoted as MN+1(t)=(fN+1(t),aN+1b(t),eN+1b(t),eN+10(t)), where, fN+1(t),aN+1b(t),eN+1b(t),andeN+10(t) represent the status of the cloud computing server EN+1, which is similar to the MEC servers above. Compared with MEC servers, cloud computing servers can provide more computing power but with longer distances and transmission latency. When the cloud computing server completes the tasks from controllers, it returns the calculation results to the ED and sends the results to the blockchain system.

3.2 Problem Formulation

3.2.1 Time Cost of Offloaded Tasks

The overall time cost of offloaded tasks is an important metric in evaluating task offloading decisions. For tasks Km, j(t), the overall time cost consists of four parts, namely transmission time between the controller and MEC/cloud server, server queuing time, server task execution time, and block finality time which includes block generation (block interval) time and validation time. The overall time is presented as

Tm,j,n(t)=Tm,j,ntran(t)+Tm,j,nqueu(t)+Tm,j,nexec(t)+Tm,j,nbloc(t),(1)

where Tm,j,ntran(t),Tm,j,nqueu(t),Tm,j,nexec(t)andTm,j,nbloc(t) are transmission latency, queuing latency, execution latency and block finality time on server En (n ∈ {1, 2, …, N + 1}), respectively.

We consider that the channel gain between controllers and servers is diverse and let gm, n(t) denote the channel gain between controller cmcon and server En. Therefore, the data transmission rate of tasks Km, j(t), between controller cmcon and server En is

Rm,j,n(t)=Wlog2⁡(1+pm(t)gm,n(t)σ2+In),(2)

where pm(t) denotes the transmission power of controller cmcon; W, σ2, In are channel bandwidth, noise power, and interference power of the channel between controller cm and server En, respectively. Each communication system channel is independent, so no more than B/W controllers can transmit data simultaneously. Therefore, the transmission latency of tasks Km, j(t) is

Tm,j,ntran(t)=dm,j(t)Rm,j,n(t)=dm,j(t)Wlog2⁡(1+pm(t)gm,n(t)σ2+In),(3)

Since these servers use a first-in-first-out (FIFO) queue, the queuing time of the task on each server is the time to execute all earlier tasks in the buffer. Consequently, the queuing time and task execution time of tasks Km, j(t) are presented as

Tm,j,nqueu(t)=enb(t)fn(t),(4)

Tm,j,nexec(t)=em,j(t)fn(t),(5)

For simplicity, we only take block generation time DI(t) and validation time DV(t) into account for block finality time. To analyze the impact of consensus latency on the blockchain more accurately, we divide the entire process into two parts, i.e., message delivery Dv and message verification Dm. Their formulas are as follows:

Tm,j,nbloc(t)=DI(t)+DV(t),(6)

DV(t)=Dv(t)+Dd(t),(7)

The validation time is largely influenced by the consensus algorithm. By comprehensively considering the efficiency and security of the system, we adopt the practical Byzantine fault tolerance (PBFT) algorithm in our architecture. The process of PBFT consists of the request, pre-prepare, prepare, commit and reply stages, as presented in Fig. 2

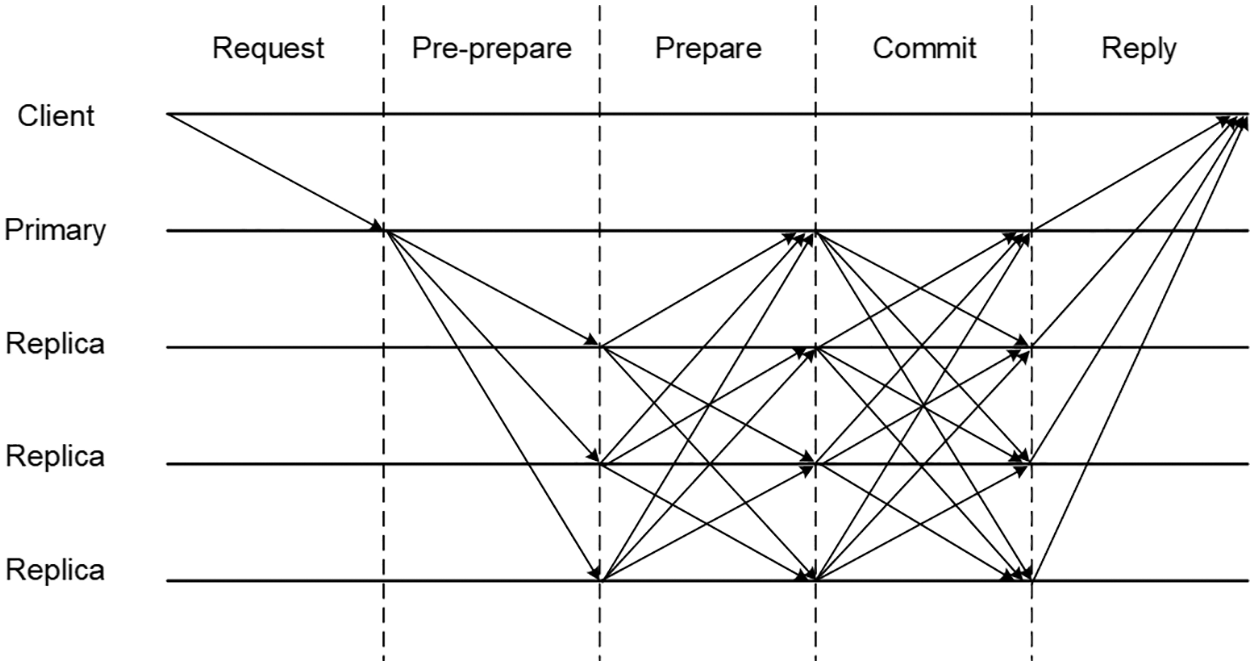
Figure 2: Process of the PBFT consensus algorithm

The PBFT consensus algorithm requires each validation node to exchange a large number of messages with others, thus guaranteeing the high security of the blockchain system with the cost of communication efficiency. Among the nodes are one primary node and many replica nodes. In the request phase, the primary node verifies every transaction and pickles it into a block. In the pre-prepare phase, the primary node sends the block to all replica nodes, and the replica nodes confirm the receipt. In the preparation phase, all replica nodes deliver the results they received in the last stage to other nodes. Meanwhile, every replica node should validate the message authentication code (MAC) and generate an identical MAC for delivery. In the commit phase, all nodes send confirmation messages to other nodes. If more than 2/3 of the messages have been agreed upon, the node sends the results to the client in the reply phase.

Then, we carry out a quantitative analysis of the latency in the consensus process. We assume that block size is BM, one block includes up to δ transactions, and there are k validation nodes in the system. Therefore, for message verification, the primary node needs to check δ signatures and finish 2δ + 4(k − 1) MAC operations. In addition, each replica node is supposed to verify δ signatures and finish δ + 4(k − 1) MAC operations. Supposing that a verify operation and a generation/check MAC operation require α and β computing cost, respectively, the delay of block information verification for primary node Dp v and replica nodes Dr v is therefore as follows:

Dvp=δα+[2δ+4(k−1)]βfp,(8)

Dvr=maxr=1,…,k;r≠pδα+[δ+4(k−1)]βfr,(9)

where fp and fr denote the compute power of the MEC servers selected to be the primary node and replica node, respectively, p, r ∈ {1, …, k p ≠ r}. For message delivery, timeout T exists in every phase to prevent endless waiting for a response from nodes.

According to the five stages of the consensus process, the latency of block message delivery is:

Dd=DdReq+Ddprep+Ddpre+Ddcom+Ddrep=(min{BMREsEp,T}+min{maxp,j=1,...,k;p≠j⁡BMREpEj,T}+min{maxi,j=1,...,k;i≠j⁡BMREiEj,T}+min{maxi,j=1,...,k;i≠j⁡BMREiEj,T}+min{maxj=1,...,k⁡BMREsEj,T})(10)

where REsEj(s, j = 1, …, k) refers to the communication rate between task-execution MEC server ES and validation MEC server Ej; REsEp refers to the communication rate between MEC server ES and primary validation MEC server Ep ; REiEj refers to the information transmission rate between two validation MEC server nodes. The overall time cost of the offloaded tasks is presented as:

Tm,j,n(t)=(dm,j(t)Wlog2(1+pm(t)gm,n(t)σ2+In)+enb(t)+em,j(t)fn(t)+max(δα+[2δ+4(k−1)]βfp,maxr=1,...,k;r≠p⁡δα+[δ+4(k−1)]βfr)+(min{BMREsEp,T}+min{maxp,j=1,...,k;p≠j⁡BMREpEj,T}+min{maxi,j=1,...,k;i≠j⁡BMREiEj,T}+min{maxi,j=1,...,k;i≠j⁡BMREiEj,T}+min{maxj=1,...,k⁡BMREsEj,T}))(11)

3.2.2 Throughput of the Blockchain System

To ensure security, we include blockchain in the architecture. Therefore, the entire assignments of the MEC server and the results of the computing tasks must be recorded for trusted traceability [35]. However, low throughput is a critical issue that prevents blockchain from being integrated into other technologies and systems. The intuition of blockchain is a distributed ledger. Before blocks are finally linked to the entire chain, many communications are executed by the consensus algorithm among nodes. We are therefore concerned that the blockchain constructed by MEC servers may also become a bottleneck in our system.

The key factors that impact the throughput of blockchain include block size BM(t) and block interval DI(t) [2]. The block size determines the number of transactions that may be contained in a block. The block interval is the time duration to generate a new block. To address the challenge, we design a model that can adjust the parameters above reference to the situation and help improve the performance of our architecture. The model is introduced in Section 3.3.

Additionally, it is important to note that the goal of this architecture is to solve as many complex computing tasks as possible and ensure all assignments/results can be validated, so once the tasks are completed, they must be recorded on the chain. In other words, the effective throughput of the entire system is only measured by the number of completed and recorded tasks. Therefore, the throughput of the system is limited by two aspects: the number of tasks executed by MEC servers and the record performance of the blockchain. Regarding the performance of the blockchain, each block in the blockchain contains two parts. The first is the task allocation record and the corresponding calculation results. The second is the redundant structure, such as a pointer and a block header. So, the calculation of effective throughput involves two aspects. First, we count the number of tasks completed, denoted by φ. Second, we calculate the throughput of the blockchain. Meanwhile, to satisfy the latency requirement of the entire system, we consider that all assignment and response data should be generated and verified in consecutive block intervals. The effective throughput of the system Ф(t) and constraint condition is

Φ(t)=min(ϕDI(t),⌊BM(t)−Sn(t)γ⌋DI(t)),(12)

Tm,j,n(t)≤ω×DI,0≤ω,(13)

where Sn(t) is the occupied space of the redundant structure; γ denotes the average size of transactions of computing result; ω denotes the number of block intervals.

3.3 Problem Analysis

Since the designed framework integrates blockchain, controllers, and MEC servers in addition to traditional IIoT systems, the states and actions are complicated and dynamic. Specifically, there are a large number of computing tasks with different scales, costs, and tolerant time in every time step that should be assigned to a computing server. Additionally, the server significantly affects queuing time and task execution time according to Eqs. (4) and (5). Meanwhile, the selection of validation nodes among MEC servers through communication rate and computational power is another critical factor that makes a significant contribution to the final throughput of the system because it is referenced to block finality time according to Eqs. (6)–(10), (12).

Obviously, the state of the system is dynamic every time step. Any action may affect the state in the next time step and rewards in the future. Therefore, based on the characteristics of the system, we describe the optimal decision-making problem as a discrete MDP by defining the state space, action space, and reward function.

3.3.1 State Space

In each time step, the agent learns action value or policy from experience by observing the state. In some scenarios, before making a decision, the agent observes the current state, defined as a set by timeslot t. The set is represented as:

s(t)=(F,R,A,e)t,(14)

where F denotes the computational power of validation nodes and task-execution servers; R denotes the communication rate among the servers for consensus and computing; A represents the number of remaining tasks in the buffer related to all servers; and e represents the required number of CPU cycles to complete the earliest task and all tasks in the buffer.

3.3.2 Action Space

Facing a complex environment, the system is required to make decisions and adjust the scheme for maximum reward in the future at every time step. We must thoroughly consider not only task-offloading behaviors but also factors that promote the throughput of blockchain and then create the action space. The action space at decision epoch t is represented by

a(t)=(V,S,I,B)t,(15)

where V denotes the set of servers as validation nodes; S denotes the server selected to handle the tasks; I denotes the block interval; B represents block size.

3.3.3 Reward

In this system, our initial goal is to improve the efficiency of task offloading under security conditions, and that involves two aspects. On the one hand, tasks must be assigned to servers rich in channel resources and computational power to ensure that they may be accomplished in a short time and make profits. On the other hand, because any allocation of computing results is required to reach consensus on the blockchain when the data size exceeds the throughput of the blockchain, the data must be put into a data pool and wait for another chance to reach consensus. The batch of the tasks cannot be counted in the effective throughput of the whole system. In sum, the decisions made by our model must take task assignments and blockchain throughput into account. Once the scale of data to be recorded on-chain is larger than throughput, part of the data cannot be recorded in time. On the contrary, if the scale of the data is smaller than the record capabilities of blockchain, it leads to inefficient space resource use.

In conclusion, our final reward consists of two parts: the information on computational tasks that are computed at the current time and the effective throughput of the entire system at the current time. To better measure completed tasks, we first get the task score of a batch of tasks by multiplying the scale (data size) and difficulty (required number of CPU cycles). To accurately measure throughput, we take the smaller value of the number of computing tasks completed by MEC/cloud servers with and throughput of the blockchain. We set the reward by multiplying the average score of finished tasks and the throughput of the entire system.

Moreover, when designing a reward function, we should consider positive and negative rewards. Here, we set two constraints when the state of the system out of which the model will be punished. First, each server has a buffer limit, and each task has a maximum tolerance time. When the number of remaining tasks in the buffer of a server is greater than the limit or the overall time of finishing tasks (including result recorded) is longer than the maximum tolerance time, we punish the final reward by subtracting tasks scores from the original reward in case of unreasonable assignment. Second, when the overall time cost of offloaded tasks does not meet Eq. (13), we set the throughput to 0. The reward function is as follows:

r(t)taskscore=∑imdi(t)×ei(t)m,(16)

r(t)thtoughput=Φ(t),(17)

maxn=1,…,N+1(enb)≤bl,(18)

Tii=1,…,m(t)≤τi(t),(19)

r(t)={r(t)taskscore×r(t)throughputif(13),(18),and(19)aresatisfiedr(t)taskscore×r(t)throughput−μ×d(t)×e(t)if(18)and(19)arenotsatisfied0if(13)isnotsatisfied,(20)

where r(t)throughput and r(t)task represent the throughput and average tasks scores at time t separately; di(t) and ei(t) represent the size and difficulty of the task that has been finished at time t, bl represents servers buffer limit; Ti(t) and τi(t) represent the execution time and maximum tolerance time of the task finished at time t; μ represents penalty coefficient. We can set different punishments by adjusting μ.

3.3.4 DQN-based Performance Optimization Algorithm

Because the system involves high-dimension features and large-scale actions, we resort to the DQN approach to deal with the MDP problem. While running the DQN algorithm, the agent frequently interacts with the environment, finally learning a smart optimization strategy based on action values. The DQN, which evaluates the value of discrete actions by neural networks based on consecutive and complicated observations, is one of the most famous action-state value functions in DRL. The value and update of action-values are defined as follows:

Qπ=(s,a)=Eπ[∑k=1∞rt+k+1|st=s,at=a],(21)

Q(s,a)←Q(s,a)+ϑ[r(s,a)+ξmaxQ(s′,a′)−Q(s,a)],(22)

where Eπ represents expectation; rt + k + 1 denotes the present reward at timeslot t + k + 1 under the strategy π;ξϵ(0,1) represents a discount factor; maxQ(s’, a’) denotes the max value action in the next state; Θ denotes the learning rate. ξ equals to zero represents that we prefer an immediate reward. On the contrary, ξ equals to 1 shows that we prefer a long-term reward. Compared with the original algorithm, DQN possesses two characteristics: experience reply and evaluate-target networks architecture.

To prevent temporal correlations issued by continuous states in the system from affecting optimization, we introduce experience replay into our approach. In the system, we focus on which agent action may acquire a maximum long-term reward in the current state, which is unrelated to previous states. Therefore, it is necessary to reduce the relevance among the states learned by the model. To achieve this, the agent stores every pair <s, a, r, s’> in memory and samples a batch of pairs at the start of training. Another improvement related to DQN is the creation of the evaluating network and the target network. The two networks have the same architecture but different update frequencies. The parameters in evaluating network are updated in real-time and the target network updates the parameters after a fixed time step. The reason is to reduce the relevance of the evaluated action-value and target action-value.

Thus, the loss function is denoted as:

L(θ)=E[(r(a,s)+ξmaxQ(s′,a′,θ−)−Q(s,a,θ))2],(23)

where θ is the parameter of the evaluate network, and θ− is the parameter of the target network.

4  Experimental Results and Discussion

In this section, we first introduce our simulation environment and significant system parameters, as well as details on the DQN algorithm. Then, we present and analyze the simulation results with different parameters and conditions.

4.1 Simulation Parameters and System Environments

In the experiments, the DQN algorithm is implemented by TensorFlow2.2.4, a widely used framework for deploying deep learning models. Our software environment is Python 3.6.9 based on the Ubuntu operating system. The DQN algorithm in our system is shown as Algorithm 1.

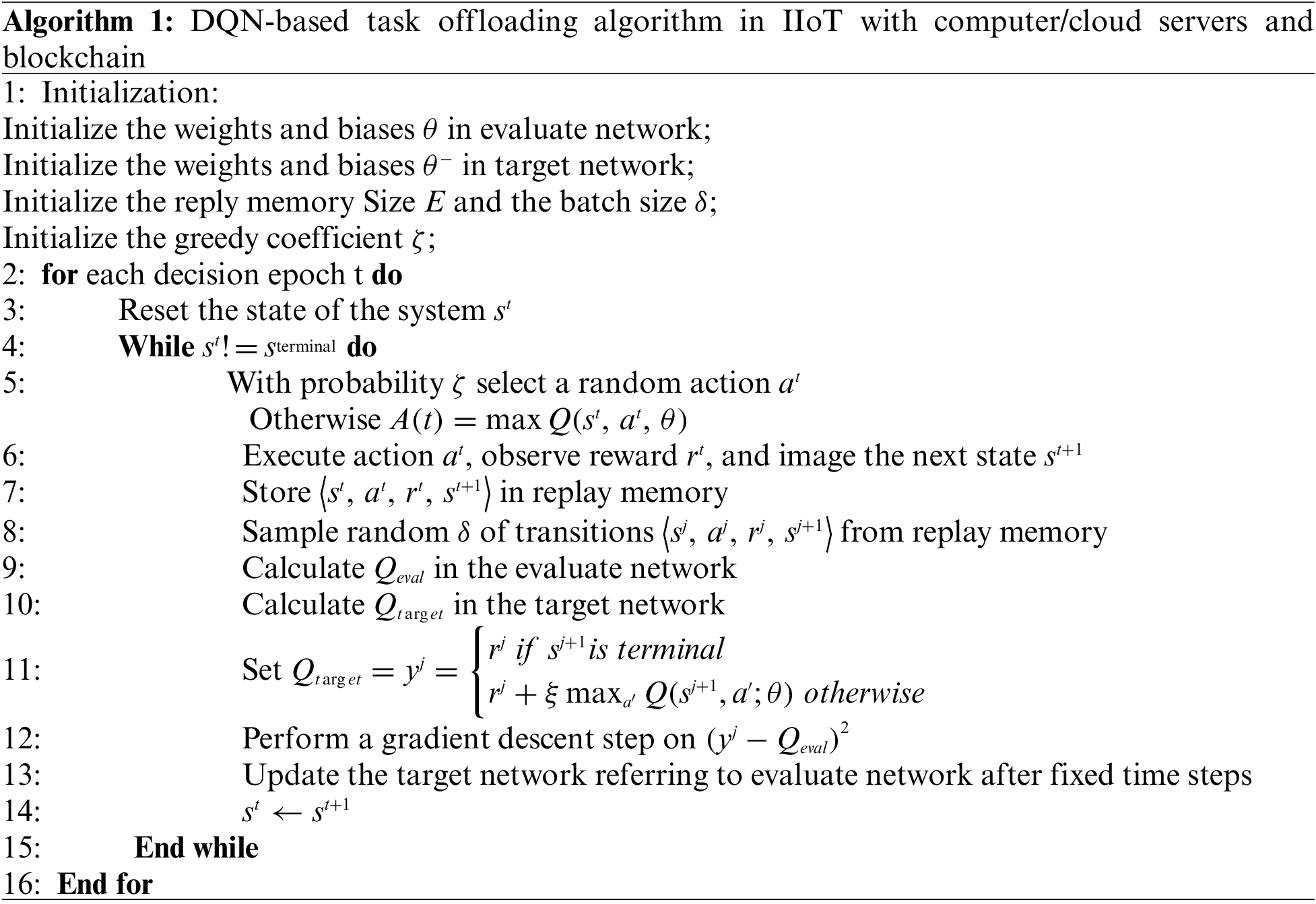
In this simulation, there are five cells and five computational servers in the blockchain-empowered IIoT scenario, including four MEC servers and one cloud server. Among all MEC servers, we set three validation nodes. Meanwhile, we allocate fixed computational resources and buffer to every server and set communication rates between different servers and controllers. Some of the parameters are given in Tab. 1.

4.2 Simulation Results and Analysis

To better measure the performance of our framework, we designed ablation studies by comparing the proposed framework and the following schemes:

1)   Proposed framework without block size adjustment

2)   Proposed framework without block interval adjustment

3)   Proposed framework without validation nodes choice

4)   Proposed framework with task offloading node choice randomly

The real IIoT environment is complex, and applications have various requirements for data size and recording time. To simulate the real IIoT scenario and verify the effectiveness of the scheme proposed in this paper, we design experiments with different factors ω and transaction sizes. Then observe whether the scheme can make use of resources according to states under as many scenarios as possible.

Fig. 3 presents the total reward obtained by schemes in different environments. Schemes 1) and 2) get lower total rewards than others when ω is smaller than 7 or transaction size is smaller than 20 KB. One of the reasons may be the system packs many transactions into a block, but the environment has rigid restrictions for data recording. The transactions cannot be reached on the chain in time, so the two schemes have been punished frequently. When ω is larger than 7 or transaction size is larger than 40 KB, Scheme 3) gets the lowest total rewards. The reason may be the scheme is more likely to choose a server to compute tasks and validate data at the same time, which will cause a long delay and low efficiency in data processing. Meanwhile, the scheme we propose performs the best because it can adjust the blockchain for making full use of block space and avoid punishments when ω is small, as well as assign tasks to optimum servers for fast response.

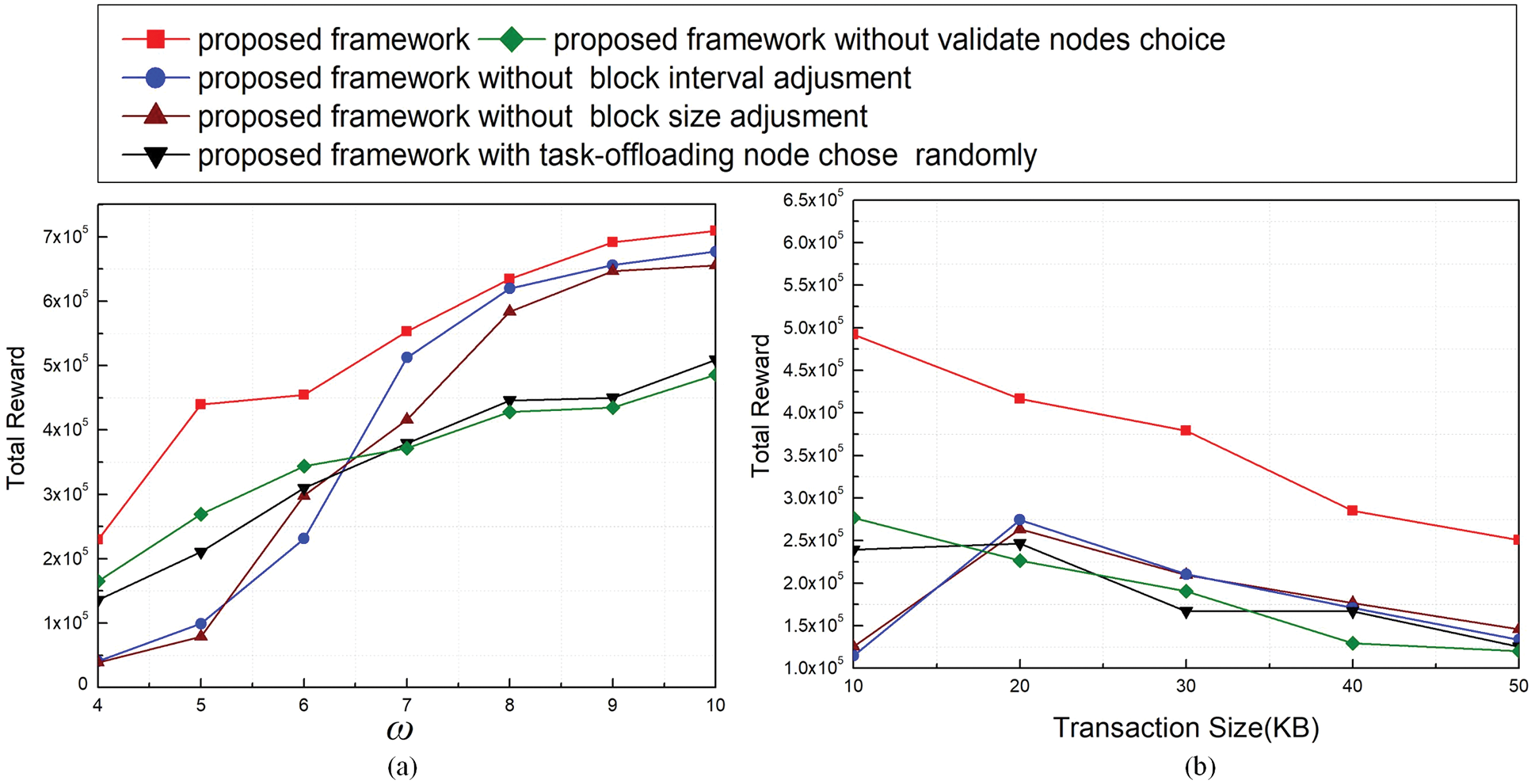
Figure 3: Total reward under different thresholds of ω (a) and transaction sizes (b)

Effective throughput is an important metric for the scheme performance in applications, which can partially reflect the ability of different methods to process data with different scales. Fig. 4 shows results of effective throughput in different situations. From Fig. 4a, we find that the throughput increases when ω increases because blockchain can record results within a relatively long time. When transaction size increases, the throughputs decreases. However, the throughputs of Schemes 1) and 2) increase than before when transaction size equals 20  KB. One of the reasons may be the blockchain can handle more transactions included in a block than before. The methods proposed in the paper acquire higher effective throughput than others.

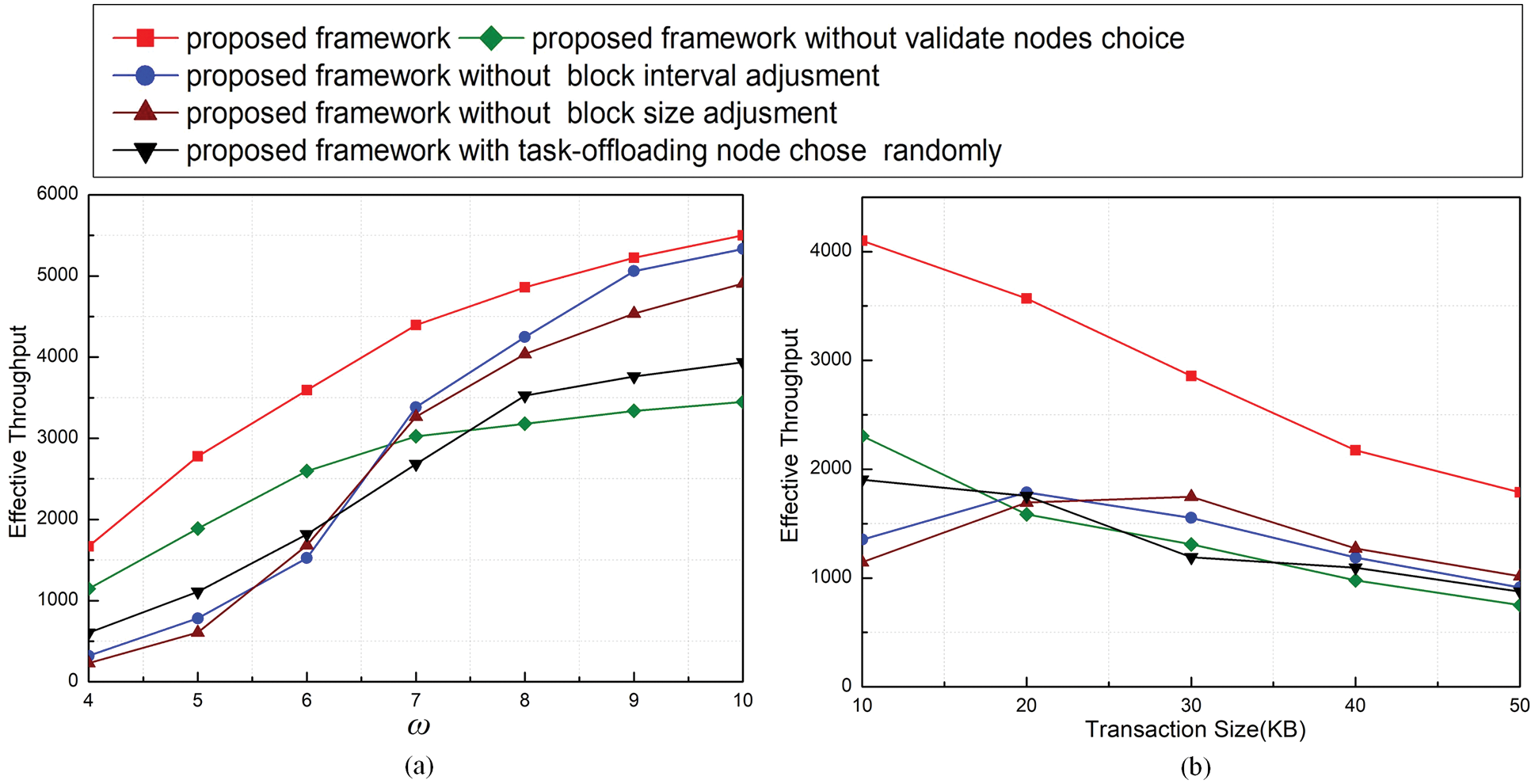
Figure 4: Effective throughput under different thresholds of ω (a) and transaction sizes (b)

The aim of our method is to solve computing tasks fast, so to better verify the performance of the optimization scheme, we generate some batches of tasks and set a value about computing circles that need to be executed according to the tasks. Then, we record the time consumption of all schemes to achieve the value. It’s noted that the scores generated by the actions that break the system constraints are calculated in the results. Fig. 5 describes the time consumption of all schemes to reach the value we set. We can see that our method takes the shortest time to solve the tasks and reach the value because our method can keep higher throughput and assign proper resources for computing tasks. Schemes 1) and 2) take a shorter time than Schemes 3) and 4) until the ω is larger than 7 or the transaction size is larger than 20  KB. One reasonable explanation is the performance of the blockchain is the bottleneck of the whole system. When the performance/constraints of the blockchain are improved/relaxed, the efficiency of offloading depends more on resource allocation.

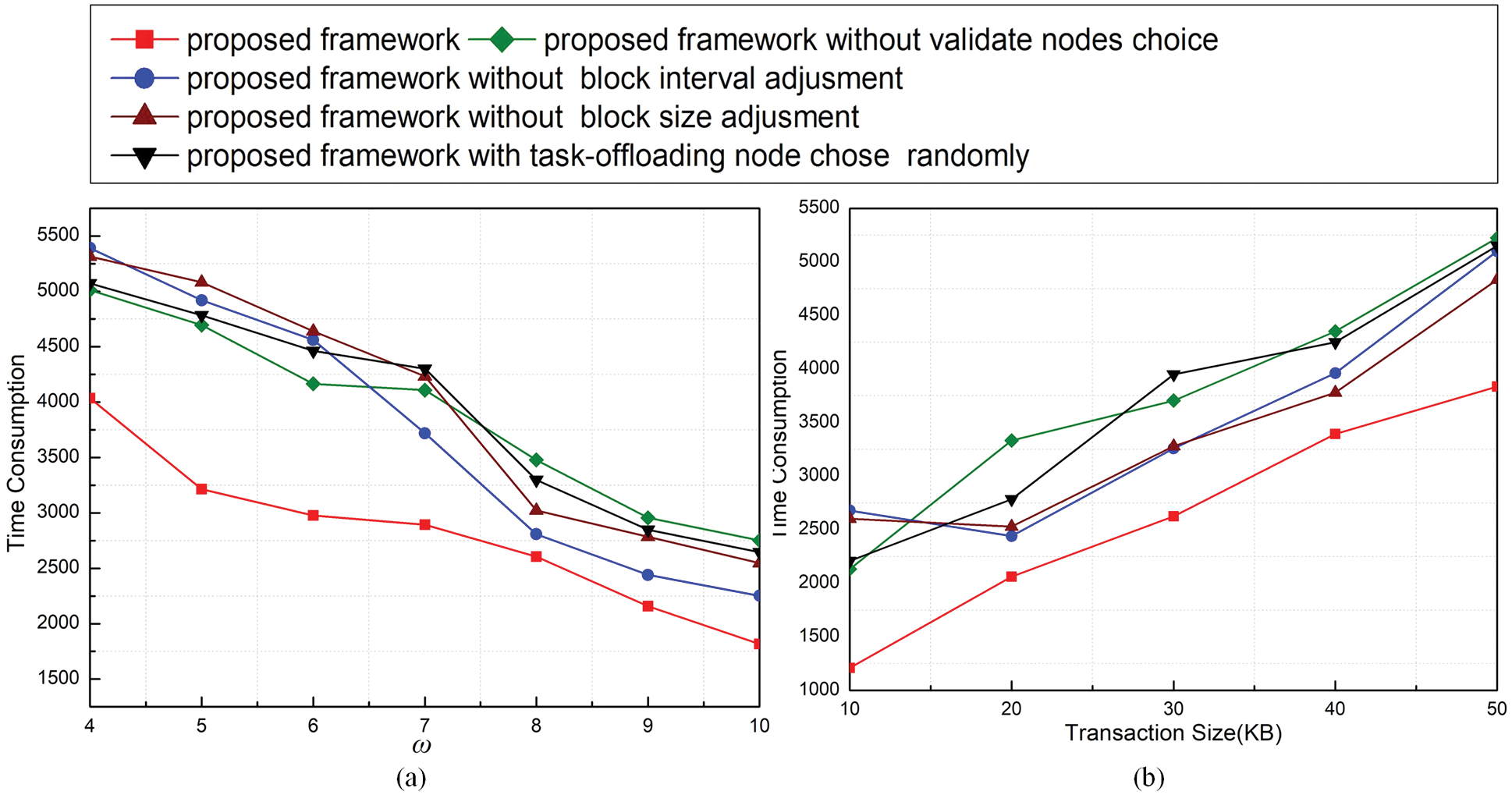
Figure 5: Time consumption under different thresholds of ω (a) and transaction sizes (b)

5  Conclusions and Future Work

In this paper, we propose an optimization scheme of trusted task offloading to ensure data security and efficiency in a dynamic IIoT scenario based on a DQN algorithm. The system performance considers overall latency and the throughput of the blockchain. We formulate the task allocation decision and blockchain performance optimization problem as an MDP. To solve the high dimensional and dynamic problem, a DQN-based approach is proposed to dynamically select actions and adjust parameters to achieve the optimal general performance of MEC and blockchain systems while the security and integrity of data can be guaranteed. The simulation results show that the proposed scheme can significantly improve the system’s performance. In future work, we will study superior verification node selection strategies and optimize the DQN algorithm to solve the multi-objective optimization problem of more action combinations. Meanwhile, the states of a real scenario is more complex, so we will improve our scheme in a real IIoT scenario.

Acknowledgement: I would like to thank Professor Mei Song for her important comments, Professor Yinglei Teng for her meaningful guidance on the architecture and my friend Ximing Xing for his contribution to the paper.

Funding Statement: This work was supported by the Projects of Software of Big Data Processing Tool (TC210804V-1) and Big Data Risk Screening Model Procurement (No. S20200).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. He, Y. Wang, C. Qiu, Q. Lin, J. Li et al., “Blockchain-based edge computing resource allocation in IoT: A deep reinforcement learning approach,” IEEE Internet of Things Journal, vol. 8, no. 4, pp. 2226–2237, 2021. [Google Scholar]

 2.  X. Wang, C. Wang, X. Li, V. C. Leung and T. Taleb, “Federated deep reinforcement learning for internet of things with decentralized cooperative edge caching,” IEEE Internet of Things Journal, vol. 7, no. 10, pp. 9441–9455, 2020. [Google Scholar]

 3.  H. Zhang, Y. Xiao, S. Bu, D. Niyato, F. R. Yu et al., “Computing resource allocation in three-tier IoT fog networks: A joint optimization approach combining stackelberg game and matching,” IEEE Internet of Things Journal, vol. 4, no. 5, pp. 1204–1215, 2017. [Google Scholar]

 4.  X. Wang, Y. Han, C. Wang, Q. Zhao, X. Chen et al., “In-edge AI: Intelligentizing mobile edge computing, caching and communication by federated learning,” IEEE Network, vol. 33, no. 5, pp. 156–165, 2019. [Google Scholar]

 5.  X. Li, X. Wang, P. J. Wan, Z. Han and V. C. Leung, “Hierarchical edge caching in device-to-device aided mobile networks: Modeling, optimization, and design,” IEEE Journal on Selected Areas in Communications, vol. 36, no. 8, pp. 1768–1785, 2018. [Google Scholar]

 6.  X. Zhang, R. Li and B. Cui, “A security architecture of VANET based on blockchain and mobile edge computing,” in Proc. IEEE Int. Conf. on Hot Information-Centric Networking (HotICN), Shenzhen, Guangdong, China, pp. 258–259, 2018. [Google Scholar]

 7.  X. Xu, X. Zhang, H. Gao, Y. Xue, L. Qi et al., “BeCome: Blockchain-enabled computation offloading for IoT in mobile edge computing,” IEEE Transactions on Industrial Informatics, vol. 16, no. 6, pp. 4187–4195, 2020. [Google Scholar]

 8.  J. Wang, B. Wei, J. Zhang, X. Yu and P. K. Sharma, “An optimized transaction verification method for trustworthy blockchain-enabled IIoT,” Ad Hoc Networks, vol. 119, no. 1, pp. 102526, 2021. [Google Scholar]

 9.  J. Y. Zhang, S. Q. Zhong, T. Wang, H. C. Chao and J. Wang, “Blockchain-based systems and applications: A survey,” Journal of Internet Technology, vol. 21, no. 1, pp. 1–14, 2020. [Google Scholar]

10. Z. Xu, W. Liang, K. C. Li, J. Xu and H. Jin, “A Blockchain-based roadside unit-assisted authentication and key agreement protocol for internet of vehicles,” Journal of Parallel and Distributed Computing, vol. 149, no. 1, pp. 29–39, 2021. [Google Scholar]

11. J. Wang, W. Chen, L. Wang, R. S. Sherratt, O. Alfarraj et al., “Data secure storage mechanism of sensor networks based on blockchain,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2365–2384, 2020. [Google Scholar]

12. J. Kang, R. Yu, X. Huang, M. Wu, S. Maharjan et al., “Blockchain for secure and efficient data sharing in vehicular edge computing and networks,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 4660–4670, 2019. [Google Scholar]

13. L. Yang, M. Li, P. Si, R. Yang, E. Sun et al., “Energy-efficient resource allocation for blockchain-enabled industrial internet of things with deep reinforcement learning,” IEEE Internet of Things Journal, vol. 8, no. 4, pp. 2318–2329, 2021. [Google Scholar]

14. J. Wang, W. Chen, Y. Ren, O. Alfarraj and L. Wang, “Blockchain based data storage mechanism in cyber physical system,” Journal of Internet Technology, vol. 21, no. 6, pp. 1681–1689, 2020. [Google Scholar]

15. R. A. Khalil, N. Saeed, M. Masood, Y. M. Fard, M. S. Alouni et al., “Deep learning in the industrial internet of things: Potentials, challenges, and emerging applications,” IEEE Internet Things, vol. 8, no. 12, pp. 11016–11040, 2021. [Google Scholar]

16. E. Sisinni, A. Saifullah, S. Han, U. Jennehag and M. Gidlund, “Industrial internet of things: Challenges, opportunities, and directions,” IEEE Trans. Ind. Inform, vol. 14, no. 11, pp. 4724–4734, 2018. [Google Scholar]

17. N. Saeed, M. S. Alouini and T. Y. AI-Naffouri, “Toward the internet of underground things: A systematic survey,” IEEE Commun. Surv. Tutor, vol. 21, no. 2, pp. 3443–3466, 2019. [Google Scholar]

18. F. Liang, W. Yu, X. Liu, D. Griffith and N. Golmie, “Toward edge-based deep learning in industrial internet of things,” IEEE Internet Thing, vol. 7, no. 1, pp. 4329–4341, 2020. [Google Scholar]

19. S. Latif, M. Driss, W. Boulila, Z. Huma, S. S. Jamal et al., “Deep learning for the industrial internet of things (IIoTA comprehensive survey of techniques, implementation frameworks, potential applications, and future directions,” Sensors, vol. 21, no. 21, pp. 7518–7562, 2021. [Google Scholar]

20. A. Islam, A. Debnath, M. Ghose and S. Chakraborty, “A survey on task offloading in multi-access edge computing,” Journal of Systems Architecture, vol. 118, no. 13, pp. 1–16, 2021. [Google Scholar]

21. P. Mach and Z. Becvar, “Mobile edge computing: A survey on architecture and computation offloading,” IEEE Communications Surveys & Tutorials, vol. 19, no. 3, pp. 1628–1656, 2017. [Google Scholar]

22. J. Liu, Y. Mao, J. Zhang and K. B. Letaief, “Delay-optimal computation task scheduling for mobile-edge computing systems,” in Proc. IEEE Int. Symp. on Information Theory (ISIT), Barcelona, Spain, pp. 1451–1455, 2016. [Google Scholar]

23. C. Shu, Z. Zhao, Y. Han, G. Min and H. Duan, “Multi-user offloading for edge computing networks: A dependency-aware and latency-optimal approach,” IEEE Internet of Things Journal, vol. 7, no. 3, pp. 1678–1689, 2019. [Google Scholar]

24. R. Xie, Q. Tang, C. Liang, F. R. Yu and T. Huang, “Dynamic computation offloading in IoT fog systems with imperfect channel-state information: A POMDP approach,” IEEE Internet of Things Journal, vol. 8, no. 1, pp. 345–356, 2021. [Google Scholar]

25. D. Miller, “Blockchain and the internet of things in the industrial sector,” IT Professional, vol. 20, no. 3, pp. 15–18, 2018. [Google Scholar]

26. H. Wu, K. Wolter, P. Jiao, Y. Deng, Y. Zhao et al., “EEDTO: An energy-efficient dynamic task offloading algorithm for blockchain-enabled IoT-edge-cloud orchestrated computing,” IEEE Internet of Things Journal, vol. 8, no. 4, pp. 2163–2176, 2021. [Google Scholar]

27. X. G. Huang, X. S. Deng, C. C. Liang and W. W. Fan, “Blockchain-enabled task offloading and resource allocation in fog computing networks,” Wireless Communications & Mobile Computing, vol. 2021, no. 1, pp. 1–12, 2021. [Google Scholar]

28. C. Qiu, F. R. Yu, H. Yao, C. Jiang, F. Xu et al., “Blockchain-based software-defined industrial internet of things: A dueling deep q-learning approach,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 4627–4639, 2019. [Google Scholar]

29. D. C. Nguyen, P. N. Pathirana, M. Ding and A. Seneviratne, “Privacy-preserved task offloading in mobile blockchain with deep reinforcement learning,” IEEE Transactions on Network and Service Management, vol. 17, no. 4, pp. 2536–2549, 2020. [Google Scholar]

30. J. Feng, F. R. Yu, Q. Pei, X. Chu, J. Du et al., “Cooperative computation offloading and resource allocation for blockchain-enabled mobile-edge computing: A deep reinforcement learning approach,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 6214–6228, 2020. [Google Scholar]

31. J. Almutairi and M. Aldossary, “Exploring and modelling IoT offloading policies in edge cloud environments,” Computer Systems Science and Engineering, vol. 41, no. 2, pp. 611–624, 2022. [Google Scholar]

32. J. Almutairi and M. Aldossary, “Investigating and modelling of task offloading latency in edge-cloud environment,” Computers, Materials & Continua, vol. 68, no. 3, pp. 4143–4160, 2021. [Google Scholar]

33. K. Sakthidasan, B. Twala, S. Yuvaraj, K. Vijayan, S. Praveenkumar et al., “State-based offloading model for improving response rate of IoT services,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3721–3735, 2021. [Google Scholar]

34. Y. Xu, Z. Jin, X. Zhang and L. Zhang, “An optimization scheme for task offloading and resource allocation in vehicle edge networks,” Journal of Internet of Things, vol. 2, no. 4, pp. 163–173, 2020. [Google Scholar]

35. J. Zhang, S. Zhong, J. Wang, X. Yu and O. Alfarraj, “A storage optimization scheme for blockchain transaction databases,” Computer Systems Science and Engineering, vol. 36, no. 3, pp. 521–535, 2021. [Google Scholar]