Hybrid Global Optimization Algorithm for Feature Selection

1  Introduction

The Concept of swarm intelligence (SI) principle, is highly inspired by the recent advancement in the field of Neuroscience and the Behavioral Science, commonly known as intelligent paradigm in Intelligence Computational domain, to solve the optimization issues of various problems in absence of any global models [1,2]. As a result, the swarm concept, inspired by the mutual attitudes of gregarious animals (like a herd of animals, birds, fishes, ants, cats, and fireflies), is used to discuss intelligent agents in a distributed system [3]. A swarm is an aggregation of identical objects which may accomplish some task, may interact among themselves in a predefined manner, may react to surrounding environments, in absence of any central governing entity. Algorithms which are based upon this kind of behavior, imitate natural appearing phenomenon, an efficient and viable solution to several complex problems [4]. In these circumstances, Particle Swarm Optimization or better known as PSO, open horizons for meta-heuristic global optimization techniques evolved from concepts of swarm intelligence [5].

Kennedy et al., proposed a particle swarm optimization algorithm, based on meta-heuristics evolved from swarm intelligence methodologies, it can emulate cordial movement patterns of flocks of birds and flying patterns of birds, it has capabilities for intercommunication among group members, to assist them in decision making processes, in a coherent synchronized manner [5].

Swarms are simulated, as if flocks are out in search of their food, any particular individual in the flock, determines its relative speed and position by calculating these two attributes of its neighbors speed and positions among the flock members. During Optimization of solution space, a swarm particle in a PSO changes its positions in a multidimensional space. This phenomenon reconciles location of particle under solution space for the problem being optimized. These particles are controlled by a tradeoff of memory between the group and the individuals. As stated in [5,6], the main idea of particle swarm optimization was influenced by bird flocks hunting food sources. Previous research has demonstrated that optimization using the PSO method yields accurate results. In a PSO algorithm, a particle’s movement is determined by its location and velocity.

Iteratively, the particle velocity determines its route. The particle velocity is determined by three key factors. The first component, a social component, tries to dominate the best position for all particles I during a single iteration or to keep the global best position till the next iteration, which is termed the current global best position (gbesti), where i is the particle’s index. The second component, a cognitive component, tries to dominate each particle I in the swarm individually, or the personal best for a given particle, until the present iteration, dubbed the current best for particle i. (pbesti). The third component, a momentum component, determines the influence of each particle’s past velocity and is considered a modification of the original PSO described in [7]. The PSO’s position and velocity are determined by Eqs. (1) and (2).

vi(t+1)=wvi(t)+((c1r1)×pbesti(t)−xi(t))+((c2r2)×gbesti(t)−xi(t))(1)

xi(t+1)=xi(t)+vi(t+1)(2)

where xi(t) denotes the location of a particle i at time t, and vi(t) denotes the velocity of a particle i at time t. w is the inertial weight that prevents particles from drifting away from their optimal places without attaining convergence; The time-variant acceleration coefficients (TVAC) c1 and c2 strive to alter the weight of two components, social and cognitive, in order to dominate personal and local optimal attitudes [8]; pbesti(t) is the best-known position of particle i at a specific time t; gbesti(t) is the best-known position of a neighbor particle to i; and r1 and r2 are independent random values in a range of [0, 1]. The PSO algorithm begins its computational steps to determine the current position of each particle, and then checks if this position is optimal to attain the best position. The next step involves computing the velocity of the particle using Eq. (1) and then updating the position of the particle using Eq. (2). Initially, when a cognitive component is large and a social component is small, the particles move around the search space instead of moving across the best population. Furthermore, when the cognitive component is low, and the social component is large, the particles converge at the global optima of the latter part of optimization.

The proposed Parallelized Linear Time-Variant Acceleration Coefficients and Inertial Weight of PSO (PLTVACIW-PSO) algorithm, based on a hybridization of the linearity of time-variant acceleration coefficients and a linear decrease of the inertial weight associated with the parallel processing of PSO fitness evaluation, will be used in this paper. The proposed algorithm will be used to optimize 12 known benchmark functions, varying in their properties and scales. The optimization of these functions tends to minimize the errors generated in the sequential iterations of the proposed PLTVACIW-PSO vs. other PSO TVAC algorithms, PSO IW algorithms, GA and DE algorithms, and, lastly, BAT and Multi-swarm BAT algorithms. The four categories mentioned before are shown in Tab. 1. The first category is the “IW family”, which consists of four parallelized and non-parallelized inertial weight-based PSO algorithms called PLIW-PSO, LIW-PSO, PNLIW-PSO, and NLIW-PSO. The second category is the “TVAC family”, which consists of four parallelized and non-parallelized TVAC based PSO algorithms called PLTV-PSO, LTV-PSO, PNLTV-PSO, and NLTV-PSO. The third category includes traditional algorithms: PSO, the Differential Evolution algorithm (DE), the Genetic algorithm (GA), and the Flower Pollination Algorithm (FPA). Finally, two bio-inspired algorithms are compared: the BAT and Multi swarm-BAT algorithms.

2  Preliminaries

The PSO algorithm utilises meta-parameters, which controls the swarm actions for efficient optimization and it effective in enhancing searchability of a particle in the swarm. The convergence characteristics parameters of PSO algorithm are dependent upon controlling parameters, hence impact on controlling parameters also impacts convergence characteristics. Therefore, the functions of these meta-parameters and their influence on the conclusive results are crucially importance for designing an efficient optimization algorithm [7].

2.1 Swarm Initialization

The random position of each particle is the initialization step in the PSO algorithm, which starts inside an iteration to keep searching for optimal solutions. The velocities and positions for each particle are determined in every iteration until the final iteration or until any stopping criteria are provided.

Non-uniformly disseminated introductory particles impact the minimal stability properties of the PSO algorithm. Furthermore, the convergence of the particle’s velocity in the swarm is dependent on the initial population [17].

2.2 Parameter Determination

The PSO algorithm’s control parameters are the inertial weight and acceleration coefficients. The correct setting of these parameters can have an impact on the PSO’s convergence. The PSO algorithm’s cognitive and social components are influenced by the acceleration coefficients c1 and c2 [18,19]. The acceleration coefficients [20] refer to the speed at which the particles are moved to the swarm’s most precise location and superior position. They tweak a particle’s distance and timing to get it into the best possible spot. If the acceleration coefficients are excessively great, the particle may go past the right place by accident. If the acceleration coefficients are too little, the particle will not be able to reach its intended position. This maximum particle’s velocity (Vmax) identifies the intention, which controls the areas between the current particle’s position and the target particle’s position [21]. If Vmax value is too high, the particles could miss well-known locations. However, if Vmax is too small, the particles may not reach very distant places. Therefore, the determination of Vmax should be tuned by using a weight factor, which should be added to the PSO equation (Eq. (1)) [20]. This weight is understood as inertial weight (w), which aims to dominate the speed of the arrival at the best location during the final iteration. An increase in the value of w enhances global searchability, whereas a decrease in the value of w enhances partial searchability.

2.3 Parameters Enhancements

To increase the performance of the PSO algorithm, the TVAC was upgraded [8,11]. TVAC may raise or reduce the swarm’s cognitive and social behavior in a linear fashion. In other words, allowing the swarm to travel the whole search area by enhancing cognitive aspects and minimizing social factors in the early phases of the optimization process. The convergence of all particles toward the global optima at the conclusion of the optimization process is improved by reducing cognitive aspects and enhancing social ones. Nonlinear inertial weight variation might be used as a benchmark for nonlinearly enhancing acceleration coefficients [10]. Instead of manually establishing the inertial weight parameters, the speed of convergence of the relevant particles in the swarm might be enhanced. The following equations indicate improvements to c1 and c2:

c1=(c1f−c1i)×(iterMAXITER)+c1i(3)

c2=(c2f−c2i)×(iterMAXITER)+c2i(4)

where c1i, c1f and c2i, c2f are the initial and final values of c1 and c2, respectively; iter is the currently running iteration; and MAXITER is the maximum number of iterations the algorithm will perform.

Another strategy for enhancing the swarm’s particle convergence rate is linear inertial weight w adaptation [9]. The upper and lower inertial weight limits are established, and a new inertial weight value is computed and evaluated in each iteration to adjust the swarm to the optimal location in the search space. The improvement in inertial weight w is seen in the following equation:

w=(wmax)−(iter×(wmax−wmin)MAXITER)(5)

where w1 and w2 are the initial and final values of w, respectively.

2.4 Parallel Processing of the PSO Algorithm

The PSO algorithm’s execution time was reduced and the fitness assessment of individual particles in the swarm was reduced by parallel processing of objective functions across multiples of the independent machine in the form of a cluster [22]. Before calculating a new velocity and location in subsequent rounds of the PSO algorithm, all participating machines must achieve global synchronization to ensure that each particle’s fitness is computed and finished. The study in [11] uses an updated version of the parallelization of the PSO method based on the distribution of the objective function evaluation and the available identified cores, which is based on the previous perspective. This viewpoint is used in this study.

3  Proposed Algorithm

The capacity of particles in the swarm to cover the search space and give consistent results will be restricted if the social factor is smaller than the cognitive element utilized in classic PSO algorithms (such as those demonstrated in [5]). As seen in [7], an incorrectly set inertial weight slows down the PSO algorithm’s convergence speed. Furthermore, as the optimization issue becomes more intricate in its intricacies, the swarm performance degrades, resulting in a longer PSO method execution time.

By introducing the technique that will be proven in this work, the aforementioned issues are alleviated. The Parallelized linear TVAC and inertial weight of PSO, or “PLTVACIW-PSO,” is a suggested method that takes use of the benefits of linearity for each time-variant acceleration coefficient described in [8,11] and the linearity of the inertial weight presented in [9]. PLTVACIW-PSO also employs the parallelization viewpoint described in [11,22]. Algorithm 1 shows the proposed PLTVACIW-PSO.

The proposed method PLTVACIW-PSO takes a benchmark function as input and treats it as the goal function. The swarm iterates in PLTVACIW-PSO based on changes made to the inertial weight w and TVAC parameters, as well as parallelization of the objective function evaluation and the optimized value produced for the given objective function at each iteration; finally, the smallest optimized value is chosen from all values produced by all executed iterations.

4  Results, Analysis, and Discussions

There are two stages to the experiment described in this study. Phase one compares three kinds of algorithms to the proposed method PLTVACIW-PSO, which is utilized to optimize twelve distinct benchmark functions. The “IW family” is the first category, which contains algorithms that use PSO’s parallelized and non-parallelized inertial weight. The “TVAC family,” which comprises algorithms based on PSO’s parallelized and non-parallelized TVAC, is the second category. Traditional algorithms such as PSO, differential evolution (DE), the genetic algorithm (GA), and the flower pollination algorithm (FPA) are included in the third category [11]. In phase two, the proposed PLTVACIW-PSO algorithm is compared against a group of algorithms that comprises two bio-inspired optimizations, the BAT and Multi-swarm BAT algorithms [16]. The experimental results found in [11,16] are also compared with the results achieved from the proposed algorithm. These functions’ definitions and attributes are used to show how efficient and successful any particular optimization strategy [23,24]. The benchmark functions utilized in this study were chosen based on two criteria. Modality (single mode or multi-mode) and separability are two of these requirements (separable or non-separable). The multi-mode function has two or more local optima, while the unimodal function has just one. A separable function is one that has no interrelations between the variables that make up the function, while a non-separable function contains interrelations between the variables that make up the function. Twelve benchmark functions from [11,16] are utilized in this study to compare the proposed PLTVACIW-PSO method to the other algorithms listed in Tab. 1 (functions F11 and F12 are mentioned in [11] only).

4.1 Model Evaluation

The proposed PLTVACIW-PSO algorithm used in phase one is a stochastic iterative PSO algorithm by nature, which indicates that an optimized result will be produced during each iteration for any given function listed in Appendix A. Therefore, the values of Worst, Best, and Mean of Mean Square Error (MSE), represented in Eq. (6), are recorded for any set of iterations produced by any given function.

MSE=∑i=1n(Ei−Pi)2n(6)

where Ei is the actual experimental values, Pi are predictive values, and n are test data being used. The value of “Worst” indicates the most significant value of MSE along with the optimization iterations. The value of “Best” is the smallest MSE value given along with the optimization iterations. Finally, the value of “Mean” is delivered by calculating the average of all MSE values along with their optimization iterations.

A series of independent runs is used to generate accurate findings from the stochastic based methods indicated in Tab. 1 [11,16]. Fifty different algorithm executions are done in this work, and the best run is picked. This run provides the best overall results for the proposed PLTVACIW-PSO method and all other algorithms for Worst, Bestm, and Mean. In this experiment, the same fifty separate runs were performed, and the best overall performance was chosen. Furthermore, for all algorithms, including the proposed PLIWTVAC-PSO, the average of the Worst, Best, and Mean values for the fifty separate executions is chosen for functions F1–3.

For the proposed PLIWTVAC-PSO, 100 separate executions are done, and the average values of Worst, Best, and Mean, as well as the best overall execution for the proposed PLIWTVAC-PSO, are chosen and compared to the BAT and MBAT algorithms.

4.2 Experimental Platform

In this paper, the implementation of both PLTVACIW-PSO algorithms was done using R language version 3.3.0, executed on a virtualized CentOS Linux operating system with a 2 GHz dual-core processor, 5 GB RAM, and 20 GB of non-volatile storage.

4.3 Experimental Parameters

For the IW family algorithms used in phase 1, inertial weight wrang = (0.4, 09), swarm size = 50, and iterations = 100. For the TVAC family algorithms used in phase one, inertial weight w = 0.721, c1rang = (1.28: 1.05), c2rang = (1.05: 1.28), and iterations = 100. For PSO, swarm size = 50, w = 0.721, c1 = 1.193, c2 = 1.193, and iterations = 100. For the DE algorithm used in phase I, population size = 50, crossover probability = 0.5, differential weighting factor = 0.8, and iterations = 100. For the GA used in phase I, population size = 50, crossover probability = 0.8, mutation probability = 0.1, and iterations = 100. For the FPA used in phase 1, population size = 25, probability switch = 0.8, and iterations = 100.

In phase II, the same configurations for phase I are used for PLTVACIW-PSO.

4.4 Result Analysis

Phase I

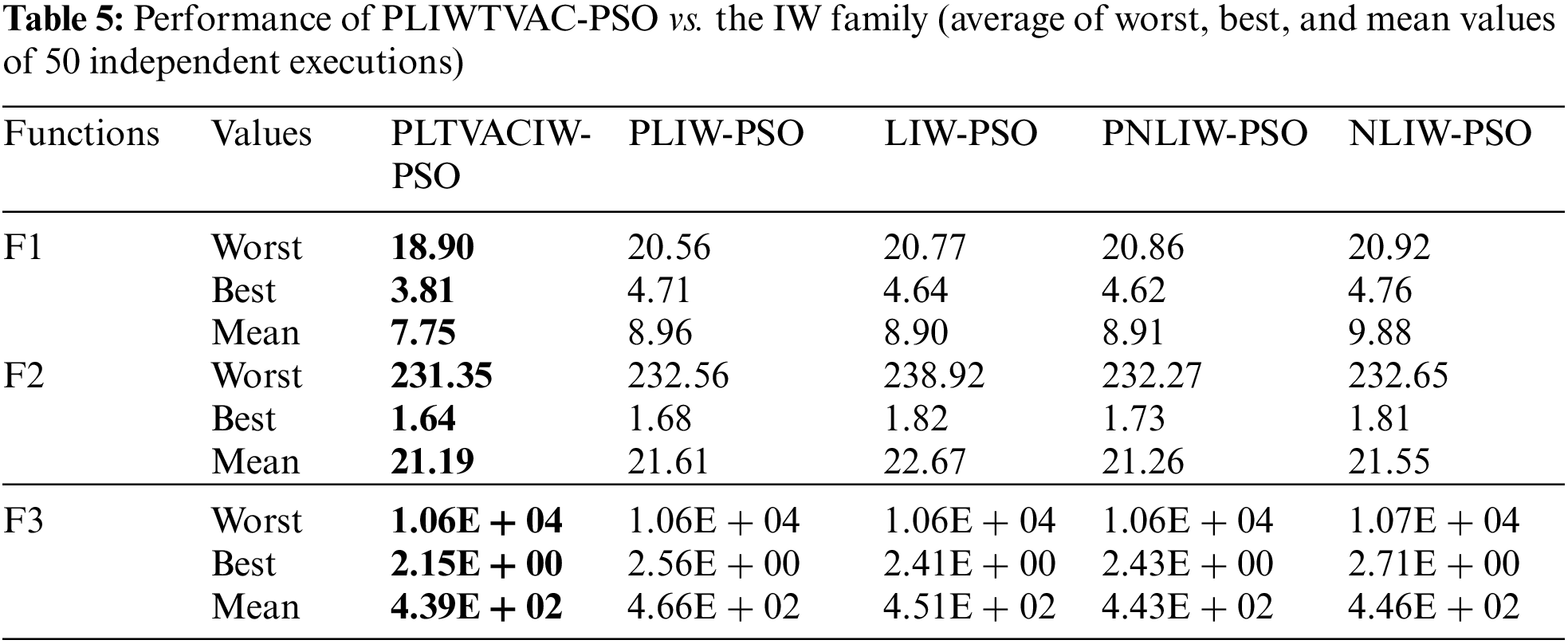
Three different experiments were conducted in phase one to illustrate the capabilities of the proposed PLTVACIW-PSO algorithm. The first experiment compares the proposed PLIWTVAC-PSO with the IW family mentioned earlier in Tab. 1. These experimental results are illustrated in Tab. 2.

The second experiment compares the proposed PLIWTVAC-PSO with the TVAC family, including the PLTV-PSO algorithm; this family is mentioned in Tab. 1. These experimental results are illustrated in Tab. 3.

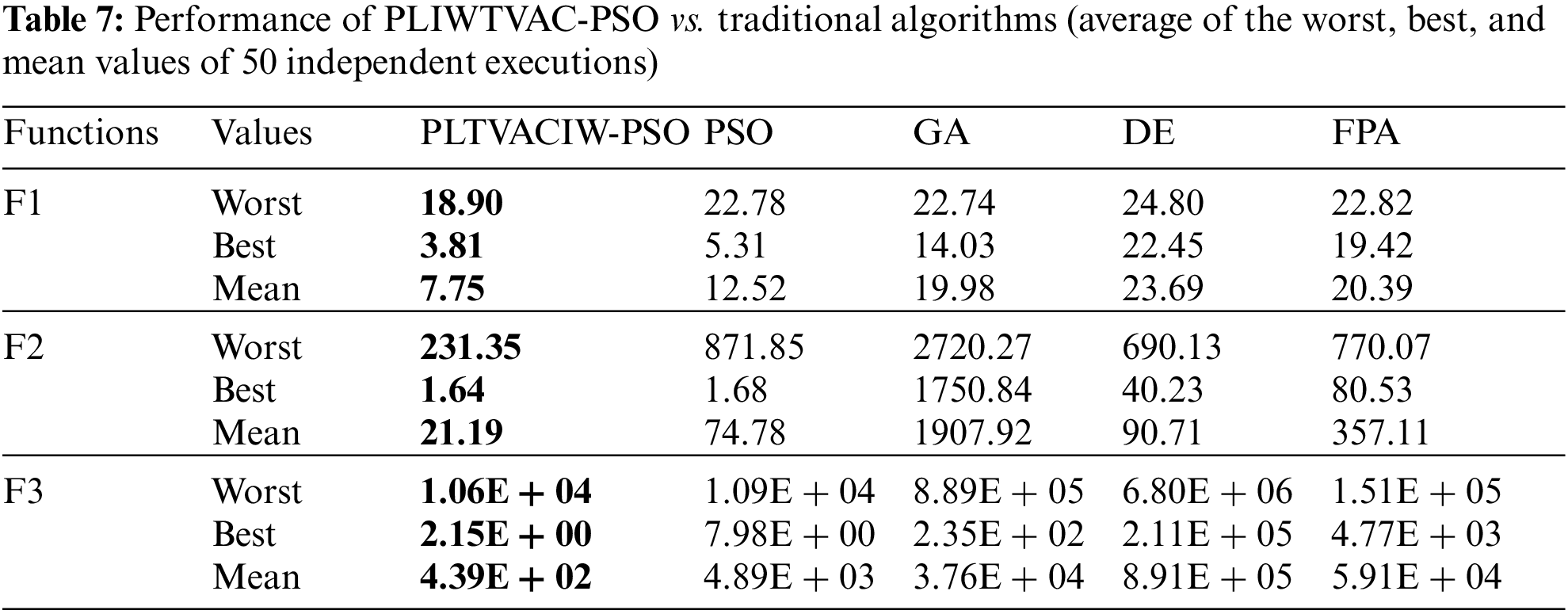
Finally, the third experiment aims at comparing the proposed PLIWTVAC-PSO with the traditional algorithms and the BAT algorithms as mentioned earlier in Tab. 1. The third experiment’s results are presented in Tab. 4. The same 50 independent executions were also carried out in this experiment, and the best overall execution is determined.

Setting the IW to the highest value, which permits particles to travel at a fast speed and participate in extensive exploration, increases the exploration behavior of particles in the proposed PLIWTVAC-PSO algorithm towards the nearest position of the optimal value. Following that, IW repeatedly declines linearly to lower levels, causing the particles to travel slowly and engage in more deliberate investigation. As a consequence, lowering the Worst values acquired in early iterations provides the swarm with greater Best values during its final rounds than other IW family algorithms. Furthermore, the mean value indicates that the proposed PLIWTVAC-PSO yields modest Worst values in early iterations and converges to optimal Best values in middle and final iterations. Tab. 3 demonstrates that there are many more improvements to the PLTV-PSO algorithm by linearly decreasing the IW method in the form of the proposed PLIWTVAC-PSO. The linear TVAC and IW may help the swarm’s overall behavior. When linear TVAC is combined with linearly decreasing IW, the exploration behavior of all particles in the swarm is significantly improved; the worst values obtained during earlier iterations are significantly reduced, and the best values are obtained during the final iterations, affecting the overall Mean values obtained by all iterations of the proposed PLIWTVAC-PSO. Tab. 4 shows demonstrates the suggested PLIWTVAC-PSO outperforms other standard algorithms for the Worst, Best, and Mean values, respectively, than PSO, DE, GA, and FPA algorithms. Other algorithms, like as GA and DE, have a lot more parameters to tune, such as crossover and mutation probabilities.

The average values of the Worst, Best, and Mean are acquired from 50 different executions for the proposed PLIWTVAC-PSO, IW family algorithms, TVAC family algorithms, and conventional algorithms to verify that the proposed algorithm PLIWTVAC-PSO obtains trustworthy results. Functions F1–3 are used in this supplementary experiment. These findings are shown in Tabs. 5–7. The data in Tabs. 5–7 demonstrate that the proposed PLIWTVAC-PSO algorithm is successful, and that the linearity of both TVAC and IW combined effectively manages the swarm toward the best outcomes. Furthermore, the optimized outcomes from 50 separate executions do not differ much from one to the next.

Phase II

We employed ten benchmark medical datasets in this phase. The datasets were taken from the University of California, Irvine’s learning machine server [25]. A short explanation of each chosen dataset may be found in Tab. 8. As can be seen, several entries in the adopted data sets are missing. In this article, the median value of all known values of the functional class is substituted by all of these missing values. The mathematical definition of the median is as follows:

s¯i,j=mediani:si,j∈WrSi,j(7)

where si, j is the missing value for a specific ith class W’s jth feature. For missing categorical values, the most typically replaced value is the missing value for a specific class function.

Three parameters are used to test PLIWTVAC-PSO selected features. Other requirements include accuracy of classification, number of specified features and CPU processing time have been considered [26]. Tab. 9 provides a distinction between feature selection, classification accuracy and processing time before and after applying PLIWTVAC-PSO.

The number of features and the mean accuracy of 10 folds are presented together with CPU processing time. Only a subset of characteristics may reduce classification efficiency, but computation time and storage can be greatly reduced. Fig. 1 depicts a comparison of feature selection and classification accuracy before and after PLIWTVAC-PSO application. Such findings illustrate the superiority of the PLIWTVAC-PSO selection method. These traits may also be utilized to increase clustering performance. Clusters made consisting of a selection of important qualities are more realistic and understandable than clusters made up of all of them, such as noise. It may also aid in the interpretation and comprehension of facts.

Figure 1: Feature selection and classification accuracy before and after applying PLIWTVAC-PSO for medical datasets

5  Conclusions

The suggested PLTVACIW-PSO algorithm outperforms PSO IW-based algorithms, TVAC algorithms, GA and DE algorithms, and even multi-swarm-based algorithms in terms of efficiency and efficacy. This demonstrates that combining the linearity of IW and TVAC may adjust a single swarm-based PSO algorithm to get optimal outcomes. Furthermore, the suggested PLTVACIW-PSO method tends to reduce the worst values from earlier iterations in order to attain the best value during the final rounds, demonstrating that the proposed algorithm is an effective and reliable global optimization technique. The suggested PLTVACIW-PSO Algorithm was used to verify ten medical datasets. The findings suggest that PLTVACIW-PSO can increase classification, consistency, the number of features picked, and convergence speed by a substantial amount.

Future work could include switching between the linearity of IW and the non-linearity of TVAC and vice versa, replacing PSO parallelization across multiple cores with a dedicated board of CPUs, and finally, instead of using a single swarm, the proposed PLTVACIW-PSO can use multiple swarms of particles. PLTVACIW-results PSO’s may be used to verify increasingly difficult challenges in science and contemporary engineering in the future.

Acknowledgement: The authors would like to thank Prince Sultan University, Riyadh, Saudi Arabia for paying the Article Processing Charges (APC) of this publication. Special acknowledgement to Automated Systems & Soft Computing Lab (ASSCL), Prince Sultan University, Riyadh, Saudi Arabia. Also, the authors wish to acknowledge the editor and anonymous reviewers for their insightful comments, which have improved the quality of this publication.

Funding Statement: This research was funded by the Prince Sultan University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. Eberhart, Y. Shi and J. Kennedy, Swarm Intelligence, Burlington, MA: Morgan Kaufmann, 2001. [Google Scholar]

 2.  G. Beni and J. Wang, Swarm Intelligence, Tokyo, Japan: RSJ Press, pp. 425–428, 1989. [Google Scholar]

 3.  M. Ab-Wahab, S. Nefti-Meziani and A. Atyabi, “A comprehensive review of swarm optimization algorithms,” PLoS One, vol. 10, no. 5, pp. e0122827, 2015. [Google Scholar]

 4.  C. Blum and D. Merkle, Swarm Intelligence: Introduction and Applications, Heidelberg, Germany: Springer verlag, 2008. [Google Scholar]

 5.  J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Internal Conf. on Neural Networks, Perth Australia, vol. 4, pp. 1942–1948, 1995. [Google Scholar]

 6.  S. Rana, S. Jasola and R. Kumar, “A review on particle swarm optimization algorithms and their applications to data clustering,” Artificial Intelligence Revision, vol. 35, pp. 211–222, 2011. [Google Scholar]

 7.  Y. Shi and R. Eberhart, “A modified particle swarm optimizer,” in IEEE Int. Conf. on Evolutionary Computation Proc., IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, USA, 4–9 May 1998. https://doi.org/10.1109/ICEC.1998.699146. [Google Scholar]

 8.  A. Ratnaweera, S. K. Halgamuge and H. C. Watson, “Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients,” IEEE Transactions on Evolutionary Computation, vol. 8, no. 3, pp. 240–255, 2004. [Google Scholar]

 9.  Y. Zheng, L. Ma, L. Zhang and J. Qian, “Empirical study of particle swarm optimizer with an increasing inertia weight,” in 2003 Congress on Evolutionary Computation (CEC ‘03), Canberra, ACT, Australia, 8–12 Dec. 2003. https://doi.org/10.1109/CEC.2003.1299578. [Google Scholar]

10. E. -S. M. El-kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information and Control, vol. 16, no. 3, pp. 831–844, 2020. [Google Scholar]

11. K. Fouad, T. Elsheshtawy and M. Dawood, “Parallelized linear time-variant acceleration coefficients of PSO algorithm for global optimization,” in 12th Int. Conf. on Computer Engineering and Systems (ICCES), Cairo, Egypt, 21–22 Oct. 2016. https://doi.org/10.1109/ICCES.2017.8275369. [Google Scholar]

12. P. Chen, C. Wu, Y. Fu and C. KO, “A PSO method with nonlinear time-varying evolution for the optimal design of PID controllers in a pendubot system,” Artif Life Robotics, vol. 14, no. 1, pp. 58–61, 2009. [Google Scholar]

13. K. Price, R. Storn and J. Lampinen, Differential Evolution-A Practical Approach to Global Optimization, Berlin Heidelberg: Springer-Verlag, ISBN 3540209506, 2006. [Google Scholar]

14. E. -S. M. El-kenawy, A. Ibrahim, S. Mirjalili, Y. Zhang, S. Elnazer et al., “Optimized ensemble algorithm for predicting metamaterial antenna parameters,” Computers Materials & Continua, vol. 71, pp. 4989–5003, 2022. [Google Scholar]

15. X. S. Yang, “Flower pollination algorithm for global optimization,” in J. Durand-Lose and N. Jonoska (Eds.) Unconventional Computation and Natural Computation. UCNC 2012, Lecture Notes in Computer Science, Berlin, Heidelberg: Springer, vol. 7445, pp. 240–249, 2012. https://doi.org/10.1007/978-3-642-32894-7_27. [Google Scholar]

16. G. Wang, B. Chang and Z. Zhang, “A multi-swarm bat algorithm for global optimization,” in IEEE Congress on Evolutionary Computation (CEC 2015), Sendai, Japan, 25–28 May 2015. https://doi.org/10.1109/CEC.2015.7256928. [Google Scholar]

17. H. Ran, W. Yong-Ji, W. Qing, Z. Jin-Hui and H. Chen-Yong, “An improved particle swarm optimization based on self-adaptive escape velocity,” Journal of Software, vol. 16, no. 12, pp. 2036–2044, 2005. [Google Scholar]

18. C. Ke, Z. Fengyu, Y. Lei, W. Shuqian and W. Yugang, “A hybrid particle swarm optimizer with sine cosine acceleration coefficients,” Information Sciences, vol. 422, pp. 218–241, 2018. [Google Scholar]

19. Z. Tang and D. Zhang, “A modified particle swarm optimization with adaptive acceleration coefficients,” in Proc. of the Asia-Pacific Conf. on Information Processing (APCIP’09), Shenzhen, China, pp. 330–332, 18–19 July 2009. [Google Scholar]

20. A. Ibrahim, H. A. Ali, M. M. Eid and E. -S. M. El-Kenawy, “Chaotic harris hawks optimization for unconstrained function optimization,” in 2020 16th Int. Computer Engineering Conf. (ICENCO), Cairo, Egypt, IEEE, pp. 153–158, 2020. [Google Scholar]

21. B. Qinghai, “Analysis of particle swarm optimization algorithm,” Computer and Information Science, vol. 3, no. 1, pp. 180–184, 2010. [Google Scholar]

22. J. Schutte, J. Reinbolt, B. Fregly, R. Haftka and A. George, “Parallel global optimization with particle swarm algorithm,” Int. J. Numerical Methods in Engineering, vol. 61, pp. 2296–231, 2004. [Google Scholar]

23. M. Jamil, X. Yang and H. Zepernick, “Test functions for global optimization: Comprehensive survey,” in X, Yang, Z. Cui, R. Xiao, A. Gandomi and M. Karamanoglu (Eds.) Swarm Intelligence and Bio-Inspired Computation, Waltham, MA: Elsevier, pp. 193–222, 2013. https://doi.org/10.1016/B978-0-12-405163-8.00008-9. [Google Scholar]

24. X. Yao, Y. Liu and G. Lin, “Evolutionary programming made faster,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 2, pp. 82–102, 1999. [Google Scholar]

25. D. Dua and C. Graff, UCI Machine Learning Repository, Irvine, CA: University of California, School of Information and Computer Science, 2019. http://archive.ics.uci.edu/ml. [Google Scholar]

26. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]