Quantum Oblivious Transfer with Reusable Bell State

1  Introduction

The concept of oblivious transfer (OT) in classical cryptography was first introduced by Rabin [1] in 1981. In the oblivious transfer protocol, a sender, Alice, wants to transfer a secret message m∈ {0,1} to a receiver, Bob. However, Bob only has a 50% probability of learning the message m. That is, Bob could either learn the message m with 100% reliability, or have zero knowledge of m. In addition, at the end of the OT protocol, Alice remains oblivious as to whether Bob learned the message m. This used to be called the all-or-nothing oblivious transfer protocol. Subsequently, the idea of one-out-of-two oblivious transfer was presented by Even et al. [2] in 1985. In one-out-of-two oblivious transfer, sender Alice wants to transfer one of two secret messages, m0 and m1, to receiver Bob, and Bob can choose which message he wishes to learn, but has no idea what the other message is. Analogously, Alice knows nothing about which message Bob learns when the protocol is over. In 1987, Crépeau [3] presented a reduction method to build a one-out-of-two OT using a p-all-or-nothing OT, in which Bob can learn the secret message m with p probability, and this reduction method is hereinafter referred to as Crépeau’s reduction. In the reduction method, Bob can learn the secret bit with p probability in each round of the all-or-nothing OT. After repeated rounds, he divides the result into two key sets, including the conclusive set key0, which is the secret bit that he learns with certainty, while he learns nothing about the secret bit for the other inconclusive set key1. According to Bob's choice j, Bob asks that Alice encrypt her message, m0 and m1, using keyj and keyJ¯, respectively. Then, Bob ultimately can learn the message mj. Using the above reduction, Crépeau proved that these two types of OT are equivalent in classical cryptography, so secure all-or-nothing OT can lead to secure one-out-of-two OT. Subsequently, ever more research into extending OT application has been undertaken, and hotly discussed [4], as with secure computation, bit commitment, remote coin-flipping, electrical contract signing, exchanging secrets simultaneously, and so on.

The classical OT protocols are based on complex mathematical problems, such as the discrete logarithm problem [4]. However, if powerful quantum computers become available in the near future, these protocols in classical cryptography will no longer be secure. Certain complex mathematical problems can be solved extremely quickly using quantum algorithms, such as Shor’s algorithm [5] or Grover’s search algorithm [6]. Therefore, as greater advances are being made toward developing quantum computing, quantum cryptography research aimed at achieving better security has begun to receive increasing attention. The security of quantum cryptography is based on physical principles rather than mathematical complexity, so it is easy to design cryptographic protocols with unconditional security, which is impossible in classical cryptography. For example, the well-known quantum key distribution (QKD) proposed by Charles Bennett and Gilles Brassard in 1984 (BB84 protocol) [7], is proven to be unconditionally secure [8,9].

Quantum oblivious transfer (QOT) has also been extensively discussed. The first all-or-nothing QOT was proposed by Crépeau et al. [10] in 1988, and Bennett et al. [11] proposed the first one-out-of-two QOT protected by quantum error correction codes (QECC) in 1991. In 1994, Crépeau presented a one-out-of-two QOT [12] based on the quantum bit commitment (QBC), but its security can only work on the assumption that Bob cannot delay the quantum measurement if the protocol lacks an auxiliary of QBC. In 1995 Yao [13] further proved that the protocol [12] is secure against coherent measurement if QBC is secure. However, in 1997, the Mayers-Lo-Chau (MLC) no-go theorem [14,15] declared that an unconditionally secure QBC does not exist, so it is impossible for any QOT protocols based on the QBC to be unconditionally secure. Following this, Lo’s no-go theorem [16] further discussed the insecurity of quantum secure computations, and posited that all one-sided two-party computations (which allow only one of the two parties to learn the result) are necessarily insecure, so an ideal one-out-of-two quantum oblivious transfer is also impossible. In addition, because of the connection between all-or-nothing OT and one-out-of-two OT, which has been proven to be equivalent in classical cryptography [3], these no-go theorems have caused difficulty in the development of both all-or-nothing and one-out-of-two QOTs.

In 2002, Shimizu et al. [17] proposed a communication scheme that is analogous to a one-out-of-two QOT with a 50% probability of completing the communication, meaning that Bob will not learn the message unambiguously to evade Lo’s theorem [16]. They [18] later improved the security of their protocol against entangled pair attacks. In 2005, Wolf et al. [19] showed a simple reduction between OT and PR-boxes, which is a non-locality machine described by Popescu et al. [20]. In 2006, He et al. [21] proposed an all-or-nothing QOT using four entangled states, and proved that the protocol does not belong to the QOT protocol defined by Lo’s no-go theorem. They found that the one-out-of-two QOT using Crépeau’s reduction [3] is not a rigorous one-out-of-two QOT black box function as specified in Lo’s theorem, because the inputs of Alice and Bob are dependent on each other. Therefore, they suggested that the equivalence between the two types of OT required a reexamination at the quantum level. He et al. [22] proved that the two types of OT are nonequivalent at the quantum level later. Because Bob inputs his choice before Alice inputs her message and Alice’s input will vary depending on Bob’s choice, the one-out-of-two QOT using Crépeau’s reduction does not satisfy the definition of ideal one-sided two-party computations in Lo’s no-go theorem. The inputs of Alice and Bob are dependent on each other, so the black box function differs from the function defined in Lo’s theorem [16]. Subsequently, Yang et al. [23] developed a one-out-of-two QOT using tripartite entangled states combined with the concept of Crépeau’s reduction [3] and considered that the one-out-of-two QOT using Crépeau’s reduction is not covered by the cheating strategy of Lo’s no-go theorem.

Once the nonequivalence of the two types of QOT was proven, more researchers discussed the issue of QOT using different methods and reduction schemes. The literature can be classified and described systematically as follows.

a) PR non-locality box: After Wolf et al. [19] showed the reduction between OT and PR-boxes, Buhrman et al. [24] presented a QBC protocol based on PR-boxes extended Wolf’s reduction method, and used a previous idea to further construct a one-out-of-two QOT. In 2011, Chou et al. [25] simulated a non-local PR box using ten-qubit entanglement, and used it to build a one-out-of-two QOT. To date, there has been little discussion on the relationship between the no-go theorems and the QOT protocols based on PR non-locality box, so its validity is open to question.

b) QBC-based QOT: When some unconditionally secure QBC can be obtained under relativistic or experimental constraints, it is a good idea to try to build QOT upon relativistic QBC. However, there are still some doubts about this method, and the most prominent question is “Can relativistic bit commitment lead to secure quantum oblivious transfer?” [26].

c) Bit-string QOT: Apart from relativistic QBC, another concept of bit-string from QBC is also applied to QOT, called bit-string QOT. Souto et al. [27], in 2015, proposed bit-string QOT inspired by Kent’s bit-string commitment [28]. However, He [29] pointed out that Souto’s all-or-nothing QOT protocol is not secure. A dishonest Alice can always mislead Bob into learning nothing and ensure that Bob cannot detect, because Bob checks Alice’s loyalty only when he learns the message correctly. This vulnerability will become a serious problem when Souto’s all-or-nothing QOT [27] is used as a building block for more complicated protocols, such as one-out-of-two QOT using Crépeau’s reduction [3]. Souto et al. [30] responded that He’s attack is not within the scope of the all-or-nothing OT protocol proposed by Rabin [1], and Souto thinks that a successful cheating strategy, which is one in which only one security criterion is violated, while the others are satisfied. Even so, to achieve the abovementioned security requirement, Souto constructed a semi-honest one-out-of-two QOT against malicious Alice relying on the use of their protocol and a secure bit commitment protocol. Recently, Plesch et al. [31] agreed with He’s viewpoint [29] that all-or-nothing QOTs with security flaws cannot be used to construct a secure one-out-of-two QOT, and introduced an improved version of the reduction protocol to remedy the weaknesses of the original protocol. This means that using Crépeau’s reduction to build a secure one-out-of-two QOT necessarily requires a perfect all-or-nothing QOT.

d) Crépeau’s reduction: After He et al. [22] proved that the one-out-of-two QOT using Crépeau’s reduction [3], where the effect of Alice’s input will be affected by Bob’s input, is not covered by Lo’s theorem [16], someone-out-of-two QOT protocols [32–35] using Crépeau’s reduction were developed, and one proposed in 2017 is a flexible one-out-of-n QOT using any two non-orthogonal states. Yang et al. [34] explained that their QOT protocol is not perfect concealing, which is the essential assumption in Lo’s theorem. Perfect concealing means that Alice has no information about Bob’s input, and the density matrix of Alice’s subsystem is independent of Bob’s measurement, so Bob can always implement an attack to read Alice’s message determinately. This type of QOT protocol is not covered by Lo’s theorem according to He’s proof [22]; however, they need to spend additional quantum resources to generate classical keys by all-or-nothing OT, then use the classical keys to achieve the goal of one-out-of-two QOT. The proposed protocol is similar to this type, but it uses the quantum resource on one-out-of-two QOT directly.

e) Others: In addition, some QOT protocols have been proposed from different viewpoints, such as practical QOT [36], which is based on technological limitations, the weak form of QOT [37,38], which weakens the security of the definition of OT, and probability-typed QOT [39] whose communication success has some probability, etc. In 2019, He used his proof [22] to propose a practical all-or-nothing QOT protocol [40] with a single photon, which helps researchers think another way to secure computation. Some researchers [41] only showed that their QOT is not built by a bit commitment protocol and is not covered by the MLC no-go theorem [14,15], but they did not mention Lo’s no-go theorem [16].

In order to address this complicated and challenging issue, in this paper we propose an innovative one-out-of-two QOT. Our novel ideas and main contributions are as follows.

a) First, we discuss previous QOT protocols in detail and provide a novel idea to build a one-out-of-two QOT using Crépeau’s reduction [3], which has been proven to not rigorously satisfy the requirement of Lo’s no-go theorem [16] in He’s proof [22]. This means that the proposed protocol is not covered by the no-go theorem.

b) Second, previous one-out-of-two QOT protocols [32–35] using Crépeau’s reduction are built upon all-or-nothing QOT, so they need to use more resources to generate classical keys for inputting Bob’s choice. The proposed protocol improves previous limits and uses the choice of different basis to replace the way Bob chooses. Therefore, our protocol can directly establish a one-out-of-two QOT, not through an all-or-nothing QOT, which means the proposed protocol can be more efficient.

c) Third, the proposed protocol has the strong ability to check the sender’s loyalty and avoid an attack from the receiver. It means that our one-out-of-two QOT protocol can prevent multiple external and internal attacks to provide significant security.

d) Moreover, the starting resource distribution is the sharing of a Bell state by Alice and Bob, and the Bell state is reusable because the entanglement property of the Bell state will not be destroyed at the end of this protocol. In this way, it can save more quantum resources. These reused entangled states can provide Alice and Bob to apply other entanglement services, such as teleportation [42], dense coding [43], quantum repeaters [44], quantum key distribution [45], quantum asymmetric key [46], quantum secure direct communication [47], and so on.

2  Preliminaries

In quantum computing, the qubit is the basic information unit. The qubits |0⟩=[10] and |1⟩=[01] are a pair of basis vectors of a 2D plane in z-basis, and the other common base is x-basis {|+⟩,|−⟩}, where |+⟩=12(|0⟩+|1⟩)and |−⟩=12(|0⟩−|1⟩). The following is an explanation of the properties of quantum mechanics, such as superposition, entanglement, quantum gates and measurement.

2.1 Superposition

The qubit differs from the classical bit, which can only have one of two states (either 0 or 1). The qubit can be represented as multiple states at the same time. That is, when the qubit |ψ〉=α|0⟩+β|1⟩ is measured in z-basis, there is |α|2 probability that the measurement result equals |0⟩, and |β|2 probability that the measurement result equals |1⟩. For example, there is a 50% probability that the measurement result in the z-basis of the qubit |+⟩=12(|0⟩+|1⟩) is either |0〉 or |1〉.

2.2 Entanglement

Another powerful property in quantum mechanics is entanglement, which occurs between two or more qubits. The common and simplest example of entanglement is called a Bell state, in which two qubits are entangled with each other; the Bell states consist of four specific entangled two-qubit states, as shown in Eq. (1).

|ϕ+⟩ab=12(|00⟩+|11⟩)ab=12(|++⟩+|−−⟩)ab

|ϕ−⟩ab=12(|00⟩−|11⟩)ab=12(|+−⟩+|−+⟩)ab

|ψ+⟩ab=12(|01⟩+|10⟩)ab=12(|++⟩−|−−⟩)ab

|ψ+⟩ab=12(|01⟩−|10⟩)ab=12(|+−⟩−|−+⟩)ab(1)

An entangled state made up of more than two qubits is called a Greenberger–Horne–Zeilinger (GHZ) state. The proposed protocol mainly uses the two following states, |GHZz⟩abc and |GHZx⟩abc shown in Eqs. (2) and (3).

|GHZz⟩abc=12(|000⟩+|111⟩)abc=12(|+++⟩+|+−−⟩+|−+−⟩+|−−+⟩)abc(2)

|GHZx⟩abc=12(|+++⟩+|−−−⟩)abc=12(|000⟩+|011⟩+|101⟩+|110⟩)abc(3)

2.3 Quantum Gate

A quantum gate is an operation in quantum computing. There are five common basic operations, including I=[1001], Z=[100−1], Y=[0−110], X=[0110] and H=12[111−1]. The operations can be performed on one qubit to change the state of that qubit, as shown in Tab. 1.

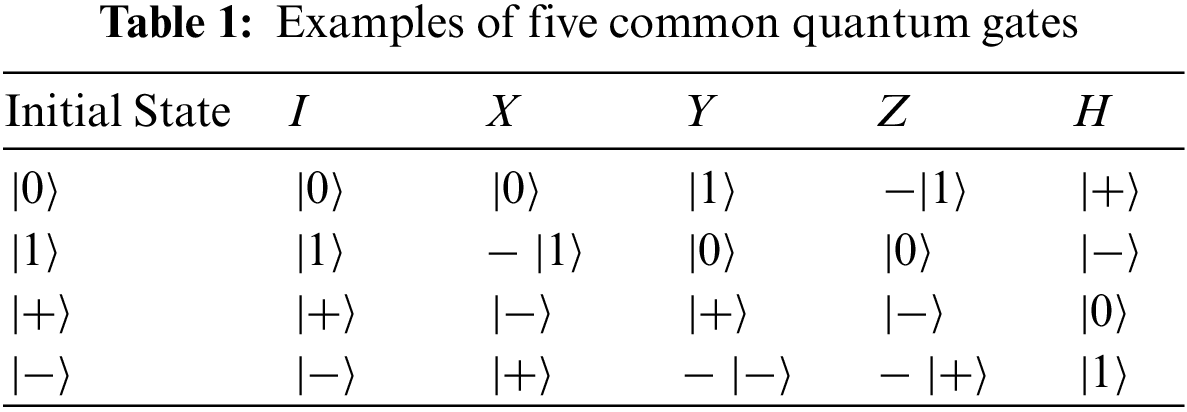
2.4 Controlled-not Gate (CNot)

In addition to the above five basic operations, the proposed protocol also uses the controlled-not gate. The controlled-not gate acts on two or more qubits, and consists of control bits and a target bit. Controlled-not gates most commonly operate in z-basis (ZCNotab) as follows: if the control bit a is |0⟩, the target bit b maintains its state; if the control bit a is |1⟩, the target bit b reverses its state. For example, if the control bit a is |1⟩, the state of target bit b will become |1⟩ from |0⟩, or become |0⟩ from |1⟩, as shown in Eq. (4). Similarly, a controlled-not gate operating in x-basis (XCNotab) can change the target bit b from |+⟩ to |−⟩ or change it from |−⟩ to |+⟩ if the control bit a is |−⟩, as shown in Eq. (5). A controlled-not gate can easily create and release the entanglement property, as shown in Eqs. (4) and (5). If controlled-not gate is performed two times continuously, the result would equal to do nothing as CNot⋅CNot=I. This is because the controlled-not gate is a unitary operator UU∗=I and CNot=CNot∗.

12(|0⟩+|1⟩)a⊗|0⟩b=12(|00⟩+|10⟩)ab

→ZCNotab12(|00⟩+|11⟩)ab→ZCNotab12(|0⟩+|1⟩)a⊗|0⟩b(4)

12(|+⟩+|−⟩)a⊗|+⟩b12(|++⟩+|−+⟩)ab→XCNotab12(|++⟩+|−−⟩)ab

→XCNotab12(|+⟩+|−⟩)a⊗|+⟩b(5)

2.5 Bell Measurement and GHZ Measurement

There are four Bell states: |ϕ+⟩, |ϕ−⟩, |ψ+⟩, and |Ψψ−⟩, and Bell measurement is used to distinguish these Bell states. Bell measurement consists of two quantum gates, including a controlled-not (ZCNot) gate in z-basis and a Hadamard (H) gate. In z-basis, the Bell measurement results of |ϕ+⟩ab, |ϕ−⟩ab, |ψ+⟩ab and |ψ−⟩ab are “00”, “01”, “10” and “11”, respectively. For example, Bell measurement is performed on the Bell state |ϕ+⟩ab=1/2(|00⟩+|11⟩)ab. First, the ZCNotab gate is performed, where qubit a is the control bit and qubit b is the target bit. Then, the Ha gate is performed on qubit a, and the measurement result is “00”, as shown in Eq. (6).

|ϕ+⟩ab=12(|00⟩+|11⟩)ab→ZCNotab12(|00⟩+|10⟩)ab→Ha|00⟩ab(6)

The GHZ measurement serves to distinguish the GHZ states, and the gates performing on |GHZ⟩ab…n are ZCNotab, ZCNotac, …, ZCNotan and Ha. For example, the GHZ measurement result of |GHZZ⟩abc is “000” in z-basis, as shown in Eq. (7).

|GHZz⟩abc=12(|000⟩+|111⟩)abc→ZCNotab12(|000⟩+|101⟩)abc

→ZCNotac12(|000⟩+|100⟩)abc→Ha|000⟩abc(7)

3  Basic Idea

This section briefly introduces the basic idea of the proposed one-out-of-two QOT protocol. That is, this section will only discuss the easiest case in which both m0 and m1 are only one bit messages; both Alice and Bob are honest, and their channel is free of external eavesdroppers. The qubit in a different state is immune to different quantum operations, as shown in Tab. 1. For example, in z-basis, operations X and Y can change the qubit |0⟩ to |1⟩, but operations I and Z cannot, that is, the qubit with z-basis is immune to operations I and Z. On the other hand, the qubit with x-basis is immune to operations I and X. The proposed protocol utilizes the property of immunity to achieve the goal of one-out-of-two OT. The basic idea of the proposed one-out-of-two QOT protocol is described below:

Step B1.Alice shares a Bell state |ϕ+⟩ab with Bob. The qubit in Alice’s hand is a, and the other qubit in Bob’s hand is b, as shown in Fig. 1①.

Step B2.Bob makes a choice j∈{0,1} as to which message mj he wants to receive from Alice, and then prepares a single qubit c according to j, and performs the CNotbc operation, as shown in Fig. 1a ②. When j=0, Bob prepares the qubit |0⟩ with the z-basis, and performs the ZCNotbc operation, as shown in Eq. (8), where Bob wants to learn m0. On the other hand, when j=1, Bob prepares the qubit |+⟩ with the x-basis, and performs the XCNotbc operation, as shown in Eq. (9). Then, Bob sends qubit b to Alice, as shown in Fig. 1a ③.

Step B3.Once Alice receives qubit b from Bob, and performs one of the I, Z, X or Y operations on qubit a or qubit b randomly, according to her messages m0 and m1, as shown in Fig. 1b ④. The I, Z, X and Y operations indicate that Alice’s messages m0 and m1, are “00”, “01”, “10” and “11”, respectively. Alice then sends the qubit performed operation to Bob, as shown in Fig. 1b ⑤. For example, it is present that Alice’s messages, m0=0 and m1=1, when she performs the Z operation on qubit b, as shown in Eq. (8).

Step B4.On receiving qubit a or b from Alice, Bob performs the controlled-not CNotac or CNotbc operation, as shown in Fig. 1c ⑥. (CNotac = ZCNotac when j= 0, and CNotac=XCNotac when j= 1; the same rule applies to CNotbc.) The controlled-not gate can bring the influence of Alice’s operation into qubit c and release the entangled relationship between qubit c and the Bell state consisting of qubits a and b. In Eq. (8), j=0, Bob performs ZCNotbc, and the influence of Alice’s operation affects the qubit c, but the entanglement property of the Bell state is not destroyed.

Step B5.Bob measures qubit c with the z-basis {|0⟩,|1⟩} when j=0, or with the x-basis {|+⟩,|−⟩} when j=1, as shown in Fig. 1d ⑦. Bob can obtain message mj, which he chose in Step B2, if the measurement result is |0⟩ or |+⟩, message mj=0; if the measurement result is |1⟩ or |−⟩, message mj=1. In Eq. (8), j=0, after Bob measures the qubit c with z-basis, and obtains the measurement result |0⟩. He learns m0=0.

Step B6. (Reusable)Through the above steps, the communication for one-out-of-two QOT between Alice and Bob is complete. It is worth noting that the controlled-not gate is used to transfer the influence of Alice’s operation into qubit c; it does not destroy the entanglement property of the Bell state. Therefore, the Bell state can be reused after adjustment. If Alice and Bob want to start the next communication, Alice simply needs to perform the same operation as in Step B3 to adjust the Bell state to return to |ϕ+⟩ab.

For clarity, another example is given to show the process of the proposed protocol. In Eq. (9), Alice’s message, m0 and m1, is still “01”, but Bob wants to learn the message m1.

12(|00⟩+|11⟩)ab⊗|0⟩c=12(|000⟩+|110⟩)abc

→ZCNotbc12(|000⟩+|111⟩)abc→Zb12(|000⟩−|111⟩)abc

→ZCNotbc12(|000⟩−|110⟩)abc=12(|00⟩−|11⟩)ab⊗|0⟩c(8)

12(|++⟩+|−−⟩)ab⊗|+⟩c=12(|+++⟩+|−−+⟩)abc

→XCNotbc12(|+++⟩+|−−−⟩)abc→Zb12(|+−+⟩+|−+−⟩)abc

→XCNotbc12(|+−−⟩+|−+−⟩)abc=12(|+−⟩+|−+⟩)ab⊗|−⟩c(9)

Figure 1: The steps of the basic idea. (a) Step B1 and Step B2, (b) Step B3, (c) Step B4, (d) Step B5

4  Relationship with the No-go Theorems

It is important at this point to discuss the relationship between this protocol and the no-go theorems, including the MLC no-go theorem [8,9] and Lo’s no-go theorem [10]. In the MLC no-go theorem, it is considered that all QOT protocols based on QBC are not secure because an unconditionally secure QBC is not possible. However, the proposed protocol is not based on QBC, so this section focuses on Lo’s no-go theorem. It then uses the viewpoint in He’s proof about Crépeau’s reduction to show that the proposed protocol can avoid the strategy in Lo’s no-go theorem.

Lo’s no-go theorem proves that any protocol is insecure if it satisfies the definition of the ideal one-side two-party secure computation, which is described in Definition A. In a secure computation, suppose Alice has a private (i.e., secret) input i∈{1,2,…,n}, Bob has a private input j∈{1,2,…,m}, and Alice helps Bob compute a prescribed function f(i,j)∈{1,2,…,r}. According to Lo’s cheating strategy, Bob can change the value of j from j0 to j1 by applying a unitary transformation to his own quantum machine; he can then learn f(i(m0,m1),j0)=m0 and f(i(m0,m1),j1)=m1.

However, He’s proof [6] showed that Lo’s no-go theorem only considered a situation of rigorous one-out-of-two OT, whose definition is described in Definition B. According to He’s proof, in the one-out-of-two QOT using Crépeau’s reduction [3] described in Definition C, Alice’s input i will vary according to Bob’s input j, and its value is not determined until Bob’s input has been completed. Therefore, the one-out-of-two OT using Crépeau’s reduction does not satisfy the rigorous one-out-of-two OT because the function should be f(i(m0,m1,j),j), not f(i(m0,m1),j). As a result, after Bob inputs j=0 and learns the message f(i(m0,m1,j0),j0)=m0, Bob cannot learn the other message by changing the value from j0 to j1 because the value f(i(m0,m1,j0),j1) is meaningless. If Bob wants to learn the other message f(i(m0,m1,j1),j1), he must change the value of i from i(m0,m1,j0) to i(m0,m1,j1). However, this is impossible without Alice’s help, so Bob’s strategy will not succeed alone. Consequently, the one-out-of-two QOT using Crépeau’s reduction is not covered by Lo’s cheating strategy.

Definition A: ideal one-side two-party secure computation

(1) Bob learns f(i,j) unambiguously.

(2) Alice learns nothing about j or f(i,j).

(3) Bob learns nothing about i more than it logically follows from the values of j and f(i,j).

Definition B: rigorous one-out-of-two OT

(1) Alice inputs i, which is a pair of messages (m0,m1).

(2) Bob inputs j=0 or j=1.

(3) At the end of the protocol, Bob learns about the message mj, but not the other message mJ¯, i.e., the protocol is an ideal one-side two-party secure computation f(i(m0,m1),j=0)=m0 and f(i(m0,m1),j=1)=m1.

(4) Alice does not know which mj Bob learned.

Definition C: One-out-of-two OT using Crépeau’s reduction

(1) Bob inputs j=0 or j=1.

(2) Alice inputs i(m0,m1),j), where Alice’s input i will vary according to Bob’s input j.

(3) At the end of the protocol, Bob learns about the message mj=f(i(m0,m1),j) but not the other message mJ¯=f(i(m0,m1,J¯),J¯).

(4) Alice does not know which mj Bob learned.

The proposed protocol is similar to Crépeau’s reduction; the function is also f(i(m0,m1,j),j), but not f(i(m0,m1),j). Bob must input the value of j before Alice inputs her messages, and the effect of Alice's input will be affected by j. As the situation where Alice's messages m0 and m1, are “01” in Eq. (8) and Eq. (9), the entangled state is 12(|000⟩−|111⟩)abc when Bob inputs j=0; conversely, the entangled state is 12(|+−+⟩+|−+−⟩)abc when Bob inputs j=1.

According to Lo’s theorem, Alice’s input and Bob’s input are independent in rigorous one-out-of-two OT, Uj⋅Ui=Ui⋅Uj so the result will be the same, whoever inputs first, Alice or Bob. After learning f(i(m0,m1),j)=mj, Bob can always find the inverse operation Uj−1to clear j by himself, and then perform UJ¯ to learn the other message f(i(m0,m1,J¯),J¯), UJ¯⋅Uj−1⋅Uj⋅Ui=UJ¯⋅Ui. However, He’s proof showed that Lo’s theorem does not cover the one-out-of-two OT using Crépeau’s reduction, in which Alice’s input i will vary according to Bob’s input j. That is Alice’s input and Bob’s input are dependent, Ui⋅Uj≠Uj⋅Ui, and if Bob uses Lo’s strategy, he will learn a meaningless value f(i(m0,m1,j),J¯) because UJ¯⋅Uj−1⋅Ui⋅Uj≠Ui⋅UJ¯. In the proposed protocol, Uj⋅Ui≠Ui⋅UJ¯ when Alice performs the Z, X or Y operation. For example, Bob inputs his choice before Alice inputs her message, and Bob can learn ,mj correctly, as shown in Eq. (9). In contrast, if Alice inputs her message before Bob makes his choice, Bob will learn nothing about the message, as shown in Eq. (10). (Because the controlled-not gate is performed twice continuously, the result will equal doing nothing as CNot⋅CNot =I, so it cannot bring the influence from Alice’s operation into qubit c, Bob cannot learn any information.) Therefore, the proposed protocol, like the one-out-of-two OT using Crépeau’s reduction in He’s proof, is secure against Lo’s cheating strategy. The proposed protocol utilizes the quantum property to implement the result using Crépeau’s reduction, which means it is simpler and more efficient.

12(|++⟩+|−−⟩)ab→Zb12(|+−⟩+|−+⟩)ab

12(|+−⟩+|−+⟩)ab⊗|+⟩c=12(|+−+⟩+|−++⟩)abc

→XCNotbc12(|+−−⟩+|−++⟩)abc

→XCNotbc12(|+−+⟩+|−++⟩)abc=12(|+−⟩+|−+⟩)ab⊗|+⟩c(10)

5  The Proposed Protocol

The starting point of the protocol is the sharing of a Bell state |ϕ+⟩ by Alice and Bob, as with many of the existing protocols, such as: the protocols in quantum teleportation, quantum dense coding, quantum repeater, quantum key distribution, quantum asymmetric key and quantum secure direct communication. This kind of start is flexible, and not limited to only one service between Alice and Bob. Furthermore, the entanglement property of the Bell state will not be destroyed at the end of this QOT protocol, so it can be reused. Moreover, secure one-out-of-two QOT must guarantee that Bob can only learn one of Alice’s messages, and ensure that Alice cannot learn Bob’s choice and choose which message Bob learns. In the proposed protocol, Bob can check Alice’s loyalty to avoid attacking, and Bob only can learn one of Alice’s messages certainly.

This section discusses the details of the one-out-of-two QOT protocol, which is based on the basic idea described in the previous section, and includes channel checking, in which we use the decoy qubits [48] to find the external eavesdroppers. Alice transfers one of two k-bit messages, m0={m01,m02,…,m0k} and m1={m11,m12,…,m1k}, to Bob. The detailed steps are as follows:

Step P1.Alice shares k Bell states |ϕ+⟩ab with Bob, as shown in Fig. 1a ①. We call the qubit sequence in Alice’s hand Sa={a1,a2,…,ak}, and the other qubit sequence in Bob’s hand Sb={b1,b2,…,bk}.

Step P2.For each i bit, Bob makes a choice ji∈{0,1} to learn mjii from Alice; the set of ji is Sj={j1,j2,…,jk},. According to Sj, Bob additionally prepares a single qubit sequence, Sc={c1,c2,…,ck},., and performs CNotbc operation, as shown in Fig. 1a ②. That is, Bob prepares the single qubit ci in state |0⟩ with z-basis, and performs ZCNotbc operation when ji=0, as in the situation in Eq. (8). On the other hand, when ji=1, Bob prepares the single qubit ci in state |+⟩ with x-basis, and performs XCNotbc operation, as in the situation in Eq. (9).

Step P3.After this, Bob randomly inserts n single qubits as decoy qubits in state {|0⟩,|1⟩,|+⟩,|−⟩} into Sb for channel checking, and then sends Sb′ consisting of Sb and decoy qubits to Alice, as shown in Fig. 1a ③.

Step P4.Once Alice has received Sb′, Alice and Bob use the decoy qubits to check the security of their communication channel. The detection process and detection rate of channel checking are described in the “External Attack” section. If they find that there is an outside eavesdropper present, they abort this communication and restart. Otherwise, they continue to the next step.

Step P5.Alice performs one of the I, Z, X or Y operations on qubit ai or bi randomly, according to the i-th bit in both of her messages, m0i and m1i, as shown in Fig. 1b ④. The I, Z, X and Y operations indicate that m0i and m1i are “00”, “01”, “10” and “11”, respectively. For example, if Alice performs the X operation on a3, then m03 is “1” and m13 is “0”, and if she performs the Z operation on b5, then m05 is “0” and m15 is “1”. The qubits on which Alice performs operations compose a new set Sd.

Step P6.As in Step P3, Alice randomly inserts n single qubits as decoy qubits in state {|0⟩,|1⟩,|+⟩,|−⟩} into Sd for channel checking, and then sends Sd′ consisting of Sd and decoy qubits to Bob, as shown in Fig. 1b ⑤.

Step P7.As in Step P4, Alice and Bob check the security of the channel and remove the decoy qubits from Sd′ to revert Sd. If they detect someone eavesdropping between them, they will stop this communication, if not, they will continue.

Step P8.As in Step P2, Bob performs the controlled-not operation CNotdc according to Sj, as shown in Fig. 1c ⑥. If ji=0, Bob performs the ZCNotdc operation, as in the situation in Eq. (8); otherwise, Bob performs the XCNotdc operation if ji=1, as in the situation in Eq. (9).

Step P9.Bob measures qubit ci with z-basis {|0⟩,|1⟩} when ji=0, as in the situation in Eq. (8), or with x-basis {|+⟩,|−⟩} when ji=1, as in the situation in Eq. (9), as shown in Fig. 1d ⑦. If the measurement result of ci is |0⟩ or |+⟩, then the message mjii is “0”; if the measurement result is |1⟩ or |−⟩, then mjii is “1”.

Step P10.Bob now utilizes some Bell states to check whether or not Alice is honest by internal attack detection, which is explained in detail in Section 6. If Bob finds that Alice is dishonest, Bob will stop the upper-layer application after this.

6  Security Analysis

In this section, the security of the proposed protocol is discussed, including both external and internal attack detection. External attack detection guards against an outside eavesdropper (Eve) stealing Alice’s message information, while internal attack detection guards against either dishonest Alice or dishonest Bob.

6.1 External Attack

Alice and Bob must ensure that the communication channel between them is secure, otherwise, Eve can eavesdrop on their messages illicitly without being spotted. In the proposed protocol, several single qubits are used as decoy qubits [48], and inserted into the transmitted sequence for channel checking, as in Step P3 and Step P6 of this protocol. The sender prepares the decoy qubits in state {|0⟩,|1⟩,|+⟩,|−⟩} randomly. If both the sender and the receiver measure the qubit with the same basis, they must obtain the same measurement results. That is, if their measurement results with the same basis differ, then an eavesdropper is present. Two common external attack strategies are discussed below, including the intercept-and-resend attack and the entangling attack.

Intercept-and-resend attack: When the sender sends the qubit sequence to the receiver, Eve intercepts all qubits to measure them in order to learn the messages during the transmission, and then resends the qubits to the receiver. In the proposed protocol, the sender will insert the decoy qubits into the qubit sequence with random states and positions. To steal the message, Eve intercepts the qubits and measures them. However, Eve may change the state of decoy qubits by measuring with wrong basis because she is unaware of the basis on which each decoy qubit is prepared. Eve will be detected with a 25% probability for each decoy qubit. With n decoy qubits, this guarantees the probability of detecting Eve by 1−(34)n.

Entangling attack: After intercepting the qubit sequence during the transmission, Eve prepares an ancillary qubit |E⟩, and performs a unitary operation U on the intercepted qubit to entangle with qubit |E⟩. If the decoy qubit in state {|0⟩,|1⟩,|+⟩,|−⟩} is entangled with the qubit |E⟩, the unitary operation U is defined in Eq. (11).

U(|0⟩|E⟩)=a|0⟩|e00⟩+b|1⟩|e01⟩

U(|1⟩|E⟩)=c|0⟩|e10⟩+d|1⟩|e11⟩

U(|+⟩|E⟩)=12(U(|0⟩|E⟩)+U(|1⟩|E⟩))

=12(|+⟩(a|e00⟩+b|e01⟩+c|e10⟩+d|e11⟩)+|−⟩(a|e00⟩−b|e01⟩+c|e10⟩−d|e11⟩))

U(|−⟩|E⟩)=12(U(|0⟩|E⟩)−U(|1⟩|E⟩))

=12(|+⟩(a|e00⟩+b|e01⟩−c|e10⟩−d|e11⟩)+|−⟩(a|e00⟩−b|e01⟩−c|e10⟩+d|e11⟩))(11)

6.2 Internal Attack

An unconditionally secure one-out-of-two QOT must guarantee that Bob can only learn one of Alice’s messages, and ensure that Alice cannot learn Bob’s choice and choose which message Bob learns. Thus, internal attacks can be divided into two parts, the first part is from the sender, Alice, while the second part is from the receiver, Bob.

Alice’s attack: In the proposed QOT protocol, if dishonest Alice wants to learn Bob’s choice by an illicit method, she must determine whether the entangled state is |GHZz⟩abc or |GHZx⟩abc after Bob inputs his choice and sends qubit b to her.

The first way of doing this might be GHZ measurement, but this is impossible because Alice does not have the whole entangled state. The second way could be through single qubit measurement. For example, Alice gets the result “01” after measuring qubit a and qubit b with z-basis. In this way, Alice can be sure that the entangled state is |GHZx⟩abc, which indicates that Bob wants message m1. However, this attack will be detected by Bob in the final step. The key point is that Alice’s attack destroys the entangled state, and Bob can check whether the entangled state is complete.

Once Bob has learned the message in Step P9, the entanglement property of the Bell state consisting of qubits a and b is not destroyed if Alice is honest, and the Bell state will become |ϕ+⟩ab, |ϕ−⟩ab, |ψ+⟩ab and |ψ−⟩ab according to Alice’s operation, I, Z, X, or Y. Without knowing Alice’s operation, Bob can use this phenomenon to detect whether Alice is honest or not. For example, if Alice’s message is “01”, the Bell state will become |ϕ−⟩ab, which Alice knows but Bob does not. Then Bob performs one of the operations, I, Z, X, or Y, on the qubit in his hands, sends it to Alice and asks Alice which operation he has performed. If Alice is honest, she can perform a Bell measurement to identify Bob’s operation by the Bell measurement result and the Bell state |ϕ−⟩ab.

Bob’s attack: If dishonest Bob wants to learn both of Alice’s messages, m0 and m1, Bob does not prepare one single qubit because it only has two states: 0 or 1, to identify one message. In order to recognize the situation of the two messages: “00”, “01”, “10” and “11”, Bob prepares different states instead of one single qubit in Step P2. Two kinds of Bob’s attacks are discussed below.

Attack 1, Bob will prepare a Bell state instead of a single qubit, and use Bell measurement to identify which operation (I, Z, X, or Y) Alice performs. For example, Alice shares |ϕ+⟩ab with Bob. Bob wants to learn both of Alice’s messages, m0 and m1, so he does not prepare a single qubit but a Bell state |ϕ+⟩ab′ instead, and sends qubit b′ to Alice, as shown in Fig. 2a. After channel checking, Alice performs one of four operations on the qubit a or qubit b randomly in Step P5, as shown in Fig. 2b. If Alice performs the operation on the qubit a and sends it to Bob, then Bob can perform the Bell measurement on qubit a and qubit b to identify Alice’s operation, as shown in Fig. 2c, and if Alice performs the operation on qubit b′ and sends it to Bob, then Bob can perform the Bell measurement on qubits b′ and c to identify Alice’s operation, as shown in Fig. 2d.

However, this strategy still cannot successfully learn both of Alice’s messages because Alice performs the operation on qubit a or qubit b′ randomly. Bob does not know which qubit Alice selected to perform the operation, so Bob cannot perform the Bell measurement on the correct Bell state to identify Alice’s operation.

Figure 2: Steps of Bob’s attack 1: (a) Step 1, (b) Step 2, (c) Step 3, and (d) Step 4

Attack 2, Bob prepares two single qubits, |0⟩ and |+⟩, and performs two types of CNot operations: ZCNot and XCNot, to learn both of Alice’s messages: m0 and m1. For example, Alice shares |ϕ+⟩ab with Bob in the beginning. Then Bob prepares the single qubit c in state |0⟩c and performs ZCNotbc. After that, Bob prepares another single qubit d|+⟩d, performs XCNotbd and sends the qubit b to Alice, as shown in Fig. 3a.

Alice performs one of four operations: I, Z, X, and Y, on qubits a or b randomly after channel checking, as shown in Fig. 3b. There are two situations. The first is that Alice performs Z operation on qubit b and sends it to Bob, which is shown in Eq. (12). Bob then performs XCNotbd and ZCNotbc in an orderly manner, as shown in Figs. 3c and 3d, and measures qubit d with x-basis and qubit c with z-basis, as shown in Fig. 3e The measurement result of qubit c is |0⟩, which indicates that m0 is “0”, and qubit d is |−⟩, which means that m1 is “1”.

The other situation, shown in Eq. (13), is where Alice performs Z operation on qubit a and sends it to Bob. However, after Bob performs XCNotad and ZCNotac in an orderly manner, he will get random measurement results in this situation by measuring qubit d with x-basis and qubit c with z-basis. It would seem that Bob can perform the Bell measurement on qubits c and d to identify Alice’s operation, as shown in Fig. 3f. Even so, Bob still cannot learn both of Alice’s message for the same reasons as in attack 1, Alice performs an operation on qubits a or b randomly. Because Bob cannot be sure which qubit Alice selected, Bob may learn the wrong message by using the wrong measurement method.

12(|00⟩+|11⟩)ab⊗|0⟩c⊗|+⟩d=12(|000⟩+|110⟩)abc⊗|+⟩d

→ZCNotbc12(|000⟩+|111⟩)ab⊗|+⟩d=12(|+++⟩+|+−−⟩+|−+−⟩+|−−+⟩)abc⊗|+⟩d

→XCNotbd12(|++++⟩+|+−−−⟩+|−+−+⟩+|−−+−⟩)abcd

→Zb12(|+−++⟩+|++−−⟩+|−−−+⟩+|−++−⟩)abcd

→XCNotbd12(|+−+⟩+|++−⟩+|−−−⟩+|−++⟩)abc⊗|−⟩d=12(|000⟩−|111⟩)abc⊗|−⟩d

→ZCNotbc12(|000⟩−|110⟩)abc⊗|−⟩d=12(|00⟩−|11⟩)ab⊗|0⟩c⊗|−⟩d(12)

12(|00⟩+|11⟩)ab⊗|0⟩c⊗|+⟩d=12(|000⟩+|110⟩)abc⊗|+⟩d

→ZCNotbc12(|000⟩+|111⟩)abc⊗|+⟩d=12(|+++⟩+|+−−⟩+|−+−⟩+|−−+⟩)abc⊗|+⟩d

→XCNotbd12(|++++⟩+|+−−−⟩+|−+−+⟩+|−−+−⟩)abcd

→Za12(|−+++⟩+|−−−−⟩+|++−+⟩+|+−+−⟩)abcd

→XCNotad12(|∓±⟩+|−−∓⟩+|+±+⟩+|±±⟩)abcd

=12(|0000⟩−|0011⟩+|1101⟩−|1110⟩)abcd

→ZCNotac12(|0000⟩−|0011⟩+|1111⟩−|1100⟩)abcd=12(|00⟩−|11⟩)ab⊗12(|00⟩−|11⟩)cd(13)

In the above, two different kinds of Bob's attacks were discussed, and it was found that Bob’s attack needs to change the state; i.e., the state will be others but not |GHZz⟩abc or |GHZx⟩abc. If Alice wants to check whether Bob is honest, she can measure the qubits a and b in her hand and then ask Bob announce his choice to compare with the measurement result. For example, Alice will know that Bob is cheating if her measurement result is “01” but Bob announces that his choice is m0, which indicates that the state should be |GHZz⟩abc.

Figure 3: Bob’s attack 2. (a) Step 1, (b) Step 2, (c) Step 3, (d) Step 4, (e) Step 5-1, (f) Step 5-2

7  Discussion and Conclusion

This study proposes a novel and efficient protocol for one-out-of-two QOT despite the difficulties presented by no-go theorems. The proposed protocol has three main contributions. First, the relationship between the no-go theorems and our protocol was described herein, and it was shown that the proposed protocol is not based on the QBC and thus does not conform to the MLC no-go theorem. The proposed protocol is similar to Crépeau’s reduction; it does not satisfy the definition of rigorous one-out-of-two QOT according He’s proof, so it is not covered by Lo’s no-go theorem. Second, compared with other QOTs, the proposed protocol uses quantum resources directly, instead of wasting the resources on generating classical keys. Third, the proposed protocol can check the sender’s loyalty and avoid attack from the receiver, so it does satisfy the two security requirements of OT. Furthermore, the entanglement property of the Bell state is reusable once communication via the protocol is complete. In summary, the proposed protocol is the first attempt to directly build a one-out-of-two QOT not covered by the no-go theorem, preventing external and internal attacks, and the quantum sources can be reused, which means that this protocol is more secure, efficient, and flexible. This paper provides a path for the future design of secure and efficient QOT.

Funding Statement: This work was supported in part by the Ministry of Science and Technology (MOST) in Taiwan under Grants MOST108-2638-E-002-002-MY2, MOST109-2222-E-005-002-MY3, MOST110-2627-M-002-002, MOST110-2221-E-260-014, MOST110-2222-E-006-011, MOST111-2218-E-005-007-MBK, and MOST111-2119-M-033-001, and was also supported in part by Higher Education Sprout Project, Ministry of Education to the Headquarters of University Advancement at National Cheng Kung University.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. O. Rabin, “How to exchange secrets by oblivious transfer,” in Technical Report TR-81, Aiken Computation Laboratory, Harvard University, 1981. [Google Scholar]

 2.  S. Even, O. Goldreich and A. Lempel, “A randomized protocol for signing contracts,” Communications of the ACM, vol. 28, no. 6, pp. 637–647, 1985. [Google Scholar]

 3.  C. Crépeau, “Equivalence between two flavours of oblivious transfers,” in Proc. Springer CRYPTO, Santa Barbara, CA, USA, pp. 350–354, 1987. [Google Scholar]

 4.  V. K. Yadav, N. Andola, S. Verma and S. Venkatesan, “A survey of oblivious transfer protocol,” ACM Computing Surveys (CSUR), Just Accepted, 2021. https://doi.org/10.1145/3503045. [Google Scholar]

 5.  P. W. Shor, “Algorithm for quantum computation: Discrete logarithms and factoring,” in Proc. IEEE FOCS, Santa Fe, NM, USA, pp. 124–134, 1994. [Google Scholar]

 6.  L. K. Grover, “A fast quantum mechanical algorithm for database search,” in Proc. ACM STOC, New York, NY, USA, pp. 212–219, 1996. [Google Scholar]

 7.  C. H. Bennett and G. Brassard, “Quantum cryptography: Public key distribution and coin tossing,” in Proc. IEEE CSSP, Bangalore, India, pp. 175–179, 1984. [Google Scholar]

 8.  H. K. Lo and H. F. Chau, “Unconditional security of quantum key distribution over arbitrarily long distances,” Science, vol. 283, no. 5410, pp. 2050–2056, 1999. [Google Scholar]

 9.  P. W. Shor and J. Preskill, “Simple proof of security of the BB84 quantum key distribution protocol,” Physical Review Letters, vol. 85, no. 2, pp. 441–444, 2000. [Google Scholar]

10. C. Crépeau and J. Kilian, “Achieving oblivious transfer using weakened security assumptions,” in Proc. IEEE FOCS, White Plains, NY, USA, pp. 42–52, 1988. [Google Scholar]

11. C. H. Bennett, G. Brassard, C. Crépeau and M. H. Skubiszewska, “Practical quantum oblivious transfer,” in Proc. Springer EUROCRYPT, Brighton, UK, pp. 351–366, 1991. [Google Scholar]

12. C. Crépeau, “Quantum oblivious transfer,” Journal of Modern Optics, vol. 41, no. 12, pp. 2445–2454, 1994. [Google Scholar]

13. A. C. C. Yao, “Security of quantum protocols against coherent measurements,” in Proc. ACM STOC, Las Vegas, Nevada, USA, pp. 67–75, 1995. [Google Scholar]

14. D. Mayers, “Unconditionally secure quantum bit commitment is impossible,” Physical Review Letters, vol. 78, no. 17, pp. 3414–3417, 1997. [Google Scholar]

15. H. K. Lo and H. F. Chau, “Is quantum bit commitment really possible?,” Physical Review Letters, vol. 78, no. 17, pp. 3410–3413, 1997. [Google Scholar]

16. H. K. Lo, “Insecurity of quantum secure computations,” Physical Review A, vol. 56, no. 2, pp. 1154–1162, 1997. [Google Scholar]

17. K. Shimizu and N. Imoto, “Communication channels analogous to one out of two oblivious transfers based on quantum uncertainty,” Physical Review A, vol. 66, no. 5, pp. 052316, 2002. [Google Scholar]

18. K. Shimizu and N. Imoto, “Communication channels analogous to one out of two oblivious transfers based on quantum uncertainty. II. closing EPR-type loopholes,” Physical Review A, vol. 67, no. 3, pp. 034301, 2003. [Google Scholar]

19. S. Wolf and J. Wullschleger, “Oblivious transfer and quantum non-locality,” in Proc. IEEE ISIT, Adelaide, SA, Australia, pp. 1745–1748, 2005. [Google Scholar]

20. S. Popescu and D. Rohrlich, “Causality and nonlocality as axioms for quantum mechanics,” in Proc. Dordrecht, ZH, Holland: Springer CLMP, pp. 383–389, 1998. [Google Scholar]

21. G. P. He and Z. Wang, “Oblivious transfer using quantum entanglement,” Physical Review A, vol. 73, no. 1, pp. 012331, 2006. [Google Scholar]

22. G. P. He and Z. Wang, “Nonequivalence of two flavors of oblivious transfer at the quantum level,” Physical Review A, vol. 73, no. 4, pp. 044304, 2006. [Google Scholar]

23. W. Yang, L. Huang, Y. Yao and Z. Chen, “Quantum oblivious transfer using tripartite entangled states,” in Proc. IEEE FGCN, Jeju-Island, Korea, pp. 464–468, 2007. [Google Scholar]

24. H. Buhrman, M. Christandl, F. Unger, S. Wehner and A. Winter, “Implications of superstrong non-locality for cryptography,” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 462, no. 2071, pp. 1919–1932, 2006. [Google Scholar]

25. Y. H. Chou, C. Y. Chen, H. C. Chao, J. H. Park and R. K. Fan, “Quantum entanglement and non-locality based secure computation for future communication,” IET Information Security, vol. 5, no. 1, pp. 69–79, 2011. [Google Scholar]

26. G. P. He, “Can relativistic bit commitment lead to secure quantum oblivious transfer?,” The European Physical Journal D, vol. 69, no. 4, pp. 1–8, 2015. [Google Scholar]

27. A. Souto, P. Mateus, P. Adão and N. Paunković, “Bit-string oblivious transfer based on quantum state computational distinguishability,” Physical Review A, vol. 91, no. 4, pp. 042306, 2015. [Google Scholar]

28. A. Kent, “Quantum bit string commitment,” Physical Review Letters, vol. 90, no. 23, pp. 237901, 2003. [Google Scholar]

29. G. P. He, “Comment on “Bit-string oblivious transfer based on quantum state computational distinguishability,” Physical Review A, vol. 92, no. 4, pp. 046301, 2015. [Google Scholar]

30. A. Souto, P. Mateus, P. Adao and N. Paunković, “Reply to “comment on ‘Bit-string oblivious transfer based on quantum state computational distinguishability’,” Physical Review A, vol. 92, no. 4, pp. 046302, 2015. [Google Scholar]

31. M. Plesch, M. Pawłowski and M. Pivoluska, “1-out-of-2 oblivious transfer using a flawed bit-string quantum protocol,” Physical Review A, vol. 95, no. 4, pp. 042324, 2017. [Google Scholar]

32. Y. G. Yang, P. Xu, J. Tian and H. Zhang, “Quantum oblivious transfer with an untrusted third party,” Optik-International Journal for Light and Electron Optics, vol. 125, no. 18, pp. 5409–5413, 2014. [Google Scholar]

33. Y. G. Yang, S. J. Sun and Y. Wang, “Quantum oblivious transfer based on a quantum symmetrically private information retrieval protocol,” International Journal of Theoretical Physics, vol. 54, no. 3, pp. 910–916, 2015. [Google Scholar]

34. Y. G. Yang, R. Yang, H. Lei, W. M. Shi and Y. H. Zhou, “Quantum oblivious transfer with relaxed constraints on the receiver,” Quantum Information Processing, vol. 14, no. 8, pp. 3031–3040, 2015. [Google Scholar]

35. Y. G. Yang, R. Yang, W. F. Cao, X. B. Chen, Y. H. Zhou et al., “Flexible quantum oblivious transfer,” International Journal of Theoretical Physics, vol. 56, no. 4, pp. 1–12, 2017. [Google Scholar]

36. Y. B. Li, Q. Y. Wen, S. J. Qin, F. Z. Guo and Y. Sun, “Practical quantum all-or-nothing oblivious transfer protocol,” Quantum Information Processing, vol. 13, no. 1, pp. 131–139, 2014. [Google Scholar]

37. A. Chailloux, G. Gutoski and J. Sikora, “Optimal bounds for semi-honest quantum oblivious transfer,” arXiv preprint arXiv:1310.3262, 2013. [Online]. Available: https://arxiv.org/abs/1310.3262. [Google Scholar]

38. G. P. He, “Secure quantum weak oblivious transfer against individual measurements,” Quantum Information Processing, vol. 14, no. 6, pp. 2153–2170, 2015. [Google Scholar]

39. N. Gisin, S. Popescu, V. Scarani, S. Wolf and J. Wullschleger, “Oblivious transfer and quantum channels as communication resources,” Natural Computing, vol. 12, no. 1, pp. 13–17, 2013. [Google Scholar]

40. G. P. He, “Practical quantum oblivious transfer with a single photon,” Laser Physics, vol. 29, no. 3, pp. 035201, 2019. [Google Scholar]

41. M. L. Zhang, J. Li, S. Shi, Y. H. Liu and Q. J. Zheng, “A novel application of probabilistic teleportation: p-Rabin quantum oblivious transfer of a qubit,” International Journal of Theoretical Physics, vol. 58, no. 10, pp. 3333–3341, 2019. [Google Scholar]

42. C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres et al., “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels,” Physical Review Letters, vol. 70, no. 13, pp. 1895–1899, 1993. [Google Scholar]

43. C. H. Bennett and S. J. Wiesner, “Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states,” Physical Review Letters, vol. 69, no. 20, pp. 2881–2884, 1992. [Google Scholar]

44. H. J. Briegel, W. Dür, J. I. Cirac and P. Zoller, “Quantum repeaters: The role of imperfect local operations in quantum communication,” Physical Review Letters, vol. 81, no. 26, pp. 5932–5935, 1998. [Google Scholar]

45. Y. S. Zhang, C. F. Li and G. C. Guo, “Quantum key distribution via quantum encryption,” Physical Review A, vol. 64, no. 2, pp. 024302, 2001. [Google Scholar]

46. F. Gao, Q. Wen, S. Qin and F. Zhu, “Quantum asymmetric cryptography with symmetric keys,” Science in China Series G: Physics Mechanics and Astronomy, vol. 52, no. 12, pp. 1925–1931, 2009. [Google Scholar]

47. K. Boström and T. Felbinger, “Deterministic secure direct communication using entanglement,” Physical Review Letters, vol. 89, no. 18, pp. 187902, 2002. [Google Scholar]

48. W. Y. Hwang, “Quantum key distribution with high loss: Toward global secure communication,” Physical Review Letters, vol. 91, no. 5, pp. 057901, 2003. [Google Scholar]