GrCol-PPFL: User-Based Group Collaborative Federated Learning Privacy Protection Framework

1  Introduction

Since the end of the last century, with the development of Internet technology, more and more people have begun to contact and use network communication equipment. In recent years, hardware devices have been continuously updated and iterated, and the level of processing data has been greatly improved. With the proposed concepts of smart home [1], Internet of Things (IoT) [2] and smart city [3], the number of mobile terminals and IoT equipment has increased significantly. It is speculated that by 2025, there will be 80 billion access devices on the Internet [4] and the generated data will be massive.

Currently, data is still in the form of isolated islands due to issues such as competitive relationships and trust levels among industries, enterprises, and even individuals. Traditional distributed machine learning [5,6] collects all data for unified training. However, in many applications, data is scattered among mobile edge devices and cannot be shared and transmitted safely and effectively. And more and more laws have made relevant provisions for the protection of personal data privacy, such as the principle of “focused collection or data minimization” outlined in the 2012 White House Report [7]. The collection of user data to servers is becoming more expensive and unrealistic.

This problem has been improved since federated learning (FL) was proposed by Google in 2016 [8,9]. FL is that the parameter server uniformly distributes the model parameter to the client. The device uses local data to train the model after receiving parameters from the server. When all users complete training, the updated parameters are sent to the parameter server. The parameter server aggregates the model globally. After several iterations, the model convergence is finally achieved. This prevents the user’s original data from being transmitted and only needs to transmit the model parameters to the server.

In recent studies [10–12], in the process of FL exchanging model gradient, malicious attackers can recover the original information of users through model parameter (i.e., gradient). This shows that FL cannot fully guarantee users’ privacy. Therefore, many researchers have proposed solutions to this problem, most of which are based on differential privacy (DP) [13–15] and secure multi-party computing (SMPC) [16–18]. The DP scheme is to add Gaussian noise or Laplacian noise to the gradient [19,20], which interferes with the local model parameters. The server uses the disturbed model parameters for global aggregation to protect privacy. But this solution will lead to the problem of low model accuracy. Moreover, the communication overhead of SMPC is large, and the computing performance decreases significantly with the increase of the number of users, and it is also not easy to deploy mobile devices. Reference [21,22] leverages conditional generative adversarial networks to achieve high-level privacy protection.

Recently, we have paid attention to [23] using the chained privacy-preserving FL framework (chain-PPFL) to add a random number to the first node of the chain. It uses this random number as noise to join the model parameters and correctly subtracts this random number on the server-side. It not only ensures the accuracy of the model, but also protects the user's data privacy. However, we found through analysis that although this method provides a new idea in privacy protection, there are still some problems to be solved. First of all, under the chained structure, [23] cannot solve the problem of two nodes on a jump discontinuity in a chain that can correctly decrypt the gradient information of the intermediate node by collusion. Secondly, due to the chained structure, the user nodes behind will have to wait for the transmission of the previous nodes, and the convergence rate of the model will slow down, resulting in the long uplink communication time.

In an environment with a large number of users and the problem of mutual collusion, we propose a novel group collaborative FL framework. We first divide a large number of users into groups, so that the groups do not affect each other. To a certain extent, the parallelism of the system uplink is improved. Secondly, we connect the users in the group in a chained structure to form a communication mode for transferring data between users. Only the last user of each group needs to upload data. The last user in each group contains the information of all users in the group. In this way, the number of nodes communicating with the edge server at the same time can be greatly reduced, which not only effectively utilizes the communication resources between users, but also relieves the pressure on bandwidth. Based on [23], we let the server distribute random numbers to each user. After each user completes training, the sum of training result and the random number is passed to the next user to protect user privacy. It can solve the problem of collusion between users.

We summarize our main results and contributions as follows:

•   We propose a user-based group collaborative federated learning privacy protection framework (GrCol-PPFL), which uses two-scale transmission methods to increase local computation on the traditional FL architecture and reduce the number of connections to the server.

•   We analyze the time consumed by GrCol-PPFL, and theoretically prove that GrCol-PPFL can find the optimal solution by changing the number of groups to minimize the uplink consumption time.

•   Our subsequent experiments prove that our scheme can effectively solve the problem of user collusion. By changing the number of groups to reduce the prolonged uplink consumption time of the system caused by the chained structure, and it is better than classic federated averaging (FedAvg).

In Section 2, we discuss existing related work. In Section 3, we discuss the design of the model as well as the basic workflow of the architecture and present our algorithm. In Section 4, we analyze the accuracy of the model, the security of the system, and the relationship between the number of groups and the uplink consumption time. In Section 5, we present comparative experiments and discuss the experimental results. Finally, we summarize the findings of this paper in Section 6.

2  Related Works

Due to the upgrading of hardware equipment and the popularization of Internet intelligence, a large amount of personal data has been generated. With the development and application of artificial intelligence, data plays an indispensable role. However, the privacy of personal data is also concerned by people, and relevant protection regulations have been proposed in law. FL plays the role of privacy protection in more and more fields, such as Google input tools [24], intelligent cognitive systems [24], relation extraction in medical field based on FL [25–27], robotics [28], etc. Its security and privacy issues [17] still exist: (1) Since the implicit knowledge in the training data can be obtained by combining the local model update and the global model parameters, the user’s personal information may be leaked to untrusted servers or other malicious users. For example, even prototype samples generated from training data from other users can potentially be stealthily stolen by malicious users. (2) Under the collusion attack of untrusted cloud servers and malicious participants, everyone’s exact private information may be leaked.

The model parameters (i.e., gradients) of each edge node need to be uploaded to the server instead of uploading the user’s original data. However, this scheme has been proved to be insecure, and attackers can deduce the user’s original data through gradient [10–12]. To address this problem, there are mainly DP [13–15] and SMPC [17].

DP mainly hides the original attributes of the data by adding noise to the data, so that the attacker cannot analyze the original information to achieve the purpose of protection. DP has strong theoretical guarantees [29], and the communication overhead is smaller than that of encryption algorithms. In their work, DP mainly uses Laplace mechanism or exponential mechanism. The model gradient information of edge nodes is added to noise by DP technology. And [20] propose a novel FL framework that uses online Laplace approximation to approximate posteriors on both the client and server side. Reference [30] presents the scheme of FL with local DP that implements a suite of selection and filtering techniques for perturbing and sharing select parameter updates with the parameter server.

SMPC is mainly performed in a network that does not trust each other. After a series of operations are performed using cryptography, the result is consistent with the plaintext computation. Reference [31] perform privacy-preserving FL on longitudinally distributed data by using entity resolution and homomorphic encryption. Reference [32] proposed a privacy-preserving asynchronous averaging algorithm using Shamir's secret sharing scheme to maintain the privacy of each individual.

In terms of communication problems in practical applications, especially when the global model is large, the network bandwidth limitation and the number of working nodes will exacerbate the communication bottleneck of FL. And the server processing capacity is limited, which will lead to the straggler problem. Under the classic FL framework, these straggling devices are usually discarded and not aggregated by the server. But this way will affect the results of model training and user experience. Although it is feasible to divide server’s computing and communication pressure into several edge servers [33], user resources are still not fully utilized, and security is not considered. Reference [34] proposes a multi-agent deep q-networks for efficient edge FL communications. Reference [35] intelligently selects client devices participating in each round of FL, balances the bias of the data, and improves the convergence rate.

In the current literature to solve the problem of bandwidth resources, they mainly use compression Reference [36] and sparsification models [37]. Reference [38] handle an optimized deduplication strategy. Cluster-based users [39] only need a small number of users to upload models after consensus communication using device-to-device (D2D) technology.

The above solutions will have problems such as low model accuracy, high communication overhead or consumption of a lot of computing resources, and none of them consider and solve the balance between security and communication. Based on [23], our scheme solves the problem of collusion between dishonest clients and shortens the uplink transmission time by changing the number of groups without changing the size of the model.

3  System Model and Method

In this section, we will introduce several basic models of the system and how the approach used by this architecture to improve safety and efficiency.

3.1 Network Model

As shown in Fig. 1, we consider a FL system with an edge server and K participants. We represent K users as group-based L clusters G1,…Gl,…GL, where Gl={1,…k,…κl}. Each group has κl=|Gl| clients, so K=∑l=1L|Gl|.

We adopt a system architecture that is different from classical FL. Within the cluster, participants can communicate with each other and pass data by D2D technology, as shown in Fig. 2.

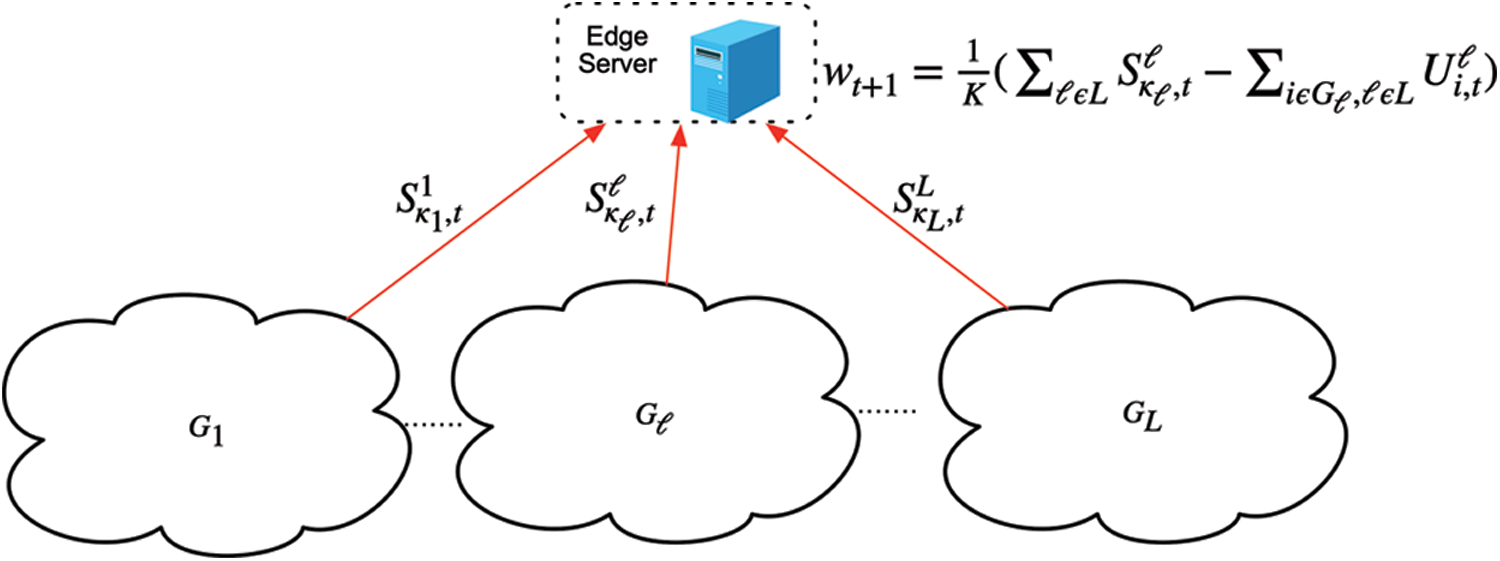
Figure 1: K clients are divided L groups

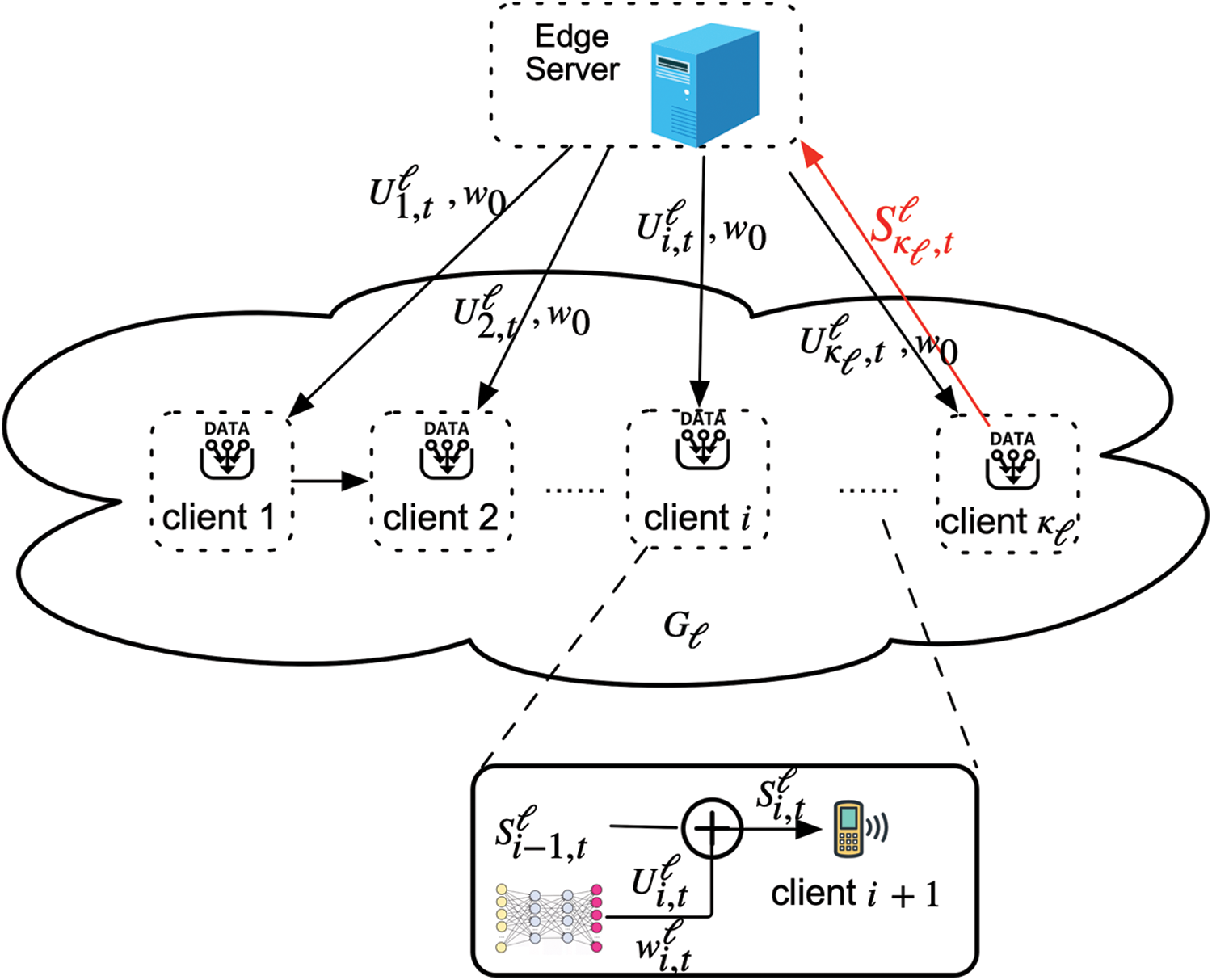
Figure 2: Users’ communication process in the group

Participating users can choose their neighbor nodes according to different networks. For example, [40] constructed a P2P network model based on a “neighbor-neighbor” list. Each node contains a list, which not only includes the names, addresses and other information of connected neighbor nodes, but also includes the neighbor node information of the neighbor nodes, in order to improve the self-healing and robustness of the network. Even if a node is attacked, it can quickly establish a connection with a new neighbor node, avoiding the loss of some nodes and the impact of offline nodes on the entire network. It can also create a D2D neighbor network graph Graph=(Gl,El) based on physical distance, transmission power and channel conditions [39], where El represents the set of edges.

3.2 FL Model

We take the group as a unit, and the participant i in the group l has a local dataset Dil of size |Dil|. In a supervised FL setting, Dil is represented as a set {xj,yj}jϵDil, where xjϵRd is a vector with d-dimensional input samples and yjϵR is a sample output label for xj. We let fjl(w,xj,yj), abbreviated as fjl(w), as the loss function of a data sample of user i, where j∈Dil. We use the parameter w to predict the sample (xj,yj) loss. Let Fil(w) be the total loss function of all local data samples Dil of user i. Then the loss function of user i after completing one round is expressed as:

Fil(w)=1|Dil|∑j∈Dilfj(w).(1)

Then the total loss function of the group l is:

F^l(w)=∑i∈Gl1κlFil(w).(2)

Therefore, the loss function of the global model is:

F(w)=∑lϵL1KF^l(w).(3)

3.3 Computation and Communication Model

The time consumed by FL mainly includes the server broadcasting the global model, the user’s local training, the transmission time of model parameters uploading to the server and the time for the server to aggregate the model. The transmission power of the server is larger than that of the upstream communication, so it can be ignored. Classic FL systems use the star topology network structure. This makes in synchronous FL, a large number of users communicate with the server at the same time, and sometimes network congestion occurs. As shown in Fig. 2, users in the group transmit model parameters through D2D propagation, and the last user in the group uploads all nodes’ information to the server, which greatly reduces the number of users connected to the server and relieves the pressure of network traffic. And we shorten the consumed time by changing the number of groups in Section 4.3.

We set the local computing capability of user i to be ail, and the number of rounds of the CPU cycle of the device when calculating data samples is Cil, so the local computing time of user i is:

τil=CilDilail.(4)

Since the local computation is synchronous, the local computation time required by the system is:

Γc=maxi∈Gl,lϵLτil.(5)

In a wireless network, we use orthogonal frequency division techniques to transmit the local FL model to the server through D2D, the transmission rate of the device is:

ril=Billog2(1+pil|hil|2Nd2Bil2).(6)

where Bil is the bandwidth, pil is the transmission power, Nd is the white noise power spectral density, and hil is the channel coefficient.

We let the FL model parameter size be z, which is a constant, so the communication duration is:

til=zril.(7)

So the communication duration of each group is:

Tcomm_l=∑i∈Gltil.(8)

3.4 GrCol-PPFL Algorithm

In this part, we will introduce the improvements made to the system security in the GrCol-PPFL framework in detail and show the specific working process.

3.4.1 Double-Masking Privacy Protection Scheme

In this paper, we consider the privacy protection problem assuming that the server is honest and the transmission channel with the participants is reliable. But we do not assume that users are honest, because in a network environment where users collude with each other, the Single-Masking chained privacy protection method [23] can still leak user’s privacy.

In each round of training, the parameter server will generate the same number of random numbers Ui,tl in advance as the participants, Ui,tl is a matrix with the same dimension as the model parameter w. Its role is to add noise to each local model parameter. Unlike DP, this does not affect the accuracy of the model. In the round t of training, the participant i in the group l will add Ui,tl to the model parameter wi,tl. This result is then passed to the next neighbor node. Except for the first participant, the other participants not only use U to add noise, but also calculate the parameters passed by the previous node at the same time, that is, we adopt the double-masking privacy protection scheme.

This mechanism makes each participant’s result contain not only the random number used as a mask, but also the information of the previous participant. This allows only the last participant in the group to upload the parameters to include the information of all users in this group. This effectively eliminates the problem of collusion between participants while assisting in the transmission of information.

3.4.2 Chain Transmission Process

Step 1:

Aggregation server: In round t of training, the server distributes the global model parameter wt. And each participating user i simultaneously obtains Ui,tl.

Step 2:

Participating users: After the users receive the information from the server, the model is trained according to the local data within a specified time. Users use mini-batch stochastic gradient descent (SGD) to train locally. When the local training of user i is completed, the model parameter wi,tl is obtained. Then it will be calculated:

Mi,tl=Ui,tl+wi,tl(9)

For the first user in the group l, M1,tl will be passed to the second user. And for other users i, in addition to calculating Mi−1,tl, it should also calculate the data of the previous user communicating with it, we express it as:

Si,tl=Ui,tl+wi,tl+Mi−1,tl(10)

Step 3:

Aggregation server: When delivered to the last user in the group l, user κl will upload Sκl,tl to the server. Since the parameter server will calculate all the random parameters ∑iϵGl,lϵLUi,tl in advance. The server only needs to add up the parameters uploaded by the last user of each group. The average is:

wt+1=1K(∑lϵLSκl,tl−∑iϵGl,lϵLUi,tl)(11)

After the server is aggregated, the model training of the round t + 1, the server regenerates Ui,t+1l, and broadcasts wt+1 and Ui,t+1l to participating users, repeat step1-step3 until the convergence of the model is reached. The specific GrCol-PPFL algorithm we propose is given in Algorithm 1.

4  Analysis and Comparison

In this section, we will analyze three aspects: (i) model accuracy; (ii) privacy protection; (iii) uplink time consumed by the system.

4.1 Model Accuracy

In the field of privacy protection, part of the accuracy is often sacrificed for the purpose of privacy. For example, DP [20] adds noise to the model parameter w, but it sometimes seriously affects the model accuracy. As shown in Eq. (11), the server subtracts all random numbers during aggregation, and the result is the average parameter of all user model parameters. Even if we add more random numbers, these random numbers are generated on the server-side, which can easily calculate the correct average aggregation result. In the experimental part, we also give the corresponding model accuracy diagram, which proves that our scheme can ensure the accuracy of the model.

4.2 Privacy Protection

In [23], the author is based on the assumption that users do not collude with each other. Only the first node in a chain receives a random number U0,t from the server-side. This node will add U0,t to the trained model parameter w1,t. Then a new U1,t will be generated. And this node continues to transmit to the next node, performing the same operation until the last node. However, in the network environment of FL, the problem of user collusion cannot be avoided. According to the chain FL strategy, when colluding with any two jumping user nodes, the model parameters of the intermediate users can be easily calculated:

Ui+1,t−Ui−1,t=(∑j=1i+1wj,t+U0,t)−(∑j=1i−1wj,t+U0,t)=wi,t(12)

As shown in the Eq. (12), the intermediate user parameter wi,t can be calculated only by subtracting the values of the two jumped nodes. This is obviously a big hidden danger in the FL privacy protection framework. In our scheme, each user has a random number for itself to cover the local model parameters. Although local computing is increased, the problem of user collusion is solved:

Si−1,tl−Si+1,tl=Ui,tl+wi,tl(13)

We can see that even if it is collusion, the calculated result is a mixed result X=Ui,tl+wi,tl. It is hard to roll out the original parameter information. Similarly, no matter how users collude with each other, the result will be the sum of the parameters of the attacked user and a random number. In theory, it is proved that our scheme can still ensure the security of local data in the network environment where users collude with each other.

4.3 Analysis of Latency

In a regional environment, the connection method of a chain will cause the transmission of information to be too slow. Therefore, in our scheme, the K users in the network are divided into several groups in order to improve the parallelism of the communication process.

But unlimitedly increase the number of groups L, that is, we set L=K, then it becomes the FedAvg. If L=1, the communication method will be the same as [23]. So, we try to find an optimal number of groups, so that our communication efficiency is the best. Since we use synchronous FL, the time to train the model locally will always wait for the slowest node, so we ignore this part of the time when comparing several algorithms. Therefore, the total time spent by the system includes the communication time Tcomm, the local extra computation time Tcomp_c in the chain mechanism and the server time Tcomp_s for calculating the model parameters, so the total time is:

Ttotal=Tcomm+Tcomp_c+Tcomp_s.(14)

We define the ability of the two devices to process information, that is, the size of the number of bytes processed per unit time. For the convenience of analysis, we express it as the number of model parameters processed per unit of time. One is the client-side, which we set as C, and the other is the server-side, which is set as S. We use the average transmission rate r¯ as the transmission speed of each user i. Each group has the same number of users. Then for FedAvg, the total time it takes to iterate K users at one round is:

TFedAvg=zr¯+KS.(15)

The total time for a round of chain-PPFL is the time for K local users to transmit information, the time for the last user to upload to the server and calculated time on the server:

Tchain−PPFL=zr¯K+(K−1)1C+1S.(16)

In our solution, since the users under the same edge server are divided into L groups, the processes between the groups are performed in parallel, which obviously reduces the total upload time. The total time TGrCol−PPFL includes the time of communicating between users in a group, uploading L users from last user of each group to the edge server and calculating on the server:

TGrCol−PPFL=KzLr¯+(KL−1)1C+LS.(17)

Since subsequent nodes need to spend more waiting time. Obviously, when there are enough users, the chain-PPFL scheme takes longer than FedAvg, that is, TFedAvg≤Tchain−PPFL. Our goal is to reduce the time of TGrCol−PPFL, so we let TGrCol−PPFL≤TFedAvg:

zr¯+KS≥KzLr¯+(KL−1)1C+LS.(18)

After simplification, the quadratic discriminant is:

ξ=(zr¯−KS+1C)2.(19)

We can observe that the ξ is greater than or equal to 0, so there is L that makes the inequality true. In the experimental part we also show that the presence of L makes the time consumed by the system better than other schemes.

5  Experiment

In this section, we describe the relevant experimental settings, and compare the model accuracy, user privacy protection, and system uplink communication time with several schemes.

5.1 Experiment Setup

We test the model accuracy of GrCol-PPFL, FedAvg, Chain-PPFL and DP. The experimental environment is the same, both are based on pytorch simulation environment. The batch size B = 10 for local training and the learning rate η = 0.1. Among them, for DP, we choose different noise variances 10−1 and 10−4, the purpose is to add different degrees of noise to the model parameters to observe the impact on the model accuracy. In terms of transmission and computation, we set the size of the model z = 28.1 kbit, and the average transmission rate of the client is 281 kbit/s. At the same time, we set C and S to 1 and 5. More importantly, we continuously adjust the number of groups L for the selected 100 users to verify whether there is an optimal number of groups that reduces the system time compared with other schemes.

The MNIST [41] handwritten digits database has a training set of 60,000 examples and a test set of 10,000 examples. The numbers are normalized and centered in the fixed-size image. We divide the data into two forms: (i) independent identically distribution (IID), the data is shuffled and divided into 100 users, each user receives 600 samples; (ii) non-IID, the data is sorted by number tags and divided into 200 shards of size 300. We allocate two shards for 100 users. In terms of models, we use the two 5 × 5 convolutional layer convolutional neural network (CNN) model, its fully connected layer has 512 units and rectified linear unit (ReLU) activation function, a softmax output layer. Then, we use the datasets of canadian institute for advanced research (CIFAR)-100 and deep leakage from gradients (DLG) algorithm [10] to recover the image by the gradient for testing the security of the system. We evaluated our model on a Dell Precision 3630 desktop computer, which uses the 9th generation Intel Core i7-9700K CPU, 16 GB.

5.2 Training Accuracy

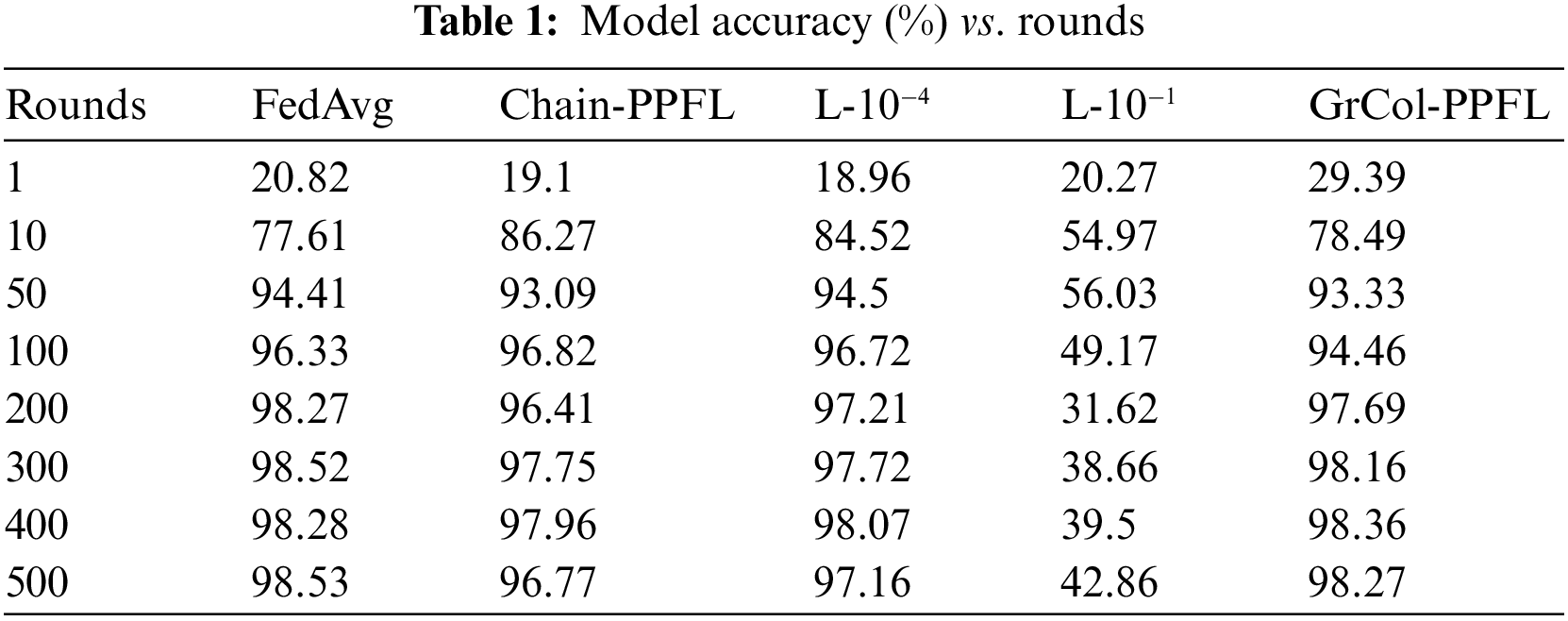
In the model accuracy test, we select the CNN model to train 500 rounds on the dataset of non-IID. As shown in Fig. 3, the accuracy of FedAvg, chain-PPFL, Laplacian noise-10−4 (L-10−4) and GrCol-PPFL can remain above 95%, which proves that our scheme does not affect the correctness of the model parameters during aggregation. In DP experiments, we can see that the size of the noise will affect the accuracy of the model. When the variance is 10−4, the accuracy of the model is generally not affected, which is consistent with that of FedAvg. When the variance is 10−1, the noise added to the model parameters is large, and the fuzzification of the parameters is obvious, which affects the accuracy of the model.

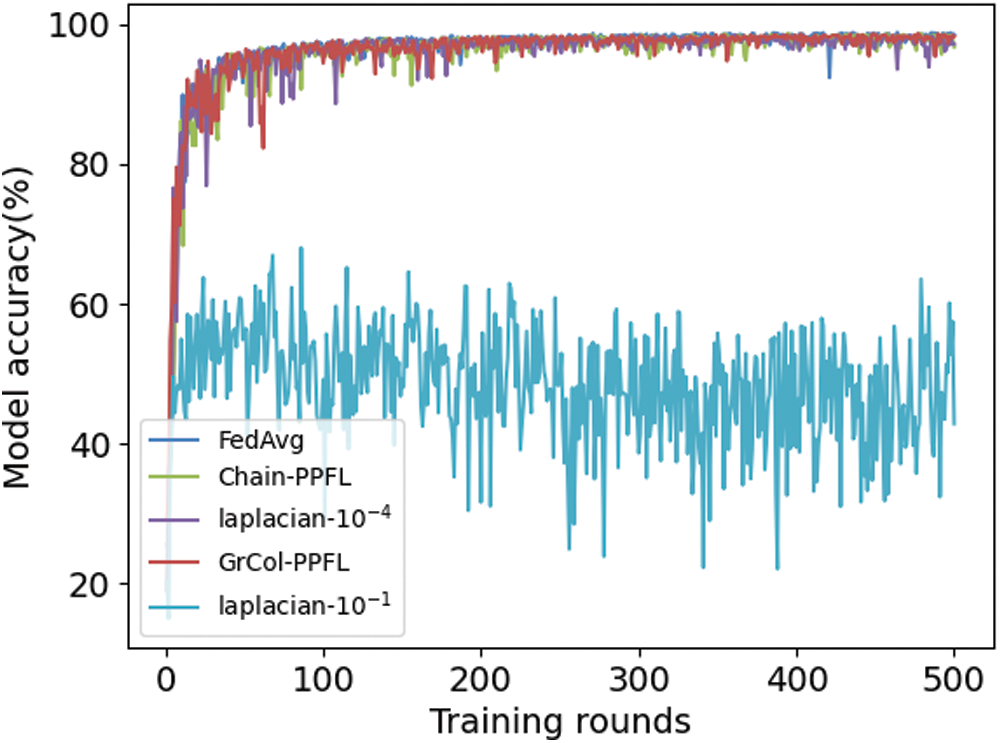
Figure 3: The accuracy of MNIST CNN non-IID

Tab. 1 shows the values of accuracy change with the increase of training rounds model. It can be seen that the accuracy of the other four cases is basically consistent except Laplacian noise-10−1 (L-10−1). Therefore, the accuracy of GrCol-PPFL scheme on non-IID dataset will not be affected. At server aggregation, the correct parameters can be obtained.

The approximate direction of the curve in Fig. 4 is consistent with Fig. 3. In order to see the change of the curve more clearly, we set the interval of the y-axis to 88–100. The curve is smoother than non-IID. Except for L-10−1, the accuracy is above 98% after 500 rounds of training. This is because the data assigned to users is IID. This situation is more similar to centralized machine learning, so the curve will be smoother. The L-10−1 has the same situation as Fig. 3, which is due to adding too much noise, but the server has no way to find the correct parameters. On the contrary, even though GrCol-PPFL and chain-PPFL have more noise than the L-10−1 policy, the server can reduce the excess noise and get the correct parameters.

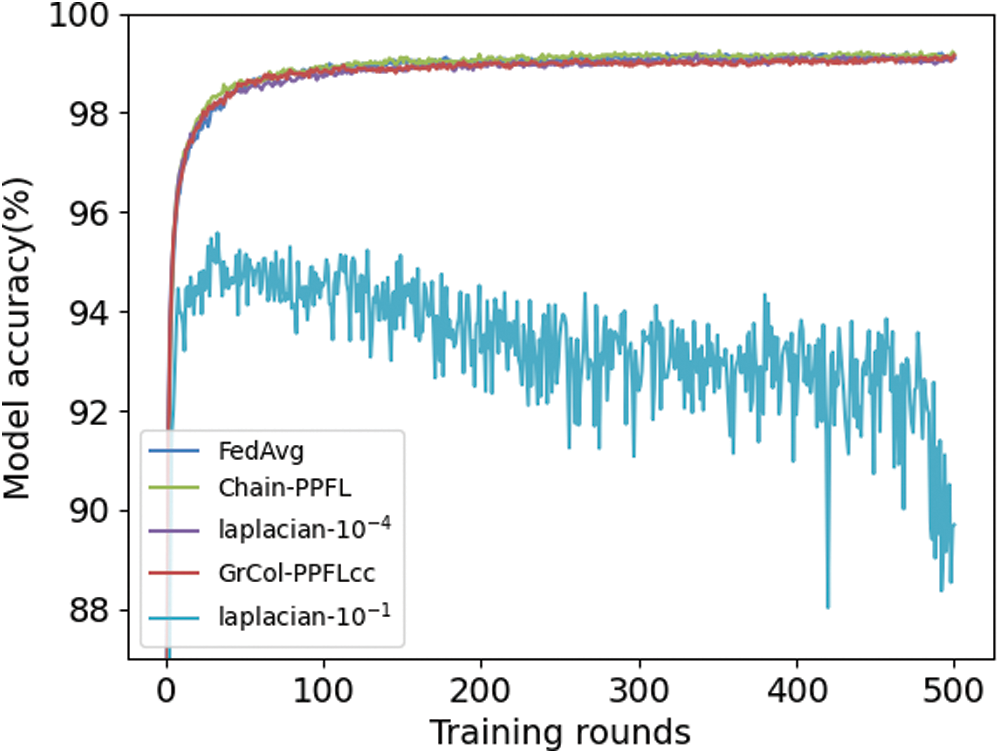
Figure 4: The accuracy of MNIST CNN IID

Tab. 2 shows the variation of the model accuracy with the number of rounds in the case of IID, which can also verify that GrCol-PPFL does not lose the model accuracy.

5.3 Privacy Preservation

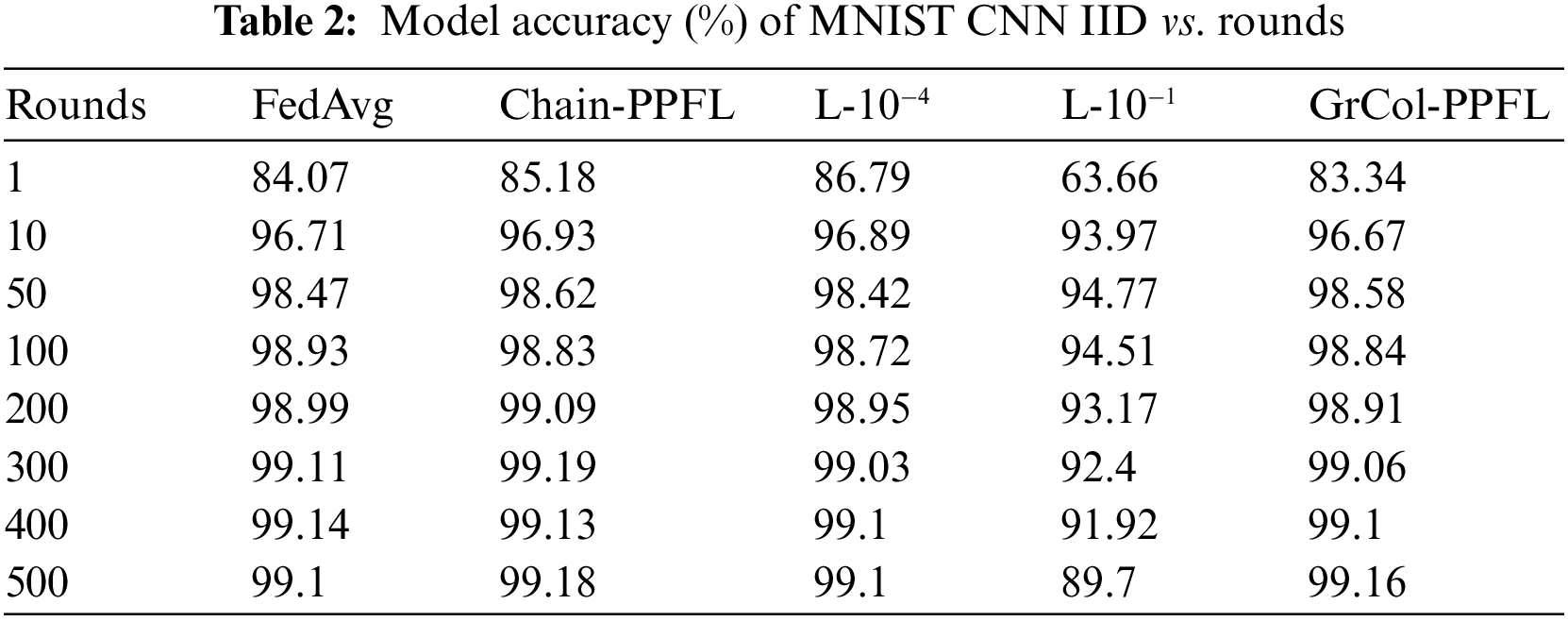
We utilize the DLG algorithm [10] to match the model gradients. The DLG algorithm uses the gradient uploaded by users to generate dummy data and labels with the same dimension. Then by calculating the dummy gradient, the distance between the dummy gradient and the real gradient is continuously reduced, and the original gradient is finally recovered. Chain-PPFL can obtain model parameters with user collusion. Therefore, chain-PPFL, like the FedAvg scheme, can expose the model parameters to the attacker to reveal the original image. So, when drawing DLG attack images, we see these two schemes as the same.

We can see from Figs. 5a and 5b that after 300 rounds of training, the gradient matching loss value of FedAvg/chain-PPFL and Laplacian noise with variance 10−4 is almost 0, which can completely leak the user’s original image information. However, the gradient matching loss value of Laplacian noise with the variance of 10−1 remained at about 8 after 300 rounds of training, and the image information is not recovered. The GrCol-PPFL scheme has a higher gradient matching loss value and also has the effect of privacy protection.

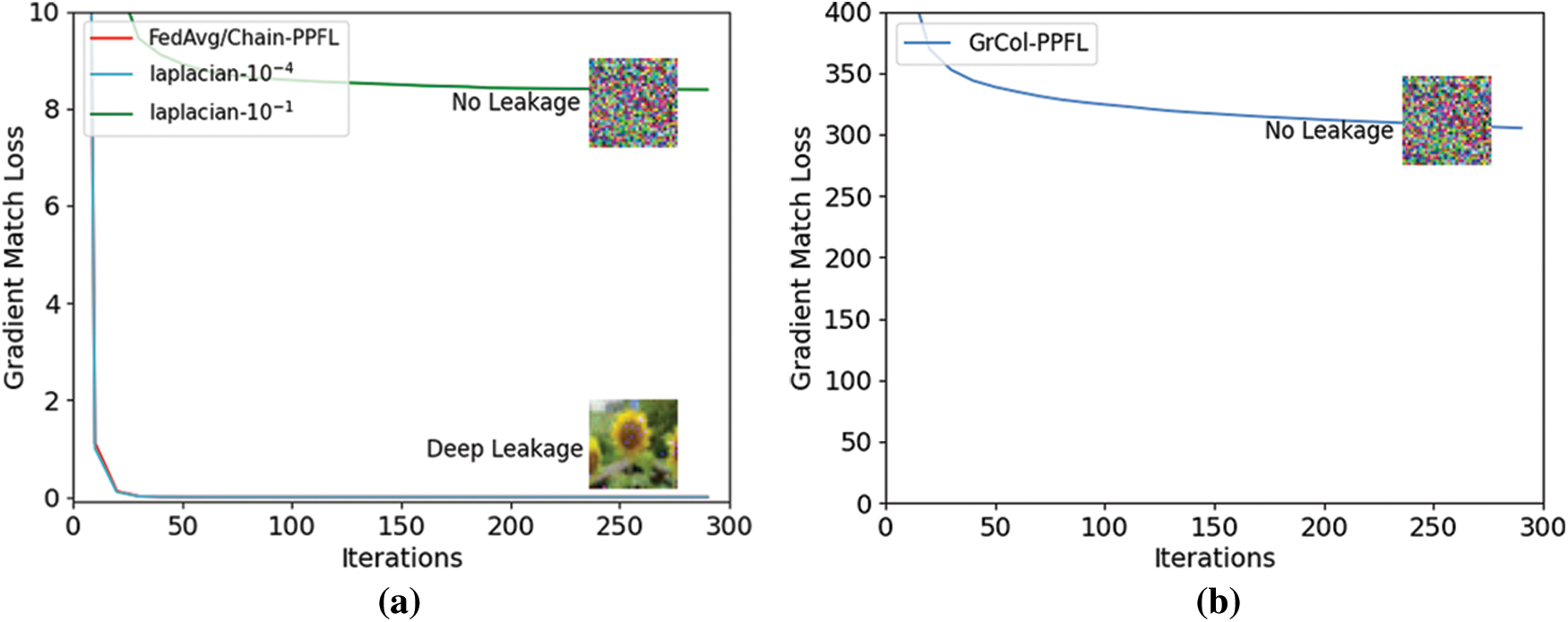
Figure 5: The gradient match loss of the DLG attack

So we can see that when the variance of the noise is larger, that is, the more interference, the stronger the ability to protect privacy. But the interference is not the bigger the better. Below we will introduce the comparison of accuracy and safety in detail.

We compare several schemes with data for non-IID distribution and training average accuracy for 500 rounds and gradient matching loss (GML) for DLG after 300 rounds. As can be seen from the Tab. 3, only L-10−1 and GrCol-PPFL have the ability to defend against DLG attacks, but the accuracy of L-10−1 has lower accuracy due to the addition of larger Laplacian noise. Our scheme can not only protect privacy in a network environment where users collude with each other, but also does not affect the accuracy of the model.

5.4 Latency

We measure the uplink consumption time of the GrCol-PPFL framework by changing the number of groups.

As shown in Fig. 6, when the number of groups is 1, GrCol-PPFL is equivalent to chain-PPFL, which has the highest communication delay, because there are many nodes that need to wait for the transmission of the previous node to complete. When L = 100, GrCol-PPFL is equivalent to FedAvg, and all users communicate with the server at the same time. Since we make TGrCol−PPFL≤TFedAvg, and users in FedAvg will not be grouped, we regard FedAvg as Baseline. We try to change the number of groups. We can see that the part below the baseline is the number of groups that are lower than FedAvg. Within these group fractions, the uplink consumption time of the system can be reduced, and an optimal group that minimize the uplink consumption time can be found.

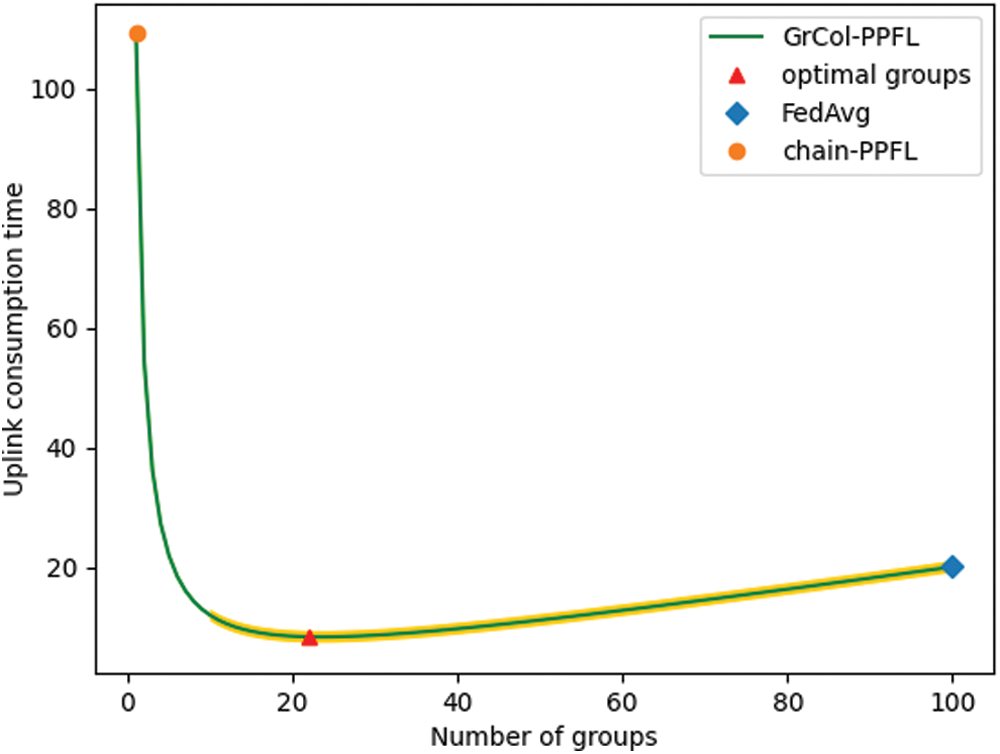
Figure 6: The relationship between the number of groups and the consumption time

In Fig. 7, the green curve represents the system uplink consumption time under the optimal group of GrCol-PPFL scheme. We can observe that the time of chain-PPFL increases significantly with the increase of users. GrCol-PPFL can dynamically adjust the number of groups with the increase of users, and the time is lower than FedAvg.

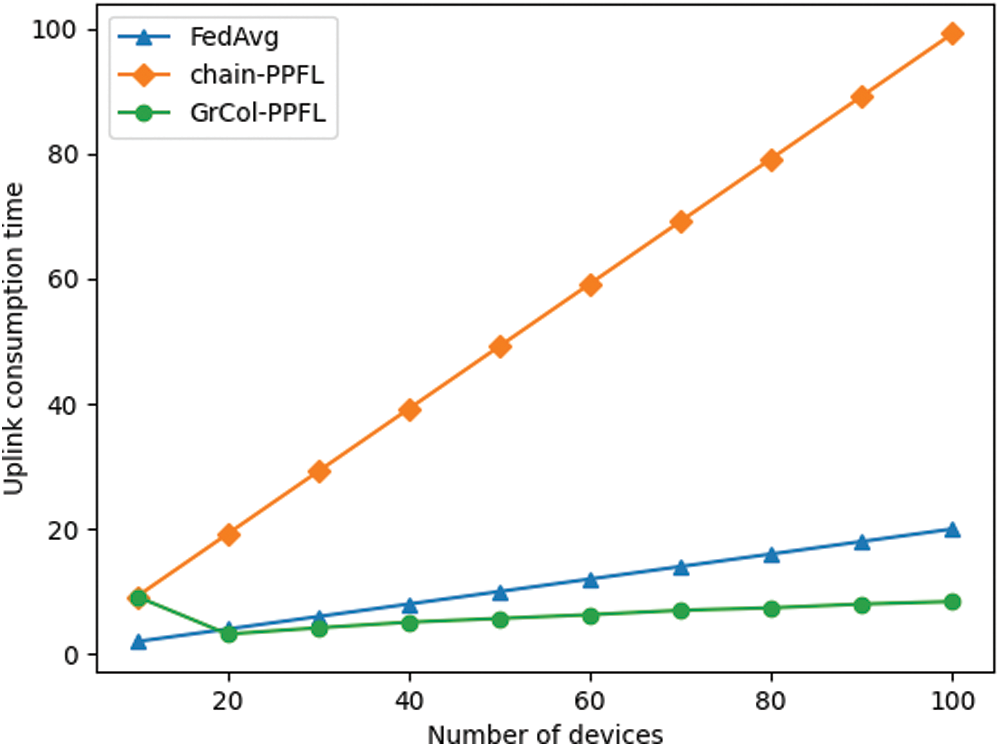
Figure 7: Uplink consumption time as devices increase

6  Conclusion and Future Work

In this paper, we propose a user-based group collaborative FL privacy protection framework, which aims to improve the system uplink communication time. Our experiments show that our method can still protect privacy even when users collude with each other, and does not affect the accuracy of model training. Through analysis and experimental verification, we can obtain the optimal number of groups that make the total uplink time of the FL system. In future work, we will continue to study the security and communication issues of FL in mobile communication networks, and propose better resource allocation schemes.

Funding Statement: This work was supported by the Major science and technology project of Hainan Province (Grant No. ZDKJ2020012), National Natural Science Foundation of China (Grant No. 62162024 and 62162022), Key Projects in Hainan Province (Grant ZDYF2021GXJS003 and Grant ZDYF2020040).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Taylor, D. Baron and D. Schmidt, “The world in 2025-predictions for the next 10 years,” in Proc. 10th Int. Microsystems, Packaging, Assembly and Circuits Technology Conf. (IMPACT), Taipei, Taiwan, pp. 192–195, 2015. [Google Scholar]

 2.  P. Tam, S. Math, C. Nam and S. Kim, “Adaptive resource optimized edge federated learning in real-time image sensing classifications,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 14, no. 1, pp. 10929–10940, 2021. [Google Scholar]

 3.  Z. H. Zheng, Y. Zhou and Y. Sun, “Applications of federated learning in smart cities: Recent advances, taxonomy, and open challenges,” Connection Science, vol. 34, no. 1, pp. 1–28, 2022. [Google Scholar]

 4.  C. T. Dinh and N. H. Tran, “Federated learning over wireless networks: convergence analysis and resource allocation,” IEEE/ACM Transactions on Networking, vol. 29, no. 1, pp. 398–409, 2021. [Google Scholar]

 5.  V. Joost and W. Matthijs, “A survey on distributed machine learning,” ACM Computing Surveys (CSUR), vol. 53, no. 2, pp. 1–33, 2020. [Google Scholar]

 6.  F. Lei, J. Cheng, Y. Yang, X. Tang and V. Sheng, “Improving heterogeneous network knowledge transfer based on the principle of generative adversarial,” Electronics, vol. 10, no. 13, pp. 1525, 2021. [Google Scholar]

 7.  White House Report, “Consumer data privacy in a networked world: A framework for protecting privacy and promoting innovation in the global digital economy,” Journal of Privacy and Confidentiality, vol. 4, no. 2, pp. 95–142, 2013. [Google Scholar]

 8.  B. McMahan, E. Moore and D. Ramage, “Communication-efficient learning of deep networks from decentralized data,” in Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, pp. 1273–1282, 2017. [Google Scholar]

 9.  J. Konečný, H. B. McMahan and F. X. Yu, “Federated learning: Strategies for improving communication efficiency,” arXiv preprint, arXiv: 1610.05492, 2016. [Google Scholar]

10. L. G. Zhu, “Deep leakage from gradients,” in Advances in Neural Information Processing Systems 32 (NeurIPS 2019Curran Associates, Vancouver, Canada, 14774–14784, 2019. [Google Scholar]

11. L. Melis and C. Song, “Exploiting unintended feature leakage in collaborative learning,” in Proc. IEEE Symp. on Security and Privacy (SP), San Francisco, California, USA, pp. 691–706, 2019. [Google Scholar]

12. B. Zhao, K. R. Mopuri and H. Bilen, “Idlg: Improved deep leakage from gradients,” arXiv preprint, arXiv:2001.02610, 2020. [Google Scholar]

13. Z. Sun, J. Feng, L. Yin, Z. Zhang and R. Li, “Fed-dfe: A decentralized function encryption-based privacy-preserving scheme for federated learning,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1867–1886, 2022. [Google Scholar]

14. S. Chen, D. Yu and Y. Zou, “Decentralized wireless federated learning with differential privacy,” IEEE Transactions on Industrial Informatics, vol. 18, no. 9, pp. 6273–6282, 2022. [Google Scholar]

15. C. Wang and C. Ma, “Protecting data privacy in federated learning combining differential privacy and weak encryption,” in Proc. Int. Conf. on Science of Cyber Security, Shanghai, China, pp. 95–109, 2021. [Google Scholar]

16. R. Nock and S. Henecka, “Entity resolution and federated learning get a federated resolution,” arXiv preprint, arXiv: 1803.04035, 2018. [Google Scholar]

17. K. Bonawitz, V. Ivanov and B. Kreuter, “Practical secure aggregation for privacy-preserving machine learning,” in Proc. of the 2017 ACM SIGSAC Conf. on Computer and Communications Security, Dallas, Texas, USA, pp. 1175–1191, 2017. [Google Scholar]

18. R. H. Xu and N. Baracaldo, “Hybridalpha: An efficient approach for privacy-preserving federated learning,” in Proc. of the 12th ACM Workshop on Artificial Intelligence and Security, London, UK, pp. 13–23, 2019. [Google Scholar]

19. X. Wu, F. Li and A. Kumar, “Bolt-on differential privacy for scalable stochastic gradient descent-based analytics,” in Proc. of the 2017 ACM Int. Conf. on Management of Data, Chicago, Illinois, USA, pp. 1307–1322, 2017. [Google Scholar]

20. L. Liu, F. Zheng and H. Chen, “A bayesian federated learning framework with online laplace approximation,” arXiv preprint, arXiv: 2102.01936, 2021. [Google Scholar]

21. Y. Wu, Y. Kang and J. Luo, “Fedcg: Leverage conditional GAN for protecting privacy and maintaining competitive performance in federated learning,” arXiv preprint, arXiv: 2111.08211, 2021. [Google Scholar]

22. J. Cheng, Y. Yang, X. Tang, N. Xiong and Y. Zhang, “Generative adversarial networks: A literature review,” KSII Transactions on Internet and Information Systems, vol. 14, no. 12, pp. 4625–4647, 2020. [Google Scholar]

23. Y. Li, Y. P. Zhou, A. Jolfaei, D. J. Dong, G. C. Xu et al., “Privacy-preserving federated learning framework based on chained secure multiparty computing,” IEEE Internet of Things Journal, vol. 8, no. 8, pp. 6178–6186, 2020. [Google Scholar]

24. S. Deep, X. Zheng, A. Jolfaei, D. Yu and P. Ostovari, “A survey of security and privacy issues in the internet of things from the layered context,” Transactions on Emerging Telecommunications Technologies, vol. 33, no. 6, pp. 1–20, 2020. [Google Scholar]

25. D. B. Sui, “Feded: federated learning via ensemble distillation for medical relation extraction,” in Proc. of the 2020 Conf. on Empirical Methods in Natural Language Processing, Punta Cana, Dominican Republic, pp. 2118–2128, 2020. [Google Scholar]

26. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

27. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

28. B. Y. Liu and L. J. Wang, “Lifelong federated reinforcement learning: A learning architecture for navigation in cloud robotic systems,” IEEE Robotics and Automation Letters, vol. 4, no. 4, pp. 4555–4562, 2019. [Google Scholar]

29. C. Dwork, “A firm foundation for private data analysis,” Communications of the ACM, vol. 54, no. 1, pp. 86–95, 2011. [Google Scholar]

30. S. Truex, L. Liu and K. H. Chow, “Ldp-Fed: Federated learning with local differential privacy,” in Proc. of the Third ACM Int. Workshop on Edge Systems, Analytics and Networking, New York, NY, United States, pp. 61–66, 2020. [Google Scholar]

31. S. Hardy, W. Henecka and H. Ivey-law, “Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption,” arXiv preprint, arXiv: 1711.10677, 2017. [Google Scholar]

32. Q. Li and M. G. Christensen, “A privacy-preserving asynchronous averaging algorithm based on shamir’s secret sharing,” in 2019 27th European Signal Processing Conf., A Coruna, Spain, pp. 1–5, 2019. [Google Scholar]

33. L. Yang, Y. Lu and J. Cao, “E-tree learning: A novel decentralized model learning framework for edge ai,” IEEE Internet of Things Journal, vol. 8, no. 14, pp. 11290–11304, 2021. [Google Scholar]

34. P. Tam, S. Math, A. Lee and S. Kim, “Multi-agent deep q-networks for efficient edge federated learning communications in software-defined iot,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3319–3335, 2022. [Google Scholar]

35. H. Wang, Z. Kaplan, D. Niu and B. Li, “Optimizing federated learning on non-IID data with reinforcement learning,” in IEEE INFOCOM, 2020-IEEE Conf. on Computer Communications, Toronto, ON, Canada, pp. 1698–1707. [Google Scholar]

36. D. Rothchild, A. Panda and E. Ullah, “Fetchsgd: Communication-efficient federated learning with sketching,” in 37th Int. Conf. on Machine Learning, Vienna, Austria, pp. 8253–8265, 2020. [Google Scholar]

37. A. F. Aji and K. Heafield, “Sparse communication for distributed gradient descent,” in Proc. EMNLP 2017: Conf. on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, pp. 440–445, 2017. [Google Scholar]

38. N. Chhabra, M. Bala and V. Sharma, “Implementation and validation of the optimized deduplication strategy in federated cloud environment,” Computers, Materials & Continua, vol. 71, no. 1, pp. 2019–2035, 2022. [Google Scholar]

39. F. P. -C. Lin, S. Hosseinalipour, S. S. Azam, C. G. Brinton and N. Michelusi, “Semi-decentralized federated learning with cooperative d2d local model aggregations,” IEEE Journal on Selected Areas in Communications, vol. 39, no. 12, pp. 3851–3869, 2021. [Google Scholar]

40. H. Zhao, C. Wang, Y. Zhu and W. Lin, “P2p network based on neighbor-neighbor lists,” Journal of Physics: Conference Series, vol. 1168, no. 3, pp. 32072, 2019. [Google Scholar]

41. L. Deng, “The MNIST database of handwritten digit images for machine learning research,” IEEE Signal Processing Magazine, vol. 29, no. 6, pp. 141–142, 2012. [Google Scholar]