Novel Optimized Feature Selection Using Metaheuristics Applied to Physical Benchmark Datasets

1  Introduction

Feature selection is the process of selecting the most significant variables in predictive modeling problems. Feature selection is considered a principal concept in the field of machine learning (ML). Some predictive modeling problems have high-dimensional datasets which may contain redundant or irrelevant variables. Employing all input variables in training the model increases the likelihood of including non-informative features. This may cause uncertainty in the predictions and reduce the model's effectiveness. Moreover, using such a large number of features in developing the model slows the training process and makes it computationally intensive. Therefore, in the process of feature selection, irrelevant and redundant attributes are discarded, and the number of features to be used in training the model is decreased. Using a reduced and significant set of features in training the model contributes in improving the prediction performance and decreases the computational complexity and time.

Feature selection techniques are categorized into supervised and unsupervised methods based on the dependence on the target variable in selecting relevant features. In supervised feature selection approaches, the relation between the input predictors and the target variable is used to distinguish the effective features. However, this is not the case in unsupervised methods. Supervised methods have been shown to provide better feature selection performance and hence are commonly used [1]. Filter, wrapper, embedded, and intrinsic methods are the most popular methods under the umbrella of supervised learning feature selection techniques [2]. In filter methods, statistical techniques are employed to evaluate the relevance between the input features and the target. Commonly, statistical correlation between the input predictors and the target variable is used as the basis for filter feature selection. A correlation score is computed for each feature, and based on these scores; the input predictors are filtered. Only features with the strongest relationship with the target are used for the model development.

In wrapper methods, multiple models are generated with different subsets of input predictors. The performance of these models is evaluated to find the best combination of features that optimizes the prediction performance. The main difference between the filter and wrapper methods is that the latter assesses the goodness of selected features based on the predictive model accuracy measure, which makes it more efficient but computationally intensive. On the other hand, the selection criteria of the filter approaches are model-independent, which makes it more popular, and has a less computational cost but is less efficient in selecting relevant features [3–5]. In order to get the advantages of both methods, the embedded approaches integrate the statistical-based and model-based feature selection into a single algorithm. Interestingly, some ML algorithms contain built-in feature selection properties such as decision trees, random forest, Lasso algorithms, and others. These algorithms automatically select the features that maximize the model performance as part of model learning. Such algorithms are referred to as intrinsic feature selection methods. It is worth mentioning that the performance of a feature selection approach is dependent on the problem in hand. In other words, the performance of a specific approach in selecting the significant features may vary from one problem to another. The type of the input and output variables, the relevance, noise, and the number of features definitely affect feature selection performance. This makes it challenging to decide on the best feature selection approach to be used especially when there are a vast number of input attributes. In this case, the feature selection problem could be tackled as an optimization problem to select the optimal set of input features. Stochastic optimization algorithms can search and select optimum features. Among the powerful and modern optimization approaches is the metaheuristic optimization algorithms. Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Simulated Annealing, Ant Colony, and Bee algorithms are the most popular metaheuristic optimization algorithms. These optimizers have been used for feature selection in many studies to enhance the performance of classification algorithms [6].

2  Literature Review

Feature selection has been widely employed in a variety of applications, including spam email filtering, disease diagnosis, text classification, fraudulent detection, deoxyribonucleic acid (DNA) microarray analysis, and others. Extracting significant features from the input dataset is crucial for creating an efficient decision-making model. To increase the accuracy of prediction models, most studies apply filter and wrapper feature selection strategies [7]. For instance, authors in [8] developed a new feature selection strategy based on an improved Chi-square algorithm to improve the performance of Arabic text classification using support vector machines (SVM) classifier. According to authors in [9], an anomaly network-based system can achieve a high detection rate and minimize false positives by employing an innovative hybrid method. The AdaBoost technique was used to classify the data, and an artificial bee colony was employed to choose features. The authors of [10] proposed a feature selection method for mammography classification utilizing a Biogeography-based optimization approach employing the adaptive neuro-fuzzy inference system and artificial neural network. According to [11], robust feature selection based on the L1, and L2 norm may eliminate outliers and identify attributes across all data points with joint sparsity while reducing loss function and regularization. The scientists utilized regression as an aim and conducted multiple tests on six datasets to evaluate the proposed model. A novel unsupervised feature selection approach based on L1, and L2 norm regularization was developed by authors in [12] for human action recognition. The model extracts and chooses features simultaneously in order to create optimum features for the classification framework. Another work [13] developed a novel linear dimensionality reduction approach called robust discriminant regression (RDR) that leverages the L2; 1-norm as the core measure for feature extraction. RDR was unable to pick features in sparse projections, according to the authors.

Finding the best combination of features is a challenging task. In response to this demand, optimization algorithms have been recently incorporated into modern feature selection approaches to select the best subset of attributes from datasets. Metaheuristic optimization algorithms have been utilized by many recent studies to find the optimal set of input features. A metaheuristic is a problem-independent algorithmic framework that gives a set of recommendations for developing heuristic optimization algorithms at a high level. Optimization algorithms often use a combination of specific algorithmic parameters and regulating parameters in the evaluation process. These parameters highly impact the feature selection process and significantly affect the performance of the employed machine learning models. Many studies used various optimization algorithms, such as the Genetic Algorithm and Particle Swarm Optimization, and others for attribute selection to improve the effectiveness of machine learning models. For instance, authors in [14] established a method for feature selection using GA by ranking genes using T-Statistics, F-Test, and signal-to-noise ratio (SNR) measurements. The selected features were fed afterward to K-nearest neighbor (KNN) and SVM classifiers. The study in [15] used the wrapper technique to develop a novel fusion method that combines GA and SVM to perform feature selection. When compared to other well-known methods, the hybrid GA-SVM produced greater classification precision. Another study [16] suggested a GA-based feature selection method that uses KNN classification error as a fitness to provide a set of features to improve the classifier performance. Moradi [17] combined a local search technique with a PSO-based feature selection method. They tested the system’s performance using various filter and wrapper-based methods and found that classifiers provided superior accuracy using the optimized features. Authors in [18] introduced a new feature selection approach based on chicken swarm optimization. The results of that study showed that the Chicken swarm optimization outperforms the original GA and PSO optimization algorithms on standard datasets. A feature selection algorithm that is based on elephant search optimization and a deep learning network was proposed in [19] to investigate microarray data. Rodrigues et al. [20] proposed a wrapper feature selection strategy based on Bat Algorithm (BA) and Optimum-Path Forest. Authors in [21] employed the Binary Dragonfly optimization algorithm to select a subset of features from UCI datasets and achieved better results than GA and PSO algorithms. Sayed et al. [22] developed a new metaheuristic method for feature selection based on the crow search algorithm. Their results showed superior results with benchmark datasets. To solve local optima and poor convergence difficulties, authors in [23] proposed a hybrid feature selection method combining a swarm algorithm with chaos theory and applied it to a variety of benchmark tasks. To reduce the number of attributes in breast cancer datasets, authors in [24] employed the Modified Correlation Rough Set feature selection method. For identifying CT images of cervical cancer, a new feature selection approach based on Artificial Bee Colony and KNN algorithms was introduced in [25]. To increase classification performance, authors in [26] proposed a new feature selection method for Arabic text classification utilizing the firefly algorithm. The authors conducted experiments on the OSAC dataset and achieved a precision of 0.994 with the firefly algorithm. Authors in [6] developed a metaheuristics-based feature selection model to select optimal features for breast cancer classification. Another study [27] introduced a new prediction framework called IGWO-KELM by combining an enhanced grey wolf optimization (IGWO) and kernel extreme learning machine (KELM). In the suggested method, a genetic algorithm (GA) was utilized to generate a diverse set of initial positions, and then grey wolf optimization (GWO) was used to update the population's current positions in the discrete searching space, resulting in the best feature subset for KELM classification. The authors claimed that the IGWO-KELM outperformed the native GA and GWO for breast cancer classification. In another study [28], a wrapper feature selection algorithm is developed using the chimp optimization algorithm (ChOA) for the classification of high-dimensional biomedical data. Authors in [29] introduced an enhanced version of the Binary Dragonfly Algorithm (BDA) to select optimal feature classification problems. They proposed a new wrapper-based Hyper Learning Binary Dragonfly Algorithm (HLBDA) in which a hyper learning strategy is utilized to improve searching and help escape local optima. Authors in [30] developed a modified Binary Grey Wolf optimizer (MbGWO) to find optimal features using the right balance between exploration and exploitation. Their proposed optimizer is based on Stochastic Fractal Search (SFS) to find the best solution for the MbGWO. KNN classifier was used to assess the performance of the selected features over nineteen datasets. Their results reveal the superiority of the introduced MbGWO.

3  Methodology

The proposed binary adaptive squirrel search optimization algorithm is based on the flying squirrels’ search mechanism [31]. To utilize the optimization algorithm in the task of feature selection, the optimization algorithm is applied, and the fitness function is evaluated for each feature; then, the resulting continuous solution is converted to binary. Therefore, this section starts with presenting the main idea of the squirrel search algorithm, followed by presenting the fitness calculation and binary conversion.

3.1 The Squirrel Search Algorithm

The basic idea of the squirrel search algorithm takes into account that squirrels travel between three different types of trees: hickory, oak, and regular trees. Nuts come from oak and hickory trees, whereas other trees provide no nourishment. For simplicity, the squirrel search (SS) algorithm treats three oak trees and one hickory tree as Nfs available food supplies for the n flying squirrels (FS). The squirrel locations (SL) and velocities (SV) are represented by the following matrices:

SL=[SL1,1SL1,2SL1,3…SL1,dSL2,1SL2,2SL2,3…SL2,dSL3,1SL3,2SL3,3…SL3,d……………SLm,1SLm,2SLm,3…SLm,d](1)

SV=[SV1,1SV1,2SV1,3…SV1,dSV2,1SV2,2SV2,3…SV2,dSV3,1SV3,2SV3,3…SV3,d……………SVm,1SVm,2SVm,3…SVm,d](2)

For the jth dimension and ith squirrel, the flying squirrel is denoted by FAi,j for i ∈ 1, 2, 3,…, n and j ∈ 1, 2, 3, …, d. The uniform distribution within upper and lower bounds is used to determine the initial locations of FAi,j. For each flying squirrel, the fitness values f = f1, f2, f3,…, fn are measured in terms of the following matrix.

f=[f1(SL1,1,SL1,2,SL1,3,…,SL1,d)f2(SL2,1,SL2,2,SL2,3,…,SL2,d)f3(SL3,1,SL3,2,SL3,3,…,SL3,d)…fm(SLm,1,SLm,2,SLm,3,…,SLm,d)](3)

As a result, flying squirrels look for food sources with a higher fitness value than those with lower fitness values. It is a hickory tree that provides the best value. The values are then rearranged in order of increasing importance. In the case of hickory nut trees, the first best solution has been determined to be FAht, followed by three further best solutions that have been determined to be FAat. The rest of the answers should be FAnt on standard trees. In mathematics, there are three possible cases to generate new locations for a flock of flying squirrels. The global and local optima of the ASSOA algorithm are shown in the plot of Fig. 1. As shown in the figure, the movement of the squirrel based on the three cases can lead to the optimum global location.

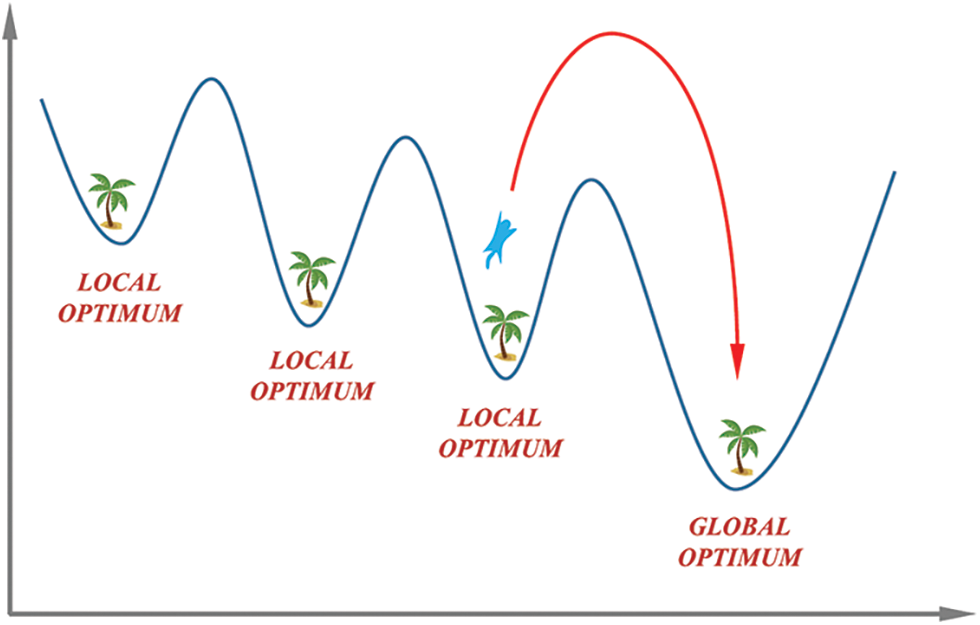
Figure 1: Global and local optima during the search by the ASSOA algorithm

Case 1: Moving to the hickory nut tree and location of FLat:

FLat(t+1)=f(x)={FLat(t)+dg×Gc(FLht(t)−FLat(t)),ifR1<PdpRandomlocation,otherwise(4)

Case 2: Moving to the acorn nut trees and location of FLnt:

FLnt(t+1)=f(x)={FLnt(t)+dg×Gc(FLht(t)−FLnt(t)),ifR2<PdpRandomlocation,otherwise(5)

Case 3: moving to the hickory nut tree and location of FLnt:

FLnt(t+1)=f(x)={FLnt(t)+dg×Gc(FLht(t)−FLnt(t)),ifR3<PdpRandomlocation,otherwise(6)

where the variables R1, R2, and R3 are selected randomly from the range [0,1], t denoted the iteration number, distance for gliding is referred to as dg, which is selected randomly. To achieve balance the exploitation and exploration, the value of Gc is set as 1.9. For the three cases, the value of Pdp is set as 0.1. More details about the ASSOA are presented in [32].

3.2 The Proposed Feature Selection Method

The binary ASSOA search strategy for selecting wrapper features is introduced in this section. Using the wrapper-based strategy, several classifiers are required to choose the optimal subset of features from a high-dimensional dataset. The wrapper-based technique is used to handle the challenge of high-dimensional feature selection.

1.    Search algorithm

2.    Feature selection basis

3.    Classification method

Classification algorithms such as SVM, KNN, and artificial neural networks (ANN) are all prevalent. As a result, this research employs the KNN classifier, which can be used simply and easily. In addition, for the feature selection problem, KNN is one of the most commonly used classifiers. SVM and ANN can also be used to evaluate the quality of features that have been picked [33–38].

The proposed bASSOA employs a KNN classifier to make sure that only decency-preserving features are used. Due to its primary goal of maximizing classification accuracy while minimizing the number of selected features and the error rate, feature selection methods aim to decrease both of these factors. As a result, Eq. (1) is employed in the proposed feature selection technique. To maximize the feature assessment norm, the proposed bASSOA approach proposes an adaptive search space exploration presented in Eq. (1).

Fitness=αγR(D)+β|C−R||C|(7)

In which the condition attribute set R in relation to the decision D has a classification quality denoted by γR(D). The total number of features is denoted by C, and the number of selected features is referred to as R. Additional parameters that affect the classification accuracy are α ∈ [0,1] and β = 1 – α. Based on the error rate and selected feature ratio, Eq. (1) can be converted into the minimization problem. Therefore, the minimization of the error rate can be performed using the following fitness function, where ER(D) is the error rate.

Fitness=αER(D)+β|R||C|(8)

To select the best set of features, the resulting best solution is converted into binary 0 or 1. To perform this conversion, the sigmoid function is usually employed as represented by the following equation where Sbest refers to the best position at iteration t.

Sd(t+1)={0,ifSigmoid(Sbest)<0.51,otherwise(9)

The steps of the proposed feature selection method are listed in Algorithm (1).

4  Experimental Results

Ten feature selection benchmark datasets from the UCI repository have been used to evaluate the proposed binary feature selection method's performance (UCI Feature selection dataset 2017). The number of features and occurrences in each of the databases is different. Tab. 1 provides a comprehensive overview of all datasets. In order to choose the best features, the suggested bASSOA was used. The suggested technique selects the optimal features based on the accuracy given by the KNN classifier. Using empirical data, the KNN classifier sets K to 5. In cross-validation, each dataset's instances are randomly divided into three sets: training, validation, and testing. The suggested bASSOA algorithm's performance was verified using K-fold cross-validation that makes use of K − 1 folds for training, validation, and testing.

4.1 Evaluation Criteria

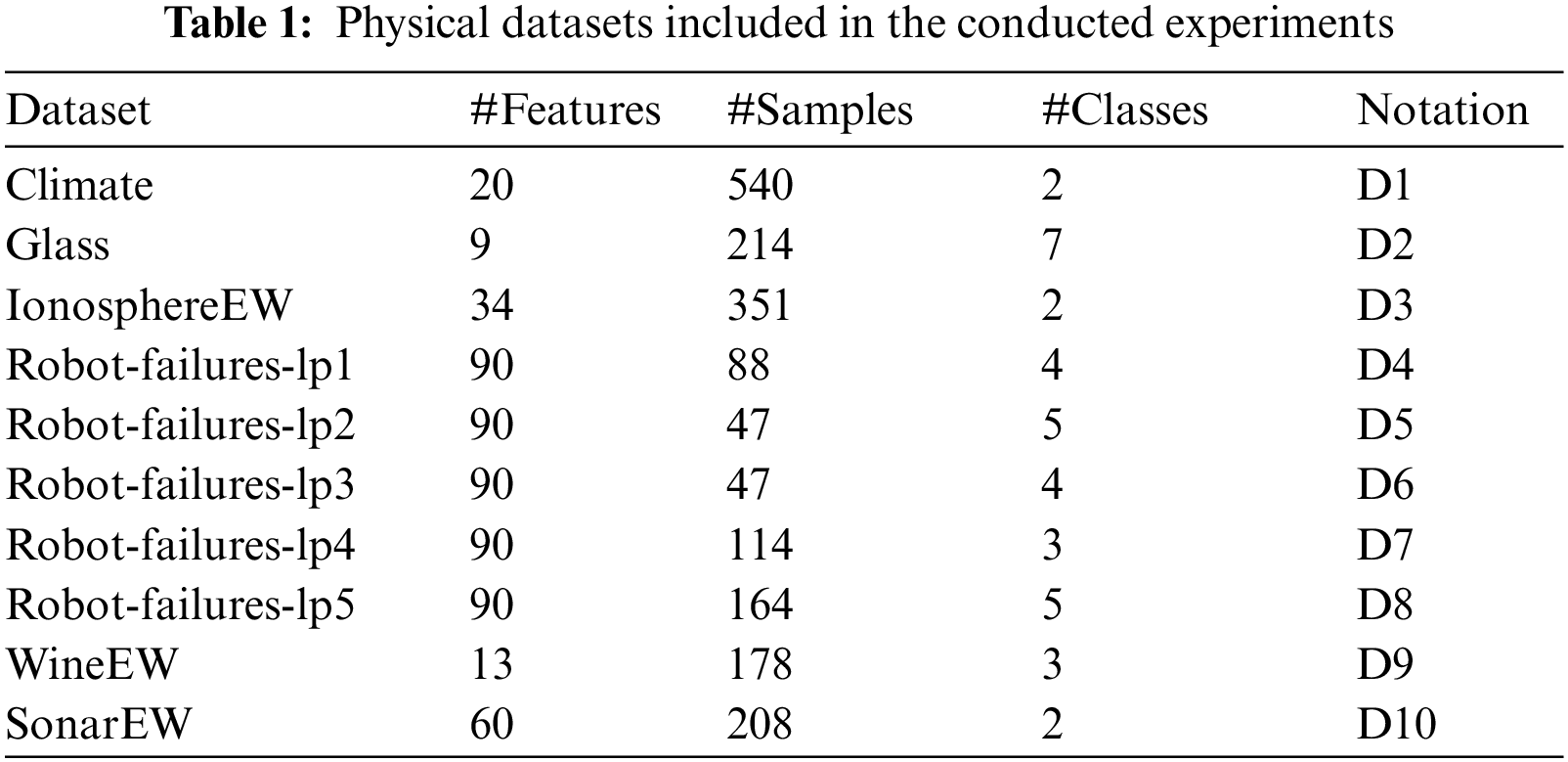
Performance evaluation measures used to evaluate the suggested strategy are shown in Tab. 2. There are six criteria that make up these metrics: standard deviation, average fitness size, mean fitness, average error, worst fitness, and best fitness. In this part, the evaluation of the proposed approach using these metrics is presented and discussed.

4.2 Algorithm Configuration

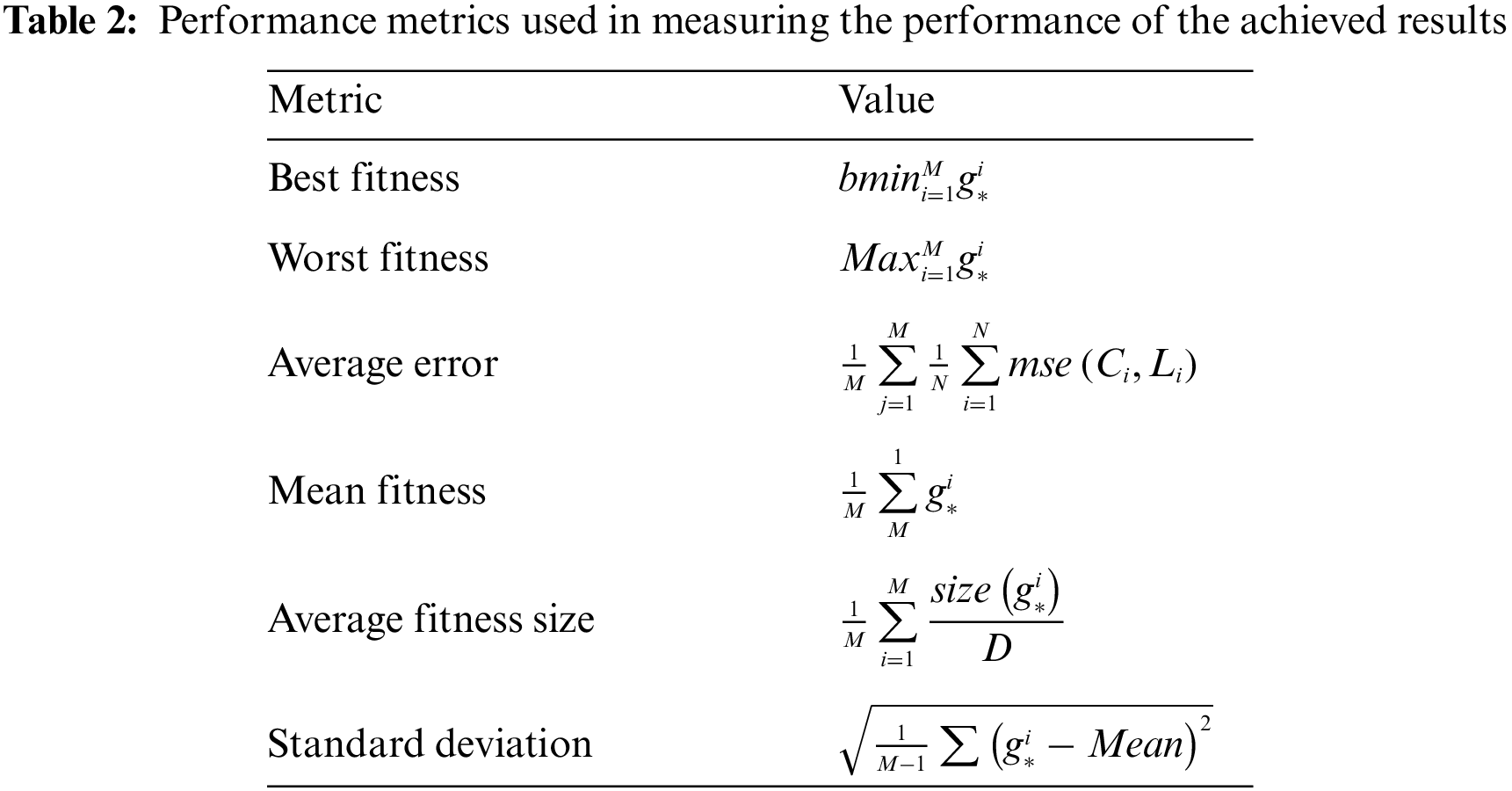
The configuration parameters of the proposed approach are presented in Tab. 3. In this table, the number of iterations is 50, and the number of search agents is 10. In addition, the ranges of the variables of the optimization equations are presented in the table.

4.3 Evaluation Results

There are eleven current state-of-the-art ways to compare the proposed bASSOA feature selection approach with; bGWO, PSO, bPSO, SFS bWOA, bMGWO and SBO, bSBO, bPSO, bGWO GA and the suggested method, bASSOA. Mean values for each approach have been obtained for comparison after each method was run 30 times. In order to evaluate the suggested bASSOA approach, the six performance criteria listed above were taken into consideration.

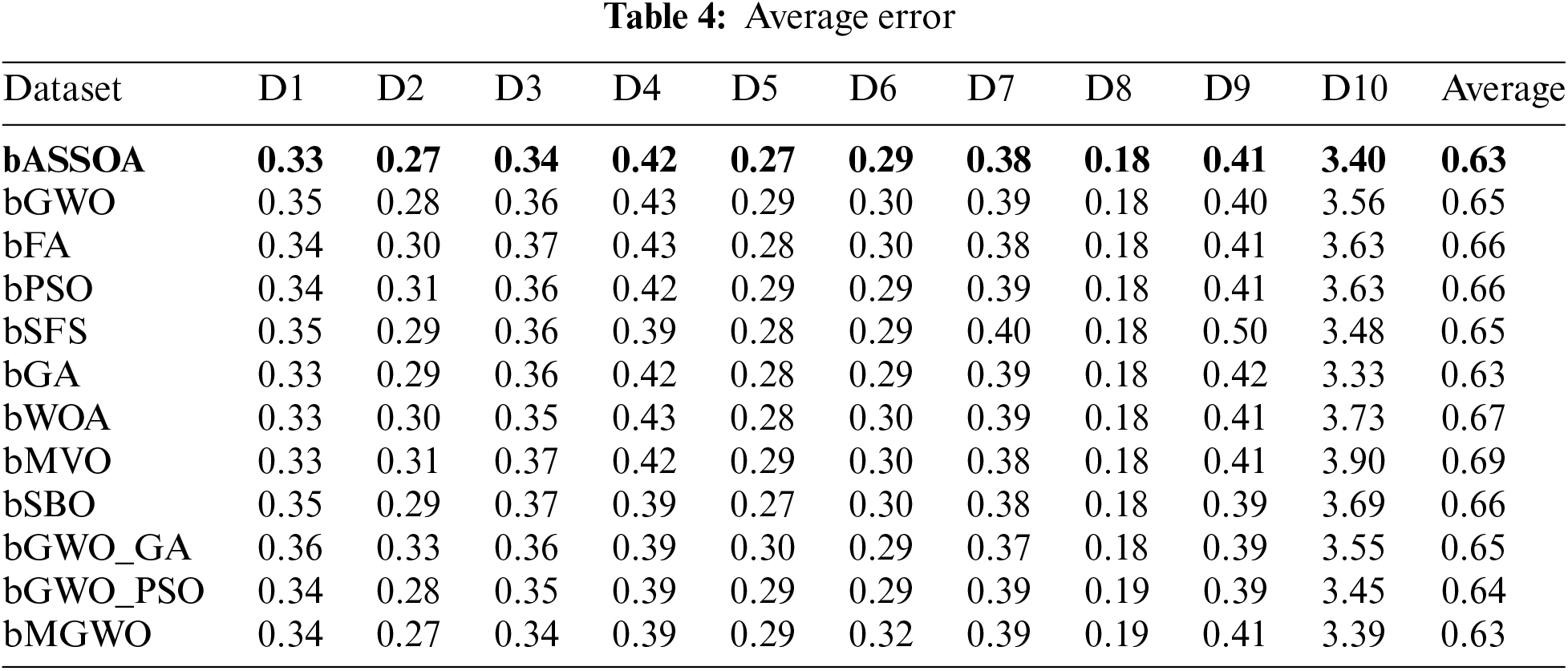
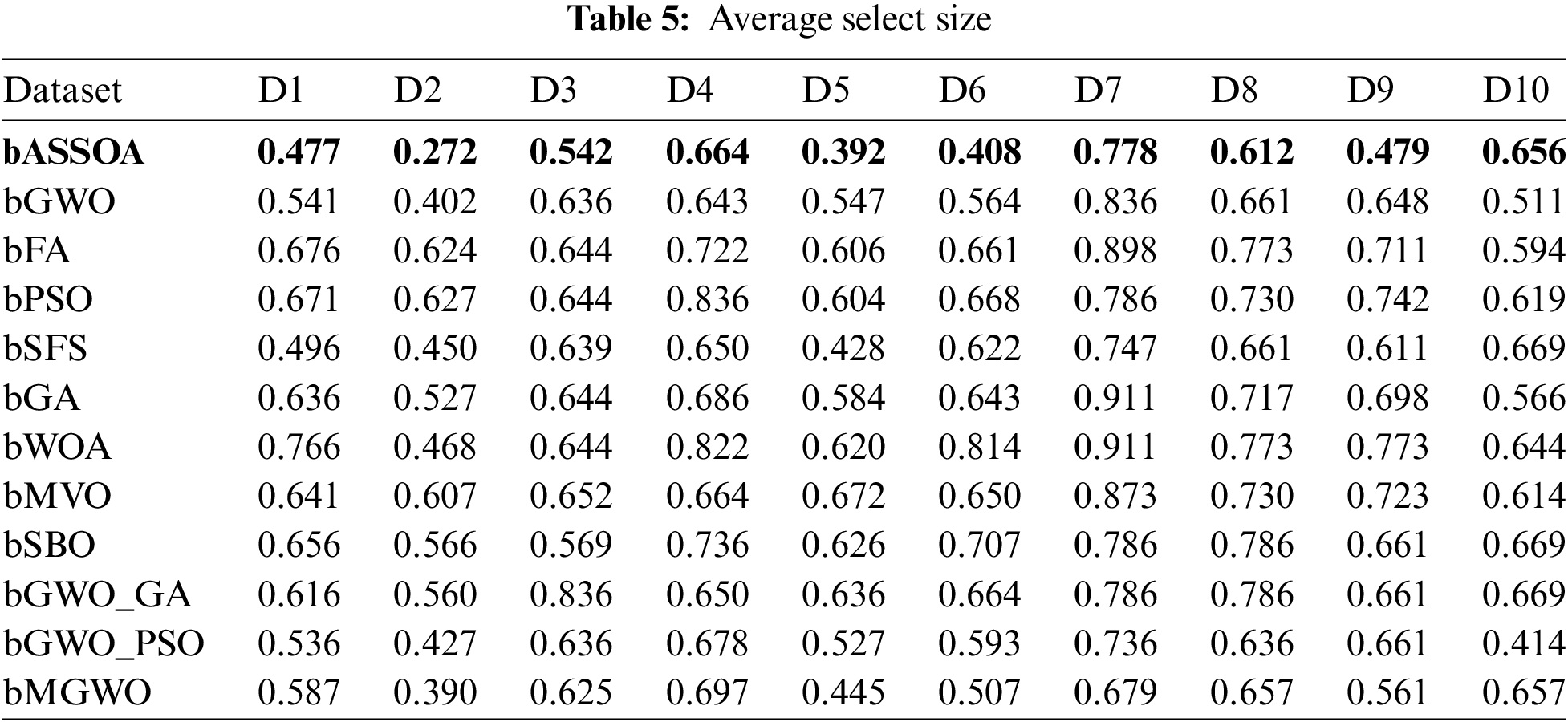
Data transformation and feature selection approaches were tested on the original datasets without deleting any attributes in order to show the impact of the suggested methods on the original datasets. Tab. 4 shows the average inaccuracy of the proposed bASSOA and the other approaches investigated. According to the table, the bASSOA technique has the best overall average error of 0.63, which is lower than the other methods' average errors. Using data transformation, we can examine the effect that the suggested technique of feature selection has on the average select size of chosen features, as shown in Tab. 5. Based on this chart, it’s clear that using bASSOA returns the largest select size.

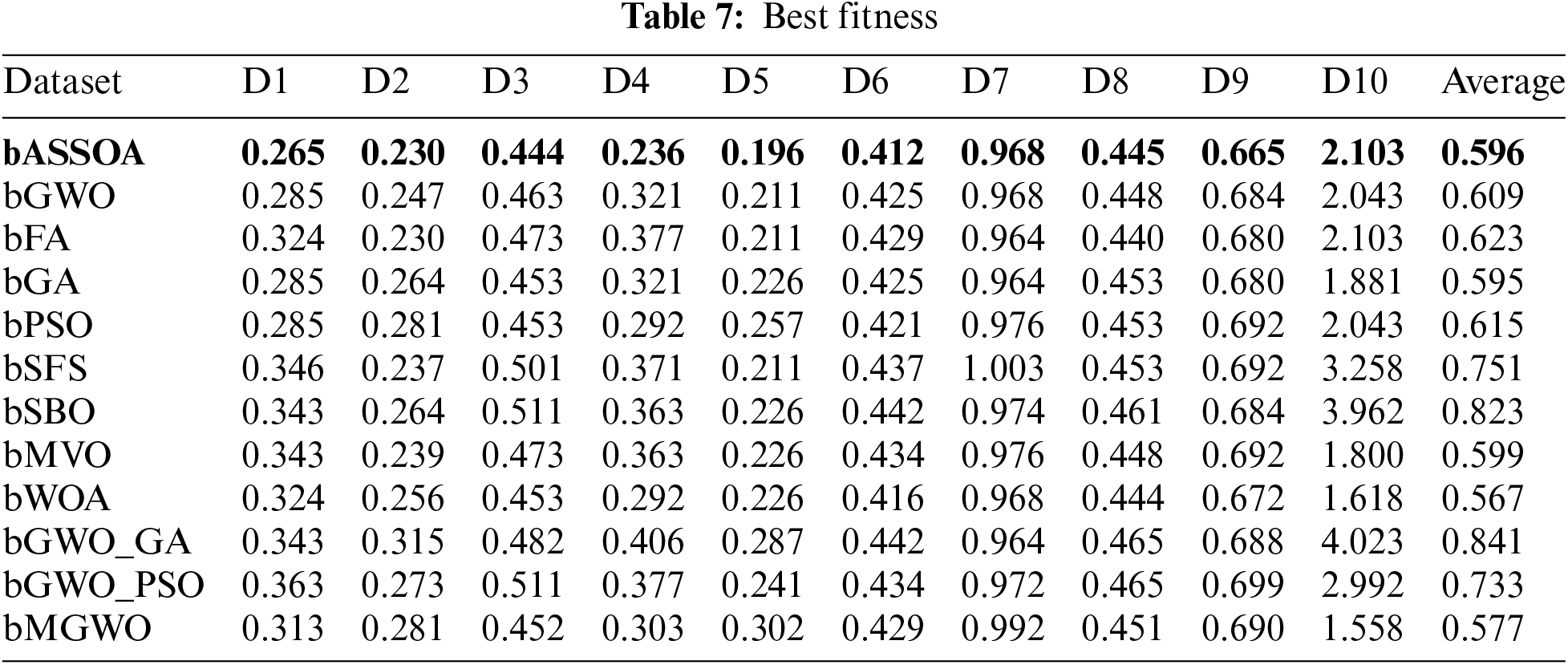
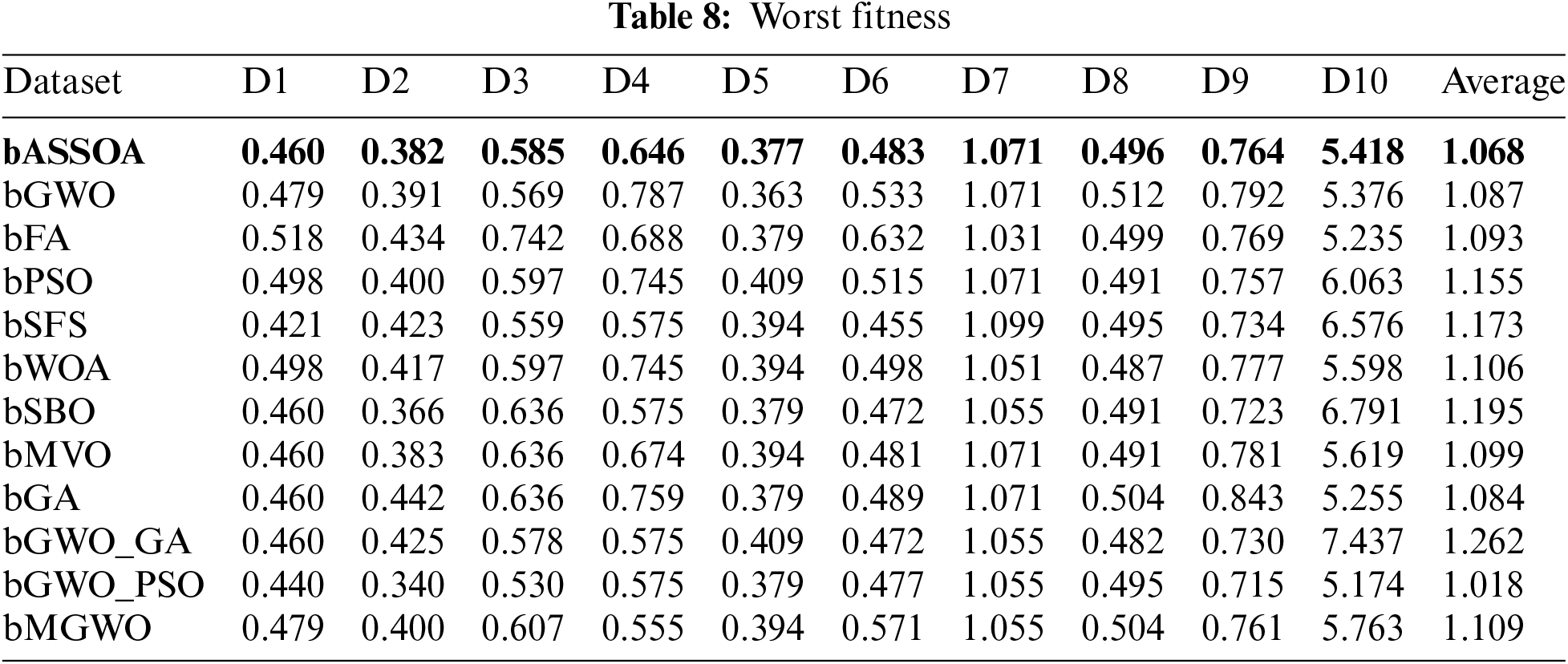
On the other hand, the average fitness of the quality of the selected features is measured, and the results are recorded in Tab. 6. As presented in this table, the overall average fitness of the proposed approach is 0.775, which is the best value among the other approaches. In addition, the best, worst, and standard deviation fitness are measured based on the selected features, and the results are presented in Tabs. 7–9, respectively. The recorded results in these tables confirm the superiority and effectiveness of the proposed feature selection algorithm.

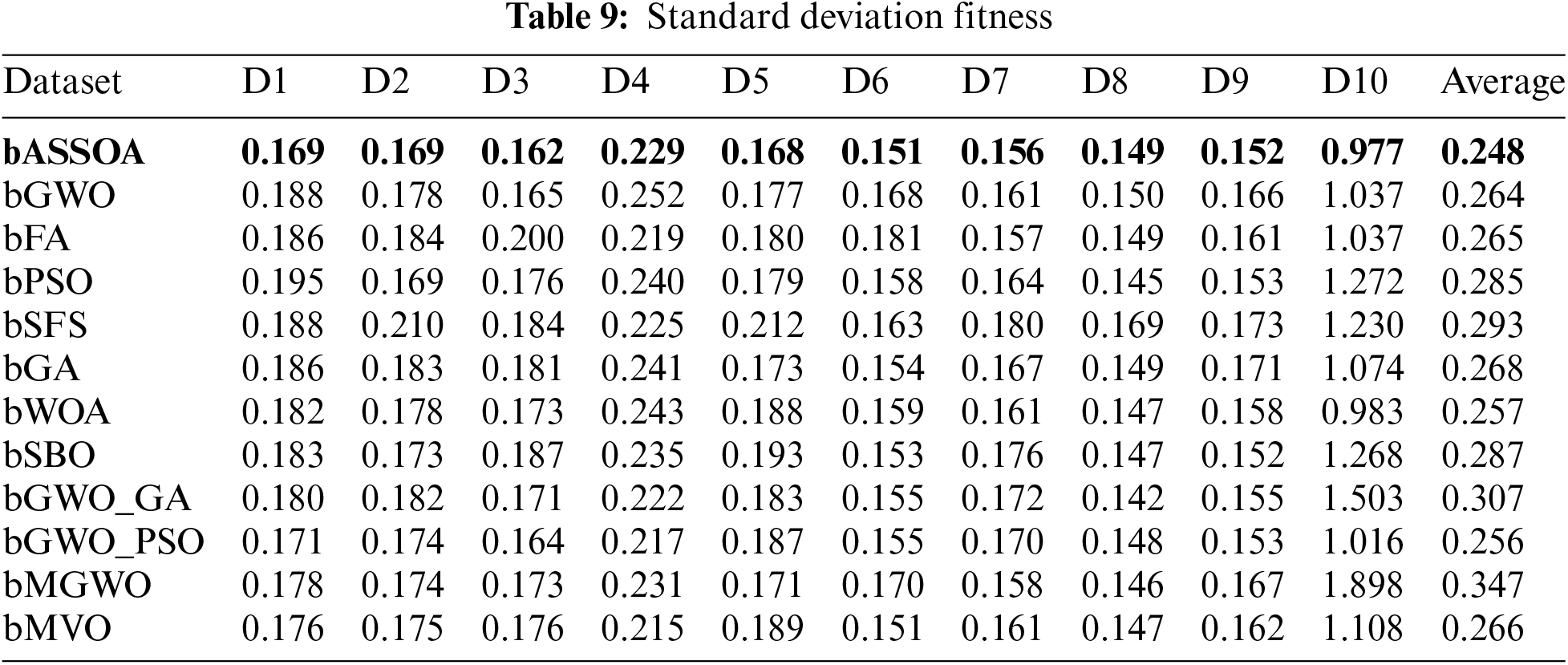
In addition, the visualization of some of the achieved results is presented in Figs. 2 and 3. In these figures, the average error and average standard deviation of the achieved fitness are shown. As depicted in these figures, the best values achieved are based on the proposed bASSOA approach. These results confirm the superiority of the proposed approach.

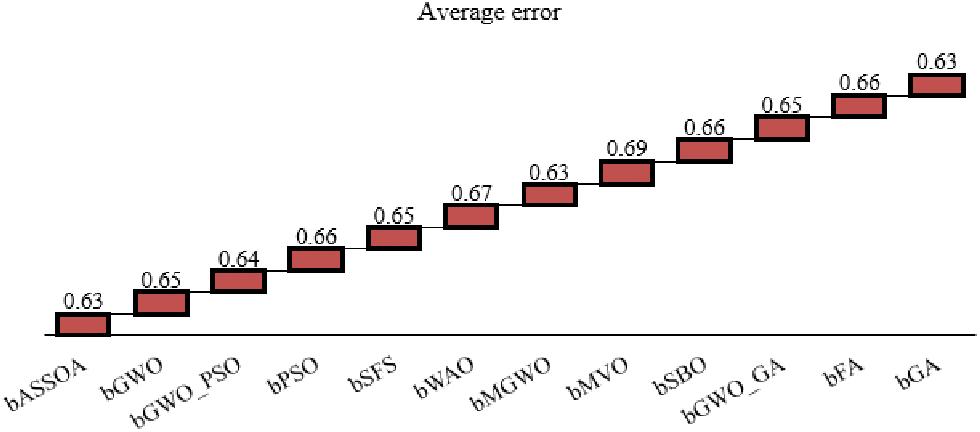
Figure 2: The average error of the achieved results using the proposed and other competing approaches

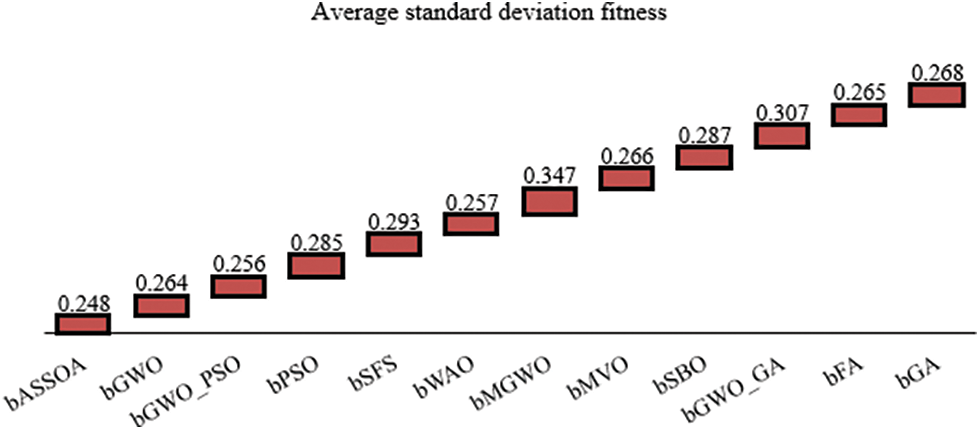
Figure 3: The average standard deviation of the achieved fitness

5  Conclusions

This paper introduces the binary adaptive squirrel search optimization algorithm (bASSOA). The suggested bASSOA approach was utilized to pick the important and non-redundant features from the high-dimensional datasets. First, the standard dataset is changed, and then an optimum selection of features is selected from the altered dataset. The performance of the proposed binary feature selection approach was evaluated using ten benchmark datasets. Six assessment criteria have been used to evaluate the proposed bASSOA technique in comparison to eleven other approaches in the literature, namely, bGWO, bGWO PSO, bPSO, bSFS, bWOA, bMGWO, bMVO, bSBO, bGWO GA, bFA, and bGA methods. Experimental results showed that the proposed bASSOA approach outperforms the other feature selection methods with an average error of 0.63. It has been shown that the bASSOA approach has the best standard deviation fitness of 0.248 when compared to the other methods. Future research will look into the possibility of increasing accuracy by adjusting various performance parameters. In addition, the proposed approach may be evaluated on additional real-world datasets.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R077), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R077), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  E.-S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, no. 1, pp. 36019–36037, 2021. [Google Scholar]

 2.  Q. Al-Tashi, H. Md Rais, S. Abdulkadir, S. Mirjalili and H. Alhussian, “A review of grey wolf optimizer-based feature selection methods for classification,” in Evolutionary Machine Learning Techniques. Algorithms for Intelligent Systems. Singapore: Springer, 2020. [Google Scholar]

 3.  Q. Al-Tashi, H. Rais and S. Abdulkadir, “Hybrid swarm intelligence algorithms with ensemble machine learning for medical diagnosis,” in 4th Int. Conf. on Computer and Information Sciences (ICCOINS), Kuala Lumpur, Malaysia, pp. 1–6, 2018. [Google Scholar]

 4.  M. Dash and H. Liu, “Feature selection for classification,” Intelligent Data Analysis, vol. 1, no. 3, pp. 131–156, 1997. [Google Scholar]

 5.  H. Liu, H. Motoda, R. Setiono and Z. Zhao, “Feature selection: An ever evolving frontier in data mining,” in Feature Selection in Data Mining, Hyderabad, India, pp. 4–13, 2010. [Google Scholar]

 6.  M. Allam and M. Nandhini, “Optimal feature selection using binary teaching learning based optimization algorithm,” Journal of King Saud University–Computer and Information Sciences, vol. 34, no. 2, pp. 329–341, 2022. [Google Scholar]

 7.  Y. Wah, N. Ibrahim, H. Hamid, S. Abdul-Rahman and S. Fong, “Feature selection methods: Case of filter and wrapper approaches for maximising classification accuracy,” Pertanika Journal of Science and Technology, vol. 26, no. 1, pp. 329–340, 2018. [Google Scholar]

 8.  S. Bahassine, A. Madani, M. Al-Sarem and M. Kissi, “Feature selection using an improved Chi-square for Arabic text classification,” Journal of King Saud University–Computer and Information Sciences, vol. 32, no. 2, pp. 225–231, 2020. [Google Scholar]

 9.  M. Mazini, B. Shirazi and I. Mahdavi, “Anomaly network-based intrusion detection system using a reliable hybrid artificial bee colony and AdaBoost algorithms,” Journal of King Saud University–Computer and Information Sciences, vol. 31, no. 4, pp. 541–553, 2019. [Google Scholar]

10. S. Thawkar and R. Ingolikar, “Classification of masses in digital mammograms using Biogeography-based optimization technique,” Journal of King Saud University–Computer and Information Sciences, vol. 32, no. 10, pp. 1140–1148, 2020. [Google Scholar]

11. F. Nie, H. Huang, X. Cai and C. Ding, “Efficient and robust feature selection via joint L2,1-norms minimization,” in Proc. of the 23rd Int. Conf. on Neural Information Processing Systems, Vancouver, Canada, pp. 1813–1821, 2010. [Google Scholar]

12. J. Wen, Z. Lai, Y. Zhan and J. Cui, “The L2,1-norm-based unsupervised optimal feature selection with applications to action recognition,” Pattern Recognition, vol. 60, no. 1, pp. 515–530, 2016. [Google Scholar]

13. Z. Lai, D. Mo, W. Keung, X. Yong, D. Miao et al., “Robust discriminant regression for feature extraction,” IEEE Transactions in Cybernetics, vol. 48, no. 8, pp. 2472–2484, 2018. [Google Scholar]

14. C. Gunavathi and K. Premalatha, “Performance analysis of genetic algorithm with KNN and SVM for feature selection in tumor classification,” International Scholarly Science Research Innovation, vol. 8, no. 8, pp. 1490–1497, 2014. [Google Scholar]

15. K. Tan, E. Teoh, Q. Yu and K. Goh, “A hybrid evolutionary algorithm for attribute selection in data mining,” Expert Systems with Applications, vol. 36, no. 4, pp. 8616–8630, 2009. [Google Scholar]

16. B. Oluleye, A. Leisa, J. Leng and D. Dean, “A genetic algorithm-based feature selection,” International Journal Electrical Communication and Computer Engineering, vol. 5, no. 4, pp. 899–905, 2014. [Google Scholar]

17. P. Moradi and M. Gholampour, “A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy,” Application Soft Computing, vol. 43, no. December, pp. 117–130, 2016. [Google Scholar]

18. A. Hafez, H. Zawbaa, E. Emery, H. Mahmoud and A. Hassanien, “An innovative approach for feature selection based on chicken swarm optimization,” in Int. Conf. of Soft Computing and Pattern Recognition (SoCPaR), Fukuoka, Japan, pp. 19–24, 2015. [Google Scholar]

19. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. E. Takieldeen, T. M. Hassan et al., “Meta-heuristics for feature selection and classification in diagnostic breast cancer,” Computers, Materials & Continua, vol. 73, no. 1, pp. 749–765, 2022. [Google Scholar]

20. D. Rodrigues, L. Pereira, R. Nakamura, K. Costa, Y. Xin-She et al., “A wrapper approach for feature selection based on bat algorithm and optimum-path forest,” Expert Systems with Applications, vol. 41, no. 5, pp. 2250–2258, 2014. [Google Scholar]

21. M. Mafarja, D. Eleyan, I. Jaber, A. Hammouri and S. Mirjalili, “Binary dragonfly algorithm for feature selection,” in Int. Conf. on New Trends in Computing Sciences (ICTCS), Amman, Jordan, pp. 12–17, 2017. [Google Scholar]

22. G. Sayed, A. Hassanien and A. Azar, “Feature selection via a novel chaotic crow search algorithm,” Neural Computing and Applications, vol. 31, no. 1, pp. 171–188, 2019. [Google Scholar]

23. G. Sayed, G. Khoriba and M. Haggag, “A novel chaotic salp swarm algorithm for global optimization and feature selection,” Application Intelligence, vol. 48, no. 1, pp. 3462–3481, 2018. [Google Scholar]

24. T. Sridevi and A. Murugan, “A novel feature selection method for effective breast cancer diagnosis and prognosis,” International Journal of Computer Applications, vol. 88, no. 11, pp. 0975–8887, 2014. [Google Scholar]

25. V. Agrawal and S. Chandra, “Feature selection using artificial bee colony algorithm for medical image classification,” in Int. Conf. on Contemporary Computing (IC3), Noida, India, pp. 171–176, 2015. [Google Scholar]

26. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

27. Q. Li, H. Chen, H. Huang, X. Zhao, Z. Cai et al., “An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis,” Computational and Mathematical Methods in Medicine, vol. 2017, pp. 1–15, 2017. [Google Scholar]

28. E. Pashaei and E. Pashaei, “An efficient binary chimp optimization algorithm for feature selection in biomedical data classification,” Neural Computing & Applications, vol. 34, no. 8, pp. 6427–6451, 2022. [Google Scholar]

29. J. Too and S. Mirjalili, “A hyper learning binary dragonfly algorithm for feature selection: A COVID-19 case study,” Knowledge-Based Systems, vol. 212, no. 1, pp. 1–31, 2021. [Google Scholar]

30. E. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

31. N. Abdel Samee, E. M. El-Kenawy, G. Atteia, M. M. Jamjoom, A. Ibrahim et al., “Metaheuristic optimization through deep learning classification of COVID-19 in chest X-ray images,” Computers, Materials & Continua, vol. 73, no. 2, pp. 4193–4210, 2022. [Google Scholar]

32. E.-S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, no. 1, pp. 36019–36037, 2021. [Google Scholar]

33. A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]

34. A. Abdelhamid and S. R. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]

35. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. E. Takieldeen, T. M. Hassan et al., “Meta-heuristics for feature selection and classification in diagnostic breast cancer,” Computers, Materials & Continua, vol. 73, no. 1, pp. 749–765, 2022. [Google Scholar]

36. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. Ibrahim, S. H. Abd Elkhalik et al., “Improved prediction of metamaterial antenna bandwidth using adaptive optimization of LSTM,” Computers, Materials & Continua, vol. 73, no. 1, pp. 865–881, 2022. [Google Scholar]

37. E. -S. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]

38. A. Abdelhamid, E.-S. M. El-kenawy, B. Alotaibi, M. Abdelkader, A. Ibrahim et al., “Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm,” IEEE Access, vol. 10, pp. 49265–49284, 2022. [Google Scholar]