Hybrid Dipper Throated and Grey Wolf Optimization for Feature Selection Applied to Life Benchmark Datasets

1  Introduction

One of the first Artificial Intelligence (AI) strategies that have been utilized in solving complex real-world research problems was search algorithms. Uninformed and informed search methods are two types of search strategies [1]. Uninformed search approaches conduct a blind search of the search space without any prior knowledge of how close or far away the optimal answer is from the current solution [2]. Brute-force search, breadth-first search, depth-first search, and bidirectional search are examples of uninformed search algorithms [3,4]. Such search algorithms are comprehensive and infeasible for computationally expensive issues because they are time-consuming. The informed search technique, sometimes referred to as heuristics, employs a heuristics assistant, which is typically a function, to estimate how the final result is near to the optimal solution. The use of such heuristic algorithms can yield an increased speed and efficiency in terms of computing and storage requirements. However, the blind search strategies have become more feasible because of recent considerable developments in computing and data storage systems; there are still a considerable number of problems that they can’t solve, specifically those having exponential growth in the search space. Hill climbing and simulated annealing are two examples of early methods of heuristic search algorithms. The main shortage of such algorithms is being application dependent and requiring an adjustment to the heuristic function to be employed in solving different problems. Metaheuristics search algorithms are well-known methods that handle such drawbacks of the heuristic methods. In these methods, the search problem is considered a black box. The heuristic info is deduced using the problem’s outcome, which is typically referred to as the fitness or cost function. The algorithm is iterated until it yields results for the objective function to find the best solution. Recently metaheuristics have become one of the leading research areas in the field of AI and have been widely used in science and industrial research problems. The main categories of the metaheuristics include Swarm intelligence, and Evolutionary Algorithms, EA. The Swarm-based search algorithms simulate the local interactions among entities in nature to solve problems collaboratively. Ant Colony is one of the early Swarm-based search approaches in which each ant makes use of her pheromone to help other ants to follow her path in discovering the sources of food. The second category, EA, such as Genetic Algorithm, GA, simulates natural evolutionary processes.

Machine learning, ML, is an area of artificial intelligence that focuses on developing an algorithm that can learn from existing examples. However, building effective learning algorithms is challenging. Metaheuristic optimization techniques are frequently used to overcome such issues. Mainly the construction of an efficient ML algorithm has four challenges. Firstly, the identification of the structure of the learning algorithms and the best learning parameters to achieve the best classification/forecasting accuracy is an optimization problem. Gradient-based approaches have been popular; however, due to the enormous number of parameters involved in the training process, they suffer from local optima stagnation. Consequently, metaheuristic techniques are becoming more reliable. Secondly, the training of the learning algorithm has a number of regulating parameters that should be tuned and optimized during the training phase. The backpropagation learning algorithm, for example, has two parameters that should be tuned during the training phase, including the momentum and learning rate. Estimating optimal values for learning parameters is necessary as it can yield great results in terms of the prediction system’s accuracy. This challenge can be handled by applying the metaheuristics search methods in the tuning of the learning parameters. The third challenge includes the formulation of a multi-objective function in which the ML application has more than one objective. The metaheuristics search methods can be utilized in finding the optimal solutions for such multiple objective applications. The fourth challenge is concerned with handling the under/overfitting problems. The over-fitting problem occurs when the learning algorithm is excessively adaptable and learns the noise in the data in addition to the fundamental data pattern. However, the under-fitting happens if the learning algorithm cannot learn the underlying pattern in the data. Discovering the correct balance between the number of samples and data records is another issue that can be handled using the metaheuristics AI search methods. Finally, the fifth challenge is the selection of input features that will be used in the training/testing of the learning algorithm. We may not need to include all of the features in the training/testing phases to achieve high forecasting/classification accuracy. Redundant and correlated features should be filtered or aggregated. Finding an optimal set of features can help in achieving the high accuracy of the prediction system. The goal of this research is to use metaheuristics paradigms to find the best set of relevant features that will result in a high-accuracy prediction system.

2  Literature Review

Generally, the nature-inspired optimizers employ new mathematical components and demonstrate greater performance. Consequently, they attract a lot of attention from researchers to create or enhance the existing optimizers for different ML problems. They can be basically classified according to the underlying mechanics into four categories, including swarm intelligence-based, evolution-based, human-related, and physics-based algorithms [5]. Natural evolution is the inspiration for evolution-based algorithms, which begin with a random population of recommended solutions. The solutions that yield good fitness with the objective function are combined in these algorithms to produce different individuals. Crossover and Mutation are used to create a new population. GA [6] is the most prominent algorithm in this category. Other algorithms include evolution strategy [7], tabu search [8], and genetic programming [9]. Only a few algorithms in the evolution-based category have been developed recently, such as the work done in [10], in which an optimized technique for selecting the significant features for the classification of images of galaxies has been introduced. The biological image matching methods can be thought of as an optimization process that aims to identify the highest degree of similarity between a pattern and a template. Therefore, many optimization algorithms were utilized in that era, such as the work done in [11] in which the chaotic differential search technique was employed to discover the presence of a pattern inside a given image. In [12], and optimized ML model has been established in wind speed predictions in a wind-power producing system. The backtracking search methods have been utilized in optimizing the learning parameters of the learning algorithm. As well as an optimized search paradigm has also been utilized in [13] in implementing a computer-aided diagnosing system for blood cancer. A stochastic search algorithm, Fractal search optimizer, has been employed along with the K-means clustering in the segmentation of blood images for Leukemia classification.

Swarm intelligence algorithms are based on the social behavior of birds, insects, fish, and animals, among other things. Particle Swarm Optimization, PSO, [14], is a prominent approach and is based on the behavior of a flock of birds that flies over the search space to find the ideal site for them. Other algorithms include ant colony optimization [15], monkey optimization [16], honey-bee swarm optimization algorithm [17], and others. Algorithms based on physics are developed by the utilization of the laws of physics, and they include Harmony search [18], simulated annealing [19], etc. Algorithms based on human behavior are mainly based on simulating human behavior. Every human being has a unique method of carrying out tasks that has an impact on their overall performance. League Championship algorithm [20], and Teaching learning-based optimization algorithm [21], others are popular algorithms.

3  Methodology

The proposed methodology is based on a hybrid dipper throated optimization and grey wolf optimization. In this section, the basics of the proposed approach, along with a presentation and discussion of the proposed approach, are explained.

3.1 Dipper Throated Optimization

Dipper throated optimization (DTO) is based on a simulation of the real process of looking for food by tracking the positions and speeds of swimming and flying birds. The following equations are used to update the position and speed of the swimming birds.

BLnd(t+1)=BLbest(t)−C1.|C2.BLbest(t)−BLnd(t)|(1)

where t is the iteration number, and BLnd(t) and BLbest(t) are the normal location and best location of the bird, and C1 and C2 are adaptive values whose values are changed during the optimization process based on the iteration number and random values. On the other hand, the update of the flying bird’s location is performed using the following equation.

BLnd(t+1)=BLnd(t)+BS(t+1)(2)

BS(t+1)=C3BS(t)+C4r1(BLbest(t)−BLnd(t))+C5r1(BLGbest−BLnd(t))(3)

where BS(t+1) is the updated speed of each bird, r1 is a random number in [0; 1], BLGbest is the global best location, and C3 is a weight value, C4 and C5 are constants.

3.2 Grey Wolf Optimization

One of the world’s apex predators, grey wolves, may be found around the world. It is common for grey wolves to live in packs. On average, the group size is between 5 and 12. Grey wolves have a fascinating social structure with a well-defined hierarchy of authority. Male and female alphas rule the pack. When it comes to key group choices like hunting, resting, and so on, the alpha is in charge. The alpha’s commands should be followed by everyone in the group. It has also been noticed that the alpha wolf follows the rest of the pack, which may be seen as a form of democracy. For this reason, they’re also known as alphas and leaders because the entire pack must obey them. Interestingly, the alpha doesn’t have to be the strongest member but rather the one who is best suited to taking the group’s leadership position. As a result, the group’s discipline and structure is more crucial than its strength [22–28].

Grey wolves have a two-tiered social structure, with Beta being the lowest. Beta wolves are subordinate wolves tasked with assisting the alpha wolf in making sound judgments and participating in group activities. While the betas are expected to show respect to the alpha, they are also in charge of the pack’s lesser ranks. They’re both a counselor to the alpha and a group enforcer at the same time. The alpha’s henchmen, the betas, are in charge of enforcing his orders across the group and providing feedback to them. Omega is the lowest-ranked grey wolf in the pack. Scapegoat: Omega performs this role. Omega wolves are constantly forced to give in to the more powerful wolves in the pack. They are also the last of the wolves to be permitted to consume meat. There is a possibility that the omegas are not considered significant members of the group, yet losing one of them might lead to internal strife and troubles for the entire group. All of the wolves in the pack are angry and frustrated, and the omegas are letting it all out. Since everyone needs to be satisfied, the omegas play a crucial function in helping to keep things in their proper order.

A wolf is considered inferior if it is not an alpha, beta, or omega wolf (or, according to some references, delta). Alphas and betas must submit to delta wolves, who rule over the omega. This group includes scouts, elders, and hunters. The alphas and betas rely on the hunters for assistance in hunting animals, and the hunters, in turn, provide food for the group. Sentinels are in charge of ensuring and defending the group’s security. A scout’s primary responsibility is to keep an eye out for any threats to the group’s territory and alert the rest of the troop. The Elders of the pack are the wolves who have previously served as alpha or beta. Grey wolves’ social structure is fascinating, but their collective hunting strategy is perhaps more fascinating. The grey wolves are surrounding their victim, as we previously stated. The following equations are suggested for mathematical modeling of encircling behavior:

D→=|C→.F→p(t)−F→(t)|(4)

F→(t+1)=F→p(t)−A→.D→(5)

where A→ and C→ are vectors of coefficients, t represents the current iteration, F→ is the grey wolf’s position vector, and F→p indicates the position vector of the prey. If there is a better solution in each iteration, F→ is updated to the best solution.

a→=2−t(2Maxiter)(6)

A→=2a→.r→1−a→(7)

C→=2r→2(8)

Loop counter t, Maxiter is the maximum number of iterations, r→1 and r→2 are random vectors in [0,1], and a→ is linearly decreasing from 2 to 0 throughout the length of iterations. Consider a two-dimensional position vector and some of the potential neighbors depicted in Fig. 2 as a starting point for exploring the impact of Eqs. (1) and (2). In this illustration, a grey wolf in position (X, Y) can adjust its position in response to the prey’s movement (X*, Y*). It is possible to go to other locations surrounding the optimal agent by modifying EA and EC vectors’ values with respect to their present location. Setting A→ = (1,0) and C→ = (1, 1), for example, will result in (X* −X, Y*). Grey wolves can travel between the places depicted in Fig. 1 using the random vectors r1 and r2. Eqs. (1) and (2) allow a grey wolf to change its posture in the vicinity of its prey at will. The same method may be used in other dimensions, and the grey wolves will move in around the best answer so far (hyper-spheres/cubes).

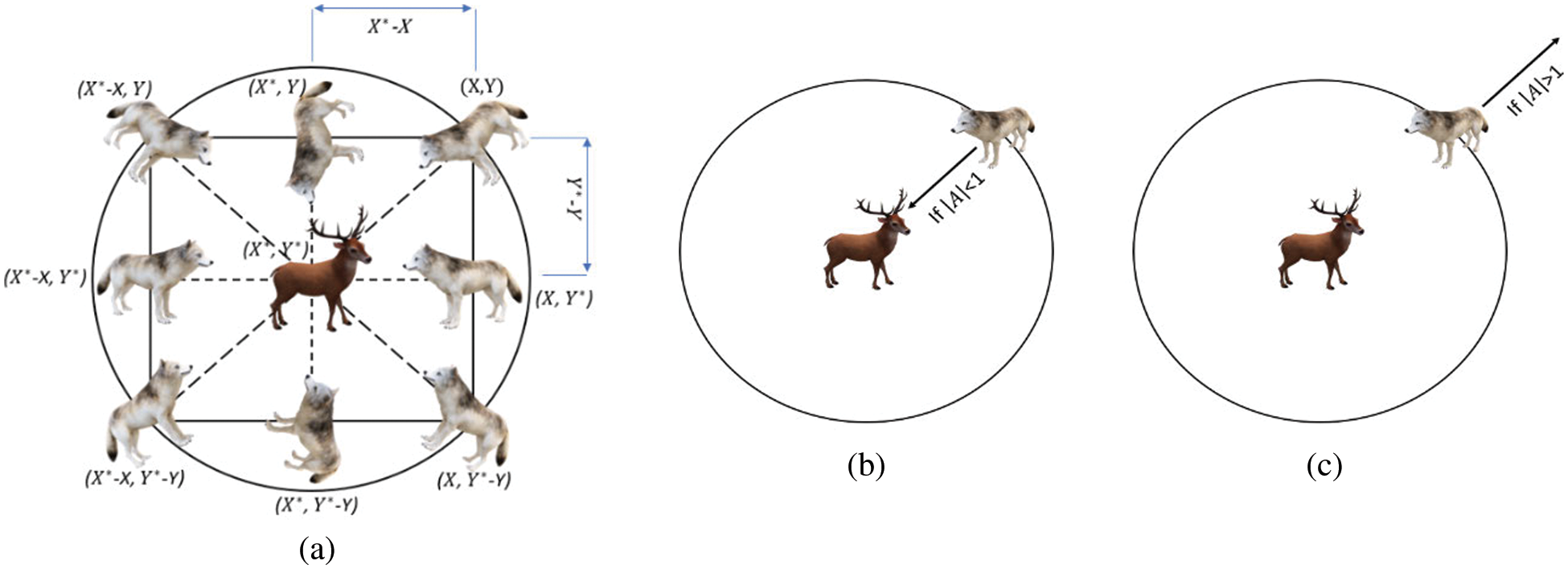
Figure 1: Hunting process: (a) potential locations of grey wolves (b) convergence (attacking the prey), (c) divergence (searching for prey)

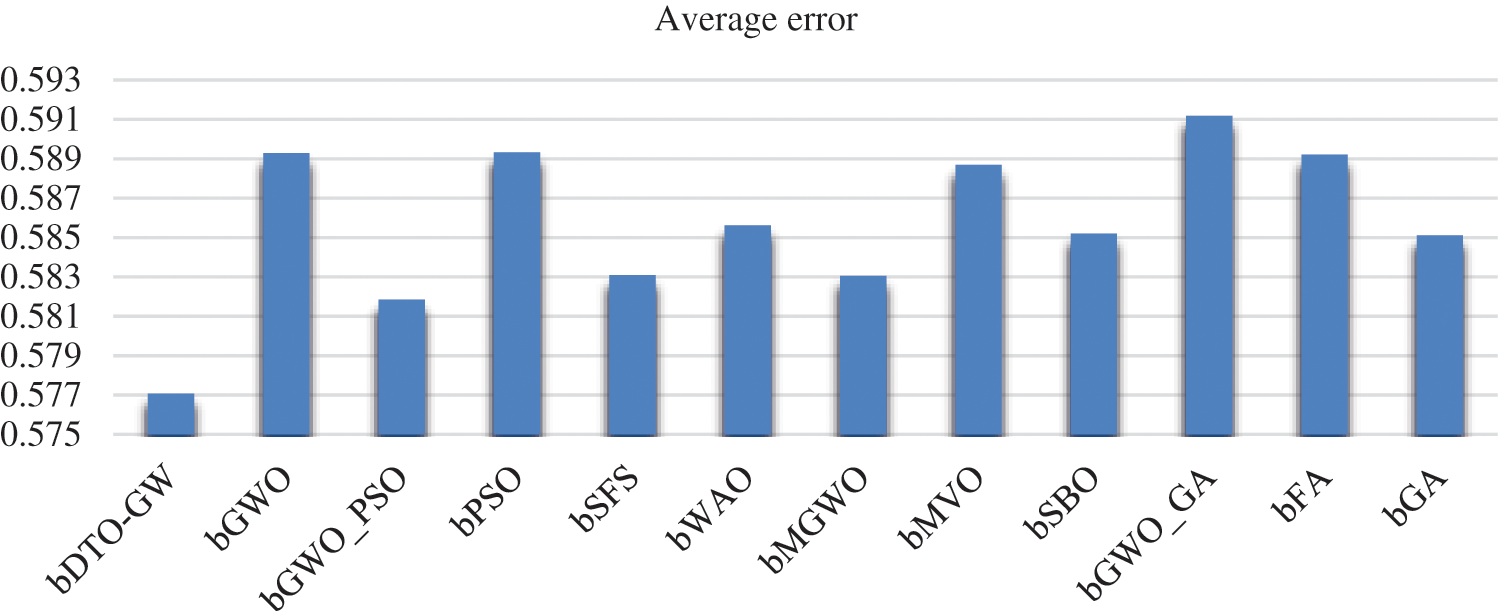
Figure 2: Visualizing the achieved average error using the proposed and competing approaches

Grey wolves have the ability to locate prey and then encircle it. The alpha is generally in charge of the entire hunt. The beta and delta occasionally join in on the action during a hunting expedition. We, on the other hand, have no notion where the prey is located in our simulated 2D search area (optimum). The alpha, beta, and delta wolves all know where to look for prey; therefore, we’ll use this assumption to model grey wolf hunting behavior statistically. As a consequence, we’ll keep the top three search results and compel the rest of the grey wolves (including the omegas) to recalculate their locations based on them. We came up with the following formulae to do this:

D→α=|D→1∗F→α−F→|,D→β=|D→2∗F→β−F→|,D→δ=|D→3∗F→δ−F→|(9)

F→1=F→α−A→1∗D→α,F→2=F→β−A→2∗D→β,F→3=F→δ−A→3∗D→δ(10)

F→(t+1)=F→1+F→2+F→33(11)

A grey wolf (a search agent) is seen in Fig. 1 moving around in a 2D search space according to alpha, beta, and delta. Fig. 1 shows that the ultimate location of a grey wolf (search agent) will be in a random location inside the search area given by the coordinates of alpha, beta, and delta. Prey’s location is estimated by alpha, beta and delta wolves; other wolves follow this guess and update their locations around the prey at random.

3.3 The Proposed DTO-GW Algorithm

The proposed bDTO-GW employs a KNN classifier to make sure that only decency-preserving features are used. Due to its primary goal of maximizing classification accuracy while minimizing the.

3.4 The Proposed Feature Selection Method

The proposed bDTO-GW employs a KNN classifier to make sure that only decency-preserving features are used. Due to its primary goal of maximizing classification accuracy while minimizing the number of features picked and the error rate, feature selection methods aim to decrease both these factors [29–33]. As a result, Eq. (1) is employed in the proposed feature selection technique. To maximize the feature assessment norm, the proposed bDTO-GW approach proposes an adaptive search space exploration presented in Eq. (1).

Fitness=αγR(D)+β|C−R||C|(12)

In which the condition attribute set R in relation to the decision D has a classification quality denoted by γR(D). The total number of features is denoted by C and the number of selected features is referred to as R. Additional parameters that affect the classification accuracy are α ∈ [0,1] and β = 1 – α. Based on the error rate and selected feature ratio, Eq. (1) can be converted into a minimization problem. Therefore, the minimization of the error rate can be performed using the following fitness function, where ER(D) is the error rate.

Fitness=αER(D)+β|R||C|(13)

To select the best set of features, the resulting best solution is converted into binary 0 or 1. To perform this conversion, the sigmoid function is usually employed as represented by the following equation where Sbest refers to the best position at iteration t.

Sd(t+1)={0,ifSigmoid(Sbest)<0.51,otherwise(14)

4  Experimental Results

The proposed binary feature selection approach was put to the test on eight benchmark datasets from the UCI repository (UCI Feature selection dataset 2017). Various databases have different numbers of attributes and occurrences. There is a complete breakdown of all datasets in Table 1. Because of this, it was utilized to choose the most significant features. The KNN classifier’s accuracy is used to choose the best features to use in this approach. K is set to 5 by the KNN classifier based on empirical data. Training, validation, and testing datasets are randomly separated for cross-validation. K-fold cross-validation, which uses K-1 folds for training, validation, and testing, was used to verify the performance of the proposed bDTO-GW method.

4.1 Evaluation Criteria

Table 2 shows the performance evaluation metrics used to assess the results of the proposed approach. These metrics are composed of six criteria, including best fitness, worst fitness, average error, average select size, average fitness size, and standard deviation. The following section presents the evaluation of each of these metrics based on the achieved results using the proposed approach.

4.2 Algorithm Configurations

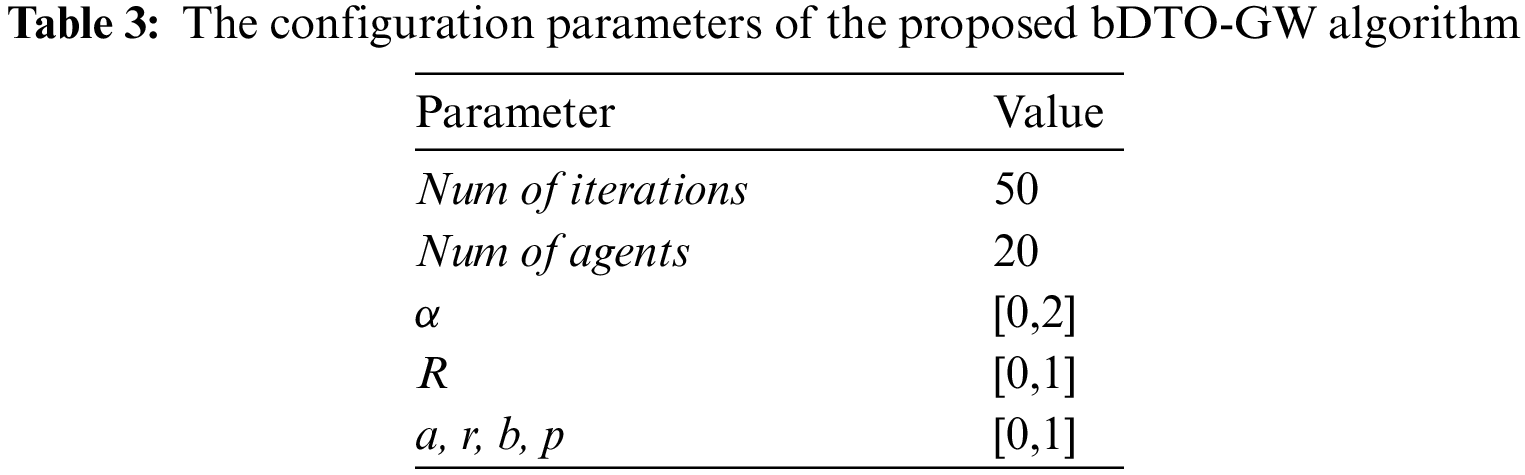
Table 3 shows the suggested approach’s setup settings. There are 50 iterations and 10 search agents in this table. Also included is a table that lists the values of the optimization equation variables.

4.3 Evaluation Results

For comparison, there are eleven existing state-of-the-art approaches, including bGWO, PSO, bPSO and SFS, bMGWO and SBO, and the proposed bDTO-GW technique bDTO-GW. We were able to derive the average values for each strategy after 30 iterations of each method for the purposes of comparison. The six performance criteria given above were used to assess the proposed bDTO-GW method.

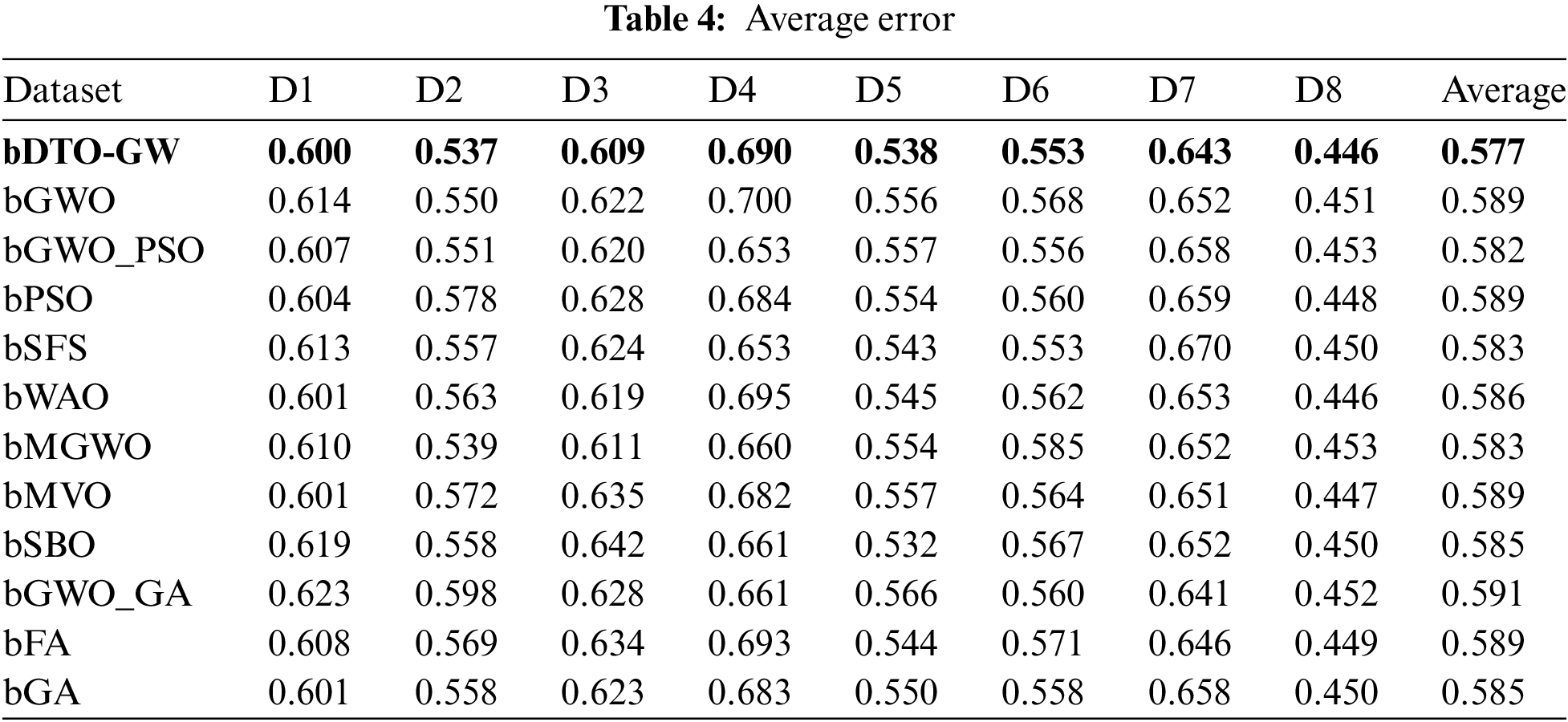
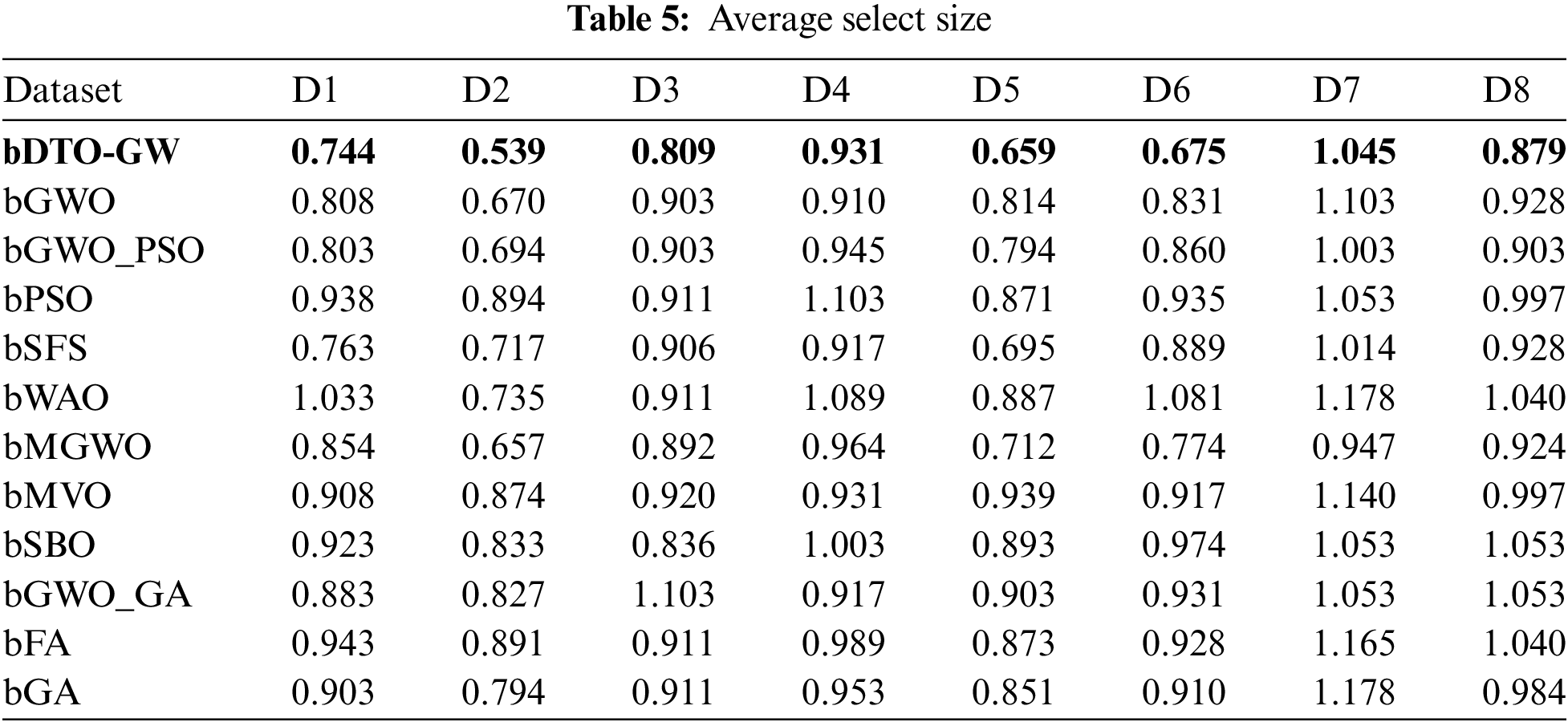
A strategy that does not remove any data from its source was used to examine the effects of data transformation and feature selection methods. The suggested bDTO-GW and the other techniques tested have an average inaccuracy shown in Table 4. Overall, bDTO-average GW’s error of 0.577 is lower than the other techniques’ average errors, according to a table. We may investigate the influence of the recommended feature selection approach on the average select size of selected features, as shown in Table 5, through data transformation. As can be seen from this graph, bDTO-GW yields the greatest possible select size.

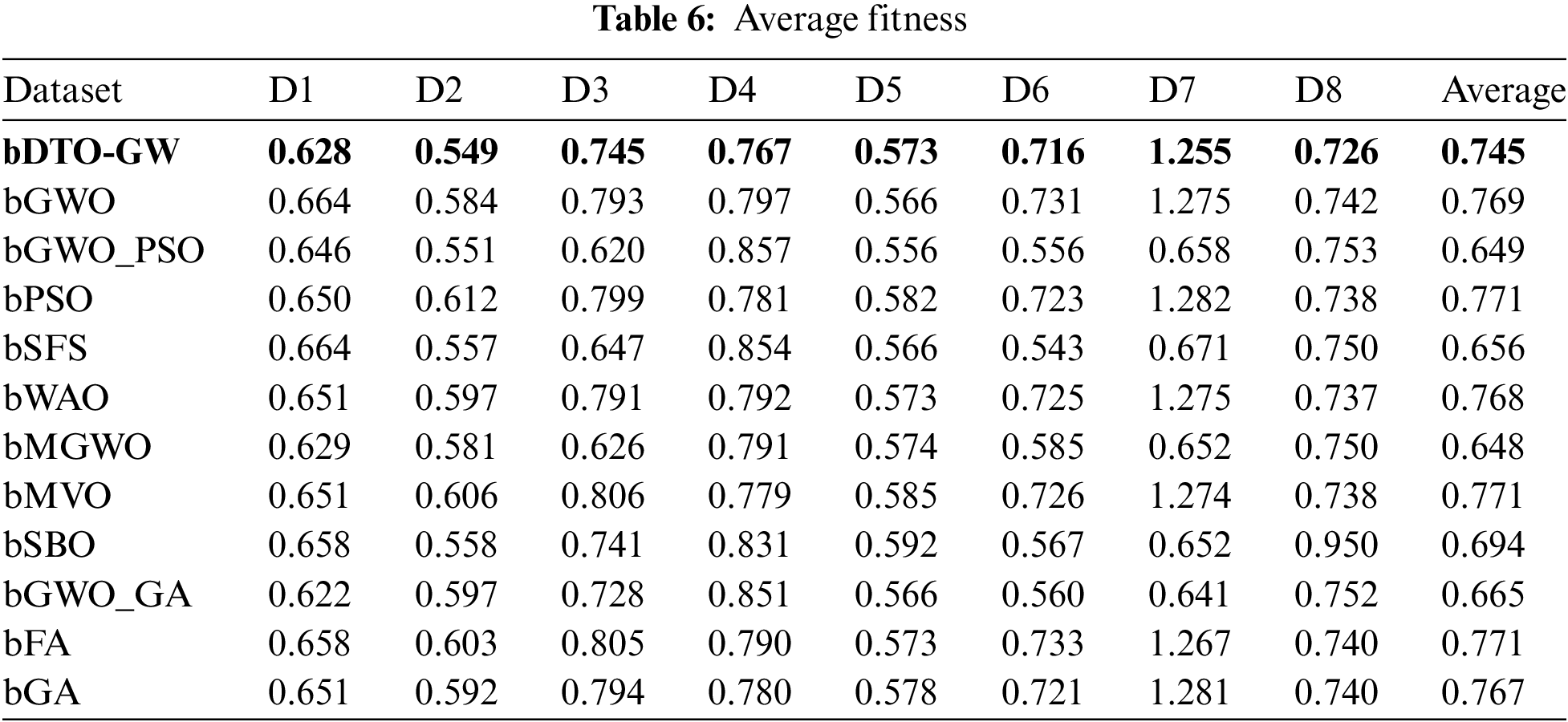
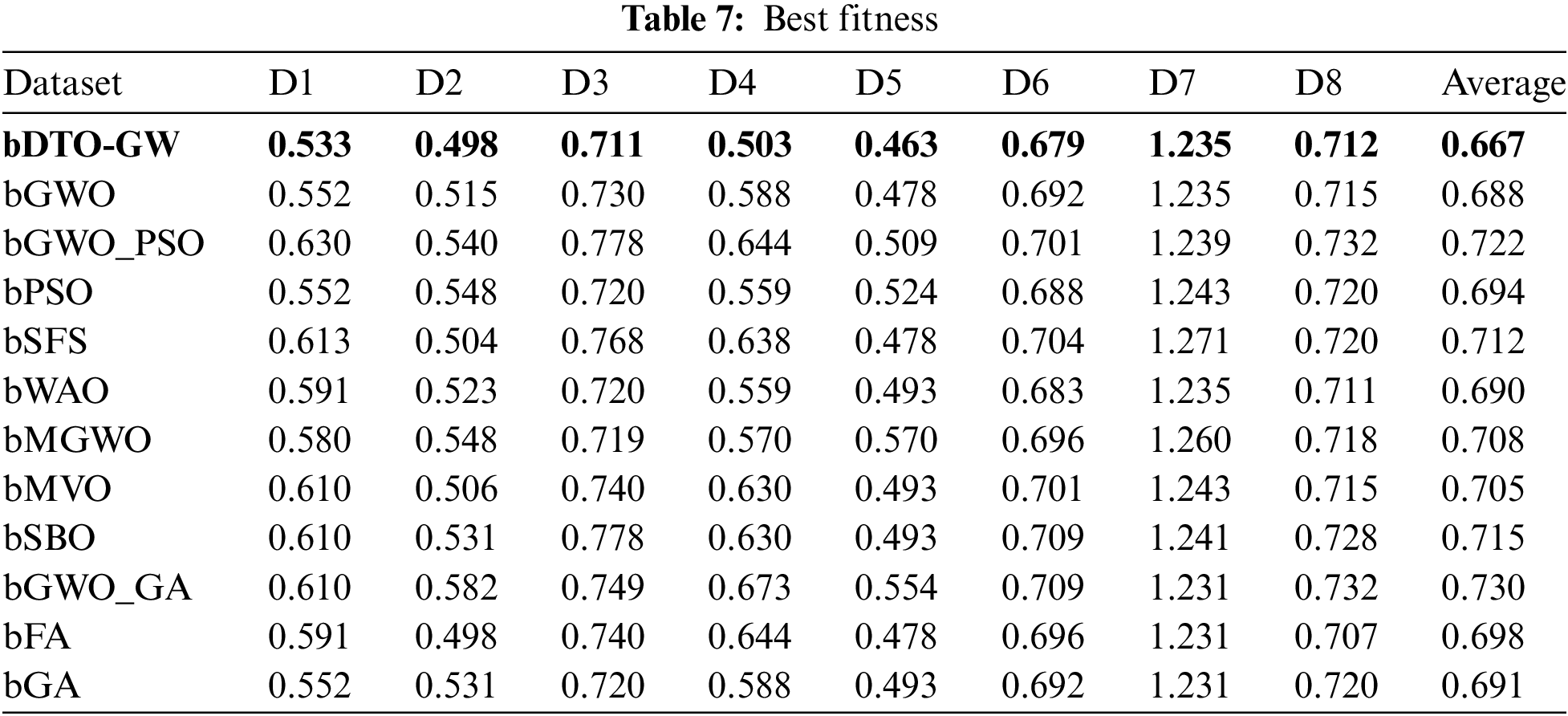
As an alternative, Table 6 shows an average of the quality of the specified features’ quality. As seen in this table, the proposed technique has an overall average fitness of 0.745, which is the best among the various alternatives. Tables 7–9 show the best, worst, and standard deviation of each feature’s fitness, respectively, depending on the selected features. These tables show that the suggested feature selection algorithm is superior and more successful than any other method that has been tried before.

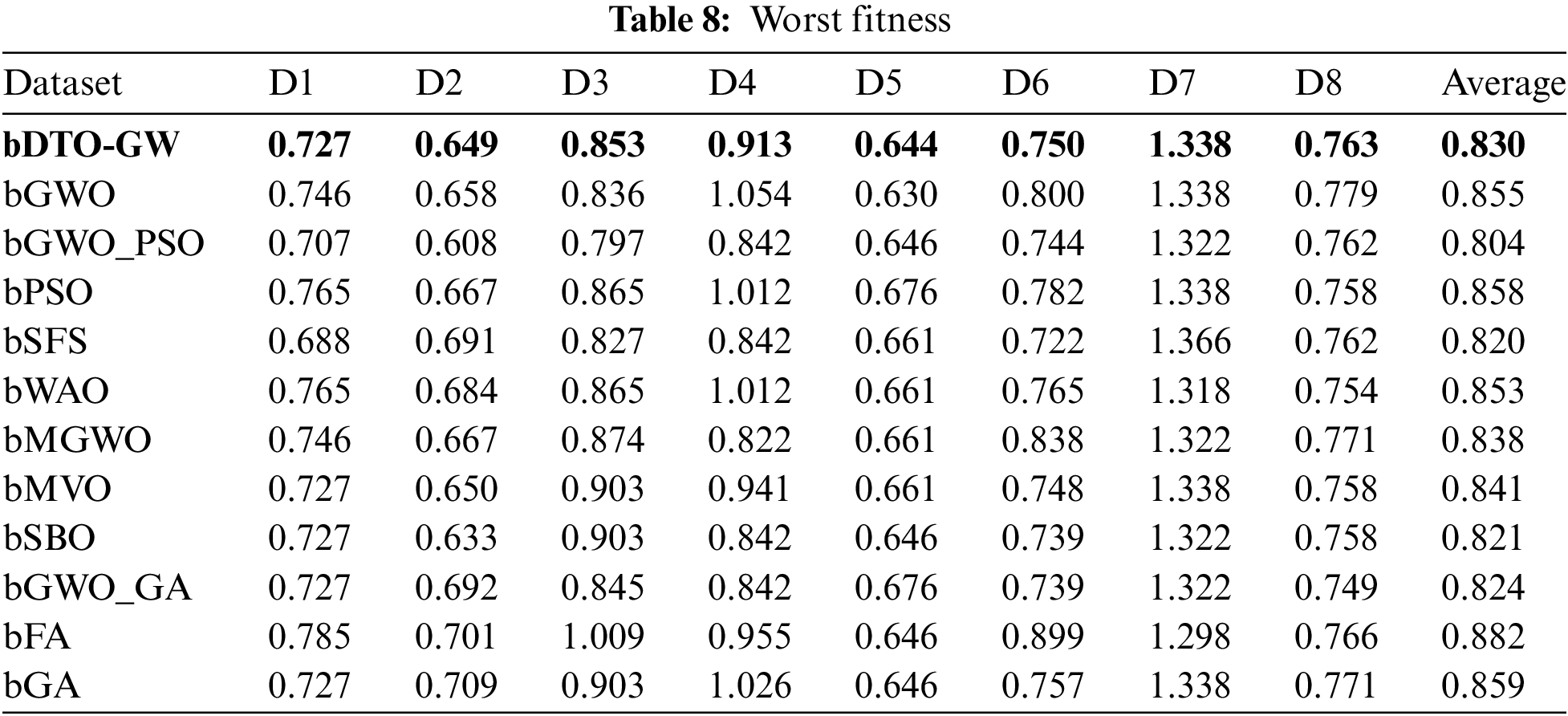
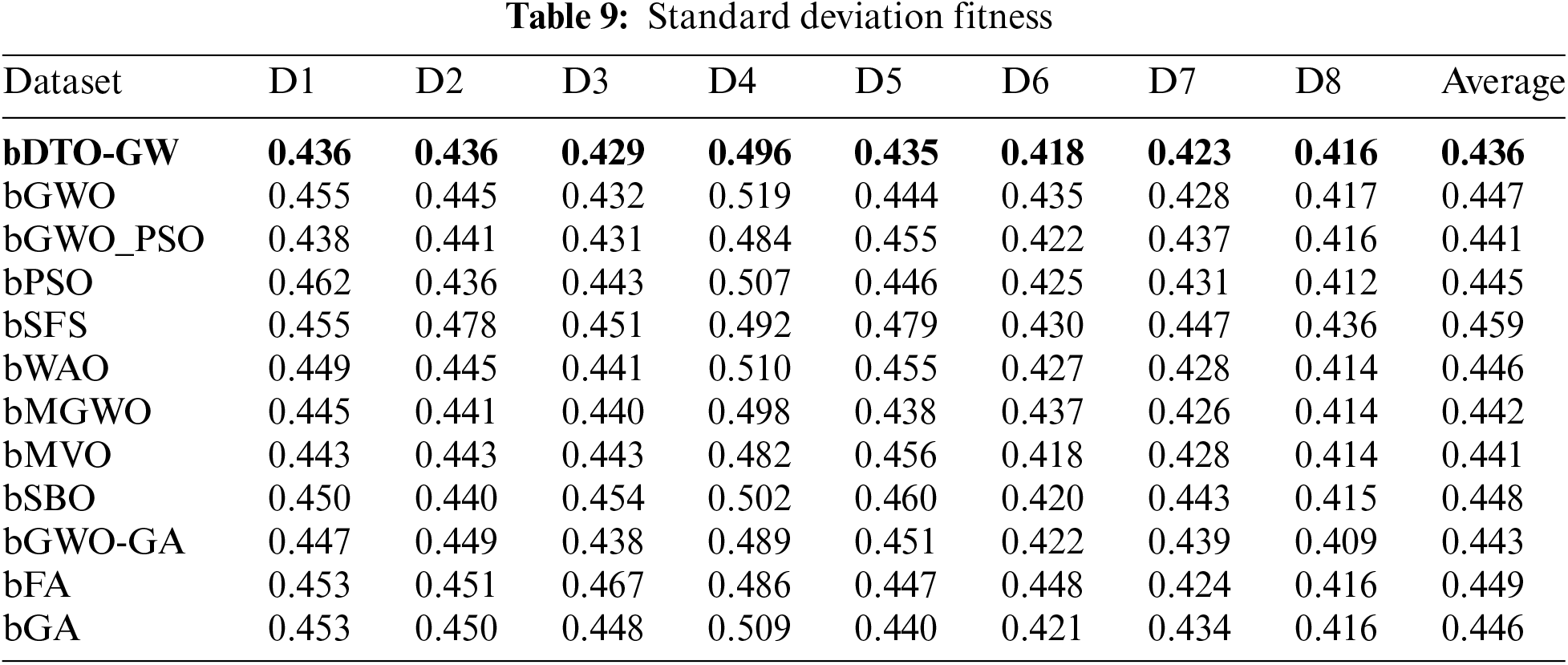
On the other hand, to clearly show the effectiveness and superiority of the proposed approach, Figs. 2 and 3 visualize the achieved average error and standard deviation of the fitness, respectively. As shown in these figures, the best results are achieved by the proposed approach, which confirms its superiority when compared to the other approaches.

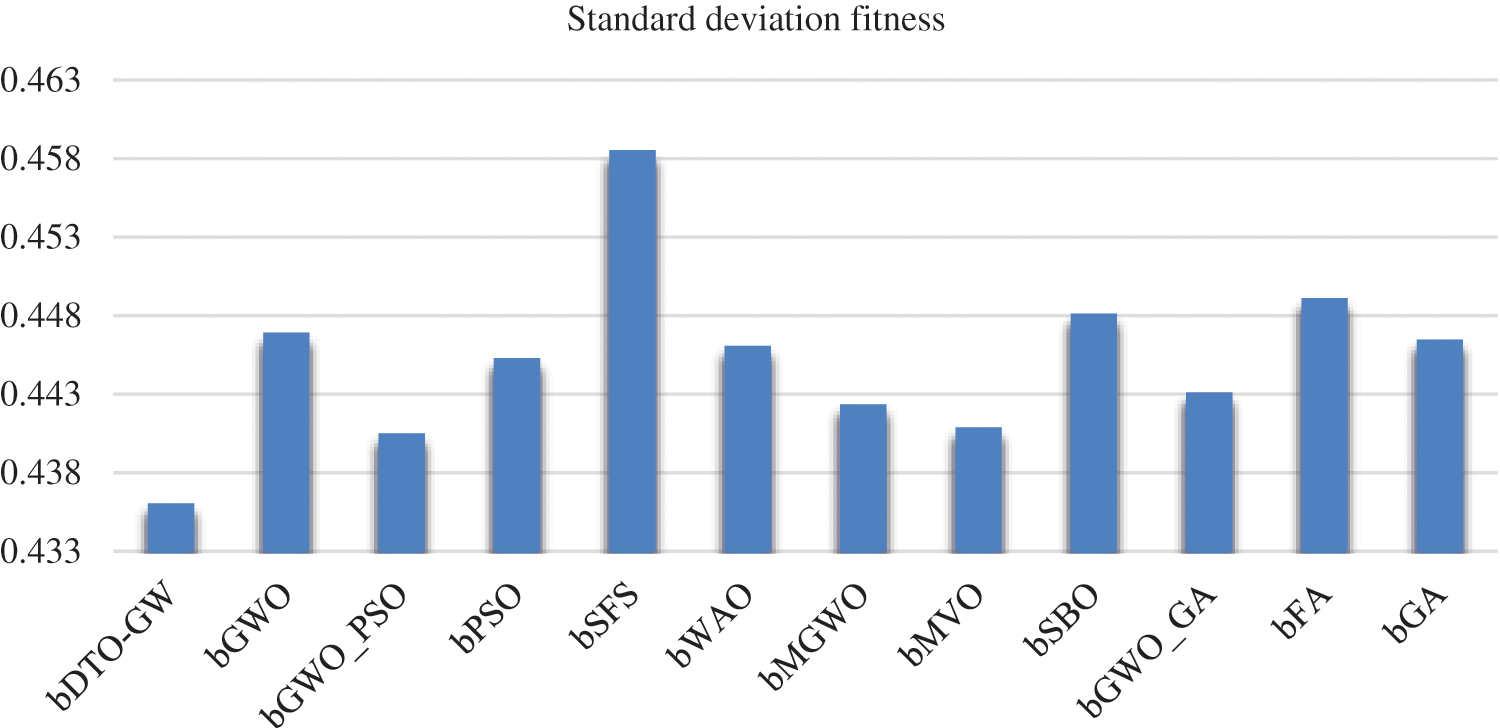
Figure 3: Visualizing the achieved standard deviation of the fitness using the proposed and other competing approaches

5  Conclusions

The binary optimization is introduced in this study by employing dipper-toothed and grey wolf optimizers (bDTO-GW). The bDTO-GW method was used to choose the most essential and non-redundant features from the large datasets. It is necessary to make changes to the standard dataset before selecting the best possible collection of features from the new dataset. In order to test the proposed binary feature selection method, eight benchmark datasets were used. bDTO-GW has been evaluated against eleven other techniques in the literature using six assessment criteria, which include bGWO, bGWO PSO, and other bGWO-related approaches as well as bPSO, bSFS, bWOA, bMGWO, bMVO, and bSBO methods as well as bFA and bGA. The suggested bDTO-GW technique outperforms the previous feature selection methods with an average error of 0.577. A standard deviation fitness of 0.436 was found for the bDTO-GW technique, which beat the competition. Future studies will investigate the possibilities of enhancing accuracy by altering various performance criteria. An extra real-world dataset is an option for testing the technique.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R300), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R300), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. Hidayat, F. Susanti and D. Wijaya, “A comparative study of informed and uninformed search algorithm to solve eight-puzzle problem,” Journal of Computer Science, vol. 17, no. 11, pp. 1147–1156, 2021. [Google Scholar]

 2.  R. Chiong, J. H. Sutanto and W. J. Jap, “A comparative study on informed and uninformed search for intelligent travel planning in borneo island,” in Proc. of the Int. Symp. on Information Technology, Kuala Lumpur, Malaysia, pp. 1–5, 2008. [Google Scholar]

 3.  S. Pooja, S. Chethan and C. Arjun, “Analyzing uninformed search strategy algorithms in state space search,” in Proc. of the Int. Conf. on Global Trends in Signal Processing, Information Computing and Communication, Jalgaon, India, pp. 97–102, 2016. [Google Scholar]

 4.  H. Khaled, “Enhancing recursive brute force algorithm with static memory allocation: Solving motif finding problem as a case study,” in Proc. of the 14th Int. Conf. on Computer Engineering and Systems, Cairo, Egypt, pp. 66–70, 2019. [Google Scholar]

 5.  M. Fouad, A. El-Desouky, R. Al-Hajj and E. -S. M. El-Kenawy, “Dynamic group-based cooperative optimization algorithm,” IEEE Access, vol. 8, no. 1, pp. 148378–148403, 2020. [Google Scholar]

 6.  F. Glover, “Future paths for integer programming and links to artificial intelligence,” Computers and Operations Research, vol. 13, no. 5, pp. 533–549, 1986. [Google Scholar]

 7.  J. H. Holland, “Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence,” in Adaptation in Natural and Artificial Systems. Bradford Books, MIT Press, 1992. [Google Scholar]

 8.  K. M. Hosny, M. A. Elaziz, I. M. Selim and M. M. Darwish, “Classification of galaxy color images using quaternion polar complex exponential transform and binary Stochastic Fractal Search,” Astronomy and Computing, vol. 31, no. 1, pp. 100383, 2020. [Google Scholar]

 9.  M. M. Eid, E. -S. M. El-Kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 4th National Computing Colleges Conf. (NCCC 2021), Taif, Saudi Arabia, IEEE, pp. 1–6, 2021. [Google Scholar]

10. L. Gan and H. Duan, “Biological image processing via Chaotic Differential Search and lateral inhibition,” Optik (Stuttg), vol. 125, no. 9, pp. 2070–2075, 2014. [Google Scholar]

11. K. G. Dhal, J. Gálvez, S. Ray, A. Das and S. Das, “Acute lymphoblastic leukemia image segmentation driven by stochastic fractal search,” Multimedia Tools and Applications, vol. 79, no. 17–18, pp. 12227–12255, 2020. [Google Scholar]

12. M. Dorigo, V. Maniezzo and A. Colorni, “Ant system: Optimization by a colony of cooperating agents,” IEEE Transactions on Systems, Managment, and Cybernetics, vol. 26, no. 1, pp. 29–41, 1996. [Google Scholar]

13. R. Zhao and W. Tang, “Monkey algorithm for global numerical optimization,” Journal of Uncertain Systems, vol. 2, pp. 165–176, 2008. [Google Scholar]

14. D. Karaboga, “An idea based on honey bee swarm for numerical optimization: Technical report - TR06,” in Technical Report, Erciyes University, 2005. [Google Scholar]

15. S. S. M. Ghoneim, T. A. Farrag, A. A. Rashed, E. -S. M. El-Kenawy and A. Ibrahim, “Adaptive dynamic meta-heuristics for feature selection and classification in diagnostic accuracy of transformer faults,” IEEE Access, vol. 9, pp. 78324–78340, 2021. [Google Scholar]

16. H. Hassan, A. I. El-Desouky, A. Ibrahim, E. -S. M. El-Kenawy and R. Arnous, “Enhanced QoS-Based model for trust assessment in cloud computing environment,” IEEE Access, vol. 8, no. 1, pp. 43752–43763, 2020. [Google Scholar]

17. Z. Geem, J. Kim and G. Loganathan, “A new heuristic optimization algorithm: Harmony search,” Simulation, vol. 76, no. 2, pp. 60–68, 2001. [Google Scholar]

18. S. Kirkpatrick, “Optimization by simulated annealing: Quantitative studies,” Journal of Statistical Physics, vol. 34, no. 5–6, pp. 975–986, 1984. [Google Scholar]

19. A. H. Kashan, “League championship algorithm: A new algorithm for numerical function optimization,” in Int. Conf. of Soft Computing and Pattern Recognition (SoCPaR), Malacca, Malaysia, pp. 43–48, 2009. [Google Scholar]

20. E. -S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and Newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

21. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” CMC-Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

22. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 125787–125804, 2021. [Google Scholar]

23. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 X-ray chest image classification,” IEEE Access, vol. 9, no. 1, pp. 36019–36037, 2021. [Google Scholar]

24. A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]

25. A. Abdelhamid and S. R. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]

26. E. -S. M. El-kenawy and M. Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information & Control, vol. 16, no. 1, pp. 831–844, 2020. [Google Scholar]

27. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. Ibrahim, H. S. Abd Elkhalik et al., “Improved prediction of metamaterial antenna bandwidth using adaptive optimization of LSTM,” Computers, Materials & Continua, vol. 73, no. 1, pp. 865–881, 2022. [Google Scholar]

28. E. -S. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]

29. A. Abdelhamid, E. -S. M. El-kenawy, B. Alotaibi, M. Abdelkader, A. Ibrahim et al., “Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm,” IEEE Access, vol. 10, pp. 49265–49284, 2022. [Google Scholar]

30. E. -S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, no. 1, pp. 107635–107649, 2020. [Google Scholar]

31. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. E. Takieldeen, T. M. Hassan et al., “Meta-heuristics for feature selection and classification in diagnostic breast cancer,” Computers, Materials & Continua, vol. 73, no. 1, pp. 749–765, 2022. [Google Scholar]

32. N. Abdel Samee, E. M. El-Kenawy, G. Atteia, M. M. Jamjoom, A. Ibrahim et al., “Metaheuristic optimization through deep learning classification of COVID-19 in chest x-ray images,” Computers, Materials & Continua, vol. 73, no. 2, pp. 4193–4210, 2022. [Google Scholar]

33. H. Nasser AlEisa, E. M. El-kenawy, A. Ali Alhussan, M. Saber, A. A. Abdelhamid et al., “Transfer learning for chest x-rays diagnosis using dipper throated algorithm,” Computers, Materials & Continua, vol. 73, no. 2, pp. 2371–2387, 2022. [Google Scholar]