A Coprocessor Architecture for 80/112-bit Security Related Applications

1  Introduction

Due to the exponential growth in technology, millions of users want to interact with the internet through IoT devices, and the requirement for this enormous connectivity raises security threats [1–3]. Therefore, several security services can be achieved either by employing symmetric or asymmetric (or public-key) cryptographic algorithms. Comparatively, the latter offers more increased security as two distinct keys are involved in cryptographic computation(s) [2]. On the other hand, a single key is needed in the case of symmetric algorithms/protocols. Moreover, each cryptographic algorithm (either related to symmetric or public-key) contains different messages and key lengths for a certain level of security achievement [4,5]. For 80-bit symmetric-key security achievement, Rivest-Shamir-Adleman (RSA) and Elliptic Curve Cryptography (ECC) require 1024-bit and 160-bit key lengths [4,5]. Similarly, for identical security to 112-bits, the RSA and ECC require 2048-bit and 224-bit key lengths. For security equivalent to AES-128, the RSA and ECC need 3072-bit and 256-bit lengths. Consequently, for a similar security level, ECC is an attractive option as it offers several additional benefits in terms of lower bandwidth, lower computational/processing efforts, lower power consumption, and lower area cost [6].

The ECC contains a four-layer model. The uppermost layer, known as the protocol layer, determines the execution of (i) encryption/decryption, (ii) signature-generation/verification, (iii) key-authentication, etc. For the computation of these operations, the most frequently used protocols are Elliptic-curve Diffie Hellman (ECDH) [7], Elliptic-curve Digital Signature Algorithm (ECDSA) [8] and Elliptic-curve Menezes Qu–Vanstone (ECMQV) [9]. The ECMQV, ECDSA and ECDH protocols are responsible to compute encryption/decryption, signature-generation/verification and key-authentication, respectively. To implement these protocols (ECDSA, ECDH and ECMQV), point multiplication (PM) is essential to execute (third layer of ECC model). Moreover, in Elliptic curves, the PM is the considerable computationally intensive operation [6,10–13]. The implementation of PM depends on the computation of layer two operations, i.e., point addition (PA), and doubling (PD). These operations (PA and PD) depend on layer one. The corresponding layer one operations are finite field (FF) addition, multiplication, squaring, inversion and reduction.

In addition to the ECC layer model, the prime, i.e., GF(P), and binary, i.e., GF(2m), fields are available choices for implementations, where m shows the field size or supported-key length. Comparatively, the prime field is more appealing for software implementations (e.g., on microcontrollers) while binary fields have a preference due to its accelerations on hardware platforms such as field-programmable-gate-array (FPGA) and application-specific-integrated-circuits (ASICs) [6,11–15]. Due to reconfigurability, ease of availability in the market, low development cost, etc, we have selected the GF(2m) field for implementations on FPGA in this work.

Over GF(2m) field, the National Institute of Standards and Technology (NIST) [16] has defined various key lengths, i.e., 163, 233, 283, 409, and 571, for implementations. The NIST is an American organization that is responsible for standardized new cryptographic primitives to ensure secure communications. The 163 and 233-bit key lengths are sufficient to secure applications that require an 80 or 112-bit security [4,17]. Therefore, the objective of this work is to protect the cryptographic applications that require 80/112-bit security by designing and implementing an Elliptic-curve processor for key-authentication using ECDH over GF(2m) with m=163 and 233 on FPGA.

Several applications demand higher security. One of the examples includes the fourth industrial revolution (also named industry 4.0) which brings rapid growth in technology, industries and societal patterns due to the demand for increasing interconnectivity of several devices over the unsecured internet. Moreover, industry 4.0 emphasizes the notion of automation of numerous applications to facilitate human daily life [14]. More specifically, in the case of digitalization, automation requires higher security, e.g., key authentication or key agreement. For example, for radio-frequency-identification-network (RFID) applications, key authentication is essential when scanning the bar codes on different products in shopping malls [18–22]. Automotive mobile vehicles are another application where authentication is critical to start secure communication [23]. Generally, these include intra or inter-mobile communications with several devices, e.g., vehicle-to-phone, vehicle-to-vehicle, phone-to-phone, etc. The term intra determines the wired/wireless communication inside the sensing network while inter means the communication with embedded devices outside the sensing network. We have provided intra-mobile connectivity of the several devices in Fig. 1 where the Node1, Node2 and Node3 are the wireless sensor nodes (WSN) that determine the connectivity of several embedded devices with the gateway.

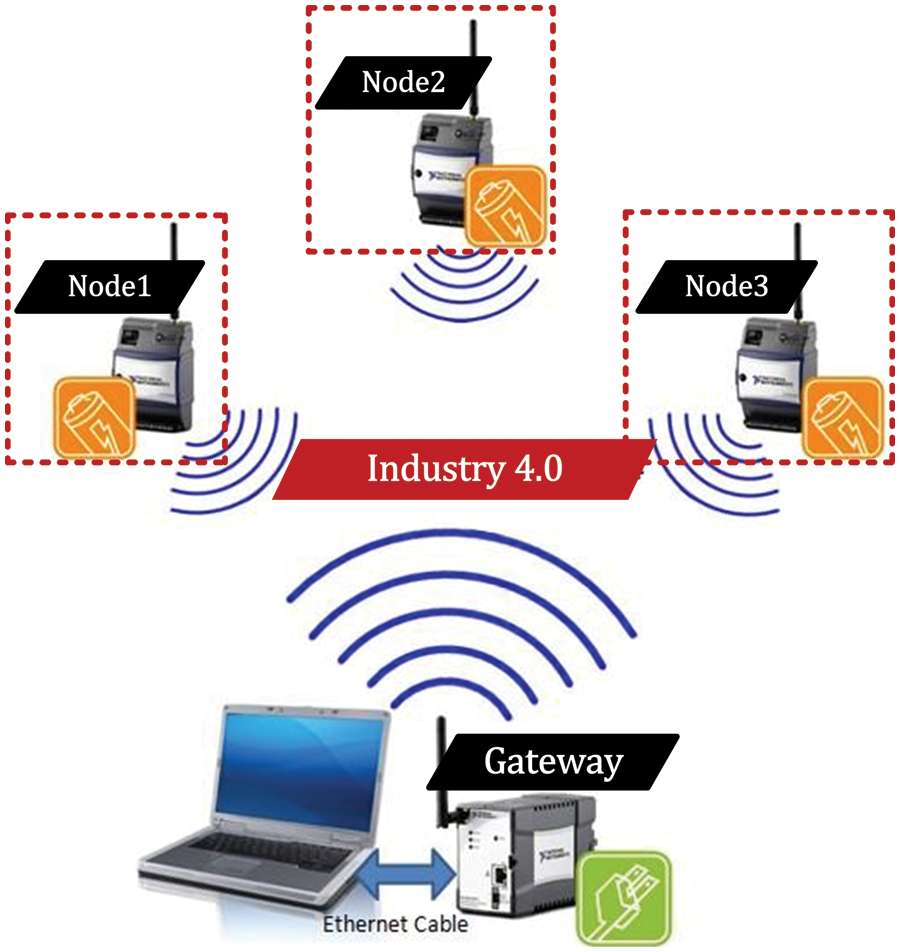
Figure 1: Intra-mobile connectivity of several devices [23]

To achieve higher security hardware-based implementations are more suitable when compared to software-based implementations. Therefore, an ECC design is described in [17] where an FPGA-based sensor node has been presented. They have targeted prime and binary fields with supported key lengths of 192 and 163. Moreover, their design is compliant with the IEEE802.15.4 standard. To reduce the hardware resources, they have reused the embedded resources of the utilized FPGA, i.e., Xilinx Artix-7.

Some ASIC and FPGA designs of ECC for RFID applications are described in [18,21]. In [18], an efficient architecture of ECC over GF(2163) for RFID applications is discussed. The synthesis results are reported for UMC 0.13 μm Complementary Metal Oxide Semiconductor (CMOS) technology. Different optimization techniques have been used for different purposes: (i) a new finite field inversion method is adopted with an intent to minimize the hardware resources, (ii) a technique for coordinate changing is discussed to minimize the complexity and decrease the computational time, (iii) a shift register design is used to minimize the area of employed register files, and (iv) the clock gating is used to reduce the power consumption. Recently in [21], an ECC-based processor over GF(2163) for RFID applications with aid to acquire low latency and the low area is presented. Additionally, flexibility is the beauty of their design. They have used three shift buffers to serially load the input parameters for two purposes: initially for acquiring low latency and then for flexibility. Moreover, the area is further optimized by reusing the hardware in inversion computation. The synthesis results are reported on various 7-series FPGA devices.

The ECC-based hardware accelerators specific to wireless sensor nodes on ASIC and FPGA platforms are described in [24–28]. In [24], a new ECC-based protocol followed with a coprocessor hardware design for key distribution in wireless sensor nodes is presented over GF(2163). Moreover, an 8-bit serial interface is discussed to load/collect the inputs/outputs to/from the coprocessor design. On Spartan-6 FPGA device, their coprocessor architecture takes 33.6 μs for one PM computation running on 33.3 MHz frequency. Similarly, a flexible design for several NIST recommended curves (substituting the reduction unit) is proposed in [25]. This partial reconfiguration determines the flexibility of their design and is accomplished on a Spartan-3 FPGA device over GF(2163) and GF(2571) fields. They have connected standard motes with the FPGA for visualization purposes while performing the actual cryptographic computations on the standard motes. An ECC-based integrated hardware architecture for wireless sensor nodes is presented in [26] over GF(2163) on Kintex-7 FPGA. Apart from the use of a Secure Hash Algorithm (SHA) or Advance Encryption Standard (AES) for authentication purposes, their design implements an Elliptic-curve based message authentication code (MAC) for efficient reuse of FPGA resources. Similarly, a PM implementation of ECC over GF(2112) and GF(2163) on different FPGA devices is provided in [27] where a Montgomery PM algorithm is employed for securing WSN. Recently in [28], an Ed25519 (Edwards curve a specialized form of Elliptic curves) curve is utilized to implement the ECDH operation for secure key-agreement over GF(P) with P=160 on two distinct nodes of MoTE-ECC.

The most recent ECC published designs for securing several other cryptographic applications are described in [11,13,29,30]. In [11], a two-stage pipelined design is reported over GF(2163) and GF(2233) for PM execution to secure cryptographic applications that require an optimal throughput and low-area for implementations such as smart cards, etc. Here, the optimal throughput determines the execution of the cryptographic operation in a reasonable time. The pipeline registers are employed to shorten the critical path of their design and ultimately improve the operational frequency which results in lower computational time. A reduced-area ECC design using the Lopez Dahab algorithm over GF(2163) on various FPGA devices is described in [13]. Recently, in [29], a Number Theoretic Transform (NTT) is utilized to enhance the performance of the PM process. A highly efficient design for 8-bit AVR-based sensor nodes is presented in [30].

The hardware accelerators of ECC are specifically concentrating on the hardware resource optimizations and decreasing the power consumption for wireless sensor nodes and RFID applications [13,18,21,24–28]. A schoolbook multiplication method is frequently employed in the literature as it reduces the hardware resources and achieves lower power consumption. With minimum hardware resources and low power consumptions, the computational time (latency or throughput) is also important to exchange the cryptographic keys in a reasonable time. It is essential to provide that the performance of polynomial multiplier determines the performance of the entire ECDH protocol as it requires frequent polynomial multiplications for computation. In literature, the most commonly used Karatsuba multiplier, as employed in [13], results in higher resources and is not feasible for wireless sensor nodes and RFID applications. The schoolbook multiplication method of [21] is expensive in terms of computational time. Therefore, an optimal multiplier is needed to achieve the low-area and high-performance footprints for meeting standards for wireless sensor nodes and RFID-related applications. Consequently, to address these issues our contributions are as follows:

•   Coprocessor architecture: We have proposed a key-authentication coprocessor architecture for 80/112-bit security-related applications over GF(2163) and GF(2233) using the ECDH protocol.

•   Flexibility: In our proposed coprocessor architecture, the flexibility is offered using a serial interface by placing input/output buffers to load/produce x and y coordinates of secret, public, and shared keys sequentially (bit-by-bit).

•   Polynomial multiplication architecture: To reduce the hardware resources and to achieve a reasonable time for cryptographic computations, we have proposed a finite field digit-serial multiplier architecture over GF(2m) field using a shift and accumulate technique. Our digit-serial multiplication operates on a digit length of 24-bits.

•   Control blocks: Finally, two finite-state-machines (FSM) are implemented to efficiently compute the public and shared keys.

The proposed coprocessor architecture is programmed using Verilog and then implemented on Xilinx Virtex-7 FPGA. Over GF(2163) and GF(2233), the proposed coprocessor architecture use 1351 and 1789 slices and the maximum operational frequency is 250 and 235 MHz. Similarly, the time required to compute one public key is 40.50 and 79.20 μs and time for one shared key generation is 81.00 and 158.40 μs. The power consumption of our architecture over GF(2163) and GF(2233) is 0.91 and 1.37 mW, respectively. The achieved results show that the proposed architecture is suitable to secure the applications that require 80/112-bits protection.

The rest of this article is organized as: Section 2 presents the relevant background. The proposed coprocessor architecture is presented in Section 3. The achieved results and performance comparison are discussed in Section 4. The article is concluded in Section 5.

2  Related Background

This section describes the essential mathematical background required for the computation of operations of ECC.

Key-authentication protocol (ECDH): As discussed earlier in Section 1, the ECDH protocol (associated with the uppermost layer model of ECC) is required to perform key agreement or key-authentication between two sensor nodes. Let us make an example to describe the key agreement mechanism of the ECDH protocol. We have shown three nodes (Node1, Node2 and Node3) in Fig. 1. If Node1 wants to communicate with Node2 then the ECDH steps include: (i) Node1 and Node2 use the same ECC configurations to prompt the required setup, (ii) computation of PM at each node (Node1 and Node2) for public key generation, (iii) exchange of generated public keys between two nodes (Node1 and Node2 in this demonstration example), and (iv) computation of PM on Node1 and Node2 for shared key generation. For mathematical structures and additional descriptions of ECDH protocol, we refer readers/designers to follow [6,14].

Point multiplication over GF(2m): It is important to highlight that each layer in ECC requires different algorithms for implementation. Therefore, the addition of k copies of PA and PD determines the PM calculation where k shows the key length. Several PM algorithms are available in the literature. According to [14,15,28,30,31], the Double and Add algorithm is more convenient for unified models of ECC, e.g., Edwards, Huff, Twisted Edwards, etc. The Lopez Dahab PM algorithm is an attractive choice for achieving instruction-level parallelism for performance improvement. The similar finite field operations for computation of PA and PD make the Montgomery PM algorithm suitable for side-channel resistant implementation of ECC. A comparison over various PM algorithms is presented in [2]. In short, we have preferred the Montgomery (Algorithm 1) PM algorithm to target the side-channel attack-protected hardware implementation of ECC for wireless sensor nodes and RFID applications.

The inputs to Algorithm 1 are (i) an initial point P with x and y coordinates, i.e., xp and yp and (ii) a scalar multiplier k. A sequence kn−1,…,k1,k0 shows the bits stream. The outputs are x and y coordinates. The PADD() and PDBL() methods represent the PA and PD instructions. For if and else statements, the sequence of instructions is shown in Table 1.

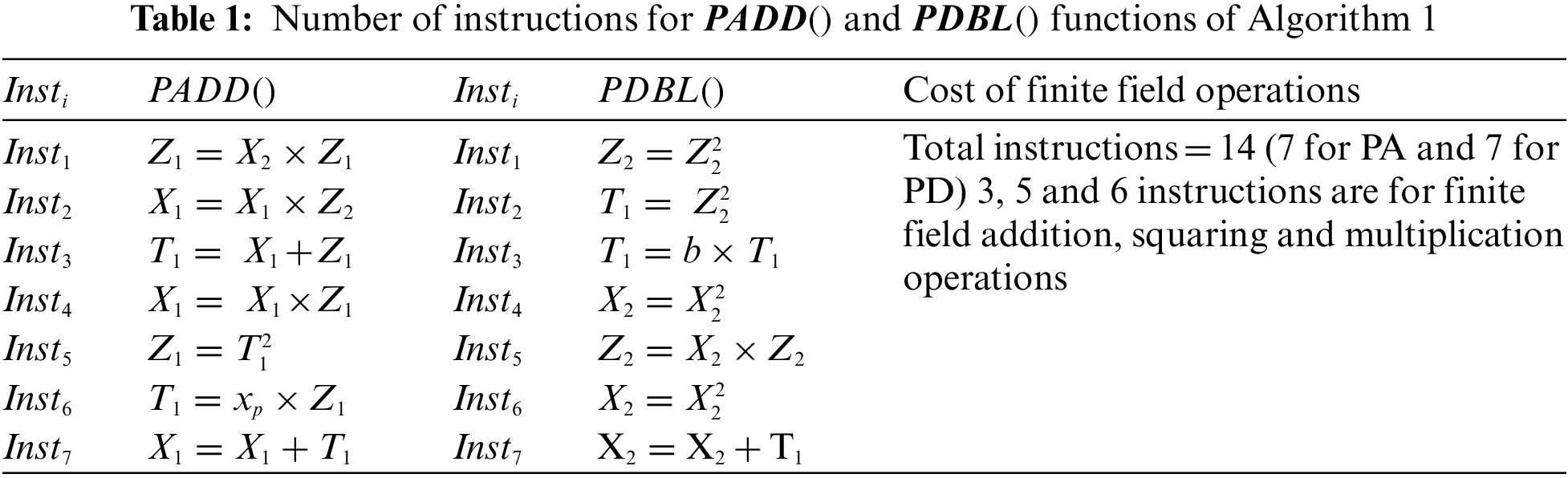
Columns one and two give the PA information in terms of sequence of instructions (i.e., Insti) and the corresponding operations, respectively. Similarly, columns three and four show the number of instructions and the respective finite field operations for PD computations. The last column presents the cost of finite field operations in PA and PD instructions.

3  Proposed Architecture

Our proposed design is presented in Fig. 2. It contains (i) a control unit, (ii) input and output buffers and (iii) an ECC unit. The related details of these blocks are as follows.

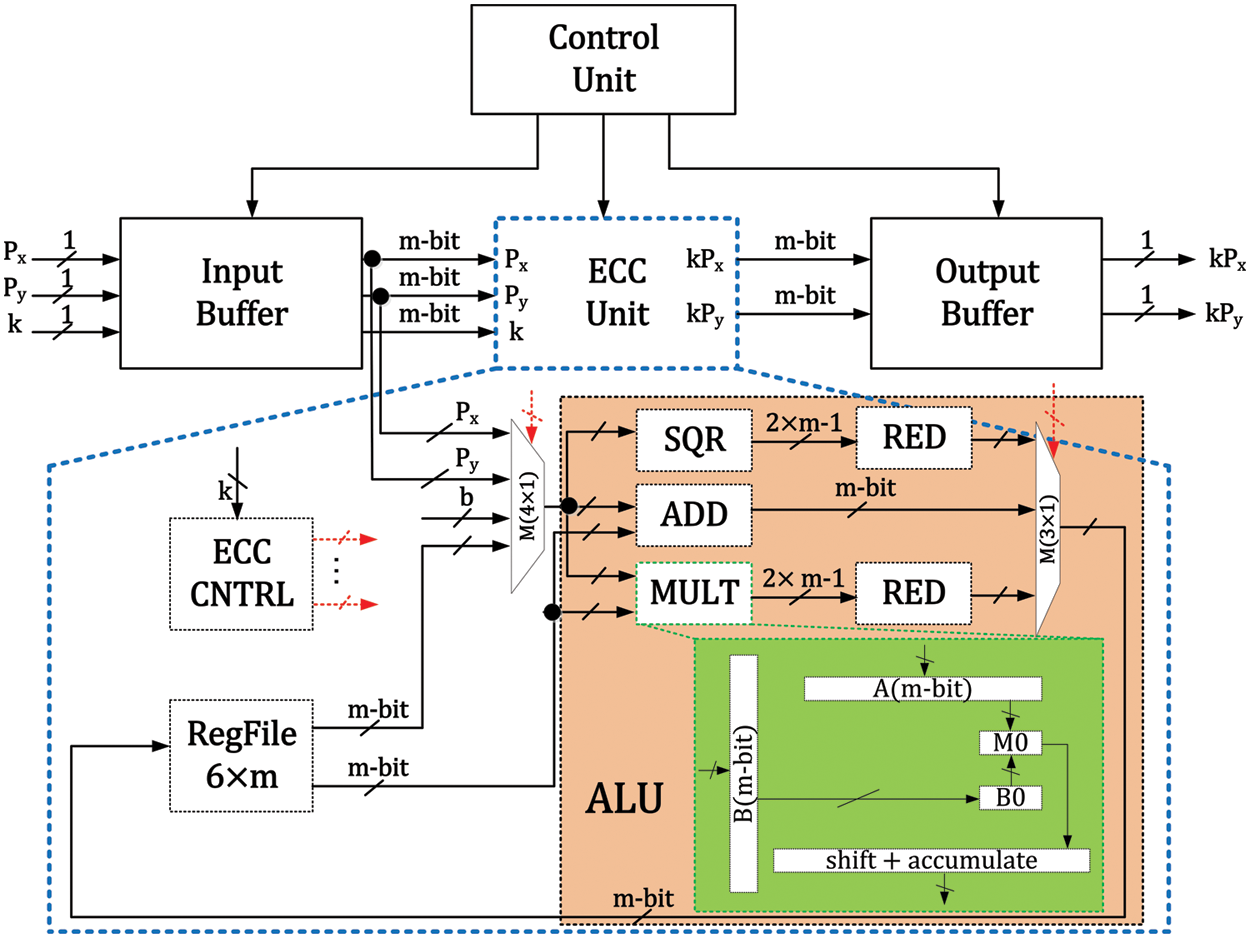
Figure 2: Proposed elliptic curve processor architecture

3.1 Control Unit

It generates the corresponding control signals for input/output buffers and the ECC unit. It contains three states: (i) LIP, (ii) SKG and (iii) LOP. The corresponding details of these states (LIP, SKG and LOP) are as follows.

LIP: It is responsible to load the input parameters, i.e., x and y coordinates of an input point P, and x and y coordinates of a public key of another node. The objective is the generation of a shared key for ECC unit. After loading the input parameters, it puts a loaddone signal (not shown in Fig. 2) as 1 for the ECC unit to start generating either public or shared keys depending on the ECDH protocol.

SKG: The ECDH protocol requires PM operation twice. The initial PM is for the generation of x and y coordinates of the public key. The second PM computation is required for the generation of x and y coordinates of a shared key. Therefore, the objective of an SKG state is to wait until the generation of x and y coordinates of either the public or shared keys. After generating the required public or shared keys, the control unit sets a KGdone signal (not presented in Fig. 2) as 1.

LOP: The purpose of the LOP states is to load the x and y coordinates of the public or shared keys on the output pins (i.e., k.Px and k.Py) of the proposed processor architecture.

3.2 Input/Output Buffers

The input buffer block comprises three m-bit buffers (not given in Fig. 2) to load x and y coordinates of a secret, public and shared keys sequentially (one-by-one-bit). It takes serial inputs and concatenates them to generate m-bit outputs. Similarly, two m-bit buffers (not shown in Fig. 2) are used in the output buffer block to serially produce the x and y coordinates of generated public or shared keys as output. For input and output buffers, m clock cycles are required for m-bit data and key lengths to load and produce output. It is essential to mention that the proposed architecture is flexible as it offers data loading (including a private and the coordinates of public & shared keys) from the outside of ECC unit, as shown in Fig. 2.

3.3 ECC Unit

The ECC unit contains (i) a storage system, (ii) an arithmetic and logic unit (ALU) and (iii) a controller (ECC CNTRL), as shown in Fig. 2. Moreover, for routing purposes, a 4×1 multiplexer is used between the storage system and ALU. As we have presented in Fig. 2, it selects an operand from the storage system and ECC parameters, i.e., Px, Py, and b, to provide input to the ALU. The architectural details of the used storage system, ALU and ECC controller blocks are given as follows.

3.3.1 Storage System (RegFile)

A 6×m size register file is used as memory to store the initial, intermediate and final outputs of the ECC unit. It contains two 6×1 sizes of multiplexers and one 1×6 size of a demultiplexer. The intent of routing multiplexers is to read two m-bit operands. Similarly, a demultiplexer is incorporated to update the memory contents. The related control signals (not given in Fig. 2) are generated by the ECC controller.

3.3.2 Arithmetic and Logic Unit (ALU)

The pink color in Fig. 2 shows the ALU that contains an adder (ADD), squarer (SQR), multiplier (MULT) and two reduction (RED) blocks (connected one after each SQR and MULT). Moreover, for routing purposes, a 3×1 multiplexer is used to select the corresponding data for writing on a storage system. Therefore, in GF(2m) field, the addition is performed by employing bitwise Exclusive-OR operations. The SQR unit in Fig. 2 is implemented by putting a ‘0’ bit after every successive data bit, as implemented in hardware accelerators of [11,13,19].

The polynomial multiplication computation specifies the performance of the PM architecture [2,11,17–19,21,27,28,30–32]. For multiplying two m-bit polynomial multiplications, several architectures have been presented in the literature [11,17–19,21,27,28,30]. These includes (i) bit-serial, (ii) bit-parallel, (iii) digit-serial and (iv) digit-parallel approaches. Moreover, some systolic polynomial multiplication designs are also described in [33–35]. In this context, the bit-serial designs are more appropriate for achieving the low-area and power-efficient architectures. But, on the other hand, the computational cost of bit-serial designs is the overhead as it utilizes m clock cycles for the multiplication of two m-bit operands. For high-speed cryptographic applications such as network servers, bit parallel and digit parallel multipliers are more attractive choices as they consume a single clock cycle for a polynomial multiplication [11,36,37]. Higher hardware resource utilization and larger power consumptions limit the use of bit and digit parallel multipliers for wireless sensor nodes and RFID applications. The digit-serial multipliers consider both area and computational cost (throughput) simultaneously for polynomial multiplication. It takes a=bc cycles for one polynomial multiplication, where a is the total digits, b is the operand length and c is digit size. Therefore, the digit-serial polynomial multipliers are the more attractive alternative for multiplying two polynomials. Consequently, our MULT contains a digit-serial architecture.

Proposed digit-serial multiplier architecture: Our proposed digit-serial polynomial multiplication architecture (24-bits) is shown with the green color in Fig. 2. The reason to select a 24-bits digit size is to obtain an optimal computational cost with minimum hardware resource utilization. The longer digit length reduces clock cycles requirement but utilizes more hardware resources and consumes more power which is not feasible for wireless sensor nodes and RFID applications [19,21]. With this compliance, we have employed a 24-bit digit size in our multiplication architecture of Fig. 2 where two m-bit polynomials, i.e., A, and B, are input to the proposed multiplier. We have stored an m-bit polynomial B in an m-bit buffer. Then, to initiate a polynomial multiplication in the first cycle, we have loaded 24-bits of polynomial B from LSB (least-significant-side) into buffer B0 for polynomial multiplications using M0 multiplier. The size of B0 is also 24-bits. In the next cycle, the next 24-bits of polynomial B are loaded into B0 for multiplication. After the second multiplication of 24-bits of polynomial B with an m-bit polynomial A, we have accumulated the current generated result with the previous result to acquire the resultant polynomial. This process will continue until all the 24-bit digits of polynomial B are multiplied with an m-bit input polynomial A. Finally, the resultant polynomial contains a 2×m−1 bit length. The computational cost of our multiplier is a=bc+1 cycles, where a is the total digits, b is the operand length (163 and 233 in this work) and c is the digit length (24-bits in this work). An additional clock cycle is needed to load an m-bit polynomial B into a buffer.

For the computation of one m-bit polynomial squaring or two m-bit polynomial multiplications, the proposed SQR and MULT units result in 2×m−1 bit polynomials length, respectively. Therefore, a reduction is needed to obtain an m-bit polynomials. The RED block in Fig. 2 is implemented using NIST defined reduction algorithms. For the corresponding reduction algorithms over GF(2163) and GF(2233), we refer readers to [6,37]. Moreover, in Algorithm 1, the reconversion from projective to affine shows that a finite field inversion operation is needed. The inversion block is not shown in Fig. 2. However, we have used an Itoh-Tsujii inversion algorithm which is initially proposed in 1988 and the corresponding mathematical formulations are completely described in [38]. For implementations, it requires frequent squaring and multiplication operations [11,13,21]. Over GF(2163) and GF(2233), the corresponding Itoh-Tsujii inversion algorithms are represented in [39,5], respectively. The Itoh-Tsujii algorithm in our design of Fig. 2 is implemented by sharing hardware resources of SQR and MULT blocks as implemented in [5,39]. This (also) allow us to save the hardware cost of our proposed design.

3.3.3 Dedicated Controller (ECC CNTRL) and Clock Cycles Calculation

The ECCCNTRL unit is responsible to generate the corresponding control signals for the routing multiplexers (i.e., M(4×1) and M(3×1)) and MULT unit. Moreover, it corresponds with the control unit block after the computation of x and y coordinates of public and shared keys. It consists of 88 states. State 0 is an idle state. However, the details for other states are as follows.

•   Affine to projective coordinates conversion: Affine to projective conversions is performed from state 1 to state 6. Each state requires one clock cycle. So a total of six clock cycles are needed to compute affine to projective conversions.

•   PM in projective coordinates: Columns two and four of Table 1 shows that each PADD() and PDBL() functions involve seven instructions (i.e., Inst1 to Inst7). Hence, a total of fourteen instructions are needed to compute each PA and PD operation. State seven is a conditional state which is responsible to check the value of key. If the ki in Algorithm 1 becomes 1 then the PA and PD operations of the if part will be computed (during states eight to twenty-one) otherwise the else part will be executed (during states twenty two to thirty-five). The last column in Table 1 shows that the six, three and five instructions are required for the computation of finite field multiplication, addition and squaring, respectively. The addition and squaring operations require only one clock cycle for computations. On the other hand, each finite field multiplication takes bc+1 clock cycles. Therefore, six multiplications take 6×bc+1 clock cycles.

•   Reconversion from projective to affine coordinates: When the processor executes the for loop statement in Algorithm 1 then the reconversions will be computed during states thirty-six to eighty-eight. Moreover, the reconversion portion of Algorithm 1 also incorporates the finite field inversion operation. Hence, over GF(2163) field, each finite field inversion requires m squares and nine multiplications. So the computational cost will be 9×(bc+1)+m clock cycles. Similarly, over GF(2233) field, each finite field inversion demands m squares and ten multiplications. In this case the computational cost will be 10×(bc+1)+m clock cycles.

3.4 Total Clock Cycle Calculations

The total clock cycles of our proposed processor architecture over GF(2163) and GF(2233) is calculated using Eqs. (1) and (2), respectively.

Totalcycles=6+m×[6×{(mc)+1}+8]+2×[9×{(mc)+1}+m]+360(1)

Totalcycles=6+m×[6×{(mc)+1}+8]+2×[10×{(mc)+1}+m]+450(2)

In Eqs. (1) and (2), m shows the targeted field length (i.e., 163 and 233) and c determines the digit length of 24-bits. The additional details are given below.

•   Affine to projective coordinates conversion: A numerical value of 6 before the square brackets determine the clock cycles for affine to projective conversions.

•   PM in projective coordinates: In Eqs. (1) and (2), 6×{(mc)+1}+8 determines the clock cycles for PM computation in projective coordinates. If we substitute m=163 and c=24 in Eq. (1) then the 48 clock cycles are required to compute six multiplication instructions of PADD() and PDBL() functions of Algorithm 1. The additional 8 clock cycles are needed to compute the addition and squares computations. Similarly, if we use m=233 and c=24 in Eq. (2) then the 66 clock cycles are needed to compute six multiplication instructions of PADD() and PDBL() functions and 8 shows the additional clock cycles for addition and squares computations. Therefore, over GF(2163) and GF(2233), the total cycles for one iteration of a loop statement of Algorithm 1 is 56 and 74, respectively. Then, the required cycles for m field operations is 9128 (163×56) and 17242 (233×74).

•   Reconversion from projective to affine coordinates: As shown in reconversion part of Algorithm 1, two finite field inversions are involved to execute the reconversion step. Therefore, over GF(2163) and GF(2233), the 2×[9×{(mc)+1}+m] and 2×[10×{(mc)+1}+m] portions of Eqs. (1) and (2) determines the inversion computation. If we use the corresponding values of m and c, the clock cycle computation becomes 468 and 682. The additional 360 and 450 cycles are needed to compute the remaining instructions of reconversion portion ofAlgorithm 1. Therefore, over GF(2163) and GF(2233), the total clock cycle requirements for reconversion is 828 and 1132, respectively.

4  Results and Comparisons

4.1 Results

To describe the implementation results, we have first provided the simulation waveform in Section 4.1.1. After that, the implementation results are reported in Section 4.1.2. Finally, the schematic waveform after the circuit place and route is shown in Section 4.1.3.

4.1.1 Simulation Waveform

The simulation waveform over GF(2163) is shown in Fig. 3. It ensures that the proposed coprocessor architecture successfully generates the shared key value when the public and private/secret keys are input to the system. The generated shared key value could be used to perform key authentication or encryption and decryption between two wireless sensor nodes.

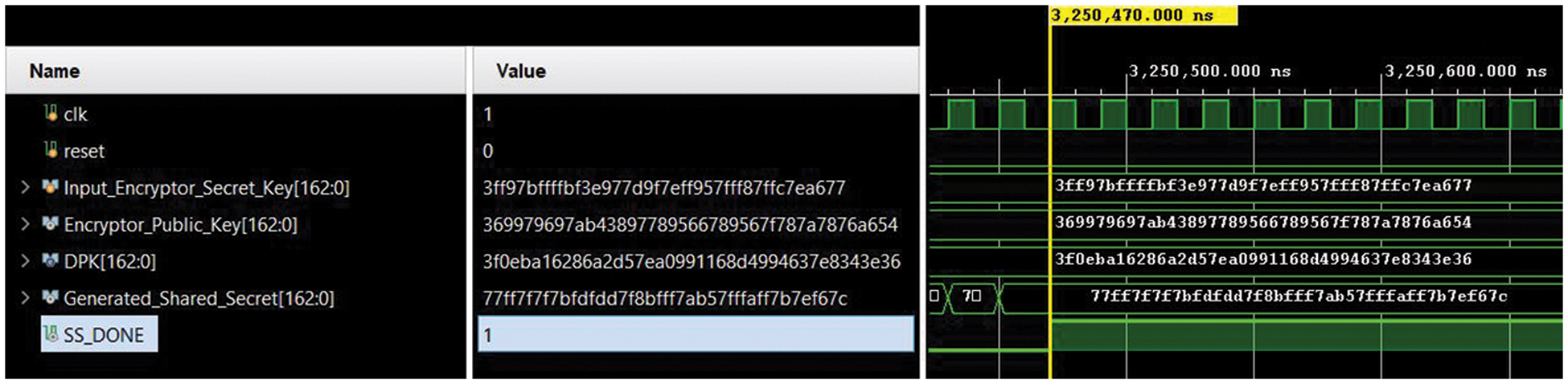
Figure 3: RTL simulation waveform (captured on Vivado 2019.2)

4.1.2 Implementation Results

Our proposed coprocessor architecture over GF(2163) and GF(2233) is implemented in Verilog, using Vivado IDE (Integrated Design Environment) tool. The implementation results is performed for a 28 nm technology on Virtex-7 (xc7vx485tffg1157-1) FPGA. The input parameters have been selected from NIST standardized document [16]. Consequently, the results are provided after place-and-route in Table 2. The field length (m) is presented in column one. Columns two, three and four present the slices, LUTs and FFs respectively. The clock frequency is presented in column five. The total number of required clock cycles (CCs) and latency (in μs) figures are given in columns six and seven, respectively. Similarly, the clock cycles (CCs) and latency (in μs) values for shared key generation are given in columns eight and nine, respectively. Finally, the consumed power (in mW) is provided in the last column. The area and frequency values are obtained from the Vivado IDE tool. The clock cycles are calculated using Eqs. (1) and (2), the details are already described in Section 3.4. The latency values are calculated using Eq. (3). To obtain power values, we have used a Vivado Power Analysis tool [40].

Latency(μs)=ClockCycles(CCs)Frequency(MHz)(3)

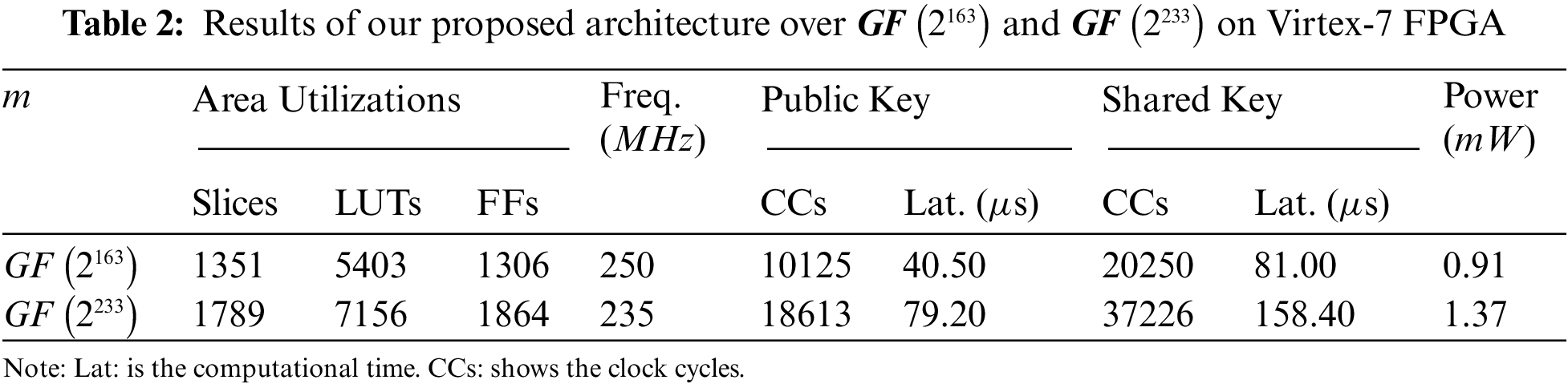
Due to different field lengths (i.e., 163 and 233), the proposed architecture over GF(2163) utilizes 1351, 5403 and 1306 FPGA slices, LUTs and FFs that are comparatively 0.75 (ratio of 1351 over 1789), 0.75 (ratio of 5403 over 7156) and 0.70 (ratio of 1306 over 1864) times lower than the design implemented over GF(2233) field. The use of a coprocessor implementation style and a digit-serial finite field multiplier results in a maximum frequency of 250 and 235 MHz over GF(2163) and GF(2233), respectively. By employing different optimization techniques such as pipelining, parallelism and scheduling for PA and PD instructions of columns two and four of Table 1, the clock frequency of our architecture could be improved for high-speed cryptographic applications.

Despite the hardware resources and operational frequency, our design requires 10125 and 20250 cycles for one public and shared keys computation over GF(2163). Similarly, for public and shared key generations, the clock cycle cost of our architecture over GF(2233) is 18613 and 37226, respectively. With some area (hardware resources) overhead, the clock cycles could be improved by employing bit-parallel or digit-parallel finite field multipliers inside the ALU of our coprocessor architecture. The computational cost in terms of latency is 40.50 and 81.00 μs over GF(2163) for one public key and shared key generation, respectively. For similar operations, the latency values over GF(2233) is 79.20 and 158.40 μs. As expected, the computational cost (in terms of both CCs and latency) increases with the increase in the binary field length (i.e., from 163 to 233). The latency of the proposed design could be improved by (i) reducing the clock cycles and (ii) maximizing the clock frequency.

Utilization of a digit-serial multiplier with a smaller digit size of 24-bit results in lower power consumption of 0.91 and 1.37 mW over GF(2163) and GF(2233), respectively. The use of smaller digit length results in a lower computational power with clock cycles overhead [11,41]. The hardware resources and power consumption of our proposed design could be improved further by employing a bit-serial multiplication architecture as used in [21].

4.1.3 Schematic Layout

The circuit layout of our proposed coprocessor architecture over GF(2163) is shown in Fig. 4. It shows that the proposed coprocessor architecture is routable on our selected Virtex-7 (xc7vx485tffg1157-1) FPGA without the DRC (design rule check) and timing violations.

Figure 4: Circuit layout of the proposed coprocessor architecture over GF(2163)

4.2 Comparisons

The comparison with state-of-the-art is shown in Table 3. The reference design and publication years are displayed in column one. The implemented binary field length along with cryptographic operation is given in column two. Column three presents the targeted FPGA device. The values presented before the parenthesis in column four are the FPGA slices while a value inside the parenthesis is the FPGA LUTs. The operational frequency (in MHz) and latency (in μs) values are presented in columns five and six, respectively. Moreover, we have used a symbol of ‘–’ in Table 3 where the relevant information is not given.

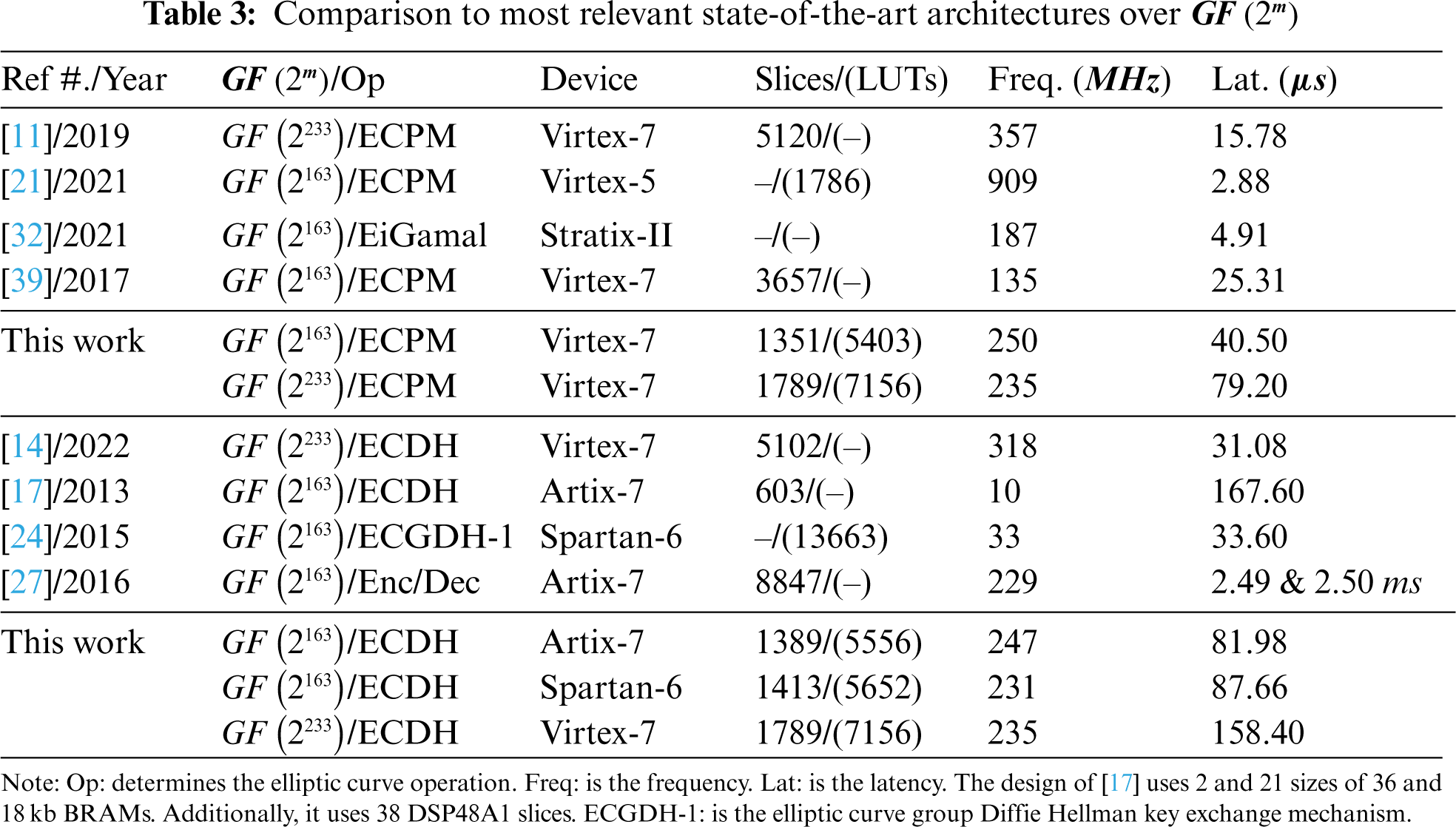
4.2.1 Comparison with ECPM Designs

On Virtex-7 over GF(2233), the proposed architecture consumes 2.86 (ratio of 5120 with 1789) times lesser slices with respect to [11]. The reason is the use of a digit-serial multiplier (24-bits). On the other hand, a 32-bit digit size is used in a parallel way in [11]. Moreover, this comparison shows that the longer digits result in higher hardware resources. Additionally, the digit-parallel multiplication approach with a digit length of 32-bits results in lower clock cycles which ultimately improves the latency value in [11]. The use of 2-stage pipelining improves the clock frequency in [17].

As shown in Table 3, the architecture of [21] over GF(2163) on Virtex-7 utilizes lower FPGA LUTs and takes less time for computation with respect to the proposed design. The reason is the computation of only the PM operation of ECC while our design considers the ECDH protocol implementation for key authentication. As the objective of our work is to generate the shared key for wireless sensor nodes and RFID applications, the proposed architecture can operate up to a maximum of 250 MHz while the architecture of [21] can operate on 909 MHz frequency as the intent is to optimize only the PM operation.

Apart from the hardware resources and timing results, the power consumption of [21] is 0.73 mW for one PM execution. In our work, a 0.91 mW is consumed for one shared key generation using ECDH protocol. Furthermore, our design utilizes Montgomery PM algorithm for the implementation of the ECDH protocol of ECC as it is inherently secure against timing and power analysis attacks. On the other hand, the Lopez Dahab PM algorithm is used in [21]. In Lopez Dahab PM algorithm, swapping between the PA and PD computations is needed whenever the inspected value of the key-bit becomes 1. The need for swapping requires additional clock cycles which shows that the architecture of [21] is not secure against the timing and power analysis attacks. To summarize, our architecture is protected against timing and power analysis attacks and consumes a comparable power than the power consumption of [21].

The Stratix-II design of [32] achieves an operational frequency of 187 MHz that is comparatively 1.33 (ratio of 250 with 187) times lower than our Virtex-7 implementation over GF(2163). In other words, our work is 1.33 times faster in terms of frequency. However, our architecture requires more computational time as we have described a flexible design while a dedicated architecture of PM is discussed in [32]. The comparison to area and power values are not possible to provide as the relevant information is not presented in the reference design. On Virtex-7 over GF(2163), our architecture utilizes 2.70 (ratio of 3657 with 1351) times lower FPGA slices than [39]. The reason is the use of a digit-serial multiplier with a digit size of 24-bits in our work while a bit-parallel Karatsuba multiplier is considered for implementation in [39]. The use of bit-parallel multiplier results in lower clock cycles which eventually improves the latency value in [39]. Moreover, our design is 1.85 (ratio of 250 with 135) times faster in terms of operational frequency. Similar to [32], the power comparison is not possible because the corresponding information is not described in the reference design.

4.2.2 Comparison to Key-Authentication Architectures

The most recent design of [14] for key-authentication using ECDH protocol over GF(2233) on Virtex-7 FPGA results in 2.85 (ratio of 5102 with 1789) times higher slices as compared to our work. On the other hand, the design of [14] is 5.09 (ratio of 158.40 with 31.08) times faster in terms of computational time as compared to our architecture. The reason is the use of bit-parallel Karatsuba multiplier in the datapath of [14] while in our design, we employed a digit-serial multiplication approach. Another reason is the use of 2-stage pipelining to shorten the critical path which eventually increases the clock frequency with an area overhead. Power comparison is not possible as the corresponding information is not given in [14].

The efficient implementation of [17] for key authentication using ECDH protocol over GF(2163) on Artix-7 results in 603 slices that is comparatively lower than our work (1389). On the other hand, the architecture of [17] uses 2 and 21 sizes of 36 and 18 kb BRAMs. In addition, it utilizes 38 DSP48A1 FPGA slices. In our design, we are not using the BRAMs as we implemented a RegFile as an array of registers to accommodate the initial, intermediate and final results. Therefore, a fair comparison to area is challenging. Despite the hardware resources, our architecture is 24 (ratio of 247 with 10) times faster in terms of clock frequency. Moreover, our architecture requires 2.40 (ratio of 167.70 with 81.98) times lower computational time (latency). Whenever, the power consumption of [17] is concerned for comparison, our architecture is 29.62 (ratio of 40 mW with 1.35 mW times efficient. The potential reason for higher power consumption and computational time in [17] is the support for various cryptographic algorithms such as SHA (Secure Hash Algorithm) for secure hashing while our design is specific to the ECDH protocol.

On similar Spartan-6 device, the design of [24] over GF(2163) for ECDH implementation is 2.41 (ratio of 13663 with 5652) times less area efficient as compared to our work. It is due to the employment of several finite field multipliers in their architecture. O the other hand, we have utilized a single serial multiplier. Moreover, the proposed design provides a speedup of 7 (ratio of 231 with 33), as far as the operational frequency is concerned. In terms of latency, the proposed design requires 2.60 (ratio of 87.66 with 33.60) times the higher computational cost. The cause is the parallelism using multiple finite field multipliers in [24]. The dynamic power in [24] at 33 MHz is 571 mW which is comparatively 435.8 (ratio of 571 mW with 1.31 mW) times higher than this work. The Artix-7 design of [27] over GF(2163) results in higher slices (i.e., 8847) as compared to our design whereas we have used only 1389. The reason is the additional encryption and decryption operations along with the ECDH protocol implementation while we have considered only the ECDH protocol for shared key computation. Due to the simpler datapath in our design, the operational frequency is 1.07 (ratio of 247 with 229) times higher. The comparison to latency is not possible as their architecture results in encryption and decryption time while we have computed a shared key generation without the encryption and decryption operations.

5  Conclusions

This article has proposed a flexible coprocessor key-authentication architecture for 80/112-bit security-related applications over GF(2m) with m=163 and 233 using an ECDH protocol. The flexibility is achieved by using a serial input/output interface to load/produce secret, public, and shared keys. Moreover, a finite field digit-serial multiplier architecture with a digit size of 24-bits is proposed using shift and accumulate methods. Two FSM controllers have been implemented to efficiently generate the control signals. The implementation results are reported on Xilinx Virtex-7 FPGA. Over GF(2163) and GF(2233), the utilized hardware resources in terms of FPGA slices are 1351 and 1789. For similar key lengths, the operational clock frequency is 250 and 235 MHz. The time required to compute one public key over GF(2163) and GF(2233) is 40.50 and 79.20 μs, respectively. Similarly, the time for one shared key generation is 81.00 and 158.40 μs. The consumed power over GF(2163) and GF(2233) is 0.91 and 1.37 mW, respectively. Consequently, the proposed architecture outperforms state-of-the-art ECDH designs in terms of hardware resources.

Funding Statement: This project has received funding by the NSTIP Strategic Technologies program under Grant Number 14-415 ELE1448-10, King Abdul Aziz City of Science and Technology of the Kingdom of Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Rana, Q. Mamun and R. Islam, “Lightweight cryptography in IoT networks: A survey,” Future Generation Computer Systems, vol. 129, pp. 77–89, 2022. [Google Scholar]

 2.  M. Rashid, M. Imran, A. R. Jafri and T. F. Al-Somani, “Flexible architectures for cryptographic algorithms: A systematic literature review,” Journal of Circuits Systems and Computers (JCSC), vol. 28, no. 3, pp. 35, 2019. [Google Scholar]

 3.  E. Anaya, J. Patel, P. Shah, V. Shah and Y. Cheng, “A performance study on cryptographic algorithms for IoT devices,” in Proc. of the Tenth ACM Conf. on Data and Application Security and Privacy, New York, USA, pp. 159–161, 2020. [Google Scholar]

 4.  A. Miri, “Advanced Security and Privacy for RFID Technologies,” Hershey, PA: IGI Global, pp. 1–342, 2013. [Online]. Available: https://www.igi-global.com/gateway/book/72161. [Google Scholar]

 5.  M. Imran and F. Shehzad, “FPGA based crypto processor for elliptic curve point multiplication (ECPM) over GF(2233),” International Journal for Information Security Research (IJISR), vol. 7, pp. 706–713, 2017. [Google Scholar]

 6.  D. Hankerson, A. J. Menezes and S. Vanstone, “Guide to Elliptic Curve Cryptography,” Henderson, NV, USA: Springer, pp. 1–311, 2004. [Online]. Available: https://link.springer.com/book/10.1007/b97644. [Google Scholar]

 7.  R. Housley, “Use of the Elliptic Curve Diffie-Hellman Key Agreement Algorithm with x25519 and x448 in the Cryptographic Message Syntax (CMS),” RFC 8418, pp. 1–18, 2018. [Online]. Available: https://www.rfc-editor.org/info/rfc8418. [Google Scholar]

 8.  T. Pornin, “Deterministic Usage of the Digital Signature Algorithm (DSA) and Elliptic Curve Digital Signature Algorithm (ECDSA),” RFC 6979, pp. 1–79, 2013. [Online]. Available: https://www.rfc-editor.org/info/rfc6979. [Google Scholar]

 9.  S. Turner, D. Brown, K. Yiu, R. Housley and T. Polk, “Elliptic Curve Cryptography Subject Public Key Information,” RFC 5480, pp. 1–20, 2009. [Online]. Available: https://www.rfc-editor.org/info/rfc5480. [Google Scholar]

10. N. Pirotte, J. Vliegen, L. Batina and N. Mentens, “Design of a fully balanced ASIC coprocessor implementing complete addition formulas on weierstrass elliptic curves,” in 21st Euromicro Conf. on Digital System Design (DSD), Prague, Czech Republic, pp. 545–552, 2018. [Google Scholar]

11. M. Imran, M. Rashid, A. R. Jafri and M. Kashif, “Throughput/area optimised pipelined architecture for elliptic curve crypto processor,” IET Computers & Digital Techniques, vol. 13, no. 5, pp. 361–368, 2019. [Google Scholar]

12. B. Rashidi, “Low-cost and fast hardware implementations of point multiplication on binary edwards curves,” in Electrical Engineering (ICEEIranian Conf. on, Mashhad, Iran, pp. 17–22, 2018. [Google Scholar]

13. M. Imran, M. Rashid and I. Shafi, “Lopez dahab based elliptic crypto processor (ECP) over GF(2163) for low-area applications on FPGA,” in 2018 Int. Conf. on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, pp. 1–6, 2018. [Google Scholar]

14. M. Rashid, H. Kumar, S. Z. Khan, I. Bahkali, A. Alhomoud et al., “Throughput/area optimized architecture for elliptic-curve diffie-hellman protocol,” Applied Sciences, vol. 12, no. 8, pp. 1–18, 2022. [Google Scholar]

15. J. Vliegen, N. Mentens, J. Genoe, A. Braeken, S. Kubera et al., “A compact FPGA-based architecture for elliptic curve cryptography over prime fields,” in 21st IEEE Int. Conf. on Application-Specific Systems, Architectures and Processors, Rennes, France, pp. 313–316, 2010. [Google Scholar]

16. NIST. “Recommended Elliptic Curves for Federal Government Use,” FIPS PUB 1862–2: USA, pp. 1–70, 1999. [Online]. Available: https://csrc.nist.gov/csrc/media/publications/fips/186/2/archive/2000-01-27/documents/fips186-2.pdf. [Google Scholar]

17. A. De la Piedra, A. Braeken and A. Touhafi, “Extending the IEEE 802.15.4 security suite with a compact implementation of the NIST P-192/B-163 elliptic curves,” Sensors, vol. 13, no. 8, pp. 9704–9728, 2013. [Google Scholar]

18. Z. Liu, D. Liu, X. Zou, H. Lin and J. Cheng, “Design of an elliptic curve cryptography processor for RFID tag chips,” Sensors, vol. 14, no. 10, pp. 17883–17904, 2014. [Google Scholar]

19. S. Khan, W. K. Lee and S. O. Hwang, “A flexible gimli hardware implementation in FPGA and its application to RFID authentication protocols,” IEEE Access, vol. 9, pp. 105327–105340, 2021. [Google Scholar]

20. A. S. R. Oliveira, N. B. Carvalho, J. Santos, A. Boaventura, R. F. Cordeiro et al., “All-digital RFID readers: An RFID reader implemented on an FPGA chip and/or embedded processor,” IEEE Microwave Magazine, vol. 22, no. 3, pp. 18–24, 2021. [Google Scholar]

21. M. Rashid, S. S. Jamal, S. Z. Khan, A. R. Alharbi, A. Aljaedi et al., “Elliptic-curve crypto processor for RFID applications,” Applied Sciences, vol. 11, no. 15, pp. 1–16, 2021. [Google Scholar]

22. T. D. P. Bai, K. M. Raj and S. A. Rabara, “Elliptic curve cryptography based security framework for internet of things (IoT) enabled smart card,” in 2017 World Congress on Computing and Communication Technologies (WCCCT), Tiruchirappalli, India, pp. 43–46, 2017. [Google Scholar]

23. C. Ankita, “Wireless Sensor Networks,” electroSome, 2013. [Online]. Available: https://electrosome.com/wireless-sensor-networks/#google_vignette. [Google Scholar]

24. L. Parrilla, D. P. Morales, J. A. López-Villanueva, J. A. López-Ramos and J. A. Álvarez-Bermejo, “Hardware implementation of a new ECC key distribution protocol for securing wireless sensor networks,” in 2015 Conf. on Design of Circuits and Integrated Systems (DCIS), Estoril, Portugal, pp. 1–6, 2015. [Google Scholar]

25. S. Peter, O. Stecklina, J. Portilla, E. de la Torre, P. Langendoerfer et al., “Reconfiguring crypto hardware accelerators on wireless sensor nodes,” in 6th IEEE Annual Communications Society Conf. on Sensor, Mesh and Ad Hoc Communications and Networks Workshops, Rome, Italy, pp. 1–3, 2009. [Google Scholar]

26. P. Jilna, P. P. Deepthi and U. K. Jayaraj, “Optimized hardware design and implementation of EC based key management scheme for WSN,” in 10th Int. Conf. for Internet Technology and Secured Transactions (ICITST), London, UK, pp. 164–169, 2015. [Google Scholar]

27. G. Leelavathi, K. Shaila and K. R. Venugopal, “Elliptic curve cryptography implementation on FPGA using montgomery multiplication for equal key and data size over GF(2m) for wireless sensor networks,” in IEEE Region 10 Conf. (TENCON), Singapore, pp. 468–471, 2016. [Google Scholar]

28. M. Das and Z. Wang, “ED25519: A new secure compatible elliptic curve for mobile wireless networks security,” Jordanian Journal of Computers and Information Technology (JJCIT), vol. 8, no. 1, pp. 57–71, 2022. [Google Scholar]

29. U. Gulen and S. Baktir, “Elliptic curve cryptography for wireless sensor networks using the number theoretic transform,” Sensors, vol. 20, no. 5, pp. 1–16, 2020. [Google Scholar]

30. S. C. Seo and H. Seo, “Highly efficient implementation of NIST-compliant koblitz curve for 8-bit AVR-based sensor nodes,” IEEE Access, vol. 6, pp. 67637–67652, 2018. [Google Scholar]

31. Z. Razali, N. Muslim, S. Kahar, F. Yunos and K. Mohamed, “Improved point 5P formula for twisted edwards curve in projective coordinate over prime field,” in Int. Conf. on Decision Aid Sciences and Applications (DASA), Chiangrai, Thailand, pp. 498–502, 2022. [Google Scholar]

32. R. Amiri and O. Elkeelany, “FPGA design of elliptic curve cryptosystem (ECC) for isomorphic transformation and EC ElGamal encryption,” IEEE Embedded Systems Letters, vol. 13, no. 2, pp. 65–68, 2021. [Google Scholar]

33. S. Devi, R. Mahajan and D. Bagai, “A low complexity bit parallel polynomial basis systolic multiplier for general irreducible polynomials and trinomials,” Microelectronics Journal, vol. 115, pp. 105163, 2021. [Google Scholar]

34. S. Devi, R. Mahajan and D. Bagai, “Low complexity design of bit parallel polynomial basis systolic multiplier using irreducible polynomials,” Egyptian Informatics Journal, vol. 23, no. 1, pp. 105–112, 2022. [Google Scholar]

35. S. E. Mathe and L. Boppana, “Bit-parallel systolic multiplier over GF(2m) for irreducible trinomials with ASIC and FPGA implementations,” IET Circuits, Devices & Systems, vol. 12, no. 4, pp. 315–325, 2018. [Google Scholar]

36. M. Thirumoorthi, M. Heidarpur, M. Mirhassani and M. Khalid, “An optimized m-term karatsuba-like binary polynomial multiplier for finite field arithmetic,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 30, no. 5, pp. 603–614, 2022. [Google Scholar]

37. H. Kumar, M. Rashid, A. Alhomoud, S. Z. Khan, I. Bahkali et al., “A scalable digit-parallel polynomial multiplier architecture for NIST-standardized binary elliptic curves,” Applied Sciences, vol. 12, no. 9, pp. 1–18, 2022. [Google Scholar]

38. T. Itoh and S. Tsujii, “A fast algorithm for computing multiplicative inverses in GF(2m) using normal bases,” Information and Computation, vol. 78, no. 3, pp. 171–177, 1988. [Google Scholar]

39. M. Imran, I. Shafi, A. R. Jafri and M. Rashid, “Hardware design and implementation of ECC based crypto processor for low-area-applications on FPGA,” in Int. Conf. on Open Source Systems & Technologies (ICOSST), Lahore, Pakistan, pp. 54–59, 2017. [Google Scholar]

40. Xilinx, “Power Analysis and Optimization,” AMD Xilinx, UG907: USA, pp. 1–112. 2016. [Online]. Available: https://docs.xilinx.com/v/u/2016.2-English/ug907-vivado-power-analysis-optimization. [Google Scholar]

41. M. Imran, Z. U. Abideen and S. Pagliarini, “An open-source library of large integer polynomial multipliers,” in 24th Int. Symp. on Design and Diagnostics of Electronic Circuits & Systems (DDECS), Vienna, Austria, pp. 145–150, 2021. [Google Scholar]