Mathematical Morphology View of Topological Rough Sets and Its Applications

Nomenclature

Abbreviations

1  Introduction and Preliminaries

Pawlak’s rough set theory [1] is a mathematical tool that is useful for studying uncertain or incomplete data in information systems and is based on the classification of data into Objects [2]. However, Pawlak’s definition of equivalence classes of an equivalence relation for the universe set is not valid for all incomplete data, particularly various real-life problems. By studying Pawlak’s rough set theory from a topological point of view, Lashin et al. [3] and Salama et al. [4] derived a general relation and observed that most of Pawlak’s properties are not held in a general sense. This led to the study of new kinds of rough sets and their applications by many researchers [5–7]. Neighborhood systems and rough sets have recently been used to represent structures, such as self-similar fractals [8] and the human heart [9], with potential applications in physics and medicine, respectively. One of the most important achievements in rough set theory is knowledge reduction in information systems, by which a membership function is used to reduce the data. Pawlak et al. [10] expanded the membership function into an initial rough membership function, while El Atik et al. [11] used this similarity as a membership function. Allam et al. [12] and Salama [13] presented new approaches for basic rough set concepts. In [14], Yao et al. address the problem of overlapping classes in rough sets and introduce object class membership, and in [15] Yu et al. introduce approximations to measure accuracy. Polkowski et al. introduced some of important mechanisms for rough sets in [16,17].

Differential equations and diffusion equations may both be used to simulate many real-world issues in the fields of science and engineering [18]. Recently, four novel mutant SARS-COV-2 strains that are thought to be 70% more lethal than the currently circulating COVID-19 virus were found in several locations [19]. By using a mathematical model, it is crucial to understand the SARS-CoV-2 dynamics in the context of immune surveillance [20]. In the COVID-19 outbreak investigation, asymptomatic transmission of the coronavirus illness and the prediction of infected individuals have become crucial [21]. For biomathematicians and medical professionals, controlling these acute illnesses has been a major priority in recent years [22].

The main aim of the present paper is to study rough set theory from another angle, that is, from the viewpoint of mathematical morphology. Mathematical morphology provides a range of techniques for image processing and analysis based on basic algebraic and geometric principles. Matheron [23] and Serra [24] first introduced the concepts of mathematical morphology, in application to petrography and mineralogy where they studied the physical properties of certain types of rocks. Mathematical morphology has since been explored in some detail (see, e.g., [25–30]) and has been applied in engineering and medicine [31–34]. A new method for scene classification from the remote sensing images is investigated in [35], but diagnosis and testing of COVID-19 chest are investigated in [36,37].

Here we propose new forms of rough morphological structures: rough dilation, rough erosion, rough closing, and rough opening. These forms are defined for application in topological and digital image processing and applied specifically for the delineation of lung occlusion from a chest x-ray of a patient with acute COVID-19 pneumonia.

This article is organized as follows; Section 2 for morphological definitions of roughness and Section 3 introduces the basic properties of rough dilation and rough erosion. Section 4 presents the application of rough morphological structures for differential analysis of chest x-ray images. Finally, Section 5 presents the conclusion and future work.

Throughout this paper Z2 denotes a discrete topological space, where Z is the set of positive integers and M,B⊆Z2. Also, U is a nonempty finite universe set, R is an equivalence relation on U and W⊆U.

Definition 1. [30] Mathematical morphology allows the extraction and analysis of discrete quantal image structures. There are two essential components: the image as a set of objects and a structure element (SE). Each object is represented by binary digits, e.g., (0=black,1=white). Objects are also represented by a coordinate (x,y) in Z2. The SE in Z2 is a small set to define the image under study. For each structure element, we define the original shape and size based on the geometric properties of the objects. Examples of SEs are shown in Fig. 1.

Figure 1: Some examples of structure elements

Definition 2. [30] For any two images, E1 and E2 in the d-dimensional product Ed of E, Minkowski addition (subtraction) is defined by

E1⊕E2={e1+e2:e1∈E1ande2∈E2};

E1⊖E2={h:e2+h∈E1∀e2∈E2}.

Note that ⊕ is commutative and ⊖ is not. Any fixed set A in Ed is said to be a structural element.

Definition 3. [30] The dilation of image called X by structure element called A is given by δA(X)=X⊕A and the erosion of X by A is εA(X)=X⊖A.

Definition 4. [1] Let (U,R) be a Pawlak’s approximation space. A lower approximation, upper approximation, and boundary region of X by R is defined by

LR(X)=∪x∈U{R(x):R(x)⊆X},

UR(X)=∪x∈U{R(x):R(x)∩X≠Φ},

BR(X)=UR(X)−LR(X).

where R(x) is the equivalence class for x according to relation R.

2  Morphological Definitions of Roughness

Dilation and erosion are basic concepts in mathematical morphology and image processing, where any image set X can be dilated (eroded) by a structure element B. Here, we consider rough set theory by scanning Z2 through a structure element with the image set, affording new definitions of rough dilation, rough erosion, rough closing, and rough opening. Below and red pixels are denoted by scan cells, and yellow pixels are denoted by the neighborhoods of red pixels.

Definition 5. A rough dilation (RD) and rough erosion (RE) are defined by

RD(X;B)={x∈Z2:B∩X≠Φ}, and

RE(X;B)={x∈Z2:B⊂X}, forX,B⊂Z2.

It is clear that X⊆RD(X;B) and RE(X;B)⊆X.

Example 1. Move and scan B1 in Z2 (see Fig. 2b) through its red pixel. By applying Definition 5, we have a rough dilation set as in Fig. 2c.

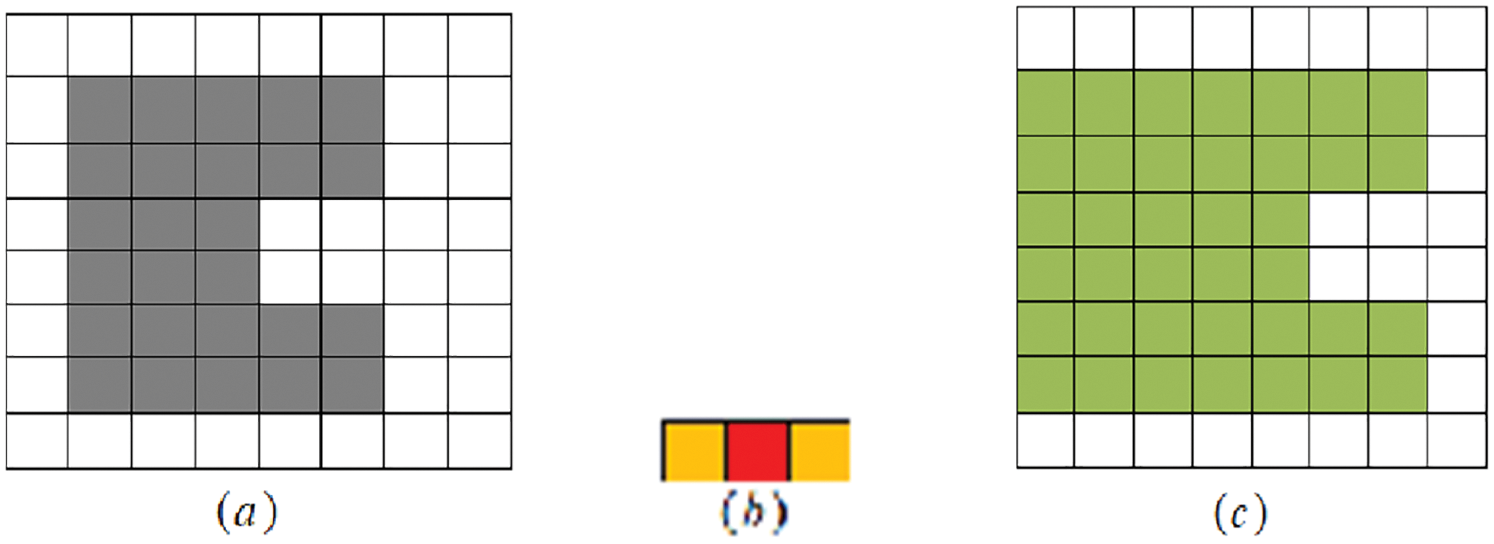
Figure 2: (a) Original image X1, (b) The SE B1, and (c) the result of processing

Example 2. Move and scan B2 in Z2 (see Fig. 3b) through its red pixel. By applying Definition 5, we have a rough erosion set in Fig. 3c.

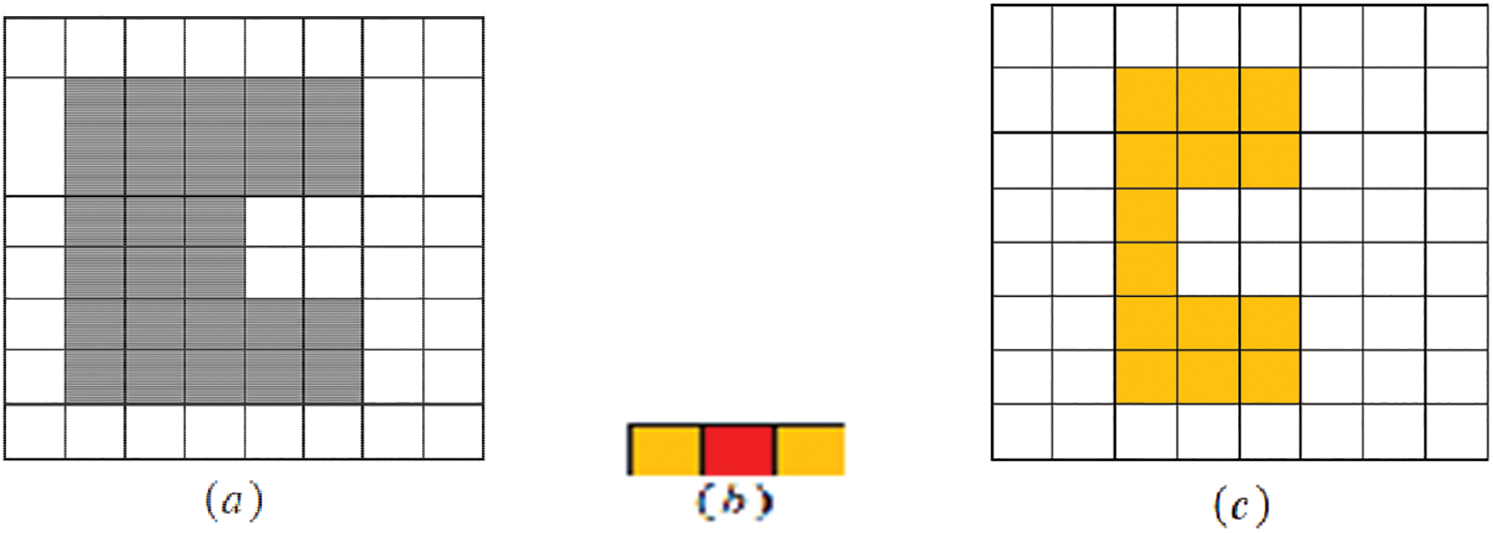
Figure 3: (a) Original image X2, (b) The SE B2, and (c) the result of processing

Definition 6. Let X and B be subsets of a discrete space Z2. The rough closing (RC) and rough opening (RO) of X by B are given by

RC(X;B)=RE(RD(X;B);B)=∪{p∈Z2:B⊆(RD(X;B))}, and

RO(X;B)=RD(RE(X;B);B)=∪{p∈Z2:B∩(RE(X;B))≠Φ}.

Example 3. Move and scan B1 in Z2 (see Fig. 4b) through its red pixel. By applying Definition 6, we have a rough closing set in Fig. 4d.

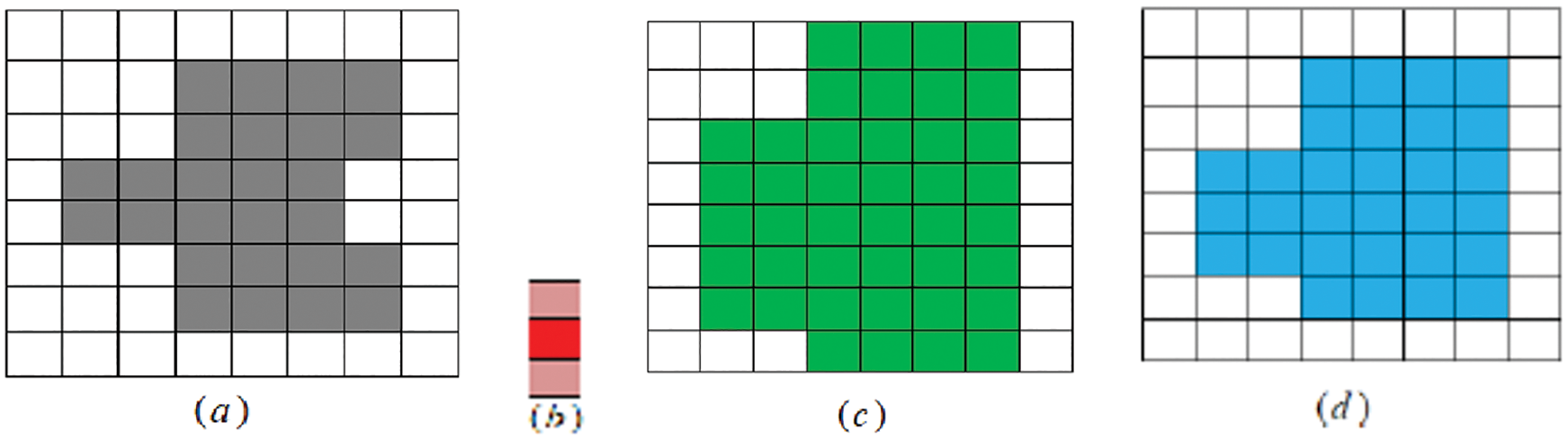
Figure 4: (a) Original image X1, (b) B1 is SE, (c) RD(X1; B1) and (d) RC(X1; B1)

Example 4. Move and scan B2 in Z2 (see Fig. 5b) through its red pixel, by applying Definition 6, we have a rough opening set in Fig. 5d.

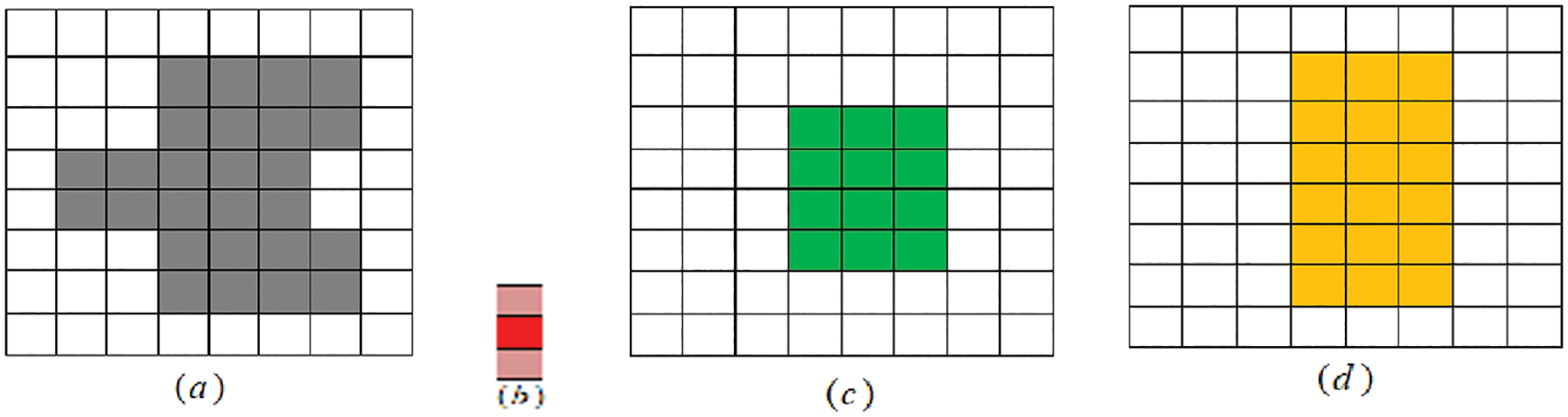
Figure 5: (a) Original image X2, (b) The SE B2, (c) RE(X2; B2) and (d) RO(X2; B2)

3  Basic Properties of Rough Dilation and Rough Erosion

In this section, we consider some topological properties based on rough dilations and rough erosions. In a topological space Z2, the closure Cl of X (ClRD(X;B)) is the smallest rough dilation of X by B containing X. The interior Int of X (IntRD(X;B)) is the largest rough erosion of X by B contains X. Cl and Int denote the closure and interior, respectively, with respect to a topological space (Z2,τ). In Lemma 1 below, it is easier to prove the relationship between RD(X;B), RD(Y;B), RE(X;B) and RE(Y;B), and so the proof is omitted.

Lemma 1. Let X and Y be image sets in Z2 such that X⊆Y, and let B be a structure element. Then, the following hold:

RD(X;B)⊆RD(Y;B).

RE(X;B)⊆RE(Y;B).

Proposition 1. Let X be an image set and B1,B2 be structure elements such that B1⊆B2. Then, RD(X;B1)⊆RD(X;B2).

Proof. Let x∈RD(X;B1). Then, x∈Z2:B1∩X≠Φ, while B1⊆B2. Therefore, B2∩X≠Φ, and so x∈RD(X;B2). Hence, RD(X;B1)⊆RD(X;B2).

Proposition 2. Let X⊆Z2 and B1,B2 be structure elements. Then, the following hold:

X⊆RD(X;B1).

RD(X;B1)⊆RD(RD(X;B1)).

RD(X;B1∪B2)=RD(X;B1)∪RD(X;B2).

RD(X;B1∩B2)⊆RD(X;B1)∩RD(X;B2).

Proof. From Proposition 1, it is easy to prove (i) and (ii).

Let x∈(X;B1∪B2)⇒x∈Z2:X∩(B1∪B2)≠Φ⇒((X∩B1)∪(X∩B2))≠Φ⇒X∩B1≠Φ or X∩B2≠Φ⇒x∈((RD(X;B1)∪RD(X;B2)). Then, RD(X;B1∪B2)⊆(RD(X;B1)∪RD(X;B2)). Conversely, let x∈(RD(X;B1)∪RD(X;B2)). Then, x∈(RD(X;B1) or x∈(RD(X;B1)⇒(X∩B1)≠Φ∪(X∩B1)≠Φ⇒(X∩(B1∪B2))≠Φ⇒x∈RD(X;B1∪B2). So, (RD(X;B1)∪RD(X;B2))⊆RD(X;B1∪B2). Therefore, RD(X;B1∪B2)=RD(X;B1)∪RD(X;B2).

Let x∈RD(X;B1∩B2)⇒x∈Z2:X∩(B1∩B2)≠Φ⇒(X∩B1)≠Φ and (X∩B2)≠Φ⇒x∈RD(X;B1) and x∈RD(X;B2). Therefore, RD(X;B1∩B2)⊆RD(X;B1)∩RD(X;B2).

Proposition 3. Let X be an image set and B1,B2 be structures such that B1⊆B2. Then, RE(X;B2)⊆RE(X;B1).

Proof. Let x∈RE(X;B2). Then, x∈Z2:B2⊆X, while B1⊆B2⇒B1⊆X⇒x∈RE(X;B1). Therefore, RE(X;B2)⊆RE(X;B1).

Proposition 4. Let X⊆Z2 and B1,B2 be structure elements. Then, the following statements hold:

RE(X;B1)⊆X.

RE(RE(X;B1))⊆RE(X;B1).

RE(X;B1)∪RE(X;B2)⊆RE(X;B1∪B2).

Proof. From Proposition 3, it is easy to prove (i) and (ii).

Let x∈(RE(X;B1)∪RE(X;B2). Then, x∈RE(X;B1)) or x∈RE(X;B2)⇒x∈Z2:B1⊆X or B2⊆X⇒x∈Z2:(B1∪B2)⊆X⇒x∈RE(X;B1∪B2). Therefore, RE(X;B1)∪RE(X;B2)⊆RE(X;B1∪B2).

Remark 1. One can easily note that RE(X;B1)∩RE(X;B2)⊆RE(X;B1∩B2), while RE(X;B1∩B2)⊈RE(X;B1)∩RE(X;B2). This can be illustrated as in Example 5.

Example 5. Move and scan B1 in Z2 through its red pixel (see Fig. 6b). Then, we have RE(X;B1) in Fig. 6c. In the same manner, by using Fig. 6d, we obtain RE(X;B2) in Fig. 6e. Similarly, move and scan B1∩B2 through its red pixel (see Fig. 6f), we get RE(X;B1∩B2) in Fig. 6g. By the moving and scanning of RE(X;B1) in Figs. 6c and 6e RE(X;B2), we obtain RE(X;B1∩RE(X;B2)) in Fig. 6h.

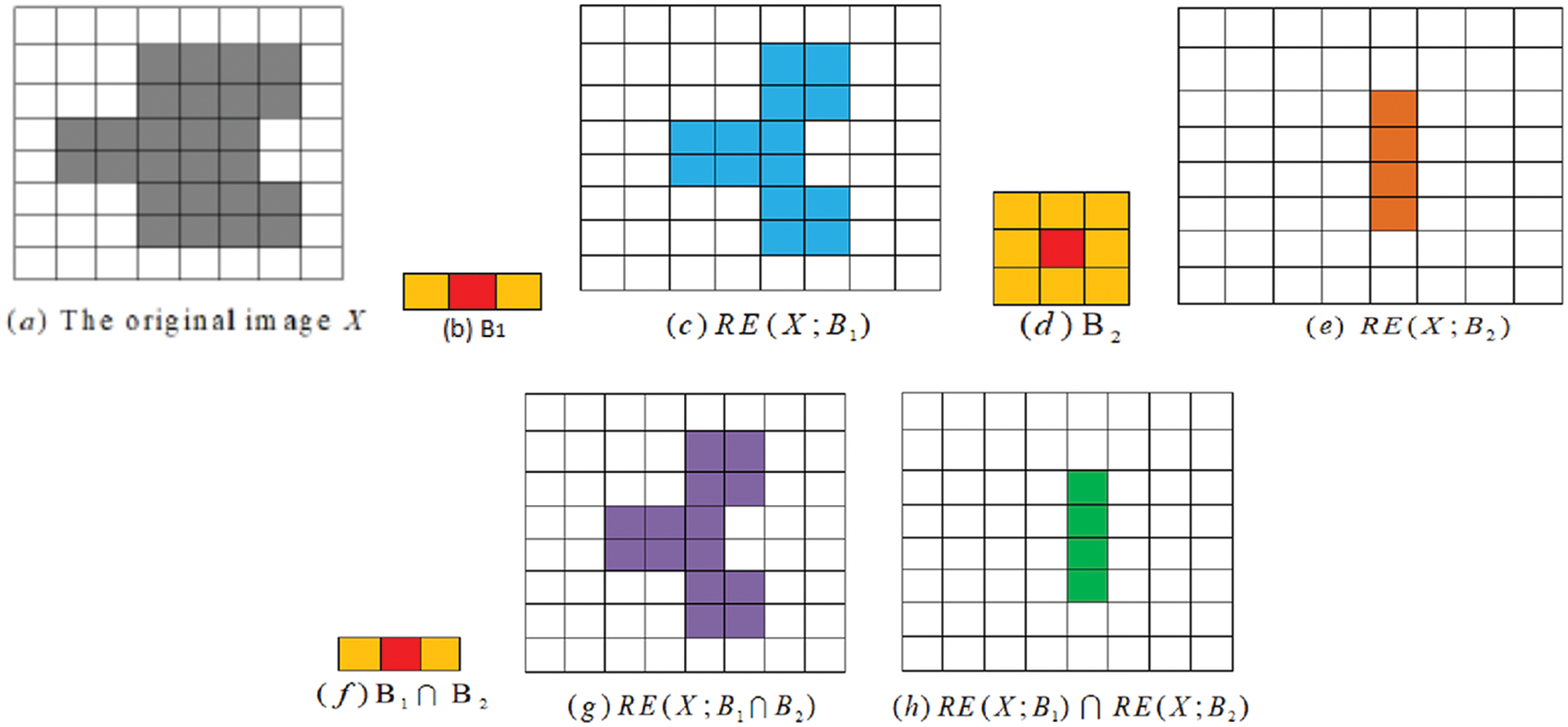
Figure 6: (a) The original image, (b) Structure element B1, (c) RE(X; B1), (d) Structure element B2, (e) RE(X; B2), (f) Structure element (B1 ∩ B2), (g) RE(X; B1 ∩ B2) and (h) RE(X; B1) ∩ RE(X; B2)

Proposition 5. The following properties hold ∀X1,X2∈Z2:

IfX=X1∪X2, thenRD(X;B)=RD(X1;B)∪RD(X2;B).

IfX=X1∩X2,RD(X;B)=RD(X1;B)∩RD(X2;B).

Proof. It is sufficient to prove only (i), as (ii) holds by similarity. As x∈RD(X;B), then x∈Z2:X∩B≠Φ, while X=X1∪X2. Hence, (X1∩B)≠Φ or (X2∩B)≠Φ⇔x∈(RD(X1;B)∪RD(X2;B)). So, RD(X;B)=RD(X1;B)∪RD(X2;B). On the other hand, with x∈RD(X;B)⇔x∈Z2:X∩B≠Φ, and X=X1∩X2, we obtain (X1∩B)≠Φ and (X2∩B)≠Φ⇔x∈(RD(X1;B)∩RD(X2;B)). Therefore, RD(X;B)=RD(X1;B)∩RD(X2;B).

Corollary 1. The following properties are held, ∀X1,X2,…,Xn∈Z2

If X=X1∪X2∪⋯∪Xn, then RD(X;B)=RD(X1;B)∪RD(X2;B)∪⋯∪RD(Xn;B).

If X=X1∩X2∩X3∩⋯∩Xn, then RD(X;B)=RD(X1;B)∩RD(X2;B)∩RD(X3;B)∩⋯∩RD(Xn;B).

Proposition 6. The following properties hold ∀X1,X2∈Z2:

If X=X1∪X2, then RE(X;B)=RE(X1;B)∪RE(X2;B).

If X=X1∩X2, then RE(X;B)=RE(X1;B)∩RE(X2;B).

Proof. As x∈RE(X;B), then x∈Z2:B⊆X, while X=X1∪X2. So, B⊆X1 or B⊆X2⇔x∈(RE(X1;B)∪RE(X2;B)). Then, RE(X;B)=RE(X1;B)∪RE(X2;B). Similarly, as x∈RE(X;B), then x∈Z2:B⊆X. But X=X1∩X2. Hence, B⊆X1 and B⊆X2⇔x∈(RE(X1;B)∩RE(X2;B)). Therefore, RE(X;B)=RE(X1;B)∩RE(X2;B).

Corollary 2. The following properties hold ∀X1,X2,…,Xn∈Z2:

If X=X1∪X2∪X3∪⋯∪Xn, then RE(X;B)=RE(X1;B)∪RE(X2;B)∪RE(X3;B)∪⋯∪RE(Xn;B).

If X=X1∩X2∩X3∩⋯∩Xn, then RE(X;B)=RE(X1;B)∩RE(X2;B)∩RE(X3;B)∩⋯∩RE(Xn;B).

Proposition 7. Let X and Y be image sets. The following hold:

RE(X)⊆X⊆RD(X).

RE(Φ)=RD(Φ)=Φ.

RD(X∪Y)=RD(X)∪RD(Y).

RE(X∩Y)=RE(X)∩RE(Y).

RE(X∪Y)⊃RE(X)∩RE(Y).

X⊆Y⇒RD(X)⊆RD(Y).

X⊆Y⇒RE(X)⊆RE(Y).

Proof. By Propositions 1 and 3, proofs of (i) and (ii) are obvious.

Since X⊆(X∪Y)⇒RD(X)⊆RD(X∪Y) and Y⊆(X∪Y), then RD(Y)⊆RD(X∪Y), and so RD(X)∪RD(Y)⊆RD(X∪Y). On the other hand, let x∈RD(X∪Y). Then, by rough dilation, x∈Z2:B∩(X∪Y)≠Φ and so (B∩X)∪(B∩Y)≠Φ. Hence, (B∩X)≠Φ or (B∩Y)≠Φ and so x∈RD(X)∪RD(Y). Then, RD(X∪Y)⊆RD(X)∪RD(Y). Therefore, RD(X∪Y)=RD(X)∪RD(Y).

Since X∩Y⊆X, then RE(X∩Y)⊆RE(X) and X∩Y⊆Y, and so RE(X∩Y)⊆RE(Y). Hence, RE(X∩Y)⊆RE(X)∩RE(Y). Conversely, let x∈RE(X)∩RE(Y). By rough erosion, x∈Z2:B⊆X∩Y and so x∈RE(X) and x∈RE(Y),x∈Z2:B⊆X and x∈Z2:B⊆Y⇒x∈Z2:B⊆X∩Y→x∈RE(X∩Y), giving RE(X)∩RE(Y)⊆RE(X∩Y). Thus, RE(X∩Y)=RE(X)∩RE(Y).

Since X⊂X∪Y, then RE(X)⊂RE(X∪Y) and Y⊂X∪Y⇒RE(Y)⊂RE(X∪Y), giving RE(X∪Y)⊃RE(X)∩RE(Y).

Let x∈RD(X). Then, B∩X≠Φ. Since X⊆Y⇒B∩X≠Φ, then x∈RD(Y), and so RD(X)⊆RD(Y).

Let x∈RE(X). Then, B⊆X. Since X⊆Y, then B⊆Y, and so x∈RE(Y). Therefore, RE(X)⊆RE(Y).

Remark 2 shows that the equalities do not hold in general. This can be seen from Examples: example 6, example 7 and example 8.

Remark 2. Let X and Y be image sets in Z2. Then

(i)   RE(Z2)≠RD(Z2)≠Z2.

(ii)   RD(X∪Y)⊈RD(X)∩RD(Y).

(iii)   RE(Xc)≠(RD(X))c.

(iv)   RD(Xc)≠(RE(X))c.

(v)   RE(RE(X))≠RD(RE(X))≠RE(X).

(vi)   RD(RD(X))≠RE(RD(X))≠RD(X).

Example 6. Let B in Fig. 7b move and scan in Z2 through its red pixel. From Remark 2 (ii), we have Fig. 7c. Also, from Fig. 7d we have RD(X∪Y)⊈RD(X)∩RD(Y).

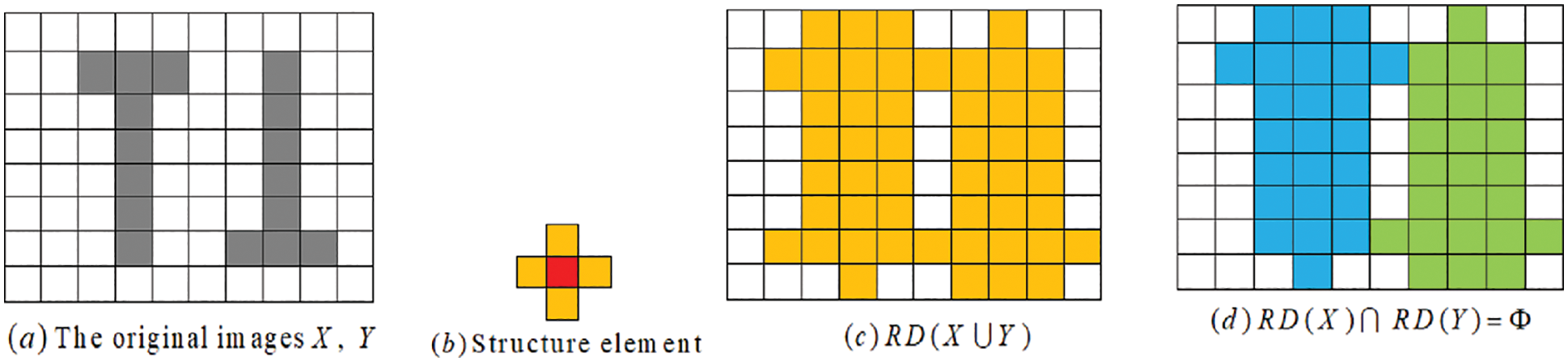
Figure 7: (a) The original images X and Y, (b) Structure element, (c) RD(X ∪ Y), and (d) RD(X) ∩ RD(Y)

Example 7. Let B in Fig. 8b move and scan in Z2 through its red pixel. From Remark 2 (iii) and (iv), we have Fig. 8d. Also, from Fig. 8f we have RE(Xc)≠(RD(X))c.

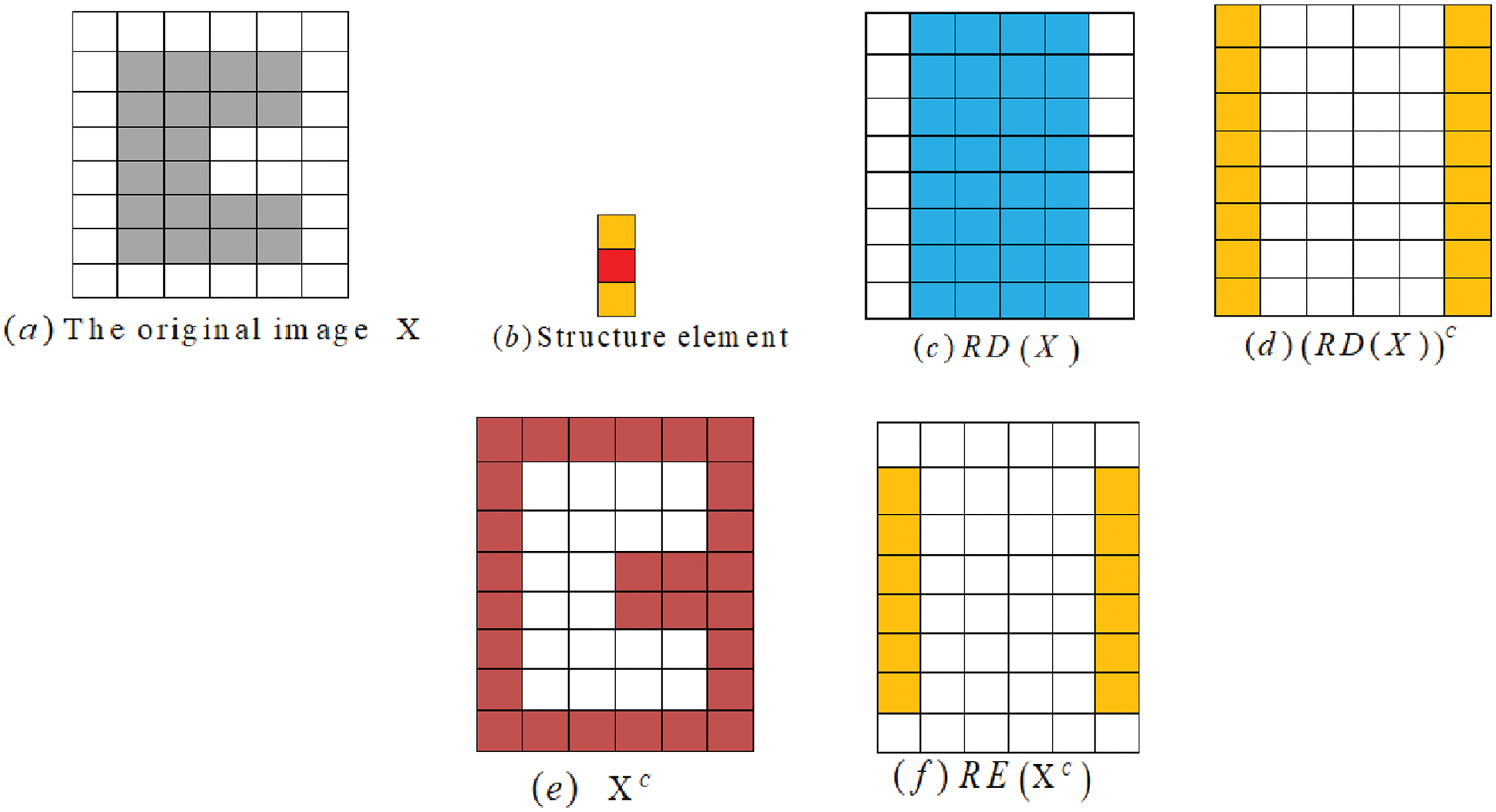
Figure 8: (a) The original image X, (b) Structure element, (c) RD(X), (d) (RD(X))C, (e) Xc, and (f) RE(XC)

The property (iv) in Remark 2 can also be seen to be satisfied in Example 8.

Example 8. Let B in Fig. 9b be a move and scan in Z2 through its red pixel. By Remark 2 (v) and (vi), we have Figs. 9c–9e. Hence, RE(RE(X))≠RD(RE(X))≠RE(X).

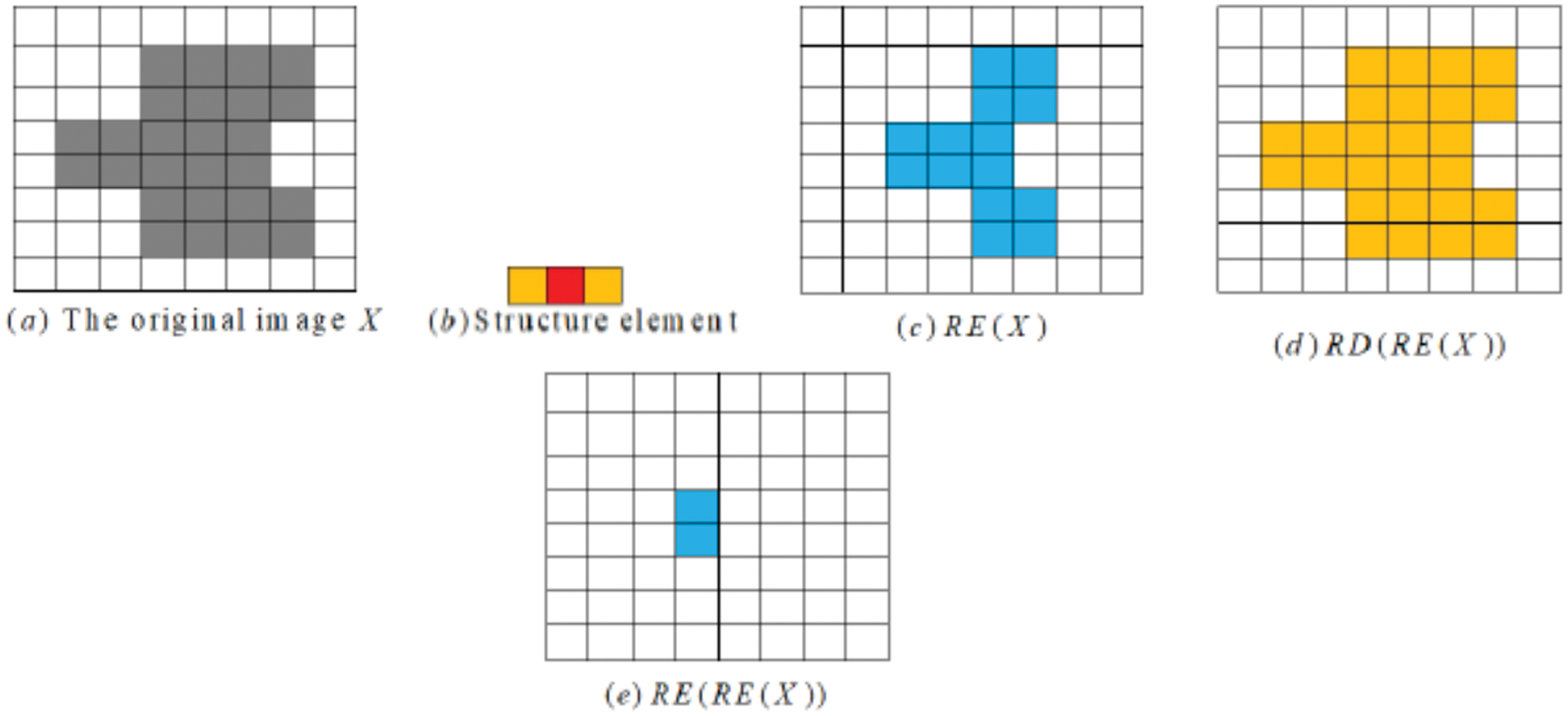
Figure 9: (a) The original image X, (b) Structure element, (c) RE(X), (d) RD(RE(X)), and (e) RE(RE(x))

Proposition 8. Let X and Y be images in Z2. Then, RE(X)∪RE(Y)⊆RE(X∪Y).

Proof. Since X⊆(X∪Y), then RE(X)⊆RE(X∪Y) and Y⊆(X∪Y). Hence, RE(Y)⊆RE(X∪Y) and so RE(X)∪RE(Y)⊆RE(X∪Y).

Proposition 9. Let X and Y be images in Z2. Then, RD(X∩Y)⊆RD(X)∪RD(Y).

Proof. Since (X∩Y)⊆X, then RD(X∩Y)⊆RD(X) and (X∩Y)⊆Y. Hence, RD(X∩Y)⊆RD(Y) and so RD(X∩Y)⊆RD(X)∪RD(Y).

4  Application of Rough Morphological Structures for Differential Analysis of Chest X-ray Images

One of the symptoms of severe SARS-CoV-2 coronavirus diseases [38] is the development of pneumonia and acute respiratory distress syndrome (ARDS) [39]. Admitted patients suspected of such severe COVID-19 disease typically undergo a radiological examination of the lungs for ARDS. While computed tomography offers the most sensitive and accurate imaging of lung condition [40,41], chest X-rays are often the front-line approach employed by many hospitals and can be performed using portable equipment [42], which can reduce patient movements and thereby lower the risk of infection [43–45]. The importance of chest X-ray imaging for the diagnosis of ARDS in COVID-19 pneumonia prompted us to examine whether rough morphological structures could be used to aid differential diagnostics.

Figs. 10 and 11 show two typical chest X-ray images, one from a health subject and another from a COVID-19 patient with ARDS.

Figure 10: A chest X-ray of a COVID-19 patient with ARDS and the corresponding binary image in Z2

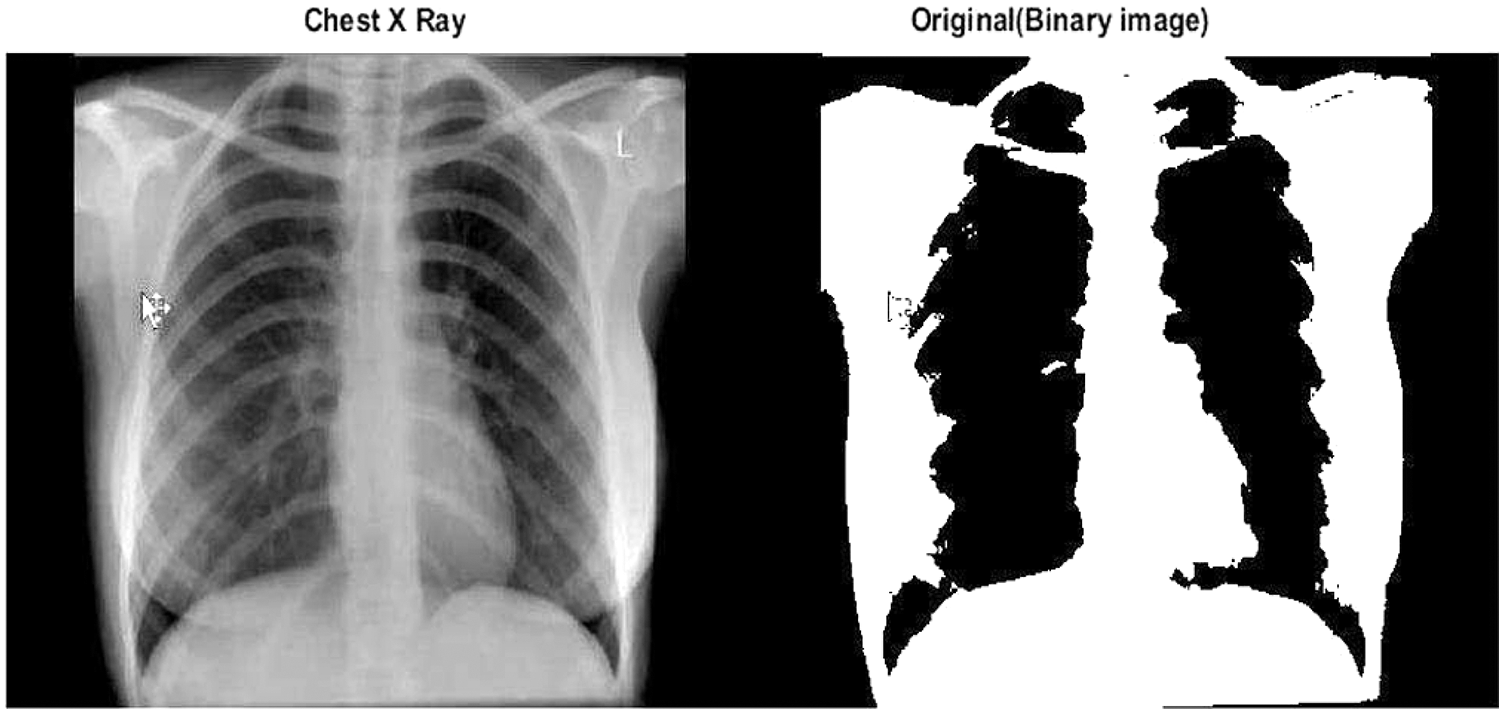
Figure 11: A chest X-ray of a healthy subject and corresponding binary image in Z2

Now we consider the rough boundary (rough opening and rough closing) using the original-rough opening and rough closing–original transforms, as shown in Figs. 12 and 13.

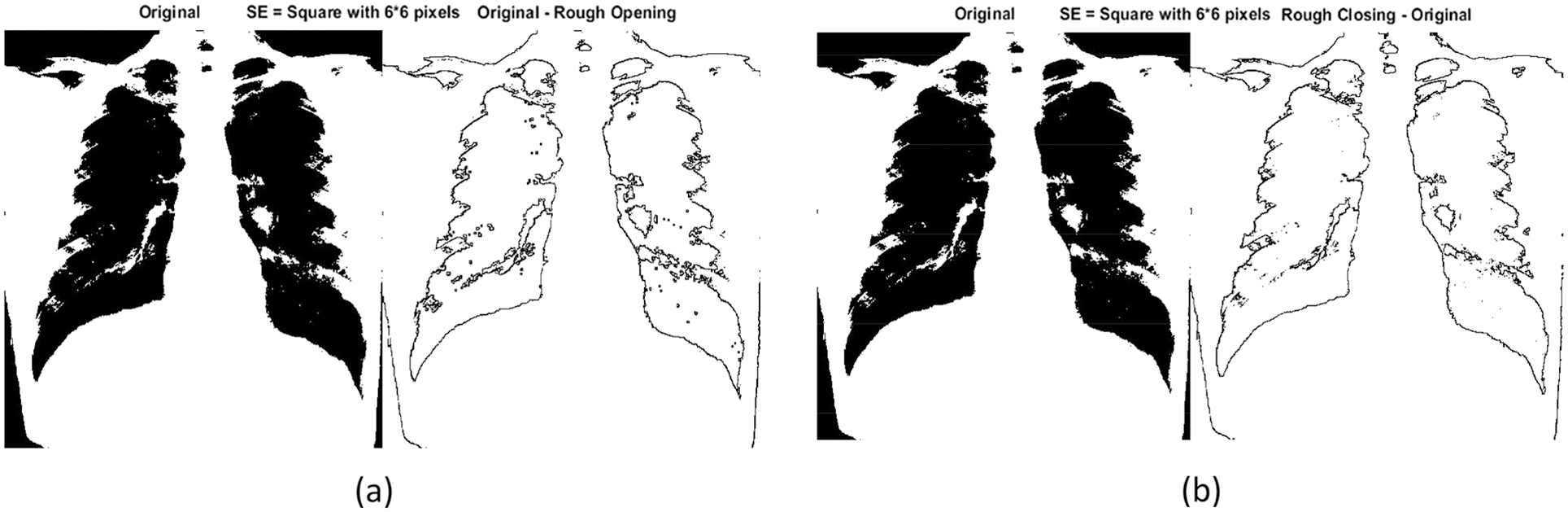
Figure 12: (a) Original-rough opening transform for the chest X-ray of a COVID-19 patient in Z2 (b) Rough closing-original transform for chest X-ray of a COVID-19 patient in Z2

Figure 13: (a) Original-rough opening transform for the chest X-ray of a healthy subject in Z2 (b) Rough closing-original transform for chest X-ray of a healthy subject in Z2

An algorithm for differential analysis of these two images is provided below: algorithm 1. Here, RD and RE are operators. The input image is the binary image of the chest X-ray (image 1; IM1) with size p(xmax,ymax), and we use square 3∗3 pixels as structural elements (B). The algorithm stores the result in image 2 (IM2) for rough dilation and image 3 (IM3) for rough erosion.

The main steps for finding the rough opening (RO) and rough closing (RC) of the chest X-ray images are shown in the following flowchart at Fig. 14.

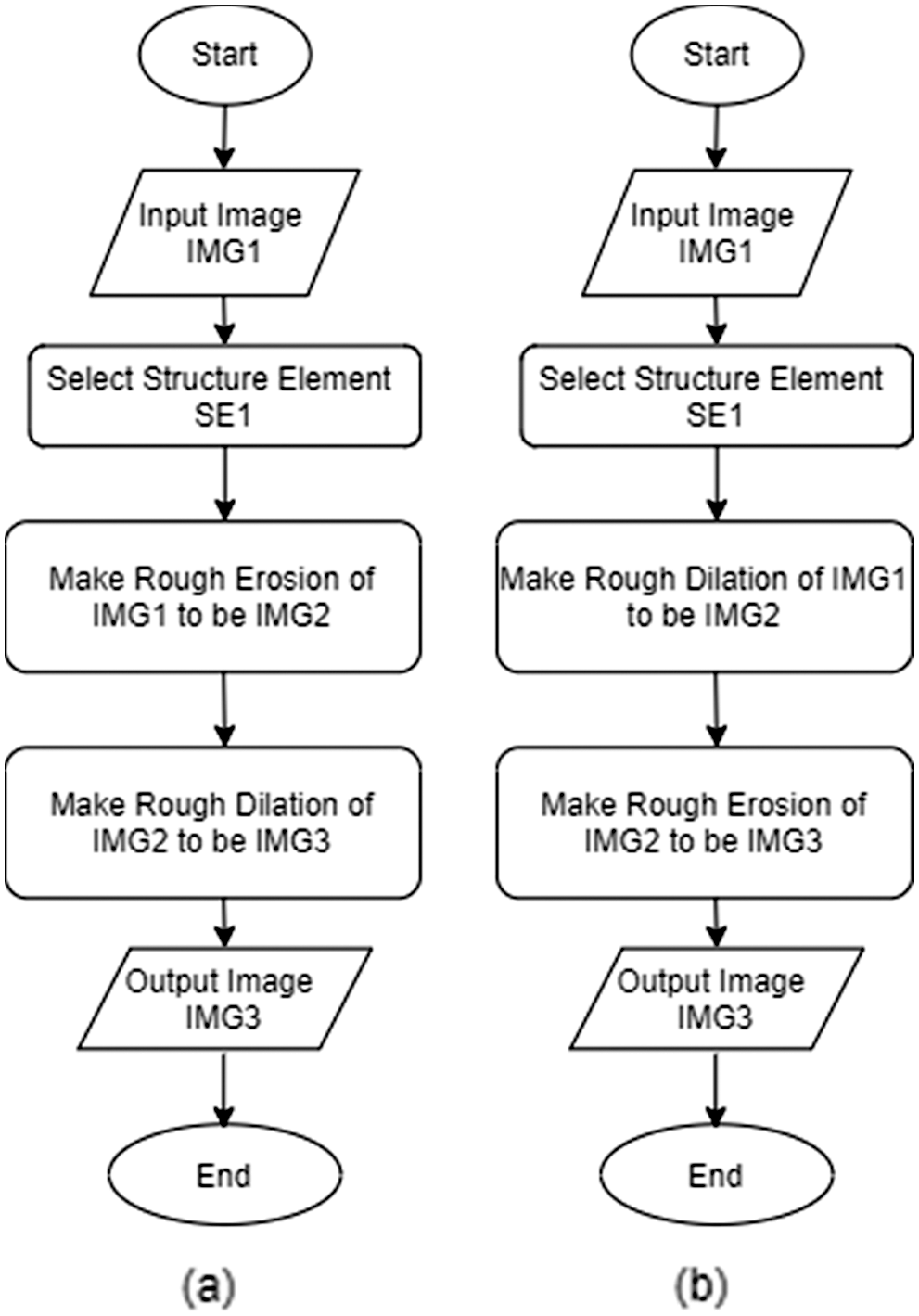
Figure 14: Flowchart of (a) rough opening and (b) rough closing on chest X-ray images

5  Conclusion and Future Work

Although mathematical morphology and rough set theory are two different fields in terms of their initial domains and implementations, there are relations between the two systems as shown in this article. Specifically, we have shown that the lower and upper approximations of rough set theory are similar to opening/erosion and closing/dilation in mathematical morphology. This principle can be used to find similarity among images with a lower approximation. The topology of the partition can be defined in images as part of the universe set using four features defined using color and image indices. Subspace topologies can also be used to model each image type. We proposed an algorithm using these rough morphological operations that could be used to delineate lung occlusion (ARDS) in COVID-19 patients from chest X-ray images. In future work, we will add the detection accuracy measured.

Authors’ Contributions: All authors read and approved the final manuscript.

Availability of Data and Materials: The datasets used and analyzed during the current study are public and available from the corresponding author on request.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interests to report regarding the present study.

References

 1.  Z. Pawlak, “Rough sets,” International Journal of Information and Computer Sciences, vol. 11, pp. 341–356, 1982. [Google Scholar]

 2.  Z. Pawlak, “Rough sets: Theoretical aspects of reasoning about data,” Springer Science & Business Media, vol. 9, 2012. [Google Scholar]

 3.  E. F. Lashin, A. M. Kozae, A. A. Abo Khadra and T. Medhat, “Rough set theory for topological spaces,” International Journal of Approximate Reasoning, vol. 40, no. 1–2, pp. 35–43, 2005. [Google Scholar]

 4.  A. S. Salama and O. G. El-Barbary, “Topological approach to retrieve missing values in incomplete information systems,” Journal of the Egyptian Mathematical Society, vol. 25, no. 4, pp. 419–423, 2017. [Google Scholar]

 5.  A. Ahmad, U. Qamar and M. S. Raza, “An optimized method to calculate approximations in dominance based rough set approach,” Applied Soft Computing, vol. 97, pp. 1–13, 2020. [Google Scholar]

 6.  Z. Huang and J. Li, “Multi-scale covering rough sets with applications to data classification,” Applied Soft Computing, vol. 110, pp. 107736, 2021. [Google Scholar]

 7.  P. Zhou, P. Li, S. Zhao and Y. Zhang, “Online early terminated streaming feature selection based on rough set theory,” Applied Soft Computing, vol. 113, pp. 1–12, 2021. [Google Scholar]

 8.  A. El Atik and A. Nasef, “Some topological structures of fractals and their related graphs,” Filomat, vol. 34, no. 1, pp. 153–165, 2020. [Google Scholar]

 9.  A. El Atik, “Reduction based on similarity and decision-making,” Journal of the Egyptian Mathematical Society, vol. 28, no. 1, pp. 1–12, 2020. [Google Scholar]

10. Z. Pawlak and A. Skowron, “Rough membership functions,” in Advances in the Dempster-Shafer Theory of Evidence, vol. 22, New York: John Wiley & Sons, pp. 251–271, 1994. [Google Scholar]

11. A. El Atik and H. Hassan, “Some nano topological structures via ideals and graphs,” Journal of the Egyptian Mathematical Society, vol. 28, no. 1, paper no. 41, pp. 1–21, 2020. [Google Scholar]

12. A. A. Allam, M. Y. Bakeir and E. A. Abo-Tabl, “New approach for basic rough set concepts,” in Proc. Int. Workshop on Rough Sets, Fuzzy Sets, Data Mining, and Granular-Soft Computing, Regina, Canada: Springer, pp. 64–73, 2005. [Google Scholar]

13. A. S. Salama, “Some topological properties of rough sets with tools for data mining,” International Journal of Computer Science Issues (IJCSI), vol. 8, no. 3, pp. 588–595, 2011. [Google Scholar]

14. Y. Y. Yao and J. P. Zhang, “Interpreting fuzzy membership functions in the theory of rough sets,” in Proc. Int. Conf. on Rough Sets and Current Trends in Computing, RSCTC 2000 Banff, Canada: Springer, pp. 82–89, 2000. [Google Scholar]

15. Z. Yu and D. Wang, “Accuracy of approximation operators during covering evolutions,” International Journal of Approximate Reasoning, vol. 117, pp. 1–14, 2020. [Google Scholar]

16. L. Polkowski and A. Skowron. “Rough mereology: A new paradigm for approximate reasoning,” International Journal of Approximate Reasoning, vol. 15, no. 4, pp. 333–365, 1996. [Google Scholar]

17. A. Skowron and L. Polkowski, “Rough mereological foundations for design, analysis, synthesis, and control in distributed systems,” Information Sciences, vol. 104, no. 1, pp. 129–156, 1998. [Google Scholar]

18. V. F. Morales-Delgado, J. F. Gómez-Aguilar, K. M. Saad, M. A. Khan and P. Agarwal, “Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: A fractional calculus approach,” Physica A, vol. 523, pp. 48–65, 2019. [Google Scholar]

19. A. u. Rehman, R. Singh and P. Agarwal, “Modeling, analysis and prediction of new variants of COVID-19 and dengue co-infection on complex network,” Chaos, Solitons & Fractals, vol. 150, pp. 111008, 2021. [Google Scholar]

20. S. M. E. K. Chowdhury, J. T. Chowdhury, S. F. Ahmed, P. Agarwal, I. A. Badruddin et al., “Mathematical modelling of COVID-19 disease dynamics: Interaction between immune system and SARS-CoV-2 within host,” AIMS Mathematics, vol. 7, no. 2, pp. 2618–2633, 2022. [Google Scholar]

21. S. M. E. K. Chowdhury, M. Forkan, S. F. Ahmed, P. Agarwal, A. B. M. Shawkat Ali et al., “Modeling the SARS-CoV-2 parallel transmission dynamics: Asymptomatic and symptomatic pathways,” Computers in Biology and Medicine, vol. 143, pp. 105264, 2022. [Google Scholar]

22. P. Agarwal, J. J. Nieto, M. Ruzhansky and D. F. M. Torres, “Analysis of infectious disease problems (COVID-19) and their global impact,” in Infosys Science Foundation Series, Singapore: Springer, 2021. [Google Scholar]

23. G. Matheron, Random Sets and Integral Geometry. New York: John Wiley and Sons, 1975. [Google Scholar]

24. J. Serra, Image Analysis and Mathematical Morphology, vol. 11. London: Academic Press, 1988. [Google Scholar]

25. E. Dougherty, Mathematical Morphology in Image Processing. Boca Raton, Florida, USA: CRC Press, 2018. [Google Scholar]

26. C. R. Giardina and E. R. Dougherty, Image Processing-Continuous to Discrete. New York: Prentice Hall, 1987. [Google Scholar]

27. C. R. Giardina and E. R. Dougherty, Morphological Methods in Image and Signal Processing. New Jersey, USA: Prentice-Hall, 1988. [Google Scholar]

28. S. R. Haralick, R. M. Sternberg and X. Zhuang, “Image analysis using mathematical morphology,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 4, pp. 532–550, 1987. [Google Scholar]

29. H. J. A. M. Heijmans, Morphological Image Operators. Boston: Academic Press, 1994. [Google Scholar]

30. H. J. A. M. Heijmans, “Mathematical morphology: Basic principles,” in Proc. of Summer School on Morphological Image and Signal Processing, Citeseer, 1995. [Google Scholar]

31. L. Guang, L. Xiaoqiong, T. Jingtian, L. Jin, R. Zhengyong et al., “De-noising low-frequency magnetotelluric data using mathematical morphology_ltering and sparse representation,” Journal of Applied Geophysics, vol. 172, pp. 103919, 2020. [Google Scholar]

32. B. Jess, O. Peter, V. Luca and M. Martijn, “Mathematical morphology directly applied to point cloud data,” ISPRS Journal of Photogrammetry and Remote Sensing, vol. 168, pp. 208–220, 2020. [Google Scholar]

33. R. Safdar, R. Tauheed, S. Mazhar and J. Shahzad, “Performance analysis of power system parameters for islanding detection using mathematical morphology,” Ain Shams Engineering Journal, vol. 2, no. 1, pp. 517–527, 2021. [Google Scholar]

34. T. Zhaonian, J. Weixing, G. Jianhua, Z. Yueyan, B. Akrem et al., “Mmsparse: 2d partitioning of sparse matrix based on mathematical morphology,” Future Generation Computer Systems, vol. 108, pp. 521–532, 2020. [Google Scholar]

35. P. Kollapudi, S. Alghamdi, N. Veeraiah, Y. Alotaibi, S. Thotakura et al., “A new method for scene classification from the remote sensing images,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1339–1355, 2022. [Google Scholar]

36. A. Mohammadi, Y. Wang, N. Enshaei, P. Afshar, F. Naderkhani et al., “Diagnosis/prognosis of COVID-19 chest images via machine learning and hypersignal processing: Challenges, opportunities, and applications,” IEEE Signal Processing Magazine, vol. 38, no. 5, pp. 37–66, 2021. [Google Scholar]

37. Y. Alotaibi and A. F. Subahi, “New goal-oriented requirements extraction framework for e-health services: A case study of diagnostic testing during the COVID-19 outbreak,” Business Process Management Journal, vol. 28, no. 1, pp. 273–292, 2022. [Google Scholar]

38. N. Chen, M. Zhou, X. Dong, J. Qu, F. Gong et al., “Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study,” Lancet, vol. 395, pp. 507–513, 2020. [Google Scholar]

39. A. Giovagnoni, “Facing the COVID-19 emergency: We can and we do,” Radiol. Med., vol. 125, no. 4, pp. 337–338, 2020. [Google Scholar]

40. C. Wang, P. W. Horby, F. G. Hayden and G. F. Gao, “A novel coronavirus outbreak of global health concern,” The Lancet, vol. 395, pp. 470–473, 2020. [Google Scholar]

41. W. Yang, A. Sirajuddin, X. Zhang, G. Liu, Z. Teng et al., “The role of imaging in 2019 novel coronavirus pneumonia (COVID-19),” European Radiology, vol. 30, no. 9, pp. 4874–4882, 2020. [Google Scholar]

42. K. F. Haque and A. Abdelgawad, “A deep learning approach to detect COVID-19 patients from chest X-ray images,” AI, vol. 1, no. 3, pp. 418–435, 2020. [Google Scholar]

43. M. K. El-Bably and A. A. El Atik, “Soft-rough sets and their application to determine COVID-19,” Turkish Journal of Mathematics, vol. 45, pp. 1133–1148, 2021. [Google Scholar]

44. S. Zhou, Y. Wang, T. Zhu and L. Xia, “Ct features of coronavirus disease 2019 (COVID-19) pneumonia in 62 patients in Wuhan, China,” American Journal of Roentgenology, vol. 214, no. 6, pp. 1287–1294, 2020. [Google Scholar]

45. N. Zhu, D. Zhang, W. Wang, X. Li, B. Yang et al., “A novel coronavirus from patients with pneumonia in China, 2019,” New England Journal of Medicine, vol. 382, no. 8, pp. 727–733, 2020. [Google Scholar]