Prediction of Uncertainty Estimation and Confidence Calibration Using Fully Convolutional Neural Network

1  Introduction

The clinical image division is important for a wide variety of applications, including anatomical modelling, cancer progress monitoring, surgical planning, and treatment evaluation [1]. Considering the depth and breadth of recent studies, it is very difficult to achieve reliable and accurate division findings for many purposes. This is often due to low image resolution, pathologically-induced random appearance, differing imaging techniques, and significant variation in segregation targets between individuals. Consequently, evaluating the uncertainty of section findings is important to determine how accurate the sections are [2]. For example, the segmentation outcomes of pixels that close the border may be uncertain due to the awkward difference between the segment target and the adjacent tissues in the larger images. The segmentation ambiguity data can be utilized to specify improperly segmented areas or guide users to interact for refinement [3].

Many medical image processing and image-guided treatment modalities depend on the clinical image category. Compared to expert manual separation, computerized automated partition systems have the power to improve section speed and reproducibility. Algorithms including regional development, atlas-based techniques, and status-packages are examples of traditional computer-assisted detection approaches. Deep learning methods the CNN have now proven to be beneficial tools for this mission. Several research studies have demonstrated that convolutional neural network based algorithms override traditional models in a variety of clinical imaging tasks, often with significant differences. As a result of the success of CNN-based models, many components of their design and training have been explored in the past few years. Most of this research focuses on network configuration and loss function. However, features such as more complex network designs have been shown to improve the performance of conventional CNN-based clinical imaging algorithms [4].

Fully convolutional neural networks (FCNNs) generally position themselves as the successful criteria for segmentation, and especially for clinical imaging. Among them, convolutional networks for biomedical image segmentation (U-Net) were used to distinguish between both conventional organs and lesions, and topped the international rankings. Predictability, uncertainty, and confidence are described as the ability of a decision-making system to accurately classify failures or failures to provide a successful opportunity to test events at predictable times. Predictions, the class probabilities of a well-measured system, should be equal to the possibility of victory of those assumptions in the lengthy run using the usual definition of ambiguity. For example, if a well-measured brain tumor dissection system effectively detects 80 pixels out of 120 pixels as carcinogenic with a probability of 0.8, the study can expect 80 pixels to be properly labelled as cancer. The weakly verified model with comparable sorting possibilities, on the other hand, is predicted to deliver a higher number of correctly classified pixels. Many current neural networks (NNs) are trained using powerful optimization techniques that are vulnerable to erroneous measurements. In misclassification, incorrectly adjusted NNs are often overconfident. Excessive confidence can be problematic in some situations, such as medical image processing or auto-driving [5].

The dice loss function is a general measure of comparing the probability outcome of segmentation with training data, setting members with labelling probabilities and adding a softening factor to the class to differentiate the error function. Dice Loss selects the modelling variable set to reduce the negatives of the waiting dice of diverse topologies. Dice losses resist class inequality and are used effectively in a variety of applications. In addition, volume normalization (BN) ensures significant integration and improves network performance for realistic image classification techniques. Some other notable characteristics of uncertainty estimates are the efficacy of a predictive model, the training phase, and the distribution of training data that is identical to test events outside of distribution. As deep networks become more interested in domain shift, the efficiency of non-localized input detection systems is important to the biomedical field, which is a common occurrence in diagnostic images. Networks trained in a magnetic resonance imaging (MRI) protocol, for example, fail to perform well on images collected with a little modification to the parameters or out-of-distribution testing. As a result, in a non-distribution model, a better display realizes and declares that it “does not know” and, if possible, seeks human help instead of silent failure [6].

The uncertainty assessment has been extensively reviewed for a wide range of existing medical image division assignments. Used form and appearance to exemplify the uncertainty of the probability segment of clinical imaging [7]. It was used to calculate the ambiguity of the graph cut-based heart image segment and was utilized to increase the flexibility of the system. To assess uncertainty in the lumen segment for specific patients’ blood flow simulation. For simultaneous brain tumor segmentation and recording, the researchers used sectarian uncertainties to guide the content-driven adaptive model. The work demonstrates the uncertainty of guided volume segmentation of brain magnetic resonance imaging (MRI) and abdomen magnetic resonance imaging (CT) images using random walker-based segmentation. To minimise user time for the 3D image segment interaction, the researchers combined vague ratings with active learning [8].

In contrast to earlier studies that have focused solely on regression or classification based ambiguity predictions and current studies that examine ambiguity based on experimental time intervals, this study elaborates on the various types of uncertainties for convolutional neural network based clinical image segmentation. In addition, the study provides a general assessment of not only the distortion of the image but also the ambiguity associated with the spatial distortions of the input, taking into account the many probable poses of the unit when capturing the image. To achieve the ambiguity associated with the change, the study improves the input image during the test time and evaluates the distributions of the rating based on increasing the testing time. Test time enrichment has been used to improve image classification performance [9]. The benefit of assessing ambiguity in the heart, brain, and prostate image classification challenge. However, past attempts have not provided a quantitative or theoretical framework for this. Inspired by these findings, the researchers put forward a mathematical framework for improving test time and evaluating its effectiveness in general uncertainty estimates in clinical imaging methods.

The important contribution of the research work is illustrated as follows.

•   To explore the selection of the error function for the semantic category in FCNs, the Dice Loss and Cross-Entropy Loss are compared on the semantic segmentation training set.

•   To propose a methodology for confidence calibration of FCNs trained with dice loss and batch normalization

•   To compare the group with the Monte Carlo dropout (MC-dropout), the study empirically measures the consequence of the number of samples on the measurement and section quality.

•   To predict the segment superiority of ambient structures, it can be utilized to identify test entries out-of-distribution, using the average entropy across the expected separated item.

•   The study measures the uncertainty and certainty of three independent segmentation tasks, such as MRI images of the brain, heart, and prostate.

•   Predicts and analyses ambiguity estimates for semantic segments using the FCNs in this paper and recommends the panel for reliable calibration and accurate predictive ambiguity prediction of individual structures.

The rest of the remaining research work is illustrated as below. Section 2 explains the prior research work on uncertainty prediction. The third section discusses the problem statement for predicting uncertainty. Section 4 describes the suggested full convolutional neural network that examines the segmentation losses. Section 5 presents test findings as well as a discussion of the suggested system. The performance of the intended work is examined in Section 6. For the performance test, we use several dataset, such as PROSTATEx, PROMISE12, MICCAI 2017 BraTS, and MICCAI 2017 ACDC. Lastly, Section 7 concludes the findings and the work that has to be done in the future.

2  Related Works

The modified learning system provided sample training on data from different domains and tasks before performing the desired task. Transmission knowledge has been shown to enhance the productivity of convolutional neural network based systems across a wide range of clinical image systems. The fact that there are only 2D images in the largest public image database and most medical images are in 3D is a barrier to learning change. Multitasking training is an alternative to transfer learning. Different from transfer learning that deals with source and target functions step by step, multi-task learning seeks to learn multiple tasks at the same time. It is predicted based on the assumption that the functions at hand are identical, and learning them simultaneously will help to learn the most effective properties and lead to improved generalization. Some research has found that multi-task learning can be used successfully in dividing clinical images [10]. Furthermore, previous research has not looked at the impact of multi-task training on the predictive measurement of the training model. The normally used deep learning approaches have been shown to be inappropriately organized. This should be of concern to applications that require high doses of protection, such as medicine. Various strategies have been provided to enhance deep learning approach validation. For example, it has been demonstrated that measurement can be improved by using the correct scoring method as an error function, by using weighted distortion, and by eliminating volume normalization. Training on hostile events has been conducted to develop the model calibration. Platt scaling was used in several studies to improve sample verification.

Non-Bayesian techniques have been developed for probability measurement and uncertainty estimates. The study discovered the issue of reliability calibration in deep neural networks. They conducted studies to examine the effects of many properties, such as width, depth, weight dissipation, and BN in measurement. Heat measurement was also used to instantly check the training samples. Ensemble has been shown to be a helpful approach to enhance deep NN classification performance across a wide range of domains, especially in the clinical picture segment. Deep group methods, on the other hand, require re-training a model from scratch, that is, computation is costly for big databases and sophisticated models [11]. The weight loss function is the one that allows training single-shot measurement values. Their approach, combined with probability depth and dropout, will increase the confidence of measurement and the accuracy of classification [12]. Other Bayesian studies have provided a way to improve ambiguity in the inattention mechanism. They improved performance in both modelling verification and observation model by training for uncertainty-conscious attention with different assumptions [13].

Evaluating medical images is a difficult endeavor that is sometimes made more difficult by artifacts, stains, low variability, and other factors. Most importantly, there is considerable inter-assessment changeability in the identification and categorization of abnormalities in chest radiography. This is often due to ambiguous data or subjective assessments of disease manifestations. Classifying anatomical perspectives based on 2D ultrasound images is another case in point. In many cases, the anatomical background depicted in a frame is not enough to identify the underlying anatomy. Current machine learning approaches to these problems often provide only probability estimates, depending on the fundamental models capable of reacting to small amounts of labelled data and large amounts of labelled noise. However, in reality, this results in more reliable methods with poor generalization of unknown data. For the compensation, the study provides a system that not only trains the probability classification assessment, but also provides an explicitly ambiguous measure that expresses the system’s confidence in the expected output. This method is needed to calculate the inherent uncertainty of clinical images obtained from various radiological tests such as computed ultrasonography, radiography, and magnetic resonance imaging. In these tests, discarded specimens based on estimated uncertainties could significantly improve the receiver operating characteristic (ROC) curve and the area under the curve (AUC), i.e., a classification of abnormalities on chest radiographs with a failure rate of 7% to less than 0.82% to 25%. Furthermore, the study demonstrates that the use of uncertainty-driven bootstrapping to filter data for training can lead to major gains in regression and performance. The greatest drawback of this method is that the probability of error is high [14].

Uncertain measurements in clinical imaging technology, such as in-depth learning, are anticipated to improve clinical acceptance and integration with human knowledge. Consequently, the study proposes a full-fledged CNN for brain tumor segregation and explores the Monte Carlo dropout (MC-dropout) rule for ambiguity by concentrating on dropout status and rates. The resulting brain tumor is presented to the survival estimation method based on age and 26 image-derived geometric parameters such as volume, surface, volume ratios, surface irregularities, and increasing tumor margin width figures. The results reveal that the MC dropout modeling and a normal weight-measuring dropout model performed identically in terms of approval ratios. A quality review also reveals that activating the MC dropout after each convolution layer may provide information ambiguity. The results indicate that, from age, only certain factors should be used to predict survival. In the BraTS17 challenge, this strategy took second place in the survival test and third place in the division tasks, which puts us in the cluster with the third best performance of the statistically different methods [15].

Automated clinical image analysis is often used to diagnose a variety of disorders in a timely manner. Computer Assisted Diagnosis (CAD) technologies allow for efficient identification and treatment of diseases. Intensive learning (DL) based CAD systems can already produce promising outcomes in most health systems. Furthermore, the uncertainty assessment in current DL approaches has received little attention in the field of clinical research. To solve this problem, Sheet Binary Introduces Binary Residual Feature fusion (BARF), an innovative, simple and efficient fusion approach with uncertainty-aware components for clinical image classification. To handle ambiguity, the researchers used the Monte Carlo (MC) drop method during hypotheses to obtain mean and constant deviations from the estimates. The proposed model uses two basic techniques: direct verification and cross-verification using four unique clinical imaging datasets. The results of these experiments show that the recommended approach to clinical picture classification is useful in real-world medical situations. This method is not suitable because the compatibility of BARF is low [16].

The study proposes a vague domain alignment framework for the domain shift problem to be solved in the cross-domain unsupervised domain adoption process. To obtain the ambiguity graph prediction, the study generates an uncertainty estimate and a segmentation module. Subsequently, a unique uncertainty-conscious cross-entropy loss was developed to improve segmentation effectiveness in greatly uncertain areas. To further enhance the effectiveness of the unsupervised domain adaptation (UDA) mission, an uncertain-knowledge self-training technique is designed to select the best target models based on ambiguous advice. Furthermore, the ambiguity feature restoration module is used to implement the framework to reduce cross-domain disagreement. The recommended configuration was tested in 2017 using a private cross-device optical coherence tomography database and a general cross-model cardiac database available from Multi-Modality Whole Heart Segmentation (MMWHS). Extensive research demonstrates that the recommended UESM is productive and convenient for assessing uncertainties. The UDA mission achieves excellent-in-class performance in both cross-modality and cross-device datasets [17].

Uncertainty ratings are a potential way to develop the strength of automated segmentation techniques. Although many uncertain assessment approaches have been suggested, tiny is known about their applicability and restrictions for brain tumor segmentation. The study examines the most widely used approaches to assessing uncertainty based on the benefits and barriers to brain tumor dissection. They were rated based on their quality measurement, section error localization, and section error detection. The study findings suggest that uncertainty approaches are often well-measured when analyzed at the database level. Significant miscalculations and restricted segment error localization (e.g., segment correction) were detected in the study, which precludes the straight use of voxel-wise uncertainty. Nonetheless, voxel-wise ambiguity was useful in identifying failed segments when uncertainty estimates were collected at the material level. Consequently, the study recommends the careful use of voxel-wise uncertainty measurements and emphasizes the need to develop solutions that meet object-level criteria for measuring and separating error localization [18].

The most difficult challenges in clinical image processing include the identification, classification, and segmentation of effective automated medical imaging. Deep learning approaches have recently had exceptional success in clinical image segmentation and classification, which have firmly established themselves as sophisticated methods. Many of these approaches, though, are still unable to offer uncertainties quantifying (UQ) for their output, and are frequently overly confident, which can have devastating effects. Bayesian Deep Learning (BDL) approaches can be used to measure the uncertainty of classic deep learning algorithms, so this solves the problem. To overcoming the uncertainty of skin cancer image classification, the study uses three ambiguity measurement approaches that are Deep Ensemble, Monte Carlo dropout, and Ensemble MC Dropout. To address the residual uncertainties after using these approaches, the study provide a unique hybrid dynamic BDL model that takes uncertainties into account and it is based on the three-way Judgment model. The suggested modelling approach allows applying various UQ approaches and deep neural networks in various categorization stages. As a result, parts of each step can be modified based on the database under review. In this work, two excellent UQ techniques are used in two well-known skin cancer databases in two classification stages, which eliminate overconfidence in diagnosing diseases. The efficiency and F1-score of the finalized strategy were 89 percent and 90.00 percent for the first database, and 91 percent and 92 percent for the latter database. These findings indicate that the recommended three-way decision-based Bayesian deep learning (TWDBDL) classical can be utilized effectively at various levels of clinical image investigation [19].

Colon polyps have been identified as precursors of colon cancer, making it one of the leading causes of cancer-related mortality worldwide. Manual examinations of the patient’s intestines are used primarily for the early detection and prevention of colon cancer. For the individual providing the test, such a technique may be difficult and demanding. As an outcome, various studies have been conducted on the development of automated devices to assist physicians during testing. Recent advances in in-depth study of object image recognition have resulted in significant advances in such automated tools as a result of advances in in-depth learning research for generally available colonic imaging and object image processing. Support networks based on CNNs have demonstrated sophisticated effectiveness in both the identification and separation of colon polyps. However, in order to be efficient in the clinical context, CNN-based models must be accurate. Furthermore, the predictions and ambiguities in the forecasts need to be fully understood [20]. To improve and assess current developments in uncertainty estimates and sample understanding in the context of semantic polyp separation from images of colonoscopy. In addition, this study provides a unique approach to calculating uncertainties related to the main characteristics of the input and shows how generalizability and ambiguity may be modelled in the decision support system (DSS) for the semantic division of colonic polyps. According to the findings, deep samples use polyphony and marginal data to make predictions. Moreover, poor forecasts have greater ambiguity than accurate estimates [21].

3  Problem Statement

Dice loss and volume normalization have a negative impact on measurement performance. FCNNs learned with volume normalization and dice loss create unmeasured probabilities, resulting in poor vague ratings. Cross-entropy losses, on the other hand, provide highly adjusted predictions and uncertain estimates because it is a rigorously accurate scoring system. However, in cases where there are such severe class differences, along with FCNNs, it can be challengeable.

4  Materials and Methods

Each section task, pre-processing processes, and database characteristics are described in the following subsections. Fig. 1 represents the uncertainty prediction flow diagram of the brain, heart, and prostate by using FCNN.

Figure 1: Uncertainty prediction from brain, heart and prostate by using FCNN

4.1 Segmentation Task

4.1.1 Heart Ventricular Tumor Segmentation

Information from the Medical Image Computing and Computer Assisted Intervention (MICCAI) 2017 in the Automated Cardiac Diagnosis Challenge (ACDC) task for automatic cardiovascular detection was utilized for heart ventricular separation. This is the four class segmentation challenge in which patients’ MRI images need to be separated into the right ventricle, left ventricle, backdrop and myocardium. This dataset comprises images of 120 patients’ end-systole (ES) and end-diastole (ED). In this investigation, the study solely used ED pictures [22].

4.1.2 Prostate Segmentation

PROSTATEx and PROMISE12 are the public databases that are used for the prostate segment. Print T2 weight images of a doubted patient having prostate cancer should be separated from the background and prostate gland. 40 photos with captions were used in the PROSTATEx database [23]. These photos were all taken in one place. The PROSTATEx database was utilized for both testing and training, while the PROMISE12 database was used only for testing. The PROMISE12 database is a multidisciplinary database that is derived using multiple MR scanners and acquisition systems. The study used 60 training images for segmentation test [24].

4.1.3 Brain Tumor Segmentation

Data from the MICCAI 2017 BraTS competition were used to classify brain tumors. This segmentation is a four-class division challenge in which multiframetric MRI images of brain tumor patients are classified as edema, enhanced tumor, non-enhanced tumor, and background. The training database included 200 multiparametric MRI sequences from brain tumor patients (differential-enhanced T1-weight, T1-weight, T2-weight and FLAIR sequences). The dataset is also separated into TCIA and CBICA. The images in the CBICA collection were obtained at the University of Pennsylvania’s Centre for Biomedical Image Computing and Analytics (CBICA). The images in the TCIA collection were obtained from various organizations and are housed in the Cancer Imaging Archive (TCIA) of the National Cancer Institute. The CBICA subcommittee was used for training and verification, while the TCIA subcommittee was stored for testing [25].

4.2 Data Pre-Processing

The resolution of the brain images was redesigned to 2 × 1×1 mm. Prostate and heart images were resized to 1 × 1 mm and 2 × 2 mm in-plane resolution, respectively. FCNN’s input size 224 × 224 pixels all print fragments are arranged in the center to create images. The intensity of the image is normalized between [0, 1].

4.3 Metrics

The semantic division could be expressed as a pixel-level categorization issue that can be manipulated by CNNs. The FCNNs are used for segmentation of the image and enables end-to-end learning by mapping every pixel of the input image with the output segmentation map. Patch-based neural networks are significantly slower in presumption time than FCNs because they use sliding window methods to predict every pixel. Also, loss functions at section-level such as dice loss are easy to implement in FCNN systems. FCNNs for segments typically have an encoder and a decoder path. The skip-links with FCNNs can unify high-level compression properties with low-level greater resolution features, resulting in effective segmentation tasks. The mixture of the cross-entropy (CE) and an inverse dice similarity coefficient (DSC), known as dice loss is used to find the loss functions of trained FCNs. Class weights are utilized to aid optimization integration and to solve the problem of class inequality. The parameter for CE loss was selected to increase the mean recording probability of the training data. The system specified for dice loss is intended to reduce the negative impact of dice on the weight of various structures. The parameter for CE loss was selected to increase the mean record probability of the training data, which is given in Eq. (1).

Cross entropy loss=−1M∑i=1MXi.log⁡X˙i+(1−X˙i). log⁡(1−Xi˙)(1)

where, Xi is the truth value and X˙i is the probability of softmax of ith class. The selected parameter for dice loss is intended to minimize the negativity of the dice by the weight of the different structures which is shown in Eq. (2).

Dice loss=1−12∑K=122∑iMXkYk∑iMXk+∑iMYk(2)

where Xk is the probability of prediction value Yk is the ground truth value.

4.4 Calibration Metrics

An FCN calculates class estimation and class probabilities for each input pixel. Class probability is a measurement for predicting ambiguity at the pixel level and can be considered as the possibility of modeling confidence or accuracy. Strict scoring procedures are utilized to test the measurement effectiveness of prediction models. Generally, the scoring systems evaluate sample uncertainty ratings by providing well-measured probability predictions. Both Negative Record Possibilities (NLL) and Fryer Score are strictly accurate score methods that have already been utilized in much researches to assess forecast uncertainties. In a segmentation issue, negative loglikelihood loss (NLL) is determined for a set of N pixels as given in Eq. (3).

Negative loglikelihood loss=−∑i=1MXi logXθ,i +(1−Xi   )log⁡(1−Xθ,i )(3)

Expected Calibration Error is obtained by adding the weight mean of the imbalances among accuracy and mean confidence which is shown in Eq. (3).

Expected Calibration error=∑i−1MXmN(Acc(Xm)−(Xm))(4)

4.5 Segment-level Predictive Uncertainty Estimation

In addition to the pixel-level confidence measurement, modelling at the segment level is desirable for segment applications that represent uncertainty. Such a statistic would be invaluable in medical decision-making. In the absence of basic truth, the study estimates that the quality of the section-level reliable measurement section for a well-measured system can be predicted. This measure can be used to identify samples that are out of distribution and difficult or confusing situations. For street view separation, such measures have already been provided.

Multi-task learning was introduced as a promising strategy for teaching FCNN-based clinical image models in research. The study suggests that instead of creating a model to separate an organ in an imaging system, a model should be trained to separate multiple elements in multiple imaging techniques. The results reveal that a typical FCNN can understand the environment and effectively separate individual elements into different imaging modes without additional inputs. According to the findings, a model trained on a wide variety of databases would be useful if not more effective than models dedicated to specific databases. Furthermore, the trained model produces better measured estimates on a variety of data. The article proposes a unique approach to identifying data outside the distribution at the time of testing based on spectral analysis of FCNN feature maps. The study demonstrates that a suggested technique can detect the undistributed data rather than a technique based on predictive ambiguity. Fig. 2 shows the representation of the full convolutional neural network function.

Figure 2: Full convolutional neural network segmentation model

5  Experiments

5.1 Dice vs. Cross-Entropy

CE loss tends to reduce the mean negative recording possibilities across pixels, whereas dice loss directly improves the division level and the quality of the dice coefficient. As outcome of the study, one expects that models trained with cross entropy will have lower NLL, while models skilled with dice loss will have higher Dice coefficients. The primary objectives of this study were to evaluate the segmentation quality of a sample trained with CE based on the calibration performance of the sample trained with dice loss and dice loss. In three section assignments, the study compares the trainees with cross entropy with those qualified with Dice.

5.2 MC Dropout

As in the Bayesian SegNet, the MC drop was accomplished by changing the base network. Dropout layers with a 0.5 dropout probability were inserted into three internal encoder and decoder layers. The Monte Carlo model was made with 60 samples at an approximate time and was used as the average final estimate of the samples.

5.3 Trusted Measurement

Coupling was used in the study to evaluate the volume normalized FCNs trained with dice loss. The study developed group estimates for three-section problems and compared them with basic methods based on measurement and segmented performance. The study compared the quality of measuring NLL and the expected calibration error (ECE) percentages of the 96th Hausdorff distance for comparable dice and split performance. Furthermore, the whole experimental data collection was second only to the pixels in the expanded border boxes surrounding the anterior areas, which created measures for measuring the quality rating on the two-sample model from the hold-out test datasets. The front areas and the surrounding background are often blurry and rough. At the same time, background pixels that are farther away from the front show less blur, but more so than the front pixels. The use of border boxes eliminates most background predictions from the images, resulting in a better highlighting of differences across models.

5.4 Uncertainty Prediction from Segmentation

This study evaluates the volume-level confidence for every category of challenge and the front labels for each. Examined the differences in the prostate segment between the Prostatex test package and the Promise-12 package. Finally, the study used bootstrapping (n = 97) to generate statistical testing and 95 percent confidence intervals (CI) in all experiments. P-values of less than 0.01 were considered. The bold text specifies the greatest outcomes for every case, and the changes in all the tables given are statistically significant.

6  Result and Discussion

Table 1 illustrates how many patients’ images are in each database and how the study divides them into training, verification, and test sets. Each section task, data characteristics, and pre-processing are significant for the study. Fig. 3 represent the accuracy prediction of training and testing datasets.

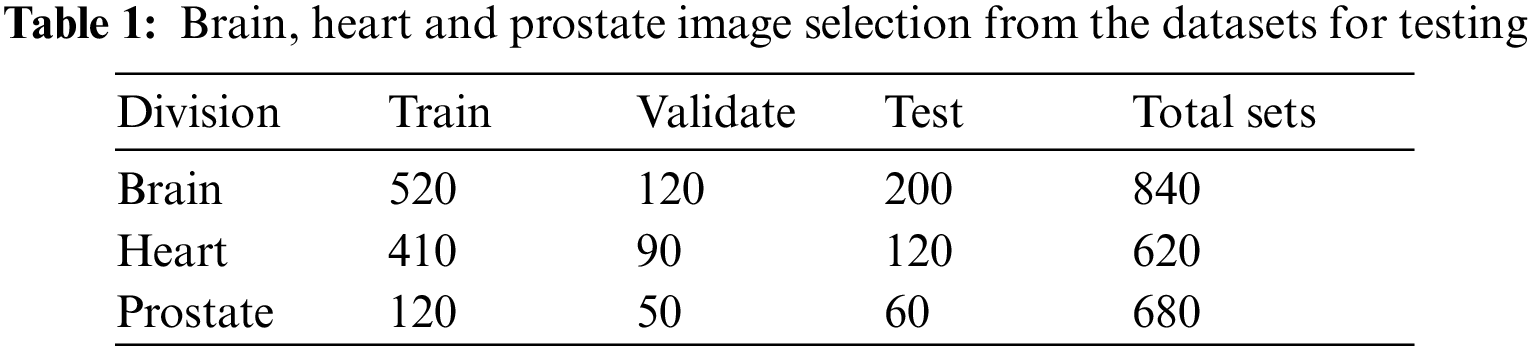
Figure 3: Training and validation accuracy of the collected datasets

Each of the training and verification curve maps represents the accuracy and loss of the entire convolutional neural network (FCNN) that was trained 10 epochs ago. Training starts at 91 percent in era 10 and stands at 99 percent, whereas verification starts at 92 percent and stabilizes at 98 percent in era 10. Start-up losses are 90% and verification is 97%. Both settled in Era 10 with 30% marks for verification and 40% marks for training.

Table 2 compares the measurement efficiency and segment accuracy of baselines and groups (N = 60) trained with CE loss to baselines and groups qualified with Dice loss and verified using MC Dropout. Average NLL, Brier score, ECE percentage, and 96% CI values are reported for boundary boxes around the section. Table 2 compares the averages of the anterior segment dice coefficients and the 96% confidence intervals for the basic methods trained with dice loss, cross-entropy loss, and baselines. Tables 1 and 2 of auxiliary measure calibration of whole block and segment performance results based on Hausdorff distances. In respect to segmentation performance, basic training with dice loss was better than training with CE loss for all tasks in all segments, while the ensemble of models qualified with dice loss performed better than all existing models.

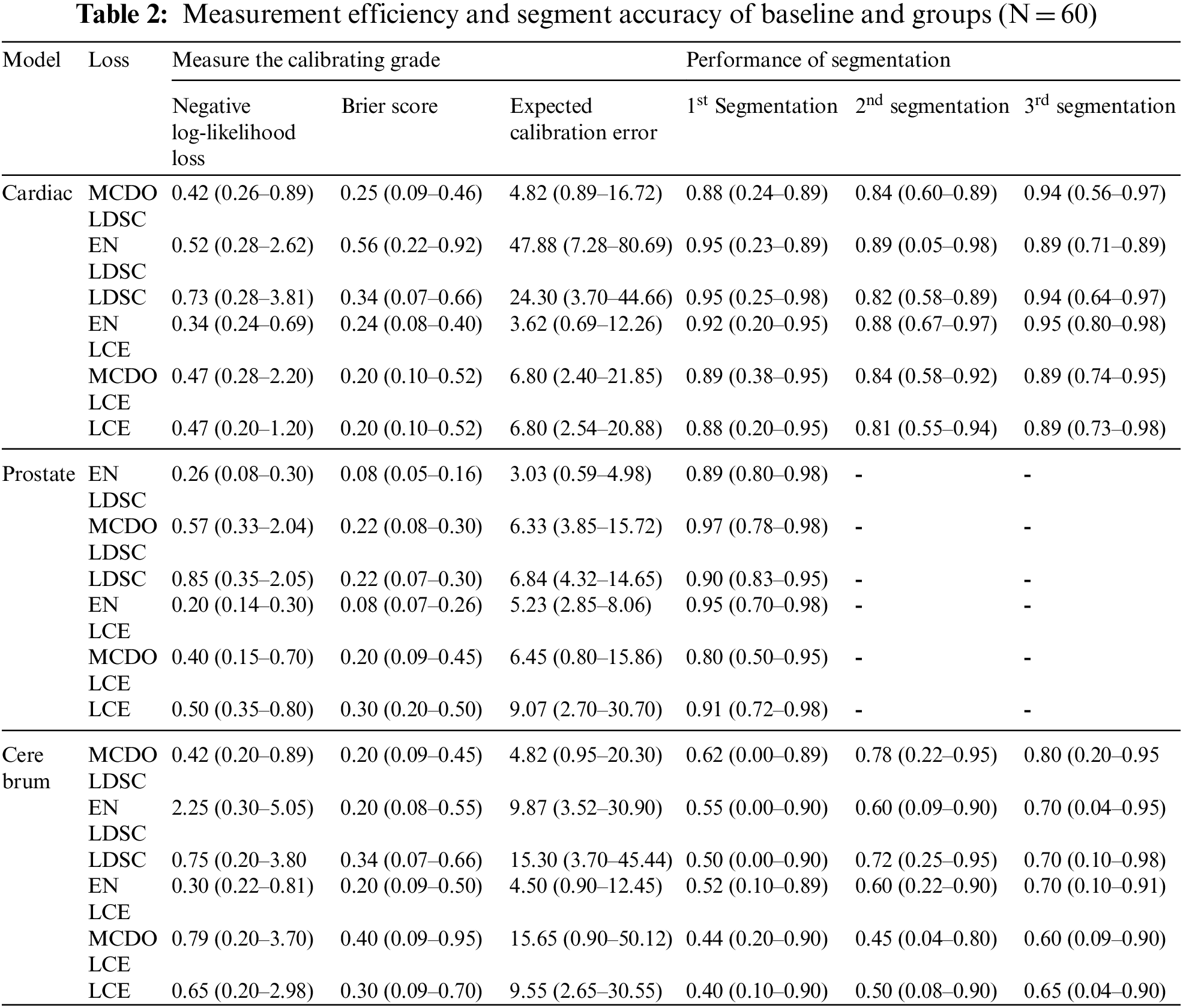
Calibration performance was importantly higher in terms of ECE and NLL percentage for basic qualified modeling with CE, compared with those qualified with dice loss for all three division methods. The process of movement for the Brier score is not steady with models qualified with CE and models qualified with dice loss. Compared with those trained with CE, the Friar scores for brain tumor and prostate separated border boxes were importantly higher for models qualified with dice loss, but the opposite was true for the heart segment. Group methods work very well in terms of measuring all tasks and all activities. Combining basics and MC dropout models that perform best in all situations, based on performance measurement. The study found that grouping significantly increased the measurement superiority of models qualified with dice loss. MC Dropout develops the measurement performance of trained models with dice loss on a consistent basis. Nevertheless, trained models with cross entropy loss, the MC dropout develop the adjustment performance of prostate modelling approaches, not brain or cardiac applications. Fig. 5 depicts a qualitative increase in calibration and separation as a function of sample size within each group of three prostate, heart, and brain tumor division functions. According to the study, even six ensembles (N = 6) of the basics trained in dice loss could reduce NLL to 67 percent, 45 percent and 63 percent, respectively, for the heart, prostate, and brain tumors. Figs. 4 and 5 shows examples of the extent of improvement as a function of the amount of samples in the ensemble.

Figure 4: Cross entropy and dice loss function of Brain

Figure 5: Cross entropy and dice loss function of Heart

The improvements in calibration as a function of sample number in groups for basic methods trained using dice loss and cross-entropy functions. For the prostate, heart, and brain tumor segments, as the number of models N grows, the measurement quality in terms of negative likelihood loss increases. For the NLL, the N = 20 scale ensemble qualified with dice loss while the basic model (N = 1) qualified with cross-entropy. In the above images, the same plot is shown with 96% confidence intervals for both total volume and boundary box data.

The scatter diagrams of the dice coefficient and the recommended section-level prediction of models qualified with dice loss are measured with uncertainty measurements and group (N = 60) shown in Figs. 6, and 7. The study found a good correlation between the dice coefficient and the logit of mean entropy in all three division tasks. In prostate division tasks, there is a clear line between the test dataset from the origin domain (PROSTATEx database) and the targeted domain (PROMISE12). Specific trials can be called examples outside the distribution because most of the worst segment events that are accurately predicted are imaged by endorectal coils.

Figure 6: Segmentation prediction analysis of Prostate

Figure 7: Segmentation prediction analysis of brain tumor

Calculation of section-level prediction ambiguity: Scatter layers and regression of linear between the dice coefficient and the median entropy of the expected section are used. Pearson’s contact coefficient (r) and the 2-tail p-value for estimating the contactlessness are given for each regression figure. Before the dice coefficients are listed and analysed, they are logged. Average entropy is strongly correlated with the dice coefficient in most cases in all three section tasks, indicating that it may be utilized as a trustworthy measure for forecasting the segment excellence of estimations during testing. Larger entropy indicates lower sureness in estimations and more erroneous categorizations, resulting in lower die coefficients.

This study examined the calibration properties of two frequently utilized loss functions and found that the loss function has a direct impact on the measuring capacity and the separation performance. As stated before, measuring excellence is an essential indicator that delivers data about the accuracy of predictions. The study believes that it is important for deep network users to be aware of the measurement characteristics associated with various loss processes. For that purpose, the study hopes that it will be interesting to examine the measurement and division performance of frequently utilized loss functions such as cross-entropy loss, dice loss, and the newly suggested Loas-Softmax loss. There is hope in splitting the medical image [26]. The study used the binary classification for the recommended section-level prediction uncertainty measurement, and the entropy of the anterior class was obtained by considering each class as a background. Furthermore, there are local interactions between classes and neighboring pixels that can be integrated further using similar techniques such as multi-glass entropy or Washerstein losses [27].

Unlike assembling, there is still a need to explore measurement approaches that do not require time-consuming training from the outset. This study looked at the uncertain rating for MR images. Despite the fact that variable changes happen more frequently in MRI than in CT, it would be more motivating to examine the uncertainties in CT images. The changes in CT parameters may be a factor in the defeat of CNNs. For example, the variation may cause prediction failures, and it is greatly desirable to predict such failures using sample sureness. The researchers hope that their findings will provide the basis for future research on uncertainty estimates and calibration of the clinical picture segment. Further research is needed on the origin of ambiguity in the medical film segment. In medical applications and Bayesian modelling, uncertainty is classified as alidoric or epistemic. Alitoric uncertainties can be the result of noise or system instability. Epistemic uncertainties, on the other hand, are established by a lack of information about the model or data. High levels of uncertainty continue to be reported in this investigation in specific areas such as borders. In prostate segment work, for example, single and multiple evaluators often express large intermediate and internal disagreements in defining the base and top of the prostate instead of the medial border of the gland.

7  Conclusion

Without any additional inputs, the basic FCNN can automatically understand the environment and properly separate the distinct elements into different imaging modes. Furthermore, a single model trained in multiple databases is less accurate than models trained in individual databases. Furthermore, a trained model on diversified data generally produces more accurate predictions. The study offers a new approach to identifying out-of-distribution (OOD) data at trial time based on spectral analysis of FCNN feature maps. This method is more precise than the method based on predictive ambiguity in detecting OOD data. Effective deployment of FCNN-based segment algorithms for medical applications needs the use of accurate OOD recognition methods to report sample failure to the user. Although this is a difficult topic due to the wide range and complexity of deep learning models, this recommended strategy provides an efficient solution. Furthermore, when the basic truth is not available, the recommended median entropy level can be utilized as an accurate prognostic measure to evaluate the effectiveness of the samples at the time of testing. We intend to adapt the most effective deep learning model and propose a hybrid deep learning model to identify non-distributed (OOD) data at trial time.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. N. Sharma and L. M. Aggarwal, “Automated medical image segmentation techniques,” Journal of Medical Physics/Association of Medical Physicists of India, vol. 35, no. 1, pp. 3, 2010. [Google Scholar]

2. J. -S. Prassni, T. Ropinski and K. Hinrichs, “Uncertainty-aware guided volume segmentation,” IEEE Transactions on Visualization and Computer Graphics, vol. 16, no. 6, pp. 1358–1365, 2010. [Google Scholar] [PubMed]

3. G. Wang, W. Li, M. Zuluaga, R. Pratt, P. Patel et al., “Interactive medical image segmentation using deep learning with image-specific fine tuning,” IEEE Transactions on Medical Imaging, vol. 37, no. 7, pp. 1562–1573, 2018. [Google Scholar] [PubMed]

4. M. H. Hesamian, W. Jia, X. He and P. Kennedy, “Deep learning techniques for medical image segmentation: Achievements and challenges,” Journal of Digital Imaging, vol. 32, no. 4, pp. 582–596, 2019. [Google Scholar] [PubMed]

5. A. Mehrtash, W. M. Wells, C. M. Tempany, P. Abolmaesumi and T. Kapur, “Confidence calibration and predictive uncertainty estimation for deep medical image segmentation,” IEEE Transactions on Medical Imaging, vol. 39, no. 12, pp. 3868–3878, 2020. [Google Scholar] [PubMed]

6. M. Ghafoorian, A. Mehrtash, T. Kapur, N. Karssemeijer, E. Marchiori et al., “Transfer learning for domain adaptation in MRI: Application in brain lesion segmentation,” In Medical Image Computing and Computer Assisted Intervention−MICCAI 2017, vol. 10435, pp. 516–524, 2017. [Google Scholar]

7. A. Saad, G. Hamarneh and T. Möller, “Exploration and visualization of segmentation uncertainty using shape and appearance prior information,” IEEE Transactions on Visualization and Computer Graphics, vol. 16, no. 6, pp. 1366–1375, 2010. [Google Scholar] [PubMed]

8. S. Sankaran, L. Grady and C. A. Taylor, “Fast computation of hemodynamic sensitivity to lumen segmentation uncertainty,” IEEE Transactions on Medical Imaging, vol. 34, no. 12, pp. 2562–2571, 2015. [Google Scholar] [PubMed]

9. H. Jin, Z. Li, R. Tong and L. Lin, “A deep 3D residual CNN for false-positive reduction in pulmonary nodule detection,” Medical Physics, vol. 45, no. 5, pp. 2097–2107, 2018. [Google Scholar] [PubMed]

10. P. Moeskops, J. Wolterink, B. van der Velden, K. Gilhuijs et al., “Deep learning for multi-task medical image segmentation in multiple modalities,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, Greece, pp. 478–486, 2016. [Google Scholar]

11. C. Guo, G. Pleiss, Y. Sun and K. Q. Weinberger, “On calibration of modern neural networks,” in Int. Conf. on Machine Learning, Australia, pp. 1321–1330, 2017. [Google Scholar]

12. S. Seo, P. H. Seo and B. Han, “Learning for single-shot confidence calibration in deep neural networks through stochastic inferences,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, California, pp. 9030–9038, 2019. [Google Scholar]

13. J. Heo, H. Lee, S. Kim, J. Lee, K. Kim et al., “Uncertainty-aware attention for reliable interpretation and prediction,” Advances in Neural Information Processing Systems, vol. 31, pp. 917–926, 2018. [Google Scholar]

14. F. Ghesu, B. Georgescu, A. Mansoor, Y. Yoo, E. Gibson et al., “Quantifying and leveraging predictive uncertainty for medical image assessment,” Medical Image Analysis, vol. 68, pp. 101855, 2021. [Google Scholar] [PubMed]

15. A. Jungo, R. McKinley, R. Meier, U. Knecht, L. Vera et al., “Towards uncertainty-assisted brain tumor segmentation and survival prediction,” in Int. MICCAI Brainlesion Workshop, Quebec City, Canada, pp. 474–485n, 2017. [Google Scholar]

16. M. Abdar, M. A. Fahami, S. Chakrabarti, A. Khosravi, P. Pławiak et al., “BARF: A new direct and cross-based binary residual feature fusion with uncertainty-aware module for medical image classification,” Information Sciences, vol. 577, pp. 353–378, Oct. 2021. [Google Scholar]

17. C. Bian, C. Yuan, J. Wang, M. Li, X. Yang et al., “Uncertainty-aware domain alignment for anatomical structure segmentation,” Medical Image Analysis, vol. 64, pp. 101732, Aug. 2020. [Google Scholar] [PubMed]

18. A. Jungo, F. Balsiger and M. Reyes, “Analyzing the quality and challenges of uncertainty estimations for brain tumor segmentation,” Front. Neurosci, vol. 14, pp. 282, Apr. 2020. [Google Scholar] [PubMed]

19. M. Abdar, M. Samami, S. D. Mahmoodabad, T. Doan, B. Mazoure et al., “Uncertainty quantification in skin cancer classification using three-way decision-based Bayesian deep learning,” Computers in Biology and Medicine, vol. 135, pp. 104418, 2021. [Google Scholar] [PubMed]

20. R. Jabbar, N. Fetais, M. Krichen and K. Barkaoui, “Blockchain technology for healthcare: Enhancing shared electronic health record interoperability and integrity,” in IEEE International Conf. on Informatics, IoT, and Enabling Technologies (ICIoT), pp. 310–317, 2020. [Google Scholar]

21. K. Wickstrøm, M. Kampffmeyer and R. Jenssen, “Uncertainty and interpretability in convolutional neural networks for semantic segmentation of colorectal polyps,” Medical Image Analysis, vol. 60, pp. 101619, 2020. [Google Scholar]

22. J. M. Wolterink, T. Leiner, M. A. Viergever and I. Išgum, “Automatic segmentation and disease classification using cardiac cine MR images,” in Int. Workshop on Statistical Atlases and Computational Models of the Heart, vol. 10663, Quebec City, Canada, pp. 101–110, 2017. [Google Scholar]

23. G. Litjens, O. Debats, J. Barentsz, N. Karssemeijer and H. Huisman, “Computer-aided detection of prostate cancer in MRI,” IEEE Transactions on Medical Imaging, vol. 33, no. 5, pp. 1083–1092, 2014. [Google Scholar] [PubMed]

24. G. Litjens, R. Toth, W. van de Ven, C. Hoeks, S. Kerkstra et al., “Evaluation of prostate segmentation algorithms for MRI: The PROMISE12 challenge,” Medical Image Analysis, vol. 18, no. 2, pp. 359–373, 2014. [Google Scholar] [PubMed]

25. B. H. Menze, A. Jakab, S. Bauer, J. Kalpathy-Cramer, K. Farahani et al., “The multimodal brain tumor image segmentation benchmark (BRATS),” IEEE Transactions on Medical Imaging, vol. 34, no. 10, pp. 1993–2024, 2014. [Google Scholar] [PubMed]

26. M. Niethammer, K. M. Pohl, F. Janoos and W. M. Wells III, “Active mean fields for probabilistic image segmentation: Connections with chan–vese and rudin–osher–fatemi models,” SIAM Journal on Imaging Sciences, vol. 10, no. 3, pp. 1069–1103, 2017. [Google Scholar] [PubMed]

27. L. Fidon, W. Li, L. C. G. P. Herrera, J. Ekanayake, N. Kitchen et al., “Generalised wasserstein dice score for imbalanced multi-class segmentation using holistic convolutional networks,” in Int. MICCAI Brainlesion Workshop, Quebec City, Canada, pp. 64–76, 2017. [Google Scholar]