Computational Investigation of Hand Foot Mouth Disease Dynamics with Fuzziness

1  Introduction

Although it can affect adults as well, HFMD is a viral illness that is only mildly contagious and often affects young children. The two viruses most frequently responsible for the spread of HFMD are coxsackievirusesA16 and enteroviruses71 [1,2]. The main symptoms of HFMD are fever, vomiting, headache, malaise, lethargy, poor appetite, and a sore throat, but many infected persons don’t have any symptoms. Another sign of HFMD is sores in the mouth or on the lips, as well as on the hands, feet, and occasionally the buttocks and legs.

After being discovered in New Zealand in 1957, HFMD has rapidly gained popularity throughout the world. It does not cause a particularly serious illness and is only moderately contagious. Recent HFMD outbreaks in China, Taiwan, Singapore, Sarawak, Malaysia, etc. have spread awareness of the disease through fatalities across the globe [3]. The HFMD virus can spread through coughing, sneezing, and infected feces. For HFMD, there is no specific treatment. Specialists recommend different medications for different symptoms, such as pain and fever that can be treated with medication. Since there is no effective therapeutic treatment against HFMD, it should be controlled by appropriate preventative measures such as isolation, personal protection against contact with infected people, etc. In general, HFMD is not a serious condition in the infected population. Only a very small minority of those infected require hospitalization, mainly due to neurological complications (encephalitis, meningitis or acute flaccid paralysis) or pulmonary edema/pulmonary hemorrhage. There is no lifelong immunity to HFMD because the disease is caused by a group of viruses very similar to influenza.

In addition to medical issues, HFMD has tremendous social and financial repercussions on countries. Understanding the spread of HFMD among susceptible populations is therefore very important that will help policymakers to maximize the effectiveness of treatment resources. The subject hasn’t been explored all that much, and there isn’t much literature on it that deals with mathematical and numerical modeling. Roy et al. developed an SEIR model in order to better understand the dynamics of HFMD and concluded that the transmission of HFMD depends more on the number of actively infected individuals in the population at the start and also on the rate of disease transmission at any given time [4].

Every community experiences changes as the climate changes. Similar to this, the parameters used in mathematical modeling are dynamic and cannot be fixed [5]. Global warming is one of the key causes of the rise in the earth’s average temperature. The varying temperatures also have an impact on how quickly the virus spreads throughout society. In an effort to forecast the relationship of HFMD with weather patterns, Urashima et al. explored the consequences of global warming [6]. By taking into account quarantine in the population of children, Liu provided a periodic model for the simulation of the dynamics of HFMD transmission [7]. Samanta investigated the discrete delay, non-uniform population size, and saturation incidence rate in the delayed HFMD model. The model of a pulsed vaccination has also been studied [8,9]. Hii et al. investigated Singapore’s HFMD incidence risk in relation to weather variables [10].

Parameters used in existing HFMD epidemic models use crisp numbers, while parameter uncertainty and population heterogeneity are very likely to occur. In order to make the model more realistic, the use of fuzzy parameters in these models is very important. Many researchers have applied fuzzy theory to study disease transmission. Barros et al. developed an epidemic model with fuzzy transmission coefficients [11]. A comparison of the average change in viral load and the average number of people infected was done to analyze the reproduction number. Ortega et al. studied a rabies model in fuzzy senses [12]. Verma et al. developed a Susceptible, Exposed, Infected and Recovered (SEIR) model with fuzzy criteria [13]. A Susceptible, Infected and Recovered (SIR) model was presented by Das et al. with imprecise parameters [14]. A model of food chain in the fuzzy environment with optimal harvesting was studied by Sadhukhan et al. [15]. Mishra et al. presented a fuzzy Susceptible, Exposed, Infected, Quarantine Recovered and Susceptible (SEIQRS) computer virus model [16]. Mangongo et al. introduced fuzzy global stability [17]. A fuzzy Susceptible, Exposed, Infected, Quarantine and Recovered (SEIQR) model was described by Allehiany et al. [18]. The model was solved using the NSFD technique in fuzzy senses, a development of Micken’s theory [19]. Dayan et al. proposed a SIR model in a fuzzy environment [20]. Euler, Runge Kutta of order 4 (RK-4) and the NSFD methods were developed with fuzzy extensions for the solution of the model. Dayan et al. also presented rumor based fuzzy model and developed an NSFD scheme for its solution [21]. Fractal fractional operators are used for the numerical solution of a tumour-immune model by Ahmad et al. [22]. Many researchers studied the NSFD schemes in stochastic senses. Arif et al. studied a stochastic SIR epidemic model [23]. A stochastic model for the numerical investigation of the computer virus was presented by Shatanawi et al. [24]. A stochastic Dengue model using NSFD schemes was proposed by Noor et al. [25]. Shoaib Arif et al. presented a stochastic model of COVID-19 and studied it using NSFD scheme [26]. Researchers studied fractional stochastic models, for example [27], for example. Naveed et al. studied a COVID-19 model with delay effect using NSFD theory [28]. Shatanawi et al. proposed a corona virus model in stochastic senses and developed numerical schemes for its solutions [29]. Baleanu et al. presented a fractional chaotic system and NSFD scheme is used to study the chaotic behavior of the model [30]. Nawaz et al. proposed a fractional order diffusive epidemic model to study the COVID-19 [31].

The existing HFMD models employing crisp numbers are insufficient in order to construct the fuzzy numerical and mathematical techniques. In this context, we examined a SEIR model with fuzzy parameters. The terms susceptible, exposed, infected and recovered are uncertain due to differences in susceptibility, exposure, infectivity and recovery among individuals in the population. Due to the different characteristics of these parameters in the population, uncertainties may arise. Different ages of the population considered may have different customs, habits, resistances, etc. because of their different origins. In many real situations, collecting numerical data as a fixed value is quite difficult, while the range of the data can be easily decided. Models are needed to deal with the above uncertainties for these different levels of individuals. The fuzzy theory facilitates us in resolving the troubles of quantifying uncertainty in mathematical modeling. In this context, mathematical models with fuzziness are more meaningful and perform better. With this in mind, we have extended a classic SEIR model by introducing fuzziness into the model. HFMD transmission, recovery and human mortality rates due to disease are considered fuzzy numbers because these parameters are direct functions of HFMD. In the case of a classical system, these parameters are not direct functions of the disease. Therefore, the fuzzy model can be considered more balanced and flexible. Thus, the use of fuzzy parameters helps us to explain HFMD transmission in more detail.

2  HFMD Model with Fuzzy Parameters

Consider the following system of 4 first order ordinary differential equations representing the SEIR model of HFMD dynamics proposed by Putri et al. [32].

dSdt=b−βIS−(μ+ω)S+ηR,(1)

dEdt=βIS−(α+μ)E,(2)

dIdt=αE−(μ+d+γ)I,(3)

dRdt=γI−(μ+ω+η)R.(4)

The corresponding fuzzy model can be written as

dSdt=b−β(ς)IS−(μ+ω)S+ηR,(5)

dEdt=β(ς)IS−(α+μ)E,(6)

dIdt=αE−(μ+d(ς)+γ(ς))I,(7)

dRdt=γ(ς)I−(μ+ω+η)R.(8)

The HFMD transmission, recovery from HFMD and the mortality rates of the infected individuals are considered fuzzy numbers due to their uncertain natures. These parameters are denoted by β(ς),γ(ς,) and d(ς) respectively, and are defined below.

β(ς)={0,ς≤ςmin ς−ςmin ςM−ςmin,ςmin<ς≤ςM1,ςM<ς,(9)

γ(ς)=γ0−1 ςMς+1,0≤ς≤ςmin,(10)

and

d(ς)={(1−ξ)−ϵ0 ςminς+ϵ0,0≤ς≤ςmin1−ξ,ςmin<ς.(11)

The death rated(ς) will be higher at the higher HFMD virus level i.e., ς0<ς and 1−ξ,(ξ≥0) is the maximum death.

2.1 The Fuzzy Basic Reproductive Number (BRN) Rhf

The BRN Rh is given by

Rh=αβ(ς)b(μ+d(ς)+γ(ς))(μ+ω)(μ+α).(12)

Since Rh being direct function of HFMD virus ς can be analyzed as follows:

Case 1: If ς<ςmin, then we have β(ς)=0 and we obtain,

Rh(ς)=0.

Case 2: If ςmin<ς≤ςM, then we have β(ς)=ς−ςminςM−ςmin and we obtain,

Rh(ς)=αβ(ς)b(μ+d(ς)+γ(ς))(μ+ω)(μ+α).

Case 3: If ςM<ς<ςmax, then we have β(ς)=1 and we obtain,

Rh(ς)=αb(μ+d(ς)+γ(ς))(μ+ω)(μ+α).

Rh(ς) can be expressed as a triangular fuzzy number as:

Rh(ς)=(0, αβ(ς)b(μ+d(ς)+γ(ς))(μ+ω)(μ+α),αb(μ+d(ς)+γ(ς))(μ+ω)(μ+α)  ).

The fuzzy reproduction number can be found as follows [17]:

 Rhf=E[Rh(ς)],

=αb(2β(ς)+1)4(μ+d(ς)+γ(ς))(μ+ω)(μ+α).

2.2 Fuzzy Equilibrium Analysis

Case 1: If ς<ςmin, we obtain:

E0( S0,E0,I0,R0)=(bμ+ω, 0, 0, 0).

Case 2: If ςmin<ς≤ςM, then we have β(ς)=ς−ςminςM−ςmin and we obtain E∗(S∗,E∗,I∗,R∗), where

S∗=(μ+α)(μ+d(ς)+γ(ς))αβ(ς),

I∗=−(μ+ω+η)[−dαβ(ς)+(μ+d(ς)+γ(ς))(μ+ω)(μ+α)](μ+α)(μ+d(ς)+γ(ς))(μ+ω+η)−αηγ(ς),

E∗=μ+d(ς)+γ(ς)α,

R∗=γ(ς)I∗μ+ω+η.

Case 3: If ςM<ς<ςmax, then we have β(ς)=1 and we obtain E∗∗(S∗∗,E∗∗,I∗∗,R∗∗), where

S∗∗=(μ+α)(μ+d(ς)+γ(ς))α,

I∗∗=−(μ+ω+η)[−dα+(μ+d(ς)+γ(ς))(μ+ω)(μ+α)](μ+α)(μ+d(ς)+γ(ς))(μ+ω+η)−αηγ(ς),

E∗∗=μ+d(ς)+γ(ς)α,

R∗∗=γ(ς)I∗∗μ+ω+η.

3  Numerical Modeling

3.1 Non-Standard Finite Difference (NSFD) Scheme

NSFD scheme for the system (5–8) is

sn+1=sn+h[b+ηrn]1+hβ(ς)in+h(μ+ω),(13)

en+1=en+hβ(ς)sn+1in1+h(α+μ),(14)

in+1=in+hαen+11+h(μ+d(ς)+γ(ς)),(15)

rn+1=rn+hγ(ς)in+11+h(μ+ω+η).(16)

3.2 Convergence Analysis

In this segment, the convergence of the developed NSFD scheme at DFE point E0(S0,E0,I0,R0) is discussed here.

The system (13–16) can be written as:

B1=s+h(b+η)1+hβ(ς)i+h(μ+ω),(17)

B2=e+hβ(ς)si1+h(α+μ),(18)

B3=i+hαe1+h(μ+d(ς)+γ(ς)),(19)

B4=r+hγ(ς)i1+h(μ+ω+η).(20)

The Jacobian matrix corresponding to the system (17–20) is

J=[∂B1∂S∂B1∂E∂B1∂I∂B1∂R∂B2∂S∂B2∂E∂B2∂I∂B2∂R∂B3∂S∂B3∂E∂B3∂I∂B3∂R∂B4∂S∂B4∂E∂B4∂I∂B4∂R]

∂B1∂S=11+hβ(ς)i+h(μ+ω),∂B1∂E=0,∂B1∂I=s+h(b+η)1+hβ(ς)i+h(μ+ω),∂B1∂R=hβ(ς)[s+h(b+η)][1+hβ(ς)i+h(μ+ω)]2,

∂B2∂S=hβ(ς)i1+h(α+μ),∂B2∂E=11+h(α+μ),∂B2∂I=hβ(ς)s1+h(α+μ),∂B2∂R=0,

∂B3∂S=0,∂B3∂E=hα1+h(μ+d(ς)+γ(ς)),∂B3∂I=11+h(μ+d(ς)+γ(ς)),∂B3∂R=0,

∂B4∂S=0,∂B4∂E=0,∂B4∂I=hγ(ς)1+h(μ+ω+η)and∂B4∂R=11+h(μ+ω+η).

The above Jacobian matrix becomes

J1=[B110B13B14B2100B22B320B23B33B4300B44]

whereB11=11+hβ(ς)i+h(μ+ω),B13=s+h(b+η)1+hβ(ς)i+h(μ+ω),B14=hβ(ς)[s+h(b+η)][1+hβ(ς)i+h(μ+ω)]2,B21=hβ(ς)i1+h(α+μ),B22=11+h(α+μ),B23=hβ(ς)s1+h(α+μ),B32=hα1+h(μ+d(ς)+γ(ς)),B33=11+h(μ+d(ς)+γ(ς)),B43=hγ(ς)1+h(μ+omega+η)andB44=11+h(μ+ω+η).

The above Jacobian matrix at the Disease Free Equilibrium (DFE) E0( S0,E0,I0,R0)=(Λμ, 0, 0, 0) is

J1∗=[B1100   0000B22B3200B33B4300B44]

The proposed NSFD scheme will be unconditionally convergent iff |λi|<1,i=1,2,3,4.

Here, λ1=11+h(μ+ω),λ2=11+h(α+μ),λ3=11+h(μ+d(ς)+γ(ς)) and λ3=11+h(μ+ω+η). Since all eigen values are less than 1, which proves the desired result.

3.3 Consistency Analysis

To check the consistency of the proposed scheme, we apply the Taylor’s series. From Eq. (13),

sn+1[1+hβ(ς)in+h(μ+ω)]=sn+h(b+ηrn).(21)

For the consistency, following procedure is adopted, considering the Taylor’s series expansion

sn+1=sn+hdsdt+h22!d2sdt2+h33!d3sdt3+…,

Substituting the value of sn+1 in the above equation and after some simplifications, we get

(hdsdt+h22!d2sdt2+h33!d3sdt3+…,)+hβ(ς)in(sn+hdsdt+h22!d2sdt2+h33!d3sdt3+…,)+h(μ+ω)(sn+hdsdt+h22!d2sdt2+h33!d3sdt3+…,)=hb+hηrn,

Taking h→0, we get

dSdt+β(ς)IS+(μ+ω)S=b+ηR,

Or

dSdt=b−β(ς)IS−(μ+ω)S+ηR.

From Eq. (14),

en+1[1+h(α+μ)]=en+hβ(ς)sn+1in(22)

The Taylor’s series expansion of the compartment E is

en+1=en+hdedt+h22!d2edt2+h33!d3edt3+…,

Substituting the value of en+1 in Eq. (22) and after some simplifications, we get

(hdedt+h22!d2edt2+h33!d3edt3+…,)+h(α+μ)(en+hdedt+h22!d2edt2+h33!d3edt3+…,)=hβ(ς)insn,

Taking h→0, we get

dEdt=β(ς)IS−(α+μ)E.

Similarly, we can get

dIdt=αE−(μ+d(ς)+γ(ς))I,

and

dRdt=γ(ς)I−(μ+ω+η)R

by applying Taylor’s series on Eqs. (13–16). It is therefore concluded that our proposed scheme is consistent of order 1.

4  Numerical Simulations

Dynamics of the subpopulations are shown in Figs. 1 and 2 for DFE at h=0.1 and h=10 respectively. All compartment of the studied model are clearly converging to their steady states in both cases. It can be concluded that the increase in the value of the time step sizes does not affect the convergence of our proposed NSFD scheme. This is an interesting feature of the developed method which many other classical methods such as Euler Maruyama, Euler’s Stochastics and RK-4 do not keep it at increasing step sizes as pointed out by Raza et al. [33].

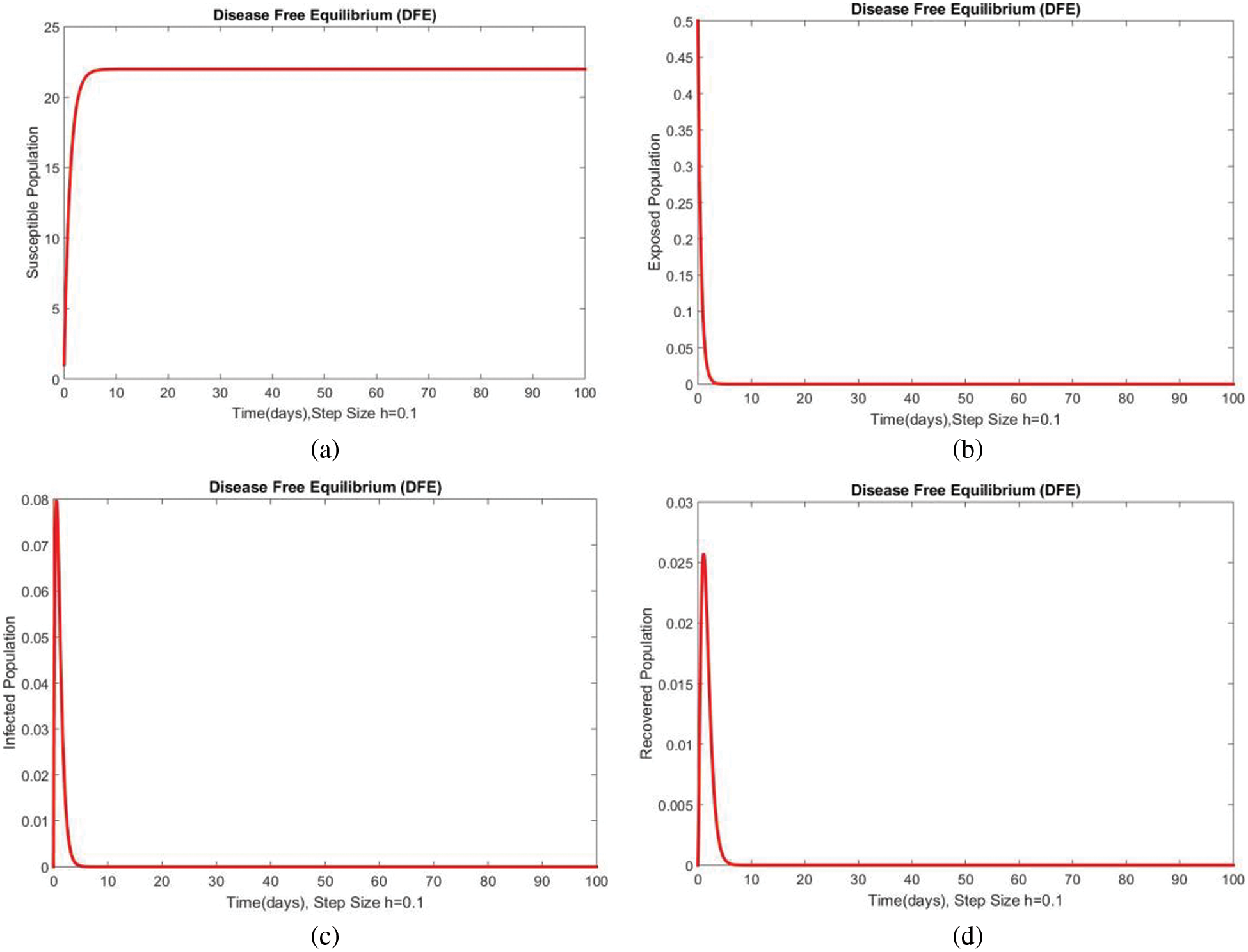
Figure 1: Dynamics of subpopulations at DFE at h=0.1

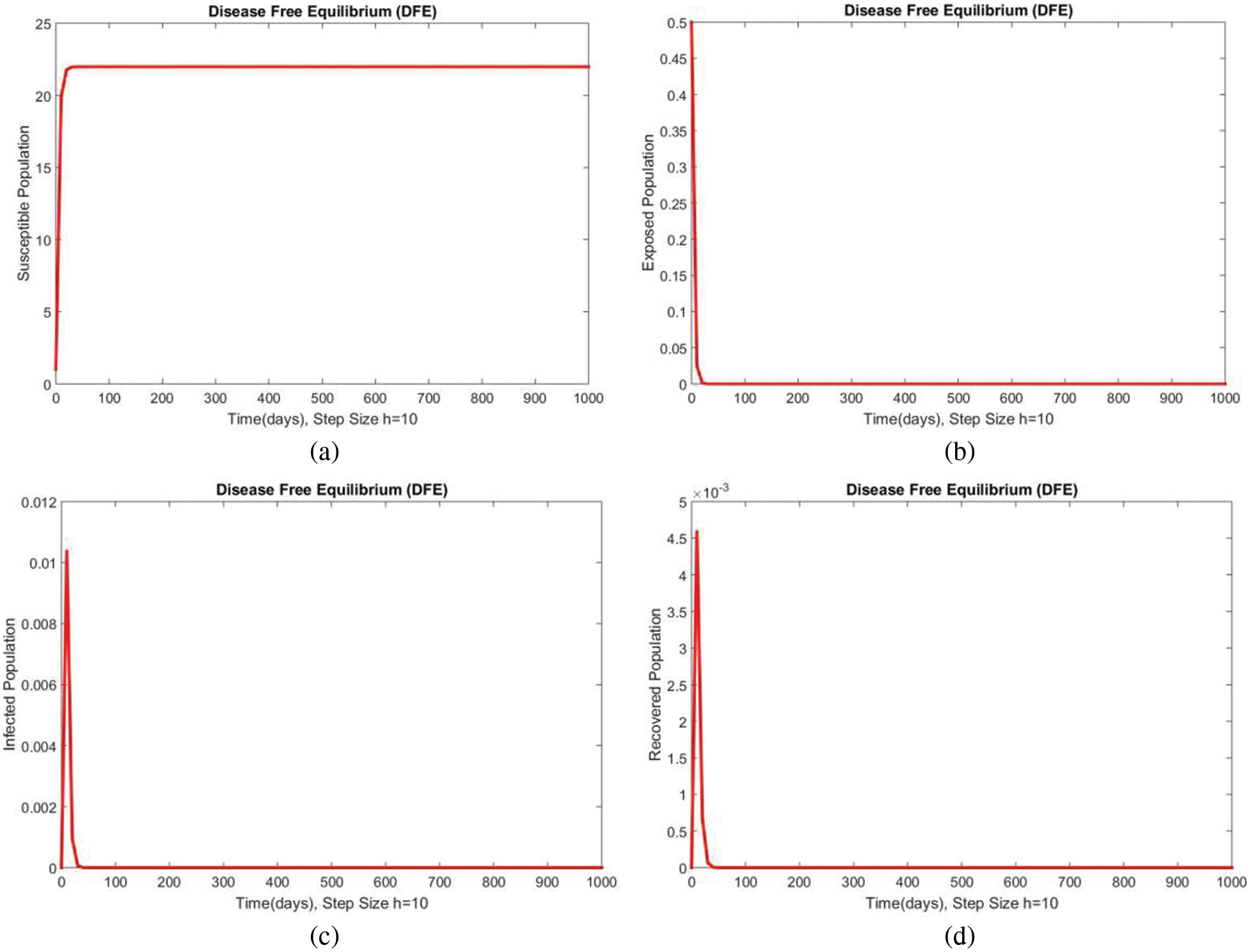
Figure 2: Dynamics of subpopulations at DFE at h=10

Fig. 3 shows the solutions of the exposed and infected compartments respectively at the first EE point, i.e., case 2 at a small step size h=0.1. Then the step size is increased to h=10, the results of which are depicted in Fig. 4. The graphs are positively converging to their steady states in both cases. We can conclude from this behavior that the constructed method is capable of reflecting the dynamics of the studied model for case 2. The typical standard schemes that exist in the literature can cause chaos and misleading variations for some passions of the discretization constraints [34].

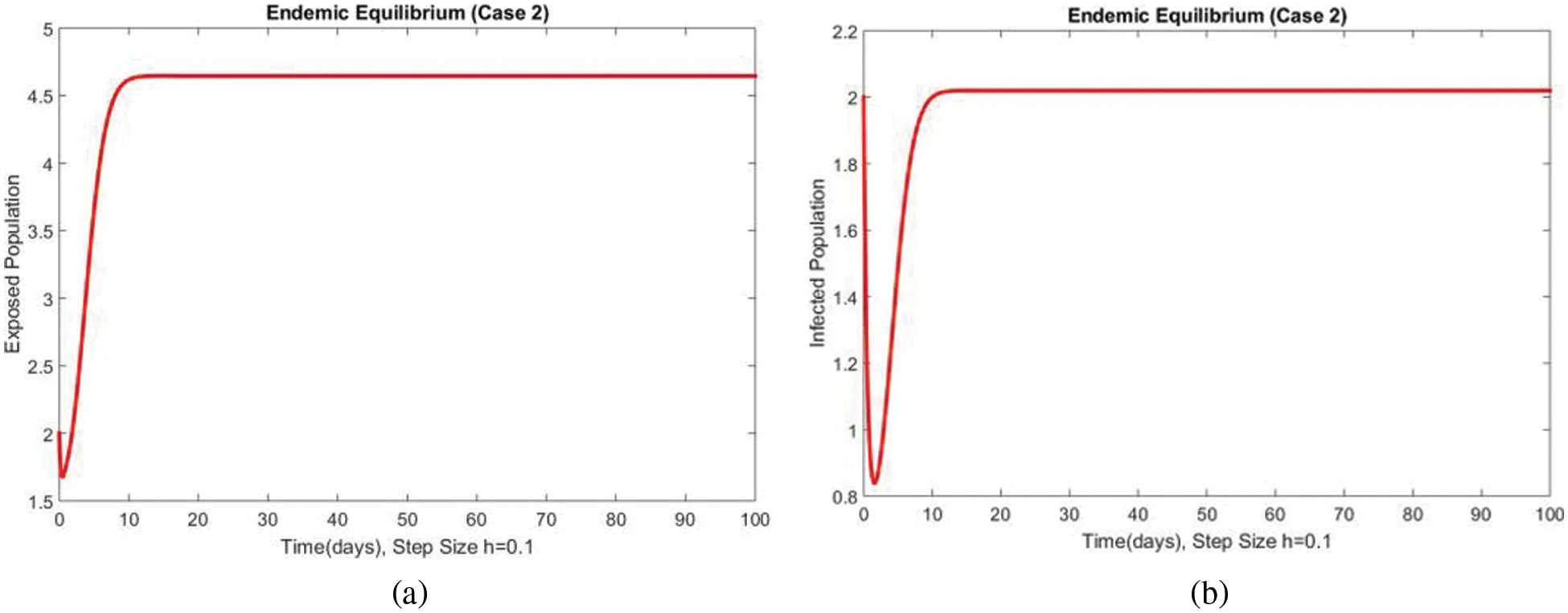
Figure 3: Dynamics of exposed and infected populations at first EE at h=0.1

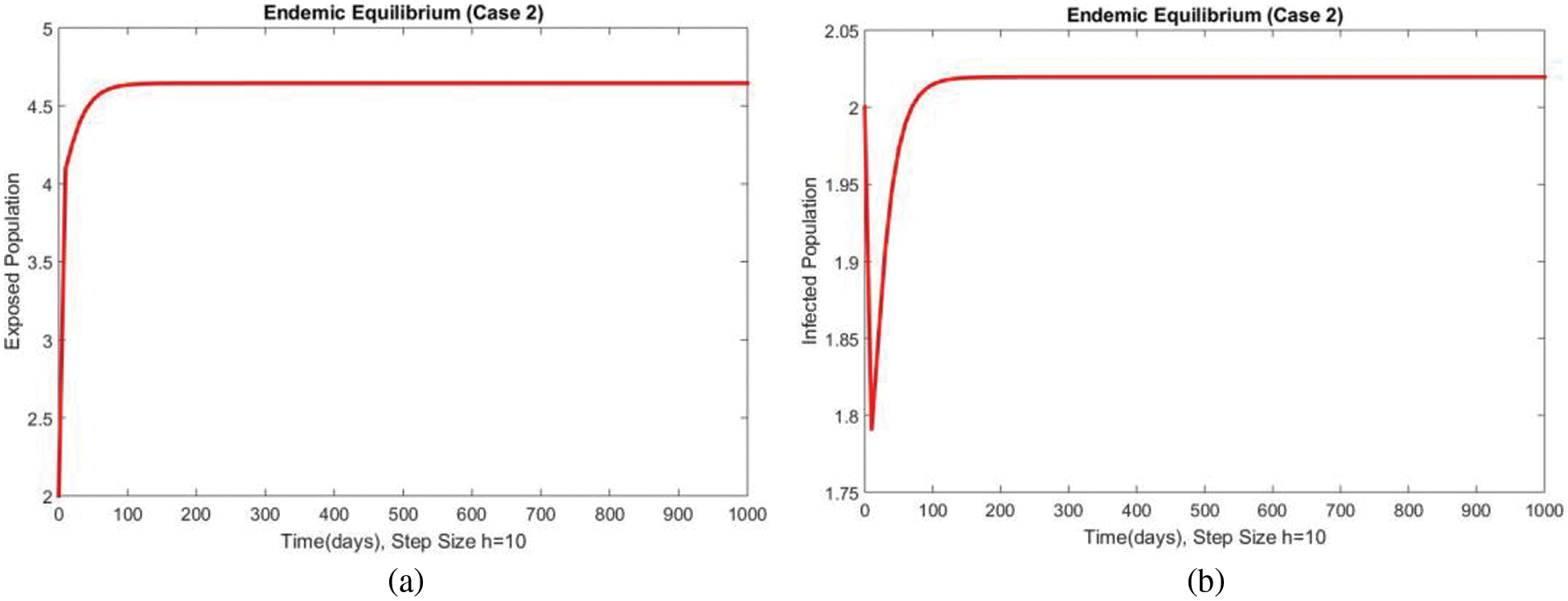
Figure 4: Dynamics of exposed and infected populations at first EE at h=10

Dynamics of the exposed and infected populations for case 3 are shown in Figs. 5 and 6 respectively. An increase in both compartments can be seen with the increase in the value of the transmission rate of the disease. The consistency, convergence and positive solutions at both smaller and large step sizes can also be observed which are the most important features of such kinds of models. Many standard schemes fail to preserve these characteristics. From the above graphs, it can be concluded that the method developed in this work can be considered a more reliable strategy for investigating the disease of FHMD in the human population at EE.

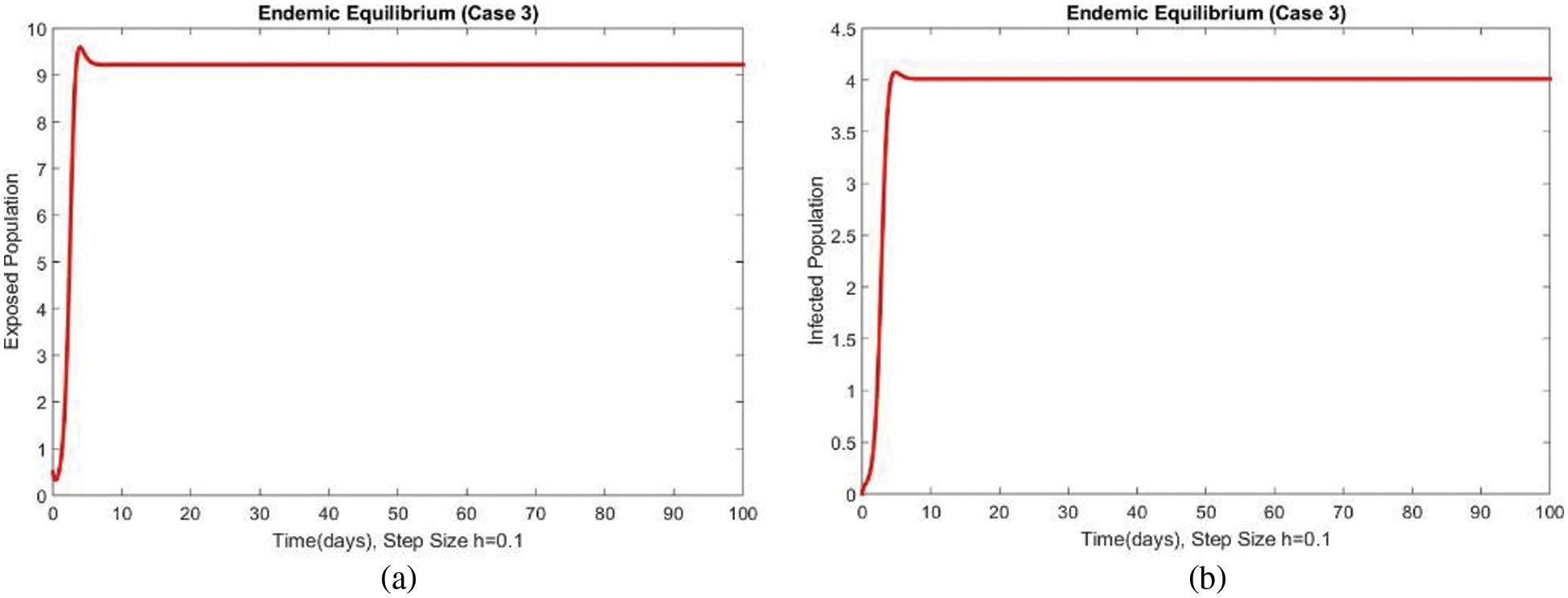
Figure 5: Dynamics of subpopulations at second EE at h=0.1

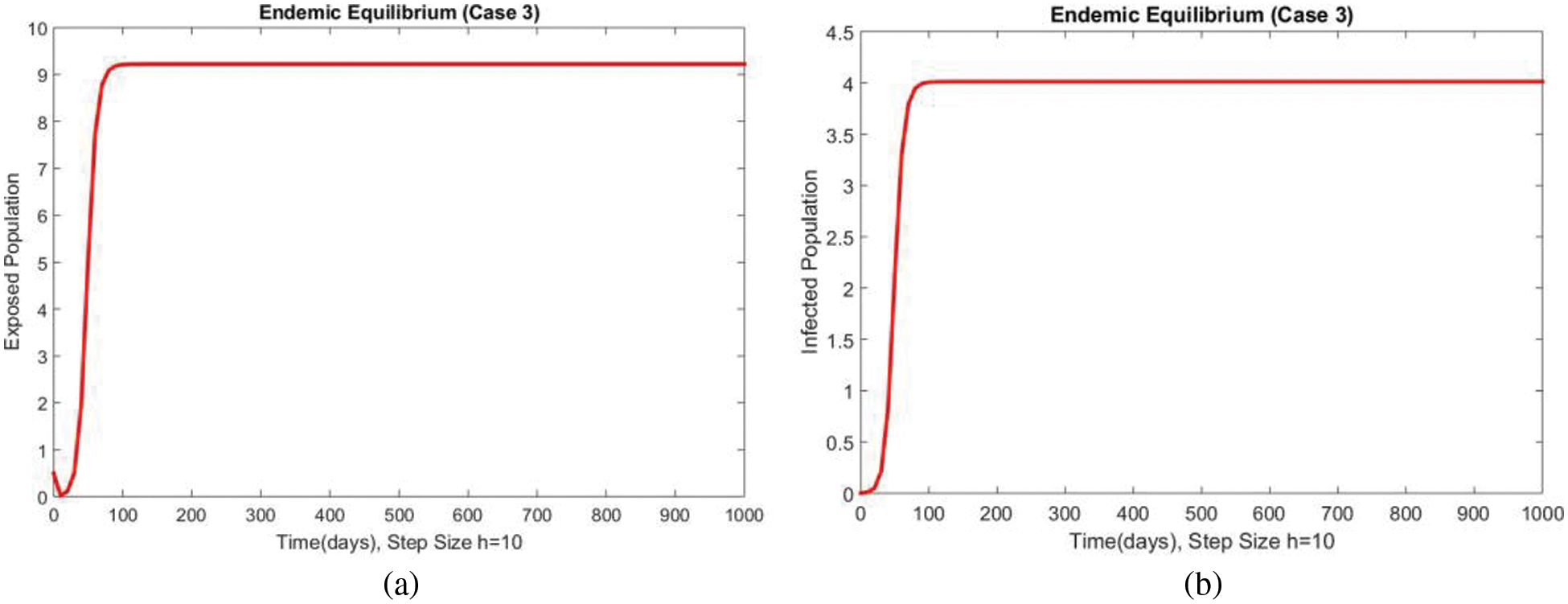
Figure 6: Dynamics of subpopulations at second EE at h=10

A comparison of the exposed and infected compartments of the studied model at DFE and EEs is shown in Figs. 7 and 8 respectively. The proposed method gives convergent solutions at both small and a large step values of h. Moreover, an increase in the compartments of exposed and infected population can also be easily observed with increasing the value of the virus load.

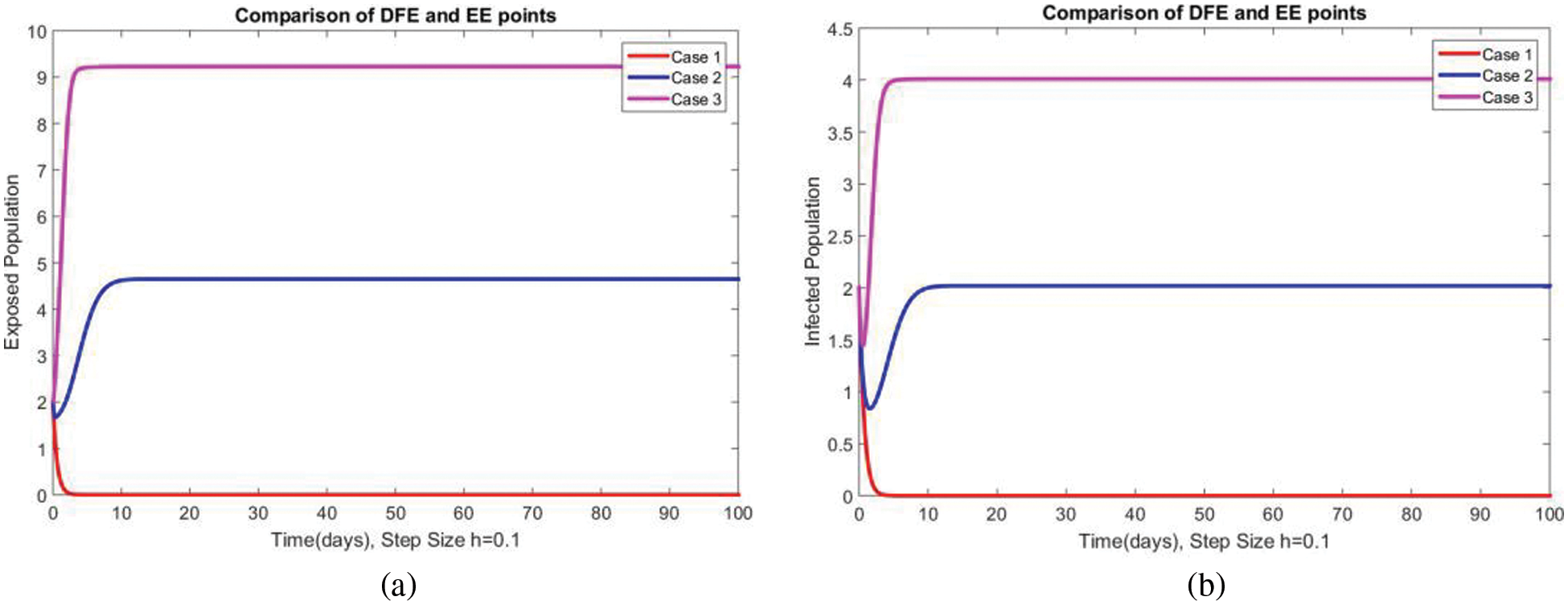
Figure 7: Comparison of subpopulations at DFE and EE at h=0.1

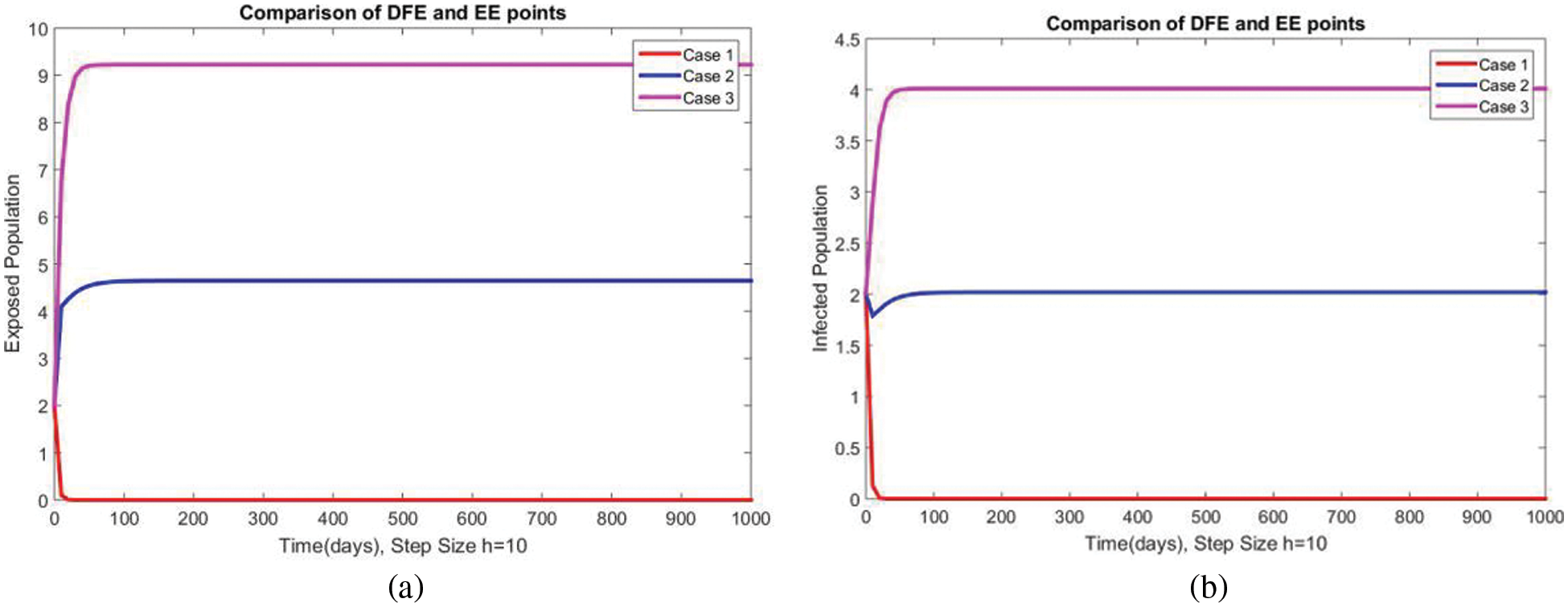
Figure 8: Comparison of subpopulations at DFE and EE at h=10

5  Conclusion

A model of HFMD with fuzzy parameters is studied in this work. In general, due to the natural immune power of mankind, with a small amount of viruses, a disease may not be effective. The system will be endemic if the virus quantity is higher. Therefore, for a small amount of virus, heavy treatment is not necessary. This phenomenon can only be observed in the fuzzy model, and the crisp model does not have the ability to sustain it. Therefore, fuzzy models are more flexible than corresponding classical models. Further, while considering the problems associated with human health in the world, more reliable models are needed and the fuzzy models are quite capable of this. The parameters β(ς),γ(ς,) and d(ς) are considered as fuzzy numbers in this study. The reproduction number and equilibrium analysis in fuzzy sense are analyzed. To solve the studied model numerically, an NSFD scheme is implemented in fuzzy environments and its stability is analyzed. Consistency of the proposed method is also studied. The proposed method preserves the convergence and positive behavior of the numerical solutions at each time step, which are the main characteristic of this type of model. This present work relies mainly on the involvement of the TFN. In future work, we will try to consider other fuzzy numbers like trapezoidal and pentagonal fuzzy numbers depending on the disease virus. This study will open some new windows for researchers in this field. Delayed, stochastic and fractional models respectively with fuzziness and many more directions can also be considered as future directions. The proposed approach can also be extended to machine learning problems as mentioned a few.

Acknowledgement: Thanks to our families and colleagues who supported us morally.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Y. Yang, Y. Chen and F. Q. Zhang, “Stability analysis and optimal control of a hand–foot–mouth disease (HFMD) model,” Journal of Applied Mathematics and Computing, vol. 41, no. 1, pp. 99–117, 2013. [Google Scholar]

2. Q. Zhu, Y. T. Hao, J. Q. Ma, S. C. Yu and Y. Wang, “Surveillance of hand, foot and mouth disease in mainland China (2008–2009),” Biomedical and Environmental Sciences, vol. 24, no. 4, pp. 349–356, 2011. [Google Scholar] [PubMed]

3. S. Sharma and G. Samanta, “Analysis of a hand foot mouth disease model,” International Journal of Biomathematics, vol. 10, no. 2, pp. 1–47, 2017. [Google Scholar]

4. N. Roy and N. Halder, “Compartmental modeling of hand, foot and mouth disease (HFMD),” Research Journal of Applied Sciences, vol. 5, no. 3, pp. 177–182, 2010. [Google Scholar]

5. P. Panja, S. K. Mondal and J. Chattopadhyay, “Dynamical study in fuzzy threshold dynamics of a cholera epidemic model,” Fuzzy Information and Engineering, vol. 9, no. 3, pp. 381–401, 2017. [Google Scholar]

6. M. Urashima, N. Shindo and N. Okabe, “Seasonal models of herpangina and hand–foot–mouth disease to simulate annual fluctuations in urban warming in Tokyo,” Japanese Journal of Infectious Diseases, vol. 56, no. 2, pp. 48–53, 2003. [Google Scholar] [PubMed]

7. J. Liu, “Threshold dynamics for a HFMD epidemic model with periodic transmission rate,” Nonlinear Dynamics, vol. 64, no. 1, pp. 89–95, 2011. [Google Scholar]

8. G. P. Samanta, “Analysis of a delayed hand–foot–mouth disease epidemic model with pulse vaccination,” Systems Science & Control Engineering: An Open Access Journal, vol. 2, no. 1, pp. 61–73, 2014. [Google Scholar]

9. G. P. Samanta, “A delayed hand–foot–mouth disease model with pulse vaccination strategy,” Computational and Applied Mathematics, vol. 34, no. 3, pp. 1131–1152, 2015. [Google Scholar]

10. Y. L. Hii, J. Rocklov and N. Ng, “Short-term effects of weather on hand, foot and mouth disease,” PLoS One, vol. 6, no. 2, pp. 99–105, 2011. [Google Scholar]

11. L. C. Barros, M. B. Ferreira Leite and R. C. Bassanezi, “The SI epidemiological models with a fuzzy transmission parameter,” Computers & Mathematics with Applications, vol. 45, no. 10, pp. 1619–1628, 2003. [Google Scholar]

12. N. R. S. Ortega, P. C. Sallum and E. Massad, “Fuzzy dynamical systems in epidemic modeling,” Kybernetes, vol. 29, no. 2, pp. 201–218, 2000. [Google Scholar]

13. R. Verma, S. P. Tiwari and R. K. Upadhyay, “Transmission dynamics of epidemic spread and outbreak of Ebola in West Africa: Fuzzy modeling and simulation,” Journal of Applied Mathematics and Computing, vol. 60, no. 1, pp. 637–671, 2019. [Google Scholar]

14. A. Das and M. Pal, “A mathematical study of an imprecise SIR epidemic model with treatment control,” Journal of Applied Mathematics and Computing, vol. 56, no. 1, pp. 477–500, 2018. [Google Scholar]

15. D. Sadhukhan, L. N. Sahoo, B. Mondal and M. Maitri, “Food chain model with optimal harvesting in fuzzy environment,” Journal of Applied Mathematics and Computing, vol. 34, no. 1, pp. 1–18, 2010. [Google Scholar]

16. B. Mishra and A. Prajapati, “Spread of malicious objects in computer network: A fuzzy approach,” Applications and Applied Mathematics: An International Journal, vol. 8, no. 2, pp. 684–700, 2013. [Google Scholar]

17. Y. Mangongo, J. Bukweli and J. Kampempe, “Fuzzy global stability analysis of the dynamics of malaria with fuzzy transmission and recovery rates,” American Journal of Operations Research, vol. 11, no. 6, pp. 257–282, 2021. [Google Scholar]

18. F. M. Allehiany, F. Dayan, F. F. Al-Harbi, N. Althobaiti, N. Ahmed et al., “Bio-inspired numerical analysis of COVID-19 with fuzzy parameters,” Computer, Materials & Continua, vol. 72, no. 2, pp. 3213–3229, 2022. [Google Scholar]

19. R. E. Mickens, “A fundamental principle for constructing non-standard finite difference schemes for differential equations,” Journal of Difference Equations and Applications, vol. 11, no. 2, pp. 645–653, 2005. [Google Scholar]

20. F. Dayan, N. Ahmed, M. Rafiq, A. Akgül, A. Raza et al., “Construction and numerical analysis of a fuzzy non-standard computational method for the solution of an SEIQR model of COVID-19 dynamics,” AIMS Mathematics, vol. 7, no. 5, pp. 8449–8470, 2022. [Google Scholar]

21. F. Dayan, M. Rafiq, N. Ahmed, D. Baleanu, A. Raza et al., “Design and numerical analysis of fuzzy nonstandard computational methods for the solution of rumor based fuzzy epidemic model,” Physica A: Statistical Mechanics and Its Applications, vol. 2022. https://doi.org/10.1016/j.physa.2022.127542 [Google Scholar] [CrossRef]

22. S. Ahmad, A. Ullah, A. Akgül and D. Baleanu, “Theoretical and numerical analysis of fractal fractional model of tumor-immune interaction with two different kernels,” Alexandria Engineering Journal, vol. 61, no. 7, pp. 5735–5752, 2022. [Google Scholar]

23. M. S. Arif, A. Raza, W. Shatanawi, M. Rafiq and M. Bibi, “A stochastic numerical analysis for computer virus model with vertical transmission over the internet,” Computers, Materials & Continua, vol. 61, no. 3, pp. 1025–1043, 2019. [Google Scholar]

24. W. Shatanawi, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Essential features preserving dynamics of stochastic Dengue model,” Computer Modeling in Engineering & Sciences, vol. 126, no. 1, pp. 201–215, 2021. [Google Scholar]

25. M. A. Noor, A. Raza, M. S. Arif, M. Rafiq, K. S. Nisar et al., “Non-standard computational analysis of the stochastic COVID-19 pandemic model: An application of computational biology,” Alexandria Engineering Journal, vol. 61, no. 1, pp. 619–630, 2022. [Google Scholar]

26. M. Shoaib Arif, A. Raza, K. Abodayeh, M. Rafiq and A. Nazeer, “A numerical efficient technique for the solution of susceptible infected recovered epidemic model,” Computer Modeling in Engineering & Sciences, vol. 124, no. 2, pp. 477–491, 2020. [Google Scholar]

27. M. Shoaib Arif, A. Raza, M. Rafiq, M. Bibi, R. Fayyaz et al., “A reliable stochastic numerical analysis for typhoid fever incorporating with protection against infection,” Computers, Materials & Continua, vol. 59, no. 3, pp. 787–804, 2019. [Google Scholar]

28. M. Naveed, M. Rafiq, A. Raza, N. Ahmed, I. Khan et al., “Mathematical analysis of novel coronavirus (2019-nCov) delay pandemic model,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1401–1414, 2020. [Google Scholar]

29. W. Shatanawi, A. Raza, M. S. Arif, K. Abodayeh, M. Rafiq et al., “An effective numerical method for the solution of a stochastic coronavirus (2019-ncovid) pandemic model,” Computers, Materials & Continua, vol. 66, no. 2, pp. 1121–1137, 2021. [Google Scholar]

30. D. Baleanu, S. Zibaei, M. Namjoo and A. Jajarmi, “A nonstandard finite difference scheme for the modeling and nonidentical synchronization of a novel fractional chaotic system,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–19, 2021. [Google Scholar]

31. Y. Nawaz, M. S. Arif, W. Shatanawi and M. U. Ashraf, “A new unconditionally stable implicit numerical scheme for fractional diffusive epidemic model,” AIMS Mathematics, vol. 7, no. 8, pp. 14299–14322, 2022. [Google Scholar]

32. A. Y. Putri, D. Handayani and R. Saragih, “The dynamic of hand-foot-mouth disease model using Takagi-Sugeno fuzzy system,” in AIP Conference Proceedings, vol. 2264, no. 1, pp. 1–10, 2020. [Google Scholar]

33. A. Raza, M. S. Arif, M. Rafiq, M. Bibi, M. Naveed et al., “Numerical treatment for stochastic computer virus,” Computer Modeling in Engineering & Sciences, vol. 120, no. 2, pp. 445–465, 2019. [Google Scholar]

34. M. Rafiq, A. Ahmadian, A. Raza, D. Baleanu, M. S. Ahsan et al., “Numerical control measures of stochastic malaria epidemic model,” Computers, Materials & Continua, vol. 65, no. 1, pp. 33–51, 2020. [Google Scholar]