Enhanced Parallelized DNA-Coded Stream Cipher Based on Multiplayer Prisoners’ Dilemma

1  Introduction

The idea presented for cryptography has shown practical and theoretical usefulness in diverse fields, including computer networks, cybersecurity and information security. Cryptography seeks to provide a secure and reliable platform for the communication of both senders and receivers in public channels. The primary categories of cryptography include asymmetric and symmetric algorithms used in encryptions. Both approaches have the specific purpose of translating input data that is easily understandable to the reader (plaintext) to a configuration that is non-readable (ciphertext). However, the applied encryption and decryption methodologies differ considerably between the two categories. On the one hand, symmetrical cryptography applies only one key for decryption and as well as encryption of the messages between the receiver and the sender. On the other hand, the asymmetrical category applies two distinct keys, referred to as the private and public key, in the process of both encryption and decryption. It is examined that the the private key are not easily accessible as their content is kept secret whereas, the other users can easily access the public key.

It is anticipated that Shift registers comprised of linear and non-linear feedback [1,2], chaos theory [3], linear finite state machines [4] and T-functions [5]. These are found as useful structures for designing conventional stream ciphers. However, in the contemporary context, cryptographic primitives are created by integrating diverse disciplines such as mathematics [6], physics and computer science [7], biology [8] and business theories [9], among others. This interconnection is useful for securing the algorithms used in the prescriptions and limiting the possibility of cryptanalysis attacks. The integration of diverse disciplines makes it more challenging for cryptanalysts to solve the behavioural patterns presented in the cipher algorithms.

The interactions that take place between parties that have mutual distrust can be well explained using the game theory. This approach is commonly applied in businesses whose diverse organisations seek to boost their market share and gain a competitive edge over their rivals. Katz [9] evaluates encryption algorithms for the implication of the game approach to make connection between cryptography and game theory. The findings revealed that game theory increases the cryptography’s efficiency and sophistication by solving some challenges inherent in typical cryptographic methods. Today, there is increasing interest among researchers in innovating security protocols and models that bridge the gap, integrating the practises practically applied in the game theory as well as in cryptography [10–15]. These techniques reveal promising outcomes when analysed based on security and performance.

DNA cryptography emerges from the integration of cryptography and biology and represents a significant field of interest. Encoding is done using DNA bases, which should be compatible with the applied computations of the DNA and security requirements. DNA cryptography contributes to the proposal of diverse schemes to enhance data security while revealing possible issues in existing approaches to security. Nevertheless, keystream generation is quite time-consuming for some DNA-based cryptography schemes. Consequently, the performance of both the processes of encryption and decryption is considered currently as unsatisfactory [16].

Recently, by considering the game theory and DNA coding, a stream cipher was introduced [17]. The cipher offers an alternative methodology that is based on generating a keystream through a game played between two players following/applying the prisoner’s dilemma paradigm. The generated keystream is then XOR-ed with plaintext to produce a stream of ciphertext, which is later coded in DNA bases. The security and performance analysis shows that the cipher is promising. However, stream ciphers are considered slower than other existing ciphers. Hence, we attempted to improve the design and create a new stream cipher that is both secure and fast.

Our main contribution focuses on two main factors: performance and security. As for security, our enhanced design uses a more complicated game model based on the ‘n-player prisoner’s dilemma’ paradigm. The new design involves a random selection of players that mimic the behaviour of benchmark strategies. Accordingly, multiple layers of randomness are added to the behaviour of the keystream generation process. In addition, parallelism is introduced to enhance the performance of the stream cipher.

The remaining sections are structured as follows. The preliminaries can be found in Section 2. Section 3 includes the discussion of associated works, and Section 4 elaborates on the proposed scheme. Section 5 presents the security analysis, and the evaluation of complexity is discussed in Sections 6 and 7. Lastly, Section 8 provide a concluding remarks on the presented research study.

2  Preliminaries

2.1 Understanding Stream Ciphers

The sender and receiver first develop secret information that they will then use in the encryption and decryption procedures applied in stream ciphers. The primary keystream generator (KSG) in stream ciphers is a pseudorandom generator with two characteristics, an initial vector (IV) and a secret key, both of which are used to generate a set of keys in a specific sequence known as the keystream. The keystream is then applied in the encryption or decryption of plaintext using the exclusive-or (XOR) operation.

The security applied to the keystream generator is the primary aspect that determines the essence of a stream cipher. Cryptanalysts focus on evaluating the keystream generator to identify possible behavioural and statistical patterns that may contribute to cryptographic vulnerabilities that are easily exploitable by attackers. Both DNA coding and game theory are useful concepts used in both encrypt/decrypt (E/D) procedures and the development of random keystreams in KSG. Section 4 of this paper provides a clear overview of the implementation process.

2.2 Iterated n-Player Prisoner’s Dilemma in Game Theory (INPPD)

INPPD is a realistic game for modelling real-life problems [18]. The INPPD model captures the social dilemma that usually takes place during a collective action. In INPPD, individuals’ defections lead to outcomes that are overall less desirable. The INPPD game has been utilised in various studies of the progress of cooperative behaviours in social and biological systems. It can be formulated by the following two statements [19]:

•   Regardless of what the other player does, each player receives a higher payoff for defecting behaviour than for cooperating behaviour.

•   All players receive a lower payoff if all players defect than if they all cooperate.

Similar to the 2IPD scenario, participants individually select to cooperate (C) or defect (D). A player’s payoff is a function of the total value of cooperators (i). Let ci and di for every participant (where i = 0, 1, . . . , n − 1) be the payoffs of a given player if that player cooperates or defects, respectively. In other words, for a particular player g, there should be i cooperators and n−i−1 defectors. Player g gets di or ci when participant g cooperates or defects, respectively. Moreover, player g for computing payoff, is required to know the total value of C and D.

Based on [18], the INPPD’s payoff function should satisfy the subsequent situations:

Condition 1: Monotonicity

If the majority of players cooperate, the payoff will be greater for additional cooperators. However, the same is true for an additional defector, as the second inequality of the monotonicity condition shows. Eqs. (1), (2) reflect the monotonicity condition:

ci>ci−1(1)

di>di−1(2)

where, for all i = 1, 2, … , n – 1, di is refered to the payoff obtained by a player who played D while i other players defected, and ci is referred to the payoff obtained by a player who played C while i other players cooperated.

Condition 2: The dominance of D over C

A short-sightedly rational player will choose to defect, since

di>ci for i=0,1,⋯,n−1(3)

Condition 3: Efficiency of cooperation over defection

The payoff for the group increases when a player starts cooperating. This condition is represented by Eqs. (4), (5), as follows:

(i+1)ci+(n−i−1)di>(i)ci−1+(n−1)di(4)

cn−1>dcn−1>d0(5)

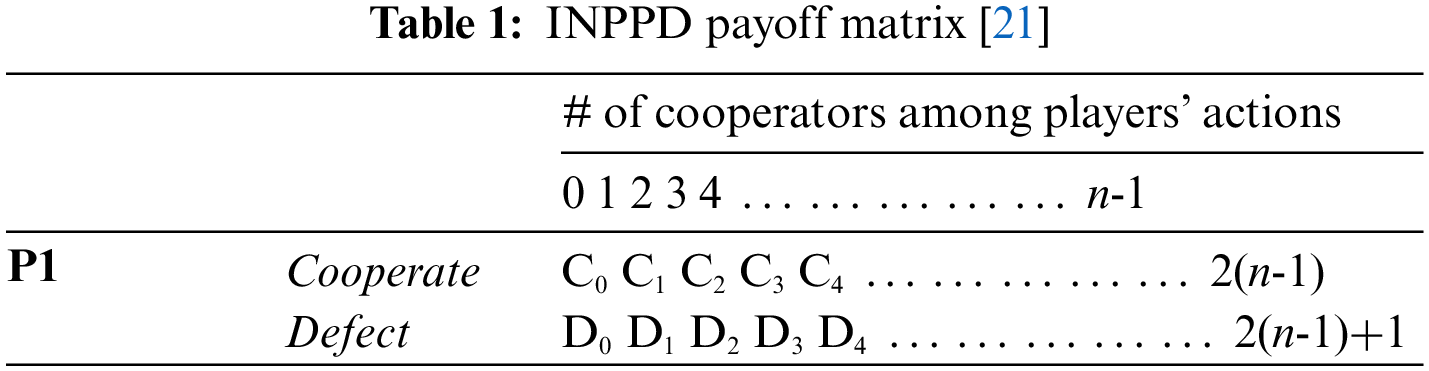
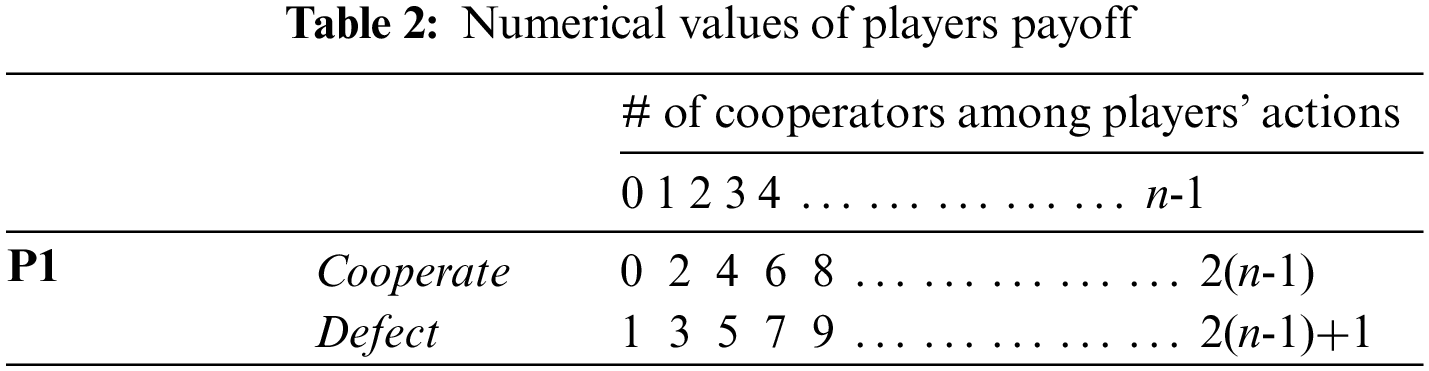
In this study, we adopt the payoff matrix presented in [20] and used in [21] to support the INPPD game since it satisfies all three conditions. The matrix is composed of multiple columns and rows (Table 1). To simplify it, we have assigned numerical values to the matrix that satisfy all three conditions (Table 2).

2.3 DNA Encoding

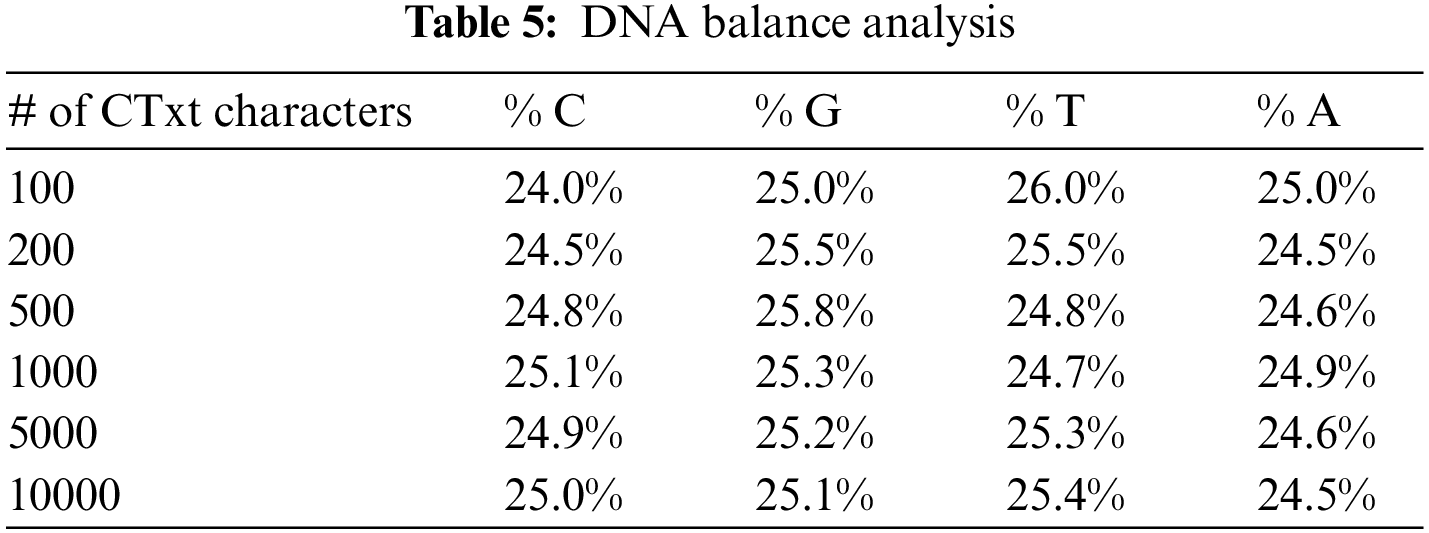
Nucleotides are the main components of DNA. They are comprised of 4 bases including adenine, cytosine, guanine and thymine (A, C, G, T). DNA cryptography includes the encryption of the plaintext and the translation of the ciphertext to DNA bases. The sender carries out a mapping procedure between the binary bits of the ciphertext and the combination of DNA bases in the encryption process. This approach is useful for increasing the encryption’s level of security. Every combination inherent in the DNA bases contributes to the formation of a sequence of DNA, and the outcome is a collection of sequences of DNA.

3  Related Works

Studies conducted by Li et al. [22] reveal the use of random DNA coding as an alternative method used in image encryption to facilitate better diffusion through a disrupted map procedure. In an attempt to improve the chaos mapping system, the scholars formulated a novel form of chaotic spatiotemporal structure. In this system, the components are combined with 2 distinct methodologies. These include tent-sine system (TSS) and coupled map lattice (CML). Also, the logistic map, TSS and Lorenz map are used to come up with the original parameters. The algorithm used in the image encryption provided increased resistance against frequent attacks.

According to Sohal et al. [23], the use of a symmetric-key scheme in cryptography can improve cloud computing systems. One of these authors’ main arguments is that while diverse algorithms are used to achieve secure data transmission in cloud computing systems, the emergence of new architecture in cloud settings has led to less favourable outcomes in different case scenarios. The researchers suggest that the solution is to apply an encryption scheme that depends solely on client-side encryption, thus ensuring its full security before disseminating it to the cloud servers. It is examined that the symmetric-key schemes are used for encryption depends primarily on DNA coding as applied in cryptography. In addition, the study included a thorough evaluation of the algorithm based on diverse encryption methodologies. These may include: Advanced Encryption Standard (AES), DNA, and Data Encryption Standard (DES). The findings revealed that the suggested algorithm encryption provided more promising results compared to the commonly applied algorithms when analysed based on the amount of time consumed during the encryption process and the general output.

A new trend in cryptography takes inspiration from natural biological phenomena to develop true randomness given the inability of computer-generated software tools to perform the same tasks. It is revealed that cryptographic systems, stimulated by biological processes, are crucial for current cryptography, which necessitates the use of devices based on machine-learning and algorithms that have a biological influence to facilitate security in the data dissemination phase [24]. The researchers applied the central dogma of molecular biology (CDMB) to recommend a new cryptosystem. The proposed methods are applied to promote a well-founded and correct simulation of the conditions necessary to promote natural and normal genetic coding, translation and transcription procedures. The input is a 16-bit dataset and a ciphertext in the form of a protein base is the consequent outcome. A bi-directional memory neural network (BAMNN) is applied to promote key generation. The study shows that the proposed scheme offers reliable and accurate encryption speed for large and small files.

Qiu-yu et al. [25] emphasise the use of an encryption technique that is more effective and comprehensive. They show that the current technologies used in encryptions, including the algorithms applied primarily in the encryption of image files, are not useful for widespread application due to security concerns. The authors’ main focus is on the diverse types of statistical analysis, including cropping, noise, differential and exhaustive attacks. Their main proposal is to apply an image encryption algorithm that depends solely on three primary elements – boosted chaotic mapping, image hashing and DNA coding – to deal with existing encryption issues. Enhancing the chaotic sequence necessitates the application of Chen’s chaotic sequence for the original framework used in the chaotic map. The findings reveal that the proposed algorithm achieves higher security levels, a larger key-space and enhanced key sensitivity.

The authors of [26] show that in the recent internet era, most images transmitted online utilise large colour spaces because they are captured by contemporary digital imaging devices that create higher dynamic range (HDR) images. For this reason, it may be difficult for any form of encryption to be carried out without compromising the quality of the transmitted file. The researchers suggested that one way to address this challenge is through a new encryption method that combines DNA coding with double-chaotic systems to conduct the encryption procedure using a bit-level for every image. The study applied the Arnold algorithm to reduce the diverse elements contained in the file (image). Then, the researchers applied the Lorenz chaotic mapping technique to obtain a meaningful double-chaos system. By using the principles of DNA coding, the researchers were able to translate the chaotic elements contained in the images and the parts of the sequences that were inherent in the DNA coding. The authors concluded that the applied methodology increases the effectiveness of image encryption while decreasing computing overhead.

Meftah et al. [27] recommend the use of a symmetric encryption algorithm using Huffman and DNA coding. The suggested technique works by applying Huffman coding on the original DNA key and then codifying the resulting secondary key. The next step involves using XOR on the codified DNA sequence and the plaintext available in the image file. Diffusing the plaintext using the permutation box technique helps to increase the security levels of the recommended encryption algorithm. Moreover, a thorough test of the encryption algorithm reveals that, given its security and performance levels, it can be considered a feasible alternative to current ciphers.

The use of DNA coding has significantly influenced and enhanced the application of high-efficiency encryption techniques. Privthran et al. [16] state that the data levels produced and disseminated through the use of the internet have been skyrocketing; therefore, the amount of both confidential and sensitive data has also been increasing. Based on this reasoning, there is an increased need for an advanced system to provide secure internet. The researchers recommend the development of a innovative cryptosystem that operates solely dependant on the frameworks of DNA cryptography, arguing that such a system would be useful in maintaining secure data dissemination over the internet. The finite automata theory further supports the use of DNA cryptography. The data sender, key generator and data receiver are the main components of the whole cryptosystem. In normal scenarios, the sender conducts data encryption by applying a secret key based on DNA. Additionally, the use of a Mealy machine helps to encode the sequence of the DNA allocated between the receiver and the sender. The findings reveal that the proposed encryption scheme facilitates increased levels of security and enhanced performance compared to current DNA-based cryptosystems.

Recently, a stream cipher based on a two-player prisoner’s dilemma (2PD) game and DNA coding was introduced in [17]. The cipher generates keystreams from rounds of PD games played between two players. The 2PD game is associated with a payoff matrix that determines the rewards that players gain from the actions they take during each game. Upon the completion of the encryption, the cipher codes the resulting bits in DNA bases. The statistical and security analysis of this cipher shows that the cipher is secure. However, the encryption speed of the cipher is much slower than that of other well-known, available ciphers.

In conclusion, the application of game theory and DNA approaches provides benefits in the cryptographic field. This work presents an enhanced design of the promising stream cipher introduced in [17]. The main contributions that our enhanced design offers are related to security and performance (Section 4).

4  The Proposed Scheme

4.1 Original Design

With reference to [17], the basic design of the algorithm needs a 256-bit secret key (SecK) and four 8-bit initial vectors (denoted as Val1, Val2, Val3 and Val4) for producing a 512-bit keystream/round. The design of the algorithm utilises randomness in most of the components (core operations) to avoid correlations and statistical dependencies. As we are enhancing the original formation of the DNA-coded stream cipher proposed in [17], we will employ the same notations used in that study:

•   ⨁ : exclusive-or operation (bitwise)

•   ||   : concatenation of bits.

•   m≫n : shift m by n bits to the right (cyclic mode)

•   m≪n : shift of m by n bits to the left (cyclic mode)

According to Fig. 1, the original design is composed of four main stages: key/IV setup, keystream bit generation, encryption and DNA encoding.

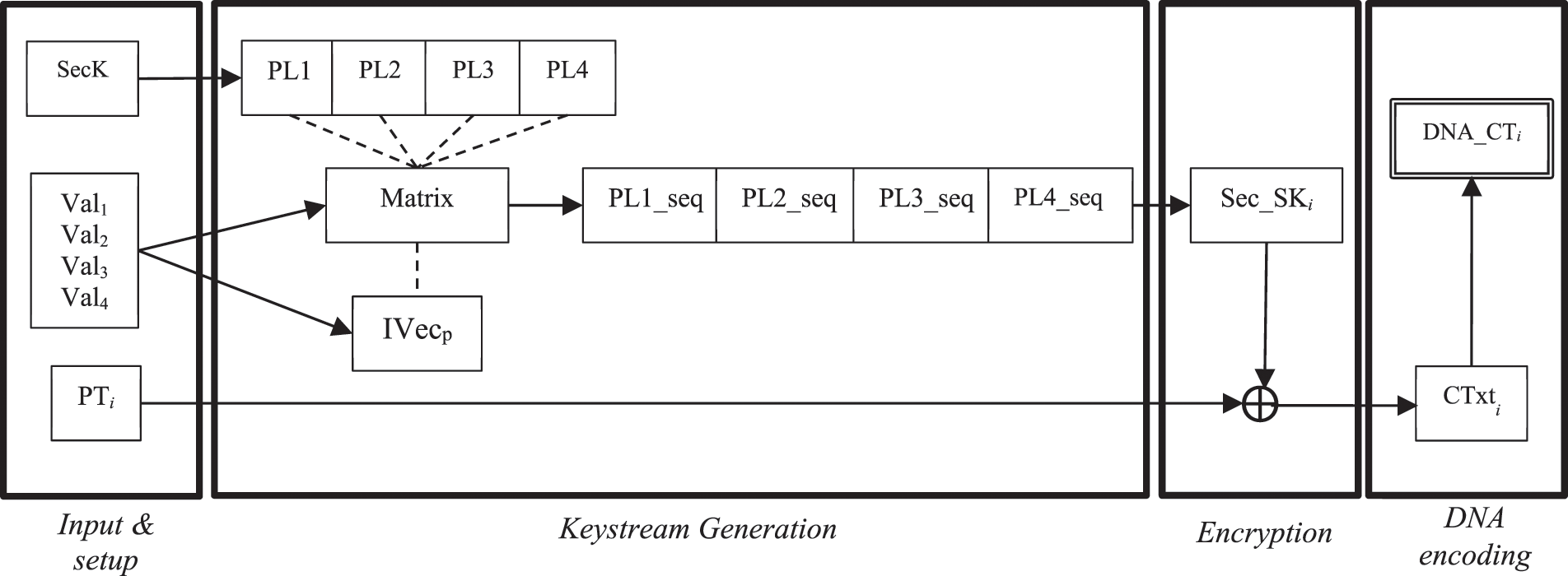
Figure 1: The original design of the original DNA-based stream cipher

4.2 Enhanced DNA-coded Stream Cipher

The main goal behind this enhanced design is to improve both the performance and security of the original stream cipher design. The original design allows only two players (represented by two bits) to play one PD game. The payoff achieved by each player is calculated based on a 2PD payoff matrix.

However, in our proposed enhanced scheme, we replace the concept of 2PD game with iterated n-player prisoner’s dilemma (INPPD) games. Hence, all IVecp bits play against all PL1 bits in a multiplayer game. In this case, the payoff is calculated according to the INPPD payoff matrix (Table 1). This replacement is expected to enhance the security by adding an extra layer of randomness. It is also expected to enhance the performance of the encryption algorithm since all players play together at one time; in contrast, the basic design assumes a bit-by-bit game. Fig. 2 illustrates the modification applied in the enhanced design. The core contributions of the enhanced stream cipher include the replacement of the 2PD game with a multiplayer PD game, the involvement of benchmark strategies in the game as a third party of players and the implementation of parallelism to increase the speed of keystream generation.

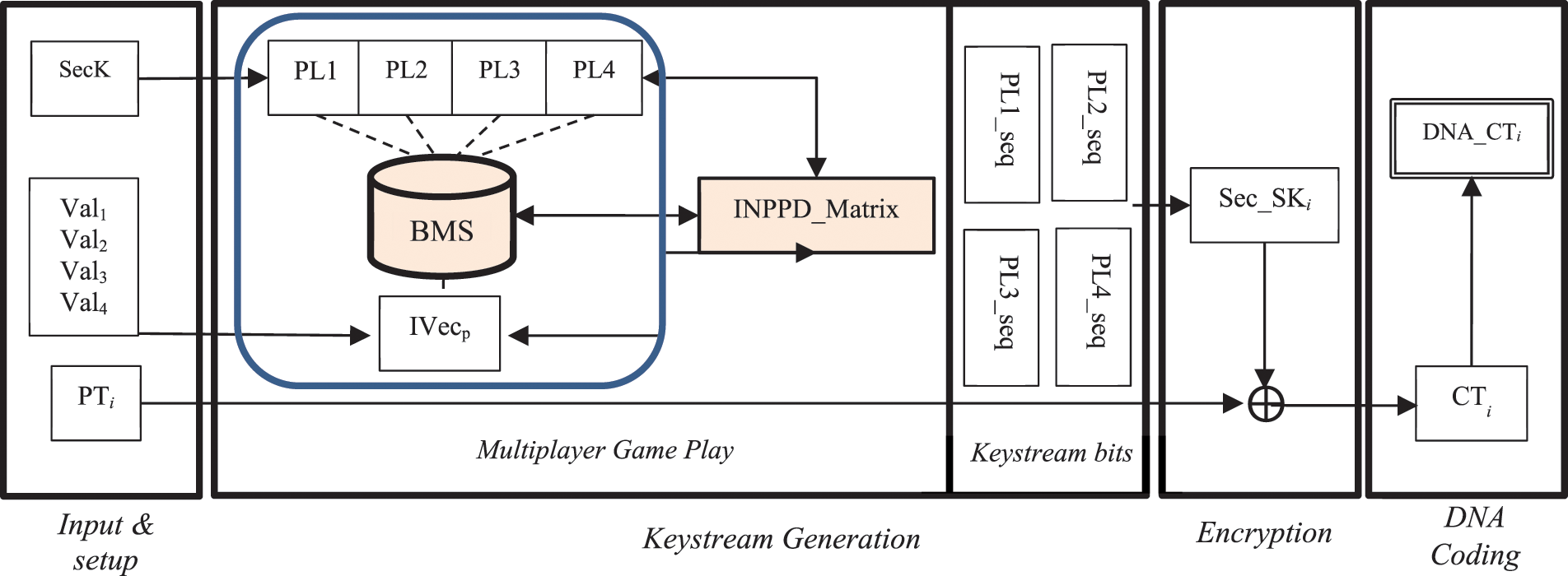
Figure 2: The enhanced design of the DNA-based stream cipher

4.2.1 Key/IV Setup

In this stage, both the SecK and IV are initialised. Like the original design, our enhanced design restricts the size of the SecK to 256 bits, while the IV is divided into four keys of 8-bit each (Val1 – Val4). The four Vi values are used to initialise the INPPD payoff matrix (Table 1) such that

C0=(Val1×Val2)+(Val3×Val4)mod 255(6)

D0=C0+1(7)

As for the general IV value (IVecp), we stick with the original scheme where IVecp is formulated according to Eq. (8). The overall algorithm of the Key/IV setup is introduced in Algorithm 1

IVp=Val3∥Val1∥Val4∥Val2∥Val3∥Val4∥Val1∥Val2(8)

4.2.2 Keystream Generation

Our enhanced stream cipher assumes different game scenarios than those that are assumed by the original design. The SecK is a set of players (PL1, PL2, PL3 and PL4) defined by Eqs. (9)–(12):

PL1[]=SecK[0−63](9)

PL2[]=SecK[64−127](10)

PL3[]=SecK[128−191](11)

PL4[]=SecK[192−255](12)

The set of PLi players plays against a set of opponents in an iterated n-player PD game. These opponents include IVecp and three randomly chosen players from a pool of players that adopt benchmark strategies (BMSs). These strategies are widely used in research papers discussing PD-based models [18]. Our pool includes the BMSs introduced in Table 3.

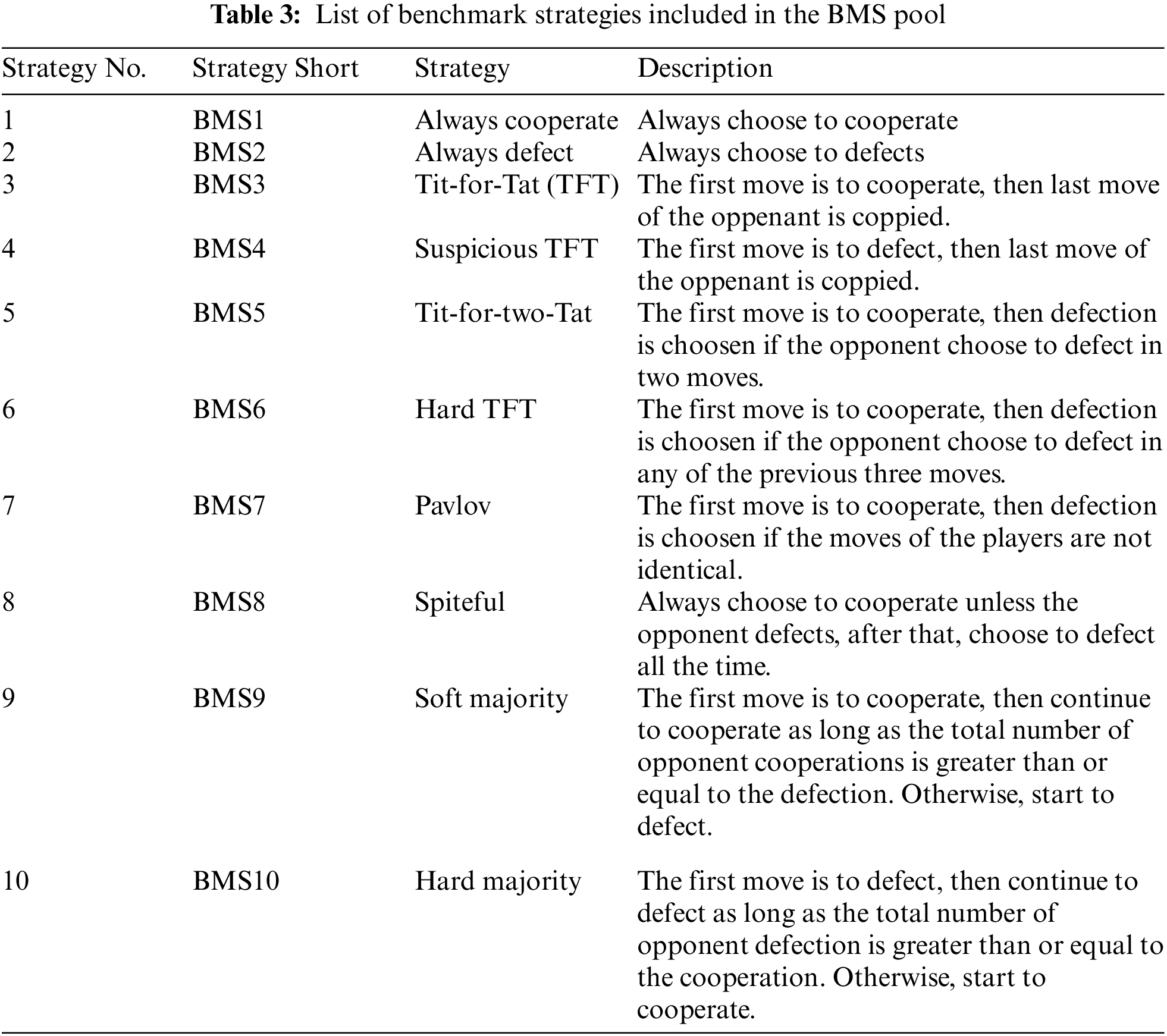
A given player can use 64 bits as part of its strategy in every single game, where bits 0 and 1 represent defection and cooperation strategies, respectively. In any game, each PLi plays against IVecp and three randomly chosen players from the BMS pool. Fig. 3 illustrates an example of a five-player PD game scenario. Note that each game is repeated Vali times, and the outcome of the last round is considered as the final output. Parallelism is implemented to expedite the process of generating keystreams (Sec_SK). Each PLi simultaneously plays against its opponents in an independent game. This is expected to dramatically enhance the performance of the stream cipher compared to the original design. The following formulas represent the parameters of each game:

Game1=Play((PL1,IVp,(BMSi,BMSj,BMSr)),INPPD_Matrix)repeatedVal1times(13)

Game2=Play((PL2,IVp,(BMSi,BMSj,BMSr)),INPPD_Matrix)repeatedVal2times(14)

Game3=Play((PL3,IVp,(BMSi,BMSj,BMSr)),INPPD_Matrix)repeatedVal3times(15)

Game4=Play((PL4,IVp,(BMSi,BMSj,BMSr)),INPPD_Matrix)repeatedVal4times(16)

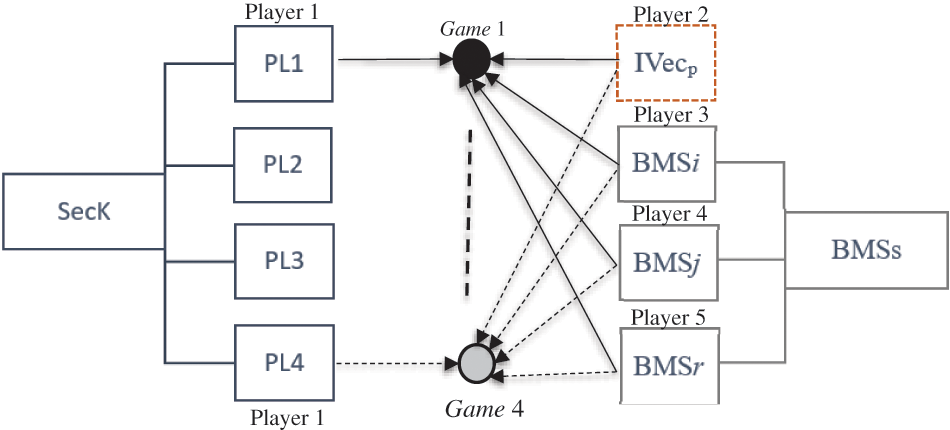
Figure 3: Parallel five-player PD game scenario

Recall that each game is composed of Vi rounds, where PL1 plays against the opponents such that PL1[k] plays against IVecp[k], BMSi[k], BMSj[k] and BMSr[k]. In relation to the INPPD matrix, each player receives a payoff value x. The value x will only be considered in the last round. The reason for repeating the game Vi times is to add more randomness to the process, as the behaviour of the players through different rounds is random and unpredictable.

When we reach the last round, the value x is appended to the sequence of PL1 (denoted by PL1_seq). The length of each sequence is 512 bits since each bit of PL1 will get a value x that is 8 bits long (8 × 64-bit = 512-bit). However, as the payoff value may exceed our range, we limit the resulting payoff value to 255, as in Eq. (17). Following the same scenario applied in PL1 to generate PL1_seq, the remaining PL2, PL3 and PL4 will play their games simultaneously to generate PL2_seq, PL3_seq and PL4_seq, respectively.

x=payoff((PL1,IVp,BMSi,BMSj,BMSr),INPPD_Matrix)mod 255(17)

Randomness is also applied in the way our design chooses the BMSi from the pool. The BMS pool is defined as a 2D array, where each strategy listed in Table 3 is mapped to one location in the array (Fig. 4). The association between the strategy code and the players is scrambled through a series of rotations: the strategy codes are rotated Val3 times to the left and Val4 times to the right. Accordingly, the actual strategy associated with the three selected BMSi in each game is chosen according to Eqs. (18)–(20):

BMSi=BMS(Val1+Val2)mod 11(18)

BMSi=BMS(Val2+Val3)mod 11(19)

BMSi=BMS(Val3+Val4)mod 11(20)

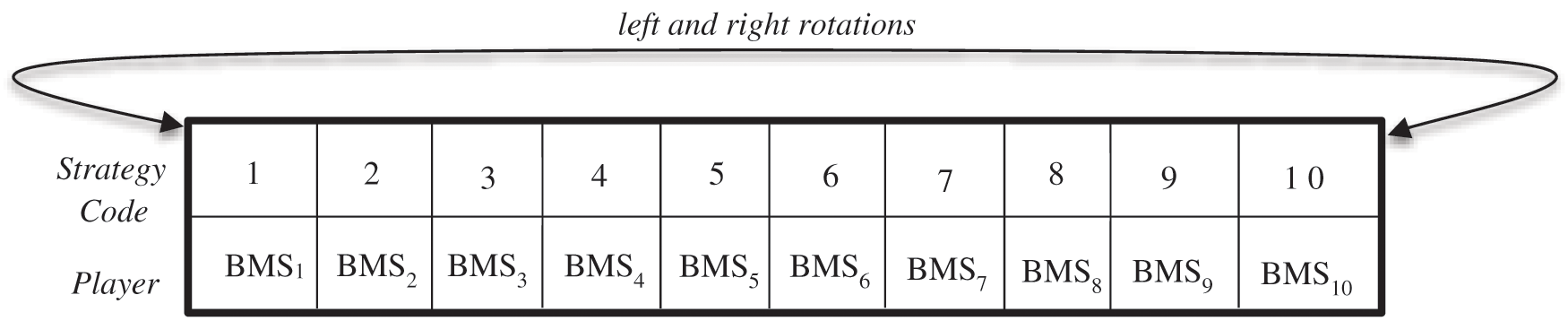
Figure 4: BMS pool structure

Like the original design, the sequences generated by each player are concatenated to generate the keystream bits. This process generates a total of 2,048 bits (4×512−bit) achieved by all participating players in one game. Hence, our enhanced scheme generates four times more bits than the original model since each player’s game is played independently. A total of 2,048 × 4 = 8,192 bits are generated by the four PLi players in each round.

As we generate the first set of keystreams, the INPPD matrix must be re-initialised with the new set of IV values (Eqs. (21)–(24)). Right and left circular rotations are applied on SecK as in Eqs. (25)–(26). This process will ensure that the next round of keystream generation is random enough to complete the encryption process.

Val1=(Val3+Val2)mod 255(21)

Val2=(Val2+Val3)mod 255(22)

Val3=(Val3+Val4)mod 255(23)

Val4=(Val4+Val3)mod 255(24)

SecK≫Val1⊕Val2(25)

SecK≪Val3⊕Val4(26)

The process of keystream generation is parallelised; multiple threads are created to run the keystream generation process over a separate copy of the BMS pool simultaneously. Each thread is associated with a player PLi to play its game against the selected opponents. Note that the actions of each player are stored in memory that is accessible by all the other players. This is important because some strategies in the BMS pool rely on opponents’ past actions to specify their own future actions. The multi-thread creation algorithm and the keystream generation processes are depicted in Algorithms 2 and 3, respectively. Upon completing the keystream generation process, the encryption method is called to encrypt the plaintext using the generated keystream.

4.2.3 Encryption and DNA Encoding

As the keystream bits are ready to use, the encryption function is called to XOR the plaintext with the keystream (Sec_SK). The encryption method uses the keystreams generated by the four threads (denoted by Sec_SK1, Sec_SK2, Sec_SK3 and Sec_SK4) sequentially. The first thread feeds the encryption method with the keystream bits (Sec_SK1) needed to complete the encryption. If the number of plaintext bits available for encryption exceeds the number of keystream bits, the second thread will feed the encryption method with more bits from Sec_SK2, and so on. Practically, once the thread consumes all its keystream bits, it will restart the process of keystream generation to create a new set of Sec_SK. Note that the encryption algorithm works sequentially on the Sec_SK to assure synchronisation with the text decryption process. The encryption process is implemented in Algorithm 4.

The DNA encoding process is implemented as in the original design of the cipher [17]. DNA encoding transform the ciphertext bits to DNA code (A, G, T and C), as depicted in Algorithm 5 [17]. Randomness over the DNA mapping is also applied to ensure the same level of security.

As for implementing the decryption process, we follow the same procedures by generating keystreams using four threads. However, DNA sequences are converted back to their binary representation based on the corresponding DNA mapping. Finally, the ciphertext is XOR’ed with the keystream to recover the plaintext.

5  Security Tests and Analysis

5.1 Balance and Statistical Analysis

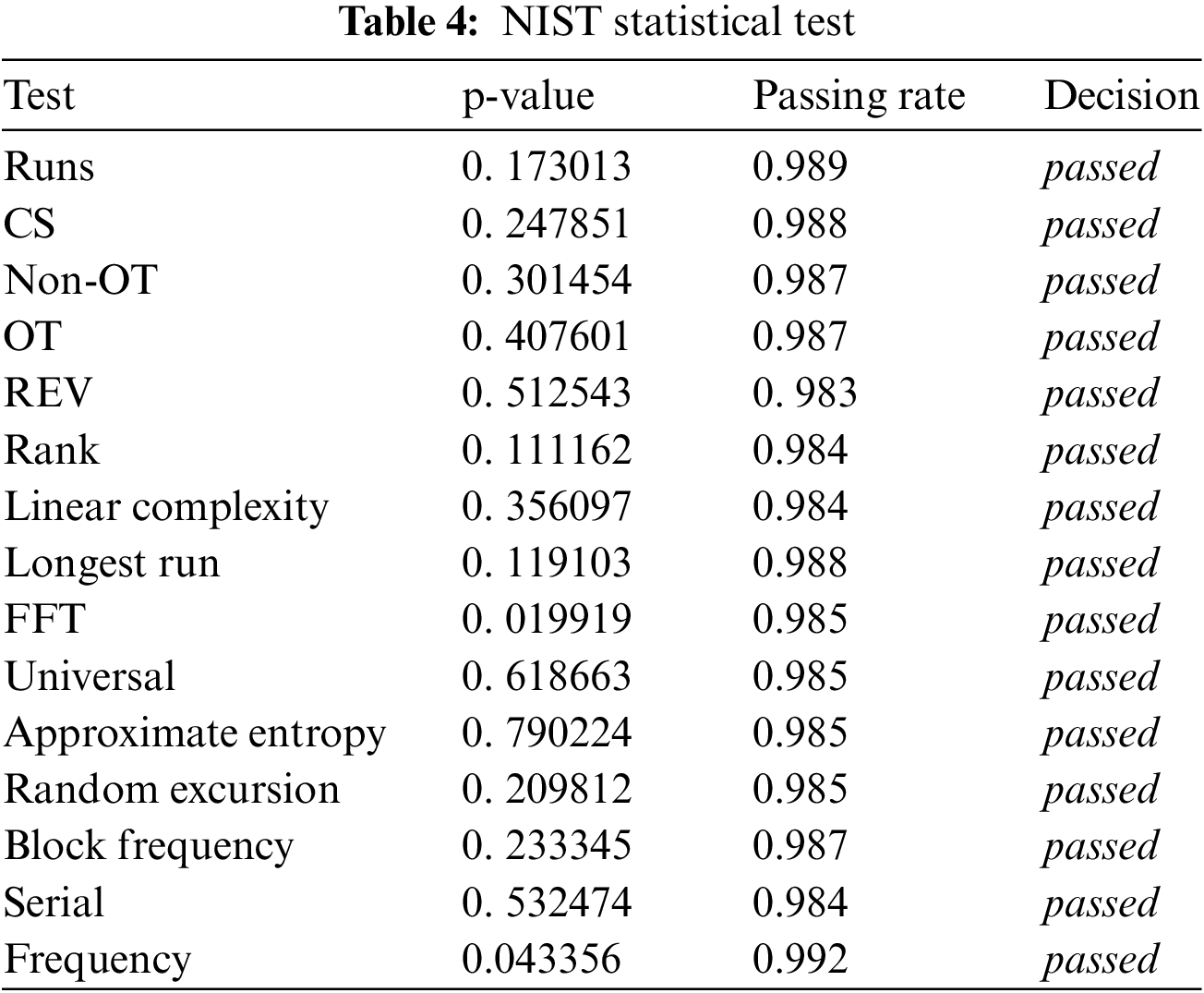
Following the evaluation standards, the NIST statistical test suite [28] was utilized to evaluate our enhanced stream cipher. Our enhanced cipher is measured in similar environments as those applied to the original cipher. Similar to [5,17], our tests relied on using a sample of size 1,000 1-Mbit. The test results indicate that our enhanced design maintains the same statistical properties and passes the NIST test (Table 4).

Since the DNA coding process is not modified, our statistical results show that no statistical bias is detected over the generated DNA bases (Table 5).

5.2 Testing the Avalanche Effect

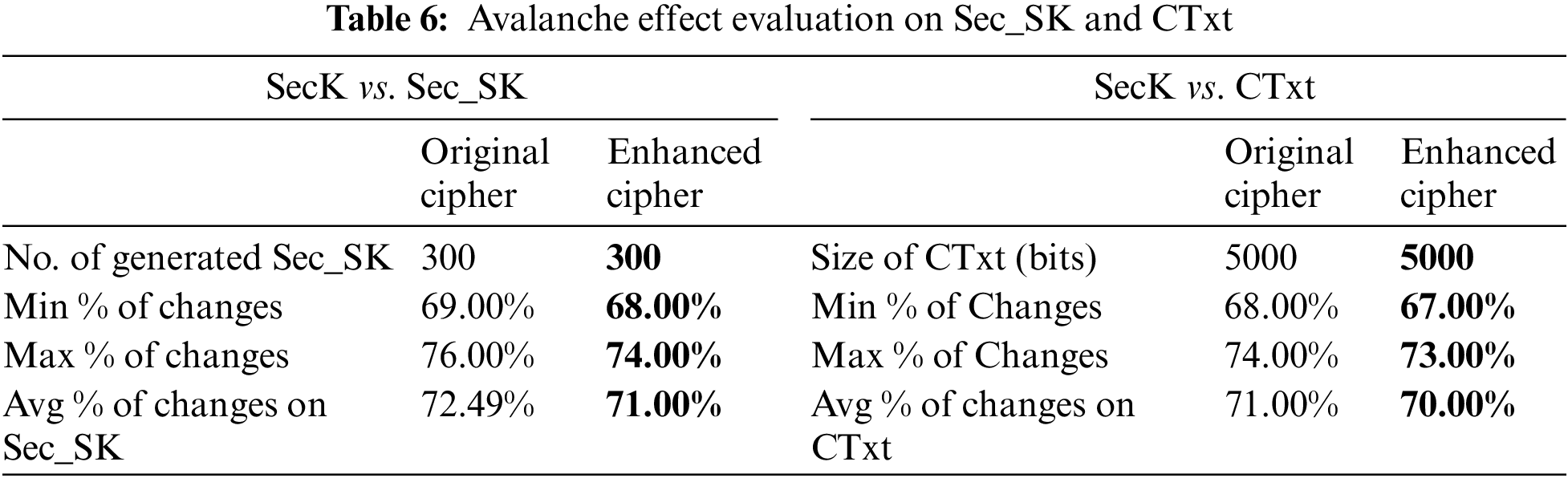
For enhanced cipher for this study, the avalanche effect of altering one bit is measured in the SecK. This is done for generating Sec_SK in comparison with the original design. It is also examined that the avalanche effect can be measured on the ciphertext. The analysis of the results presents that around 70% of the bits are altered right after modifying 1 bit in the SecK (Table 6), which is similar to the ratio achieved by the original design.

5.3 Security Attacks (Cryptanalysis)

5.3.1 Ciphertext-Only Attack

Our enhanced design relies on an INPPD matrix to produce encryption keys. Consequently, for any two exactly similar ciphertexts, the sequences of DNA that are generated are completely different. Therefore, the presented cipher is found resistant to ciphertext-only attacks.

5.3.2 Known-Plaintext Attack

The ciphertext is produced as a sequence of binary bits that result of implying XOR to the plaintext and the secret keys. This sequence of binary bits are later coded in DNA bases. As the DNA bases are chosen randomly, this guarantees that the cipher will produce two completely different ciphertexts for any two similar plaintexts. Accordingly, our algorithm presented in this study is found resistant to known-plaintext attacks.

5.3.3 Differential Attack

Our enhanced algorithm also showed resistance to differential attacks. The Sec_SK is not repeated in the generation procedure of the Sec_SK. Generating new Sec_SK requires re-initialising both the IVs and INPPD matrix by new random numbers. Accordingly, identical plaintext will be transferred to a totally different ciphertext, which conserve the presented cipher against differential attacks.

5.3.4 Brute-Force Attacks

In our enhanced cipher, the modification does not change the size of the input keys. Therefore, this attack has to compute 2256 + 232 guesses (for each thread) to disclose both the IV and the key. The time required to reveal the two keys is considered impossible to be achieved with available computational resources [17].

6  Complexity Analysis

Our complexity analysis shows that our enhanced cipher involves one extra process, which is responsible for generating multiple threads. This process is found to have a complexity of O(n). The other difference is found in the encryption algorithm, whose complexity is O(n2) due to the involvement of multiple loops applied over different plaintext segments received from different threads (Table 7).

7  Performance Analysis

The enhanced cipher is coded in Python and installed on a laptop with Intel Core i7® and 6 GB RAM, 500 GB HDD, 128 GB SSD and MS Windows 11 as the operating system. We used 20 Newsgroup dataset, which has also been used in similar research papers [15,17,29].

In addition to the original design, we compared the performance of our enhanced cipher to that of AES-128, RC4 ciphers [5,30] and the DNA-cipher proposed in [15]. The modifications applied in the enhanced cipher improve the average throughput of the encryption process, which is found to be around 1,877.22 Mbit/s. Indeed, our enhanced cipher achieved a throughput that is about 34% higher than that of the original design. As a result, it outperforms the original design and nearly matches the performance of the RC4 and AES-128 ciphers.

The reason for this improvement in the throughput is the parallelism implemented in the enhanced design. Four threads operate simultaneously over an independent set of parameters to generate the keystream sequences. However, super-linear speedup could not be achieved since the encryption process is carried out sequentially over the plaintext sequences. Table 8 presents the different throughputs achieved by the tested stream ciphers.

8  Conclusion

In this paper, we presented an enhanced design of the DNA-coded stream cipher introduced in [17]. We focused on improving two main areas: security and performance. The original design of the DNA-coded stream cipher was secure and performed well compared to other DNA-based stream ciphers. However, its performance did not reach a sufficiently competitive level to replace well-known stream ciphers.

One contribution of our enhanced design was to replace the 2PD game model with an INPPD game model. This replacement added one more layer of randomness to the behaviour of the keystream generation. In addition, we introduced a new pool of benchmark strategies, which includes 10 well-known strategies to represent the behaviour of three randomly chosen players included in each game. This contribution allowed our new design to enhance the overall security of the keystream generation process.

However, adding these extra layers makes the encryption method more time-consuming. Hence, parallelism is introduced through the multi-threading paradigm. Multiple threads are created to run independently in order to generate keystream sequences for encryption purposes. The experimental results show that the multi-threading model assisted our stream cipher to achieve a throughput of 1,877 Mbit/s. This throughput represents a 34% enhancement ratio compared to the original design. The achieved throughput expands the capabilities of stream cipher in different security applications.

From the security and statistical perspectives, our analysis shows that the enhanced design maintained the same level of high security against cryptographic attacks. NIST statistical tests also showed that no statistical biases were detected in the generated keystream. These results enabled our enhanced DNA-coded stream cipher to reach a practical level of performance, and it can be considered a secure alternative stream cipher in many applications.

Acknowledgement: The author presents his thanks to the Arab Open University, Saudi Arabia for providing consistant support in completing this research.

Funding Statement: No funding was needed in the study.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

1. P. Ekdahl and T. Johansson, “A new version of the stream SNOW,” in Selected Areas in Cryptography. Berlin, Heidelberg: Springer, pp. 47–61, 2003. [Google Scholar]

2. C. De Cannière, O. Dunkelman and M. Knežević, “KATAN and KTANTAN — A family of small and efficient hardware-oriented block ciphers,” in Cryptographic Hardware and Embedded Systems - CHES 2009, vol. 5747. Berlin, Heidelberg: Springer, pp. 272–288, 2009. [Google Scholar]

3. D. Moon, D. Kwon, D. Han, J. Lee, G. Ryu et al., T-Function Based Stream Cipher TSC-4. ECRYPT Stream Cipher Project, 2006. [Online]. Available: https://www.ecrypt.eu.org/stream/papersdir/2006/024.pdf. [Accessed 10 September 2022]. [Google Scholar]

4. C. Jansen, T. Helleseth and A. Kholosha, “Cascade jump controlled sequence generator and pomaranch stream cipher,” in New Stream Cipher Designs, vol. 4986. Berlin, Heidelberg: Springer, pp. 224–243, 2008. [Google Scholar]

5. J. Teh and A. Samsudin, “A Stream cipher based on spatiotemporal chaos,” IETE Journal of Research, vol. 63, no. 3, pp. 346–357, 2017. [Google Scholar]

6. A. Kosek, An Exploration of Mathematical Applications in Cryptography. Ohio: Ohio State University, 2015. [Google Scholar]

7. F. Cavaliere, J. Mattsson and B. Smeets, “The security implications of quantum cryptography and quantum computing,” Network Security, vol. 2020, no. 9, pp. 9–15, 2020. [Google Scholar]

8. X. Wang and Y. Su, “An audio encryption algorithm based on dna coding and chaotic system,” IEEE Access, vol. 8, pp. 9260–9270, 2020. [Google Scholar]

9. J. Katz, “Bridging game theory and cryptography: Recent results and future directions,” Theory of Cryptography, vol. 4948, pp. 251–272, 2008. [Google Scholar]

10. X. Liang, Z. Yan, R. Deng and Q. Zheng, “Investigating the adoption of hybrid encrypted cloud data deduplication with game theory,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 3, pp. 587–600, 2021. [Google Scholar]

11. S. Ergün, B. Kırlar, S. Gök and G. Weber, “An application of crypto cloud computing in social networks by cooperative game theory,” Journal of Industrial & Management Optimization, vol. 16, no. 4, pp. 1927, 2020. [Google Scholar]

12. J. Zhou, J. Li and X. Di, “A novel lossless medical image encryption scheme based on game theory with optimized roi parameters and hidden roi position,” IEEE Access, vol. 8, pp. 122210–122228, 2020. [Google Scholar]

13. B. Kırlar, S. Ergün, S. Gök and G. Weber, “A game-theoretical and cryptographical approach to crypto-cloud computing and its economical and financial aspects,” Annals of Operations Research, vol. 260, no. 1, pp. 217–231, 2018. [Google Scholar]

14. S. Liu, A. Paul, G. Zhang and G. Jeon, “A game theory-based block image compression method in encryption domain,” The Journal of Supercomputing, vol. 71, no. 9, pp. 3353–3372, 2015. [Google Scholar]

15. S. Zhu and C. Zhu, “Secure image encryption algorithm based on hyperchaos and dynamic dna coding,” Entropy, vol. 22, no. 7, pp. 772, 2020. [Google Scholar] [PubMed]

16. P. Pavithran, S. Mathew, S. Namasudra and P. Lorenz, “A novel cryptosystem based on DNA cryptography and randomly generated mealy machine,” Computers & Security, vol. 104, no. 1, pp. 102160, 2021. [Google Scholar]

17. K. Suwais, “Stream cipher based on game theory and dna coding,” Intelligent Automation & Soft Computing, vol. 33, no. 3, pp. 1815–1834, 2022. [Google Scholar]

18. S. Almanasra, “Evolutionary model for the iterated n-players prisoners’ dilemma based on particle swarmoptimization,” Journal of Theoretical and Applied Information Technology, vol. 97, no. 5, pp. 1555–1570, 2019. [Google Scholar]

19. S. Almanasra, K. Suwais and M. Rafie, “Adaptive automata-based model for iterated n-players prisoners’ dilemma,” International Arab Journal of Information Technology, vol. 13, no. 1, pp. 85–92, 2016. [Google Scholar]

20. X. Yao and P. Darwen, “An experimental study of N-person iterated prisoner's dilemma games,” in Progress in Evolutionary Computation, X. Yao (Ed.vol. 956, pp. 90–108, Berlin: Springer,1995. [Google Scholar]

21. S. Almanasra and K. Suwais, “3D model for optimising the communication topologies of iterated N-players prisoners’ dilemma,” International Journal of Applied Decision Sciences, vol. 11, no. 4, pp. 420–439, 2018. [Google Scholar]

22. X. Li, C. Zhou and N. Xu, “A secure and efficient image encryption algorithm based on DNA coding and spatiotemporal chaos,” International Journal of Network Security, vol. 20, pp. 110–120, 2018. [Google Scholar]

23. M. Sohal and S. Sharma, “BDNA-A DNA inspired symmetric key cryptographic technique to secure cloud computing,” Journal of King Saud University- Computer and Information Sciences, vol. 34, no. 1, pp. 1417–1425, 2018. [Google Scholar]

24. S. Basu, M. Karuppiah, M. Nasipuri, A. Halder and N. Radhakrishnan, “Bio-inspired cryptosystem with DNA cryptography and neural networks,” Journal of Systems Architecture, vol. 94, no. 4–5, pp. 24–31, 2019. [Google Scholar]

25. Z. Qiu-yu, J. Han and Y. Ye, “An image encryption algorithm based on image hashing, improved chaotic mapping and DNA coding,” IET Image Processing, vol. 13, no. 6, pp. 2905–2915, 2019. [Google Scholar]

26. Q. Liu and L. Liu, “Color image encryption algorithm based on DNA coding and double chaos system,” IEEE Access, vol. 8, pp. 83596–83610, 2020. [Google Scholar]

27. M. Meftah, A. Pacha and N. Hadj-Said, “DNA encryption algorithm based on Huffman coding,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 25, no. 6, pp. 1831–1844, 2022. [Google Scholar]

28. A. Rukhin, J. Soto and J. Nechvatal, A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. USA: National Institute of Standards and Technology, 2010. [Google Scholar]

29. K. Lang, “20 Newsgroups,” [Accessed 10 October 2021], 2008. [Online]. Available: http://qwone.com/~jason/20Newsgroups/ [Google Scholar]

30. “ECRYPT Stream Cipher Project,” [Accessed 20 September 2021], 2012. [Online]. Available: https://www.ecrypt.eu.org/stream/ [Google Scholar]