Optimization of Resource Allocation in Unmanned Aerial Vehicles Based on Swarm Intelligence Algorithms

1  Introduction

The Internet of Things has evolved and advanced over the past few years as a result of the development of wireless communication technology, specifically fifth-generation mobile communication technology (5G) and 5G beyond [1]. The IoT has been implemented in numerous fields, including agriculture [2], healthcare [3], smart infrastructure [4], and industry [5]. The high data rate, low latency, cost-effectiveness, and consistent Quality of Service (QoS) [6] are examples of Internet of Things with 5G challenges that must be overcome. According to the application scenario, these challenges transformed into optimization issues. Numerous researchers have been drawn to these problems, and many promising solutions have been attempted. You et al., for instance, provides an overview of several promising AI research directions for 5G technologies [7].

Sensors play a vital role in the Internet of Things systems. IoT systems, which are required for decision-making and execution, require data. In a typical scenario, sensors collect data and transmit it through networks to a location for further processing in real-time. In addition, the form sensors can operate independently or be integrated into a complex device. For scenarios such as environment monitoring and collecting multiple types of data, sensors with distinct functions can form a specialized unit.

In this paper, a potential scenario for a marine sensor system is presented. The sensors system consists of multiple sensor stations located in the ocean, beyond the range of terrestrial wireless communication networks. These sensor stations float at a specific location on the sea cliff. These stations lack a hardwired power and communication connection. Since solar and ocean waves generate the station’s energy, its energy resource is quite limited (it can not support satellite communication). The collected data are saved on storage and do not require real-time transmission. Then, a solution for retrieving data from this system is provided. Unmanned Aerial Vehicles (UAVs) are utilized as data retrievers in this system. The UAVs are fuel-powered and rich in resources. They retrieve data daily or weekly, depending on operational requirements. Using Wireless Power Transfer (WPT) technology, the UAVs provide power to the communication module on the sensor stations as they fly over them. The module is activated when it has sufficient power [8–10]. The uplink transmits the sensor station’s data to the UAV. Data transmission should conclude during the valid pass-through time, and sensor stations’ excess energy should be conserved. Maximize the minimum data rate to ensure that data can be transmitted quickly.

This paper’s contribution is summarized in the following section. First, a scenario of the UAV application is described in this paper. The model corresponds to the specification, and the optimization problem is formulated. A method that converts multi-decisions into a row vector is then implemented to qualify the problem for most swarm intelligence algorithms. Two cutting-edge swarm intelligence algorithms are then utilized to solve the optimization problem. The outcomes of the two algorithms are analyzed and compared.

Section 2 reviews some related work in IoT and UAV-assisted systems. In Section 3, two swarm intelligence algorithm is introduced, and the scheme with them is claimed. Section 4 represents the system model and the settings of the proposed method. In Section 4, the experiment is performed, and a discussion is made on the results. The conclusion of this paper is made at Section 5.

2  Related Works

As IoT technologies advance, IoT systems cover more perspectives and can be implemented in a wider variety of scenarios. Numerous related works improve IoT. Qian et al. [11] proposed an edge computing-IoT over power line communication paradigm to reduce transmission latency. They created a platform for distributed edge computing to serve IoT devices and then proposed a cache-enabled method for storing popular content. In the context of small-cell base-station networks, Li et al. [12] investigated a computing task offloading problem. A belief propagation algorithm is proposed to optimize task allocation, and the objective function is decomposed into several local utilities. They are ultimately transformed into estimates of marginal distributions before being solved by a distributed belief propagation algorithm.

IoT technologies are applicable not only on land but also on the water. Internet of Things-based marine environment monitoring system designed by Haitao C. et al. The system is comprised of the information management subsystem, the data collection subsystem, and the monitoring terminal subsystem. It is constructed with 4G and Zigbee communication technologies. Luccio et al. introduced the Internet of Floating Things (IoFT) in [13], which extends the Internet of Things to the maritime scenario. This study presented a framework for collecting coastal data from sensors and devices installed on marine equipment. The marine data was collected and utilized to predict specific applications. Nonetheless, both IoT systems in works [13] and [14] on the coast are covered by shore-based cellular stations. Kavuri et al. [15] analyzed the onshore Narrow Band-IoT (NB-IoT) performance for container tracking during near-shore vessel navigation using three different schemes. The relay-based solution effectively distributes transmission requests, enhancing the system’s operation. Moreover, UAV relaying is used to extend base station coverage. While the sensors system may be far from land or even in the middle of the ocean, sending data from the system away from the land-based communication method is impossible. Satellite communication is a promising but limited method. The capacity of satellite communication to transmit data is significantly greater than that of cellular networks. Therefore, UAVs could be utilized to address this issue. Song et al. [16] reviewed UAV communications prototypes and experiments. Two promising paradigms of UAV communications are discussed, namely cellular-connected UAVs and UAV-enabled aerial communication platforms, along with their respective scenarios. Furthermore, UAVs are also utilized to solve problems in various fields [17–19].

There are numerous applications for UAVs in wireless networks described in other works. Khalifeh et al. [20] incorporated UAVs into smart city wireless sensor networks. They propose using UAVs as data mules to transfer monitoring data from sensor nodes to the remote control center for further analysis and decision-making. H. Peng and X. Shen investigate a resource management problem for UAV-assisted vehicular networks in the reference [21]. Feng et al. [22] outlined a UAV-assisted millimeter-wave multiple-input-multiple-output non-orthogonal multiple-access network and attempted to maximize its downlink sum rate. The Mobile Edge Computing (MEC) server resource allocation is formulated as a distributive optimization problem in order to maximize the number of QoS-offloaded tasks. Li et al. [23] proposed an algorithm to optimize the energy efficiency of communication services based on UAVs. Due to their high mobility, agility, and low cost, UAVs are utilized to provide communication services in areas where none exist. Sharma et al. [24] utilized UAVs for forest fire detection applications. The proposed is an effective architecture for energy-efficient UAV communications under general constraints.

Optimization issues in UAV communication networks are widely discussed. There are works concerned with optimizing force and trajectory [25,26]. Some components optimized the network’s time or latency [27,28]. They may employ standard and conventional mathematical or cutting-edge techniques in these works. Alnagar et al. [26] proposed a power control scheme for UAV-assisted networks based on a Q-learning algorithm. In addition, works [29,30] have considered both time and energy allocation. However, these two studies focus on the model using Matlab’s CVX tools (CVX is the name of a Matlab-based modeling system for convex optimization), whereas the optimization method requires more attention.

In addition, additional works address resource allocation in UAV-related communications. Xu et al. [31] proposed a long short-term memory with generative adversarial networks framework to solve the resource allocation problem that maximizes the sum rate of UAVs-served communications jointly, taking transmission power, transmission mode, frequency spectrum, relay selection, and the trajectory into account. The proposed framework has the benefit of tracking and predicting the mobility of UAVs. In work [32], a similar method is used to maximize bandwidth efficiency by adopting network slicing and simultaneously ensuring the transmission rate and latency. Their additional work [33] combines the deep deterministic policy gradient and long short-term memory network in order to optimize the resource allocation problem of UAV-assisted energy harvesting-powered device to device Communications. A deep deterministic policy gradient is utilized to determine the optimal strategy, and a long short-term memory network is employed to accelerate convergence by extracting previous information. Hosseini et al. [34] created a resource allocation scheme for UAV-supported vehicular communication. Difference-of-concave-functions approximation-based radio resource allocation and Stackelberg game-based radio resource allocation are used to solve the resource allocation-formed mixed-integer non-linear programming problem. The effectiveness of the scheme and the Stackelberg game-based method has been demonstrated. There are numerous communication scenarios in which UAVs participate, and resource allocation optimization methods are designed for specific procedures.

3  Optimization Algorithms

3.1 Harris Hawks Optimization

Harris hawks optimization (HHO) is a swarm-based metaheuristic algorithm designed by Heidari et al. [35]. The most specific method used by Harris hawks to capture prey is known as the “surprise pounce,” in which multiple hawks attack the prey from different directions and simultaneously converge on it with a quick dive. The duration of the entire behavior is brief, and Harris hawks capture their prey in a matter of seconds.

The HHO can be generally divided into three phases: the exploitation phase, the transition from exploration to exploitation, and the exploitation phase. In addition, the exploitation phase consists of four strategies: soft besiege, hard besiege, soft besiege with quick dives, and hard besiege with quick dives. The three phases are executed sequentially, and the four strategies are implemented in accordance with the various situations.

In the algorithm, the exploration phase is modeled as

X(t+1)={Xrand(t)−u1|Xrand(t)−2u2X(t)|,q≥0.5(Xprey(t)−Xm(t))−u3(LB+u4(UB−LB)),q<0.5(1)

where X(t+1) is the position vector of the hawk in the next iteration, Xprey is the position of the prey, Xrand(t) is the position vector of a randomly selected hawk, Xm(t) is the average position of the current population of hawks, X(t) is the current position vector of the hawk, q is a random number that decides which method is used to update the position, and its range is (0,1), r1, r2, r3, and r4 are random numbers in the field of (0,1), helping the update of position, LB and UB are the lower bound and upper bound of solution.

The average position of hawks is obtained by

Xm(t)=1N∑i=1NXi(t)(2)

where Xi(t) is the position vector of each hawk in the current iteration, and N denotes the number of the hawk population.

The prey’s energy decreases, so exploration transit to exploitation. Hence, the formula is given as

Eprey=2Einit(1−tT)(3)

The algorithm considers a complex situation between hawks and the prey. A variable v describes the chance of the prey performing a successful escape. In short, the soft besiege will be executed when Eprey≥0.5, while the hard besiege will be performed when Eprey<0.5, and if r<0.5, a rapid dive will be added with besieging.

When r≥0.5 and Eprey≥0.5, soft besiege is performed. The position vector is updated as

X(t+1)=ΔX(t)−Eprey|JXprey(t)−X(t)|(4)

ΔX(t)=Xprey(t)−X(t)(5)

where ΔX(t) is the difference between the position vector of the prey and the current location in the current iteration, J=2(1−r5) denotes the random jump strength of the prey when escaping, and r5 is a random number in the range of (0,1).

When r≥0.5 and Eprey<0.5, hard besiege is performed. The position vector is updated as

X(t+1)=Xprey(t)−Eprey|ΔX(t)|(6)

When r< 0.5 and Eprey≥0.5, soft besiege with rapid dives is performed. The position vector is updated as

X(t+1){Y, if F(Y)<F(X(t))Z, if F(Z)<F(X(t))(7)

Y=Xprey(t)−Eprey|JXprey(t)−X(t)|(8)

Z=Y+S×LF(D)(9)

where D is the dimension of the problem and S is a random vector with the size of 1×D. LF is the levy flight function, which is calculated by using

LF(x)=0.01×w×ϖ|k|1λ(10)

ϖ=(Γ(1+λ)×sin⁡(πλ2)Γ(1+λ2)×λ×2(λ−12))1λ(11)

where w, k are random values within (0,1), λ is a constant set to 1.5.

When r<0.5 and Eprey≥0.5, soft besiege with rapid dives is performed. The position vector is updated as

X(t+1){Y, if F(Y)<F(X(t))Z, if F(Z)<F(X(t))(12)

Y=Xprey(t)−Eprey|JXprey(t)−Xm(t)|(13)

Z=Y+S×LF(D)(14)

where Xm(t) is the average position of hawks is obtained by Eq. (2).

3.2 Whale Optimization Algorithm

Whale Optimization Algorithm (WOA) is also a metaheuristic algorithm based on a swarm [36]. It was conceptualized by Mirjalili et al. based on the humpback whale’s predation process. The humpback whales use a unique method to hunt their prey, which consists of producing distinctive bubbles along a path shaped like a number nine.

The whale optimization algorithm consists of three phases: prey search, prey encirclement, and bubble-net attack. This follows the order in which whales hunt their prey, and the purpose of each stage is readily apparent.

The coefficient vectors A and C are introduced for the mathematical model, and they are calculated as

A=2a⋅g−a(15)

C=2g(16)

where a is linearly decreased from 2 to 0 in the iterations and g is a random vector in [0,1].

When searching for prey, the position vector of the whale can be updated by

X(t+1)=Xrand(t)−A⋅G(17)

G=|C⋅Xrand(t)−X(t)|(18)

where Xrand(t) is a random position vector from the current population.

When encircling prey, the position vector of the whale can be updated by

X(t+1)=Xbest(t)−A⋅G(19)

G=|C⋅Xbest(t)−X(t)|(20)

where Xbest(t) is the position vector of the best solution in the current iteration, which can be updated in each iteration if a better solution is found.

For the bubble-net attack, there have two approaches: shrinking encircling mechanism and spiral updating position. One of the two approaches is used each time according to p, a random number in [0,1]. The position vector of the whale can be updated by

X(t+1){Xbest(t)−A⋅G,p<0.5G′⋅ebl⋅cos⁡(2πl)+Xbest(t),p≥0.5(21)

G′=|Xbest(t)−X(t)|(22)

where b is a constant that defines the shape of the spiral, i is a random number in [−1,1].

4  Research Methodology

4.1 System Model

A UAV-assisted marine sensors system can have many UAVs and sensors. This paper discusses the scenario with two UAVs flying through two neighboring sensors to express the problem and show the result easily. In such a system, sensors exist as floating sensor stations.

Fig. 1 shows a planned view of the selected part during the two UAVs flying, there is a start point where UAV1 has built a connection with Sensors Station 1, and UAV2 has made a connection with Sensors Station 2. In the figure, the line with ‘*’ is the trajectory of UAVs, and the big red star is the location of the sensor station. The location of each sensor station can be represented as Loci=(xi,yi,0),i∈{1,2}, i represents the code of Sensors Station. Furthermore, the endpoints are the points that they cut off the connection. For this part, the total period is characterized as T. Then, the flight time T is divided into n parts equally, each of which is called a time slot. These time slots can be made into a set, showing 𝒩={1,2,⋅⋅⋅,n}. The length of each time slot is calculated as δ=Tn. As each time slot interval is short, it can be assumed that UAVs are hovering on the exact position in each time slot. Therefore, the positions of UAVs can be described with a set, as Posj={ (xj[ 1 ],yj[ 1 ],zj[ 1 ]),(xj[ 2 ],yj[ 2 ],zj[ 2 ]),xj[ 3 ],yj[ 3 ],(zj[ 3 ]),⋅⋅⋅,(xj[ n ],yj[ n ],zj[ n ]) }, j represents the code of UAV, and n represents the n−th time slot. The distance between Sensors Station i and UAV j in time slot n can be calculated as,

disi,j[n]=|Posj[n]−Loci|, i,j∈{1,2}(23)

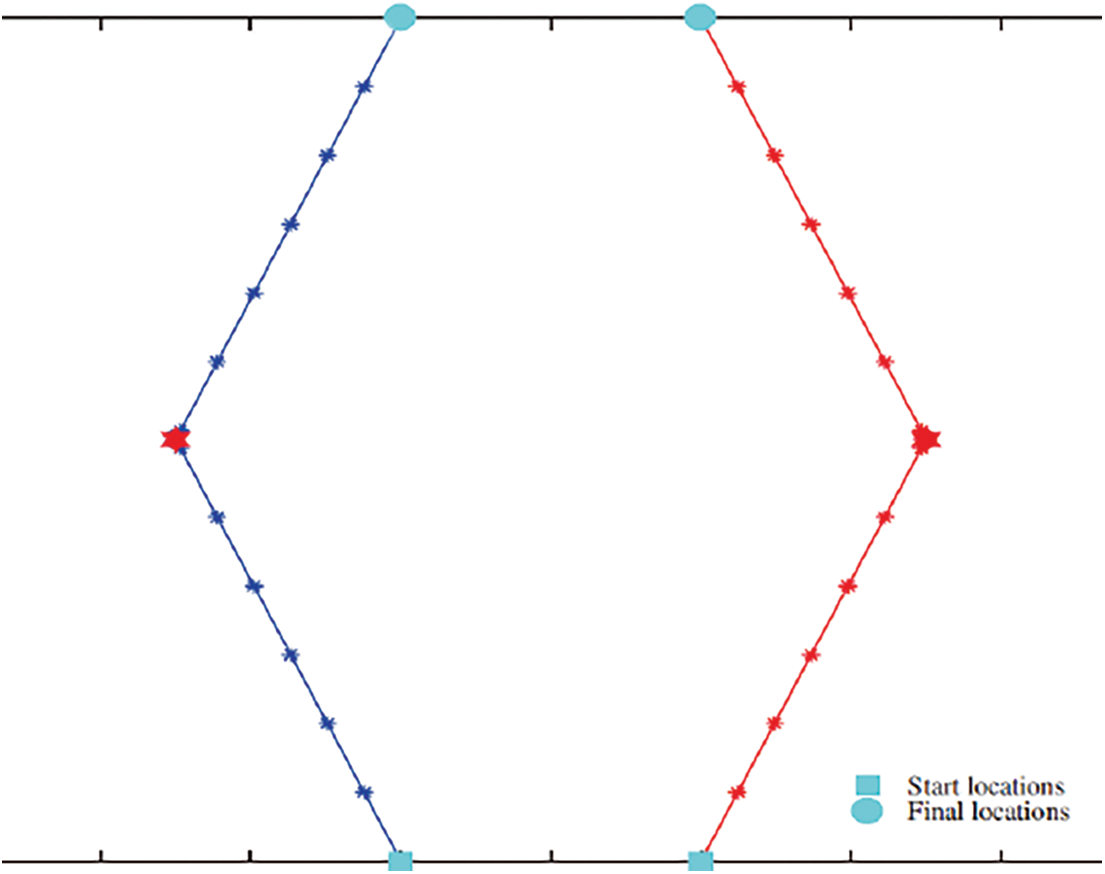
Figure 1: Plan view of two UAVs flying trajectory

In order to maximize efficiency, the flight paths of two unmanned aerial vehicles (UAVs) are predetermined based on the known locations of sensor stations. Each UAV possesses sufficient energy. Before sensors are detected, they will continually transmit power on a particular channel using WPT technologies. When they are within a specific range of sensor stations, they will gain enough energy to transmit a unique beacon to alert the UAV to their presence. Then, unmanned aerial vehicles can prepare to receive data from the sensors station. To ensure the integrity and validity of the data collected by UAVs from sensor stations, the sensor stations will only transmit their data to the first UAV that connects and will complete the transmission before disconnecting.

The channel power gain between Sensors Station i and UAV j in time slot n is given by [37].

hi,j[n]=βdisi,j2[n]=β|Posj[n]−Loci|2, i,j∈{1,2}(24)

where β is the reference channel power gain.

While transmitting data, it can receive energy from the other UAVs without the interface for the communication link. But if not only one communication link is sending data, it will cause an interface for each other. Therefore, the time used to transmit data at Sensors Station i during time slot n is represented as δDi[n], and the time used to transfer energy at Sensors Station i during time slot n is defined as δEi[n]. Suppose that Sensors Station i will transmit its data to UAV i.

For the case that δEi[n]>δDi[n], Sensors Station can harvest the energy from both UAV i and UAV j. The energy harvested at Sensors Station i from UAV i can be calculated as

Ei,i[n]=δEi[n]ηPhi,i[n](25)

where η is the energy conversion efficiency at Sensors Station, P is the energy power sent from the UAV.

The energy harvested at Sensors Station i from UAV j can be calculated as

Ei,j[n]=(δEi[n]−δDi[n])ηPhi,j[n](26)

Total energy received by Sensors Station i is given by

Ei[n]=Ei,i[n]+Ei,j[n]=δEi[n]ηPhi,i[n]+(δEi[n]−δDi[n])ηPhi,j[n](27)

The signal-to-interference plus noise ratio at UAV i can be calculated as

γi[n]=qi[n]hi,i[n]σ2(28)

where qi[n] is the transmission power for data of Sensors Station i in time slot n, σ2 is the received noise power.

Then, the average data rate can be calculated as

ri[n]=δDi[n]δlog2(1+qi[n]hi,i[n]σ2)(29)

For the case that δEi[n]<δDi[n], Sensors Station can harvest the energy only from UAV i. And there exists an interference for part of data transmission. The energy harvested at Sensors Station i from UAV i can be calculated as

Ei[n]=Ei,i[n]=δEi[n]ηPhi,i[n](30)

The data rate can be calculated similarly to Eq. (29) for the period when interference does not occur. For the rest period with interference, the signal-to-interference plus noise ratio at UAV i can be calculated as

γi,j[n]=qi[n]hi,i[n]qj[n]hj,i[n]+σ2(31)

The data rate for the interference part should be calculated by

ri[n]wi=δDi[n]−δEi[n]δlog2(1+qi[n]hi,i[n]qj[n]hj,i[n]+σ2)(32)

As for the data rate for the whole time slot, it consisted of two parts described, and it should be given as

ri[n]=δDi[n]δlog2(1+qi[n]hi,i[n]σ2)+δDi[n]−δEi[n]δlog2⁡(1+qi[n]hi,i[n]qj[n]hj,i[n]+σ2)(33)

4.2 Problem Formulation

The cumulative energy harvested by Sensors Station i at the time slot k should be calculated by

Eki=∑n=1kEi[n](34)

The cumulative energy consumed by Sensors Station to transmit data at the time slot k should be calculated by

qki=∑n=1kqi[n]δDi[n](35)

The average data rate throughput from Sensors Station i to UAV i during the whole flight time T and the final average data rate throughput is calculated as

Ri=1N∑n=1Nri[n](36)

R=R1+R22(37)

It should have enough throughput to ensure the data can be totally transmitted. The purpose is to maximize the minimum data throughput by jointly optimizing the time allocation and transfer power under limited conditions. The optimization problem is formulated as

max{T,Q}⁡minRs.t. qki≤Eki,∀i∈{1,2}, ∀k∈𝒩,0≤δDi[n]≤δ,∀n∈N0≤δEi[n]≤δ,∀n∈N δDi[n]+δEi[n]≤δ,∀n∈N(38)

where 𝒯={δEi[n], δDi[n]},∀i∈{1,2},∀n∈N is the time allocation set, and 𝒬={qi[n]},∀i∈{1,2},∀n∈N is the transmit power allocation set.

4.3 Optimization Implementation

During the optimization of the model, two sets of variables must be considered, wherein the time allocation includes a portion of the energy allocation. The number of time slots has a significant impact on the number of variables, as allocations are made accordingly. On the assumption that UAV i is responsible for the data transmission of Sensors Station i, each time slot should contain i variables. The situation regarding transmit power allocation, a crucial factor in energy allocation, is comparable to the previous instance. Consequently, the optimal representation of allocation decisions is two matrices of two dimensions. In swarm intelligence algorithms, one population unit is represented as a one-dimensional row vector. A mapping matrix is introduced to remap the allocations into a row vector in order to resolve this mismatch. In addition, each decision is accessible via the remapped index.

The allocation decision must rigorously adhere to the constraints. A portion of the constraints are ensured by the process that generates the allocation decision, but the remainder must be verified whenever the allocation changes. Therefore, a check function is implemented to ensure the constraints. If an allocation decision does not satisfy the constraint, it is immediately replaced with one generated at random.

5  Results and Discussion

In this section, numerical results are provided to validate the performance of the proposed solution. The algorithms are coded in MATLAB 2021a, and all tests are performed on a PC with Intel i5-8250U@3.2 GHz and 8GB of RAM.

In the simulation, the noise power that the UAV receives σ2 is assumed to be −100 dBm. The reference channel power gain β0 is set as −30 dB. The UAVs fly over the sensors station at a height of 5 m. The valid pass-through time is 30 s and is separated into 48 time slots. The power that the WPT module on UAVs sent out is 10 watts. And the energy harvesting efficiency on the sensors station is set as 60%.

Experiments are taken to evaluate the model’s performance and the proposed scheme. The solution set gets by completely random and is made as a reference. Apart from HHO and WOA, four algorithms are included in the experiments as compare, which are Particle Swarm Optimization (PSO) [38], Grey Wolf Optimizer (GWO) [39], Genetic Algorithm (GA) [40] and Simulated Annealing (SA) [41].

As the primary indicator of the work’s performance, the minimum data throughput of the model optimized by the aforementioned algorithms serves as the objective. In order to evaluate the efficacy of algorithms on the model, the processing time required by the algorithm is also considered. In conclusion, a swarm intelligence algorithm is a random and self-optimizing algorithm, and the outcome would vary each time. The repeatability and consistency of these results should also be investigated.

Each algorithm executes 200 times, and each execution contains 500 iterations. Table 1 shows the minimum maximized minimum throughput, the average maximized minimum throughput, and the maximum maximized minimum throughput. Besides the minimum, average, and maximum processing time are also shown in Table 2.

Table 1 shows that the WOA gets the highest average maximized minimum throughput among algorithms taken into the experiment. Although HHO has the maximum maximized minimum throughput, its average maximized minimum throughput is lower than WOA. The minimum maximized minimum throughput of HHO is relatively low, which is lower than that of GWO. The considerable difference between the minimum and maximum indicates that the algorithm may need to be more stable. The average result of the PSO algorithm is middle-lower compared to the other algorithms in the comparison, and the fluctuation range of the result is middle-level. The average result of the GA algorithm is the worst of any random algorithm, and there is a significant difference between the minimum and maximum values and a vast fluctuation range. The average result of SA is marginally inferior to that of GWO, while the fluctuation range is relatively large.

Processing time reflects the complexity of the algorithm, and it can be observed in Table 2. Undoubtedly, the random approach has the shortest processing time. But considering its performance on the primary indicator, other suitable methods exist. The average processing time of WOA is 1.1690 s, and the average processing time of HHO is 1.6930 s. The performance of WOA in processing time is also better than HHO. Though PSO has a shorter processing time of 0.8655 s, its primary indicator is still away from WOA. GA requires the longest processing time of all tested algorithms, roughly double the average processing time of HHO. The average processing time of SA is the shortest of all tested algorithms, except random, and its processing time variation is also minimal.

Fig. 2 shows the convergence curve of the algorithms taken into experiments. As the random method cannot lead the result to have a certain convergence tendency, the curve of the random method is excluded from the figure. The curve is drawn using the average value of each iteration of 200 times’ execution.

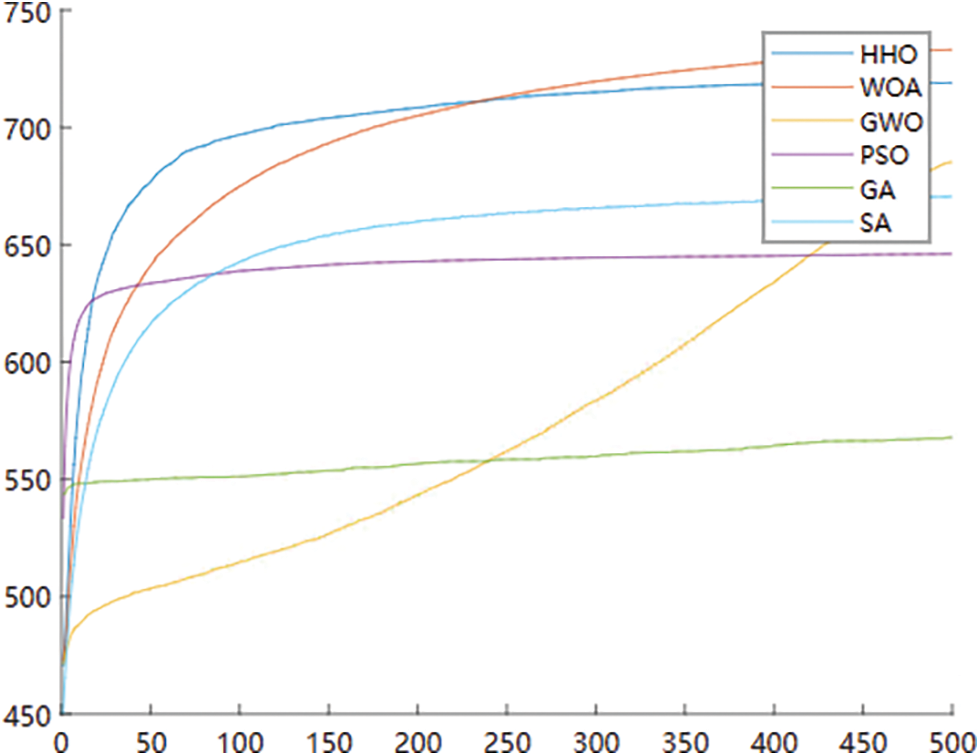
Figure 2: Convergence curve of the algorithms for optimization

Fig. 2 demonstrates that HHO converged rapidly during the first hundred iterations before slowing down. WOA has a similar situation to HHO, but its deceleration rate is slower. WOA has a superior convergence outcome than HHO. PSO has the fastest initial convergence speed, but the throughput optimized by PSO tends to increase gradually. GWO appears to optimize the output gradually, and its throughput growth rate is slower than that of all other algorithms tested. After a period of rapid growth in the first few iterations, the growth rate of GA decelerates to very small increments in subsequent iterations. SA has a faster growth rate for the first 150 iterations, after which it slows.

Then, the results of the execution of these algorithms in the 200 times are shown in Fig. 3, indicating the stability of these algorithms on the optimization problem.

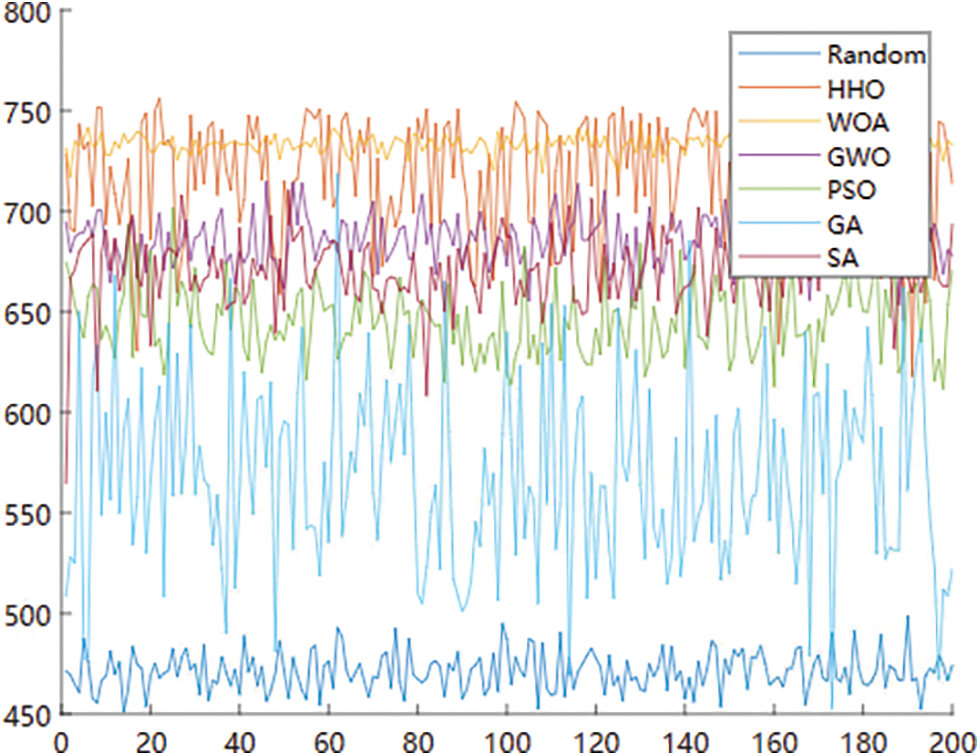
Figure 3: Stability of 200 executions of the algorithms for optimization

Fig. 3 shows that WOA fluctuates in a small range in most cases, and the line of WOA is the most stable in the figure, indicating that WOA on this optimization problem has excellent stability. The lines of other algorithms fluctuate more than that of WOA, which the data in Table 1 can also prove. While the line of HHO fluctuates violently, it represents that the HHO has awful stability on this optimization problem. The 200 results of GA fluctuate significantly, and the curve appears to be extremely unstable, as confirmed by Table 1’s large fluctuation range for GA. In the illustration, the fluctuation of the SA result curve is greater than that of WOA and GWO and comparable to that of HHO. The performance of WOA regarding the variability of results is optimal.

Based on the results of the experiments, it can be concluded that WOA is the optimal solution for the optimization problem presented in this paper. HHO has both benefits and drawbacks. The instability of HHO makes it possible to find the optimal solution. HHO can be used to execute the algorithm multiple times and then select the optimal solution.

6  Conclusion

This paper describes an optimization strategy for the resource allocation of UAVs in an IoT network. Formulation of the corresponding optimization problem that maximizes the minimum uplink throughput for the sensor station. The article then selects HHO and WOA as the optimization method. Adapting the existing optimization problem to a swarm intelligence algorithm is described. Following this, numerical experiment results are obtained using the algorithms discussed. By analyzing the results, it is possible to conclude that WOA performs the best and can be used as a general optimization technique for the posed problem. In addition, HHO can be utilized in certain circumstances.

In future work, a more promising solution to the problem described in this work will be attempted. In addition, modifications to WOA and HHO would be investigated to improve the outcome, and the two algorithms could be combined.

Funding Statement: This research was funded by the National Key Research and Development Program of China under Grant 2018YFB1404400.

Author Contributions: The authors confirm contribution to the paper as follows: conceptualization, S.F. and Y.C.; methodology, S.F. and Y.C.; software, Y.C.; validation, S.F., M.H. and F.S.; formal analysis, S.F. and Y.C.; investigation, Y.C.; resources, M.H.; data curation, Y.C.; writing—original draft preparation, Y.C.; writing—review and editing, S.F. and Y.C.; visualization, Y.C.; supervision, M.H. and F.S.; project administration, M.H. and F.S.; funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Liu, M. Peng, G. Shou, Y. Chen and S. Chen, “Toward edge intelligence: Multiaccess edge computing for 5G and internet of things,” IEEE Internet of Things Journal, vol. 7, no. 8, pp. 6722–6747, 2020. [Google Scholar]

2. O. Friha, M. Ferrag, L. Shu, L. Maglaras and X. Wang, “Internet of things for the future of smart agriculture: A comprehensive survey of emerging technologies,” IEEE/CAA Journal of Automatica Sinica, vol. 8, no. 4, pp. 718–752, 2021. [Google Scholar]

3. S. Bhattacharya, M. M. Hossain, K. Hoedebecke, M. Bacorro, O. Gokdemir et al., “Leveraging unmanned aerial vehicle technology to improve public health practice: Prospects and barriers,” Indian Journal of Community Medicine, vol. 45, no. 4, pp. 396, 2020. [Google Scholar] [PubMed]

4. P. Chanak and I. Banerjee, “Internet-of-things-enabled SmartVillages: An overview,” IEEE Consumer Electronics Magazine, vol. 10, no. 3, pp. 12–18, 2021. [Google Scholar]

5. S. Khisa and S. Moh, “Priority-aware fast mac protocol for UAV-assisted industrial IOT systems,” IEEE Access, vol. 9, pp. 57089–57106, 2021. [Google Scholar]

6. K. Shafique, B. A. Khawaja, F. Sabir, S. Qazi and M. Mustaqim, “Internet of things (IOT) for next-generation smart systems: A review of current challenges, future trends and prospects for emerging 5G-IOT scenarios,” IEEE Access, vol. 8, pp. 23022–23040, 2020. [Google Scholar]

7. X. You, C. Zhang, X. Tan, S. Jin and H. Wu, “AI for 5G: Research directions and paradigms,” Science China Information Sciences, vol. 62, no. 2, pp. 1–13, 2018. [Google Scholar]

8. H. Hu, K. Xiong, G. Qu, Q. Ni, P. Fan et al., “Aoi-minimal trajectory planning and data collection in UAV-assisted wireless powered IOT networks,” IEEE Internet of Things Journal, vol. 8, no. 2, pp. 1211–1223, 2021. [Google Scholar]

9. X. Yuan, T. Yang, Y. Hu, J. Xu and A. Schmeink, “Trajectory design for UAV-enabled multiuser wireless power transfer with nonlinear energy harvesting,” IEEE Transactions on Wireless Communications, vol. 20, no. 2, pp. 1105–1121, 2021. [Google Scholar]

10. Y. Che, Y. Lai, S. Luo, K. Wu and L. Duan, “UAV-aided information and energy transmissions for cognitive and sustainable 5G networks,” IEEE Transactions on Wireless Communications, vol. 20, no. 3, pp. 1668–1683, 2021. [Google Scholar]

11. Y. Qian, L. Shi, J. Li, X. Zhou, F. Shu et al., “An edge-computing paradigm for internet of things over power line communication networks,” IEEE Network, vol. 34, no. 2, pp. 262–269, 2020. [Google Scholar]

12. J. Li, A. Wu, S. Chu, T. Liu and F. Shu, “Mobile edge computing for task offloading in small-cell networks via belief propagation,” in Proc. ICC, Kansas City, MO, USA, pp. 1–6, 2018. [Google Scholar]

13. D. D. Luccio, A. Riccio, A. Galletti, G. Laccetti, M. Lapegna et al., “Coastal marine data crowdsourcing using the internet of floating things: Improving the results of a water quality model,” IEEE Access, vol. 8, pp. 101209–101223, 2020. [Google Scholar]

14. H. Chi, Y. Du and P. M. Brett, “Design of a marine environment monitoring system based on the internet of things,” Journal of Coastal Research, vol. 110, no. sp1, pp. 256–260, 2020. [Google Scholar]

15. S. Kavuri, D. Moltchanov, A. Ometov, S. Andreev and Y. Koucheryavy, “Performance analysis of onshore Nb-IOT for container tracking during near-the-Shore Vessel navigation,” IEEE Internet of Things Journal, vol. 7, no. 4, pp. 2928–2943, 2020. [Google Scholar]

16. Q. Song, Y. Zeng, J. Xu and S. Jin, “A survey of prototype and experiment for UAV communications,” Science China Information Sciences, vol. 64, no. 4, pp. 1–21, 2021. [Google Scholar]

17. Y. Qian, F. Wang, J. Li, L. Shi, K. Cai et al., “User association and PATH planning for UAV-aided mobile edge computing with energy restriction,” IEEE Wireless Communications Letters, vol. 8, no. 5, pp. 1312–1315, 2019. [Google Scholar]

18. J. Li, Q. Liu, P. Wu, F. Shu and S. Jin, “Task offloading for UAV-based mobile edge computing via deep reinforcement learning,” in Proc. ICCC, Beijing, China, pp. 798–802, 2018. [Google Scholar]

19. Q. Song, S. Jin and F. -C. Zheng, “Completion time and energy consumption minimization for UAV-enabled multicasting,” IEEE Wireless Communications Letters, vol. 8, no. 3, pp. 821–824, 2019. [Google Scholar]

20. A. Khalifeh, K. A. Darabkh, A. M. Khasawneh, I. Alqaisieh, M. Salameh et al., “Wireless Sensor Networks for smart cities: Network design, implementation and performance evaluation,” Electronics, vol. 10, no. 2, pp. 218, 2021. [Google Scholar]

21. H. Peng and X. Shen, “Multi-agent reinforcement learning based resource management in MEC- and UAV-assisted vehicular networks,” IEEE Journal on Selected Areas in Communications, vol. 39, no. 1, pp. 131–141, 2021. [Google Scholar]

22. W. Feng, N. Zhao, S. Ao, J. Tang, X. Zhang et al., “Joint 3D trajectory and power optimization for UAV-aided mmwave MIMO-Noma networks,” IEEE Transactions on Communications, vol. 69, no. 4, pp. 2346–2358, 2021. [Google Scholar]

23. L. Li, X. Wen, Z. Lu, W. Jing and H. Zhang, “Energy-efficient multi-uavs deployment and movement for emergency response,” IEEE Communications Letters, vol. 25, no. 5, pp. 1625–1629, 2021. [Google Scholar]

24. A. Sharma and P. K. Singh, “UAV-based framework for effective data analysis of forest fire detection using 5G networks: An effective approach towards smart cities solutions,” International Journal of Communication Systems, vol. e4826, pp. 1–23, 2021. [Google Scholar]

25. Y. Liu, F. Wu and J. Wu, “Cellular uav-to-device communications: Joint trajectory, speed, and power optimisation,” IET Communications, vol. 15, no. 10, pp. 1380–1391, 2021. [Google Scholar]

26. S. I. Alnagar, A. M. Salhab and S. A. Zummo, “Q-Learning-based power allocation for secure wireless communication in UAV-aided relay network,” IEEE Access, vol. 9, pp. 33169–33180, 2021. [Google Scholar]

27. W. -T. Li, M. Zhao, Y. -H. Wu, J. -J. Yu, L. -Y. Bao et al., “Collaborative offloading for UAV-enabled time-sensitive MEC networks,” EURASIP Journal on Wireless Communications and Networking, vol. 2021, no. 1, pp. 1–17, 2021. [Google Scholar]

28. L. Li, M. Wang, K. Xue, Q. Cheng, D. Wang et al., “Delay optimization in multi-uav edge caching networks: A robust mean field game,” IEEE Transactions on Vehicular Technology, vol. 70, no. 1, pp. 808–819, 2021. [Google Scholar]

29. L. Xie and J. Xu, “Cooperative trajectory design and resource allocation for a two-UAV two-user wireless powered communication system,” in Proc. ICCS, Chengdu, China, pp. 7–12, 2018. [Google Scholar]

30. W. Lu, P. Si, F. Lu, B. Li, Z. Liu et al., “Resource and trajectory optimization in UAV-powered wireless communication system,” Science China Information Sciences, vol. 64, no. 4, pp. 50–63, 2021. [Google Scholar]

31. Y. -H. Xu, X. Liu, W. Zhou and G. Yu, “Generative adversarial LSTM networks learning for resource allocation in UAV-served M2M communications,” IEEE Wireless Communications Letters, vol. 10, no. 7, pp. 1601–1605, 2021. [Google Scholar]

32. Y. -H. Xu, J. -H. Li, W. Zhou and C. Chen, “Learning-empowered resource allocation for air slicing in UAV-assisted cellular V2X communications,” IEEE Systems Journal, pp. 1–4, 2022. [Google Scholar]

33. Y. -H. Xu, Q. -M. Sun, W. Zhou and G. Yu, “Resource allocation for UAV-aided energy harvesting-powered D2D communications: A reinforcement learning-based scheme,” Ad Hoc Networks, vol. 136, pp. 102973, 2022. [Google Scholar]

34. M. Hosseini, R. Ghazizadeh and H. Farhadi, “Game theory-based radio resource allocation in noma vehicular communication networks supported by UAV,” Physical Communication, vol. 52, pp. 101681, 2022. [Google Scholar]

35. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja et al., “Harris hawks optimization: Algorithm and applications,” Future Generation Computer Systems, vol. 97, pp. 849–872, 2019. [Google Scholar]

36. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

37. J. Chen and D. Gesbert, “Efficient local map search algorithms for the placement of flying relays,” IEEE Transactions on Wireless Communications, vol. 19, no. 2, pp. 1305–1319, 2020. [Google Scholar]

38. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. ICNN, Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]

39. S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

40. D. Whitley, “A genetic algorithm tutorial,” Statistics and Computing, vol. 4, no. 2, pp. 65–85, 1994. [Google Scholar]

41. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar] [PubMed]