 Open Access
Open Access
ARTICLE
Asymmetric Key Cryptosystem for Image Encryption by Elliptic Curve over Galois Field
1 Department of Mathematics, College of Science, King Khalid University, Abha, 61421, Saudi Arabia
2 Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
* Corresponding Author: Hafeez Ur Rehman. Email:
Computers, Materials & Continua 2023, 76(2), 2033-2060. https://doi.org/10.32604/cmc.2023.040629
Received 26 March 2023; Accepted 29 May 2023; Issue published 30 August 2023
Abstract
Protecting the integrity and secrecy of digital data transmitted through the internet is a growing problem. In this paper, we introduce an asymmetric key algorithm for specifically processing images with larger bit values. To overcome the separate flaws of elliptic curve cryptography (ECC) and the Hill cipher (HC), we present an approach to picture encryption by combining these two encryption approaches. In addition, to strengthen our scheme, the group laws are defined over the rational points of a given elliptic curve (EC) over a Galois field (GF). The exclusive-or (XOR) function is used instead of matrix multiplication to encrypt and decrypt the data which also refutes the need for the inverse of the key matrix. By integrating the inverse function on the pixels of the image, we have improved system security and have a wider key space. Furthermore, through comprehensive analysis of the proposed scheme with different available analyses and standard attacks, it is confirmed that our proposed scheme provides improved speed, security, and efficiency.Keywords
Communication technology, multimedia data technology, and Internet protocol communication via wireless networks have experienced rapid growth in this decade. However, the transmission of sensitive information over an open wireless network like the internet poses a security risk. Therefore, it is crucial to develop new methods that can guarantee the confidentiality of sensitive information transmitted over such networks. It takes a variety of encryption methods, including substitution box (S-box) and chaotic maps in all three dimensions, to protect the security of data being transmitted via communication channels. The three main techniques for securing information—steganography, watermarking, and encryption—are used to hide data from unauthorized readers. Additionally, there are two categories of key cryptosystems in cryptography: symmetric (also known as a private key) and asymmetric (also known as the public key). One key is used in a symmetric key cryptosystem to perform both encryption and decryption. The private key used by each user in an asymmetric cryptosystem, in contrast, is distinct from the private key used by the other user. In recent years, digital information technology and multimedia data have rapidly evolved, and security has become a crucial factor in sharing confidential information. Utilising standard-based cryptosystems and using photos as a base is one trustworthy way to accomplish this. Images are frequently employed for ordinary or unique actions in personal, institutional, military, medical, and other contexts where they are required. Hence, to prevent cyber-attacks, the images should be protected from attackers [1]. Several algorithms have been developed to guarantee secure image transmission, including the image encryption scheme based on the two-dimensional (2D) Salomon map, a two-dimensional hyperchaotic system using optimization benchmark functions, and the 2D eπ-map which is a 2D chaotic map based on Euler and Pi numbers [2–5] by Erkan et al. Moreover, various algorithms have been proposed for encrypting and decrypting digital audios and images [6–9] by Gao et al. In these algorithms, the sender converts the original data to an enciphered data before transmitting it to the other user over the internet (receiver) and the receiver decrypts the ciphered data and restores it to its original state. Also, ECC was suggested separately by [10,11] as an example of an effective public-key cryptography technique [12] because ECC has the advantages of small key size, fast computation, and better security [13]. Furthermore, ECC is promoted because the same security level is possible with shorter keys, less computation, and less memory usage. ECC’s 160-bit key is as a 1024-bit Rivest-Shamir-Adleman (RSA) key but provides ten times better speed when using a 128-bit key. Furthermore, ECC uses mathematical problems that are harder to solve than those used by RSA, making it more difficult for attackers to break the encryption. ECC is also simpler and uses smaller keys, which require less storage without sacrificing security. Binary extension fields have been suggested as an alternative to prime fields for ECC, which can reduce the amount of computation needed [14].
The HC technique is one of the symmetric algorithms used to encrypt a picture in numerous researches because of its straightforward structure and speedy computations. In order to address the problem with the inverse key matrices, which are typically not available in HC algorithms, Acharya et al. [15] introduced the picture encryption utilising an advanced HC approach, obviating the need for the receiver to compute the inverse key. With the aid of interlacing and iterations, Acharya et al. [16] enhanced the original HC by adding an unconscious key. However, because the solution was limited to one grayscale image, the analysis was faulty and the outcome was unreliable. In order to increase the security of the original HC technique, Hamissa et al. [17] proposed a unique encoder-decoder approach for picture encryption employing logistic map due functions. To increase the entropy of the encrypted image, researchers developed a system with three phases, including the HC. First, the two original images’ pixel values are transformed to eight binary bits each, after which some fixed k bits are rotated and inverted. The lower nibbles of the image’s pixels are then switched. The pixel values are then subjected to the HC method [18]. The ciphertext’s numerical values are converted into points on the ECC via scalar multiplication using the HC algorithm, which is also utilised to produce another innovative encryption method. This strategy increases security while lengthening computation time [19]. The HC was further improved by Mahmoud et al. [20] to defend against assaults utilising statistics, brute force, and plaintext ciphertext. Later, Sun et al. [21] combined the contourlet-based steganography technique with the HC in their proposed picture encryption technology. Simultaneously, Naveenkumar et al. [22] offered a hybrid of Chaos and HC-based picture encryption that incorporates permutation and diffusion techniques as a different option to the traditional HC algorithm. Additionally, Sazaki et al. [23] integrated the advanced HC with the affine transform. The method used in [23] is slightly updated in [24] by Goutham et al. with regard to the 128-bit key utilised. Due to the fact that the HC uses the same key for both encoding and decoding, it offers a low level of security. To fix this weakness, Hamissa et al. [17] introduced a revolutionary image encryption algorithm called Elliptic Curve Cryptosystem with Hill Cipher (ECCHC). This combination method results in the asymmetry of the ECCHC method. A binary extension field-based ECC system was subsequently proposed by Rabah [14] as a result. In this article, the fundamental EC and Diffie-Hellman design concepts are discussed. According to Farwa et al. [25], the group rule stated over the rational points of an EC over the GF also provides remarkable benefits when applied to block ciphers for the byte replacement process. A specific EC over the
The following are the primary justifications for suggesting this approach to boost the HC’s speed and effectiveness by combining it with the EC over the GF.
• The fundamental flaw in the original HC technique was that it occasionally failed to recover plaintext since there was not a key matrix inverse because not all matrices could be inverted.
• Because the encryption and decryption operations used the same key, the HC also had the drawback of offering insufficient security.
• Agrawal et al. [19] suggested employing scalar multiplication to initially produce the ciphertext using numerical values before translating them into points on the ECC. Although the computing time was increased by this concept, the security level was increased.
• Although ECC was a novel and effective method, using big primes to achieve the required results increases computation time and complicates the algorithm [25].
In order to increase security and create a new approach that follows the idea presented in [12], we offered a novel idea for image encryption that combines ECC over GF and HC with a modification in the key matrix utilised for the encoding and decoding process. According to [25], it stands to reason that the issue of handling large primes in ECC should be approached from a different angle. By using prime power fields, particularly binary extension fields, and a few certain elliptic curves, we can boost complexity while requiring little additional computation, avoiding this problem. This motive is the driving force for the method presented in this paper, which produces the private and public keys using ECC over the binary extension field as opposed to a prime field. The secret key can then be generated by both the sender and the receiver without being shared online or over an unsecured communication route. One of the critical problems in the HC method is that the inverse of the key matrix does not always exist. The decryption procedure will therefore fail and the receiver will not be able to recover the original data if the key matrix is not invertible. This method solves the issue of locating the inverse of the key matrix for decryption even though it uses the XOR operation because the same key matrix is utilised for both encryption and decryption. Additionally, the algorithm is strengthened against different cryptographic attacks by using the inverse function of the appropriate GF. The proposed scheme is presented in Section 3 of the remaining work, which also discusses the building of the Galois field, EC over the GF, and the original HC algorithm. We assessed the suggested algorithm performance indices in Section 4 and contrasted them to other existing S-boxes. Moreover, Section 4 provides an illustration of the suggested approach. The final segment will cover the conclusion.
This section will discuss some basic definitions and concepts regarding EC and HC.
2.1 Elliptic Curve over a Finite Field
An EC over a field
where
Let
where
Let
where
The binary field
EC over the binary extension field is of the form
where
This curve has unique characteristics because of its rational points. The above curve has total 15 points including a point at infinity.
An EC makes an additive group that adds points using group law [28]. Here, we discuss only the point doubling and the point addition laws for the EC over the GF.
Let
where
Let
where
The symmetric block cipher algorithm known as the HC was created by Lester Hill in 1929 [29]. Both the sender and the receiver use the same key matrix for ciphering and decoding. The fundamental idea is to give each letter a numerical value, such as a = 0, b = 1, …, z = 25. Depending on the size of the key matrix having order
If
For decryption, the receiver must find
This section provides a novel proposed technique that combines EC over the GF with HC, which is more efficient and secure than the original HC method. This technique has the important benefit of avoiding the difficult calculations involved in matrix multiplication using XOR which speeds up decryption computations by removing the need to compute the inverse of the key matrix. Additionally, employing GF operations expedites the procedure and strengthens the suggested scheme. Let us assume that the sender (a) chooses to use this approach to send an image to the recipient (b) across an insecure channel. First, they should agree on the EC function E, and then the domain parameters
The Public key for a is
Then it evaluates
The above values generate the initial key matrix that is given as
The sender and the receiver then work together to construct the key matrix. Subsequently, an encrypted message cannot be decoded by the recipient because it is not always possible to create an invertible key matrix. However, the inverse key matrix will not need to be evaluated because this suggested method uses the XOR for encryption and decryption. In this technique, the image will be divided into sixteen pixel-sized chunks, which are then converted into a matrix of size
over
over
After dividing the values of image pixels into 16 size blocks that are transformed into the size of a
For
An inverse map is applied after assessing each
such that
Here,
The decryption procedure can start after the encrypted image has been received. Because we utilise XOR instead of matrix multiplication, we can skip computing the inverse key matrix. First, we arrange all of the
such that
where
For
After evaluating
3.4 Proposed Technique Using ECC
User (a)
1. Choose a private key
2. Calculate the public key
3. Evaluate initial key
4. Compute
5. Here
6. Then finally, the key matrix of size
over
User (b).
1. Select a private key
2. Calculate the public key
3. Evaluate initial key
4. Compute
5. Here
6. Then finally, the key matrix of size
over
1. Divide
2. Apply the operation of XOR to each
3. After obtaining
4. Similarly, apply the same technique to all of the
1. Separate
2. Apply an inverse function under
3. Similarly, take all matrices of size
4. Apply XOR operation to each
5. Finally, combine all of the matrices
Let a person
over

For the chosen curve, we get a generator point
All other points are given in Table 2.

As the generator point is
User (a)
1. Select a random value as a private key
2. Calculate the public key
3. Evaluate initial key
4. Compute
5. Here
6. Then finally, the key matrix of size
User (b)
1. Select a private key
2. Calculate the public key
3. Evaluate initial key
4. Compute
5. Here
6. Then finally, the key matrix of size
1. Choose an image of size
2. Apply the operation of XOR to
3. Likewise, apply the same procedure to each matrix
4. Apply an inverse function under the
5. Similarly, take all of the matrices
1. Separate
2. Apply an inverse to each entry of the matrix
3. Similarly, apply an inverse function under
4. After obtaining
5. Finally, combine all of the matrices
In this article, we encrypted images of Lena, Cameraman and Baboon and their respective encrypted images are depicted in Fig. 1. After analyzing them, we conclude that our approach is more robust against cryptographic attacks compared to the existing schemes mentioned in Section 5.

Figure 1: (a) Original Images: Lena, Cameraman, and Baboon. (b) Encrypted images. Lena, Cameraman, and the Baboon
To check the performance of the proposed encryption technique, some parameters or measures are used to check the efficiency of the greyscale image and compare the original image with the encrypted image. The resulting encrypted images were also subjected to various performance tests, which will be discussed in the following subsections, to assess their security against different types of attacks. A comparison has also been made between the existing schemes and this new approach.
Entropy is the measurement of randomness and statistical parameter used to evaluate image enciphering. It represents the trends that occur most frequently. The formula for calculating entropy is given below.
where
For the greyscale image of size
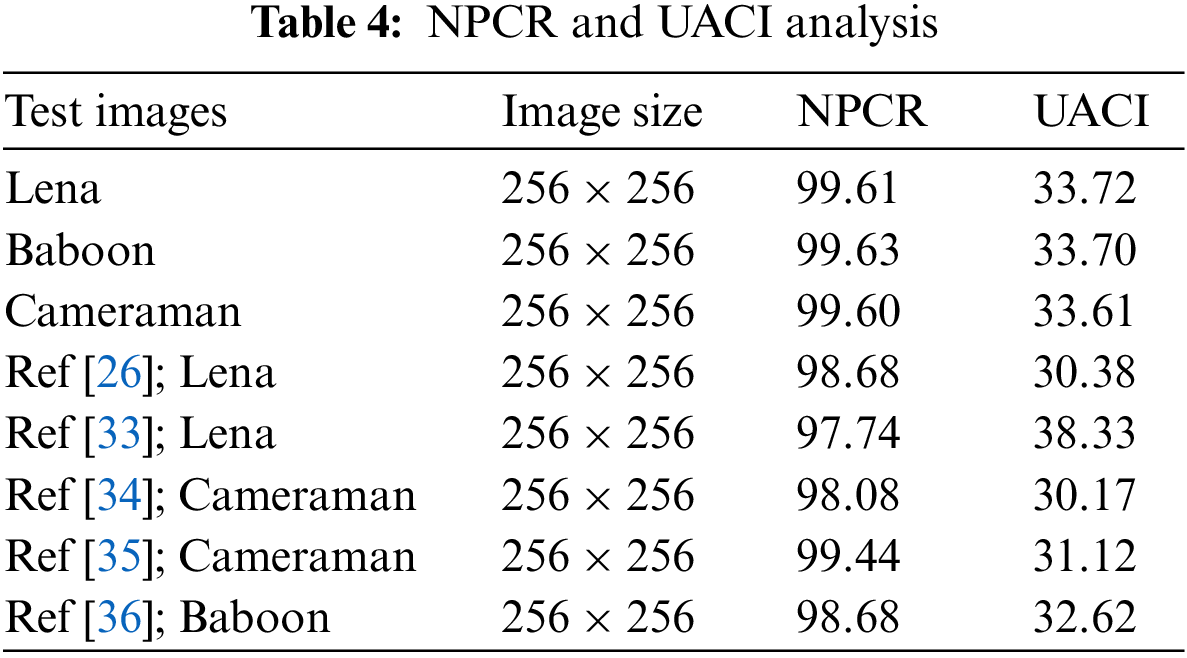
To measure the difference between the original and encrypted images, we use the number of pixels changes rate (NPCR) and the unified average changing intensity (UACI) tests. They are used to test the strength of the encryption process. The NPCR is used to check the number of changing pixels between the original and ciphered images. In contrast, the UACI measures the average change in intensity between the original and ciphered image. Its value depends upon the size and the format of the image. These two tests are used to show the resistance of the algorithm to different attacks. The formula for calculating NPCR is given as
UACI can be evaluated as
The value of UACI for the greyscale image of size
Histogram analysis is one of the most straightforward methods to illustrate image encryption quality. It is a graph that shows the number of pixels of an image at different intensity values found in the image. For good encryption, the graph of the histogram should be uniformly distributed. It is used to show how an algorithm is resistant to statistical attacks. The corresponding histogram of the original, encrypted, and decrypted image is given below. The original and decrypted image has the same graph, so there is no data loss. In contrast, the histogram of the encrypted image is flat, indicating that the encryption scheme is good. Fig. 2 shows the histograms of the original images and corresponding ciphered images of Lena, Cameraman, and Baboon.
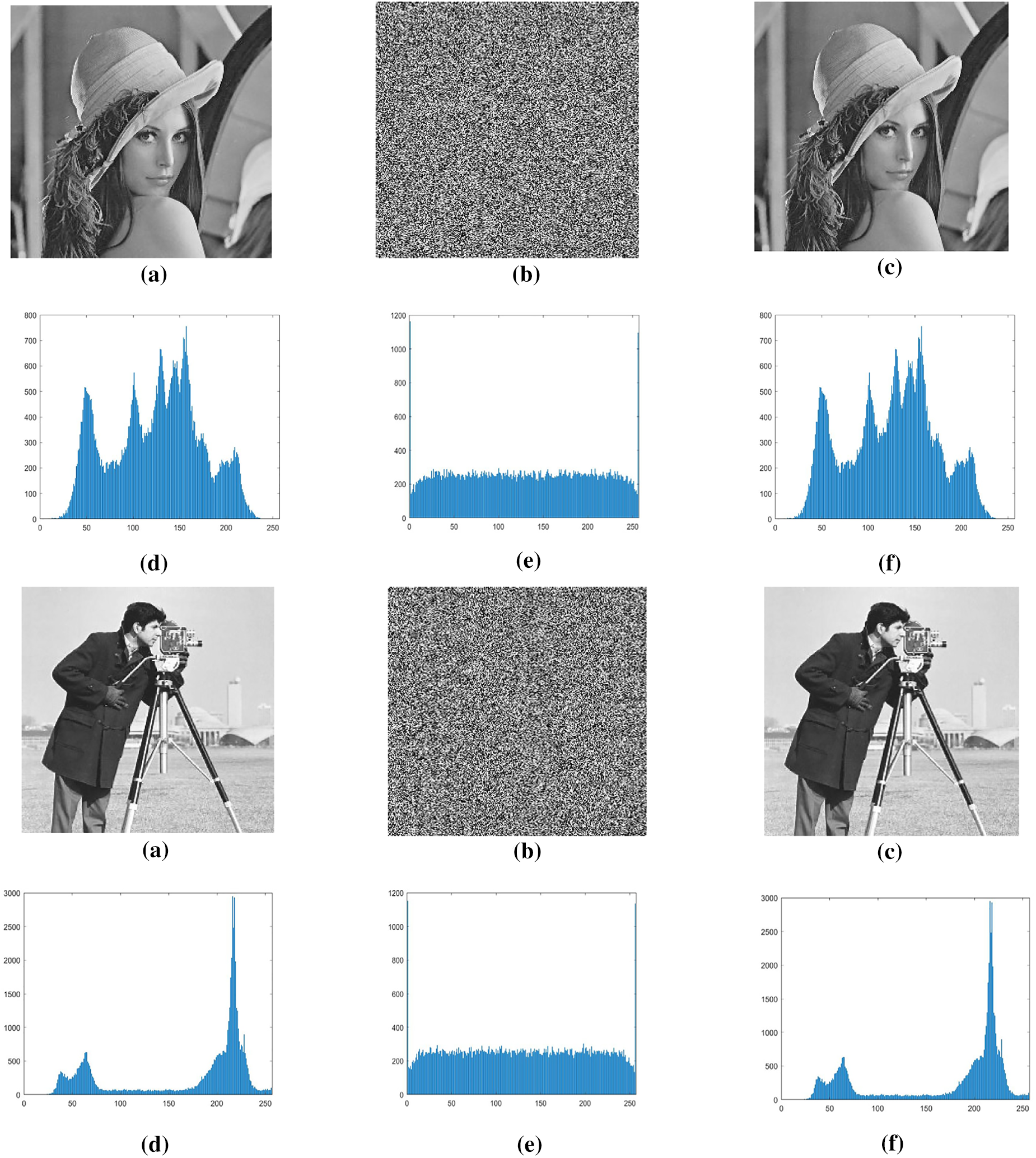
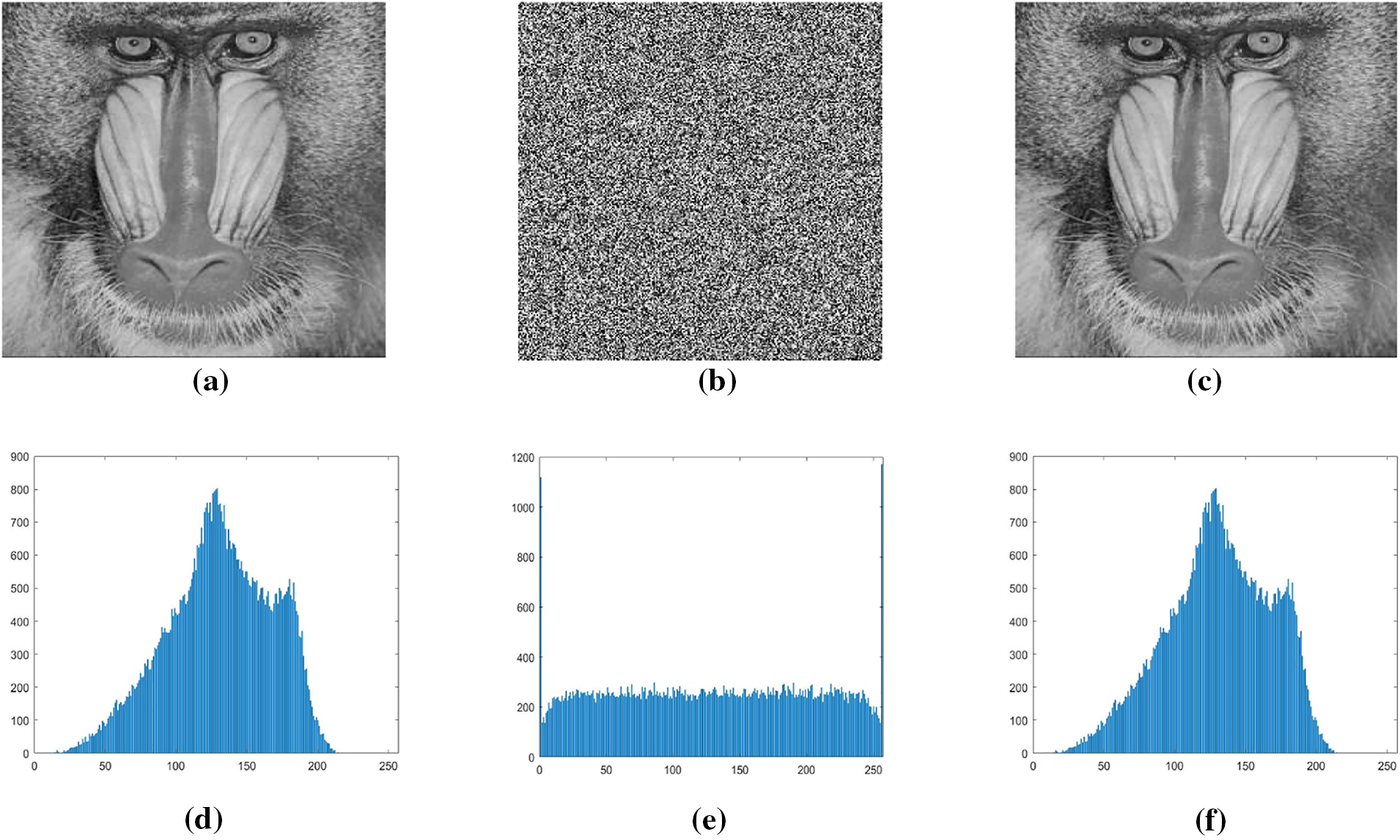
Figure 2: (a) Original Images: Lena, Cameraman, and Baboon. (b) Encrypted Images. Lena, Cameraman, and Baboon. (c) Decrypted images. Lena, Cameraman, and Baboon. (d) Histogram of original images. Lena, Cameraman, and Baboon. (e) Histogram of encrypted images. Lena, Cameraman, and Baboon. (f) Histogram of decrypted images. Lena, Cameraman, and Baboon
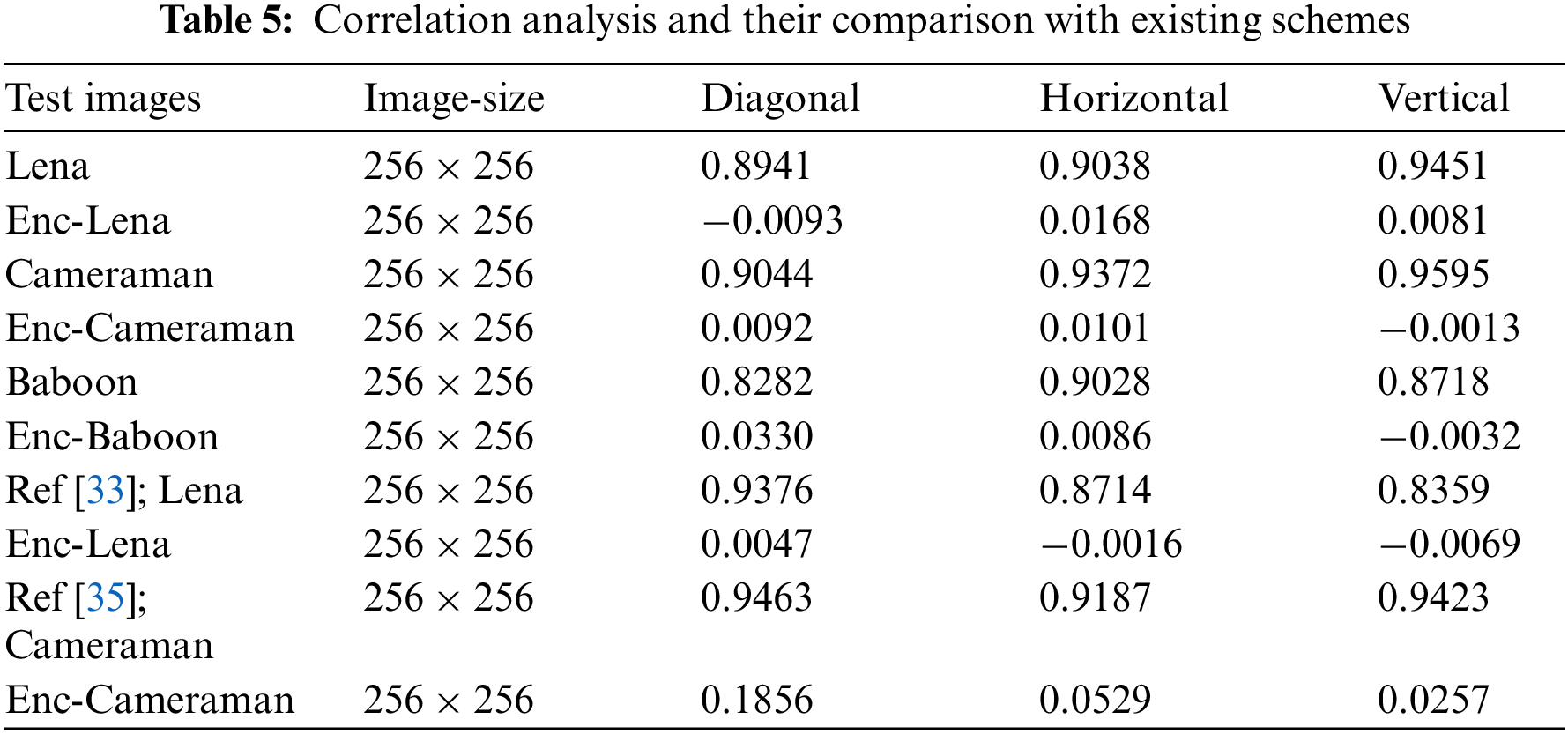
4.4 Correlation Coefficient Analysis
Correlation measures the degree of relationship between two adjacent pixels in an image and the degree of association between two adjacent pixels. Standard images we see daily have a high correlation of pixel values with their neighbors. There will be a very low correlation of pixel values with their neighbors for good image encryption. Generally, if the correlation coefficient is equal to zero or is about zero, then the plain image and its encrypted image are different. This means the encrypted image is highly independent of the plain image. A correlation coefficient of less than 0.1 between the plain and ciphered images is preferable. It is calculated as
where
Table 5 displays the experimental outcomes of the correlation test of the original and cipher images.
Additionally, compared to some existing relevant literature, the correlation coefficient results demonstrate that the suggested encryption system is significantly more effective and immune to statistical attacks (Figs. 3–5).
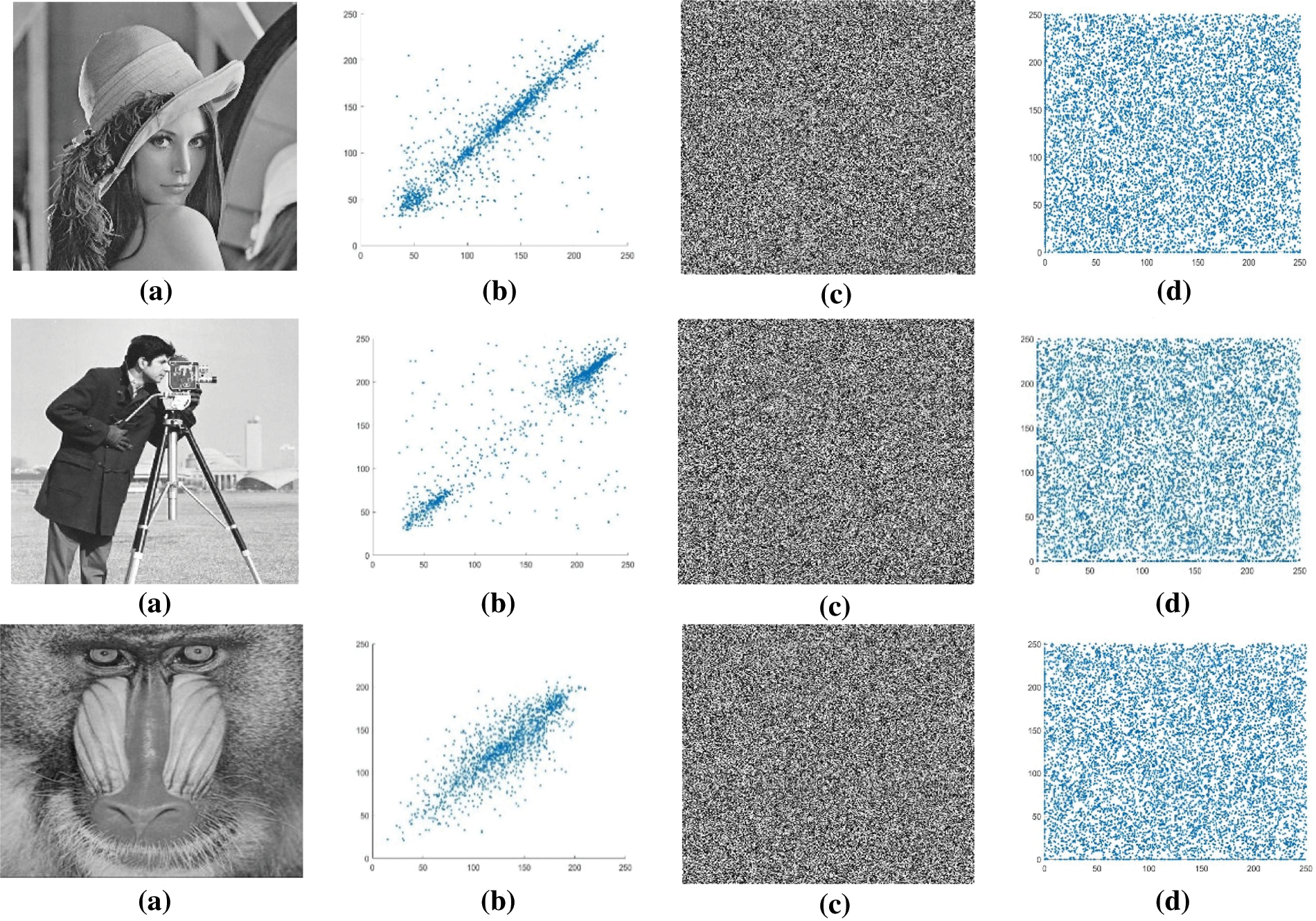
Figure 3: (a) Original Images. Lena, Cameraman, and Baboon. (b) Diagonal correlation of original images. Lena, Cameraman, and Baboon. (c) Encrypted images. Lena, Cameraman, and Baboon. (d) Diagonal correlation of encrypted images. Lena, Cameraman, and Baboon
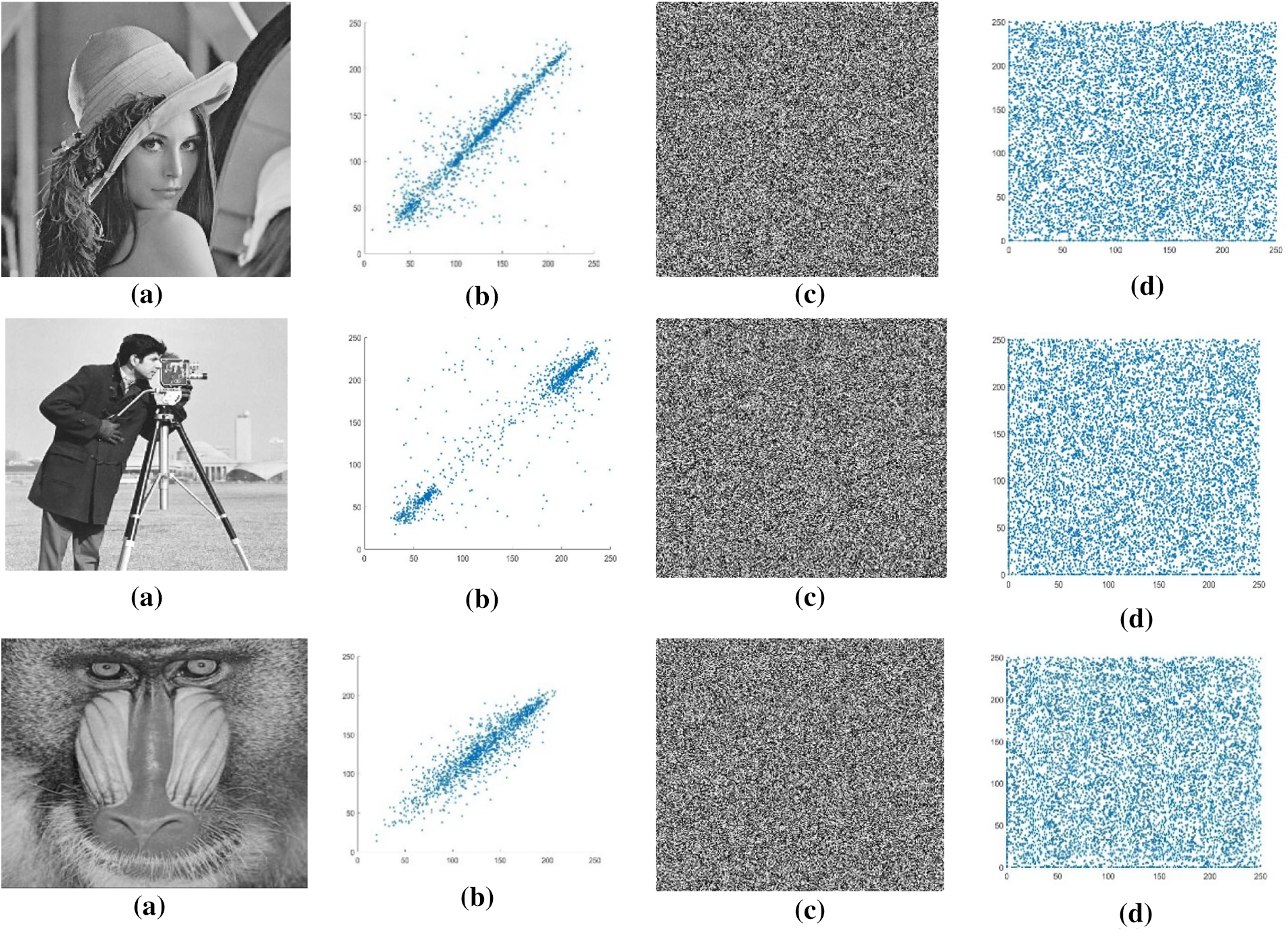
Figure 4: (a) Original images. Lena, Cameraman, and Baboon. (b) Horizontal correlation of original images. Lena, Cameraman, and Baboon. (c) Encrypted images. Lena, Cameraman, and Baboon. (d) Horizontal correlation of encrypted images. Lena, Cameraman, and Baboon
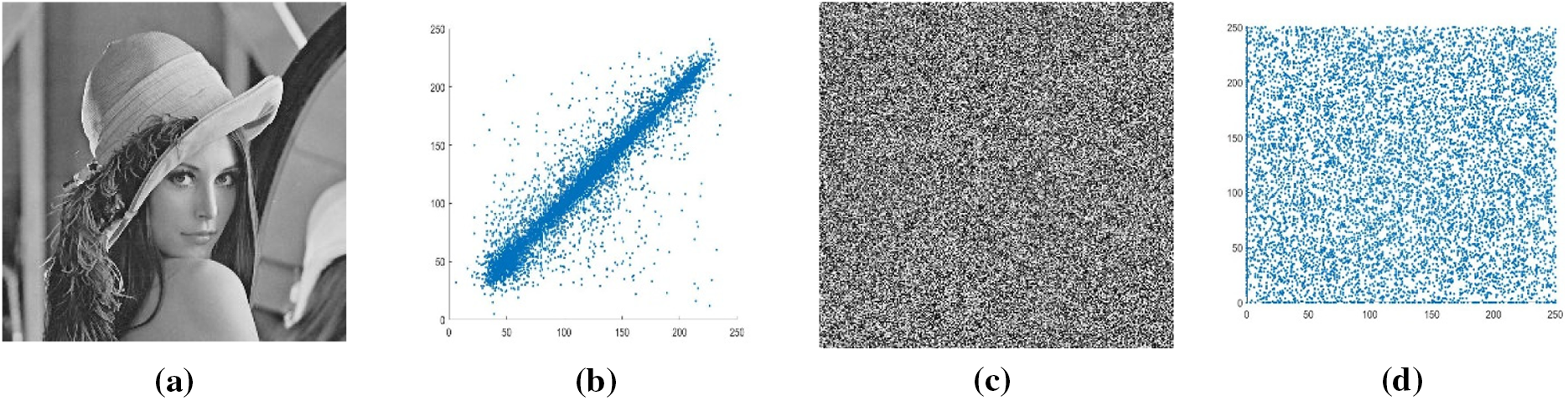
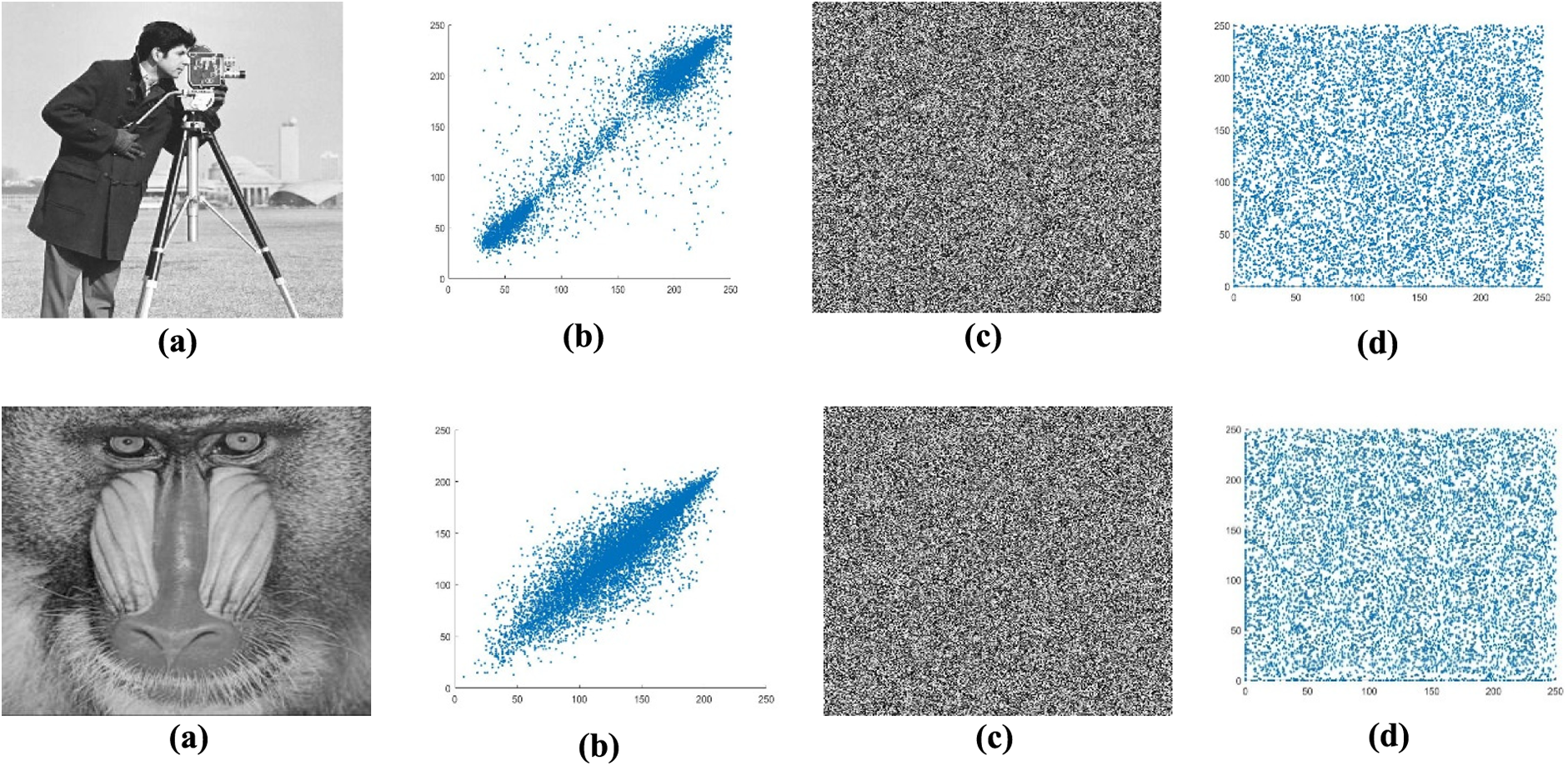
Figure 5: (a) Original images. Lena, Cameraman, and Baboon. (b) Vertical correlation of original images. Lena, Cameraman, and Baboon. (c) Encrypted images. Lena, Cameraman, and Baboon. (d) Vertical correlation of encrypted images. Lena, Cameraman, and Baboon
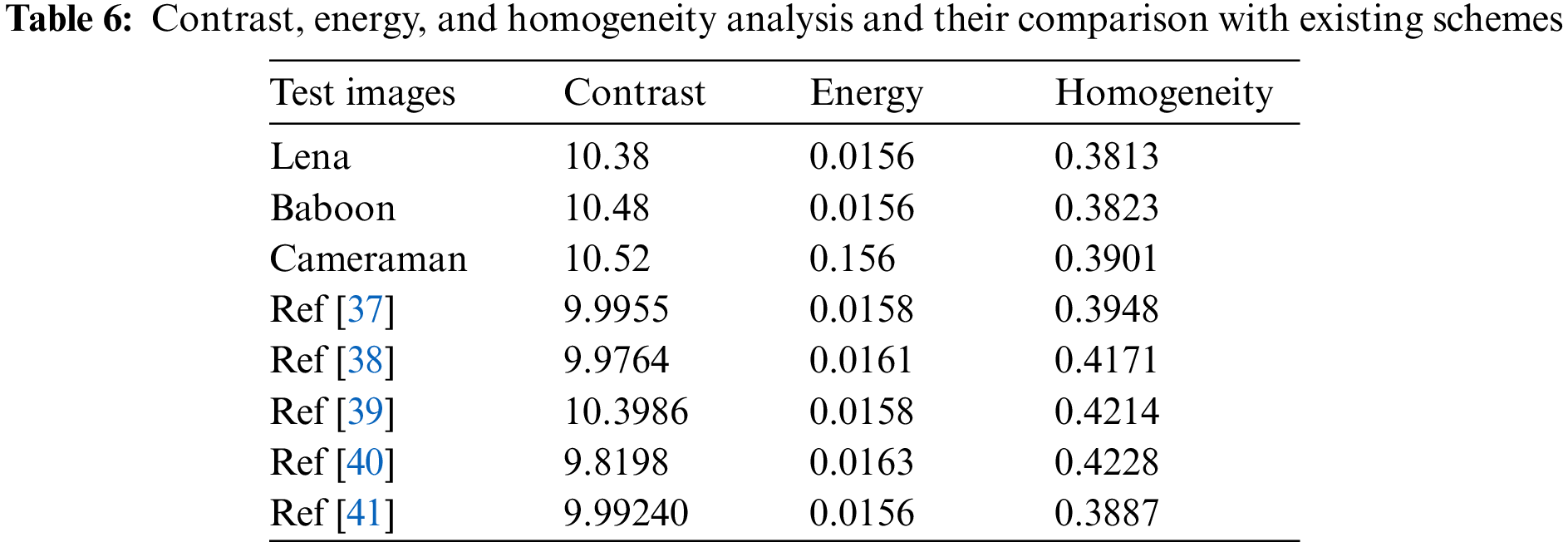
The contrast ratio is an essential feature of picture quality because it allows the viewer to identify the object in the image. Contrast analysis is a technique for determining the intensity level of contrast about pixels in an image. The encryption system is said to pass the contrast test if the contrast ratio in the ciphered image is high. The following is the mathematical expression of the contrast coefficient:
where
The GLCMs of the encrypted image are used in the energy analysis of an image. The energy test calculates the square root of the angular second moment to determine pixel intensity uniformity. To calculate energy, apply the following mathematical equation.
where
Images have intrinsically dispersed contents when seized. GLCM dispersed elements are compared to the GLCM diagonal using this methodology to see how closely they are related. Additionally, a gray-tone spatial dependence matrix of it has been recorded. The following equation represents the search for homogeneity mathematically
The homogeneity score for Lena’s ciphered image is deficient, as depicted in Table 6. As a result, it implies that the GLCM difference is more considerable.
A crucial element of a cryptosystem’s security is the size of its key-space. A higher cardinality in the set of keys used in the encryption algorithm makes it more resistant to brute-force attacks, also known as exhaustive key search. This new scheme employs the order, base fields of elliptic curves, coefficients of the elliptic curve, and inverse function as secret keys. The article provides a broad concept that relies mainly on the GF and the corresponding bit values of the image. A larger key space can be achieved by increasing the order of the binary extension and using images with higher bit values. Furthermore, the use of XOR and inverse functions in the encryption process makes it more difficult for attackers to guess the key. The algorithm also uses ECC over GF, which offers a high level of security and makes it resistant to attacks based on prime factorization. Overall, the key space analysis indicates that the proposed image encryption algorithm is highly secure and offers strong protection against various types of attacks by taking higher order of the binary extension and images with higher bit values.
4.9 Resistant to Cryptographic Attacks
In the proposed scheme, an algorithm for image encryption is designed combining an elliptic curve, a hill cipher, and an invertible function under the Galois field. This algorithm has been designed to resist various types of attacks, including ciphertext-only, known-plaintext, chosen-plaintext, and chosen-ciphertext attacks. The EC provides a secure key exchange mechanism, while the hill cipher permutes the plaintext and confuses the encryption process. The 2-time invertible function under the Galois field provides diffusion to ensure that any changes made to the ciphertext will significantly impact the decrypted image. Using these three cryptographic primitives in combination provides a high level of security and makes it difficult for an attacker to break the encryption. Additionally, using an EC in the key exchange process ensures that the algorithm resists attacks. Overall, this proposed algorithm is a robust and effective method for image encryption that provides resistance to various attacks. With the increasing importance of secure image transmission in today’s digital world, this algorithm is an essential contribution to the field of cryptography.
In this section, we examine the effectiveness of the encryption-decryption algorithm in the presence of noise. When multimedia data is transmitted through a communication channel, various types of noise can cause distortion or errors. Consequently, to evaluate the decryption efficiency of the proposed scheme, we intentionally added some noise to the encrypted image before sending it through the communication channel. The different types of noise added for this purpose are discussed briefly below.
Salt and pepper noise, also known as impulsive or fat-tail distribution, causes sudden and sharp disturbances in an image’s dark and bright regions, resulting in randomly scattered dark and white pixels. Bit errors typically cause this noise during signal transmission or analogue-to-digital signal conversion. Thus, several algorithms and techniques like non-local means, block-matching 3D filtering (BM3D), dark frame subtraction, and interpolation are used to remove salt and pepper noise. In this study, we added salt and pepper noise, Speckle noise to the encrypted image of Apple and then decrypted the noisy encrypted images, as shown in Figs. 6 and 7. Figs. (a–c) depict the noisy encrypted images, while Figs. (d–f) display the corresponding decrypted images. Hence, despite the presence of noise in the encrypted images, the decrypted images are still recognizable, as seen from the figures.

Figure 6: Slat and Peppers analysis of Apple image: (a–c) Apple ciphered image with salt and pepper variance 0.05, 0.005, 0.0005 and 0.5. (d–f) Corresponding deciphered images

Figure 7: Speckle analysis of Apple image: (a–c) Apple ciphered image with noise addition 0.003, 0.0003, 0.00003 and 0.5. (d–f) Corresponding deciphered images
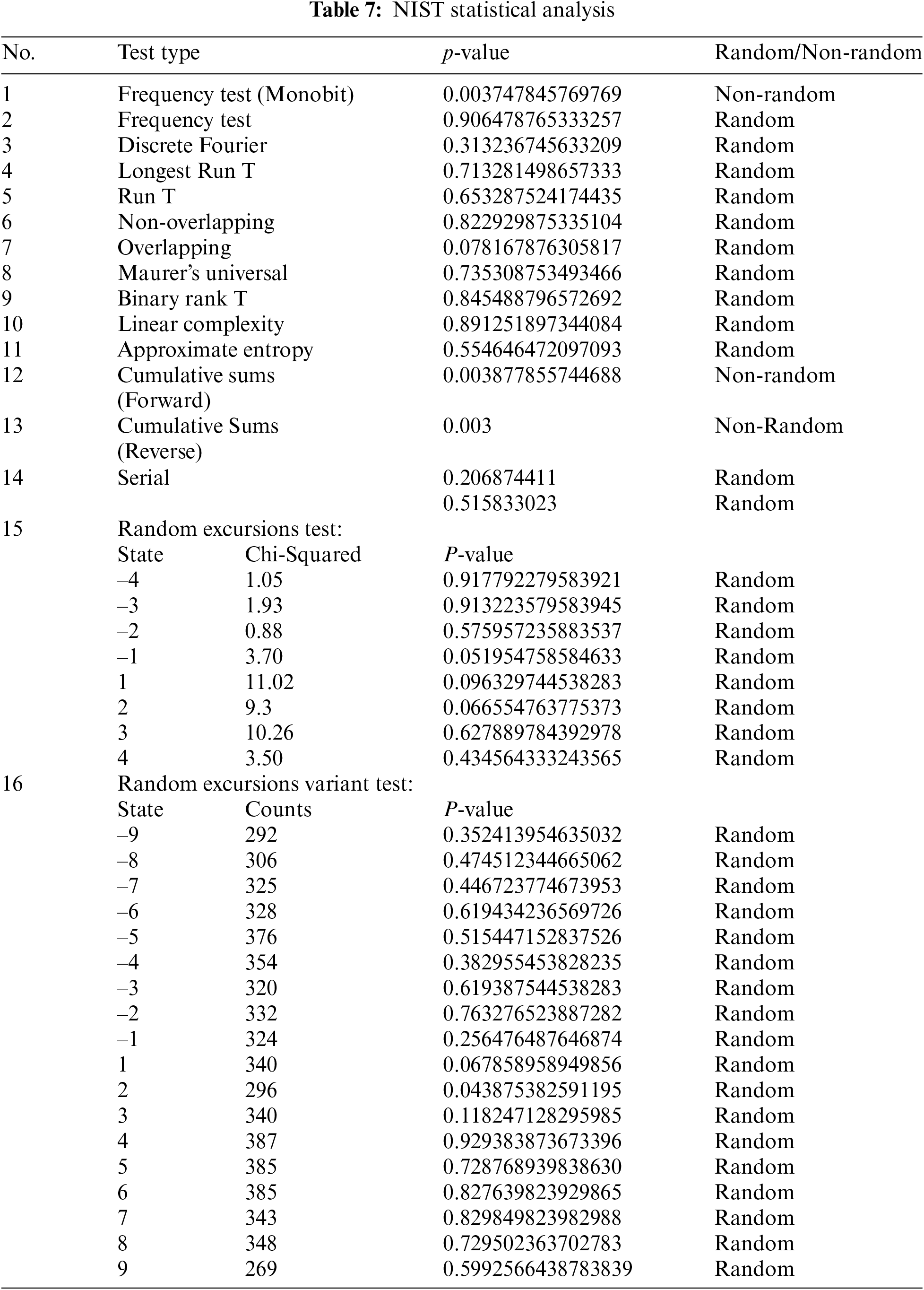
4.11 National Institute of Standard and Technology (NIST)
The NIST testing suite comprises of various tests used to determine the randomness of sequences, which can be generated using different techniques such as cryptographic algorithms. In 2001, collaborative efforts between the NIST statistics and computer security departments led to the publication of the NIST testing suite. Table 7 shows the simulation outcomes of the testing tool applied to the pixels of the encrypted image. In this research study, our pseudo random number sequences (ES-PRNS) are evaluated by setting β = 0.01, which imply that a sequence is accepted as random with confidence 0.99 unless its P value is greater than 0.01.
In this article, we combined EC over GF with a traditional HC algorithm. The ECC approach creates a new encryption and decryption key which offers increased security because it is not shared over the internet. As XOR is used for encryption and decryption, which reduces calculation time and complexity with parallel increased speed, it eliminates the requirement to determine the invertible key matrix during decryption. It also reduces the computational work by employing the GF instead of large primes. Moreover, the use of inverse functions in place of substitution techniques makes the encryption algorithm more resistant to cryptographic attacks because inverse functions are more complex and challenging to reverse-engineer. From a futuristic point of view, XOR and inverse functions can be easily combined with other encryption techniques to create new and more robust encryption algorithms, making them a flexible and adaptable option for image encryption. In addition, this idea can also be extended to generate multiple initial matrices and use them in different cryptographic protocols.
Funding Statement: The authors extend their gratitude to the deanship of Scientific research at King Khalid University for funding this work through the research group’s program under Grant Number R. G. P. 2/5/44.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. N. Thein, H. A. Nugroho, T. B. Adji and I. M. Mustika, “Comparative performance study on ordinary and chaos image encryption schemes,” in 2017 Int. Conf. on Advanced Computing and Applications (ACOMP), Ho Chi Minh, Vietnam, IEEE, pp. 122–126, 2017. [Google Scholar]
2. U. Erkan, A. Toktas and Q. Lai, “2D hyperchaotic system based on Schaffer function for image encryption,” Expert Systems with Applications, vol. 213, pp. 1–12, 2023. [Google Scholar]
3. Q. Lai, G. Hu, U. Erkan and A. Toktas, “A novel pixel-split image encryption scheme based on 2D Salomon map,” Expert Systems with Applications, vol. 213, pp. 118845, 2023. [Google Scholar]
4. U. Erkan, A. Toktas and Q. Lai, “Design of two-dimensional hyperchaotic system through optimization benchmark function,” Chaos, Solitons & Fractals, vol. 167, pp. 1–13, 2023. [Google Scholar]
5. U. Erkan, A. Toktas, F. Toktas and F. Alenezi, “2D eπ-map for image encryption,” Information Sciences, vol. 589, pp. 770–789, 2022. [Google Scholar]
6. S. Gao, R. Wu, X. Wang, J. Liu, Q. Li et al., “Asynchronous updating Boolean network encryption algorithm,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 1, pp. 1, 2023. [Google Scholar]
7. S. Gao, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, pp. 1–13, 2023. [Google Scholar]
8. S. Gao, R. Wu, X. Wang, J. Liu, Q. Li et al., “Encryption for face recognition based on the chaos and semi-tensor product theory,” Information Sciences, vol. 621, pp. 766–781, 2023. [Google Scholar]
9. W. Rui, S. Gao, X. Wang, S. Liu, Q. Li et al., “AEA-NCS: An audio encryption algorithm based on a nested chaotic system,” Chaos, Solitons & Fractals, vol. 165, pp. 112770, 2022. [Google Scholar]
10. V. S. Miller, “Use of elliptic curves in cryptography,” in Conf. on the Theory and Application of Cryptographic Techniques, Berlin, Germany, Springer, pp. 417–426, 1986. [Google Scholar]
11. N. Koblitz, “Elliptic curve cryptosystems,” Mathematics of Computation, vol. 48, no. 177, pp. 203–209, 1987. [Google Scholar]
12. Z. E. Dawahdeh, S. N. Yaakob and R. R. B. Othman, “A new image encryption technique combining Elliptic Curve Cryptosystem with Hill Cipher,” Journal of King Saud University-Computer and Information Sciences, vol. 30, no. 3, pp. 349–355, 2018. [Google Scholar]
13. X. Zhang, G. Zhu, W. Wang and M. Wang, “Design and realization of elliptic curve cryptosystem,” in 2012 Int. Symp. on Instrumentation & Measurement, Sensor Network and Automation (IMSNA), Sanya, China, IEEE, pp. 302–305, 2012. [Google Scholar]
14. K. Rabah, “Elliptic curve cryptography over binary finite field GF (2m),” Information Technology Journal, vol. 5, no. 1, pp. 204–229, 2006. [Google Scholar]
15. B. Acharya, G. S. Rath, S. K. Patra and S. K. Panigrahy, “Novel methods of generating self-invertible matrix for hill cipher algorithm,” International Journal of Security, vol. 1, no. 1, pp. 14–21, 2007. [Google Scholar]
16. B. Acharya, M. D. Sharma, S. Tiwari and V. K. Minz, “Privacy protection of biometric traits using modified hill cipher with involutory key and robust cryptosystem,” Procedia Computer Science, vol. 2, no. 1, pp. 242–247, 2010. [Google Scholar]
17. G. Hamissa, A. Sarhan, H. Abdelkader and M. Fahmy, “Securing JPEG architecture based on enhanced chaotic hill cipher algorithm,” in The 2011 Int. Conf. on Computer Engineering & Systems, Cairo, Egypt, IEEE, pp. 260–266, 2011. [Google Scholar]
18. H. T. Panduranga, “Advanced partial image encryption using two-stage hill cipher technique,” International Journal of Computer Applications, vol. 60, no. 16, pp. 14–19, 2012. [Google Scholar]
19. K. Agrawal and A. Gera, “Elliptic curve cryptography with hill cipher generation for secure text cryptosystem,” International Journal of Computer Applications, vol. 106, no. 1, pp. 18–24, 2014. [Google Scholar]
20. A. Mahmoud and A. Chefranov, “Hill cipher modification based on pseudo-random eigenvalues,” Applied Mathematics & Information Sciences, vol. 8, no. 2, pp. 505–516, 2014. [Google Scholar]
21. S. Sun and Y. Guo, “A novel image steganography based on contourlet transform and hill cipher,” Journal of Information Hiding and Multimedia Signal Processing, vol. 6, no. 5, pp. 889–897, 2015. [Google Scholar]
22. S. K. Naveenkumar and H. T. Panduranga, “Chaos and hill cipher-based image encryption for mammography images,” in 2015 Int. Conf. on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, IEEE, pp. 1–5, 2015. [Google Scholar]
23. Y. Sazaki and R. S. Putra, “Implementation of affine transform method and advanced hill cipher for securing digital images,” in 2016 10th Int. Conf. on Telecommunication Systems Services and Applications (TSSA), Denpasar, Indonesia, IEEE, pp. 1–5, 2016. [Google Scholar]
24. L. Goutham, M. S. Mahendra, A. P. Manasa and S. N. Prajwalasimha, “Modified hill cipher based image encryption technique,” International Journal for Research in Applied Science & Engineering Technology, vol. 5, no. 4, pp. 342–345, 2017. [Google Scholar]
25. S. Farwa, A. Sohail and N. Muhammad, “A novel application of elliptic curves in the dynamical components of block ciphers,” Wireless Personal Communications, vol. 115, no. 2, pp. 1309–1316, 2020. [Google Scholar]
26. D. Hankerson, A. J. Menezes and S. Vanstone, “Elliptic curve arithmetic,” in Guide to Elliptic Curve Cryptography. New York, USA: Springer Science & Business Media, no. 3, pp. 75–112, 2006. [Google Scholar]
27. J. Hoffstein, J. Pipher and J. H. Silverman, “Elliptic curves and cryptography,” in An Introduction to Mathematical Cryptography. New York, USA: Springer, no. 5, pp. 299–371, 2014. [Google Scholar]
28. J. H. Silverman, “The arithmetic of elliptic curves,” in Graduate Texts in Mathematics, New York, USA: Springer, vol. 106, no. 2, 2009. [Google Scholar]
29. L. S. Hill, “Cryptography in an Algebraic Alphabet,” The American Mathematical Monthly, vol. 36, no. 6, pp. 306–312, 1929. [Google Scholar]
30. C. K. Volos, I. M. Kyprianidisand and I. N. Stouboulos, “Image encryption process based on chaotic synchronization phenomena,” Signal Processing, vol. 93, no. 5, pp. 1328–1340, 2013. [Google Scholar]
31. X. Wei, L. Guo, Q. Zhang, J. Zhang and S. Lian, “A novel color image encryption algorithm based on DNA sequence operation and hyper-chaotic system,” Journal of Systems and Software, vol. 85, no. 2, pp. 290–299, 2012. [Google Scholar]
32. X. Wang, C. Liu and D. Xu, “Image encryption scheme using chaos and simulated annealing algorithm,” Nonlinear Dynamics, vol. 84, no. 3, pp. 1417–1429, 2016. [Google Scholar]
33. L. C. Washington, Elliptic Curves: Number Theory and Cryptography. New York, USA: CRC Press, 2008. [Online]. Available: https://doi.org/10.1201/9781420071474 [Google Scholar] [CrossRef]
34. K. Kedarisetti, R. Gamini and V. Thanikaiselvan, “Elliptical curve cryptography for images using fractal based multiple key kill cipher,” in 2018 Second Int. Conf. on Electronics, Communication and Aerospace (ICECA), Coimbatore, India, IEEE, pp. 643–649, 2018. [Google Scholar]
35. M. A. Bakr, M. A. Mokhtar and A. E. S. Takieldeen, “Elliptic curve cryptography modified Hill Cipher dependent on circulant matrix,” International Journal of Industrial Electronics and Electrical Engineering, vol. 6, no. 1, pp. 24–29, 2018. [Google Scholar]
36. X. Wang, X. Zhu and Y. Zhang, “An image encryption algorithm based on Josephus traversing and mixed chaotic map,” IEEE Access, vol. 6, pp. 23733–23746, 2018. [Google Scholar]
37. H. U. Rehman, T. Shah, A. Aljaedi, M. M. Hazzazi and A. R. Alharbi, “Design of nonlinear components over a mordell elliptic curve on Galois fields,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1313–1329, 2022. [Google Scholar]
38. S. Hussain, S. S. Jamal, T. Shah and I. Hussain, “A power associative loop structure for the construction of non-linear components of block cipher,” IEEE Access, vol. 8, pp. 123492–123506, 2020. [Google Scholar]
39. M. I. Haider, A. Ali, D. Shah and T. Shah, “Block cipher’s nonlinear component design by elliptic curves, an image encryption application,” Multimedia Tools and Applications, vol. 1, no. 80, pp. 4693–4718, 2021. [Google Scholar]
40. Y. Naseer, T. Shah, D. Shah and S. Hussain, “A novel algorithm of constructing highly nonlinear Sp-boxes,” Cryptography, vol. 3, no. 1, pp. 1–13, 2019. [Google Scholar]
41. H. U. Rehman, T. Shah, M. M. Hazzazi, A. Alshehri and B. Zaid, “Mordell elliptic curve-based design of nonlinear component of block cipher,” Computers, Materials & Continua, vol. 73, no. 2, pp. 2913–2930, 2022. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF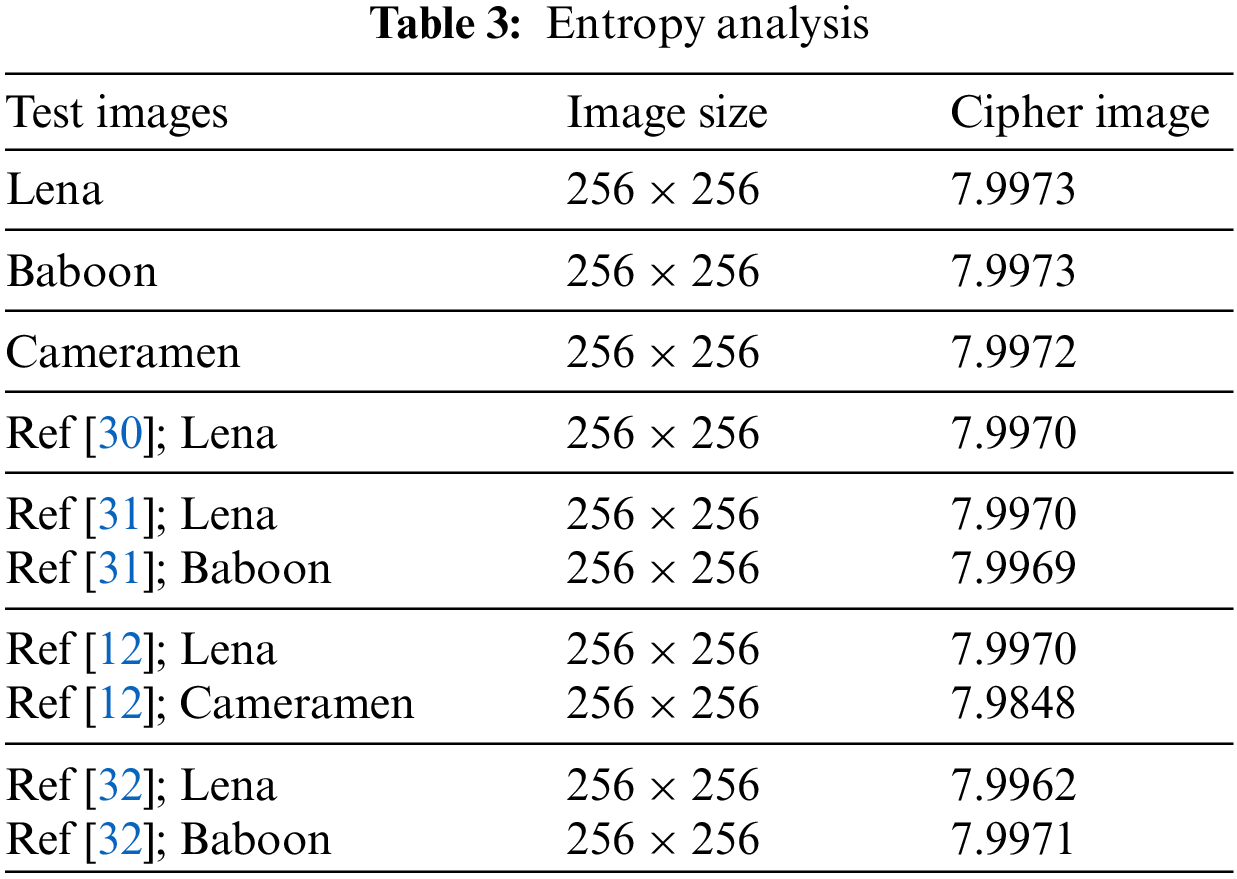
 Downloads
Downloads
 Citation Tools
Citation Tools