Human Gait Recognition for Biometrics Application Based on Deep Learning Fusion Assisted Framework

1  Introduction

Human verification or identification is crucial in various domains, including public security systems, information security, automated teller machines, and point-of-sale machines [1]. Several aspects of the human body, including internal and external characteristics such as epidermis, hair, blood samples, ear shape, recognition of a face, bite by dental forensics, and walking pattern by gait analysis, can be examined to identify a person [2]. However, popular biometric technologies like facial recognition and fingerprint verification have their limitations. For instance, face recognition needs a regulated atmosphere and appropriate distance to function properly. Fingertip contact is necessary for fingerprint authentication.

Alternately, human gait analysis [3] is a method for classifying individuals from a distance by examining their walking manner, also known as gait [4]. Typically, model-free and model-based approaches are used for gait recognition. Certain body parts like the neck, limbs, feet, hands, and legs are tracked in the model-based approach to derive dynamic and static parameters [5]. This method involves modeling the skeleton joints and bones of the human. On the other hand, the model-free process concentrates on the geometry and shape of an object, which is particularly advantageous for object recognition systems [6].

Human gait recognition (HGR) has multiple applications, including individual recognition, health care [7], cyber security, and sports science. The gait contains 24 distinguishing characteristics that are used to identify an individual. Multiple studies and investigations have shown that every individual has a distinct muscular-skeletal framework, making it possible to identify individuals based on their gait [8]. Gait recognition has several advantages over other biometric identifiers [9]. First, gait can be recorded from a distance without the participant’s cooperation [10].

In contrast, other biometrics require the individual to physically and mentally interact with sensors used to acquire the data [11]. Second, HGR can be applied to low-resolution videos and images, while facial recognition may not function well in these situations [12]. Thirdly, minimal apparatus is required to implement gait recognition systems, like an accelerometer, floor sensor, camera, or radar [13]. Generally speaking, HGR models consist of four major mechanisms [14]. Initially, locomotion data are extracted from video and situations in real-time using a variety of gears and methods [15]. The shape of the human body is detected, and background noise is eliminated using different techniques depending on the properties of the image and the region of interest. Thirdly, contour detection is carried out after segmentation to fill in any gaps between joints or missing body components. It can be used for object identification and form analysis. Extraction of features based on human qualities, such as shape, geometry, and more, is the last phase. The features are then classified using classifiers based on machine learning [16]. Before proceeding to the next level, like feature extraction, enhancing each image or frame for image processing in various applications is essential. The enhancement method depends on high-frequency and low-frequency elements [17]. High-frequency pixel components represent the scene and objects in the image, whereas low-frequency pixel components denote subtle characteristics, such as certain lines and tiny points. To enhance the image, it is imperative to keep the low-frequency components while increasing the high-frequency components [18]. Deep learning has recently demonstrated significant success in various fields, including identifying objects, gait recognition, and action identification. Deep learning extracts features from unprocessed images using a deep learning architecture with multiple hidden layers, including convolutional, pooling, and fully connected layers. Building a deep learning algorithm on the augmented dataset can result in improved features that enhance the model’s accuracy in the future [19]. Sometimes, since single networks perform poorly on complicated and huge datasets, we combined many convolutional neural network (CNN) models to boost recognition accuracy using the fusion process. After the fusion process, several characteristics are produced, reducing accuracy and lengthening calculation time. Therefore, this problem is tackled by several feature optimization strategies, including ant colony, variance-based optimization, firefly, whale, and tree-based optimization, among others [20]. The feature selection method comprises finding and choosing a smaller group of essential features or variables from a larger pool of alternatives in order to increase the precision and efficacy of a machine learning model. The goal of this approach is to reduce the model’s complexity and get rid of duplicate or unneeded traits that could cause overfitting and poor performance. The individual dataset and situation at hand must be taken into consideration while selecting the best feature selection approach, and for best results, a combination of several strategies may be used. A critical step in the machine learning process, feature selection may lead to models that are more straightforward and understandable, exhibit improved generalization, and train more quickly. The best feature vector is eventually sent to the various machine learning (ML) and neural network (NN) classifiers for action classifications, including K-Nearest Neighbor (KNN), Tree, support vector machine (SVM), Ada boost, linear discriminant (LDA), and Neural Network classifier [21]. Our major contributions to this work are as follows:

•   Fine-tuned two pre-trained lightweight deep models and initialized the static hyperparameters except for the learning rate. The particle swarm optimization algorithm has opted to select the learning rate.

•   Propose an improved version of the feature selection algorithm named Harris Hawks controlled Sine-Cosine optimization.

•   A correlation-based feature fusion technique is developed for the combination of optimal features.

2  Related Work

Numerous techniques for classifying human gait recognition based on deep learning are described in the literature. Few of them focused on traditional techniques such as handcrafted features, and others used deep learning. A few of them also focused on the fusion and feature selection techniques, improving accuracy and reducing computational time. Kececi et al. [22] created a framework for recognizing human locomotion using an enhanced optimization of ant colonies (IACO) algorithm and deep learning. They selected the most efficient features for machine learning classifiers using the IACO algorithm. Multiple experiments demonstrated that the IACO method is more precise and decreases the cost of computation compared to other cutting-edge techniques. Dou et al. [23] proposed a framework for (HGR) based on deep learning (DL) and kurtosis-controlled entropy (KcE) and video sequences. The objective was to surmount obstacles presented by human angular shift, clothing, and movement style. The authors extracted features using the ResNet101 deep model and employed the KcE method to pick the best features. On the CASIA-B dataset, the proposed framework obtained accuracies of 95.26 and 96.60%, respectively. Zhu et al. [24] proposed a framework for human gait recognition that employs a singular stream of optimum deep learning combined features. After performing data augmentation, the authors utilized two already trained models, namely Inception-ResNet-V2 and NASNet mobile. Combining and optimizing the derived features from both deep learning models using the whale optimizer. In the end, machine learning classifiers were applied to the optimized features, yielding an accuracy of 89%.

Huang et al. [25] proposed a technique for gait recognition using multisource sensing data. They retrieved 3D human features data during a walk by analyzing the human body’s shape and multisource stream data. Because every person’s gait is distinctive, these characteristics can be utilized to determine a person. The experimental procedure was conducted on the CASIA A dataset, and the suggested approach obtained a precision of 88.33%. To enhance gait recognition using low-device wearable sensors, the authors [26] presented a modified residual block and a new shallow convolutional layer to improve gait recognition using low-device sensors on clothing. To analyze the subject’s locomotion, they inserted wearable sensors in objects that might be placed on the individual’s body, such as watches, necklaces, and cellphones. Traditional matching of templates and conventional matching methods were ineffective for low-device connected devices and did not enhance performance. The enhanced residual block and narrow convolutional neural network attained an 85% accuracy on the IMU-based dataset. To address the challenges of irregular walking, patient apparel, and angular changes in arthritic patients, the authors [27] presented a deep learning (DL) and modular extreme learning machine-based approach to human gait analysis.

In contrast to conventional techniques that concentrate solely on selecting features, the researchers employed an effective approach to address these problems. The experimental procedure utilized two pre-trained models, VGG16-Net and Alex Net, improving accuracy. Next, Tian et al. [28] discussed the problem of identifying gait sequences taken under unregulated unidentified view angles and dynamically varying view angles during the walk, also known as the free-view gait identification problem. The researchers proposed a novel method, walking trajectory fitting (WTF), to surmount the limitations of conventional methods. In addition, they presented the joint gait manifold (JGM) method for assessing gait similarity.

3  Proposed Methodology

The suggested framework for recognizing human gait is depicted in Fig. 1. This diagram illustrates the steps involved in the proposed HGR structure, including frames extraction, fine-tuning the pre-trained CNN models using transfer learning, deep feature extraction from both streams, optimizing the features, and fusing the optimized feature vectors, and finally, classification is performed. Below is a concise numerical and mathematical explanation of each phase.

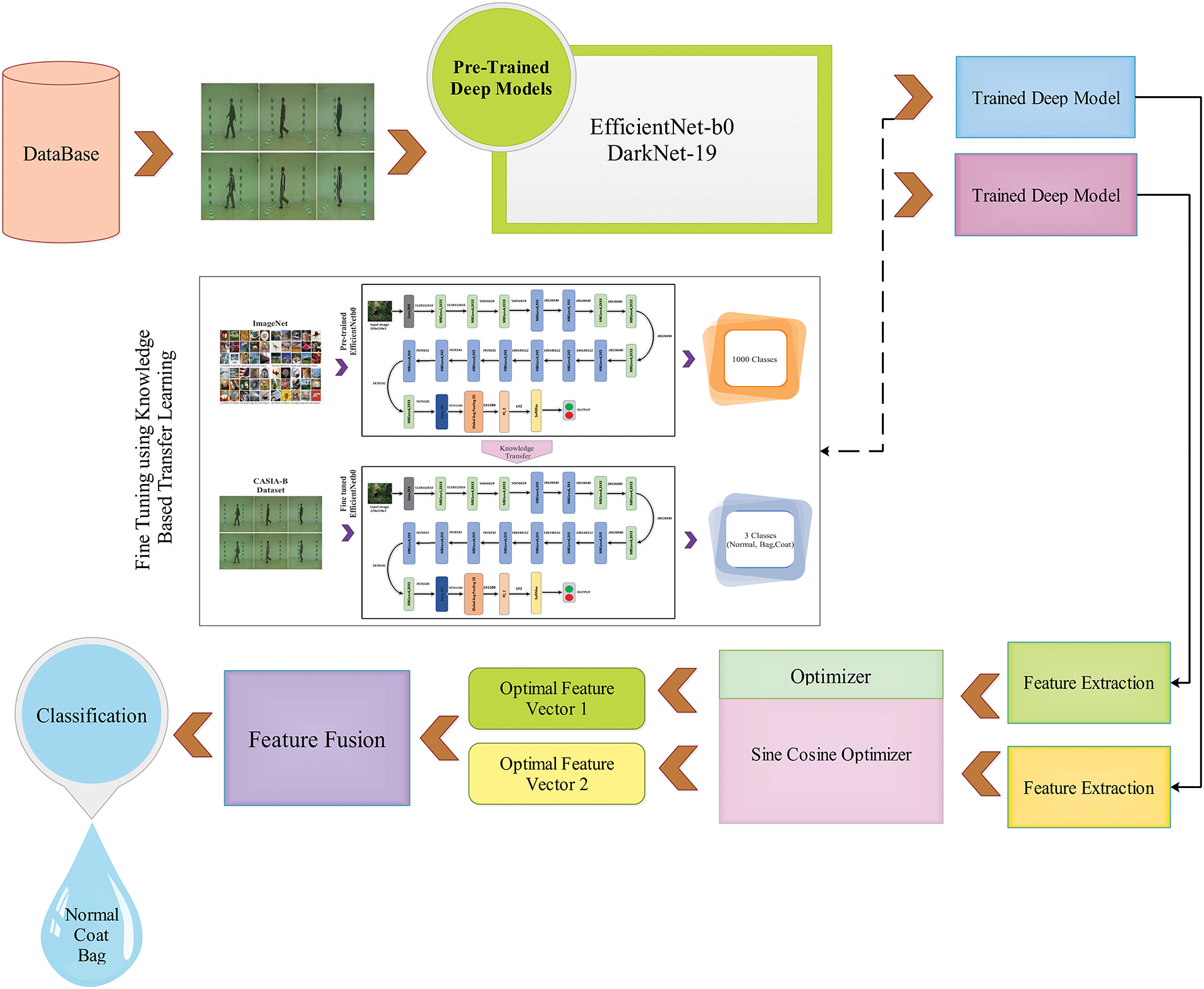
Figure 1: A proposed deep learning-based framework for HGR

3.1 Preprocessing

A machine learning or deep learning system uses preprocessing techniques to prepare video frames for further processing. This preliminary stage can improve the accuracy and efficacy of the analysis by suppressing noise, excluding irrelevant data, and highlighting significant characteristics. Separating frames from action recordings is the primary objective of the preprocessing procedure in this study. Initially, each video frame had dimensions of 512 by 512 by k, with k set to 3. After the fact, the frames are scaled down to 256 × 256 × 3 pixels.

3.2 Pre-Trained Deep CNN Models

Convolutional neural networks (CNNs) are neural networks in which at least one layer, as opposed to matrix multiplication, executes a convolution operation. Using CNNs, HGR recognition/classification accuracy is currently being improved. Convolutional, pooling, and FC layers constitute the fundamental components of a CNN. Numerous filters with variable parameters are applied to the image to obtain the convolution layer’s intricate details. The two most important parameters for this layer are the number of kernels and size. The convolutional procedure can be defined as follows:

L[a×b]=(m∗n)[a×b]=∑l⁡∑k ⁡n[l, k]m[a−l,b−k](1)

Here, ‘m’ represents the image being read in, ‘n’ stands for the kernel, and ‘a’ and ‘b’ indicate the rows and columns. The symbol for the convolutional operator is *, and the letter L indicates the output. After the convolutional layer, a ReLu activation layer is added to replace negative values with 0.

ReLu=Max(0,z), z∈L(2)

A pooling layer is used to dramatically reduce the size of the vector to speed up computation. In pooling layers, among others, the average and maximum procedures are carried out. Use the max pooling layer if you want the highest value; use the average pooling layer if you want the average value. Before sending the classification result to the output layer, a neural network uses the FC layer to smooth it out. Here is a mathematical description of the FC layer:

G0out=L[a×b](3)

Ghin=Gh−1out∗Lh+bh(4)

Ghout=△h(Ghin)(5)

where G0out  denotes the outermost FC layer. The layer number is represented by h, while the activation function is indicated by △. After the FC layer, the SoftMax layer is added for classification.

SoftMax(Ghout)=exp(Ghout)∑k ⁡Gkout(6)

3.3 Transfer Learning Based Feature Extraction

In this work, we derive features using two convolutional neural networks (CNN) models (Efficientnet-b0 and Darknet19). Efficientnet-b0 consists of one input layer measuring 224 by 224 by 3, one layer of global average pooling, one layer of fully connected neurons, and one layer of 18 convolutional blocks. Initially, we utilized a model called Efficientnet-b0 that was trained on the 1000-class ImageNet dataset. Before being transferred to the CASIA-B dataset and trained with the aid of the transfer learning concept, this deep CNN model was refined by omitting the final fully connected (FC) layer and adding additional dense layers. Fig. 2 shows the Efficientnet-b0 architecture.

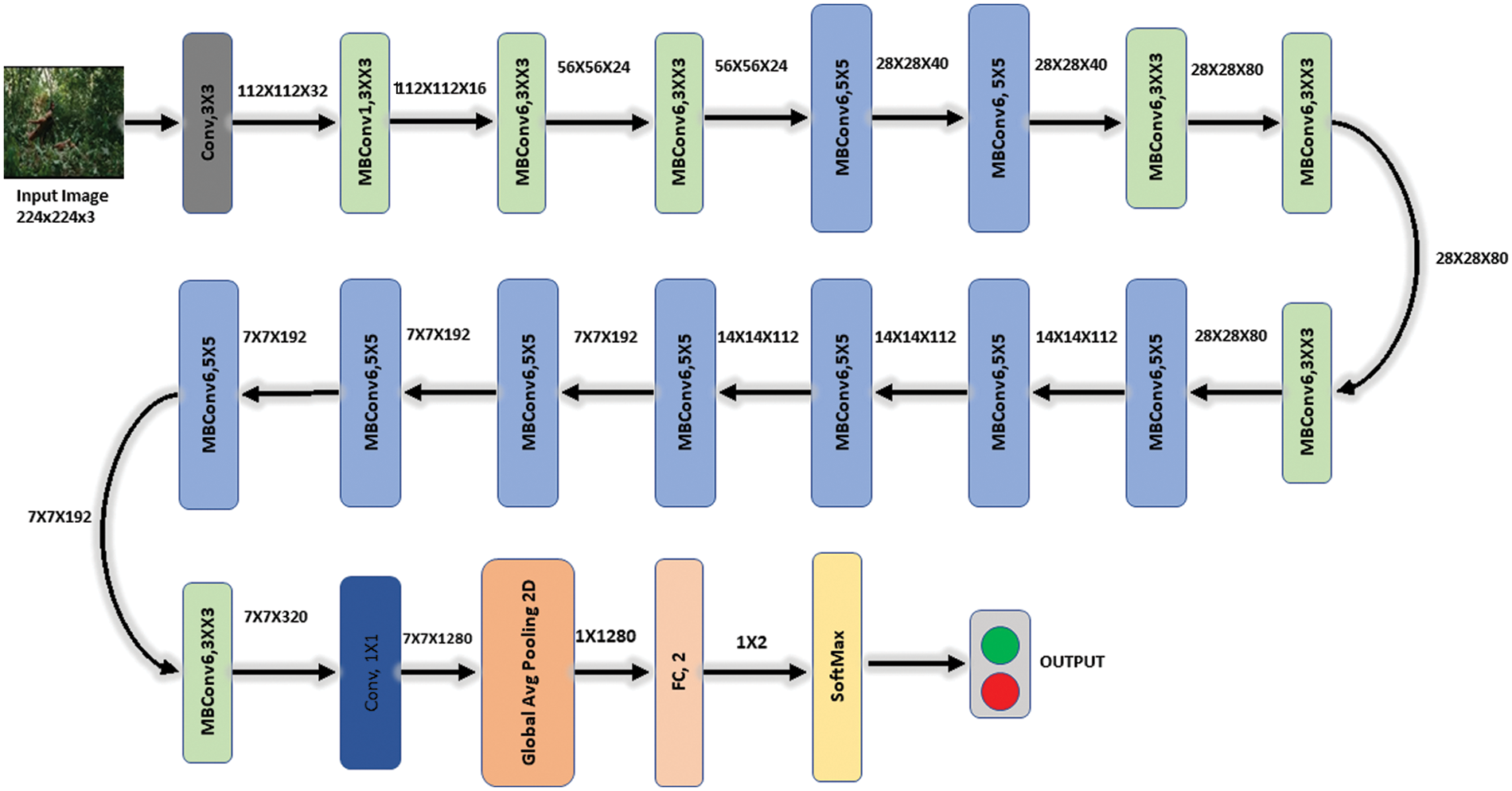
Figure 2: Architecture of Efficientnet-b0 deep model

In computer vision, the Darknet19 architecture for deep CNN is used for applications like object recognition and categorization. Darknet19 is a condensed version of Joseph Redmon’s Darknet architecture, with 19 layers. Nineteen layers comprise the Darknet19 architecture; eighteen are convolutional, and one is the FC layer. It uses the same underlying building elements as the larger Darknet53 design but with fewer layers, making it more computationally efficient and quicker to train. Fig. 3 shows the TL process for HGR.

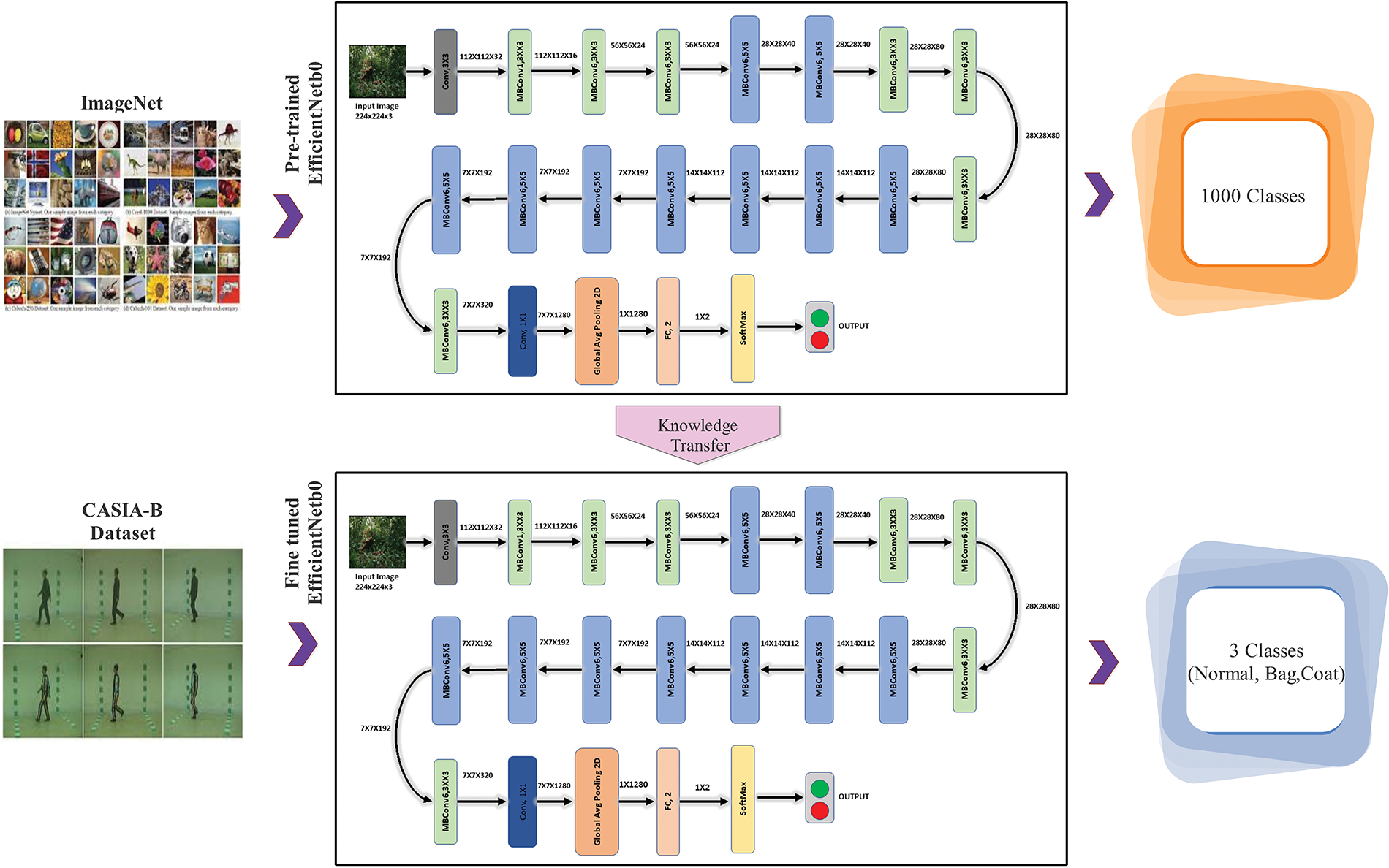
Figure 3: Knowledge-based transfer learning process for HGR

These models were initially trained on the 1,000-label ImageNet dataset. To make these models compatible with the CASIA-B dataset, the final FC layer was eliminated, and additional dense layers were added. These datasets were subjected to transfer learning techniques, and the resulting models were improved. Training and testing portions of the dataset were allocated 70% and 30%, respectively. The values for the hyperparameters were 250 epochs, 0.001 initial learning rate, 0.2 dropouts, and 16 for the mini-batch size. After being refined using transfer learning, the new deep model was finally trained.

The deep features of the fine-tuned Efficientnet-b0 model are extracted using a Global Avg Pooling layer. This layer yields a feature vector designated by Vec1 with dimensions (N × 1280). The features of the Darknet19 model are extracted using a 2-dimensional global average pooling (2gap) layer. As a result, the Vec2 representation of the extracted feature vector has a size of (N × 1024).

3.4 Feature Selection

Over the past two years, feature selection has been pivotal in machine learning. Many methods have been introduced, but they all have drawbacks, such as compromising on key aspects or cherry-picking the most relevant ones. These factors can lengthen the computation time and decrease accuracy. Since many of the first-generation optimization methods suffer from performance issues when applied to real-world, large datasets, researchers have seen the feature selection literature expand with modifications and hybridizations that leverage the strengths of different methods to improve search efficiency.

3.4.1 Harris Hawks Optimization (HHO)

HHO is a swarm-based metaheuristic algorithm inspired by the hunting techniques of Harris Hawks. Hawks often hunt in groups, seeing their prey from above and then swooping to strike. Once located, the hawks will close in and make a concerted effort to capture the prey before it can escape. The authors [29] used this method to develop the HHO cornerstones of exploration and exploitation. Exploration, the transition from exploration to exploitation, and exploitation are the three main stages of the HHO. These stages are triggered based on the parameter F (the prey’s fleeing energy) and a random variable called random (.). To avoid being caught, the fleeing energy factor F decreases with time (as shown mathematically in Eq. (7)).

F=2F0(1−ttmaximum)(7)

where F0 is the starting energy, t is the number of iterations, and tmaximum is the maximum number of iterations. When |F| is less than 1, the HHO enters its exploratory mode, indicating that the prey is too far away to attempt a capture.

Exploration phase: To begin searching, HHO generates a population of N possible solutions randomly distributed over the search space then assesses their fitness. For the first set of iterations, t = [1, 2, …, tmaximum], where tmaximum is the maximum number of iterations, |F| ≥ 1, Eq. (2) is used to probe the search space.

yjt+1={yrandom−random ()|yrandom ()−2random ()yjt|if random≥0.5(yprey−y¯t)−random()[lcj+random()(ucj−lcj)]if random()<0.5(8)

When called, random() is a function that always produces a unique random integer between 0 and 1. Generation t + 1’s jth solution is denoted by yj+1j, the best site so far by yprey, the dimensional mean of all solutions by y¯t, and the bottom and upper bounds of the searching space by lc and uc, respectively.

Exploitation phase: When HHO is in this stage, it is surrounding its prey (a rabbit, for example) and preparing to make a surprise attack, having previously identified a promising search region. As the prey tries to evade capture, the hawks can employ one of four different attack strategies, as determined by their collective intelligence: a soft besiege (SB), a soft attack with rapid falls (SBRD), a hard besiege (HB), or a hard besiege with dives (HBRD). Apart from hard besiege, these local search algorithms provide sufficient randomization to prevent a lack of variety in solutions throughout the optimization process. The following exploitation strategies are defined in HHO utilizing the escaping energy variable E and the chance of escape calculated using random ():

Step one: We will use a gentle besiege technique (|F| 0.5, random () 0.5). Harris Hawks are using this strategy because their prey has the strength to get away from them. It is done so the locally designated area can be thoroughly searched before concurrence. In mathematical terms, the step is expressed as:

yjt+1=(yprey−yjt)−F|Kyprey−yjt|,(9)

K=2(1−random())

Step two: hard assault (|F| 0.5, random () 0.5) this phase, in contrast to the preceding one, is performed when the searching agent almost discovers the nearby solution. If the prey is too tired to escape, the hawks have a better chance of catching it. You may summarize the scenario using Eq. (10):

yjt+1=yprey−F|yprey−yjt|(10)

Step three: a gentle assault with sharp dives (|E| ≥ 0.5, random () < 0.5). This search method employs a Levy flight-style search of the region of interest. In this situation, the hawks will do a series of low, quick dives around the victim until it gives up. This action is mathematically expressed in Eq. (11).

yjt+1={Aif  f(A)<f(yjt)Bif  f(B)<f(yjt)(11)

A=(yprey−F|Kyprey−yjt|)

B=A+Vrandom×Levy(C)

where C is the number of dimensions in the issue, and Vrandom is a vector of random numbers created using the random () function.

Step four: a tense siege with frequent dives (|F| < 0.5, random () < 0.5). This maneuver uses the swarm’s knowledge while making arbitrary Levy flying maneuvers. The hawks can get closer to their quarry because HHO significantly reduces the prey’s escaping energy. The relative expression is found by using Eq. (12).

yjt+1={Aif  f(A)<f(yjt)Bif  f(B)<f(yjt)(12)

A=(yprey−F|Kyprey−y¯t|)(13)

B=A+Vrandom×Levy(C)(14)

where C is the number of dimensions in the issue and Vrandom is a vector of random numbers created using the random () function.

In older formulations, the Levy flight function was written as Eq. (15).

Levy(C)=0.01×random×σ|V|1β

σ=(Γ(1+β)×sin⁡(πβ2)Γ((1+β)2)×β2β−12)(15)

where β is a constant and, by convention, β = 1.5, the step size is controlled by a second constant value of 0.01 in Eq. (7), although this value is also variable.

3.4.2 Sine-Cosine Algorithm

Recently, reference [30] formalized the use of Sine and Cosine—two trigonometric functions—into a search technique they dubbed the Sine-Cosine algorithm (SCA). The SCA is a straightforward example of a stochastic algorithm that works with populations based on the fundamental optimization principles of discovery and use.

In this case, we update the answer in all dimensions by applying Eq. (16) to each N search agent in the population.

yj,it+1={yj,it+1=yj,it+ρ×sin⁡(random( ))×|random( )ybest it−yj,it|  if random( )<0.5yjit+1=yjit+ρ×cos⁡(random( ))×|random( )ybest it−yit|  if random( )≥0.5(16)

where ybest it  is the ith dimension of the optimal solution identified so far, and yj,it+1 represents the ith dimension of the jth candidate solution. Eq. (8) uses a random number generator function called random (), which always returns a random value between [0, 1]. The variables t and t + 1 represent the current and next-generation counters. Adjusting the value of ρ parameter that governs exploration and exploitation yields Eq. (17).

ρ=α−tαT, Default value of α=2(17)

where α is a constant that may be adjusted by the user according to the nature of the optimization task at hand. SCA, like HHO, uses an adaptable range of Sine and Cosine functions to transfer from the exploration to exploitation phases.

3.5 Fusion

Fusion is a method used to enhance recognition accuracy by integrating many feature vectors into a single vector. Here, we employed a modified correlation extended serial technique to combine optVec1 and optVec2, two ideal feature vectors. Using the following formula, we can determine the relationship between j and i using the vectors optVec1∈Kj and optVec2∈Li.

Corelation=∑⁡(Kj−K¯)(Li−L¯)∑⁡(Kj−K¯)2(Li−L¯)2(18)

where Vec3 contains features with a positive correlation, whereas Vec4 contains features with a negative correlation as calculated by the formula. Following this, we compare each feature to the mean value of Vec4 as shown below:

CT={Vec4~for Vec4≥μignore,otherwise(19)

At last, we combine Vec4 and Vec3 to form a new vector, Vec5, by use of the following equation:

Vec5(i)=(Vec3(i)m×n Vec4~(i)m×n)(20)

N × Vec5 is the final vector’s dimension. Finally, the various neural network classifiers use the final vector, Vec5, to recognize human gait.

4  Results and Discussion

The numerical results and discussion of the proposed framework have been discussed in this section. Initially, the detail of the selected dataset is given and then the experimental setup. After that, the detailed results are discussed and compared with recent techniques followed.

4.1 Datasets and Performance Measures

The CASIA-B dataset was used to assess the suggested approach. This dataset has a total of 11 angles, namely, zero, 18, 36, 54, 72, 90, 108, 126, 144, 162, and 180. Each angle has three classes: Bag, Coat, and Normal, as illustrated in Fig. 4 [31]. Five classifiers—Wide Neural Network (WNN), Narrow Neural Network (NNN), Medium Neural Network (MNN), Tri-layered Neural Network (Tri-Layered NN), and Bi-layered Neural Network (Bi-Layered NN) were used to categorize the activities and computed the performance of each classifier in term of accuracies.

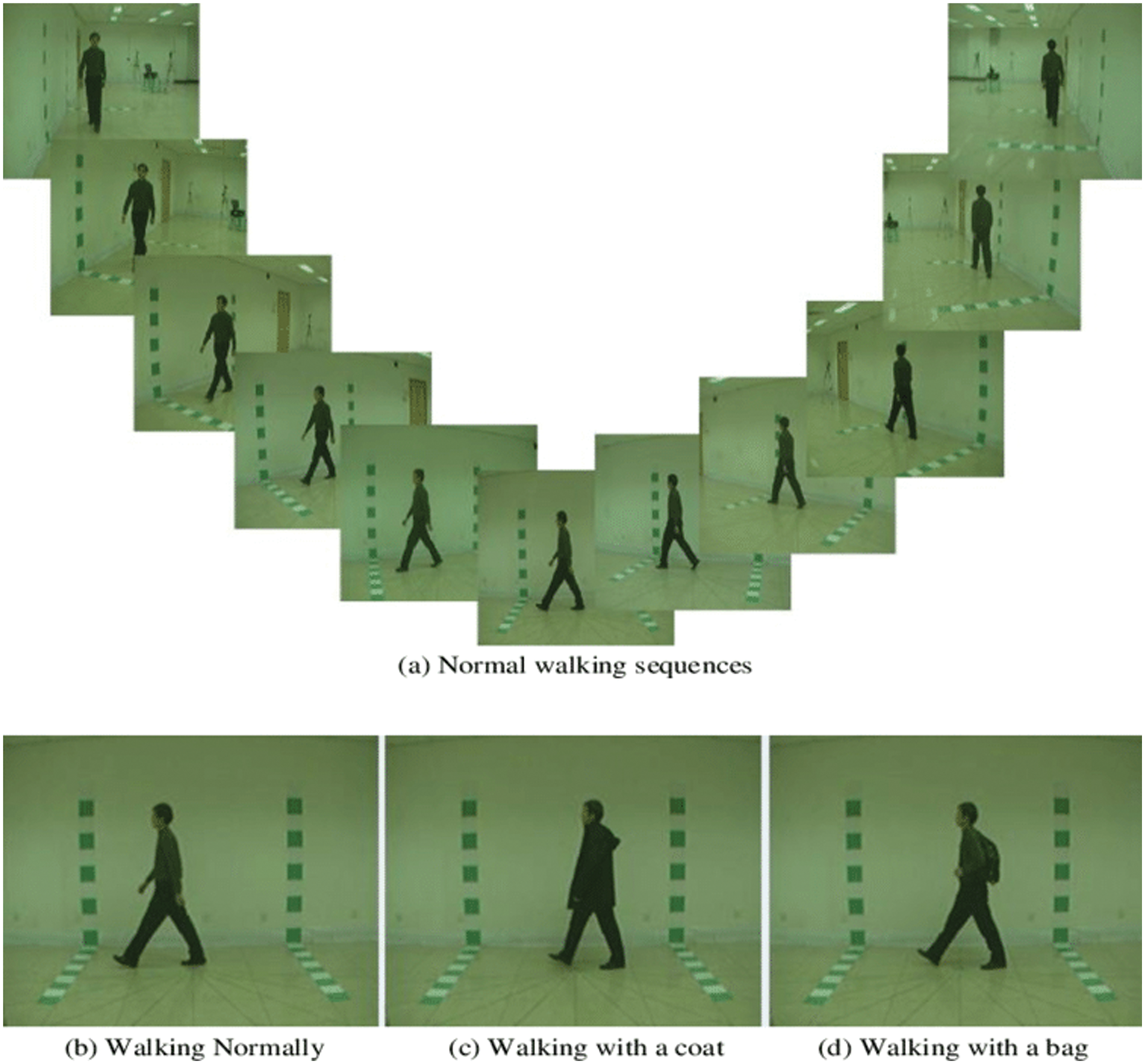
Figure 4: Sample frames of the CASIA-B dataset for all angles. Copyright @ 2018, SPIE Digital Library [32]

4.2 Experimental Setup

The neural networks were trained using several hyperparameters, including a minibatch size of 32, a learning rate of 0.0001, a value of momentum of 0.7, 150 epochs, 10-fold cross-validation, and the Adam optimizer for learning rate optimization. Training and testing set was created from the dataset in a 70:30 split. On a PC with a Core-i7 CPU, 8 GB of RAM, and a 2 GB graphics card, the suggested approach was put into practice using MATLAB 2022a.

4.3 Numerical Results

The outcomes of the proposed framework are shown in tabular form. The results are presented in five different experiments. In the first experiment, Efficientnet-b0 model features are extracted and applied to neural networks for classification. Five neural networks are used for classification accuracy: WNN, NNN, MNN, Bi-layered NN, and Tri-layered NN. The accuracy is computed for each angle separately. For angle zero, the 96.2% highest accuracy is achieved by WNN. On angle 18, the WNN attained the best accuracy of 98.7%, whereas this classifier performed well for the other angles, such as 36, 54, 72, 90, 108, 126, 144, 162, and 180, and attained the accuracy of 97.7%, 97.1%, 85.3%, 88.9%, 93.2%, 88.2%, 90.9%, 93.9%, and 99.9%. The results of each angle of the dataset evaluation are reported individually. The results of the CASIA-B dataset in terms of accuracies are shown in Table 1 by analyzing Efficientnet-b0 deep features.

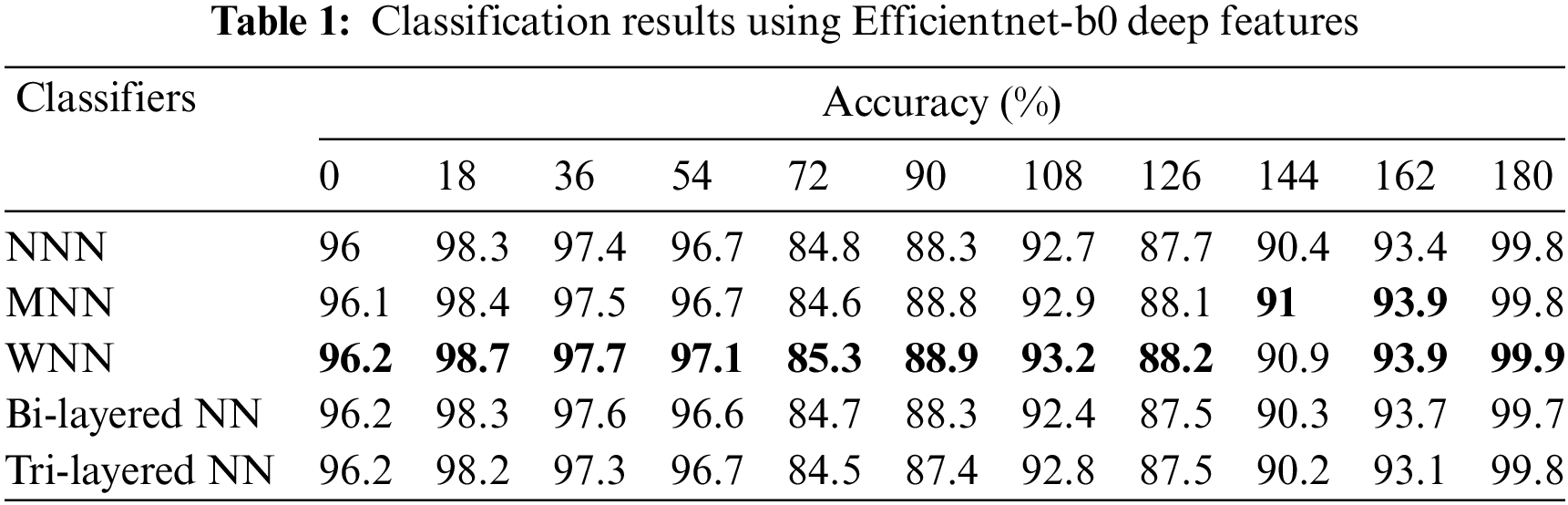
In the second experiment, Darknet19 model features are extracted and applied neural networks for classification. The accuracy is computed for each angle separately. For angle zero, the 96.7% highest accuracy is achieved by Tri-Layered NN. On angle 18, the Tri-Layered NN attained the best accuracy of 99.8%, whereas this classifier performed well for the other angles such as 36, 54, 72, 90, 108, 126, 144, 162, and 180 and attained the accuracy of 98.1%, 97.4%, 81.6%, 87.1%, 90.2%, 85.5%, 88.3%, 93.6%, and 96.7%. The results of each angle of the dataset evaluation are reported individually. The results of the CASIA-B dataset in terms of accuracies are shown in Table 2 by analyzing Darknet19 deep features.

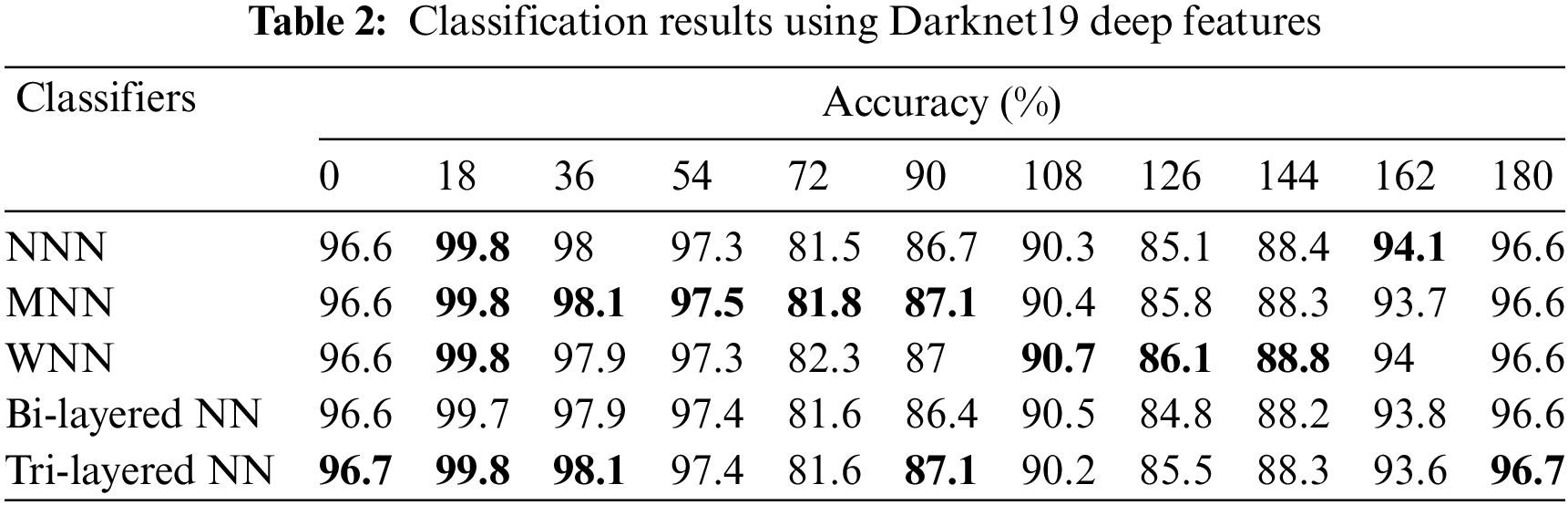
In the third experiment, Efficientnet-b0 model features are optimized using the Sine-Cosine optimizer and applied neural networks for the classification. The accuracy is computed for each angle separately. For angle zero, the 96.7% highest accuracy is achieved by Tri-Layered NN. On angle 18, the Tri-Layered NN attained the best accuracy of 99.8%, whereas this classifier performed well for the other angles such as 36, 54, 72, 90, 108, 126, 144, 162, and 180 and attained the accuracy of 98.1%, 97.4%, 81.6%, 87.1%, 90.2%, 85.5%, 88.3%, 93.6%, and 96.7%. The results of each angle of the dataset evaluation are reported individually. The results of the CASIA-B dataset in terms of accuracies are shown in Table 3 by analyzing the best features of the Efficientnet-b0 model.

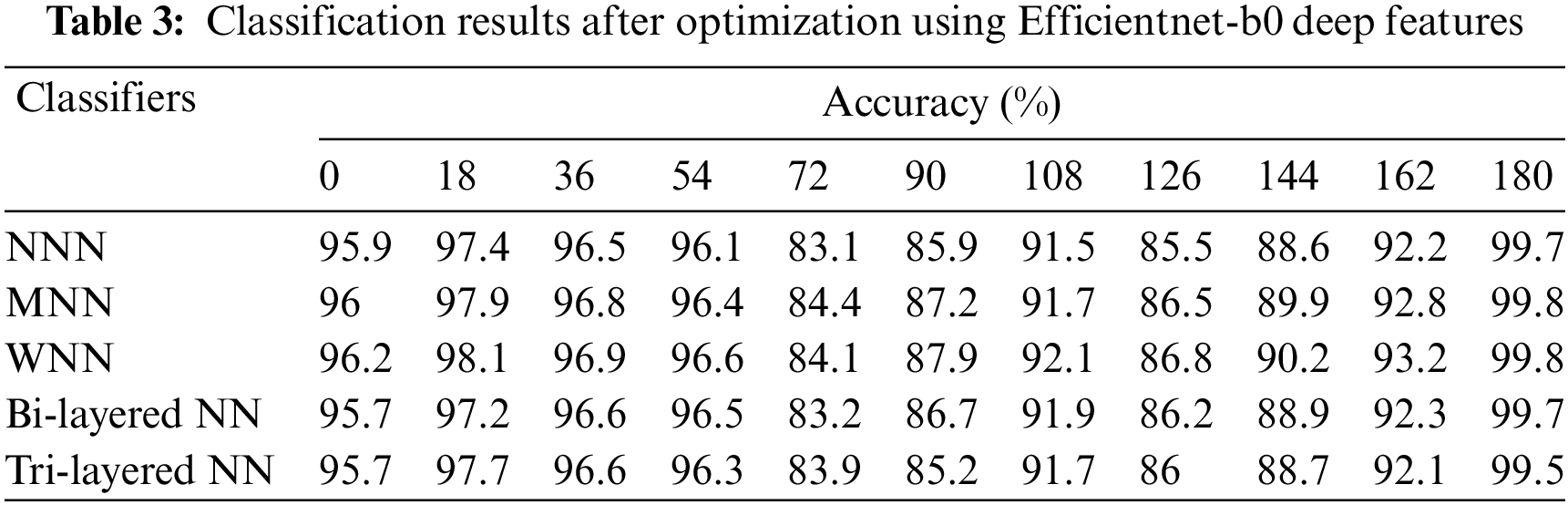
In the fourth experiment, Darknet19 model features are optimized using the sine-cosine optimizer and applied neural networks for the classification. The accuracy is computed for each angle separately. For angle zero, the 96.2% highest accuracy is achieved by WNN. On angle 18, the WNN attained the best accuracy of 99.7%, whereas this classifier performed well for the other angles, such as 36, 54, 72, 90, 108, 126, 144, 162, and 180, and attained the accuracy of 97.5%, 97.2%, 81.5%, 86.8%, 90.1%, 85.6%, 87.7%, 93.1%, and 99.8%. The results of each angle of the dataset evaluation are reported individually. The results of the CASIA-B dataset in terms of accuracies are shown in Table 4 by analyzing the best features of the Darknet19 model.

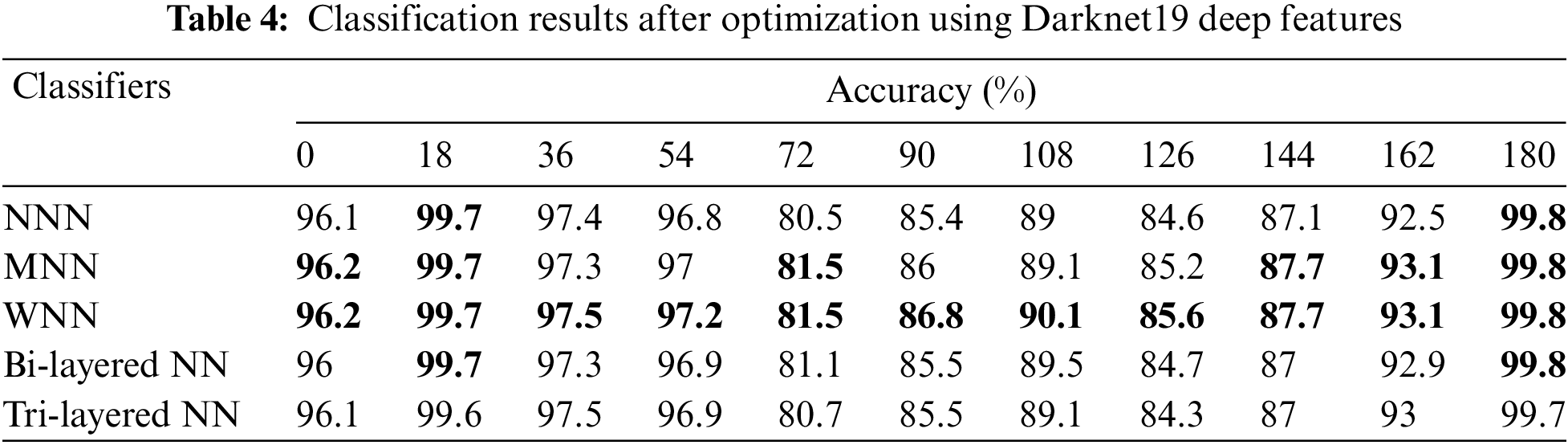
In the final experiment, the fusion of both optimized feature vectors is performed, and the final optimal fused vector is passed to neural networks for classification. The accuracy is computed for each angle separately. For angle zero, the 96.8% highest accuracy is achieved by WNN. On angle 18, the WNN attained the best accuracy of 99.9%, whereas this classifier performed well for the other angles, such as 36, 54, 72, 90, 108, 126, 144, 162, and 180, and attained the accuracy of 98.7%, 98.1%, 85.5%, 89.5%, 93.3%, 87.9%, 91.3%, 94.7%, and 100%. The results of each angle of the dataset evaluation are reported individually. The results of the CASIA-B dataset in terms of accuracies are shown in Table 5 by analyzing the final fused optimal vector. In the last, the proposed framework accuracy is visualized in a graphical form, as shown in Fig. 5. In this figure, it is observed that the fusion process improved the accuracy.

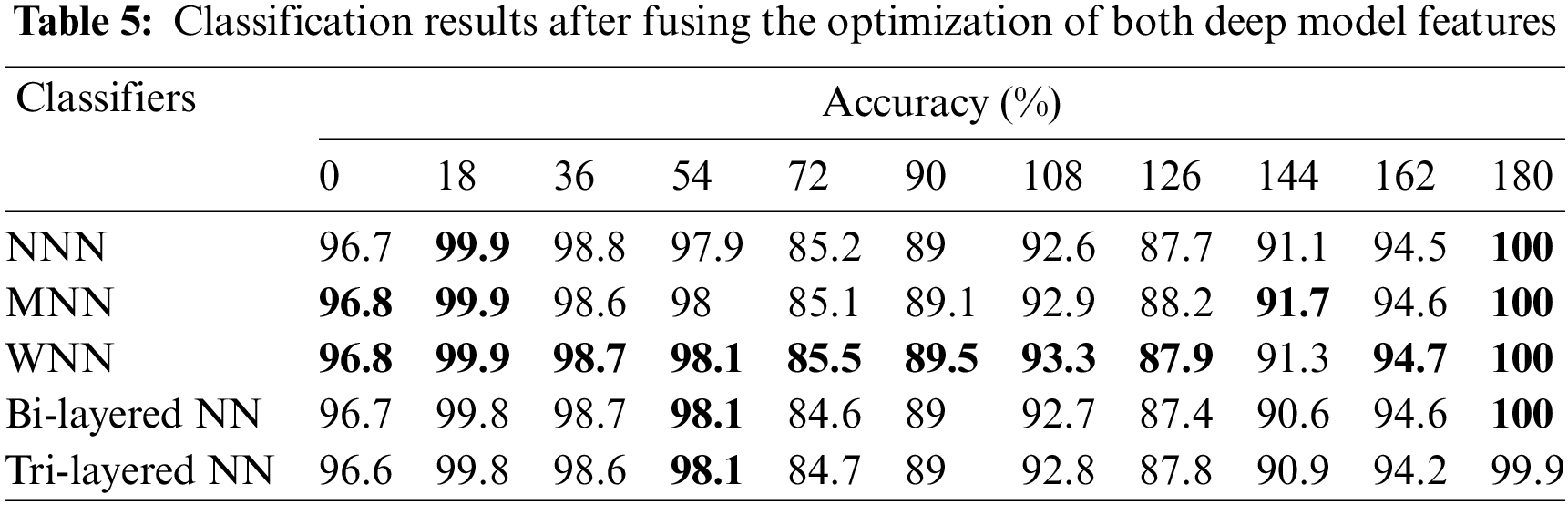
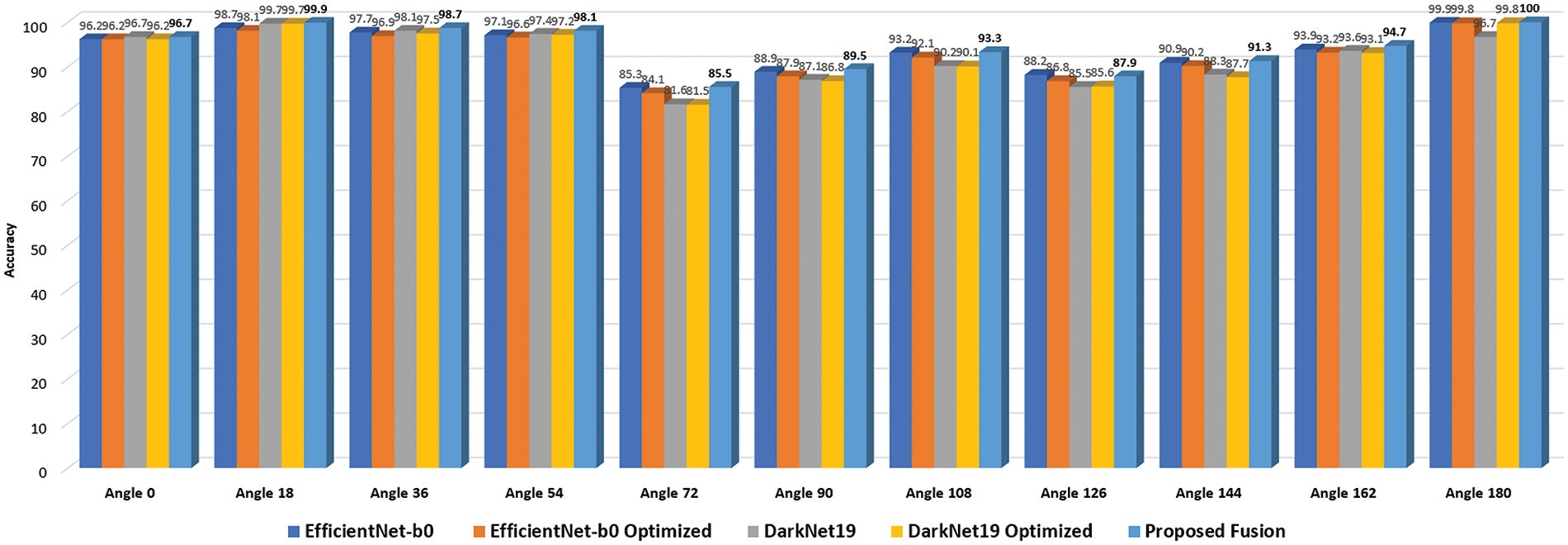
Figure 5: Visual investigation of the proposed framework’s intermediate phases

The accuracy of the suggested approach was compared against state-of-the-art (SOTA) methods using different angles of the CASIA-B dataset, with the results shown in Table 6. The recommended framework outperformed the most recent methods with a improved accuracy rate of HGR. The data in this table shows that overall, the proposed HGR framework produced better accuracy than SOTA techniques.

5  Conclusion

A deep learning and optimal feature selection using Harris Hawks controlled Sine-Cosine based framework is proposed in the work to classify covariate factors such as carrying a bag and wearing a coat. Two pre-trained CNN architectures are tweaked and trained using deep transfer learning in the first step using static hyperparameters. The learning rate is selected by employing the particle swarm optimization (PSO) algorithm. Then, features are retrieved from both trained models using a Harris Hawks-controlled Sine-Cosine optimization approach. This algorithm chooses the best features, which are then combined in a novel correlation-based manner. Finally, neural networks are employed for the classification of selected features. The publicly accessible dataset, the CASIA-B dataset, has been utilized for the experimental process and attained an improved accuracy of 94.14%. Comparison is also conducted with recent techniques and shows an improvement in accuracy. Overall, we conclude that the learning rate selection using a static manner decreased the accuracy. In addition, the selection of best features improved the accuracy and reduced the computational time compared to the existing experiments.

Acknowledgement: The authors are thankful to Princess Nourah bint Abdulrahman University Researchers Supporting Project, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This work was supported by the “Human Resources Program in Energy Technology” of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and Granted Financial Resources from the Ministry of Trade, Industry, and Energy, Republic of Korea (No. 20204010600090). The funding of this work was provided by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2023R410), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: All authors in this work contributed equally. All authors read it and agree for the submission.

Availability of Data and Materials: The CASIA-B dataset used in this work is publicly available.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. A. K. Jain, A. Ross and S. Prabhakar, “An introduction to biometric recognition,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 14, pp. 4–20, 2004. [Google Scholar]

2. A. K. Jain, A. Ross and S. Pankanti, “Biometrics: A tool for information security,” IEEE Transactions on Information Forensics and Security, vol. 1, pp. 125–143, 2006. [Google Scholar]

3. L. Liu, H. Wang, H. Li, J. Liu, S. Qiu et al., “Ambulatory human gait phase detection using wearable inertial sensors and hidden Markov model,” Sensors, vol. 21, no. 4, pp. 1347, 2021. [Google Scholar] [PubMed]

4. F. Deligianni, Y. Guo and G. Z. Yang, “From emotions to mood disorders: A survey on gait analysis methodology,” IEEE Journal of Biomedical and Health Informatics, vol. 23, no. 6, pp. 2302–2316, 2019. [Google Scholar] [PubMed]

5. R. Liao, Z. Li, S. S. Bhattacharyya and G. York, “PoseMapGait: A model-based gait recognition method with pose estimation maps and graph convolutional networks,” Neurocomputing, vol. 501, pp. 514–528, 2022. [Google Scholar]

6. D. Gafurov, “A survey of biometric gait recognition: Approaches, security and challenges,” in Annual Norwegian Computer Science Conf., Norway, pp. 19–21, 2007. [Google Scholar]

7. M. A. Khan, S. Kadry, P. Parwekar, R. Damaševičius, A. Mehmood et al., “Human gait analysis for osteoarthritis prediction: A framework of deep learning and kernel extreme learning machine,” Complex & Intelligent Systems, vol. 9, pp. 2665–2683, 2021. [Google Scholar]

8. V. Bijalwan, V. B. Semwal and T. Mandal, “Fusion of multi-sensor-based biomechanical gait analysis using vision and wearable sensor,” IEEE Sensors Journal, vol. 21, no. 13, pp. 14213–14220, 2021. [Google Scholar]

9. N. Bayat, E. Rastegari and Q. Li, “Human gait recognition using bag of words feature representation method,” arXiv:2203.13317, 2022. [Google Scholar]

10. M. Derlatka and M. Borowska, “Ensemble of heterogeneous base classifiers for human gait recognition,” Sensors, vol. 23, no. 1, pp. 508, 2023. [Google Scholar] [PubMed]

11. D. Kim and J. Paik, “Gait recognition using active shape model and motion prediction,” IET Computer Vision, vol. 4, no. 1, pp. 25–36, 2010. [Google Scholar]

12. L. Wang, Y. Li, F. Xiong and W. Zhang, “Gait recognition using optical motion capture: A decision fusion based method,” Sensors, vol. 21, no. 10, pp. 3496, 2021. [Google Scholar] [PubMed]

13. R. Liao, W. An, Z. Li and S. S. Bhattacharyya, “A novel view synthesis approach based on view space covering for gait recognition,” Neurocomputing, vol. 453, pp. 13–25, 2021. [Google Scholar]

14. J. Slemenšek, I. Fister, J. Geršak, B. Bratina, V. M. van Midden et al., “Human gait activity recognition machine learning methods,” Sensors, vol. 23, no. 2, pp. 745, 2023. [Google Scholar] [PubMed]

15. D. Pinčić, D. Sušanj and K. Lenac, “Gait recognition with self-supervised learning of gait features based on vision transformers,” Sensors, vol. 22, no. 19, pp. 7140, 2022. [Google Scholar] [PubMed]

16. C. Wan, L. Wang and V. V. Phoha, “A survey on gait recognition,” ACM Computing Surveys, vol. 51, no. 5, pp. 1–35, 2018. [Google Scholar]

17. C. Xu, Y. Makihara, X. Li and Y. Yagi, “Occlusion-aware human mesh model-based gait recognition,” IEEE Transactions on Information Forensics and Security, vol. 18, pp. 1309–1321, 2023. [Google Scholar]

18. H. Zhu, Z. Zheng and R. Nevatia, “Gait recognition using 3-D human body shape inference,” in Proc. of the IEEE/CVF Winter Conf. on Applications of Computer Vision, NY, USA, pp. 909–918, 2023. [Google Scholar]

19. L. F. Shi, Z. Y. Liu, K. J. Zhou, Y. Shi and X. Jing, “Novel deep learning network for gait recognition using multimodal inertial sensors,” Sensors, vol. 23, no. 2, pp. 849, 2023. [Google Scholar] [PubMed]

20. F. Shehzad, M. Attique Khan, A. E. Yar, M. Sharif, M. Alhaisoni et al., “Two-stream deep learning architecture-based human action recognition,” Computers, Material & Continua, vol. 74, no. 2, pp. 21–39, 2023. [Google Scholar]

21. M. A. Khan, M. Mittal, L. M. Goyal and S. Roy, “A deep survey on supervised learning based human detection and activity classification methods,” Multimedia Tools and Applications, vol. 80, pp. 27867–27923, 2021. [Google Scholar]

22. A. Kececi, A. Yildirak, K. Ozyazici, G. Ayluctarhan, O. Agbulut et al., “Implementation of machine learning algorithms for gait recognition,” Engineering Science and Technology, an International Journal, vol. 23, no. 4, pp. 931–937, 2020. [Google Scholar]

23. H. Dou, W. Zhang, P. Zhang, Y. Zhao, S. Li et al., “VersatileGait A large-scale synthetic gait dataset with fine-grainedattributes and complicated scenarios,” arXiv:2101.01394, 2021. [Google Scholar]

24. Z. Zhu, X. Guo, T. Yang, J. Huang, J. Deng et al., “Gait recognition in the wild: A benchmark,” in Proc. of the IEEE/CVF Int. Conf. on Computer Vision, Shengai, China, pp. 14789–14799, 2021. [Google Scholar]

25. C. Huang, F. Zhang, Z. Xu and J. Wei, “The diverse gait dataset: Gait segmentation using inertial sensors for pedestrian localization with different genders, heights and walking speeds,” Sensors, vol. 22, no. 4, pp. 1678, 2022. [Google Scholar] [PubMed]

26. M. A. M. Hasan, F. Al Abir, M. Al Siam and J. Shin, “Gait recognition with wearable sensors using modified residual block-based lightweight CNN,” IEEE Access, vol. 10, pp. 42577–42588, 2022. [Google Scholar]

27. W. An, S. Yu, Y. Makihara, X. Wu, C. Xu et al., “Performance evaluation of model-based gait on multi-view very large population database with pose sequences,” IEEE Transactions on Biometrics, Behavior, and Identity Science, vol. 2, no. 4, pp. 421–430, 2020. [Google Scholar]

28. Y. Tian, L. Wei, S. Lu and T. Huang, “Free-view gait recognition,” PLoS One, vol. 14, no. 4, pp. e0214389, 2019. [Google Scholar] [PubMed]

29. K. Hussain, N. Neggaz, W. Zhu and E. H. Houssein, “An efficient hybrid sine-cosine Harris hawks optimization for low and high-dimensional feature selection,” Expert Systems with Applications, vol. 176, pp. 114778, 2021. [Google Scholar]

30. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, pp. 120–133, 2016. [Google Scholar]

31. H. Chao, Y. He, J. Zhang and J. Feng, “GaitSet: Regarding gait as a set for cross-view gait recognition,” in Proc. of the AAAI Conf. on Artificial Intelligence, NY, USA, pp. 8126–8133, 2019. [Google Scholar]

32. T. Hassan, A. Sabir and S. Jassim, “Data-independent versus data-dependent dimension reduction for gait-based gender classification,” Mobile Multimedia/Image Processing, Security, and Applications 2018, vol. 31, pp. 95–102, 2018. [Google Scholar]

33. M. A. Khan, Y. D. Zhang, S. A. Khan, M. Attique, A. Rehman et al., “A resource conscious human action recognition framework using 26-layered deep convolutional neural network,” Multimedia Tools and Applications, vol. 80, pp. 35827–35849, 2021. [Google Scholar]

34. P. S. Rao, G. Sahu, P. Parida and S. Patnaik, “An adaptive firefly optimization algorithm for human gait recognition,” in Smart and Sustainable Technologies: Rural and Tribal Development Using IoT and Cloud Computing: Proc. of ICSST 2021, New Delhi, India, Springer, pp. 305–316, 2022. [Google Scholar]

35. L. Wang, X. Zhang, R. Han, J. Yang, X. Li et al., “A benchmark of video-based clothes-changing person re-identification,” arXiv:2211.11165, 2022. [Google Scholar]

36. M. Asif, M. I. Tiwana, U. S. Khan, M. W. Ahmad, W. S. Qureshi et al., “Human gait recognition subject to different covariate factors in a multi-view environment,” Results in Engineering, vol. 15, pp. 100556, 2022. [Google Scholar]

37. R. Anusha and C. Jaidhar, “Clothing invariant human gait recognition using modified local optimal oriented pattern binary descriptor,” Multimedia Tools and Applications, vol. 79, pp. 2873–2896, 2020. [Google Scholar]