A Normalizing Flow-Based Bidirectional Mapping Residual Network for Unsupervised Defect Detection

1  Introduction

In recent years, machine vision and deep learning technology have been widely used in defect detection [1]. Nevertheless, owing to the ongoing enhancements and optimization of novel materials, equipment, and production processes [2,3], there has been a remarkable increase in the yield of industrial products. This progress, while commendable, introduces a notable challenge in the practical realm—namely, the scarcity of available defect samples for collection and labeling. Consequently, the task of anomaly detection becomes increasingly intricate. Traditional supervised methods [4–6], designed for scenarios with ample labeled data, prove inadequate for industrial defect detection under these evolving conditions. Consequently, we propose an innovative unsupervised deep-learning defect detection method that exclusively relies on normal samples, circumventing the need for actual defective samples.

Recent research mainly focuses on density evaluation-based detection methods, which use CNN pre-trained on the ImageNet dataset to extract comprehensive visual features of the detection system and detect anomalies in the feature space. Some methods [7,8] simulate the thinking way of human beings to identify unknown defects and use the features of normal samples to build a memory bank, which is compared with the test features in the inference stage to detect and locate abnormalities. However, building memory banks usually consumes a lot of computation time and online memory storage, making their application in industrial scenarios challenging. Normalizing flow methods [9–11] directly learn the distribution of normal samples in the feature space. They can gradually transform the features with complex distribution into space with normal distribution through several flow steps to detect anomalies. This class of methods can update the network by minimizing the log-likelihood loss. In the testing phase, normal features are mapped into the normal distribution, and abnormal features are mapped out to detect anomalies. Other methods [12,13] usually train a CNN to reconstruct the input features as an alternative to image reconstruction methods [14–16], which significantly reduces the computation time. Among them, the Bidirectional Pre-trained Feature Mapping Network (B-PFM) [13] considers the difference of features extracted by different pre-trained CNN. In order to obtain a more comprehensive feature representation, B-PFM uses two different pre-trained CNN to extract features, which are defined as Source domain Neural Network (SNN) and Target domain Neural Network (TNN). The core idea of B-PFM is shown in Fig. 1a, where the input image x obeys a certain complex distribution pX(x), and the features are embedded by pre-training SNNs and TNNs, whose source and target domain features obey a certain complex distribution pY(y) and pU(u), respectively. Thus, the B-PFM detects the anomalies in the spaces of the two pre-trained features with complex distributions. However, the distribution of the ImageNet [17] data set is not the same as that of the training image dataset, and the use of such a biased pre-trained CNN cannot extract features well, which limits the detection performance of such methods. Using two pre-trained CNN in the B-PFM network undoubtedly exacerbates this problem. Meanwhile, although there are some differences, the features extracted using different configurations of networks under the same architecture (e.g., ResNet18, ResNet34, etc.) still have a certain amount of redundancy of feature information, which further limit the performance of B-PFM.

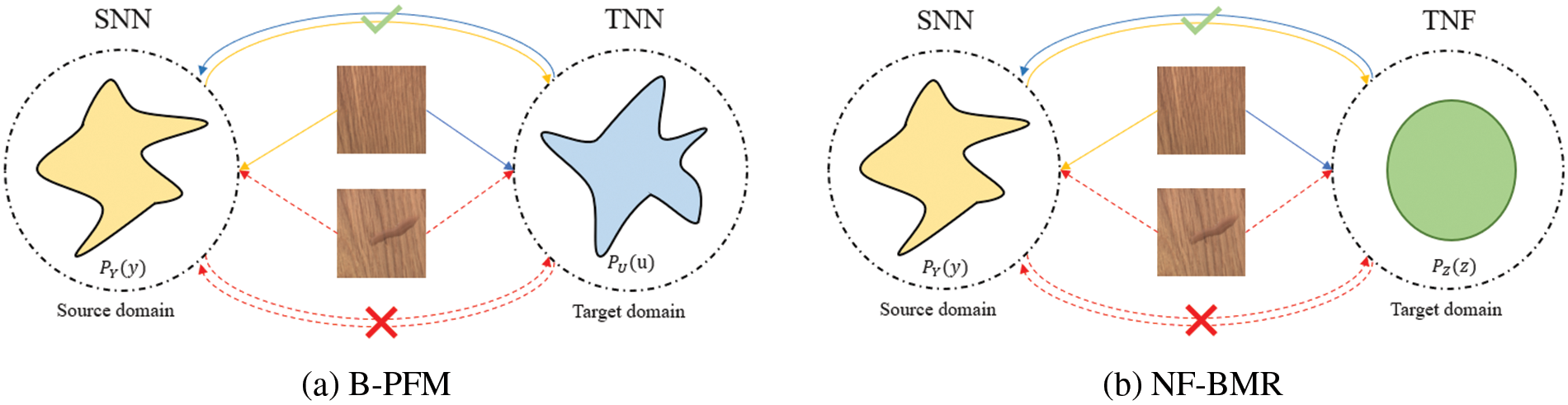
Figure 1: Spatial mapping anomaly detection diagram of Baseline method and the method proposed in this paper

To solve the above problems, this paper uses the normalizing flow as the Target domain Normalizing Flow network (TNF) instead of TNN to construct the target domain feature space to alleviate the problems caused by biased pre-training CNN. At the same time, TNF completely differs from the traditional CNN framework. It can construct a more discriminative target domain space so that the two detection spaces can effectively complement their shortcomings and detect features from two perspectives, to improve the detection performance. This paper takes B-PFM as our baseline, based on this work, we propose a bi-directional mapping residual network based on normalizing flow (NF-BMR), as shown in Fig. 1b, we use the normalizing flow network (NF) to construct the target domain, due to the characteristic of the NF, it can transform the source domain Y with complex distribution pY(y) to the target domain Z that obeys the normal distribution N(0,I). Therefore, the proposed NF-BMR network can detect anomalies in the source domain with complex distribution and the target domain with simple distribution. In addition, the output of NF can also be used as the anomaly score, which can map the anomalies outside of the distribution of the normal samples to further improve the defect detection performance. Meanwhile, to better learn the source and target domain features, we also propose a bi-directional mapping residual network (BMR), and the detailed network structure is shown in Section 3.3. Fig. 2a shows the distribution of normal and abnormal areas of the TNF network output results. The distribution of abnormal samples shows that TNF can map abnormal samples outside the distribution of normal samples. In Fig. 2b, the first column shows the input defect image, the second column shows the real defect label, the third column shows the output visualization result of the pre-trained EfficientNet-b3, and the fourth column shows the output visualization result of TNF. It clearly shows that the TNF network can capture the defect features that the pre-trained CNN cannot extract.

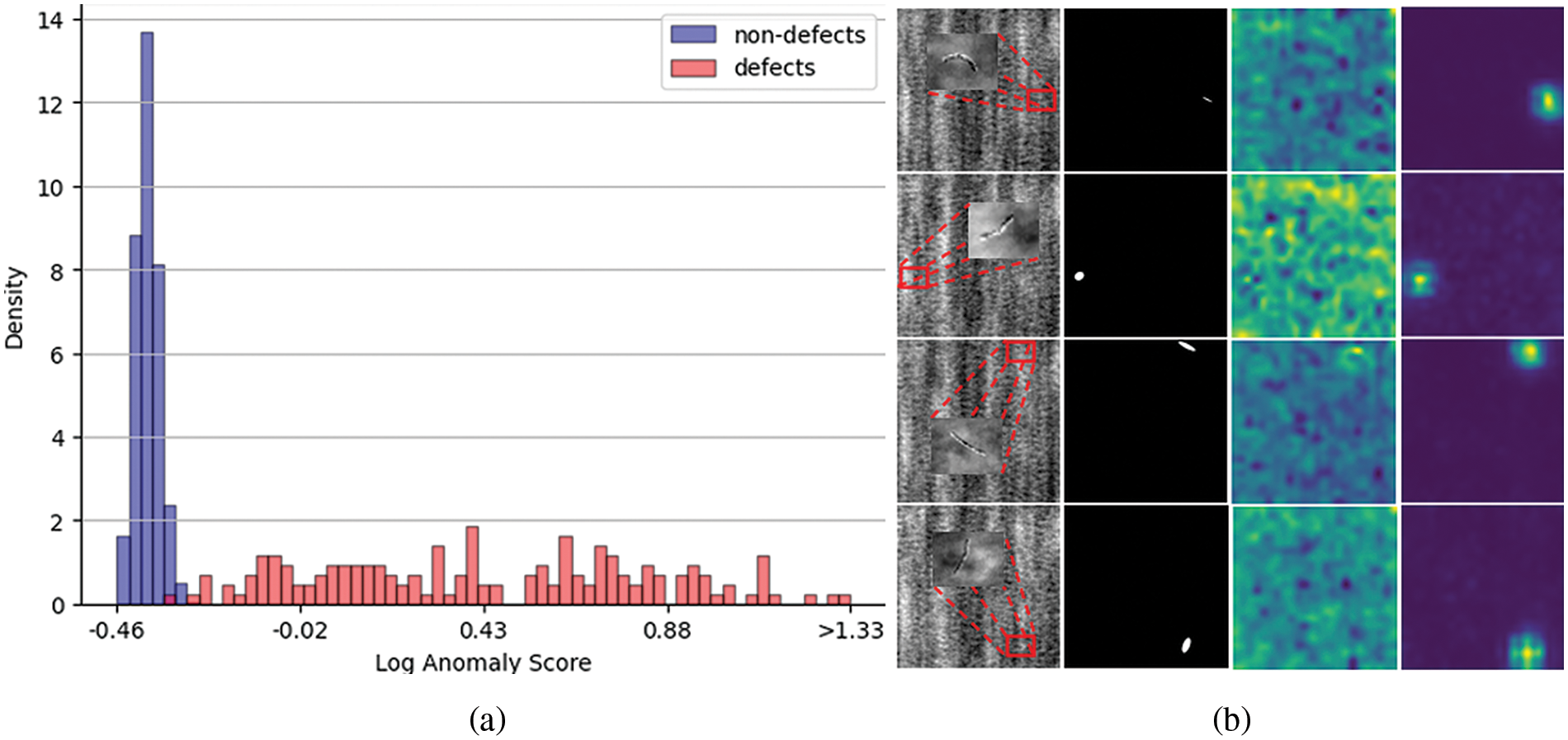
Figure 2: Demonstration of experimental results for Class8 class of the DAGM dataset ((a) Log-likelihood histogram of the TNF output results, (b) Visualization of the outputs of EfficientNet-b3 and TNF)

The main contributions of this paper are:

(1) A normalizing flow network different from the CNN framework is introduced as TNF to construct a more discriminative target domain space to solve the problems existing in the B-PFM framework.

(2) A bidirectional mapping residual network (BMR) is proposed to learn the feature representation of the source and target domains to improve the detection performance further.

(3) Multiple comparative experiments are conducted on the MVTec AD and DAGM datasets to verify the effectiveness and efficiency of the proposed method. Compared with the state-of-the-art methods, the proposed method achieves the best performance.

2  Related Works

In the following, we will review previous work on anomaly detection and pre-training feature mapping related to the method proposed in this paper.

2.1 Anomaly Detection

2.1.1 Reconstruction-Based Methods

Reconstruction-based methods generally use autoencoders (AE) [18] and Generative Adversarial Networks (GAN) [19,20]. The core idea is to train the model on normal image samples to reconstruct normal images well. During testing, the model generates significant reconstruction errors in the defective regions of the image and achieves defect detection and localization. However, in practical applications, neural networks have strong learning abilities [21,22], and they can still reconstruct abnormal image areas well even if no abnormal images are used in the training stage, which leads to ineffective abnormality discrimination. Therefore, some works begin to use masks to cover the abnormal regions of the image to alleviate the influence of abnormal areas on the reconstruction model. Yan et al. [23] proposed a Semantic Context-based Abnormal Detection Network (SCADN), which designs a multi-scale stripe mask to remove a part of the area from normal sample images and reconstruct the missing area to match the input image. RIAD [24] solves the problem that the autoencoder can reconstruct the abnormal area of the image by randomly deleting part of the image area and reconstructing the image from part of the image. Although masks alleviate the effect of abnormal regions to some extent, this effect still exists as the mask does not entirely obscure the anomalous regions due to their random size, localization, and shape.

2.1.2 Method Based on Density Estimation

The density-based methods primarily rely on useful feature vectors of pre-trained CNN on the ImageNet dataset [17]. In the training process, normal sample data distribution is acquired by inputting normal images. During inference, anomaly detection and localization are performed by computing the distance between the abnormal and normal sample data distribution. Cohen et al. [8] proposed a new abnormal segmentation method, SPADE, which uses K Near Neighbor (KNN) to obtain K normal images that are most similar to an abnormal image at the image level and then uses the retrieved K normal images to get feature pyramid information under different layers of the neural network for alignment. This method has achieved good results in defect detection and localization. Defard et al. [7] further improved this method. They proposed a new network called PaDiM, which uses the features between different semantic layers of a pre-trained CNN for patch embedding while using a multivariate Gaussian distribution to obtain the probability density representation of normal samples. However, the assumption of a Gaussian distribution is a significant simplification, which makes the network inflexible in training distributions. In contrast, because Normalizing flow networks can perform precise density evaluation, recent works [9–11] have begun to use Normalizing flow models for anomaly detection and achieved good results. Rudolph et al. [11] proposed the DifferNet network, which uses a CNN to extract descriptive feature information and uses Normalizing flow for probability density evaluation. However, this network lacks important contextual semantic information and positional information, and can only be used for image-level detection rather than pixel-level localization. CS-Flow, a Normalizing flow method proposed in [10], uses multi-scale features and introduces fully convolutional networks to achieve good results in both detection and localization.

2.2 Pre-Training Feature Mapping

PFM [13] only inputs normal images into the pre-trained SNN and TNN in the training phase to obtain the normal embedded features of the source and target domains. Then, PFM is used to map the embedded features of the source domain to the target domain. L2 loss shrinks the distance between the mapped and target domain embedded features. During testing, defect image features will not be mapped to the target domain by the PFM network. They will result in a significant error, which is used for defect detection and localization. Due to the significantly lower parameter number in the PFM network than in the SNN and TNN, adding a reverse mapping neural network to the PFM during inference will not result in excessive computation and time consumption. Therefore, the author further proposed a bi-directional pre-trained feature mapping network B-PFM, in which the overall network parameters are optimized by the bi-directional mapping L2 loss during the training stage. During testing, image features can be mapped to both the source and target domains by the B-PFM for comparison. Compared to the PFM network, both directions are fully utilized in the B-PFM, and the defect detection performance can be improved. Finally, to fully use the feature information from different layers of the pre-trained CNN to improve defect detection and localization, the multilayer bi-directional pre-trained feature mapping network MB-PFM was also proposed in [13].

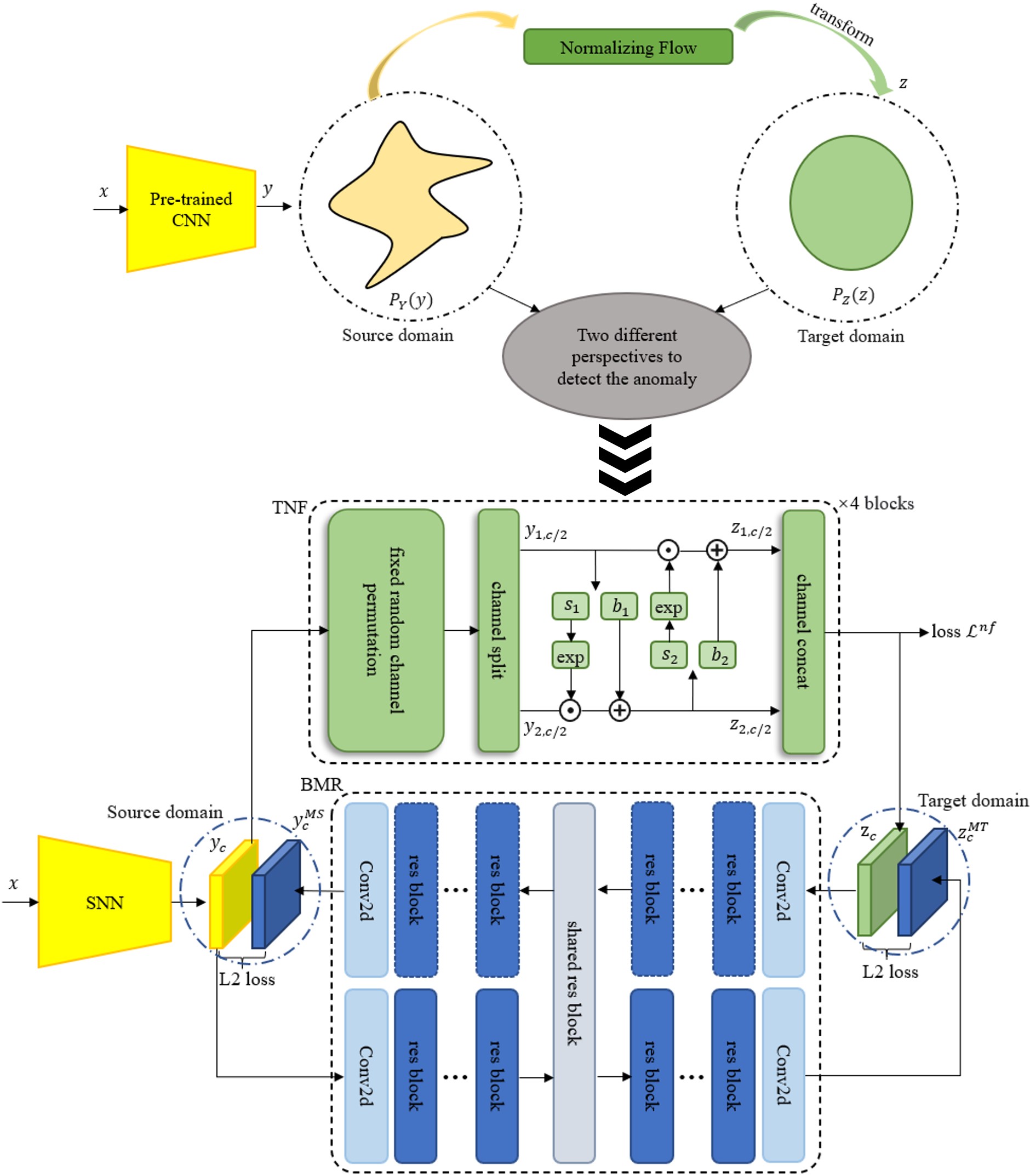
This paper proposes a bi-directional mapping residual network based on normalizing flow (NF-BMR), as shown in Fig. 3. Our network does not use TNN to embed target domain features but trains a separate TNF to transform features with a complex distribution into target domain features with a simple distribution. Then, the proposed bidirectional mapping residual network BMR is used to detect defects in two spatial domains with different distributions. Experimental results show that our NF-BMR can perform better defect detection results.

Figure 3: NF-BMR network structure

3  NF-BMR Framework

This section will describe the proposed NF-BMR network framework in detail. Our core idea is to use the pre-trained CNN and TNF networks to construct the source and target domains, respectively. Fig. 1b shows that the normal image features can freely pass through the bidirectional mapping network. In contrast, the abnormal image features cannot be mapped normally through the network to the source and target domains. The overall framework is shown in Fig. 3, which consists of three parts: the pre-trained SNN, the TNF, and the BMR. In the training phase, the pre-trained SNN is used to construct the source domain, followed by training the TNF to build the target domain that obeys normal distribution. Finally, the BMR is trained to shrink the gap of normal image features between the source domain and the target domain through the loss of mean-square error. When the defective image features are input in the inference phase, the BMR will not map the defective features between the source and target domains to achieve defect detection and localization results.

3.1 Source Domain

We use the output of a particular layer of the pre-trained SNN to build the source domain feature space. An image x∈X is inputted into SNN to embed it into the source domain feature space Y, and the embedded feature representation is:

SNN(x;θS)=yc(1)

where θS represents the pre-trained parameters of the SNN, yc denotes the embedded feature with a channel number of c, and yc∈Yw×h×c.

3.2 Target Domain

We train a normalizing flow model based on Real-NVP [25]. But the difference in our training process is that instead of using the output of the flow model directly as the anomaly score, a more discriminative target domain feature space is constructed for the BMR network. In addition, the trained TNF maps the source domain feature space Y to the target domain feature space Z that follows a normal distribution N(0,I). The mapping of the feature representation is as follows:

TNF(yc;θnf)=zc(2)

where θnf represents the parameters trained by the TNF network, zc represents the embedded features. The mapping operation does not change the number of channels or the size of the feature maps, i.e., the number of channels is c and zc∈Zw×h×c.

The normalizing flow model consists of multiple affine coupling blocks. The input source domain feature yc is randomly selected along its channel dimension and divided into two parts with a fixed arrangement. These two parts are then equally split into y1,c/2 and y2,c/2. The scale and shift parameters provided by the subnetworks si and bi, i = {1,2}, are used to perform affine transformations on the two parts separately to obtain the corresponding outputs z1,c/2 and z2,c/2. Finally, the two tensor parts are concatenated along the channel dimension to obtain the output zc, with the channel dimension restored to c. The above process is described as follows:

y1,c/2,y2,c/2=split(yc)(3)

z2,c/2=es1(y1,c/2)⊙y2,c/2+b1(y1,c/2)(4)

z1,c/2=es2(y2,c/2)⊙y1,c/2+b2(y2,c/2)(5)

zc=concat(z1,c/2,z2,c/2)(6)

where the split(⋅) and concat(⋅) functions perform splitting and concatenating operations along the channel dimension, ⊙ stands for pixel-by-pixel multiplication, and si(⋅) and bi(⋅), i = {1,2}, can be set to arbitrarily complex functions to learn the two parameters of an affine transformation.

The mapping Y→Z uses a bijective function to project the image feature y∈pY(y) onto the latent variable z∈pZ(z). For this bijective function, a variable formula is used to define the model’s distribution on y:

pY(y)=pZ(z)|det∂z∂x|(7)

In our proposed method, the prior distribution of the mapped target domain space Z is defined as a normal distribution z∼N (0,I). The training objective is minimizing −log⁡pY(y). The corresponding loss function is as follows:

ℒnf=−log⁡pY(y)=‖z‖222−log⁡|det∂z∂y|(8)

3.3 Bidirectional Mapping Residual Network

B-PFM [13] is composed by five layers of 1 × 1 convolutional kernels, which reduces the network complexity but is not enough to learn the normal feature distribution in both the source and target domains. In order to obtain a better performance in defect detection, we propose a bidirectional residual mapping network BMR and validate it in the ablation study in Section 4.4. As shown in Fig. 4, the BMR network consists of the Source domain Mapping Neural Network (SMNN) and the Target domain Mapping Neural Network (TMNN). The mapping network is internally composed of multiple stacked residual blocks. They share a residual block parameter in the middle of the network to reduce the number of parameters. The number of residual blocks (denoted as res block in Fig. 4) on the left and right sides of the shared res block is symmetrically set to n. A convolutional layer is added to the first and last layers of the network to increase and decrease the channel number, respectively. A single residual block consists of a 1 × 1, 3 × 3, and 1 × 1 convolutional sequence, and a ReLU activation function follows each convolutional layer.

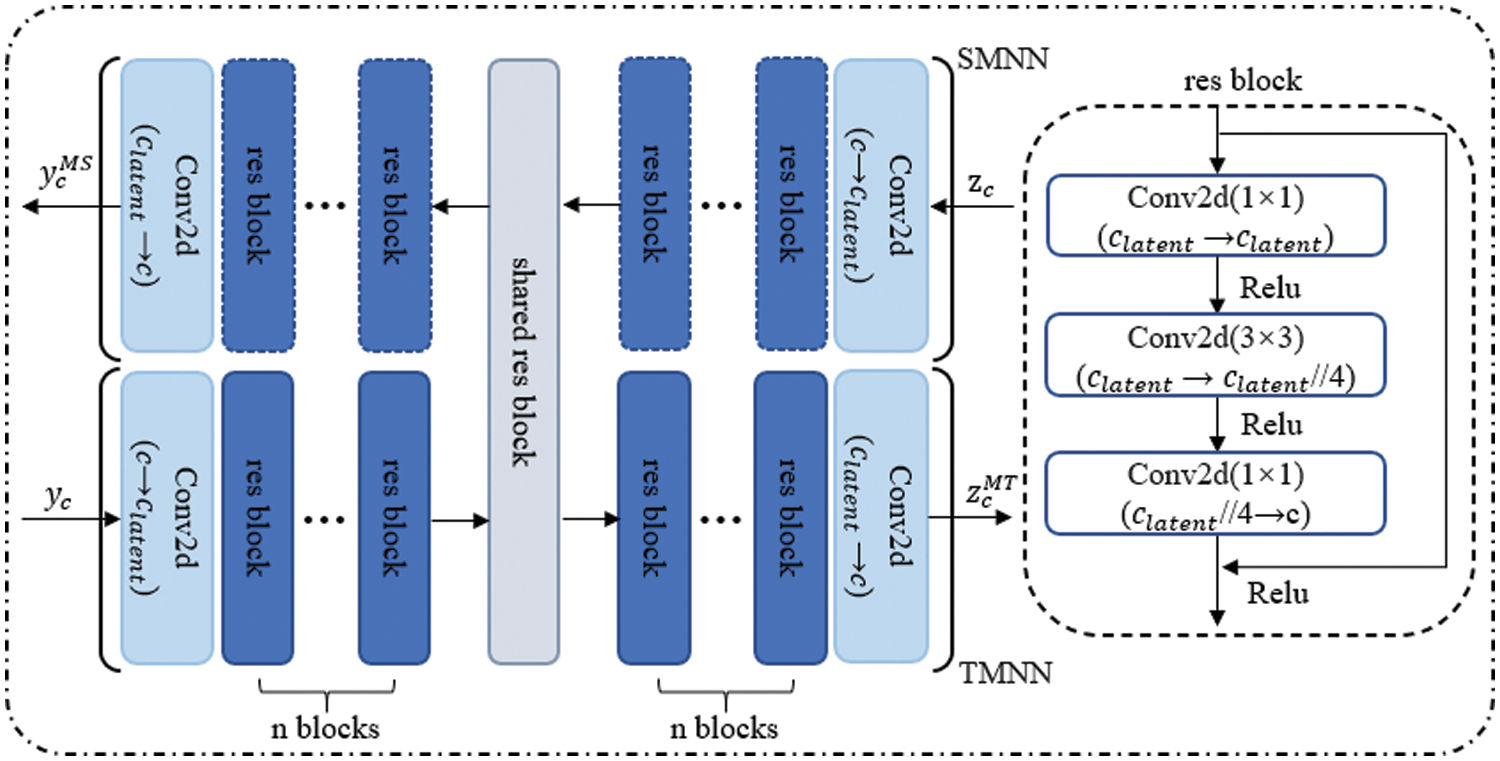
Figure 4: BMR network structure

When a training image x∈X is input into the pre-trained SNN, the source domain feature yc∈Yw×h×c can be obtained. Then, by using the trained TNF network, yc is transformed into the target domain feature zc∈Zw×h×c. Subsequently, yc is mapped to the target domain space according to the TMNN network. The mapped feature is represented as zcMT. Similarly, zc is mapped to the source domain space by the SMNN, and the mapped feature is represented as ycMS. The above mapping process is represented as follows:

zcMT=TMNN(yc;θMT)(9)

ycMS=SMNN(zc;θMS)(10)

losss=1w×h×c‖yc−ycMs‖22(11)

lossT=1w×h×c‖zc−zcMT‖22(12)

lossNF−BMR=losss+lossT(13)

For test images, the Anomaly Score Map (ASM) of an image can be calculated as follows:

ASM(i,j)=‖yc(i,j)−ycMs(i,j)‖22+‖zc(i,j)−zcMT(i,j)‖222(14)

where (i, j) denotes the pixel position.

4  Experiments

4.1 Datasets

The performance of our proposed method is evaluated on the MVTec AD [26] dataset and the DAGM [27] dataset.

(1) MVTec AD is an industrial anomaly detection benchmark dataset encompassing various objects and anomalies, constituting 15 categories, including 10 object classes and 5 texture classes. This dataset provides 3629 normal images for training, 467 normal images, and 1258 abnormal images for testing. The test set encompasses defects of different sizes, shapes, and types, such as cracks, scratches, and deformations. Each defect type can have up to 8 variations, resulting in 70 defect types.

(2) DAGM is a well-known benchmark surface defect detection dataset comprising synthetically generated images depicting various defective surfaces. The dataset consists of 16,100 images, equally divided between training and testing sets, categorized into ten image classes. Within each class, the ratio of defective images to normal images is 1:7. This paper exclusively conducts training on the normal images within the training set.

4.2 Implementation Details

The images were uniformly pre-processed by resizing them to 768 × 768. The hardware configuration used for testing is Intel(R) Core (TM) i9-10900X CPU@3.70 GHz and NVIDIA GeForce RTX3080Ti.

(1) Source domain: The outputs of the 36th layer of EfficientNet-b5 [28] are used to construct the source domain features as the feature embedding layer of the SNN. The EfficientNet-b5 is pre-trained on ImageNet [17]. The input image is fed into the SNN, and the source domain feature maps with 304 channels of 24 × 24 are obtained.

(2) Target domain: The TNF network is used to construct the target domain, 4 coupling blocks are adopted. Each coupling block has been designed as shallow neural networks with a hidden layer. The number of hidden layer channels is set to 1024, and its output is split into two parts along the channel dimension to provide the translation and scaling components for affine transformation. Adam’s [29] algorithm is used for optimization with a learning rate of 2×10−4, weight decay of 10−5, and batch size of 8. The number of training epochs is set as 300.

(3) BMR: The SNN and TNF parameters were kept fixed during the BMR training process. The detailed structures of SMNN and TMNN were shown in Fig. 4, with the number of internal left and right residual blocks symmetrically set to n=2, the number of input feature map channels c=304, hidden layer channels clatent=1024. The BMR network training process was optimized by the Adam algorithm with a learning rate of 3 × 10−4, a weight decay of 10−5, batch size set to 8, and 300 training epochs are performed on the MVTec AD dataset.

(4) Evaluation criteria: Image-level Receiver Operator Curve (ROC) and Area Under the Receiver Operator Curve (AUROC) were used to compare the superiority of the proposed method with other methods. Meanwhile, the precision, recall, and F1-Score of NF-BMR are further reported.

4.3 Comparison with Existing Methods

We evaluate the performance of NF-BMR on two popular public defect detection datasets to verify the superiority of the proposed method over other methods.

(1) MVTec AD dataset detection results: Table 1 shows the average AUROC comparison results on the object and texture classes with all categories on the dataset. In five categories, our method achieved 100% AUROC. The average AUROC values of the texture classes and object classes reached 99.4% and 98.3%, respectively. The average AUROC value of our NF-BMR in all categories achieved the best performance, with an AUROC of 98.7%. Compared with the baseline network MB-PFM, the average AUROC of all categories is increased by 1.2%. The overall performance improvement benefits from the improvement on the object classes, with a considerable improvement of 1.8%. This verified the superiority of the proposed method. Table 2 shows the detection results of the proposed method in terms of precision, recall, and F1-Score evaluation metrics. The average precision is 97.5%, the average recall is 97.0%, and the average F1-Score is 97.2% for all categories. In Fig. 5, we also plotted the ROC curves of NF-BMR in fifteen categories, which shows that our model has good classification performance in all categories.

(2) The detection results on the DAGM dataset are shown in Table 3. The results of the baseline MB-PFM were obtained through replication experiments, while the remain results were taken from the original papers. Supervised methods achieved perfect AUROC scores on the DAGM dataset, while unsupervised methods performed poorly. However, the AUROC score of our proposed NF-BMR method reached 98.5% without any data augmentation or parameter tuning, which is 1.2% higher than the MB-PFM method. Moreover, its performance is already very close to the supervised methods, which also validates the excellent effectiveness and robustness of the proposed method. Table 4 further shows the experimental results of NF-BMR on the DAGM dataset for precision, recall, and F1-Score evaluation metrics. The results show an average precision of 91.5%, an average recall of 92.0%, and an average F1-Score of 91.4% across all categories. Fig. 6 provides a bar chart of the detection results of each method on the DAGM dataset.

(3) Visualization: In Fig. 7, ‘S’ represents the source domain, ‘T’ represents the target domain, and ‘NF’ represents the conversion of ‘S’ to ‘T’ through the NF network. The illustration presents a top-to-bottom t-SNE dimensionality reduction visualization of embedding source domain features with EfficientNet-b5, embedding target domain features with EfficientNet-b3, and converting source domain features embedded with EfficientNet-b5 to target domain features using the NF network. Only four categories from the DAGM dataset are displayed in the figure, namely Class2, Class4, Class6, and Class8. From the ‘S’ and ‘T’ rows, it is evident that the embedded features obtained by different pre-trained CNN exhibit a complex distribution. Conversely, the NF network in the third row can transform source domain features with a complex distribution into target domain features with a simple distribution, mapping abnormal features outside the distribution.

Figure 7: t-SNE visualization of normal and abnormal samples in four categories on the DAGM dataset

In this paper, we only improve the defect detection performance of the bidirectional network and do not report the defect localization performance in detail. Fig. 8 shows the qualitative visualization results of NF-BMR on the MVTec AD dataset. The experimental results show that the proposed method can accurately localize defective regions even when no anomalous images have been seen during the training phase, which demonstrates the potential for defect localization. Fig. 9 further reports the qualitative visualization results on the DAGM dataset, demonstrating that NF-BMR still maintains relatively robust localization performance on some synthetic anomaly images that are difficult to recognize by the human eye.

Figure 8: Qualitative visualization results of NF-BMR method on MVTec AD data set

Figure 9: Qualitative visualization results of NF-BMR method on DAGM data set

4.4 Ablation Study

To validate the limitations of the proposed framework and its superiority compared to the baseline network, we conducted ablation experiments on the MVTec AD dataset.

(1) Influence of the number of residual blocks: In rows 1, 2, and 3 of Table 5, the influence of the change in the number of residual blocks on the classification performance of the NF-BMR network was explored. The highest average AUROC value was reached when the number of residual blocks was n = 2, and the number of residual blocks continued to increase. In contrast, the average AUROC value decreased slightly by 0.2%. Therefore, the optimal number of residual blocks n = 2 was determined.

(2) Influence of BMR Network: In the comparison experiment of the first three rows and the fourth row in Table 5, the AUROC of NF combined with B-PFM is 96.2%. The minimum and maximum AUROC values of NF combined with BMR are 97.4% and 98.7%, which is 1.2% and 2.5% higher than the method of NF combined with B-PFM, respectively. This verifies that the proposed BMR network is better than the B-PFM network. It can better learn the normal feature distribution in the two spatial domains and improve defect detection performance.

In the last row of Table 5, we show the detection performance of the NF network alone; AUROC only reaches 94.2%. When NF is combined with B-PFM, AUROC increases by 2%. When NF is combined with BMR, AUROC increases up to 4.5%. These results verified the effectiveness and superiority of the proposed method. Fig. 10 shows the AUROC results for all ablation experiments for 15 categories on the MVTec AD dataset. The black line represents the configuration with NF alone, which offers the worst performance in almost all 15 categories, especially in the target class. From comparing the dark yellow line with the blue, red, and light blue lines, NF performs worst in almost all categories when combined with B-PFM. Combining the BMR of different residual block Settings improves the detection results for all classes, especially in the more difficult object classes to detect. This further indicates that compared with B-PFM, BMR can learn the feature information of both spatial domains more fully. The red line performs leading defect detection in almost all categories and represents the best NF-BMR network configuration.

Figure 10: Results of ablation experiments on the MVTec AD dataset

5  Conclusion

This paper proposes a new normalizing flow-based bi-directional mapping residual network for unsupervised defect detection. Unlike the previous work that uses two different pre-trained CNN to embed source and target domain features, we introduce NF instead of pre-trained TNN to construct a more discriminative target domain feature space, which can alleviate the problems caused by biased pre-trained CNN. Moreover, a bidirectional mapping residual network BMR was proposed to learn thoroughly. Experiments on MVTec AD and DAGM datasets verified the superiority of our proposed NF-BMR network. Since the proposed network only performs defect detection on single-scale features and no particular optimization was done for defect localization, we will focus on improving defect localization performance in future works.

Acknowledgement: The authors thank Dr. Fanghui Zhang from the School of Artificial Intelligence at Henan University for her support and help with this study. The authors also thank reviewers for their contributions to the revision of this paper.

Funding Statement: This work was supported in part by the National Key R&D Program of China 2021YFE0110500, in part by the National Natural Science Foundation of China under Grant 62062021, in part by the Guiyang Scientific Plan Project [2023] 48-11.

Author Contributions: Lanyao Zhang: Software; Formal analysis; Methodology; Writing-original draft (equal). Shichao Kan: Writing-review & Editing. Yigang Cen: Supervision; Methodology (equal); Writing-review & Editing. Xiaoling Chen: Validation. Linna Zhang: Supervision; Funding acquisition; Writing-review & Editing. Yansen Huang: Funding acquisition; Validation.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. F. Zhang, S. Kan, D. Zhang, Y. Cen, L. Zhang et al., “A graph model-based multiscale feature fitting method for unsupervised anomaly detection,” Pattern Recognition, vol. 138, pp. 109373, 2023. [Google Scholar]

2. X. Yu, Y. Shang, L. Zheng and K. Wang, “Application of nanogenerators in the field of acoustics,” ACS Applied Electronic Materials, vol. 5, no. 9, pp. 5240–5248, 2023. [Google Scholar]

3. Z. Yi, Z. Chen, K. Yin, L. Wang and K. Wang, “Sensing as the key to the safety and sustainability of new energy storage devices,” Protection and Control of Modern Power Systems, vol. 8, no. 1, pp. 1–22, 2023. [Google Scholar]

4. A. Bochkovskiy, C. Y. Wang and H. Y. M. Liao, “YOLOv4: Optimal speed and accuracy of object detection,” arXiv preprint arXiv:2004.10934, 2020. [Google Scholar]

5. C. Y. Wang, I. H. Yeh and H. Y. M. Liao, “You only learn one representation: Unified network for multiple tasks,” arXiv preprint arXiv:2105.04206, 2021. [Google Scholar]

6. X. Zhu, S. Lyu, X. Wang and Q. Zhao, “TPH-YOLOv5: Improved YOLOv5 based on transformer prediction head for object detection on drone-captured scenarios,” in Proc. of 2021 IEEE/CVF Int. Conf. on Computer Vision (ICCV), Montreal, Canada, pp. 2778–2788, 2021. [Google Scholar]

7. T. Defard, A. Setkov, A. Loesch and R. Audigier, “Padim: A patch distribution modeling framework for anomaly detection and localization,” in Proc. of 2021 25th Int. Conf. on Pattern Recognition Workshops and Challenges, Milano, Italy, pp. 475–489, 2021. [Google Scholar]

8. N. Cohen and Y. Hoshen, “Sub-image anomaly detection with deep pyramid correspondences,” arXiv preprint arXiv:2005.02357, 2020. [Google Scholar]

9. D. Gudovskiy, S. Ishizaka and K. Kozuka, “Cflow-ad: Real-time unsupervised anomaly detection with localization via conditional normalizing flows,” in Proc. of 2022 IEEE/CVF Winter Conf. on Applications of Computer Vision (WACV), Waikoloa, HI, USA, pp. 98–107, 2022. [Google Scholar]

10. M. Rudolph, T. Wehrbein, B. Rosenhahn and B. Wandt, “Fully convolutional cross-scale-flows for image-based defect detection,” in Proc. of 2022 IEEE/CVF Winter Conf. on Applications of Computer Vision (WACV), Waikoloa, HI, USA, pp. 1088–1097, 2022. [Google Scholar]

11. M. Rudolph, B. Wandt and B. Rosenhahn, “Same same but differnet: Semi-supervised defect detection with normalizing flows,” in Proc. of 2021 IEEE/CVF Winter Conf. on Applications of Computer Vision (WACV), Waikoloa, HI, USA, pp. 1907–1916, 2021. [Google Scholar]

12. J. Yang, Y. Shi and Z. Qi, “DFR: Deep feature reconstruction for unsupervised anomaly segmentation,” arXiv preprint arXiv:2012.07122, 2020. [Google Scholar]

13. Q. Wan, L. Gao, X. Li and L. Wen, “Unsupervised image anomaly detection and segmentation based on pretrained feature mapping,” IEEE Transactions on Industrial Informatics, vol. 19, no. 3, pp. 2330–2339, 2022. [Google Scholar]

14. Z. You, K. Yang, W. Luo, L. Cui, Y. Zheng et al., “ADTR: Anomaly detection transformer with feature reconstruction,” in Proc. of 2022 29th Int. Conf. on Neural Information Processing (ICONIP), pp. 298–310, 2022. [Google Scholar]

15. W. Zhang, X. Sun, Y. Li, H. Liu, N. He et al., “A multi-task network with weight decay skip connection training for anomaly detection in retinal fundus images,” in Proc. of 2022 Int. Conf. on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Singapore, pp. 656–666, 2022. [Google Scholar]

16. L. Chen, Z. You, N. Zhang, J. Xi and X. Le, “UTRAD: Anomaly detection and localization with U-transformer,” Neural Networks, vol. 147, pp. 53–62, 2022. [Google Scholar] [PubMed]

17. J. Deng, W. Dong, R. Socher, L. J. Li, K. Li et al., “ImageNet: A large-scale hierarchical image database,” in Proc. of 2009 IEEE conf. on Computer Vision and Pattern Recognition, Miami, FL, USA, pp. 248–255, 2009. [Google Scholar]

18. D. P. Kingma and M. Welling, “Auto-encoding variational bayes,” Stat, vol. 1050, pp. 1, 2014. [Google Scholar]

19. S. Akcay, A. Atapour-Abarghouei and T. P. Breckon, “Ganomaly: Semi-supervised anomaly detection via adversarial training,” in Proc. of 2018 14th Asian Conf. on Computer Vision, Perth, Australia, pp. 622–637, 2018. [Google Scholar]

20. T. Schlegl, P. Seeböck, S. M. Waldstein, G. Langs and U. Schmidt-Erfurth, “f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks,” Medical Image Analysis, vol. 54, pp. 30–44, 2019. [Google Scholar] [PubMed]

21. L. C. Chen, G. Papandreou, I. Kokkinos, K. Murphy and A. L. Yuille, “DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 40, no. 4, pp. 834–848, 2017. [Google Scholar] [PubMed]

22. B. J. Wheeler and H. A. Karimi, “A semantically driven self-supervised algorithm for detecting anomalies in image sets,” Computer Vision and Image Understanding, vol. 213, pp. 103279, 2021. [Google Scholar]

23. X. Yan, H. Zhang, X. Xu, X. Hu and P. A. Heng, “Learning semantic context from normal samples for unsupervised anomaly detection,” in Proc. of 2021 AAAI conf. on Artificial Intelligence, pp. 3110–3118, 2021. [Google Scholar]

24. V. Zavrtanik, M. Kristan and D. Skočaj, “Reconstruction by inpainting for visual anomaly detection,” Pattern Recognition, vol. 112, pp. 107706, 2021. [Google Scholar]

25. L. Dinh, J. Sohl-Dickstein and S. Bengio, “Density estimation using real NVP,” arXiv preprint arXiv:1605.08803, 2017. [Google Scholar]

26. P. Bergmann, M. Fauser, D. Sattlegger and C. Steger, “MVTec AD–A comprehensive real-world dataset for unsupervised anomaly detection,” in Proc. of 2019 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 9592–9600, 2019. [Google Scholar]

27. M. Wieler and T. Hahn, “Weakly supervised learning for industrial optical inspection,” in Proc. of 29th DAGM Symp., Heidelberg, Germany, 2007. [Google Scholar]

28. M. Tan and Q. Le, “Efficientnet: Rethinking model scaling for convolutional neural networks,” in Proc. of 2019 36th Int. Conf. on Machine Learning, Long Beach, California, USA, pp. 6105–6114, 2019. [Google Scholar]

29. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014. [Google Scholar]

30. I. Golan and R. El-Yaniv, “Deep anomaly detection using geometric transformations,” arXiv preprint arXiv:1805.10917, 2018. [Google Scholar]

31. F. Ye, C. Huang, J. Cao, M. Li, Y. Zhang et al., “Attribute restoration framework for anomaly detection,” IEEE Transactions on Multimedia, vol. 24, pp. 16–127, 2020. [Google Scholar]

32. Y. Ma, X. Jiang, N. Guan and W. Yi, “Anomaly detection based on multi-teacher knowledge distillation,” Journal of Systems Architecture, vol. 138, pp. 102861, 2023. [Google Scholar]

33. S. Akçay, A. Atapour-Abarghouei and T. P. Breckon, “Skip-ganomaly: Skip connected and adversarially trained encoder-decoder anomaly detection,” in Proc. of 2019 Int. Joint Conf. on Neural Networks (IJCNN), Budapest, Hungary, pp. 1–8, 2019. [Google Scholar]

34. M. Salehi, A. Eftekhar, N. Sadjadi, M. H. Rohban and H. R. Rabiee, “Puzzle-AE: Novelty detection in images through solving puzzles,” arXiv preprint arXiv:2008.12959, 2020. [Google Scholar]

35. C. L. Li, K. Sohn, J. Yoon and T. Pfister, “CutPaste: Self-supervised learning for anomaly detection and localization,” in Proc. of 2021 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Nashville, TN, USA, 2021. [Google Scholar]

36. J. Božič, D. Tabernik and D. Skočaj, “End-to-end training of a two-stage neural network for defect detection,” in Proc. of 2020 25th Int. Conf. on Pattern Recognition (ICPR), Milan, Italy, pp. 5619–5626, 2021. [Google Scholar]