 Open Access
Open Access
ARTICLE
Particle Swarm Optimization Algorithm for Feature Selection Inspired by Peak Ecosystem Dynamics
School of Information Engineering, Nanchang Institute of Technology, Nanchang, 330099, China
* Corresponding Author: Shaobo Deng. Email:
Computers, Materials & Continua 2025, 82(2), 2723-2751. https://doi.org/10.32604/cmc.2024.057874
Received 29 August 2024; Accepted 20 November 2024; Issue published 17 February 2025
Abstract
In recent years, particle swarm optimization (PSO) has received widespread attention in feature selection due to its simplicity and potential for global search. However, in traditional PSO, particles primarily update based on two extreme values: personal best and global best, which limits the diversity of information. Ideally, particles should learn from multiple advantageous particles to enhance interactivity and optimization efficiency. Accordingly, this paper proposes a PSO that simulates the evolutionary dynamics of species survival in mountain peak ecology (PEPSO) for feature selection. Based on the pyramid topology, the algorithm simulates the features of mountain peak ecology in nature and the competitive-cooperative strategies among species. According to the principles of the algorithm, the population is first adaptively divided into many subgroups based on the fitness level of particles. Then, particles within each subgroup are divided into three different types based on their evolutionary levels, employing different adaptive inertia weight rules and dynamic learning mechanisms to define distinct learning modes. Consequently, all particles play their respective roles in promoting the global optimization performance of the algorithm, similar to different species in the ecological pattern of mountain peaks. Experimental validation of the PEPSO performance was conducted on 18 public datasets. The experimental results demonstrate that the PEPSO outperforms other PSO variant-based feature selection methods and mainstream feature selection methods based on intelligent optimization algorithms in terms of overall performance in global search capability, classification accuracy, and reduction of feature space dimensions. Wilcoxon signed-rank test also confirms the excellent performance of the PEPSO.Keywords
In recent years, with the rapid development of machine learning and data mining algorithms, features have been widely introduced into datasets. Feature selection has become a crucial preprocessing step for these algorithms. High-dimensional datasets often contain numerous features in the data mining process across various domains. The presence of redundant and irrelevant features not only increases the complexity of data processing but also reduces the accuracy of subsequent classification algorithms to a certain extent [1]. Preprocessing high-dimensional datasets to reduce redundant and irrelevant features is an important research focus in data mining.
Feature selection aims to select the most informative subset of features from the original feature set, with the lowest redundancy and highest relevance, to reduce the number of features without altering their meanings and improve classification accuracy. As an effective data dimensionality reduction technique, feature selection is a combinatorial optimization task. It not only filters out important features of the data, avoiding the problem of low classification accuracy caused by the curse of dimensionality, but it also reduces computational complexity and enhances the performance of classification models [2].
Feature selection techniques have been widely and successfully applied in various expert and intelligent systems, including bioinformatics [3], where applying feature selection techniques to biology and biomedicine can identify genes with unknown functions, reveal the intrinsic natural structure of gene expression data, reduce the dimensionality of microarrays, and identify hidden relationships between genes. However, gene microarray datasets still face many challenges: (1) severe sample imbalance, with the number of features far exceeding the number of samples; (2) a large proportion of useless and redundant features; (3) gene features are complex and may contain ambiguous noise. In image processing [4], feature selection methods are applied to image classification, object detection, and image clustering. Due to the presence of many image features in practical applications, the selection of image features directly determines the performance of target applications. Examples of image features include corners, edges, raw pixels, orientation gradient histograms, color channels, and gradient values [5]. Additionally, in text mining [6], the classic model for representing documents is the bag-of-words model. Feature selection is used to improve the efficiency and performance of subfields of text mining, such as text classification and text clustering, and can also be used in intrusion detection systems. One of the key tasks of intrusion detection systems is to identify the highest quality features representing the entire original dataset and remove irrelevant and redundant features from the dataset. In controller design processes [7], various techniques, including feature selection, are adopted to improve the performance of controllers for more effective and efficient retrieval of information. Feature selection techniques are also used in other industrial applications [8] to improve the accuracy of fault detection.
Although feature selection has been an active research topic, it remains a challenging task. Feature selection is an optimization problem with multiple competing criteria, mainly minimizing the number of selected features and maximizing classification accuracy. Because reducing the number of features during the feature selection process may lead to information loss and affect classification accuracy, retaining more features to improve accuracy may increase model complexity and computational costs. Therefore, feature selection can be regarded as a multi-objective optimization problem to find a set of trade-off solutions between these two objectives.
The earliest feature selection methods were based on classical methods and search algorithms such as dynamic programming, branch and bound, etc. [9]. However, to better accomplish feature selection tasks, a more powerful and efficient search algorithm is needed.
Swarm intelligence optimization algorithms are well known for their powerful global search capabilities, especially suitable for multi-objective optimization. PSO, proposed by Kennedy and Eberhart in 1995, is a population-based search algorithm that belongs to the category of optimization techniques [10]. This algorithm, similar to evolutionary algorithms and genetic algorithms, uses algebraic updates to search for global optimal solutions and belongs to the realm of metaheuristic stochastic optimization methods. Due to its advantages of fewer parameters, fast convergence speed, and good stability of particle collaboration, the particle swarm algorithm has received widespread attention. Several feature selection methods based on particle swarm algorithms have been developed for feature selection tasks.
For example, the feature selection technology based on catfish strategy and binary particle swarm algorithm [11] introduced catfish particles to replace the worst particles trapped in local optima. However, this method has not been validated on a wider range of datasets, including high-dimensional datasets, imbalanced classes, or datasets from specific domains. In the feature selection method based on chaotic binary particle swarm algorithm [12], two chaotic maps, namely, logistic map and tent map, were embedded, and the binary version of CBPSO was used to determine the inertia weight values, but this method suffers from late convergence. The method based on bare bones particle swarm algorithm [13] still faces difficulties in stagnation and falling into local optima. In the method based on hybridization of genetic algorithm and particle swarm optimization [14], although the classification accuracy of the algorithm has slightly improved, the running time has significantly increased. In the method based on a novel local search strategy and hybrid particle swarm optimization [15], HPSO-LS is a wrapper-based method, and the algorithm needs to learn the model to compute the fitness of each solution in each iteration, so it suffers from long running time. The main limitation of the hybrid particle swarm optimization method with a spiral-shaped mechanism for feature selection [16] is that for many datasets, the selected number of features is large, and the ability to remove redundant and irrelevant features needs to be improved. In the method of feature selection based on two-level particle cooperation for many-objective optimization [17], strict particles usually have better objective values, may dominate the update process, gradually replace ordinary particles, and lose the diversity of the population.
The capability of PSO to select optimal or near-optimal feature subsets is highly regarded. However, it is important to note that some drawbacks of PSO have been overlooked in previous studies. One major drawback of existing feature selection methods based on PSO is the loss of population diversity during the search process, which reduces the efficiency of searching for optimal feature subsets. Additionally, the original learning strategies fail to effectively balance between exploring global optimal solutions and refining local solutions during the search process, potentially compromising algorithm performance [18]. Moreover, particles primarily rely on known optimal solution information to guide the search process, which can lead to the algorithm getting trapped in local optima, especially in complex solution spaces or high-dimensional feature spaces.
To address the aforementioned issues, this paper proposes a PSO that simulates the evolutionary survival of species in mountain ecosystems for feature selection. This approach utilizes a multi-strategy approach to drive the feature selection method towards obtaining the optimal feature subset for classification. The main contributions of this paper are as follows:
1. Simulating Mountain Ecosystems: Utilizing a pyramid topology structure to mimic the characteristics of mountain ecosystems. Each particle is hierarchically arranged based on the competitive results of fitness, with higher fitness particles assigned to higher levels in the pyramid structure. As iterations progress, particles ascend or descend to different levels based on their fitness performance.
2. Dual-Mode Adaptive Learning Strategy: Designing a dual-mode adaptive learning strategy to replace self-learning and global learning strategies. During iterations, winner and loser particles are determined based on fitness comparisons. The algorithm automatically adjusts based on particle performance (i.e., winner or loser), selecting different learning strategies to update their positions and velocities.
3. High-Peak-Guided Genetic Mutation Strategy: Introducing a genetic mutation strategy guided by high peaks, which mutate powerful s top-level particles defined in the topology structure under specific conditions.
The remaining sections of this paper are organized as follows: Section 2 introduces related work. Section 3 elaborates on the proposed PEPSO and feature selection method. Section 4 analyzes and discusses the experimental setup and results. Finally, Section 5 summarizes the work of the paper and outlines future research directions.
2.1 Evolutionary Algorithm-Based Feature Selection
In contrast to many early conventional (non-evolutionary computing) feature selection methods [19], evolutionary algorithm-based feature selection does not require domain knowledge or any assumptions about the search space, such as whether the search space is linearly separable or nonlinearly separable, or differentiable. Another significant advantage of evolutionary computation techniques is their population-based mechanism, which can generate multiple solutions in a single run. Evolutionary algorithm-based feature selection methods are categorized based on three different criteria: evolutionary computing paradigm, evaluation, and number of objectives, which are key components of feature selection methods.
In feature selection, evolutionary algorithms are primarily used as search techniques. Virtually all major evolutionary algorithms have been applied to feature selection. Khushaba et al. [20] proposed the first feature selection method based on the differential evolution method. They used a real-valued optimizer and applied differential evolution operators to feature indices, allowing the same feature to be encountered multiple times in the solution vector. Al-Ani [21] utilized locally important features and the overall performance of feature subsets in the feature space to search for optimal solutions in a feature selection technique based on the ant colony algorithm. Kanan et al. [22] proposed an improved feature selection method based on the ant colony algorithm, which did not require prior information about the features. This method used the length of the feature vector and the accuracy of the classifier as heuristic information for the ant colony algorithm. Genetic algorithms rely on a simple scalar performance measure that does not require derivative information, which has attracted the interest of researchers due to their simplicity in implementation. However, in genetic algorithms, once the population changes, previous knowledge of the problem is discarded [23]. In contrast, algorithms such as differential evolution, ant colony optimization, and particle swarm optimization tend to achieve higher accuracy in similar feature selection problems. This is primarily due to their ability to incorporate cooperative mechanisms. For example, in ant colony algorithms and particle swarm optimization, particles or ants share information among themselves, enabling constructive cooperation that helps guide the search process more effectively [24,25].
Numerous studies have shown that PSO are equally effective as genetic algorithms, differential evolution, and ant colony algorithms in solving global optimization problems and sometimes even outperform them. Therefore, PSO have demonstrated great potential and application value in various tasks, including feature selection.
In the PSO, each particle has a position vector representing a potential candidate solution within the search space. To find the global optimum, each particle adjusts its direction of movement based on its own previous best position and the best positions of all other particles [26,27]. More specifically, let the dimension of the search space D be denoted as d. The position and velocity of the i-th particle at time t are represented as
where
In canonical PSO,
where
2.3 Topological Structures of Particle Swarm Optimization Algorithm
The topological structure of the PSO is one of its key concepts, defining the interaction among particles and the flow of information. Different topological structures influence the algorithm’s global search capability and local exploration efficiency, therefore determining the performance of the PSO.
The two fundamental topological structures of the PSO are the local best topology and the global best topology. In the local best topology, each particle is only connected to a few neighboring particles (typically neighboring on both sides), facilitating local information exchange and aiding in fine exploration but potentially limiting global search capability. Conversely, in the global best topology, each particle is connected to all other particles in the swarm, promoting rapid information dissemination across the entire swarm, which is beneficial for fast global search but potentially leads to premature convergence.
In addition to these two classic topologies, several other innovative topological structures have been proposed to balance the need for global search and local exploration, as depicted in Fig. 1. After evaluating cycle, random graph, star, and ring topologies on four 30-dimensional functions, Kennedy [28] found that no single topology could perform optimally across all types of problems and metrics. When designing or selecting the topological structure of the PSO, it is necessary to consider the characteristics of the specific problem, such as the complexity of the solution space, the size of dimensions, and the nature of optimization objectives. Wang et al. [29] proposed a novel topology called Multilayer Particle Swarm Optimization (MLPSO), which utilized multiple swarms to enhance diversity in the search space for improved performance. Inspired by a mixed hierarchical structure, Yang et al. [30] introduced a hierarchical-based Large-Scale Optimization Learning Particle Swarm. Leveraging this topology, the proposed PSO outperforms several state-of-the-art PSO variants in terms of computational efficiency and solution quality.
Figure 1: Circular topology structure diagram and wheel topology structure diagram
2.4 Competition and Cooperation in Particle Swarm Optimization Algorithm
In the PSO, a dynamic relationship of competition and cooperation exists among particles. Particles compete with each other as they strive to find solutions that are better than the current best solution. At the same time, particles also cooperate because each particle’s movement is influenced by its own best experience and the best experiences of other particles in the swarm. This mechanism of competition and cooperation helps the entire swarm conduct the effective search in the solution space, as shown in Eq. (1).
Various studies have attempted innovative mechanisms to enhance the diversity of the PSO. Wu et al. introduced the Lotka-Volterra model into PSO [31] and found that after studying the cooperation and competition strategies within and between species, this strategy increased the diversity of PSO and achieved good performance. Wu et al. [32] discovered that the cooperation mechanism of particles on hub and/or non-hub nodes of scale-free networks can enhance diversity and flexibility. Cheng et al. [33] proposed a competitive group optimizer for large-scale optimization, which introduced a pairwise competition mechanism where losers learn from corresponding winners. Extensive experiments showed that this algorithm outperforms several comparative advanced methods. Zhang et al. [34] classified particles into different types through competition and then designed an adaptive learning strategy to enhance the diversity of the particle swarm. Li et al. [35] proposed a Switching Particle Swarm Optimizer (RSPSO) based on a ranking system, where particles are assigned to different types of neighborhoods by the ranking system, and the learning strategies and parameter settings used adaptively change according to the search stage. Liang et al. [36] introduced a Comprehensive Learning Particle Swarm Optimization (CLPSO) algorithm, which utilizes personal best information from all other particles to update the velocity of a given particle. Song et al. [37] proposed a Variable-Size Cooperative Coevolutionary Particle Swarm Optimization (VS-CCPSO) algorithm. This algorithm decomposes the high-dimensional feature selection problem into multiple low-dimensional subproblems and adopts a variable-size subpopulation evolutionary mechanism, significantly improving the scalability of PSO in handling high-dimensional data. Similarly, Song et al. [38] later proposed a three-phase hybrid feature selection algorithm based on correlation-guided clustering and particle swarm optimization (HFS-C-P), which effectively reduces the search space by filtering and clustering relevant features in the early stages, thereby enhancing the overall computational efficiency.
Although much research has delved into most of the topological structures of PSO, the pyramid-shaped topology remains underexplored. By introducing a hierarchical concept based on the pyramid-shaped topology and drawing inspiration from real-world hierarchical social structures such as governmental systems, family pedigrees, and academic hierarchies, along with incorporating novel competition and cooperation strategies among particles, information flow between hierarchies can be effectively facilitated. To enhance the algorithm’s diversity and exploration capabilities, a mutation strategy guided by high-level particles is devised. On this basis, this paper presents a novel approach to enhance PSO’s performance, applied specifically to feature selection.
3 Particle Swarm Optimization Algorithm Based on Mountain Ecological Pattern Strategy and Its Application in Feature Selection
In this section, we present a PSO tailored for feature selection, inspired by the ecological patterns observed in mountainous terrain. We introduce a competitive-cooperative strategy and a high-level particle mutation approach, integrated within a pyramid-shaped topology. This algorithm aims to strike a balance between global exploration and local fine-tuning, therefore mitigating premature convergence to local optima and enhancing the efficacy in searching for the optimal feature combination.
3.1 Application of Information Gain and ReliefF Pre-Screening
In the pre-screening phase, we integrate the concepts of Information Gain and ReliefF to assess the relevance between each feature and the target variable, considering both the individual feature-target relationship using Information Gain and the interactions among features using ReliefF. To begin with, Information Gain is utilized to swiftly filter out a smaller subset of candidate features from the entire feature pool, and efficiently discarding features that are evidently unrelated or contribute minimally. Subsequently, ReliefF is applied to the candidate feature set for a more in-depth analysis, further refining the selection to identify features most beneficial for classification. This combined strategy harnesses the swift screening capability of Information Gain while leveraging the advantages of ReliefF in handling complex data relationships, therefore enhancing the efficiency and accuracy of feature selection.
Information Gain employs entropy to quantify the predictive capacity of features. While entropy measures dataset uncertainty, Information Gain quantifies the reduction in uncertainty after incorporating a feature. Higher Information Gain indicates that a feature is more effective in classifying data, reducing uncertainty, and thus, is more useful. Utilizing Information Gain helps identify and select the most useful features, reducing the dimensionality of the feature space, and enhancing model performance and efficiency [39]. The formula for Information Gain is as follows:
where
ReliefF is a filter-based algorithm that assigns weights to features based on their capacity to differentiate between samples belonging to different classes. By employing the Euclidean distance, the ReliefF algorithm identifies both “near-hit” (samples belonging to the same class) and “near-miss” (samples belonging to a different class) instances for a given sample R. Feature weights are then updated in accordance with their contribution to the separation of classes. The assignment of higher weights indicates that the respective features possess greater discriminative power. The formula for the ReliefF is as follows:
In the Eqs. (4) and (5), A represents a feature, R represents a randomly selected sample from the training data, H and M stands for “close to hit” and “close to miss”, respectively, p(C) is the prior probability that the sample belongs to the class C, the variable k denotes the number of neighboring samples to be selected, and max(A) and min(A) stand for the maximum and minimum values of the feature A, respectively.
3.2 Particle Swarm Optimization Algorithm Based on Peak Ecological Model Strategy
3.2.1 Construction of Mountain Ecological Model
A typical PSO can be viewed as employing a two-layer structure: the top layer consists of globally optimal leader particles, while the bottom layer comprises particles exploring the solution space. Bottom-layer particles update solely based on their own experiences and guidance from the top-layer leader, leading to insufficient diversity during the search process. Consequently, the entire population may quickly converge towards the currently perceived optimal solution set, increasing the risk of premature convergence to local optima and limiting the algorithm’s ability to explore the potential solution space thoroughly. Inspired by the real-world phenomenon of “multi-layered” structures, a unique multi-layered topological structure called the “mountain ecological model” is proposed, simulating the hierarchical characteristics of mountain ecological patterns found in nature.
In this ecological model, the particle swarm is organized into a hierarchical structure resembling mountains, with the peak positions occupied by the most proficient particles, symbolizing the top predators or leaders in the ecosystem. The layers below consist of particles with relatively inferior performance, akin to different tiers of biological communities in mountain ecology. Similarly, the quality of particles determines their hierarchical placement within the mountain ecological model; the higher a particle’s performance, the higher its level within the model. Specifically, the top-tier particles, positioned at the ecological peaks, possess the ability to guide the entire swarm’s search direction, exerting a decisive influence on the search process of the entire ecosystem. Meanwhile, particles in lower tiers are primarily responsible for exploring different regions of the search space. While they can learn from the particles directly above them, their learning and search behaviors are more localized and refined due to the constraints of their influence range.
Without loss of generality, this paper assumes that the optimization problem is a minimization problem and utilizes the magnitude of particle fitness to determine their assigned levels. The fitness of each particle is calculated as the average accuracy across 5-fold cross-validation, with each fold’s accuracy defined as:
where k = 5, and
Assuming a swarm of N particles

From the pseudocode, it’s evident that the Peak Ecosystem possesses the following properties:
(1) Each particle is allocated to a specific level.
(2) Higher-quality particles are positioned at higher levels, with the global best particle located at the top level and the poorest particles at the bottom level.
(3) Particles within the same level exhibit close fitness values.
3.2.2 Competition-Cooperation Mechanism
In traditional PSO, the competition-cooperation mechanism is achieved through the sharing of information among particles, whereby each particle updates its velocity and position based on its own best experience and the global best position. This approach encourages particles to converge towards a globally optimal solution; however, it often limits diversity, therefore increasing the risk of premature convergence to local optima.
This paper introduces a competition-cooperation mechanism within a Mountain Ecological Model with the objective of enhancing the particle swarm’s search ability. In this model, peaks represent optimal solution points, with top-level particles occupying peak positions as current optimal solutions, and lower-level particles exploring at the “foothills” to maintain diversity. By emulating ecological patterns where species compete and adapt to survive, strategies are established for the “winners” (more adaptable particles) to refine their positions, while the “losers” continue to explore in order to improve their fitness.
To implement the mountain ecological system strategy, firstly, when constructing the peaks, all particles participate in sorting to determine their levels in the mountains. This process involves all particles and is referred to as the species competition strategy. Secondly, after placing each particle at a specific level, different treatments can be applied to particles within the same level to improve efficiency. Based on this, another level of competition strategy is introduced. At specific “ecological niches,” namely within levels, particles are randomly paired and compete, adapting and optimizing their positions through direct competition. The particles are then divided into winners and losers based on the competition results. This strategy simulates the competition and adaptation process that occurs in nature as species compete for resources and living space within specific ecological niches. Winners have the opportunity to learn from particles at higher levels and at the top level, while losers seek opportunities for improvement within their level and choose to learn from winners within the same level. Since the competition involves only particles within the same level, it is referred to as the ecological niche competition adaptation strategy.
This niche competition approach can be further detailed in Algorithm 2, which outlines the operational steps of this strategy.

Employing the ecological niche competition strategy ensures that the global optimum particle remains positioned at the top tier through continual competition. Unlike conventional PSO paradigms, where learning is confined solely to the global optimum particle, all particles have the opportunity to glean insights from various superior counterparts. Consequently, the ecological niche competition strategy enriches the population diversity within the PSO framework.
Mathematically, under the ecological niche adaptation strategy, both winners and losers of each tier
where
In addition to collaborating with their own historical best, losers learn from paired winners, and each winner collaborates with random particles from the upper tier and random particles from the top tier. Collaborating particles are all superior to learners. Therefore, by expanding the scope and depth of cooperation between particles, the algorithm’s performance in global search processes can be enhanced, avoiding premature convergence and exploring the solution space more effectively.
3.2.3 Summit-Guided Genetic Mutation Strategy (SGGMS)
In traditional PSO, particles adjust their search directions and velocities based on individual and collective experiences to find the global optimum solution. However, this algorithm suffers from a lack of population diversity and fast convergence rates, leading to the problem of getting trapped in local optimum solutions. In nature, genetic mutation is a significant source of biological evolution, introducing new gene variations to help populations adapt to environmental changes and increase survival opportunities. Therefore, this paper proposes the Summit-Guided Genetic Mutation Strategy.
Summits represent the locations where globally superior particles reside. The Summit-Guided Genetic Mutation Strategy evolves particles towards better-performing solutions, simulating the random mutation mechanism in biological genetic evolution in nature. This strategy defines the top three layers of particles in the summit structure as summit particles and introduces slight random mutations to these summit particles. Compared to traditional mutation strategies that randomly apply changes across the entire population, our method focuses specifically on the summit particles. Since these particles are already closer to the global optimum, mutating them increases the likelihood of discovering new, high-quality solutions. This approach not only ensures a more focused and efficient search but also strikes a balance between exploration and exploitation, helping the algorithm avoid premature convergence and thoroughly explore the solution space.
In the Summit-Guided Genetic Mutation Strategy, the top three layers of particles in the summit structure are traversed, and it is determined for each particle whether to perform a mutation operation. After the mutation is completed, the fitness of the particles is recalculated to evaluate whether the mutation operation contributes to improving the solution, and then the particle set of the corresponding layer is updated.
The Summit-Guided Genetic Mutation Strategy can be described as Algorithm 3.

The Summit-Guided Genetic Mutation Strategy has been employed to introduce mutation operations to the particles in the top layers of the pyramid structure. This operation aims to enhance the algorithm’s exploration capabilities and prevent premature convergence to local optimum solutions. This process simulates the mutation process in genetic algorithms, where particle states are randomly altered in the hope of discovering better solutions.
3.2.4 Overall Algorithm Framework of PEPSO
The proposed PEPSO encompasses three main concepts: the summit structure, the cooperative strategy that divides particles into losers and winners within the same layer through competition and updates their velocity and position using different rules, and the introduction of slight random mutations to the summit particles.
Combining these three concepts, the framework of the proposed PEPSO can be described as Algorithm 4. The algorithm begins with initialization, tracking the total number of iterations executed using an iteration counter. The algorithm enters the main loop, where in each iteration, a summit structure is constructed by considering the fitness of particles. Subsequently, particles within each layer are paired, and the competitive-cooperative strategy is executed. Finally, mutation operations are performed on the summit particles in the top three layers. At the end of each iteration, the particle fitness, as well as the global best solution and global best fitness, are updated. The algorithm stops when the maximum number of iterations is reached.

4 Experimental Results and Discussion
In this section, the performance of PEPSO is evaluated through a large number of experiments. Particularly, comparisons are made with some variants of PSO and other advanced evolutionary algorithms available in the literature. Parameter comparison experiments are conducted on PEPSO to verify the influence of different parameters on algorithm performance, and the optimal parameter settings for PEPSO are discussed.
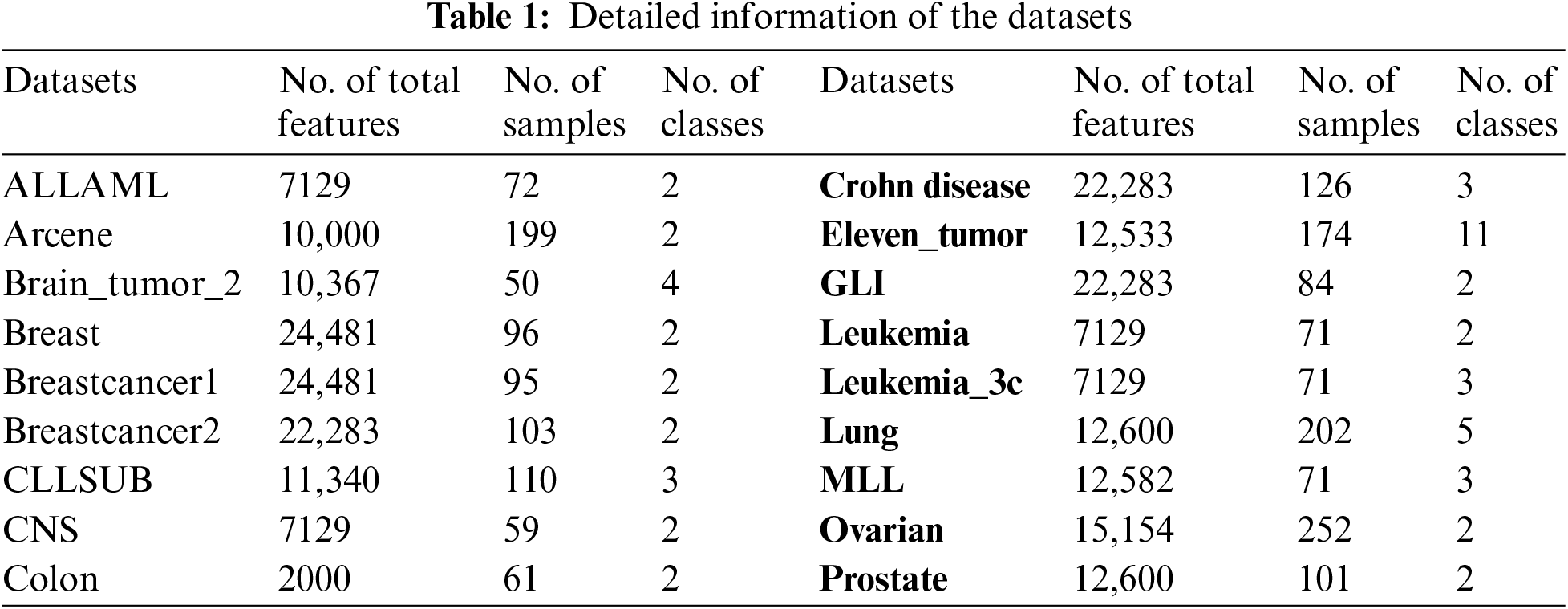
Eighteen gene microarray datasets were selected for experiments to validate the performance of the algorithm. Table 1 describes the detailed information of these datasets, including the number of features, the number of samples, and the number of class labels.
For the real-valued algorithm conversion to binary algorithm for feature selection problem, the following method is used for conversion. First, generate a matrix a of size N × D, where
In Table 2, detailed information about the comparative algorithms and parameters used in PEPSO is presented. To ensure fairness, the overall size of all algorithms is set to N = 100 with an iteration count of 100. Given the small sample sizes, 5-fold cross-validation is applied for robust evaluation, with 80% of the samples allocated to training and 20% to testing in each fold. Each experiment is repeated 10 times, and the average performance is recorded to reduce random fluctuations. All algorithms utilize the ReliefF method for feature filtering, retaining only the top k = 5% of features. Classification accuracy, recall, F1 score, and runtime are evaluated using a K-Nearest Neighbors (KNN) classifier with K = 5. All experiments are conducted on a PC with an Intel Core i7-8550U CPU @ 1.80 GHz processor, running Windows 10 64-bit.
4.2 Self-Experiment Comparison
4.2.1 The Impact of Peak Structures on PEPSO
To assess the impact of peak structures on PEPSO, this study fixed other parameters and conducted 100 iterations on 18 datasets by adjusting the peak structures. Four types of peak structures were used: “L = 6, ni = [2,4,5,16,32,38]” (PEPSO6), “L = 7, ni = [2,6,8,10,14,20,40]” (PEPSO7), “L = 8, ni = [2,4,6,8,10,20,20,30]” (PEPSO), and “L = 9, ni = [2,4,6,8,10,14,16,18,22]” (PEPSO9) to run PEPSO. The population size was fixed at 100. The experimental results are shown in Table 3. Classification accuracy, runtime, number of selected features, recall rate, and F1 score were used as evaluation parameters.
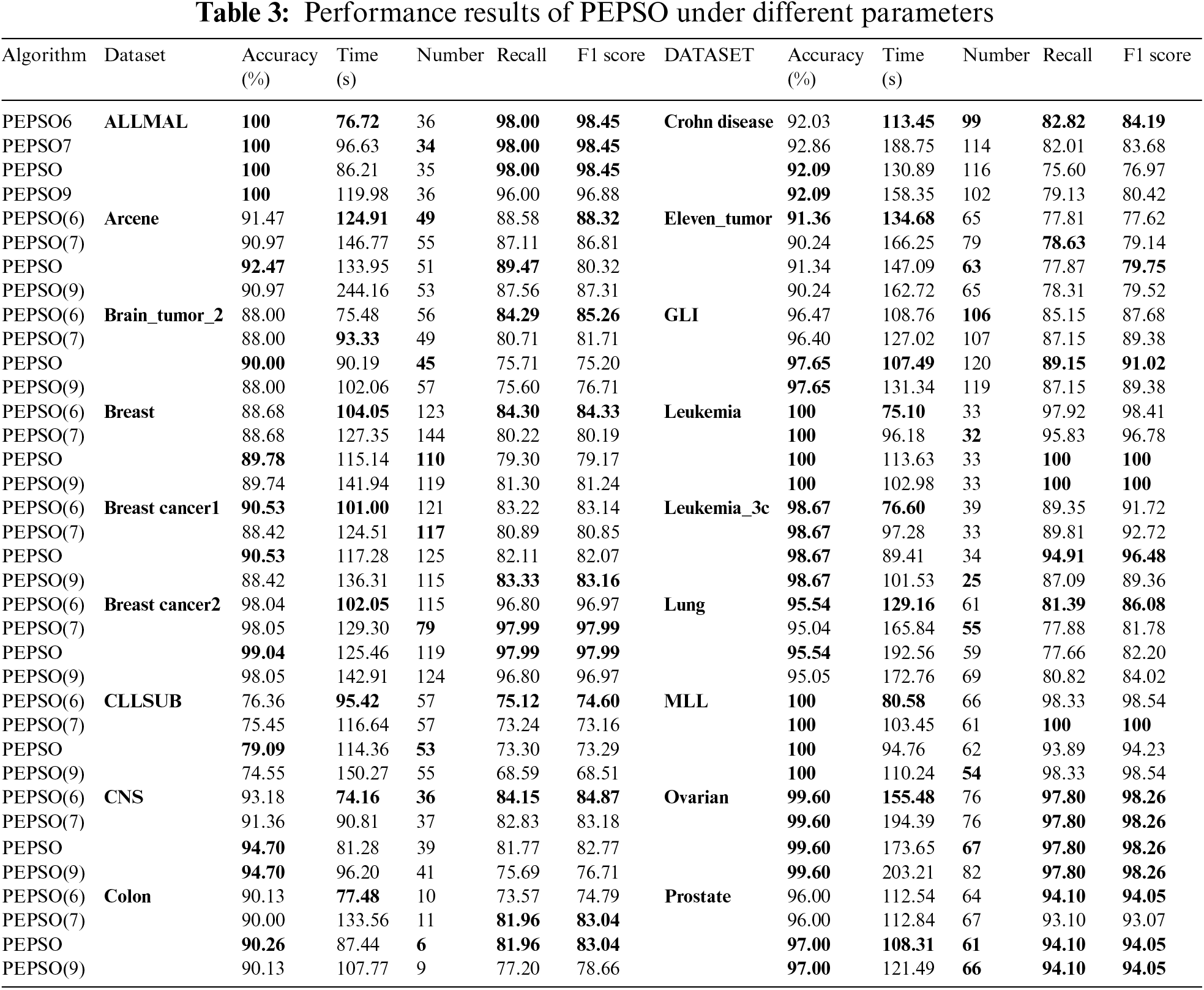
Considering these five key performance indicators, the PEPSO and its variants demonstrated outstanding performance across the 18 datasets. In terms of classification accuracy, PEPSO outperformed other algorithms on 17 datasets except for Eleven_Tumor. As the number of peak layers increased, the complexity of particle interactions and intra-layer calculations also increased, leading to an overall increase in algorithm runtime. However, PEPSO still achieved the best performance on 2 datasets and remained competitive with the best runtime on other datasets. Regarding the number of selected features, the performance of the four algorithms was generally comparable, with PEPSO typically selecting a number of features between those of other variants. This indicates that PEPSO is more precise in feature selection, avoiding excessive feature selection while retaining necessary features. In terms of F1 score, PEPSO generally matched or slightly outperformed its variants, indicating its ability to achieve a good balance between precision and recall.
In summary, although certain variants may perform better on specific datasets and performance metrics, PEPSO provides a comprehensive balance, especially in terms of accuracy and F1 score, while maintaining reasonable runtime and feature selection. PEPSO exhibits balanced performance relative to its variants. Therefore, the parameters of PEPSO should be selected for subsequent experiments.
4.2.2 Fitness Function Comparison
To further assess the effectiveness of the fitness function used in our feature selection process, we conducted experiments on four datasets: Arcene, Prostate, Breast Cancer1, and GLI. These datasets were selected due to their varying Feature-Sample Ratios (FSR), representing a diverse range of data characteristics.
As shown in Table 4, when accuracy was used as the fitness function, it produced the best overall results in terms of both classification accuracy and runtime across the four selected datasets. While recall, as a fitness function, resulted in the selection of the fewest features in three of the datasets, its performance in other key metrics was not as strong.
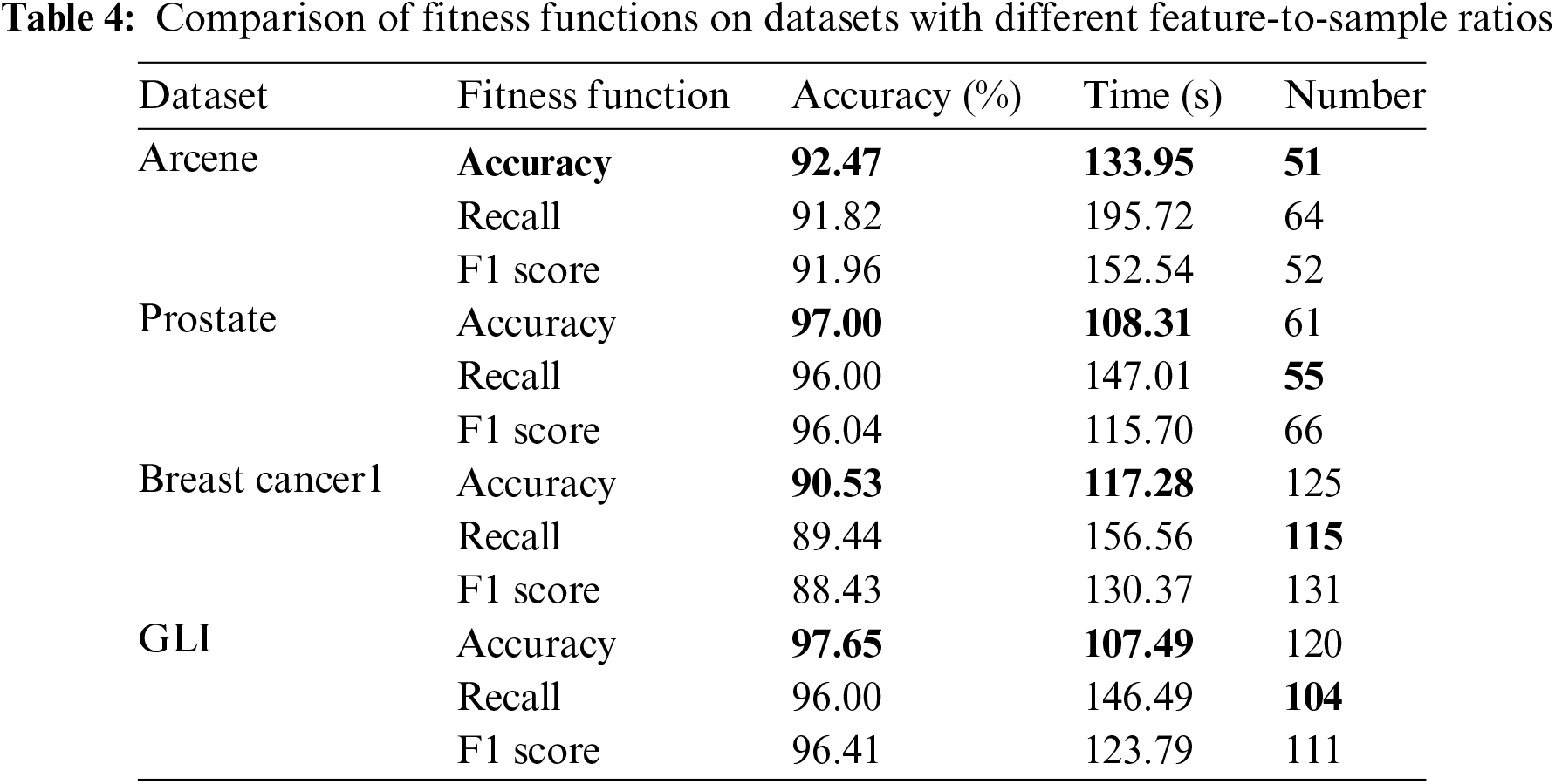
Given these results, accuracy was ultimately selected as the fitness function for our experiments, as it provided the most balanced and reliable outcomes across all the datasets, particularly in terms of the overall effectiveness of feature selection and computational efficiency.
4.3 Comparison with Other Algorithms
This subsection compares PEPSO with other competing algorithms from various perspectives, including classification accuracy, the number of selected features, and runtime.
The experiment result is shown in Table 5. Table 5 presents the evaluation of the classification accuracy of PEPSO and other comparative algorithms on 18 gene microarray datasets. To assess the statistical significance of the difference in average accuracy between PEPSO and other comparative algorithms, the Wilcoxon signed-rank test is employed with a significance level of 0.05. In Table 5, symbols “+”, “≈”, and “−” indicate whether the performance of PEPSO is better, similar, or worse than the corresponding comparative algorithm, respectively.
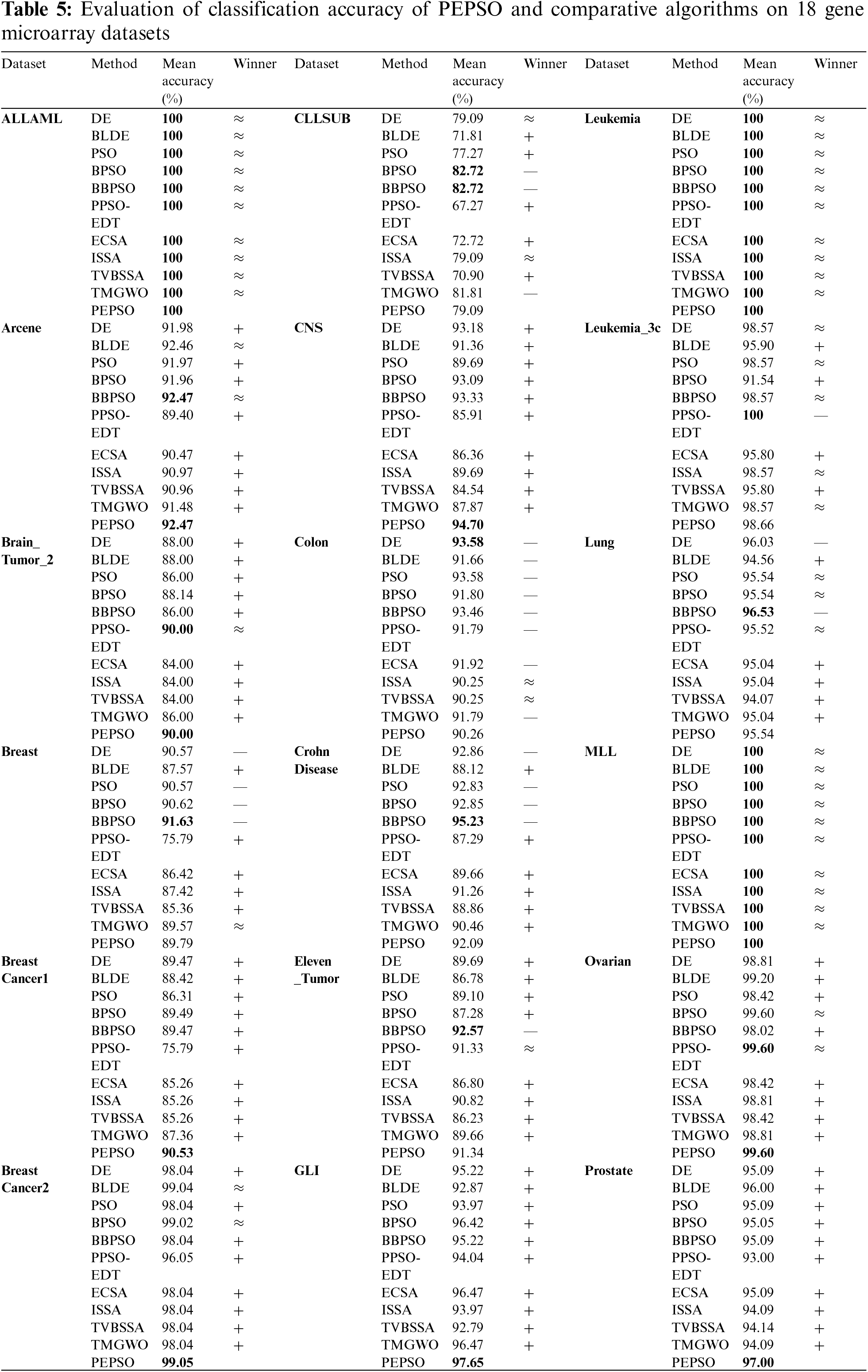
Except for the three datasets where all algorithms achieve a classification accuracy of 100%, PEPSO demonstrates superior classification accuracy on 9 datasets, indicating its strong capability in data fitting and generalization. In the Wilcoxon signed-rank test, except for the Ovarian dataset, 17 out of 18 datasets show more than half of the results marked as “+”. In some datasets, even if PEPSO’s classification accuracy is not the best, the “+” in its Wilcoxon test results still indicates a significant difference in classification accuracy compared to other algorithms. PEPSO exhibits outstanding performance on multiple datasets, demonstrating competitiveness not only in classification accuracy but also in statistical significance compared to other algorithms.
More information regarding the accuracy of classifying is shown in Fig. 2. The comparison results are represented using violin plots, providing information about changes in data probability density and median. Each violin plot represents the distribution of classification accuracy for all algorithms on a dataset.
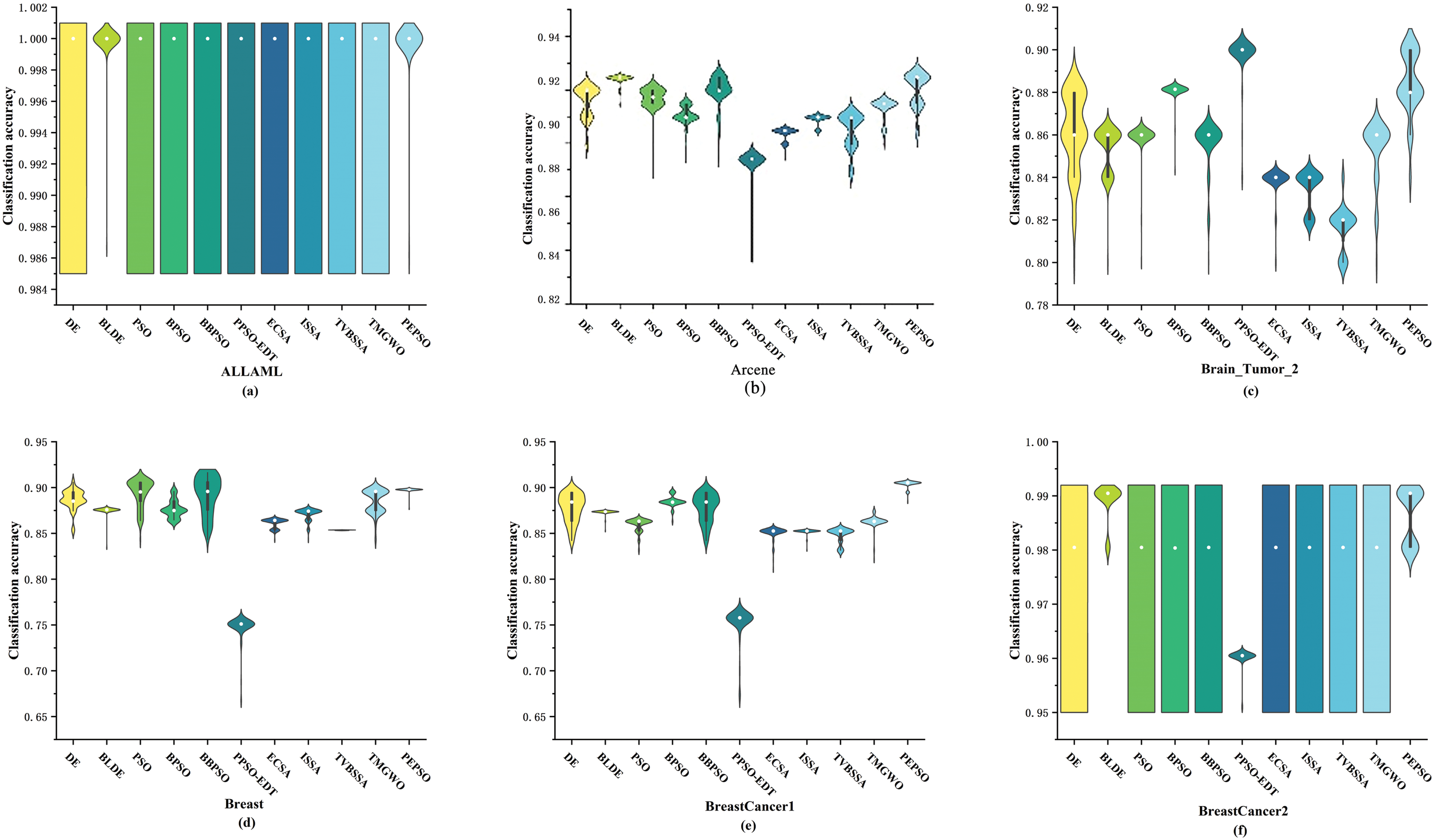
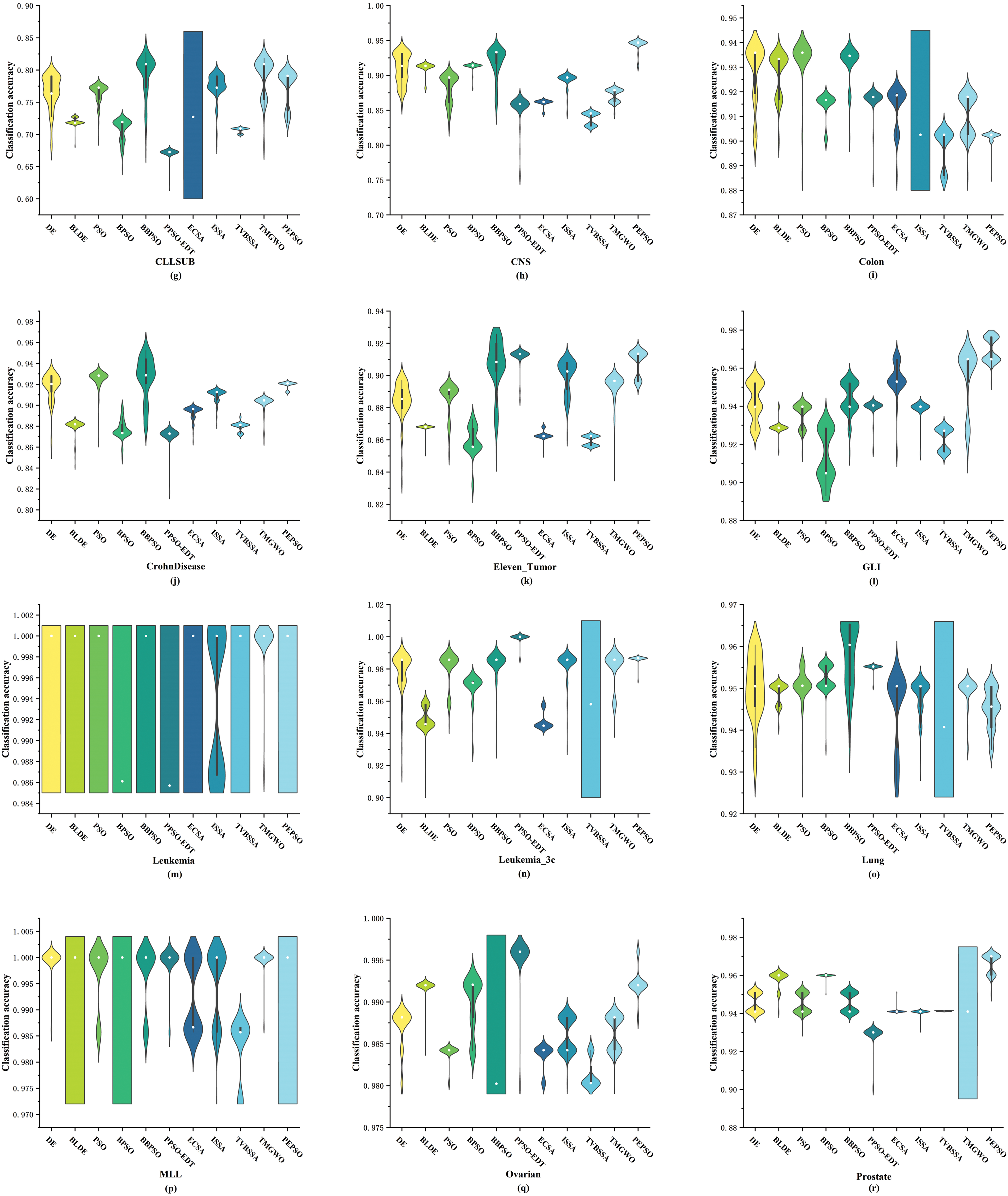
Figure 2: Comparison of classification accuracy between PEPSO and nine comparative algorithms on fifteen datasets
From Fig. 2, it can be observed that the PEPSO exhibits lower dispersion and higher density on each dataset. In most datasets, the classification accuracy of the PEPSO in both early and late iterations surpasses that of other algorithms. By comparing the boxplots within the violin plots, it can be noted that the interquartile range of the PEPSO is smaller than that of most algorithms, especially on datasets such as BreastCancer1 (Fig. 2e) and CNS (Fig. 2h), where the classic deviation of the PEPSO is smaller, indicating lower dispersion of intermediate data. The white dots within the boxplots provide information about the median classification accuracy of the PEPSO on the respective datasets. The median classification accuracy of the PEPSO is lower than that of other comparative algorithms only on datasets CLLSUB (Fig. 2g), Colon (Fig. 2i), Crohn Disease (Fig. 2j), and Lung (Fig. 2o), while remaining the highest or similar on other datasets, indicating the efficiency and comparability of the PEPSO compared to other algorithms.
4.3.2 Analysis of Feature-Sample Ratio
This study analyzes the impact of Feature-Sample Ratio (FSR) on algorithm performance. Sorted by FSR from low to high, a higher FSR indicates an extreme imbalance between the number of features and the number of samples, implying the presence of a large number of noisy features. Fig. 3 illustrates the results of PEPSO and other comparative algorithms on various datasets. In datasets with low FSR, such as Ovarian and LUNG, the difference in classification accuracy between algorithms is minimal. As FSR increases, there is a significant improvement in classification accuracy between our algorithm and other comparative algorithms, indicating a notable enhancement in the performance of our algorithm on datasets with high FSR compared to other algorithms. Even with an increase in FSR, PEPSO does not drop in its ranking among the algorithms, which demonstrates the robustness of the PEPSO.
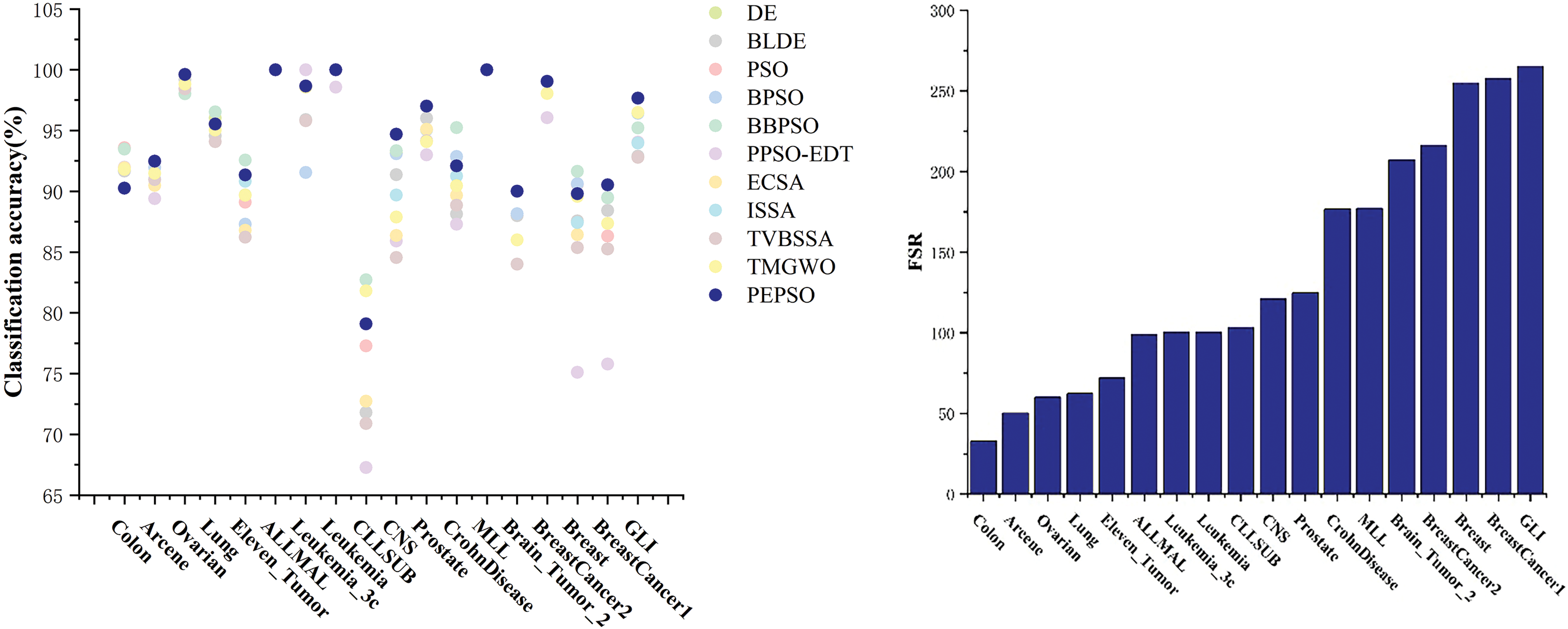
Figure 3: Impact of feature-sample ratio on algorithm performance
4.3.3 Iteration Effects of PEPSO and Comparative Algorithms on Datasets with Different Feature-Sample Ratios
Fig. 4 displays the classification accuracy variation of the PEPSO and other algorithms over 100 iterations on four datasets with low, medium, and high Feature-Sample Ratios. It can be observed that PEPSO maintains a lead or performs comparably to other algorithms at the beginning of iterations. As the number of iterations increases, the classification accuracy of PEPSO converges rapidly to the highest accuracy and remains stable, indicating the effectiveness and fast convergence of the algorithm. Across different FSR levels, PEPSO outperforms other algorithms, especially at high FSR levels, where PEPSO achieves higher accuracy, faster convergence, and superior performance.
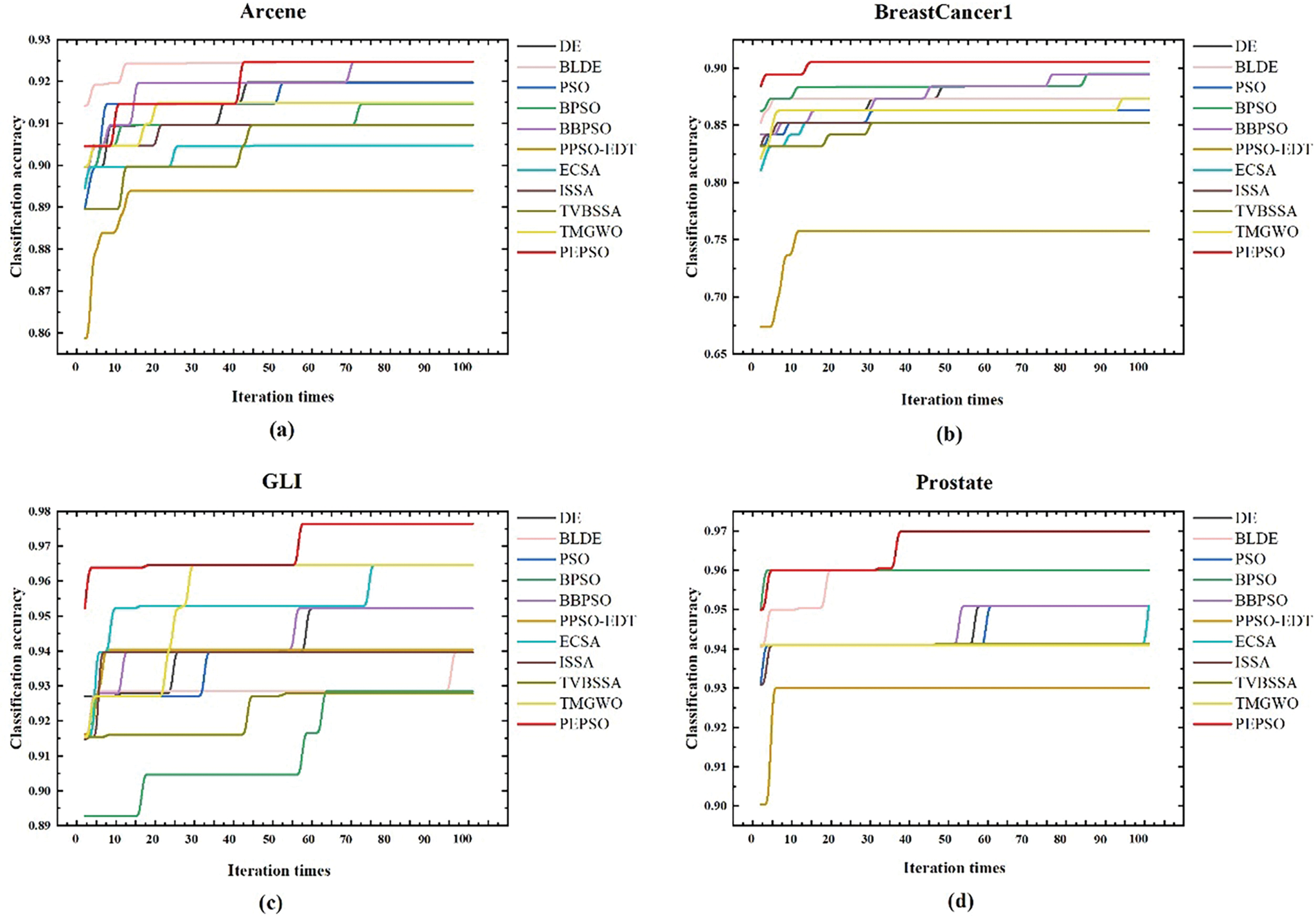
Figure 4: Iteration effects of PEPSO and comparative algorithms on different feature sample ratios dataset
4.3.4 Number of Selected Features
In feature selection, a smaller number of features often implies lower model complexity. A simplified model not only improves computational efficiency but also helps reduce performance degradation caused by overfitting. In many cases, removing redundant or irrelevant features can make the model more accurate and stable. Especially when dealing with large-scale datasets, fewer features mean less data for the algorithm to process when learning and optimizing model parameters, leading to a significant reduction in training time and enhancing the model’s generalization ability.
Fig. 5 illustrates the comparison of the number of selected features by PEPSO and other comparative algorithms during the feature selection process. It can be observed that PEPSO selects fewer features than other algorithms across 18 datasets, yet the classification accuracy is not compromised and even improved on most datasets. These results indicate the superior performance of PEPSO in effectively identifying and retaining informative features.
Figure 5: Comparison of number of selected features by PEPSO and comparative algorithms
The runtime of an algorithm is an important metric for evaluating its performance, directly impacting its efficiency. The scalability of an algorithm is also closely related to its runtime. If an algorithm’s runtime grows too quickly as the dataset size increases, it may limit its application in processing large-scale data.
Table 6 presents the comparison results of runtime between the PEPSO and other algorithms. Experimental results show that the TVBSSA exhibits the shortest runtime across 18 datasets, indicating its significant advantage in computational efficiency despite its relatively lower classification accuracy compared to PEPSO. However, it is worth noting that the PEPSO achieves the best runtime on 2 datasets and is second only to TVBSSA on the remaining 13 datasets, demonstrating its competitiveness in runtime efficiency. Compared to other reference algorithms, the runtime of PEPSO is shortened by 2 to 5 times in most cases. This result implies that the PEPSO significantly improves computational efficiency while maintaining high classification accuracy.
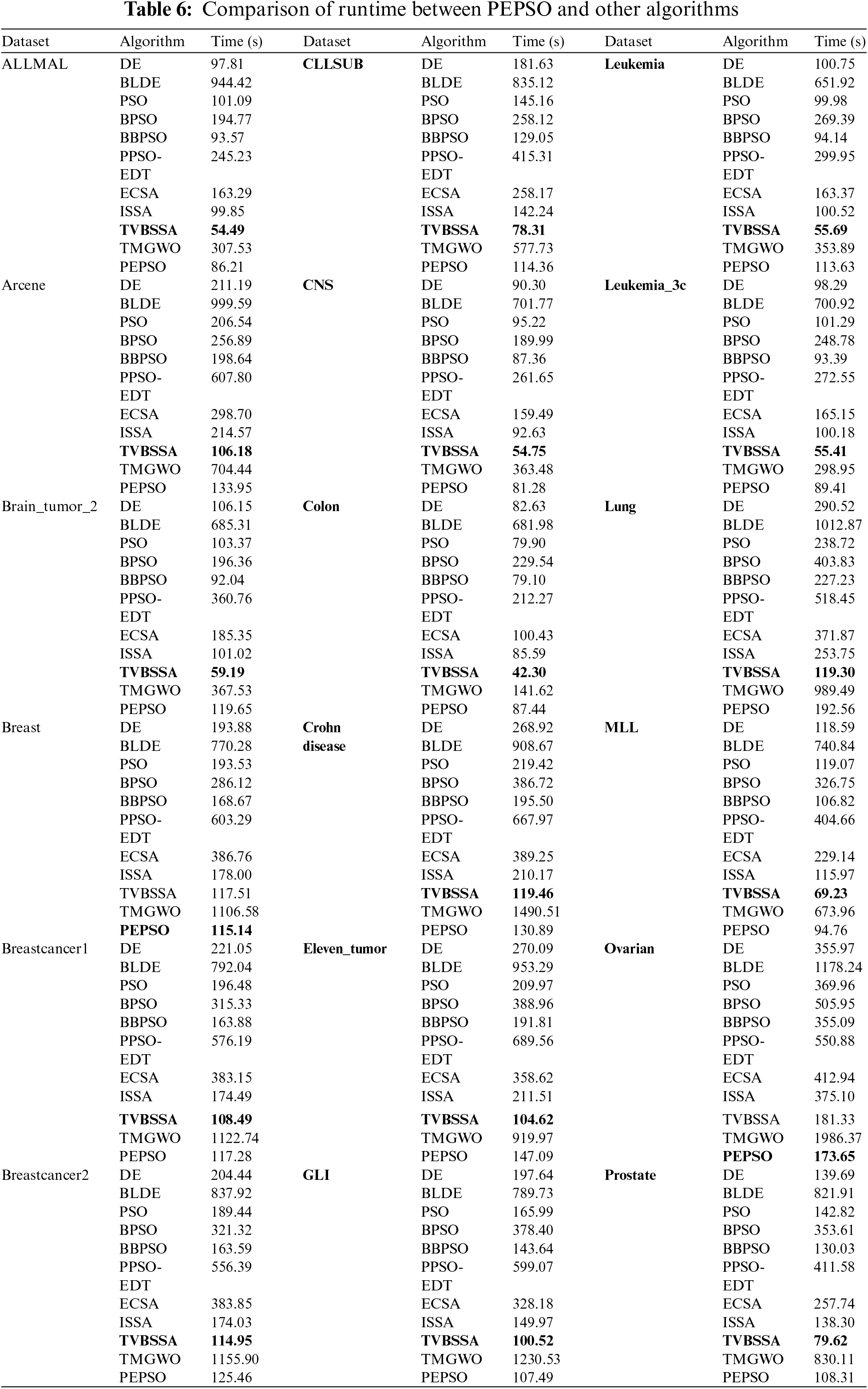
A detailed examination of PEPSO’s performance on different datasets reveals that, although the Breast dataset is approximately ten times larger than the Colon dataset, the runtime increases by less than onefold. This indicates that PEPSO is capable of effectively handling larger datasets without significantly increasing computational cost, demonstrating a certain degree of scalability.
This paper introduces a variant of PSO for feature selection, integrating the patterns and strategies of species survival evolution in mountain ecosystems into PSO to enhance the classification accuracy of feature selection problems. The proposed PEPSO makes several contributions: (1) Simulating the characteristics of mountain ecosystems using a pyramid topology structure. (2) Designing a dual-mode adaptive learning strategy to replace the self-learning and global learning strategies. (3) Introducing a high-peak-guided genetic mutation strategy.
Comprehensive comparisons with state-of-the-art algorithms on 18 gene microarray datasets validate the effectiveness of PEPSO. Numerical results demonstrate that PEPSO achieves higher classification accuracy and smaller feature subsets compared to other methods on most datasets, making it a competitive feature selection approach. Therefore, PEPSO proves to be a promising method for addressing feature selection problems.
In future research, we plan to optimize PEPSO further to enhance its applicability across various domains. We will focus on optimizing and improving the time consumption and parameter adjustment mechanisms of the PEPSO.
Acknowledgement: We thank the Nanchang Institute of Technology for support of this paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shaobo Deng; analysis and interpretation of results: Meiru Xie; draft manuscript preparation: Bo Wang; data collection: Shuaikun Zhang; supervision: Sujie Guan; project administration: Min Li. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Shaobo Deng, upon reasonable request.
Ethics Approval: This article does not contain any research involving humans or animals.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Z. Wang et al., “Application of ReliefF algorithm to selecting feature sets for classification of high resolution remote sensing image,” in 2016 IEEE Int. Geosci. Remote Sens. Symp. (IGARSS), Beijing, China, 2016, pp. 755–758. doi: 10.1109/IGARSS.2016.7729190. [Google Scholar] [CrossRef]
2. S. S. HE, “Feature extraction and selection research of sub-health recognition based on pulse wave,” Xi’an Univ. Sci. Technol., vol. 1, no. 1, pp. 37–38, Jul. 2020. doi: 10.27397/d.cnki.gxaku.2020.000590. [Google Scholar] [CrossRef]
3. M. Ghosh, S. Begum, R. Sarkar, D. Chakraborty, and U. Maulik, “Recursive memetic algorithm for gene selection in microarray data,” Expert Syst. Appl., vol. 116, no. 6, pp. 172–185, Jun. 2019. doi: 10.1016/j.eswa.2018.06.057. [Google Scholar] [CrossRef]
4. X. Zhou, X. Gao, J. J. Wang, H. Yu, Z. Y. Wang and Z. R. Chi, “Eye tracking data guided feature selection for image classification,” Pattern Recognit., vol. 63, pp. 56–70, Sep. 2017. doi: 10.1016/j.patcog.2016.09.007. [Google Scholar] [CrossRef]
5. K. Brkić, “Structural analysis of video by histogram-based description of local space-time appearance, Disertacija,” in Sveučilište u Zagrebu. Austrija: Fakultet elektrotehnike i računarstva, Tehničko sveučilište u Grazu, 2013. [Google Scholar]
6. X. Bai, X. Gao, and B. Xue, “Particle swarm optimization based two-stage feature selection in text mining,” in 2018 IEEE Congr. Evol. Comput. (CEC), Rio de Janeiro, Brazil, 2018, pp. 1–8. doi: 10.1109/CEC.2018.8477773. [Google Scholar] [CrossRef]
7. Y. Y. Zhang, X. Y. Li, L. Gao, and P. Li, “A new subset based deep feature learning method for intelligent fault diagnosis of bearing,” Expert Syst. Appl., vol. 110, pp. 125–142, May 2018. doi: 10.1016/j.eswa.2018.05.032. [Google Scholar] [CrossRef]
8. Z. Manbari, F. AkhlaghianTab, and C. Salavati, “Hybrid fast unsupervised feature selection for high-dimensional data,” Expert Syst. Appl., vol. 124, no. 4, pp. 97–118, Jan. 2019. doi: 10.1016/j.eswa.2019.01.016. [Google Scholar] [CrossRef]
9. M. A. Hall, “Correlation-based feature selection for machine learning,” Ph.D. thesis, Dept. of Computer Science, Univ. of Waikato, Hamilton, New Zealand, 1998. [Google Scholar]
10. B. Xue, M. Zhang, W. N. Browne, and X. Yao, “A survey on evolutionary computation approaches to feature selection,” IEEE Trans. Evol. Comput., vol. 20, no. 4, pp. 606–626, Aug. 2016. doi: 10.1109/TEVC.2015.2504420. [Google Scholar] [CrossRef]
11. L. Y. Chuang, S. W. Tsai, and C. H. Yang, “Improved binary particle swarm optimization using catfish effect for feature selection,” Expert Syst. Appl., vol. 38, no. 10, pp. 12699–12707, Apr. 2011. doi: 10.1016/j.eswa.2011.04.057. [Google Scholar] [CrossRef]
12. L. Y. Cuang, C. H. Yang, and J. C. Li, “Chaotic maps based on binary particle swarm optimization for feature selection,” Appl. Soft Comput., vol. 11, no. 1, pp. 239–248, Nov. 2011. doi: 10.1016/j.asoc.2009.11.014. [Google Scholar] [CrossRef]
13. Y. Zhang, D. W. Gong, Y. Hu, and W. Q. Zhang, “Feature selection algorithm based on bare bones particle swarm optimization,” Neurocomputing, vol. 148, no. 5, pp. 150–157, Sep. 2012. doi: 10.1016/j.neucom.2012.09.049. [Google Scholar] [CrossRef]
14. P. Ghamisi and J. A. Benediktsson, “Feature selection based on hybridization of genetic algorithm and particle swarm optimization,” IEEE Geosci. Remote Sens. Lett., vol. 12, no. 2, pp. 309–313, Feb. 2015. doi: 10.1109/LGRS.2014.2337320. [Google Scholar] [CrossRef]
15. P. Moradi and M. Gholampour, “A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy,” Appl. Soft Comput., vol. 43, pp. 117–130, Jan. 2016. doi: 10.1016/j.asoc.2016.01.044. [Google Scholar] [CrossRef]
16. K. Chen, F. Y. Zhou, and X. F. Yuan, “Hybrid particle swarm optimization with spiral-shaped mechanism for feature selection,” Expert Syst. Appl., vol. 128, no. 1–2, pp. 140–156, Mar. 2020. doi: 10.1016/j.eswa.2019.03.039. [Google Scholar] [CrossRef]
17. Y. Zhou, J. H. Kang, and H. N. Guo, “Many-objective optimization of feature selection based on two-level particle cooperation,” Inf. Sci., vol. 532, no. 1, pp. 91–109, May 2020. doi: 10.1016/j.ins.2020.05.004. [Google Scholar] [CrossRef]
18. Z. H. Zhan, J. Zhang, Y. Li, and H. S. H. Chung, “Adaptive particle swarm optimization,” IEEE Trans. Syst. Man Cybern. B, vol. 39, no. 6, pp. 1362–1381, Dec. 2009. doi: 10.1109/TSMCB.2009.2015956. [Google Scholar] [PubMed] [CrossRef]
19. M. Dash and H. Liu, “Feature selection for classification,” Intell. Data Anal., vol. 1, no. 1–4, pp. 131–156, 1997. doi: 10.3233/IDA-1997-1302. [Google Scholar] [CrossRef]
20. R. N. Khushaba, A. Al-Ani, and A. Al-Jumaily, “Differential evolution based feature subset selection,” in 2008 19th Int. Conf. Pattern Recognit., Tampa, FL, USA, 2008, pp. 1–4. doi: 10.1109/ICPR.2008.4761255. [Google Scholar] [CrossRef]
21. A. Al-Ani, “Ant colony optimization for feature subset selection,” presented at the 2nd World Enformatika Conf. (WEC’05), Istanbul, Turkey, Feb. 25–27, 2005. [Google Scholar]
22. H. R. Kanan and K. Faez, “An improved feature selection method based on ant colony optimization (ACO) evaluated on face recognition system,” Appl. Math. Comput., vol. 205, no. 2, pp. 716–725, May 2018. doi: 10.1016/j.amc.2008.05.115. [Google Scholar] [CrossRef]
23. D. E. Goldberg and J. H. Holland, “Genetic algorithms and machine learning,” Mach. Learn., vol. 3, no. 2, pp. 95–99, Oct. 1988. doi: 10.1023/A:1022602019183. [Google Scholar] [CrossRef]
24. F. Karimi, M. B. Dowlatshahi, and A. Hashemi, “SemiACO: A semi-supervised feature selection based on ant colony optimization,” Expert Syst. Appl., vol. 214, no. 6, Mar. 2023, Art. no. 119130. doi: 10.1016/j.eswa.2022.119130. [Google Scholar] [CrossRef]
25. Y. -T. Kao and E. Zahara, “A hybrid genetic algorithm and particle swarm optimization for multimodal functions,” Appl. Soft Comput., vol. 8, no. 2, pp. 849–857, Mar. 2008. doi: 10.1016/j.asoc.2007.07.002. [Google Scholar] [CrossRef]
26. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. ICNN’95-Int. Conf. Neural Netw., Perth, WA, Australia, 1995, vol. 4, pp. 1942–1948. doi: 10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]
27. J. Tang, G. Liu, and Q. Pan, “A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends,” IEEE/CAA J. Automatica Sinica, vol. 8, no. 10, pp. 1627–1643, Oct. 2021. doi: 10.1109/JAS.2021.1004129. [Google Scholar] [CrossRef]
28. J. Kennedy, “Small worlds and mega-minds: Effects of neighborhood topology on particle swarm performance,” in Proc. 1999 Congr. Evol. Comput.-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 1999, vol. 3, pp. 1931–1938. doi: 10.1109/CEC.1999.785509. [Google Scholar] [CrossRef]
29. L. Wang, B. Yang, and Y. H. Chen, “Improving particle swarm optimization using multi-layer searching strategy,” Inf. Sci., vol. 274, no. 1, pp. 70–94, Feb. 2014. doi: 10.1016/j.ins.2014.02.143. [Google Scholar] [CrossRef]
30. Q. Yang, W. N. Chen, J. D. Deng, Y. Li, T. Gu and J. Zhang, “A level-based learning swarm optimizer for large-scale optimization,” IEEE Trans. Evol. Comput., vol. 22, no. 4, pp. 578–594, Aug. 2018. doi: 10.1109/TEVC.2017.2743016. [Google Scholar] [CrossRef]
31. X. Wu et al., “Empirical study of particle swarm optimization inspired by Lotka-Volterra model in ecology,” Soft Comput., vol. 23, no. 14, pp. 5571–5582, 2019. doi: 10.1007/s00500-018-3215-9. [Google Scholar] [CrossRef]
32. D. Wu, N. Jiang, W. Du, K. Tang, and X. Cao, “Particle swarm optimization with moving particles on scale-free networks,” IEEE Trans. Netw. Sci. Eng., vol. 7, no. 1, pp. 497–506, Jan. 1–Mar. 2020. doi: 10.1109/TNSE.2018.2854884. [Google Scholar] [CrossRef]
33. R. Cheng and Y. Jin, “A competitive swarm optimizer for large scale optimization,” IEEE Trans. Cybern., vol. 45, no. 2, pp. 191–204, Feb. 2015. doi: 10.1109/TCYB.2014.2322602. [Google Scholar] [PubMed] [CrossRef]
34. Y. F. Zhang, X. X. Liu, F. X. Bao, J. Chi, C. M. Zhang and P. D. Liu, “Particle swarm optimization with adaptive learning strategy,” Knowl.-Based Syst., vol. 196, no. 3, 2020, Art. no. 105789. doi: 10.1016/j.knosys.2020.105789. [Google Scholar] [CrossRef]
35. H. Li, J. Li, P. S. Wu, Y. C. You, and N. Y. Zeng, “A ranking-system-based switching particle swarm optimizer with dynamic learning strategies,” Neurocomputing, vol. 494, no. 2, pp. 356–367, Apr. 2022. doi: 10.1016/j.neucom.2022.04.117. [Google Scholar] [CrossRef]
36. J. J. Liang, A. K. Qin, P. N. Suganthan, and S. Baskar, “Comprehensive learning particle swarm optimizer for global optimization of multimodal functions,” IEEE Trans. Evol. Comput., vol. 10, no. 3, pp. 281–295, Jun. 2006. doi: 10.1109/TEVC.2005.857610. [Google Scholar] [CrossRef]
37. X. -F. Song, Y. Zhang, Y. -N. Guo, X. -Y. Sun, and Y. -L. Wang, “Variable-size cooperative coevolutionary particle swarm optimization for feature selection on high-dimensional data,” IEEE Trans. Evol. Comput., vol. 24, no. 5, pp. 882–895, Oct. 2020. doi: 10.1109/TEVC.2020.2968743. [Google Scholar] [CrossRef]
38. X. -F. Song, Y. Zhang, D. -W. Gong, and X. -Z. Gao, “A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high-dimensional data,” IEEE Trans. Cybern., vol. 52, no. 9, pp. 9573–9586, Sep. 2022. doi: 10.1109/TCYB.2021.3061152. [Google Scholar] [PubMed] [CrossRef]
39. J. R. Gao, Z. Q. Wang, T. Jin, J. J. Cheng, Z. Y. Lei and S. C. Gao, “Information gain ratio-based subfeature grouping empowers particle swarm optimization for feature selection,” Knowl.-Based Syst., vol. 286, no. 2, Feb. 2024, Art. no. 111380. doi: 10.1016/j.knosys.2024.111380. [Google Scholar] [CrossRef]
40. R. Storn and K. Price, “Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces,” J. Glob. Optim., vol. 11, no. 4, pp. 341–359, Dec. 1997. doi: 10.1023/A:1008202821328. [Google Scholar] [CrossRef]
41. Y. Chen, W. C. Xie, and X. F. Zou, “A binary differential evolution algorithm learning from explored solutions,” Neurocomputing, vol. 149, no. part B, pp. 1038–1047, Feb. 2015. doi: 10.1016/j.neucom.2014.07.030. [Google Scholar] [CrossRef]
42. J. Kennedy and R. Eberhart, “A discrete binary version of the particle swarm algorithm,” presented at the IEEE Int. Conf. Syst., Man, Cybern., Orlando, FL, USA, Oct. 12–15, 1997, vol. 5, pp. 4104–4108. doi: 10.1109/ICSMC.1997.637339. [Google Scholar] [CrossRef]
43. J. Kennedy, “Bare bones particle swarms,” in IEEE Swarm Intell. Symp., Indianapolis, IN, USA, Apr. 24–26, 2003, pp. 80–87. doi: 10.1109/SIS.2003.1202251. [Google Scholar] [CrossRef]
44. X. Y. Pan, M. Z. Lei, and J. Sun, “An evolutionary feature selection method based on probability-based initialized particle swarm optimization,” Int. J. Mach. Learn. Cybern., vol. 15, no. 8, pp. 3533–3552, Mar. 2024. doi: 10.1007/s13042-024-02107-5. [Google Scholar] [CrossRef]
45. S. Ouadfel and M. A. Elaziz, “Enhanced crow search algorithm for feature selection,” Expert Syst. Appl., vol. 159, no. 1, Oct. 2020, Art. no. 113572. doi: 10.1016/j.eswa.2020.113572. [Google Scholar] [CrossRef]
46. M. Tubishat, N. Idris, L. Shuib, M. A. M. Abushariah, and S. Mirjalili, “Improved salp swarm algorithm based on opposition based learning and novel local search algorithm for feature selection,” Expert Syst. Appl., vol. 145, no. 13, Mar. 2020, Art. no. 113122. doi: 10.1016/j.eswa.2019.113122. [Google Scholar] [CrossRef]
47. H. Faris et al., “Time-varying hierarchical chains of salps with random weight networks for feature selection,” Expert Syst. Appl., vol. 140, no. 5, Feb. 2020, Art. no. 112898. doi: 10.1016/j.eswa.2019.112898. [Google Scholar] [CrossRef]
48. M. Abdel-Basset, D. El-Shahat, I. El-henawy, V. H. C. de Albuquerque, and S. Mirjalili, “A new fusion of grey wolf optimizer algorithm with a two-phase mutation for feature selection,” Expert Syst. Appl., vol. 139, no. 3, Jan. 2020, Art. no. 112824. doi: 10.1016/j.eswa.2019.112824. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF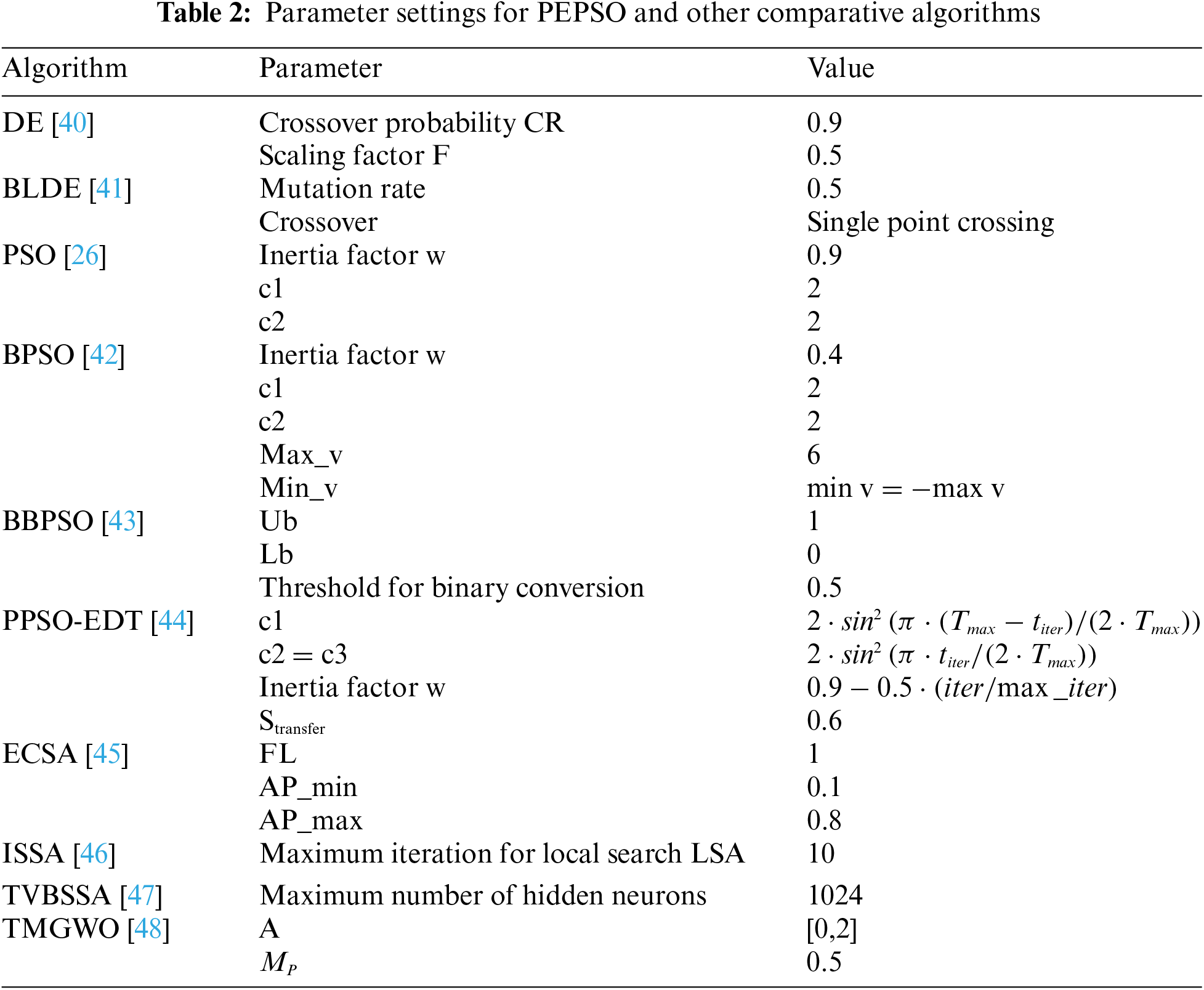
 Downloads
Downloads
 Citation Tools
Citation Tools