Application of Multi-Relationship Perception Based on Graph Neural Network in Relationship Prediction

1  Introduction

The knowledge graph (KG) is one of the core technologies for processing natural language tasks. Knowledge graph represents the knowledge base (KB) in the form of a directed graph. The structured knowledge of knowledge graph exists in the form of triples (head entity, relationship, tail entity). This representation method not only retains the basic semantic information of knowledge, but also provides efficient information retrieval and management mechanisms. Therefore, it is applied to various aspects, such as recommendation system [1], question-answering system [2], semantic search [3], and others. However, due to the continuous expansion and evolution of knowledge, the existing KG often fails to include comprehensive information. The existing knowledge graph frequently faces the problem of incomplete information, which limits its effectiveness in practical tasks.

In order to solve this problem and improve the representational ability of the knowledge graph, the knowledge graph completion (KGC) task has emerged. The goal of KGC is to enrich and enhance the knowledge graph by predicting potential triples. This task typically involves three key steps: model learning, candidate processing, and fact recognition. The core of model learning is to efficiently predict the correctness of candidate triples. The knowledge graph processed by KGC can mine and infer missing entity relationships, which improves the graph’s expressive ability for downstream tasks of the knowledge graph, such as combining the knowledge graph with the recommendation systems. By using the knowledge graph generated by the KGC method, a more comprehensive user preference model can be constructed, which helps address the problem of data sparsity and improves the accuracy of recommendations. However, the traditional KGC method faces many challenges when processing large-scale-multi-relationship graphs, such as the difficulty in accurately modeling complex structures and relationship patterns in multi-relationship graphs. Link prediction is a specific task within knowledge graph completion that focuses on predicting the missing relationships between entities.

Knowledge graph embedding (KGE) is a key technology for KGC. By mapping entities and relations into continuous vector space, it realizes the vectorized representation and calculation of triples. While simplifying operations, it retains the inherent structure of the knowledge graph [4]. The specific implementation processes of KGE are also diverse, such as the translation-based model TransE proposed by Bordes et al. [5], the TransR proposed by Lin et al. [6], the TransH proposed by Wang et al. [7], the semantic matching-based model DistMult proposed by Yang et al. [8], and the neural network-based model ConvE proposed by Dettmers et al. [9]. In addition, Sun et al. [10] proposed a new knowledge graph embedding method RotatE. This model infers various relational patterns by defining each relation as a rotation (such as symmetry, antisymmetry, inversion, etc.) from the source entity to the target entity in a complex vector space, thereby capturing more semantic information when modeling relational patterns. According to the summary of previous studies [11], since the translation-based method has higher interpretability and the neural network-based method has higher accuracy, these two methods have attracted the research interest of many scholars. For example, Xie et al. [12] integrated ConvE with the inception network and proposed a relation-aware network that combines local and global structural information. Various evaluation indicators show that Inception network can further increase the interaction between head embedding and relation embedding. Li et al. [13] obtained the interactive embedding of entities and relations by introducing the interaction matrix, and then further used the inception network to learn query embedding, and finally constructed the semantic relationship path using logical rules. However, with the increase in the scale and complexity of the graph, the traditional KGE method does not distinguish the importance of different relations when dealing with multi-relational complex knowledge graphs, and cannot perform targeted calculations on complex knowledge graph relationship patterns. Therefore, the accuracy has not been significantly improved, which limits the progress of KGC tasks.

In order to solve this problem, many scholars have begun to study the combination of the KGE method and graph neural networks (GNN) to improve the model’s ability to capture complex relationships. For example, KBGAT [14] combines a graph convolutional network (GCN) with an attention mechanism, assigning different weights to neighboring nodes through the attention layer, and then proposes a new KGE method with the encoder-decoder structure. CompGCN [15] solves the problem where GCN only processes simple undirected graphs. As a new graph convolution framework, CompGCN expands the application scope of GCN by jointly embedding entities and relationships. This method addresses the existing shortcomings of GCN. Li et al. [16] explored more detailed and interpretable knowledge combinations by representing KGs as irregular graphs and processing graph structure information with multiple independent channels, avoiding the problem that the general KGE model can only process triples independently without considering the relevance of knowledge. Moreover, the high relevance of KG is used to analyze the features of any given entity and its surrounding entities and relationships [17]. The KGE method that uses neighborhood features to evaluate candidate triples can more effectively identify the correct triples. These methods still have limitations when dealing with multi-hop relations and multi-path attention allocation. They usually only allocate attention between direct neighbors, fail to sufficiently model the multi-hop relationship paths, and insufficiently utilize the interactive information between entities and relationships.

Therefore, this paper proposes a new two-hop relationship graph attention network (TRGAT) based on the attention mechanism. This neural network introduces a new message function to obtain the interactive embedding of entities and relationships under complex topological structures, and expands the adjacent forward relationships of the central node. It establishes a relationship model containing five relation patterns such as two-hop forward relations and reverse relations, in order to comprehensively obtain node information in complex graph structures for attention calculation. Through this improvement, TRGAT can more comprehensively aggregate node information and allocate attention, significantly improving the performance of knowledge graph completion tasks. Fig. 1 shows the tasks involved in knowledge graph completion. The red node represents the central node, the yellow nodes represent the neighbor nodes of the central node, the blue nodes represent the peripheral nodes that are not directly connected to the central node, the blue edges represent the actual edges in the graph, and the red edges represent the edges that need to be inferred. Fig. 2 is an example of graph completion using the method in this study. It is centered on the central node and based on the original adjacent edges (solid lines in the figure), with added reverse, spin, two-hop forward and two-hop reverse relations(the added edges are dotted lines) to calculate graph attention, the blue edges represent the edges involved in the attention calculation, and their attention values are marked on the edges, indicating their importance to the central node, the gray edges represent those that do not participate in the attention calculation.

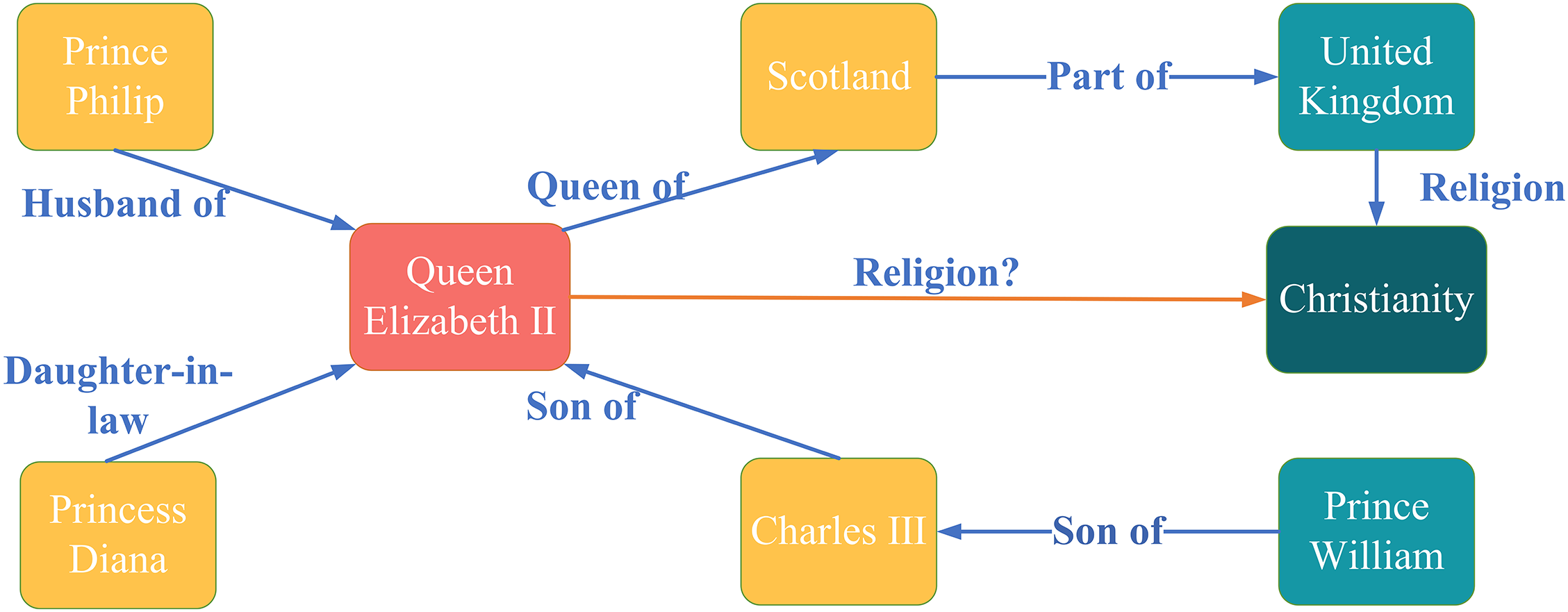
Figure 1: Example of knowledge graph completion task

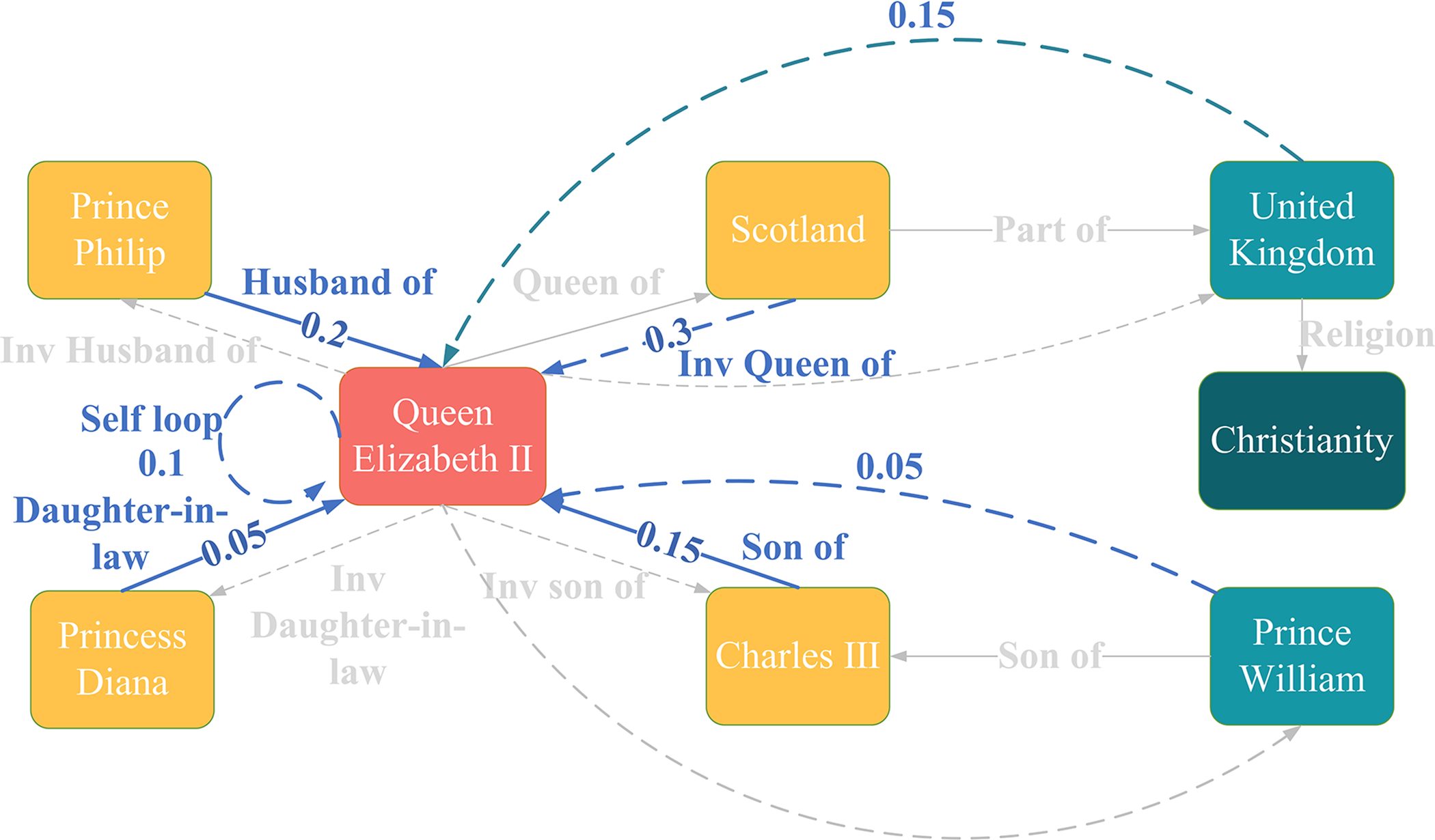
Figure 2: Example of using TRGAT on knowledge graph completion task

The main contributions of this study are summarized as follows:

1.    Introducing a new message function into the graph neural network, which can jointly map entities and relationships to complex vector spaces, thereby improving relationship awareness.

2.    Introducing the two-hop path into attention calculations to enrich the semantic information of each entity, so that message transmission is no longer limited to the direct neighboring nodes of each node, but also includes nodes indirectly connected to it. This improves the ability to aggregate information in multi-relational complex knowledge graphs.

3.    Conducting experiments on the relationship prediction task using the standard datasets WN18RR and FB15K-237. Comprehensive experimental results show that TRGAT outperforms most KGE methods, verifying the effectiveness of the method proposed in this study.

2  Related Works

2.1 Knowledge Graph Completion

In recent years, many technologies for knowledge graph completion have been continuously updated, which are roughly based on the following models: rule-based reasoning models, path-based reasoning models, and representation learning-based models.

2.1.1 Rule-Based Reasoning Model

The idea of rule-based reasoning is to use predefined rules to reason about unknown knowledge. These models are highly interpretable and are usually combined with reinforcement learning for hybrid reasoning. Logical rule-based reasoning combines Markov models with logical rules for reasoning and learns the weights of rules through training. For example, InterERP [14] combines rule reasoning and representation learning models, uses the Inception network to learn query embedding, and then uses the logical rule framework AMIE+ to build a relationship path matrix to handle the embedding of multi-relational knowledge graphs. DeepPath [18] employs reinforcement learning to automatically generate rules and conduct research. It combines deep learning to automatically discover rules to enhance the adaptability and expressiveness of the model. Although rule-based reasoning models are highly interpretable, they face some challenges in automatically discovering rules. Since rule-based methods are difficult to generalize link patterns that have not been seen before, there are some problems with generalization ability.

2.1.2 Path-Based Reasoning Model

The idea of path-based reasoning models is to use the path information between entities to capture complex relational patterns. A typical example is the PRA [19] algorithm, which transforms the relationship reasoning path into a ranking problem and uses the paths between entities for link reasoning. The MINERVA [20] algorithm is a hybrid reasoning algorithm that introduces reinforcement learning into the ordinary path reasoning model, dynamically searching for paths in the graph, and predicts unknown entities through this dynamically generated path. The greatest advantage of both rule-based reasoning models and path-based reasoning models is their strong interpretability, but it is challenging to find sufficient paths for effective reasoning in sparse graphs, and their reasoning ability is highly dependent on the structure and integrity of the graph.

2.1.3 Representation Learning-Based Models

Models based on representation learning can improve the generalization ability of the model and are not limited by the sparsity of the knowledge graph. By mapping entities and relationships to a low-dimensional vector space, large-scale knowledge graphs can be processed more effectively, and some problems inherent in rule-based reasoning and path-based reasoning models, such as poor generalization ability, ineffective completion effect on complex sparse graphs, and over-reliance on manual intervention, can be solved. Models based on representation learning include translation-based models, tensor decomposition-based models, convolutional neural network (CNN)-based models, and GNN-based models, etc.

The translation-based model is one of the earliest translation models. The idea is to project the entities and relations of the knowledge graph triple into a vector space. The head entity vector can be translated to the tail entity vector through the relationship vector to obtain the inferred triple. If the head entity plus the relationship vector is closer to the tail entity vector, the triple is considered more likely to be correct. The most typical algorithm is TransE [5], which is a foundational model in translation-based methods. This algorithm attempts to project the head entity, relationship, and tail entity into a low-dimensional vector space, and simplifies the knowledge graph completion task by minimizing the gap between the sum of the head entity vector and the relationship vector and the tail entity vector. However, TransE cannot handle symmetric and antisymmetric relationships. To solve this problem, the RotatE [10] model improves upon TransE by introducing complex numbers into the vector representation of entities and relations using Euler formula. The relation r is regarded as the rotation vector from the head entity h vector to the tail entity t vector on the complex plane, and the expectation is t=h∗r, where h,r,t∈C and |r|=1, C is the complex plane. This operation can model three relation types: symmetric/antisymmetric, inversion, and synthesis. This paper constructs the message function based on the idea of the RotatE model.

Tensor decomposition-based models are based on the idea of decomposing a high-order tensor into the product of lower-order tensors. The representative model is DistMult [8]. The interaction between entities and relationships is modeled by matrix multiplication, and the vector representation of entities and relationships is calculated by dot product to compute the score of triples. The score measures the correctness of the predicted triples.

The CNN-based model applies convolutional neural networks to KGC. The representative model is ConvE [9]. Its idea is to represent the embedding of entities and relationships as a two-dimensional matrix, and then process it through a convolutional neural network to learn local patterns and interactions between entities and relationships. ConvE has several improved variants, such as InteractE [21], which introduces an interaction function to simulate the interaction between entities and relationships. This model modifies the interaction mechanisim between entities and relationships, replacing standard embedding interactions with cross-embedding, allowing it to capture more complex information. This paper uses InteractE as the decoder for ConvE. RIECN [22] introduces a new approach to generating relation-based dynamic convolution filters (RDCF), enriching the feature maps of each entity and improving the accuracy of KGC tasks, especially in complex relations scenario. Although CNN-based models can capture local relationship features through convolution operations, they still face the problems of low training efficiency and overfitting on large-scale graphs.

The GNN-based model applies graph neural networks to KGC, updates node states through a message passing mechanism, captures flowing information between nodes, including both local information and global information, thus modeling complex dependencies between nodes. RGCN [23] is the first model to apply GNNs to knowledge graph embedding. It uses graph neural networks to learn neighborhood information between entities. The model CompGCN [15] simultaneously learns entities and relations embeddings, and uses entity-relation combinations to process multi-relational informations. This paper draws inspiration from CompGCN to construct the TRGAT model. RGHAT [24] uses the graph attention mechanism to perceive the valuable information in the neighbors of each entity, and then employs a two-layer attention mechanism to focus on both relations and entities, thereby highlighting the importance of different adjacent entities under the same relationship. In large-scale knowledge graphs, the topological structure of the graph is often highly complex, and the transmission of information may be affected by the sparsity of nodes and edges. These models do not adequately capture some high-order dependency relationships across distant nodes, especially in multi-hop reasoning tasks of knowledge graphs. It is difficult to effectively transmit information between distant nodes and relationships. Therefore, how to better utilize the transmission of complex multi-hop information to improve knowledge graph completion capability remains an urgent problem to solve.

2.2 Graph Neural Networks (GNNs)

Graphs are composed of nodes and relationships, and the interactions between nodes and relationships contain a significant amount of information. To capture this information structure, scholars have employed deep learning methods to analyze graph structures, and graph neural networks came into being.

2.2.1 Graph Convolutional Network (GCN)

GCN is one of the most basic and widely used models in GNNs. The GCN model proposed by Kipf et al. in 2017 [25] aggregates the feature information of nodes from neighboring nodes to target nodes through a method of convolution over the graph structure, so that the high-level representation of nodes can be learned. GCN has achieved excellent performance in tasks such as graph node classification and link prediction.

2.2.2 Graph Attention Network (GAT)

GAT introduces an attention mechanism to assign different weights to each neighboring node, making the information aggregation process more flexible and adjustable. The GAT model proposed by Velickovic et al. [26] in 2018 introduced a self-attention mechanism, which further improved the model’s expressive power by weighting the different importance levels of neighboring nodes.

2.2.3 Graph Neural Networks and Knowledge Graphs

The application of GNNs in KGs has made significant progress, especially in tasks such as KGC, entity linking prediction, and relation inference. In recent years, GNNs have been widely used in KGC tasks, and can better handle high-order relationships and complex structures in graphs through message passing mechanisms and dependencies between nodes. For example, DisenKGAT [27] uses micro disentanglement and macro disentanglement to represent knowledge graphs, respectively, and achieves macro disentanglement and micro disentanglement through novel relation-aware aggregation and mutual information as regularization, and it uses disentanglement to achieve adaptive representation for given scenarios. Zhang et al. [28] proposed a graph attention network, DRR-GAT, with dynamic relation representation and global information, using Transformer to achieve dynamic representation of relations and capture the unique semantic connotation of the same relation between different triples. Dai et al. [29] designed a multi-relation graph attention network (MRGAT) to calculate the attention of the central node to its neighbors from the perspectives of neighbors and relations. GNNs have demonstrated great potential in tasks such as knowledge graph completion and multi-hop reasoning through their powerful graph structure learning ability, and has promoted the research and development in the field of knowledge graphs.

3  TRGAT Model Introduction

In this section, the model proposed in this paper will be described in detail. The TRGAT model proposed in this study based on the CompGCN model and the RotatE model, is a model based on representation learning. It addresses the problem of CompGCN being unable to distinguish the importance of different relationships well, and the inability of RotatE to capture transitive relationships. This paper refers to the idea of CompGCN’s joint embedding representation of entity relationships and uses graph attention to calculate relationship-level attention. The importance of relationships can be distinguished through the value of graph attention, and the dissemination and aggregation of information can be guided more accurately. This study also draws on the RotatE model, which uses the idea of rotating relationships in the complex plane to construct the message function of the graph neural network. By expanding the scope of relationship path acquisition, the relationship path reasoning is performed on the two-hop path, and the transitive relationship pattern can be calculated, solves the problem that RotatE cannot capture transitive relationships, thereby improving the accuracy of the knowledge graph relation prediction task.

First of all, the symbols and definitions used in this study are introduced. For the multi-relationship knowledge graph, it is represented by G=(V,R,E,X,Z), where V is the vertex set, R is the relationship set, E is the edge set, 𝒳∈R|𝒱|×d0 represents the d0th dimension input node, Rd is the embedding space, 𝒵∈R|ℛ|×d0 represents the initial relationship feature, each triple (u,v,r) means that there is relationship r∈R from node u∈V to node v∈V. Get the embeddings for entity u and relationship r, represented as eu and er.

The example of the relational model can be seen in Fig. 3, which is the knowledge graph after abstracting entities and relationships into symbols in Fig. 2. u is the central node, v1, v2, v3 and v4 are neighbors of u, v5 and v6 are two-hop neighbors of u, all belonging to node set V. The solid lines are the original edges in the graph, and the dotted lines are the relationship paths added in the relationship model of this study. Among them, r1, r2, r3 and r4 are one-hop forward edges, r1_inv, r2_inv, r3_inv and r4_inv are one-hop reverse edges, r0 is a spin edge, r3r5, r4r4 are two-hop forward edges, and r5r3_inv and r4r4_inv are two-hop reverse edges.

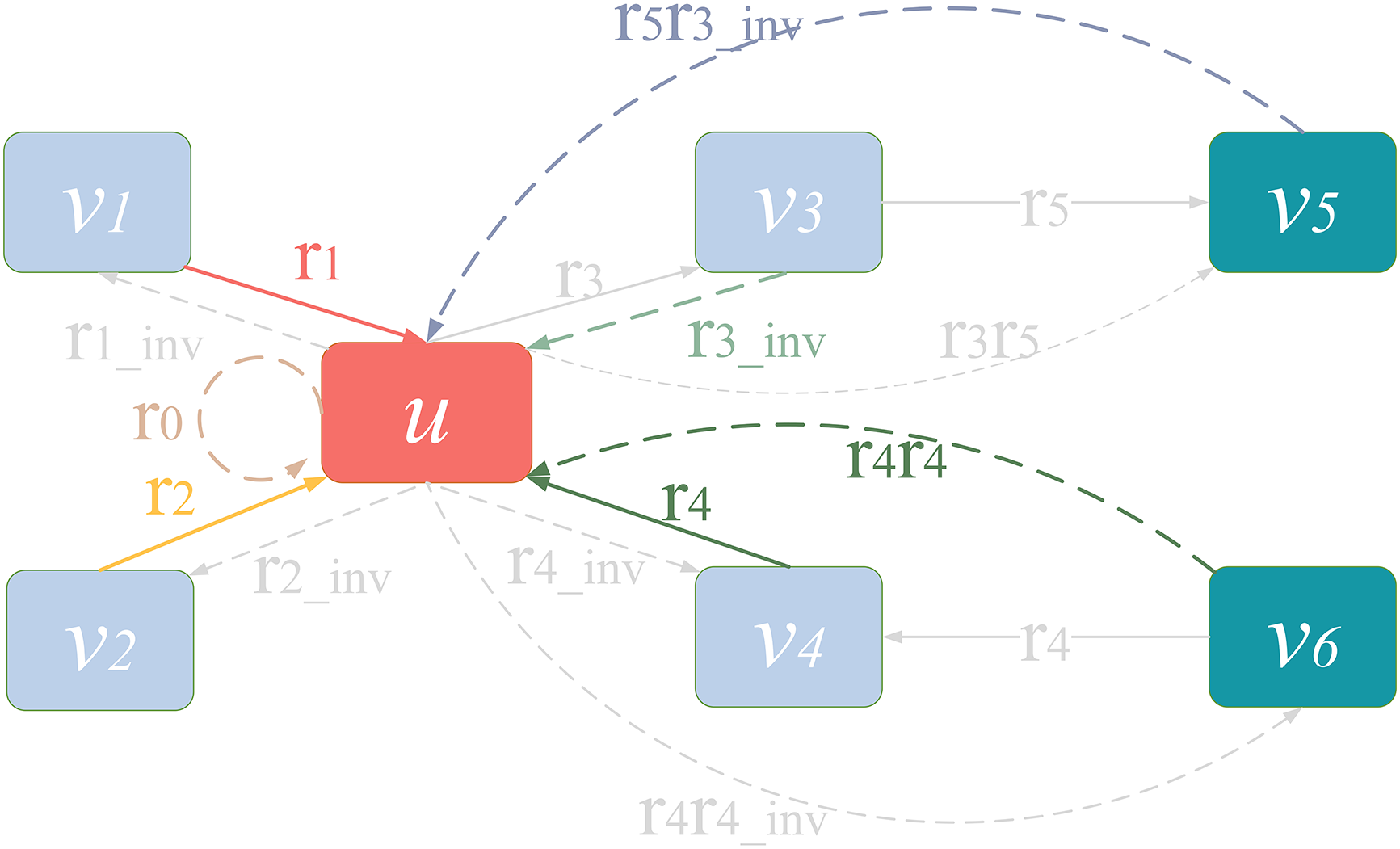
Figure 3: Example of the relational model

The overall architecture of the model is shown in Fig. 4, which performs completion tasks based on the knowledge graph relationship model example in Fig. 3.

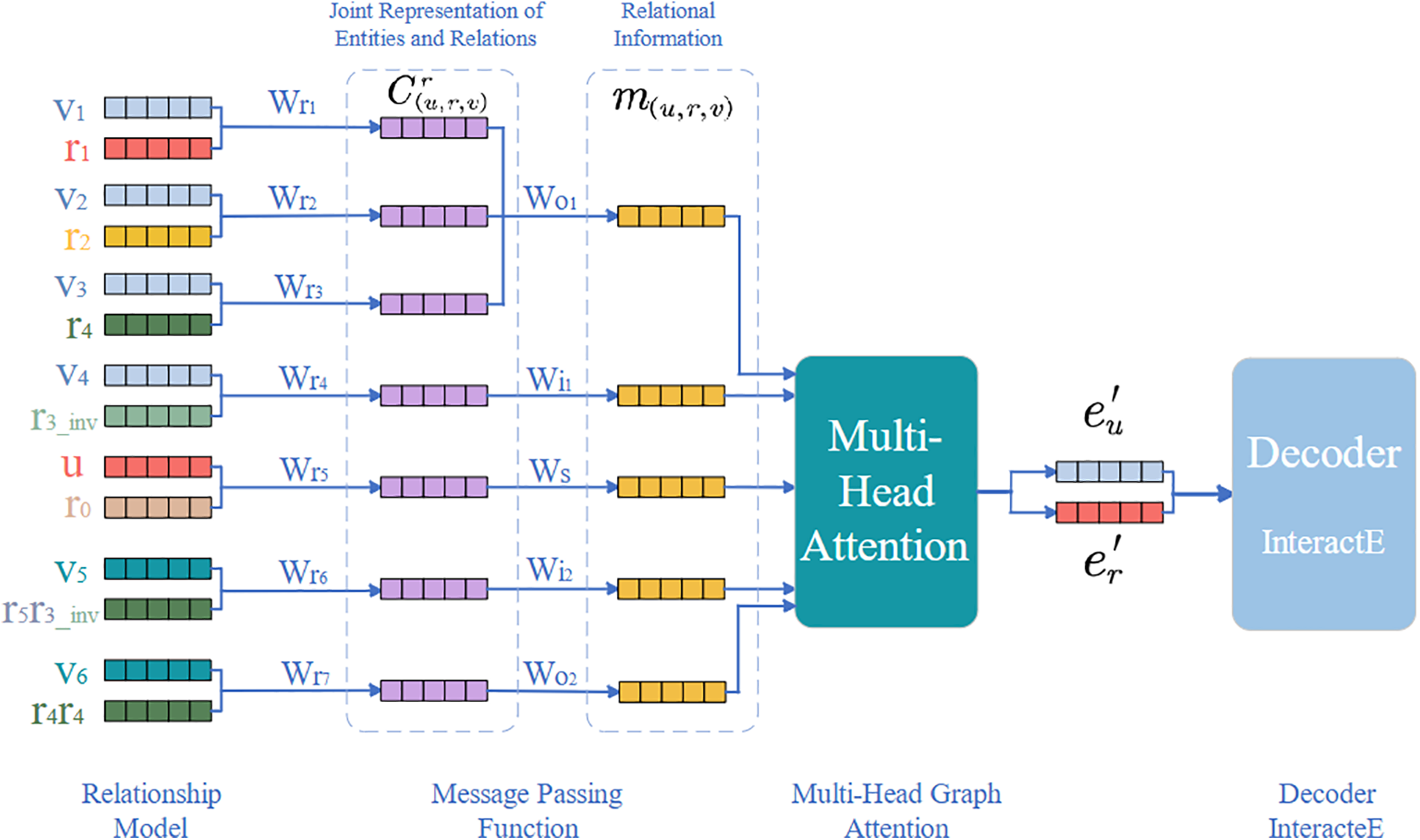
Figure 4: TRGAT model architecture

The model consists of four main components: relationship model, message passing function, multi-head graph attention network and decoder. First of all, this paper introduces a novel relationship model, which incorporates two-hop forward and two-hop reverse relationships into the relationship model. This expands the scope of message acquisition and enables calculations for different relationship patterns. Secondly, a new message function is proposed, capable of capturing the joint representation of entities and relationships: C(u,r,v)r, to distinguish different path types, and calculate the relationship information of each path m(u,r,v). Subsequently, a multi-head graph attention network is employed to calculate the attention weights of different entity-relationship pairs, and update entity embedding eu and relationship embedding er. Finally, the updated entity embedding eu′ and relationship embedding er′ are passed to the decoder for decoding operations.

3.1 Relationship Model

This section introduces the relationship model adopted in this study. There are numerous complex relationships in the links of the knowledge graph. The five most common relationship patterns are symmetric/antisymmetric, inversion, composition, transitive/non-transitive and reflexive, as shown in Table 1. These relationship types are complex, the same relationship path may belong to multiple relationship types, and multiple relationship paths can be combined into another relationship type. Relationship paths are also directional. Therefore, it is necessary to build a model that covers most relationship patterns to better capture graph information and complete the knowledge graph.

The relationship model we established takes the central node as the core and includes five relationship paths: spin relationship, forward relationship, reverse relationship, two-hop forward relationship, and two-hop reverse relationship. It effectively covers these five relationship patterns: spin includes the reflexive relationship pattern; forward and reverse relationship includes symmetric/antisymmetric and inversion relationship patterns; and two-hop forward and two-hop inverse relationship include synthesis and transitive/non-transitive relationships.

The original edge set ε adds reverse edges and multi-hop edges, expanding to ε′. The relationship set R adds reverse relationships and multi-hop relationships, and is expanded to R′. Suppose u is the central node, v is the node connected to it, w is the two-hop neighbor of v, and r′ is the relationship of the second-hop path, then the expanded edge set ε′ is:

ℰ′=ℰ∪{(v,u,r−1)|u,v∈𝒱r∈ℛ}∪{(u,u,⊤)|u∈𝒱}∪{(u,r,r′,w)|u,w∈𝒱r,r′∈ℛ}∪{(w,r′,r,u)|u,w∈𝒱r,r′∈ℛ}(1)

And R′=R∪Rinv∪⊤∪Rtwo−hop∪Rtwo−hop−inv, where Rinv={r−1|r∈R} is the inverse relationship, ⊤ is the spin relationship, Rtwo−hop={(r,r′)|r,r′∈R} is the two-hop forward relationship, and Rtwo−hop−inv={(r′,r)|r,r′∈R} is the two-hop inverse relationship.

3.2 Message Passing Function

In GNNs, the message passing function is a core mechanism. It enables graph networks to learn and propagate neighbor information across the graph. Through this mechanism, nodes in the graph can aggregate information from their neighbor nodes to update their own states (i.e., representations). This iterative process enables the network to capture dependencies and patterns in the graph structure. In the GNN learning process, a crucial component is the neighbor aggregation strategy. That is, the message passing function obtains neighbor entity relationship information to form a message vector that updates the node’s own information. This enables each node to learn the local and global patterns of the graph by integrating information from its local neighborhood.

The RotatE model achieves the purpose of link prediction by rotating the relationship vector from head entity vector to tail entity vector in the complex plane space. While the TransE model can only model two relationship modes (inversion and synthesis), and the DistMult model can only model symmetry/Anti-symmetric relationship mode calculation, RotatE can handle these three relationship modes (symmetry, inversion, synthesis) after demonstration. Thus, we construct a new message function by referring to the RotatE’s scoring function, which is called “Self-Training parameter RotatE” (STRotatE), as the non-parametric synthesis operator that calculates the attention value of each different relationship type. This message function can effectively map entity relationships to three types of relationships: symmetric/antisymmetric, inversion, and transitive.

The RotatE model maps entities and relationships to a complex vector space, treating each relationship as a rotation from the source entity to the target entity. Its rotation model is based on Euler’s identity.

Let there be a triplet (h,r,t), where h, r, t are the embedding vectors of the head, relationship and tail respectively, and expect t=h∘r, where |ri|=1. For each element of the embedding in each dimension of the complex plane have ti=hiri, where ∘ represents the Hadamard product, and i represents the i-th element of the embedding. ri=eiθr, corresponding to the i-th element of the relational embedding being rotated counterclockwise by θr,i degrees from the origin around the complex plane. The distance function of RotatE is:

dr(h,t)=‖h∘r−t‖(2)

Inspired by the idea of RotatE, we define the joint representation of head entities and relationships as:

C(u,r,v)r=Wr∗eu∗er(3)

where eu is the entity embedding, er is the relationship embedding, and Wr is the weight matrix to be trained, initialized as a diagonal matrix.

We perform multi-head attention calculations on all relationships connected to the central node, learn an independent weight matrix Wr for each relationship, and calculate the joint representation of entities and relationships C(u,r,v)r for all relationships with the central node as the core in the graph. Since in the complex plane space, er=eiθ=cosθ+isinθ, by combining the above joint representation with weight training, the message function STRotatE of TRGAT can be obtained as:

C(u,r,v)r=Wreu(cosθ+isinθ)(4)

i represents the i-th element of the embedding, θ is the angle of rotation of the relational embedding from the origin about the complex plane.

Then, a path-specific weight matrix Wdir(r) is established for the five different forms of relationship paths in the relationship model.

Wdir(r)={WO1,r∈ℛWI1,r∈ℛinvWS,r=⊤(self−loop)WO2,r∈ℛtwo−hopWI2,r∈ℛtwo−hop−inv(5)

These weights correspond to five relationship path situations: WO1 represents the path weight of the forward relationship R directly connected to the central node, WI1 represents the path weight of the reverse relationship Rinv, Ws represents the weight of the spin relationship, WO2 and WI2 represent the weights of the two-hop forward relationship Rtwo−hop and the two-hop reverse relationship Rtwo−hop−inv. By multiplying the path weight by the entity-relationship joint representation C(u,r,v)r, the relationship information m(u,r,v) of each path can be obtained, and used for multi-head attention calculation:

m(u,r,v)=Wdir(r)C(u,r,v)r(6)

In this way, attention calculations can be performed for different relationship paths. From the previously mentioned relationship model, these five situations can cover five relationship patterns (symmetric/antisymmetric, inversion, composition, transitive/non-transitive and reflexive). By dynamically updating weights, the model reflects the importance of different relationship paths for relationship prediction.

3.3 Multi-Head Graph Attention Network

This model uses multi-head graph attention to calculate the importance of different relationship paths to the central node. First, it is necessary to aggregate the path relationship information m(u,r,v) in Eq. (6) and use LeakyReLU as the activation function for graph attention calculation. Then, the relative attention parameter of the relationship path is:

fu,r=LeakyRelu(Wattm(u,r,v))(7)

where Watt is the weight value of each relationship. LeakyRelu is the activation function. After obtaining the relative attention value, calculate the absolute attention parameter αu,r.

αu,r=softmax(fu,r)(8)

The above attention calculation is performed for one head. We need to calculate the attention value of each head through multi-head attention, and then average them to update the entity embedding eu and the relationship embedding er.

eu′=f(1H∑h=1H∑(u,r)∈𝒩(u)αu,rhm(u,r,v))(9)

er′=Wreer(10)

Among them, u is the central node entity, r represents all the relationships connected to it, H is the number of multi-head attention heads, h represents all heads traversed from 1 to H, f is the nonlinear activation function, N(u) represents all the forward, backward, spin, two-hop forward, and two-hop backward relational paths connected to u. Wre is the weight matrix that updates the relationship embedding. Finally, the updated entity embedding eu′ and relationship embedding er′ are input into the decoder for relation prediction.

3.4 Decoder

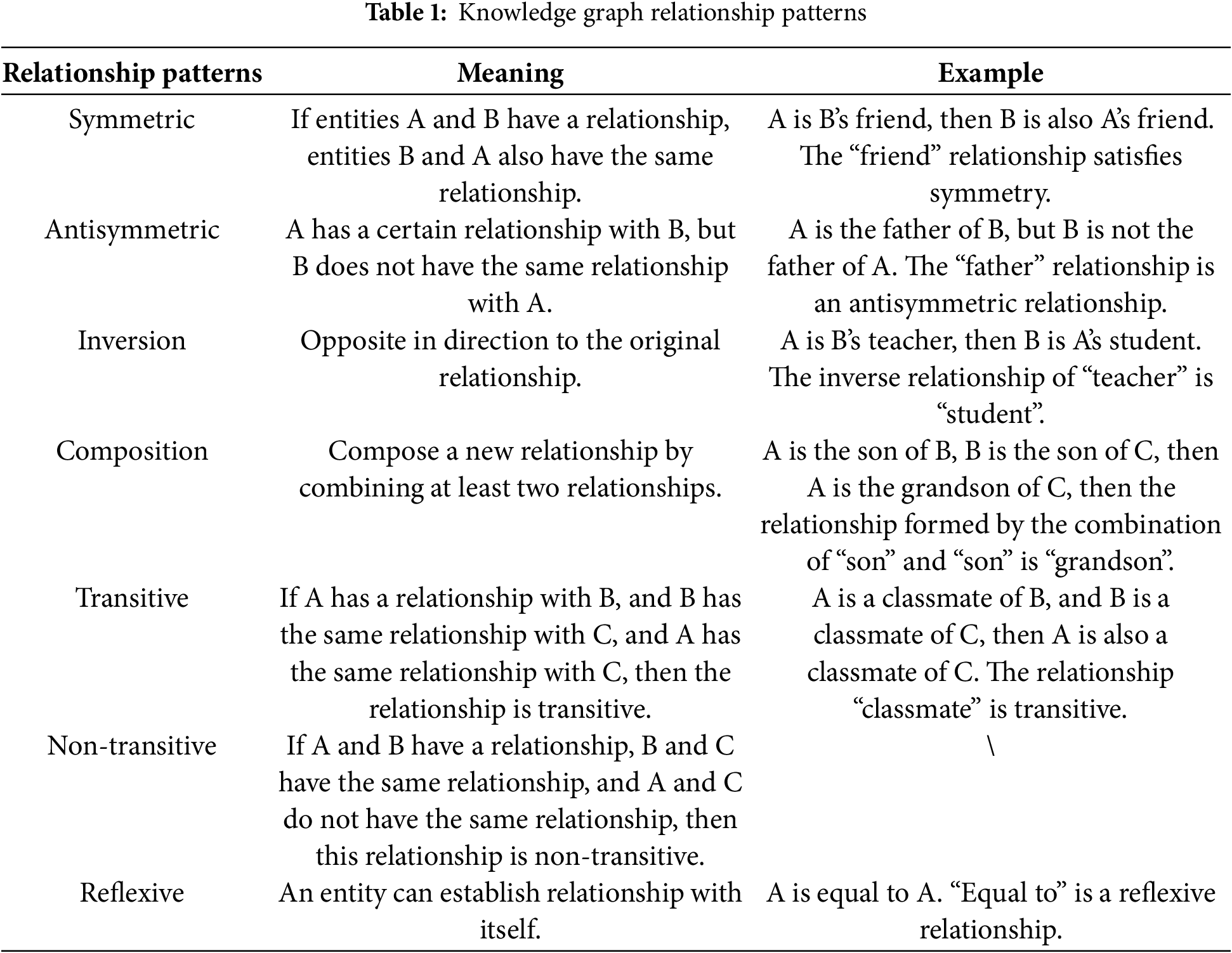
InteractE is a knowledge graph embedding model based on CNN, which consists of feature replacement, checkerboard reorganization and circular convolution. Feature replacement refers to randomly arranging entity and relationship features to enable the model to learn the interaction between entities and relationships. Checkerboard reorganization involves cross-arranging head entity embeddings and relationship embeddings in a checkerboard format. Circular convolution refers to enhancing the global interaction capability of features by connecting input boundaries. As a decoder, InteractE transforms the feature-permuted and grid-reorganized embedding matrix. The model diagram of InteractE is shown in Fig. 5, which includes the following parts:

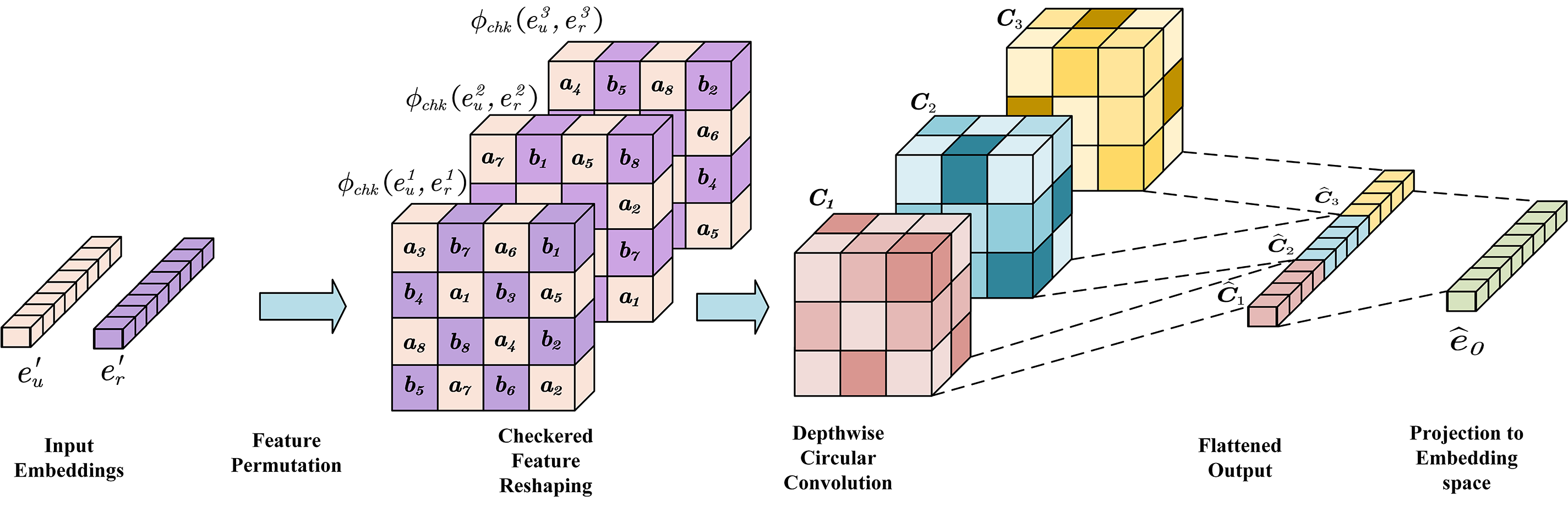
Figure 5: InteractE decoder

1.   Input Embeddings: Entity embedding eu′ and relationship embedding er′ are fully arranged t times to generate t channels. Let the result of random arrangement be Pt=[(eu1,er1);…;(eut,ert)], and t=3 in the Fig. 5.

2.   Feature Permutation: Use the grid reorganization method to cross-arrange head entity embeddings and relationship embeddings. Thus, the updated entity embeddings and relation embeddings from the encoder are input into the decoder and are represented as (eu,er).

3.   Checkered Feature Reshaping: Assume ϕ(eui,eri) represents the chessboard operation function. Then the reorganization result is:

ϕ(𝒫t)=[ϕ(eu1,er1);…;ϕ(eut,ert)](11)

4.   Depthwise Circular Convolution: This operation makes the content of the boundary interact during convolution. Let k be the convolution kernel size, put the left content of ⌊k2⌋ on the right side, and the right content of ⌊k2⌋ on the left side, similarly, put the lower side on the upper side, and put the upper side on the lower side.

5.   Fully Connected: The mapping dimension is eu. First, flatten the circular convolution tensor into a first-order tensor, and then project it into the embedding space Rd as e^o.

The scoring function of the InteractE decoder is:

ψ(u,r,v)=g(vec(f(ϕ(𝒫k)⊛ω))W)eo(12)

where f is the ReLU activation function, g is the sigmoid function, vec(⋅) represents the flattening operation, ϕ(Pk) is the result of the checkerboard entity-relationship embedding, ⊛ represents the convolution operation, ω is the learnable parameter, eo represents the output entity embedding, and W is the learned weight matrix. The loss function adopts the label-smoothed cross-entropy loss function.

4  Experiment

This section presents the experimental settings used in this study and the experiment results on the knowledge graph completion task.

4.1 Datasets

This study utilizes two of the most commonly used knowledge graph datasets: WN18RR and FB15K-237. Table 2 shows the sizes of these two datasets. FB15K-237 is a subset of the FB15K dataset, with all inverse relationships removed to address the issue of reversible relationships. WN18RR is a subset of the WN18 dataset, which contains structured data from English dictionaries and also removes inverse relationships.

4.2 Experimental Parameter Settings

The experimental parameters are as follows: this study adopts a two-step training method. First, the encoder is trained, and the graph attention network is used to calculate the importance of different edges to the central node. Then the InteractE decoder is trained to perform preliminary relationship decoding. This study uses two-hop relationship paths to aggregate more information from the sparse matrix. The Adam algorithm is employed for end-to-end training. In order to improve the model convergence speed and avoid overfitting, this study uses dropout and Batch Normalization while performing joint calculations of entity-relationship embeddings at each layer of the model. For the two datasets, we selected the optimal hyperparameters through extensive experiments. The hyperparameter settings are shown in Table 3. Due to the large amount of data in the two-hop dataset of FB15K-237, which was constrained by the available experimental resources, we selected the ten most frequent two-hop relationship pairs and conducted experiments on one percent of these pairs.

4.3 Evaluation Indicators

This study employs the relationship prediction task to assess the model’s performance. Specifically, it uses the known head entities and relationships to predict the missing tail entity (h,r,?), and uses the known tail entities and relationships to predict the missing head entity (?,r,t). After replacing the unknown entities with the predicted entities, we generate candidate triples that are not present in the original dataset. Then score these candidate triples and perform score ranking. It is necessary to filter out the triples that exist in the training set, validation set, and test set from the candidate triples. Finally, the ranking of the original triples is computed within the set of candidate triplets. Evaluation indicators include mean reciprocal rank (MRR), mean rank (MR), and the percentage of correct entities ranked in the top 1, top 3, and top 10 (Hit@1, Hit@3, Hit@10). The baseline models used for comparison have been introduced in a previous study, so they will not be repeated here.

4.4 Performance Comparison

To evaluate the effectiveness of the TRGAT model, we compared its performance with other existing knowledge graph models. On both datasets, TRGAT outperforms most models in terms of Hit@3 and MRR. The performance comparison of the TRGAT model is presented in Table 4, with the best results highlighted in bold.

The structure of TRGAT is an encoder-decoder structure, where the decoder is InteractE. Therefore, we compare the model with InteractE. As shown in Table 4, TRGAT consistently outperforms InteractE across MRR, Hit@1, Hit@3, and Hit@10. Notably on WN18RR, TRGAT achieved a 5% increase in Hit@1 and an improvement of 2510 in MR value, demonstrating that the GAT-based approach effectively captures the complex information inherent in the knowledge graph. Additionally, we design different weight matrices for various relationship types to capture the significance of information features of different relationships. By jointly representing entities and relationships, TRGAT leverages message passing functions to capture and propagate relevant information.

In addition, attention mechanisms are performed for edge types of varying lengths and directions in the multi-hop knowledge graph, to achieve the purpose of predicting link entities more accurately. In addition, CompGCN is a precursor to combining GCN with message functions. Comparing TRGAT with CompGCN, it is observed that TRGAT outperforms CompGCN in terms of Hit@1, Hit@3, Hit@10, and MRR on both datasets. Specifically, on WN18RR it achieved a 3% increase in Hit@3, a 4% increase in Hit@10, and a 2% increase in MRR value, which proves that the message function adopted in this study adds a joint representation of entity and relationship embeddings, and captures complex topological structures, calculates the importance of different relationship paths, leading to improved performance.

4.5 Ablation Experiment

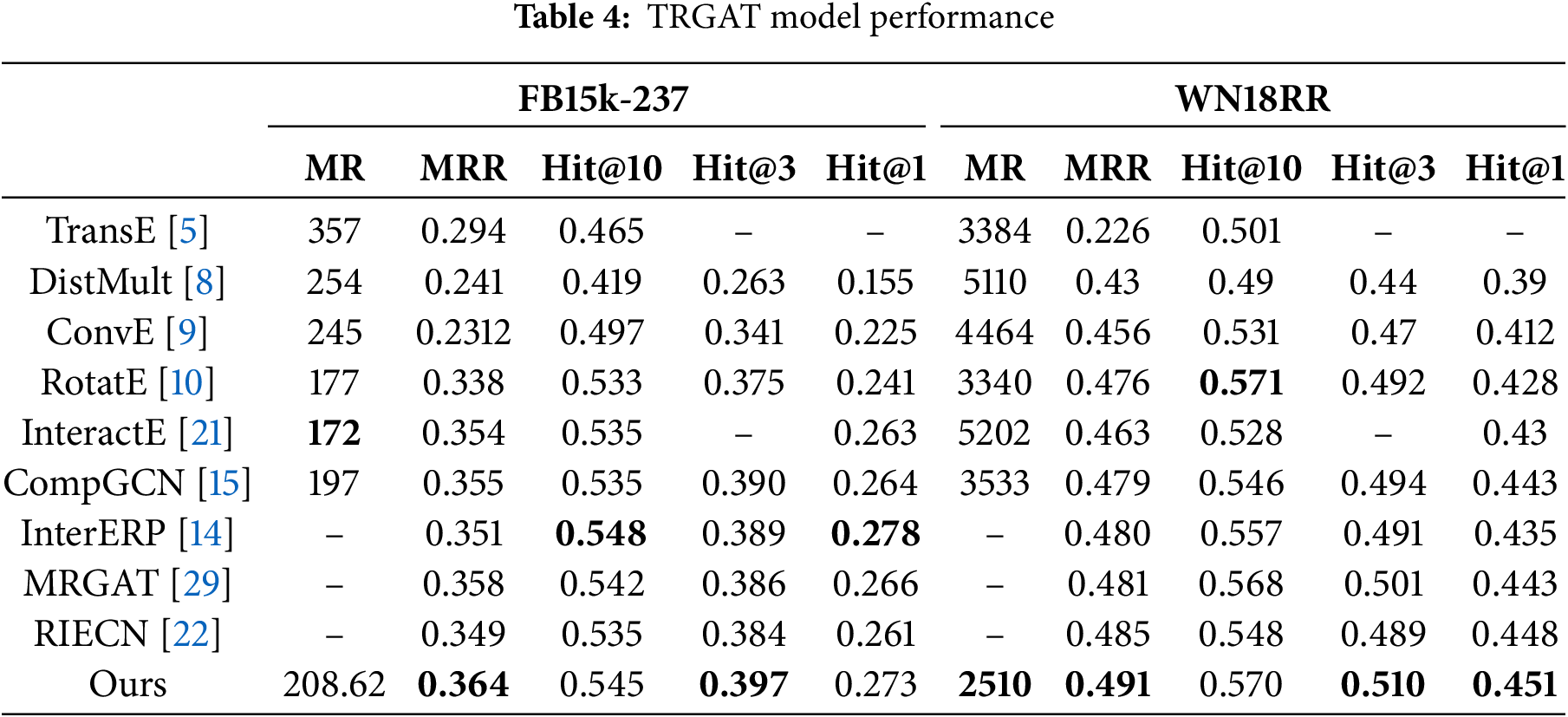
In order to clarify the impact of the two-hop path and message function on the performance of the TRGAT model, we conduct an ablation study. Specifically, we evaluate the model by removing the two-hop path (denoted as “w/o TR”), removing the message function (denoted as “w/o RO”), and simultaneously removing both two-hop paths and message functions (denoted as “w/o TR&RO”). The experiments were performed on the WN18RR dataset. Table 5 shows the results of the ablation experiment, demonstrating the effectiveness of the two methods adopted in this study.

4.6 Message Functions, Decoders, and Aggregation Methods

In order to study the effectiveness of the message function, decoder, and aggregation methods employed in this study. We selected multiple aggregation methods, message functions, and decoders for experiments, all used the WN18RR dataset.

There are three aggregation methods used in this study: ADD is a weighted average aggregation of nodes, MEAN is an average aggregation of nodes, and MAX is a maximum aggregation of nodes. These three aggregation methods are applied to process the edge indices. Comparative experiments were performed using the ADD, MEAN, and MAX aggregation methods. The iterative experiment results are shown in Fig. 6. As the number of iterations increases, the MRR values of the ADD and MEAN aggregation methods achieve better results faster than the MAX method, while the LOSS value increases with iteration. Although the LOSS decline rates for all three aggregation methods are similar, the ADD aggregation method demonstrates more stable LOSS reduction. The final test set results are shown in Fig. 7. The ADD aggregation method outperforms the other two aggregation methods in terms of MRR, Hit@1, and Hit@10. We infer that this may be due to the inclusion of a two-hop path in the relationship model. To calculate relational attention, the first-hop path and the second-hop path need to be ADD merged, and MEAN or MAX cannot reflect the relationship between paths of length 2. Therefore, the ADD aggregation method is chosen in this study.

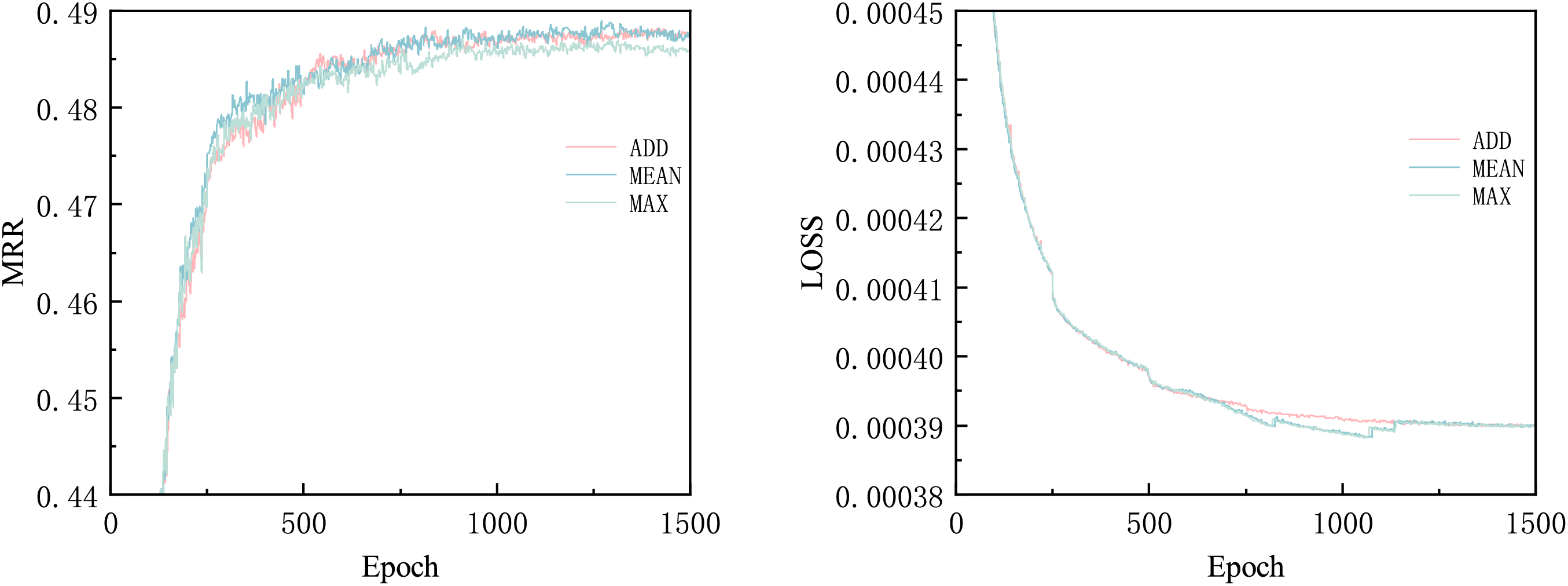
Figure 6: Aggregation methods iteration effects

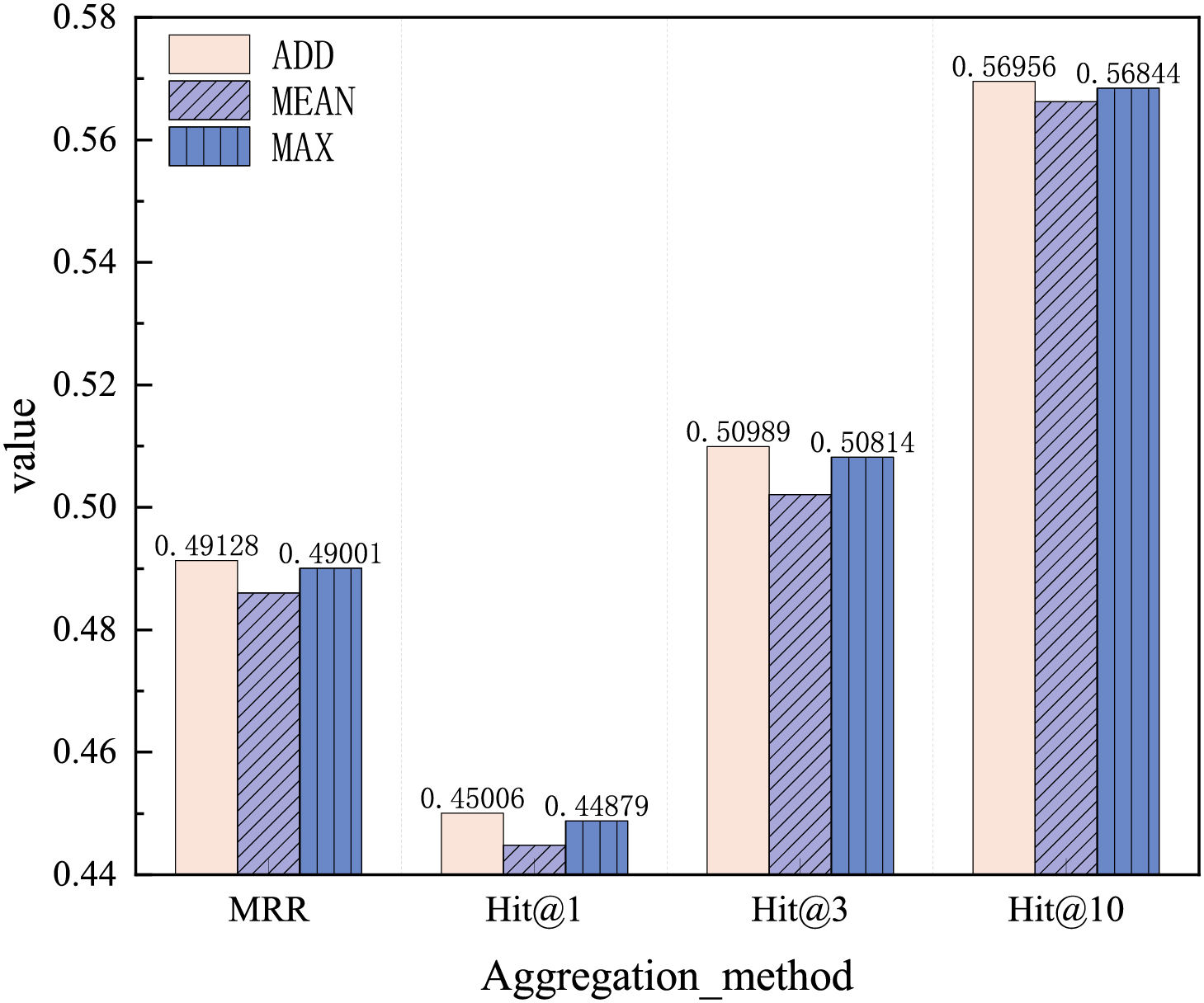
Figure 7: Aggregation methods test results

In addition to the message function STRotatE used in this study, we also refer to the three message functions proposed by CompGCN:

1.    Circular-correlation (Corr): ϕ(eu,er)=eu⋆er

2.    Subtraction (Sub): ϕ(eu,er)=eu−er

3.    Multiplication (Mult): ϕ(eu,er)=eu∗er

Among them, eu is the head entity embedding, er is the relationship embedding, the ϕ function is the synthesis operator without parameters, and ⋆ is the loop operation. The iterative experimental results are shown in Fig. 8. As the number of iterations increases, the MRR value of STRotatE increases more slowly than that of Corr, but the LOSS value decreases more rapidly. Based on the final test set results (shown in Fig. 9), STRotatE outperforms the other three message functions in MRR, Hit@1, and Hit@10. Overall, STRotatE performs better than other message functions. The possible reason is that it integrates the mapping information of entities and relationships for attention training, which better aligns with the relationship model of multi-relationship, complex-path knowledge graphs, allowing for more appropriate model training in symmetry, inversion, and spin modes.

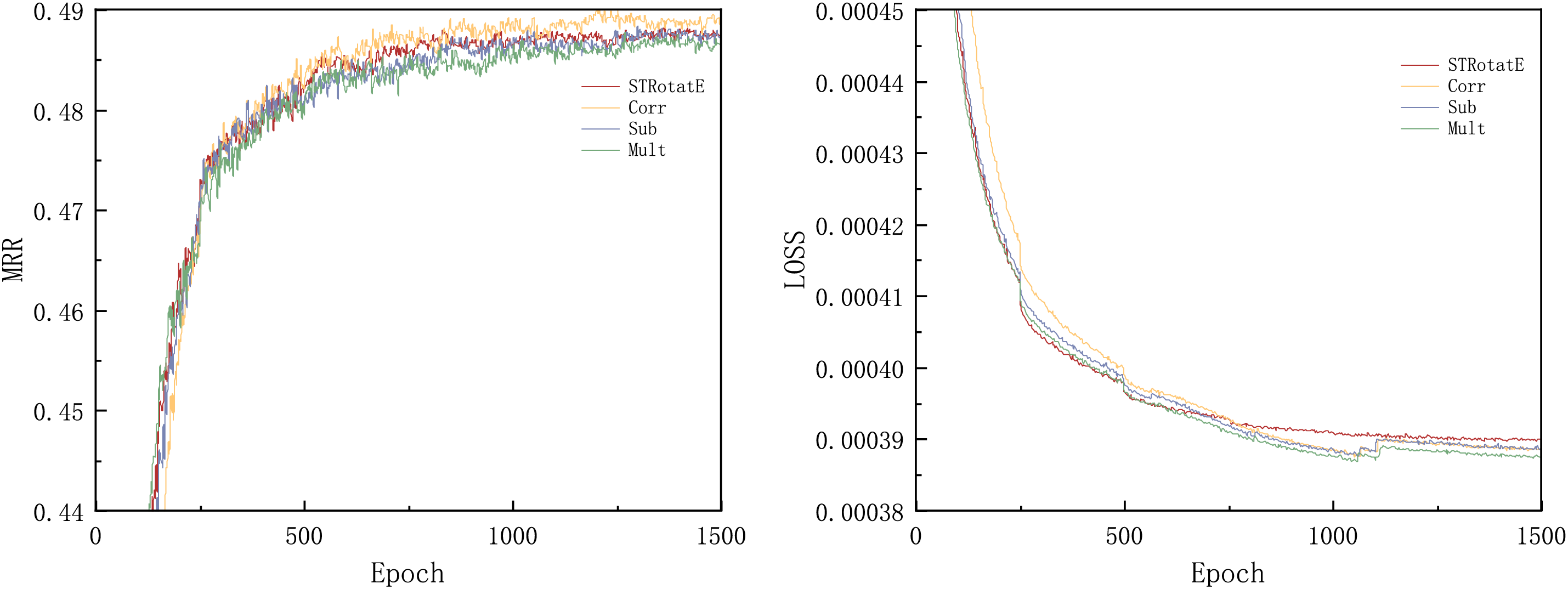
Figure 8: Message function iteration effects

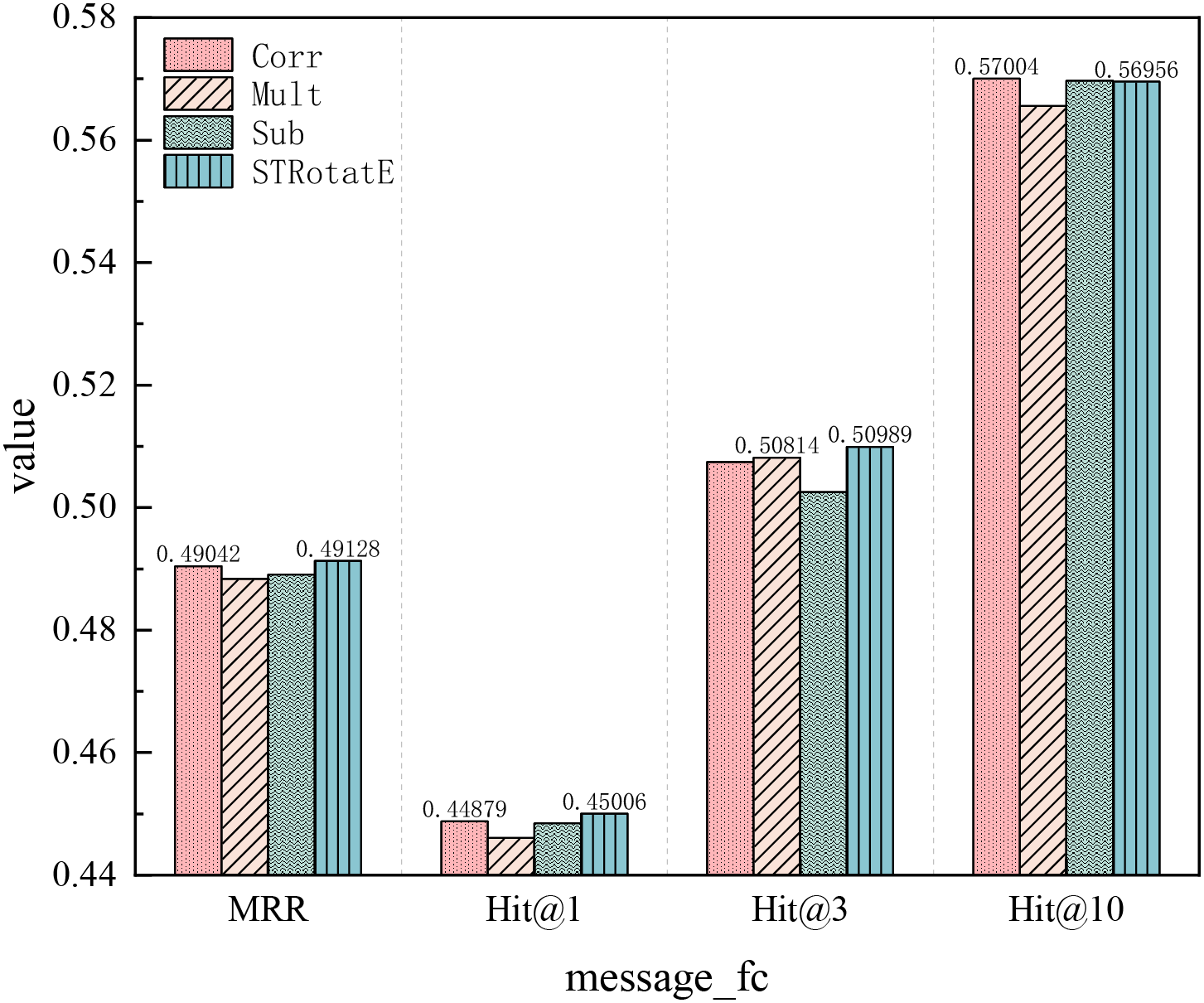
Figure 9: Message function test results

Regarding the decoder, this study uses three decoders to conduct comparative experiments, namely ConvE, DistMult and InteractE. The results of the iterative experiments are shown in Fig. 10. InteractE achieved a significant improvement in the MRR, while the LOSS value decreased to the minimum at the fastest speed. The test set results are presented in Fig. 11. As a decoder, InteractE demonstrates a considerable advantage over the other two decoders in terms of MRR, Hit@1, Hit@3, and Hit@10. Compared to ConvE, the MRR value increased by 3%, and Hit@10 improved by 2.55%. Therefore, using InteractE as the decoder yields superior results. We attribute this improvement to the unique characteristics of InteractE: which include feature replacement, random arrangement of entities and relationships, chessboard cross reorganization, and the interaction of entities and relationships can be learned, which collectively contribute to better decoding performance.

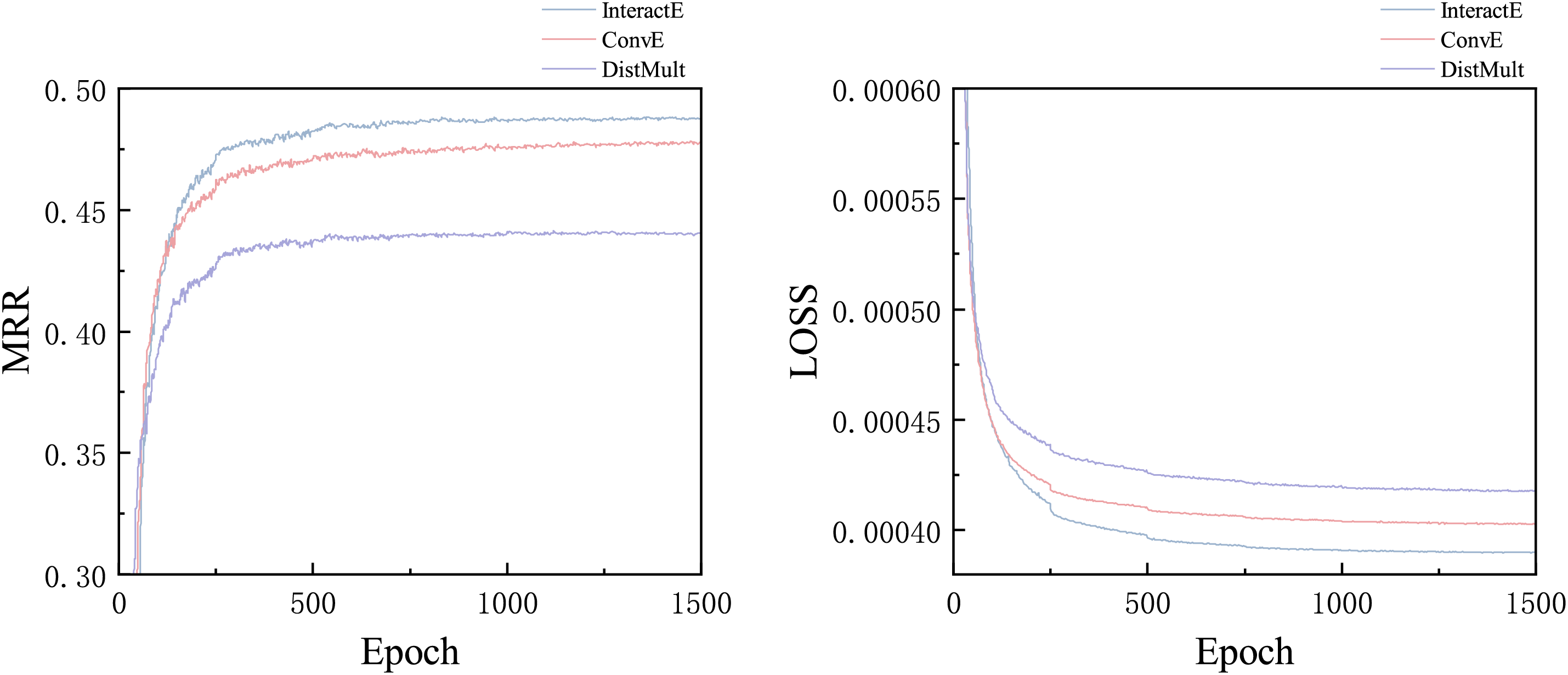
Figure 10: Decoder iteration effects

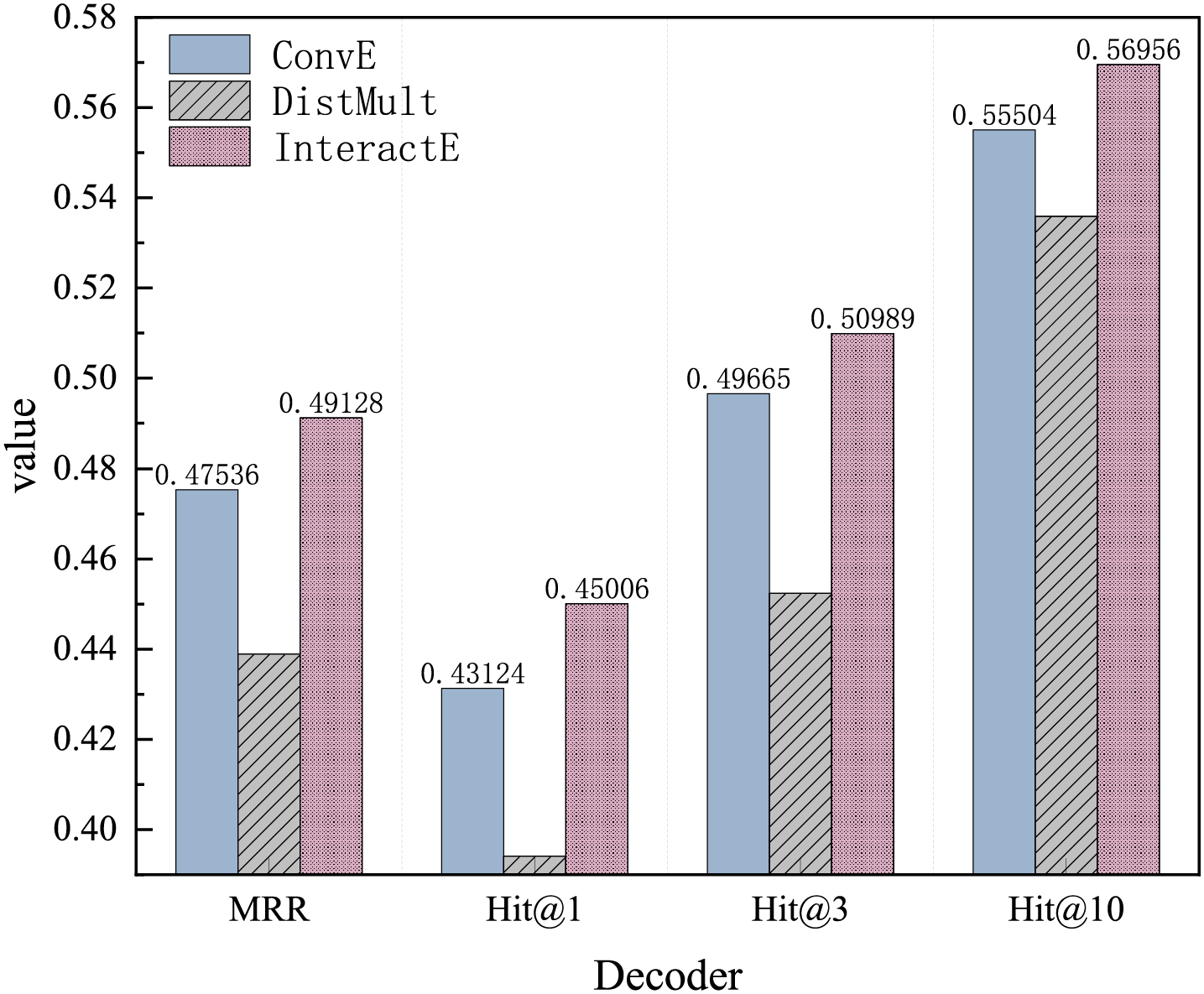
Figure 11: Decoder test results

4.7 Hyperparameter Analysis

This section analyzes the impact of TRGAT’s hyperparameters on the results, including learning rate and embedding dimension. The experiments were conducted using the WN18RR dataset.

For the learning rate, we used four values for comparative experiments, namely: 0.0001, 0.0005, 0.001, and 0.002. The iteration results are shown in Fig. 12. The performance effect of the learning rate of 0.0001 was the worst. The iterations of MRR values and LOSS values with learning rates of 0.0005, 0.001, and 0.002 were nearly identical. The test results, shown in Fig. 13, indicate that the learning rate of 0.0005 yields the best performance.

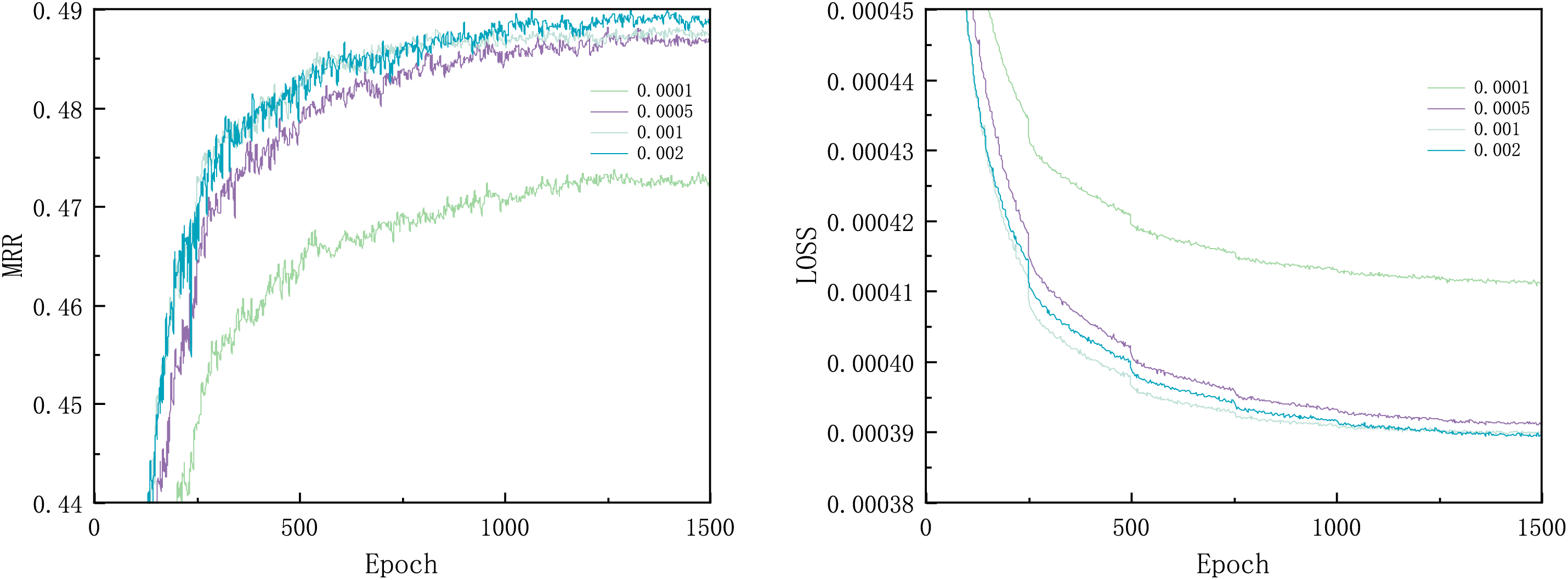
Figure 12: Learning rate iteration effects

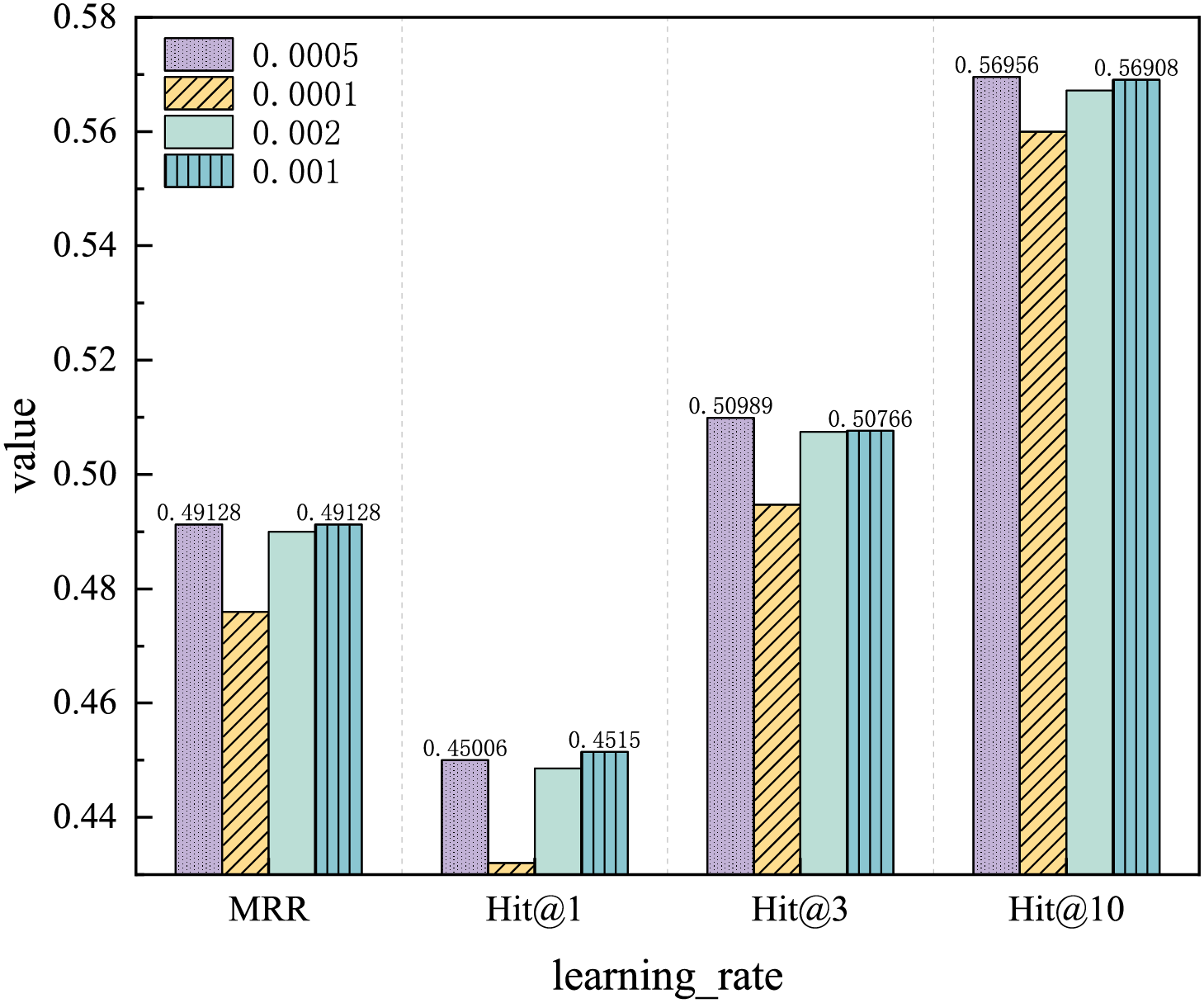
Figure 13: Learning rate test results

This study tests five values for the embedding dimension: 150, 200, 250, 300, and 350. As shown in the iteration results (Fig. 14), an embedding dimension of 350 produces the best performance. However, the test set results (Fig. 15) indicate that an embedding dimension of 200 yields the best performance. Therefore, considering the calculation cost and time, an embedding dimension of 200 is preferred, as the cost of using an embedding dimension of 350 is too high. The likely reason for this is that as the embedding dimension increases, the model may become over-parameterized, leading to overfitting on the training data and reducing the generalization ability of the model.

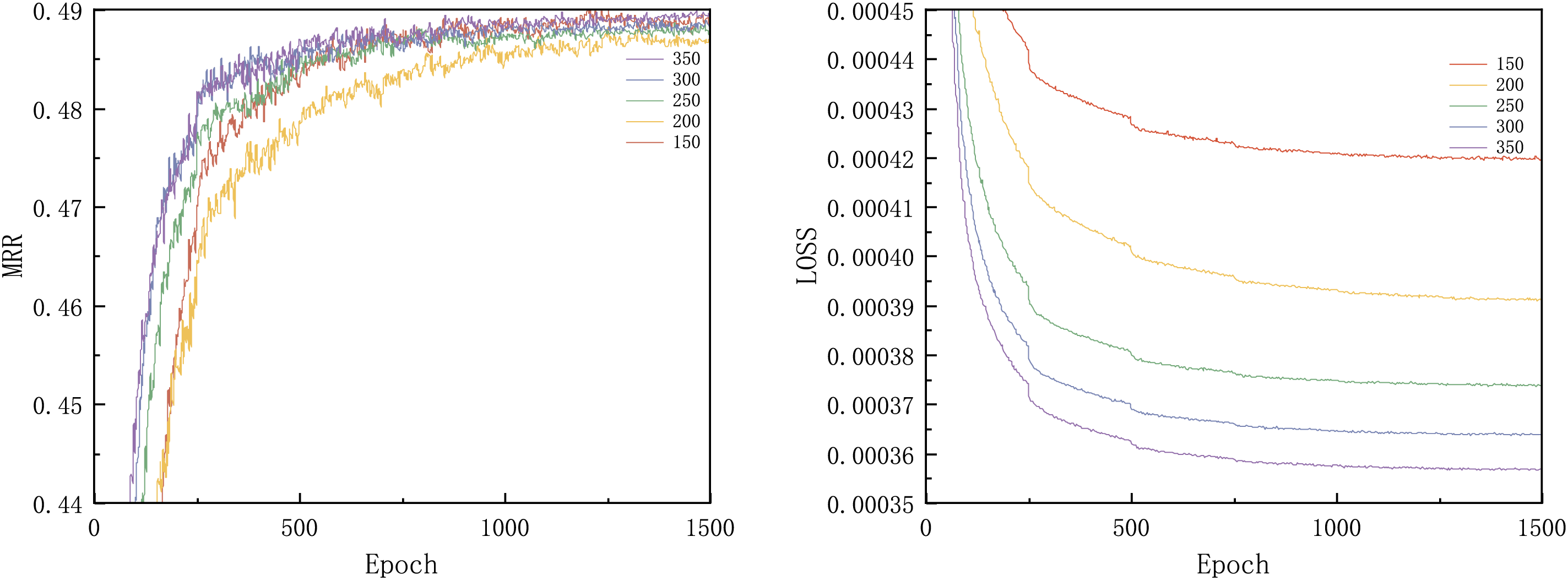
Figure 14: Embedded dimension iteration effects

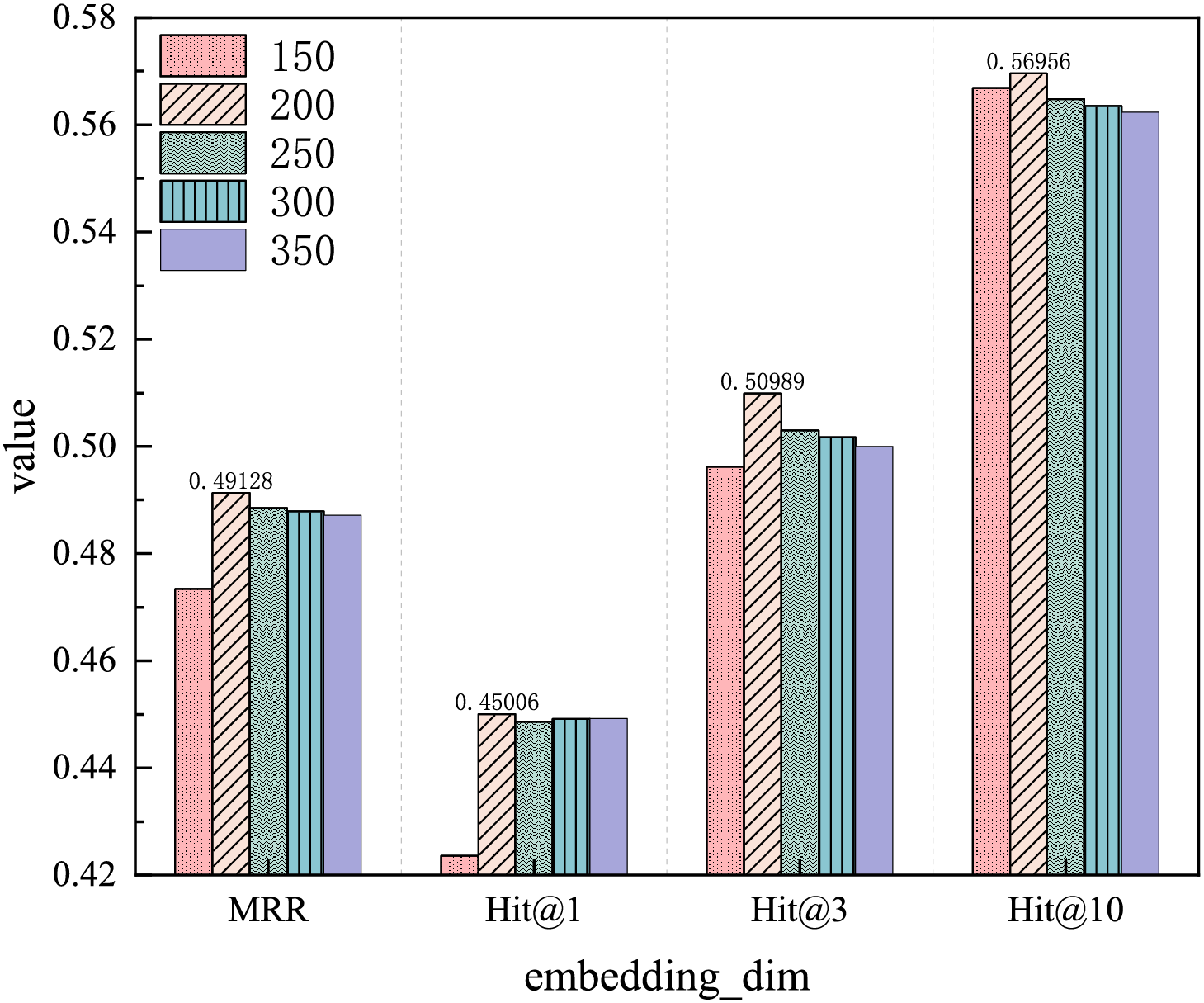
Figure 15: Embedding dimension test results

5  Conclusion

This study introduces a new method that uses graph neural networks to improve the accuracy of KGC in knowledge graphs. The method draws on the principles of the RotatE model and constructs a new message function, which performs entity-relationship mapping by representing relationships as rotations in a complex vector space. It also performs relationship attention calculations, thus capturing the importance of different relationship paths. In addition, this method uses two-hop neighbor entity pairs and their relationships to capture richer structural information, and divides the relationships between entities into five categories: forward, reverse, spin, two-hop forward, and two-hop reverse. This results in the creation of a new relationship model that enriches the diversity of relationships and aggregates more neighborhood information. Experimental results on the WN18RR and FB15k-237 datasets demonstrate that our approach outperforms existing link prediction techniques. This research enhances the ability of graph neural networks to capture complex relationship information in knowledge graphs and distinguish the importance of different relationships, thereby achieving the goal of improving the accuracy of KGC tasks.

However, there are some limitations to this work. Due to computational constraints, this study focuses on the one-hop and two-hop cases of multi-hop relationship information transmission. Future work could explore the influence of longer-distance neighbor paths on the central entity. Additionally, this study is based on publicly available knowledge graph datasets and does not address domain-specific knowledge graph datasets. It could be applied to knowledge graphs in a broader range of fields (e.g., medical, financial or social network fields), which would help validate the generalization ability of TRGAT and optimize its adaptability. Finally, the attention model used in this study is relatively conventional. Future research could explore combining it with pre-trained models to achieve better performance. The approach described in this study could also be applied to downstream tasks of knowledge graphs, such as recommendation systems, to further enhance the practical application ability of TRGAT.

Acknowledgement: This research would not have been possible without the unwavering support and guidance from my academic advisor, whose expertise and patience have been invaluable throughout the course of this project. I am deeply grateful for his insightful comments and constructive criticism, which have significantly contributed to the quality of this work. I would also like to express my gratitude to my fellow students for providing a stimulating and collaborative research environment. Special thanks go to my lab mates, who have been a source of inspiration and camaraderie, especially during the challenging times.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shaoming Qiu, Xinchen Huang; data collection: Xinchen Huang; Software: Xinchen Huang, Liangyu Liu; analysis and interpretation of results: Xinchen Huang, Jingfeng Ye, Bicong E; draft manuscript preparation: Xinchen Huang, Bicong E. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: This study uses public datasets (WN18RR, FB15k-237), which can be downloaded and used on the Internet.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zamanzadeh Darban Z, Valipour MH. GHRS: graph-based hybrid recommendation system with application to movie recommendation. Expert Syst Appl. 2022;200(6):116850. doi:10.1016/j.eswa.2022.116850. [Google Scholar] [CrossRef]

2. Do P, Phan THV. Developing a BERT based triple classification model using knowledge graph embedding for question answering system. Appl Intell. 2022;52(1):636–51. doi:10.1007/s10489-021-02460-w. [Google Scholar] [CrossRef]

3. Zheng W, Zou L, Peng W, Yan X, Song S, Zhao D. Semantic SPARQL similarity search over RDF knowledge graphs. Proc VLDB Endow. 2016;9(11):840–51. doi:10.14778/2983200.2983201. [Google Scholar] [CrossRef]

4. Shen T, Zhang F, Cheng J. A comprehensive overview of knowledge graph completion. Knowl Based Syst. 2022;255(2):109597. doi:10.1016/j.knosys.2022.109597. [Google Scholar] [CrossRef]

5. Bordes A, Usunier N, Garcia-Duran A, Weston J, Yakhnenko O. Translating embeddings for modeling multi-relational data. In: Burges C, editor. Advances in neural information processing systems. Neural Information Processing Systems Foundation, Inc. (NeurIPS); 2013. Vol. 26. [Google Scholar]

6. Lin Y, Liu Z, Sun M, Liu Y, Zhu X. Learning entity and relation embeddings for knowledge graph completion. Proc AAAI Conf Artif Intell. 2015;29(1):2181–7. doi:10.1609/aaai.v29i1.9491. [Google Scholar] [CrossRef]

7. Wang Z, Zhang J, Feng J, Chen Z. Knowledge graph embedding by translating on hyperplanes. Proc AAAI Conf Artif Intell. 2014;28(1):1112–9. doi:10.1609/aaai.v28i1.8870. [Google Scholar] [CrossRef]

8. Yang B, Yih WT, He X, Gao J, Deng L. Embedding entities and relations for learning and inference in knowledge bases. arXiv:1412.6575. 2014. [Google Scholar]

9. Dettmers T, Minervini P, Stenetorp P, Riedel S. Convolutional 2D knowledge graph embeddings. Proc AAAI Conf Artif Intell. 2018;32(1):1811–8. doi:10.1609/aaai.v32i1.11573. [Google Scholar] [CrossRef]

10. Sun Z, Deng ZH, Nie JY, Tang J. RotatE: knowledge graph embedding by relational rotation in complex space. arXiv:1902.10197. 2019. [Google Scholar]

11. Chen X, Jia S, Xiang Y. A review: knowledge reasoning over knowledge graph. Expert Syst Appl. 2020;141:112948. doi:10.1016/j.eswa.2019.112948. [Google Scholar] [CrossRef]

12. Xie Z, Zhou G, Liu J, Huang JX. ReInceptionE: relation-aware inception network with joint local-global structural information for knowledge graph embedding. In: Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. Online; 2020; Stroudsburg, PA, USA: ACL. p. 5929–39. doi:10.18653/v1/2020.acl-main.526. [Google Scholar] [PubMed] [CrossRef]

13. Li W, Peng R, Li Z. Improving knowledge graph completion via increasing embedding interactions. Appl Intell. 2022;52(8):9289–307. doi:10.1007/s10489-021-02947-6. [Google Scholar] [CrossRef]

14. Sun Z, Vashishth S, Sanyal S, Talukdar P, Yang Y. A re-evaluation of knowledge graph completion methods. arXiv:1911.03903. 2019. [Google Scholar]

15. Vashishth S, Sanyal S, Nitin V, Talukdar P. Composition-based multi-relational graph convolutional networks. arXiv:1911.03082. 2019. [Google Scholar]

16. Li C, Peng X, Niu Y, Zhang S, Peng H, Zhou C, et al. Learning graph attention-aware knowledge graph embedding. Neurocomputing. 2021;461(5):516–29. doi:10.1016/j.neucom.2021.01.139. [Google Scholar] [CrossRef]

17. Borrego A, Ayala D, Hernández I, Rivero CR, Ruiz D. CAFE: knowledge graph completion using neighborhood-aware features. Eng Appl Artif Intell. 2021;103(2):104302. doi:10.1016/j.engappai.2021.104302. [Google Scholar] [CrossRef]

18. Xiong W, Hoang T, Wang WY. DeepPath: a reinforcement learning method for knowledge graph reasoning. arXiv:1707.06690. 2017. [Google Scholar]

19. Lao N, Cohen WW. Relational retrieval using a combination of path-constrained random walks. Mach Learn. 2010;81(1):53–67. doi:10.1007/s10994-010-5205-8. [Google Scholar] [CrossRef]

20. Das R, Dhuliawala S, Zaheer M, Vilnis L, Durugkar I, Krishnamurthy A, et al. Go for a walk and arrive at the answer: reasoning over paths in knowledge bases using reinforcement learning. arXiv:1711.05851. 2017. [Google Scholar]

21. Vashishth S, Sanyal S, Nitin V, Agrawal N, Talukdar P. InteractE: improving convolution-based knowledge graph embeddings by increasing feature interactions. Proc AAAI Conf Artif Intell. 2020;34(3):3009–16. doi:10.1609/aaai.v34i03.5694. [Google Scholar] [CrossRef]

22. Wang W, Shen X, Zhang H, Li Z, Yi B. RIECN: learning relation-based interactive embedding convolutional network for knowledge graph. Neural Comput Appl. 2023;35(11):8343–56. doi:10.1007/s00521-022-08109-0. [Google Scholar] [CrossRef]

23. Schlichtkrull M, Kipf TN, Bloem P, van den Berg R, Titov I, Welling M. Modeling relational data with graph convolutional networks. In: The Semantic Web: 15th International Conference, ESWC 2018; 2018 Jun 3–7; Heraklion, Greece. p. 593–607. [Google Scholar]

24. Zhang Z, Zhuang F, Zhu H, Shi Z, Xiong H, He Q. Relational graph neural network with hierarchical attention for knowledge graph completion. Proc AAAI Conf Artif Intell. 2020;34(5):9612–9. doi:10.1609/aaai.v34i05.6508. [Google Scholar] [CrossRef]

25. Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. arXiv:1609.02907. 2016. [Google Scholar]

26. Veličković P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y. Graph attention networks. arXiv: 1710.10903. 2017. [Google Scholar]

27. Wu J, Shi W, Cao X, Chen J, Lei W, Zhang F, et al. DisenKGAT: knowledge graph embedding with disentangled graph attention network. In: Proceedings of the 30th ACM International Conference on Information & Knowledge Management; 2021; Virtual Event, Queensland, Australia: ACM; 2021. p. 2140–9. doi:10.1145/3459637.3482424. [Google Scholar] [CrossRef]

28. Zhang X, Zhang C, Guo J, Peng C, Niu Z, Wu X. Graph attention network with dynamic representation of relations for knowledge graph completion. Expert Syst Appl. 2023;219(2):119616. doi:10.1016/j.eswa.2023.119616. [Google Scholar] [CrossRef]

29. Dai G, Wang X, Zou X, Liu C, Cen S. MRGAT: multi-relational graph attention network for knowledge graph completion. Neural Netw. 2022;154(9):234–45. doi:10.1016/j.neunet.2022.07.014. [Google Scholar] [PubMed] [CrossRef]